DOI:
10.1039/D3LC00413A
(Paper)
Lab Chip, 2024,
24, 20-33
Measuring the electrophoretic mobility and size of single particles using microfluidic transverse AC electrophoresis (TrACE)†
Received
11th May 2023
, Accepted 23rd October 2023
First published on 8th November 2023
Abstract
The ability to measure the charge and size of single particles is essential to understanding particle adhesion and interaction with their environment. Characterizing the physical properties of biological particles, like cells, can be a powerful tool in studying the association between the changes in physical properties and disease development. Currently, measuring charge via the electrophoretic mobility (μep) of individual particles remains challenging, and there is only one prior report of simultaneously measuring μep and size. We introduce microfluidic transverse AC electrophoresis (TrACE), a novel technique that combines particle tracking velocimetry (PTV) and AC electrophoresis. In TrACE, electric waves with 0.75 to 1.5 V amplitude are applied transversely to the bulk flow and cause the particles to oscillate. PTV records the particles' oscillating trajectories as pressure drives bulk flow through the microchannel. A simple quasi-equilibrium model agrees well with experimental measurements of frequency, amplitude, and phase, indicating that particle motion is largely described by DC electrophoresis. The measured μep of polystyrene particles (0.53, 0.84, 1, and 2 μm diameter) are consistent with ELS measurements, and precision is enhanced by averaging ∼100 measurements per particle. Particle size is simultaneously measured from Brownian motion quantified from the trajectory for particles <2 μm or image analysis for particles ≥2 μm. Lastly, the ability to analyze intact mammalian cells is demonstrated with B cells. TrACE systems are expected to be highly suitable as fieldable tools to measure the μep and size of a broad range of individual particles.
1. Introduction
Particle characterization based on physical properties, whether biological, organic, or inorganic particles, has become essential in many fields, from clinical to environmental analyses.1 For example, the unique physical properties of cells play important roles in regulating essential biological processes, including differentiation, migration, and metabolic activities.2,3 Additionally, the physical properties of cells are considered a potential biomarker for identifying cell types and diseases.3 Thus, measuring the physical properties of cells can serve as a powerful tool in understanding the association between the changes in cells' physical properties and the development of diseases. In fields involving water quality and environmental analysis, detecting and characterizing contaminants, such as microplastics, is a critical step in developing a reliable purification method.4
Particle characterization techniques can be classified as ensemble or single-particle methods. The most appropriate method for a particular application depends on the analytical needs. For example, ensemble measurement techniques such as laser diffraction and dynamic light scattering (DLS) determine an average size over a distribution of the members of the sample population.5–10 Ensemble methods can sample much greater numbers of particles than single-particle measurement techniques as they measure numerous particles simultaneously. However, detailed information on individual particles is lost in averaging.8 On the other hand, single particle techniques, such as various types of microscopy and the Coulter counter, detect and characterize individual particles.11–13 Although single-particle techniques usually analyze a reduced number of particles compared to ensemble techniques, they record specific characteristics of each particle. Thus, single-particle techniques provide significantly more information than ensemble measurements. Nonetheless, the characterization of individual particles remains challenging as these methods typically yield a low signal-to-noise ratio, require longer processing time, and have lower sample throughput.8
Several techniques have been developed to measure particle size, although each method has a size range over which it works best. Optical microscopy best measures the sizes of single particles larger than 0.5 μm, but the measurements depend heavily on the instrument and experimental settings, such as the light source's wavelength and the refractive index of the buffer medium.8 Another commonly used ensemble measurement method for particle sizing is dynamic light scattering (DLS). DLS uses light scattering to quantify a particle's Brownian motion and determine the hydrodynamic diameter distribution of particles smaller than 10 μm. Although DLS is fast and non-invasive, the method is primarily suitable for spherical particles and struggles with aggregates and polydisperse samples.8 A more recent technique called nanoparticle tracking analysis (NTA) couples light scattering and imaging to measure the size of single particles in suspension. However, NTA is appropriate only for nanometer-sized particles with a low seeding density, and high user variability has been reported.8,11
Electrophoretic techniques, such as capillary electrophoresis and electrophoretic light scattering, enable measurements of the particle's surface charge or zeta potential. The surface charge of particles not only plays a critical role in their interactions with the surrounding environment, but it is also a measurable property that can be used for particle characterization and classification. A particle's surface charge is most frequently measured through electrophoretic mobility (μep).14–16 Electrophoretic mobility is the ratio of the electrophoretic velocity (v) to the applied electric field (E), μep = v/E, which is dependent on the particle's size, shape, and charge.9,17 Capillary electrophoresis (CE) is a widely used bulk separation method in which analyte elution order depends on their electrophoretic mobilities. CE has been used to separate and characterize molecular species and can also be used for inorganic particles, cells, and microorganisms.18,19 However, when CE is used for particle analysis or separation, especially with biological particles like bacteria, particle aggregation is often problematic as aggregates can preclude the observation of resolved peaks.18,20 While CE can provide unparalleled separation efficiencies for molecules, one critical challenge with CE is surface adsorption in the capillary, which alters the electroosmotic flow (EOF). The observed or total mobility is the sum of the electrophoretic mobility and the electroosmotic mobility, μobs = μep + μEOF. Thus, variability in EOF reduces the accuracy of the μep measurements.17 Neutral markers or current monitoring are commonly used to measure the EOF in CE.21,22 If adequately measured, the contribution of the EOF to the observed mobility can be subtracted to yield the μep. Electrophoretic light scattering (ELS) is an ensemble measurement method based on electrophoresis and DLS that measures the mean μep for a population of particles.23 The main challenge with ELS is the bubble formation that distorts the electric field in the measurement zone, decreasing the reproducibility of the μep values.24 EOF can be present in AC systems and decreases with increasing frequency.25,26 Consequently, a higher frequency is often used in ELS to decrease EOF to a negligible level.
There have been previous reports of measuring particle electrophoretic mobility in microfluidic devices. One important challenge has been applying a high electric field. A strong electric field is desirable to increase the particle's electrophoretic velocity when measuring a particle's μep. Although both Miller and Strubbe's groups applied high voltages to their systems (35 and 80 V, respectively), a long distance between electrodes limited the strength of the electric field within the microchannel (7 and 51 V cm−1). Strubbe's group measured μep by applying an AC wave with a frequency >300 Hz along the length of a microchannel.15 While this method determined the μep of particles with different charges by tracking the particle centroid, the standard deviation varied from 4 to 22%, and a low sample throughput (n < 12) was reported. On the other hand, Miller's group used an innovative approach to combine DC electrophoresis and particle tracking velocimetry (PTV) to measure the particles' size and μep simultaneously.14 In PTV, particle displacements are tracked over time in a moving or suspended fluid to calculate the particle velocities.27 In this method, Brownian motion, measured by the random fluctuations in the particle velocity, determined the sizes of particles ranging from 456 nm to 1.05 μm. The bead diameter was measured to ∼12%, while the particle's μep measurements had a relative standard deviation (RSD) from ∼4 to 7% among different particles. Trajectory fluctuations beyond the level predicted by Brownian motion were observed, indicating that experimental noise was significant. However, the measurement accuracy could be improved by calibrating with standards. Miller's DC electrophoresis system is the only previously published method that simultaneously measures a single particle's μep and size, and it demonstrates the challenges of precisely measuring the individual particle's size and μep.
This paper introduces a novel technique called microfluidic transverse AC electrophoresis (TrACE) that simultaneously measures the μep and size of single particles from oscillating particle trajectories. The transverse AC electric field drives the particle oscillations that are recorded using PTV. TrACE utilizes a low-frequency AC electrophoresis, in the low Hz range, unlike most AC electrophoresis methods that use frequencies ≥ kHz wave. A simple TrACE device requires only a single microchannel, a pair of electrodes, and a small transverse electric potential to create a high electric field (Fig. 1). The voltages applied in TrACE fall below the threshold for electrolysis and avoid bubble formation within the detection window, which would otherwise distort the electric field and stop the analysis. In addition, the low potential and low current in TrACE results in low power dissipation and negligible Joule heating, which is beneficial for analyzing thermally sensitive biological particles, such as extracellular vesicles (EVs).28 The low-frequency, low-voltage, and low-power waveforms needed to operate the system can be easily generated with a smartphone, simplifying the potential integration of TrACE into fieldable diagnostic tools. A set of unique characteristics describes the capability of the TrACE system. The configuration allows the bulk flow rate to be controlled independently from the electrophoretic motion of the particles. The bulk flow controls the residence time of the particles in the detection window, which can be varied from short to very long observation time. Additionally, multiplexing is possible in TrACE, as any number of particle trajectories can be recorded in parallel by controlling the sample's seeding density and the number of crossovers in the trajectories. The TrACE device can be used with any particle suspension that does not clog the microchannel and for which a trajectory can be recorded. Optical microscopy is not inherently required for particle detection, although it is beneficial for recording precise trajectories when high spatial resolution is required. We present a simple time-dependent model that largely describes the particle oscillations in the microchannel. We experimentally characterize the system's operation and measure the electrophoretic mobility and size while imaging single particles.
 |
| | Fig. 1 Schematic representation of the device. (A) Top view and (B) cross-sectional view show the microchannel, electrodes, and reservoirs. The important dimensions include: channel width (Cw) = 300 μm, channel height (CH) = 50 μm, channel length (CL) = 11 mm, electrode length (eL) = 1 mm, and electrode spacing (es) = 100 μm. In (B), the parabolic profile of a hydrodynamic flow is illustrated to represent the variability in flow velocity as a function of microchannel height (z-dimension). (C) Image of a completed TrACE device. (D) A microscopic image of a pair of electrodes (black rectangles) shows parallel and straight edges of the electrodes. The white circles represent a particle's oscillating positions in response to a sine wave. | |
2. Experimental setup
2.1 Materials
All reagents are used without purification. Sodium phosphate dibasic anhydrous is obtained from VWR, whereas sodium phosphate monobasic and Tergitol (NP40) are from Sigma Aldrich. 1 and 2 μm FluoSpheres carboxylate-modified microspheres are from Invitrogen Thermo Fisher Scientific, and 0.84 and 0.53 μm Sphero carboxyl fluorescent microspheres are from Spherotech, Inc. SYLGARD 184 silicone elastomer kit is purchased from Dow company. The silicon wafers are from University Wafer, Inc. Cr/Au coated borate glass slide is from Telic Company.
2.2 TrACE device fabrication
The TrACE devices were fabricated from two main components: a polydimethylsiloxane (PDMS) layer with the microchannel and the glass slide with the electrodes. First, a silicon wafer mold was patterned with SU-8 using a photolithography method. The SU-8 layer had a height of 50 μm and included a single microchannel (300 μm (W) × 11 mm (L)) and reservoirs (3 mm in diameter) at each end of the microchannel. A PDMS solution, prepared by mixing a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of PDMS to curing agent, was poured over the mold and cured overnight at 65 °C to make a PDMS microchannel. Next, electrodes are patterned, as shown in Fig. 1via a standard wet etching process on a Cr/Au coated glass slide (Telic Company). A total of 9 devices were patterned onto each glass slide, and a glass cutter was used to cut out individual devices. Then, a PDMS microchannel and patterned electrodes slide was placed in a plasma cleaner using atmospheric gas (Harrick Plasma model PDC-32G) to clean the surfaces and produce reacting groups for one minute. Immediately after the plasma treatment, a PDMS microchannel was aligned to the patterned electrode slide using an in-house constructed x–y–z stage and pressed firmly for attachment. After the assembly, a weight was placed on top of the device and heated at 65 °C overnight to ensure complete attachment. Finally, an electrical wire was soldered onto an electrode to supply electric potentials to the device.
1 ratio of PDMS to curing agent, was poured over the mold and cured overnight at 65 °C to make a PDMS microchannel. Next, electrodes are patterned, as shown in Fig. 1via a standard wet etching process on a Cr/Au coated glass slide (Telic Company). A total of 9 devices were patterned onto each glass slide, and a glass cutter was used to cut out individual devices. Then, a PDMS microchannel and patterned electrodes slide was placed in a plasma cleaner using atmospheric gas (Harrick Plasma model PDC-32G) to clean the surfaces and produce reacting groups for one minute. Immediately after the plasma treatment, a PDMS microchannel was aligned to the patterned electrode slide using an in-house constructed x–y–z stage and pressed firmly for attachment. After the assembly, a weight was placed on top of the device and heated at 65 °C overnight to ensure complete attachment. Finally, an electrical wire was soldered onto an electrode to supply electric potentials to the device.
2.3 TrACE experimental procedure
First, the PDMS microchannel and reservoirs were cleaned by injecting isopropyl alcohol (IPA) solution and flushing the solution out with a vacuum. DI water was used immediately after to wash off any remaining IPA solution inside the channel. These cleaning steps were repeated three times to ensure no debris was found inside the microchannel. The sample solution was prepared by diluting the concentrated particles in a 0.1 mM phosphate buffer (PB) solution (pH 7.4) to the desired seeding density. Additionally, 1 μL of 0.1% NP40 was added to 1 mL of sample solution to prevent the particles from sticking to the microchannel. Three conditions were tested: 1) bulk flow in the x-direction, 2) no flow or suspended particles in an aqueous solution, and 3) stationary particles captured in a thin film of PDMS. The height difference between the inlet and outlet reservoir solutions created the bulk flow. Particles were suspended in an aqueous solution by ensuring no height difference between the solutions in inlet and outlet reservoirs. Lastly, beads were mixed with PDMS solution and cured into a thin film on a glass slide for stationary particles. Particles with varying diameters (0.53 ± 0.013 μm, 0.84 ± 0.016 μm, 1 ± 0.016 μm, and 1.9 ± 0.095 μm reported by the manufacturers) were used in this study. A TrACE device was placed on an inverted fluorescent microscope (Zeiss Axio Vert.A1) to record the particle trajectories. The particles were imaged using a high-speed camera (Phantom VEO-E 340L) operating at 1000 fps at 20 or 40× magnification. For fluorescence imaging of the particles, a 532 nm laser (Opto Engine LLC) was used as a light source, and the microscope was adjusted to focus on the center of the microchannel to avoid edge effects. The electric field wave, either a square or sine wave, was applied between an electrode pair using a function generator (Keysight Technologies Model 33210A). The image stack acquisition of 1000 frames was initiated by an external synchronizer (TSI Inc) for accurate synchronization of the applied electric field. The applied potentials are measured by the oscilloscope (Pico Technology), so the potential is known for calculations of μep.
2.4 Particle tracking velocimetry (PTV)
The raw digital images were processed using the Crocker–Grier centroid-finding algorithm29 with five steps: preprocessing raw images, locating candidate particle position, refining the center of particles, detecting ‘ghost’ particles, and linking time-resolved particle position. First, a median filter was applied to time stack the raw images to reduce the background noise level. The candidate centroids of particles were detected with the pixel-wise local maxima intensity method. Then, the centroids were refined based on intensity weight near the candidate centroids to provide subpixel accuracy. Since particles move with the flow or via Brownian motion, time-resolved centroids detection removes non-particle identification. Finally, the interframe linking algorithms selected the minimum overall linking distance among the subnetworks between two frames. A single frame gap closing method was utilized to construct long trajectories to tackle particle vanishing phenomena.22
2.5 Calculation of the electrophoretic mobility
Only y-positions were considered in calculations for the electrophoretic mobility (Fig. 4), as electrophoresis drives particles in the y-direction. Y-Positions of each particle were recorded using a PTV center detection algorithm in every frame, and the positions are plotted over time to get the particle trajectory. Next, the y-velocities of an individual particle were calculated over time by taking the derivative of the y-positions. The maximum velocity was found for every half of a wave cycle and was divided by the known electric field to calculate the electrophoretic mobility through μep = v/E. Since each particle was subjected to several cycles of an electric wave, multiple μep values were calculated per particle, and an average was taken to describe the μep of a single particle. A commercially available ELS instrument, the Zetasizer by Malvern, is used to measure and compare the μep of different particle populations.
2.6 Particle size analysis
In TrACE, particle sizes were measured based on two approaches: 1) the particle's spatial fluctuations due to Brownian motion in the x-dimension, or 2) pixel intensity from raw images. To measure particle size using Brownian motion analysis, particles in the center of the channel were considered. Also, a constant bulk flow rate was assumed, and that the particles traveled along the microchannel in the same XY plane. Particle sizes were calculated based on diffusion coefficients calculated from the measured diffusion lengths using  , where D is the diffusion coefficient, and t is the time between frames. Pixel intensity from raw images of the particles was also used to determine the particle size in ImageJ. The intensity threshold, about five times larger than the background, was used to measure particle diameters.
, where D is the diffusion coefficient, and t is the time between frames. Pixel intensity from raw images of the particles was also used to determine the particle size in ImageJ. The intensity threshold, about five times larger than the background, was used to measure particle diameters.
3. Theoretical
3.1 A theoretical time dependent DC electrophoresis model
The goal of this time dependent DC electrophoresis model is to capture the basic particle motion. Particle velocity is found using a DC electrophoretic mobility equation. See Table 1 for symbols used in the following equations. In a wide channel, we assume that the electric field is defined and uniform between the electrodes (|y| < a/2) and takes the form| |  | (1) |
where we consider both sinusoidal and square wave electric potentials. For the sinusoidal potential, we use| | Φ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (t) = Φ0 (t) = Φ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt), sin(ωt), | (2) |
where Φ0 is the amplitude of the applied voltage,ω is its angular frequency, and f is its frequency. Newton's second law,| | m![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) = qE + mg − m′g − 3πDη( = qE + mg − m′g − 3πDη(![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) − u), − u), | (4) |
describes the position r, velocity ṙ = dr/dt, and acceleration ![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) = d2r/dt2 of a particle of mass (m) and charge (q) as it moves through the channel with the fluid velocity (u), where g = −gẑ is the gravitational acceleration vector and
= d2r/dt2 of a particle of mass (m) and charge (q) as it moves through the channel with the fluid velocity (u), where g = −gẑ is the gravitational acceleration vector and| | 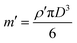 | (5) |
is the mass of the buffer solution that is displaced by a particle. The terms on the right side of eqn (4) respectively describe the electric force, the gravitational force, the buoyant force, and the Stokes drag force on the particle.
Table 1 List of symbols and their descriptions used in the equations
| Symbol |
Description |
Symbol |
Description |
|
a
|
Electrode separation |
e
L
|
Electrode length |
|
f
|
Voltage frequency |
e
s
|
Electrode spacing |
|
Φ
0
|
Voltage amplitude |
E
|
Electric field |
|
g
|
Gravitational acceleration |
v
e
|
Electrophoretic velocity |
|
η
|
Buffer solution viscosity |
ω
|
Angular frequency |
|
μ
|
Particle electrophoretic mobility |
ṽ
z
|
Vertical velocity |
|
ρ
|
Particle mass density |
C
w
|
Channel width |
|
m
|
Particle mass |
C
H
|
Channel height |
|
m′ |
Displaced mass |
C
L
|
Channel length |
|
q
|
Particle charge |
ū
|
Average fluid velocity |
|
D
|
Particle diameter |
|
|
When we substitute the Cartesian position r = x![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + yŷ + zẑ into eqn (4), we obtain the following component equations:
+ yŷ + zẑ into eqn (4), we obtain the following component equations:
| |  | (7) |
| | m![[z with combining umlaut]](https://www.rsc.org/images/entities/i_char_007a_0308.gif) + 3πDηż = (m′ − m)g + 3πDηż = (m′ − m)g | (8) |
As described in eqn (6)–(8), the Poiseuille flow drives x(t), y(t) is driven by the electric potential, and the balance between buoyancy and gravity drives z(t). We can further simplify eqn (6)–(8) in a quasi-equilibrium solution where the particle responds quickly to changes in the electric potential, and the net force on the particle and its acceleration are assumed at zero. Setting ẍ = ÿ = ![[z with combining umlaut]](https://www.rsc.org/images/entities/i_char_007a_0308.gif) = 0 in eqn (6)–(8), we can simplify the equations to give
= 0 in eqn (6)–(8), we can simplify the equations to give
| |  | (9) |
| | ẏ = ṽy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) sin(ωt) | (10) |
From
eqn (9)–(11), we focus on
eqn (10), where the particle response is driven mainly by the electric potential.
Eqn (10) describes that the transverse component of the quasi-equilibrium velocity is determined by the electrophoretic response to the applied potential with a velocity amplitude given by
ṽy,
| |  | (12) |
A particle's transverse position is solved by integrating the velocity equation (eqn (10)), for the sine and square wave over time. Since the amplitude of the velocity (ṽy) described here is a constant, integration of a sine wave yields a cosine particle trajectory (Fig. 2D–F). Likewise, the integration of the square wave produces a saw-tooth particle trajectory (Fig. 2A–C). A direct correlation is observed between the frequency of the applied electric wave and the particle trajectory. The particle oscillates at the same frequency as the electric field wave that drives its motion. As we increase the frequencies of both sine and square waves, the frequencies of the respective particle trajectories increase accordingly (Fig. 2). Additionally, the amplitude of the particle trajectory is proportional to the frequency of the applied potential because the longer excursions at lower frequency increase the amplitude (Fig. 2). Furthermore, changing the amplitude of the electric potential (Φ0) affects the velocity amplitude as described in eqn (10). As the amplitude of the electric wave increases, the distance traveled during a half-wave cycle increases as well (Fig. 3). Overall, the quasi-equilibrium solutions to a simple theoretical model based on DC electrophoresis sufficiently captures the basic particle response to the externally applied sine or square wave electric field.
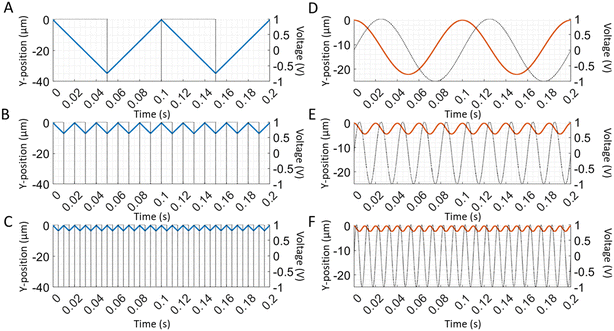 |
| | Fig. 2 Predicted frequency dependence of particle trajectory for the square and sine wave. (A–C) The time-dependent particle trajectories are calculated when driven by square waves of 1 V amplitude at frequencies of 10, 50, and 100 Hz. (D–F) The time-dependent particle trajectories are calculated when driven by sine waves of 1 V amplitudes at frequencies of 10, 50, and 100 Hz. The particle trajectories are plotted using eqn (10) and (12) with the following values for the electrode spacing and electrophoretic mobility: a = 100 μm and μ = 3.48 cm2 V−1 s−1.14 The particle trajectories are plotted on the left y-axis with the blue and orange lines, while the applied electric waves are plotted on the right y-axis with the dotted black lines. | |
 |
| | Fig. 3 Predicted amplitude dependence of particle trajectory for the square wave. (A–C) The particle positions as a function of time are calculated for a square wave with 0.5, 1, and 1.5 V amplitudes at 10 Hz using eqn (10) and (12). A particle's predicted positions are shown on the left y-axis with the blue lines, and the applied electric waves are illustrated on the right y-axis with the dotted black lines. | |
3.2 Ratio between electrophoretic mobility and Brownian motion
For a precise electrophoretic mobility measurement, electrophoresis must be a primary force driving a particle motion in the y-dimension. The ratio of particle displacements from electrophoresis and Brownian motion is critical in the evaluation of the potential precision of the electrophoretic mobility measurement. Thus, we define the ratio by using the following equations.
Given that electrophoretic mobility is defined as
distance traveled by a particle can be defined as
and path length traveled due to Brownian motion can be defined as
| |  | (15) |
Thus, the ratio between these two distances can be defined as
| | 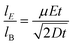 | (16) |
based on
eqn (15) and
(16). Rearranging
eqn (17), a final equation can be further simplified to
| | 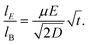 | (17) |
A large

improves the precision at which the electrophoretic mobility can be measured; measurement precision increases as
μ and
E increase and as the square root of the diffusion coefficient decreases. To achieve a precision within 1%, the ratio of particle displacements from electrophoresis and Brownian motion must be greater than 100.
4. Results and discussion
4.1 Overview of device design and operation
TrACE microfluidic devices have a simple design, making them easy to fabricate as they require only a single microchannel and a pair of opposing electrodes (Fig. 1). Although three pairs of electrodes are shown in Fig. 1A–C, only one pair is required. Devices with three pairs of electrodes were fabricated for improved fabrication efficiency, to compare the performance of electrode pairs, and to provide adequate surface area for adhesion of the PDMS layer to the glass substrate. The pair of opposing electrodes in TrACE creates an electric field perpendicular to the bulk flow through the microchannel. A low-frequency (≤100 Hz) AC wave is applied to these electrodes, forcing charged particles to move through the microchannel with an oscillating trajectory. Experimentally, the spatial movements of the particles are a summation of the three phenomena: electrophoresis, hydrodynamic bulk flow, and Brownian motion. A PTV algorithm measures the net particle displacement at a given frame (Fig. 4). While high electric fields provide greater electrophoretic velocities and can improve measurement precision, because the electrodes are in the microchannel, there is a practical limit to the electric field strength created by electrolysis. Electrolysis produces bubbles, hydrogen at the cathode and oxygen at the anode. 1 V amplitude is below the electrolysis threshold and given the 100 μm electrode spacing, a 1 V amplitude creates an electric field of ∼100 V cm−1. We found that amplitudes up to 1.75 V provide reliable performance without observable trajectory perturbation from electrolysis (Fig. S1†).
 |
| | Fig. 4 Forces acting on a particle and the movement of a particle. A net particle movement results from three phenomena acting on the imaged particle: electrophoresis in the y-direction, bulk flow in the x-direction, and Brownian motion in any direction. Since Brownian motion is random, the direction of its vector representation is arbitrary. The white dotted line around the particle represents possible particle displacements (one sigma length not to scale) caused by Brownian motion. The framewise particle trajectories represent the sum of these forces and the number of frames can be easily modified. An overlay of 5 images shows the movements of a single particle over 5 frames at 10 Hz and 1 V amplitude square wave. An extended view (bottom) of the same particle after n′ frames is included. | |
4.2 Experimental measurement of particle trajectories as a function of frequency, amplitude, and phase comparison with the theoretical model
The motion of individual particles is measured in the TrACE system driven by a square or sine wave at different frequencies and voltage amplitudes. The quasi-equilibrium model uses steady-state velocities that are observed in DC electrophoresis with faradaic current. Experimentally observed particles' responses to square and sine waves are shown in Fig. 5 and 6, respectively. The experimental frequency, amplitude, and phase of the particle trajectories are compared with the quasi-equilibrium theoretical model, and remarkably good agreement is found for frequency, phase, and amplitude at higher frequencies. The good agreement supports the hypothesis that particle movement is largely driven by DC electrophoresis. The increasing amplitude deviation with decreasing frequency suggests that electrode charging influences the particle movement in TrACE. The effects of electrode charging on the trajectory appear to be enhanced at low frequencies and by voltages below the electrolysis threshold.
 |
| | Fig. 5 Experimental particle trajectory to the square wave. Trajectories of carboxyl functionalized polystyrene microspheres with a nominal diameter of 1.9 ± 0.095 μm are recorded. The individual traces show trajectories of individual particles with different electrophoretic mobilities. The following conditions are applied: 1 V amplitude square wave at a frequency of (A) 10 Hz, (B) 50 Hz, and (C) 100 Hz. Images are taken at 1000 fps for 1 s. The first cycle of all trajectories in each condition is shown in the insets. Normalized trajectories are shown in the insets, so the first point is at zero to better display decreasing amplitude of the particle trajectories with increasing frequencies as well as the overall shape of the trajectories. | |
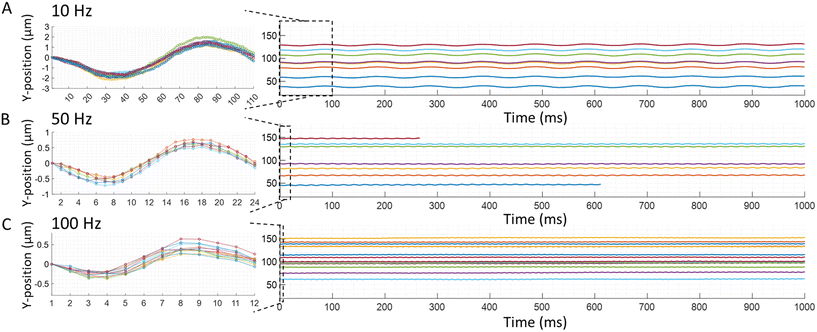 |
| | Fig. 6 Experimental particle trajectory to a sine wave. Trajectories of carboxyl functionalized polystyrene microparticles with a nominal diameter of 1.9 ± 0.095 μm are recorded. The same parameters reported in Fig. 5. Are used for the sine waves to record the trajectories of individual particles to demonstrate the flexibility of the type of electric wave used in the TrACE system: (A) 10 Hz, (B) 50 Hz, and (C) 100 Hz. Images are taken at 1000 fps for 1 s. The individual traces with different colors show trajectories of different particles with different electrophoretic mobilities. The first cycle of all trajectories in each condition is shown in the insets using the same method reported in Fig. 5. The insets show the decreasing amplitude of the trajectories with the increasing frequency and the overall shape of the measured trajectories. | |
4.2.1 Particles response to varying frequencies of the electric waves.
A direct correlation between an applied electric field's frequency and particle trajectories are observed. In other words, the oscillating frequency of the particles is the same as the frequency of the driving electric field wave. The responses of particles to electric square or sine waves with frequencies of 10, 50, or 100 Hz are shown in Fig. 5 and 6, respectively. For example, when a 10 Hz square wave is applied to the electrodes, all particles oscillate at 10 Hz as they travel through the microchannel (Fig. 5A). Likewise, when a 10 Hz sine wave is applied to the electrodes, all particles oscillate at 10 Hz down the microchannel (Fig. 6A). Therefore, these experimental results show good agreement with the quasi-equilibrium model as the observed and predicted frequencies are the same as the frequencies of the driving electric waves. Additionally, in the recorded particles responses, the frequency of the electric wave and the particle trajectory amplitude are inversely proportional (Fig. 5 and 6). Likewise, this relation between the amplitude and frequency is shown in a quasi-equilibrium solution of the theoretical model (Fig. 2).
While there is good agreement in the shape of the trajectory at higher frequencies, a deviation from the simple theoretical model is observed to increase as the electric field frequency decreases for square waves. The model predicts a sawtooth trajectory for a square wave, and in each segment of the sawtooth trajectory, a constant particle velocity is shown. However, experimentally, the particle velocity decreases after the polarity of the electric field changes, causing the y-velocity to continually decrease after each change in polarity of the electric field. This decreasing velocity produces a trajectory in which the slope of the y-position decreases monotonically and approaches zero at frequencies ≤10 Hz (Fig. 5A). Thus, the measured initial velocity is closest to the velocity predicted by the DC mobility, particularly for sub-faradaic voltages. Electrode charging is a likely cause of this decreasing particle velocity after the polarity of the electric field is reversed, which can reduce the local electric field that drives the particle's electrophoretic motion. Specifically, in TrACE, electrode charging is likely to play an important role because the applied voltages are below the threshold for electrolysis, and charge transfer is presumed negligible. The fundamentals of electrode charging and the current-time dependence at the electrodes have been modeled with an RC circuit in chronoamperometry.30 The contribution of electrode charging or charge transfer on particle migration in a low-frequency AC electrophoresis system at sub-faradaic voltages will be investigated in future work.
4.2.2 Particles response to varying amplitudes of the electric waves.
The amplitude represents the strength of the electric field and the force that drives particle migration. A direct correlation between the amplitude of the electric potential and the amplitude of the particle trajectories is observed, which agrees with the quasi-equilibrium model. As the electric potential increases from 0.75 to 1.5 V amplitude, the amplitude of the particle trajectories, calculated by the first and last points of each half-cycle of trajectories, increases due to the greater electric force applied to each particle during the cycle (Fig. 7). However, a change in the particle response near the electrolysis potential is observed where the deviation from the quasi-equilibrium model is present but decreases above the threshold as the particles' y-displacements become more linear. The difference in the trajectory shape near the electrolysis potential is most notable in the latter portion of each half-wave cycle, as the slope in the latter portion increases. The observed increase in the particle trajectories' slope above the electrolysis potential corroborates the likely role of electrode charging driving the particle movements below the redox limit.
 |
| | Fig. 7 Experimental particles responses to electric waves with different amplitudes. (A) Square waves with 0.75, 1, 1.25, and 1.5 V amplitude (top to bottom graphs) at 10 Hz are applied, and the particle trajectories are recorded. Images are taken at 1000 fps for 1 s, although the graphs include cycles up to 0.5 s. (B) Amplitudes of particle trajectories are calculated by taking the first and last y-positions in each half-wave cycles. Mean trajectory amplitude is plotted as a function of voltage at 0.75, 0.9, 1, 1.1, 1.25, and 1.5 V amplitude. Standard deviations of the trajectory amplitudes are plotted using error bars, and a linear fit line is plotted. | |
As the electric potential is increased above the redox threshold potential, the amplitude enhancement exceeds the linear relationship observed at lower voltages. In this work, the onset of electrolysis appears to be between 1.2 V and 1.5 V amplitude, as shown in Fig. 7B. At amplitudes ≥1.5 V and at a low frequency, after the initial rapid response, the slope of the trajectory is increased during the latter part of the half-wave cycle. Thus, as the amplitude increases above the redox threshold, the contribution of the faradaic current increases, increasing the electrophoretic velocity during each half-wave cycle. A voltage sweep from 0 to ±3 V conducted with the TrACE device shows similar electric potential thresholds (around 1.2 V and −1.5 V) where the current increases and decreases significantly (Fig. S2†). Applying a high voltage amplitude is beneficial as it increases the electrophoretic velocity, but if the voltage amplitude is too high, bubble formation (Fig. S1†) perturbs the electric field and decreases the lifespan of the electrodes.
4.2.3 Phase difference between the electric field wave and the particle trajectories.
The particle trajectories are also examined to determine if a measurable phase lag is observed. The inertial response constant is defined by the ratio between the particle's mass and Stokes' drag force,  , indicating that the inertial response should be on the order of 50 nanoseconds for a 2 μm particle which is five orders of magnitude faster than the 1 ms period between each frame. A synchronizer triggered the camera and the function generator to image and apply electric waves simultaneously. Experimentally no phase lag is observed (Fig. 5), consistent with an inertial time constant on the order of 50 ns and predicted by the quasi-equilibrium solution. In the case of a sine wave, the phase difference between the electric field wave and particle trajectories is ¼ of a wave (Fig. 6), consistent with the solution of the quasi-equilibrium theoretical model (Fig. 2D–F). Although this may be perceived as a phase lag, when the applied electric field has the shape of a sine wave, the particle trajectories have a cosine shape, which is consistent with the particles moving the fastest when the forcing by the electric field is the strongest. For the square wave, the electric field changes abruptly, and the change in particle trajectory is immediate and just as abrupt as the change in the electric field wave. In summary, no measurable phase lag is observed.
, indicating that the inertial response should be on the order of 50 nanoseconds for a 2 μm particle which is five orders of magnitude faster than the 1 ms period between each frame. A synchronizer triggered the camera and the function generator to image and apply electric waves simultaneously. Experimentally no phase lag is observed (Fig. 5), consistent with an inertial time constant on the order of 50 ns and predicted by the quasi-equilibrium solution. In the case of a sine wave, the phase difference between the electric field wave and particle trajectories is ¼ of a wave (Fig. 6), consistent with the solution of the quasi-equilibrium theoretical model (Fig. 2D–F). Although this may be perceived as a phase lag, when the applied electric field has the shape of a sine wave, the particle trajectories have a cosine shape, which is consistent with the particles moving the fastest when the forcing by the electric field is the strongest. For the square wave, the electric field changes abruptly, and the change in particle trajectory is immediate and just as abrupt as the change in the electric field wave. In summary, no measurable phase lag is observed.
4.3 Brownian motion measurement
Brownian motion imparts random motion in all three dimensions. To study the effect of Brownian motion on the particle trajectories, Brownian motion is first measured from the suspended particles in TrACE with the bulk flow stopped. The changes in particles' x and y-positions between frames are mainly from Brownian motion since the particles are suspended in a static solution. The measured displacements follow a normal distribution; one sigma defines the experimental diffusion length. Initially, the σmeasured displacement of the particles of all sizes are larger than the expected diffusion lengths from Brownian motion. In the TrACE system, the sources of measurement noise can include imprecision of the particle center detection, vibrations, instrumentation, etc. Therefore, the contribution of σmeasurement noise is quantified from the center detection algorithm on stationary particles and subtracted from the σmeasured displacement to determine the experimental diffusion length (Table S1†). Experimental diffusion lengths of 0.53 and 1 μm particles fall within their respective theoretical diffusion lengths. However, because Brownian motion decreases as particle size increases, the experimental diffusion length of 2 μm particles is not sufficiently above the noise to provide an accurate measurement.
4.3.1 Effect of Brownian motion along the microchannel height.
Brownian motion in the z-dimension can alter the particle velocity in the x and y-dimensions and consequently affect the particle trajectory analysis. The parabolic profile of the hydrodynamic flow along the channel height (Fig. 1B) changes the particle's velocity in the x-direction as the particle's z-position changes. Based on the experimental diffusion length of the smallest particle from Table S1,† two-thirds of 0.53 μm particles will have a deviation of <0.12 μm along the z-axis between images at 100 fps. However, as the particle size increases, the diffusion length decreases and the diffusive variance in the particle trajectory decreases. Additionally, Brownian motion along the z-axis can alter the particle's velocity in the y-direction due to the variation in the electric field strength as a function of microchannel height. Ideally, in a TrACE device, the electric field is homogenous, so all particles experience the same electric field regardless of their positions in the microchannel. However, in this first version of the device, the micropatterned electrodes are on the substrate surface, and the divergence of the electric field increases as the height above the device substrate increases along the z-axis. A numerical analysis at the center of the microchannel shows a 0.2% variation in the magnitude of the electric field as the channel height increases from 2.5 to 5 μm (Fig. S3†). Therefore, when a particle randomly moves up to 0.12 μm along the z-axis from Brownian motion, even less than 0.2% variation in the electric field strength is expected with a negligible impact on the particle's y-velocity.
4.4 Electrophoretic mobility measurement of single particles
In TrACE, the electrophoretic mobility of single particles can be determined from the individual particle trajectories, while oscillating trajectories increase the number of measurements taken per particle. Initially, a square wave is selected because of the constant field of the electric wave before a change in direction, which simplifies the electrophoretic mobility calculations. Experimentally, a sine wave is less demanding on the voltage source; thus, electrophoretic mobility measurements using a sine wave will be investigated in the future. To reduce the effects of wall interactions in these initial analyses, we focused only on the trajectories recorded in the region near the center of the microchannel. To keep the consistent z-positions for measurements, particles in focus are analyzed only. In our non-confocal fluorescence imaging system, the particle must move more than the ±4 μm from the focal plane to appear out of focus. Thus, a difference less than 4 μm in the particles' initial z-positions or displacements caused by Brownian motion from the focal plane will not be apparent in images.
Electrophoretic mobility is calculated for each particle upon every change in the direction of the electric field. As noted in Fig. 5, the time-dependent trajectories are not linear, but are nearly linear at the onset of each voltage transition of the square wave. Given the time-dependent velocity after each half-wave electric field transition, one simple approach is calculating the electrophoretic mobility from the maximum particle y-velocity measured after the electric field changes direction. Therefore, the number of measurements taken per particle equals the number of half-wave cycles recorded for each particle trajectory. First, multiple reads taken on a single 2 μm particle at electric wave frequencies of 10, 50, and 100 Hz are averaged, and the standard error of the mean values are calculated to compare the measurement precision (Table 2). Higher frequencies provide more reads, but the maximum read rate is limited by the maximum fps of the camera and the distance each particle travels between frames. Also, due to instrumental limitations of the waveform generator, the greatest deviation of the applied potential wave is observed at each square wave transition, which has a greater contribution to the total wave with increasing frequency (Fig. S4†). Yet, the instrumental deviations from a perfect square are considered to be minor. Thus, the precision of the electrophoretic mobility measurement, as indicated by the standard error of the mean value, improves about the square root of the number of half-wave cycles as the frequency increases with some expected outliers (Fig. S5†). The following analyses perform electrophoretic mobility calculations using the particle trajectories recorded while applying a 1 V amplitude square wave at 50 Hz. 50 Hz is selected because a sufficiently small standard error of the mean value is calculated without compromising the trigger speed of the synchronizer or the waveform generator.
Table 2 Electrophoretic mobility measurements at different frequencies. The electrophoretic mobility of three 2 μm carboxyl-functionalized polystyrene particles, one at each frequency, is calculated for 10, 50, and 100 Hz electric field waves. The number of measurements equals the number of half-wave cycles equals. The standard error of the mean is calculated by dividing the standard deviation by the square root of the number of half-wave cycles
| Frequency (Hz) |
Number of half-cycles |
Electrophoretic mobility (μm cm V−1 s−1) |
Standard error of the mean |
| 10 |
12 |
−5.25 |
0.16 |
| 50 |
100 |
−4.92 |
0.03 |
| 100 |
199 |
−4.62 |
0.02 |
Electrophoretic mobility values of individual carboxyl-functionalized particles with diameters of 0.53, 0.84, 1, and 2 μm are measured in the TrACE system and validated with ELS. While there is significant heterogeneity within each nominal bead size, the populations for each size are differentiated with TrACE. Observable difference in the electrophoretic mobility distributions measured between the particle groups fabricated by different companies suggest that there is a difference in charge functional group density on the surface of the particles (Fig. 8). Furthermore, the electrophoretic mobility values reported with the TrACE system are compared to the measurements done using a commercially available ELS instrument (Table 3). Since ELS is an ensemble measurement technique, unlike a single particle method like TrACE, average electrophoretic mobility of the distribution of the population is reported. A relative standard deviation (RSD) as high as ∼9% is observed in the sample population measured using ELS. However, the TrACE system can measure individual particles' electrophoretic mobility with greater precision by taking ∼100 measurements per particle in which the precision is demonstrated by a standard error of the mean as close as ∼2% to the true mean. The population mean electrophoretic mobilities measured with ELS reports different values from the TrACE system for 0.84 and 0.53 μm particles. However, it is uncertain which method reports a more accurate electrophoretic mobility without a good standard.
 |
| | Fig. 8 Simultaneous electrophoretic mobility and size measurement. Analysis of the TrACE trajectories of four types of carboxyl-functionalized polystyrene particles. Particle size is calculated from σx where accuracy increases as size decreases. The electrophoretic mobility is determined directly from particle's y-velocity. The 0.53 and 0.84 μm nominal OD particles are from Spherotech, Inc., and the 1 and 2 μm nominal OD particles are from Invitrogen. Each circle represents a single particle. | |
Table 3 Measured electrophoretic mobilities using TrACE and ELS. The electrophoretic mobility of each particle type is reported by TrACE and ELS. TrACE reports the electrophoretic mobility of a single particle in each group. In contrast to TrACE, ELS reports the mean electrophoretic mobility of the particle population as ELS performs an ensemble measurement. A significant run-to-run variability has been shown in ELS
|
|
TrACE |
Zetasizer |
| Particle size (μm) |
Electrophoretic mobility (μm cm V−1 s−1) |
Standard error of the mean |
Electrophoretic mobility (μm cm V−1 s−1) |
Standard deviation |
| 0.53 |
−5.68 |
0.14 |
−5.09 |
0.48 |
| 0.84 |
−5.81 |
0.11 |
−5.23 |
0.35 |
| 1 |
−4.87 |
0.05 |
−4.85 |
0.27 |
| 2 |
−4.92 |
0.03 |
−4.96 |
0.27 |
Electrophoresis is the primary force driving the particle motion in the y-dimension in TrACE; however, Brownian motion also influences the particle motion and affects the measurement precision. Fundamentally, the precision of the electrophoretic mobility measurement is limited by Brownian motion, which increases with decreasing particle size. Thus, the ratio between the electrophoretic motion and Brownian motion also plays a key part in making a precise electrophoretic mobility measurement. Experimentally, the ratio between electrophoresis and Brownian motion is calculated per particle using eqn (17). Although the ratio decreases as the particle size decreases due to increasing Brownian motion, the precision of the electrophoretic mobility measurements remains high as the mean ratios are well above 100 in all sizes (Fig. S6†).
EOF exists in DC and AC free solution electrophoresis and could contribute to the observed transverse velocity (μobs = μEOF + μep). Given the negative zeta potential of the microchannel surface and the closed configuration of the system, EOF in the center of the microchannel should be in the same direction as the anionic particles.26 However, the increased frictional resistance in closed systems is expected to increase the time to reach steady-state EOF compared to open systems, such as CE. A report on an AC EOF mixer with a very similar design to TrACE found that the electroosmotic mixing decreased rapidly with increasing frequency above 1 Hz.26 Additionally, EOF decreases with increasing frequency in AC electrophoresis systems.25 Thus, at higher frequencies μobs = μep. In our system, two approaches found no measurable EOF at frequencies ≥50 Hz. First, the addition of PVP, a dynamic coating of polyvinylpyrrolidone (PVP) that suppresses the EOF,31 did not significantly alter the mobility for a wave with a frequency of 50 Hz (Table S2†). Second, the dependence of μobs on the frequency shows significant EOF at 1 Hz, little EOF at 10 Hz, and negligible EOF at frequencies ≥50 Hz.
4.5 Particle sizing
To accommodate a larger particle size range, both imaging and Brownian motion analysis can be used for particle size measurement in TrACE. The size-dependent spatial fluctuations caused by Brownian motion are measured in the x-direction from trajectory analysis and are used to calculate smaller particles' size. Image analysis is used to measure the size for large particles in this study (diameters ≥2 μm), where imaging is presumed to be more precise than Brownian motion. The particle size limit for where imaging becomes more precise than Brownian motion has not yet been clearly defined in our system, as both approaches have not been fully refined. A histogram of measured spatial fluctuations of particles with diameters of 0.53, 0.84, 1, and 2 μm shows distinct peaks at 0.049, 0.040, 0.028, and 0.025 μm, respectively (Fig. S8†). As expected, measured spatial fluctuations decrease as the particle size increases due to a decrease in Brownian motion. In TrACE, the diameter of each particle is calculated based on measured spatial fluctuations in the x-dimension as the bulk flow along the x-axis is assumed to be constant, while the electrophoretic mobility is simultaneously calculated from the particle displacement in the y-dimension of each particle trajectory (Fig. 8). Since the spatial fluctuations measure the diffusion lengths from Brownian motion, the diffusion coefficient for each particle can be determined and used to calculate the particle diameter. The mean diameter measured in each particle population from spatial fluctuations is 6 to 35% smaller compared to the nominal diameters reported by the manufacturers using a Coulter counter (Table 4). Brownian motion analysis can be refined by improving the precision of the particle center detection algorithm. However, the performance of the TrACE device is expected to improve as the particle size decreases with increasing magnitude in Brownian motion. Image analysis is better for measuring particle size for particles with diameters ≥2 μm, where the magnitude of spatial fluctuations is dominated by measurement noise. In this case, a particle diameter is calculated using the image area function in ImageJ using an intensity threshold value above 1250. For the particle population with a vendor-reported diameter of 1.9 ± 0.095 μm, the mean diameter measured using image analysis is 1.72 ± 0.18 μm. Often, particles imaged with a non-confocal fluorescence microscope can vary widely due to optical properties, including the wavelength of the light source, focal plane, light scattering, etc. Overall, TrACE's capability to support a wider particle size range using either Brownian motion and image analysis is demonstrated, and refinement of both approaches and calibration from known size standards is expected to improve the size analysis.
Table 4 Comparison between nominal and measured diameter. Nominal diameters are reported as the mean diameter ± standard deviation of a population by the manufacturers. Measured diameters are also of a mean diameter ± standard deviation of a population determined based on Brownian motion measured in the TrACE system
| Nominal diameter (μm) |
Mean measured diameter (μm) |
| 0.53 ± 0.013 |
0.36 ± 0.06 |
| 0.84 ± 0.024 |
0.54 ± 0.07 |
| 1 ± 0.016 |
1.07 ± 0.13 |
| 1.9 ± 0.095 |
1.41 ± 0.22 |
4.6 Multiplexing
One of the main drawbacks of single-particle measurements is a reduction of sample throughput, as most single-particle measurement methods typically measure one particle at a time and require a low seeding density. While the linear bulk flow in this first report is fairly low (∼200 μm s−1), the TrACE system is capable of multiplexing as many particles that can be tracked simultaneously by the PTV algorithm. For 2D PTV, the maximum density of particles is determined by the camera speed and the flowrate since the seeding density can be high as long as the particles' moving distance is less than the distance from the neighboring particles.32 Here, we have tracked up to ten particles simultaneously (Fig. 9). However, the maximum number of particles tested can be easily adjusted by modifying the camera speed and flow rate appropriate for the application.
 |
| | Fig. 9 Multiplexing. Ten particles are tracked simultaneously as they oscillate across the microchannel when a 1 V amplitude square wave at 50 Hz frequency is applied. The white circles illustrate their initial relative spatial orientations, which remain relatively constant throughout. In this experiment, the detection window is 1 mm. | |
4.7 Variability of observation time
In TrACE, particle motion in the x-dimension is driven by the hydrodynamic flow and is effectively decoupled from the particle's electrophoretic motion in the y-dimension. There is no relation between the bulk flow velocity and the electrophoretic mobility (Fig. S9†). The bulk flowrate can be varied by simply changing the height of the solutions in inlet and outlet reservoirs. Easy control over the bulk flow rate has many benefits. As the bulk flow approaches 0 μm s−1, the residence time of the particle(s) in the detection window approaches infinity, and the measured oscillations increase. As shown in Table 2, an average taken with a larger number of measurements can improve the measurement precision. On the other hand, increasing the bulk flowrate allows more particles through the detection window to be analyzed and increases throughput. It is anticipated that the ability to easily tailor the flow rate to balance particle throughput with precision and observation time will enhance the applicability of TrACE.
4.8 TrACE of mammalian cells
A critical question for assessing whether TrACE can characterize living cells is – do the electric field waves used in TrACE drive detectable oscillations while avoiding cell lysis? B-lymphoblastoid cells are selected for initial testing in TrACE because they are non-adhering spherical cells. When a 10 Hz square wave with 2 V amplitude is applied to the TrACE system, the transverse electric field forces B-cells to oscillate across the microchannel similarly to the polystyrene particles (ESI† Video SV1). The μep of individual B-cells are calculated based on their transverse velocities and the measured μep values varied from −9.5 ± 0.1 to −12.9 ± 0.3 μm cm V−1 s−1. There is a growing research interest in the mechanical manipulation of mammalian cells, and numerous studies have reported on electroporation of cells.33–35 At intermediate electric fields, cells electroporate, and in higher fields, cells lyse.34 These experiments with intact cells indicate that the electric field in the TrACE system is strong enough to drive B-cells' oscillation, yet the electric field is below the cell lysis threshold. Additionally, in TrACE, slowing the bulk flow close to 0 μm s−1 can hold the cells in one position in the microchannel, where cells can be stimulated and observed for a long time. This application will emphasize the temporal analysis over high throughput, which serves as a good complement to instruments like flow cytometry.
5. Conclusion
We describe a new microfluidic TrACE system that simultaneously measures single particles' electrophoretic mobility and size using particle trajectories. Thus, TrACE provides a new method for measuring charge via electrophoretic mobility and size of single particles, for which few methods have been reported. Particle movement in TrACE is captured with a simple time-dependent DC model, indicating that DC electrophoresis drives particle migration. A deviation in amplitude increases with decreasing frequency of square waves, although this deviation is presumably caused by electrode charging and will be the subject of further studies. Additionally, TrACE shows improved precision achieved by averaging multiple measurements taken on a single particle from the oscillating particle trajectories.
The TrACE system has unique performance characteristics for single particle measurements: simultaneous high-precision electrophoretic mobility and size measurements, a long observation time, and multiplexing capability. A low bulk flow velocity and long detection window provide a longer observation time to increase the number of measurements for improved precision or tailor to experiments in which a long observation time is desired. Additionally, a high precision of electrophoretic mobility is achieved with high electric fields created by the short gap between the electrodes and simultaneous size measurements are made with either Brownian motion or image analysis. Compared with DC free solution electrophoresis, electromigration and bulk flow are decoupled, and the contribution of longitudinal EOF to migration is eliminated. Multiplexing via simultaneous tracking of multiple particle trajectories in the detection window alleviates low particle throughput. At a more practical level, the simple design of the TrACE device allows for a low-cost fabrication and the low voltage amplitudes, and currents avoid bubble formation and excessive heat generation. Optical microscopy in the TrACE system provides high-resolution trajectories and allows for imaging of particle aggregation.
To further improve the precision of the electrophoretic mobility measurements, a more homogenous electric field within a microchannel can be created using vertical electrodes and utilizing a 3D PTV technique for direct measurement of particle's z-positions.36 Overall, the combination of low-frequency, low-voltage AC electrophoresis, and PTV has the potential to characterize biological particles, specifically cells and bacteria, as the interest in describing biological particles grows each day. We anticipate that the measurement precision and capabilities of the TrACE system will expand as our understanding of particle motion in reversing electric fields improves.
Conflicts of interest
The authors declare the following competing financial interest: A. T. T. has a financial interest in FluidiSpec LLC.
Acknowledgements
The authors acknowledge the support from the National Science Foundation (NSF) (Grant No. 1808678). We want to acknowledge Dr. F. Brad Johnson for providing B lymphoblastoid cell line (AG09387).
References
- W. T. Liu, J. Biosci. Bioeng., 2006, 102, 1–7 CrossRef CAS PubMed.
- Y. Zheng, J. Nguyen, Y. Wei and Y. Sun, Lab Chip, 2013, 13, 2464–2483 RSC.
- G. Y. H. Lee and C. T. Lim, Trends Biotechnol., 2007, 25, 111–118 CrossRef CAS PubMed.
- J. R. Thompson, L. M. Wilder and R. M. Crooks, Chem. Sci., 2021, 12, 13744–13755 RSC.
- Z. Ma, H. Merkus, J. Smet, C. Heffels and B. Scarlett, Powder Technol., 2000, 111, 66–78 CrossRef CAS.
- L. Treuel, K. A. Eslahian, D. Docter, T. Lang, R. Zellner, K. Nienhaus, G. U. Nienhaus, R. H. Stauber and M. Maskos, Phys. Chem. Chem. Phys., 2014, 16, 15053–15067 RSC.
- R. Xu, Particuology, 2015, 18, 11–21 CrossRef.
- J. Gross-Rother, M. Blech, E. Preis, U. Bakowsky and P. Garidel, Pharmaceutics, 2020, 12, 1112 CrossRef CAS PubMed.
- K. R. Riley, S. Liu, G. Yu, K. Libby, R. Cubicciotti and C. L. Colyer, J. Chromatogr. A, 2016, 1463, 169–175 CrossRef CAS PubMed.
- C. Manzo and M. F. Garcia-Parajo, Rep. Prog. Phys., 2015, 78, 124601 CrossRef PubMed.
- V. Filipe, A. Hawe and W. Jiskoot, Pharm. Res., 2010, 27, 796–810 CrossRef CAS PubMed.
- W. Zhang, Y. Hu, G. Choi, S. Liang, M. Liu and W. Guan, Sens. Actuators, B, 2019, 296, 126615 CrossRef CAS.
- R. Haskell, J. Pharm. Sci., 1997, 87, 125–129 CrossRef PubMed.
- A. Palanisami and J. H. Miller, Jr., Electrophoresis, 2010, 31, 3613–3618 CrossRef CAS PubMed.
- I. Amer Cid, Y. Y. Ussembayev, K. Neyts and F. Strubbe, Electrophoresis, 2021, 42, 1623–1635 CrossRef CAS PubMed.
- B. Jachimska, M. Wasilewska and Z. Adamczyk, Langmuir, 2008, 6866–6872 CrossRef CAS PubMed.
- M. Gordon, X. Huang, S. J. Pentoney and R. Zare, Science, 1988, 242, 224–228 CrossRef CAS PubMed.
- M. A. Rodriguez and D. W. Armstrong, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2004, 800, 7–25 CrossRef CAS PubMed.
- V. Kostal and E. A. Arriaga, Electrophoresis, 2008, 29, 2578–2586 CrossRef CAS PubMed.
- B. J. Huge, M. M. Champion and N. J. Dovichi, Anal. Chem., 2019, 91, 4649–4655 CrossRef CAS PubMed.
- X. Huang, M. J. Gordon and R. N. Zare, Anal. Chem., 1988, 60, 1837–1838 CrossRef CAS.
- A. Hellqvist, Y. Hedeland and C. Pettersson, Electrophoresis, 2013, 34, 3252–3259 CrossRef CAS PubMed.
- G. Huang, B. Xu, J. Qiu, L. Peng, K. Luo, D. Liu and P. Han, Colloids Surf., A, 2020, 587, 124339 CrossRef CAS.
- F. Varenne, J. Botton, C. Merlet, J.-J. Vachon, S. Geiger, I. C. Infante, M. M. Chehimi and C. Vauthier, Colloids Surf., A, 2015, 486, 218–231 CrossRef CAS.
- M. Minor, A. Van der Linde, H. Van Leeuwen and J. Lyklema, J. Colloid Interface Sci., 1997, 189, 370–375 CrossRef CAS.
- H. Song, Z. Cai, H. M. Noh and D. J. Bennett, Lab Chip, 2010, 10, 734–740 RSC.
- B. S. Schuster, L. M. Ensign, D. B. Allan, J. S. Suk and J. Hanes, Adv. Drug Delivery Rev., 2015, 91, 70–91 CrossRef CAS PubMed.
- S. Hassanpour Tamrin, A. Sanati Nezhad and A. Sen, ACS Nano, 2021, 15, 17047–17079 CrossRef CAS PubMed.
- D. G. Grier and J. C. Crocker, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef.
-
A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical methods: fundamentals and applications, John Wiley & Sons, 2022 Search PubMed.
- T. Kaneta, T. Ueda, K. Hata and T. Imasaka, J. Chromatogr. A, 2006, 1106, 52–55 CrossRef CAS PubMed.
- K. Ohmi and H.-Y. Li, Meas. Sci. Technol., 2000, 11, 603 CrossRef CAS.
- N. Bao, Y. Zhan and C. Lu, Anal. Chem., 2008, 80, 7714–7719 CrossRef CAS PubMed.
- P. A. Garcia, Z. Ge, J. L. Moran and C. R. Buie, Sci. Rep., 2016, 6, 1–11 CrossRef PubMed.
- H. Lu, M. A. Schmidt and K. F. Jensen, Lab Chip, 2005, 5, 23–29 RSC.
- A. Huhle, D. Klaue, H. Brutzer, P. Daldrop, S. Joo, O. Otto, U. F. Keyser and R. Seidel, Nat. Commun., 2015, 6, 5885 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a,
Liu
Hong
c,
Leonardo P.
Chamorro
*a,
Liu
Hong
c,
Leonardo P.
Chamorro
 c,
Boyd
Edwards
d and
Aaron T.
Timperman
c,
Boyd
Edwards
d and
Aaron T.
Timperman
 *ab
*ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of PDMS to curing agent, was poured over the mold and cured overnight at 65 °C to make a PDMS microchannel. Next, electrodes are patterned, as shown in Fig. 1via a standard wet etching process on a Cr/Au coated glass slide (Telic Company). A total of 9 devices were patterned onto each glass slide, and a glass cutter was used to cut out individual devices. Then, a PDMS microchannel and patterned electrodes slide was placed in a plasma cleaner using atmospheric gas (Harrick Plasma model PDC-32G) to clean the surfaces and produce reacting groups for one minute. Immediately after the plasma treatment, a PDMS microchannel was aligned to the patterned electrode slide using an in-house constructed x–y–z stage and pressed firmly for attachment. After the assembly, a weight was placed on top of the device and heated at 65 °C overnight to ensure complete attachment. Finally, an electrical wire was soldered onto an electrode to supply electric potentials to the device.
1 ratio of PDMS to curing agent, was poured over the mold and cured overnight at 65 °C to make a PDMS microchannel. Next, electrodes are patterned, as shown in Fig. 1via a standard wet etching process on a Cr/Au coated glass slide (Telic Company). A total of 9 devices were patterned onto each glass slide, and a glass cutter was used to cut out individual devices. Then, a PDMS microchannel and patterned electrodes slide was placed in a plasma cleaner using atmospheric gas (Harrick Plasma model PDC-32G) to clean the surfaces and produce reacting groups for one minute. Immediately after the plasma treatment, a PDMS microchannel was aligned to the patterned electrode slide using an in-house constructed x–y–z stage and pressed firmly for attachment. After the assembly, a weight was placed on top of the device and heated at 65 °C overnight to ensure complete attachment. Finally, an electrical wire was soldered onto an electrode to supply electric potentials to the device.
 , where D is the diffusion coefficient, and t is the time between frames. Pixel intensity from raw images of the particles was also used to determine the particle size in ImageJ. The intensity threshold, about five times larger than the background, was used to measure particle diameters.
, where D is the diffusion coefficient, and t is the time between frames. Pixel intensity from raw images of the particles was also used to determine the particle size in ImageJ. The intensity threshold, about five times larger than the background, was used to measure particle diameters.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (t) = Φ0
(t) = Φ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt),
sin(ωt),![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) = qE + mg − m′g − 3πDη(
= qE + mg − m′g − 3πDη(![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) − u),
− u),![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) = d2r/dt2 of a particle of mass (m) and charge (q) as it moves through the channel with the fluid velocity (u), where g = −gẑ is the gravitational acceleration vector and
= d2r/dt2 of a particle of mass (m) and charge (q) as it moves through the channel with the fluid velocity (u), where g = −gẑ is the gravitational acceleration vector and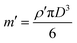
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + yŷ + zẑ into eqn (4), we obtain the following component equations:
+ yŷ + zẑ into eqn (4), we obtain the following component equations:
![[z with combining umlaut]](https://www.rsc.org/images/entities/i_char_007a_0308.gif) + 3πDηż = (m′ − m)g
+ 3πDηż = (m′ − m)g![[z with combining umlaut]](https://www.rsc.org/images/entities/i_char_007a_0308.gif) = 0 in eqn (6)–(8), we can simplify the equations to give
= 0 in eqn (6)–(8), we can simplify the equations to give
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt)
sin(ωt)



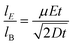
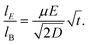
 improves the precision at which the electrophoretic mobility can be measured; measurement precision increases as μ and E increase and as the square root of the diffusion coefficient decreases. To achieve a precision within 1%, the ratio of particle displacements from electrophoresis and Brownian motion must be greater than 100.
improves the precision at which the electrophoretic mobility can be measured; measurement precision increases as μ and E increase and as the square root of the diffusion coefficient decreases. To achieve a precision within 1%, the ratio of particle displacements from electrophoresis and Brownian motion must be greater than 100.

 , indicating that the inertial response should be on the order of 50 nanoseconds for a 2 μm particle which is five orders of magnitude faster than the 1 ms period between each frame. A synchronizer triggered the camera and the function generator to image and apply electric waves simultaneously. Experimentally no phase lag is observed (Fig. 5), consistent with an inertial time constant on the order of 50 ns and predicted by the quasi-equilibrium solution. In the case of a sine wave, the phase difference between the electric field wave and particle trajectories is ¼ of a wave (Fig. 6), consistent with the solution of the quasi-equilibrium theoretical model (Fig. 2D–F). Although this may be perceived as a phase lag, when the applied electric field has the shape of a sine wave, the particle trajectories have a cosine shape, which is consistent with the particles moving the fastest when the forcing by the electric field is the strongest. For the square wave, the electric field changes abruptly, and the change in particle trajectory is immediate and just as abrupt as the change in the electric field wave. In summary, no measurable phase lag is observed.
, indicating that the inertial response should be on the order of 50 nanoseconds for a 2 μm particle which is five orders of magnitude faster than the 1 ms period between each frame. A synchronizer triggered the camera and the function generator to image and apply electric waves simultaneously. Experimentally no phase lag is observed (Fig. 5), consistent with an inertial time constant on the order of 50 ns and predicted by the quasi-equilibrium solution. In the case of a sine wave, the phase difference between the electric field wave and particle trajectories is ¼ of a wave (Fig. 6), consistent with the solution of the quasi-equilibrium theoretical model (Fig. 2D–F). Although this may be perceived as a phase lag, when the applied electric field has the shape of a sine wave, the particle trajectories have a cosine shape, which is consistent with the particles moving the fastest when the forcing by the electric field is the strongest. For the square wave, the electric field changes abruptly, and the change in particle trajectory is immediate and just as abrupt as the change in the electric field wave. In summary, no measurable phase lag is observed.






