Self-absorption correction of NEXAFS spectra for intermediate sample thicknesses applied to organo-sulfur model compounds

Abstract

Near-Edge X-ray Absorption Fine Structure (NEXAFS) spectra tend to be damped due to self-absorption effects when measured in fluorescence-yield mode in samples which are neither thin nor dilute. While established self-absorption correction methods are only valid for infinitely thick samples and partly inapplicable if the samples are too concentrated, the novel forward correction presented here is widely applicable, especially for intermediately thick and concentrated samples. Aiming towards quantitative analysis supporting the development of lithium sulfur battery materials, which are intermediately thick and not dilutable, the forward correction is applied to organo-sulfur liquid films as a proof of concept.

---

1 Introduction

Properties of materials depend mainly on the chemical state of the atoms, the crystal and the local structure. A chemical state being determined by bonding partners, the oxidation state, the conformation or other parameters results in a certain electronic configuration. Depending on the probed atom, these electronic states have discrete, characteristic transition energies. Probing the interaction of X-rays with the electrons, the measured spectrum gives insights into this electronic structure which enables the recognition of chemical properties and species. The knowledge and monitoring of these properties are important to understand macroscopic behaviours of the sample.

One commonly used method of probing unoccupied electronic states is X-ray Absorption Spectroscopy (XAS). Depending on the energy of the incident monochromatic X-ray beam, electrons from the deep atomic core shells get excited to a previously unoccupied state. The states close to the Fermi level are probed near the respective absorption edges in the Near-Edge X-ray Absorption Fine Structure (NEXAFS).¹ Since the chemical state and the binding partners of a probed atom mainly affect the electronic levels close to the Fermi level, NEXAFS is a powerful tool to observe these properties and is widely used throughout many fields such as material science,^2,3 surface science and nanotechnology,^4,5 biomedical applications,⁶ cultural heritage studies⁷ and energy device development.^8–10

Originally, the intensity of the transmitted X-ray beam was measured in relation to the incident beam intensity depending on the incident energy to find the mass attenuation coefficient¹¹ of the sample. Since this works only for thin films, measuring the Fluorescence Yield (FY) is an alternative approach.¹² The FY is the response to the excitation of electrons to an unoccupied state where an electron from another shell fills the core hole by emitting fluorescence X-rays. The intensity of this secondary radiation can be used as a measure of the photo-absorption coefficient of the material. The photo-absorption coefficient describes the probability for photo-ionisation of the element of interest for the incident X-rays. The yield for the following fluorescence process is typically constant. The signature of this spectrum can be used to identify a certain chemical species or to quantify several different species, typically by a linear combination of the respective photo-absorption coefficients.

When XAS is conducted in FY mode, the fluorescence signal varies depending on the sample thickness.¹² It resembles the photo-absorption coefficient only for infinitely thin or dilute samples. If this is not the case, the self-absorption effect damps the fluorescence signal due to the varying penetration depth of the excitation beam into the sample.^13,14 This confines the applicability of a direct linear combination fitting without an appropriate self-absorption correction.

If possible, the influence of the self-absorption effect is minimized by a manipulation of the experiment geometry towards normal incidence and grazing detection, as shown in early works on FY-XAS.^15,16 Later, Tröger et al.¹³ for Extended X-ray Absorption Fine Structure (EXAFS) and Eisebitt et al.¹⁴ for Near-Edge X-ray Absorption Fine Structure (NEXAFS) found methods how to correct for the self-absorption effect via variation of the geometry, which has been slightly modified by Carboni et al.¹⁷ The Inverse Partial Fluorescence Yield (IPFY) approach by Achkar et al.¹⁸ also has a minor angular dependence. However, having batteries or parts of them typically as samples in coin cells, the possibilities of varying the experiment geometry are limited due to the appearance of the sample. Furthermore, all of the mentioned methods^{1,12–14,17–19} use an approximation which is only valid in the limit of infinitely thick samples.

Booth and Bridges²⁰ developed a self-absorption correction of EXAFS spectra which is valid for any sample thickness and among the three algorithms implemented to the widely used ATHENA software package.²¹ However, the only algorithm which is implemented to ATHENA for NEXAFS spectra, the backward correction as proposed by Haskel,¹⁹ is only valid for infinitely thick samples and applicable for dilute samples. This leaves a gap for intermediate sample thicknesses in order of the respective element's X-ray attenuation length and highly concentrated samples. In addition, the question arises what makes a sample infinitely thin, dilute or infinitely thick in the sense of the correction of the self-absorption effect. The answers suggest which correction methods are possible and whether they are reliable with a limited uncertainty for a given experimental setup.

In energy storage devices such as rechargeable batteries, energy is transferred by changing the chemical state of involved atoms. Knowledge about the spectroscopic signature reveals the contributions of certain states to improve the understanding of ongoing processes. In preparation of operando characterization of lithium sulfur (LiS) batteries, FY-NEXAFS measurements on both organo-sulfur liquid films and LiS battery cathodes containing sulfur in different chemical states have been conducted at the sulfur K-edge in previous works.^8,22 In all of these applications, the mass deposition of sulfur is between 10 μg cm⁻² and 100 μg cm⁻² for the liquid films and 1 mg cm⁻² for cathodes. This corresponds neither to an infinitely thin sample, where the FY is not damped, nor an infinitely thick sample, so that the approximations of established correction methods are invalid. Thus, future applications of quantitative FY-NEXAFS experiments require an advanced correction for the self-absorption effect for intermediate sample thicknesses. This is necessary for the identification of chemical species and the reliability of linear combinations in order to quantify electrochemically relevant properties as the sulfur strand length or concentrations of certain species.

The presented procedure is a forward calculation which does not explicitly require tabulated data, but can be used to check for self-consistency regarding the corresponding fitting parameters, as demonstrated later. Incorporating a model spectrum may lead to a systematic error, but also facilitates a quantitative analysis. Additionally, the forward direction of correction excludes a significant increase of relative uncertainties which occurs in the backward correction for highly concentrated samples. This will be demonstrated applying the forward correction methods to the organo-sulfur model samples.

2 Theory

Irradiating a sample with thickness z_s with an incident X-ray beam of photon flux P₀ and energy E₀, hitting the sample in an angle of ϑ_i with respect to its surface, results in a detected fluorescence count rate P_f(E₀) which can be described asas it occurs in many publications in this or slightly simplified versions.^{1,12–14,16–20} Here, Ω is the solid angle covered by the detector with efficiency ε_det which has an angle of ϑ_f with the sample surface. The geometric denotation is visualized in Fig. 1. ε_f is the fluorescence yield, and μ_t is the linear absorption coefficient of the total sample, taken at the incident energy E₀ or the fluorescence energy E_f which is below the absorption edge of the element of interest. The quantity to be analysed in the measurement is the photo-absorption coefficient τ(E₀) of the element of interest, as defined by Mantler.¹¹ The derivation of eqn (1) can be found in the ESI.†

Fig. 1 Schematic depiction of the geometric denotation used in the theoretical calculations.

The fluorescence signal is practically normalized to the incoming photon flux P₀(E₀) and this ratio is further normalized to a value at an energy E₀⁺ well above the main absorption edge where the fluorescence intensity becomes approximately constant. Following the procedure described by Haskel,¹⁹ this normalized count rate N(E₀) is given by

with the relative absorption coefficients [small tau, Greek, macron](E₀) = τ(E₀)/τ(E⁺₀), γ(E₀) = μ_b(E₀)/τ(E⁺₀), γ′ = μ_b(E⁺₀)/τ(E⁺₀), β = μ_t(E_f)/τ(E⁺₀),
and the effective sample thickness
where μ_t(E₀) = τ(E₀) + μ_b(E₀) was used in order to obtain the absorption coefficient of the element of interest. The absorption coefficient μ_b therefore includes all background interaction between the photons and the electrons except for excitation of the observed shell, i.e. other shells, scattering and contributions from other atoms in the sample.

The measured fluorescence signal N(E₀) is a non-linear function of the relative photo-absorption coefficient [small tau, Greek, macron](E₀) with further dependencies on other elements in the matrix. Now, the question is which limits simplify this formula in order to know (i) in which cases one needs a self-absorption correction at all and (ii) how to correct the spectrum if needed. There are two cases where the normalized fluorescence count rate N(E₀) described in eqn (2) approximates the relative photo-absorption coefficient , namely the case of thin samples and the case of relatively heavy matrices or dilute samples where the major absorption of photons happens in the matrix.

Starting with thin samples, i.e., the exact normalized fluorescence signal can be approximated by

as shown in the ESI,† which is in the first order independent of the matrix. The difference γ(E₀) − γ′ is small, as shown later in Chapter 3, so that [small tau, Greek, macron](E₀) − 1 dominates the numerator in the linear order. Allowing relative deviations of 1% and assuming maximal relative absorption coefficients of [small tau, Greek, macron](E₀) ≤ 5, the approximation N(E₀) ≈ [small tau, Greek, macron](E₀) holds for t ≤ 0.005.

The other case of relatively heavy matrices is meant such that the relative absorption coefficients originating from the matrix, [small beta, Greek, macron], γ(E₀) and γ′ are large in the sense of γ(E₀)+[small beta, Greek, macron] ≈ γ′+[small beta, Greek, macron] = ζ ≫ 1, which yields

as shown in the ESI,† which is in the first order independent of the effective sample thickness t. Assuming maximal relative absorption coefficients of [small tau, Greek, macron](E₀) ≤ 5 and allowing relative deviations of 1%, the approximation N(E₀) ≈ [small tau, Greek, macron](E₀) holds for γ(E₀) + [small beta, Greek, macron] ≈ γ′ + [small beta, Greek, macron] = ζ ≥ 400.

There is one more way of simplifying eqn (2). For thick samples t ≫ 1, the last factor can be sized up to

such that the relative deviation remains under 1% for t > ln(101) ≈ 4.62 if the whole expression is larger than 1, i.e. [small tau, Greek, macron](E₀) + γ(E₀) ≥ 1 + γ′ ⇔ [small tau, Greek, macron](E₀) ≥ 1 + γ′ − γ(E₀) ≈ 1 in regions of resonant fluorescence. In this case, the self-absorption effect can analytically be corrected by solving the approximated version of eqn (2) to findNote that if the neglected factor is smaller than 1, i.e. [small tau, Greek, macron](E₀) + γ(E₀) < 1 + γ′ ⇔ [small tau, Greek, macron](E₀) < 1 + γ′ − γ(E₀) ≈ 1 in regions of low absorption, the relative deviation can be higher. Eqn (5) is an analytical backward correction to find the relative photo-absorption coefficient directly from the experimental spectrum, as proposed by Haskel¹⁹ already. However, relative uncertainties in this correction can be so large that it is impossible to analyse the result if the matrix is not heavy enough, i.e. the sample is too highly concentrated. This is also demonstrated later with a highly increased variance of measurement points using this correction method in the experimental results.

For clarification, assuming a concentrated sample with certain matrix contributions of γ(E₀) + [small beta, Greek, macron] ≈ γ′ + [small beta, Greek, macron] = ζ, the correction in eqn (5) simplifies to so that the uncertainty becomes . Thus, the relative uncertainty does not only increase with the fraction , which denotes the strength of the damping and can be large in the case of concentrated, thick samples, but also with 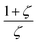which increases faster than 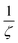being another particularly large factor for highly concentrated samples (ζ ≪ 1). This makes the backward correction inapplicable for concentrated and thick samples due to highly increased uncertainties and can favour a forward calculation even though the backward correction is theoretically possible within small deviations.

2.1 Guideline for handling of self-absorption correction

A summarized guideline for handling of self-absorption correction can be found in Table 1 with the assumption of [small tau, Greek, macron](E₀) ≤ 5 which is valid in the case of organo-sulfur samples. For thin samples with effective sample thickness and samples in low concentrations or heavy matrices with relative absorption coefficient contributions γ(E₀) + [small beta, Greek, macron] ≈ γ′ + [small beta, Greek, macron] = ζ ≥ 400, the experimental normalized spectrum N(E₀) approximates the relative absorption coefficient within 1% according to eqn (3) and (4), respectively. Thick samples t ≥ 5 allow for an approximated backward correction following eqn (5) within deviations of 1%, which might be inapplicable though due to potentially much higher uncertainties. All other configurations with effective sample thickness 0.005 < t < 5 and non-heavy matrix contribution ζ < 400, i.e. intermediately thick samples, demand the exact forward calculation during the spectrum deconvolution routine for achieving results which do not exceed relative deviations of 1% or potentially highly increased uncertainties.

Table 1 Guideline for handling of self-absorption correction: necessity of exact forward calculation, possibility of backward correction and approximations with relative deviations of the experimental normalized spectrum N(E₀) from the relative absorption coefficient for different effective sample thicknesses and relative absorption coefficient contributions of the matrix ζ = γ′ + [small beta, Greek, macron] ≈ γ(E₀) + [small beta, Greek, macron] with the assumption of [small tau, Greek, macron](E₀) ≤ 5

		Relative absorption coefficient contribution of the matrix
		ζ = γ′ + [small beta, Greek, macron] ≈ γ(E0) + [small beta, Greek, macron]
		ζ < 400	ζ ≥ 400
Effective sample thickness	t ≤ 0.005	N(E0) ≈ [small tau, Greek, macron](E0) within 1% (eqn (3))	N(E0) ≈ [small tau, Greek, macron](E0) well within 1% (eqn (3) and (4))
	0.005 < t < 5	Exact forward calculation necessary (eqn (2))	N(E0) ≈ [small tau, Greek, macron](E0) within 1% (eqn (4))
	t ≥ 5	Appr. backward correction possible within 1% (eqn (5))

---

Fig. 2 visualizes the self-absorption effect on a modeled NEXAFS spectrum with only one resonance at E₀ = 2472 eV for different relative sample thicknesses t and matrix contributions ζ = γ′ + [small beta, Greek, macron] ≈ γ(E₀) + [small beta, Greek, macron]. For thin samples with t = 0.01, the self-absorption effect is negligible, independent of the matrix. At t = 100, the sample satisfies the condition of infinitely thick samples which is also represented by covering the grey lines for the respective values of ζ. Intermediate sample thicknesses represented by t = 1 show a complex behaviour where the influence of ζ also depends on the actual thickness. In dilute samples with large ζ, the self-absorption effect is negligible even for thick samples, whereas concentrated samples experience a strong damping depending on the sample thickness. Note that the damping in thick samples is especially determined by the matrix, so that a quantitative measurement might be sensitive to ζ.

Fig. 2 Self-absorption simulation of a modeled NEXAFS spectrum with only one resonance at E₀ = 2472 eV for different relative thicknesses t and matrix contributions ζ = γ′ + [small beta, Greek, macron] ≈ γ(E₀) + [small beta, Greek, macron]. For t = 0.01, the self-absorption effect is negligible, for t = 100, we are in the limit of infinitely thick samples which is also represented by the grey lines for the respective values of ζ throughout all plots for comparison. Intermediate sample thicknesses represented by t = 1 show a complex behaviour where the influence of ζ also depends on the actual thickness. Concentrated samples with intermediate thicknesses are significantly self-absorption damped, but do not fulfil the requirements of infinitely thick samples where established correction methods can be applied.

3 Experimental setup and materials

3.1 Sample preparation and NEXAFS measurements

As in previous investigations,^8,22 NEXAFS spectra have been recorded at the Four Crystal Monochromator (FCM) beamline in the PTB laboratory at BESSY II using the Si (111) crystals.²³ The experimental setup is optimized for X-ray spectrometric measurements on batteries,⁹ therefore the samples were prepared in CR2032 coin cell housings to fit in the previously used sample holder. This procedure also allows for measurements on liquid samples in a UHV setting. The exciting X-ray beam reaches the liquid samples through a 12.7 μm thick Kapton window covering a hole in the positive case of the coin cell housing with a diameter of 2 mm. The NEXAFS signal was detected in fluorescence mode using an energy-dispersive silicon drift detector (SDD) in a 90° geometry relative to the incident X-ray beam, where the angle between the probe and the respective incoming and outgoing radiation is 45° (see Fig. 3a). The measurements were done at the sulfur K-edge with the typical S–S peak located at an incident X-ray energy of 2472.1 eV. Since the cells were also used for transmission measurements, they had a second hole in the negative case of the coin cell housing, which was also covered by a Kapton window. The cells were assembled in an Argon glovebox, so that the material between the liquid films moistening the windows is Argon gas (see Fig. 4). Transmission spectra were recorded in normal incidence geometry using a photo diode (see Fig. 3b). All measurements presented here were conducted with thin samples where the liquids just moistened the windows in a thin film. The performance of multiple measurements verified that the results are reproducible and there is no significant beam damage.

Fig. 3 Schematic depiction of the experimental setup and the geometric denotation in top view for (a) fluorescence and (b) transmission experiments.

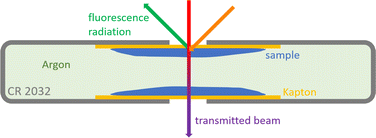Fig. 4 Schematic depiction of the prepared coin cell sample in top view with beam paths sketched for fluorescence and transmission measurements.

Note that the results already reported in²² were measured in a 60° geometry and included thick samples where the coin cells were fully filled with the liquids. Thus, the backward correction following Haskel's method¹⁹ can be applied for these measurements and is shown here for comparison. Due to slightly changed beamline settings, the energy axes from the different measurement campaigns differ by 0.04 eV. The energy axis of the latest measurements has therefore been shifted to be aligned with the previously reported²² energy positions.

Three organo-sulfur liquids shown in Fig. 5 have been used to assess the quality of the forward self-absorption correction. 97.5% dimethyl trisulfide (DMTS) was purchased from Thermo Scientific, 98% dipropyl disulfide (DPDS) and 97% dipropyl sulfide (DPS) were purchased from Sigma-Aldrich Chemie GmbH. All chemicals have not been diluted.

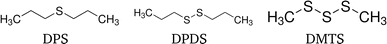Fig. 5 Structural formulae of the three organo-sulfur liquids dipropyl sulfide (DPS), dipropyl disulfide (DPDS) and dimethyl trisulfide (DMTS).

3.2 Realisation of the correction

The mathematical basis in terms of a linearly combined spectrum of a sample with different constituents is always given by the photo-absorption coefficient τ(E₀) which is imaged in the transmission spectra but gets distorted when measured in fluorescence mode. Thus, in an application where different species of the element of interest are to be quantified in an unknown sample which can only be measured in fluorescence mode (which is the case for light elements and especially for sulfur battery applications), it is necessary to be able to calculate the fluorescence spectrum from a linearly combined photo-absorption coefficient.

The presented correction is a forward calculation that simulates the normalized detected fluorescence intensity N(E₀) in dependence of the relative photo-absorption coefficient [small tau, Greek, macron](E₀), based on eqn (2). [small tau, Greek, macron](E₀) can either be modeled as described in the following section, or taken as a previously experimentally or theoretically observed spectrum. The fluorescence signal is a non-linear function of the photo-absorption coefficient. Other dependencies are the relative detector efficiency, which we approximate as 1 over the narrow near-edge energy range, and contributions to the interaction of the photons with the sample by other shells and atoms (bulk, index b). If the exact stoichiometry of the sample is known, these contributions can be taken from tabulated values. Since this is not always the case in many applications including the analysis of various battery materials, they can be approximated by empirical relations.

In the following results and calculations, the starting point is 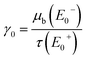, i.e. the ratio of the bulk X-ray attenuation coefficient μ_b at the lowest measured NEXAFS energy below the edge of interest E⁻₀ and the photo-absorption coefficient τ at the highest measured NEXAFS energy above the edge of interest E⁺₀. Fixing E₀⁻ = 2467 eV and E⁺₀ = 2490 eV, tabulated values²⁴ for C and S suggest fixed values for β and γ′ given by and . The energy-dependent γ(E₀) is approximated as a linear function determined by γ₀ and γ′.

Measuring the sample in transmission mode, μ_b can directly be evaluated at E⁻₀. Its decrease until E⁺₀ fixes [small tau, Greek, macron](E⁺₀) such that one finds γ₀. If the correction is used in the inverse problem simulating the forward calculation in order to recover the fluorescence intensity for a measured or simulated self-absorption free spectrum, γ₀ can be passed as a fit parameter.

The effective thickness t can not only be determined by transmission measurements, but also using reference-free X-ray Fluorescence analysis (XRF).²⁵ When t is not known, it can also be passed as a fit parameter.

3.3 Model spectrum and fitting procedure

When the self-absorption correction is used in a fitting routine where the self-absorption free spectrum is not known a priori, a model spectrum is used which consists of a certain amount of normalized Voigt profiles (mostly two) summed to a simple edge function.^1,26 The parameters describing this model spectrum are the Voigt profiles, the properties of the edge jump as well as the relative peak intensities. The Voigt profiles consist of Lorentzian and Gaussian contributions corresponding to the natural line broadening due to the finite lifetime of the excited state and the experimental resolution, respectively. Since the bulk contributions and effective thicknesses are typically not known in this scenario either, γ₀ and t remain as additional fit parameters during the correction routine.

In the fitting routine, a model spectrum or a linear combination of several spectra represents the self-absorption corrected, normalized NEXAFS spectrum (which is equivalent to the physical quantity of the relative photo-absorption coefficient [small tau, Greek, macron](E₀)). The model spectrum is either an initially known spectrum from transmission experiments or theoretical calculations, or a parametrized spectrum as described above.

The presented forward self-absorption calculation is applied to the model spectrum and fitted to resemble the experimental fluorescence data which can be taken at samples with different thicknesses and concentrations. Note that both the properties of the spectra and the experimental parameters are fitted simultaneously. The fit result can be determined more precisely when there exist different measurements with exactly one varying parameter. More specifically, measuring fluorescence NEXAFS spectra of the same molecule with different sample thicknesses, the same transmission spectrum should resemble both spectra for exactly the same set of parameters except for a different effective sample thickness. This method increases the significance of the recovery method of the unknown self-absorption free spectrum.

4 Results

As a proof of concept, the NEXAFS spectra of dipropyl sulfide (DPS), dipropyl disulfide (DPDS) and dimethyl trisulfide (DMTS) were measured both in transmission and in fluorescence modes. Due to the experimental setup, the transmission spectra needed to be corrected for the contributions of the Kapton window and the Argon from the glovebox, but are self-absorption free. However, the attenuation in Kapton dominates the total X-ray attenuation so that the absolute scale of the resulting sulfur transmission has an increased uncertainty. From the transmission spectra, the mass deposition of the three samples was determined to be in the order of 10 to100 μg cm⁻² corresponding to thicknesses of just below 1 μm or effective thicknesses of around 0.1. According to Table 1, this identifies the samples as intermediately thick such that the forward correction is needed. The contributions of other shells and atoms to the X-ray attenuation can also be determined in the transmission mode, hence the forward calculation could be done without any further assumptions.

For the fluorescence mode, not only the NEXAFS spectra were taken, but the calibrated instrumentation of PTB allowed for an additional reference-free XRF quantification of the sulfur content. The sulfur mass depositions and the liquid film thicknesses obtained by the transmission measurements could be confirmed within deviations up to 25%, respectively, which is a confirmation of the self-consistency of this method. Reference-free XRF might also serve as a good alternative when the properties of the sample do not allow transmission measurements. The exact mass depositions and sample thicknesses from both transmission and fluorescence measurements can be found in the ESI.† Note that only one of the sample films contributed to the fluorescence signal, whereas the transmitted X-ray beam was attenuated by both films. An uneven thickness distribution over the two sample films may also contribute to the deviation of the measured thicknesses.

Fig. 6a shows the measured transmission (dots) and fluorescence (pluses) signals, as well as the forward calculated fluorescence spectra (crosses) in between. Note that the experimental data from the transmission measurement are calculated from the transmitted X-ray intensity and therefore represents an assumed fluorescence spectrum without self-absorption, even though this is not physically realisable. This self-absorption free spectrum allows to assess the quality of the forward calculation and suggests that the structure of the spectra significantly changes due to the self-absorption effect. Looking at the residues in Fig. 6b, the calculation appears to recover the correct peak height ratios in the damped fluorescence spectra which is especially valuable when it comes to quantification of different sulfur species in the further applications of this method. Remarkably, DMTS experiences the strongest damping since the molar ratio of sulfur is the highest in this molecule leading to the highest effective thickness. The calculation does not fully recover the measured spectrum, but it does recover its shape without any residual structure. The only deviation that remains is an almost constant factor which can be interpreted as a constant deviation in the edge jump height. Thus, this correction method fulfils all necessary requirements to quantify concentrations of different chemical species.

Fig. 6 (a) NEXAFS spectra of dipropyl sulfide (DPS, blue), dipropyl disulfide (DPDS, orange) and dimethyl trisulfide (DMTS, green). The self-absorption free (undamped) spectra, directly calculated from transmission measurements, are depicted with dots, the measured fluorescence spectra are marked with pluses, and the crosses in between are the forward calculated fluorescence spectra predicted using transmission and tabulated data. (b) The residues for the measured transmission and the predicted fluorescence spectra relative to the measured fluorescence spectra visualize that the forward calculation makes up for the damping of the NEXAFS signal and especially recovers the peak height ratios in the damped fluorescence spectra. The full data over the whole energy axis are shown in the ESI.†

Using the self-absorption correction based on forward calculation introduced above, the NEXAFS spectra of model compounds from ref. 22 can be fitted again with a detailed consideration of the self-absorption effect. Here, NEXAFS spectra have been taken in fluorescence mode with a 60° geometry for a thick sample and a thin liquid film which only moistened the window. The results are shown in Fig. 7 for DPDS together with the full spectra, and in Fig. 8 for DPS and DMTS just for the region of resonance. The plots feature the experimental data, the self-absorption corrected spectrum, the corresponding non-corrected spectra and, for comparison, the backward corrected spectra following Haskel's method¹⁹ as well as the self-absorption free spectrum taken from the transmission measurements. By varying the effective sample thickness t, the experimental data for both thin and thick samples can be described with the same self-absorption corrected spectrum using fixed matrix contributions to the relative absorption coefficient.

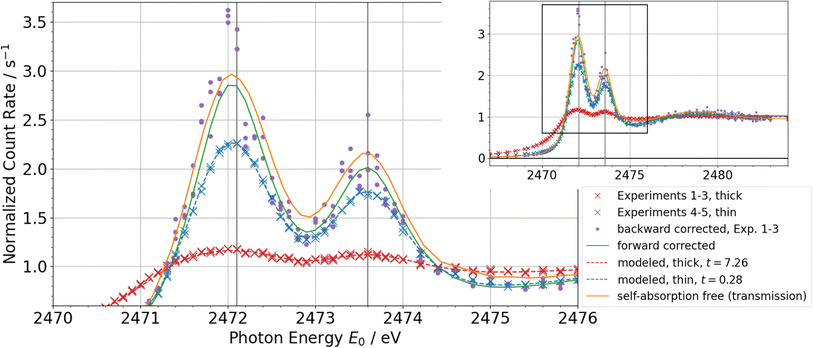Fig. 7 NEXAFS spectra of dipropyl disulfide (DPDS). The self-absorption corrected model spectrum describes the experimental spectra of thin and thick samples from ref. 22 with varying the effective sample thickness t. The variance of the backward corrected spectra using Haskel's FLUO code¹⁹ are significantly larger than relative uncertainties in the experiment. The self-absorption free calculation from the transmission measurement and the forward corrected spectrum are in good agreement.

Fig. 8 NEXAFS spectra of (a) dipropyl sulfide (DPS) and (b) dimethyl trisulfide (DMTS) in the same depiction as in Fig. 7. Due to the smaller molar ratio of sulfur in DPS, the effective sample thickness is smaller compared to DPDS which increases the quality of both the recovered self-absorption free spectrum and the backward correction by Haskel.¹⁹ DMTS has a much larger mass density and molar ratio of sulfur and thus a large effective sample thickness. This damps the resonances of the fluorescence signal in thick samples strongly and thus makes the backward correction less reliable. The forward correction agrees reasonably well with the self-absorption free spectrum predicted using the transmission measurement.

Focusing on DPDS for a detailed discussion, the effective sample thickness of the thick sample was fitted to t ≈ 7 which is already in the limit of infinitely thick samples. As shown in Fig. 2, measurements on infinitely thick samples are sensitive to and depend only on the matrix contribution ζ. Subsequently, this information fixes the effective sample thickness t of the intermediately thick samples to values of t ≈ 0.28. This value is almost two orders of magnitude higher than the infinitely thin sample limit, which can also be seen in the clear deviation from the self-absorption corrected spectrum.

One significant feature checking for the self-consistency of this correction method is the fact that all experimental data cross the N(E₀) = 1 axis at the same energies. This is in line with eqn (2) where N(E₀) ≈ 1 if and only if [small tau, Greek, macron](E₀) ≈ 1 which has to be at the same energies for the same material. Additionally, the matrix contributions predicted by the fit are in line with both the value from the transmission measurements and the theoretical assumption taking tabulated values into account.

The self-absorption free spectrum which is shown for comparison is measured in transmission mode. However, the main attenuation happens in the Kapton windows and the Argon inside the cell, thus the uncertainty of the absolute scale of the spectrum is relatively high. A deviation of 0.1 in the normalized NEXAFS spectrum corresponds to a thickness uncertainty of the Kapton film of approximately 1%. The uncertainty of both the corrected and the self-absorption free spectra makes it difficult to compare their absolute scales. However, the energy positions as well as the relative peak areas and shapes agree well within the uncertainties.

Since the thick samples are beyond the limit of infinitely thick samples, the backward correction following Haskel's FLUO code¹⁹ can be applied. However, there is no need to use tabulated values in this case since the optimization with forward calculation already gives the optimal set of necessary parameters fitting to the calculated spectrum in order to compare the different methods. The purple-coloured dots, representing the backward corrected spectra for each of the thick sample measurements, roughly resemble the self-absorption corrected spectrum. However, the variance of these data points is significantly larger than the relative uncertainty of the actually measured data because of the strong non-linearity and therefore a significant increase of uncertainty in backward correction for thick and highly concentrated samples. This makes the backward correction not applicable for the shown experiments. A further advantage of the forward correction method is the fit result being a full modeled spectrum function rather than a conglomeration of single corrected measurement points. This makes the further analysis more straight forward and is subsequently more suitable for quantitative conclusions, especially when there is a good model function for the spectrum or a database of theoretic spectra.

The equivalent spectra of dipropyl sulfide (DPS) and dimethyl trisulfide (DMTS) are shown in Fig. 8. Due to the smaller molar and weight ratio of sulfur in DPS, the sulfur mass deposition and thus the effective sample thickness is smaller compared to DPDS which increases the quality of both the recovered self-absorption corrected spectrum and the backward correction by Haskel.¹⁹ DMTS has a much larger mass density and molar ratio of sulfur and thus a more than doubled sulfur mass deposition leading to a significantly larger effective sample thickness than the DPDS sample. This damps the resonances of the fluorescence signal in thick samples strongly and thus makes the backward correction less reliable, which is also visualised by the strongly increasing variance of the backward corrected spectrum. The forward correction agrees reasonably well with the self-absorption free spectrum employed from the transmission measurement. Here, the shape of the spectrum is not fully recovered because the model spectrum can not resemble any arbitrary shape. Furthermore, the thinner samples are close to the limit of infinitely thick samples so that they do not differ as clearly as for the samples with lower sulfur content. For a potential quantification of sulfur species, it might be helpful to utilize a self-absorption free spectrum, e.g. from a transmission measurement or a theoretical calculation, in order to increase the significance of the fit in such a case.

In the application of the chemical speciation of an element of interest, the key fitting parameters are the peak areas which are mainly dependent on the correct determination of the sample thickness. In the fitting routine, the energy positions, the peak heights and the sample thicknesses have the most robust convergence behaviour, especially with samples of significantly different thicknesses and even with conservative parameter limitations. The width contributions of Gaussian and Lorentzian in the Voigt profiles are mainly anti-correlated and have a minor impact on the peak shape. Generally, the widths and thus the peak areas can be determined robustly which makes the presented self-absorption correction a promising tool for speciation applications. The number of different chemical species in one sample that can be quantified depends on how distinct their characteristic peak positions are. In the case of strong damping due to the self-absorption effect, e.g. for DMTS, the determination of the peak widths becomes less significant. Hence, some stricter limitations of these parameters were applied to get a physically reasonable result. In this case, the resulting peak ratios would have an increased uncertainty.

In some applications, e.g. battery materials, there is neither the possibility to examine differently thick samples, i.e. intermediate and infinitely thick sample thicknesses, nor to perform transmission experiments. Since the matrix contributions to the absorption coefficient and the effective sample thickness t have inversely correlated influence regarding the self-absorption effect, this might lead to the need of fixing one of the parameters to a certain pre-calculated value. If the stoichiometry of the sample is known, the impact of the bulk can be found from tabulated values conveniently. Sometimes, the thickness or the mass deposition of the sample is also known, e.g. by XRF analysis, to calculate the effective sample thickness t. Better knowledge of these parameters might optimize the fit so that the self-absorption corrected spectrum resembles the actual relative photo-absorption coefficient .

The self-absorption corrected spectra in Fig. 7 and 8, however, are free fits without using any a priori parameters which give reasonable values for γ₀ and t. These results were confirmed regarding self-consistency by stoichiometric calculations and determination of the actual sample thicknesses. This justifies an application of the presented method for self-absorption correction of NEXAFS spectra of intermediately thick samples which can not be measured in transmission mode. The application of this method promises the enabling of quantitative chemical speciation as well as the quantification of complex material properties such as the sulfur strand length of sulfur cathodic materials and working batteries.⁸

5 Conclusion

We have presented a self-absorption correction method for NEXAFS spectra which is applicable to samples with intermediate thickness. In a proof of concept, using self-absorption free data measured in transmission mode, we predicted NEXAFS spectra including self-absorption (fluorescence mode). The predicted spectra are in good agreement with spectra independently acquired in fluorescence mode. The determined fitting parameters such as the sulfur mass deposition were confirmed by transmission and reference-free XRF measurements. This proves the consistency of the theoretical assumptions and the concept of the forward correction. The correction method has then been successfully applied to a set of fluorescence mode measurements of samples with different thicknesses to recover the self-absorption corrected spectrum without employing transmission data. A remarkable finding is that the consideration of thick samples increases the quality of the fit result because of the damping being sensitive to the matrix contributions in these samples. Compared to established correction methods, the presented correction is not limited to infinitely thick samples. Furthermore, it excels with decreased uncertainty which makes the correction of strongly damped spectra more reliable. This enables future applications to intermediately thick samples which can not be measured in transmission mode, e.g. battery materials. The described method is promising to enable a quantitative chemical speciation as well as the quantification of complex material properties such as sulfur strand lengths using fluorescence mode NEXAFS spectrometry.

Data availability

Data for this article, including all presented experimental NEXAFS spectra, are available in the Open Access Repository of the Physikalisch-Technische Bundesanstalt (PTB-OAR) at https://doi.org/10.7795/720.20241009.

Author contributions

KS developed the theoretical section, implemented the correction method and performed the data analysis. KS and MM developed the concept, prepared the samples and measured NEXAFS spectra. MM, MW and MS designed the full project and all authors participated in writing.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We acknowledge funding by the German Research Foundation (DFG) through the Priority Programme “Polymer-based Batteries” (SPP 2248) under the projects CH 2376/2-1, MU 4632/1-1 and WA 1687/12-1.

References

1. J. Stöhr, NEXAFS Spectroscopy, Springer Science & Business Media, 2013, vol. 25.
2. J. Evans, X-Ray Absorption Spectroscopy for the Chemical and Materials Sciences, John Wiley & Sons, 2018.
3. C. S. Schnohr and M. C. Ridgway, X-Ray Absorption Spectroscopy of Semiconductors, Springer, 2015.
4. A. Nefedov and C. Wöll, in Surface Science Techniques, Springer, 2013, pp. 277–303.
5. P. Guttmann and C. Bittencourt, Beilstein J. Nanotechnol., 2015, 6, 595–604.
6. G. G. B. de Souza and J. C. Gonzalez, Radiation in Bioanalysis: Spectroscopic Techniques and Theoretical Methods, 2019, pp. 287–312.
7. F. Farges and M. Cotte, X-Ray Absorption and X-Ray Emission Spectroscopy: Theory and Applications, 2016, pp. 609–636.
8. R. Matsidik, K. Skudler, S. de Kock, A. Seifert, M. Müller, M. Walter, S. Choudhury and M. Sommer, ACS Appl. Energy Mater., 2023, 6, 9466–9474.
9. C. Zech, P. Hönicke, Y. Kayser, S. Risse, O. Grätz, M. Stamm and B. Beckhoff, J. Mater. Chem. A, 2021, 9, 10231–10239.
10. F. Hausen, N. Scheer, B. Ying and K. Kleiner, Electrochem. Sci. Adv., 2023, e2300017.
11. M. Mantler, Handbook of Practical X-Ray Fluorescence Analysis, Springer Science & Business Media, 2007, pp. 309–327.
12. J. Jaklevic, J. Kirby, M. Klein, A. Robertson, G. Brown and P. Eisenberger, Solid State Commun., 1977, 23, 679–682.
13. L. Tröger, D. Arvanitis, K. Baberschke, H. Michaelis, U. Grimm and E. Zschech, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 3283–3289.
14. S. Eisebitt, T. Böske, J.-E. Rubensson and W. Eberhardt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 14103–14109.
15. Y. Suzuki, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 3393–3395.
16. D. Pease, D. Brewe, Z. Tan, J. Budnick and C. Law, Phys. Lett. A, 1989, 138, 230–234.
17. R. Carboni, S. Giovannini, G. Antonioli and F. Boscherini, Phys. Scr., 2005, 2005, 986.
18. A. J. Achkar, T. Z. Regier, H. Wadati, Y.-J. Kim, H. Zhang and D. G. Hawthorn, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 081106.
19. D. Haskel, Computer program and documentation, available from, https://www.aps.anl.gov/xfd/people/haskel/fluo.html, accessed January 4, 2009, 1999.
20. C. Booth and F. Bridges, Phys. Scr., 2005, 2005, 202.
21. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
22. S. de Kock, K. Skudler, R. Matsidik, M. Sommer, M. Müller and M. Walter, Phys. Chem. Chem. Phys., 2023, 25, 20395–20404.
23. M. Krumrey, J. Synchrotron Radiat., 1998, 5, 6–9.
24. T. Schoonjans, A. Brunetti, B. Golosio, M. S. Del Rio, V. A. Solé, C. Ferrero and L. Vincze, Spectrochim. Acta, Part B, 2011, 66, 776–784.
25. B. Beckhoff, J. Anal. At. Spectrom., 2008, 23, 845–853.
26. L. G. Parratt, Rev. Mod. Phys., 1959, 31, 616–645.

---

Footnote

† Electronic supplementary information (ESI) available: Theoretical calculations, determined mass depositions and sample thicknesses, full spectra. See DOI: https://doi.org/10.1039/d4ja00232f

---