 Open Access Article
Open Access ArticleStatistical behaviour of laser-induced plasma and its complementary characteristic signals†
Jakub
Buday
 *ab,
Daniel
Holub
*ab,
Daniel
Holub
 ab,
Pavel
Pořízka
ab and
Jozef
Kaiser
ab
ab,
Pavel
Pořízka
ab and
Jozef
Kaiser
ab
aFaculty of Mechanical Engineering, Brno University of Technology, Technická 2896/2, Brno, Czech Republic. E-mail: buday@vutbr.cz
bCEITEC BUT, Central European Institute of Technology, Brno University of Technology, Purkyňova 123, Brno 612 00, Czech Republic
First published on 4th September 2024
Abstract
In this work, we present a study aimed at the statistical distribution of characteristic signals of laser-induced plasmas. This work mainly focuses on observing statistical distribution for repetitive measurement of spectra, plasma plume imaging, and sound intensity. These were captured by using various laser irradiances, spanning between 1.72 and 6.25 GW cm−2 for a 266 nm laser. Their distributions were fitted by Gaussian, generalized extreme value (GEV), and Burr distributions, as typical representation models used in LIBS. These were compared using the Kolmogorov–Smirnov (KS) test by its null hypothesis on whether these models are suitable or fail to describe the statistical distribution of the data. The behavior of the data distribution has shown a certain connection to the plasma plume temperature. This was observed for all the used ablation energies. Performances of the statistical models were further compared in the outlier filtering process, where the relative standard deviation of the filtered data was observed. The results presented in this work suggest that an appropriate selection of a statistical model for the data representation can lead to an improvement in the LIBS performance.
Introduction
In laser-induced breakdown spectroscopy (LIBS), a laser pulse of high energy fluence is focused on a sample, vaporizing a small portion of it and creating a luminous microplasma. By detecting the characteristic emission radiation of the generated laser-induced plasma (LIP), the sample's elemental composition can be determined.1For the past years, this method has been used in various fields;2e.g., biology,3 geology,4 alloy analysis,5 forensic applications,6,7etc. However, this method suffers from certain disadvantages, i.e., pulse-to-pulse fluctuation of the spectral signal or relatively small sensitivity limits.8,9 One of the main contributors to these limitations is the nature of laser–matter interaction and consequent LIP expansion. The ablation process itself is comprised of several complex processes, where each of them is connected to certain aspects of the LIBS mechanisms, or sample properties. To minimize these disadvantages, various complementary methods are being added to the experiment. This is done to bring more insight into the complex processes of the ablation, and possibly to improve certain aspects of the LIBS analysis.
An example of these techniques is direct plasma plume imaging or sound measurement systems. The direct imaging method is generally used to analyze temporal and spatial morphological properties of the plasma plume.10–12 Moreover, a spatial distribution of specific atoms, ions, or molecules of interest can be observed when imaging specific ranges of the spectrum.13–16 It is also possible to observe their spatial distribution dependence on the experimental parameters, such as laser focus,17,18 wavelength,19,20 energy,21 or various ambient properties.22
A shock wave is generated during the ablation process, expanding into the ambient atmosphere with a certain energy. This can be observed through shadowgraphs23 or sound detection.24 Several studies were carried out on sound signals in LIBS. It has been shown that there is a certain relation between the mass of the ablated material and the intensity of the generated shock wave.25,26 Its expansion energy is dependent on several experimental conditions, such as the focus of the laser beam,27 and laser properties.28 The intensity of the sound wave can also be used in combination with the LIBS spectra,29 where a relation between the LIBS spectra and the sound intensity has been observed.27 It may even lead to partial elimination of the matrix effect.24
Both techniques are used to improve the analytical performance of LIBS. For this, the main assumption is that the complementary signals show a high correlation with the spectral signal. To decrease the pulse-to-pulse signal fluctuation of LIBS, there is a possibility to implement image information in the correction process.30,31 This can lead to a decrease in the relative standard deviation for the spectra. One of the problems in LIBS is also the matrix effect, which leads to different spectral signals of elements with the same concentration contained in different samples or matrices. This effect can be minimized by using a plasma-image-assisted method for spectra correction.32
In general, a certain signal is used for the standardization of another signal.33 This is a common approach in the case of using total spectral intensity to standardize a specific spectral line, the signal of a major element for the standardization signal of a minor element,34 or the complementary signals as mentioned above. The purpose is to decrease the RSD of the observed signal and to improve the precision of the measurement.35 In general, one signal can be used for the standardization of another one if it bears a high level of correlation.36 This is mostly fulfilled for the spectral signal, but in the case of complementary signals, this may not be true in certain instances.
With the high correlation, there is also an assumption that these data share the same statistical distribution, which is generally considered to be Gaussian. This is however not always true since the data can exhibit tailing in their distribution. In this case, other statistical models can be used for the data representation, such as generalized extreme value distribution (GEVD),37–39 Weibull,40 Burr,41 or other models. Therefore, in certain instances, the data do not show major similarities in their statistical distribution. Subsequently, their correlation is poor and cannot be used in their mutual standardization. To determine the goodness of these distributions concerning the measured data, the Kolmogorov–Smirnov (KS) test is performed.40,42
This work focuses on studying the statistical distribution of various data originating from the LIP, be it characteristic spectroscopy signals, plasma plume properties, or sound intensity under various laser irradiances. Two datasets of 400 laser shots (presented here) and 900 laser shots (results in the Supplementary sections) were analyzed. Changes in the laser irradiance led to non-linear changes in the plasma plume temperature, which affected the statistical distribution of the individual data. Here, we observed the validity of three statistical models for the data description, Gaussian, GEV, and Burr distribution. These models were picked based on previous experience37 and the accurate capabilities of the Burr model for both symmetrical and asymmetrical data.43 However, there are dozens of possible models that could be used for this purpose. Here we focused only on these three, as a representative of general assumption (Gaussian), previously used on the LIBS data (GEVD) and more universal model (Burr). Their goodness was determined by the null hypothesis derived from the KS test. The distribution of selected data together with the temperature of the plasma plume was observed under different laser irradiances used for the ablation. Changes in the statistical distribution concerning the laser irradiance and the plasma plume temperature can be utilized for example in outlier filtering. Here relative standard deviation (RSD) concerning filtering based on the selected distribution was observed. It has been found that the commonly used Gaussian model does not always provide a good representation of the data, and other models can be used to achieve more accurate results, be it in the data representation or subsequential data handling.
Instrumentation and methods
Instrumentation
A specialized tabletop system was used for the experiments, allowing the possibility of measuring all the data simultaneously; i.e., LIBS spectra, images of the LIP plume, and the sound intensity of the shock wave. The body of the chamber system has several ports for a sample view, laser focusing, and data collection components. The sample was placed on a 3-axis motorized stage with 2 μm movement resolution. An ablation Nd:YAG laser (266 nm, 10 ns, 6 mm diameter, 50 Hz) was guided using a series of laser line mirrors and focused on the sample with a fused silica triplet (50 mm focal length) resulting in a 60 μm laser spot. Radiation of the plasma plume was collected with a collimator (38.5 mm focal length) and transmitted with an optical fiber (400 μm core diameter) to a Czerny–Turner spectrometer (245–407 nm range, 0.04 nm resolution). The collection of the LIBS spectra was set to 1 μs after the ablation for 50 μs, as well as for the plasma plume imaging. Images of the plasma plume and sound signals of the ablation were collected with the characteristic LIBS spectra. As for the sound, we analyzed the amplitude domain of the shock wave, more specifically its first peak, representing the shock front of the generated shock wave. Since this information is connected to the ablation of a sample, it brings relevance to studying this phenomenon.23 Detailed information about the setup for the complementary signals and their respective analysis can be found in our previous study.36Methods
 | (1) |
 | (2) |
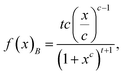 | (3) |
| D = max|F0(x) − Fn(x)|, | (4) |
 , where n is the number of measurements. In our case, the threshold value for the null hypothesis is 0.068 for 400 measurements. Hence, if the KS test for a specific statistical distribution results in a value higher than the calculated threshold, the statistical distribution will be considered as not ideal for the data representation. On the other hand, a lower value means the goodness of the distribution for the data, while the lower the value D is, the better the fit.46
, where n is the number of measurements. In our case, the threshold value for the null hypothesis is 0.068 for 400 measurements. Hence, if the KS test for a specific statistical distribution results in a value higher than the calculated threshold, the statistical distribution will be considered as not ideal for the data representation. On the other hand, a lower value means the goodness of the distribution for the data, while the lower the value D is, the better the fit.46
| Fe | ||
|---|---|---|
| Wavelength (nm) | E k (eV) | A kl × 107 (s−1) |
| 367.99 | 3.37 | 0.14 |
| 368.75 | 4.22 | 0.80 |
| 372.26 | 3.42 | 0.50 |
| 373.49 | 4.18 | 9.01 |
| 374.34 | 4.30 | 2.60 |
| 376.55 | 6.53 | 9.51 |
| 382.78 | 4.80 | 10.50 |
| 400.52 | 4.65 | 2.04 |
| Minor elements | ||
|---|---|---|
| Line (nm) | E k (eV) | A kl × 107 (s−1) |
| Cu I 324.74 | 3.81 | 13.98 |
| Ni I 352.44 | 3.54 | 10.00 |
There are several approaches on how to perform the outlier filtering. Probably the most common is based on Normal distribution, which approaches the outlier filtering symmetrically, where the same amount of data is filtered from both the bottom and the top of its interval. However, the data can also be asymmetrical, not following the Normal distribution. Hence, we performed the outlier filtering for all three observed models and determined their performance based on the RSD of the resulting data. To test this, we filtered from 5 to 30% of all the measured data with the step of 5%. Visualization of the data filtering is shown in Fig. 2. The approach was to filter data symmetrically to the highest probability density value of the selected fit in the EDF. For example, in the case of filtering 15% based on the Gaussian model, 7.5% from the bottom and the top are filtered. However, if for one of the other models the highest probability density value was at 40% concerning the data population, the filtering would keep the data from −2.5 to 87.5%, which is not possible. Therefore, any percentage crossing the 0 or 100% data interval would be transferred to the other end of the interval. This will lead to filtering from 0 to 85% in the presented example.
Results and discussion
To determine the goodness of specific statistical distribution fit to the experimental data, we calculated EDF and CDF for all the acquired data. The EDF provides information about the skewness that points to the asymmetry of the data. It also refers to the tailing behavior of the data distribution. Such an example is shown in Fig. 3A, where the EDF of spectral intensity of Fe I 373.49 nm for the steel sample is presented. In this case, we can see that the skewness of the data is of a positive value, meaning that the data distribution is tailed to the right. Moreover, we show theoretical fit to the data using Gauss, GEVD, and Burr models. It is evident from the data fit that the Gaussian distribution may fail under specific conditions when describing the acquired data. On the other hand, GEVD and Burr's models respond quite well to tailed data, resulting in a better fit. Examples of the EDFs for the rest of the data, such as the size of the plasma plume, sound intensity, or total spectral intensity are shown in the ESI data (Fig. 1S).†To calculate how well each model performs, the KS test was used to determine the goodness of their fit to the experimental data. This can be seen on the CDF of the selected iron spectral line (Fig. 3B). Here we show the results of the KS test, denoted as D for each statistical model. The threshold value for the null hypothesis is connected to the selected level of confidence and the number of measurements, resulting in a value of 0.068. By comparing the calculated values for every data type with the threshold value we can determine not only which model is better for a description of the specific data, but also if it fails to describe the data. Therefore, every D value higher than the threshold value means that the specific model fails to describe the data distribution. From the presented CDF (Fig. 3B), it is clear that in the case of Fe I 373.49 nm using the irradiance of 4.20 GW cm−2 the Gaussian model is not suitable for the data representation, while the remaining two models fulfill the null hypothesis.
A detailed list of the KS test and skewness of all the selected data under various irradiances are shown in Table 2. As for the examined data, we selected the size of the plasma plume, the sound intensity of the generated shock wave, spectral lines of Fe as the major matrix element together with Cu and Ni as two trace elements, and the total spectral intensity. Detailed information about the size of the plasma plume and sound intensity analysis can be found in our previous work.36 As for the laser energy, it was simultaneously measured for every laser pulse, and it had the Normal distribution in all instances.
| Signal | Irradiance (GW cm−2) | Gauss | GEV | Burr | Skewness |
|---|---|---|---|---|---|
| Plasma plume | 1.72 | 0.0550 | 0.0600 | 0.0550 | 0.0271 |
| 2.53 | 0.0625 | 0.0750 | 0.0525 | 0.5668 | |
| 3.37 | 0.1050 | 0.0525 | 0.0475 | 1.0155 | |
| 4.20 | 0.1125 | 0.0500 | 0.0450 | 1.0569 | |
| 5.04 | 0.1075 | 0.0575 | 0.0475 | 0.6583 | |
| 5.74 | 0.1300 | 0.0700 | 0.0350 | 1.2517 | |
| 6.25 | 0.1097 | 0.0648 | 0.0499 | 1.2070 | |
| Sound intensity | 1.72 | 0.0450 | 0.0975 | 0.0500 | 0.3844 |
| 2.53 | 0.0700 | 0.0750 | 0.0650 | 0.8018 | |
| 3.37 | 0.0825 | 0.0450 | 0.0600 | 0.7627 | |
| 4.20 | 0.1250 | 0.0725 | 0.0600 | 1.0351 | |
| 5.04 | 0.0975 | 0.1325 | 0.0675 | 0.2079 | |
| 5.74 | 0.0950 | 0.2050 | 0.0475 | −0.1552 | |
| 6.25 | 0.0684 | 0.0997 | 0.0473 | 0.2635 | |
| Fe I 373.49 nm | 1.72 | 0.1125 | 0.0600 | 0.0525 | 0.9183 |
| 2.53 | 0.0525 | 0.0775 | 0.0600 | 0.1141 | |
| 3.37 | 0.0625 | 0.0525 | 0.0525 | 0.6873 | |
| 4.20 | 0.0880 | 0.0530 | 0.0450 | 0.8790 | |
| 5.04 | 0.0625 | 0.0650 | 0.0500 | 0.5364 | |
| 5.74 | 0.0525 | 0.0625 | 0.0550 | 0.3910 | |
| 6.25 | 0.0473 | 0.0798 | 0.0598 | −0.1010 | |
| Cu I 324.74 nm | 1.72 | 0.0550 | 0.0525 | 0.0625 | 0.3798 |
| 2.53 | 0.0400 | 0.0800 | 0.0475 | 0.6562 | |
| 3.37 | 0.0650 | 0.0525 | 0.0450 | 0.7421 | |
| 4.20 | 0.0975 | 0.0625 | 0.0575 | 0.8658 | |
| 5.04 | 0.0675 | 0.0525 | 0.0450 | 0.4971 | |
| 5.74 | 0.0400 | 0.0575 | 0.0525 | 0.4132 | |
| 6.25 | 0.0498 | 0.0748 | 0.0523 | −0.3116 | |
| Ni I 352.44 nm | 1.72 | 0.0750 | 0.0525 | 0.0450 | 0.6089 |
| 2.53 | 0.0525 | 0.0725 | 0.0600 | 0.6089 | |
| 3.37 | 0.0650 | 0.0500 | 0.0500 | 0.6959 | |
| 4.20 | 0.0825 | 0.0525 | 0.0500 | 0.8469 | |
| 5.04 | 0.0625 | 0.0625 | 0.0550 | 0.4967 | |
| 5.74 | 0.0500 | 0.0575 | 0.0500 | 0.4334 | |
| 6.25 | 0.0448 | 0.0773 | 0.0598 | −0.0279 | |
| Total sp. intensity | 1.72 | 0.0775 | 0.0450 | 0.0500 | 0.0374 |
| 2.53 | 0.0425 | 0.0850 | 0.0525 | 0.2123 | |
| 3.37 | 0.0700 | 0.0550 | 0.0425 | 0.7778 | |
| 4.20 | 0.0800 | 0.0675 | 0.0375 | 0.7780 | |
| 5.04 | 0.0725 | 0.0650 | 0.0650 | 0.6254 | |
| 5.74 | 0.0448 | 0.0650 | 0.0500 | 0.2392 | |
| 6.25 | 0.0300 | 0.0623 | 0.0448 | −0.4032 |
Fig. 4 shows the temperature dependence of the plasma plume (A), calculated from the Boltzmann plot (Table 1 and Fig. 1), on laser irradiance together with the skewness of the selected data (B). In the instances of low laser irradiances, the variations in the plasma plume temperature follow the Gaussian distribution, and the relationship between the temperature and laser irradiance is fairly linear. In this low-irradiance region, the selected acquired data mainly show Gaussian distribution as well. As the laser irradiance increases (between 4.20 and 5.04 GW cm−2 for our conditions), the temperature of the plasma plume starts to saturate, deviating from the linear dependence. The Normal distribution of the laser energy no longer results in a Normal distribution in the plasma plume temperature, which is in this case tailing to the left. This also leads to changes in the data behavior, where they start to exhibit right-tailed behavior. In this region, the Gaussian model fails to describe the majority of the detected data, due to their increased skewness. However, for the highest irradiance values, the plasma plume temperature reaches its plateau. Here, the data starts to lose their tailing behavior and can be in most cases described as symmetrical, fulfilling the null hypothesis for the Normal distribution. However, the plasma plume temperature remains left-tailed. A nearly identical trend in the plasma plume temperature was also observed in the 900 dataset measurement (see ESI data, Fig. 2S†).
 | ||
| Fig. 4 Temperature of the plasma plume dependence on the laser irradiance (A), and skewness of the selected data (B). | ||
The size of the plasma plume follows the same trend as its temperature but only for lower irradiances, where the size exhibits normal distribution. For the highest laser irradiance, it remains heavily tailed to the right. This is also connected to the plasma plume temperature, where it is left-tailed. Here, the plasma plume temperature and its size are inversely proportional. If the plasma plume has less profound expansion and is smaller, the energy of the plasma plume is distributed into a smaller volume, hence the temperature is higher and vice versa. As the laser irradiance increases, the initial energy of the plasma plume expansion is also higher, since more energy is deposited onto the sample surface and the ablation process. This causes a higher expansion speed of the plasma plume, leading to its increased size, hence decreasing its temperature within the region of signal collection. For all the measured laser irradiances, the distribution of the plasma plume size can be described by the Burr distribution, while the Normal distribution fulfills the null hypothesis only for the two lowest irradiance values.
In the case of the energy of the generated shock wave represented by the recorded sound, it shows Normal distribution only for the lowest laser irradiance value. As the laser irradiance increases, the shock wave energy starts to exhibit tailing behavior similar to the size of the plasma plume. This is also represented by a high correlation between these signals. As the laser irradiance reaches higher values, the skewness starts to decrease and is closer to zero. In all instances, the Burr distribution fulfills the null hypothesis for the data description.
It is important to mention the iron spectral lines for the lowest irradiance regime. Here, the iron spectral lines with high Einstein coefficients (such as Fe I 373.49, 376.55 or 382.78, see Table 1) show higher tailing represented by the skewness and deviate from the expected Normal distribution, failing the null hypothesis. Opposite to this, the spectral lines with lower Einstein coefficients (such as Fe I 367.99, 368.75 or 389.97, see Table 1) have lower skewness values and can be described by the Normal distribution model, similar to the plasma plume temperature. As the laser energy is relatively low for ablating a complex sample such as steel, any fluctuations caused by the experimental conditions and laser–mater interaction can have a higher impact on the iron spectral lines with higher transition probabilities. Contrary to this, those with lower transition probabilities are not as susceptible to any fluctuations and, therefore follow the distribution of the plasma plume temperature, and are less skewed. This is an important behavior in case any experiment is conducted under similar conditions with relatively low laser irradiance, as individual spectral lines can behave differently. This is no longer visible for 3.37 GW cm−2 and higher values of the irradiance. Here, the fluctuation is relatively small, the energy is evenly distributed between the individual possible transitions and all the observed iron spectral lines show nearly the same behavior. As for the trace elements, Cu and Ni, they follow a similar trend as the iron spectral lines with low Einstein coefficients.
In general, the data are symmetrically distributed for the lower irradiance values, except for certain spectral lines based on the Einstein coefficient, and for the highest irradiance values. Here, the Gaussian distribution fulfills the null hypothesis in most cases but fails for the other laser irradiances. On the other hand, the GEV model has inverse performance, where it fails for the symmetrical distributions, but is capable of describing the data when they start to be skewed. However, the Burr distribution can describe all the data under various laser irradiances. On average from the selected data in Table 2, the Gaussian DGauss = 0.073 (52% success rate), GEVD reached DGEVD = 0.069 (64% success rate) and Burr distribution resulted in average DBurr = 0.052 (100% success rate). Therefore, other statistical models are more viable for the data handling in the LIBS analysis than the commonly assumed Gaussian distribution. Similar trends in the results were observed also in the 900 dataset (see ESI data, Table 1S†). Here the statistical models performed slightly worse compared to the threshold value D for the KS test. However, on average the Burr model performed the best reaching the exact value of the threshold (50% success rate), while the GEVD (19% success rate) and Gauss (8% success rate) models did not fulfill the null hypothesis. Moreover, the Gaussian model performed slightly better on average compared to the GEVD in this 900 dataset, but still failed the most. The decreased performance and success rate are attributed to the larger dataset.
As 900 data points resulted in a more strict threshold value D for the KS test, instabilities within the physical processes typical for the LIBS experiment as well as instability of the plasma plume morphology decreased the performance of the individual statistical models.
To further test the capability of the Gaussian model, we randomly averaged a specific number of measured data (four and five data points, see ESI data†) based on the central limit theorem and performed the KS test again on both datasets. In the case of the presented 400 dataset, the success rate of the Gauss model increased from 50 to 71%, GEVD from 64 to 95% and Burr decreased from 100 to 90% (see ESI data, Table 2S†). As for the 900 dataset, the success rate of the Gauss model increased from 8 to 78%, GEVD from 19 to 58% and Burr from 50 to 97% (see ESI data, Table 3S†). It is clear that randomly averaging the number of data points will improve the performance of the Gauss model, bringing the distribution of the data closer to symmetrical distribution. Moreover, it improved the performance of the other two models (except Burr for the 400 dataset). However, in the LIBS analysis the process of averaging the data points does not always have to be desirable, even though it will improve the statistical behavior of the data. Hence the performance of the analyzed statistical models without the averaging was tested in the typical outlier filtering.
In general, there are several data processing options in the analysis pipeline. One of the generally used processes is outlier filtering, which is commonly cutting away the outlier values symmetrically. However, based on the results presented above, the distribution of the data is highly dependent on several parameters and does not always follow the Gaussian symmetrical distribution. Therefore, we performed outlier filtering based on the three observed statistical models. Detailed information about the filtering of the data based on the statistical distribution is shown in Fig. 2. Here, the results can indicate whether the fact that one of the statistical models is more accurate in the data fitting can help in the data processing. Therefore, various percentages of the data population were filtered concerning the selected statistical distribution and the RSD was calculated. To capture the variance of the deviations using the selected statistical models, the final RSD value that is presented is an average of RSD signals shown in Fig. 4.
An example of filtering 15% is displayed in Fig. 5. It shows that selecting the outlier filtering based on specific statistical distribution may lead to a further decrease in uncertainty while keeping the same amount of data points. Consequently, more reliable filtering is performed. The differences in the results for the selected statistical distribution are mainly tied to the goodness of fit to the measured data. For example, in the case of 2.53 GW cm−2, the average D value (see Table 2) for all the selected data is 0.52, 0.77, and 0.55 for the Gaussian, GEV and Burr distributions respectively. The changes in the resulting RSD based on selective filtering follow the same pattern in most instances. Here, the Gaussian leads to 8.45%, GEV to 9.75% and the Burr to 8.79% RSD. The filtering based on the Gaussian distribution leads to the best results in the RSD, since in this case, it shows the best performance in the data fitting derived from the KS test. For the rest of the laser irradiances, the Burr distribution provides the best fit or is very similar to other distributions on average. Hence, in the case of outlier filtering, the selection of the Burr model led to better results in the majority of the cases and therefore it is capable to filter the extreme values with higher precision. The same behavior was observed in filtering from 5 to 30% of the data, with a 5% step.
 | ||
| Fig. 5 Dependence of the RSD for non-filtered data and filtered data concerning the selected statistical distribution, where 15% of the data were filtered. | ||
It is important to note that the RSD value decreased with the higher laser irradiance to a moment when the temperature of the plasma plume reached the saturation point. Here the RSD of the data remains nearly constant and even shows higher values with further increase of the laser irradiance. Since in the saturation point, the temperature itself exhibits relatively low variations, all the observed data exhibit the same behavior, as they are closely related to the temperature.
Conclusions
In this work, we examined the statistical distribution of the LIBS spectra, the size of the plasma plume, and the sound intensity of the generated shock wave with 400 (presented here) and 900 (presented in the ESI† section) datasets for repeatability purposes. The sample used for the experiments was certified SUS-1R and the laser irradiance ranged from 1.72 to 6.25 GW cm−2 (2–10 mJ). We tested three statistical models for the data description against the null hypothesis derived from the distance of the model from the measured data in CDF. The tested models were Gaussian, GEVD, and Burr. The first two models were selected based on experience and previous research work, as typical representation of the statistical analysis of the LIBS data. The Burr model was selected due to its capability of a good fit for both symmetrical and asymmetrical data distributions. The goodness of these models was calculated with the Kolmogorov–Smirnov test, and the resulting value was compared to the threshold value based on the null hypothesis. Together with the goodness of the fit we also calculated the skewness of the data and compared the data distribution with the temperature of the plasma plume.The behavior in the data distribution is to a certain extent dependent on the plasma plume temperature. Our experimental conditions resulted in the temperature saturation at a certain laser irradiance. This may be attributed to the formation of a self-regulating regime. At the point of saturation, the skewness of all the data reached the highest values, resulting in a failed fit of the data by the Gaussian model. However, for the lowest and the highest laser irradiance used in the measurement, the Gaussian model was good enough to fulfill the null hypothesis. Here, the skewness of the data was close to 0, meaning that the distribution of the data was close to Normal. Interestingly enough, the energy of the laser displayed the Normal distribution for each irradiance value. As the temperature of the plasma plume starts to reach the saturation point, symmetrical deviations in the laser energy, plasma plume morphology, and other factors result in an asymmetrical distribution of the temperature relative to the saturation curve. The same factors impact all the connected signals as well.
Another interesting behavior was observed in the low-irradiance regime for Fe spectral lines with different transition probabilities. Those with lower values tend to copy the plasma plume temperature distribution. In this case, the spectral lines with a lower Einstein coefficient and lower transition probability show Gaussian distribution. On the other hand, those with higher values of the Einstein coefficient and higher transition probability tend to show tailing in their distribution and deviate from the Gaussian model. Therefore other models are proposed to be used. As for the spectral lines of trace elements, they show similar behavior as iron spectral lines with a low Einstein coefficient. This highlights the necessity of an appropriate statistical approach to the specific data and/or spectral lines when additional data handling is needed. Moreover, the GEVD and Burr models passed the null hypothesis in the majority of the cases (400 dataset). On average, the GEVD reached DGEVD = 0.069 (64% success rate) from all the selected data, while the threshold value for the null hypothesis is 0.068. The Burr distribution resulted in on average DBurr = 0.052 (100% success rate) and Gaussian DGauss = 0.073 (50% success rate). The results suggest that if the plasma plume temperature is close to its saturation, the Gaussian model starts to fail, while the GEVD and Burr models show a good fit to the experimental data. On average, the Burr model shows better accuracy in the description of the observed data. This is mainly because this model is suitable for either heavily tailed or normally distributed data, while the GEDV works well mainly for tailed data.
Nearly identical values and trends were observed in the 900 dataset as well in terms of the KS testing. This means that the two analyzed datasets (400 and 900) were taken under similar conditions, allowing us to observe the repeatability of our selected statistical approach. Here the threshold value for the null hypothesis is 0.045. The Burr distribution resulted in on average DBurr = 0.045 (50% success rate), Gaussian DGauss = 0.063 (8% success rate), and GEVD DGEVD = 0.071 (19% success rate). The Burr model was on average successful again, while the other two models failed in the majority of the cases. The only difference is that in the case of the 900 dataset, the Gauss performed slightly better than the GEVD. This comes mainly from the fact that even though both experiments (conducted with several months gap in between) resulted in similar outcomes (temperature and KS testing), the results are not completely identical. The main reason is the signal instability and fluctuation originating in the laser–matter interaction and unstable morphology of the plasma plume. This only underlines the fact that considering the statistics of the data in the analysis process can improve the performance of LIBS.
Moreover, based on the central limit theorem, we averaged a selected amount of data points and performed the KS test to check whether the Gaussian model improved. In the case of the presented 400 dataset, the success rate of the Gauss model increased from 50 to 71%, GEVD from 64 to 95% and Burr decreased from 100 to 90% (see ESI data, Table 2S†). As for the 900 dataset, the success rate of the Gauss model increased from 8 to 78%, GEVD from 19 to 58%, and Burr from 50 to 97%. In the case of the worst performance (900 dataset), the Gauss model performance improved the most. It is clear that this approach will improve its performance, as the theorem suggests. However, other models performed better as well. In some applications, the approach of the central limit theorem would not be desirable. For example, when applying complementary signals, such as plasma plume imaging or sound analysis, you need one-on-one data points combination to fully exploit the advantages of this combination.
Applying this information in the outlier filtering process, we have shown that considering the data distribution may further reduce the RSD of the measured data. In general, outlier filtering is carried out assuming the Gaussian distribution of the data. However, filtering the data based on the Burr or GEV distribution might further reduce the RSD. If the specific statistical model shows better performance in the data fitting process, it is most likely that it will perform better also in the outlier filtering selection. Therefore, we propose a different approach, where the data are filtered based on the statistical behavior that they exhibit. As this is dependent on several factors, properties of individual spectral lines as well as the temperature of the plasma plume, it is not possible to say which statistical model is best in all instances. However, certain models, such as the Burr model, are accurate for both symmetrical and asymmetrical data, making it a potential candidate for this approach.
Data availability
Data for this article are available at https://doi.org/10.5281/zenodo.12527742.Author contributions
Jakub Buday: conceptualization, methodology, formal analysis and investigation, writing—original draft preparation, writing—review and editing. Daniel Holub: conceptualization, writing—review and editing. Pořízka Pavel: writing—review and editing, supervision. Jozef Kaiser: writing—review and editing, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This research was financially supported by the FSI–S-23-8389, CEITEC VUT/FSI-J-23-8365, the Technology Agency of the Czech Republic (FW06010042), and the Czech Science Foundation (23-05186K).References
- R. Noll, Laser-Induced Breakdown Spectroscopy - Fundamentals and Applications, Springer, 2012, ISBN: 978-3-642-20667-2 Search PubMed.
- L. Radziemski and D. Cremers, A brief history of laser-induced breakdown spectroscopy: From the concept of atoms to LIBS 2012, Spectrochim. Acta, Part B, 2013, 87, 3–10 CrossRef CAS.
- T. Brennecke, L. Čechová, K. Horáková, L. Šimoníková, J. Buday, D. Prochazka, P. Modlitbová, K. Novotný, A. W. Miziolek, P. Pořízka and J. Kaiser, Imaging the distribution of nutrient elements and the uptake of toxic metals in industrial hemp and white mustard with laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2023, 205, 106684 CrossRef CAS.
- D. Prochazka, T. Zikmund, P. Pořízka, A. Břínek, J. Klus, J. Šalplachta, J. Kanický, J. Novotný and J. Kaiser, Joint utilization of double-pulse laser-induced breakdown spectroscopy and X-ray computed tomography for volumetric information of geological samples, J. Anal. At. Spectrom., 2018, 33, 1993–1999 RSC.
- Y. Zhang, C. Sun, Z. Yue, S. Shabbir, W. Xu, M. Wu, L. Zou, Y. Tan, F. Chen and J. Yu, Correlation-based carbon determination in steel without explicitly involving carbon-related emission lines in a LIBS spectrum, Opt. Express, 2020, 28, 32019–32032 CrossRef CAS PubMed.
- C. R. Dockery and S. R. Goode, Laser-induced breakdown spectroscopy for the detection of gunshot residues on the hands of a shooter, Appl. Opt., 2003, 42, 6153 CrossRef CAS PubMed.
- P. Pořízka, S. Kaski, A. Hrdlička, P. Modlitbová, L. Sládková, H. Häkkänen, D. Prochazka, J. Novotný, P. Gadas, L. Čelko, K. Novotný and J. Kaiser, Detection of fluorine using laser-induced breakdown spectroscopy and Raman spectroscopy, J. Anal. At. Spectrom., 2017, 32, 1966–1974 RSC.
- A. Miziolek, V. Palleschi and I. Schechter, LIBS – Fundamentals and Applications, Cambridge University Press, 2006 Search PubMed.
- S. S. Harilal, B. E. Brumfield, N. L. Lahaye, K. C. Hartig and M. C. Phillips, Optical spectroscopy of laser-produced plasmas for standoff isotopic analysis, Appl. Phys. Rev., 2018, 5, 021301 Search PubMed.
- J. Buday, P. Pořízka and J. Kaiser, Imaging laser-induced plasma under different laser irradiances, Spectrochim. Acta, Part B, 2020, 168, 105874 CrossRef CAS.
- E. Képeš, I. Gornushkin, P. Pořízka and J. Kaiser, Spatiotemporal spectroscopic characterization of plasmas induced by non-orthogonal laser ablation, Analyst, 2021, 146, 920–929 RSC.
- M. Mohan, J. Buday, D. Prochazka, P. Gejdoš, P. Pořízka and J. Kaiser, Laser-induced plasma on the boundary of two matrices, J. Anal. At. Spectrom., 2023, 38, 2433–2440 RSC.
- V. Motto-Ros, Q. L. Ma, S. Grégorie, W. Q. Lei, X. C. Wang, F. Pelascini, F. Surma, V. Detalle and J. Yu, Dual-wavelength differential spectroscopic imaging for diagnostics of laser-induced plasma, Spectrochim. Acta, Part B, 2012, 74–75, 11–17 CrossRef CAS.
- E. Negre, V. Motto-Ros, F. Pelascini and J. Yu, Classification of plastic materials by imaging laser-induced ablation plumes, Spectrochim. Acta, Part B, 2016, 122, 132–141 CrossRef CAS.
- X. Bai, Q. Ma, V. Motto-Ros, J. Yu, D. Sabourdy, L. Nguyen and A. Jalocha, Convoluted effect of laser fluence and pulse duration on the property of a nanosecond laser-induced plasma into an argon ambient gas at the atmospheric pressure, J. Appl. Phys., 2013, 113, 013304 CrossRef.
- X. Bai, F. Cao, V. Motto-Ros, Q. Ma, Y. Chen and J. Yu, Morphology and characteristics of laser-induced aluminum plasma in argon and in air: A comparative study, Spectrochim. Acta, Part B, 2015, 113, 158–166 CrossRef CAS.
- Y. Tian, L. Wang, B. Xue, Q. Chen and Y. Li, Laser focusing geometry effects on laser-induced plasma and laser-induced breakdown spectroscopy in bulk water, J. Anal. At. Spectrom., 2019, 34, 118–126 RSC.
- V. Motto-Ros, E. Negre, F. Pelascini, G. Panczer and J. Yu, Precise alignment of the collection fiber assisted by real-time plasma imaging in laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2014, 92, 60–69 CrossRef CAS.
- Q. Ma, V. Motto-Ros, F. Laye, J. Yu, W. Lei, X. Bai, L. Zheng and H. Zeng, Ultraviolet versus infrared: Effects of ablation laser wavelength on the expansion of laser-induced plasma into one-atmosphere argon gas, J. Appl. Phys., 2012, 111, 053301 CrossRef.
- X. Bai, Q. Ma, M. Perrier, V. Motto-Ros, D. Sabourdy, L. Nguyen, A. Jalocha and J. Yu, Experimental study of laser-induced plasma: Influence of laser fluence and pulse duration, Spectrochim. Acta, Part B, 2013, 87, 27–35 CrossRef CAS.
- Y. Zhao, L. Zhang, J. Hou, W. Ma, L. Dong, W. Yin, L. Xiao, S. Jia and J. Yu, Species distribution in laser-induced plasma on the surface of binary immiscible alloy, Spectrochim. Acta, Part B, 2019, 158, 105644 CrossRef CAS.
- Q. Ma, V. Motto-Ros, X. Bai and J. Yu, Experimental investigation of the structure and the dynamics of nanosecond laser-induced plasma in 1-atm argon ambient gas, Appl. Phys. Lett., 2013, 103, 204101 CrossRef.
- J. Buday, P. Pořízka, M. Buchtová and J. Kaiser, Determination of initial expansion energy with shadowgraphy in laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2021, 182, 106254 CrossRef CAS.
- C. Chaléard, P. Mauchien, N. Andre, J. Uebbing, J. L. Lacour and C. Geertsen, Correction of matrix effects in quantitative elemental analysis with laser ablation optical emission spectrometry, J. Anal. At. Spectrom., 1997, 12, 183–188 RSC.
- L. Grad and J. Možina, Acoustic in situ monitoring of excimer laser ablation of different ceramics, Appl. Surf. Sci., 1993, 69, 370–375 CrossRef CAS.
- C. Stauter, P. Gérard, J. Fontaine and T. Engel, Laser ablation acoustical monitoring, Appl. Surf. Sci., 1997, 109–110, 174–178 CrossRef.
- B. Chide, S. Maurice, A. Cousin, B. Bousquet, D. Mimoun, O. Beyssac, P. Y. Meslin and R. C. Wiens, Recording laser-induced sparks on Mars with the SuperCam microphone, Spectrochim. Acta, Part B, 2020, 174, 106000 CrossRef CAS.
- T. W. Murray and J. W. Wagner, Laser generation of acoustic waves in the ablative regime, J. Appl. Phys., 1999, 85, 2031–2040 CrossRef CAS.
- A. Hrdlička, L. Zaorálková, M. Galiová, T. Čtvrtníčková, V. Kanický, V. Otruba, K. Novotný, P. Krásenský, J. Kaiser, R. Malina and K. Páleníková, Correlation of acoustic and optical emission signals produced at 1064 and 532 nm laser-induced breakdown spectroscopy (LIBS) of glazed wall tiles, Spectrochim. Acta, Part B, 2009, 64, 74–78 CrossRef.
- P. Zhang, L. Sun, H. Yu, P. Zeng, L. Qi and Y. Xin, An Image Auxiliary Method for Quantitative Analysis of Laser-Induced Breakdown Spectroscopy, Anal. Chem., 2018, 90, 4686–4694 CrossRef CAS PubMed.
- Q. Li, Y. Tian, B. Xue, N. Li, W. Ye, Y. Lu and R. Zheng, Improvement in the analytical performance of underwater LIBS signals by exploiting the plasma image information, J. Anal. At. Spectrom., 2020, 35, 366–376 RSC.
- D. Zhang, Y. Chu, S. Ma, S. Zhang, H. Cui, Z. Hu, F. Chen, Z. Sheng, L. Guo and Y. Lu, A Plasma-Image-Assisted Method for Matrix Effect Correction in Laser-Induced Breakdown Spectroscopy, Anal. Chim. Acta, 2020, 1107, 14–22 CrossRef CAS PubMed.
- M. M. ElFaham, W. M. Elthalabawy, O. Elzahed, M. A. Zakaria and M. Abdelhamid, Mechanical hardness estimation of heat-treated DIN50Cr3 spring steel utilizing laser-induced breakdown spectroscopy (LIBS) inverse calibration, Appl. Phys. A: Mater. Sci. Process., 2020, 126, 1–9 CrossRef.
- D. W. Hahn and N. Omenetto, Laser-induced breakdown spectroscopy (LIBS), part II: Review of instrumental and methodological approaches to material analysis and applications to different fields, Appl. Spectrosc., 2012, 66, 347–419 CrossRef CAS PubMed.
- P. Pořízka, J. Klus, D. Prochazka, E. Képeš, A. Hrdlička, J. Novotný, K. Novotný and J. Kaiser, Laser-Induced Breakdown Spectroscopy coupled with chemometrics for the analysis of steel: The issue of spectral outliers filtering, Spectrochim. Acta, Part B, 2016, 123, 114–120 CrossRef.
- J. Buday, D. Prochazka, A. Záděra, V. Kaňa, P. Pořízka and J. Kaiser, Correlation of characteristic signals of laser-induced plasmas, Spectrochim. Acta, Part B, 2022, 194, 106476 CrossRef CAS.
- J. Klus, P. Pořízka, D. Prochazka, J. Novotný, K. Novotný and J. Kaiser, Effect of experimental parameters and resulting analytical signal statistics in laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2016, 126, 6–10 CrossRef CAS.
- Y. T. Fu, W. L. Gu, Z. Y. Hou, S. A. Muhammed, T. Q. Li, Y. Wang and Z. Wang, Mechanism of signal uncertainty generation for laser-induced breakdown spectroscopy, Front. Phys., 2021, 16, 22502 CrossRef.
- A. P. M. Michel and A. D. Chave, Analysis of laser-induced breakdown spectroscopy spectra: The case for extreme value statistics, Spectrochim. Acta, Part B, 2007, 62, 1370–1378 CrossRef.
- K. Abbas, A. Nawazish, N. Feroze and N. Ahmed, Selection of Appropriate Probability Distributions for Rock Analysis using Laser-induced Breakdown Spectroscopy, J. Min. Environ., 2022, 13, 997–1013 Search PubMed.
- A. Moshrefi, H. Aghababa and O. Shoaei, Statistical estimation of delay in nano-scale CMOS circuits using Burr Distribution, Microelectronics J, 2018, 79, 30–37 CrossRef.
- E. Képeš, P. Porízka and J. Kaiser, On the application of bootstrapping to laser-induced breakdown spectroscopy data, J. Anal. At. Spectrom., 2019, 34, 2411–2419 RSC.
- C. Stuart, An Introduction to Statistical Modeling of Extreme Values, Springer, 2002, p. 208, ISBN 978-1-84996-874-4 Search PubMed.
- T. B. Arnold and J. W. Emerson, Nonparametric goodness-of-fit tests fordiscrete null distributions, The R Journal, 2011, 3, 34–39 CrossRef.
- M. A. Stephens, EDF statistics for goodness of fit and some comparisons, J. Am. Stat. Assoc., 1974, 69, 730–737 CrossRef.
- F. Chang, J. Yang, H. Lu and H. Li, Repeatability enhancing method for one-shot LIBS analysis: Via spectral intensity correction based on probability distribution, J. Anal. At. Spectrom., 2021, 36, 1712–1723 RSC.
- S. Zhang, X. Wang, M. He, Y. Jiang, B. Zhang, W. Hang and B. Huang, Laser-induced plasma temperature, Spectrochim. Acta, Part B, 2014, 97, 13–33 CrossRef CAS.
- J. El Haddad, L. Canioni and B. Bousquet, Good practices in LIBS analysis: Review and advices, Spectrochim. Acta, Part B, 2014, 101, 171–182 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ja00126e |
| This journal is © The Royal Society of Chemistry 2024 |



