Open Access Article
Open Access ArticleDesigning green chemicals by predicting vaporization properties using explainable graph attention networks†
Yeonjoon
Kim‡
 ab,
Jaeyoung
Cho‡
cd,
Hojin
Jung
ab,
Jaeyoung
Cho‡
cd,
Hojin
Jung
 ae,
Lydia E.
Meyer
c,
Gina M.
Fioroni
c,
Christopher D.
Stubbs
a,
Keunhong
Jeong
ae,
Lydia E.
Meyer
c,
Gina M.
Fioroni
c,
Christopher D.
Stubbs
a,
Keunhong
Jeong
 a,
Robert L.
McCormick
a,
Robert L.
McCormick
 c,
Peter C.
St. John
c,
Peter C.
St. John
 *c and
Seonah
Kim
*c and
Seonah
Kim
 *ac
*ac
aDepartment of Chemistry, Colorado State University, Fort Collins, CO 80523, USA. E-mail: seonah.kim@colostate.edu
bDepartment of Chemistry, Pukyong National University, Busan 48513, Republic of Korea
cNational Renewable Energy Laboratory, 15013 Denver W Pkwy, Golden, CO 80401, USA. E-mail: pstjohn@nvidia.com
dDepartment of Aerospace and Mechanical Engineering, The University of Texas at El Paso, El Paso, TX 79968, USA
eDepartment of Chemical and Biomolecular Engineering, Yonsei University, Seoul 03722, Republic of Korea
First published on 3rd September 2024
Abstract
Computational predictions of vaporization properties aid the de novo design of green chemicals, including clean alternative fuels, working fluids for efficient thermal energy recovery, and polymers that are easily degradable and recyclable. Here, we developed chemically explainable graph attention networks to predict five physical properties pertinent to performance in utilizing renewable energy: heat of vaporization (HoV), critical temperature, flash point, boiling point, and liquid heat capacity. The predictive model for HoV was trained using ∼150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points, considering their uncertainties and temperature dependence. Next, this model was expanded to the other properties through transfer learning to overcome the limitations due to fewer data points (700–7500). The chemical interpretability of the model was then investigated, demonstrating that the model explains molecular structural effects on vaporization properties. Finally, the developed predictive models were applied to design chemicals that have desirable properties as efficient and green working fluids, fuels, and polymers, enabling fast and accurate screening before experiments.
000 data points, considering their uncertainties and temperature dependence. Next, this model was expanded to the other properties through transfer learning to overcome the limitations due to fewer data points (700–7500). The chemical interpretability of the model was then investigated, demonstrating that the model explains molecular structural effects on vaporization properties. Finally, the developed predictive models were applied to design chemicals that have desirable properties as efficient and green working fluids, fuels, and polymers, enabling fast and accurate screening before experiments.
Introduction
Decarbonizing the power sector is urgently needed for most countries to realize net-zero carbon emissions in the foreseeable future.1 This will require advanced power generation technologies from renewable thermal resources (solar heat, geothermal, biomass, waste heat, etc.), necessitating an efficient thermodynamic cycle that works in the low-to-mid temperature range. The organic Rankine cycle (ORC) has been recognized as a promising technology owing to its functionality over a wide temperature.2,3 The ORC's performance heavily relies on the vaporization properties of the organic working fluid.4 For example, a working fluid with a high heat of vaporization (HoV) is known to give a higher unit work output at the given temperature of the heat source.5 In this regard, extensive research has been conducted on the structure–property relationships for the working fluid's vaporization properties.6–9The vaporization properties of working fluids are also closely related to the performance of refrigeration cycles (or heat pumps)10 that consume ∼23% of residential sector electricity in the United States.11 Since the Montreal Protocol banned the use of chlorofluorocarbons, there have been constant demands for green working fluids with low global warming and ozone depletion potential.12 Developing such chemicals must be preceded by thoroughly understanding structure–property relationships for vaporization properties.
The structure–property relationships of vaporization properties have been extensively studied to design clean (low-emission) alternative fuels.13–15 Specifically, the HoV has been considered one of the key factors for determining the combustion characteristics of liquid fuels. Fuel vaporization in the engine cylinder leads to a significant drop in temperature and pressure, affecting propulsion systems’ thermal efficiency and emission characteristics.16–18 For example, a predictive model for particulate matter emissions from spark-ignition engines utilizes fuel HoV to account for the influence of its vaporization properties on the emission characteristics.19 Similarly, the importance of HoV in the thermal efficiency of propulsion systems is evident as shown in the relationships of HoV vs. cetane number (CN)20 and HoV vs. octane number (ON).21 Therefore, considering chemicals’ vaporization properties can lead to the discovery of green chemicals with low emission that are relevant to one of the twelve Principles of Green Chemistry (#3 – Less hazardous/toxic materials).22
A de novo design of green chemicals demands a predictive model for the vaporization properties of arbitrary molecules. For HoV, various approaches have been applied to develop the predictive models, including equation-based,23,24 group contribution (GC) models,25–27 and their combination with regression methods or neural networks.28–30 Besides GC-based methods, quantitative structure–property relationship (QSPR) models have been built using various structural descriptors.31–35 Similar approaches have also been adopted for other vaporization properties,27,31,36–69 including critical temperature (TC), flash point (FP), and boiling point (TB). More generally, numerous QSPR-based predictive models have been developed for organic molecules’ properties relevant to chemical regulations70 and safety in fire and explosion,71 and for other physicochemical, biological, technological properties.72
Despite the remarkable advances in prediction accuracy over decades, these models still have several limitations. First, some equation-based models assume knowledge of prior information of other physical properties (e.g., TB predictive equation as a function of HoV and vapor pressure). This assumption is sometimes problematic when assessing a novel molecular structure whose physical properties have not been measured. Second, most models have not considered the temperature dependency of vaporization properties (e.g., HoV), which constrains the general applicability of the model to the broader temperature range. Most existing predictive models for HoV are valid for one temperature (room temperature or boiling point).28–30,32,33 Third, the models do not properly account for the uncertainties in experimental measurements. Training the model with uncertainty quantification can improve model accuracy and provide a confidence bound for the predicted value.73
Lastly, there have been fewer discussions regarding the chemical interpretation of predictive models than those regarding their accuracy. Prediction results from GC-based methods can be regarded as chemically explainable, since one can find chemical reasons of different atom-wise contribution values of each substructural moiety in a molecule. However, there are three limitations of GC-based predictive models; first, further investigation is needed to elucidate the effects of temperatures on atom-wise GC values and vaporization properties such as HoV. Second, the GC values are typically assigned to fragments consisting of only first-nearest atoms around one atom, possibly leading to the lack of considering non-local intramolecular interactions. The influence of ‘Nth-nearest-neighboring’ atoms on vaporization properties should be included to achieve more reliable prediction and interpretation. Third, the non-linear relationship between GC and property values should be taken into account, in addition to linear additivity. When it comes to non-GC machine learning (ML) models (tree-based, neural networks, etc.), many studies did not even report chemical explanation of models, despite the availability of several available tools for interpretation, including attention weights (vide infra for details).
A chemically explainable model can give the predicted value as well as rational principles for designing green working fluids and low-emission fuels. In that regard, this study developed chemically interpretable models through analyzing (i) attention weights for each atom and (ii) sensitivity of individual atoms when HoV is changed with varying temperatures. Objective (i) aims to identify crucial structural components that contribute to significant variations in property values among closely related molecules. Objective (ii) provides insights into which molecular substructures are responsible for significant changes in HoV under different temperature conditions. Such approaches provide chemical explanation of prediction results even for deep learning models such as neural networks.
Here, we introduce a novel strategy to develop a reliable and chemically explainable ML predictive model for vaporization properties (Fig. 1). First, databases of vaporization properties were collected and curated to use as inputs for training and evaluation of the model. The raw databases are not structured; particularly, molecules’ simplified molecular-input line-entry system (SMILES) strings are unavailable in some data sources. Therefore, we generated and canonicalized their SMILES strings to input molecules as two-dimensional representations into our ML model (details in the Methods section). A graph attention network (GAT) model was then built and trained against the databases. The GAT is an advanced graph neural network structure where atoms and bonds of a molecule are described as nodes and edges. It can consider the effects of interactions among atoms on target molecular properties (i.e., vaporization properties in this study). Attention weights of each atom in GAT are related to structural importance, and investigating them is beneficial regarding their interpretability. Hence, this approach has been utilized in predicting and analyzing numerous chemical properties.74–83
 | ||
| Fig. 1 Flow diagram of the overall procedure for developing predictive models for vaporization properties. | ||
Besides GAT, tree-based ML algorithms have also succeeded in various chemistry applications, e.g., drug discovery.84 However, in this work, we did not consider molecular descriptor-based models, including tree-based ones, because our GAT showed better accuracy than the recent descriptor-based models (vide infra). Second, GAT does not usually need exhaustive molecular feature generation and selection. Reasonable accuracy was accomplished using only a few features (atom features and connectivity). Without incorporating additional molecular features, the model can infer overall molecular structural effects on HoV through local graph convolution, which can consider more than first-nearest neighbors around each atom. Therefore, it could be generalizable to a broader scope of molecules compared to descriptor-based models, and its accuracy can be comparable to or better than conventional group contribution methods, which usually consider only first-nearest atoms. Third, GAT is not computationally expensive when using a graphical processing unit (GPU). Details are available in the following sections regarding the architecture and accuracy of the GAT model.
To reach the maximal accuracy, a grid search and ten-fold cross-validation found the optimal hyperparameters of the GAT. The mean absolute error (MAE) of validation sets from ten folds was evaluated for each hyperparameter, and the hyperparameter that showed the lowest MAE was selected. Among the ten models from the optimal hyperparameter set, the best model with the lowest validation set MAE was selected. The final accuracy of the model with optimal hyperparameters was assessed for the held-out test set of HoV, with analyses of functional group effects and outliers. This training and accuracy evaluation process was then repeated for other properties: flash point (FP), critical temperature (TC), boiling point (TB), heat capacity of liquid (CP), and melting point (TM). The predictive model for HoV was also validated by comparing our experimentally measured HoVs with predicted values.
Subsequently, the chemical structural effects on HoV were investigated by analyzing the GAT model. Attention weights of each atom in a molecule were then compared to find key substructures or functional groups determining HoV. Such investigations demonstrate that our predictive model is accurate and chemically explainable. Finally, our predictive models for vaporization properties were applied to the practical design of green chemicals (i.e., working fluid, renewable fuel candidates, and polymers). The following sections describe each step's detailed procedure and results outlined in Fig. 1.
Results and discussion
Databases of vaporization properties used for the model development
Table 1 summarizes the data sources and the number of data points for the six properties studied in this work. The present study only considers the molecules consisting of C, H, and O atoms, most common in fuels and working fluids readily synthesizable from natural sources. Halogens were omitted from the consideration owing to their potential impacts on ozone depletion.| Property | N data | References | Comments |
|---|---|---|---|
| Heat of vaporization (HoV) | 153![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 105 |
NIST Web Thermo Tables (NIST-WTT)85 | • 7400 molecules at different temperatures |
| • Experimental + calculated values | |||
| Critical temperature (TC) | 7362 | • Temperature at which HoV is zero | |
| Flash point (FP) | 708 | Design Institute for Physical Properties (DIPPR) database + literature28,30,32,33,47–49,51,53–55,57,86 | • Total 3282 data points were found from DIPPR and other literature sources, but only those from DIPPR (708 data points) were used for training and validation of the model due to the inconsistency among different data sources |
| Boiling point (TB) | 3034 | N/A | |
| Heat capacity of liquid at 298 K (CP) | 777 | DIPPR database86 | • Control properties irrelevant to vaporization |
| Melting point (TM) | 920 |
For the HoV prediction model, we used 153![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 data points of 7400 molecules in the NIST Web Thermo Tables (NIST-WTT). Fig. 2 illustrates the HoV values of five molecules in the NIST-WTT85 as examples, depicting the sensitive nature of HoV to molecular structures. NIST-WTT contains the HoV values of each molecule at varying temperatures below TC where HoV becomes zero. The database also provides error bars from experimental measurements or extrapolations from experimental values, which were utilized for uncertainty quantification of predicted HoVs. A tenth of the molecules (740) were reserved for the held-out test set for splitting the data. The rest 6660 molecules were divided into ten folds to carry out the ten-fold cross-validation and hyperparameter tuning. Detailed information about each split data set is available in section S1 of ESI.†
105 data points of 7400 molecules in the NIST Web Thermo Tables (NIST-WTT). Fig. 2 illustrates the HoV values of five molecules in the NIST-WTT85 as examples, depicting the sensitive nature of HoV to molecular structures. NIST-WTT contains the HoV values of each molecule at varying temperatures below TC where HoV becomes zero. The database also provides error bars from experimental measurements or extrapolations from experimental values, which were utilized for uncertainty quantification of predicted HoVs. A tenth of the molecules (740) were reserved for the held-out test set for splitting the data. The rest 6660 molecules were divided into ten folds to carry out the ten-fold cross-validation and hyperparameter tuning. Detailed information about each split data set is available in section S1 of ESI.†
Meanwhile, the same data source collected TC values of 7362 molecules. Molecular FPs were gathered from the Design Institute for Physical Properties (DIPPR) database86 and other literature.58 We removed the ambiguous FPs, which are significantly different among multiple literature sources, leading to 3282 data points,47–49,51,53–55,57,86 708 of which are from the DIPPR database. The FPs from the DIPPR database were only used for training and validating the model since combining all data from different sources deteriorates the predictive accuracy, presumably due to the different reliability of standard and non-standard experimental methods (vide infra for details). The same procedure was repeated for TB, resulting in 3034 data points in total.28,30,32,33,86 All TB values correspond to those measured in the atmospheric pressure condition. In addition, 777 CP values in the liquid phase and 920 TM values were acquired from the DIPPR database.86CP and TM were considered a control group to compare the accuracy of predicting vaporization properties with those unrelated to vaporization. Liquid CP was also utilized with vaporization properties such as TB, TC, and HoV when designing new working fluids (vide infra).
Development of graph attention networks for predicting HoV
Fig. 3a shows a schematic diagram of our GAT model for predicting the HoV and other properties outlined in Table 1. The model first generates the 16-dimensional atom feature vectors from a SMILES molecular representation. For each atom, five features (atom type, number of bonds and hydrogens, ring state, and aromatic state) are encoded as one-hot feature vectors. A connectivity matrix is also created from SMILES. This matrix encodes whether there is a bond between two atoms, and does not contain information about bond orders. These atom features and connectivity matrix comprise an input layer, and it should be emphasized that no three-dimensional coordinates of atoms in a molecule are needed for the prediction. Of note, SMILES strings can distinguish stereoisomers and diastereomers, and atom feature vectors can encode information about stereocenters. However, the current HoV model does not consider stereocenters since only 13% of the molecules in NIST-WTT contain the stereochemistry information (1106 and 7400 molecules with and without stereochemistry, respectively). In addition, the mean HoV difference between two stereoisomers (e.g., cis vs. trans, (E)- vs. (Z)-, and (R)- vs. (S)-) is 1.54 kJ mol−1, being lower than the mean uncertainty of HoVs in NIST-WTT (3.44 kJ mol−1, section S2 in ESI†). Thorough consideration of stereochemistry effects on HoV is beyond the scope of current work and will be future work.The input atom features then pass through the graph convolutional layers updated with considering adjacent atoms. Detailed formulations for graph convolution and attention matrices can be found in Methods and the literature.74 Meanwhile, to consider temperature dependence on HoV, an input temperature value is embedded into a global feature vector. Next, the global feature vector updates the atom feature vectors from the last convolution layer, and those atom vectors again update the global feature vector (crossed arrows in Fig. 3a). More technical details about the global feature update scheme can be found in Wen et al.87 and Methods section of the present paper.
It should be noted that GATs have better capabilities than convolutional neural networks and graph neural networks having no attention mechanisms, when they learn global features. In GATs, the attention coefficients in an attention matrix are shared throughout multiple GAT layers and attention heads, resulting in a more robust consideration of non-local structural effects on HoV.74,88–90 Such attention mechanisms alongside global update blocks of temperatures lead to a rigorous quantification of the influence of temperatures on HoV. The global update scheme effectively enhances model's accuracy through reinforcing the introduction of relational inductive biases to the model.91 Predictive models utilizing global updates have demonstrated superior accuracy compared to those without global updates in predicting chemicals’ bond dissociation enthalpies, cetane numbers, and solubilities.87,92–94
The averaged atom feature vector and global vector are then concatenated and undergo three readout layers with ReLU activation functions to provide the predicted HoV (Hpred) and its uncertainty (σpred). In other words, the predicted HoV of a molecule is given as not a specific value but a normal distribution Q whose mean and standard deviation are Hpred and σpred, respectively (Fig. 3b). This distribution is compared with another normal distribution P ∼ N(HNIST, σ2NIST) acquired from the NIST database. The model is trained to maximize the overlap between P and Q.
Methods for quantifying σpred include Bayesian neural networks (BNNs) where trainable weights and biases of readout layers are given as probability distributions instead of specific values. BNNs are appropriate for considering the epistemic uncertainty stemming from fitting the model to limited data. However, we assumed that the database is sufficiently extensive (153![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 data points, Table 1) and focused on aleatoric uncertainties arising from the variability from experimental measurements or extrapolation of experimental data. Such uncertainties may depend on uniquely complex molecular structures and can be irreducible regardless of database size.95 In this regard, the final readout layer directly quantifies σpred as a function of molecular structure and outputs the distribution Q instead of determining σpred from BNNs or ensembles of NNs. Elucidating the relationship between chemical structure and uncertainties informs how distant the molecule is from the chemical space of well-known compounds and the fidelity of the predicted values when designing new molecules.96–99 Recent studies have also adopted similar approaches and obtained reliable results from the graph neural network-based prediction of molecular properties with uncertainty quantification.96,97
105 data points, Table 1) and focused on aleatoric uncertainties arising from the variability from experimental measurements or extrapolation of experimental data. Such uncertainties may depend on uniquely complex molecular structures and can be irreducible regardless of database size.95 In this regard, the final readout layer directly quantifies σpred as a function of molecular structure and outputs the distribution Q instead of determining σpred from BNNs or ensembles of NNs. Elucidating the relationship between chemical structure and uncertainties informs how distant the molecule is from the chemical space of well-known compounds and the fidelity of the predicted values when designing new molecules.96–99 Recent studies have also adopted similar approaches and obtained reliable results from the graph neural network-based prediction of molecular properties with uncertainty quantification.96,97
In the first step of the model development, cross-validation and hyperparameter tuning were performed to find the best model architecture (Fig. 1). Using five layers with five attention heads minimizes the validation set MAE; fewer or more layers or attention heads do not improve the accuracy (section S3 in ESI†). It should be noted that the mathematical definition of the loss function is another key hyperparameter for developing a reliable model. The Kullback-Leibler (KL) divergence loss function, DKL(P||Q), was adopted to minimize the difference between two normal distributions (Fig. 3b) of HoVs from the database and prediction. It has been successfully applied to recent ML models relevant to physics, chemistry, and biochemistry.100–103 Detailed formula of the KL divergence is available in eqn (5) of the Methods section. Surprisingly, the KL divergence showed higher accuracy than the typical mean-squared-error loss function without uncertainty quantification, indicating that considering uncertainty is pivotal for a reliable prediction. In addition, the GAT model with the KL divergence is more accurate than the graph convolutional networks without attention, and the GAT prediction based on Watson's equation (details in section S3, ESI†). Optimization of other hyperparameters is explained in section S4 of ESI.†
The weights of graph convolution layers from the HoV model were then used to expand the prediction to five other properties (Fig. 3a). A transfer learning approach was adopted to overcome the limitation due to fewer data points of these properties (700–7500 data points, Table 1) compared to HoV (∼105). Its feasibility was examined by comparing the accuracies of the models trained with and without transfer learning (for details, vide infra). These properties do not have a temperature effect, so only the graph convolution layers were adopted from the HoV model. The averaged atom feature vectors obtained from the transfer learning pass through another series of readout layers to predict vaporization properties.
The five-layer GAT model (Fig. 3a) can distinguish the different local environments of atoms in a molecule, as shown in the t-stochastic neighbor embedding (t-SNE) analysis of atom feature vectors in hidden layers (Fig. 3c). The first layer's 2D t-SNE representations of atom features display a clear clustering according to the four basic atom types. Those in the third layer are more dispersed except for a few clusters near the center, and the fifth layer shows the most scattered atom features. This indicates that, as a molecular graph passes through more layers, the model updates atom feature vectors to differentiate more detailed local environments leading to different HoVs.
For further demonstration, we selected two representative compounds, butyl sec-butyl ether, and dibutyl ether, which have slight structural differences in Fig. 3c. The former has one branched methyl group (methyl group on a tertiary carbon), whereas the latter does not. The terminal methyl carbons in the butyl group were chosen from each compound, and their atom feature vectors were compared. They show similar 2D t-SNEs until the third layer; interestingly, they become distinct in the fifth layer. These two carbons share the same substructure until the fourth-nearest neighbors. Their fifth-nearest ones are different, and the model captures this structural dissimilarity, ultimately leading to different HoVs of these compounds.
The feasibility of the model shown in Fig. 3a was assessed by training the model using the databases of HoVs at TB from the literature and comparing the prediction accuracies from previously reported models (Table 2). The previous studies used various techniques such as genetic algorithms, multivariate regression, group contribution, and artificial neural networks. For a fair comparison, we applied the splits of data sets into training, validation, and test sets identical to those reported in the literature. Although only C/H/O-containing molecules were chosen, the training![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) validation
validation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) test set ratio is maintained at approximately 8
test set ratio is maintained at approximately 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (or training
1 (or training![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) test 4
test 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), which is reasonable for training our model and comparing the accuracy with other models. Our model generally shows better accuracy; a test set MAE 0.1 kJ mol−1 higher was demonstrated in only one case, which could be attributed to experimental uncertainties. The raw data obtained for the analysis shown in Table 2 is available via an Excel spreadsheet file uploaded as ESI.†
1), which is reasonable for training our model and comparing the accuracy with other models. Our model generally shows better accuracy; a test set MAE 0.1 kJ mol−1 higher was demonstrated in only one case, which could be attributed to experimental uncertainties. The raw data obtained for the analysis shown in Table 2 is available via an Excel spreadsheet file uploaded as ESI.†
| Reference | Method | N data (training/validation/test)a | Mean absolute error (training/validation/test) | Comments | |
|---|---|---|---|---|---|
| Literature (kJ mol−1) | This work (GAT, kJ mol−1) | ||||
| a Database from the literature. C/H/O-containing molecules only. | |||||
| Gharagheizi et al.32 | Genetic algorithm-based multivariate regression | 2291/—/571 | 1.01/—/0.99 | 0.73/—/0.79 | HoVs at boiling point (TB) |
| Gharagheizi et al.30 | Group contribution + artificial neural network | 2312/287/275 | 0.86/1.21/1.05 | 0.84/1.20/1.16 | HoVs at TB |
| Jia et al.33 | Features from quantum chemistry calculations + QSPR | 219/—/61 | 1.13/—/1.12 | 0.88/—/0.92 | HoVs at TB. Less extensive database but contains new oxygenates (alcohols, ethers, esters, ketones, etc.) |
Accuracy of the HoV model trained using the largest database
Ultimately, our GAT model was trained using a much more extensive database than any other models in the literature. There are 124![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 HoVs at varying temperatures in the training, 13
100 HoVs at varying temperatures in the training, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634 in the validation, and 15
634 in the validation, and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 in the test sets. In the best-case model, we achieved reasonable accuracy for this extensive database, with the MAEs of 3.33, 4.21, and 4.77 kJ mol−1 for each split data set. Although the MAEs are relatively higher than those of HoVs at TB (Table 2, 0.7–1.2 kJ mol−1), it should be emphasized that the errors are comparable to the mean uncertainty of HoVs in the database (3.44 kJ mol−1, section S2, ESI†). Given the MAEs similar to the database's mean uncertainty, it can be deduced that the GAT model architecture and the trained model are less susceptible to overfitting. Moreover, the model was trained using the largest database ever (153
371 in the test sets. In the best-case model, we achieved reasonable accuracy for this extensive database, with the MAEs of 3.33, 4.21, and 4.77 kJ mol−1 for each split data set. Although the MAEs are relatively higher than those of HoVs at TB (Table 2, 0.7–1.2 kJ mol−1), it should be emphasized that the errors are comparable to the mean uncertainty of HoVs in the database (3.44 kJ mol−1, section S2, ESI†). Given the MAEs similar to the database's mean uncertainty, it can be deduced that the GAT model architecture and the trained model are less susceptible to overfitting. Moreover, the model was trained using the largest database ever (153![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 data points) compared to any other previous studies, considering the temperature effects of HoV.
105 data points) compared to any other previous studies, considering the temperature effects of HoV.
A learning curve was obtained (Fig. 4a) by training the model with increasing training set data points, where triplicate runs were performed for each training set to consider the variance of MAEs stemming from the randomness of training. A clear improvement in test set accuracy was shown as the number of training set molecules increased, suggesting that the model accuracy could be further improved using a more extensive database.
More analysis on the model error was then carried out (details in section S5, ESI†). Most of the errors (∼80%) are within ± 5.0 kJ mol−1. Next, the MAEs by 13 categorized functional groups were analyzed. All functional groups showed lower MAEs (2.24–4.57 kJ mol−1) than the overall test set MAE (4.77 kJ mol−1) except for fused ring compounds whose MAE is 5.03 kJ mol−1. Fused rings have fewer data points per molecule at different temperatures (17.56 data points per molecule) than other functional groups (19–22 data points per molecule), while their structures are more complex, presumably leading to their higher MAE.
The molecular structure of the top 5 outliers was further analyzed. Interestingly, methane showed the highest MAE (81.4 kJ mol−1), which may be attributed to the temperature range (90–150 K) and atom type (a carbon with four hydrogens) that rarely appear in the database. The molecules with the second to fifth highest MAE are complex cyclic compounds. The 2nd and 5th outliers have 26- and 24-membered rings, respectively, and their structures are highly twisted and deviated from typical conformations (chair and boat, etc.) of cyclic compounds. The remaining two compounds are cyclopropene with ketone and phenyl rings and quinone with four linearly fused rings (pentacenequinone). Such structural distinctiveness is hard to be captured by GATs that use 2D structures as inputs, so they became outliers from predictions. However, these large-sized or fused ring structures are uncommon and far from desirable fuel candidates or working fluids. To further examine the feasibility of uncertainty quantification, we compared the accuracy of this model with one that used a mean-squared-error loss function without considering uncertainty. A lower training set MAE of 2.21 kJ mol−1 was observed, but validation and test set MAEs are 4.67 and 5.09 kJ mol−1, respectively, indicating that overfitting occurs if uncertainty is not considered (section S5, ESI†).
Next, we investigated the Pearson and Spearman rank correlation coefficients (ρ) between the absolute errors from the prediction (|HNIST − Hpred|) and uncertainties quantified from the model (σpred), as listed in Table 3. In principle, these two quantities should show a positive correlation; if the uncertainty is low, the prediction error should also be low. The KL divergence formula (eqn (5), Methods section) also well reflects this trend; the numerator and denominator contain |HNIST − Hpred| and σpred, respectively. A stronger positive correlation leads to the numerator and denominator being closer, thus minimizing divergence values. Meanwhile, the first term of eqn (5) prevents |HNIST − Hpred| and σpred from simultaneously diverging to infinity. The logarithm of the ratio between σpred and σNIST minimizes σpred to be closer to the uncertainty tabulated in the database (σNIST).
| Dataset | N molecule | N data | Pearson ρ | Spearman ρ |
|---|---|---|---|---|
| Training | 5994 | 124![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
0.60 | 0.57 |
| Validation | 666 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 634 634 |
0.49 | 0.47 |
| Test | 740 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371 371 |
0.54 | 0.50 |
A Pearson ρ close to 1 indicates that two variables have a relationship close to monotonic proportionality. A Spearman ρ equal to 1 corresponds to identical ranks of two variables. Our GAT model showed a decent positive Pearson correlation: 0.60, 0.49, and 0.54 for training, validation, and test set, respectively. The Spearman rank correlation values were located within 0.47–0.57. This is comparable to the ρ = 0.469 obtained from the state-of-the-art message-passing neural network, which quantified the uncertainty for molecular properties of 133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 compounds in the QM9 dataset.96 All these results manifest that our model gives an accurate HoV prediction and a reasonable quantification of uncertainties.
885 compounds in the QM9 dataset.96 All these results manifest that our model gives an accurate HoV prediction and a reasonable quantification of uncertainties.
Expansion of the predictive model to other vaporization properties
The predictive model for HoV was expanded to predict other vaporization properties listed in Table 1 by adopting the transfer learning approach (Fig. 3a). This overcomes the limited number of data points for these properties while utilizing the pre-trained HoV model that learned chemical structural effects on vaporization from the large database. Transfer learning can be done by varying the number of layers transferred from the HoV model. Here, we hypothesized that the relevance to HoV is different for each of the properties in Table 1, and transferring more layers is optimal when a property has higher relevance. For each property, the GAT models were trained by changing the number of transferred layers (0 to 6, seven cases) to find the optimal number of transferred layers and the model with the best accuracy. Twenty different data set splits were tested for each of the seven cases to prevent the model from obtaining biased results regarding accuracies.Fig. 5a illustrates the mean and standard deviation of test set MAEs from the 20 TC, FP, and TB models with different numbers of transferred layers. The standard deviation of MAEs does not exceed 2 K for TC, FP, and TB, indicating that changing the data splits does not affect the overall trends of MAEs. These low deviations also demonstrate that the models from transfer learning are not susceptible to overfitting specific data splits. These three vaporization properties are relevant to HoV, so transferring all or part of the layers from the HoV model effectively maximizes the predictive accuracy. The means of test set MAEs converged for TC and FP with the difference below 1 K when four to six layers were transferred (16.1–17.1 K for TC, 9.2–9.4 K for FP). Transferring two to five layers is optimal for TB (means of test set MAEs ranging from 11.1 to 11.7 K).
In contrast, CP of liquid at 298 K and TM are unrelated to HoV. These two properties were examined additionally to justify that the optimal number of transferred layers is relevant to the relationship of a given property with HoV (Fig. 5b). Transferring 0–1 layers showed the best mean of test set MAEs (98.4–98.6 J kg−1 K−1) for CP. The optimal number of transferred layers is 1–2 for TM. However, the means of MAEs (32–33 K) are much higher than those of other properties (9–17 K) shown in Fig. 5a. Also, the standard deviations of MAEs are very high in all cases: 11–14 K. These two contrasting examples further demonstrate our hypothesis that the number of transferred layers is related to the correlation between HoV and vaporization properties.
We also compared the Pearson correlation coefficient between HoVs and other vaporization properties (Table 4) to verify that a property strongly correlates with HoV if the model becomes more accurate when more layers are transferred. The first target property is TC; TC is the temperature where HoV becomes zero. Watson's equation estimates that the HoVs at different temperatures T are proportional to (TC − T).23 In other words, there is a direct formulaic relationship between TC and HoV, which can be associated with a high Pearson ρ (0.86) between HoV at room temperature and TC. Transferring four to all six layers showed the best accuracy in predicting TC, also in line with these high Pearson ρ values. The Pearson ρ between FPs and HoVs at FP (0.91) is comparable to that in the case of TC, resulting in the identical range of the optimal number of transferred layers (4–6 layers). Previous studies46,52 quantified the relationship between FP and HoV. They derived an equation for estimating FP as a function of HoV, TB, and other descriptors such as the number of carbons, surface area, etc., explaining the Pearson ρ value for FPs.
| Property | Number of transferred layers vs. correlation with HoV | Model accuracies | |||||
|---|---|---|---|---|---|---|---|
| Number of transferred layersa | Pearson coeff. | Correlation betweenb | N data (training/validation/test) | MAE – best-case model (training/validation/test) | MAE – all models (training/validation/test) | Unit | |
| a Numbers of layers where the mean of test set MAEs is within 1 K (1 J kg−1 K−1 for CP) compared to the lowest. b HoVs are from the GAT predictive model, and the target properties are from the database. | |||||||
| Critical temperature (TC) | 4–6 | 0.86 | HoV at 298 K vs. TC | (5890/736/736) | (15.9/16.1/14.9) | (16.5 ± 0.6/16.7 ± 1.0/16.9 ± 1.0) | K |
| Flash point (FP) | 4–6 | 0.91 | HoV at FP vs. FP | (566/71/71) | (6.4/7.1/6.5) | (8.6 ± 1.0/8.4 ± 1.5/9.3 ± 1.5) | K |
| Boiling point (TB) | 2–5 | 0.68 | HoV at TBvs. TB | (2427/304/303) | (7.2/8.9/9.2) | (9.6 ± 1.5/10.6 ± 0.9/11.4 ± 1.1) | K |
| Melting point (TM) | 1–2 | 0.18 | HoV at TMvs. TM | (736/92/92) | (19.1/26.2/21.7) | (19.7 ± 4.8/30.5 ± 12.4/32.8 ± 12.9) | K |
| Liquid heat capacity at 298 K (CP) | 0–1 | −0.10 | HoV at 298 K vs. CP | (622/78/77) | (65.1/78.3/81.0) | (60.5 ± 14.0/77.8 ± 11.7/98.5 ± 13.3) | J kg−1 K−1 |
T B is also known to have a relationship with HoV, according to the Clausius–Clapeyron equation and other studies regarding FP and TB.46,52 Therefore, transfer learning shows better accuracy than training the model without transferring layers from the HoV model, with slightly fewer numbers of transferred layers (2–5) than TC and FP. It should be emphasized that the model for each vaporization property has been developed without prior knowledge regarding the relationships among these properties, while the results are consistent with their underlying physical equations.
Meanwhile, the best-case model for each property should be chosen for screening desirable working fluids and fuel candidates. Table 4 summarizes the best-case models with their number of data points and MAEs for training, validation, and test sets. The best-case models showed the test set MAE of 14.9 K, 6.5 K, and 9.2 K for TC, FP, and TB, respectively. TC could also be predicted by estimating the temperature where the predicted HoV becomes zero; however, the HoV prediction near TC was less accurate than that at lower temperature ranges (Fig. 4b). As can be seen in Fig. 2, the uncertainties of NIST-WTT HoVs increase near TC, leading to less reliable predictions of HoVs when they approach zero. Transfer learning was carried out instead of predictions from the HoV model to obtain the best TC prediction accuracy, resulting in the best model shown in Table 4.
It should be noted that the test set MAE is lower than the training set MAE for the best-case model of TC. Such an anomaly could occur when the molecules in the test set have relatively plain structures that make the prediction more accurate. To avoid the artificial bias from data splitting, we also evaluated the mean and standard deviation of MAEs for all models with different data splits (20 per each number of transferred layers, Table 4). As a result, all properties showed lower averaged training set MAEs than averaged test set MAEs, indicating that our models were evaluated under no specific ‘privileged’ data splits.
The FP prediction model was developed using only the DIPPR database. We also attempted to train the model using a larger integrated database, but the MAEs increased (section S6, ESI†). The less accuracy for the larger database is presumably due to the inconsistency arising from different data sources, including FPs measured using non-standard methods,47–51,53–57,86 rather than the deficiency of the model. The best model from training against the DIPPR database showed the MAEs of 6.4–7.1 K for training, validation, and test sets. These errors are comparable to the typical experimental errors of FP measurements using standard methods (5.0–8.0 K).58,85,86 On the other hand, the model for TM showed a higher test set MAE (21.7 K) than other properties, but it was not used for designing green chemicals. The lowest MAEs for CP of liquids are 65–81 J kg−1 K−1. This accuracy is acceptable to be utilized in the design of working fluids (vide infra).
While numerous models have been reported for ‘one independent predictive model per one property’, all these results manifest the general applicability of the temperature dependence of HoV to other properties relevant to vaporization. Such approaches would lead to robust predictive models consistent with the underlying physics of vaporization and integrated into one model architecture. As discussed in the next section, the model can be more powerful if it is chemically interpretable.
Chemical interpretation of the model
The interpretability of an accurate predictive model is a key aspect of chemistry-informed design.104,105 To demonstrate our model's chemical interpretation, we chose ethers and esters as representative molecules among various fuel candidates. They have drawn attention as promising biofuel candidates due to their favorable reactivity, emission characteristics, and synthetic viability from biomass.106,107 First, the attention weights of atoms were analyzed to find the key substructures that lead to HoV differences. The literature108 and section S7 in ESI† explain the detailed procedure for evaluating atom-wise attention weights.The attention weight analysis for three C8 ethers is illustrated in Fig. 6a. The predicted HoVs showed a good agreement with those in the NIST-WTT. More methyl branches result in lower HoVs (dibutyl ether > butyl isobutyl ether > diisobutyl ether), presumably due to decreased molar surface area and, thus, intermolecular interactions.109 The attention weights also explain this trend; the highest attention weights were observed in the tertiary carbons of two branched ethers since they have methyl branches and lower HoV than a linear one. The γ carbons in dibutyl ether showed the most significant attention because they are adjacent to terminal methyl carbons and determine the continuation or termination of alkyl chains.
This analysis was repeated for esters (Fig. 6b). The hydroxy (OH) substitution at beta carbon of ethyl 3-hydroxyhexanoate (E3OHH) leads to higher HoVs than ethyl hexanoate (EH) because it can form intramolecular and intermolecular hydrogen bonds. HoVs of the hydroxyester with a shorter carbon chain (methyl 3-hydroxypropanoate: M3OHP) are still higher than EH, indicating the significance of OH groups in determining HoV. Our model also captured this structural feature; the beta carbons having an OH group showed the highest attention weights among atoms in E3OHH and M3OHP. On the other hand, the effect of OH position on HoVs was investigated. The HoVs of methyl 2-hydroxypropanoate (M2OHP) are lower than M3OHP. In both cases, the carbon atom with an OH group showed the highest attention, regardless of whether it is a terminal carbon.
It should be noted that, as the critical point is approached, the prediction accuracy of GAT model, particularly for esters in Fig. 6b, gets worse as it is relatively harder to catch the molecular interaction in dense states. This challenge around the critical point is also reflected in the large error bar of experimental data near the critical points. Still, it is interesting that the prediction for M2OHP deviates from the experimental data more than their uncertainty bound, while those of the other ethers and esters in the figures are within the experimental error bar. This large discrepancy in M2OHP can be attributed to its unique molecular structure, where a OH group is attached to the alpha-site of the ester functional group which is rarely observed in other molecules and may cause the intricate intramolecular interaction.
The OH group also influences the temperature dependence of a molecule on HoV. For example, the HoV of E3OHH is higher than that of EH at all temperatures. To explain the reason for these HoV differences, we compared the response of atom feature vectors to the global updates, which is evaluated by the L2-norm of feature vector difference before and after the update: ||v − v′|| (eqn (2) in Methods and Fig. 6c). At 400 K, all atoms in EH and E3OHH show a low response value to the temperature except the OH group, alpha, and beta carbons of E3OHH. The overall responses increase at 600 K, but these three atoms in E3OHH respond most sensitively to the temperature, contributing to higher HoVs of E3OHH than EH at the given temperature range. This indicates that the OH substitution at the beta position is a key factor for increasing the HoV of esters via hydrogen bonds.
The above analysis on attention weights and temperature dependence demonstrates our model's capability of capturing chemical structural effects on HoV. The predicted HoVs are accurate and are consistent with the chemical knowledge pertinent to HoV, such as molecular surface area and hydrogen bonds. The structural insights from this chemical interpretation would inform the discovery and design of new working fluids and (bio)fuel candidates. It should be emphasized that the chemical interpretation method using attention weights can also be applied to the GAT models trained through transfer learning for other vaporization properties (section S8, ESI†).
Experimental validation of the model
We carried out in-house measurements of HoVs at temperatures near TB for further assessment of the model using external data besides NIST-WTT. HoVs were measured for three beta-hydroxy esters and six ethers shown in Fig. 7a. They are promising biofuel candidates derivable from biomass and have high reactivity and low soot emission.106,107,110 They also have diverse structural features, such as linear/branched, symmetric/asymmetric alkyl chains, hydroxy, ether, and ester groups, which are suitable for model evaluation. Notably, three (4-butoxyheptane, methyl 3-hydroxyhexanoate, and methyl 3-hydroxytetradecanoate: I, VII, and IX) do not exist in NIST-WTT. The remaining six compounds are found in NIST-WTT, but the GAT model has never seen HoVs at the temperatures in Fig. 7a during the model training. Therefore, the feasibility of our external validation is further justified by the unavailability of these nine molecules at the given temperatures.We predicted the HoVs of these molecules at the same temperature using our model and compared the measured and predicted values. As a result, our GAT model showed reasonable accuracy with an MAE of 2.6 kJ mol−1 for these nine molecules. It should be emphasized that all measured and predicted values overlap if uncertainties are considered (Fig. 7b), which manifests the importance of considering confidence intervals in the ML prediction of HoV.
Application of the model to green chemical screening
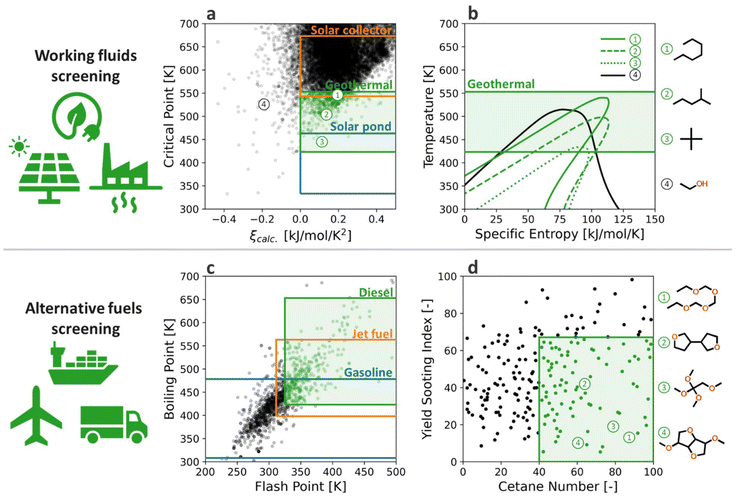
The developed GAT models for vaporization properties prediction can have numerous potential applications for designing green chemicals. Here, we applied our GAT models to screening green chemicals for three purposes: working fluids, alternative fuels, and sustainable polymers. It should be emphasized that other molecular properties relevant to ‘greenness’ of chemicals were examined together with the vaporization properties for the practical consideration of Green Principles during the screening. Such additional molecular traits are fuels’ emission characteristics (yield sooting index – YSI) and polymers’ glass transition temperature which are relevant to degradability. In addition, when screening working fluids, renewable energy sources were taken into account, such as solar and geothermal energy (vide infra for details).The first example is to screen for optimal ORC working fluids with desirable vaporization properties that maximize the utility of renewable thermal resources. Xu et al.111 discussed the relevance of working fluids’ TC on the thermal efficiency of sub-critical pressure ORC. Their simulation study revealed that the thermal efficiency of ORC at a given temperature of heat source (TH) is maximized with the working fluids having TC between TH − 30 K and TH + 100 K, suggesting TC as an essential criterion for screening the optimal working fluids. Meanwhile, the “dryness” of working fluids was also widely accepted as an important property relevant to ORC's thermal efficiency and work output.112–114 The working fluid is considered dry if the fluid stays in the vapor phase upon isentropic expansion of the saturated vapor, which is essential to ensure the absence of liquid droplets at the turbine exit. The dryness of the working fluid can be determined with the temperature sensitivity of the specific entropy (ξ = ds/dT) of saturated vapors; that is, the working fluid is dry if ξ > 0 or wet otherwise. Liu et al.112 suggested an analytic equation for predicting ξ of organic compounds from their vaporization characteristics as below:
 | (1) |
 is the reduced temperature of the heat source (=TH/TC), n is an empirical coefficient that ranges from 0.375 to 0.38,115 and HoVH is the HoV at TH. This study assumes the TH as TB for the brevity in molecular screening.
is the reduced temperature of the heat source (=TH/TC), n is an empirical coefficient that ranges from 0.375 to 0.38,115 and HoVH is the HoV at TH. This study assumes the TH as TB for the brevity in molecular screening.
To screen working fluids based on their dryness and TC, Fig. 8a depicts the distribution of ∼27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 organic molecules from the database (NIST WTT, DIPPR, PubChem, etc.85,86,116) on TC–ξ axis, where all the relevant molecular properties – TC, TB, CP,l, and HoVH – were evaluated from the present GAT model. The TC screening criteria for solar collector, geothermal, and solar pond were based on their typical temperature range (573 K, 453 K, and 353 K, respectively117), while ξ was restricted to positive. Most (96%) tested molecules fall into the dry working fluid. Meanwhile, more compounds at higher TC provide more viable options for working fluid selection for high-temperature heat sources such as solar collectors. On the other hand, the low-temperature heat sources (geothermal and solar ponds) have limited choices for the dry working fluid.
000 organic molecules from the database (NIST WTT, DIPPR, PubChem, etc.85,86,116) on TC–ξ axis, where all the relevant molecular properties – TC, TB, CP,l, and HoVH – were evaluated from the present GAT model. The TC screening criteria for solar collector, geothermal, and solar pond were based on their typical temperature range (573 K, 453 K, and 353 K, respectively117), while ξ was restricted to positive. Most (96%) tested molecules fall into the dry working fluid. Meanwhile, more compounds at higher TC provide more viable options for working fluid selection for high-temperature heat sources such as solar collectors. On the other hand, the low-temperature heat sources (geothermal and solar ponds) have limited choices for the dry working fluid.
The validity of working fluid screening based on the GAT model was confirmed on the T–s diagram of the selected working fluids for geothermal ORC (Fig. 8b), where the thermodynamic properties of liquid–vapor transition were collected from CoolProp.118 The n-heptane met the screening criteria as a working fluid for geothermal ORC, and its T–s diagram in Fig. 7b depicts the ideal shape in geothermal temperature with clear dryness, proving the soundness of ML-based screening of ORC working fluid. Similarly, the iso-hexane and neo-pentane also satisfied the screening criteria for geothermal ORC but with lower TC than n-heptane, which is consistent with their T–s diagram in Fig. 8b. This finding is in line with previous studies on n-heptane, iso-hexane, and neo-pentane as ORC working fluids,119,120 all of which showed a plausible performance in geothermal power generation. As a counterexample, we depicted the T–s diagram of ethanol, which shows the negative temperature sensitivity of specific entropy (thus, wet) as predicted from the ML-based working fluid screening. In summary, the GAT model from the present study can provide useful guidance on screening ORC working fluid for renewable thermal resources with varying temperatures.
As another example, the present GAT model can be utilized to discover alternative fuel candidates for decarbonizing the transportation sections. Our previous study110 suggested ether fuels as a promising alternative to conventional fuels owing to their high reactivity and low soot emission characteristics while being synthesizable from biomass conversion. Such ethers can be derived through catalytic Guerbet coupling and dehydration of biomass-derived alcohols.110,121 Despite the extensive studies from both experimental and theoretical approaches, the optimal structure of ether-containing molecules is still under investigation due to their various degrees of freedom. In this regard, the present study examined the utility of the GAT model in screening ether fuels based on their vaporization and combustion characteristics.
ASTM standards122–124 restrict various molecular properties of transportation fuels to ensure safety and operability in the propulsion systems. TB range is one of the important criteria for categorizing the fuel molecules into diesel, jet fuels, and gasoline, and it affects the vaporization process of the injected fuels in the combustion chamber. Meanwhile, fuel safety and inflammability are controlled by regulating the FP above specific criteria. Fig. 8c presents the distribution of ∼1300 saturated ethers on TB–FP axis, where both properties are predicted from the GAT model from the present study. All the tested ethers are from existing databases that contain experimentally observed molecules; thus, they are all synthesizable. We set the boundary of TB for diesel, jet fuel, and gasoline as 423–653 K, 398–563 K, and 308–473 K, respectively.125 The lower limit of FP of diesel and jet fuels was set as 325 K and 311 K, while those of gasoline are not constrained, as described in ASTM standards. Consequently, 30.3% of tested ethers fall into the diesel regime, while 45.3% and 78.5% are in the jet-fuels, and gasoline range, respectively. Of note, the currently oxygenated compounds such as ethers are not acceptable as alternatives to conventional jet fuels owing to their poor thermal stability and low specific energy.125 Therefore, here we focused on diesel fuel candidates, although it can also be applied to the design of renewable fuels for other engines, including gasoline and aviation.
The 387 diesel-range ethers were then further analyzed on the cetane number (CN) and yield sooting index (YSI) axis, which represents the reactivity and sooting tendency of fuel candidates, as shown in Fig. 8d. The CN and YSI of ether compounds were estimated from the multivariate linear regression model suggested by Cho et al.110 The screening criteria for CN was set to be higher than 40 as dictated in ASTM standard for diesel fuels,123 while YSI was assumed below those of n-dodecane (YSI = 67.1), which is a typical surrogate fuel for conventional diesel. Consequently, 60 of 387 diesel-range ethers satisfied the criteria for combustion characteristics. Fig. 8d shows four of the selected ethers fuels, all of which contain multiple oxygen atoms to increase the reactivity and suppress the soot formation, as envisioned by Cho et al.110 Of note, the candidates with lower YSI indicate that they are closer to green chemicals that mitigate adverse health and environmental impacts. In summary, the GAT model from the present study can provide an additional window for screening alternative fuels based on their vaporization characteristics, which significantly reduces efforts for combustion properties characterization.
For the last example, we applied our models to polymer screening by predicting cohesive energy and glass transition temperature of polymers from the HoVs of their monomers. Cohesive energy could be a criterion to consider in designing polymers since it is relevant to molecular interactions of polymers and the polarity and binding energy of polymer chains. It affects many thermophysical and mechanical properties, for example, glass transition temperature (Tg). Although polymers typically degrade before vaporizing, we can use the cohesive energy of a given polymer to approximate the HoV of its structural analogs. The validity of this approximation is presumably due to the shared need to break molecular interactions required by both liquid vaporization and polymer degradation.
We attempted to predict the cohesive energies of polymers (Ecoh, pred) by linear regression of monomer HoVs (HoVpred, mono, Fig. 9). The 5-fold cross-validation was performed using the literature values of cohesive energies of 93 polymers at room temperature.126 High test set accuracies were obtained, with Q2 and MAE of 0.97 and 2.20 kJ mol−1, respectively. Moreover, the coefficients (c1 and c2) from five regressions showed very low standard deviations (0.01 and 0.43), indicating a robust relationship between the monomer's HoV and the polymer's cohesive energy. Reliable extrapolation from monomers to polymers was possible by our accurate predictive models for HoV, demonstrating the potential applicability of our GAT models to polymers.
 | ||
| Fig. 9 Application of the GAT model for screening polymers through the prediction of polymer's cohesive energy and glass transition temperature using monomer's HoV. | ||
Next, we also predicted Tg of polymers by the linear regression of monomer's HoV normalized by the number of functional groups representing molecular oscillations (Noscil). This was motivated by a previous study which quantified the linear relationship between Tg and cohesive energies per Noscil.127 The 5-fold cross-validation for 28 polymers126,127 resulted in test set Q2 and MAE of 0.94 and 15.8 K, respectively, against the experimental Tg values. The linear regression coefficients (c3 and c4) showed low deviations among five training sets, highlighting the relationship between HoV and Tg. However, a polymer's glass transition is a complicated phenomenon that cannot be accounted for solely by HoVs, as can be seen by a weak correlation between HoV and Tg for the seven polymers with alcohol moieties (section S9 in ESI†). Despite this limitation, predicting polymer properties from monomer's HoV is a fast and robust approach for designing and screening new polymers. The prediction results in Fig. 9 include polymers that can be synthesized from renewable sources such as biomass: for example, those with ethers, esters, and phenolic moieties (I–VI in Fig. 9).
Conclusions
A GAT model was developed to predict vaporization properties. The extensive NIST-WTT HoV database consisting of ∼150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points was utilized for model development considering the temperature dependence of HoV and uncertainty quantification. The model showed good prediction accuracy with reasonable uncertainty estimation. The predictive model for HoV was expanded to other vaporization properties, whose databases are less extensive than HoV. Adopting transfer learning approaches for TC, FP, and TB was beneficial, using the trained layer weights from the HoV model. The transfer learning models showed lower errors in estimating these properties than the models from non-transfer training. The prediction and chemical interpretation were possible by analyzing attention weights and temperature response of atom feature vectors, leading to the elucidation of molecular structural effects on HoV. This workflow encompassing uncertainty quantification, transfer learning, and chemical interpretation was applied to the practical design of working fluids and (bio)fuel candidates.
000 data points was utilized for model development considering the temperature dependence of HoV and uncertainty quantification. The model showed good prediction accuracy with reasonable uncertainty estimation. The predictive model for HoV was expanded to other vaporization properties, whose databases are less extensive than HoV. Adopting transfer learning approaches for TC, FP, and TB was beneficial, using the trained layer weights from the HoV model. The transfer learning models showed lower errors in estimating these properties than the models from non-transfer training. The prediction and chemical interpretation were possible by analyzing attention weights and temperature response of atom feature vectors, leading to the elucidation of molecular structural effects on HoV. This workflow encompassing uncertainty quantification, transfer learning, and chemical interpretation was applied to the practical design of working fluids and (bio)fuel candidates.
Our predictive models and their applications are relevant to some of the 12 Green Chemistry Principles:22 (i) less hazardous/toxic materials, (ii) energy efficient by design, (iii) renewable rather than designing new material, and (iv) design products for degradation. Principle (i) was considered by including fuel candidates’ YSI and vaporization properties that influence emissions as screening criteria. Principle (ii) was taken into account since vaporization properties also affect chemicals’ energy efficiency when being used as working fluids and alternative fuels. In addition, we mainly considered compounds that are derivable from biomass, which is related to Principle (iii). Predicting glass transition temperatures of polymers can lead to Principle (iv).
The computational approaches introduced in this contribution can be used for other molecular properties related to the design of green chemicals, facilitating clean and sustainable energy production. Particularly, our predictive models can be expanded to Green Indices that quantify environmental impacts, emissions, and carbon economy. One can adopt other databases of Green Indices and re-train the GAT models.128 Transfer learning can also be applied if the target properties of interest are correlated with the vaporization properties.
Methods
The following procedure was carried out for the data collection and curation. SMILES strings of molecules were generated by converting their IUPAC names or CAS numbers into SMILES via Chemical Identifier Resolver developed by the National Institutes of Health (NIH)129 and the PubChemPy package.130 The RDKit cheminformatics package131 was utilized for canonicalizing SMILES strings and generating atom features and connectivity of molecules that are used as inputs of our GAT model. Our GAT model was programmed in Python 3.7132 using the Deep Graph Library 0.7133 with the TensorFlow 2.4134 backend. In the GAT, the given 16-dimensional input features H(0) pass through graph convolution layers considering attention weights (α) that impose different convolution weights to each bond based on other surrounding atoms. The updated atom feature vector of atom i at the (l + 1)-th layer is:
is: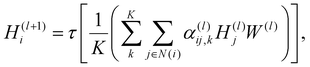 | (2) |
Such attention weights with multiple attention heads are capable of capturing long-range, non-local, global effects of molecular structures on HoV. Next, the two-stage global update scheme was combined with our attention mechanisms to incorporate temperature information into the model. The first update is carried out by:
| v′ = v + τ[ϕ1(v) + ϕ2(u)], | (3) |
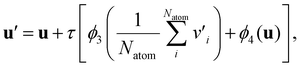 | (4) |
The first update propagates the temperature condition to individual atoms in a molecule. The subsequent update is for the aggregation of the atom-wise responses to temperature changes and the incorporation of the collected information into the updated global feature vector. Overall, atom and global feature vectors are updated mutually, simulating the effects of a molecule on its surroundings during vaporization and vice versa, which leads to a physics-informed description of vaporization.
The KL divergence is defined as
 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 data points for 200 epochs using one V100 GPU took about two hours.
105 data points for 200 epochs using one V100 GPU took about two hours.
Experimental details of HoV measurements
Pure component symmetric ethers and beta hydroxy hexanoate esters investigated for HoV measurement were purchased in >98% purity from Sigma Aldrich. Asymmetric ethers were custom synthesized by Advanced Molecular Technologies of Melbourne, Australia. A Differential Scanning Calorimeter/Thermogravimetric Analyzer (DSC/TGA) (TA Instruments, Q600-series) was utilized to perform HoV measurements. It was based on a previous method developed for gasoline samples.135,136 The instrument was calibrated per the manufacturer's specifications, and a correction factor was calculated for the instrument (1.17) using n-butyl benzene because its HoV is well documented.137,138 Utilizing a similar methodology to that developed by Luning Prak and coworkers,139 each pure component was placed in an aluminum pan (TA Instruments, Tzero Pan 901683.901) with a hermetically sealed pinhole lid (TA Instruments, Tzero Hermetic Lid w/Pin Hole 901685.901). The DSC/TGA was held isothermally for one minute and then ramped at a rate of 30 °C per minute until it reached a temperature of 15–20 °C below the boiling point of the pure component. The DSC/TGA was then held isothermally for 30 seconds before again being ramped at a rate of 10 °C per minute until it reached a temperature within 5 °C of the boiling point. It then remained isothermal until the sample had completely evaporated, as determined by the TGA. The heat flow was integrated from the isothermal ramp's start until the sample evaporation's end. The HoV was calculated as the combined heat flow divided by the mass loss recorded by the TGA. Each sample was run in triplicate, and the average HoV was reported.Author contributions
Y. K., J. C., R. L. M., P. C. S. J., and S. K. conceptualized the manuscript. Y. K. developed the Python code for ML models of vaporization properties. Y. K. and H. J. did the database curation of vaporization properties. L. E. M., G. M. F., and R. L. M. carried out the HoV experiments. K. J. performed 10-fold cross-validation and hyperparameter tuning of the model. J. C. applied the ML models to the design of working fluids and fuels and analyzed the results. All authors contributed to preparing and reviewing the manuscript.Data availability
Our GitHub repository (https://github.com/BioE-KimLab/HoVpred) contains Python source codes and predictive models with detailed instructions about how to run predictions for new molecules. The molecules used for training the model are available through the GitHub repository, although subscriptions are required to access the property data in NIST-WTT and DIPPR databases. The data points from literature were not redacted and are available through the GitHub repository.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge Chris Muzny and Demian Riccardi (NIST) for their help accessing NIST-WTT. The ExxonMobil Technology and Engineering Company funded this research. The views represented are those of the authors and do not necessarily reflect those of ExxonMobil Technology and Engineering Company. The computer time was provided by the NSF Extreme Science and Engineering Discovery Environment (XSEDE), Grant no. TG-CHE210034 and by the National Renewable Energy Laboratory Computational Science Center. This work was partly authored by Alliance for Sustainable Energy, LLC, the Manager and Operator of the National Renewable Energy Laboratory for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains, and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work or allow others to do so for U.S. Government purposes. H. Jung acknowledges the support by the MOTIE (Ministry of Trade, Industry, and Energy) in Korea under the Fostering Global Talents for Innovative Growth Program (P0008747) supervised by the Korea Institute for Advancement of Technology (KIAT). Y. Kim acknowledges that this work was supported by the Global Joint Research Program funded by the Pukyong National University (202411660001).References
- J. E. Bistline and G. J. Blanford, Energy Clim. Change, 2021, 2, 100045 CrossRef CAS.
- R. Loni, O. Mahian, C. N. Markides, E. Bellos, W. G. le Roux, A. Kasaeian, G. Najafi and F. Rajaee, Renewable Sustainable Energy Rev., 2021, 150, 111410 CrossRef CAS.
- A. Haghighi, M. R. Pakatchian, M. E. H. Assad, V. N. Duy and M. Alhuyi Nazari, J. Therm. Anal. Calorim., 2021, 144, 1799–1814 CrossRef CAS.
- J. Bao and L. Zhao, Renewable Sustainable Energy Rev., 2013, 24, 325–342 CrossRef CAS.
- H. Chen, D. Y. Goswami and E. K. Stefanakos, Renewable Sustainable Energy Rev., 2010, 14, 3059–3067 CrossRef CAS.
- A. I. Papadopoulos, M. Stijepovic and P. Linke, Appl. Therm. Eng., 2010, 30, 760–769 CrossRef CAS.
- W. Su, L. Zhao and S. Deng, Appl. Energy, 2017, 202, 618–627 CrossRef CAS.
- Y. Peng, W. Su, N. Zhou and L. Zhao, Energy Convers. Manage., 2020, 221, 113204 CrossRef CAS.
- X. Luo, Y. Wang, J. Liang, J. Qi, W. Su, Z. Yang, J. Chen, C. Wang and Y. Chen, Energy, 2019, 174, 122–137 CrossRef CAS.
- A. Piña-Martinez, S. Lasala, R. Privat, V. Falk and J.-N. Jaubert, ACS Sustainable Chem. Eng., 2021, 9, 11807–11824 CrossRef.
- K. Nakolan, Annual Energy Outlook 2022, Energy Information Administration, 2022 Search PubMed.
- C. Choudhari and S. Sapali, Energy Procedia, 2017, 109, 346–352 CrossRef CAS.
- P. C. St. John, S. Kim and R. L. McCormick, Energy Fuels, 2019, 33, 10290–10296 CrossRef CAS.
- H. Liu, K. H. Yoo, A. L. Boehman and Z. Zheng, Energy Fuels, 2018, 32, 1884–1892 CrossRef CAS.
- D. B. Hulwan and S. V. Joshi, Appl. Energy, 2011, 88, 5042–5055 CrossRef CAS.
- Y. Huang, Y. Li, K. Luo and J. Wang, Proc. Inst. Mech. Eng., Part D, 2020, 234, 2988–3000 CrossRef CAS.
- P.-M. Yang, Y.-C. Lin, K. C. Lin, S.-R. Jhang, S.-C. Chen, C.-C. Wang and Y.-C. Lin, Energy, 2015, 90, 266–273 CrossRef CAS.
- M. A. Ratcliff, B. Windom, G. M. Fioroni, P. St. John, S. Burke, J. Burton, E. D. Christensen, P. Sindler and R. L. McCormick, Appl. Energy, 2019, 250, 1618–1631 CrossRef CAS.
- P. C. St. John, S. Kim and R. L. McCormick, Energy Fuels, 2019, 33, 10290–10296 CrossRef CAS.
- S. Mishra, K. Anand and P. S. Mehta, Energy Fuels, 2016, 30, 10425–10434 CrossRef CAS.
- C. Wang, S. Zeraati-Rezaei, L. Xiang and H. Xu, Appl. Energy, 2017, 191, 603–619 CrossRef CAS.
- R. A. Sheldon, ACS Sustainable Chem. Eng., 2018, 6, 32–48 CrossRef CAS.
- K. M. Watson, Ind. Eng. Chem., 1943, 35, 398–406 CrossRef CAS.
- D. L. Morgan, Fluid Phase Equilib., 2007, 256, 54–61 CrossRef CAS.
- K. G. Joback and R. C. Reid, Chem. Eng. Commun., 1987, 57, 233–243 CrossRef CAS.
- Q. Wang, P. Ma, Q. Jia and S. Xia, J. Chem. Eng. Data, 2008, 53, 1103–1109 CrossRef CAS.
- F. Z. Serat, A. M. Benkouider, A. Yahiaoui and F. Bagui, Fluid Phase Equilib., 2017, 449, 52–59 CrossRef CAS.
- Q. Jia, Q. Wang and P. Ma, J. Chem. Eng. Data, 2010, 55, 5614–5620 CrossRef CAS.
- F. Gharagheizi, P. Ilani-Kashkouli, W. E. Acree Jr., A. H. Mohammadi and D. Ramjugernath, Fluid Phase Equilib., 2013, 360, 279–292 CrossRef CAS.
- F. Gharagheizi, O. Babaie and S. Mazdeyasna, Ind. Eng. Chem., 2011, 50, 6503–6507 CrossRef CAS.
- R. Li, J. M. Herreros, A. Tsolakis and W. Yang, Fuel, 2021, 304, 121437 CrossRef CAS.
- F. Gharagheizi, Fluid Phase Equilib., 2012, 317, 43–51 CrossRef CAS.
- Q. Jia, X. Yan, T. Lan, F. Yan and Q. Wang, J. Mol. Liq., 2019, 282, 484–488 CrossRef CAS.
- M. R. Fissa, Y. Lahiouel, L. Khaouane and S. Hanini, J. Mol. Graphics Modell., 2019, 87, 109–120 CrossRef PubMed.
- A. R. Aouichaoui, S. S. Mansouri, J. Abildskov and G. Sin, AIChE J., 2022, e17696 CrossRef CAS.
- X. Yao, Y. Wang, X. Zhang, R. Zhang, M. Liu, Z. Hu and B. Fan, Chemom. Intell. Lab. Syst., 2002, 62, 217–225 CrossRef CAS.
- M. Banchero and L. Manna, Molecules, 2018, 23, 1379 CrossRef.
- L. M. Egolf, M. D. Wessel and P. C. Jurs, J. Chem. Inf. Comput. Sci., 1994, 34, 947–956 CrossRef CAS.
- A. R. Katritzky, L. Mu and M. Karelson, J. Chem. Inf. Comput. Sci., 1998, 38, 293–299 CrossRef CAS.
- B. E. Turner, C. L. Costello and P. C. Jurs, J. Chem. Inf. Comput. Sci., 1998, 38, 639–645 CrossRef CAS.
- D. Sola, A. Ferri, M. Banchero, L. Manna and S. Sicardi, Fluid Phase Equilib., 2008, 263, 33–42 CrossRef CAS.
- M. A. Sobati and D. Abooali, Thermochim. Acta, 2015, 602, 53–62 CrossRef CAS.
- G. Espinosa, D. Yaffe, A. Arenas, Y. Cohen and F. Giralt, Ind. Eng. Chem., 2001, 40, 2757–2766 CrossRef CAS.
- F. Gharagheizi and M. Mehrpooya, Mol. Divers., 2008, 12, 143–155 CrossRef CAS.
- X. Yao, X. Zhang, R. Zhang, M. Liu, Z. Hu and B. Fan, Comput. Chem., 2002, 26, 159–169 CrossRef CAS.
- L. Catoire and V. Naudet, J. Phys. Chem. Ref. Data, 2004, 33, 1083–1111 CrossRef CAS.
- A. R. Katritzky, I. B. Stoyanova-Slavova, D. A. Dobchev and M. Karelson, J. Mol. Graphics Modell., 2007, 26, 529–536 CrossRef CAS.
- Y. Pan, J. Jiang and Z. Wang, J. Hazard. Mater., 2007, 147, 424–430 CrossRef CAS.
- F. A. Carroll, C.-Y. Lin and F. H. Quina, Energy Fuels, 2010, 24, 4854–4856 CrossRef CAS.
- X. Liu and Z. Liu, J. Chem. Eng. Data, 2010, 55, 2943–2950 CrossRef CAS.
- F. A. Carroll, C.-Y. Lin and F. H. Quina, Ind. Eng. Chem., 2011, 50, 4796–4800 CrossRef CAS.
- F. Gharagheizi, A. Eslamimanesh, A. H. Mohammadi and D. Richon, Ind. Eng. Chem., 2011, 50, 5877–5880 CrossRef CAS.
- J. M. Godinho, C.-Y. Lin, F. A. Carroll and F. H. Quina, Energy Fuels, 2011, 25, 4972–4976 CrossRef CAS.
- D. A. Saldana, L. Starck, P. Mougin, B. Rousseau, L. Pidol, N. Jeuland and B. Creton, Energy Fuels, 2011, 25, 3900–3908 CrossRef CAS.
- D. Mathieu and T. Alaime, J. Hazard. Mater., 2014, 267, 169–174 CrossRef CAS.
- L. Y. Phoon, A. A. Mustaffa, H. Hashim and R. Mat, Ind. Eng. Chem., 2014, 53, 12553–12565 CrossRef CAS.
- T. C. Le, M. Ballard, P. Casey, M. S. Liu and D. A. Winkler, Mol. Inf., 2015, 34, 18–27 CrossRef CAS.
- X. Sun, N. J. Krakauer, A. Politowicz, W. T. Chen, Q. Li, Z. Li, X. Shao, A. Sunaryo, M. Shen and J. Wang, Mol. Inf., 2020, 39, 1900101 CrossRef CAS.
- J. Tetteh, T. Suzuki, E. Metcalfe and S. Howells, J. Chem. Inf. Comput. Sci., 1999, 39, 491–507 CrossRef CAS.
- Y.-m. Dai, Z.-p. Zhu, Z. Cao, Y.-f. Zhang, J.-l. Zeng and X. Li, J. Mol. Graphics Modell., 2013, 44, 113–119 CrossRef CAS PubMed.
- A. R. Katritzky, V. S. Lobanov and M. Karelson, J. Chem. Inf. Comput. Sci., 1998, 38, 28–41 CrossRef CAS.
- L. Jin and P. Bai, Chemom. Intell. Lab. Syst., 2016, 157, 127–132 CrossRef CAS.
- L. Jin and P. Bai, Fluid Phase Equilib., 2016, 427, 194–201 CrossRef CAS.
- B. Osaghi and F. Safa, Rev. Roum. Chim., 2019, 64, 183–189 CrossRef.
- D. Ericksen, W. V. Wilding, J. L. Oscarson and R. L. Rowley, J. Chem. Eng. Data, 2002, 47, 1293–1302 CrossRef CAS.
- J. h. Zhang, Z. m. Liu and W. r. Liu, J. Chemom., 2014, 28, 161–167 CrossRef CAS.
- G. Espinosa, D. Yaffe, Y. Cohen, A. Arenas and F. Giralt, J. Chem. Inf. Comput. Sci., 2000, 40, 859–879 CrossRef CAS PubMed.
- M. N. Aldosari, K. K. Yalamanchi, X. Gao and S. M. Sarathy, Energy AI, 2021, 4, 100054 CrossRef.
- E. Al Ibrahim and A. Farooq, Energy Fuels, 2020, 34, 817–826 CrossRef CAS.
- C. Nieto-Draghi, G. Fayet, B. Creton, X. Rozanska, P. Rotureau, J.-C. de Hemptinne, P. Ungerer, B. Rousseau and C. Adamo, Chem. Rev., 2015, 115, 13093–13164 CrossRef CAS.
- Z. Jiao, H. U. Escobar-Hernandez, T. Parker and Q. Wang, Process Saf. Environ. Prot., 2019, 129, 280–290 CrossRef CAS.
- A. R. Katritzky, M. Kuanar, S. Slavov, C. D. Hall, M. Karelson, I. Kahn and D. A. Dobchev, Chem. Rev., 2010, 110, 5714–5789 CrossRef CAS.
- B. C. Koenig, W. Ji and S. Deng, Proc. Combust. Inst., 2023, 39, 5229–5238 CrossRef.
- P. Veličković, G. Cucurull, A. Casanova, A. Romero, P. Lio and Y. Bengio, arXiv:1710.10903, 2017.
- S. Ryu, J. Lim, S. H. Hong and W. Y. Kim, arXiv:1805.10988, 2018.
- S.-Y. Louis, Y. Zhao, A. Nasiri, X. Wang, Y. Song, F. Liu and J. Hu, Phys. Chem. Chem. Phys., 2020, 22, 18141–18148 RSC.
- W. Zhu, Y. Zhang, D. Zhao, J. Xu and L. Wang, J. Chem. Inf. Model., 2023, 63, 43–55 CrossRef CAS.
- M. Withnall, E. Lindelöf, O. Engkvist and H. Chen, J. Cheminf., 2020, 12, 1 CAS.
- Z. Xiong, D. Wang, X. Liu, F. Zhong, X. Wan, X. Li, Z. Li, X. Luo, K. Chen, H. Jiang and M. Zheng, J. Med. Chem., 2020, 63, 8749–8760 CrossRef CAS PubMed.
- X.-b. Ye, Q. Guan, W. Luo, L. Fang, Z.-R. Lai and J. Wang, Pattern Recognit., 2022, 128, 108659 CrossRef.
- M. Wiercioch and J. Kirchmair, Expert Syst. Appl., 2023, 213, 119055 CrossRef.
- S. S. Omee, S.-Y. Louis, N. Fu, L. Wei, S. Dey, R. Dong, Q. Li and J. Hu, Patterns, 2022, 3, 100491 CrossRef.
- A. R. N. Aouichaoui, F. Fan, S. S. Mansouri, J. Abildskov and G. Sin, J. Chem. Inf. Model., 2023, 63, 725–744 CrossRef CAS.
- D. Jiang, Z. Wu, C.-Y. Hsieh, G. Chen, B. Liao, Z. Wang, C. Shen, D. Cao, J. Wu and T. Hou, J. Cheminf., 2021, 13, 12 CAS.
- K. Kroenlein, C. Muzny, A. Kazakov, V. Diky, R. Chirico, J. Magee, I. Abdulagatov and M. Frenkel, NIST/TRC Web Thermo Tables (WTT), NIST Standard Reference Subscription Database 3—Professional Edition, version 2-2012-1-Pro; Thermodynamics Research Center (TRC), National Institute of Standards and Technology, Boulder, CO, 2011.
- W. Wilding, T. Knotts, N. Giles and R. Rowley, Design Institute for Physical Properties, AIChE, New York, NY, 2020 Search PubMed.
- M. Wen, S. M. Blau, E. W. C. Spotte-Smith, S. Dwaraknath and K. A. Persson, Chem. Sci., 2021, 12, 1858–1868 RSC.
- Y. Ye and S. Ji, IEEE Trans. Knowl. Data Eng., 2023, 35, 905–916 Search PubMed.
- S. Brody, U. Alon and E. Yahav, arXiv preprint arXiv:2105.14491, 2021.
- H. Xu, X. Yang, W. Wang, J. Du and J. Gao, Meas. Sci. Technol., 2023, 34, 125026 CrossRef.
- P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez, V. Zambaldi, M. Malinowski, A. Tacchetti, D. Raposo, A. Santoro and R. Faulkner, arXiv preprint arXiv:1806.01261, 2018.
- Y. Kim, J. Cho, N. Naser, S. Kumar, K. Jeong, R. L. McCormick, P. C. St. John and S. Kim, Proc. Combust. Inst., 2023, 39, 4969–4978 CrossRef.
- Y. Kim, H. Jung, S. Kumar, R. S. Paton and S. Kim, Chem. Sci., 2024, 15, 923–939 RSC.
- F. H. Vermeire and W. H. Green, Chem. Eng. J., 2021, 418, 129307 CrossRef CAS.
- M. Thomas, A. Boardman, M. Garcia-Ortegon, H. Yang, C. de Graaf and A. Bender, Applications of artificial intelligence in drug design: opportunities and challenges, in Artificial Intelligence in Drug Design, 2022 Search PubMed.
- A. P. Soleimany, A. Amini, S. Goldman, D. Rus, S. N. Bhatia and C. W. Coley, ACS Cent. Sci., 2021, 7, 1356–1367 CrossRef CAS.
- C.-I. Yang and Y.-P. Li, ChemRxiv Preprint, 2022, DOI:10.26434/chemrxiv-22022-qt26449t.
- K. Gubaev, E. V. Podryabinkin and A. V. Shapeev, J. Chem. Phys., 2018, 148, 241727 CrossRef PubMed.
- N. S. Eyke, W. H. Green and K. F. Jensen, React. Chem. Eng., 2020, 5, 1963–1972 RSC.
- F. Noé, S. Olsson, J. Köhler and H. Wu, Science, 2019, 365, 1001 CrossRef.
- I. Anishchenko, S. J. Pellock, T. M. Chidyausiku, T. A. Ramelot, S. Ovchinnikov, J. Hao, K. Bafna, C. Norn, A. Kang, A. K. Bera, F. DiMaio, L. Carter, C. M. Chow, G. T. Montelione and D. Baker, Nature, 2021, 600, 547–552 CrossRef CAS PubMed.
- S. Bhakat, RSC Adv., 2022, 12, 25010–25024 RSC.
- L. I. Vazquez-Salazar, E. D. Boittier, O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2021, 17, 4769–4785 CrossRef CAS PubMed.
- M. Ihme, W. T. Chung and A. A. Mishra, Prog. Energy Combust. Sci., 2022, 91, 101010 CrossRef.
- P. Sharma, W. T. Chung, B. Akoush and M. Ihme, Energies, 2023, 16, 2343 CrossRef CAS.
- N. A. Huq, X. Huo, G. R. Hafenstine, S. M. Tifft, J. Stunkel, E. D. Christensen, G. M. Fioroni, L. Fouts, R. L. McCormick and P. A. Cherry, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 26421–26430 CrossRef CAS.
- D. J. Gaspar, C. J. Mueller, R. L. McCormick, J. Martin, S. Som, G. M. Magnotti, J. Burton, D. Vardon, V. Dagle and T. L. Alleman, et al., Top 13 Blendstocks Derived from Biomass for Mixing-Controlled Compression-Ignition (Diesel) Engines: Bioblendstocks with Potential for Decreased Emissions and Improved Operability, Pacific Northwest National Lab. (PNNL), Richland, WA (United States), 2021, Report No.: PNNL-31421 DOI:10.2172/18065642.
- H. Lim and Y. Jung, Chem. Sci., 2019, 10, 8306–8315 RSC.
- J. Garai, Fluid Phase Equilib., 2009, 283, 89–92 CrossRef CAS.
- J. Cho, Y. Kim, B. D. Etz, G. M. Fioroni, N. Naser, J. Zhu, Z. Xiang, C. Hays, J. V. Alegre-Requena and P. C. S. John, Sustainable Energy Fuels, 2022, 6, 3975–3988 RSC.
- J. Xu and C. Yu, Energy, 2014, 74, 719–733 CrossRef CAS.
- B.-T. Liu, K.-H. Chien and C.-C. Wang, Energy, 2004, 29, 1207–1217 CrossRef CAS.
- T. Zhang, L. Liu, J. Hao, T. Zhu and G. Cui, Appl. Therm. Eng., 2021, 188, 116626 CrossRef CAS.
- X. Zhang, C. Zhang, M. He and J. Wang, J. Therm. Sci., 2019, 28, 643–658 CrossRef CAS.
- B. E. Poling, J. M. Prausnitz and J. P. O'Connell, Properties of Gases and Liquids, McGraw-Hill Education, New York, 5th edn, 2001 Search PubMed.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen and B. Yu, Nucleic Acids Res., 2019, 47, D1102–D1109 CrossRef PubMed.
- H. Zhai, Q. An, L. Shi, V. Lemort and S. Quoilin, Renewable Sustainable Energy Rev., 2016, 64, 790–805 CrossRef CAS.
- I. H. Bell, J. Wronski, S. Quoilin and V. Lemort, Ind. Eng. Chem., 2014, 53, 2498–2508 CrossRef CAS.
- I. H. Aljundi, Renewable Energy, 2011, 36, 1196–1202 CrossRef CAS.
- J. M. Zinsalo, L. Lamarche and J. Raymond, Energy, 2022, 245, 123259 CrossRef CAS.
- N. M. Eagan, B. M. Moore, D. J. McClelland, A. M. Wittrig, E. Canales, M. P. Lanci and G. W. Huber, Green Chem., 2019, 21, 3300–3318 RSC.
- ASTM International, ASTM D4814-21c, Standard Specification for Automotive Spark–Ignition Engine Fuel, 2021 Search PubMed.
- ASTM International, ASTM D975-22, Standard Specification for Diesel Fuel, 2022 Search PubMed.
- ASTM International, ASTM D1655-22, Standard Specification for Aviation Turbine Fuels, 2022 Search PubMed.
- J. Holladay, Z. Abdullah and J. Heyne, Sustainable Aviation Fuel: Review of Technical Pathways, Office of Energy Efficiency & Renewable Energy, US Department of Energy, 2020, ch. 2, pp. 7–16, https://www.energy.gov/sites/prod/files/2020/09/f78/beto-sust-aviation-fuel-sep-2020.pdf.
- G. Wypych, Handbook of polymers, Elsevier, 2022 Search PubMed.
- U. T. Kreibch and H. Batzer, Angew. Makromol. Chem., 1979, 83, 57–112 CrossRef.
- G. H. Thomson, Int. J. Thermophys., 1996, 17, 223–232 CrossRef CAS.
- NCI/CADD Chemical Identifier Resolver. Accessed June 13, 2024. https://cactus.nci.nih.gov/chemical/structure.
- M. Swain, PubChemPy documentation, 2014 Search PubMed.
- S. Riniker and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2562–2574 CrossRef CAS PubMed.
- G. Van Rossum , USENIX annual technical conference, 2007, vol. 41, p. 36.
- M. Wang, L. Yu, D. Zheng, Q. Gan, Y. Gai, Z. Ye, M. Li, J. Zhou, Q. Huang and C. Ma, Python Programming Language, 2019 Search PubMed.
- M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving and M. Isard, 12th USENIX symposium on operating systems design and implementation, 2016, pp. 265–283.
- G. M. Fioroni, L. Fouts, E. Christensen, J. E. Anderson and R. L. McCormick, Energy Fuels, 2018, 32, 12607–12616 CrossRef CAS.
- G. Fioroni, C. K. Hays, E. D. Christensen and R. L. McCormick, SAE Int. J. Fuels Lubr., 2021, 14, 175–276 CAS.
- Benzene, n-butyl-. Accessed October 8, 2021. https://webbook.nist.gov/cgi/cbook.cgi?ID=C104518&Mask=4#ref-12.
- W. V. Steele, R. D. Chirico, S. E. Knipmeyer and A. Nguyen, J. Chem. Eng. Data, 2002, 47, 648–666 CrossRef CAS.
- D. J. Luning Prak, M. P. Foley, L. Dorn, P. C. Trulove, J. S. Cowart and D. P. Durkin, Energy Fuels, 2020, 34, 4046–4054 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Detailed information about split data sets, prediction uncertainty, hyperparameter optimization. See DOI: https://doi.org/10.1039/d4gc01994f |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2024 |