Multi-objective optimization strategy for green solvent design via a deep generative model learned from pre-set molecule pairs†
Jun
Zhang
a,
Qin
Wang
*b,
Huaqiang
Wen
a,
Vincent
Gerbaud
 c,
Saimeng
Jin
c,
Saimeng
Jin
 a and
Weifeng
Shen
a and
Weifeng
Shen
 *a
*a
aSchool of Chemistry and Chemical Engineering, Chongqing University, Chongqing 400044, China. E-mail: shenweifeng@cqu.edu.cn
bSchool of Chemistry and Chemical Engineering, Chongqing University of Science and Technology, Chongqing 401331, China. E-mail: wangq356@mail2.sysu.edu.cn
cLaboratoire de Génie Chimique, Université de Toulouse, CNRS, INP, UPS, Toulouse, France
First published on 6th December 2023
Abstract
Green solvent design is usually a multi-objective optimization problem that requires identification of a set of solvent molecules to balance multiple, often trade-off, properties. At the same time, process constraints need to be addressed since solvent properties impact the process feasibility like in the extractive distillation separation process. Hence, a green solvent multi-objective optimization framework is proposed with EH&S properties, process constraints, and energy consumption analysis, where the molecular design optimization model relies upon the ability of the proposed infinite dilution activity coefficient (IDAC) direct prediction model to accurately predict process properties in addition to molecular properties. The process properties are short-cut properties of the extractive distillation process, namely selectivity and solution capacity. To this end, the proposed IDAC direct prediction model is employed to prepare molecule pairs with selectivity and solution capacity improvement constraints to train the molecular multi-objective optimization model, which can learn the optimization path from the pre-set molecule pairs and then optimize a given solvent via the prediction of a disconnection site and molecular fragment addition or removal at that site. An extractive distillation process to separate a cyclohexane/benzene mixture is taken as an example to demonstrate the proposed framework. As a result, three candidate green solvents are optimized and designed to recover benzene from mixtures of benzene and cyclohexane. The proposed green solvent multi-objective optimization framework is flexible enough to be employed in other chemical separation processes, where solvent property assessment is needed to evaluate the feasibility and performance of the processes.
1 Introduction
In many separation processes, such as azeotropic or extractive distillation or liquid–liquid extraction, a solvent is needed to perform the desired separation. Solvent design is inherently a constrained multi-objective optimization problem.1,2 The first set of constraints concerns matching the desired solvent property values. These properties are multiple and usually cover not only molecular properties related to the primary function of the solvent, such as solubilizing an active principle or having a preferred affinity with one of the molecules in a mixture, but also other properties that may ease the process operation. Model-based property predictions are numerous but are confronted with various challenges, such as coping with stereoisomers for group-contribution methods, or correctly sampling the vast solvent search space spanning the chemistry field for computer-costly quantum mechanical methods.Besides, in separation processes, the process feasibility sets additional constraints on the solvent. Hence, a search simultaneously combining molecular and process constraints is a challenge, which is the purpose of our study, and which would be facilitated by using model-based approaches to optimize the structure of solvent molecules. But successive optimal solvent design first followed by an optimal process design bears a risk of error propagation that could rule out the whole procedure.
In this case, we proposed a molecular multi-objective optimization model to purposefully modify the structure of solvent molecules with some drawbacks (such as EH&S negative impact) to obtain the green solvent with the desired separation performance rather than simply utilizing a molecular generative model to enlarge the chemical space for subsequent solvent screenings with multi-index constraints. The multi-objective optimization model can learn the optimization path from the pre-set molecule pairs. Every pair of molecules (Mx and My) in the pre-set molecule pairs had similar molecular structures and only had a single different disconnection site, but the scores of both selectivity and solution capacity of My were at least 20% larger than those of Mx. The prepared pre-set molecular pairs were used to train the proposed molecular multi-objective optimization model, which can learn the difference between the molecular pairs and can learn the optimization path from Mx to My. To prepare the molecule pairs, an improved deep learning-based IDAC direct prediction model trained over a COSMO-SAC database was developed for predicting the selectivity and solution capacity of the molecule pairs. The proposed IDAC direct prediction method can provide superior predictive performance compared with the IDAC indirect prediction method, which first predicted the VCOSMO and 51 σ-profile and then calculated the IDAC using the COSMO-SAC model. The indirect IDAC prediction method resulted in more information lost during the prediction and COSMO-SAC calculation processes. The improved deep learning-based direct IDAC prediction model was integrated with the molecular multi-objective optimization model to form the proposed green solvent multi-objective and multi-scale optimization framework with EH&S properties and process constraints, and energy and economic analysis. The proposed green solvent multi-objective and multi-scale optimization framework can: (1) simultaneously optimize multiple trade-off properties such as the selectivity and solution capacity of the solvent; (2) learn from the pre-set molecule pairs that have similar molecular structures but have differences in their properties of interest; (3) visualize the optimization path of the solvent's molecular structure; and (4) accurately and directly predict the IDAC of the molecules.
The paper is organized as follows: the next section (Section 2) gives a non-exhaustive overview of solvent design issues, related computer-aided approaches, and connections to some process design issues for extractive distillation processes. Section 3 describes the integrated molecular multi-objective and multi-scale optimization framework. Section 4 describes and evaluates the performance of the improved model for the direct prediction of the infinite dilution activity coefficient using deep learning techniques. Section 5 introduces the molecular multi-objective optimization model. Section 6 is an illustrative case study about solvent optimization and design for an extractive distillation process.
2 Background
When designing a solvent for separation process, one should match target values with properties that directly impact the process separation feasibility such as the selectivity and solution capacity in liquid–liquid separation, melting point in solid separation processes, etc. At the same time, properties that affect the process performance and operation, in terms of economics and energy requirements, should also be considered, such as the boiling point for the distillation process and the molar volume for batch processes along with properties related to transport phenomena like viscosity, surface tension, heat capacity, etc.3 Nowadays, the sustainability of new solvents (e.g., toxicity, safety, environmental impact, etc.)4–6 is also becoming a key design objective,7 which is especially important for the green solvent design task, and for complying with regulations such as the US Toxicity Characteristic Leaching Procedure (TCLP) or the EU Registration, Evaluation, Authorization, and Restriction of Chemicals (REACH), which affect process authorization. Considering the vast number of potential solvents, the trial-and-error method for solvent identification may be highly time-consuming and even unrealistic when one considers only a single property. In addition, promising solvents could be missed if the trial-and-error method relies on a fixed solvent database. Hence, model-based solvent selection or design methods, like computer-aided molecular design (CAMD), are extremely desirable to address the issue of exploring the vast solvent search space.8In support of any computer-aided solvent design approach, one needs to access solvent property values. Evaluation of the solvent thermodynamic properties requires measuring them or calculating them using property estimation models because they are more appropriate in a preliminary process design phase. Hence, property calculation or estimation models play a significantly important role in model-based solvent design methods since they can correlate molecular structures with solvent thermodynamic properties. For any property of interest in a real process, there exist a variety of property models, and choosing the most suitable models is a key step.9 Each model bears different accuracies, predictive capabilities, and computation costs.10 The property estimation methods mainly include descriptor-based methods,11 group-contribution (GC) methods,12 quantum mechanical (QM) methods,13 and deep learning (DL) methods.14,15 For example, for extractive distillation, the process we select for illustration, one real property of relevance might be stated as having a preferential affinity with one of the compounds in the mixture to be separated. It can be evaluated by various models, by comparing the similarity of the Hansen solubility parameter values between the solvent and the molecule of interest, a simple correlative model with no access to temperature dependency; by solving the thermodynamic phase equilibrium for computing solubility with temperature dependency; or by comparing interaction surface potentials, like the COSMO sigma potential curves, which requires quantum mechanics calculations. The GC method is one of the most widely utilized and efficient techniques to evaluate macroscopic physicochemical properties. However, the performance of first-order GC models, with contributions regressed over experimental data directly related to the occurrence of simple chemical groups like –CH2, –OH, etc., is sometimes weakened because they cannot take account of the proximity effects and distinguish between isomers.3,16 To address these issues, second- and third-order GC models have been developed for discriminating the structural isomers.17 but they are still deficient of many stereoisomers such as cis/trans isomers.18 These issues can be tackled with quantum mechanical-based (QM-based) solvation models, such as COSMO-RS19,20 and COSMO-SAC.21,22 With only a few parameters such as the surface charge density profile (σ-profile) and the cavity volumes (VCOSMO), the COSMO-based models can achieve a decent accuracy for the calculation of thermodynamic properties. However, the initial QM calculations bear a heavy computational cost and are highly time-consuming, and even unrealistic when exploring the vast search space of solvent molecules.23 To this end, the GC-COSMO techniques have been proposed as a shortcut to more efficiently access the VCOSMO and σ-profile.24,25 However, due to the inherent GC limitations, these GC-COSMO techniques not only have difficulties in appropriately handling isomers and proximity effects but are also limited in the variety of functional groups available in open-source databases. With the availability of the COSMO-type databases (e.g., the VT-200526), as alternatives, deep learning-based (DL-based) techniques27–30 can be applied as another shortcut to obtain the σ-profile and VCOSMO.31,32 However, the VT-2005 database only contains 1431 compounds, which may not be enough to train a DL-based prediction model with satisfying generalization ability. Additionally, such DL-based prediction models are developed to predict the VCOSMO and the σ-profile, and then the predicted parameters are used to calculate the IDAC. This indirect IDAC calculation process could lead to a decline in accuracy.
Once property estimation models are available, computer-aided molecular design33 (CAMD) is an effective approach for screening existing solvents and designing new ones. In CAMD, pre-prepared molecular functional groups are assembled to generate potential solvents through mixed integrated linear programming (MILP) or mixed integrated non-linear programming (MINLP) or stochastic algorithms with objective functions and constraints (such as molecular structural, property, and process operating constraints).34–37 However, with the increase in the number of preselected functional groups, the CAMD method may face the problem of combination explosion.3,38
Recent advancements in the domain of artificial intelligence have accelerated the development and application of techniques for inverse molecular design.39–42 For instance, molecular generation models have been applied in many fields.38,43 Molecular graph generation techniques44 as an outstanding representative have become one of the most widely adopted approaches for molecular design. Recently, a fragment-based hierarchical encoder–decoder model for molecular generation was proposed by Jin et al.45 Fragments extracted from the training molecules were analogous to the molecular functional groups used in the group-contribution methods. The molecular fragments could integrate knowledge from the chemistry domain interpretability into the model.46 The molecules can be optimized by predicting a disconnection site and performing molecular fragment addition or removal at that site. However, this model cannot simultaneously optimize multiple trade-off properties of the solvent molecules. Therefore, this kind of single objective optimization model is very difficult to couple with the multi-dimensional and highly nonlinear chemical separation process. Although there are deep molecular optimization models labeled “multi-objective”,47,48 these models usually aggregate multiple objectives into a single scalar objective.
However, solvent property knowledge is only a first step in the design of a performing separation process, for which the process model can be highly nonlinear because the process feasibility is often directly related to the characteristics of the solvent. For example, there are some trade-off properties such as the selectivity and solution capacity that are not perfectly correlated and, therefore, molecular multi-objective optimization cannot be addressed by these models. Hence, some authors have explored the simultaneous design of the solvent and the process attributes in a so-called reverse engineering computer aided molecule and process design (CAMPD) approach. For example, some authors have proposed a framework for the integrated design of a solvent and extractive distillation process by solving a multi-objective optimization problem addressing constraints related to thermodynamic process feasibility, along with process operation, a process model, and molecular constraints,49 or a more rigorous rate-based model.50 In these studies, the property prediction in a molecular scale is addressed using COSMO approaches while the process model can be a pinch-based model based on a minimum solvent flow rate and minimum energy demand49 or a more rigorous rate-based model.50 The use of such process models is relevant for an accurate process design but there exist simpler criteria for assessing extractive distillation feasibility, such as solvent capacity and selectivity,51 which are further related to infinite dilution activity coefficients (IDAC), and univolatility curves.52 In this study, we propose a molecular multi-objective and multi-scale optimization framework for the combined molecular and process design with the predicted process constraints (solvent selectivity and capacity based on IDAC) where the process-related properties are directly used to train the molecular structure optimization model, with the help of deep-learning techniques.
3 The deep learning-based molecular multi-objective and multi-scale optimization framework for a green solvent design
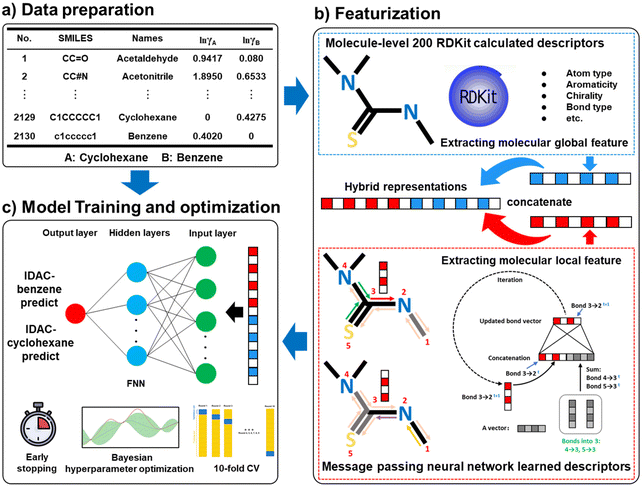
The deep learning-based molecular multi-objective and multi-scale optimization framework for a green extraction distillation solvent design is presented by integrating an improved deep learning-based model for IDAC direct prediction (in Section 4) and a data-driven deep molecular multi-objective optimization model (in Section 5) as shown in Fig. 1. Meanwhile, the EH&S property constraints, process constraints, and energy consumption analysis are considered to ensure the sustainability and technological economy of green solvents.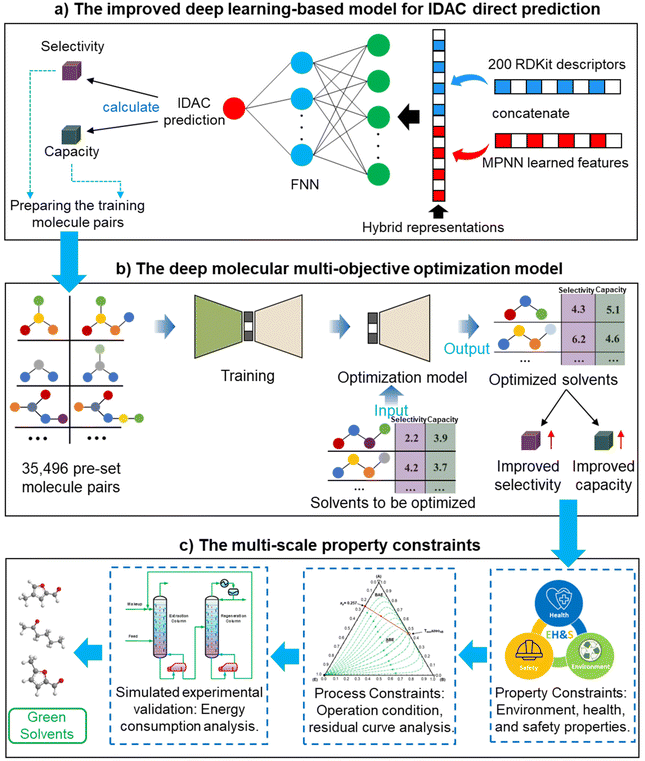 | ||
| Fig. 1 The green solvent multi-objective and multi-scale optimization framework towards the extractive distillation processes. | ||
The proposed framework for a green solvent design will be applied to an extractive distillation process to separate cyclohexane and benzene mixtures (in Section 6).
4 An improved deep learning model for direct prediction of the infinite dilution activity coefficient
4.1 Data preparation
The COSMO-SAC model22 is utilized in this study for the IDAC calculation. The UD database53 contains the quantum mechanically derived VCOSMO and σ-profile for 2261 compounds. Heuristically, the increase in molecular weight of a solvent results in a higher normal boiling point, which usually means higher energy consumption for an extractive distillation process, and reduces its economic viability. Therefore, only molecules with less than 12 root atoms (hydrogen atoms ignored) are considered in this study. Additionally, as a collected dataset, it is essential to apply data cleaning to remove outliers. The Pauta criterion,54 also known as the three Sigma rule, is employed for the data cleaning process. After the data preparation process, 2130 compounds remain in the UD database. The quantum mechanically derived VCOSMO and σ-profile of the 2130 compounds (2125 compounds for model training and 5 compounds for external testing) are provided in Table S1 in the ESI.† The calculated IDAC of the 2130 compounds in cyclohexane (A) and benzene (B) is detailed in Table S2 in the ESI.†4.2 Development of the deep learning model for IDAC direct prediction
There are two paths to calculate the IDAC of a molecule in a certain solvent: (1) the VCOSMO and 51 σ-profile predictive models are trained, and then the IDACs of different compounds in a certain solvent are calculated utilizing the COSMO-SAC with the estimated parameters as shown in Fig. 2a. This indirect IDAC calculation process can be termed as an indirect method (IM) in this work; (2) the IDACs of different compounds in a certain solvent are directly calculated by employing the COSMO-SAC, and then the calculated IDAC information is utilized to train an IDAC predictive model as illustrated in Fig. 2b. This direct IDAC calculation path can be termed a direct method (DM). The IM-based IDAC calculation path has been introduced in our previous work.32,55 In this study, the DM-based IDAC predictive model is developed to evaluate which IDAC calculation path performs better.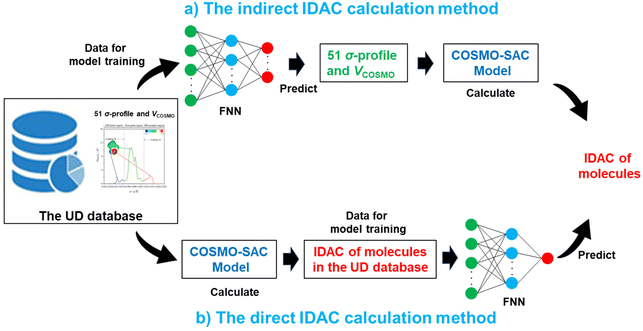 | ||
| Fig. 2 The schematic diagram for IDAC calculation. (a) An indirect method (IM). (b) A direct method (DM). | ||
First, the IDACs of the 2130 compounds in benzene and cyclohexane are calculated using the COSMO-SAC model with their VCOSMO and σ-profile information from the UD database. Subsequently, the hybrid representations28,32 of the 2125 compounds (five additional compounds are used as the external validation data) are utilized as input to train the feedforward neural network for the IDAC prediction in benzene and cyclohexane (IDAC-benzene and IDAC-cyclohexane) as shown in Fig. 3. The message-passing neural network (MPNN) is a graph neural network, which consists of two phases, namely, the message-passing phase and the readout phase.28 In the message-passing phase, the MPNN updates information on the directed bonds, as shown in Fig. 3. In the readout phase, a readout function is utilized to provide a vector representation of the molecular structure. The MPNN learned descriptors mainly focus on the local information about molecular structure due to the message updating mechanism. Therefore, the molecule level 200 dimensional RDKit calculated descriptors (as shown in Fig. 3) that can capture the global information of the molecular structure are employed to integrate with the MPNN learned features to form the molecular hybrid representation, which can retain the molecular local and global information as much as possible. The data split setting for training the two proposed models is 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1. The early stopping technique is employed to avoid overfitting. Finally, the 10-fold cross-validation (10-fold CV) method is applied to improve the stability of the two proposed models. In this study, the hidden size of MPNN, the depth of MPNN, the layer number of FNN, and the dropout of FNN are optimized using the Bayesian optimization method embedded in the Python package hyperopt.56
0.1. The early stopping technique is employed to avoid overfitting. Finally, the 10-fold cross-validation (10-fold CV) method is applied to improve the stability of the two proposed models. In this study, the hidden size of MPNN, the depth of MPNN, the layer number of FNN, and the dropout of FNN are optimized using the Bayesian optimization method embedded in the Python package hyperopt.56
4.3 The performance evaluation of the proposed deep learning prediction models
The optimal hyperparameter combinations for the proposed IDAC-benzene and IDAC-cyclohexane predictive models are summarized in Table 1.| Hyperparameters | Range | IDAC-benzene | IDAC-cyclohexane |
|---|---|---|---|
| Hidden size | [300,3000] | 1200 | 1300 |
| Depth | [2,7] | 6 | 6 |
| Dropout | [0,0.4] | 0.0 | 0.0 |
| Number of layers | [1,5] | 3 | 3 |
In this study, three evaluating metrics, i.e. the mean absolute error (MAE), the mean squared error (MSE), and the coefficient of determination (R2), were adopted as the evaluation criteria. The prediction performance of the IM and DM with the UD database is summarized in Table 2. In addition to the FNN model, the prediction performance using random-forest and support-vector machine approaches is also summarized in Table 2 to explore which machine learning approach is more suitable for IDAC prediction. The optimal hyperparameter combinations of the random forest and support vector machine-based approaches are detailed in Table S3.† Based on the statistical analysis, the FNN-based models (IM and DM models) had superior predictive performance over the random forest and support vector machine-based models. The performance of the 10-fold CV of the proposed DM models for the IDACs in benzene and cyclohexane prediction on the test sets was better than that of the IM predictive model.
| 10 CV MAE | 10 CV MSE | 10 CV R2 | |
|---|---|---|---|
| (a) IM 32 (FNN-based model) | |||
| IDAC-benzene | 0.1216 ± 0.0140 | 0.0720 ± 0.0163 | 0.8651 ± 0.0338 |
| IDAC-cyclohexane | 0.1755 ± 0.0180 | 0.1435 ± 0.0341 | 0.9123 ± 0.0198 |
| (b) DM (FNN-based model) | |||
| IDAC-benzene | 0.1146 ± 0.0108 | 0.0506 ± 0.0084 | 0.9036 ± 0.0128 |
| IDAC-cyclohexane | 0.1652 ± 0.0173 | 0.1126 ± 0.0262 | 0.9257 ± 0.0226 |
| (c) Random forest-based model | |||
| IDAC-benzene | 0.2224 ± 0.0198 | 0.1581 ± 0.0221 | 0.6985 ± 0.0314 |
| IDAC-cyclohexane | 0.3381 ± 0.0264 | 0.3394 ± 0.0689 | 0.7814 ± 0.0367 |
| (d) Support vector machine-based model | |||
| IDAC-benzene | 0.2516 ± 0.0164 | 0.1456 ± 0.0206 | 0.7213 ± 0.0389 |
| IDAC-cyclohexane | 0.3571 ± 0.0263 | 0.2965 ± 0.0476 | 0.8089 ± 0.0196 |
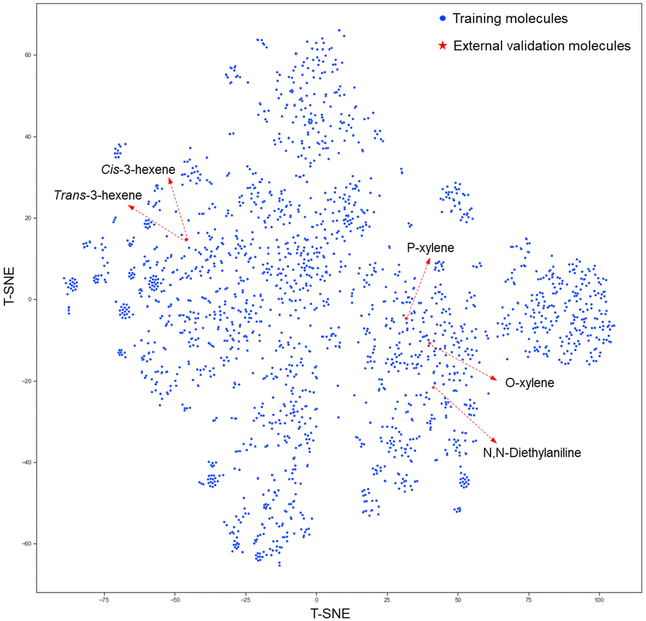
In addition to the above-mentioned statistical analysis, five molecules in the external validation dataset were utilized as examples to evaluate the ability of the proposed predictive models to discriminate the stereoisomers and structural isomers and to deal with complex molecules. In this work, the external validation dataset consisted of N,N-diethylaniline (complex compounds), P-xylene and O-xylene (structural isomers), and cis-3-hexene and trans-3-hexene (cis/trans isomers). The heteroatomic nitrogen in N,N-diethylaniline has an inducing effect on the delocalized π electron system of the aromatic ring, which could lead to a poor prediction performance by some quantitative structure–property relationship (QSPR) models.31o-Xylene and p-xyleneare a pair of structural isomers and trans-3-hexene and cis-3-hexene are a pair of cis/trans isomers. The predictive performance of the IM and DM models is tabulated in Table 3. Regarding N,N-diethylaniline, the proposed DM models can achieve a better predictive performance than the IM models. Regarding the structural and cis/trans isomers, both the IM and DM models have a satisfactory ability to differentiate isomers. Additionally, we visualized the chemical space of the training and external dataset by projecting the Morgan fingerprints (radius = 2, 1024 bits) of the molecules onto the 2D space (as shown in Fig. 4) via the t-SNE approach.57 As shown in Fig. 4, the five external data were not very similar to the well-represented molecules in the training dataset. Moreover, the five external data were scattered in different regions of the chemistry space of the training dataset. Therefore, the proposed DM models had decent IDAC predictive performance and good generalization ability.
| Compounds names | IDAC-cyclohexane | IDAC-benzene | ||||
|---|---|---|---|---|---|---|
| QM derived values | IM | DM | QM derived values | IM | DM | |
| N,N-Diethylaniline | 0.3215 | 0.2398 | 0.3028 | −0.1047 | −0.0745 | −0.1033 |
| p-Xylene | 0.2230 | 0.2194 | 0.2295 | 0.0008 | 0.0109 | −0.0004 |
| o-Xylene | 0.2654 | 0.2683 | 0.2472 | 0.0007 | −0.0037 | 0.0014 |
| cis-3-Hexene | 0.0550 | 0.0505 | 0.0463 | 0.1860 | 0.1847 | 0.2072 |
| trans-3-Hexene | 0.0457 | 0.0475 | 0.0505 | 0.2325 | 0.2165 | 0.2183 |
Based on the predictive performance analysis mentioned above, the proposed DM models had a better generalization ability than the IM models. Additionally, the proposed IDAC prediction models can discriminate the isomers, including the isomers and cis/trans isomers, and can deal with complex compounds such as hetero-atom compounds.
5 An interpretable molecular multi-objective optimization model learned from pre-set molecule pairs
5.1 Training data preparation for molecular multi-objective optimization
The ChEMBL dataset58 processed by Olivecrona59 was used to construct the molecule pairs, which were employed as the training data for solvent molecular multi-objective optimization. There were 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 179
179![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477 compounds in the processed ChEMBL dataset. Each compound was restricted to contain 10–50 root atoms and only had atoms in {H, B, C, N, O, F, Si, P, S, Cl, Br, and I}. The training molecule pairs were constructed as follows. First, 18
477 compounds in the processed ChEMBL dataset. Each compound was restricted to contain 10–50 root atoms and only had atoms in {H, B, C, N, O, F, Si, P, S, Cl, Br, and I}. The training molecule pairs were constructed as follows. First, 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 155 molecules were identified from the processed ChEMBL dataset with root atoms of not more than 12. We adopted the 12 root atom threshold because larger molecules usually have a higher normal boiling point, and a molecule with a high normal boiling point is not suitable for use as a solvent to separate the benzene and cyclohexane via extractive distillation. Second, C18
155 molecules were identified from the processed ChEMBL dataset with root atoms of not more than 12. We adopted the 12 root atom threshold because larger molecules usually have a higher normal boiling point, and a molecule with a high normal boiling point is not suitable for use as a solvent to separate the benzene and cyclohexane via extractive distillation. Second, C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1552 = 164
1552 = 164![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 792
792![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 935 molecule pairs (Mx and My) were constructed from 18
935 molecule pairs (Mx and My) were constructed from 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 155 processed molecules. Third, 1
155 processed molecules. Third, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590
590![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 molecule pairs had similarities, sim(Mx, My) ≥ 0.4. The similarities of the molecule pairs can be measured by the Tanimoto coefficient over 2048-dimension binary Morgan fingerprints with radius 1. The similarity threshold was adopted because the proposed molecular optimization model needed the training molecule pairs with only one fragment different at one disconnection site, which can improve the learning efficiency of the molecular optimization model. Fourth, the DF-GED algorithm was used to extract molecule pairs that had only one fragment different at one disconnection site, which can improve the learning efficiency of the molecular multi-objective optimization model. 100
350 molecule pairs had similarities, sim(Mx, My) ≥ 0.4. The similarities of the molecule pairs can be measured by the Tanimoto coefficient over 2048-dimension binary Morgan fingerprints with radius 1. The similarity threshold was adopted because the proposed molecular optimization model needed the training molecule pairs with only one fragment different at one disconnection site, which can improve the learning efficiency of the molecular optimization model. Fourth, the DF-GED algorithm was used to extract molecule pairs that had only one fragment different at one disconnection site, which can improve the learning efficiency of the molecular multi-objective optimization model. 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 molecule pairs were extracted from 1
629 molecule pairs were extracted from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590
590![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350 pairs of molecules. Fifth, among the 100
350 pairs of molecules. Fifth, among the 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 pairs of molecules, we selected the molecule pairs that met the following property constraints: for selectivity, the selectivity score of My should be improved by at least 20% compared with Mx in a molecule pair, that is,
629 pairs of molecules, we selected the molecule pairs that met the following property constraints: for selectivity, the selectivity score of My should be improved by at least 20% compared with Mx in a molecule pair, that is,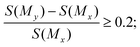 | (1) |
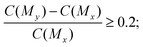 | (2) |
As a result, 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 496 molecule pairs (detailed in Table S4 in the ESI†) were identified that can be used as the training data with the property constraints.
496 molecule pairs (detailed in Table S4 in the ESI†) were identified that can be used as the training data with the property constraints.
5.2 Development of the multi-objective optimization model of solvent molecules
The proposed multi-objective molecular optimization approach of the solvent molecules extended the hierarchical generation model to multi-objective molecular optimization by learning the molecule pairs with improved selectivity and solution capacity.In the hierarchical encoding process, a molecule can be represented by a hierarchical graph with three layers,45i.e., an atom layer, an attachment layer, and a fragment layer, as seen in Fig. 5a. The details of the fragment extraction approach and the hierarchical encoding method were introduced in the studies presented by Jin et al.45 and Chen et al.46 In the hierarchical molecular representation framework, a molecule graph 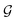 can be represented as a set of fragments
can be represented as a set of fragments 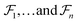 , and their attachments
, and their attachments 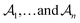 . Each attachment
. Each attachment 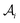 in this layer denotes a specific attachment configuration of fragment
in this layer denotes a specific attachment configuration of fragment 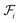 , including the connection information between
, including the connection information between 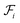 and one of its neighbor fragments. In the atom layer, a molecule can be depicted as graph
and one of its neighbor fragments. In the atom layer, a molecule can be depicted as graph 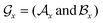 , where
, where 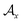 and
and 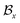 represent the atoms and corresponding bonds in Mx. In the attachment layer, molecule
represent the atoms and corresponding bonds in Mx. In the attachment layer, molecule 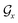 is constituted by a series of fragments
is constituted by a series of fragments 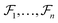 extracted from the Mx. In the fragment layer, a molecule Mx is represented as a tree-constructed graph
extracted from the Mx. In the fragment layer, a molecule Mx is represented as a tree-constructed graph 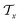 . The tree-constructed representation can be depicted as
. The tree-constructed representation can be depicted as 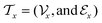 ,44 where all the fragments in Mx are extracted as nodes in
,44 where all the fragments in Mx are extracted as nodes in 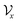 ; nodes with the same atoms are connected with edges in
; nodes with the same atoms are connected with edges in 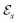 . The encoder encodes the molecule pairs (Mx, My) as graph (
. The encoder encodes the molecule pairs (Mx, My) as graph (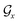 and
and 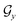 ) using message passing networks, and as a tree-constructed graph (
) using message passing networks, and as a tree-constructed graph ( and
and  ) using tree message passing networks.
) using tree message passing networks.
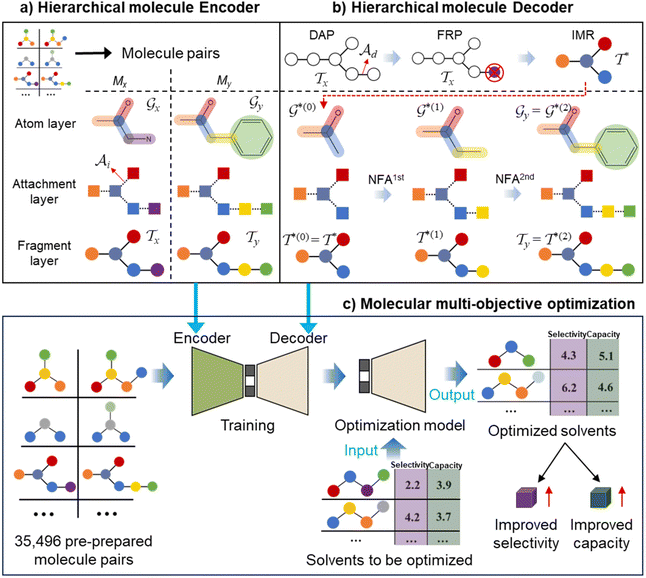 | ||
| Fig. 5 The schematic diagram of the hierarchical molecule (a) encoder, (b) decoder, and (c) multi-objective optimization process. | ||
In the hierarchical decoding process, the decoder conducts a series of modified operations that optimize Mx into My, as seen in Fig. 5b. The details of the hierarchical decoding method are introduced in the studies presented by Jin et al.45 and Chen et al.46 First, the decoder performs disconnection attachment prediction (DAP) to find an attachment  in
in 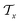 as the disconnection site. Second, at the neighbors of
as the disconnection site. Second, at the neighbors of 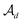 , the decoder performs fragment-removing prediction (FRP) to remove fragments attached to
, the decoder performs fragment-removing prediction (FRP) to remove fragments attached to 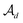 . Third, an intermediate representation (IMR) for the remaining scaffold
. Third, an intermediate representation (IMR) for the remaining scaffold 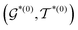 is produced after the fragment removal operation. Fourth, over
is produced after the fragment removal operation. Fourth, over 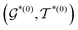 , the decoder conducts new fragment attachment (NFA) prediction iteratively to optimize Mx into My. The optimal graph edit paths can be identified by the DF-GED algorithm.60
, the decoder conducts new fragment attachment (NFA) prediction iteratively to optimize Mx into My. The optimal graph edit paths can be identified by the DF-GED algorithm.60
By learning from the selectivity and solution capacity of improved molecule pairs (training molecule pairs), the hierarchical molecular multi-objective optimization model can realize the multi-objective optimization of the solvent molecules as illustrated in Fig. 5c.
6 Case study of the green solvent multi-objective and multi-scale optimization framework
A case study using extraction distillation to separate aliphatic and aromatic mixtures61 was used to evaluate the proposed green solvent multi-objective optimization framework. In this work, the aromatic/aliphatic mixtures were simplified as mixtures of cyclohexane (A)/benzene (B).62 The green extractive distillation solvent multi-objective optimization framework can be decomposed into three steps, i.e., molecular multi-objective optimization, property constraints, and process constraints, as introduced in Section 2.6.1 The extractive distillation solvent multi-objective optimization
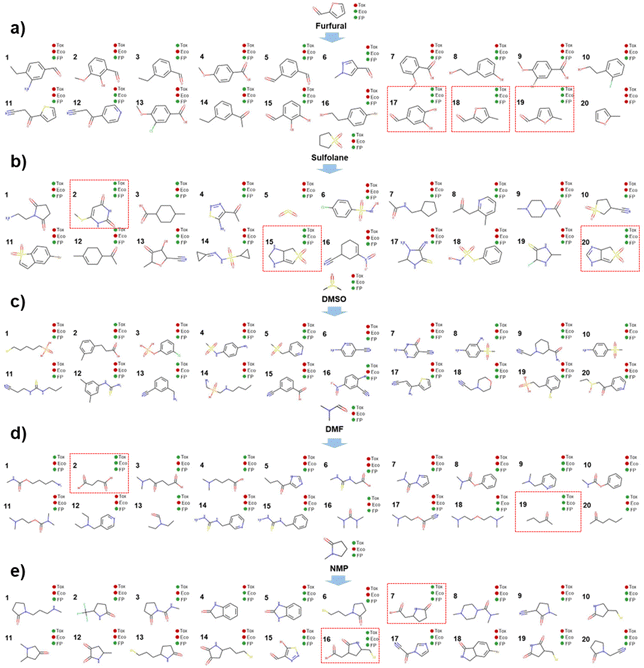
In this step, as the inputs of the molecular multi-objective optimization model, industrial extractive solvent molecules that need to be optimized should be first identified. Five widely employed extractive distillation solvents for separating the mixtures of cyclohexane (A) and benzene (B) are listed in Table 4 based on extensive literature research.61,63–66 However, all these solvents have some drawbacks, such as toxicity or ecological hazard. The toxicity and ecological information of these solvents (with experimentally measured or predicted properties) is available in the Syntelly database.67Taking the five common industrial solvent molecules as inputs of the molecular multi-objective optimization model, 20 optimized solvent molecules are generated for every single widely used solvent (as seen in Fig. 4a–e) via the trained molecular multi-objective optimization model introduced in Section 4. Accordingly, 100 optimized solvent molecules are generated as tabulated in Table S5 in the ESI.†
6.2 EH&S property constraints
In this step, the 100 optimized solvent molecules are screened using EH&S properties. In terms of environmental properties, three ecological indicators are taken into account, i.e., the bioconcentration factor, 40 hours of Tetrahymena pyriformis IGC50, and 48 hours of Daphnia magna LC50. If a solvent negatively affects the environment, it will be marked in red, as shown in Fig. 6. The health properties can be quantified by the rat oral dosage. The threshold value for toxicity is 2000 mg kg−1. If the rat oral dosage of a given solvent is 500 mg kg−1, it will negatively affect health and will be marked in red, as shown in Fig. 6. Safety can be quantified using the flash point. For a given solvent, the higher its flash point, the better for storage security. In this work, if the flash point is above 280 K,36 it will positively impact the storage security and it will be marked in green, as shown in Fig. 6. All the EH&S information can be collected from the Syntelly database.67 As a result, 10 solvent molecules remain screened by EH&S properties constraints and are displayed in Table 5.| Namesa | Smiles | Structure | Melting point/K | Boiling point/K |
|---|---|---|---|---|
| a The names correspond to the serial numbers in Fig. 6. | ||||
| a17 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cc1ccc(O)c(O)c1 Cc1ccc(O)c(O)c1 |
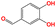
|
413.15 | 550.15 |
| a18 | Cc1coc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)c1 O)c1 |

|
303.15 | 455.15 |
| a19 | Cc1ccc(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)o1 O)o1 |

|
293.15 | 460.15 |
| b2 | CSc1cc(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[nH]c( O)[nH]c(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[nH]1 O)[nH]1 |
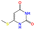
|
523.15 | 578.15 |
| b15 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1( S1(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)C O)C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2NCNC2C1 C2NCNC2C1 |
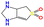
|
473.15 | 564.15 |
| b20 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S1( S1(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)C O)C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2NC C2NC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NC2C1 NC2C1 |
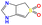
|
473.15 | 547.15 |
| d2 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(O)CCC( C(O)CCC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O O)O |
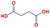
|
461.15 | 546.15 |
| d19 | CCCCC(C)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
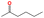
|
217.65 | 400.75 |
| e7 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(O)CC1CCC( C(O)CC1CCC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)N1 O)N1 |
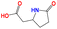
|
430.15 | 570.15 |
| e16 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(O)CC1CC(CS)NC1 C(O)CC1CC(CS)NC1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
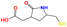
|
430.15 | 559.15 |
6.3 Process constraints
In this step, process operation conditions are quantified by normal melting point and normal boiling point. The melting point of the solvent should be below 310 K (ref. 36) to ensure that it is in the liquid state at the operating temperature. The boiling point of the solvent should be below 580 K (ref. 36) for relatively economical separation energy consumption. There are 3 solvent molecules (i.e., a18, a19, and d19, whose names are 4-methyl furfural, 5-methyl furfural, and 2-hexanone, respectively) remaining after the operation condition screening. Detailed information on the normal melting point and boiling point of the 10 solvent molecules after EH&S property screening is provided in Table 5.To further screen solvents that would make the extractive distillation process feasible, the residue curve analyses of the 3 screened solvents were conducted and the results are shown in Fig. 7. According to a review by Gerbaud et al.,52 the combined analysis of residual curve maps (RC) and univolatility line can help evaluate whether a solvent is suitable formixture separation via extractive distillation, or not.68 As illustrated in the RC maps, every single curve originates from the azeotrope point and terminates in the pure component. Additionally, there is one distillation region for each of the three RC maps. In the residue curve map, A or B is a saddle point of the distillation region and cannot be obtained by azeotropic distillation. On the other hand, the univolatility line splits the ternary diagram into two volatility order regions for all three solvents. With the feeding of the solvent at another location than the main feed, the extractive distillation process enables the most volatile component in the volatility order regions to be obtained where the solvent is found.52 This is the case for cyclohexane with the 3 green candidate solvents. Therefore, it is possible to separate the benzene/cyclohexane mixtures as pure products, first by removing cyclohexane from the extractive distillation column, then by recovering benzene as a distillate from the regeneration column where a high-purity solvent is obtained at the bottom and then recycled to the extraction distillation column. The intersection point xp of the isovolatility curve with the triangle edge largely determines the minimum usage of the solvent.52,69,70 The lower the xp, the less the amount of solvent required. As we can see, the mole amount of 2-hexanone used is more than that of 4-methyl furfural and 5-methyl furfural. The results of the combined residue curve and univolatility analyses can further prove that the proposed IDAC predictive models can achieve reliable and accurate prediction performance.
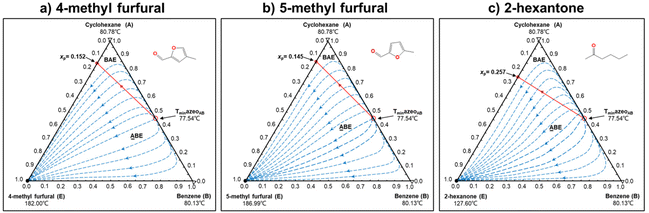 | ||
| Fig. 7 The residue curve maps of (1) 4-methyl furfural, (2) 5-methyl furfural, and (3) 2-hexanone in the cyclohexane (A)/benzene (B) mixtures. | ||
6.4 Energy consumption analysis
The energy of the extraction column (QE) and regeneration column (QR) of the five widely employed solvents and three candidate green solvents are summarized in Table 6. The detailed operation conditions of the eight solvents are tabulated in Table S6.†Additionally, the information on the rat oral and bioconcentration factor is tabulated in Table 6. The results indicate that there is a trade-off between energy consumption and sustainable performance (such as EH&S properties), where a decrease in energy consumption usually comes at the expense of sustainability. The toxicity of 4-methyl furfural and 5-methyl furfural is reduced by about 95% compared with furfural. The bioconcentration factor of 2-hexanone is reduced by about 62% compared with DMF. Policies worldwide are moving the application of chemical separation processes in the direction of green chemistry.6 It is worth noting that the reboiler temperature of the extraction and regeneration columns of 2-hexanone is lower than 150 °C. However, the reboiler temperatures of the extraction and regeneration column of 4-methyl furfural and 5-methyl furfural are both higher than 150 °C. This means that the reboiler using 2-hexanone can use low pressure steam while the reboiler using the other two solvents needs to use medium pressure steam.
6.5 Analysis based on knowledge of the chemistry domain
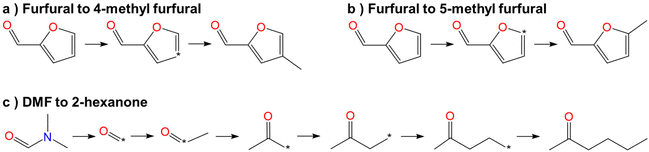
To make a more intuitive observation, the optimization processes of the three candidate green solvents are shown in Fig. 8. Among the three solvents, 4-methyl furfural and 5-methyl furfural are the derivatives of furfural. Interestingly, the branching of methyl to the furan ring could significantly reduce the toxicity of furfural. This could be due to the steric effect resulting from the aromatic ring substitution. The oral dosages of 4-methyl furfural, 5-methyl furfural, and furfural to rats are 2404, 2405, and 129 mg kg−1 (the higher the better), respectively. 2-Hexanone is obtained by optimizing the structure of DMF. The dialkylation of the carbonyl carbon in DMF can not only improve the selectivity and solution capacity but also reduce the ecological hazards. This is because the amide in DMF plays a very pivotal role in the growth and metabolism of microorganisms and can ensure that microbes get enough protein and other important metabolites, thus promoting their growth and reproduction, which could have a negative impact on the environment.In summary, 4-methyl furfural, 5-methyl furfural, and 2-hexanone can be used as candidate green solvents to isolate mixtures of cyclohexane and benzene with extractive distillation. In this study, to evaluate the validity of the green solvent multi-objective optimization framework, only 20 molecules were generated from every widely used solvent. More candidate green solvents will be identified if more molecules are optimized and generated for every widely used solvent.
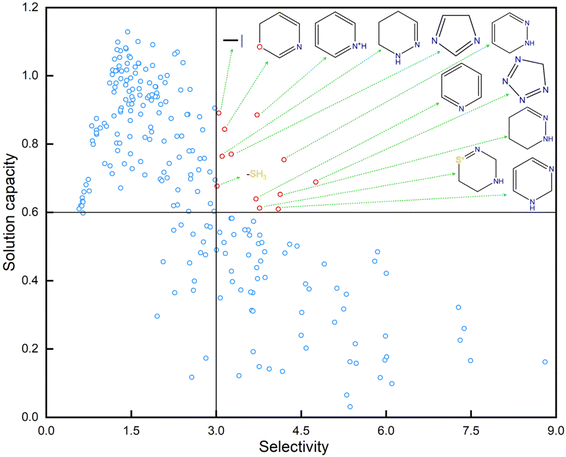
6.6 Molecular fragment analysis
To further explore the relationship between the molecular fragments and the optimization processes, the fragments were first extracted from the prepared training molecule pairs shown in Table S4 in the ESI.† The IDACs of these fragments in benzene and cyclohexane are predicted by the proposed IDAC perdition models. The selectivity and solution capacity of these fragments are calculated based on the predicted IDACs of these fragments. The detailed information on these fragments is tabulated in Table S7 in the ESI.† The results of the selectivity and solution capacity of these fragments are shown in Fig. 9. In this figure, molecular fragments with selectivity greater than 3 and solution capacity greater than 0.6 are marked in red. To more intuitively explore the common characteristics between the molecular fragments, the molecular structures of the fragments marked in red are shown in Fig. 9. As we can see, most of these visualized molecular fragments are heteroatom-containing aromatic compounds. From the optimization results shown in Fig. 6, we can also find that many optimized molecules are modified with these molecular fragments. However, these fragments can easily lead to toxicity and ecological hazards. Therefore, there appears to be a trade-off between the separation performance (such as selectivity and solution capacity) and sustainable performance (such as EH&S properties) of the solvents. In this study, the proposed green solvent design framework can efficiently balance the trade-off between the separation performance and sustainable performance of the solvents and find green solvents with multi-constraints.7 Conclusions
In this study, we propose a molecular multi-objective and multi-scale optimization framework for the design of green solvents fit for extractive distillation that can simultaneously optimize multiple trade-off properties such as selectivity and solution capacity, both related to molecular and process constraints. The molecular multi-objective optimization model relies upon its ability to optimize process properties rather than molecular properties, as in common computer-aided molecular design approaches. The process properties are short-cut properties of the extractive distillation process, namely selectivity and solution capacity, which are evaluated via infinite dilution activity coefficients (IDAC).A deep hierarchical molecular multi-objective optimization model was developed to learn the optimization path from our pre-set molecule pairs (Mx and My) and generate new solvents by fragment addition or removal. Every pair of molecules in the pre-set molecule pairs had similar molecular structures, but the scores of both selectivity and solution capacity of My were at least 20% larger than those of Mx. To prepare the molecule pairs, an improved deep learning-based IDAC direct prediction model trained over a COSMO-SAC database was developed for calculating the selectivity and solution capacity of the molecule pairs. The IDAC direct predictive model with the ability to discriminate stereoisomers achieved a better prediction performance than the IDAC indirect predictive model. As a result, 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 496 molecule pairs were identified that can be used as training data to train the deep hierarchical molecular multi-objective optimization model. Finally, the proposed IDAC prediction model and molecular multi-objective optimization model were integrated into a green solvent multi-objective and multi-scale optimization framework with EH&S properties and process constraints.
496 molecule pairs were identified that can be used as training data to train the deep hierarchical molecular multi-objective optimization model. Finally, the proposed IDAC prediction model and molecular multi-objective optimization model were integrated into a green solvent multi-objective and multi-scale optimization framework with EH&S properties and process constraints.
The proposed green solvent multi-objective and multi-scale optimization framework was applied to an extractive distillation process to separate the mixtures of cyclohexane and benzene. The results showed that 4-methyl furfural, 5-methyl furfural, and 2-hexanone can be utilized as candidate green solvents. Among the three solvents, 4-methyl furfural and 5-methyl furfural are derivatives of furfural. Interestingly, the branching of methyl to the furan ring could significantly reduce the toxicity of furfural. This could be due to the steric effect resulting from the aromatic ring substitution. 2-Hexanone was obtained by optimizing the structure of DMF. The dialkylation of the carbonyl carbon in DMF can not only improve the selectivity and solution capacity but also reduce the ecological hazards. This is because amide compounds play a very important role in the growth and metabolism of microorganisms and help microbes get enough protein and other important metabolites, thus promoting their growth and reproduction, which could have a negative impact on the environment.
Author contributions
Jun Zhang: conceptualization (lead), data curation (lead), formal analysis (lead), methodology (lead), software (lead), validation (lead), writing – original draft (lead), and writing – review and editing (equal). Qin Wang: conceptualization (equal), funding acquisition (equal), methodology (equal), project administration (equal), supervision (equal), and writing – review and editing (equal). Huaqiang Wen: formal analysis (equal), methodology (equal), software (equal), and validation (equal). Vincent Gerbaud: conceptualization (equal), methodology (equal), and writing – review and editing (equal). Saimeng Jin: conceptualization (equal), methodology (equal), and writing – review and editing (equal). Weifeng Shen: conceptualization (equal), funding acquisition (lead), methodology (equal), project administration (lead), supervision (lead), writing – original draft (equal), and writing – review and editing (lead).Data availability
The data that support the findings of this study are available in the ESI of this article on https://zenodo.org/records/10097726.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the financial support provided by the National Natural Science Foundation for Excellent Young Scientists of China (No. 22122802); the National Natural Science Foundation of China (No. 22278044); the Chongqing Science Foundation for Distinguished Young Scholars (No. CSTB2022NSCQ-JQX0021); the Chongqing Innovation Support Key Program for Returned Overseas Chinese Scholars (No. cx2023002); and the Research Foundation of Chongqing University of Science and Technology (No. ckrc2019006).References
- J. C. Fromer and C. W. Coley, Computer-aided multi-objective optimization in small molecule discovery, Patterns, 2023, 4, 100678 CrossRef CAS PubMed.
- X. C. Ma, Q. Zhang, C. He, Q. L. Chen and B. J. Zhang, Computer-aided naphtha liquid–liquid extraction: Molecular reconstruction, sustainable solvent design and multiscale process optimization, Fuel, 2023, 334, 126651 CrossRef CAS.
- S. Chai, Z. Song, T. Zhou, L. Zhang and Z. Qi, Computer-aided molecular design of solvents for chemical separation processes, Curr. Opin. Chem. Eng., 2022, 35, 100732 CrossRef.
- A. Doolin, R. G. Charles, C. D. Castro, R. G. Rodriguez and M. L. Davies, Sustainable solvent selection for the manufacture of methylammonium lead triiodide (MAPbI 3) perovskite solar cells, Green Chem., 2021, 23, 2471–2486 RSC.
- J. H. Clark, Green chemistry: Challenges and opportunities, Green Chem., 1999, 1, 1–8 RSC.
- J. H. Clark, Green chemistry: Today (and tomorrow), Green Chem., 2006, 8, 17–21 RSC.
- J. Y. Ten, Z. H. Liew, X. Y. Oh, M. H. Hassim and N. Chemmangattuvalappil, Computer-aided molecular design of optimal sustainable solvent for liquid–liquid extraction, Process Integr. Optim. Sustain, 2021, 5, 269–284 CrossRef.
- Y. S. Lee, A. Galindo, G. Jackson and C. S. Adjiman, Enabling the direct solution of challenging computer-aided molecular and process design problems: Chemical absorption of carbon dioxide, Comput. Chem. Eng., 2023, 174, 108204 CrossRef CAS.
- I. Rodriguez-Donis, S. Thiebaud-Roux, S. Lavoine and V. Gerbaud, Computer-aided product design of alternative solvents based on phase equilibrium synergism in mixtures, C. R. Chim., 2018, 21, 606–621 CrossRef CAS.
- M. Korichi, V. Gerbaud, P. Floquet, A. H. Meniai, S. Nacef and X. Joulia, Computer aided aroma design I – Molecular knowledge framework, Chem. Eng. Process., 2008, 47, 1902–1911 CrossRef CAS.
- H. Sun, A universal molecular descriptor system for prediction of logP, logS, logBB, and absorption, J. Chem. Inf. Comput. Sci., 2004, 44, 748–757 CrossRef CAS.
- A. Fredenslund, R. L. Jones and J. M. Prausnitz, Group-contribution estimation of activity coefficients in nonideal liquid mixtures, AIChE J., 1975, 21, 1086–1099 CrossRef CAS.
- T. J. Sheldon, M. Folić and C. S. Adjiman, Solvent design using a quantum mechanical continuum solvation model, Ind. Eng. Chem. Res., 2006, 45, 1128–1140 CrossRef CAS.
- J. G. Rittig, K. B. Hicham, A. M. Schweidtmann, M. Dahmen and A. Mitsos, Graph neural networks for temperature-dependent activity coefficient prediction of solutes in ionic liquids, Comput. Chem. Eng., 2023, 171, 108153 CrossRef CAS.
- Z. Wang, Y. Su, S. Jin, X. Zhang and J. H. Clark, A novel unambiguous strategy of molecular feature extraction in machine learning assisted predictive models for environmental properties, Green Chem., 2020, 22, 3867–3876 RSC.
- Z. Wang, Y. Su, W. Shen, S. Jin, J. H. Clark, J. Ren and X. Zhang, Predictive deep learning models for environmental properties: the direct calculation of octanol–water partition coefficients from molecular graphs, Green Chem., 2019, 21, 4555–4565 RSC.
- T. Zhou, K. McBride, S. Linke, Z. Song and K. Sundmacher, Computer-aided solvent selection and design for efficient chemical processes, Comput. Chem. Eng., 2020, 27, 35–44 Search PubMed.
- R. Gani, Group contribution-based property estimation methods: advances and perspectives, Curr. Opin. Chem. Eng., 2019, 23, 184–196 CrossRef.
- F. Eckert and A. Klamt, Fast solvent screening via quantum chemistry: COSMO–RS approach, AIChE J., 2002, 48, 369–385 CrossRef CAS.
- A. Klamt and F. Eckert, COSMO-RS: A novel and efficient method for the a priori prediction of thermophysical data of liquids, Fluid Phase Equilib., 2000, 172, 43–72 CrossRef CAS.
- S.-T. Lin, Quantum mechanical approaches to the prediction of phase equilibria: solvation thermodynamics and group contribution methods, University of Delaware, 2001 Search PubMed.
- S.-T. Lin and S. I. Sandler, A priori phase equilibrium prediction from a segment contribution solvation model, Ind. Eng. Chem. Res., 2002, 41, 899–913 CrossRef CAS.
- I. H. Bel, E. Mickoleit, C.-M. Hsieh, S.-T. Lin, J. Vrabec, C. Breitkopf and A. Jäger, A benchmark open-source implementation of COSMO-SAC, J. Chem. Theory Comput., 2020, 16, 2635–2646 CrossRef.
- Q. Liu, L. Zhang, K. Tang, L. Liu, J. Du, Q. Meng and R. Gani, Machine learning-based atom contribution method for the prediction of surface charge density profiles and solvent design, AIChE J., 2021, 67, e17110 CrossRef CAS.
- T. Mu, J. Rarey and J. Gmehling, Group contribution prediction of surface charge density distribution of molecules for COSMO-SAC, AIChE J., 2009, 55, 3298–3300 CrossRef CAS.
- E. Mullins, R. Oldland, Y. A. Liu, S. Wang, S. I. Sandle, C.-C. Chen, M. Zwolak and K. C. Seavey, Sigma-profile database for using COSMO-based thermodynamic methods, Ind. Eng. Chem. Res., 2006, 45, 4389–4415 CrossRef CAS.
- Y. Su, Z. Wang, S. Jin, W. Shen, J. Ren and M. R. Eden, An architecture of deep learning in QSPR modeling for the prediction of critical properties using molecular signatures, AIChE J., 2019, 65, e16678 CrossRef.
- J. Zhang, Q. Wang, Y. Su, S. Jin, J. Ren, M. Eden and W. Shen, An accurate and interpretable deep learning model for environmental properties prediction using hybrid molecular representations, AIChE J., 2022, 68, e17634 CrossRef CAS.
- F. Jirasek, R. A. Alves, J. Damay, R. A. Vandermeulen, R. Bamler, M. Bortz, S. Mandt, M. Kloft and H. Hasse, Machine learning in thermodynamics: Prediction of activity coefficients by matrix completion, J. Phys. Chem. Lett., 2020, 11, 981–985 CrossRef CAS PubMed.
- G. Chen, Z. Song, Z. Qi and K. Sundmacher, Neural recommender system for the activity coefficient prediction and UNIFAC model extension of ionic liquid–solute systems, AIChE J., 2021, 67, e17171 CrossRef CAS.
- G. Chen, Z. Song and Z. Qi, Transformer-convolutional neural network for surface charge density profile prediction: Enabling high-throughput solvent screening with COSMO-SAC, Chem. Eng. Sci., 2021, 246, 117002 CrossRef CAS.
- J. Zhang, Q. Wang and W. Shen, Message-passing neural network based multi-task deep-learning framework for COSMO-SAC based σ-profile and VCOSMO prediction, Chem. Eng. Sci., 2022, 254, 117624 CrossRef CAS.
- R. Gani and E. Brignole, Molecular design of solvents for liquid extraction based on UNIFAC, Fluid Phase Equilib., 1983, 13, 331–340 CrossRef CAS.
- T. Zhou, Z. Song, X. Zhang, R. Gani and K. Sundmacher, Optimal solvent design for extractive distillation processes: A multiobjective optimization-based hierarchical framework, Ind. Eng. Chem. Res., 2019, 58, 5777–5786 CrossRef CAS.
- L. Zhang, J. Pang, Y. Zhuang, L. Liu, J. Du and Z. Yuan, Integrated solvent-process design methodology based on COSMO-SAC and quantum mechanics for TMQ (2,2,4-trimethyl-1,2-H-dihydroquinoline) production, Chem. Eng. Sci., 2020, 226, 115894 CrossRef CAS.
- S. Chai, E. Li, L. Zhang, J. Du and Q. Meng, Crystallization solvent design based on a new quantitative prediction model of crystal morphology, AIChE J., 2021, e17499 Search PubMed.
- J. Heintz, J. P. Belaud, N. Pandya, M. T. D. Santos and V. Gerbaud, Computer aided product design tool for sustainable product development, Comput. Chem. Eng., 2014, 71, 362–376 CrossRef CAS.
- A. S. Alshehri, R. Gani and F. You, Deep learning and knowledge-based methods for computer-aided molecular design—toward a unified approach: State-of-the-art and future directions, Comput. Chem. Eng., 2020, 141, 107005 CrossRef CAS.
- A. Graves, Generating sequences with recurrent neural networks, arXiv, 2013, preprint, arXiv:1308.0850.
- V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra and M. Riedmiller, Playing atari with deep reinforcement learning, arXiv, 2013, preprint, arXiv:1312.5602.
- D. P. Kingma and M. Welling, Auto-encoding variational bayes, arXiv, 2013, preprint, arXiv:1312.6114.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Inverse molecular design using machine learning: Generative models for matter engineering, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- A. S. Alshehri and F. You, Deep learning to catalyze inverse molecular design, Chem. Eng. J., 2022, 444, 136669 CrossRef CAS.
- W. Jin, R. Barzilay and T. Jaakkola, Junction tree variational autoencoder for molecular graph generation, arXiv, 2018, preprint, arXiv:1802.04364, arXiv.org e-Print archive.
- W. Jin, R. Barzilay and T. Jaakkola, Hierarchical generation of molecular graphs using structural motifs, arXiv, 2020, preprint, arXiv:2002.03230v2.
- Z. Chen, M. R. Min, S. Parthasarathy and X. Ning, A deep generative model for molecule optimization via one fragment modification, Nat. Mach. Intell., 2021, 3, 1040–1049 CrossRef.
- J. Wang, C.-Y. Hsieh, M. Wang, X. Wang, Z. Wu, D. Jiang, B. Liao, X. Zhang, B. Yang and Q. He, Multi-constraint molecular generation based on conditional transformer, knowledge distillation and reinforcement learning, Nat. Mach. Intell., 2021, 3, 914–922 CrossRef.
- D. Polykovskiy, A. Zhebrak, B. Sanchez-Lengeling, S. Golovanov and A. Zhavoronkov, Molecular sets (MOSES): A benchmarking platform for molecular generation models, Front. Pharmacol., 2020, 11, 565644 CrossRef CAS PubMed.
- J. Scheffczyk, P. Schäfer, L. Fleitmann, J. Thien, C. Redepenning, K. Leonhard, W. Marquardt and A. Bardow, COSMO-CAMPD: A framework for integrated design of molecules and processes based on COSMO-RS, Mol. Syst. Des. Eng., 2018, 3, 645–657 RSC.
- L. Polte, L. Raßpe-Lange, F. Latz, A. Jupke and K. Leonhard, COSMO-CAMPED–solvent design for an extraction distillation considering molecular, process, equipment, and economic optimization, Chem. Ing. Tech., 2023, 95, 416–426 CrossRef CAS.
- S. Kossack, K. Kraemer, R. Gani and W. Marquardt, A systematic synthesis framework for extractive distillation processes, Chem. Eng. Res. Des., 2008, 86, 781–792 CrossRef CAS.
- V. Gerbaud, I. Rodriguez-Donis, L. Hegely, P. Lang, F. Denes and X. Q. You, Review of extractive distillation. Process design, operation, optimization and control, Chem. Eng. Res. Des., 2019, 141, 229–271 CrossRef CAS.
- R. Fingerhut, W.-L. Chen, A. Schedemann, W. Cordes, J. r. Rarey, C.-M. Hsieh, J. Vrabec and S.-T. Lin, Comprehensive assessment of COSMO-SAC models for predictions of fluid-phase equilibria, Ind. Eng. Chem. Res., 2017, 56, 9868–9884 CrossRef CAS.
- L. Li, Z. Wen and Z. Wang, Outlier detection and correction during the process of groundwater lever monitoring base on Pauta criterion with self-learning and smooth processing, in Theory, Methodology, Tools and Applications for Modeling and Simulation of Complex Systems, Springer, Singapore, 2016 Search PubMed.
- J. Zhang, Q. Wang, M. Eden and W. Shen, A deep learning-based framework towards inverse green solvent design for extractive distillation with multi-index constraints, Comput. Chem. Eng., 2023, 177, 108335 CrossRef CAS.
- J. Zhang, Q. Wang and W. Shen, Hyper-parameter optimization of multiple machine learning algorithms for molecular property prediction using hyperopt library, Chin. J. Chem. Eng., 2022, 52, 115–125 CrossRef CAS.
- D. S. Karlov, S. Sosnin, I. V. Tetko and M. V. Fedorov, Chemical space exploration guided by deep neural networks, RSC Adv., 2019, 5151–5157 RSC.
- A. Gaulton, A. Hersey, M. Nowotka, A. P. Bento, J. Chambers, D. Mendez, P. Mutowo, F. Atkinson, L. J. Bellis and E. Cibrián-Uhalte, The ChEMBL database in 2017, Nucleic Acids Res., 2017, 45, D945–D954 CrossRef CAS.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, Molecular de-novo design through deep reinforcement learning, J. Cheminf., 2017, 9, 1–14 Search PubMed.
- Z. Abu-Aisheh, R. Raveaux, J. Y. Ramel and P. Martineau, An exact graph edit distance algorithm for solving pattern recognition problems, International Conference on Pattern Recognition Applications & Methods, PRT, Setubal , 2015, 1, 271–278 Search PubMed.
- L. Sun, Q. Wang, L. Li, J. Zhai and Y. Liu, Design and control of extractive dividing wall column for separating benzene/cyclohexane mixtures, Ind. Eng. Chem. Res., 2014, 53, 8120–8131 CrossRef CAS.
- Q. Wang, J. Y. Chen, M. Pan, C. He, C. C. He, B. J. Zhang and Q. L. Chen, A new sulfolane aromatic extractive distillation process and optimization for better energy utilization, Chem. Eng. Process., 2018, 128, 80–95 CrossRef CAS.
- L. Li, Y. Tu, L. Sun, Y. Hou, M. Zhu, L. Guo, Q. Li and Y. Tian, Enhanced efficient extractive distillation by combining heat-integrated technology and intermediate heating, Ind. Eng. Chem. Res., 2016, 55, 8837–8847 CrossRef CAS.
- F. M. Lee, Use of organic sulfones as the extractive distillation solvent for aromatics recovery, Ind. Eng. Chem. Process. Des. Dev., 1986, 25, 949–957 CrossRef CAS.
- M. K. Praharaj, A. Satapathy, P. Mishra and S. Mishra, Ultrasonic analysis of intermolecular interaction in the mixtures of benzene with N,N-dimethylformamide and cyclohexane at different temperatures, J. Chem. Pharm. Res., 2013, 5, 49–56 CAS.
- C. Yang, Z. Liu, H. Lai and P. Ma, Thermodynamic properties of binary mixtures of N-methyl-2-pyrrolidinone with cyclohexane, benzene, toluene at (303.15 to 353.15) K and atmospheric pressure, J. Chem. Thermodyn., 2007, 39, 28–38 CrossRef CAS.
- Syntelly: Better than chemists can do., https://syntelly.com, (accessed 11 Sep., 2023).
- W. Shen, L. Dong, S. Wei, J. Li, H. Benyounes, X. You and V. Gerbaud, Systematic design of an extractive distillation for maximum-boiling azeotropes with heavy entrainers, AIChE J., 2015, 61, 3898–3910 CrossRef CAS.
- J. Gu, X. You, C. Tao, L. Jun and G. Vincent, Energy-saving reduced-pressure extractive distillation with heat integration for separating the biazeotropic ternary mixture tetrahydrofuran–methanol–water, Ind. Eng. Chem. Res., 2018, 57, 13498–13510 CrossRef CAS.
- A. Yang, W. Shen, S. A. Wei, L. Dong, J. Li and V. Gerbaud, Design and control of pressure-swing distillation for separating ternary systems with three binary minimum azeotropes, AIChE J., 2019, 65, 1281–1293 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3gc04354a |
| This journal is © The Royal Society of Chemistry 2024 |