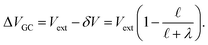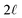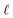DOI:
10.1039/D3FD00114H
(Paper)
Faraday Discuss., 2024,
249, 267-288
Water molecules mute the dependence of the double-layer potential profile on ionic strength
Received
1st June 2023
, Accepted 3rd July 2023
First published on 5th July 2023
Abstract
We present the results of molecular dynamics simulations of a nanoscale electrochemical cell. The simulations include an aqueous electrolyte solution with varying ionic strength (i.e., concentrations ranging from 0–4 M) between a pair of metallic electrodes held at constant potential difference. We analyze these simulations by computing the electrostatic potential profile of the electric double-layer region and find it to be nearly independent of ionic concentration, in stark contrast to the predictions of standard continuum-based theories. We attribute this lack of concentration dependence to the molecular influences of water molecules at the electrode–solution interface. These influences include the molecular manifestation of water’s dielectric response, which tends to drown out the comparatively weak screening requirement of the ions. To support our analysis, we decompose water’s interfacial response into three primary contributions: molecular layering, intrinsic (zero-field) orientational polarization, and the dipolar dielectric response.
1 Introduction
The interface between an electrode and an electrolyte solution can support persistent electric fields that serve to promote various modes of chemical reactivity.1–4 These fields reflect spatial variations in the electrostatic potential that arise due to the accumulation of charge on the electrode surface and the associated screening response of the electrolyte solution.5–11 Certain features of the interfacial potential profile can be systematically modified, for example by changing the applied potential or the chemical composition of the electrolyte solution.5,7,10,12 In this manuscript, we study the effects of changing electrolyte concentration on the interfacial potential profiles, specifically comparing the predictions of continuum-level theory and all-atom molecular dynamics (MD) simulation. We highlight that the potential profile derived from MD simulation exhibits little apparent dependence on ionic strength, in stark contrast to the predictions of the standard textbook theory of Gouy and Chapman.
We demonstrate that the source of this discrepancy is that the continuum theory does not account for the molecular effects of the solvent and its polarization response. Our simulation data reveals that these effects play a dominant role in shaping the interfacial potential profile. By analyzing the simulations of neat liquid water between charged electrodes, we attempt to deconstruct water’s various contributions to the interfacial potential profile. These contributions include oscillations from molecular layering, a symmetric potential drop between each electrode and the bulk from the inherent orientational bias of water–metal interactions, and a modified dielectric response due to excluded volume effects at the electrode boundary.
It has long been appreciated that the performance of electrochemical systems can be systematically modified by the concentration of ions in the supporting electrolyte. Since catalytic electrochemical reactions often proceed through surface intermediate species that reside in the electrochemical double layer (EDL), tuning screening behavior in the EDL (e.g. by changing the ionic strength of the solution) can meaningfully change electrochemical reaction rates and mechanisms. In the case of reactions with outer-sphere mechanisms described by Marcus kinetics, theoretical,13,14 and experimental,15 work has demonstrated that the reorganization energy (and hence reaction rate) is sensitive to the screening length-scale set by the electrolyte ionic strength. For inner-sphere electrochemical mechanisms, the effect of changing the ionic strength on the reaction rate can be more difficult to model, yet there are a number of experimental studies that have experimentally characterized the effects of changes in electrolyte composition and ionic strength on hydrogen evolution and CO2 reduction kinetics.16,17
Establishing the boundaries of validity for standard theories and models, and identifying the molecular origins of their failures, is vital to our ability to advance the field of electrochemistry. Here, we utilize MD simulation to explore water’s role in mediating the screening response of the aqueous interface. We compare our results to the predictions of standard theories, which generally treat liquid water as a dielectric continuum. Since molecular dynamics simulations fully represent the molecular structure, e.g., size, shape, and orientational correlation, they are well suited for validating the assumptions that underlie common theories and models. The manuscript is organized as follows. In the following section, we review double-layer theory. Then, in Section 3, we present results exploring the effects of changing ionic strength on the electrostatic potential profile of the interface. In Section 4 we evaluate the specific roles that water plays in mediating these effects and in shaping the potential profile more generally. Finally, following a brief conclusion, we describe our theoretical and simulation methodology.
2 Theoretical descriptions of the electric double-layer
The region of excess electrolyte concentration that builds up at an electrode interface is commonly known as the electric double-layer (EDL).7–9 Theoretical descriptions of EDL structure and its role in screening phenomena have a rich history. Helmholtz and Perrin advanced the first mathematical model for the EDL, and assumed that the electrode surface charge was perfectly neutralized by a flat plane of ions residing at the “outer Helmholtz plane” (OHP), separated from the electrode by a distance 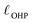 .18–20 Under this assumption, as illustrated in Fig. 1A, the EDL is a microscopic parallel-plate capacitor, with a constant electric field between the electrode and the OHP, and no variation in the potential from the OHP onwards. This EDL theory of Helmholtz and Perrin offers important physical insight into the role of ions in screening fields originating from electrodes, but has significant limitations.
.18–20 Under this assumption, as illustrated in Fig. 1A, the EDL is a microscopic parallel-plate capacitor, with a constant electric field between the electrode and the OHP, and no variation in the potential from the OHP onwards. This EDL theory of Helmholtz and Perrin offers important physical insight into the role of ions in screening fields originating from electrodes, but has significant limitations.
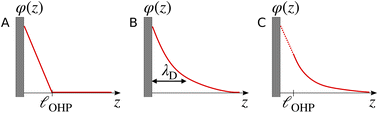 |
| | Fig. 1 Schematic electrical potential profiles in the EDL predicted by (A) Helmholtz–Perrin theory, (B) GC theory, and (C) GC theory with the Stern correction, where the dashed section represents the linear decay in the Stern layer. | |
The complete screening layer of Helmholtz and Perrin is entropically unfavorable and therefore not stable under standard thermal conditions. Entropic effects cause the screening layer to spread, broadening the width of the EDL. Physically reasonable electrostatic screening configurations therefore feature a diffuse cloud of neutralizing ionic density. An elementary description of potential variations in the EDL that accounts for such entropic effects originates from the Poisson–Boltzmann equation,21,22
| | 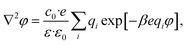 | (1) |
where
φ is the electrostatic potential,
c0 is the bulk ion concentration,
e is the fundamental charge, 1/
β =
kBT is the Boltzmann constant times temperature, and
ε and
ε0 are the continuum dielectric permittivity and the vacuum permittivity, respectively. The summation runs over all ionic components of the solution, indexed by
i, where
qi represents the charge number of the ion (
e.g. qi = +1 for a monovalent cation like Na
+).
For conditions of dilute ionic configurations, this equation can be simplified by linearizing the exponential term in eqn (1) and leveraging the fact that the salt formula is electroneutral 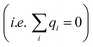 . The resultant mathematical description predicts an exponentially decaying electrostatic potential,
. The resultant mathematical description predicts an exponentially decaying electrostatic potential,
where
z is the separation from the electrode interface,
Vext is the applied potential, and
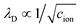
is the Debye screening length of the electrolyte solution.
Gouy–Chapman (GC) theory,21,22 as described in eqn (2), is applied widely when considering screening phenomena in the EDL, especially when they are of relevance to interpreting the results of electrochemical experiments. GC theory is particularly attractive because it advances the same simple physical picture as Debye–Hückel (DH) theory,23i.e., that a single tagged charge is surrounded by a diffuse neutralizing “cloud” of mobile ionic counter-charges. A single characteristic length scale emerges in both GC and DH, which is the so-called Debye length, λD. While physically intuitive, the theory for potential decay presented in eqn (2) involves a number of strong assumptions, many of which may be violated in electrochemically-relevant electrolyte systems.7,8,24,25
First, GC theory assumes that the ions in the electrolyte can be modeled as point charges that occupy no volume. Second, GC theory assumes that the solvent environment can be accurately represented by a dielectric continuum with single dielectric permittivity, ε, neglecting both the finite size of solvent molecules, as well as possible correlations between their positions and orientations.7,26 While these assumptions may be accurate in some cases, they can result in qualitatively inaccurate predictions on the length scale that characterizes the EDL. For example, in 1 M monovalent aqueous electrolyte, the Debye length λD = 3 Å, which is comparable to the hydrated radius of a single solvated ion; at this scale, the intuitive physical picture of a diffuse ionic charge screening cloud of width λD becomes untenable.24,26 Additionally, GC theory does not model the strong molecular interactions between a planar electrode surface and solvent dipoles, which have been shown to exhibit strong orientational preferences within a few molecular layers of an electrode surface.25,27,28
Some of the issues associated with the second assumption are remedied by the so-called Stern correction, which posits that there is a molecular layer (the “Stern layer”) of specifically adsorbed ions at the electrode surface.8,29 Including the Stern correction in the theory developed in eqn (2) results in an electrostatic potential profile that decays linearly in the Stern layer, and then exponentially out to the bulk. Fig. 1C depicts schematic descriptions of potential decay as described by each of the theories discussed.
3 Dependence of the interfacial potential profile on ionic concentration
We study electrostatic screening in the EDL using molecular dynamics (MD) simulations of aqueous NaCl electrolytes at various different concentrations, confined between two Pt electrodes. Fig. 2A depicts a representative snapshot of the molecular simulation cell, with the z axis oriented normal to the planar electrode surface. In our simulation model, the electrodes are held at constant potential, as if they were connected to an external potentiostat. To accomplish this, we use the fluctuating charges method originally developed by Siepmann and Sprik, and later extended by Reed and Madden.30–32 In this method, the partial charges on the electrode atoms are adjusted between each MD timestep in order to maintain a constant potential difference between the two electrodes. For the simulations presented in this section, the left electrode is held at a potential of VL = −Vext and the right electrode is held at VR = Vext, where Vext = 0.5 V, thus imposing an overall potential difference of ΔV = 1 V between the two electrodes.
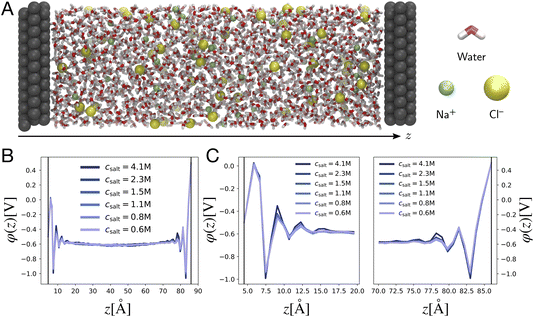 |
| | Fig. 2 Poisson potential computations from molecular dynamics simulations. (A) Representative snapshot of a molecular dynamics simulation cell, depicting an aqueous 1 M NaCl electrolyte between two Pt electrodes. The left electrode is the cathode (held at VL = −0.5 V), and the right electrode is the anode (held at VR = +0.5 V). By convention, the z axis runs perpendicular to the electrode surfaces. (B) Traces of the equilibrium-averaged, plane-averaged Poisson potential φ(z), estimated from molecular dynamics simulations run at various electrolyte salt concentrations. (C) Traces of φ(z) zoomed in on the cathode and anode, highlighting oscillatory and concentration independent short distance screening behavior. | |
The simulation box has dimensions 3.1 nm × 3.1 nm × 9.3 nm, and is periodically replicated in the directions lateral to the electrode surface. Previous studies have shown that the local dielectric constant of water approaches the bulk value within 35 Å of an interface.33 With a wall separation of 80 Å our simulation cell is large enough to host two non-overlapping EDLs at each of the electrodes, with a well-formed bulk in the central region. The number of water molecules and ions in the simulation cell vary with electrolyte concentration and are presented in Table 1 in the Methods section. The intermolecular potential, or “force field” describing the water molecules is the standard TIP3P force field,34 whereas the ion and Pt atom interaction parameters are taken from studies reported in the literature.35,36 These parameters were chosen due to the excellent correlation of calculated and experimental ion hydration properties for this particular force field.36 Ion solvation properties are known to play an important role in ion distribution preferences at interfaces.10,37 The results presented here depend on the details of the intermolecular interaction potentials, but the qualitative screening structures reported should be broadly conserved between force fields.
Our primary basis of comparison between continuum theory and atomistic simulation is the average electrostatic potential profile, i.e., the Poisson potential, φ. In this work, we represent this profile as an average over an equilibrium ensemble of single snapshot potentials. Specifically, we define the mean Poisson potential as,
| | 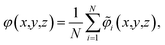 | (3) |
where
![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) i
i(
x,
y,
z) is an instantaneous representation of the Poisson potential for the
ith MD snapshot. Computing
![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) i
i(
x,
y,
z) for a single configuration of a point-charge species requires first defining a spatially continuous charge density profile,
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i
i(
x,
y,
z), on a regular lattice. We accomplish this with a proportional charge spreading scheme, which interpolates the charges on atomic centers to nearby points on the regular lattice. The details of this charge-spreading scheme are described in the Methods section. After defining
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i
i, we compute
![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) i
i from the Poisson equation, ∇
2![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) i
i = −
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i
i/
ε0.
The averages presented below are derived from equilibrated simulations of 10 ns with snapshots taken every 100 ps (i.e., N = 100). We define the one-dimensional potential profile as,
| | 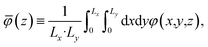 | (4) |
where
Lx and
Ly are the length of the electrolyte region in the
x and
y directions, respectively. Defining the potential in this way enables straightforward comparison to the one-dimensional profiles predicted from continuum theory and admits the analysis of microscopic potential fluctuations
via the statistics of
![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif)
(
x,
y,
z).
Fig. 2B depicts traces of the plane-averaged Poisson potential for several different electrolyte ion concentrations. The thin black lines represent the approximate planes of constant potential imposed in the MD simulation, where the voltages are pinned at VL = −0.5 V and VR = +0.5 V. It is apparent that the electrostatic screening structure is well established over the course of the simulations, with two distinct EDL regions confined within 10–15 Å of the electrode surfaces, and a bulk region with a flat electrostatic potential profile, thus indicating the absence of static fields from the electrodes. Fig. 2C shows zoomed-in snapshots of the EDLs at the left and right electrodes, highlighting the electrostatic potential variation in these regions. Although the plane-averaged potential profiles exhibit electrostatic potential decay from the electrode surface to the bulk, in line with continuum descriptions of electrostatic screening, they are strikingly dissimilar from the profiles depicted in Fig. 1. First, the profiles are markedly non-monotonic, exhibiting relatively large oscillations in the local electrostatic potential on the scale of Vext. Second, and perhaps most strikingly, the electrostatic potential profiles show little variation over the entire range of ion concentrations studied here, instead of becoming more compact at higher concentrations, as predicted by GC theory.
The marked deviations from GC behavior in Fig. 2 raises the question: in what manner does GC-like screening manifest in the atomistic system, if at all? To answer this question, we attempt to separate the contributions of ions and water molecules to interfacial screening. We accomplish this by analyzing the screening profile of ions only, via the construction of the ionic screening function, which for the left EDL is defined as,
| | 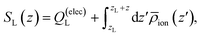 | (5) |
where
zL denotes the position of the left electrode, and
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) ion
ion(
z) is the
xy-plane-averaged ionic charge density, obtained by restricting the proportional spreading procedure (described in Section 6) only to the atom-centered charges on the ionic species, and neglecting the charges of the solvent molecules entirely. The screening function for the right electrode is defined analogously to that of
eqn (5) but with an integral extending from
zR to
zR −
z. Intuitively, the screening function
S(
z) tallies the amount of electrode charge that remains unscreened by the mobile ionic charges of a given distance into the bulk; it takes the value
Q(elec) at the electrode surface (
z = 0), and levels off upon reaching the bulk region of the simulation cell. We observe that
S(
z) ≈ 0 for values of
z beyond the EDL width.
Fig. 3A depicts traces of the normalized ionic screening function ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (z) ≡ SL(z)/SL(0) for various different ionic concentrations. According to GC screening theory, this normalized screening function should decay from unity to zero in an exponential manner, with associated length scale λD, the Debye length. The profiles in Fig. 3A show signatures of the GC screening behavior; the profiles are more diffuse at lower salt concentrations, and analysis of the length scale by exponential fitting, as illustrated in Fig. 3C, shows that the decay length is roughly λD for each ion concentration.
(z) ≡ SL(z)/SL(0) for various different ionic concentrations. According to GC screening theory, this normalized screening function should decay from unity to zero in an exponential manner, with associated length scale λD, the Debye length. The profiles in Fig. 3A show signatures of the GC screening behavior; the profiles are more diffuse at lower salt concentrations, and analysis of the length scale by exponential fitting, as illustrated in Fig. 3C, shows that the decay length is roughly λD for each ion concentration.
 |
| | Fig. 3 Signatures of ionic and dipolar screening behavior. (A) Traces of the normalized screening function, S(z)/S(0) at various electrolyte concentrations, reflecting concentration dependent ionic screening behavior. (B) Traces of the local concentration of water molecules (solid lines) and Na+ cations (dashed lines), normalized by their respective bulk concentrations, at various electrolyte concentrations. (C) Empirical screening length, λ derived by fitting ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (z)/ (z)/![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (0) to a decay function exp(−(z − 8 Å)/λ). The Gouy–Chapman prediction, where λ = λD, is plotted as a solid black line. (0) to a decay function exp(−(z − 8 Å)/λ). The Gouy–Chapman prediction, where λ = λD, is plotted as a solid black line. | |
Although the ionic statistics are in line with expectations from GC theory, the molecular dynamics simulations provide ample evidence that the solvent molecules play an important role in electrostatic screening. Fig. 3B shows traces of the bulk-normalized concentration of water molecules (solid lines) and sodium cations (dashed lines) in the simulation for the different ionic concentrations examined. At these concentrations, the first density peak of the water molecules appears closer to the left electrode than the first density peak of the cations. Additionally, the height of the peak, normalized to the bulk density of water, is roughly independent of the ion concentration, indicating that the water molecules are able to screen the electrode charge at distances closer than the typical cation approaches the electrode.
4 Deconstructing water’s influence on the interfacial potential profile
In continuum theories, such as those based on the seminal work of Debye and Hückel,23 the role of solvent in determining the electrostatic potential profile is reduced to that of a simple dielectric medium.7,8 Any notable variations in the shape of the potential are thus attributed to the spatial redistribution of mobile charge carriers. The results in the previous section reveal that water plays a more significant role than ions do in shaping the potential profile within the EDL. To isolate this role, we consider simulations of neat water confined between two electrodes under varying applied potential.
The neat water simulations utilize a similar simulation size and setup to the system presented in Section 3, but use the SPC/E force field for water and electrode atom force field parameters for graphite rather than platinum, while still maintaining constant potential in the same way. The SPC/E force field was used because it provides a dielectric constant closer to experiment than TIP3P. The switch to graphite was motivated by the observation that water chemisorbs onto platinum at positive potentials as demonstrated by ab initio simulations.38,39 Water chemisorption is expected to influence the quantitative details of the interfacial potential profile, and this feature cannot be captured with classical force fields. However, water does not chemisorb onto graphene at the potentials used in our simulations.40 Therefore, we expect our simulations will at least qualitatively capture the reorientation of interfacial water, which is expected to contribute to the inner-layer capacitance of the interface.41 We carried out simulations with the electrodes held at constant potentials of Vext = 0.00, 0.25, 0.50, and 1.00 V, imposing an overall potential difference of ΔV = 0.00, 0.50, 1.00, and 2.00 V. Additional details are provided in the Methods section. Again, we analyze these simulations by computing the mean Poisson potential profile, φ(z).
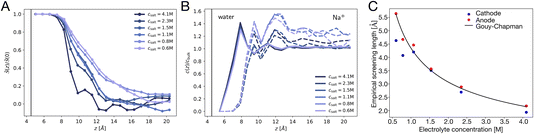
The potential profile computed for unbiased conditions, i.e., Vext = 0, is plotted in Fig. 4A. This potential profile exhibits oscillations near the electrode, similar to those appearing in Fig. 2. The bulk potential for neat water at Vext = 0 is flat with a value of φbulk ≈ −0.55 V. We note that this interfacial potential drop and the oscillations are not accounted for in the treatment of water as a simple dielectric continuum.
 |
| | Fig. 4 The potential profiles for neat water with and without applied potential. (A) The Poisson potential, φ(z), for neat liquid water between neutral electrodes (Vext = 0). The calculated bulk potential, φbulk ≈ −0.55 V. (B) Poisson potential for neat water with an applied electrode potential difference of 2 V (Vext = 1 V). The bulk electric field, Ebulk, is the slope of the calculated potential (black line) evaluated with the bulk region. For reference, schematic potentials with slopes E0 = Vext/L and E0/εw are plotted in blue and green, respectively. | |
A potential profile computed under a 2 V bias (Vext = 1 V) is plotted in Fig. 4B. This profile exhibits similar features to those of the unbiased profile with the addition of a finite slope in the bulk. This slope implies the presence of a static electric field, thereby indicating incomplete screening of the applied electrode potential by water, as expected for a neutral solvent. This partial screening is reminiscent of the effect of a uniform dielectric on the field between a parallel-plate capacitor, as we discuss further in Section 4.3. However, the observed slope in the potential differs from the expectations of dielectric continuum theory.
Taken together, the potential profiles plotted in Fig. 4 reveal three primary contributions that water makes in shaping the interfacial potential profile. These contributions are: (1) pronounced oscillations over molecular length scales, (2) a roughly 0.5 V drop in potential over the first 1 nm of the interface at both electrodes, leading to a bulk-level potential that is not at the midpoint of the electrode potentials, (3) a reduction in the electric field within the bulk under applied electrode potential. In the following subsections, we discuss the molecular origins of each of these contributions and how they relate to the dielectric properties of the water–electrode interface.
4.1 Molecular scale oscillations in the interfacial potential profile
Both ab initio and classical molecular dynamics simulations have revealed molecular scale oscillations in the electrostatic potential profile of solid–liquid interfaces.6,27,42 These oscillations are attributed to the consequences of molecular layering at the electrode surface, which serves to break translational symmetry. An increased density (relative to the bulk) of water molecules at the contact plane of the electrode exclude the adjacent plane, resulting in a subsequent decrease in density. This phenomenon, which has an analog in the oscillation of a radial distribution function, results in the emergence of well-defined hydration layers, as illustrated in Fig. 5.
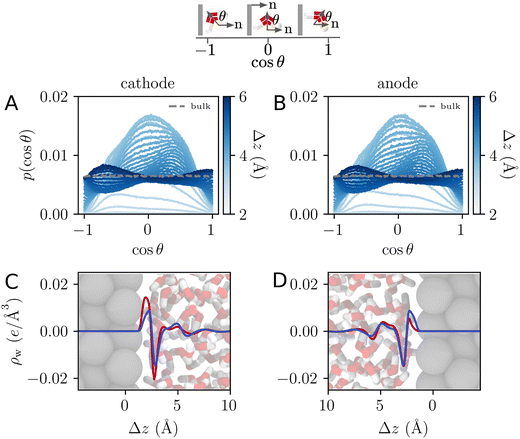 |
| | Fig. 5 (A) and (B) The orientational distribution function for the angle, θ, made between the water dipole vector and the electrode surface normal, as illustrated schematically above. The differently shaded lines correspond to populations of water molecules a given distance, Δz, from the electrode surface. The dashed grey line is the distribution corresponding to bulk water. (C) and (D) The charge density profile is computed for the population of water molecules at the interface of the electrode. Blue and red lines correspond to charge densities at Vext = 0.0 V and Vext = 1.0 V, respectively. Snapshots of the interface over the same horizontal axis scale are included to establish a sense of molecular lengths. | |
The oscillating water density profile leads to a similarly oscillating charge density field. When subject to the Poisson equation, this oscillating charge profile naturally results in an oscillating potential profile. The length scale of oscillation is determined by the molecular size and can be modeled with classical density functional theory.43 Oscillations like this, but persisting well beyond λD, emerge in ionic liquids.12 Since these oscillations have been previously well studied using MD simulation, we refrain from elaborating on them further herein.
4.2 Water’s interfacial potential drop
One striking feature of the unbiased potential profile plotted in Fig. 4 is the potential drop between the neutral electrodes and the bulk liquid. This potential drop is also evident in the biased system plotted in Fig. 4B and in the aqueous electrolyte systems plotted in Fig. 2. Analysis of molecular dynamics simulation data reveals that this effect originates from anisotropy in the orientations of water molecules in the first hydration layer. This anisotropy is intrinsic to the water–electrode interactions and thus symmetric between the left and right electrodes. The anisotropy is apparent in the distribution of molecular orientations plotted in Fig. 5, which reveals a preference for interfacial water molecules to direct their hydrogens toward the electrode (away from the bulk). This orientation prevails because it provides favorable coulomb interactions between the image charges in the electrode and the partial positive charges of the hydrogen atoms.
The orientational bias of interfacial water molecules leads to a charge density wave that is net charge neutral, as illustrated in Fig. 5. According to the Poisson equation, a neutral density wave of this form (negative charge oriented toward increasing z) yields a finite potential drop. At the opposite electrode, this charge density wave is mirrored leading to an equal and opposite potential rise. The quantitative details of this effect depend sensitively on the water–metal interactions as well as the distribution of charge within the water molecule. The magnitude of this effect is thus expected to depend sensitively on the choice of force field and on the simulation conditions.
To understand this effect, we consider a simple model of dipolar solvent polarization at constant potential boundaries. This model includes a one-dimensional charge density profile extending along the z coordinate, as illustrated in Fig. 6. The charge density profile is described on a lattice with lattice spacing 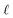 , representing the approximate radius of a water molecule. Under unbiased conditions with neat water, both the electrodes and bulk liquid have charge densities of ρ = 0. We model the charge density wave associated with solvent polarization with a discrete charge density wave, ρ(−L) = ρw and ρ(−L + 1) = −ρw, with a symmetric contribution at the other electrode, ρ(L) = ρw and ρ(L − 1) = −ρw.
, representing the approximate radius of a water molecule. Under unbiased conditions with neat water, both the electrodes and bulk liquid have charge densities of ρ = 0. We model the charge density wave associated with solvent polarization with a discrete charge density wave, ρ(−L) = ρw and ρ(−L + 1) = −ρw, with a symmetric contribution at the other electrode, ρ(L) = ρw and ρ(L − 1) = −ρw.
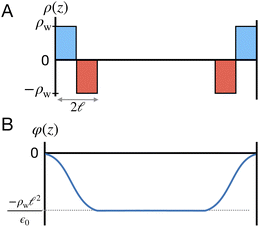 |
| | Fig. 6 A schematic model of the influence of a symmetric charge wave on the electrostatic potential profile. (A) A piecewise representation of a water-like interfacial charge wave localized within 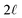 of the interface. (B) The Poisson potential arising from the density profile in (A) has a systematic drop in the bulk, analogous to that observed in the analysis of atomistic simulations. of the interface. (B) The Poisson potential arising from the density profile in (A) has a systematic drop in the bulk, analogous to that observed in the analysis of atomistic simulations. | |
The potential profile that results from the lattice charge density wave is plotted in Fig. 6B. The potential profile of this lattice charge density is sigmoidal, becoming constant at 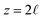 with a bulk potential value of
with a bulk potential value of 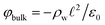 . Taking
. Taking 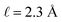 , the polarization density required to achieve a value of φbulk = −0.55 V is ρw = 0.57e nm−3.
, the polarization density required to achieve a value of φbulk = −0.55 V is ρw = 0.57e nm−3.
If the inherent orientation of water molecules at the interface is inverted, i.e., with hydrogen atoms pointed away from the electrode, then the resulting charge density wave results in a bulk potential that has a higher value than that of the neutral electrode.
4.3 Partial screening of external electric fields within the bulk
A dielectric medium, such as liquid water, has the general effect of reducing the strength of electric fields originating externally, such as from extended charged surfaces, or internally, such as from charge solutes. If a medium with dielectric constant ε is exposed to an external electric field of magnitude E0, then the field within the bulk medium is Ebulk = E0/ε. Liquid water has a large dielectric constant, εw ≈ 80, owing to its large molecular dipole and can thus significantly reduce the strength of external fields.
However, when liquid water is located between parallel electrodes held at constant potential, the dielectric effect simultaneously amplifies and reduces the fields originating from the electrode. The reduction arises due to the polarization of solvent dipoles and the amplification arises due to the concomitant charging of the electrodes in order to maintain their potential. For a uniform dielectric continuum, these effects exactly cancel, yielding no net reduction in the bulk electric field. To maintain this, the electrode charge density qel = εq0, where q0 is the charge density required to maintain potential in vacuum (ε = 1).
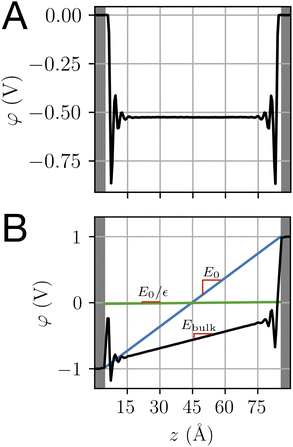
The electric fields in our simulations of neat water under constant potential bias are lower than expectations based on a constant potential dielectric continuum, yet higher than expectations based on constant charge parallel plate capacitors. This is illustrated in Fig. 4. Fig. 7 contains a plot of Ebulkvs. applied potential, indicating that the partial screening of the external electrode fields is a linear function of applied potential.
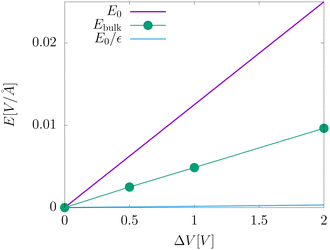 |
| | Fig. 7 A plot of the electric field in the bulk liquid at different values of the applied electrode potential ΔV = 2Vext. The plot also includes an indication of the predictions from dielectric continuum theory between surfaces of fixed potential, E0, and fixed charge, E0/εw. | |
Analysis of our MD simulation data indicates the influence of liquid water on the electrode charge density is similar to that of a standard dielectric medium, yet not identical to that of a homogeneous dielectric continuum. The presence of water results in an amplification of electrode charge density relative to the case where the electrodes are separated by a vacuum, and the strength of the electric field from this amplification is significantly reduced in the bulk relative to that of bare electrodes. However, the strength of each of these effects implies a different value of the dielectric constant. Furthermore, neither effect is consistent with the dielectric constant of this model of liquid water.
The partial screening of the electric fields from the electrodes can be quantified in terms of an effective dielectric constant, ε(E)eff, which is defined in relation to the slopes of the potential originating from the bare electrodes and the potential within bulk liquid. Specifically, Ebulk = Eel/ε(E)eff, where Eel = qel/ε0 is the field originating from an infinite plate with surface charge density qel and Ebulk is the slope of φ(z) within the bulk, as indicated in Fig. 4. The value we compute for this effective dielectric constant is ε(E)eff ≈ 60, and roughly independent of applied potential. Specifically, ε(E)eff = 59.8 when ΔVext = 0.5, ε(E)eff = 61.5 when ΔVext = 1.0, and ε(E)eff = 60.1 when ΔVext = 2.0. This effective dielectric constant is similar in magnitude to that reported in the literature for this water model, εSPC/E = 73.44
The amplification of electrode charge due to water can be quantified in terms of a different effective dielectric constant, ε(q)eff, which is defined in relation to the charge density of the electrodes separated by liquid water and separated by vacuum. Specifically, qel = ε(q)effq0, where q0 is the charge density to maintain the potential in vacuum. The value we compute for this effective dielectric constant is ε(q)eff ≈ 24, and also roughly independent of applied potential. Specifically, ε(q)eff = 24.4 when ΔVext = 0.5, ε(q)eff = 24.3 when ΔVext = 1.0, and ε(q)eff = 23.4 when ΔVext = 2.0. This effective dielectric is significantly smaller than that of the liquid.
We assert that these seemingly incommensurate observations arise from deviations from dielectric continuum theory due to molecular effects at the water interface. As a dielectric continuum, water is assumed to be spatially uniform and everywhere charge neutral. Both of these assumptions break down at the charged electrode–water interface. Excluded volume effects limit the plane of closest approach for water molecules and orientational anisotropy due to the external electric field leading to narrow planes of charge buildup with equal magnitude and opposite sign at either electrode. Fig. 8A illustrates the concept and Fig. 8B demonstrates that there is indeed a positive net charge buildup at the negative electrode. There is an analogous negative buildup at the positive electrode. The position of this charge plane is displaced from the electrode surface by a finite distance, 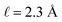 , and its magnitude scales with Vext.
, and its magnitude scales with Vext.
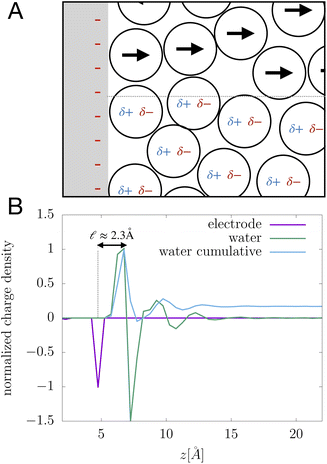 |
| | Fig. 8 (A) A schematic depiction of an interface between an electrode and a neutral dipolar liquid. In the top half and bottom half of the schematic, the net dipole orientation is rendered as arrows and partial charges, respectively. At a negative electrode surface, the orientation of the first hydration layer results in a narrow plane of net positive charge at the interface, subsequent planes of alternating charge cancel out as the degree of molecular layering diminishes. (B) Charge density profiles derived from simulation data of neat water at the left electrode with potential −1 V. Purple and green lines indicate the normalized charge density contributions of electrode atoms ρel(z) and water molecules ρw(z), respectively. The blue line represents the cumulative water charge density, 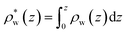 , illustrating that at the negative electrode, there is a positive net charge from water. There is an equal and opposite net positive charge at the adjacent positive electrode (not plotted). We denote the distance, , illustrating that at the negative electrode, there is a positive net charge from water. There is an equal and opposite net positive charge at the adjacent positive electrode (not plotted). We denote the distance, 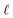 between the first peaks of ρel and ρw which contributes to the effective dielectric response of the water–electrode interface. between the first peaks of ρel and ρw which contributes to the effective dielectric response of the water–electrode interface. | |
This physical picture implies a simple one-dimensional model of the charge density field of an electrochemical cell with two opposing polar solvent–electrode interfaces, as illustrated in Fig. 9. In this model, one electrode is located at position z = −L and held at potential V = −Vext and the other electrode is located at position z = L and held at potential V = +Vext. The charge density of the electrodes are represented by Gaussian distributions centered at z = −L and z = L:
| | 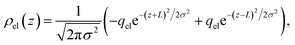 | (6) |
and the water polarization layers are represented by similar distributions displaced into the bulk by a distance
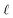
,
| | 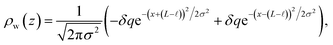 | (7) |
where
σ is atomic in scale. The full charge density field is given by a sum of these two contributions,
| | | ρ(z) = ρel(z) + ρw(z), | (8) |
as illustrated in
Fig. 9. The value of
qel is determined by the constant potential condition that
φ(
L) −
φ(−
L) = 2
Vext and the value of
δq determines water’s interfacial dielectric response.
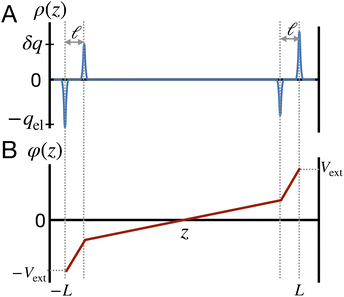 |
| | Fig. 9 A model for understanding the interfacial dielectric response of a polar liquid at constant potential boundaries. (A) A depiction of the charge density field which combines the electrode surface charge, with amplitude qel and the water polarization surface charge, with amplitude δq. (B) The potential profile derived from the Poisson equation in the limit that the Gaussian distributions narrow to delta functions. The slope of the potential in the bulk region is that of a parallel plate capacitor with charge density ρel − δρ. | |
The potential differences between the electrode and the center of the bulk can be computed directly from the Poisson equation. In this model, by construction, φ(0) − φ(−L) = φ(L) − φ(0) = Vext. In the limit that the Gaussian distributions are infinitely narrow, this expression is simply,
| | 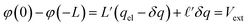 | (9) |
where
L′ =
L/
ε0 and
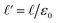
. The
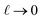
limit of this expression corresponds to the standard dielectric continuum picture. In this limit,
qel −
δq =
Vext/
L′ =
E0. Noting that
E0 =
q0/
ε0 =
ε−1qel/
ε0, we see that
δq =
qel(1 −
ε−1).
The deviations from dielectric continuum theory that we highlighted above (i.e. that ε(E)eff ≈ 60 and ε(q)eff ≈ 24) arise from the case where 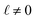 . In this case, eqn (9) can be manipulated to yield,
. In this case, eqn (9) can be manipulated to yield,
| | 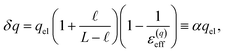 | (10) |
thus indicating that the degree of interfacial solvent polarization is directly proportional to that of the electrode. The proportionality constant,
α, depends on
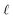
,
L, and the effective dielectric constant,
ε(q)eff.
Eqn (10) provides a basis for understanding the unexpectedly low value of ε(q)eff = 24. We note that δq is related to water’s bulk dielectric constant via a simple parallel plate capacitor model,
| | 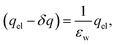 | (11) |
where
εw is water’s bulk dielectric constant. Substituting
δq from this expression into
eqn (9) yields,
| | 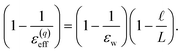 | (12) |
This expression reveals that the relationship between
ε(q)eff and
εw is mediated by the ratio
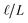
, with
ε(q)eff =
εw in the
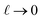
limit. In our system, where
L = 8 nm,
εw = 73, and
ε(q)eff = 24, we find
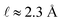
, which is consistent with the results plotted in
Fig. 8.
The physical picture that this model advances is like that of the Stern layer. Some fraction of the applied potential drops due to water’s interfacial dielectric response in the 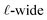 region between the electrode and the first solvent plane. The magnitude of this drop is effectively equal to
region between the electrode and the first solvent plane. The magnitude of this drop is effectively equal to 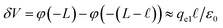 . The remaining potential drop, ΔVGC = Vext − δV, is thus what remains to be screened by the migration of ions (e.g., following Gouy–Chapman theory). In a pure water system, this quantity is,
. The remaining potential drop, ΔVGC = Vext − δV, is thus what remains to be screened by the migration of ions (e.g., following Gouy–Chapman theory). In a pure water system, this quantity is,
| | 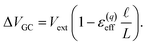 | (13) |
This expression has the feature that for a macroscopic system,
i.e.,
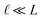
, Δ
VGC =
Vext. In other words,
δV → 0 as
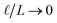
.
4.4 The role of ions in amplifying water’s interfacial dielectric response
The implication of the above analysis is that the interfacial potential drop due to water (i.e., δV) is only appreciable in nanoscale systems. This conclusion is specific to a pure solvent system, where there are no mobile charge carriers to participate in screening. In this case, any unscreened potential drop (e.g., ΔVGC), must extend across the entire length of the system. Potentials dropped over macroscopic length scales require only small electrode charges. In reality, neat water contains dilute concentrations of “water ion”, i.e., H3O+ and OH−, that can contribute to attenuating potential drops to microscopic scales (λD ∼ 1 μm in water at neutral pH). When this is the case, the analysis above must be adjusted to account for the influence of ionic screening. Assuming the first hydration layer excludes ions (so Gouy–Chapman-like screening occurs at the left electrode starting from 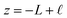 ) and that the potential is fully attenuated over the distance
) and that the potential is fully attenuated over the distance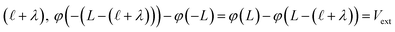 , and thus
, and thus 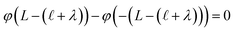 . Eqn (9) can thus be revised as,
. Eqn (9) can thus be revised as,| | 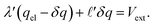 | (14) |
where λ′ = λ/ε0. It can be shown that with ionic screening qel = ε0Vext/λ, whereas without ionic screening qel = ε0Vext/(εL). With this expression, the interfacial potential drop, 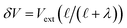 and likewise,
and likewise,| | 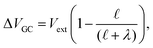 | (15) |
implying that the amount of potential that must be screened by ions is a decreasing function of ionic strength (increasing function of λ). If 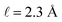 , then according to this expression, ΔVGC ≈ 0.63Vext for a 0.6 M solution (λD = 3.96 Å) and ΔVGC ≈ 0.52Vext for a 1.5 M solution (λD = 2.47 Å).
, then according to this expression, ΔVGC ≈ 0.63Vext for a 0.6 M solution (λD = 3.96 Å) and ΔVGC ≈ 0.52Vext for a 1.5 M solution (λD = 2.47 Å).
5 Conclusions
The predictions of Gouy–Chapman theory are based on the assumption that water is a homogeneous dielectric continuum. In this manuscript, we have used all-atom molecular dynamics simulation to demonstrate that this assumption breaks down in multiple important ways. Water molecules take up physical space which leads to the appearance of molecular layering at solid–liquid interfaces and an associated displacement of the solvent polarization layer away from the electrode into the bulk. In addition, the molecular orientations of water molecules at the interface are anisotropic, owing to the specific details of non-spherically symmetric water–metal interactions. Together, these effects play a dominant role in shaping the interfacial potential profile, thus obscuring the comparatively minor effects of classical Debye–Hückel-like ionic screening.
6 Methods
6.1 Simulation details for systems with varying ionic concentration
Simulations at varying concentrations included the number of ions and water molecules indicated in Table 1.
Table 1 Number of atoms contained in each simulation at the specified concentrations
| Concentration [M] |
N
water
|
N
NaCl
|
| 0.6 |
2557 |
28 |
| 0.8 |
2548 |
37 |
| 1.1 |
2536 |
51 |
| 1.5 |
2512 |
73 |
| 2.3 |
2464 |
113 |
| 4.1 |
2344 |
202 |
6.2 Simulation details for neat water systems
The dimensions of the simulation cell were 2.8 nm × 2.9 nm × 9.3 nm. Water was modeled with the SPC/E water model45 and the number of water molecules was 2042. The charges on the electrode atoms were allowed to fluctuate to maintain constant potential with the ELECTRODE package46 in LAMMPS.47 For each Vext = 0.00, 0.25, 0.50, and 1.00 V, we generated 100 trajectories each 1 ns in length. From each of these trajectories, the last 0.8 ns were used for data analysis. This provided an aggregate total of 80 ns of simulation data for each Vext.
6.3 Computational details for Poisson potential computation
Given a molecular simulation trajectory, we would like to devise a numerical scheme to determine the Poisson potential at any point in the simulation volume. The Poisson potential φ is defined by the Poisson equation,where ρ is the free charge density field. The geometry under consideration has two periodic dimensions, denoted x and y, and one closed dimension z, which is the coordinate normal to the planar electrodes. The appropriate boundary conditions are,| | | ∂xφ(0,y,z) = ∂xφ(Lx,y,z) | (19) |
| | | ∂yφ(x,0,z) = ∂yφ(x,Ly,z) | (20) |
where Vleft and Vright are the applied potentials on the left and right electrodes, situated at z = 0 and z = Lz, respectively.
To start developing a numerical scheme, we can discretize eqn (16) on a three-dimensional rectangular grid. Given a specification of the number of grid points N = (Nx,Ny,Nz), we can define a vector of grid spacings Δ ≡ (Nx−1,Ny−1,[Nz + 1]−1). Note that the z-coordinate has a slightly different grid spacing because we would like to impose Dirichlet boundary conditions in this coordinate, requiring an extra boundary point. Now, grid points can be indexed by an index tuple n ∈ {0,…,Nx − 1} × {0,…,Ny − 1} × {0,…,Nz}. The spatial location of a grid point with index tuple n is simply rn = Δ·n. Eqn (16) can be naturally discretized using a second-order Laplacian stencil. Under a row-major indexing scheme for the coordinates, this produces a sparse representation of the Laplacian operator.
Solving eqn (16), discretized on a grid, is relatively straightforward if we have a way to evaluate the free charge density field, ρ, on the grid points. However, particles in a molecular simulation are, in general, not situated on a uniform grid. Hence, we need a scheme for interpolating a non-uniform charge density field onto a uniform grid of points. Formally, for a particle with index k carrying charge qk localized at position rk = (xk,yk,zk), we identify eight points bounding the voxel containing the particle. The index tuples of these eight points can be computed using the following equations,
| | | nk1 = (⌈xk/Lx⌉,⌊yk/Ly⌋,⌊zk/Lz⌋) | (23) |
| | | nk2 = (⌊xk/Lx⌋,⌊yk/Ly⌋,⌊zk/Lz⌋) | (24) |
| | | nk3 = (⌈xk/Lx⌉,⌈yk/Ly⌉,⌊zk/Lz⌋) | (25) |
| | | nk4 = (⌊xk/Lx⌋,⌈yk/Ly⌉,⌊zk/Lz⌋) | (26) |
| | | nk5 = (⌈xk/Lx⌉,⌊yk/Ly⌋,⌈zk/Lz⌉) | (27) |
| | | nk6 = (⌊xk/Lx⌋,⌊yk/Ly⌋,⌈zk/Lz⌉) | (28) |
| | | nk7 = (⌈xk/Lx⌉,⌈yk/Ly⌉,⌈zk/Lz⌉) | (29) |
| | | nk8 = (⌊xk/Lx⌋,⌈yk/Ly⌉,⌈zk/Lz⌉), | (30) |
where ⌊·⌋ and ⌈·⌉ represent the integer floor and integer ceiling functions, respectively. Along each dimension
d ∈ (
x,
y,
z), the particle position partitions the line segment connecting two adjacent grid points into two segments, one of length
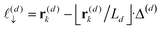
, and another of length
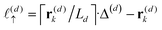
. Note that
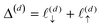
, due to the properties of the ceiling and floor functions. For notational convenience, define,
| | 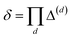 | (31) |
Now, we assign each point bounding the voxel a weight,
| | 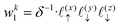 | (32) |
| | 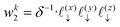 | (33) |
| | 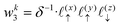 | (34) |
| | 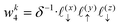 | (35) |
| | 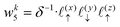 | (36) |
| | 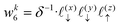 | (37) |
| | 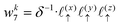 | (38) |
| | 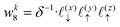 | (39) |
The charge density on all grid points is computed by incrementing the charge density on each point
i ∈ 1,…,8 bounding the voxel containing particle
k by its charge weight
qkwki, and repeating for all particles in the simulation.
6.4 Poisson–Boltzmann theory for electrode charge
We can adapt Poisson–Boltzmann theory to generate a potential profile for the system architecture summarized in Fig. 9. To begin, consider the case where 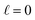 , i.e., traditional continuum approximation. In this case, linearized Poisson–Boltzmann theory yields potential profile of,
, i.e., traditional continuum approximation. In this case, linearized Poisson–Boltzmann theory yields potential profile of,| | 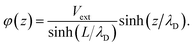 | (40) |
According to this model, the potential due to the electrode is given by,| | 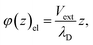 | (41) |
which implies (through a parallel-plate capacitor model) a surface charge density for the left electrode of,| | | qel = −Vext/λD = −(δq + qion), | (42) |
where qion is the integrated excess ionic density profile in the interfacial screening layer. As the second equality suggests, charge neutrality necessitating that the charge contribution arising from the solution (i.e., δq + qion) must exactly counter the electrode charge.
We can adapt the equations above to describe the case where 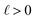 . In this case, the electrode charge is separated by the onset of the Poisson–Boltzmann screening layer (eqn (40)) by a distance
. In this case, the electrode charge is separated by the onset of the Poisson–Boltzmann screening layer (eqn (40)) by a distance 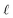 . The potential dropped over this distance is
. The potential dropped over this distance is 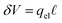 , leaving the remaining potential ΔVGC to be dropped by solvent/ions. According to eqn (42), the charge in the solution will be,
, leaving the remaining potential ΔVGC to be dropped by solvent/ions. According to eqn (42), the charge in the solution will be,
| | | δq + qion = −ΔVGC/λ = −qel, | (43) |
where again, the second equality arises due to charge neutrality. Now, noting that
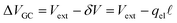
, we find that,
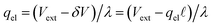
and thus
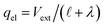
. With this,
| | 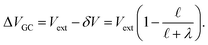 | (44) |
Author contributions
AL carried out and analyzed simulations of varying ionic concentration. DS carried out and analyzed simulations of neat water under varying bias. All authors contributed to writing the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Air Force Office of Scientific Research (AFOSR) under award number FA9550-18-1-0420. DS acknowledges the Burroughs Wellcome Fund for support. We would like to thank the late Professor Phill Geissler for helpful advice and discussion.
References
- V. R. Stamenkovic, D. Strmcnik, P. P. Lopes and N. M. Markovic, Nat. Mater., 2017, 16, 57–69 CrossRef CAS.
- J. Masa, C. Andronescu and W. Schuhmann, Angew. Chem., Int. Ed., 2020, 59, 15298–15312 CrossRef CAS.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- K. Sakaushi, T. Kumeda, S. Hammes-Schiffer, M. M. Melander and O. Sugino, Phys. Chem. Chem. Phys., 2020, 22, 19401–19442 RSC.
- D. Martin-Jimenez, E. Chacon, P. Tarazona and R. Garcia, Nat. Commun., 2016, 7, 12164 CrossRef CAS.
- O. M. Magnussen and A. Groß, J. Am. Chem. Soc., 2019, 141, 4777–4790 CrossRef CAS PubMed.
- G. Gonella, E. H. G. Backus, Y. Nagata, D. J. Bonthuis, P. Loche, A. Schlaich, R. R. Netz, A. Kühnle, I. T. McCrum, M. T. M. Koper, M. Wolf, B. Winter, G. Meijer, R. K. Campen and M. Bonn, Nat. Rev. Chem., 2021, 5, 466–485 CrossRef CAS.
- J. Wu, Chem. Rev., 2022, 122, 10821–10859 CrossRef CAS PubMed.
- A. Groß and S. Sakong, Curr. Opin. Electrochem., 2019, 14, 1–6 CrossRef.
- K. Ojha, K. Doblhoff-Dier and M. T. M. Koper, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2116016119 CrossRef CAS.
- G. Caniglia, G. Tezcan, G. N. Meloni, P. R. Unwin and C. Kranz, Annu. Rev. Anal. Chem., 2022, 15, 247–267, DOI:10.1146/annurev-anchem-121521-122615.
- G. Jeanmairet, B. Rotenberg and M. Salanne, Chem. Rev., 2022, 122, 10860–10898 CrossRef CAS PubMed.
- A. M. Limaye, W. Ding and A. P. Willard, J. Chem. Phys., 2020, 152, 114706 CrossRef CAS.
- S. Ghosh, S. Horvath, A. V. Soudackov and S. Hammes-Schiffer, J. Chem. Theory Comput., 2014, 10, 2091–2102 CrossRef CAS PubMed.
- R. E. Bangle, J. Schneider, E. J. Piechota, L. Troian-Gautier and G. J. Meyer, J. Am. Chem. Soc., 2020, 142, 674–679 CrossRef CAS.
- A. Serva, N. Dubouis, A. Grimaud and M. Salanne, Acc. Chem. Res., 2021, 54, 1034–1042 CrossRef CAS PubMed.
- B. Liu, W. Guo and M. A. Gebbie, ACS Catal., 2022, 12, 9706–9716 CrossRef CAS.
- H. Helmholtz, Ann. Phys., 1879, 243, 337–382 CrossRef.
- H. Helmholtz, Ann. Phys., 1853, 165, 211–233 CrossRef.
- D. C. Grahame, Chem. Rev., 1947, 41, 441–501 CrossRef CAS PubMed.
- M. Gouy, J. Phys. Theor. Appl., 1910, 9, 457–468 CrossRef.
- D. L. Chapman, London, Edinburgh Dublin Philos. Mag. J. Sci., 1913, 25, 475–481 CrossRef.
- P. Debye and E. Huckel, Phys. Z., 1923, 24, 185 CAS.
- S. Seyedi, D. R. Martin and D. V. Matyushov, J. Phys.: Condens. Matter, 2019, 31, 325101 CrossRef CAS PubMed.
- J. de Souza, A. A. Kornyshev and M. Z. Bazant, J. Chem. Phys., 2022, 156, 244705 CrossRef CAS PubMed.
- D. V. Matyushov, J. Phys. Chem. B, 2021, 125, 8282–8293 CrossRef CAS.
- A. P. Willard, S. K. Reed, P. A. Madden and D. Chandler, Faraday Discuss., 2009, 141, 423–441 RSC.
- D. T. Limmer and A. P. Willard, Chem. Phys. Lett., 2015, 620, 144–150 CrossRef CAS.
- O. Stern, Z. Elektrochem. Angew. Phys. Chem., 1924, 30, 508–516 CrossRef CAS.
- J. I. Siepmann and M. Sprik, J. Chem. Phys., 1995, 102, 511–524 CrossRef CAS.
- S. K. Reed, O. J. Lanning and P. A. Madden, J. Chem. Phys., 2007, 126, 084704 CrossRef PubMed.
- S. K. Reed, P. A. Madden and A. Papadopoulos, J. Chem. Phys., 2008, 128, 124701 CrossRef PubMed.
- J.-F. Olivieri, J. T. Hynes and D. Laage, J. Phys. Chem. Lett., 2021, 12, 4319–4326 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- H. Heinz, T.-J. Lin, R. Kishore Mishra and F. S. Emami, Langmuir, 2013, 29, 1754–1765 CrossRef CAS PubMed.
- S. Mamatkulov and N. Schwierz, J. Chem. Phys., 2018, 148, 074504 CrossRef PubMed.
- D. Bastos-González, L. Pérez-Fuentes, C. Drummond and J. Faraudo, Curr. Opin. Colloid Interface Sci., 2016, 23, 19–28 CrossRef.
- A. Bouzid and A. Pasquarello, J. Phys. Chem. Lett., 2018, 9, 1880–1884 CrossRef CAS.
- J.-B. Le, Q.-Y. Fan, J.-Q. Li and J. Cheng, Sci. Adv., 2020, 6, eabb1219 CrossRef CAS.
- X.-Y. Li, X.-F. Jin, X.-H. Yang, X. Wang, J.-B. Le and J. Cheng, J. Chem. Phys., 2023, 158, 084701 CrossRef CAS.
- K. Doblhoff-Dier and M. T. Koper, Curr. Opin. Electrochem., 2023, 39, 101258 CrossRef CAS.
- S.-J. Shin, D. H. Kim, G. Bae, S. Ringe, H. Choi, H.-K. Lim, C. H. Choi and H. Kim, Nat. Commun., 2022, 13, 174 CrossRef CAS.
- G. Jeanmairet, B. Rotenberg, D. Borgis and M. Salanne, J. Chem. Phys., 2019, 151, 124111 CrossRef.
- S. P. Kadaoluwa Pathirannahalage, N. Meftahi, A. Elbourne, A. C. Weiss, C. F. McConville, A. Padua, D. A. Winkler, M. Costa Gomes, T. L. Greaves and T. C. Le,
et al.
, J. Chem. Inf. Model., 2021, 61, 4521–4536 CrossRef CAS.
- H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- L. J. V. Ahrens-Iwers, M. Janssen, S. R. Tee and R. H. Meißner, J. Chem. Phys., 2022, 157, 084801 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ’t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen,
et al.
, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Dylan
Suvlu†
,
Dylan
Suvlu†
 and
Adam P.
Willard
and
Adam P.
Willard
 *
*
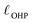 .18–20 Under this assumption, as illustrated in Fig. 1A, the EDL is a microscopic parallel-plate capacitor, with a constant electric field between the electrode and the OHP, and no variation in the potential from the OHP onwards. This EDL theory of Helmholtz and Perrin offers important physical insight into the role of ions in screening fields originating from electrodes, but has significant limitations.
.18–20 Under this assumption, as illustrated in Fig. 1A, the EDL is a microscopic parallel-plate capacitor, with a constant electric field between the electrode and the OHP, and no variation in the potential from the OHP onwards. This EDL theory of Helmholtz and Perrin offers important physical insight into the role of ions in screening fields originating from electrodes, but has significant limitations.
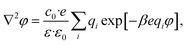
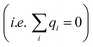 . The resultant mathematical description predicts an exponentially decaying electrostatic potential,
. The resultant mathematical description predicts an exponentially decaying electrostatic potential,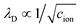 is the Debye screening length of the electrolyte solution.
is the Debye screening length of the electrolyte solution.
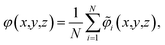
![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) i(x,y,z) is an instantaneous representation of the Poisson potential for the ith MD snapshot. Computing
i(x,y,z) is an instantaneous representation of the Poisson potential for the ith MD snapshot. Computing ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) i(x,y,z) for a single configuration of a point-charge species requires first defining a spatially continuous charge density profile,
i(x,y,z) for a single configuration of a point-charge species requires first defining a spatially continuous charge density profile, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i(x,y,z), on a regular lattice. We accomplish this with a proportional charge spreading scheme, which interpolates the charges on atomic centers to nearby points on the regular lattice. The details of this charge-spreading scheme are described in the Methods section. After defining
i(x,y,z), on a regular lattice. We accomplish this with a proportional charge spreading scheme, which interpolates the charges on atomic centers to nearby points on the regular lattice. The details of this charge-spreading scheme are described in the Methods section. After defining ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i, we compute
i, we compute ![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) i from the Poisson equation, ∇2
i from the Poisson equation, ∇2![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) i = −
i = −![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i/ε0.
i/ε0.
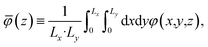
![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) (x,y,z).
(x,y,z).
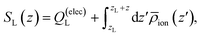
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) ion(z) is the xy-plane-averaged ionic charge density, obtained by restricting the proportional spreading procedure (described in Section 6) only to the atom-centered charges on the ionic species, and neglecting the charges of the solvent molecules entirely. The screening function for the right electrode is defined analogously to that of eqn (5) but with an integral extending from zR to zR − z. Intuitively, the screening function S(z) tallies the amount of electrode charge that remains unscreened by the mobile ionic charges of a given distance into the bulk; it takes the value Q(elec) at the electrode surface (z = 0), and levels off upon reaching the bulk region of the simulation cell. We observe that S(z) ≈ 0 for values of z beyond the EDL width.
ion(z) is the xy-plane-averaged ionic charge density, obtained by restricting the proportional spreading procedure (described in Section 6) only to the atom-centered charges on the ionic species, and neglecting the charges of the solvent molecules entirely. The screening function for the right electrode is defined analogously to that of eqn (5) but with an integral extending from zR to zR − z. Intuitively, the screening function S(z) tallies the amount of electrode charge that remains unscreened by the mobile ionic charges of a given distance into the bulk; it takes the value Q(elec) at the electrode surface (z = 0), and levels off upon reaching the bulk region of the simulation cell. We observe that S(z) ≈ 0 for values of z beyond the EDL width.
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (z) ≡ SL(z)/SL(0) for various different ionic concentrations. According to GC screening theory, this normalized screening function should decay from unity to zero in an exponential manner, with associated length scale λD, the Debye length. The profiles in Fig. 3A show signatures of the GC screening behavior; the profiles are more diffuse at lower salt concentrations, and analysis of the length scale by exponential fitting, as illustrated in Fig. 3C, shows that the decay length is roughly λD for each ion concentration.
(z) ≡ SL(z)/SL(0) for various different ionic concentrations. According to GC screening theory, this normalized screening function should decay from unity to zero in an exponential manner, with associated length scale λD, the Debye length. The profiles in Fig. 3A show signatures of the GC screening behavior; the profiles are more diffuse at lower salt concentrations, and analysis of the length scale by exponential fitting, as illustrated in Fig. 3C, shows that the decay length is roughly λD for each ion concentration. , representing the approximate radius of a water molecule. Under unbiased conditions with neat water, both the electrodes and bulk liquid have charge densities of ρ = 0. We model the charge density wave associated with solvent polarization with a discrete charge density wave, ρ(−L) = ρw and ρ(−L + 1) = −ρw, with a symmetric contribution at the other electrode, ρ(L) = ρw and ρ(L − 1) = −ρw.
, representing the approximate radius of a water molecule. Under unbiased conditions with neat water, both the electrodes and bulk liquid have charge densities of ρ = 0. We model the charge density wave associated with solvent polarization with a discrete charge density wave, ρ(−L) = ρw and ρ(−L + 1) = −ρw, with a symmetric contribution at the other electrode, ρ(L) = ρw and ρ(L − 1) = −ρw.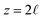 with a bulk potential value of
with a bulk potential value of 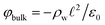 . Taking
. Taking 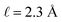 , the polarization density required to achieve a value of φbulk = −0.55 V is ρw = 0.57e nm−3.
, the polarization density required to achieve a value of φbulk = −0.55 V is ρw = 0.57e nm−3.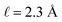 , and its magnitude scales with Vext.
, and its magnitude scales with Vext.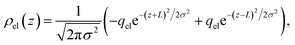
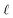 ,
,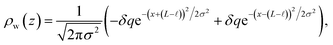
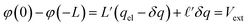
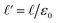 . The
. The 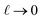 limit of this expression corresponds to the standard dielectric continuum picture. In this limit, qel − δq = Vext/L′ = E0. Noting that E0 = q0/ε0 = ε−1qel/ε0, we see that δq = qel(1 − ε−1).
limit of this expression corresponds to the standard dielectric continuum picture. In this limit, qel − δq = Vext/L′ = E0. Noting that E0 = q0/ε0 = ε−1qel/ε0, we see that δq = qel(1 − ε−1).
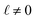 . In this case, eqn (9) can be manipulated to yield,
. In this case, eqn (9) can be manipulated to yield,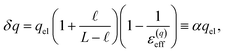
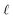 , L, and the effective dielectric constant, ε(q)eff.
, L, and the effective dielectric constant, ε(q)eff.
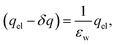
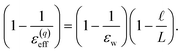
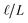 , with ε(q)eff = εw in the
, with ε(q)eff = εw in the 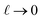 limit. In our system, where L = 8 nm, εw = 73, and ε(q)eff = 24, we find
limit. In our system, where L = 8 nm, εw = 73, and ε(q)eff = 24, we find 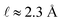 , which is consistent with the results plotted in Fig. 8.
, which is consistent with the results plotted in Fig. 8.
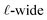 region between the electrode and the first solvent plane. The magnitude of this drop is effectively equal to
region between the electrode and the first solvent plane. The magnitude of this drop is effectively equal to 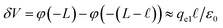 . The remaining potential drop, ΔVGC = Vext − δV, is thus what remains to be screened by the migration of ions (e.g., following Gouy–Chapman theory). In a pure water system, this quantity is,
. The remaining potential drop, ΔVGC = Vext − δV, is thus what remains to be screened by the migration of ions (e.g., following Gouy–Chapman theory). In a pure water system, this quantity is,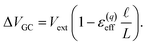
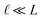 , ΔVGC = Vext. In other words, δV → 0 as
, ΔVGC = Vext. In other words, δV → 0 as 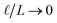 .
.
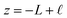 ) and that the potential is fully attenuated over the distance
) and that the potential is fully attenuated over the distance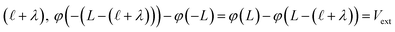 , and thus
, and thus 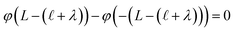 . Eqn (9) can thus be revised as,
. Eqn (9) can thus be revised as,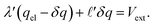
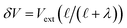 and likewise,
and likewise,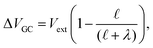
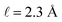 , then according to this expression, ΔVGC ≈ 0.63Vext for a 0.6 M solution (λD = 3.96 Å) and ΔVGC ≈ 0.52Vext for a 1.5 M solution (λD = 2.47 Å).
, then according to this expression, ΔVGC ≈ 0.63Vext for a 0.6 M solution (λD = 3.96 Å) and ΔVGC ≈ 0.52Vext for a 1.5 M solution (λD = 2.47 Å).
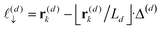 , and another of length
, and another of length 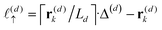 . Note that
. Note that 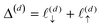 , due to the properties of the ceiling and floor functions. For notational convenience, define,
, due to the properties of the ceiling and floor functions. For notational convenience, define,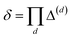
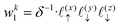
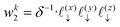
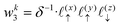
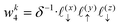
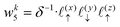
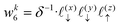
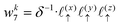
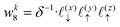
 , i.e., traditional continuum approximation. In this case, linearized Poisson–Boltzmann theory yields potential profile of,
, i.e., traditional continuum approximation. In this case, linearized Poisson–Boltzmann theory yields potential profile of,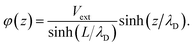
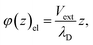
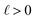 . In this case, the electrode charge is separated by the onset of the Poisson–Boltzmann screening layer (eqn (40)) by a distance
. In this case, the electrode charge is separated by the onset of the Poisson–Boltzmann screening layer (eqn (40)) by a distance 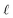 . The potential dropped over this distance is
. The potential dropped over this distance is 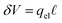 , leaving the remaining potential ΔVGC to be dropped by solvent/ions. According to eqn (42), the charge in the solution will be,
, leaving the remaining potential ΔVGC to be dropped by solvent/ions. According to eqn (42), the charge in the solution will be,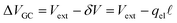 , we find that,
, we find that, 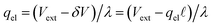 and thus
and thus 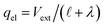 . With this,
. With this,