Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Techno-economic assessment of different small-scale electrochemical NH3 production plants†
Boaz
Izelaar
a,
Mahinder
Ramdin
a,
Alexander
Vlierboom
a,
Mar
Pérez-Fortes
 b,
Deanne
van der Slikke
a,
Asvin
Sajeev Kumar
b,
Deanne
van der Slikke
a,
Asvin
Sajeev Kumar
 a,
Wiebren
de Jong
a,
Fokko M.
Mulder
a,
Wiebren
de Jong
a,
Fokko M.
Mulder
 c and
Ruud
Kortlever
c and
Ruud
Kortlever
 *a
*a
aProcess and Energy Department, Faculty of Mechanical Engineering, Delft University of Technology, 2628 CB Delft, The Netherlands. E-mail: R.Kortlever@tudelft.nl
bEngineering, Systems and Services Department, Faculty of Technology, Policy and Management, Delft University of Technology, 2628 BX Delft, The Netherlands
cChemical Engineering Department, Faculty of Applied Sciences, Delft University of Technology, 2629 HZ Delft, The Netherlands
First published on 3rd October 2024
Abstract
Electrochemical ammonia synthesis via the nitrogen reduction reaction (NRR) has been poised as one of the promising technologies for the sustainable production of green ammonia. In this work, we developed extensive process models of fully integrated electrochemical NH3 production plants at small scale (91 tonnes per day), including their techno-economic assessments, for (Li-)mediated, direct and indirect NRR pathways at ambient and elevated temperatures, which were compared with electrified and steam-methane reforming (SMR) Haber–Bosch processes. The levelized cost of ammonia (LCOA) of aqueous NRR at ambient conditions only becomes comparable with SMR Haber–Bosch at very optimistic electrolyzer performance parameters (FE > 80% at j ≥ 0.3 A cm−2) and electricity prices (<$0.024 per kW h). Both high temperature NRR and Li-mediated NRR are not economically comparable within the tested variable ranges. High temperature NRR is very capital intensive due the requirement of a heat exchanger network, more auxiliary equipment and an additional water electrolyzer (considering the indirect route). For Li-mediated NRR, the high lithium plating potentials, ohmic losses and the requirement for H2, limits its commercial competitiveness with SMR Haber–Bosch. This incentivises the search for materials beyond lithium.
Broader contextElectrochemical ammonia synthesis based on the nitrogen reduction reaction (NRR), wherein nitrogen gas and a proton source are electrochemically reduced with renewable electricity, holds the promise of enabling the production of carbon-free ammonia. The NRR can occur at ambient conditions, elevated temperatures in a solid oxide cell and via lithium as an active mediator the proton source can originate “direct” from water or “indirect” via hydrogen gas. A large majority of the current research in the field focusses on improving the electrolyzer performance instead of exploring the overall techno-economic feasibility of the mentioned NRR pathways. Here, we have developed comprehensive conceptual process models of direct and indirect NRR pathways at ambient and elevated temperatures, Li-mediated NRR and the electrified Haber–Bosch process as a sustainable benchmark. This gives key insights into the required electrolyzer performance metrics to reach economic parity with SMR Haber–Bosch. Overall, we find that the inherently low energy efficiencies of the electrolysis steps (NRR or water electrolyzers) are limiting the economic competitiveness of electrochemical ammonia synthesis. |
Introduction
Ammonia (NH3) ranks among the largest produced synthetic chemicals in the world with an annual market size of ∼180 Mt, total market capitalization of around $76 billion USD and an expected annual growth of 3–5%.1,2 The majority of NH3 (80%) is processed into N-based fertilizers such as urea and ammonium nitrate, where the latter is also used for the production of explosives (5%). Other applications are in the manufacturing of cleaning detergents, pharmaceuticals, rubber and other polymers (15%).3,4 The vast majority of NH3 is produced by the conventional thermochemical Haber–Bosch process, where high temperatures (300–500 °C) and pressures (200–300 atm) are required to reach sufficient NH3 conversions from N2 and H2 over an iron catalyst.5 Due to these intensive process conditions, this process requires substantial capital investments, with costs reaching billions of USD for plants producing >2000 tonnes ammonia per day to minimize costs by economy of scale.6 The downside of these centralized plants are the increasing transportation costs, especially to remote areas. However, small scale plants (typically <100 tonnes per day) catering to local markets with regional price agreements have been reported.7The most energy efficient method for H2 feed production is steam methane reforming (SMR) based on natural gas, but this has significant environmental consequences as it releases 1.22 tCO2 per tNH3 alongside additional emissions related to burning fuel, natural gas extraction and other losses.8 Approximately 1.2% of the anthropogenic CO2 emissions are caused by the NH3 sector, necessitating a transition to greener production alternatives to meet the net-zero emissions goal in 2050.9 A significant reduction in emissions can be accomplished if the SMR or coal gasification plant is substituted by greener alternatives, such as water electrolysis. This “electrified” version of the Haber–Bosch process, first implemented in 1928 (Rjukan, Norway), was discontinued in the 1960's when SMR became more competitive because of the cheap availability of natural gas; however, it is now poised for a comeback.10 This is mainly due to the decreasing costs for renewable electricity from onshore wind and solar photovoltaics.11 Moreover, the expected decline in manufacturing costs of alkaline and proton-exchange membrane electrolyzers (decreasing 3.0% and 4.8% each year)12 for water electrolysis further enhances the competitiveness for the electrified Haber–Bosch in the near future.8,13,14
Alternative technologies for sustainable NH3 production are based on the electrochemical nitrogen reduction reaction (NRR), where nitrogen gas in combination with a proton source can in theory be electrochemically reduced with electricity from renewable energy sources. The proton source can be “direct” from water or “indirect” from hydrogen produced by water electrolysis. Both the direct and indirect NRR electrolyzer can in theory operate at ambient temperatures and pressures, thereby saving energy and capital expenditure on compressors and heat exchangers. Another promising approach is NRR at elevated temperatures, harvesting waste heat from the chemical industry to produce NH3 at higher rates and energy efficiencies.
Most of the current research in electrochemical NRR emphasizes the development of active, selective and stable electrocatalysts for the electrolyzers. Only a handful of studies have assessed the techno-economic feasibility of NRR technologies on a system level,15 and focus mostly on the electrolyzer costs.16,17 Particularly, there is a lack of knowledge about the future design, energy consumption and techno-economic feasibility of a fully integrated electrochemical NH3 process plant, including upstream and downstream separation units, heat integration and storage. To that end, we have developed comprehensive conceptual process models of direct and indirect NRR pathways at ambient and elevated temperatures, Li-mediated NRR and the electrified Haber–Bosch process as a sustainable benchmark. Moreover, we have used a consistent set of assumptions to perform a comparative analysis between these technologies, which gives key insights into the required electrolyzer performance metrics and the minimum ammonia production price necessary to enable carbon emission-free ammonia.
Process design assumptions and descriptions
It is expected that electrochemical ammonia plants operate in a decentralized manner.15,18 Therefore, a small capacity of 91 tNH3 per day is considered, which is based on the smallest commercial SMR HB plant that supplies only to local markets.7 The synthesis process is assumed to be continuous, which means that a variable availability of renewable energy is outside the scope of the current study and capacity factors of the process are high.The majority of the mass balance and economic calculations were performed in conventional spreadsheet software. Aspen PlusTM was used to model distinct unit operations, such as distillation and adsorption columns, flash evaporation, pump and compressor duties and heat integration if necessary. All NRR electrolyzers are considered as stoichiometric black box models. The total cell voltage (Ecell) is defined as:
| Ecell = Eeq + ηcat + ηan + ηmem + ηohmic, | (1) |
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1) and α the transfer coefficient (α = 0.5). Electrocatalytic reactions occurring at higher temperatures have typically an j0 larger than j, meaning that the hyperbolic sine approximation stated in eqn (3) is more appropriate.19
485 C mol−1) and α the transfer coefficient (α = 0.5). Electrocatalytic reactions occurring at higher temperatures have typically an j0 larger than j, meaning that the hyperbolic sine approximation stated in eqn (3) is more appropriate.19 | (3) |
The power consumption in watt of the electrolyzer (Pelect) is a function of Ecell and the total current in amperes (I):
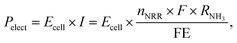 | (4) |
We defined the energy efficiency (EE) of the electrolyzer or the entire process as the ratio between the LHV of NH3 (18.6 GJ per tNH3) and the total energy input (ein):
 | (5) |
Methane-fed Haber–Bosch with a single SMR unit, electrified Haber–Bosch and the NRR based processes require an air separation unit (ASU) to produce a high purity N2 feed for the synthesis loop and the NRR electrolyzers. Otherwise, small quantities of oxygen will poison the iron catalyst (in the synthesis reactor) or will initiate the oxygen reduction reaction (ORR) as a parasitic side reaction in the NRR electrolyzers. The selection of a specific ASU technology depends on the N2 capacity, where pressure swing adsorption (PSA) is more economical below 500 tN2 per day and cryogenic distillation above 500 tN2 per day.22 If a PSA is integrated in the process, the oxygen waste stream can not be sold as commodity because its purity is below market grade (<99.9%), which is not the case for cryogenic distillation. Argon is also a by product of the ASU, but is excluded from the analysis.
For the electrified Haber–Bosch process (see Fig. 1a), an alkaline electrolyzer (AEL) or proton exchange membrane electrolyzer (PEMEL) is integrated in the model to produce H2. The main advantage of PEMEL over AEL is its load flexibility, compact design, high pressure operation and a better energy efficiency, but PEMEL is significantly more costly.23 Therefore, it is valuable to understand the economic benefit of both scenarios. The implementation of a solid-oxide electrolyzer (SOEL) in the electrified Haber–Bosch process was excluded from this analysis because of reported issues with thermal degradation of the electrode material reducing its overall lifetime (<5000 h) in comparison with AEL (55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–96
000–96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h) and PEMEL (60
000 h) and PEMEL (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–100
000–100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h), respectively.8,23 Additionally, it is estimated that the capital costs of the SOEL will be relatively high due to expensive material costs, which limits its economic attractiveness as a water electrolyzer for the electrified Haber–Bosch process.24,25
000 h), respectively.8,23 Additionally, it is estimated that the capital costs of the SOEL will be relatively high due to expensive material costs, which limits its economic attractiveness as a water electrolyzer for the electrified Haber–Bosch process.24,25
N2 and H2 are both pressurized to 155 bar in an intercooled multi-stage compressor before entering the Haber–Bosch reactor. The thermocatalytic NH3 reaction is exothermic (−53.8 kJ mol−1 at 155 bar, 400 °C) and excess heat can be harnessed to pre-heat the reactor feed. Hence, no additional heat source is required. The N2/H2/NH3 mixture is cooled down to −5 °C and separated by flash evaporation into a 99.5 mol% NH3 product stream and 4 mol% NH3/N2/H2 gaseous mixture. The latter is recycled back to the compressor and mixed with the other feed gases.
Fig. 1b illustrates our proposed design for aqueous based electrochemical ammonia synthesis at ambient conditions (aqueous NRR). The aqueous NRR electrolyzer is modelled as a hybrid gas–liquid flow cell with a N2 gas compartment, a catholyte and anolyte compartment. A gas diffusion electrode (GDE) separates the gas and liquid compartments. The NRR occurs at the triple phase boundary (TPB) at the liquid catholyte side of the GDE, where, it is assumed that produced NH3 will directly dissolve into the electrolyte due to its high solubility (540 g per LH2O at 20 °C).26 H2 is formed as a byproduct at the TPB and flows back through the GDE into the gas compartment. Two design alternatives for the utilization of the gaseous N2/H2 product stream were considered; the N2/H2 product stream can simply be purged (referred as “purge scenario”) or partly separated via the N2/H2 PSA to sell H2 as a commodity (“PSA scenario”). However, N2/H2 separation is non-trivial and may require at least 60 mol% H2 in the PSA feed to be technically feasible.27 Therefore, we incorporated an accumulation loop in the PSA scenario that recycles a N2/H2 mixture back to the GDE to satisfy this requirement (see Fig. S3, ESI†). Another potential strategy is to harvest the energy of the N2/H2 mixture by the generation of heat via combustion. The latter is not desirable because N2 forms NOx-related greenhouse gases upon combustion,28 which require additional DeNOx installations. Dissolved NH3 in 1 M KOH aqueous solution is separated by distillation with a distillate purity of 99.5 mol% and 99.9% NH3 recovery. The energy consumption of the column depends mainly on the NH3 composition in the feed (see Fig. S7, ESI†). From our analysis, a minimum of 10 mol% NH3 is implemented to limit the distillation energy consumption.
High temperature NRR occurs in a solid oxide electrolyzer (SOEL) that operates at 550 °C and 1 atm. This pathway is divided into two similar process variations, wherein the SOEL reduces N2 with water oxidation (NRR SOEL with water oxidation, Fig. 1c) or hydrogen oxidation including an additional water electrolyzer for H2 production (NRR SOEL with hydrogen oxidation, Fig. 1d). The SOEL operates in thermoneutral mode, meaning that the heat balance within the cell is in equilibrium.23 A heat exchanger network is designed to minimize the required heat input for the SOEL feed, by integrating inlet with outlet streams, as can be seen in the PFDs (Fig. S4 and S5, ESI†). The NH3/N2/H2 product mixture cannot be separated by flash evaporation because the stream is at atmospheric pressure. NH3 condensation is only techno-economically feasible when higher pressures (≥150 bar) are considered (as for the electrified Haber–Bosch process).8 For low pressure systems, adsorption by zeolites or absorption in alkaline earth metal salts are poised as promising separation technologies.29 In this process, NH3 is separated by an adsorption step with an NH3 product purity of 99.5 mol% and recovery of 90%. The other 10% cannot be recycled because NH3 will decompose directly (>400 °C). Due to the complexity of the heat integration system, it was not possible to further separate the N2/H2 stream in a similar fashion as the aqueous NRR process (PSA scenario).
The electrolyzer design in the Li-mediated NRR process (Fig. 1e) is inspired on the continuous flow cell recently developed by Chorkendorff and coworkers.30 The electrolyzer is modelled as a hybrid flow cell with two gas compartments (for N2 and H2), which are separated by an organic electrolyte that contains 1 M lithium bis(fluorosulfonyl)imide (LiFSI) in 0.25 vol% EtOH/THF. The gas and liquid compartments are separated by GDEs. We selected 1 M LiFSI due to its high conductivity with respect to other Li salts, while we are aware that the highest FEs in a batch-type cell were obtained with 2 M LiBF4 and 2 M LiTFSI.31,32 Again, it is assumed that NH3 will directly dissolve in the organic electrolyte and can be separated by distillation with a distillate purity of 99.5 mol% and 99.5% NH3 recovery.
Identification of energy losses in different NRR electrolyzers
The energetics of the electrolyzer often dominate the overall energy input of an electrochemical process. Here we used a simple modelling approach by using the Nernst law, approximations from the Butler–Volmer equation and expressions for the ohmic losses, to estimate the current–voltage relationship (Fig. 2) and energy losses of the considered NRR electrolyzers (with eqn (1)–(5), respectively). This gives us a preliminary estimate of the energy efficiency of each process and how this relates to the energy efficiency of SMR Haber–Bosch. | ||
| Fig. 2 Build-up of the current–voltage relationship by stacking the individual voltage contributions of the equilibrium potentials, overpotentials and ohmic losses for: (a) aqueous NRR, (b) NRR SOEL with water, (c) NRR SOEL with hydrogen and (d) Li-NRR. Relevant input data is listed in Table S15 (ESI†) and assumptions are discussed in “Process Design Assumptions and Descriptions” in the main text and “Supplemental methods” in the ESI.† | ||
An important advantage of the aqueous NRR compared to the electrified Haber–Bosch is the process intensification step, where NH3 can potentially be synthesized in a single electrolyzer with a considerably lower E0 (1.17 V) versus 1.23 V for H2O electrolysis, with a thermodynamic minimum of 19.9 GJ per tNH3 with respect to 21.3 GJ per tNH3 for H2O electrolysis (based on the LHV of stoichiometric amount of H2).8 However, NRR involves six proton-coupled electron transfer steps, where the intermediates impose thermodynamic constraints. As a result, a minimum barrier in the form of an ηNRR (0.4–0.6 V) is required to activate the reaction.5,20,33 The j–E curve in Fig. 2a indicates that below 0.42 A cm−2, the activation overpotentials (ηNRR and ηOER) are higher than the ohmic losses (ηΩ). At higher j, ohmic losses become more significant due to the relatively low conductivity of the 1 M KOH electrolyte (0.215 S cm−1 at 25 °C). At 0.3 A cm−2 and 90% FE, taken as electrolyzer aspirational values from the US Department of Energy ARPA-e REFUEL program,34 the ohmic losses are so severe that the electrolyzer's EE decreases to 39% (see Fig. 3a). This can partly be circumvented by considering a 25 wt% KOH aqueous solution as a more conductive electrolyte, thereby increasing the EE with +9%.
 | ||
| Fig. 3 Contour plots of the electrolyzer's EE as a function of j and FE for: (a) aqueous NRR at ambient conditions, (b) high temperature NRR in a SOEL with water oxidation, (c) high temperature NRR in a SOEL with hydrogen oxidation and (d) Li-NRR with hydrogen oxidation. Both (c) and (d) include an additional energy input term for H2 production with an alkaline H2O electrolyzer (28.4 GJ per tNH3 based on the commercial AEL type “A484” of Nel Hydrogen).23 Star symbol indicates the calculated EE at the US DoE Arpa-e electrolyzer aspirational values (0.3 A cm−2 and 90% FE). It is important to note that the plots imply a low j (<0.1 A cm−2) seems appealing. However, there is an economic trade-off between the EE and j, where the former has an effect on the OPEX and the latter on the capital costs. The optimal electrolyzer operation parameters will be discussed in the economic analysis. | ||
An advantage of high temperature NRR is the lower activation barrier for both the NRR (0.04 V at 1 A cm−2) and the H2O oxidation reaction (0.1 V at 1 A cm−2) as illustrated in Fig. 2b. In contrast to a water SOEL, the E0 of NRR increases with temperature (1.17 V at 25 °C to 1.21 V at 550 °C) due to a negative change in reaction entropy (see Fig. S8–S10, ESI†). The main reason why SOELs operate at such high temperatures is to increase the conductivity of the solid electrolytes. Ce0.8Sm0.2O2 is commonly used as an electrolyte and it has a conductivity of 0.014 S cm−1 at 650 °C, which is an order of magnitude lower than 1 M KOH (0.215 S cm−1), but this is typically compensated by using a thin slab of 0.05 mm. At 0.3 A cm−2, the voltage losses account for 13% of Ecell, thus the E0 dictates the energy efficiency. By substituting the oxygen evolution reaction (OER) for the hydrogen oxidation reaction (HOR), the E0 decreases to 0.19 V (see Fig. 2c). Nevertheless, the net energy gain of the cell voltage is compensated by the additional requirement for H2 (alkaline water electrolysis consumes 28.4 GJ per tNH3 based on the Nel Hydrogen type “A485”). Fig. 3b and c clearly demonstrates that the indirect approach is more energy intensive (without considering the up- and downstream units), where the EE of NRR SOEL with water is +14% higher than NRR SOEL with H2 (including AEL).
Li-mediated NRR is fundamentally energy intensive due to the required presence of metallic Li, with an E0 of −3 V vs. SHE for Li-plating. This results in a thermodynamic minimum of 51 GJ per tNH3 when Li-plating is combined with hydrogen oxidation (at 0 V vs. SHE), which is already 16 GJ per tNH3 higher than electrified Haber–Bosch. Fig. 2d shows that the actual energy input will be even more severe due to activation overpotentials and ohmic losses. Among the Li-salts, Li bis(trifluoromethanesulfonyl)imide (LiTFSI) and Li bis(fluorosulfonyl)imide (LiFSI) are reported as having the highest conductivities in organic solvents and contain fluorinated functional groups. Especially the latter is important for the formation of a stable and selective SEI.31 By assuming 1 M LiFSI dissolved in 0.1 M EtOH/THF as electrolyte with a conductivity of 0.015 S cm−1 (electrolyte gap = 2 mm), the ohmic resistance becomes so significant, that ohmic losses start to dominate Ecell at current densities >0.3 A cm−2. Unsurprisingly, the EE diagram in Fig. 3d indicates that Li-NRR (including AEL for green H2 production) has the lowest EE in comparison with other NRR electrolyzers.
Energy losses in sustainable NH3 processes
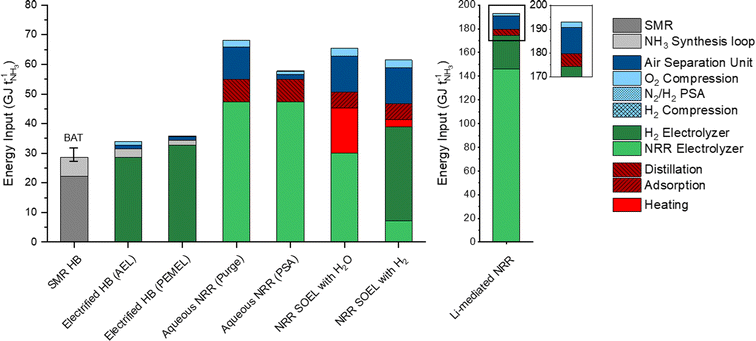
The total energy inputs for the NH3 production processes, including the electrolyzers, upstream and downstream unit operations, are illustrated in Fig. 4. For comparison, the energy requirement of SMR Haber–Bosch is also included and was taken from previous literature reports.8,35 The energy input of the AEL (28.4 GJ per tNH3) and PEMEL (32.8 GJ per tNH3) for the electrified Haber–Bosch process and indirect NRR pathways are based on commercially available models from Nel Hydrogen (A485) and Siemens Energy (Silyzer 300) with an EE of 75% and 65% (using the LHV of the stoichiometric amount of H2).23 The energy requirements for the NRR electrolyzers were calculated with our electrochemical model using the US DoE ARPA-e aspirational values (0.3 A cm−2 and 90% FE) as input parameters. The following highlights the main findings from our energy analysis and discusses several energy saving strategies.The energy consumption in the synthesis loop is significantly higher in the methane fed Haber–Bosch process (6.45 GJ per tNH3) than in the electrolysis based process.8,35 These losses in SMR Haber–Bosch can be assigned to low efficiencies of the steam turbine cycles (42–48%) that drive the feed-gas, recycle and refrigeration compressors.8 Additional losses of 1.7 GJ per tNH3 are associated with the necessity to purge a part of the product mixture for the recycle loop. In electrified Haber–Bosch, the losses in the NH3 synthesis loop are solely related to the compressor duty since there is no requirement for purging. These compressors need to be electrically driven due to the absence of a high pressure steam network in the electrified Haber–Bosch process. These types of compressors have a significantly higher driver efficiency (up to 95%), meaning that losses in the synthesis loop are limited. Additionally, commercially available PEMEL systems have the ability to produce H2 at 35–50 bar, which can save up to 56% of the compressor duty. After the synthesis loop, the NH3/N2/H2 mixture is separated by condensation (typically at −5 °C and 145 bar).36 Although the temperature gradient between the condenser and the synthesis reactor seems large, heat integration in the synthesis loop (Section S4.8 in the ESI†) recovers most of the heating and cooling duties. The energy input of the ASU is directly proportional to the stoichiometric demand of N2 for the reactor because unreacted N2 is separated and recycled back to the synthesis loop. Therefore, the ASU energy demand is limited to 1.3 GJ per tNH3. Although the electrified version of the Haber–Bosch is less energy efficient (33.9 GJ per tNH3) than the best available technology (BAT) (27.4–31.8 GJ per tNH3) due to the water electrolyzers, it is expected that innovations in the PEMEL system will improve the EE in the foreseeable future.37
The aqueous NRR electrolyzer consumes 47.4 GJ per tNH3, which accounts for 57% of the total energy loss. It is assumed that NH3 dissolves directly into the electrolyte after electrosynthesis and has to be separated downstream by distillation. The NH3 feed composition plays an important role in determining the energy input of the distillation unit. Fig. S7 (ESI†) shows that the reboiler duty decays exponentially with increasing NH3 feed concentration, with a minimum at approximately 10 mol%. Even at 10 mol%, the duty of both the reboiler and condenser are still considerable (7.5 GJ per tNH3). Implementing a N2 recycle stream can reduce the demand of “fresh” N2 from the ASU. To study this effect, we considered two process design alternatives for the N2/H2 product stream, where the product stream is simply purged (Fig. S2, ESI†) or separated by a PSA with N2 recycling and H2 recovery (Fig. S3, ESI†). The purge scenario shows a 7-fold increase of the ASU duty (10.9 GJ per tNH3) with respect to the PSA scenario. This indicates the importance of a recycle stream in order to save up to −9.3 GJ per tNH3.
NRR SOEL with water oxidation is the most energy efficient NRR electrolyzer (62%), meaning that the voltage losses at high temperature electrolysis are minimal. However, this is a false minimum since roughly 15 GJ per tNH3 of additional heat is necessary to sustain the NRR SOEL operational temperature (550 °C). Even though heat integration is included, there is a mismatch between the heat capacities of the reactants (N2, H2O(g)) and products (N2, NH3, O2). This implies that external heat must be supplied. By combining the additional heat and energy input of the SOEL, the EE decreases to 41%. Unfortunately, 3.8 GJ per tNH3 of this heat is labelled as “high quality heat” (to raise the feed temperature to 550 °C), which is challenging to obtain by steam, but can be harnessed from electric heating or waste heat from neighbouring chemical plants.38 For a stand-alone plant, a “green” furnace based on biogas or H2 from water electrolysis are also possible options. For now, it is assumed that the heat is imported from neighbouring chemical industries for the natural gas price. To save energy on the ASU (−10.2 GJ per tNH3), the N2 enriched waste stream from the separation step can in principle be recycled and mixed with the reactant stream. However, an additional 3.3 GJ per tNH3 of high quality heat is necessary to elevate the recycle temperature from 200 °C to 550 °C. This means that there is a trade-off between the import of heat and ASU energy savings. For simplicity, the recycle stream is excluded from further analysis. Separating the low pressure N2/H2/NH3 product mixture of the NRR SOEL by condensation is not economically attractive due to the excessive compressor costs.8 While still in the research phase, adsorption with zeolites is a promising approach for low pressure NH3 separation.29,39 The energy input for separation by adsorption (5.5 GJ per tNH3) depends on the heat of adsorption (2.76 GJ per tNH3), feed compression (2.32 GJ per tNH3) and desorption vacuum swing (0.46 GJ per tNH3). The compression duty is required to overcome the large pressure gradient (around 2 bar) across the densely packed column. The heat of adsorption depends on the interaction strength between the adsorbent and adsorbate. Since NH3 binds strongly to zeolites, a significant amount of heat must be supplied for desorption, although this is much less than would be required with metal halides.29
The enormous energy input of the Li-NRR electrolyzer (146 GJ per tNH3) accounts for 84% of the process losses, which are inherently related to the Li-plating potential and the low conductive nature of organic Li-salt electrolytes. These specific physical properties cannot be improved, but the electrolyte gap between the electrodes can be minimized by implementing a zero-gap membrane electrode assembly (MEA).40 Fig. S11 (ESI†) indicates that the electrolyzer EE can be increased by 8% when the electrolyte gap is completely eliminated. An alternative strategy is to find an active mediator with a lower plating potential than Li.41 Ca has recently been identified as an active mediator besides Li.42 However, the net energy gain of using Ca is limited since its plating potential only differs ∼0.2 V from Li. Theoretical work of Bagger, Stephens and coworkers have proposed Mg and Al as promising alternatives.43,44 Experimental work performed by Krebsz et al. proved that electroplated Mg is able to activate N2 by forming a surface layer of MgNx, which can be hydrolysed into ammonia via a two-step approach.45 An overview of the E0 and ΔG of these mediators paired with hydrogen oxidation is displayed in Fig. S12 (ESI†). When assuming an E0 of −2.36 V vs. SHE for Mg plating and 0 V vs. SHE for hydrogen oxidation, the thermodynamic minimum of this electrolyzer would be 40.2 GJ per tNH3, which is still relatively high in comparison with other NRR electrolyzers. Al is in terms of its low plating potential the most propitious element, but remains yet to be experimentally explored and verified.
Assumptions for the techno-economic analysis
The techno-economic analysis is based on small scale NH3 plants with the same capacity (91 tNH3 per day) that operate 333 days per year, with a life time of 20 years for electrolysis based ammonia processes and 40 years for SMR Haber–Bosch. It is assumed that the electrolyzer stacks do not have to be replaced during the life time of the plant. The investment cost for a 91 tNH3 per day SMR Haber–Bosch plant is $2022 936 M taken from ref. 7 (with inflation correction). The capital costs of the sustainable ammonia processes were estimated based on the equipment costs of all the process units in the plant. Standard process equipment, such as compressors, heat exchangers, pumps and columns are designed based on industrial heuristics. The equipment costs (CE) were calculated via different equipment capacity (S) correlation functions: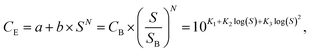 | (6) |
The electrolyzer costs, electricity and hydrogen prices for the base case scenario are inter- and extrapolated from 2022–2050 cost projections taken from numerous available sources (see Fig. 5 and Table S17 for referencing, ESI†).11,55–58 Other base case parameters, such as the price of O2 ($0.14 per kg),59 natural gas ($3.78 per GJ),60 H2O ($7.5 per m3),61 CO2 tax ($58 per tCO2),62 labor and O&M (3% of total capital costs) are kept constant.23,36 These numbers are mostly based on North American price indexing if available. For each cost parameter, more conservative and optimistic price projections reported by other literature sources were also included in the analysis (see Table S17 for more details, ESI†). This wide range of model input data allows us to predict under what conditions green NH3 becomes feasible and in which timeframe.
 | ||
| Fig. 5 Price projections for; (a) renewable electricity for a conservative, base case and optimistic scenario; (b) base case water electolyzer costs of PEMEL, AEL and SOEL in $ per unit power; (c) base case electrolyzer costs of NRR electrolyzers in $ per unit area. Data used for these figures is listed in Table S17 (ESI†). | ||
It is important to note that there is no available capital cost data of NRR electrolyzers. Therefore, their capital costs were derived from commercial H2O electrolyzers and compared with other cost data from the literature for validation.25,63 Electrolyzer costs, often expressed in $ per unit power, were converted with their respective power density (kW per m2) to $ per unit area to include the effect of the current density on the economics. The power density is related to the j–E characteristics of the electrolyzer, hence the $ per m2 is different for each particular system as can be seen in Fig. 5c. Additional statements regarding the electrolyzer capital cost assumptions and an extended discussion on the calculations are available in the ESI† (Section S4.9).
The inflation was corrected with the chemical engineering plant cost index (CEPCI). The total capital cost was estimated from the equipment cost with the Lang factorial method.47 These factors include the installation costs, contingency and working capital (more details can be found in Table S18, ESI†). It is important to note that the installation costs in the “inside battery limit” (ISBL) are temperature, pressure and material dependent, therefore the ISBL was calculated for each piece of equipment independently. The electrolyzer installation costs were not estimated via the Lang factors, but were assumed to be 10% of the equipment costs.23 General assumptions regarding the OPEX are mentioned in Table S19 (ESI†). The end-of-life net present value (NPV) was calculated using eqn (7) with 25% tax rate, 25% salvage value and a linear depreciation scheme by taking the cumulative sum of the cash flow (CF) discounted with 4.28% interest rate (median between 1954–2023 US interest rates):64
 | (7) |
The levelized cost of ammonia (LCOA) is used as an indicator to estimate and compare the economic feasibility of the different ammonia production plants. The LCOA is a function of the product revenue present value (eqn (8)), which can be obtained by adjusting the NH3 selling price until the NPV is equal to zero.15,65 The total capital cost is incurred during the first construction year of the plant (t = 0), where it assumed that the plant is fully operational at t ≥ 1.
| NPV = 0 = Product revenue PV (LCOA) − Operating cost PV − total capital costs | (8) |
Economic comparison of methane-based versus electrified Haber–Bosch
With the implementation of the base case assumptions, the LCOA of the small scale SMR Haber–Bosch plant is $555 per tNH3 as illustrated in Fig. 6a and d, which is in line with previous literature reports.15,66 These figures indicate that the price for grey ammonia (from SMR Haber–Bosch) remains considerably lower than ammonia from sustainable sources, such as the electrified Haber–Bosch process. The sensitivity analysis implies that the natural gas price and carbon tax are the main cost drivers for SMR Haber–Bosch (Fig. S13, ESI†). For a while, these plants have benefitted from relatively low natural gas prices (∼$3 per GJ), but the 2022 energy crisis in Europe has shown that SMR Haber–Bosch can be vulnerable.67 The US EIA states that natural gas prices can rise above $5 per GJ by 2050 which will put a lot of pressure on conventional Haber–Bosch economics.17 Additionally, societies demand more compensation for emitted greenhouse gases from the chemical industries in the form of an emission trading system or tax to stimulate the transition towards renewable alternatives. The latest IPCC report predicts that a carbon tax of $58 per tCO2 is necessary to incentivise the implementation of carbon capture and storage technologies by the chemical industry.62 Other economists and climate scientists claim that the CO2 tax should increase even further to $174–417 per tCO2.68–70 Hence, a more conservative price scenario ($175 per tCO2, $5.66 per GJ) is necessary to incentivise a shift towards carbon free NH3.Fig. 6a and d illustrate that electrified Haber–Bosch is too expensive under the current economic conditions (in 2022) compared with SMR Haber–Bosch, even when considering conservative price assumptions (∼$800 per tNH3). The sensitivity analysis in Fig. 6c and f show that the electricity price has the largest influence on the LCOA. By saving $0.01 per kW h on the OPEX, the LCOA reduces with roughly $100 per tNH3 (electrified HB with PEMEL), while a cost reduction of $100 per kW of the stack, lowers the LCOA with only $60 per tNH3 (approximately −5%). When considering the base case cost projection, electrified HB with PEMEL becomes cost competitive with SMR HB at $615 per kW (PEMEL investment costs) and $0.035 per kW h (electricity price). This means that the manufacturing of PEMEL systems and the cost of electricity has to be reduced by −68% and −38% within the upcoming decades. Other combinations of electrolyzer CAPEX and electricity prices can also lead to cost competitive ammonia production (see Fig. S14b, ESI†). Replacing PEMEL with AEL demands an additional investment of 29% for larger compressors because commercially available AELs deliver H2 at atmospheric pressure. Therefore, PEMEL is in this context a more suitable source for H2.
Economic analysis of aqueous NRR at ambient conditions
The LCOA of aqueous NRR at ambient conditions for the process scheme with a N2/H2 purge or PSA recovery unit are under the base case conditions not competitive with SMR Haber–Bosch, and require more optimistic price projections (see Fig. 7a and d). The main economic issue with aqueous NRR is the relatively high operational costs (∼$450 per tNH3) related to the electrolyzer due to unavoidable energy losses by activation overpotentials and ohmic losses. Consequently, Fig. 7e indicates that approximately 70% of the electricity costs and 50% of the OPEX are associated with the electrolyzer's electrical input. The capital costs of the NRR electrolyzer comprises 55% of the total capital cost and is ∼$2000 per tNH3 more expensive than a PEMEL. The latter is justifiable since a hybrid flow cell configuration is more complex in operation due to potential flooding issues of the GDE. This problem is typically circumvented by carefully controlling the pressure gradient over the GDE.71 The hybrid flow cell does also consumes more power per tNH3, therefore, the balance of plant (BoP) can be higher due to additional pressure regulators, rectifiers with a larger capacity, and miscellaneous auxiliary equipment.The process design with a N2/H2 purge (Fig. S2, ESI†), hence without a N2 recycle, consumes evidently more “fresh” N2 feedstock from the ASU. Consequently, the CAPEX of the ASU (18% of total capital costs) is roughly $1200 per tNH3 more expensive than when a N2 recycle is considered. For electrified Haber–Bosch, recycling N2 or a N2/H2 mixture is more straightforward because N2/H2 can be re-compressed, mixed with the N2/H2 feedstock and fed into the synthesis reactor. A mixture of N2/H2 can in principle be used as feed for the NRR electrolyzer since H2 is inert. But, if H2 is not separated from the recycle loop, it will accumulate, cross-over to the anode and form an explosive mixture with O2 or recombine into water. To realize a H2 separation step, an additional capital injection of 11% has to be invested into a N2/H2 PSA ($638 per tNH3), storage infrastructure for recycle buffering ($1286 per tNH3) and H2 compressors ($488 per tNH3) with a −4% gain of the OPEX. It becomes clear that by comparing the LCOA trend in Fig. 7a and d, purging the N2/H2 product stream is from an economic point of view more attractive because N2/H2 separation is considered to be technically challenging, wherein a minimum feed composition of 60 mol% H2/N2 is typically required with very low H2 recoveries (∼50%).27
Steering towards H2 production with NH3 as a by-product (FE < 50%) is not preferred because NH3 has more intrinsic value, and H2 can be produced more efficiently in a PEMEL or AEL. This indicates that steering towards a near unity ammonia FE should be the main objective as is supported by our sensitivity analysis (Fig. 7c). When considering the purge scenario, O2 market price fluctuations have a substantial effect on the LCOA (±27%), especially in comparison with electrified Haber–Bosch (Fig. 6c and f). This is related to the vast quantities of O2 (230 tonnes per day) that are being produced by the cryogenic distillation unit due to the large demand for N2. In case the location of the plant does not allow O2 export to the market, the LCOA increases by ∼$550 per tNH3.
The necessary cost reductions to reach SMR Haber–Bosch parity (∼$800 per tNH3) are highlighted in Fig. S14c (ESI†). It becomes clear that very optimistic electrolyzer costs ($5600 per m2) and electricity prices ($0.025 per kW h) have to be realized for cost competitive NH3 production. Additionally, the LCOA is heavily influenced by the electrolyzer performance metrics. Fig. 7f presents an optimal j window between 0.5–0.9 A cm−2, where the LCOA is approaching its minima. By assuming an electrolyzer CAPEX of $5850 per m2 (base case) and a very optimistic electricity price of $0.02 per kW h, a “minimum” FE as a function of the j can be estimated. The results are displayed in Fig. S15 (ESI†) and highlights three regions: FE > 80% at 0.3 A cm−2, FE > 70% at 0.4 A cm−2 and FE > 65% between 0.5–1 A cm−2. Operating at j < 0.3 A cm−2 is not preferable because the capital costs increase exponentially with the electrode area. The earlier used aspirational values from the ARPA-e REFUEL program (90% FE, 0.3 A cm−2) are reasonable and fall within the estimated range. Nevertheless, this analysis extends the aqueous NRR opportunity window and can be used as guideline for experimentalists.
Economic analysis of NRR at elevated temperatures
Fig. 8a and c show that both the NRR SOEL with water and with hydrogen pathways are under the base case assumptions not cost competitive with SMR Haber–Bosch, and require a more optimistic economic scenario. In contrast with aqueous NRR, the CAPEX and OPEX of the NRR SOEL unit are not dominating the plant costs. The majority of the investment is related to conventional process units, such as heat exchangers, air separation units and adsorption columns, which account for roughly 65% of the fixed capital costs. According to our analysis, NRR SOEL with hydrogen (containing two electrolyzers) is more cost effective than the NRR SOEL with water. This is counterintuitive, but can be explained based on differences in the heat integration and the electrolyzer capital costs. NRR SOEL with hydrogen has almost an ideal heat integration scenario, limiting the demand for high quality heat, which saves up to $100 per tNH3 on the OPEX. Additionally, Fig. 8b illustrates that the NRR SOEL unit with hydrogen oxidation is less capital intensive due to its lower power density (1.6 versus 5.9 kW per m2 for NRR SOEL with water oxidation), which directly affects the BoP as discussed previously.The sensitivity analysis in Fig. 8e and Fig. S16 (ESI†) indicates that the electricity price has the largest effect on the feasibility. Unsurprisingly, the absence of a N2 recycle in the high temperature process means that the ASU is producing large quantities of O2, which have to be sold for additional revenue. At the ARPA-e REFUEL aspirational values (FE = 90%, j = 0.3 A cm−2), Fig. S14e (ESI†) illustrates that NRR SOEL with hydrogen only becomes competitive with SMR Haber–Bosch at very optimistic electricity prices (≤$0.02 per kW h) and SOEL capital costs ($800 per m2). We estimated new aspirational values for the NRR SOEL with hydrogen oxidation using the same approach as discussed for aqueous NRR. By assuming a NRR SOEL and AEL CAPEX of $1209 per m2 and $564 per kW (base case assumptions in 2050) at an electricity price of $0.02 per kW h, the trend in Fig. S17 (ESI†) can be divided into three segments: FE > 90% at 0.4 A cm−2, FE > 85% at 0.5 A cm−2 and FE > 80% between 0.6–1 A cm−2. These performance requirements are significantly higher than aqueous NRR because improvements in the CAPEX and OPEX of the NRR SOEL unit have only a limited effect on the plant's economics.
NRR SOEL with water has even a smaller opportunity window, wherein electricity must decrease to unrealistic market prices (≤$0.018 per kW h) when assuming an electrolyzer CAPEX of $3000 per m2. Electricity prices up to $0.01 per kW h have been reported during peak periods of surplus renewable power.72 An electrochemical NH3 plant could theoretically operate along the volatile trend of low electricity market prices. The scale of the plant increases according to an assumed capacity factor, which results in higher investment costs. Wang et al. investigated the matter and observed an increase of the LCOA with $100 per tNH3 at a 0.2–0.3 capacity factor.15 Another issue is the compatibility with intermittent operation, which can especially be challenging for high temperature electrolysis, upstream and downstream units.
Economic assessment of Li-mediated NRR
Among the assessed sustainable NH3 pathways, Li-mediated NRR is the most expensive process and cannot become cost competitive with SMR Haber–Bosch even when considering the most optimistic cost factors (Fig. 9a). Due to the complexity of the electrolyzer system (hybrid flow cell, compatibility with organic electrolytes, moisture free operation) and significant power demand, the BoP will be excessive and comparable with other energy intensive electrochemical processes, such as chlor-alkali (∼$30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 per m2).63 With a base case estimate of $18
000 per m2).63 With a base case estimate of $18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 per m2 (in 2050), approximately 75% of the capital intensity is directly related to the electrolyzer system (Fig. 9b). The operational costs in Fig. 9c show that the electricity consumption of the Li-NRR electrolyzer accounts for almost 50% of the total OPEX (∼$1360 per tNH3), mainly due to its low EE. By changing to a more compact cell design, a zero gap membrane electrode assembly without ohmic losses, the LCOA can be reduced by ∼50% (Fig. S18a, ESI†), but this is still not sufficient.
650 per m2 (in 2050), approximately 75% of the capital intensity is directly related to the electrolyzer system (Fig. 9b). The operational costs in Fig. 9c show that the electricity consumption of the Li-NRR electrolyzer accounts for almost 50% of the total OPEX (∼$1360 per tNH3), mainly due to its low EE. By changing to a more compact cell design, a zero gap membrane electrode assembly without ohmic losses, the LCOA can be reduced by ∼50% (Fig. S18a, ESI†), but this is still not sufficient.
Another strategy is to find an alternative mediator with a significantly lower deposition potential. Although Ca has recently been identified as an active mediator besides Li,42 its reduction potential differs only +0.2 V vs. Li, which results in a limited gain in the OPEX. We decided to do a preliminary techno-economic screening, whereby Mg and Al are implemented as potential mediators (+0.7 V and +1.37 vs. Li). We assume a zero-gap electrolyzer configuration with the Li-plating activation overpotential and the same upstream and downstream units as used in the Li-NRR process. Under the base case assumptions (in 2050), Mg-NRR or Al-NRR allow a LCOA reduction of −$262 and −$547 per tNH3 with respect to Li-NRR in MEA configuration. These cost saving scenarios are insufficient and do not allow mediated NRR to compete with other sustainable ammonia processes (as illustrated in Fig. S18, ESI†). This incentivises the search for mediators beyond Al in order to enable mediated NRR as a compelling approach.
Future outlook
SMR Haber–Bosch will be around for several decades until the technology can be phased out with a zero-emissions alternative. The transition rate towards green ammonia will mainly depend on the level of inducible carbon tax by governmental policies, future levelized cost of renewable electricity and reductions in the electrolyzer manufacturing costs. Among the options for sustainable ammonia synthesis at a small scale plant (91 tonnes per day), electrified Haber–Bosch remains the most promising technology in terms of maturity, costs and energy efficiency (see Fig. 10). Nonetheless, research exploration for alternative pathways must continue. | ||
| Fig. 10 LCOA versus the energy consumption of the ammonia production routes discussed in this work. The y-error bars indicate the LCOA at optimistic and conservative cost scenarios in 2050 (from Table S17, ESI†). The data points represent the average between the optimistic and conservative cost assumptions, and not necessarily the base case assumptions. The x-error bar of SMR HB (black) represents the best available technology (27.4–31.8 GJ per tNH3). The variation among the reported literature values on the LCOA ($827 ± 398 per tNH3) and energy input (38.6 ± 7.1 GJ per tNH3) of electrified HB at a similar production capacity were taken from ref. 8 and 73–75, and added for comparison (sapphire). | ||
Aqueous NRR at ambient conditions is thermodynamically the most favorable approach, but the energy losses associated with activation overpotentials, ohmic losses, N2 feedstock production and distillation are often overlooked and decrease the energy efficiency of the process significantly. The low single-pass conversion and inability to recycle unreacted N2 demands an ASU with a large capacity, which will also produce vast quantities of O2. Selling O2 as a commodity is therefore essential to stimulate cash flow. Unfortunately, the current state of the aqueous NRR field is orders of magnitude away (j < 0.001 A cm−2, FE < 1%) from reaching our newly defined electrolyzer aspirational values (FE > 80% at 0.3 A cm−2, FE > 70% at 0.4 A cm−2 and FE > 65% between 0.5–1 A cm−2). Moreover, numerous publications that claim to have activated N2 are dubious and irreproducible,76–79 which can mostly be assigned to extraneous sources of NH3 or the electroreduction of NOx species.80 It remains to be seen if aqueous NRR will ever be experimentally demonstrated unambiguously at the intended j and FE.
High temperature NRR combined with water oxidation is as challenging as aqueous NRR at room temperature, wherein reported j (<0.01 A cm−2) and FE (<1%) remain at a bare minimum.81 On the contrary, high temperature NRR with H2 oxidation allows N2 activation to be more selective (FE > 70%).81 Yet, both the FE and the current densities obtained at lab scale do not meet with the bare minimum j and FE (FE > 90% at 0.4 A cm−2), hence remain impractical for industrial applications. More progress has been made in the Li-NRR field, where current densities of 1 A cm−2 and FEs near unity were reported,31,32 continuous flow and membrane electrode assembly cells have been developed,30,40,82 and Ca has been identified as an active N2 mediator.42 These achievements have progressed the mediated NRR field tremendously, but due to the fundamentally low energy efficiencies of the electrochemical conversion step and the overall complexity of the process, ammonia production at a competitive cost price will be a major challenge for its future application.
Conclusion
In this work, we designed detailed process models for the electrochemical production of NH3 to gain insights into the main bottlenecks of the process and to understand what process conditions are required to reach economic parity with SMR Haber–Bosch. Electrified Haber–Bosch with PEMEL is so far the most attractive process. However, current PEMEL investment costs and electricity prices need to be reduced to $615 per kW and $0.035 per kW h, which can be achieved within two decades according to future price projections. Aqueous NRR at ambient conditions needs even more optimistic scenarios and only becomes promising if the electricity price drops below $0.025 per kW h at $5600 per m2 (electrolyzer CAPEX). In addition to this, the NRR performance has to be increased to FE > 80% and j ≥ 0.3 A cm−2, a daunting task when comparing to the current state of the field. On the contrary, numerous experimental reports show that NRR in a SOEL with hydrogen oxidation is more selective (FE > 70%), but current densities remain at industrially irrelevant scales. Additionally, we find that SOEL based processes tend to be more capital intensive due to the additional requirement of heat exchangers and more auxiliary equipment. Hence, high temperature NRR is only cost competitive at the most optimistic and perhaps unrealistic economic scenario (≤$0.02 per kW h, ≤$800 per m2). Li-NRR has progressed tremendously over the last years in terms of scale, continuity, ammonia yield and selectivity. Unfortunately, the inherently low energy efficiency (<13%) of the electrolyzer causes disproportionally high operational costs. The EE can be improved by developing MEA-type electrolyzers to circumvent electrolyte conductivity losses or by implementing an alternative mediator with a more positive plating potential than Li, such as Mg or Al. For a small scale plant at 91 tonnes per day, Li-mediated NRR is under the most optimistic economic assumptions not economically feasible. This means that Li-NRR and also Ca-NRR remain interesting subjects for scientific research, but might never be integrated into a profitable application or process. Future research has to focus on the identification of mediators beyond Li and Ca. For now, electrified Haber–Bosch remains the only compelling electrolysis based pathway for sustainable ammonia production.Author contributions
B. I. and R. K. conceived the work. A. V. and D. V. D. S. developed initial versions of the process models and B. I. finalized them. M. R., M. P. F., A. S. K., W. D. J., F. M. M. and R. K. gave mentorship during the design phase of the process models. The economic analysis was performed by B. I. and A. V. with input from M. R. The manuscript was written by B. I. The project was supervised by R. K. All authors helped interpretating the results and contributed in the editing and revision process of the manuscript.Data availability
The data supporting this article have been included as part of the ESI.† Additional data is available on reasonable request at the authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the Nitrogen Activation and Ammonia Oxidation project within the Electron to Chemical Bonds consortium with project number P17-08, and the Open Technology research program with project no. 15234, which are both financed by The Netherlands Organization for Scientific Research (NWO) and affiliated industrial partners.References
- Food and Agriculture Organization of the United Nations, World Fertilizer Trends and Outlook to 2022, 2019.
- IMARC, Ammonia Market: Global Industry Trends, Share, Size, Growth, Opportunity and Forecast 2023–2028, 2022.
- International Energy Agency, Ammonia Technology Roadmap – Towards more sustainable nitrogen fertiliser production, 2021.
- J. Lim, C. A. Fernández, S. W. Lee and M. C. Hatzell, ACS Energy Lett., 2021, 6, 3676–3685 CrossRef CAS.
- C. J. M. Van Der Ham, M. T. M. Koper and D. G. H. Hetterscheid, Chem. Soc. Rev., 2014, 43, 5183–5191 RSC.
- G. Soloveichik, Nat. Catal., 2019, 2, 377–380 CrossRef CAS.
- T. Brown, The capital intensity of small-scale ammonia plants, https://www.ammoniaenergy.org/articles/the-capital-intensity-of-small-scale-ammonia-plants/, (accessed 13-9-2023).
- C. Smith, A. K. Hill and L. Torrente-Murciano, Energy Environ. Sci., 2020, 13, 331–344 RSC.
- P. Arias, N. Bellouin, E. Coppola, R. Jones, G. Krinner, J. Marotzke, V. Naik, M. Palmer, G.-K. Plattner and J. Rogelj, Climate Change 2021: the physical science basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; technical summary, 2021.
- T. Smolinka, H. Bergmann, J. Garche and M. Kusnezoff, Electrochemical power sources: fundamentals, systems, and applications, Elsevier, 2022, pp. 83–164 Search PubMed.
- International Rewenable Energy Agency (IRENA), Renewable power generation costs in 2022, 2022.
- G. Glenk and S. Reichelstein, Nat. Energy, 2019, 4, 216–222 CrossRef CAS.
- R. Michael Nayak-Luke and R. Bañares-Alcántara, Energy Environ. Sci., 2020, 13, 2957 RSC.
- Z. Cesaro, M. Ives, R. Nayak-Luke, M. Mason and R. Bañares-Alcántara, Appl. Energy, 2021, 282, 116009 CrossRef CAS.
- M. Wang, M. A. Khan, I. Mohsin, J. Wicks, A. H. Ip, K. Z. Sumon, C.-T. Dinh, E. H. Sargent, I. D. Gates and M. G. Kibria, Energy Environ. Sci., 2021, 14, 2535–2548 RSC.
- C. A. Fernandez and M. C. Hatzell, J. Electrochem. Soc., 2020, 167, 143504 CrossRef.
- G. Hochman, A. S. Goldman, F. A. Felder, J. M. Mayer, A. J. M. Miller, P. L. Holland, L. A. Goldman, P. Manocha, Z. Song and S. Aleti, ACS Sustainable Chem. Eng., 2020, 8, 8938–8948 CrossRef.
- N. Lazouski, Z. J. Schiffer, K. Williams and K. Manthiram, Joule, 2019, 3, 1127–1139 CrossRef.
- D. Noren and M. A. Hoffman, J. Power Sources, 2005, 152, 175–181 CrossRef.
- E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245 RSC.
- M. Ni, M. K. Leung and D. Y. Leung, Int. J. Hydrogen Energy, 2008, 33, 4040–4047 CrossRef CAS.
- A. Sánchez and M. Martín, Sustainable Prod. Consumption, 2018, 16, 176–192 CrossRef.
- A. Buttler and H. Spliethoff, Renewable Sustainable Energy Rev., 2018, 82, 2440–2454 CrossRef CAS.
- H. Zhang, L. Wang, J. Van Herle, F. Maréchal and U. Desideri, Appl. Energy, 2020, 259, 114135 CrossRef CAS.
- M. Ramdin, B. De Mot, A. R. Morrison, T. Breugelmans, L. J. Van Den Broeke, J. M. Trusler, R. Kortlever, W. De Jong, O. A. Moultos and P. Xiao, Ind. Eng. Chem. Res., 2021, 60, 17862–17880 CrossRef CAS PubMed.
- International Chemical Safety Cards (ICSCs), Ammonia (anhydrous) – Physical & Chemical Information, (https://www.ilo.org/dyn/icsc/showcard.display?p_lang=en&p_card_id=0414&p_version=2).
- M. Yáñez, F. Relvas, A. Ortiz, D. Gorri, A. Mendes and I. Ortiz, Sep. Purif. Technol., 2020, 240, 116334 CrossRef.
- J. A. Miller and C. T. Bowman, Prog. Energy Combust. Sci., 1989, 15, 287–338 CrossRef CAS.
- K. H. Rouwenhorst, A. G. Van der Ham and L. Lefferts, Int. J. Hydrogen Energy, 2021, 46, 21566–21579 CrossRef CAS.
- X. Fu, J. B. Pedersen, Y. Zhou, M. Saccoccio, S. Li, R. Sažinas, K. Li, S. Z. Andersen, A. Xu and N. H. Deissler, Science, 2023, 379, 707–712 CrossRef CAS.
- S. Li, Y. Zhou, K. Li, P. C. K. Vesborg, J. K. Nørskov, S. Li, Y. Zhou, K. Li, M. Saccoccio, R. Sa, I. Chorkendorff, S. Z. Andersen, J. B. Pedersen, X. Fu, V. Shadravan and D. Chakraborty, Joule, 2022, 6, 2083–2101 CrossRef CAS.
- H.-L. Du, M. Chatti, R. Y. Hodgetts, P. V. Cherepanov, C. K. Nguyen, K. Matuszek, D. R. MacFarlane and A. N. Simonov, Nature, 2022, 609, 722–727 CrossRef CAS.
- E. Dražević and E. Skúlason, iScience, 2020, 23, 101803 CrossRef.
- G. Soloveichik, Renewable Energy to Fuels Through Utilization of Energy-Dense Liquids (REFUEL) Program Overview, 2016 Search PubMed.
- I. Dybkjaer, in Ammonia – Catalysis and Manufacturing, ed. A. Nielsen, Springer-Verlag, 1995, pp. 199–327 Search PubMed.
- M. Appl, Ammonia: Principles and Industrial Practice, 1999.
- M. Chatenet, B. G. Pollet, D. R. Dekel, F. Dionigi, J. Deseure, P. Millet, R. D. Braatz, M. Z. Bazant, M. Eikerling, I. Staffell, P. Balcombe, Y. Shao-Horn and H. Schäfer, Chem. Soc. Rev., 2022, 51, 4583–4762 RSC.
- Innovation for Cool Earth Forum (ICEF), Industrial Heat Decarbonization Roadmap, 2019 Search PubMed.
- J. Helminen, J. Helenius, E. Paatero and I. Turunen, AIChE J., 2000, 46, 1541–1555 CrossRef CAS.
- X. Cai, Z. Shadike, X. Cai, X. Li, L. Luo, L. An, J. Yin, G. Wei, F. Yang, S. Shen and J. Zhang, Energy Environ. Sci., 2023, 16, 3063–3073 RSC.
- D. Jin, A. Chen and B.-L. Lin, J. Am. Chem. Soc., 2024, 146, 12320–12323 CrossRef CAS PubMed.
- X. Fu, V. A. Niemann, Y. Zhou, S. Li, K. Zhang, J. B. Pedersen, M. Saccoccio, S. Z. Andersen, K. Enemark-Rasmussen and P. Benedek, Nat. Mater., 2023, 1–7 Search PubMed.
- R. Tort, A. Bagger, O. Westhead, Y. Kondo, A. Khobnya, A. Winiwarter, B. J. Davies, A. Walsh, Y. Katayama and Y. Yamada, ACS Catal., 2023, 13, 14513–14522 CrossRef CAS PubMed.
- A. Bagger, R. Tort, M. M. Titirici, A. Walsh and I. E. Stephens, ACS Energy Lett., 2024, 9, 4947–4952 CrossRef CAS.
- M. Krebsz, R. Y. Hodgetts, S. Johnston, C. K. Nguyen, Y. Hora, D. R. MacFarlane and A. N. Simonov, Energy Environ. Sci., 2024, 17, 4481–4487 RSC.
- G. Towler and R. Sinnott, Chemical engineering design: principles, practice and economics of plant and process design, Butterworth-Heinemann, 2021 Search PubMed.
- R. Smith, Chemical process: design and integration, John Wiley & Sons, 2005 Search PubMed.
- E. E. Ludwig, Applied Process Design for Chemical and Petrochemical Plants, Gulf Professional Publishing, 1997, vol. 2 Search PubMed.
- R. Turton, R. C. Bailie, W. B. Whiting and J. A. Shaeiwitz, Analysis, synthesis and design of chemical processes, Pearson Education, 2008 Search PubMed.
- E. R. Morgan, Techno-economic feasibility study of ammonia plants powered by offshore wind, University of Massachusetts Amherst, 2013 Search PubMed.
- A. Mivechian and M. Pakizeh, Korean J. Chem. Eng., 2013, 30, 937–948 CrossRef CAS.
- R. Bañares-Alcántara, G. Dericks Iii, M. Fiaschetti, G. Philipp, J. M. Lopez, E. Tsang, A. Yang, L. Ye and S. Zhao, Dep. Eng. Sci. Rep. (Univ. Oxford), 2015, 1–150 Search PubMed.
- M. Marsidi, Technology Factsheet – Electric Industrial Boiler, (https://energy.nl/wp-content/uploads/electric-industrial-boiler-7.pdf).
- M. Marsidi, L. Beurskens and A. Uslu, The role of renewable heat technologies in industry – a review of Dutch sectoral industry roadmaps, 2018 Search PubMed.
- B. Lane, J. Reed, B. Shaffer and S. Samuelsen, Int. J. Hydrogen Energy, 2021, 46, 27293–27306 CrossRef CAS.
- International Rewenable Energy Agency (IRENA), Making The Breakthrough – Green hydrogen policies and technology costs, 2021.
- International Rewenable Energy Agency (IRENA), Future of Solar Photovoltaic: Deployment, investment, technology, grid integration and socio-economic aspects (A global Energy Transformation: paper), 2019.
- D. Bogdanov, J. Farfan, K. Sadovskaia, A. Aghahosseini, M. Child, A. Gulagi, A. S. Oyewo, N. S. de Souza, L. Barbosa and C. Breyer, Nat. Commun., 2019, 10, 1–16 CrossRef.
- INDEXBOX, EU – Oxygen – Market Analysis, Forecast, Size, Trends and Insights, 2022.
- U.S. Energy Information Administration, Henry Hub Natural Gas Spot Price, https://www.eia.gov/dnav/ng/hist/rngwhhdm.htm, (accessed 20-9, 2023).
- J. N. Hausmann, R. Schlögl, P. W. Menezes and M. Driess, Energy Environ. Sci., 2021, 14, 3679–3685 RSC.
- I. A. Bashmakov, L. J. Nilsson, A. Acquaye, C. Bataille, J. M. Cullen, S. D. L. R. D. Can, M. Fischedick, Y. Geng and K. Tanaka, IPCC, Climate Change 2022: Mitigation of Climate Change, Industry, 2022.
- M. Ramdin, A. R. Morrison, M. De Groen, R. Van Haperen, R. De Kler, E. Irtem, A. T. Laitinen, L. J. Van Den Broeke, T. Breugelmans and J. M. Trusler, Ind. Eng. Chem. Res., 2019, 58, 22718–22740 CrossRef.
- Macrotrends, Federal Funds Rate – 62 Year Historical Chart, (https://www.macrotrends.net/2015/fed-funds-rate-historical-chart).
- J. M. Spurgeon and B. Kumar, Energy Environ. Sci., 2018, 11, 1536–1551 RSC.
- C. Philibert, IAE, 2017 Search PubMed , https://cdi.mecon.gob.ar/bases/docelec/az3521.pdf.
- Fertilizers Europe, Europe's fertilizer industry victim of EU's energy chaos, (https://www.fertilizerseurope.com/wp-content/uploads/2022/08/Fertilizers-Europe-Press-release_Europe-fert-industry-victim-of-EU-energy-chaos-1.pdf).
- R. S. Pindyck, J. Environ. Econ. Manage., 2019, 94, 140–160 CrossRef.
- K. Ricke, L. Drouet, K. Caldeira and M. Tavoni, Nat. Clim. Change, 2018, 8, 895–900 CrossRef.
- K. Rennert, F. Errickson, B. C. Prest, L. Rennels, R. G. Newell, W. Pizer, C. Kingdon, J. Wingenroth, R. Cooke and B. Parthum, Nature, 2022, 610, 687–692 CrossRef.
- H. P. Iglesias van Montfort, S. Subramanian, E. Irtem, M. Sassenburg, M. Li, J. Kok, J. Middelkoop and T. Burdyny, ACS Energy Lett., 2023, 8, 4156–4161 CrossRef.
- International Energy Agency (IEA), Real-Time Electricity Tracker – United States, (https://www.iea.org/data-and-statistics/data-tools/real-time-electricity-tracker?from=2023-4-9&to=2024-4-8&category=price&country=USA).
- R. M. Nayak-Luke and R. Bañares-Alcántara, Energy Environ. Sci., 2020, 13, 2957–2966 RSC.
- E. R. Morgan, J. F. Manwell and J. G. McGowan, ACS Sustainable Chem. Eng., 2017, 5, 9554–9567 CrossRef.
- Institute for Sustainable Process Technology (ISPT), Power to Ammonia – Feasibility study for the value chains and business cases to produce CO2-free ammonia suitable for various market applications, 2017.
- J. Choi, B. H. R. Suryanto, D. Wang, H. L. Du, R. Y. Hodgetts, F. M. Ferrero Vallana, D. R. MacFarlane and A. N. Simonov, Nat. Commun., 2020, 11, 1–10 CrossRef.
- B. Izelaar, D. Ripepi, S. Asperti, A. I. Dugulan, R. W. Hendrikx, A. J. Böttger, F. M. Mulder and R. Kortlever, ACS Catal., 2023, 13, 1649–1661 CrossRef PubMed.
- S. Z. Andersen, V. Čolić, S. Yang, J. A. Schwalbe, A. C. Nielander, J. M. McEnaney, K. Enemark-Rasmussen, J. G. Baker, A. R. Singh, B. A. Rohr, M. J. Statt, S. J. Blair, S. Mezzavilla, J. Kibsgaard, P. C. K. Vesborg, M. Cargnello, S. F. Bent, T. F. Jaramillo, I. E. L. Stephens, J. K. Nørskov and I. Chorkendorff, Nature, 2019, 570, 504–508 CrossRef.
- L. F. Greenlee, J. N. Renner and S. L. Foster, ACS Catal., 2018, 8, 7820–7827 CrossRef.
- B. Izelaar, D. Ripepi, D. D. van Noordenne, P. Jungbacker, R. Kortlever and F. M. Mulder, ACS Energy Lett., 2023, 8, 3614–3620 CrossRef PubMed.
- V. Kyriakou, I. Garagounis, E. Vasileiou, A. Vourros and M. Stoukides, Catal. Today, 2017, 286, 2–13 CrossRef.
- S. Li, Y. Zhou, X. Fu, J. B. Pedersen, M. Saccoccio, S. Z. Andersen, K. Enemark-Rasmussen, P. J. Kempen, C. D. Damsgaard and A. Xu, Nature, 2024, 1–3 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee03299c |
| This journal is © The Royal Society of Chemistry 2024 |