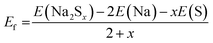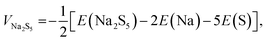Three-step thermodynamic vs. two-step kinetics-limited sulfur reactions in all-solid-state sodium batteries

Abstract

The investigation of all-solid-state sodium–sulfur batteries (ASSSBs) is still in its early stage, where the intermediates and mechanism of the complex 16-electron conversion reaction of the sulfur cathode remain unclear. Herein, this study presents a comprehensive investigation of the sulfur reaction mechanism in ASSSBs by combining electrochemical measurements, ex situ synchrotron X-ray absorption spectroscopy (XAS), in situ Raman spectroscopy, and first-principles calculations. This work, for the first time, proved that the sulfur cathode undergoes an intrinsic three-step solid–solid redox reaction following the thermodynamic principle under the extreme low rate (C-rates ≤ C/100) or at high temperature (≥ 90 °C), where S₈ is first reduced to long-chain polysulfides (Na₂S₅ and Na₂S₄), then to Na₂S₂, and finally to Na₂S, resulting in a three-plateau voltage profile. However, under conventional battery test conditions, i.e., temperatures ≤60 °C and C-rates ≥C/20, the Na₂S₂ phase is bypassed due to kinetic limitations, leading to a direct conversion from Na₂S₄ to Na₂S, resulting in the commonly observed two-plateau voltage profile. First-principles calculations reveal that the formation energy of Na₂S₂ is only 4 meV per atom lower than the two-phase equilibrium of Na₂S₄ and Na₂S, explaining its absence under kinetics-limited conditions. This work clarified the thermodynamic and kinetics-limited pathways of the 16-electron conversion reaction of the sulfur cathode in ASSSBs, providing valuable insights into the solid-state sodium–sulfur reaction mechanisms.

---

Broader context

The development of advanced energy storage systems with high energy density, low cost, and high safety is paramount for the effective extension of the electric vehicle, utilization of renewable energy sources, and the reduction of greenhouse gas emissions. All-solid-state batteries (ASSBs) have emerged as one of the most promising candidates due to their superior safety, higher energy density, and longer life cycle, and the sodium–sulfur (Na–S) system is highly attractive to the industry due to their natural abundance benefiting the mass production at low cost. This work demonstrates a comprehensive investigation of the sulfur reaction mechanism in all-solid-state sodium–sulfur batteries (ASSSBs) from both experimental and simulation to address critical challenges in understanding the complex 16-electron conversion reaction of the sulfur cathode. By elucidating the thermodynamic and kinetics-limited pathways of this reaction, the research provides vital insights into the sulfur reduction reaction (SRR) in the all-solid-state Na–S system. These fundamental findings not only advance energy and material science but also benefit the development of high-performance sustainable energy storage solutions. Improved ASSSBs can lead to more efficient energy storage from portable electronics and electric vehicles to grid stabilization, ultimately supporting the global transition to clean and renewable energy systems.

Introduction

Sodium–sulfur (Na–S) batteries have emerged as promising candidates for next-generation energy storage systems due to their high theoretical energy density, low cost, and the natural abundance of sodium and sulfur.^1,2 However, conventional Na–S batteries with liquid electrolyte (LE) suffer from both safety concerns due to the flammable nature of the electrolyte and the shuttle effect, where soluble polysulfide intermediates diffuse between the electrodes, leading to rapid capacity decay and poor cycling performance. All-solid-state sodium–sulfur batteries (ASSSBs), which replace the LE with a solid-state electrolyte (SE), have the potential to overcome these challenges, enhance safety, eliminate shuttle effect, and further promote energy density on the cell level.

Despite the advantages of ASSSBs, the reaction mechanism of the sulfur cathode in ASSSBs remains inadequately understood. Tatsumisago's group proved that the final discharge product of ASSSBs is crystalline Na₂S, yet the polysulfide intermediates (Na₂S_n, n = 2–8) have not been clearly identified.³ Most of the previous research and simulations focusing on identifying the polysulfide intermediates were based on the LE-based Na–S system with a solid–liquid–solid two-phase conversion of the sulfur.⁴ The two-plateau voltage feature corresponds to the solid–liquid (from S₈ to soluble long-chain polysulfide) and liquid–solid (from soluble long-chain polysulfide to insoluble sulfide species) conversion processes, where solvents played a crucial role.⁵ However, in the ASSSBs, the absence of solvents results in a different reaction mechanism.

Based on the findings from the all-solid-state lithium-sulfur batteries (ASLSBs), a one-step solid–solid conversion was recognized without long-chain polysulfide (Li₂S_n, n ≥ 4) formation.^6,7 Nevertheless, in the latest report, the presence of Li₂S₄ was identified in ASLSBs under the thermodynamic pathway, and it disappeared due to kinetic reasons.⁸ The all-solid-state Na–S system is even more complex than the Li–S system. According to the phase diagram, there are more thermodynamically stable solid polysulfides in Na–S than Li–S system.^9,10 In addition, the larger size of Na compared to Li results in sluggish kinetics, and its lower charge density makes it more reducing, facilitating electron loss. What's more, the sulfide intermediates in the electrochemical reaction process may not be stable with uncertain chemical reactions between the various polysulfide species over time.⁴ Therefore, careful and delicate investigation driving both thermodynamic and kinetic factors is important for understanding the sulfur cathode's conversion mechanism in ASSSBs. In this process, in situ characterization is necessary to collect the most reliable data during battery cycling.¹¹

In this work, we present a comprehensive investigation of the reaction mechanism of the sulfur cathode in ASSSBs, combining electrochemical measurements, synchrotron X-ray absorption spectroscopy (XAS), in situ Raman spectroscopy, and first-principles calculations. By carefully controlling the operating conditions, this study identified the intrinsic thermodynamic and the kinetics-controlled electrochemical behaviors of the sulfur reactions in ASSSBs. We further investigated the chemical conversions of the sulfur cathode using ex situ S K-edge X-ray absorption near-edge structure (XANES) and in situ Raman spectroscopy. For the first time, this work identified the intrinsic three-step solid–solid redox reaction of the sulfur cathode following the thermodynamic principle under the very low rate (C/100) for both the charge and discharge process. The three-step solid–solid electrochemical reaction has never been explored in either LE or SE-based Na–S systems before. In addition, the in situ Raman investigation revealed the mechanism of the commonly observed two-plateau electrochemical reaction: the specific phase (Na₂S₂) is skipped over in the conversion process due to slow kinetics. This work provides valuable insights into the complex polysulfide conversion and the role of intermediates in the sulfur cathode, paving the way for the optimization of ASSSB performance.

Results & discussion

The diverse properties of Na and Li, as well as the differences between LE and SE, potentially lead to varied sulfur electrochemical reaction mechanisms in ASSSBs and ASLSBs. Thermodynamically, lithium sulfide (Li₂S) is the only stable solid phase in the binary Li–S phase diagram (Fig. 1a).⁹ In contrast, in the Na–S system, sodium sulfide (Na₂S), sodium disulfide (Na₂S₂), sodium tetrasulfide (Na₂S₄), and sodium pentasulfide (Na₂S₅) are all thermodynamically stable at room temperature (Fig. 1b).¹⁰ Additionally, the larger atom size of Na than Li results in sluggish kinetics of Na due to the slower atom movement. However, the larger atomic radius and lower charge density of Na facilitate electron loss and hinder electron attraction, making it more reducing.¹² The abovementioned differences raise questions about the sulfur reaction processes in ASSSBs (Fig. 1c): what are the chemical intermediates in ASSSBs? How many conversion steps does sulfur undergo during charge (oxidation) and discharge (reduction) reactions? How does kinetics affect these intermediates and conversion processes?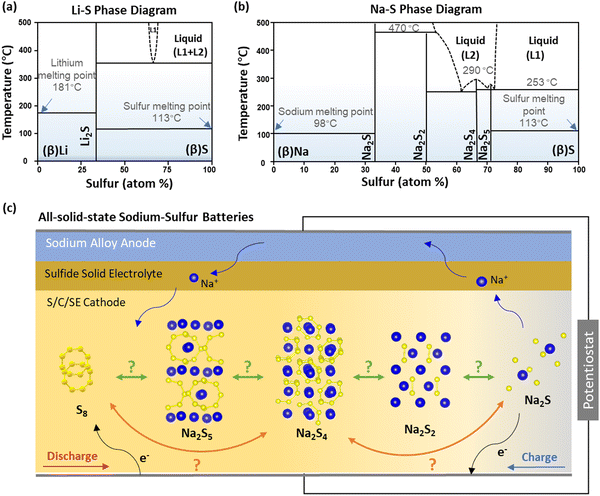

Fig. 1 Potential electrochemical reaction pathways in all-solid-state sodium–sulfur batteries. Phase diagrams of (a) Li–S and (b) Na–S systems converted from ref. 13. (c) Schematic illustration of the potential solid–solid electrochemical reaction pathways during charge and discharge in ASSSB.

To answer the above questions, we prepared a composite sulfur cathode by applying a lab-made high surface area polyacrylonitrile-derived porous carbon fiber (PPCF) as the electroconductive additive,¹⁴ combined with a sulfur-compatible sulfide-based sodium solid electrolyte, Na₃PS₄. Na–Sn alloy (Na₁₅Sn₄, with the electrochemical potential of 0.1 V vs. Na/Na⁺) as the anode because of its good chemical stability with the solid electrolyte.^15,16 Electrochemical measurements including galvanostatic charge and discharge under different temperatures and different rates, cyclic voltammetry (CV) tests, and galvanostatic intermittent titration technique (GITT) were performed to explore the intrinsic electrochemical behaviors of the sulfur cathode in ASSSBs under different temperature and rate. To identify the sulfide species during the discharging and charging process, both ex situ and in situ characterization methods were applied. ex situ S K-edge XANES of the sulfur cathode operated under different temperatures were collected to identify the polysulfide intermediates following the thermodynamic path. In situ Raman was further applied to track the conversion of the sulfur cathode under kinetic limitations. For successful in situ Raman testing, we developed a homemade cell with an open cross-section and stacking pressure, measured by a Raman instrument in the argon-filled glovebox (Fig. S1, ESI†).¹⁷ Through the combination of electrochemical measurements, ex situ and in situ characterizations, and first-principles calculations, we explored the reaction mechanism of the sulfur cathode in ASSSBs, addressing the questions raised above.

Electrochemical behavior of sulfur cathode in ASSSBs

The galvanostatic charge and discharge of the ASSSBs were performed under different temperatures (25, 60, and 90 °C) and rates (C/20 and C/100) to explore the electrochemical behaviors of the sulfur cathode under various conditions. At 25 °C and a rate of C/20 (Fig. 2a), the ASSSB achieved a decent initial discharge capacity of 1475 mA h g⁻¹ but a low charge capacity of 871 mA h g⁻¹, resulting in a low initial coulombic efficiency (ICE) of 59.1%. In the subsequent cycle, the discharge and charge capacities remained around 870 mA h g⁻¹, indicating limited utilization of the sulfur material. To enhance the sulfur cathode utilization, the cells were further tested at elevated temperatures of 60 and 90 °C to reduce the limitations from kinetics. These temperatures are still below the melting points of sulfur and other sulfide products, maintaining the all-solid-state nature of the materials. The cells tested at 60 and 90 °C exhibited improved initial discharge capacities of 1595 and 1607 mA h g⁻¹, respectively, which are close to the theoretical capacity of sulfur (1672 mA h g⁻¹) (Fig. 2b and c). This indicates that higher temperatures benefit sulfur utilization in ASSSBs. The charge capacities of the cells at 60 and 90 °C were 1531 and 1599 mA h g⁻¹, with ICEs of 96.0 and 99.5%, respectively, exhibiting great reversibility of the sulfur cathode in ASSSBs. The second cycles of the cells at both 60 and 90 °C closely matched the first cycle, demonstrating the great electrochemical reversibility of the sulfur cathode at high temperature.

Fig. 2 Electrochemical behavior of sulfur cathode in ASSSBs. Galvanostatic discharge and charge profiles of the all-solid-state sodium sulfur batteries under C/20 at (a) 25 °C, (b) 60 °C, and (c) 90 °C and corresponding dQ/dV curves (d) 25 °C, (e) 60 °C, and (f) 90 °C. Galvanostatic charge and discharge profiles of the ASSSBs under C/100 at (g) 25 °C, (h), 60 °C, and (i) 90 °C and corresponding dQ/dV curves (j) 25 °C, (k) 60 °C, and (l) 90 °C.

In addition to varying capacity retentions at different temperatures, the number of plateaus on the voltage profiles also changes. To clearly identify the plateaus of the discharge and charge profiles, the differential capacity (dQ/dV) curves were calculated to convert the voltage plateaus of the discharge and charge profiles to reduction and oxidation peaks (Fig. 2d–f). At 25 °C, only one pair of reduction and oxidation peaks was clearly observed at 1.01 and 1.91 V (vs. Na₁₅Sn₄/Na⁺) with two board non-zero regions starting from 1.77 to 1.38 V for the reduction curve and from 2.13 to 2.57 V for the oxidation curve. At 60 °C, in addition to the shifting of the first pair of peaks to 1.14 and 1.71 V, respectively, due to the reduced overpotential at the higher temperature, another pair of reduction and oxidation peaks emerged at the positions of 1.81 V and 2.08 V, corresponding with the above-mentioned non-zero regions observed at 25 °C. For the dQ/dV curve of the cell tested at 90 °C, a third oxidation peak (at 1.79 V) appeared between the first and second peaks (at 1.62 V and 2.04 V). The cyclic voltammetry (CV) tests further validated this trend, as shown in Fig. S2 and S3 (ESI†). These data indicate that the electrochemical behavior of the sulfur cathode in the ASSSB varies at different temperatures. Three redox peaks and higher capacity are obtained under 90 °C.

Since temperature can affect both the thermodynamics and kinetics of the electrochemical reaction, to identify the intrinsic reason for the change in the electrochemical behaviors, we further reduced the rate of the electrochemical reaction to C/100 at all temperatures, as shown in Fig. 2g–i and calculated their corresponding dQ/dV curves (Fig. 2j–l). Under the extremely low rate of C/100, the electrochemical behaviors of the cells operated under 25 and 60 °C are clearly changed. In addition to an improved charge capacity of the cell operated under 25 °C (Fig. 2g), the number of the charge/discharge plateaus or reaction peaks also changed. All three cells show three oxidation peaks for the charging process (Fig. 2j–l). Note, the small oxidation peak observed at the high voltage range (>2.5 V vs. Na₁₅Sn₄/Na⁺) in Fig. 2k and i is attributed to the decomposition of the SE (Discussion S1, and Fig. S4, S5, ESI†). The consistent appearance of the three-peak behavior in all cells indicates that the three-plateau feature is an intrinsic electrochemical behavior of the sulfur cathode of the ASSSBs. To observe the transition from the two-plateau profile to the three-plateau profile, additional rates (C/10 and C/50) test were performed at 90 °C and compared with the results at C/20 and C/100, as shown in Fig. S6 (ESI†). It is clear that with the reducing of the C-rate, the second plateau gradually formed.

The above results demonstrated that raising the temperature and reducing the C-rate enhanced the performance of the sulfur cathode. Firstly, higher temperatures and slower rates resulted in enhanced sulfur utilization with a capacity closer to its theoretical value. Additionally, these conditions also promoted better capacity retention over multiple cycles, indicating improved reversibility of the sulfur cathode. Most notably, the emergence of the additional voltage plateau and reaction peak at higher temperatures or lower rates provided strong evidence for the intrinsic three-plateau feature of the electrochemical reaction of the sulfur cathode in ASSSBs. These findings underscore the crucial role of kinetics in the performance and underlying reaction pathways of the sulfur cathode in ASSSBs.

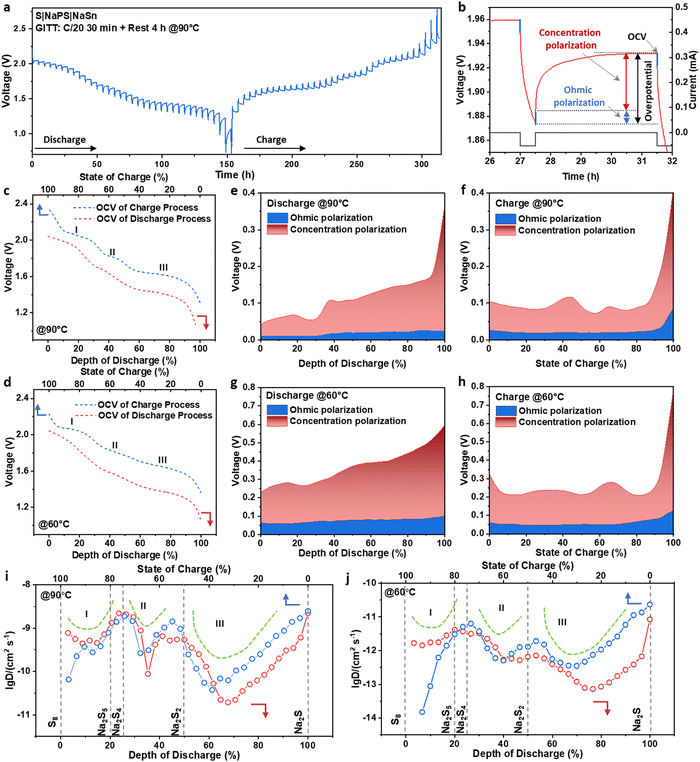
To further explore the thermodynamic and kinetic information of the ASSSBs, the galvanostatic intermittent titration technique (GITT) tests were performed by discharging and charging the cells at C/20 (1C = 1672 mA g⁻¹) for 30 minutes followed by 4 hours of relaxation at both 90 °C (Fig. 3a) and 60 °C (Fig. S7, ESI†). Fig. 3b presents a zoomed-in view of the GITT profile, where we can identify the open circuit voltage (OCV), which is the thermodynamic equilibrium voltage of the battery, and the overpotential due to kinetic reasons.¹⁸Fig. 3c and d show the OCV curves at different depths of discharge (DOD) and states of charge (SOC) obtained from the GITT tests at 90 °C and 60 °C, respectively. Both curves exhibit three plateaus. The three discharge plateaus are at 2.00, 1.71, and 1.42 V vs. Na₁₅Sn₄/Na⁺, corresponding to 2.10, 1.81, and 1.52 V vs. Na/Na⁺. The three charge plateaus are at 2.16, 1.92, and 1.72 V vs. Na/Na⁺. Notably, the galvanostatic voltage profile of the ASSSBs operated at 60 °C under C/20 shows only two plateaus. However, there are three plateaus appeared in the OCV curve in the GITT test of the cell also operated at 60 °C under C/20. This phenomenon suggests that under this condition (60 °C and C/20), the electrochemical reaction corresponding to the second plateau may not occur during the galvanostatic discharge and charge process, but the intermediate of this reaction can still be obtained after sufficient rest due to thermodynamic reaction. The phenomena will be further analyzed in the following section.

Fig. 3 Galvanostatic intermittent titration technique (GITT) analysis of ASSSBs. (a) GITT test profile of the ASSSBs at 90 °C, and (b) zoom-in view of the GITT profile for illustrating the ohmic and concentration polarizations and open circuit voltage (OCV). OCV during discharging and charging processes at (c) 90 °C and (d) 60 °C. The evaluation of the overpotentials at 90 °C during (e) discharging and (f) charging processes. The evaluation of the overpotentials at 60 °C during (g) discharging and (h) charging processes at 60 °C. Apparent diffusion coefficient during discharging and charging processes at (i) 90 °C and (j) 60 °C.

Fig. 3e–h present the evaluations of the overpotentials of the cells during the discharging and charging processes at both 90 °C and 60 °C. At 60 °C, there is a significant overpotential (∼0.2–0.6 V), reflecting the slow kinetics of the sulfur cathode in ASSSBs. The cell operating at 90 °C has a much smaller overpotential than the cell at 60 °C, suggesting improved kinetics at higher temperatures. The overpotential during the electrochemical reaction is attributed to two factors: Ohmic polarization and concentration polarization.¹⁸ Ohmic polarization, also known as iR-drop, where R is the sum of the charge transfer resistance R_ct and the other uncompensated resistance R_u, is primarily related to the overall ionic and electron transfer within the cell.¹⁹ As shown in Fig. 3e–h, the Ohmic polarizations are relatively stable and account for only a small portion of the overall overpotential for the cells operated at 90 °C and 60 °C. Most of the overpotential is attributed to concentration polarization, which is related to the ion diffusion within the active material.¹⁸ Therefore, the kinetic limitation of the sulfur cathode in ASSSBs primarily arises from the poor ion diffusivity of the active materials.

The apparent diffusion coefficient was calculated based on the GITT test through the conventional method based on Fick's law, as described in equation (S1) (ESI†) and shown in Fig. 3i and j. The Na–S system contains several solid polysulfide phases. In the two-phase region, the ions are transported through both the movement of the interphase boundary and the ionic diffusion within each phase.²⁰ Based on the study of the GITT of the phase transition materials, because of the mismatch of the ion-transport mechanism with Fick's law, a significant reduction of the apparent diffusion coefficient occurs in the two-phase region, resulting in a U-shaped diffusion coefficient curve.²⁰ In both Fig. 3i and j, three U shapes in the diffusion coefficient curve were observed for both discharging and charging processes. On account of this feature, a three-step phase transformation process can be initially identified, corresponding to the three-plateau feature of the charge/discharge profile. By converting the DOD and SOC to the degree of sodiumization of sulfur (x in Na₂S_x), we can anticipate that the three-phase transformation processes could be S₈ to Na₂S₅ or Na₂S₄, Na₂S₅ or Na₂S₄ to Na₂S₂, and Na₂S₂ to Na₂S. Specific intermediaries will be identified in the following study.

We also evaluated the cycling performance of the ASSSBs at 60 °C, as shown in Fig. S8 (ESI†). The cell was initially cycled at C/20 and then further cycled at C/3. The discharge capacity at C/3 increased from 921 mA h g⁻¹ to 1125 mA h g⁻¹ in the first 15 cycles and then gradually decayed. The increase of the capacity is a common phenomenon of sulfur cathodes in all-solid-state batteries, resulting from the gradual activation of the sulfur cathode.^21,22 Fig. S9 (ESI†) provided the voltage profiles, indicating the highly reversible electrochemical reactions of the sulfur cathode in ASSSBs.

Ex situ XANES investigation of polysulfide intermediates at various SOC and DOD

To identify the reaction intermediates during the charge and discharge process in ASSSBs, we employed XAS for its high sensitivity to sodium–sulfur compounds. Fig. 4a shows the reference S K-edge XANES spectra of Na₂S, Na₂S₂, Na₂S₄, and S₈, while Fig. S10 (ESI†) displays the spectrum for Na₃PS₄. All spectra were calibrated using a standard sulfur (S₈) sample, with the absorption edge set to 2472.0 eV. In the calibrated spectra, the sulfur “white line” feature appears at 2472.7 eV, attributing to the S 1s to S–S π* state transition of elemental sulfur. The XANES spectra of long-chain polysulfides, Na₂S_x (x = 4, 5), exhibit similar features at 2472.7 eV from the long-chain S–S bond and a low-energy shoulder feature at 2471.0 eV, which is assigned to the S 1s to π* state transition associated with linear polysulfides.²³ We only obtained the standard sample of Na₂S₄, not Na₂S₅ (Fig. 4a). The intensity of the shoulder feature is related to the strength of sulfur species coordination with the other ions, thus Na₂S₅ has a slightly weaker shoulder feature than Na₂S₄.²⁴ However, due to the similar features, it is challenging to clearly identify the specific species of long-chain polysulfides by this single technique, which will be further identified in the in situ Raman study. For Na₂S₂, the pre-edge becomes the main feature and shifts negligibly to 2470.9 eV, while the feature at 2472.0 eV nearly disappears. The final reduction product, Na₂S, exhibits two features at 2472.3 eV and 2474.7 eV.

Fig. 4 Ex situ X-ray absorption spectroscopy (XAS) investigation of ASSSBs. (a) S K-edge XANES spectra of Na₂S, Na₂S₂, Na₂S₄, and S. Ex situ S K-edge XANES measurements for the ASSSBs operated at (b) 25 °C, (c) 60 °C, and (d) 90 °C. (e) The voltage profile and intensity mapping of the ex situ S K-edge XANES of the cell operated at 90 °C.

The ex situ S K-edge XANES spectra of the sulfur cathodes at different DOD and SOC states operated at 25, 60, and 90 °C under the rate of C/20 are shown in Fig. 4b–d. Due to the nature of the ex situ test, all cells are rested for more than 48 hours before the XAS measurements. As discussed in the GITT test, (Fig. 3c and d), the rest period allows the cathode active material to reach the OCV with the three-plateau feature. Therefore, the ex situ XANES measurements provided chemical information on the three-plateau feature of the sulfur cathode under different DOD and SOC.

The XANES spectrum recorded for the pristine composite cathode (Fig. 4b) shows one clear feature at 2472.7 eV related to the cathode active material, S₈. No features arising from the SE component, Na₃PS₄, were observed. However, the presence of SE caused a negligible shift of the absorption edge to lower energy for the pristine cathode spectrum when compared with the standard S₈ sample (Fig. S11, ESI†). At 25 °C, during the discharge process from pristine to 75% DOD, the “white line” intensity decreased gradually with a low-energy pre-edge feature arising, attributed to the transition of 1s electron to the lowest available unoccupied S 3p σ* antibonding states hybridized with 3d metal (e_g states). This change corresponds to the reduction of the long-chain S–S bonds and formation of the Na–S bonds, indicating the conversion from S₈ to long-chain polysulfides, Na₂S_x (x = 4 or 5), and then to Na₂S₂ (Fig. 4b). From 75% to 100% DOD, two features at 2472.3 and 2474.7 eV gradually appeared, indicating that the final reduction product of the sulfur cathode in ASSSBs is Na₂S. Nevertheless, the XANES spectrum of the 100% DOD at 25 °C still has the shoulder feature at 2471.0 eV and a feature at 2472.7 eV, indicating there are still polysulfide species retained due to the insufficient electrochemical reaction corresponding with the limited discharge capacity of 1475 mA h g⁻¹ at 25 °C compared with 1595 and 1607 mA h g⁻¹ obtained at 60 and 90 °C. The charging process is the reverse of the discharge process from Na₂S to Na₂S₂ and further converts to Na₂S_x (x = 4 or 5). However, the XANES spectrum recorded of 100% SOC is more similar to the XANES spectrum of 25% DOD rather than that of the pristine state (Fig. S12, ESI†), indicating that the final charging product of the ASSSBs operated at 25 °C has the long-chain S–S structure but not fully revert to S₈.

The XANES spectra of the sulfur cathodes operated at 60 °C and 90 °C show a similar trend with that at 25 °C for the initial discharge process from pristine to 75% DOD, indicating the reduction process of S₈ to Na₂S_x (x = 4 or 5), to Na₂S₂, and finally to Na₂S. At 100% DOD, only two features at 2472.3 eV and 2474.7 eV are clearly observed, indicating a more complete electrochemical reaction to Na₂S than 25 °C. Additionally, at 100% SOC, the cathodes of the cell operated at 60 °C and 90 °C successfully converted back to S₈ (Fig. S13, ESI†), which corresponded well with the great ICEs of 96.0 and 99.5% obtained from the electrochemical tests.

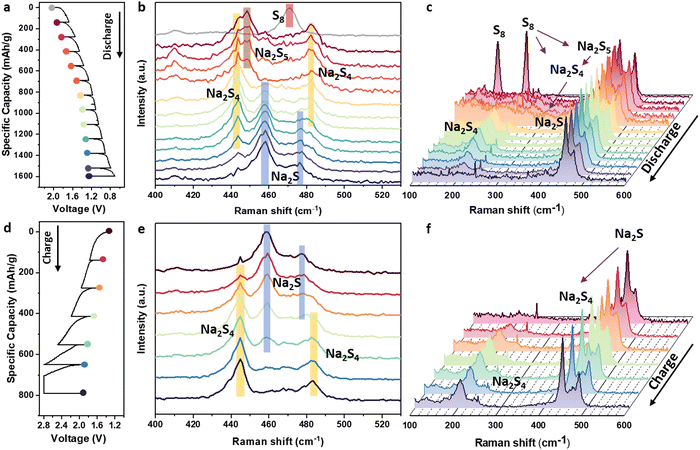
Since the cell operated at 90 °C exhibited a more complete reaction, a visual intensity mapping of the XANES spectra was created for the samples tested at 90 °C alongside the corresponding voltage profile (Fig. 4e). In addition to the appearance and disappearance of the features related to S₈, Na₂S_x (x = 4,5), Na₂S₂, and Na₂S, we also observed the shift of the absorption edge position. The lowest absorption edge at 50% DOD and SOC further indicates the formation of Na₂S₂. Since XANES spectra of both Na₂S₂ and Na₂S₄ have the feature around 2471 eV, we further did the linear combination fitting of the sample at 50% SOC to quantitatively identify the content of them. Based on the fitting result as shown in Fig. S14 (ESI†), 65.5 wt% of the sulfur element in the composite cathode belongs to Na₂S₂, and only 17.2% of them belong to Na₂S₄. The rest of the signal comes from our SE (Na₃SP₄). Furthermore, sulfide species of the electrochemical reactions corresponded well to the voltage plateaus and the capacities, where S₈ converted to Na₂S₄ through the first plateau with 4 electron transfer (accounting for 25% of the total capacity), and further reduced to Na₂S₂ in the second plateau with additional 4 electron transfer (accounting for additional 25% of the total capacity), and finally converted to Na₂S with addition 8 electrons transfer (accounting for the last 50% of the total capacity) in the third plateau, completing the 16 electrons transfer from S₈ to Na₂S.

In situ Raman spectroscopy reveals the mechanism of the absence of the second electrochemical reaction plateau

Although we identified the intermediate and the final product of the sulfur cathode in ASSSBs through the ex situ XAS study, the kinetic effects and the reason for the change in plateau numbers under relatively low temperatures and high rates remain unclear. To address this, we further conducted the in situ Raman measurement for the ASSSB operated at room temperature (20–25 °C) at the current density of 0.09 mA cm⁻² (approximately C/12). Since the Raman spectrum has high space resolution, we focused the laser on the area with the strongest sulfur signal and the weakest SE signal (Fig. S15, ESI†). Due to the lack of pressure on the topmost surface layer of the cross-section in the in situ cell, the sulfur cathode on the topmost surface has difficulty engaging in the reaction during cycling (Fig. S16, ESI†). Consequently, we scratched the surface layer after each hour of charge and discharge and collected the Raman spectra for the freshly exposed sulfur cathode layer. The results are shown in Fig. 5.

Fig. 5 In situ Raman investigation of the ASSSBs operated at room temperature. (a) Voltage profiles, (b) Raman spectra and (c) waterfall plot of the Raman spectra of the discharging process. (d) voltage profiles, (e) Raman spectra and (f) waterfall plot of the Raman spectra of the charging process.

During the initial discharge process (Fig. 5b), Na₂S₅ and Na₂S₄ were identified by the Raman peaks at 450 cm⁻¹ for Na₂S₅ and 443 cm⁻¹ and 482 cm⁻¹ for Na₂S₄.²⁵ As discharging progressed, Na₂S₅ gradually disappeared while Na₂S₄ remained. Subsequently, peaks at 459 and 478 cm⁻¹ emerged, indicating the formation of Na₂S. In the following process, Na₂S₄ gradually converted to Na₂S, and there was no Raman signal from Na₂S₂ detected. Fig. 5c presents a waterfall plot of the in situ Raman spectra, where S₈ first converts to Na₂S₅ and Na₂S₄, and then Na₂S₄ is directly reduced to Na₂S without the formation of Na₂S₂. During the charging process (Fig. 5d–f), Na₂S oxidized to Na₂S₄ through a one-step reaction without the formation of Na₂S₂. Due to the limitation of the in situ cell, no S₈ was detected after charging because the large overpotential caused an early termination of the electrochemical reaction during the charging process.

We further examined the final product of the charging process under different temperatures under C/20 by ex situ Raman spectroscopy (Fig. S17, ESI†). At 25 °C and C/20 rate, charging capacity limited to 870 mA h g⁻¹ resulted in Na₂S₄ as the final product, whereas at 60 °C and 90 °C, complete conversion to S₈ was achieved. Combined with the electrochemical data (Fig. 2a and g), S₈ is confirmed as the fully charged product of ASSSBs from the thermodynamic side, but the big overpotential caused by the sluggish kinetics under low temperature or high rate will cause an early termination of the electrochemical reaction.

Note, that the presence of Na₂S₂ in the ex situ XANES measurement (Fig. 4b) and its absence in the in situ Raman spectrum (Fig. 5b and e) tested under 25 °C can be attributed to differences in the samples caused by the preparation process of the ex situ and in situ characterization techniques. The ex situ nature allows a long rest time, enabling the sample to get a more thermodynamically stable state. As discussed in the GITT section, resting during the GITT test can form a three-plateau OCV curve instead of the two-plateau voltage profile in the galvanostatic test. In addition, a recent report on the LE-based Li–S system demonstrated that the formation of Li₂S₆ results from a chemical reaction between Li₂S₈ and Li₂S₄ rather than the electrochemical reactions.²⁶ Therefore, the in situ Raman spectroscopy provides real-time, dynamic information about the species present during the two-plateau electrochemical reaction, while ex situ XANES provides the chemical information of the three-plateau OVC curve. The absence of Na₂S₂ in the Raman spectra suggests that this phase is not formed as part of the electrochemical reaction at 25 °C and C/12 rate. Given the higher reliability of in situ measurements and the evidence from the electrochemical tests, we conclude that Na₂S₂ is not a significant intermediate in the electrochemical reaction at 25 °C and the rate of C/12, which explains the absence of the second plateau and the formed the formation of the two-plateau voltage profile.

In summary, the in situ Raman data confirmed the long-chain polysulfide species, specifically Na₂S₅ and Na₂S₄, and revealed that the reaction proceeds directly from Na₂S₄ to Na₂S without forming Na₂S₂ under room temperature. This direct reaction pathway is responsible for the two-plateau feature in the voltage profile under kinetically limited conditions instead of the three-plateau feature following the thermodynamic path.

First-principles calculations for all-solid-state Na–S system

In order to understand the fundamental mechanism of the findings above, we further conducted the first-principles calculations. We calculated the crystal structures of Na₂S₅, Na₂S₄, Na₂S₂, and Na₂S in the Na–S phase diagram, depending on the Na concentration. The crystal structures, including lattice constants and internal atomic positions, were fully optimized using DFT calculations. Fig. 6a presents the crystal structures of S₈ and Na₂S_x (x = 5, 4, 2, and 1) polysulfides, highlighting the interesting S–S chain structures that vary with composition, such as the S₅ (Na₂S₅) and S₄ (Na₂S₄) chains, and the S₂ dimers (Na₂S₂). Na₂S features Na–S bonds with Na in a tetrahedral coordination.

Fig. 6 DFT calculations of the Na–S system. (a) Crystal structures of S cathode and Na–S phases. Large and small atoms are Na and S atoms respectively. S–S bonds are shown by sticks in S₈, Na₂S₅, Na₂S₄, and Na₂S₂. (b) The formation energy of Na–S phases calculated by r2scan at 0 K, with the phonon contribution at 300 K and 400 K calculated with the phonopy package.²⁷ (c) The depth of energy convex hull of each phase at three temperatures. (d) OCV plateaus of the Na–S phases as a function of the Na content.

Table S1 (ESI†) presents the lattice constants and unit cell volumes fully optimized using DFT calculations with the r2scan functional (details provided in the Methods section) alongside experimental values from the literature.^28–33 The calculated lattice constants show good agreement with the experimental values, with an overestimation in the range of 0.2 to 2.0%. The calculated volumes per atom are 22.954, 21.810, 22.414, and 23.041 ų per atom for Na₂S, Na₂S₂, Na₂S₄, and Na₂S₅ respectively, which are 16.4–20.8% smaller than the 27.56 ų per atom for S₈. For comparison, Na metal in its hexagonal structure has a calculated equilibrium volume of 36.738 ų per atom.

Fig. 6b shows the formation energy per atom of the Na–S system. The formation energy E_f (eV per atom) at 0 K temperature is calculated by using total free energies of Na₂S_x [E(Na₂S_x)] and of the elemental phases of bcc Na [E(Na)] and S [E(S)] as:

All four considered polysulfides, Na₂S_x (x = 5, 4, 2, and 1), are thermodynamically stable at the three evaluated temperatures (0 K, 300 K, and 400 K), as shown in Fig. 6b. Among these, Na₂S is the most stable, having the lowest formation energy. The calculated formation energies at 0 K (−1.224, −0.976, −0.687, and −0.591 eV per atom for Na₂S, Na₂S₂, Na₂S₄, and Na₂S₅, respectively) are in good agreement with our experimental values. Fig. 6c illustrates the depth of the energy convex hull for the four intermediate phases, defined as the difference between the formation energy of the Na₂S_x polysulfide and the two-polysulfide mixture of its neighboring structure. For example, Na₂S₅ has a depth of −67 meV per atom relative to the two-polysulfide mixture of S and Na₂S₄, and Na₂S₄ has a depth of −14 meV per atom relative to the two-polysulfide mixture of Na₂S₅ and Na₂S₂. Similarly, Na₂S₂ is the shallowest, with a value of −4 meV per atom compared to the two-polysulfide mixture of Na₂S₄ and Na₂S, while Na₂S is the deepest, with −512 meV per atom lower than the two-polysulfide mixture of Na₂S₂ and Na.

We further calculated the OCV of the ASSSBs. Assuming a pristine S cathode reacts with Na during discharge, all the Na–S polysulfides shown in Fig. 6a are experienced depending on the Na concentration in the cathode. The final product at the end of discharge should be Na₂S (2Na + S → Na₂S), which can be further broken down into concentration-dependent reactions as follows:

The open circuit voltage associated with each intermediate polysulfide formation reaction can be estimated by using the DFT calculated total energies (E) of the phases before and after the reaction as:

As shown in Fig. 6d, the calculated OCV is 2.07 V for the Na content 0–2/7 producing Na₂S₅ and decreases to 2.03 V for the Na content 2/7–1/3 for polysulfide Na₂S₄. The calculated voltage decreases to 1.84 V for the lower Na content between 1/3 and 1/2 leading to Na₂S₂, and further to 1.72 V between 1/2 to 2/3 to structure Na₂S. Calculated OCvs. for Na₂S₅ and Na₂S₄ are very close, leading to a merged single plateau for the two reactions in experimental voltage–capacity curves. Therefore, we conclude from these theoretical findings that three plateaus will be observed in the voltage profile for ASSSBs, if the reactions proceed until the Na₂S formations in accordance with the Na–S phase diagram at temperatures lower than the melting points of these species. The results are well aligned with our experimental findings.

Based on the calculated OCV, we further went back to check the Galvanostatic discharge voltage profiles of the cells under a rate of C/20 and lower temperature (≤60 °C) (Fig. 2a and b). Due to the large polarization, the operating voltage of the second plateau (<1.60 V vs. Na/Na⁺) is not only lower than the theoretical potential of the chemical reaction from Na₂S₄ to Na₂S₂ (1.84 V) but also lower than that from Na₂S₂ to Na₂S₂ (1.72 V). In addition, the calculated formation energy of Na₂S₂ is very close to the two-polysulfide value of Na₂S₄ and Na₂S, (with a value of −4 meV per atom), indicating that this structure can be easily bypassed during the cycling of the Na–S system when kinetic factors are considered. This result remains qualitatively unchanged at finite temperatures, with the Na₂S₂ polysulfide being the easiest to skip. Overall, under the kinetic limitation condition, the Na₂S₂ phase was skipped in the electrochemical reaction of the sulfur cathode and cause the observed two-plateau voltage profile of the ASSSBs instead of the three-plateau voltage profile.

Sulfur reaction pathways: thermodynamic equilibrium and kinetic limitations in ASSSBs

The solid electrochemical reactions of sulfur in ASSSBs were thoroughly investigated through both experimental and theoretical studies. The three-plateau voltage profile represents the intrinsic thermodynamic equilibrium path of the sulfur cathode in ASSSBs, where S₈ is first reduced to Na₂S₅ and Na₂S₄ in the first plateau, and further converted to Na₂S₂ in the second plateau, and finally reduced to Na₂S in the third plateau (Fig. 7a). However, due to the sluggish kinetics at low temperatures (≤60 °C) and under the common rates (≥C/20), the sulfur reduction pathway is altered, in addition to the increase at the overpotential. In this kinetically limited scenario, the Na₂S₂ phase is skipped, resulting in a conversion directly from Na₂S₄ to Na₂S during discharge and from Na₂S to Na₂S4 during charge. This change in the reaction pathway leads to a two-plateau voltage profile. Furthermore, the incomplete conversion from Na₂S₄ to S₈ during the charging process due to the sluggish kinetics at room temperature results in a low charging capacity in the first cycle, which subsequently affects the capacity in the following cycles (Fig. 7b).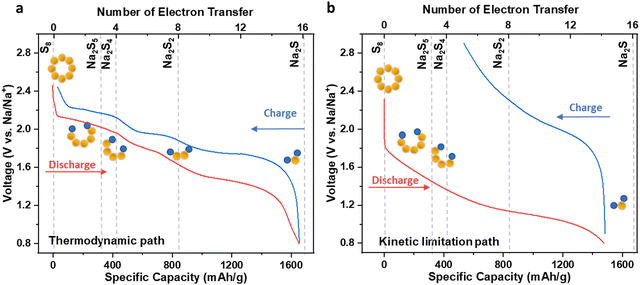

Fig. 7 Reaction pathways under thermodynamic and kinetic effects. The voltage profiles of the ASSSBs operated under (a) the thermodynamic path and (b) the kinetic limitation path.

While the final reduction product of the sulfur cathode in ASSSBs is Na₂S with 16 electron transfer under different temperatures, the sluggish kinetics cause a big overpotential during discharge and charge and further impede the full utilization and reaction of the sulfur active materials, causing low coulombic efficiency. In the kinetic limited scenario, the conversion between different polysulfides is not the major barrier, especially during the SRR. The major obstacle of the kinetics is the slow sodium diffusion in the cathode material. Reducing the size or increasing the surface area of sulfur and adding highly ionic conductors remain effective strategies to address the kinetic limitations in ASSSBs.

Conclusions

In summary, our study presented a comprehensive investigation into the reaction mechanism of sulfur cathodes in ASSSBs using electrochemical measurements, ex situ S K-edge XANES, in situ Raman spectroscopy, and first-principles calculations. Starting with electrochemical measurements, we explored the different electrochemical behaviors at various temperatures and C-rates. The intrinsic thermodynamic path was first explored by providing a high temperature of 90 °C and a longer reaction time at a low rate of C/100 as well as the GITT test. For the first time, the three-plateau voltage profile has been confirmed as the intrinsic thermodynamic behavior of the sulfur cathode in ASSSBs. Ex situ XANES identified the species of the polysulfide intermediates. During the SRRs of the sulfur cathode, S₈ is first reduced to long-chain polysulfide, Na₂S_x (x = 4,5), further converted to Na₂S₂, and finally reduced to Na₂S. In situ Raman further investigated the conversion pathway of the sulfur cathode under the kinetic limitations condition, revealing that the Na₂S₂ phase was skipped from the reduction reaction from Na₂S₄ to Na₂S, resulting in a two-plateau voltage profile during charge and discharge. The first principal calculation proved that Na₂S₅, Na₂S₄, Na₂S₂, and Na₂S are thermodynamic stable in the Na–S system. However, the formation energy of Na₂S₂ is only 4 meV per atom less than the intermediates of Na₂S₄ and Na₂S. Therefore, under kinetic limited conditions (such as at 25 °C and rate ≥ C/20), the Na₂S₂ phase is bypassed during the electrochemical reaction due to the sluggish kinetics. This study offers insights into the reaction mechanism of the sulfur cathode in ASSSBs considering both the thermodynamics-favored and kinetics-limited conditions through a combination of experimental and theoretical computation, inspiring the understanding and development of high-performance ASSSBs.

Experimental

Preparation of the sulfur composite cathode

The sulfur cathode was composed of 35 wt% of sulfur (Sigma, 99.98%), 15 wt% of carbon additive, and 50 wt% of solid electrolyte–Na₃PS₄. The synthesis of the carbon additive, polyacrylonitrile-derived porous carbon fibers (PPCF), was reported in our previous work.¹⁴ A high surface area with a dense core of PPCF can provide intimate contact with sulfur and excellent electrical conductivity. The solid electrolyte, Na₃PS₄, was prepared by the dry method. Na₂S (Thermo Scientific, anhydrous) and P₂S₅ (Sigma, 99%) were mixed with the mole ratio of 3 : 1 and further ball milled at 500 rpm for 10 hours followed by annealing at 270 °C for 2 hours.³⁴ To prepare the sulfur composite cathode, the sulfur–carbon (S–C) composite was first prepared by a melt-diffusion method,³⁵ in which sulfur and PPCF were mixed by ball milling and followed with heating to 155 °C for 12 hours under vacuum. Solid electrolyte, Na₃PS₄, was further mixed with the S–C composite by ball milling at 400 rpm for 2 hours to produce the final product of sulfur composite cathode.

Preparation of Na–Sn–C anode

Na–Sn–C composite was used as the anode material for the all-solid-state Na–S battery because of the good compatibility with Na3PS4 solid electrolyte.¹⁵ Na (Sigma, >99.9%, cubes) and Sn (Sigma, ≥99%, powder) were mixed with a mole ratio of 15 : 4 by ball milling, and 10 wt% of carbon black was added to improve the electron conductivity.

Fabrication of all-solid-state sodium–sulfur batteries

The all-solid-state sodium–sulfur batteries (ASSSBs) were fabricated by the cold pressing method in the argon-filled glovebox. 126 mg of Na₃PS₄ was first pre-pressed into the cell with a diameter of 12.7 mm. 2 mg of sulfur composites cathode and 15 mg of Na–Sn–C anode were added to two sides of the solid electrolyte separately. Aluminum foil was used as the current collector for both sides. All cells were rested for 5 hours before tests.

Electrochemical measurement

For the galvanostatic charge and discharge and cycling tests, all cells were discharged and charged between 0.7 to 2.8 V (vs. Na₁₅Sn₄/Na⁺) by the battery tester (Landt Instrument, China) at different temperatures. The galvanostatic intermittent titration technique (GITT) test was conducted on the battery tester (Landt Instrument, China) with 30 mins constant-current discharge/charge at the rate of C/20 followed by 4 hours rest. The cyclic voltammetry (CV) test was scanned on the potentiostat (BioLogic, SP-150) from 0.5 V to 3 V at different temperatures with various scan speeds.

X-ray absorption spectroscopy (XAS) measurement of the sulfur cathode

The XAS samples of the sulfur cathode at different depths of discharge (DoD) and states of charge (SoC) were prepared by discharging and charging the battery to different cut-off voltages. The cut-off voltages were determined by the voltage at the different DoDs and SoCs of the charge and discharge profile of the first cycle of the ASSSB cycled at C/20. After discharging and charging the cell to different DoDs and SoCs, the whole cell pellet was moved out of the PEEK case and removed the aluminum current at the cathode side to explore the cathode material. The pellet was sealed using a polypropylene film. Sulfur K-edge XAS of the sulfur cathode were collected in fluorescence mode using a silicon drift detector (Canberra) at the tender energy X-ray absorption spectroscopy (TES, 8-BM) beamline of the National Synchrotron Light Source II (NSLS-II) at Brookhaven National Laboratory. The Athena software from the Demeter software package was utilized to process the XAS data.³⁶

In situ Raman measurement

A special all-solid-state sodium–sulfur cell with a removable side wall was assembled for the in situ Raman test with the same method as mentioned for the regular ASSSBs. 70 mg of Na₃PS₄, 1.2 mg of sulfur composites cathode, and 10 mg of Na–Sn–C anode were used. After assembling the cell, a side wall was opened to explore the cross-section of the ASSSB for the in situ Raman measurement. The in situ Raman cell was discharged at the current density of 0.09 mA cm⁻² to 0.7 V and then charged to 2.8 V with a voltage hold at 2.8 V for one hour. After every one-hour discharge and charge, the surface of the cross-section was gently scratched by a glass sheet. Raman spectra were collected at room temperature in a backscattering geometry using a commercial Raman instrument (WiTec) in an argon-filled glovebox with a 532 nm leaser at the power of 300 μW and a 1800 cm⁻¹ grating. For the best quality, each Raman spectrum acquisition took 60 seconds and averaged 3 times.

First-principles calculations

Density functional theory (DFT) calculations within the projector augmented wave (PAW) formalism were performed, as implemented in the Vienna ab initio simulation package (VASP).³⁷ We employed a higher-fidelity calculation with the meta-GGA functional (r2SCAN).³⁸ Each calculation was performed with an energy cut-off of 680 eV. K-Point grid scheme are different depending on the calculated phase: 3 × 3 × 3 for Na₂S, 5 × 5 × 2 for Na₂S₂, 4 × 4 × 4 for Na₂S₄, and 4 × 3 × 1 for Na₂S₅.

Phonon calculations at finite temperatures

The phonopy package²⁷ is used in combination with VASP to produce phonon frequencies. To obtain the force constants (FCs) in phonopy, the atoms are manually displaced in the center cell by Δx in the three directions, and then calculate the IFCs of the perturbed structure.

Author contributions

H. Z. supervised this study and revised the manuscript. T. J. conducted the electrochemical experiments; Q. T. performed the first-principles calculations; T. J. and D. W. collected the ex situ S K-edge XANES spectra. T. J., Y. Z., and D. W. analyzed the S K-edge XANES data. T. J., V. P., Y. W., and K. B. conducted the in situ Raman test. J. W. contributed to the electrochemical experiments design and data analysis. T. J. and Q. T. wrote the original draft of the manuscript; H. Z., T. J., Q. T., Y. Z. D. W., V. W., J. W., Y. W., K. B., and Y. Y. modified the manuscript. All authors have read and agreed to the published version of the manuscript.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

H. Z. acknowledges the financial support from the Office of Science in Department of Energy under Award Number DE-SC0024528. V. P. and K. S. B. acknowledge the primary support of the US Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences under award number DE-SC0018675. This research used resources of the 8-BM (TES) beamline of the National Synchrotron Light Source II, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory under Contract no. DE-SC0012704.

References

1. Y. Wang, D. Zhou, V. Palomares, D. Shanmukaraj, B. Sun, X. Tang, C. Wang, M. Armand, T. Rojo and G. Wang, Energy Environ. Sci., 2020, 13, 3848–3879.
2. W. Yao, K. Liao, T. Lai, H. Sul and A. Manthiram, Chem. Rev., 2024, 124, 4935–5118.
3. N. Tanibata, M. Deguchi, A. Hayashi and M. Tatsumisago, Chem. Mater., 2017, 29, 5232–5238.
4. F. Jin, B. Wang, J. Wang, Y. Wang, Y. Ning, J. Yang, Z. Zhang, P. Liu, Y. Zhou, D. Wang, H. Liu and S. Dou, Matter, 2021, 4, 1768–1800.
5. L. Zhao, Y. Tao, Y. Zhang, Y. Lei, W.-H. Lai, S. Chou, H.-K. Liu, S.-X. Dou and Y.-X. Wang, Adv. Mater., 2024, 36, 2402337.
6. D. Cao, X. Sun, F. Li, S. M. Bak, T. Ji, M. Geiwitz, K. S. Burch, Y. Du, G. Yang and H. Zhu, Angew. Chem., Int. Ed., 2023, 62, e202302363.
7. J. T. Kim, A. Rao, H.-Y. Nie, Y. Hu, W. Li, F. Zhao, S. Deng, X. Hao, J. Fu, J. Luo, H. Duan, C. Wang, C. V. Singh and X. Sun, Nat. Commun., 2023, 14, 6404.
8. J. Gu, W. Hu, Y. Wu, F. Ren, Z. Liang, H. Zhong, X. Zheng, R. Ma, Y. Luo, X. Chen, J. Shi and Y. Yang, Chem. Mater., 2024, 36(9), 4403–4416.
9. R. A. Sharma, J. Electrochem. Soc., 1972, 119, 1439.
10. J. Sangster and A. Pelton, J. Phase Equilib., 1997, 18, 89–96.
11. R. Zhang, Y. Wu, Z. Chen, Y. Wang, J. Zhu and X. Zhuang, J. Mater. Chemi. A, 2023, 11, 19195–19209.
12. L. Lin, C. Zhang, Y. Huang, Y. Zhuang, M. Fan, J. Lin, L. Wang, Q. Xie and D. L. Peng, Small, 2022, 18, 2107368.
13. P. Adelhelm, P. Hartmann, C. L. Bender, M. Busche, C. Eufinger and J. Janek, Beilstein J. Nanotechnol., 2015, 6, 1016–1055.
14. X. Sun, Q. Li, D. Cao, Y. Wang, A. Anderson and H. Zhu, Small, 2022, 18, 2105678.
15. H. Nguyen, A. Banerjee, X. Wang, D. Tan, E. A. Wu, J.-M. Doux, R. Stephens, G. Verbist and Y. S. Meng, J. Power Sources, 2019, 435, 126623.
16. N. Tanibata, A. Hayashi and M. Tatsumisago, J. Electrochem. Soc., 2015, 162, A793.
17. M. J. Gray, N. Kumar, R. O’Connor, M. Hoek, E. Sheridan, M. C. Doyle, M. L. Romanelli, G. B. Osterhoudt, Y. Wang and V. Plisson, Rev. Sci. Instrum., 2020, 91, 073909.
18. J. Wang, Y. Xu, Z. Xu, Y. Shan, J. Yang, Z. Luo, H. Yang, X. Guo and J. Lu, Small Methods, 2023, 7, 2300662.
19. S. D. Kang and W. C. Chueh, J. Electrochem. Soc., 2021, 168, 120504.
20. Y. Zhu and C. Wang, J. Phys. Chem. C, 2010, 114, 2830–2841.
21. L.-J. Jhang, D. Wang, A. Silver, X. Li, D. Reed and D. Wang, Nano Energy, 2023, 105, 107995.
22. G. Xu, Z. Yan, H. Yang, X. Zhang, Y. Su, Z. Huang, L. Zhang, Y. Tang, Z. Wang, L. Zhu, J. Lin, L. Yang and J. Huang, Small, 2023, 19, 2300420.
23. M. Cuisinier, P.-E. Cabelguen, S. Evers, G. He, M. Kolbeck, A. Garsuch, T. Bolin, M. Balasubramanian and L. F. Nazar, J. Phys. Chem. Lett., 2013, 4, 3227–3232.
24. J. Gao, M. A. Lowe, Y. Kiya and H. D. Abruna, J. Phys. Chem. C, 2011, 115, 25132–25137.
25. O. El Jaroudi, E. Picquenard, N. Gobeltz, A. Demortier and J. Corset, Inorg. Chem., 1999, 38, 2917–2923.
26. R. Liu, Z. Wei, L. Peng, L. Zhang, A. Zohar, R. Schoeppner, P. Wang, C. Wan, D. Zhu, H. Liu, Z. Wang, S. H. Tolbert, B. Dunn, Y. Huang, P. Sautet and X. Duan, Nature, 2024, 626, 98–104.
27. A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001.
28. S. J. Rettig and J. Trotter, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1987, 43, 2260–2262.
29. Y. Xu, M. Yamazaki and P. Villars, Jpn. J. Appl. Phys., 2011, 50, 11RH02.
30. P. Böttcher and R. Keller, Z. Naturforsch. B, 1984, 39, 577–581.
31. R. Tegman, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 1463–1469.
32. P. Böttcher, J. Getzschmann and R. Keller, Z. Anorg. Allg. Chem., 1993, 619, 476–488.
33. P. R. Bonneau, R. F. Jarvis Jr and R. B. Kaner, Inorg. Chem., 1992, 31, 2127–2132.
34. A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Nat. Commun., 2012, 3, 856.
35. L. Huang, J. Li, B. Liu, Y. Li, S. Shen, S. Deng, C. Lu, W. Zhang, Y. Xia and G. Pan, Adv. Funct. Mater., 2020, 30, 1910375.
36. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
37. J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078.
38. J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee03160a

‡ These authors contributed equally to this work.

---