Discerning rise time constants to quantify charge carrier extraction in perovskite solar cells†
Received
19th June 2023
, Accepted 18th December 2023
First published on 28th December 2023
Abstract
The small-perturbation analysis of perovskite solar cells (PSCs) highlights a fundamental conundrum – while time domain measurements yield two time constants corresponding to the rise and subsequent decay of the photovoltage or photocurrent, the corresponding frequency domain methods only yield one time constant from the analysis of the negative imaginary part of the transfer function. To solve this problem, we propose a modification of the frequency domain transfer function that focusses on the transition of its real part to negative values at high frequencies. After verification using drift-diffusion simulations and equivalent circuit analysis, the application of the method to experimental intensity-modulated photovoltage spectroscopy data of a PSC allows calculation of the hidden rise time constant, showing a good agreement with rise time constants obtained from transient photovoltage measurements. Combining these measurements with transient photoluminescence measurements allows calculation of the figure of merit (FOM) that determines the charge collection efficiency. We determine large FOM values between 0.7–0.95 at or close to the 1 sun open-circuit voltage, indicating a significant electric field exists in the transport layers that allows fast charge collection in these conditions.
Broader context
Small-perturbation methods in the time and frequency domain are widely-used tools to understand the physics of operation of solar cells. Though they are connected via the Laplace transform, the equivalence of information obtained from both domains has not been established. To solve this problem, we develop a novel analysis method that focusses on the characteristic time constants measured in the time and frequency domain. This method extracts a time constant from the frequency domain data that is previously inaccessible using the traditional analysis method. This time constant corresponds to the rise of the photovoltage or photocurrent in a transient measurement and contains information regarding the speed of charge extraction from the bulk to the electrodes. This strategy is used to analyse intensity-modulated photovoltage spectroscopy (IMVS – frequency domain) and transient photovoltage (TPV – time domain) spectra of a thin-film perovskite solar cell, yielding a good agreement between the calculated rise time constants. In combination with recombination lifetimes obtained from transient photoluminescence measurements, the rise time constants allow calculation of a figure of merit that determines the charge collection efficiency. Such an analysis opens the possibility to determine charge extraction losses across all bias points of the current–voltage curve of the solar cell.
|
Introduction
Small perturbation techniques are powerful tools for the analysis of physical mechanisms in perovskite solar cells (PSCs). The main advantage of using a small perturbation is the possibility to linearise the mathematical description of higher-order processes, thereby facilitating the data analysis. In the time domain, these techniques include transient photovoltage (TPV) and transient photocurrent (TPC) measurements, that record the rise and subsequent decay of the external voltage and current respectively, as a function of time after the application of a short laser pulse. The corresponding frequency domain techniques are intensity-modulated photovoltage spectroscopy (IMVS), intensity-modulated photocurrent spectroscopy (IMPS) and impedance spectroscopy (IS).
Among the time domain techniques, TPV is widely used to study PSCs, where the decay of the photovoltage is typically fitted with a mono or bi-exponential function, with the corresponding characteristic time constants subsequently assigned to different physical mechanisms such as trap-mediated recombination and recombination limited by the injection of electrode charges.1–4 The rise time of the photovoltage is typically not analysed in the PSC community, though its time constant has been interpreted as the charge carrier transport time from the bulk to the electrodes in the case of dye-sensitized solar cells.5 Recently, Krückemeier et al. have shown that the photovoltage rise time in PSCs is determined by the speed of charge carrier exchange between the perovskite absorber and the electrodes via the transport layers.6 In the case of frequency domain methods, the typical approaches for data analysis are based on using models such as the diffusion-recombination model,7–9 fitting of equivalent circuits10–13 and calculation of time constants as a function of DC parameters.14–17 In this regard, the traditional analysis method involves calculating the time constants from the maxima of the negative imaginary part of the transfer function versus angular frequency ω. In the case of IS, the analysis of the capacitance and its evolution versus angular frequency and DC voltage are also used to obtain parameters such as doping and defect densities.18 Irrespective of the different analysis methods, the same information is expected to be contained in a time domain measurement and its corresponding frequency domain measurement (e.g. TPV → IMVS), since the time domain data can be converted to the frequency domain using a Laplace transform, which is a lossless transformation.19 However, this equivalence between the time and frequency domain methods has not been established experimentally.
In this work, we connect the analysis methods for both the time domain and frequency domain small perturbation techniques through the analysis of their characteristic time constants. We find that while the time-domain methods (TPV and TPC) naturally yield two time constants that correspond to the rise and subsequent decay of the photovoltage or photocurrent, the corresponding frequency domain methods of IMVS and IMPS yield only one time constant, the decay time constant, using the traditional analysis method. To identify the hidden rise time constant in the frequency domain data, we propose a modification of the transfer function that causes the traditional analysis method to focus on the evolution of the transfer function's real part versus angular frequency. Using drift-diffusion simulations and equivalent circuit analysis, we show that the transformation allows clearly observing both the rise and decay time constants. We further apply this method to experimental IMVS spectra of a perovskite solar cell, identifying similar magnitudes of the two time constants compared to the corresponding TPV measurements. We thus prove that the same information is contained in both the time and frequency domain spectra, albeit in different forms. Additionally, in combination with transient photoluminescence (tr-PL) measurements, we identify the voltage-dependent charge extraction and recombination lifetimes, which determine the figure of merit governing the charge collection efficiency.
Definitions
In a TPV measurement, the device is held at open circuit (typically using a load resistance of 1 MΩ) under a given DC illumination, and a short pulse of photons is impinged on it. The deflection Vext of the external voltage Vext is subsequently recorded as a function of time t. As there is no current flowing across the terminals at open circuit, Vext is equal to the difference between the electron quasi-Fermi level at the cathode minus the hole quasi-Fermi level at the anode (referred to as Velec). For the case of TPC measurements, the load resistance is reduced to typically 50 Ω and the current deflection j (where j is the current density at the terminals) is measured. The frequency-domain counterparts of TPV and TPC are IMVS and IMPS respectively – IMVS measures the AC external voltage while IMPS measures the AC current at the terminals upon application of an AC small perturbation of photon flux Φ (represented as a current density jΦ = qΦ). The IMVS transfer function is thus given by| | 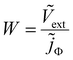 | (1) |
and the IMPS transfer function is given by| | 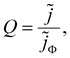 | (2) |
where the tilde represents an AC quantity. A third transfer function called the impedance is defined by measuring the AC terminal current upon the application of an AC small perturbation of the external voltage, given by| | 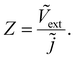 | (3) |
In general, these methods can be measured at any DC condition, however, IMPS is traditionally measured at short circuit20 while IMVS is measured at open circuit21 (IS is measured across a range of DC conditions22). The frequency domain data are usually represented by plotting the real versus the negative imaginary part of the transfer function (termed W/Q/Z-plane plot depending on the transfer function). Fig. 1(a) and (b) show simulated TPV and TPC data respectively of a typical p–i–n PSC and Fig. 1(c)–(e) show the corresponding simulated IMVS, IMPS and IS spectra respectively (see Table S1 and Section A1 in the ESI,†23–27 for simulation parameters and their discussion). For simplicity, in the simulations in Fig. 1, we do not include mobile ions and consider an arbitrarily high relative permittivity in the perovskite layer to ensure the absence of an electric field.
 |
| | Fig. 1 Typical representation of the data obtained from the time and frequency domain measurements. Drift-diffusion simulations of (a) transient photovoltage (TPV) and (b) transient photocurrent (TPC) spectra of a p–i–n perovskite solar cell that shows the voltage deflection and current deflection respectively upon application of a laser pulse at t = 0. Dashed lines show the rise of the photovoltage/photocurrent that is governed by the rise time constant while solid lines show the decay of the photovoltage/photocurrent governed by the decay time constant. Simulated (c) intensity-modulated photovoltage spectroscopy (IMVS), (d) intensity-modulated photocurrent spectroscopy (IMPS) and (e) impedance spectroscopy (IS) spectra of the same solar cell. The corresponding characteristic time constants obtained from the maxima of the negative imaginary part of the transfer function is also shown. See Table S1 in the ESI,† for simulation parameters. | |
Results
Connection between time and frequency domain spectra
In this section, we will analyse the data in Fig. 1 with the goal of accurately modelling the device physics and hence obtaining parameters of photovoltaic operation. We first analyse drift-diffusion simulations of the TPV and TPC spectra in Fig. 1(a) and (b), for a p–i–n perovskite solar cell. In both cases, we see a rise of the photovoltage or the photocurrent upon application of the laser pulse, which then reaches a peak followed by a decay back to the steady-state value. In the PSC community, only the decay of the photovoltage or photocurrent is typically analysed by fitting an exponential to obtain the characteristic decay time constant.1,2,4,28 However, in the case of dye-sensitized solar cells, the characteristic rise time constants of the photovoltage were analysed and attributed to electron transport across the TiO2 layer5 while for organic solar cells, the rise of the photocurrent was analysed to get insight into charge trapping.29,30
To provide a consistent interpretation of the rise and decay of the photovoltage and photocurrent in a TPV or TPC measurement in the case of PSCs, we will briefly describe a charge carrier exchange model that has been developed in ref. 6 and 31. In addition to the fundamental mechanisms of charge carrier generation, radiative and non-radiative (via deep traps) bulk recombination, the model explicitly accounts for non-ideal charge extraction from the perovskite to the collecting electrodes, via the transport layers. The model assumes a symmetric, thin-film PSC with an intrinsic perovskite layer and homogeneous distribution of deep traps, with negligible electric field in the perovskite layer due to ionic shielding32 and flat Femi levels in the device at open-circuit condition. Furthermore, the reported large diffusion lengths of electronic carriers33,34 compared to the perovskite layer thickness d (typically ∼350 nm) implies that the electronic carrier concentration is position-independent immediately after photogeneration. The concentration of electrons and holes is thus given by
| |  | (4) |
where
ni is the intrinsic carrier concentration,
Vint = (
Efn −
Efp)/
q is the internal voltage and
Efn and
Efp are the electron and hole quasi-Fermi levels in the perovskite layer. The continuity equation is given by
| | 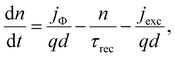 | (5) |
where
jΦ =
qΦ is the photon flux represented as a current density and
τrec is the parallel combination of the radiative lifetime and Shockley–Read–Hall (SRH) non-radiative lifetime
35 –
| |  | (6) |
where
Brad is the radiative recombination coefficient. The exchange current density
jexc between the perovskite and transport layer is given by
| |  | (7) |
where
Sexc is the charge exchange velocity, given by
31| |  | (8) |
where
μTL is the mobility in the transport layer,
FTL is the electric field in the transport layer and Δ
Epero,TL is the band offset between the perovskite layer and the transport layer. We note that
Sexc depends on
Velec because the electric field in the undoped transport layer is given by
| |  | (9) |
where
Vbi,TL is the built-in electrostatic voltage in the transport layer,
dTL is the thickness of the transport layer and
k is a factor that determines the magnitude of
Velec going to the transport layer (
k = 2 for our symmetric device). Applying a small perturbation to
eqn (4), (5) and (7) and solving them (derivation shown in Section A2 in the ESI
†), we obtain the photocurrent deflection in a TPC measurement as
| |  | (10) |
and the external voltage deflection
Vext in a TPV measurement as
| |  | (11) |
In
eqn (10) and (11),
τrise and
τdecay are characteristic time constants that determine the speed of the rise or decay of the measured quantity respectively, hereafter referred to as rise and decay time constants. Δ
Vext,0 and Δ
j0 are the peak photovoltage and photocurrent deflections respectively, that are also a function of the laser pulse intensity. The analytical solutions from the model for the time constants obtained from TPV measurements are
| |  | (12) |
| | 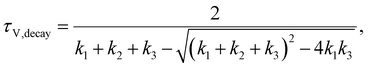 | (13) |
and the time constants in the case of TPC measurements are
| |  | (14) |
| |  | (15) |
where
| |  | (16) |
In
eqn (16),
τexc =
d/
Sexc is a charge carrier exchange lifetime that determines how efficiently charge carriers are transferred from (to) the perovskite bulk to (from) the electrodes
via the charge transport layers, while
Rexc is the corresponding transport layer resistance (see eqn (S6) in the ESI
†).
Rrec is the recombination resistance (eqn (S8) in the ESI
†),
Rs is the external series resistance and
Cg is the geometric capacitance. Since some of the inverse time constants in
eqn (16) are functions of
Vint or
Velec, the rise and decay time constants are also functions of
Vint or
Velec. This means that different time constants will dominate the response depending on the DC condition at which the TPV or TPC measurement is carried out. These matrices and their solutions are also applicable to the corresponding frequency domain small-perturbation measurements (TPV → IMVS, TPC → IMPS), since they are connected
via the Laplace transform. A deep analysis of the model and its predicted time constants as a function of DC parameters has been carried out recently.
6,31
In the case of the frequency domain spectra in Fig. 1(c)–(e), the characteristic frequencies ωchar are obtained from the frequency of the maxima of the negative imaginary part versus angular frequency ω (ω = 2πf, where f is the frequency in Hz), allowing to calculate the characteristic time constants τchar using
| |  | (17) |
Alternately, the frequency of the maxima of the negative imaginary part can also be obtained from the maxima of the
y-axis in the
W/
Q/
Z-plane plot, which corresponds to the top of the arc or arcs observed in these plots, as shown in
Fig. 1(c)–(e). We note that there are other methods of data analysis, such as the direct fitting of the diffusion-recombination model
7,8 or the analysis of capacitance steps
versus time
36 or frequency
37 and equivalent circuit fitting.
11,12 Here, we promote the method of studying the evolution of the measured time constants as a function of DC parameters such as external voltage, current density and light intensity, which can then be associated to fundamental physical mechanisms using our developed model, based on their characteristic evolution
versus DC parameters.
We begin our analysis by comparing the time constants obtained from drift-diffusion simulations of the TPV and IMVS spectra of a p–i–n perovskite solar cell at DC open-circuit condition under 100 mW cm−2 illumination using a blue LED (459 nm), for different mobilities of the transport layers (see Fig. S1 in the ESI,† for the band diagram and Table S1 in the ESI,† for simulation parameters). For simplicity, the simulations assume the ETL and HTL mobility to be equal and do not consider any mobile ionic densities within the perovskite layer. Furthermore, the relative permittivity of the perovskite layer is arbitrarily increased to ensure the absence of an electric field in the perovskite layer. The influence of Shockley–Read–Hall (SRH) recombination35 is simulated using a density of mid-gap traps. Fig. 2(a) shows that the rise of the photovoltage is strongly dependent on the mobility of the transport layers, with faster rises and higher peaks in the photovoltage observed for increasing mobilities of the transport layers. This is because charge carriers are transported from the perovskite layer to the electrodes via the transport layers to build up the photovoltage or drive the photocurrent. The decay of the photovoltage is mostly independent of the transport layer mobility, indicating that the dominant mechanism is bulk recombination. We note that the calculation of recombination lifetimes from the decay time constants is limited by charge carrier redistribution in the case of low mobility of charge carriers in the absorber layer, as in the case of organic solar cells.38 However, this limitation does not apply for thin-film PSCs due to the large mobilities or diffusion coefficients of the charge carriers.33,34
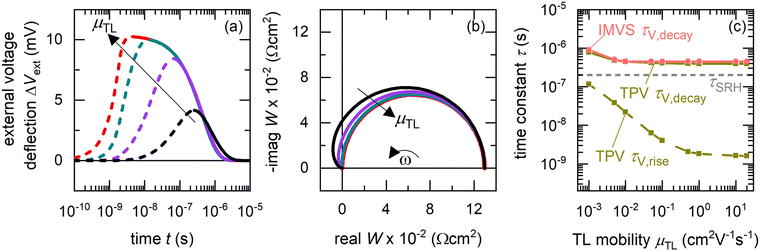 |
| | Fig. 2 Calculation of time constants from the time and frequency domain data – Drift-diffusion simulations of (a) TPV and (b) IMVS spectra at DC open-circuit conditions under illumination with a blue LED (459 nm), for different transport layer mobilities (the largest transport layer mobility corresponds to the situation μTL = μpero). (c) Shows the corresponding calculated rise (dashed lines) and decay (solid lines) time constants from fitting the TPV spectra using eqn (11) (fitting shown in Fig. S2 in the ESI†), and the IMVS time constant (circles) obtained from (b) using eqn (17). While TPV yields both the rise and decay time constants, IMVS yields only the decay time constant. The transport layer mobilities were set equal for simplicity and no ionic densities were considered in the perovskite layer. The relative permittivity of the perovskite layer was arbitrarily increased to ensure the absence of an electric field in it. For the TPV simulations, a laser pulse width of 2 ns was used. All simulation parameters are shown in Table S1 in the ESI.† For clarity, only a few of the simulated spectra are shown in (a) and (b). | |
The corresponding IMVS spectra in Fig. 2(b) show a single arc in the W-plane plot for all cases. For lower transport layer mobilities, the real part of W makes a pronounced transition (larger amplitudes) to the second quadrant, showing a negative value at high frequencies before reaching the origin. The occurrence of a single arc in the W-plane plot implies one observable time constant from IMVS, whereas the rise and decay of the photovoltage implies two time constants from TPV measurements (see Fig. S2 in the ESI,† for fitting using eqn (11)). Fig. 2(c) shows that there is a good agreement between the slower time constant (decay time constant) from TPV and IMVS, which approaches the SRH recombination lifetime (τSRH) for higher transport layer mobilities. The faster time constant, which corresponds to the rise time constant, shows a strong dependence on the transport layer mobility, rising from a few nanoseconds when the transport layer mobilities equal that of the perovskite to 100 nanoseconds for the lowest transport layer mobility chosen.
However, Fig. 2 raises the question – why is the rise time constant observed in the time domain but not in the frequency domain? Since the transformation from the time domain to the frequency domain is a lossless one, we conclude that the rise time constant is hidden in the frequency domain data. This effect can be understood by taking the Laplace transform of eqn (11), which yields the IMVS transfer function
| |  | (18) |
where
W0 is a constant with the units of Ω cm
2 s
−1. For time constants well-separated in magnitude (
τV,decay ≫
τV,rise), the first term in the RHS of
eqn (18) is much bigger than the second term. In such a situation, the second term in the RHS drops out (see Section A3 in the ESI,
† for derivation) and the characteristic time constant calculated from the frequency maximum of the negative imaginary part of
W is
| | 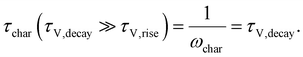 | (19) |
Eqn (19) shows that the rise time constant cannot be observed from the typical analysis of the frequency maximum of the negative imaginary part of the transfer function when it is significantly smaller than the decay time constant. Since the rise time constant is in many cases related to charge extraction from the absorber to the contacts, the situation where
τV,decay ≫
τV,rise is likely to be frequently encountered, especially at low forward biases.
6 Therefore, even though the transfer function contains two time constants, only the slower time constant is expressed, leading to a single arc in the frequency domain spectrum. We thus require a data analysis method that allows visualising both time constants clearly. In the case of time domain measurements, we note that both the absolute value and the slope of the photovoltage or photocurrent can be obtained from the plot of photovoltage or photocurrent
versus time. In the case of frequency domain measurements, the slope of the real part of the transfer function is not defined and hence not analysed. Based on this intuition, we define a new transfer function
| | | MW = iωW = −ω(imagW) + iω(realW), | (20) |
whose imaginary part is the product of the angular frequency and the real part of the IMVS transfer function
W. Using
eqn (18) in
eqn (20), we obtain
| |  | (21) |
Fig. 3(a) and (b) show the simulated negative imaginary parts of
W and
MWversus angular frequency for different transport layer mobilities of the PSC. While − imag
W shows only one peak that corresponds to a single time constant, − imag
MW shows a peak each in the upper and lower quadrant that corresponds to two time constants (see Section A4 in the ESI,
† for derivation). The additional time constant is obtained from the region at high frequencies where the real part of the IMVS transfer function
W transitions to a negative value (
i.e. moves to the second or third quadrant), consequently making a peak in the opposite quadrant to that of the decay time in
Fig. 3(b). Therefore, while the transition to the negative real part of the transfer function has been attributed to different physical mechanisms such as diffusion,
7 trapping
39 and ionic effects,
40 this effect also arises from a simple consideration of non-ideal charge extraction from the bulk to the electrodes in a transient measurement. The amplitude of this transition to the negative real part is proportional to the rise time constant (see derivation in Section A5 in the ESI
†), which is also observed from
Fig. 2(a) and (b) for lower transport layer mobilities, which show larger (slower) rise time constants.
Fig. 3(c) shows that the additional time constant obtained from
MW is indeed the rise time constant calculated from the TPV data, while the slow time constant is obtained from both
W and
MW. We note that the divergence in the calculated rise time constants from both TPV and IMVS occurs only when the rise time constants are of the order of the time width of the laser pulse (2 ns) in the TPV simulation. In summary, the transformation of the IMVS transfer function from
W to
MW allows determination of both the rise and decay time constants.
 |
| | Fig. 3 Transformation of IMVS data to obtain the rise and decay time constants – Drift-diffusion simulations of the negative imaginary part of (a) IMVS transfer function W and (b) transformed transfer function MW = iωW versus angular frequency, for different transport layer mobilities (the largest transport layer mobility corresponds to the situation μTL = μpero). The negative imaginary part of MW shows both the rise (dashed lines) and decay (solid lines) time constants, while that of W only shows the decay time constant. (c) shows the calculated rise and decay time constants from the negative imaginary part of MW in (b) and the TPV simulations in Fig. 2. The calculated rise and decay time constants from both the TPV and the transformed IMVS data are almost identical. For clarity, only a few of the simulated spectra are shown in (a) and (b). | |
Effect of electric field and mobile ionic densities
The mobile ion densities in PSCs are known to have a significant impact on the charge extraction and recombination rates in the device.41–43 Therefore, in this section, we will focus on how the electric field and mobile ionic densities in the perovskite layer can affect the rise and decay time constants obtained from TPV and IMVS simulations. We therefore set the relative permittivity of the perovskite layer to εr = 30 and assume equal densities of mobile cations and anions in the perovskite layer. The effect of the electric field is observed by simulations at open-circuit conditions for different DC light intensities. The band diagrams for three situations of high, intermediate and low light intensities are shown in Fig. 4(a), (c) and (e) respectively. For ease of observation, these figures show only the conduction bands of the perovskite and the electron transport layer. For the case with the lowest ionic density (1013 cm−3), an electric field exists in the perovskite layer whose magnitude increases with reducing light intensity. Only in the situation of high light intensity where the open-circuit voltage is close to or above the 1 sun open-circuit voltage, do we observe a negligible electric field in the perovskite layer. Upon increasing the mobile ion density, a reduction of the electric field is observed in all cases, leading to an approximately field-free perovskite bulk with potential drops occurring in a small region at the ETL/perovskite and HTL/perovskite interfaces for ion densities of 1017 cm−3.
 |
| | Fig. 4 Drift-diffusion simulations of band diagrams of the perovskite solar cell for different densities of mobile ions in the perovskite layer (the relative permittivity of the perovskite layer was set to εr = 30), at open-circuit condition corresponding to (a) high, (c) intermediate and (e) low light intensities, using a blue LED (459 nm). (b), (d) and (f) respectively show the corresponding time constants obtained from the simulated TPV and IMVS spectra (shown in Fig. S3 in the ESI†). | |
The corresponding TPV and IMPS spectra are shown in Fig. S3 in the ESI.† Most of the spectra show an exponential rise and decay that is well-described by eqn (11), though some spectra show an additional peak in the rise or decay, due to the influence of the mobile ionic density. The time constants obtained from the simulated TPV and IMVS data for these situations are shown in Fig. 4(b), (d) and (f). In all cases, we are successfully able to extract the rise and decay time constants using our developed analysis method. The rise time constants at a given ion density increase in magnitude with increasing light intensity, which occurs due to the reduced electric field in the transport layer at higher light intensities (shown in Fig. 4(a), (c) and (e)) that reduces the charge extraction velocity Sexc (see eqn (8)). Fig. 4(b), (d) and (f) also show that the rise time constant remains approximately constant as a function of ion density, only showing an increase for the case of the largest ion density (Nion = 1017 cm−3). The decay time constants correspond to the SRH lifetime at high light intensities (Fig. 4(b)), which transitions to much larger magnitudes at lower light intensities (Fig. 4(d) and (f)). These large magnitudes are related to the fact that at low quasi-Fermi level splitting (low light intensity), the decay time constant is limited by the slow re-injection of charges from the geometric capacitance and their subsequent recombination (τdecay = RrecCg).3,4,31 A third time constant is obtained from the low frequency arc in the IMVS spectra, whose magnitude is in the order of tens of milliseconds. This time constant is related to the slow movement of ions in the perovskite layer.44 In summary, we find that our model and the developed analysis method is applicable to obtain and interpret the time constants for the case of including mobile ionic densities in the perovskite layer.
Time constants from equivalent circuit modelling
In this section, we will verify the validity of the developed analysis method by using it to extract the time constants from the typical frequency domain spectra (IMVS, IMPS and IS), using an equivalent circuit of the PSC, shown in Fig. 5. This equivalent circuit is derived from the kinetic model of the PSC described in the previous section (see Section A2 in the ESI,† for definitions). The transfer functions are given by31| | 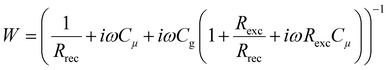 | (22) |
| |  | (23) |
| | 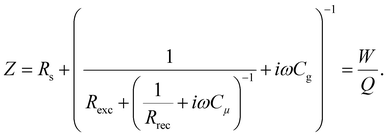 | (24) |
We thus generalise the transformation method in the previous section and extend it to the IMPS and IS transfer functions. In case of IS, the series resistance is subtracted from the total impedance and then transformed to MZ to obtain the time constants. This is because while the characteristic frequency of the impedance transfer function Z is independent of Rs, the characteristic frequency of the modified transfer function MZ is dependent on Rs in the form of a linear, additive term and hence needs to be subtracted out to remove its influence (see Section A6 in the ESI,† for derivation). A summary of these transfer functions and their transformations to obtain the rise and decay time constants are shown in Table 1.
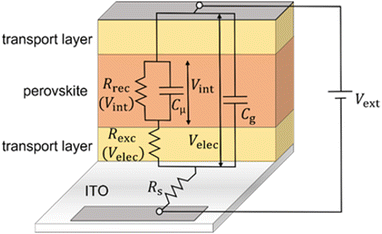 |
| | Fig. 5 Derived equivalent circuit from the model, which is used to verify the validity of the developed transformation method for the frequency domain data. Rrec is the recombination resistance (eqn (S8) in the ESI†), Rexc is the charge carrier exchange resistance that models the potential drop across the transport layers (eqn (S6) in the ESI†), Rs is the series resistance, Cμ is the chemical capacitance (eqn (S3) in the ESI†) and Cg is the geometric capacitance of the perovskite layer. The model used to derive the equivalent circuit is described extensively in ref. 31. | |
Table 1 Summary of frequency domain transfer functions and their corresponding transformations to obtain the rise and decay time constants from the data
| Transfer function |
Transformation |
Time constants |
|
W (IMVS) |
M
W = iωW |
Inverse extrema of −imag W versus ω |
|
Q (IMPS) |
M
Q = iωQ |
Inverse extrema of −imag Q versus ω |
|
Z (IS) |
M
Z = iω(Z − Rs) |
Inverse extrema of −imag Z versus ω |
Fig. 6 shows the calculated rise and decay time constants from simulations of the IMVS, IMPS and IS spectra respectively at open-circuit conditions using the equivalent circuit in Fig. 5 (see Table S2 in the ESI,† for parameters and Fig. S4 in the ESI,† for the peaks in the negative imaginary part of the modified transfer functions that correspond to the two time constants). The IMVS and IS response are identical, with the rise time constant corresponding to τexc at low open-circuit voltages followed by a transition to the product RexcCg, causing it to exponentially decrease at large open-circuit voltages. The decay time constant follows the recombination lifetime τrec, decreasing exponentially at large open-circuit voltages followed by a very short saturation at lower open-circuit voltages. This corresponds to the dominance of radiative recombination at high open-circuit voltages and SRH recombination at lower open-circuit voltages. The short saturation in the decay time constant is rapidly followed by an exponential increase at lower open-circuit voltages corresponding to the product RrecCg. This effect has been observed and analysed from both electrical and luminescence methods,3,4,45,46 where the recombination is limited by the back-injection of charges from the electrodes into the absorber. This effect is also observed in the simulations in Fig. 4, where the magnitude of the decay time significantly increases at low light intensities (low quasi-Fermi level splitting). In the case of IMPS, the rise time constant is identical to that of IMVS and IS, while the decay time constant corresponds to τrec at large open-circuit voltages and transitions to the product RsCg (generally called RC attenuation) at low open-circuit voltages. Thus, our new method for the analysis of frequency domain spectra allows determination of the rise time constant, which was inaccessible from the standard analysis of the negative imaginary part of the transfer function. The rise time constant contains information regarding the extraction of charges from the perovskite layer to the electrodes and is a function of transport layer parameters such as the mobility and built-in voltage (eqn (8) and eqn (S5) in the ESI†).
Analysis of experimental spectra
We now proceed to study experimental TPV and IMVS spectra obtained from measurements of p–i–n thin film perovskite solar cells, using our developed analysis method. The structure of the samples used was ITO/SAMs/PTAA/Cs0.05FA0.8MA0.15PbI2.25Br0.75/C60/BCP/Ag (fabrication details provided in the methods section, current–voltage curves provided in Fig. S5 in the ESI†), where SAMs is a mixture of self-assembled monolayers (Me-4PACz and MeO-2PACz), poly(triaryl amine) (PTAA) is the hole transport layer and C60/BCP (Bathocuproine) is the electron transport layer. The bandgap of the perovskite layer is 1.68 eV. For both the TPV and IMVS measurements, the spectra were collected at different DC bias light intensities under open-circuit conditions, with the open-circuit condition set using a 1 MΩ load resistor (further experimental details provided in the methods section).
 |
| | Fig. 6 Calculated rise time constants τrise (red, open circles) and decay time constants τdecay (blue, open circles) versus DC open-circuit voltage, obtained from simulated (a) IMVS, (b) IMPS and (c) IS spectra of the equivalent circuit in Fig. 5, using the transformation method summarised in Table 1. These time constants correspond to different RC products as shown, depending on the DC open-circuit voltage. Rs is the series resistance, Rrec is the recombination resistance (eqn (S8) in the ESI†), Rexc is the charge carrier exchange resistance that models the potential drop across the transport layers (eqn (S6) in the ESI†), Cg is the geometric capacitance, τrec is the recombination lifetime (eqn (6)) and τexc is the charge carrier exchange lifetime (eqn (S5) in the ESI†). The parameters used for the equivalent circuit simulations are summarised in Table S2 in the ESI.† | |
Fig. 7(a) shows an example of the W – plane plots of the IMVS transfer function, measured at different open-circuit voltages (see Fig. S6 in the ESI,† for all IMVS and TPV spectra). These plots show the same general shape, consisting of two arcs, one at high frequency and one at low frequencies below ≅500 Hz. The low-frequency arc in the frequency domain spectra has been well-studied and is attributed to ionic effects in the PSC.44 The high frequency arc shows the same behaviour as seen from the simulations in Fig. 2(b), with a transition to a negative real part of the transfer function at high frequencies. We thus transform the IMVS transfer function to MW and analyse the evolution of the negative imaginary part of MWversus angular frequency ω, shown in Fig. 7(b). We observe peaks in the positive and negative directions, which correspond to the rise and decay time constants of the photovoltage. Fig. 7(c) shows an example of the measured TPV spectra at different open-circuit voltages and their corresponding fitting with eqn (11) to obtain the rise and decay time constants of the photovoltage in the time domain. We note that the rise of the photovoltage at short times is affected by reflections of the output voltage at the 1 MΩ load resistance.
 |
| | Fig. 7 Measured (a) real versus negative imaginary part of the IMVS transfer function W and (b) negative imaginary part of transformed IMVS transfer function (MW = iωW) versus angular frequency ω and (c) TPV spectra of Cs0.05FA0.8MA0.15PbI2.25Br0.75 perovskite solar cells, measured at different DC open-circuit voltages using the PAIOS instrument developed by Fluxim. The data in (c) was fitted using eqn (11) to obtain the rise and decay time constants. The frequencies of the peaks in (b) (dashed lines) correspond to the rise and decay time constants of the photovoltage. The entire set of measured spectra is shown in Fig. S6 in the ESI.† | |
Fig. 8(a) shows the calculated rise and decay time constants of the photovoltage from both TPV and IMVS measurements. The time constants from both methods show a good agreement with each other. To identify the physical mechanisms that generate these time constants, we define a slope factor θ using
| |  | (25) |
where
τ0 is a constant with a unit of seconds. Depending on the coupling between the voltage-dependent and voltage-independent resistances and capacitances described in the previous section, different values of the slope factor are expressed, allowing to differentiate the mechanisms. Fig. S7 in the ESI,
† shows the calculated slope factors for the measured time constants of IMVS and TPV. The decay time constant
τV,decay from both IMVS and TPV shows an exponential evolution
versus open-circuit voltage with a slope factor close to 2. This corresponds to a time constant that is limited by the first-order recombination of charge carriers that are re-injected into the intrinsic perovskite layer from the electrodes, expressed as the product of the recombination resistance
Rrec (eqn (S8) in the ESI
†) and the geometric capacitance
Cg.
3,4,46 The rise time constant
τV,rise from TPV remains approximately constant at high open-circuit voltages (large slope factor
θ = 5.97), with a magnitude ranging between 2 × 10
−8 s 4 × 10
−8 s. At lower open-circuit voltages, a small increase in magnitude is observed. A similar evolution and magnitude of the rise time constant was observed from TPV measurements on a thin-film CH
3NH
3PbI
3 solar cell.
6 For the corresponding voltage range,
τV,rise from IMVS shows a similar behaviour with a larger magnitude of
τV,rise ≅ 10
−7 s. To confirm if the high frequency data is free of ionic effects, we carried out IMVS measurements after preconditioning the solar cell under LED white light illumination (155 W m
−2) at open-circuit condition for 120 seconds. The IMVS spectra before and after preconditioning are shown in Fig. S8(a) in the ESI.
† The high frequency region of the spectra is almost identical, while the only differences occur in the low frequency arc of the spectra.
 |
| | Fig. 8 (a) Calculated rise and decay time constants from the experimental IMVS and TPV spectra shown in Fig. 7 and Fig. S6 in the ESI.† The triangles correspond to the decay time constants while the spheres correspond to the rise time constants. Based on their slope factors θ calculated using eqn (25) (see Fig. S7 in the ESI,† for fitting), the decay time constant is ascribed to the recombination of charge carriers back-injected by the electrodes, while the rise time constant is ascribed to the speed of charge carrier extraction from the perovskite to the electrodes, via the transport layers. (b) Calculated decay time versus Fermi-level splitting from transient photoluminescence measurements of a glass/ITO/PTAA/Cs0.05FA0.8MA0.15PbI2.25Br0.75/C60/BCP stack, with the decay times from TPV and IMVS in (a) plotted for ease of comparison. ‘HTL’and ‘ETL’ refer to the hole and electron transport layers respectively. (c) Calculated figure of merit (see eqn (28) and (30)) using the ratio of the exchange lifetimes (calculated from TPV and IMVS rise time constants in (a)) and recombination lifetimes (calculated from the tr-PL decay time in (b)). | |
This is further confirmed by the identical rise and decay time constants obtained from both spectra, and the ionic time constant in the order of millliseconds (see Fig. S8(b) in the ESI†). We further verified this in the time domain by carrying out current–voltage curves in the reverse and forward directions at different scan speeds (see Fig. S9 in the ESI†). The hysteresis is minimised for slow scan speeds around 0.1 V s−1 and for high scan speeds around 2400 V s−1 (which corresponds to a frequency of 1000 Hz). We conclude that the data at frequencies above several kHz should be devoid of any ionic influences.
Based on the model discussed in the previous section and the large slope factor, we conclude that the rise time constant corresponds to the exchange lifetime τexc. We can thus include the effect of non-ideal charge extraction in the traditional equation of the current–voltage curve (see Section A7 in the ESI,† for the derivation), which yields6
| |  | (26) |
where
G is the generation rate and
d is the perovskite layer thickness.
Velec is connected to the external voltage through the series resistance as
eqn (26) is the traditional current–voltage curve with a pre-factor that is determined by the ratio of the voltage-dependent charge exchange and recombination lifetimes. We can thus define a figure of merit (FOM) that quantifies the quality of charge extraction with respect to the rate of recombination, given by
6| | 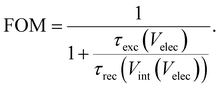 | (28) |
For the case of the exchange lifetime being much faster than the recombination lifetime, the FOM becomes 1 and we obtain the traditional current–voltage curve equation. For other cases of the recombination lifetime being similar in magnitude or faster than the exchange lifetime, the FOM is smaller than 1 and the entire current–voltage curve is reduced by this factor. We note that
τexc is a function of
Velec (see
eqn (8) and (14) and
Fig. 6) for an intrinsic perovskite layer and undoped transport layers, while
τrec is a function of the internal voltage (quasi-Fermi level splitting) (
eqn (6)), that can also vary as a function of the light intensity and
Velec.
47 Therefore, the FOM is also a function of
Velec (
eqn (28)) and can be used to calculate losses related to non-ideal charge extraction at each bias point of the current–voltage curve. The FOM is particularly useful to determine losses at short-circuit and low forward bias that can strongly affect the fill factor in state-of-the-art PSCs.
6,48
In general, the short-circuit current density jsc can be described by the equation  where G(x) is the position-dependent photogeneration and fc(x) is the position-dependent collection efficiency in the absorber layer of thickness d. In case of constant photogeneration, we obtain
where G(x) is the position-dependent photogeneration and fc(x) is the position-dependent collection efficiency in the absorber layer of thickness d. In case of constant photogeneration, we obtain  where jgen = qdG is the total photogenerated current density in the absorber layer and fc,av is the average collection efficiency. In such situations, fc,av can be calculated from eqn (26) (assuming zero external series resistance) as
where jgen = qdG is the total photogenerated current density in the absorber layer and fc,av is the average collection efficiency. In such situations, fc,av can be calculated from eqn (26) (assuming zero external series resistance) as
| |  | (29) |
where the subscript ‘sc’ indicates the value at short-circuit (
Velec = 0).
Eqn (29) is the average collection efficiency in the case of a p–i–n device with an approximately field-free absorber with excellent charge carrier transport (
i.e. diffusion lengths of electrons and holes much larger than the absorber thickness, as is the case for the thin-film PSC
34), where the charge collection is limited by the transport layers. The product
Sexc,scτrec,sc has the unit of length and is similar to the charge carrier collection length
lc defined for a p–i–n solar cell where charge collection is limited by drift in the absorber (for constant photogeneration, we have
fc,av = (
lc/
d)[1 − exp(−
d/
lc)], where
lc is given by the sum of the mobility-lifetime product of electrons and holes multiplied by the electric field in the absorber).
49
In situations where the experimental rise time constant corresponds to τexc and the decay time constant corresponds to τrec, the FOM at a given Velec can be calculated using
| |  | (30) |
However, we cannot calculate the FOM from the time constants in
Fig. 8(a) because the decay time constant is dominated by the contribution of the geometric capacitance. We therefore carried out transient photoluminescence (tr-PL) measurements of a glass/ITO/PTAA/Cs
0.05FA
0.8MA
0.15PbI
2.25Br
0.75/C
60/BCP stack with the measured tr-PL spectrum of a Cs
0.05FA
0.8MA
0.15PbI
2.25Br
0.75 perovskite film on glass as reference, shown in Fig. S10(a) in the ESI.
† We calculated the differential tr-PL decay time using the equation
45| |  | (31) |
where
Φ is the emitted photon flux and
t is the time.
τdiff is plotted as a function of the quasi-Fermi level splitting Δ
Ef (assuming an intrinsic perovskite layer), shown in Fig. S10(b) (ESI
†). To discriminate the different mechanisms governing the tr-PL decay time, we employ
eqn (25) with
qVoc replaced by Δ
Ef. We first analyse the tr-PL spectrum of the perovskite film on glass. For an intrinsic layer, we expect SRH recombination
via deep traps to yield a constant
τdiff while radiative recombination yields
θ = 2 (
eqn (4) and (6)).
45 The decay time shows an ‘S’-shaped evolution, showing a sharp rise at large Δ
Ef, a comparitively slower increase between the magnitudes
τdiff = 3 × 10
−7–10
−5 s for intermediate Δ
Ef and a sharp rise again at low Δ
Ef. The calculated values from the tr-PL decay time are also shown in Fig. S10(b) (ESI
†). We obtain
θ = 1.9 for low Δ
Ef between 0.9–1 eV, transitioning to a region with
θ = 3.7 for Δ
Ef between 1–1.3 eV, followed by a region with
θ = 1.3 at high Δ
Ef above 1.3 eV. The large values between 1–1.3 eV followed by the transition at lower Δ
Ef has recently been interpreted as originating from SRH recombination
via shallow traps.
50,51 The origin of the slope factor at large Δ
Ef is unclear, though we speculate it could be influenced by transport effects due to the position-dependent generation profiles of carriers in the perovskite at very early times. In the case of the glass/ITO/PTAA/Cs
0.05FA
0.8MA
0.15PbI
2.25Br
0.75/C
60/BCP stack, we observe a similar ‘S’-shaped evolution of the decay time (shown in Fig. S10(b), ESI
†), though the magnitudes of the decay times are approximately one order lower than that of the perovskite film on glass. This observation is consistent with the fact that the perovskite/transport layer interfaces contain defect densities that lead to additional non-radiative recombination, reducing the effective recombination lifetime of the glass/ITO/PTAA/Cs
0.05FA
0.8MA
0.15PbI
2.25Br
0.75/C
60/BCP stack compared to that of the perovskite film on glass.
In order to compare the time constants obtained from electrical measurements on the full device with those obtained from tr-PL measurements on the glass/ITO/PTAA/Cs0.05FA0.8MA0.15PbI2.25Br0.75/C60/BCP stack, we assume that the ΔEf of the stack is identical to the open-circuit voltage of the full device under the same illumination conditions (as has been previously observed52). We further note that the tr-PL decay times of the stack could be influenced by charge exchange between the perovskite and the transport layers only at early times,45 quite far from the region of ΔEf where the IMVS and TPV time constants are measured. We thus calculate the FOM (eqn (28)) using the τexc from the rise time constants of both the IMVS and TPV measurements (Fig. 8(a)), in unison with the τrec obtained from the tr-PL data (Fig. 8(b)). This FOM is shown in Fig. 8(c), yielding values between 0.9–0.95 for the TPV + tr-PL data and between 0.7–0.9 for the IMVS + tr-PL data. The large values of the FOM indicate that charge extraction is efficient close to and at the 1 sun open-circuit voltage. Therefore, we expect that a significant electric field still exists in the transport layers at applied voltages at or close to the one sun open-circuit voltage, that allows fast charge extraction.
Experimental
Materials
Cesium iodide (CsI), N,N′-dimethylformamide (DMF), dimethyl sulfoxide (DMSO) and ethyl acetate were purchased from Sigma Aldrich. Self-assembled monolayers Me-4PACz and MeO-2PACz, bathocuproine (BCP, 99.0%), lead iodide (PbI2, 99.99%) were purchased from TCI. Lead bromide (PbBr2, 98%) was purchased from Acros Organics. Formamidinium iodide (FAI) and 4-fluoro-phenethylammonium iodide (F-PEAI) were purchased from Greatcell Solar Materials. Methylammonium bromide (MABr) was obtained from Dyesol. C60 was obtained from Ossila. Poly[bis-(4-phenyl)-(2,4,6-trimethylphenyl)-amine] (PTAA, Mn = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900, Mw = 33
900, Mw = 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) was purchased from Xi’an Polymer Light Technology Corp (China).
000) was purchased from Xi’an Polymer Light Technology Corp (China).
Device fabrication
The patterned indium doped tin oxide (ITO) substrates (20 mm × 20 mm) from KINTEC were sequentially cleaned through Hellmanex III, deionized water, acetone, and 2-propanol for 10 min each followed by oxygen plasma (Diener Zepto, 100 W) for 10 min and then transferred to a N2-filled glovebox. The solution of mixture of Me-4PACz and MeO-2PACz (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (1 mmol mL−1 in total in ethanol) was deposited on ITO substrate at 3000 rpm for 30 s and then annealed at 100 °C for 10 min. Then the PTAA solution (0.5 mg ml−1 in toluene) was dropped on the substrates at 4000 rpm for 30 s and annealed at 100 °C for 10 min. The perovskite precursor solution (1.7 M for 1000 nm thick perovskite film) was prepared by dissolving 22.08 mg CsI, 28.5 mg MABr, 233.8 mg FAI, 190.5 mg PbBr2 and 559.5 mg PbI2 in 1 mL DMF
1) (1 mmol mL−1 in total in ethanol) was deposited on ITO substrate at 3000 rpm for 30 s and then annealed at 100 °C for 10 min. Then the PTAA solution (0.5 mg ml−1 in toluene) was dropped on the substrates at 4000 rpm for 30 s and annealed at 100 °C for 10 min. The perovskite precursor solution (1.7 M for 1000 nm thick perovskite film) was prepared by dissolving 22.08 mg CsI, 28.5 mg MABr, 233.8 mg FAI, 190.5 mg PbBr2 and 559.5 mg PbI2 in 1 mL DMF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO (3
DMSO (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol ratio) solvent. F-PEAI was added into the perovskite precursor solution for passivation (0.8 mg ml−1). The perovskite precursor solution was dropped on the substrates and spin coated at 2000 rpm for 40 s, then 5000 rpm for 4 s. 250 μL ethyl acetate was slightly dropped on the center of the substrate when the spin coating speed reached 5000 rpm. The film then was annealed on a hot plate at 100 °C for 20 min. Finally, 20 nm C60, 8 nm BCP and 80 nm Ag was deposited sequentially in a K. J. Lesker Mini Spectros System attached to the glovebox (<5 × 10−6 Pa) using a metal shadow mask. The cell area is 0.16 cm2.
1 vol ratio) solvent. F-PEAI was added into the perovskite precursor solution for passivation (0.8 mg ml−1). The perovskite precursor solution was dropped on the substrates and spin coated at 2000 rpm for 40 s, then 5000 rpm for 4 s. 250 μL ethyl acetate was slightly dropped on the center of the substrate when the spin coating speed reached 5000 rpm. The film then was annealed on a hot plate at 100 °C for 20 min. Finally, 20 nm C60, 8 nm BCP and 80 nm Ag was deposited sequentially in a K. J. Lesker Mini Spectros System attached to the glovebox (<5 × 10−6 Pa) using a metal shadow mask. The cell area is 0.16 cm2.
Transient photovoltage (TPV) measurements
A quote from ref. 46 is provided to describe the TPV measurements – “For the transient photovoltage measurements, we used a pulsed UV-solid-state laser (Coherent Flare NX, 343 nm, 1 ns pulse length, 0 to 2 kHz repetition rate, set to 100 Hz in our case). This radiation passes through an optical fibre and impinges at an angle of 30° on the sample surface. The illumination spot has an elliptical shape with a diameter of 3.8 mm. In addition, a solid-state laser with 532 nm (Coherent Sapphire SF) is used to provide the bias illumination. The resulting voltage transients are measured with an oscilloscope (LeCroy Waverunner HRO 66Zi 600 MHz analog bandwidth, 12 Bit analog to digital conversion).” The open-circuit condition was set using a 1 MΩ load resistance.
Intensity-modulated photovoltage spectroscopy (IMVS) measurements
IMVS measurements were made using a PAIOS system developed by Fluxim AG. These measurements were made at different open-circuit voltages by varying the light intensity of a white LED. The frequency range used for the measurements was 1–107 Hz. The AC light intensity perturbation was set to 10% of the DC light intensity.
Transient photoluminescence (tr-PL) measurements
The transient photoluminescence decay of the perovskite film was measured using a gated CCD recording setup. An intensified CCD camera (iStar DH720 from Andor Solis) was employed to detect the spectrally dispersed photoluminescence signals through a spectrometer (iHR 320 from Horiba Jobin Yvon). The excitation source, a 343 nm UV laser, was utilized with a repetition rate of 100 Hz. The diameter of the resulting spot was approximately 3.07 mm. The applied excitation fluence was approximately 0.9 μJ cm−2 and the sample was illuminated from the glass side.
Fast hysteresis measurements
The fast hysteresis measurements were obtained by using the measurement setup developed by FastChar UG. The setup automates the scan-rate dependent current–voltage measurement by applying a triangular voltage pulse to the cell, starting from 1.2 V to −0.1 V and then back to 1.2 V (reverse scan, followed by forward scan).
Drift-diffusion simulations
Drift-diffusion simulations were carried out using SETFOS developed by Fluxim AG.
Conclusions
Time domain small-perturbation techniques such as transient photovoltage (TPV) and transient photocurrent (TPC), and their frequency domain counterparts – intensity-modulated photovoltage spectroscopy (IMVS), intensity-modulated photocurrent spectroscopy (IMPS) and impedance spectroscopy (IS) are widely used for the characterization of perovskite solar cells (PSCs). However, the different analysis and representation methods for each technique make it difficult to reliably extract information and compare calculated parameters. This effect manifests itself in the case of the measured time constants, where time domain measurements naturally yield two time constants that correspond to the rise and subsequent decay of the photovoltage or photocurrent, while the corresponding frequency domain method yields only one time constant.
We solve this problem by defining a modified transfer function that focusses on the evolution of the real part of the transfer function versus frequency. Analysis of the modified transfer function shows an additional time constant at high frequencies that is invisible in the unmodified transfer function. From drift-diffusion simulations and analysis of an equivalent circuit, we find that this additional time constant corresponds to the rise time constant observed in the time domain measurements, while the time constant observed in the unmodified transfer function is the decay time constant. We further verify the validity of the transformation method by applying it to experimental IMVS data of perovskite solar cells, to obtain both the rise and decay time constants of the photovoltage. These time constants are similar in magnitude to those obtained from TPV measurements, showing the first equivalence between parameters obtained from time domain and frequency domain measurements for PSCs. This result confirms that the same information is contained in both time and frequency domain measurements, although in different forms. By combining the IMVS and TPV measurements on p–i–n devices with transient photoluminescence (tr-PL) measurements of the corresponding glass/ITO/HTL/perovskite/ETL stack, we identify the exchange lifetimes and recombination lifetimes at different open-circuit voltages. These lifetimes are used to calculate a figure of merit that quantifies the efficiency of charge extraction for the PSC. We determine this figure of merit to range between 0.7–0.95 for our devices, indicating that a significant electric field likely exists in the transport layers at applied voltages close to or at the one sun open-circuit voltage, that maximises the charge extraction efficiency.
Author contributions
Conceptualization: SR methodology: SR sample preparation: YW investigation: SR, LK, SJ, GY, YW visualization: SR, LK supervision: SR writing – original draft: SR writing – review & editing: SR, SJ, YW, LK.
Data availability
All data are available in the main text or in the ESI.† All simulation files are uploaded to the Zenodo database with the identifier https://doi.org/10.5281/zenodo.8004545.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG) through a Walter-Benjamin fellowship – project number 462572437, the Helmholtz association via the POF IV, the innovation platform SolarTap and the project ‘Beschleunigter Transfer der nächsten Generation von Solarzellen in die Massenfertigung - Zukunftstechnologie Tandem-Solarzellen’, Forschungszentrum Jülich via the HITEC graduate school.
Notes and references
- S. Wheeler, D. Bryant, J. Troughton, T. Kirchartz, T. Watson, J. Nelson and J. R. Durrant, J. Phys. Chem. C, 2017, 121, 13496–13506 CrossRef CAS.
- R. S. Sanchez, V. Gonzalez-Pedro, J.-W. Lee, N.-G. Park, Y. S. Kang, I. Mora-Sero and J. Bisquert, J. Phys. Chem. Lett., 2014, 5, 2357–2363 CrossRef CAS.
- D. Kiermasch, A. Baumann, M. Fischer, V. Dyakonov and K. Tvingstedt, Energy Environ. Sci., 2018, 11, 629–640 RSC.
- Z. S. Wang, F. Ebadi, B. Carlsen, W. C. Choy and W. Tress, Small Methods, 2020, 4, 2000290 CrossRef CAS.
- B. C. O'Regan, K. Bakker, J. Kroeze, H. Smit, P. Sommeling and J. R. Durrant, J. Phys. Chem. B, 2006, 110, 17155–17160 CrossRef PubMed.
- L. Krückemeier, Z. Liu, T. Kirchartz and U. Rau, Adv. Mater., 2023, 35, 2300872 CrossRef PubMed.
- A. Bou, H. ĀboliŅš, A. Ashoka, H. Cruanyes, A. Guerrero, F. Deschler and J. Bisquert, ACS Energy Lett., 2021, 6, 2248–2255 CrossRef CAS.
- J. S. Laird, S. Ravishankar, K. J. Rietwyk, W. Mao, U. Bach and T. A. Smith, Small Methods, 2022, 6, 2200493 CrossRef CAS.
- W. Peng, C. Aranda, O. M. Bakr, G. Garcia-Belmonte, J. Bisquert and A. Guerrero, ACS Energy Lett., 2018, 3, 1477–1481 CrossRef CAS.
- A. J. Riquelme, K. Valadez-Villalobos, P. P. Boix, G. Oskam, I. Mora-Seró and J. A. Anta, Phys. Chem. Chem. Phys., 2022, 24, 15657–15671 RSC.
- S. Ravishankar, C. Aranda, S. Sanchez, J. Bisquert, M. Saliba and G. Garcia-Belmonte, J. Phys. Chem. C, 2019, 123, 6444–6449 CrossRef CAS.
- A. O. Alvarez, S. Ravishankar and F. Fabregat-Santiago, Small Methods, 2021, 5, 2100661 CrossRef CAS.
- A. Guerrero, J. Bisquert and G. Garcia-Belmonte, Chem. Rev., 2021, 121, 14430–14484 CrossRef CAS.
- A. Todinova, J. Idígoras, M. Salado, S. Kazim and J. A. Anta, J. Phys. Chem. Lett., 2015, 6, 3923–3930 CrossRef CAS PubMed.
- A. Pockett, G. E. Eperon, T. Peltola, H. J. Snaith, A. Walker, L. M. Peter and P. J. Cameron, J. Phys. Chem. C, 2015, 119, 3456–3465 CrossRef CAS.
- B. Hailegnaw, N. S. Sariciftci and M. C. Scharber, Phys. Status Solidi A, 2020, 217, 2000291 CrossRef CAS.
- A. Riquelme, F. E. Gálvez, L. Contreras-Bernal, H. Míguez and J. A. Anta, J. Appl. Phys., 2020, 128, 133103 CrossRef CAS.
- O. Almora, M. García-Batlle and G. Garcia-Belmonte, J. Phys. Chem. Lett., 2019, 10, 3661–3669 CrossRef CAS.
- J. Bisquert and M. Janssen, J. Phys. Chem. Lett., 2021, 12, 7964–7971 CrossRef CAS.
- E. Ponomarev and L. Peter, J. Electroanal. Chem., 1995, 396, 219–226 CrossRef.
- E. Guillén, F. J. Ramos, J. A. Anta and S. Ahmad, J. Phys. Chem. C, 2014, 118, 22913–22922 CrossRef.
- I. Zarazua, G. Han, P. P. Boix, S. Mhaisalkar, F. Fabregat-Santiago, I. Mora-Seró, J. Bisquert and G. Garcia-Belmonte, J. Phys. Chem. Lett., 2016, 7, 5105–5113 CrossRef CAS PubMed.
- S. Sami, P. A. Haase, R. Alessandri, R. Broer and R. W. Havenith, J. Phys. Chem. A, 2018, 122, 3919–3926 CrossRef CAS.
- M. Sendner, P. K. Nayak, D. A. Egger, S. Beck, C. Müller, B. Epding, W. Kowalsky, L. Kronik, H. J. Snaith and A. Pucci, Mater. Horiz., 2016, 3, 613–620 RSC.
- Z. Liu, L. Krückemeier, B. Krogmeier, B. Klingebiel, J. A. Màrquez, S. Levcenko, S. Öz, S. Mathur, U. Rau, T. Unold and T. Kirchartz, ACS Energy Lett., 2019, 4, 110–117 CrossRef CAS.
- J. Maibach, E. Mankel, T. Mayer and W. Jaegermann, J. Mater. Chem. C, 2013, 1, 7635–7642 RSC.
- F. Staub, H. Hempel, J.-C. Hebig, J. Mock, U. W. Paetzold, U. Rau, T. Unold and T. Kirchartz, Phys. Rev. Appl., 2016, 6, 044017 CrossRef.
- L. Su, M. Méndez, J. Jiménez-López, M. Zhu, Y. Xiao and E. J. P. Gil, ChemPlusChem, 2021, 86, 1316–1321 CrossRef CAS PubMed.
- C. R. McNeill, I. Hwang and N. C. Greenham, J. Appl. Phys., 2009, 106, 024507 CrossRef.
- M. Neukom, S. Züfle, S. Jenatsch and B. Ruhstaller, Sci. Technol. Adv. Mater., 2018, 19, 291–316 CrossRef CAS.
- S. Ravishankar, Z. Liu, Y. Wang, T. Kirchartz and U. Rau, PRX Energy, 2023, 2, 033006 CrossRef.
- M. Cai, N. Ishida, X. Li, X. Yang, T. Noda, Y. Wu, F. Xie, H. Naito, D. Fujita and L. Han, Joule, 2018, 2, 296–306 CrossRef CAS.
- C. Stavrakas, G. Delport, A. A. Zhumekenov, M. Anaya, R. Chahbazian, O. M. Bakr, E. S. Barnard and S. D. Stranks, ACS Energy Lett., 2020, 5, 117–123 CrossRef CAS PubMed.
- L. M. Herz, ACS Energy Lett., 2017, 2, 1539–1548 CrossRef CAS.
- W. Shockley and W. Read Jr, Phys. Rev., 1952, 87, 835 CrossRef CAS.
- M. H. Futscher, J. M. Lee, L. McGovern, L. A. Muscarella, T. Wang, M. I. Haider, A. Fakharuddin, L. Schmidt-Mende and B. Ehrler, Mater. Horiz., 2019, 6, 1497–1503 RSC.
- R. A. Awni, Z. Song, C. Chen, C. Li, C. Wang, M. A. Razooqi, L. Chen, X. Wang, R. J. Ellingson and J. V. Li, Joule, 2020, 4, 644–657 CrossRef CAS.
- M. Azzouzi, P. Calado, A. M. Telford, F. Eisner, X. Hou, T. Kirchartz, P. R. F. Barnes and J. Nelson, Solar RRL, 2020, 4, 1900581 CrossRef CAS.
- D. Cardenas-Morcoso, A. Bou, S. Ravishankar, M. García-Tecedor, S. Gimenez and J. Bisquert, ACS Energy Lett., 2020, 5, 187–191 CrossRef CAS.
- A. Pockett, M. Spence, S. K. Thomas, D. Raptis, T. Watson and M. J. Carnie, Solar RRL, 2021, 5, 2100159 CrossRef CAS.
- L. J. Bennett, A. J. Riquelme, J. A. Anta, N. E. Courtier and G. Richardson, Phys. Rev. Appl., 2023, 19, 014061 CrossRef CAS.
- V. M. Le Corre, J. Diekmann, F. Peña-Camargo, J. Thiesbrummel, N. Tokmoldin, E. Gutierrez-Partida, K. P. Peters, L. Perdigón-Toro, M. H. Futscher, F. Lang, J. Warby, H. J. Snaith, D. Neher and M. Stolterfoht, Solar RRL, 2022, 6, 2100772 CrossRef CAS.
- J. Thiesbrummel, V. M. Le Corre, F. Peña-Camargo, L. Perdigón-Toro, F. Lang, F. Yang, M. Grischek, E. Gutierrez-Partida, J. Warby, M. D. Farrar, S. Mahesh, P. Caprioglio, S. Albrecht, D. Neher, H. J. Snaith and M. Stolterfoht, Adv. Energy Mater., 2021, 11, 2101447 CrossRef CAS.
- H. Wang, A. Guerrero, A. Bou, A. M. Al-Mayouf and J. Bisquert, Energy Environ. Sci., 2019, 12, 2054–2079 RSC.
- L. Krückemeier, B. Krogmeier, Z. Liu, U. Rau and T. Kirchartz, Adv. Energy Mater., 2021, 11, 2003489 CrossRef.
- L. Krückemeier, Z. Liu, B. Krogmeier, U. Rau and T. Kirchartz, Adv. Energy Mater., 2021, 11, 2102290 CrossRef.
- D. Grabowski, Z. Liu, G. Schöpe, U. Rau and T. Kirchartz, Solar RRL, 2022, 6, 2200507 CrossRef CAS.
- U. Rau, V. Huhn and B. E. Pieters, Phys. Rev. Appl., 2020, 14, 014046 CrossRef CAS.
- R. S. Crandall, J. Appl. Phys., 1983, 54, 7176–7186 CrossRef CAS.
-
Y. Yuan, G. Yan, C. Dreessen, M. Hülsbeck, B. Klingebiel, U. Rau and T. Kirchartz, Res. Sq. preprint, 2023, URL: https://assets.researchsquare.com/files/rs-2514593/v1/0398c512303ecfd5def49f7d.pdf?c=1674796116.
- Y. Wang, S. Akel, B. Klingebiel and T. Kirchartz, Adv. Energy Mater., 2023, 2302614 CrossRef.
- M. Stolterfoht, P. Caprioglio, C. M. Wolff, J. A. Márquez, J. Nordmann, S. Zhang, D. Rothhardt, U. Hörmann, Y. Amir and A. Redinger, Energy Environ. Sci., 2019, 12, 2778–2788 RSC.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Lennard
Kruppa
a,
Sandra
Jenatsch
*a,
Lennard
Kruppa
a,
Sandra
Jenatsch
 b,
Genghua
Yan
b,
Genghua
Yan
 a and
Yueming
Wang
a
a and
Yueming
Wang
a
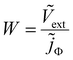
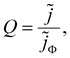
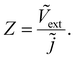


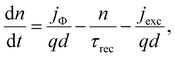







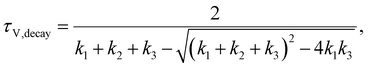






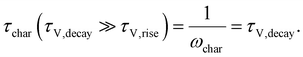



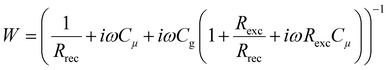








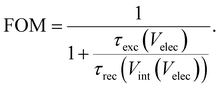
 where G(x) is the position-dependent photogeneration and fc(x) is the position-dependent collection efficiency in the absorber layer of thickness d. In case of constant photogeneration, we obtain
where G(x) is the position-dependent photogeneration and fc(x) is the position-dependent collection efficiency in the absorber layer of thickness d. In case of constant photogeneration, we obtain  where jgen = qdG is the total photogenerated current density in the absorber layer and fc,av is the average collection efficiency. In such situations, fc,av can be calculated from eqn (26) (assuming zero external series resistance) as
where jgen = qdG is the total photogenerated current density in the absorber layer and fc,av is the average collection efficiency. In such situations, fc,av can be calculated from eqn (26) (assuming zero external series resistance) as


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900, Mw = 33
900, Mw = 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) was purchased from Xi’an Polymer Light Technology Corp (China).
000) was purchased from Xi’an Polymer Light Technology Corp (China).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) (1 mmol mL−1 in total in ethanol) was deposited on ITO substrate at 3000 rpm for 30 s and then annealed at 100 °C for 10 min. Then the PTAA solution (0.5 mg ml−1 in toluene) was dropped on the substrates at 4000 rpm for 30 s and annealed at 100 °C for 10 min. The perovskite precursor solution (1.7 M for 1000 nm thick perovskite film) was prepared by dissolving 22.08 mg CsI, 28.5 mg MABr, 233.8 mg FAI, 190.5 mg PbBr2 and 559.5 mg PbI2 in 1 mL DMF
1) (1 mmol mL−1 in total in ethanol) was deposited on ITO substrate at 3000 rpm for 30 s and then annealed at 100 °C for 10 min. Then the PTAA solution (0.5 mg ml−1 in toluene) was dropped on the substrates at 4000 rpm for 30 s and annealed at 100 °C for 10 min. The perovskite precursor solution (1.7 M for 1000 nm thick perovskite film) was prepared by dissolving 22.08 mg CsI, 28.5 mg MABr, 233.8 mg FAI, 190.5 mg PbBr2 and 559.5 mg PbI2 in 1 mL DMF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO (3
DMSO (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol ratio) solvent. F-PEAI was added into the perovskite precursor solution for passivation (0.8 mg ml−1). The perovskite precursor solution was dropped on the substrates and spin coated at 2000 rpm for 40 s, then 5000 rpm for 4 s. 250 μL ethyl acetate was slightly dropped on the center of the substrate when the spin coating speed reached 5000 rpm. The film then was annealed on a hot plate at 100 °C for 20 min. Finally, 20 nm C60, 8 nm BCP and 80 nm Ag was deposited sequentially in a K. J. Lesker Mini Spectros System attached to the glovebox (<5 × 10−6 Pa) using a metal shadow mask. The cell area is 0.16 cm2.
1 vol ratio) solvent. F-PEAI was added into the perovskite precursor solution for passivation (0.8 mg ml−1). The perovskite precursor solution was dropped on the substrates and spin coated at 2000 rpm for 40 s, then 5000 rpm for 4 s. 250 μL ethyl acetate was slightly dropped on the center of the substrate when the spin coating speed reached 5000 rpm. The film then was annealed on a hot plate at 100 °C for 20 min. Finally, 20 nm C60, 8 nm BCP and 80 nm Ag was deposited sequentially in a K. J. Lesker Mini Spectros System attached to the glovebox (<5 × 10−6 Pa) using a metal shadow mask. The cell area is 0.16 cm2.
