Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modulating quantum tunnelling of magnetization in Dy isotopologue dimers†
Ting-Ting
Ruan
a,
Eufemio
Moreno-Pineda
 *bcd,
Sagar
Paul
*bcd,
Sagar
Paul
 d,
Michael
Schulze
d,
Sören
Schlittenhardt
d,
Michael
Schulze
d,
Sören
Schlittenhardt
 a,
Asato
Mizuno
a,
Asato
Mizuno
 e,
Wolfgang
Wernsdorfer
e,
Wolfgang
Wernsdorfer
 *d and
Mario
Ruben
*d and
Mario
Ruben
 *afg
*afg
aInstitute of Nanotechnology (INT), Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, D-76344, Eggenstein-Leopoldshafen, Germany. E-mail: mario.ruben@kit.edu
bUniversidad de Panamá, Facultad de Ciencias Naturales, Exactas y Tecnología, Depto. de Química-Física, Panamá, 0824, Panamá. E-mail: eufemio.moreno@up.ac.pa
cUniversidad de Panamá, Facultad de Ciencias Naturales, Exactas y Tecnología, Grupo de Investigación de Materiales, Panamá, 0824, Panamá
dPhysikalisches Institut, Karlsruhe Institute of Technology (KIT), Engesserstraße 15, D-76131, Karlsruhe, Germany. E-mail: wolfgang.wernsdorfer@kit.edu
eDivision of Chemistry, Department of Materials Engineering Science, Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560-8531, Japan
fInstitute of Quantum Materials and Technologies (IQMT), Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, D-76344, Eggenstein-Leopoldshafen, Germany
gCentre Européen de Sciences Quantiques (CESQ), Institutde Science et d'Ingénierie Supramoléculaires (ISIS), 8 allée Gaspard Monge, BP 70028, 67083, Strasbourg Cedex, France
First published on 1st October 2024
Abstract
Qudits are anticipated to streamline quantum computation by minimizing iterations, lowering error rates, and facilitating error correction. It has been shown that Dy(III)-based molecular systems can act as qudits with expanded Hilbert spaces. Achieving a robust intramolecular interaction, whether exchange or dipolar, is crucial for spanning the Hilbert space of qudits; hence, short Dy(III)⋯Dy(III) distances are required. Looking for multilevel systems that can be employed as qudits, we have synthesized and characterized two dysprosium-based isotopologues: [163Dy2(BTFA)4(PHZP)2]0 (1(I=5/2)) and [164Dy2(BTFA)4(PHZP)2]0 (2(I=0)), where BTFA = 3-benzoyl-1,1,1-trifluoroacetone and PHZP = N′-[(E)-(pyrazin-2-yl)methylidene]pyrazine-2-carbohydrazonate. Both complexes showed slow magnetic relaxation at zero applied magnetic field. μSQUID investigations, at milli-Kelvin temperatures, and direct and alternating current magnetic measurements reveal distinctions in the magnetic behavior between the two complexes and an operative interaction between the Dy(III) centers. We find that the presence or absence of the nuclear spin plays a minor role in the magnetic properties above 2 K. On the contrary, at milli-Kelvin temperatures, μSQUID studies show enhanced relaxation in 1(I=5/2), attributed to several quantum tunnelling pathways enabled by hyperfine and quadrupole interactions. The interplay between the antiferromagnetic coupling and enhanced relaxation indicates that the exchange coupling influences the relaxation mechanisms at different temperature ranges.
Introduction
The study of Single-Molecule Magnets (SMMs) has witnessed significant advancements in recent decades, driven by the quantum nature of their magnetic properties and their potential applications in quantum computing1–4 and spintronics.5–7 Lanthanides, such as Dy(III), Tb(III), Ho(III), and Er(III), have particularly gained prominence due to their substantial magnetic anisotropy and large magnetic moment.8–12 Additionally, lanthanide-based SMMs (Ln-SMMs) have been suggested as frameworks for Quantum Information Processing (QIP) schemes,13–17 functioning as quantum bits (qubits) or qudits. This proposition was validated by implementing a quantum algorithm,18 in a single molecular unit from the prototypical [TbPc2]0 SMM, incorporated within a hybrid spintronic structure.13,15,19The magnetization dynamics of Ln-SMMs result in magnetic bistability, which is essential for their potential applications. The factors influencing the magnetization dynamics of SMMs are complex, with the magnetic anisotropy of the spin carriers and their interactions being the most important parameters. Typically, the intrinsic nature of the f-electrons, shielded by the outer shell electrons, is responsible for the weak magnetic interactions between the lanthanide centers. However, interactions and anisotropy have been shown to influence the relaxation dynamics of multinuclear lanthanide SMMs.20–26
Upon reviewing the literature related to SMMs, we were prompted to focus more on systems wherein magnetic units are linked through bridging ligands to form high-dimensional frameworks.27 In such molecules, the selection of organic moieties (ligands) is meticulous, aiming to adjust the physical properties of the resulting compounds.28–30 Our research team has successfully synthesized two dinuclear dysprosium SMMs with isotopic enrichment, using a highly π-conjugated polyheteroaromatic molecule as a bridging ligand.23 The findings presented in the study demonstrated that the strength of the intramolecular interaction (exchange or dipolar) is a crucial factor for spanning the Hilbert space of qudits, foreseeing a preference for shorter Dy(III)⋯Dy(III) configurations.23
The group of ligands based on 1,2,4,5-tetrazine31–34 is noteworthy in coordination chemistry due to their easy functionalization and redox activity, which can augment magnetic communication among metal ions.35–38 In this context, the ligand 3,6-dipyrazin-2-yl-1,2,4,5-tetrazine (BPTZ) emerges as an appealing choice. By introducing isotopically enriched 163Dy(III) and 164Dy(III), we attempted the syntheses of BPTZ-based Dy(III) complexes. To our surprise, instead of obtaining two BPTZ-containing compounds, we discovered the creation of two distinct isotopologues: [163Dy2(BTFA)4(PHZP)2]0 (1(I=5/2)) and [164Dy2(BTFA)4(PHZP)2]0 (2(I=0)). The BPTZ ligand was found to have been transformed into a new ligand, N′-[(E)-pyrazin-2-yl)methylidene]pyrazine-2-carbohydrazonate (PHZP), as illustrated in Scheme 1. The two complexes showed SMM characteristics at zero applied magnetic field. We investigate the impact of the metal–metal distance on the intramolecular interaction as well as the effect of the nuclear spins on the dynamic properties of two dinuclear Dy(III)-SMMs through studies involving AC magnetic susceptibility and single crystal μSQUID data conducted at sub-Kelvin temperatures. We find similar relaxation behaviors down to 2 K temperature for both systems, which is a direct consequence of the short Dy(III)⋯Dy(III) distance-enhancing the intramolecular interaction (exchange or dipolar). However, low-temperature μSQUIDs investigations of the magnetization reversal reveal significant differences in the relaxation mechanism between the two isotopologues (I = 0, 5/2).
Results and discussion
Syntheses and structures
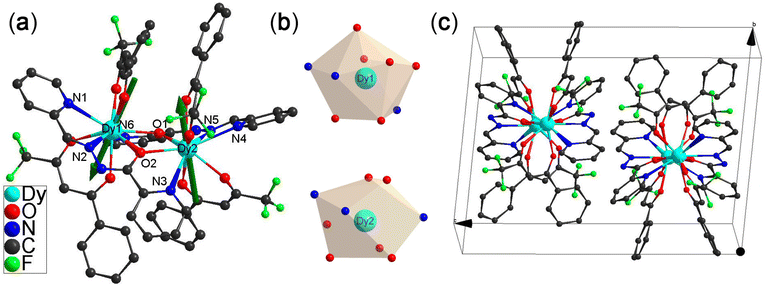
Complexes 1(I=5/2) and 2(I=0) were obtained by reacting one equivalent of ligand BPTZ with two equivalents of Ln(BTFA)3(H2O)2 precursor, in which Ln = 163Dy(III) (I = 5/2) for 1(I=5/2) and 164Dy(III) (I = 0) for 2(I=0), respectively (see ESI† for details). Crystals of 1(I=5/2) and 2(I=0), suitable for single crystal X-ray studies, were grown from a mixture of ethanol and dichloromethane. X-ray single crystal studies reveal both complexes to be isomorphic, crystallizing in the triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group with two symmetry-related molecules residing in the unit cell (Fig. 1c).
space group with two symmetry-related molecules residing in the unit cell (Fig. 1c).
The ligand BPTZ is highly susceptible to nucleophilic attack by OH−, causing the opening of the tetrazine ring and generating the asymmetrical N′-[(E)-pyrazin-2-yl)methylidene]pyrazine-2-carbohydrazonate (PHZP) ligand (Scheme 1).39–41 Both Dy(III) ions are bridged by two PHZP ligands. Each Dy(III) coordinates in a tridentate chelating mode (N1, N2, and O2) with one of the ligands and a bidentate mode with the second ligand (O1 and N6). Two BTFA units complete the coordination sphere, forming a N3O6 nine-coordinated environment around each metal center (Fig. 1a). The Dy–O and Dy–N bond lengths are in the range of 2.325(3)–2.460(3) Å and 2.497(3)–2.721(3) Å for 1(I=5/2) and 2.325(2)–2.460(2) Å and 2.485(3)–2.712(3) Å for 2(I=0), respectively. The amide oxygen atoms (O1 and O2) within the PHZP ligands form bonds in the deprotonated imidic acid mode (O−), acting as bridges between the two Dy(III) ions and resulting in the formation of a Dy2O2 quadrilateral geometry. The Dy1–O–Dy2 angles are 115.7° for 1(I=5/2) and 2(I=0). The intramolecular Dy⋯Dy distance for 1(I=5/2) and 2(I=0) is 4.065(5) Å and 4.064(3) Å, respectively. Analysis of the degree of distortion of the coordination environment of the lanthanides is performed using SHAPE,42 resulting in different N3O6 environments for Dy1 and Dy2 for 1(I=5/2) and 2(I=0) (Table S2†). The nine-coordinated Dy1 ions in both 1(I=5/2) and 2(I=0) represent a spherical tricapped trigonal prism motif with the same D3h symmetry, and the continuous shape measure (CShM) values are determined to be 1.885 and 1.858, respectively. Dy2 in 1(I=5/2) and 2(I=0) ions represent the uniform Muffin arrangement with the same Cs symmetry, and the continuous shape measure (CShM) values are determined to be 2.253 and 2.250, respectively (Fig. 1b).
The purity of the phases in the polycrystalline samples of 1(I=5/2) and 2(I=0) was assessed through powder X-ray diffraction (PXRD) analysis. The observed PXRD patterns for both 1(I=5/2) and 2(I=0) demonstrated good agreement with the simulated patterns (Fig. S2†), indicating that both samples consist of a single crystalline phase.
Magnetic properties
The magnetization-field curves (M(H)) for both complexes were also examined within the magnetic field range of 0 to 7 T and a temperature range of 2 to 5 K, revealing a swift rise at low magnetic fields, as depicted in the insets of Fig. 2. At high magnetic fields, the magnetization shows near horizontal behaviour, with recorded values of 10.1μB for 1(I=5/2) and 10.4μB for 2(I=0), at 7 T. These M(H) values closely align with the anticipated values for two Dy(III) ions featuring a well-defined J = 15/2 ground doublet, approximately ∼10μB.
 , which slowly shifts towards higher frequencies with increasing temperature up to 8 K. Employing a generalized Debye model, the symmetric semicircle Cole–Cole data are fitted between 2 and 6.8 K (Fig. S4 and S4†). This fitting process allows for the extraction of relaxation times (τ) and the distribution of relaxation times (α values): 0.05(3) < α < 0.18(4) for 1(I=5/2), 0.04(3) < α < 0.14(6) for 2(I=0), tending to be larger at lower temperatures (Fig. S3 and S4†). This observation suggests a relatively narrow distribution of relaxation times for 1(I=5/2) and 2(I=0). The temperature dependence of the relaxation times (τ(T)) is practically equal for both complexes (see Fig. 3b, d, S6 and S7†) and can be effectively fitted using the following eqn (1):
, which slowly shifts towards higher frequencies with increasing temperature up to 8 K. Employing a generalized Debye model, the symmetric semicircle Cole–Cole data are fitted between 2 and 6.8 K (Fig. S4 and S4†). This fitting process allows for the extraction of relaxation times (τ) and the distribution of relaxation times (α values): 0.05(3) < α < 0.18(4) for 1(I=5/2), 0.04(3) < α < 0.14(6) for 2(I=0), tending to be larger at lower temperatures (Fig. S3 and S4†). This observation suggests a relatively narrow distribution of relaxation times for 1(I=5/2) and 2(I=0). The temperature dependence of the relaxation times (τ(T)) is practically equal for both complexes (see Fig. 3b, d, S6 and S7†) and can be effectively fitted using the following eqn (1):τ−1 = τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/kBT) + CTn + τQTM−1 exp(−Ueff/kBT) + CTn + τQTM−1 | (1) |
 profiles, the relaxation parameters are nearly identical. Note that the n parameter of the Raman process was found to be small.45,46 Low Raman n parameters have been ascribed to low vibrational modes,47 which can be better described by the sum of contributions arising from phonon modes, with the second term in (1) being replaced by:
profiles, the relaxation parameters are nearly identical. Note that the n parameter of the Raman process was found to be small.45,46 Low Raman n parameters have been ascribed to low vibrational modes,47 which can be better described by the sum of contributions arising from phonon modes, with the second term in (1) being replaced by: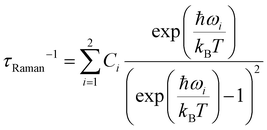 | (2) |
 | ||
Fig. 3 Experimental frequency-dependent magnetic susceptibility data at zero applied DC (HDC) field and variable temperatures  for (a) 1(I=5/2) and (b) 2(I=0); (c) temperature dependence of the magnetic relaxation time τ(T) under zero field for 1(I=5/2) (pale blue) and 2(I=0) (light orange). The solid red lines in panels are the best fit to eqn (1) with the second term being that given in eqn (2), consisting of the Orbach and Raman relaxation processes, while the dashed and dashed-dotted lines are the decomposition for each process. for (a) 1(I=5/2) and (b) 2(I=0); (c) temperature dependence of the magnetic relaxation time τ(T) under zero field for 1(I=5/2) (pale blue) and 2(I=0) (light orange). The solid red lines in panels are the best fit to eqn (1) with the second term being that given in eqn (2), consisting of the Orbach and Raman relaxation processes, while the dashed and dashed-dotted lines are the decomposition for each process. | ||
In (2) the ωi describe the active vibrational modes. The best fit requires the inclusion of a single vibrational mode, yielding Ueff = 29.9(7) K (20.8(5) cm−1), τ0 = 1.4(1) × 10−6 s, C1 = 1497(783) s−1, ω1 = 3.8(9) cm−1, τQTM = 9.8(2) × 10−4 s, R2 = 1.9 × 10−4 for 1(I=5/2), and Ueff = 30.1(1) K (20.9(6) cm−1), τ0 = 1.5(2) × 10−5 s, C1 = 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542(1064) s−1, ω1 = 6.4(4) cm−1, τQTM = 9.0(6) × 10−4 s, R2 = 1.8 × 10−4 (Fig. 3b and d). The ωi are found to be low, as expected for molecular systems.45,48,49
542(1064) s−1, ω1 = 6.4(4) cm−1, τQTM = 9.0(6) × 10−4 s, R2 = 1.8 × 10−4 (Fig. 3b and d). The ωi are found to be low, as expected for molecular systems.45,48,49
The hysteresis loops are a common feature for two Ising-like spins that are antiferromagnetically coupled: around zero field, they exhibit an S-shaped curve with two tunnel steps at positive and negative fields.44,58,59 The presence of S-shaped loops and the observation of the tunnel steps for μ0Hz < ±0.2 T suggest the existence of two antiferromagnetically coupled Dy(III) ions within the system. The occurrence of these steps is attributed to the transition from parallel (ferromagnetic) to antiparallel (antiferromagnetic) alignment of the Dy(III) anisotropic moments. An additional step is observed at zero field, which corresponds to the pinning of some molecules to the ferromagnetic state.44,60,61 Upon comparing the hysteresis curves for 1(I=5/2) and 2(I=0), it is apparent that the nuclear spin-bearing system results in narrower loops, signifying a more effective relaxation mechanism, as previously observed.44
The before-mentioned results showcase that for temperatures above 2 K, both relaxation mechanisms are not affected by the presence or absence of nuclear spins, while notable differences are visible at sub-Kelvin temperatures. The CASSCF obtained single-ion electronic characteristics show that relaxation is viable through the first excited state. However, although the magnetic anisotropy in Ln-SMMs complexes typically arises from individual Dy(III) ions, the slow relaxation dynamics of the complexes are notably impacted by interactions between Dy–Dy pairs, hence, the description of the relaxation must be that of dimeric species. To assess the interactions operating between the Dy(III) pairs, the χMT(T) and M(H) were simultaneously fitted using the Lines model69 as implemented in PHI.70 The Lines model, employs an isotropic exchange between the spin component of the angular momenta of the Dy(III) ions (S = 5/2). A Hamiltonian of the following form was employed:
 | (3) |
 is the ligand field Hamiltonian expressed as Steven's operators (Oqk), and Bqk are the ligand field parameters obtained from CASSCF. ĴLn, ŜLn and gJ are the spin–orbit, spin-only state and Landé g-factor for Dy(III), respectively. The best simultaneous fits for 1(I=5/2) and 2(I=0) yields: JLines = +0.141(1) K (+0.098(1) cm−1) for 1(I=5/2) and +0.178(1) K (+0.124(1) cm−1) for 2(I=0). The Lines exchange fitted parameters can be projected onto the total spin of the Dy(III) ion, i.e., (J = 15/2) leading to JLines(J = 15/2) = +16 mK (+0.01 cm−1) for 1(I=5/2) and +20 mK (+0.014 cm−1) for 2(I=0).
is the ligand field Hamiltonian expressed as Steven's operators (Oqk), and Bqk are the ligand field parameters obtained from CASSCF. ĴLn, ŜLn and gJ are the spin–orbit, spin-only state and Landé g-factor for Dy(III), respectively. The best simultaneous fits for 1(I=5/2) and 2(I=0) yields: JLines = +0.141(1) K (+0.098(1) cm−1) for 1(I=5/2) and +0.178(1) K (+0.124(1) cm−1) for 2(I=0). The Lines exchange fitted parameters can be projected onto the total spin of the Dy(III) ion, i.e., (J = 15/2) leading to JLines(J = 15/2) = +16 mK (+0.01 cm−1) for 1(I=5/2) and +20 mK (+0.014 cm−1) for 2(I=0).
Furthermore, the μSQUID loops reveal the exchange field (Hex), with Hex = JtotalmJ/gJμβ, where mJ = 15/2, gJ = 4/3 and μβ is the Bohr magneton, which allows the extraction of the exchange interaction by identifying the inflexion points in the hysteresis loops. The derivative of the temperature-dependent hysteresis loops (Fig. 5) shows a tunnelling event occurring at ±0.130 T in 2(I=0), whereas, for 1(I=5/2), tunnelling is spread out over a ±0.200 T range. The total (exchange + dipolar) coupling can be estimated by examining the tunnelling event that occurs at ±0.130 T in 2(I=0), resulting in Jtotal = +15.5 mK (+0.011 cm−1). This value is very close to the strongest component of the dipolar matrix (i.e., Jdipzz = +14 mK (+0.01 cm−1)) for a 164Dy⋯164Dy distance of 4.064(3) Å (see ESI section 1.5†) and to the JLines, all projected onto a J = 15/2 state, hence the interaction in the isotopologues is mainly dipolar.
 | ||
| Fig. 5 Zeeman diagram obtained (top) and derivative of the temperature-dependent hysteresis loops from μSQUID studies (bottom) for (a) 2(I=0) and (b) 1(I=5/2). | ||
Based on the Lines model, it is readily visible that the SMM character in 1(I=5/2) and 2(I=0) arises from the thermal population of the first excited state lying at ∼2 K above the ground state. In this scenario, relaxation occurs between the first excited coupled states and the second coupled excited state (at ∼90 K) via the Orbach mechanism (Table S15†). Note that experimentally obtained barriers are smaller than the separation gap between these two states, hence, the Raman process and QTM play a role (see Fig. 3b and d). At temperatures above 2 K, the relaxation dynamic is dominated by the strong exchange interaction operating between the Dy(III) ions, which shifts to relatively high fields (±0.130 T) the commonly occurring [at zero field] QTM.
Nevertheless, at very low temperatures the situation is different, as evidenced by the μSQUID loops. Below 2 K, the thermally mediated mechanisms are less efficient, and QTM becomes predominant. By understanding the magnetic characteristics at lower energy levels for 1(I=5/2) and 2(I=0), one can elucidate the specific impact of the presence or absence of nuclear spins in both complexes. The large Hilbert space of the isotopologues here studied and the number of parameters involved, e.g., Ligand Field Parameters, g-values, Euler angles, nuclear spins and exchange interaction, a J = 15/2 makes the rationalization of the sub-Kelvin temperature data computationally expensive. Hence, to bypass this problem, the spin effective formalism (Seff = ½) is invoked, with pure axial g-tensors i.e., gxx = gyy = 0; gzz = 20 and the Euler angles for each Dy(III) ion obtained from the CASSCCF calculations. Nonetheless, Seff = ½, at first order, mixed strongly by transverse fields, prompting huge tunnelling splitting not representative mJ = ±15/2 states, thus, we employ a fictitious S = 3/2 systems with an arbitrarily large Zero Field Splitting (D) parameter D = −100 cm−1. The g-values were maintained isotropic (gxx = gyy = gzz = 20/3) since the anisotropy is projected on the ZFS, while the anisotropy of the D term was rotated employing the Euler angles obtained from CASSCF.
To initiate our low-temperature analysis, we first concentrate on the magnetic properties of the nuclear spin-free 2(I=0) system, for simplicity. The CASSCF results indicate that the single ion magnetic properties of the isotopologues are dominated by the spin–orbit coupling and the interaction with the ligands, yielding a large separation between the ground mJ = ±15/2 and the first excited multiplet. This allows us to define the complex as two isolated Ising spins coupled through an effective interaction Jtotal(Ŝ1·Ŝ2), where Jtotal is an effective coupling and Ŝ1·Ŝ2, are effective spin for each Dy(III). Hence, in the presence of an external magnetic field applied along the easy axis, the Hamiltonian for 2(I=0) is defined as:
 | (4) |
The first term in (4) is the Zeeman term, the second one being the exchange interaction and the last one being the zero-field splitting. geff = 20/3 and Jtotal is the interaction between the ions (projected on a S = 3/2 basis). The non-colinear nature of the easy axes of the system is also taken into consideration by employing the Euler rotations [in Z–Y′–Z′′ convention], as obtained from the CASSCF results (see ESI section 1.5†).
A crossing between the ground and the first excited state occurs at ±0.121 T when setting Jtotal = +15.5 mK (+0.011 cm−1) as derived previously from the μSQUID exchange field. Refinement of the interaction to the crossing point at ±0.130 T yields Jtotal = 16.7 mK (+0.012 cm−1). The difference between the Jtotal obtained from μSQUID studies and the values obtained by fitting the Zeeman diagram to the level crossing at ±0.130 T arise from the non-collinearity between the anisotropy axes of the Dy(III) ions.
Without an interaction operating between the Dy(III) ions, QTM would be active at zero field, as observed for most SMMs, with relaxation occurring also through the first excited state (vide supra). In contrast, the presence of an exchange interaction causes the zero-field crossing to shift towards larger fields (Fig. 5a). Furthermore, the interaction decreases the tunnelling transition probability within the ground doublet and the first excited coupled state since it would involve a double spin–flip process. Hence, for a field sweep from −0.5 T to +0.5 T the following processes occur: (i) at μ0Hz = −0.5 T (with the field chosen along the easy axis of the Dy(III) ions) the sample is polarized and all the spins are in the ground state |−15/2, −15/2〉; (ii) as the magnetic field is swept from negative to the positive field, the molecules remain in the ground state until the external field compensates for the bias field and the spins make a transition from the ferromagnetic to the antiferromagnetic order by QTM. Notice that |±15/2, ∓15/2〉 state is split in two due to the non-colinear arrangement of the easy axes, hence the crossings occur at μ0Hr ∼ −0.110 T and −0.130 T; (iii) the next crossing occurs at zero-field, where some of the spins that remain pinned to the ferromagnetic excited state can tunnel via the antiferromagnetic excited state |±15/2, ∓15/2〉; and (iv) the last transition happens at μ0Hr ∼ +0.120 T where the molecules relax non-adiabatically from the state |±15/2, ∓15/2〉 to |+15/2, +15/2〉. As observed, in the case of 2(I=0), QTM occurs at the three intersections between the ground singlet and the excited doublet (∼±0.130 T), with the strongest transition occurring at the zero-field crossing.
Additionally, it must be noted that the M(H) curves (at 30 mK) for 2(I=0) (Fig. 4c) exhibit thermal relaxation in addition to QTM, observed as a slow change in magnetization, clearly visible at faster sweep rates. In fact, in this case, thermal relaxation and QTM compete at such temperatures dramatically. While ramping the field from negative saturation towards positive saturation, a large population remains in the ferromagnetic state |−15/2, −15/2〉 due to a small QTM gap at the crossings with |±15/2, ∓15/2〉 at −0.120 T (see Fig. 5a). For faster sweep rates, a large fraction of this population remains pinned to |−15/2, −15/2〉 even after crossing zero field, due to a small QTM gap between states |−15/2, −15/2〉 and |+15/2, +15/2〉. Next, due to the direct relaxation events following the QTM event between states |±15/2, ∓15/2〉 and |+15/2, +15/2〉 around +0.110 T (possibly increasing the spin temperature), the thermal relaxation for the leftover population from the state |−15/2, −15/2〉 is triggered causing an avalanche of relaxation eventually to |+15/2, +15/2〉. This results in a large derivative for fast sweep rates at +0.110 T (see star in Fig. 5a). For slow sweep rates, this specific peak is smaller since most of the population could tunnel from |−15/2, −15/2〉 to |+15/2, +15/2〉 at zero field. Hence, the change in magnetization at +0.110 T is mainly due to QTM between states |±15/2, ∓15/2〉 to |+15/2, +15/2〉 and not enhanced by an avalanche of relaxation from the state |−15/2, −15/2〉. Eventually, a pure thermal relaxation event between states |±15/2, ∓15/2〉 to |+15/2, +15/2〉 is observed, which shifts towards higher fields for slower sweep rates, as evidenced by the last peak near positive saturation in Fig. 5a moving towards +0.3 T for slower sweep rates.60
In contrast, the M(H) curve (at 30 mK) for 1(I=5/2) in Fig. 4a exhibits fast transitions at the crossing fields, as the curves at different sweep rates fall on top of each other indicating QTM-dominated transitions. The different relaxation behavior between Fig. 4a and c is attributed to the presence of nuclear spin in the latter and is discussed next. The four previously discussed processes [(i) to (iv)] also occur in 1(I=5/2). Contrary, however, 1(I=5/2) bears a nuclear spin capable of inducing hyperfine-QTM. The presence of a nuclear spin in 1(I=5/2) changes the form of the Hamiltonian, which now incorporates the hyperfine (Ahyp) and quadrupolar (Pquad) interactions as follows:
 | (5) |
The Zeeman diagram for 1(I=5/2), as shown in Fig. 5b, was obtained by fixing Jtotal as for 2(I=0), while the hyperfine and quadrupolar interactions were fixed to Ahyp = 107.1 mK (0.074 cm−1) [projected from an mJ = 15/2 to a S = 3/2 basis] and Pquad = 19.6 mK (0.014 cm−1).
As depicted in Fig. 5b, in addition to the interaction between the Dy(III) centers, the Zeeman diagram shows (2I + 1)n hyperfine states with numerous crossings over a wider field range than for 2(I=0). Mainly at the crossings that conserve nuclear spin (i.e. ΔmI = 0), hyperfine-QTM is active, facilitating the relaxation of the system at a larger field span or causing the QTM occurrence to shift from ±0.130 T to various field values. This is evidenced in the much stronger hf-QTM shown at the ±0.130 T crossing compared to the crossing at zero field. Another effect that can enhance QTM further in such systems is the non-axial arrangement of the quadrupole tensor. For simplicity, the quadrupole interaction axis is assumed to be aligned with the ligand field axis and the interaction is uniaxial. However, generally, this axis can be tilted from the ligand field easy-axis. Moreover, the quadrupole term can be expandable to axial and non-axial terms.71 Together with the inter ionic couplings, the exact quadrupole terms introduce transverse interactions in the spin Hamiltonian, which can explain QTM gap openings at crossings between the hyperfine states without conserving nuclear spin, i.e. ΔmI ≠ 0. This yields further positions in the field for QTM events.71 In our system, due to the larger field range/a greater number of positions in which hf-QTM is active, the electronic spins can tunnel with higher probabilities. Hence, a smaller number of spins remain pinned to the ferromagnetic excited state, causing a smaller number of spins to tunnel at the zero-field crossing occurring in the ferromagnetic excited state (see smaller derivative at zero field in Fig. 5b).
Conclusions
Utilizing a 1,2,4,5-tetrazine-based ligand, we have successfully synthesized and characterized two isotopologues of dinuclear dysprosium complexes, featuring the 163/164Dy isotopes. Both complexes exhibit an antiferromagnetic interaction between the lanthanide ions. Computational methods, as well as AC and μSQUID data, provide validation for the observed experimental behavior. Our results evidenced that a suitable exchange interaction can render both isotopologues high-temperature (>2 K) magnetic characteristics alike, and solely by performing sub-Kelvin studies the differences due to nuclear spin can be unraveled. Due to the intra-molecular coupling and small QTM gaps between the states, the Dy dimer isotopologue without nuclear spin shows a dramatic competition between thermal and QTM pathways of relaxation at 30 mK temperature. On the other hand, enhanced QTM is evident for the isotopologue with nuclear spin, attributed to many QTM pathways available by the hyperfine and nuclear quadrupole interactions. This phenomenon, as also observed previously in other similar systems,40 can be utilized to enforce a purely antiferromagnetic (for Ising dimers) and cyclic/toroidal (for Ising trimers) ground state at low temperature without the need to enhance interionic coupling. While the observed slow magnetic relaxation primarily stems from single-ion relaxation, the results indicate that the exchange coupling between the lanthanide ions influences the relaxation mechanism at different temperature ranges. Albeit the coupling between the lanthanide ions remains modest, investigating analogous dinuclear systems becomes crucial for understanding the effect and strength of the interaction into the relaxation characteristics of SMMs.Data availability
The data supporting this article has been included as part of the ESI.†All the magnetic data was processed employing Origin Pro 2023. The Debye analysis and relaxation fits were also performed using Origin Pro 2023, while the χMT susceptibility data was fitted employing PHI (J. Comput. Chem., 2013, 34, 1164–1175). The Zeeman diagrams of the angular dependence of the μSQUID studies were obtained using Easyspin implemented in MATLAB (J. Magn. Reson., 2006, 178(1), 42–55).
Full crystallographic details can be found in CIF format: in the Cambridge Crystallographic Data Centre database (CCDC 2337590 and 2337589).†
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
We acknowledge the DFG-CCR 1573 “4f for future” (project B3) and the Karlsruhe Nano Micro Facility (KNMF, https://www.kit.edu/knmf) for the provision of access to instruments at their laboratories. T. T. R. acknowledges the China Scholarship Council (No. 201806650008). A. M. acknowledges the Alexander von Humboldt (AvH) Foundation for a postdoctoral fellowship, a Grant-in-Aid for the JSPS Research Fellowship program, and the financial support by JSPS KAKENHI Grant Numbers JP22KJ3097 and JP23K13723. W. W. thanks the German Research Foundation (DFG) concerning the Gottfried Wilhelm Leibniz-Award, ZVN-2020_WE 4458-5. E. M.-P. thanks the Alexander von Humboldt fellowship for experienced researchers for support.References
- M. N. Leuenberger and D. Loss, Nature, 2001, 410(6830), 789–793 CrossRef CAS PubMed.
- D. Aravena and E. Ruiz, Dalton Trans., 2020, 49, 9916–9928 RSC.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS.
- G. Gabarro-Riera, G. Aromi and E. C. Sanudo, Coord. Chem. Rev., 2023, 475, 214858 CrossRef CAS.
- F. Paschke, T. Birk, V. Enenkel, F. Liu, V. Romankov, J. Dreiser, A. A. Popov and M. Fonin, Adv. Mater., 2021, 33, e2102844 CrossRef.
- F. Paschke, T. Birk, V. Enenkel, F. Liu, V. Romankov, J. Dreiser, A. A. Popov and M. Fonin, Adv. Mater., 2021, 33, 2102844 CrossRef CAS.
- W. J. Xu, Q. C. Luo, Z. H. Li, Y. Q. Zhai and Y. Z. Zheng, Adv. Sci., 2024, 11, e2308548 CrossRef.
- L. E. Darago, M. D. Boshart, B. D. Nguyen, E. Perlt, J. W. Ziller, W. W. Lukens, F. Furche, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2021, 143, 8465–8475 CrossRef CAS PubMed.
- D. A. Galico, E. M. Rodrigues, I. Halimi, J. Toivola, H. Zhao, J. Xu, J. O. Moilanen, X. Liu, E. Hemmer and M. Murugesu, Nat. Commun., 2024, 15, 3498 CrossRef CAS PubMed.
- D. Reta, J. G. Kragskow and N. F. Chilton, J. Am. Chem. Soc., 2021, 143, 5943–5950 CrossRef CAS PubMed.
- A. H. Vincent, Y. L. Whyatt, N. F. Chilton and J. R. Long, J. Am. Chem. Soc., 2023, 145, 1572–1579 CrossRef CAS.
- S. Thiele, R. Vincent, M. Holzmann, S. Klyatskaya, M. Ruben, F. Balestro and W. Wernsdorfer, Phys. Rev. Lett., 2013, 111(3), 037203, DOI:10.1103/PhysRevLett.111.037203.
- M. R. Wasielewski, M. D. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith and T. Goodson III, Nat. Rev. Chem., 2020, 4, 490–504 CrossRef CAS.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344(6188), 1135–1138 CrossRef CAS.
- F. Luis, A. Repollés, M. J. Martínez-Pérez, D. Aguilà, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, A. Camón and J. Sesé, Phys. Rev. Lett., 2011, 107(11), 117203 CrossRef CAS.
- M. Martínez-Pérez, S. Cardona-Serra, C. Schlegel, F. Moro, P. Alonso, H. Prima-García, J. Clemente-Juan, M. Evangelisti, A. Gaita-Ariño and J. Sesé, Phys. Rev. Lett., 2012, 108(24), 247213 CrossRef.
- C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119(18), 187702 CrossRef CAS PubMed.
- C. Godfrin, R. Ballou, E. Bonet, M. Ruben, S. Klyatskaya, W. Wernsdorfer and F. Balestro, npj Quantum Inf., 2018, 4(1), 53 CrossRef.
- K. Pramanik, Y.-C. Sun, P. Brandão, N. C. Jana, X.-Y. Wang and A. Panja, New J. Chem., 2022, 46, 11722–11733 RSC.
- Y.-Q. Zhou, W. Deng, S.-N. Du, Y.-C. Chen, Z.-Y. Ruan, S.-G. Wu, J.-L. Liu and M.-L. Tong, Inorg. Chem. Front., 2024, 11, 1061–1069 RSC.
- A. Palii, B. Tsukerblat, S. Klokishner, K. R. Dunbar, J. M. Clemente-Juan and E. Coronado, Chem. Soc. Rev., 2011, 40(6), 3130–3156 RSC.
- T.-T. Ruan, E. Moreno-Pineda, M. Schulze, S. r. Schlittenhardt, T. Brietzke, H.-J. r. Holdt, S. K. Kuppusamy, W. Wernsdorfer and M. Ruben, Inorg. Chem., 2023, 62(37), 15148–15156 CrossRef CAS.
- Y. N. Guo, G. F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H. J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951 CrossRef CAS PubMed.
- Z. Zhu and J. Tang, Natl. Sci. Rev., 2022, 9, nwac194 CrossRef.
- Z. Zhu and J. Tang, Chem. Soc. Rev., 2022, 51, 9469 RSC.
- K. Liu, X. Zhang, X. Meng, W. Shi, P. Cheng and A. K. Powell, Chem. Soc. Rev., 2016, 45(9), 2423–2439 RSC.
- T. Okubo, K. Himoto, K. Tanishima, S. Fukuda, Y. Noda, M. Nakayama, K. Sugimoto, M. Maekawa and T. Kuroda-Sowa, Inorg. Chem., 2018, 57(5), 2373–2376 CrossRef CAS PubMed.
- P. Chábera, Y. Liu, O. Prakash, E. Thyrhaug, A. E. Nahhas, A. Honarfar, S. Essén, L. A. Fredin, T. C. Harlang and K. S. Kjær, Nature, 2017, 543(7647), 695–699 CrossRef.
- D. I. Alexandropoulos, K. R. Vignesh, T. C. Stamatatos and K. R. Dunbar, Chem. Sci., 2019, 10(6), 1626–1633 RSC.
- S. Goswami, H. S. Jena and S. Konar, Inorg. Chem., 2014, 53(14), 7071–7073 CrossRef CAS PubMed.
- M. A. Lemes, H. N. Stein, B. Gabidullin, S. N. Steinmann and M. Murugesu, ACS Omega, 2018, 3(8), 10273–10277 CrossRef CAS.
- S. Patra, T. A. Miller, B. Sarkar, M. Niemeyer, M. D. Ward and G. K. Lahiri, Inorg. Chem., 2003, 42(15), 4707–4713 CrossRef CAS.
- X.-H. Bu, H. Liu, M. Du, L. Zhang, Y.-M. Guo, M. Shionoya and J. Ribas, Inorg. Chem., 2002, 41(7), 1855–1861 CrossRef CAS.
- M. A. Lemes, H. N. Stein, B. Gabidullin, K. Robeyns, R. Clérac and M. Murugesu, Chem. – Eur. J., 2018, 24(17), 4259–4263 CrossRef CAS PubMed.
- B. Li, X.-N. Wang, A. Kirchon, J.-S. Qin, J.-D. Pang, G.-L. Zhuang and H.-C. Zhou, J. Am. Chem. Soc., 2018, 140(44), 14581–14585 CrossRef CAS.
- J. Wang, S. Zhou, C. Chen, L. Lu, B. Li, W. Hu, A. Kumar and M. Muddassir, Dyes Pigm., 2021, 187, 109068 CrossRef CAS.
- T. J. Woods, M. F. Ballesteros-Rivas, S. M. Ostrovsky, A. V. Palii, O. S. Reu, S. I. Klokishner and K. R. Dunbar, Chem. – Eur. J., 2015, 21(29), 10302–10305 CrossRef CAS PubMed.
- P. Richardson, R. Marin, Y. Zhang, B. Gabidullin, J. Ovens, J. O. Moilanen and M. Murugesu, Chem. – Eur. J., 2021, 27(7), 2361–2370 CrossRef CAS.
- S. G. Tolshchina, G. L. Rusinov and V. N. Charushin, Chem. Heterocycl. Compd., 2013, 49, 66–91 CrossRef CAS.
- D. Hunter and D. G. Neilson, J. Chem. Soc., Perkin Trans. 1, 1985, 1081–1086, 10.1039/P19850001081.
- P. Alemany, D. Casanova, S. Alvarez, C. Dryzun and D. Avnir, Continuous Symmetry Measures: A New Tool in Quantum Chemistry, Rev. Comput. Chem., 2017, 30, 289–352 CAS.
- E. Moreno-Pineda, M. Damjanovic, O. Fuhr, W. Wernsdorfer and M. Ruben, Angew. Chem., Int. Ed., 2017, 56(33), 9915–9919 CrossRef CAS.
- E. Moreno-Pineda, G. Taran, W. Wernsdorfer and M. Ruben, Chem. Sci., 2019, 10(19), 5138–5145 RSC.
- M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143(34), 13633–13645 CrossRef CAS PubMed.
- K. N. Shrivastava, Phys. Status Solidi B, 1983, 117(2), 437–458 CrossRef CAS.
- F. S. Santana, M. Perfetti, M. Briganti, F. Sacco, G. Poneti, E. Ravera, J. F. Soares and R. Sessoli, Chem. Sci., 2022, 13, 5860–5871 RSC.
- J. Wang, J. J. Zakrzewski, M. Zychowicz, Y. Xin, H. Tokoro, S. Chorazy and S. i. Ohkoshi, Angew. Chem., Int. Ed., 2023, 62, e202306372 CrossRef CAS PubMed.
- J. Flores Gonzalez, F. Pointillart and O. Cador, Inorg. Chem. Front., 2019, 6(4), 1081–1086 RSC.
- G. Huang, X. Yi, J. Jung, O. Guillou, O. Cador, F. Pointillart, B. Le Guennic and K. Bernot, Eur. J. Inorg. Chem., 2018, 2018(3–4), 326–332 CrossRef CAS.
- Y. Kishi, F. Pointillart, B. Lefeuvre, F. Riobe, B. Le Guennic, S. Golhen, O. Cador, O. Maury, H. Fujiwara and L. Ouahab, Chem. Commun., 2017, 53(25), 3575–3578 RSC.
- F. Pointillart, K. Bernot, S. Golhen, B. Le Guennic, T. Guizouarn, L. Ouahab and O. Cador, Angew. Chem., 2015, 127(5), 1524–1527 CrossRef.
- F. Ortu, D. Reta, Y. S. Ding, C. A. P. Goodwin, M. P. Gregson, E. J. L. McInnes, R. E. P. Winpenny, Y. Z. Zheng, S. T. Liddle, D. P. Mills and N. F. Chilton, Dalton Trans., 2019, 48, 8541–8545 RSC.
- F. Luis, M. J. Martínez-Pérez, O. Montero, E. Coronado, S. Cardona-Serra, C. Martí-Gastaldo, J. M. Clemente-Juan, J. Sesé, D. Drung and T. Schurig, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 060403 CrossRef.
- J. Flores Gonzalez, H. Douib, B. Le Guennic, F. Pointillart and O. Cador, Inorg. Chem., 2021, 60, 540–544 CrossRef CAS.
- J. Flores Gonzalez, B. Lefeuvre, B. Degraeve, O. Cador and F. Pointillart, Dalton Trans., 2021, 50, 11466–11471 RSC.
- W. Wernsdorfer, N. E. Chakov and G. Christou, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(13), 132413 CrossRef.
- M. Dolai, E. Moreno-Pineda, W. Wernsdorfer, M. Ali and A. Ghosh, J. Phys. Chem. A, 2021, 125(37), 8230–8237 CrossRef CAS.
- J. Long, F. Habib, P. H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2011, 133(14), 5319–5328 CrossRef CAS PubMed.
- E. Moreno-Pineda, S. Klyatskaya, P. Du, M. Damjanovic, G. Taran, W. Wernsdorfer and M. Ruben, Inorg. Chem., 2018, 57(16), 9873–9879 CrossRef CAS PubMed.
- S. A. Sulway, R. A. Layfield, F. Tuna, W. Wernsdorfer and R. E. Winpenny, Chem. Commun., 2012, 48(10), 1508–1510 RSC.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez Galvan, N. Ferre, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. A. Malmqvist, T. Muller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Marti, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37(5), 506–541 CrossRef CAS PubMed.
- D. Ma, G. Li Manni and L. Gagliardi, J. Chem. Phys., 2011, 135(4), 044128 CrossRef PubMed.
- P. E. M. Siegbahn, J. Almlöf, A. Heiberg and B. O. Roos, J. Chem. Phys., 1981, 74(4), 2384–2396 CrossRef.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137(6), 064112 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Chem, 2017, 23(15), 3708–3718 CrossRef CAS PubMed.
- S. Mondal and A. Lunghi, npj Comput. Mater., 2023, 9(1), 120 CrossRef.
- A. Lunghi and S. Sanvito, Sci. Adv., 2019, 5(9), eaax7163 CrossRef CAS PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137(6), 064112 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34(13), 1164–1175 CrossRef CAS PubMed.
- G. Taran, E. Bonet and W. Wernsdorfer, J. Appl. Phys., 2019, 125, 142903 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2337590 and 2337589. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt01769b |
| This journal is © The Royal Society of Chemistry 2024 |