Precursor molecules for 1,2-diamidobenzene containing cobalt(II), nickel(II) and zinc(II) complexes – synthesis and magnetic properties

Abstract

Molecular magnetic materials based on 1,2-diamidobenzenes are well known and have been intensively studied both experimentally and computationally. They possess interesting magnetic properties as well as redox activity. In this work, we present the synthesis and investigation of potent synthons for constructing discrete metal–organic architectures featuring 1,2-diamidobenzene-coordinated metal centres. The synthons feature weakly bound dimethoxyethane (dme) ligands in addition to the 1,2-diamidobenzene. We characterize these complexes and investigate their magnetic properties by means of static and dynamic magnetometry and high-field electron paramagnetic resonance (HFEPR). Interestingly, the magnetic and magnetic resonance data strongly suggest a dimeric formulation of these complexes, viz. [M^II(bmsab)(dme)]₂ (bmsab = 1,2-bis(methanesulfonamido)benzene; dme = dimethoxyethane) with M = Co, Ni, Zn. A large negative D-value of −60 cm⁻¹ was found for the Co(II) synthon and an equally large negative D of −50 cm⁻¹ for the Ni(II) synthon. For Co(II), the sign of the D-value is the same as that found for the known bis-diamidobenzene complexes of this ion. In contrast, the negative D-value for the Ni(II) complex is unexpected, which we explain in terms of a change in coordination number. The heteroleptic Co(II) complex presented here does not feature slow relaxation of the magnetization, in contrast to the homoleptic Co(II) 1,2-diamidobenzene complex.

---

Introduction

Single-molecule magnets (SMMs) offer the possibility to store data on a molecular level, which would allow a much higher storage densities than currently possible. Careful ligand field design can induce strong magnetic anisotropy due to zero-field splitting (ZFS) in transition metal complexes, which is a prerequisite for SMM behaviour. Compounds of 1,2-bis(sulfonamido)benzenes have been shown to be excellent ligands for engendering very large ZFS D-values in various metal centres due to their acute bite angle, which leads to a strong axial distortion of the resulting complex. For diamidobenzene complexes of cobalt(II) very large negative D-values were found, making these complexes excellent SMMs.^1–4 Related nickel(II) complexes exhibit large positive D values (in the region of 60 cm⁻¹).^2,18–20 The investigations of various ligand systems based on 1,2-diamidobenzenes showed that the magnetic properties of especially cobalt(II) complexes of these ligands are very robust and the large ZFS is conserved also with different sulfonamido moieties. The strongly electron-withdrawing nature of the sulfonamido substituents provides an additional advantage, as it stabilizes the complexes in their anionic state and makes them stable towards air and moisture. This is a beneficial aspect with respect to possible future applications. Despite the strong anisotropy, true magnetic bistability was not observed in transition metal complexes of 1,2-diamidobenzenes, due to efficient under-barrier relaxation. Underbarrier processes may be suppressed in analogous polynuclear metal complexes, where the spin centres are strongly coupled. The coupling strength must be at least comparable to the magnitude of the ZFS to prevent formation of low-lying spin-excited states that facilitate magnetic relaxation. In practice, this means using radical bridging ligands.^6–9 Along these lines, our groups recently presented a binuclear, radical bridged cobalt(II) complex based on similar ligands,⁵ which displays superior magnetic relaxation properties compared to its mononuclear counterpart. However, the synthetic procedure for obtaining this compound was not convenient, and the desired product could only be obtained in low yields by manual sorting of crystals. Hence a rational and modular approach to such compounds necessitates novel precursors, in which precisely one 1,2-diamidobenzene ligand is firmly bound to the central metal, while the coordination sphere is completed by labile co-ligands. Such novel synthons would open ways to develop multinuclear systems and other heteroleptic complexes of 1,2-diamidobenzenes. This approach (among others) was reviewed by Pedersen, Bendix and Clérac in 2014,¹⁰ and is illustrated in Scheme 1 for the present case.

Scheme 1 Conceptual approach: a modular route to functional heteroleptic structures requires appropriate synthons.

In this work, the synthetic route as well as an in-depth magnetic characterization of the heteroleptic complexes of the composition [M^II(bmsab)(dme)] is presented (dme = dimethoxyethane, M = Co, Ni, Zn).

Synthesis and characterization

Our synthetic route is based on previous work by Khusniyarov and Wieghardt who reported the synthesis of an extremely air-sensitive six-coordinate heteroleptic 1,2-diamidobenzene Fe(II) complex from a diamido iron(II) precursor and 1,2-diamidobenzene as the limiting reagent.¹¹ Similarly, we used divalent amides of the respective metals as starting materials for the synthesis of the three complexes [Zn^II(bmsab)(dme)] (1), [Ni^II(bmsab)(dme)] (2) and [Co^II(bmsab)(dme)] (3), since they are readily accessible and provide a strong internal base in the correct stoichiometry. In the case of Co(II) and Zn(II), the well-known hexamethyldisilazides were used.¹² For the corresponding Ni(II) complex, the hexamethyldisilazide was recently reported as its THF adduct.¹³ However, this is a rather unsuitable starting material, due to its thermal instability.¹⁴ Instead, for 2, the divalent Ni(II) amide Ni[N(SiMe₃)(DIPP)]₂ (DIPP = diisopropyphenyl) as described by Tilley et al.¹⁵ was chosen as a starting material. The heteroleptic metal complexes were then obtained by dropwise addition of a solution of the metal amide in dme (for Co(II) and Zn(II)) or toluene (Ni(II)) to a cooled (−20 °C) suspension of H₂bmsab in dme (see Scheme 2). After warming to room temperature, the products were precipitated by addition of hexane. After filtration and drying under high vacuum, pink (Co(II)), red (Ni(II)) or colorless (Zn(II)) amorphous powders are isolated. The complexes themselves are air- and moisture-sensitive and insoluble in all common solvents, apart from acetonitrile. Dissolving into acetonitrile leads to a ligand exchange reaction, which can be followed by ¹H NMR spectroscopy (vide infra). Consequently, characterization is demanding, but elemental analysis is consistent with a formulation where each compound contains one dianionic (bmsab)²⁻ and one molecule of dme per metal ion. This suggests the presence of four-coordinate metal centres. Magnetochemical and theoretical investigations (vide infra) point towards dimeric structures in the solid state for the nickel(II) and cobalt(II) complexes 2 and 3.

Scheme 2 Synthetic route towards the heteroleptic precursor compounds. Magnetometric measurements and calculations indicate a dimeric structure for 2 and 3.

The identity of the compounds in solution was probed by means of (paramagnetic) ¹H NMR spectroscopy. The structurally well characterized homoleptic compounds² served as a reference. All spectra were recorded in deutero-acetonitrile.

The most straightforward case is 1, since Zn(II) is diamagnetic and hence the characterization by ¹H NMR is rather straightforward (Fig. S1‡). Three NMR resonances were found at δ = 7.26 (m, 2 H, bmsab-H-3,6), 6.73 (m, 2 H, bmsab-H-4,5), and 2.89 (s, 6 H, SO₂Me) ppm, which are similar to those observed for the homoleptic [Zn^II(bmsab)₂]²⁻ (7.36, 6.61, and 2.83 ppm, Fig. S2‡). Further resonances are observed at 3.45 and 3.28 ppm, which can be assigned to free dme, which points to the exchange of the weakly bound dme by acetonitrile. Similar behavior is found for 2, where signals at 3.45 and 3.28 ppm point again to free dme. The resonance lines for [Ni^II(bmsab)(dme)] are found at δ = 26.24 (6 H), 5.41 (2 H) and −5.27 (2 H) ppm and are almost identical to the homoleptic compound (albeit broadened), indicating that the coordination geometry in the dissolved complex 2 and the homoleptic counterpart are comparable (Fig. S3 and S4‡). This is supported by UV/Vis/NIR measurements. A solution of 2 in acetonitrile shows bands at 400 and 540 nm (Fig. S7‡). These features are very similar to those observed for the homoleptic complex in acetonitrile solution (Fig. S8 and Table S1‡).

In contrast, complex 3 shows different behaviour: while the heteroleptic cobalt(II) complex 3 displays resonances in a range of 35 ppm (ESI Fig. S5‡), the homoleptic analogue features NMR resonances that span a range of about 150 ppm (ESI Fig. S6‡). This indicates a different coordination environment of 3 in acetonitrile. UV/Vis/NIR spectra of an acetonitrile solution of 3 showed bands at 405 nm and 1120 nm (Fig. S9‡) that are not found in the homoleptic analogue (Table S1‡). These bands can be tentatively assigned to the ⁴T_2g ← ⁴T_1g and the ⁴T_1g(P) ← ⁴T_1g transitions of an octahedrally coordinated high-spin d⁷ system.¹⁶ Hence, we propose that upon dissolution in acetonitrile, the labile dme ligands are replaced by four solvent molecules per Co(II) centre to give a pseudo-octahedral coordination geometry. While the facile ligand exchange hampers the characterization of the dme adducts in solution, this exchange process indicates that we successfully isolated a suitable precursor with a labile co-ligand, which allows the stepwise building of heteroleptic, potentially polynuclear coordination compounds.

Magnetism and EPR spectroscopy

A thorough magnetic characterization was performed to further characterize the heteroleptic species. For 3, a room temperature χT value of 3.33 cm³ K mol⁻¹ is found, which is the value expected for a high spin Co(II) centre (S = 3/2) with g_iso = 2.66. Upon cooling, χT decreases gradually until 12 K, which indicates a significant ZFS. On further cooling below 12 K, a steep drop in χT is observed. This drop cannot be simulated considering a large ZFS alone (see below), but must be due to other phenomena such as intramolecular antiferromagnetic interactions or slow dynamics of the magnetic moment. Simulations of the magnetic data were carried out based on the spin Hamiltonian in eqn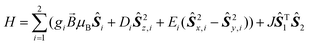 (1).

Here, JŜ^T₁Ŝ₂ is the isotropic exchange interaction term, while the other terms describe the Zeeman, and the axial, and rhombic zero-field splittings, respectively. A good agreement of the experimental susceptibility temperature product with the simulated one is obtained considering two S = 3/2 centres with g_iso = 2.68(5), D = −60(5) cm⁻¹, E = 0 and J = 0.25(3) cm⁻¹. Hence, the simulation indicates that a non-negligible exchange interaction is present. This is evident when comparing simulations with and without such an interaction (Fig. 1). Magnetization curves at different temperatures can be simulated in good accordance with the experiment based on a slightly larger g-value of g_iso = 2.75(3) and a slightly larger exchange interaction of J = 0.30(3) cm⁻¹ (Fig. S10‡).

Fig. 1 Susceptibility temperature product of 2 and 3 as a function of the temperature (black symbols) recorded on pressed powder samples at external fields of 0.1 T (T < 40 K) and at 1 T (T > 40 K). Lines are fits according to eqn (1). The parameters are given in Table 1.

On the basis of the elemental analysis data and the magnetometry, it is already possible to obtain insight into the molecular structure of 3 in the solid state. Since the elemental analysis is in good agreement with one dme and one bmsab ligand for one Co(II) centre, the smallest structure that can feature some intramolecular exchange interaction is a dimer, with two bridging dme ligands between two Co(II)(bmsab) moieties. Similar bridging structures have been reported for the Co(II)(bmsab) fragment in 2022 by Shao et al.²⁹ Further proof of such a structural motif was obtained by means of HFEPR spectroscopy (see below).

Due to its pronounced negative zero-field splitting, 3 is expected to be EPR-silent at X-band frequencies (9.5 GHz): a large negative D leads to a substantial energetic separation between the Kramers doublets and renders the m_S = ±3/2 doublet the ground state.¹⁷ The intradoublet transition within the m_S = ±3/2 doublet is EPR-forbidden. Indeed, powder EPR experiments on 3 at 9.5 GHz yield no signal over a temperature range of 4.5 K to 300 K. In contrast, a frozen solution of 3 in acetonitrile gives an intense, broad signal at 4.5 K with effective g-values of 4.99, 3.69 and 2.92, when using an S_eff = 1/2 model (see Fig. 2). These values are in good accordance with literature known effective g-values for octahedral Co(II) complexes and are hence indicative for a formation of an octahedrally coordinated high-spin Co(II) species of 3 in acetonitrile.^32,33 This is a further confirmation for the ligand exchange reaction described above.

Fig. 2 Top: Experimental X-band EPR spectrum of an acetonitrile solution of 3 at 4 K, and a simulation considering a pseudo S = 1/2 system. Bottom: HFEPR spectra of 3 as a pressed powder at 230, 300 and 375 GHz, in magnetic fields of up to 15 T and at 5 K (black). The corresponding HFEPR simulation based on two interacting pseudo S = 1/2 systems is shown in red.

To gain additional insight into the electronic structure of 3, high-field electron paramagnetic resonance (HFEPR) spectra were recorded at frequencies of up to 375 GHz on the same sample which was used for magnetometry. HFEPR measurements of samples of 3 gave reasonably well resolved spectra at 230, 300 and 375 GHz at a temperature of 5 K. Three main experimental features are observed in the 375 GHz measurement: sharp signals at fields of 12.76 T (g_eff = 2.1) and 6.38 T (g_eff = 4.2) as well as a broader feature at 3.99 T (g_eff = 6.7). The sharp signal at g_eff = 2.0 is due to an impurity in the experimental setup. For a direct comparison of the spectra of 3 at various frequencies, it is useful to plot the spectra on a g-value scale (Fig. 2). Here, a frequency dependency of the effective g-values is observed: the sharp signal at g_eff = 2.1 (375 GHz) and the central feature at g_eff = 4.2 (375 GHz) trend to lower g-values with decreasing frequency, while their spacing is also gradually decreasing (from 2.10 down to 1.81). The broad feature at g_eff = 6.7 (375 GHz) moves to higher effective g-values at the lower frequencies (g_eff = 8.2 at 230 GHz). These shifts must therefore be due to a field-independent interaction. A first approach to modelling the HFEPR data is a description featuring two interacting pseudo S = 1/2 systems. This approach is valid due to the large ZFS of 3, which results in a strongly isolated ground Kramers doublet. For this approach, effective g-values are used. An adequate simulation (see Fig. 2) of the frequency dependency of the signals at low g-values in the HFEPR spectra at 230, 300 and 375 GHz is obtained by using effective g-values of g_x′ = 2.30(3), g_y′ = 4.50(5), g_z′ = 5.20(5). The frequency dependence of the g-values is taken into account by an anisotropic exchange interaction of J_x,y,z = (5.5(2), 6.0(1), 0.2(2)) cm⁻¹.

In the description with two pseudo S = 1/2 systems, the anisotropy of each magnetic centre is projected onto the exchange interaction. To expand the description of the HFEPR measurements and to obtain more in-depth insight into the spin system of 3, especially into the coupling situation, a second modelling approach was implemented, which features two coupled S = 3/2 centres. The best agreement of the simulations based on eqn (1) with the HFEPR experiments is obtained with parameters of (for each S = 3/2 centre) g = 1.75(3), D = −60(10) cm⁻¹, E = 0.1D and J = 0.67(5) cm⁻¹. Even though the experiment is well reproduced (Fig. 3), the parameter values are very different from those obtained from the analysis of the magnetic data. On the basis of the simulations, the most informative signal in the HFEPR spectra is the one at high g-values that shows the largest g-value shift with frequency. The distance of this signal to the signal at low g-values is sensitive towards the magnitude of J and hence allows determination of the exchange strength and strongly supports the model of a dimer structure of 3. Inspection of the spin levels of 3 (Fig. S11‡) reveals that the observed signals in the HFEPR spectra are only observable due to the existence of a small exchange interaction: the Kramers doublets of each centre are separated by a value of 2D (Fig. S11,‡ middle) and hence inter-doublet transitions are not observable at the frequencies and fields available in HFEPR. In the limiting case of purely axial ZFS, the intradoublet m_S = ±3/2 transition is EPR-forbidden. However, due to the exchange interaction, the ground Kramers doublet shows a splitting, which can be probed by means of HFEPR and is in line with the observed transitions (Fig. S11,‡ bottom).

Fig. 3 Measured HFEPR spectra of 3 at the indicated frequencies at 5 K (black). Simulations are shown in red. Simulations are based on two interacting S = 3/2 systems using the parameters given in Table 1.

The g-value from HFEPR is much lower (g_iso = 1.75) than that found by means of magnetometry (g_iso = 2.68), which is too large to be attributed to weighing errors. In fact, it is unphysically low for a more than half-filled d-shell. The rhombicity (E = 0.1D) is larger than the value found by simulating the temperature dependence of the susceptibility-temperature product, where it was not used, which is due to the fact that magnetometry measurements are not very sensitive to E. In the HFEPR simulations, a sizeable E is needed in order to allow some transitions. Simulations based on the magnetometry parameters do not show any signals in the region of the experimental signals (Fig. S12‡). Conversely, fits of the magnetic data on the basis of the spin Hamiltonian parameters derived from HFEPR are not reasonable. Furthermore, best fits of the magnetic data and EPR spectra, assuming a positive D-value are also not satisfactory (Fig. S13–S15‡). However, in spite of our best efforts, better fits on the basis of one parameter set for all experiments (HFEPR and magnetometry) could not be achieved. Further work would be required to elucidate this matter.

Since the homoleptic analogue of 3 ([Co(bmsab)₂]²⁻) shows exceptional magnetic relaxation behaviour, AC susceptibility measurements were carried out on 3.^1,2 In these measurements, only a minor out-of-phase signal (χ′′), that features two distinct peaks, is observed. The magnitude of this out-of-phase component is only 3% of the in-phase component χ′ of the dynamic susceptibility. Consequently, only a minor fraction of the sample relaxes slowly, which is attributed to a small impurity, potentially of the homoleptic bis-bmsab complex (Fig. S16 and S17‡). Hence, even though the heteroleptic dme complex 3 features a large, negative ZFS, it does not show signs of slow relaxation of the magnetization. This underlines how important the details of the coordination environment are for the magnetic properties of molecules and their relaxation behavior.

In the case of 2, the room temperature χT value is with 1.20 cm³ K mol⁻¹ (Fig. 1), in good agreement with g_iso = 2.19 and the d⁸ configuration of Ni(II) (S = 1). Upon decreasing temperature, χT remains nearly constant down to 100 K, while on further temperature lowering, it decreases slightly to a value of 1.10 cm³ K mol⁻¹ at 50 K. Upon further cooling from 50 K to 1.8 K, χT decreases faster with decreasing temperature until it reaches 0.46 cm³ K mol⁻¹ at 1.8 K. This suggests a rather large ZFS or a large exchange interaction also in the case of 2. To quantify this, spin Hamiltonian simulations were carried out under a first assumption of a large and positive D, based on the parameters of the homoleptic [Ni(bmsab)₂]²⁻.² The best fit based on eqn (1), constraining the sign of D to be positive (index “pos”), gave g_x,y,pos = 2.10(2), g_z,pos = 2.64(5), D_pos = 35(5) cm⁻¹ and E_pos = D/3. The exchange interaction strength was determined more precisely by using the magnetization measurements and was found to be J_x,y,z,pos = (10(2), −8(1), 16(3)) cm⁻¹. Nevertheless, the temperature dependence of χT and the magnetization curves are not well-reproduced (Fig. S18 and S19‡) and the large anisotropy of the exchange tensor is rather unconvincing. Consequently, we removed the constraint of positive D for 2 and carried out simulations for negative D-values (index “neg”). With this approach, an adequate agreement of experimental data and simulation was obtained with parameters of g_iso,neg = 2.20(3), D_neg = −50(5) cm⁻¹, E_neg = 0 and J_iso,neg = 0.5(1) cm⁻¹ (Table 1). The magnetization curves were successfully simulated using the same parameters, with the additional inclusion of a small nonzero E-value of E/D = 0.04 (Fig. S20‡). Negative axial ZFS values have been reported for Ni(II) for higher coordination numbers than four, e.g., in octahedral geometries.^35–40 Hence, one alternative geometry might be a pseudo-octahedral geometry, where the sulfonyl oxygens saturate the coordination sphere around the Ni(II) centres. As mentioned above, large, negative ZFS D-values, exceeding −20 cm⁻¹ for octahedral or square bipyramidal Ni(II) are known in literature.^35–40

Table 1 Overview over the spin Hamiltonian parameters for 2 and 3. In the case of 2, two parameter sets, either with a positive or a negative D are found (see text). In this table, only the best-fit parameters are shown. For simulations, where nonzero E did not improve the results, the rhombic ZFS term was not used in order to avoid overparameterization

	[Ni^II(bmsab)(dme)]2 (2)
	g	D/cm^−1	E/D	J/cm^−1
HFEPR	—	—	—	—
χT vs. T	2.20(3)	−50(5)	Unused	0.5(1)
M vs. H	2.20(3)	−50(5)	0.04	0.5(1)
CASSCF	g x,1 = 2.22	−10.66	0.28	0.68
	g y,1 = 2.27	−9.29	0.06
	g z,1 = 2.33
	g x,2 = 2.23
	g y,2 = 2.24
	g z,2 = 2.30

---

	[Co^II(bmsab)(dme)]2 (3)
	g	D/cm^−1	E/D	J/cm^−1
HFEPR	1.75(2)	−60(10)	0.1	0.65(5)
χT vs. T	2.68(5)	−60(5)	Unused	0.25(3)
M vs. H	2.75(3)	−60(5)	Unused	0.30(3)
CASSCF	g x,1 = 2.16	−34.5	0.003	−0.1
	g y,1 = 2.18	−30.2	0.025
	g z,1 = 2.58
	g x,2 = 2.17
	g y,2 = 2.20
	g z,2 = 2.55

---

Quantum chemical calculations

Because no single crystals suitable for X-ray diffraction could be obtained, the direct determination of the molecular structure was not possible. Therefore, quantum chemical calculations of the electronic structure and the magnetic properties were used to complement the experimental findings. On the basis of the experimentally obtained structure of the homoleptic [M(bmsab)₂]²⁻ complexes,² we constructed dimeric starting geometries for 2 and 3, each featuring two bridging dme ligands between the two M(II) centres. The geometries were then optimized by DFT calculations (PBE0, def2-TZVP). In the case of 3, the geometry optimization (Table S2‡ and Fig. 4) on DFT level resulted in a comparable geometry around the Co(II) centres to those found experimentally for other Co(II)-bmsab complexes.^1,2 This can be highlighted, when the different Co–N and intraligand C–N distances of 3 are compared to the experimental ones of the homoleptic complexes. Here, similar values are found and hence the theoretical structure of 3 is in good agreement with the expected bond lengths in the bmsab²⁻ ligand (Table S6‡). Since the N–Co(II)–N bond angle of the ligands to the metal centre strongly influences the ZFS,³⁰ it is of great interest to compare this for 3 with experimentally found values for the homoleptic cases, where values for this bite angle range from 79.97° to 81.36°.² In the optimized structure of the heteroleptic complex 3, values of 81.33 and 81.55° are found. This leads to the conclusion, that the binding geometry at the bmsab²⁻ side in 3 matches the one in the homoleptic complex. For the O–Co(II)–O angles, angles of 106.34° or 110.21° are calculated for each one of the centres, i.e. much larger than the N–Co–N angle. Hence only one ligand–metal–ligand angle is highly acute and this is expected to lead to a decrease in axial ZFS.

Fig. 4 DFT optimized geometries of possible dme bridged dimers for the case of 2 and 3. Cobalt ions are shown in dark blue, nickel ions in green, oxygen in red, sulfur in yellow, nitrogen in light blue and carbon in grey. Hydrogens are omitted for clarity.

Since for the Ni(II) complex 2, the magnetometry results suggest an octahedral or pseudo-octahedral geometry, a six-coordinate geometry around each Ni(II) centre was assumed in the starting geometry for the DFT geometry optimization. This is justified by experimental data of a number of structurally characterized Ni(II) complexes where sulfonamido groups act as bidentate donors via N,O coordination.^44–46 Starting from a six-coordinate geometry in which the sulfonyl oxygen atoms act as axial donors, an optimum geometry was found (Table S3‡). Consequently, the geometry around the Ni(II) centre is a slightly distorted octahedron. The bond distances between the Ni(II) centres and the bmsab²⁻ ligands range from 1.957 Å up to 2.223 Å, while the distances between the metal centres and the dme donors lie between 2.089 and 2.126 Å. The calculated distances between the two Ni(II) centres and the sulfonyl oxygens lie between 2.096 Å and 2.224 Å. Reported values of this structural motif are in the range of 2.09⁴⁴ to 2.43 Å,⁴⁶ hence the computations are in line with experimental precedence.

In order to calculate the magnetic properties of theoretical dimer structures and compare these with the experimental data, CAS(7,5) (Co(II)) or CAS(8,5) (Ni(II)) (def2-TZVPP for Co/Ni, N, O and def2-SVP for other elements) calculations were carried out to obtain values for the g-tensor and as well as parameters for the ZFS. Electron correlation was modeled on the NEVPT2 level. For these calculations, one of the Co(II) or Ni(II) centres were substituted by a diamagnetic Zn(II), while the geometry was unchanged. An effective Hamiltonian analysis of the projected relativistic states then allows access to the g-tensor and the ZFS parameters. These were found to be g_x = 2.16, g_y = 2.18, g_z = 2.58, D = −34.5 cm⁻¹, E = |0.003D| in the case of Co(II) for one centre (Table 1). For the second centre, nearly similar g-values (g_x = 2.17, g_y = 2.20, g_z = 2.55), but marginally different ZFS parameters of D = −30.2 cm⁻¹ and E = |0.025D| were found, making the two spin-systems almost identical. This agrees with the comparable coordination geometry of both. For both centres, the first excited quartet state is the major contributor to the ZFS D-parameter (Tables S7 and S8‡). Good agreement is observed between the ab initio calculated values and the experimentally found spin Hamiltonian parameters in the case of 3 (Table 1). The calculated ZFS parameter D is nearly identical to the one obtained from experiments. For the g-values, smaller numbers are calculated, but the g-tensor anisotropy is also axial.

In the Ni(II) case, values of g_x = 2.22, g_y = 2.27, g_z = 2.33, D = −10.66 cm⁻¹, E = |0.28D| were calculated for Ni1 (Table 1). For Ni2, g_x = 2.23, g_y = 2.24, g_z = 2.30, D = −9.29 cm⁻¹ and E = |0.06D| are found. For both Ni(II) centres, the same magnitude for D and also a negative sign is found, being in line with the experimental findings. In the case of 2, it was observed that for both centres the first three triplet states play a major role for the magnitude of the ZFS D parameter (ESI Tables S9 and S10‡). For Ni1, g_iso = 2.27 and for Ni2 g_iso = 2.26 is calculated, which is in good agreement with the experimentally observed isotropic value. Clearly, the magnitude of D is highly underestimated in the calculations, which suggested that the real structure may differ from the theoretically predicted one.

Further evidence for the bridging motif was gathered by calculating the properties of the monometallic structures (Fig. S21, S22 and Tables S7–S10‡). In the case of Co(II), a significantly larger ZFS D-parameter of −116.0 cm⁻¹ is calculated for the hypothetical mononuclear species. The anisotropy of the g-values is with g_x = 1.91, g_y = 2.02 and g_z = 3.29 also in better agreement with the monomeric homoleptic complex [Co^II(bmsab)₂]²⁻.¹ For Ni(II) the g-values of the monometallic structure are calculated as g_x = 2.10, g_y = 2.49 and g_z = 2.56 and result in a comparable isotropic g-value of g_iso = 2.38, which is in the same region as in the dimeric case. In contrast to this, a large, but positive ZFS D-parameter of 64.6 cm⁻¹ is found, which is in line with the homoleptic complex that features two bmsab²⁻ ligands,² but clearly not with the experimentally observed values and behaviour in the case of 2. For both Co(II) and Ni(II), the dinuclear structures provide a better agreement between calculated and experimentally observed values than the mononuclear models. Hence, dme-bridged structures are viable models to reconcile the observed composition of the compounds with their spectroscopic and magnetometric properties in the absence of structural data.

To complete the theoretical picture of the dimer motif, we carried out broken symmetry DFT calculations (PBE0, def2-TZVPP for metal centres and for the first coordination sphere, def2-SVP for all other atoms) on the DFT optimized dimer structures.³⁴ For 3, an energy difference of the high-spin state (i.e. both Co(II) spins aligned parallel, leading to a total spin of S = 3) and the low-spin state (both spins aligned antiparallel, leading to a singlet state S = 0) of −0.425 cm⁻¹ is found. This energy gap hence suggests a ferromagnetic coupling and transfers to an exchange interaction of J = −0.1 cm⁻¹ in the H = JŜ^T₁Ŝ₂ formalism used in this work.^41–43 The order of magnitude of the exchange interaction in 3 is slightly underestimated compared the experimentally observed exchange, and its sign is calculated opposite. Consequently, the calculated interaction for 3 must be treated with caution. For 2, the same procedure resulted in a high-spin/low-spin energy gap of 1.353 cm⁻¹ (corresponds to an antiferromagnetic interaction of J = 0.68 cm⁻¹), which is in good agreement with the experimentally observed exchange interaction of J_iso = 0.5 cm⁻¹.

Further complexation experiments

To probe the synthetic applicability of the presented synthons, we reacted the diamagnetic [Zn^II(bmsab)(dme)] synthon with 4,4′-di-tert-butyl-2,2′-bipyridyl (DTBBPy) (Scheme 3) to obtain complex 4 in a yield of 85%.

Scheme 3 Complexation of [Zn^II(bmsab)(dme)] with DTBBPy.

The chemical identity of 4 was established by means of ¹H- and ¹³C NMR and mass spectrometry (MS) (see Fig. S22–S27‡). Three resonances at δ = 8.64 (d, J = 5.54 Hz, 2 H), 8.31 (s, 2 H, J = 1.15 Hz), 7.76 (m, 2 H, J = 5.63 Hz, 1.76 Hz) ppm can be assigned to the aromatic protons of the DTBBPy ligand. The bmsab²⁻ signals are observed at 7.39–7.34 (m, 2 H) and 6.88–6.83 (m, 2 H) ppm. Two further singlets are found at 2.89 (s, 6 H) and 1.48 (s, 18 H) ppm. These can be assigned to the sulfonamide methyl groups and to the tertbutyl groups of the DTBBPy ligand. The molecular structure of 4 was validated by means of single-crystal X-ray diffractometry and is shown in Fig. 5. The coordination geometry around the zinc atom is a distorted tetrahedron with N–Zn–N angles of 83.50° for the bmsab²⁻ ligand and 80.59° for DTBBPy. The neutral DTBBPy ligand shows bond lengths of 2.007 and 2.041 Å between the N donors and the central metal. The dianionic bmsab²⁻ ligand shows shorter metal–ligand bond distances of 1.974 and 1.953 Å. The coordinated DTBBPy displays a twist of 14.17° along the C–C bond of the two pyridine rings. Both rings are bent towards each other with angles of 114° for the N–C–C unit and 124° for the C–C–C unit of the atoms around the connecting bond (compare Fig. S23‡). The crystal structure shows that the distorted tetrahedral coordination geometry of the homoleptic compounds^1,2 can be transferred to a heteroleptic compound via a targeted, high-yielding synthetic route.

Fig. 5 ORTEP representation of the crystal structure of 4. Zn is shown in blue, nitrogens in light blue, carbon in grey, sulfur in yellow and oxygen in red. Thermal ellipsoids are drawn at 50% probability. Hydrogen atoms have been omitted for clarity.

This highlights the synthetic potential of the presented precursors 1, 2 and 3 as synthons for the construction of heteroleptic, tetrahedral complexes. With this route at hand, a variety of complexes based on the [(bmsab)M] motif and its attractive magnetic properties become accessible.

Experimental section

General remarks and instrumentation

All syntheses were performed under a dry Ar atmosphere. Dme was distilled from K, while hexane and toluene were obtained from a solvent purification system (GS Glovebox Systemtechnik). All solvents were stored over activated molecular sieves and degassed by vigorous bubbling with dry Ar. The ligands H₂bmsab²¹ and LiN(Dipp)(SiMe₃)^22,23 were prepared according to published procedures. Anhydrous CoCl₂, anhydrous ZnCl₂, NaN(SiMe₃)₂ and LiN(SiMe₃)₂ were obtained from abcr. [NiCl₂(dme)] was obtained from Sigma-Aldrich. 4,4′-Di-tert-butyl-bipyridine was obtained from BLDpharm. Commercially available chemicals were used without further purification.

SQUID magnetometry

Samples were measured as pressed powder pellets wrapped in Teflon tape. The instrument used was a Quantum Design MPMS3 SQUID magnetometer. Data were corrected for ferromagnetic impurities as well as for the diamagnetic contribution to the susceptibility by means of Pascal's constants.²⁴

High-field EPR

HFEPR measurements were carried out in a frequency range from 230 GHz to 375 GHz at a temperature of 5 K on a homebuilt spectrometer.²⁵ In this setup, an amplifier-multiplier chain (VDI) is used to obtain the desired frequency. The initial radiation is generated by a synthesizer at a frequency of up to 20 GHz. The radiation is propagated via a quasi-optical setup (Thomas Keating) to the sample and then to the detector (QMC InSb hot electron bolometer). The sample is placed in an Oxford Instruments 15/17T cryomagnet, equipped with a VTI which is allowing temperatures from 1.5 K to 300 K. The HFEPR data was collected on the same pellets as the SQUID magnetometry data.

EPR

EPR spectra at X-band frequencies were measured on a Bruker EMX spectrometer, equipped with an Oxford 4102ST flow cryostat and a standard TE102 cavity. Measurements were carried out in quartz glass tubes.

Simulations

All simulations were carried out with the EasySpin toolbox (Version 5.2.35) for Matlab (R2021b).²⁶

Quantum chemical calculations

All quantum chemical calculations were carried out with the ORCA quantum chemistry program package (Version 5.0.3).³¹ Geometry optimizations were performed on DFT level using the PBE0 functional. The Spin Hamiltonian parameters were calculated on CASSCF level. For the metal centres and the first coordination sphere, the def2-TZVPP basis set was used. For the other atoms, the def2-SVP basis set was used. Self-consistent field calculations were tightly converged by using the “tightscf” keyword. For sample inputs, see the ESI.‡

Single-crystal X-ray diffraction

Single crystals were grown as described in the Experimental section. X-ray diffraction was performed on a Bruker APEXII Duo using a fine-focus Molybdenum source at 160 K. Reflections were collected using ω- and φ-scans. The structure was solved using SHELXL-2014/7.⁴⁷ Disordered heptane was eliminated from the final structure by using the Platon/SQUEEZE procedure.

Synthesis of the divalent metal amides

Bis(bis(trimethylsilyl)amido)cobalt(II) – THF adduct. The synthetic procedure was adapted from the literature.²⁷ Na(N(SiMe₃)₂) (3.67 g, 20 mmol, 2 eq.) is dissolved in THF. Anhydrous CoCl₂ (1.3 g, 10 mmol, 1 eq.) is suspended in THF and cooled to 0 °C. The Na(N(SiMe₃)₂) solution is added dropwise via canula to the CoCl₂ slurry under vigorous stirring. The reaction mixture is stirred and allowed to warm to room temperature overnight, resulting in a dark green solution and copious precipitate. After removal of volatiles, the product is extracted with 60 ml of hexane and filtered over a Celite-padded Schlenk frit. After removal of volatiles, the crude green product is purified by sublimation (1 × 10⁻³ mbar, 75 °C) to yield the pure product as a bright green solid (2.08 g, 46%). The analytical data agree with the literature.

¹H NMR (250 MHz, 25 °C, C₆D₆) δ = 170.85 (4 H, THF), 101.99 (4 H, THF), −17.45 (36 H, SiMe₃) ppm.

Bis(bis(trimethylsilyl)amido)zinc(II). The synthetic procedure was adapted from the literature.²⁸ Na(N(SiMe₃)₂) (3.67 g, 20 mmol, 2 eq.) and anhydrous ZnCl₂ (1.56 g, 10 mmol, 1 eq.) are suspended in 60 ml diethyl ether and stirred under reflux conditions for 4 h. After cooling down and removal of volatiles, the product is extracted with 60 ml of hexane and filtered over a Celite-padded Schlenk frit. After removal of volatiles, the crude product is purified by distillation (1 × 10⁻³ mbar, 85 °C) to yield the pure product as a colorless oil (1.86 g, 48%). The analytical data agree with the literature.

¹H NMR (250 MHz, 25 °C, C₆D₆) δ = 0.2 ppm.

Bis(N-diisopropylphenyl-N-trimethylsilylamido)nickel(II). The synthetic procedure was adapted from the literature.¹⁵ A 250 ml Schlenk flask was charged with Li(N(Dipp)(SiMe₃)) (5 g, 19.57 mmol, 2 eq.) and NiCl₂(dme) (2.15 g, 9.78 mmol, 1 eq.). Toluene (80 ml) was added and the reaction mixture was stirred for 12 h, resulting in an intensely colored purple solution and copious precipitate. After removal of volatiles, the solid was extracted with hexane (60 ml) and filtered over a Celite-padded Schlenk frit. The solution was concentrated under high vacuum until crystallization commenced and subsequently stored at −80 °C for 20 h which gave deep purple crystals. The crystalline material was isolated by filtration and dried under high vacuum to give the pure product (0.8 g, 15% yield). The analytical data agree with the literature.

¹H NMR (250 MHz, 25 °C, C₆D₆): δ = 66.75 (4 H), 57.05 (4 H), 42.16 (12 H), 12.00 (12 H), 6.53 (18 H), −93.33 (2 H) ppm.

Synthesis of heteroleptic precursors [M^II(bmsab)(dme)] (M = Co, Ni, Zn)

General procedure. A Schlenk flask is charged with finely powdered H₂bmsab (0.26 g, 1 mmol, 1 eq.), to which dimethoxyethane is added (10 ml). The suspension is cooled to −20 °C. The diamido metal complex (1.1 mmol, 1.1 eq.) is dissolved in dimethoxyethane (Co, Zn) or toluene (Ni) and the solution is added dropwise to the slurry of H₂bmsab. The reaction mixture is brought to room temperature over the course of 1.5 h and then stirred for an additional 1.5 h, after which approximately half of the solvent is removed. Hexane (10 ml) is added and the reaction mixture stirred for 10 min. The supernatant is filtered off and the product is obtained as a fine powder after drying under high vacuum for 6 h. The products are air- and moisture-sensitive and hardly soluble in their native form. At this point, CHNS analysis appears to be the only feasible way of determining the purity of the product.

[Co(bmsab)(dme)]. Obtained as a pink powder in 65% yield.

Anal. calcd for C₁₂H₂₀N₂CoO₆S₂: C 35.04, H 4.90, N 6.81, S 15.59; found: C 35.13, H 5.07, N 6.67, S 15.08.

[Ni(bmsab)(dme)]. Obtained as a maroon powder in 42% yield.

Anal. calcd for C₁₂H₂₀N₂NiO₆S₂: C 35.06, H 4.90, N 6.81, S 15.60; found: C 35.09, H 5.098, N 6.60, S 14.89.

[Zn(bmsab)(dme)]. Obtained as a colorless powder in 73% yield.

Anal. calcd for C₁₂H₂₀N₂ZnO₆S₂: C 34.50, H 4.83, N 6.71, S 15.35; found: C 33.89, H 4.93, N 6.50, S 15.07.

Synthesis of [Zn(bmsab)DTBBPy] (4). A Schlenk flask was charged with the [Zn(bmsab)(dme)] (40 mg, 1 eq.), cooled to −20 °C and acetonitrile (10 ml) was added. 4,4′-Di-tert-butyl-2,2′-bipyridyl (1 eq.) was dissolved in acetonitrile (5 ml) or tetrahydrofuran (2 ml) and added dropwise at −20 °C. The mixture was stirred for 2 h, the solvent was removed and the resulting powder dried under high vacuum. [Zn(bmsab)DTBBPy] was obtained as an air-stable off-white powder in 85% yield. An off-white microcrystalline solid was achieved by slow diffusion of ether into a dichloromethane solution of the complex. A needle-shaped crystal suitable for single-crystal diffraction was grown from a slowly evaporating solution of the compound in DCM/heptane.

¹H NMR (400 MHz, 25 °C, CD₂Cl₂): 8.64 (d, J = 5.54 Hz, 2 H, DTBBPy-H), 8.31 (s, 2 H, DTBBPy-H), 7.76 (m, 2 H, DTBBPy-H), 7.36 (m, 2 H, bmsab-H), 6.85 (m, 2 H, bmsab-H), 2.89 (s, 6 H, SO₂CH₃), 1.48 (s, 18 H, tBu-H) ppm.

¹³C NMR (100 MHz, 25 °C, CD₂Cl₂): 148.95 (DTBBPy-C), 136.94 (quaternary carbon), 125.19 (DTBBPy-C), 120.26 (bmsab-C), 119.41 (DTBBPy-C), 115.62 (bmsab-C), 39.480 (SO₂CH₃) 36.309 ((CH₃)₃C-aryl), 30.466 ((CH₃)₃C-aryl). Not all quaternary carbons were visible in the NMR.

(+)-ESI: m/z: 595.14 [M]⁺, signal matches with the simulated signal for C₂₆H₃₄N₄O₄S₂Zn 617.12 [M + Na]⁺, 269.20 [dtbbpy]⁺.

Anal. calcd for C₂₆H₃₄N₄O₄S₂Zn: C 52.39, H 5.75, N 9.40, S 10.76; found C 52.40, H 5.79, N 9.31, S 10.67.

Conclusions

We have presented a series of heteroleptic metal complexes of the stoichiometry [M^II(bmsab)(dme)] with M = Co, Ni, Zn. All compounds may serve as versatile precursors for a variety of molecules with a wide range of desirable properties such as redox activity or single-molecule magnetism. Solution studies show that the dme ligand is only weakly bound and is easily replaced by a coordinating solvent such as acetonitrile. This is a prerequisite for the construction of more complex molecular architectures with this building block. The paramagnetic Ni(II) (2) and Co(II) (3) complexes behave magnetically different than their homoleptic counterparts. While a large negative ZFS is also present in 3, no slow relaxation of the magnetization is observed. For 2, also a large negative ZFS is found. In both cases, intramolecular exchange interactions are experimentally observed and the experimental findings are supported on a theoretical level. This leads to a basic model of the solid state structure of 2 and 3 as [M^II(bmsab)(dme)]₂ that features a dme bridged dimeric motif. Whereas for the Co(II) complex 3, a tetrahedral geometry around the metal ion is in line with the experimental findings, for the Ni(II) complex 2, an octahedral geometry is found. Hence, even without the availability of a crystal structure, a viable structural model for 2 and 3 is established. The magnetic properties are, as in the homoleptic counterparts, dominated by the large ZFS of both paramagnetic systems. The synthetic utility of the new compounds is exemplified by the straightforward preparation of a heteroleptic, tetrahedral Zn(II) complex in high yields. In conclusion, this work provides an insight into the chemistry and the physical properties of important synthons of magnetic materials that can be used as building blocks for rational chemical design of new multinuclear materials.

Author contributions

B. S. and J. v. S. conceived the research and supervised the work. Synthetic work, NMR- and UV/Vis/NIR spectroscopy was performed by S. S., based on previous work done by U. A. Magnetic characterization and EPR spectroscopy was performed and analyzed by D. H. The complexation tests were carried out by V. B. Single-crystal-diffraction measurements and structure solving was carried out by W. F. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Timo Holzmann for the preliminary work on the magnetochemistry and the spectroscopy of the Co(II) complex. This work was funded by the Landesgraduiertenförderung Baden-Württemberg, and by the German Science Foundation, DFG, SL104/10-1, SA1840/9-1.

References

1. Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 268.
2. H. Bamberger, U. Albold, J. Dubnická Midlíková, C.-Y. Su, N. Deibel, D. Hunger, P. P. Hallmen, P. Neugebauer, J. Beerhues, S. Demeshko, F. Meyer, B. Sarkar and J. van Slageren, Inorg. Chem., 2021, 60, 2953–2963.
3. M. S. Fataftah, J. M. Zadrozny, D. M. Rogers and D. E. Freedman, Inorg. Chem., 2014, 53, 10716–10721.
4. H.-H. Cui, F. Lu, X.-T. Chen, Y.-Q. Zhang, W. Tong and Z.-L. Xue, Inorg. Chem., 2019, 58, 12555–12564.
5. U. Albold, H. Bamberger, P. P. Hallmen, J. van Slageren and B. Sarkar, Angew. Chem., Int. Ed., 2019, 58, 9802–9806.
6. I. Jeon, J. Park, D. Xiao and D. Harris, J. Am. Chem. Soc., 2013, 135(45), 16845–16848.
7. J. Rinehart, M. Fang, W. Evans and J. Long, Nat. Chem., 2011, 3, 538–542.
8. J. Rinehart, M. Fang, W. Evans and J. Long, J. Am. Chem. Soc., 2011, 133(36), 14236–14239.
9. S. Demir, J. Zadrozny, M. Nippe and J. Long, J. Am. Chem. Soc., 2012, 134(45), 18546–18549.
10. K. S. Pedersen, J. Bendix and R. Clérac, Chem. Commun., 2014, 50, 4396–4415.
11. M. Khusniyarov, T. Weyhermüller, E. Bill and K. Wieghardt, Angew. Chem., Int. Ed., 2008, 47, 1228–1231.
12. M. F. Lappert, A. V. Protchenko, P. P. Power and A. L. Seeber, Metal Amide Chemistry, John Wiley & Sons, Chichester, 1st edn, 2008.
13. M. Faust, A. M. Bryan, A. Mansikkamäki, P. Vasko, M. M. Olmstead, H. M. Tuononen, F. Grandjean, G. J. Long and P. P. Power, Angew. Chem., Int. Ed., 2015, 54, 12914–12917.
14. A. Reckziegel, B. Battistella, A. Schmidt and C. G. Werncke, Inorg. Chem., 2022, 61, 7794–7803.
15. M. Lipschutz and T. D. Tilley, Chem. Commun., 2012, 48, 7146–7148.
16. A. B. P. Lever, Inorganic Electronic Spectroscopy, Studies in physical and theoretical chemistry 33, Elsevier, Amsterdam, 2nd edn, 2nd impression with corr., 1986.
17. R. Boča, Coord. Chem. Rev., 2004, 248, 757–815.
18. S.-D. Jiang, D. Maganas, N. Levesanos, E. Ferentinos, S. Haas, K. Thirunavukkuarasu, J. Krzystek, M. Dressel, L. Bogani, F. Neese and P. Kyritsis, J. Am. Chem. Soc., 2015, 137, 12923–12928.
19. J. van Slageren, S. Vongtragool, B. Gorshunov, A. A. Mukhin, N. Karl, J. Krzystek, J. Telser, A. Müller, C. Sangregorio, D. Gatteschi and M. Dressel, Phys. Chem. Chem. Phys., 2003, 5, 3837–3843.
20. A. T. Kowal, I. C. Zambrano, I. Moura, J. J. Moura, J. LeGall and M. K. Johnson, Inorg. Chem., 1988, 27, 1162–1166.
21. H.-Y. Cheng, P.-H. Cheng, C.-F. Lee and S.-M. Peng, Inorg. Chim. Acta, 1991, 181, 145–147.
22. Y. W. Chao, P. A. Wexler and D. E. Wigley, Inorg. Chem., 1989, 28, 3860–3868.
23. D. K. Kennepohl, S. Brooker, G. M. Sheldrick and H. W. Roesky, Chem. Ber., 1991, 124, 2223–2225.
24. G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532.
25. P. Neugebauer, D. Bloos, R. Marx, P. Lutz, M. Kern, D. Aguilà, J. Vaverka, O. Laguta, C. Dietrich, R. Clérac and J. van Slageren, Phys. Chem. Chem. Phys., 2018, 20, 15528–15534.
26. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
27. Inorganic Syntheses, ed. P. P. Power, John Wiley and Sons, Hoboken, 2018, vol. 37.
28. R. Yang, G. Xu, C. Lv, B. Dong, L. Zhou and Q. Wang, ACS Sustainable Chem. Eng., 2020, 8, 18347–18353.
29. D. Shao, S. Moorthy, Y. Zhou, S. Wu, J. Zhu, J. Yang, D. Wu, Z. Tian and S. K. Singh, Dalton Trans., 2022, 51, 9357.
30. P. Ferreira, A. Cerdeira, T. Cruz, N. Bandeira, D. Hunger, A. Allgaier, J. van Slageren, M. Almeida, L. Pereira and P. Gomes, Inorg. Chem. Front., 2022, 9, 4302.
31. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
32. G. Gransbury, M. Boulon, R. Mole, R. Gable, B. Moubaraki, K. Murray, L. Sorace, A. Soncini and C. Boskovic, Chem. Sci., 2019, 10, 8855.
33. E. Misochko, A. Akimov, D. Korchagin, J. Nehrkorn, M. Ozerov, A. Palii, J. Clemente-Juan and S. Aldoshin, Inorg. Chem., 2019, 58, 16434.
34. E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400.
35. M. Atanasov, P. Comba, S. Helmle, D. Müller and F. Neese, Inorg. Chem., 2012, 51, 12324–12335.
36. J. Titis and R. Boca, Inorg. Chem., 2010, 49, 3971–3973.
37. R. Herchel, R. Boca, J. Krzystek, A. Ozarowski, M. Duran and J. van Slageren, J. Am. Chem. Soc., 2007, 129, 10306–10307.
38. P. J. Desrochers, J. Telser, S. A. Zvyagin, A. Ozarowski, J. Krzystek and D. A. Vicic, Inorg. Chem., 2006, 45, 8930–8941.
39. A. Maslejova, R. Boca, L. Dlhan, B. Papankova, I. Svoboda and H. Fuess, Chem. Phys. Lett., 2001, 347, 397–402.
40. R. Boca, L. Dlhan, W. Haase, R. Herchel, A. Maslejova and B. Papankova, Chem. Phys. Lett., 2002, 373, 402–410.
41. A. P. Ginsberg, J. Am. Chem. Soc., 1980, 102(1), 111–117.
42. L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743.
43. L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109(1), 131–143.
44. S. Ogoshi, H. Ikeda and H. Kurosawa, Angew. Chem., Int. Ed., 2007, 46, 4930.
45. J. Davies, D. Janssen-Müller, D. P. Zimin, C. S. Day, T. Yanagi, J. Elfert and R. Martin, J. Am. Chem. Soc., 2021, 143, 4949.
46. A. Sousa-Pedrares, J. A. Viqueira, J. Antelo, E. Labisbal, J. Romero, A. Sousa, O. R. Nascimento and J. A. García-Vázquez, Eur. J. Inorg. Chem., 2011, 2011, 2273.
47. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.

---

Footnotes

† Dedicated to Prof. Dr. Axel Klein on the occasion of his 60th birthday.

‡ Electronic supplementary information (ESI) available: Additional experimental data (PDF). CCDC 2325488. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt01115e

§ These authors contributed equally.

---