Modulated spin dynamics of [Co₂] coordination helicates via differential strand composition

Abstract

Coordination supramolecular chemistry provides a versatile entry into materials with functionalities of technological relevance at the nanoscale. Here, we describe how two different bis-pyrazolylpyridine ligands (L1 and L2) assemble with Co(II) ions into dinuclear triple-stranded helicates, in turn, encapsulating different anionic guests. These constructs are described as (Cl@[Co₂(L1)₃])³⁺, (SiF₆@[Co₂(L1)(L2)₃])²⁺ and (ClO₄@[Co₂(L2)₃])³⁺, as established by single-crystal X-ray diffraction. Extensive magnetic and calorimetric measurements, numerical treatments and theoretical calculations reveal that the individual Co(II) centers of these supramolecular entities exhibit field-induced slow relaxation of magnetization, dominated by direct and Raman mechanisms. While the small variations in the spin dynamics are not easily correlated with the evident structural differences among the three species, the specific heat measurements suggest two vibronic pathways of magnetic relaxation: one that would be associated with the host lattice and another linked with the guest.

---

Introduction

The discovery of single-molecule magnets (SMMs) has been one of the most fascinating events in the area of molecular magnetism.^1–3 SMMs are capable of preserving their magnetization below a certain temperature without any cooperative effect, thus behaving as individual magnets.⁴ It was first described on an oxide/acetate bridged coordination cluster of 12 Mn ions with a total spin ground state S = 10.⁵ The ten years following this landmark witnessed large efforts to produce and study transition metal (TM) clusters as improved SMMs by pursuing larger S ground state values and axial anisotropy parameters, D. Both terms contribute to enhancing the energy barrier that prevents the relaxation of magnetization, thus increasing the blocking temperature. In 2003, it was shown that complexes of one sole lanthanide ion could display slow relaxation of magnetization, outperforming most 3d SMMs thanks to their large magnetic anisotropy.⁶ This sparked a frenetic race to develop Ln SMMs,⁷ which furnished breakthrough mononuclear Dy(III) complexes exhibiting magnetic hysteresis near^8,9 or above the temperature of liquid N₂.¹⁰ In this process, it became clear that the anisotropy in single 3d metals^11–13 (and not only lanthanides) was also sufficient to yield barriers to the magnetic relaxation larger than most polynuclear TM complexes. Molecules behaving as SMMs composed of only one metal ion have also been termed single-ion magnets (SIMs). The perfect marriage between the large anisotropy of lanthanides and large spin states arising from exchange interactions is represented by the cluster (Cp^iPr5)₂Dy₂I₃ recently published.¹⁴ It formally features a Dy(II) ion coupled very strongly to a Dy(III) center via the overlap of their 5d_z² orbitals, which share one electron, yielding an M_J = ±31/2 ground state doublet (from the ¹²N_31/2 term).

The emerging prospect of using molecular spins as qubits for the coherent manipulation of quantum information^15–18 opens new opportunities to explore the implementation of SIMs (or SMMs). These could be considered as potential hardware hosting the permanent memory used by spin-based molecular quantum processors. Depending on the ceiling of temperature imposed by the quantum coherence of the qubits and qugates of these processors, the blocking temperature of the associated SIM memory may not need to be as high as originally sought. The main challenge is rather to design mechanisms for the transfer of information among the parts of this potential molecular device, and this is yet an unresolved problem. The magnitude of the challenge notwithstanding, assembling these components as part of supramolecular architectures is a very attractive idea. For some time, we have successfully designed ligands, L, that interact with M(II) metals to form triple stranded dinuclear helicates, [M₂L₃]⁴⁺. The nature of M can furnish functional properties to the assembly such as spin switching abilities (M = Fe)^19,20 or SIM behaviour (M = Co).²¹ These helicates possess a central cavity that has always been found to encapsulate a guest, offering an avenue for modulating the properties of the host. The size and symmetry of the guest depend on the exact nature of L. The latter can be tailored to encapsulate TM-based qubit prototypes such as [M′(ox)₃]³⁻ (ox = oxalate) complexes, which have been shown to display quantum coherence and Rabi oscillations (for M′ = Fe³⁺, Cr³⁺, Ru³⁺).²² We have attempted to encapsulate Cr and Fe analogues within a [M₂L₃]⁴⁺ helicate and observed drastic changes in their spin dynamics.^23,24

In this paper, we present the use of two bis-pyrazolylpyridine (pzpy) ligands, L1 and L2 (Fig. 1), to generate three coordination dinuclear helicates of Co(II) of varying lengths and compositions depending on the combination of ligands and the nature of the guest; (Cl@[Co₂(L1)₃])³⁺, (SiF₆@[Co₂(L1)₂(L2)])²⁺ and (ClO₄@[Co₂(L2)₃])³⁺ (cations of 1, 2 and 3, respectively). The adequacy of the guest size and symmetry to the ligand strands of the corresponding helicates is discussed. Compounds 2 and 3 are reported here for the first time, while 1 (with the full formula Cl@[Co₂(L1)₃]Cl(PF₆)₂) was previously reported by our group and shown to display SMM properties.²¹ The magnetic properties of this cluster are analogous to those of its heterometallic counterpart (Cl@[ZnCo(L1)₃])³⁺, also part of that study,²¹ suggesting that the behaviour of the helicates can be rationalized as that of two SIMs contained in the same molecule. The slow relaxation of the Co(II) ions in all these helicates is analysed in detail here and compared in relation to the structural features conferred to these ions by the supramolecular construct. This study opens perspectives to explore future associations of qubits as guests of coordination hosts bearing SIMs. The analysis of the relaxation of magnetization carried out here will be useful towards this fascinating goal.

Fig. 1 Ligands 1,3-bis-(1-(pyridine-2-yl)-pyrazol-3-yl)-benzene (L1) and 3,3′-bis(3-(4-picolin-2-yl)-1H-pyrazol-5-yl)-1,1′-biphenyl (L2).

Results and discussion

Synthesis

Ligands L1 and L2 were prepared as previously reported by us,^19,25 as well as Cl@[Co₂(L1)₃]Cl(PF₆)₂ (1).²¹ The complex was obtained by mixing stoichiometric amounts of hydrated CoCl₂, L1 and NBu₄PF₆ in MeOH. Compound SiF₆@[Co₂(L1)₂(L2)](PF₆)₂ (2) was obtained by mixing stoichiometric amounts of Co(BF₄)₂, L1 and L2 with excess NBu₄PF₆ in MeOH. Indeed, mixing L1 and L2 obeyed the purpose of obtaining heteroleptic assemblies. During previous work, it was observed serendipitously that helicates incorporating both ligands and Fe(II) ions were formed with SiF₆⁻ as a guest, leading to the supramolecular cation (SiF₆@[Fe₂(L1)₂(L2)])²⁺.²⁵ The accidental discovery of this cation occurred because of the generation of SiF₆²⁻ following the transfer of BF₄⁻ fluoride ions to the silica (SiO₂) glass of the tubes.²⁶ No other guests (not even PF₆⁻) have conduced so far to the assembly of both L1 and L2 in one molecule. On the other hand, SiF₆²⁻ has been seen as a guest only when both types of ligands are combined, but never with only one of them. Homoleptic helicates of the longer ligand L2 were accessed previously with the assistance of the guest ClO₄⁻ through the reaction of Fe(ClO₄)₂ and L2 in MeOH in the presence of excess NBu₄ClO₄.²⁵ The analogous process with Co(ClO₄)₂ yields compound ClO₄@[Co₂(L2)₃](ClO₄)₃ (3). Compounds 1, 2 and 3 are all obtained as pure single-crystal phases in very moderate yields, presumably due to their high solubility, following diffusion of diethyl ether into the reaction mixtures, as confirmed in the bulk by microanalysis and determined via single-crystal X-ray diffraction (SCXRD).

Molecular structures

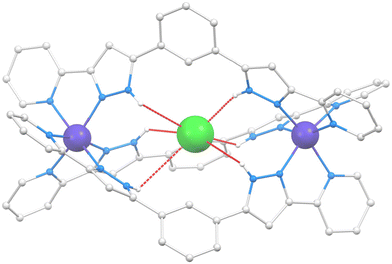
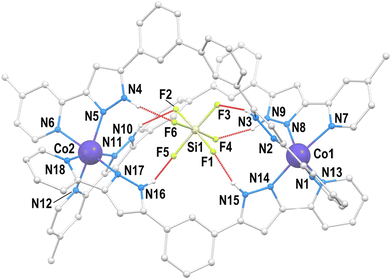
The structure of Cl@[Co₂(L1)₃]Cl(PF₆)₂ (1) was described by us on a previous paper;²¹ therefore, a full description is not provided here. Only the structural features useful for the comparison with the new helicates presented in this manuscript will be given. The cation of 1 (Fig. 2 and S1†) is a triple-stranded helicate comprising three L1 ligands bridging two six-coordinated Co(II) ions by chelating them with their pzpy moieties.

Fig. 2 Representation of the supramolecular cation (Cl@[Co₂(L1)₃])³⁺ of 1. The large blue balls are Co(II) ions, the small white balls are H atoms from N–H groups (remaining hydrogen atoms are not shown), the grey balls are C atoms, the blue balls are N atoms, and the central green ball is the Cl atom. Hydrogen bonds are shown as red dashed lines.

Compound SiF₆@[Co₂(L1)₂(L2)](PF₆)₂ (2) crystallizes in the monoclinic space group P2₁/n (Table S1†). The asymmetric unit is made by the main cation SiF₆@[Co₂(L1)₂(L2)]²⁺ (Fig. 3 and S2†), two PF₆⁻ groups and two molecules of MeOH, in addition to partially occupied diffuse solvent molecules (0.42 Et₂O and 1.76 MeOH). The unit cell contains four such groups. The metallic host is made of two pseudo-octahedral Co(II) ions lying 10.120 Å apart, bridged by chelation to one L1 and two L2 ligands, forming a hetero-(triple)stranded dinuclear helicate, the first of its kind for Co(II). This coordination assembly is the host to one SiF₆²⁻ guest anion residing inside the central cavity, poised conveniently to establish six N–H⋯F hydrogen bonds with the pyrazolyl (pz) rings of the ligands (Table S2†). The symmetry and electronic properties of SiF₆²⁻ seem to perfectly fit the cavity only when it is formed by two ligands of L2 type and one like L1 (Fig. 4). Consequently, this anion acts as a template for the construction of a heteroleptic helicate that would not form otherwise. The Co(II) ion may be used to define the pseudo axis of this helicate, albeit it lacks ternary symmetry because of its heteroleptic nature. The cation in 2 is chiral (not superimposable to its mirror image) with both enantiomers present in the crystal lattice, which is therefore racemic. The helical moieties interact among them through π⋯π interactions. Each moiety establishes such contacts with four other equivalent species (Fig. S3†). The closest intermolecular Co⋯Co distance (9.819 Å) is shorter than the separation of the metals within the helicate (vide supra).

Fig. 3 Representation of the supramolecular cation SiF₆@[Co₂(L1)₂(L2)]²⁺ of 2 with labelled heteroatoms. The grey balls are C atoms and the small white balls are H atoms from N–H groups (remaining hydrogen atoms are not shown). Hydrogen bonds are shown as red dashed lines.

Fig. 4 Two views of the SiF₆²⁻ guest present in 2, emphasizing the six N–H⋯F hydrogen bonds (shown as red dashed lines) with the core of ligands L1 (orange) and L2 (turquoise). Si is cream colour, F atoms are green colour and H atoms from N–H groups are white colour.

The lattice of compound 3 as determined through SCXRD (Table S1†) belongs also to the monoclinic space group P2₁/n. The unit cell contains four asymmetric units, which are composed of one supramolecular cation (ClO₄@[Co₂(L2)₃])³⁺, three ClO₄⁻ anions, nine molecules of MeOH, one of H₂O and a molecule of Et₂O, the latter presenting 50% occupancy. The supramolecular cationic assembly (ClO₄@[Co₂(L2)₃])³⁺ (Fig. 5 and S4†) is a triple-stranded dinuclear helicate with three ligands L2 as strands that bridge two Co(II) ions (Co⋯Co distance of 11.379 Å) via coordination through the pzpy chelating groups. The metals exhibit a very similar coordination geometry that is best described by a distorted octahedron (Table 1). The ClO₄⁻ guest resides in the cavity without restrictions, assisted by N−H⋯O hydrogen bonds with ligand strands of varying intensities and configurations (Fig. 5). This anion is closer to one Co centre than the other (Cl1⋯Co1 and Cl1⋯Co2 distances of 5.272 and 6.110 Å, respectively). Near Co1, one O atom of the anion forms three short H-bonds with the three available pz groups. On the other side, each of the three remaining O atoms of ClO₄⁻ form one longer H-bond with a different pz ring of the three such groups lying in this part of the cavity (Table S2†). The lattice is held together by a numerous set of weak intermolecular interactions (mostly C–H⋯π together with very few feeble π⋯π contacts; Fig. S5†).

Fig. 5 Representation of the supramolecular cation ClO₄@[Co₂(L2)₃]³⁺ of 3 with labelled heteroatoms. The grey balls are C atoms and the small white balls are H atoms from N–H groups (remaining hydrogen atoms are not shown). Hydrogen bonds are shown as red dashed lines.

Table 1 Distances to the ideal octahedron (O_h) or to a trigonal prism (D_3h) of the Co ions of compounds 1, 2 and 3 obtained with symmetry measured using the SHAPE program²⁷

	Complex 1		Complex 2		Complex 3
	Oh	D3h	Oh	D3h	Oh	D3h
Co1	2.789	9.279	1.946	10.498	1.524	13.802
Co2	1.765	11.463	1.993	10.992	1.408	14.979

---

The proximity of the coordination geometry of the Co(II) ions of compounds 1, 2 and 3 to the ideal octahedron (O_h) was calculated using the SHAPE program (Table 1).²⁷ For comparison, the distances to the perfect trigonal prism were also obtained. Compound 3 exhibits metals with most regular octahedral coordination geometries while complex 1 features two coordination geometries best described by the regular octahedron, but at quite different distances. Complex 2 exhibits very similar pseudo-octahedral geometries for both ions.

Static magnetic properties

The effect of the supramolecular scaffold in 1, 2 and 3 on the magnetism of the Co(II) ions was first examined through variable-temperature susceptibility and field-dependent magnetization measurements. The analysis incorporates also the heterometallic version of 1, (Cl@[CoZn(L1)₃])³⁺, previously published as a 35% component of a solid solution with (Cl@[Zn₂(L1)₃])³⁺ (4).²¹ The temperature dependence of the magnetic susceptibility of polycrystalline samples, shown as χT vs. T plots in Fig. 6, S6 and S8,† is very similar for the three systems (χ being the molar paramagnetic susceptibility). In all cases, the χT values at 300 K lie between 6.3 and 6.8 cm³ K mol⁻¹. These numbers, significantly above the spin-only value of 3.75 cm³ K mol⁻¹ for two Co(II) ions, reflect on the influence of spin–orbit coupling. The latter is also responsible for the decline of the curves upon cooling, down to 3.75–3.88 cm³ K mol⁻¹ at 2 K, in good agreement with the magnetization measurements (insets in Fig. 6 and Fig. S6†). A more pronounced decrease of χT occurring for 3 below 10 K could be attributed to weak antiferromagnetic interactions that are not present in the other two compounds. However, this would not be the result of closer intramolecular/intermolecular Co⋯Co distances (9.771/8.898, 10.120/8.723 and 11.379/10.251 for 1, 2 and 3 respectively). Furthermore, the observed superposition of the χT vs. T curves from 1 and 4 (normalized to one mole of Co(II), Fig. S7†) suggests that there is no relevant active spin–spin interaction (neither inter- nor intramolecular), at least in this specific system and down to 2 K. To analyze these results, the electronic structures of compounds 1, 2 and 3 have been investigated at the complete active space self-consistent field (CASSCF) level using OpenMolcas.²⁸ Due to the large separation between Co(II) ions, we assume that the measured magnetic properties in 1–3 arise from the independent contribution of each ion. Thus, for each compound, we define two analogues (X^a and X^b) where one of the Co(II) ions has been substituted by its structurally analogous diamagnetic Zn(II) ion – dipolar interaction estimates were then calculated between each ion.

Fig. 6 Temperature dependence of χT for compounds 1, 2 and 3, as indicated. Insets: magnetization isotherms at 2 and 5 K as indicated. Full red lines are the corresponding magnitudes obtained from the CASSCF-RASSI-SO-calculated electronic structure and g-tensors.

Details of the procedure and results are given in the ESI (Tables S4–S11†). Focusing on the spin–orbit coupled states, the first 3 Kramers doublet (KD) states were calculated to dominate the measured magnetic properties, spanning ca. 500 cm⁻¹, and being almost 100% composed of the first three spin-only states, i.e., linear combinations of the ⁴T_1g states coming from the ⁴F free ion term. This pattern is maintained for all three compounds and conforms to the T = P formalism, relevant also in other Co(II) complexes.²⁹ Only compound 1 presents significantly different g-tensors and energy splitting of the low-lying states when comparing the two metal centers of the molecule, likely due to a slightly different coordination geometry. In any case, the calculated overall susceptibility and magnetization curves remain very similar among the three compounds and are in good agreement with the experimental data (see Fig. 6 and S8†), validating the description of the low-energy magnetic states in these compounds.

Dynamic magnetic properties

The spin dynamics of the Co(II) centers were first studied through frequency-dependent AC susceptibility measurements at 2 K under different constant magnetic fields (Fig. S9†). At zero field, no out-of-phase signal of the susceptibility (χ′′) is detected; however, an external field of 100 Oe is sufficient to observe this component, characteristic of the slow dynamics of the magnetization, as previously observed with other Co(II) systems.³⁰ This has been ascribed to electronuclear spin entanglement, which masks the relaxation phenomenon at zero field while opening forbidden relaxation channels. The frequency dependence data were used to determine the corresponding characteristic relaxation times τ. In all cases, the relaxation rate τ⁻¹ is relatively fast, in comparison with analogous Co(II) systems with large anisotropy.^11,30 At low fields, the rate slightly decreases with increasing fields but then it increases markedly at fields above 0.2–0.3 T (Fig. 7a). The latter most likely corresponds to the direct relaxation mechanism becoming dominant at high fields. Although there are differences in the absolute values, the overall shape of the field dependence of τ⁻¹ is very similar for all compounds. It is satisfactorily reproduced (Table S12†) by the expression:
in which the first term expresses the field (B) dependence of the direct process and the second is the Brons–van Vleck expression describing the (low) field dependence of the Raman process.³¹ The relaxation of the Co(II) ions in (Cl@[CoZn(L1)₃])³⁺, diluted within solid solution 4, is slower than in 1, likely a consequence of their separation within the lattice, even though this is not discerned in the static measurements. There are also differences in relaxation rates among the three pure helicates, with τ(1)⁻¹ < τ(2)⁻¹ < τ(3)⁻¹. They seem correlated with the intramolecular Co⋯Co distances; i.e. the relaxation rate increases with larger separations. This is however the opposite effect expected from decreasing spin–spin interactions. Moreover, the observed trend in τ does not correlate with the shortest intermolecular Co⋯Co separations observed within the lattice. It is therefore clear that the observed differences in spin dynamics are not associated with the modulation of magnetic interactions caused by different Co⋯Co separations. Additionally, it should be noted that the presence of a second much slower relaxation mode becomes evident at low frequencies for fields above 0.3 T, which is the dominant mode at higher fields (Fig. S10†). The corresponding relaxation rates slowly decrease with increasing applied magnetic field, also displaying a similar variation for the three pure helicates (Fig. S11†).

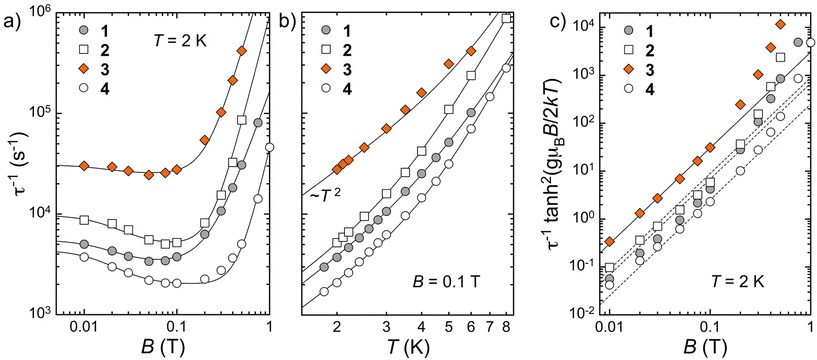Fig. 7 (a) Field and (b) temperature dependence of the magnetization relaxation rates of compounds 1–4, as indicated, respectively, at 2 K and 0.1 T. Full lines are fit to the expressions τ⁻¹ = CBⁿ + D(1 + EB²)/(1 + FB²) and τ⁻¹ = AT² + BT^m, respectively (see the text and Tables S4 and S5†). (c) Field dependence of τ⁻¹ tanh²(gμ_BB/2kT). Full and dashed lines are ∝B².

Isothermal frequency-dependent AC susceptibility data were also obtained at increasing temperatures under 0.03 and 0.1 T, respectively (Fig. S12 and S13†). This allows us for establishing the temperature dependence of the relaxation rate τ⁻¹ (Fig. 7b and S14†), unveiling the same τ(4)⁻¹ < τ(1)⁻¹ < τ(2)⁻¹ < τ(3)⁻¹ trend. For most of the temperatures explored, in particular for 3, this dependence follows an ATⁿ expression with n < 3 (Fig. S16†), suggesting the presence of a phonon bottleneck phenomenon.

Looking again at the field dependence of τ⁻¹, the low field data actually also support the presence of a phonon bottleneck. Again, the data for 3 show the most clear-cut situation, as it exhibits a B² coth²(gμ_BB/2k_BT) behavior, as expected for the presence of a phonon bottleneck (Fig. 7c).³² The other compounds show a relatively similar trend. This implies that the derived parameters for the above Brons–van Vleck expression should be taken with caution, since the Raman process is not affected by the phonon bottleneck. In any case, with these strong indications of the phonon bottleneck, the temperature dependence of τ⁻¹ was simulated considering the expression:

τ⁻¹ = AT² + BT^m

in which the direct process is considered to be dominated by the phonon bottleneck (Table S13†). We note that the Orbach process is not relevant in the studied ranges of time and temperature as it necessarily involves real excited states, which lie at >174 cm⁻¹ (as estimated from the zero-field splitting in 1).²¹ As intuited, the phonon-bottlenecked direct process is dominant up to ca. 6 K in the case of 3 and below 3–4 K for the other compounds, with A = 849, 1103, 6700 and 513 s⁻¹ K⁻², respectively, for 1, 2, 3 and 4. The Raman process becomes relevant only at higher temperatures, with m spanning 4.5–5.4 (Fig. 7b and S14, S15, Table S13†). Considering that two processes with m = 7 and m = 9 are expected for a Kramers ion, the later values of m are probably resulting from the limited temperature range available.

A phonon bottleneck results from an inefficient energy transfer from the phonons responsible for the spin relaxation to the temperature bath. The rate determining process of the energy transfer can take place in space, through the thermal bath surrounding the crystal surface, or in frequency, where lattice vibrations with energies of the order of k_BT form the bath.^33,34 A spatial phonon bottleneck occurs when the crystal radius is larger than the phonon mean-free path. It is a well-documented phenomenon, also in molecular magnets,^35–38 following the study of different forms/sizes of the same material. This mechanism is probably not at work here since all samples were polycrystalline micron-size powders, as confirmed by SEM images (Fig. S17†).

To understand their different spin relaxation behaviours, heat capacity data were acquired for 1–3 from 0.35 up to 200 K (Fig. 8). Interestingly, a low-temperature component in the zero-field heat capacity is observed that follows the same trend as the relaxation rate, i.e., the signal appears at increasing temperatures in the series 1–2–3. A possible origin for this signal would be spin–spin interactions. We estimated these interactions assuming that they are dipolar in nature. The derived average dipolar magnetic fields <B_dip> seen by each Co(II) would be ca. 6, 24 and 28 mT, respectively, for 1, 2 and 3. While this indeed follows the τ(1)⁻¹ < τ(2)⁻¹ < τ(3)⁻¹ trend observed in both field and temperature dependences, it disagrees with the intramolecular and intermolecular Co⋯Co separations in the three compounds. The calculated dipolar coupling (Tables S9–11†) indeed predicts that 1 presents a value twice as big as that for 3, in agreement with longer Co⋯Co separations in the latter. Since intramolecular interaction through the guest anion can be considered negligible, the origin of the low temperature heat capacity is a priori not due to spin–spin interactions and remains unclear.

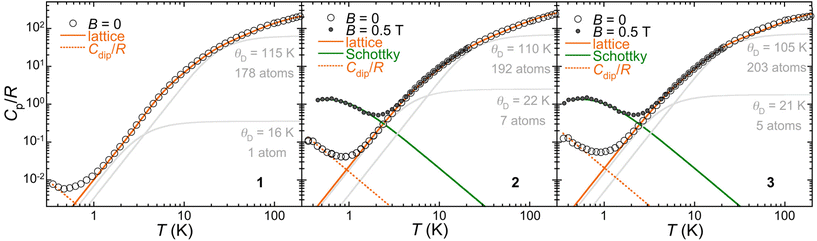Fig. 8 Specific heat capacities of 1, 2 and 3 in zero and 0.5 T applied fields, as indicated. The full orange lines are the calculated lattice heat capacity resulting from the sum of two Debye components shown as grey lines and ascribed to the lattice of helicate hosts on one hand and the anion guests on the other hand, in addition to both higher frequency Einstein components. The dashed orange line is a high temperature series of spin–spin dipolar interactions (see the text and the ESI†). The green lines are the Schottky anomaly calculated for an S = 3/2 with g = 2.

Turning to the analysis of the lattice heat capacity, it is difficult to define a (low) temperature range over which the typical Debye T³ dependence is observed, especially in the cases of 2 and 3. In fact, the Debye heat capacity calculated for the adequate number of atoms that best reproduces the low temperature part of the lattice heat capacity systematically deviates from it at higher temperatures (Fig. S18†). Using a lattice with a higher Debye temperature θ_D and the correct number of atoms would require adding Einstein components with ratios θ_E/θ_D inferior to unity, i.e., considering vibrations with frequencies below the Debye cut-off, which has no physical meaning. To rule out any magnetic contribution at unusually high temperatures, the heat capacities of 2 and 3 were measured in a 0.5 T applied field. The resulting low temperature anomaly perfectly matches the expected Schottky feature of an S = 3/2 spin, while the higher temperature data end up coinciding with the zero-field heat capacity. We therefore consider the hypothesis that a portion of the lattice may have a different, smaller θ_D. The guest anion in 1–3 indeed might be somewhat “excluded” from the overall lattice vibrations by the helicate host. As shown in Fig. 7, the lattice heat capacity is very well reproduced by the sum of two Debye components, one corresponding to the guest anion with a small θ_D of the order of 20 K on one hand and another for the helicate host with a larger θ_D of the order of 110 K, with additional higher frequency Einstein components. Despite the excellent agreement with the experimental data, the validity of this treatment remains hypothetical, but the heat capacity of 1–3 clearly hints at the existence of low frequency vibrations, much below the typical cut-off of the Debye temperature of the overall solid. These could act as a temperature bath for phonon modes resonant with the spin system, becoming the rate-determining process for the phonon relaxation time. In such a two-phonon process, the spin-phonon relaxation is indeed predicted to have a T² dependence,³³ as observed.

Conclusions

Two ligands (L1 and L2) containing two pyrazolylpyridine moieties with different spacers combine with Co(II) ions to yield dinuclear triple-stranded helicates, always incorporating a guest, G; G@[Co₂(L1)_x(L2)_y]⁺ⁿ (n = +2 or +3). Assemblies with three different ligand combinations and three different guests can be accessed. The variable temperature magnetic susceptibility in these compounds is well reproduced by calculations at the CASSCF level, allowing a good description of the electronic structure of the individual Co(II) anions. The host in all of them exhibits slow relaxation of magnetization under a small external magnetic field. The relaxation dynamics of the Co(II) centers differ slightly among the three compounds. Exhaustive analysis of their relaxation time unveils the presence of both, a direct and a Raman relaxation mechanism, with the former being dominated by the phenomenon of phonon bottleneck. It is not clear whether the different dipolar interactions between both Co(II) ions of the helicates can explain the observed differences in relaxation rates. However, heat capacity experiments suggest, interestingly, that the vibrations of the guest and host may provide for independent relaxation pathways, mediated by two different vibronic energy regimes.

This work opens the possibility of investigating supramolecular assemblies based on metallohelicates with SMM properties as potential hosts of qubits that could benefit from the nearby existence of permanent magnets of molecular origin below a certain blocking temperature.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

G. A. and H. B. thank the NextGenerationEU/PRTR-C17.I1 (from “Plan Complementario en Comunicación Cuántica” funded by Generalitat de Catalunya, the Basque Government and the European Union). H. B. thanks the IKUR Strategy on behalf of the Department of Education of the Basque Government. D. R. thanks the Basque Government for the IT1584-22 grant and Marcus Giansiracusa for helpful discussion on the calculation of dipolar interactions. G. A. and O. R. thank the Spanish Ministry of Innovation for grants PID2020-118329RB-I00, PID2022-137764OB-I00 and TED2021-129214B-I00. This research used resources of the ALBA synchrotron and of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DEAC02-05CH11231.

References

1. R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816.
2. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143.
3. A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, J. Am. Chem. Soc., 1991, 113, 5873–5874.
4. D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006.
5. R. Bagai and G. Christou, Chem. Soc. Rev., 2009, 38, 1011–1026.
6. N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
7. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
8. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449.
9. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439.
10. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403.
11. G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147.
12. S. Gómez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018.
13. P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. Van Slageren, F. Neese and J. R. Long, Science, 2018, 362, eaat7319.
14. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E. S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202.
15. A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309.
16. M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352.
17. G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546.
18. D. Aguilà, O. Roubeau and G. Aromí, Dalton Trans., 2021, 50, 12045–12057.
19. M. Darawsheh, L. A. Barrios, O. Roubeau, S. J. Teat and G. Aromí, Chem. – Eur. J., 2016, 22, 8635–8645.
20. D. Y. Aleshin, R. Diego, L. A. Barrios, Y. V. Nelyubina, G. Aromí and V. V. Novikov, Angew. Chem., Int. Ed., 2022, 61, e202110310.
21. R. Diego, A. Pavlov, M. Darawsheh, D. Aleshin, J. Nehrkorn, Y. Nelyubina, O. Roubeau, V. Novikov and G. Aromí, Inorg. Chem., 2019, 58, 9562–9566.
22. M. J. Graham, J. M. Zadrozny, M. Shiddiq, J. S. Anderson, M. S. Fataftah, S. Hill and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 7623–7626.
23. M. Darawsheh, L. A. Barrios, O. Roubeau, S. J. Teat and G. Aromí, Angew. Chem., Int. Ed., 2018, 57, 13509–13513.
24. L. A. Barrios, R. Diego, M. Darawsheh, J. I. Martínez, O. Roubeau and G. Aromí, Chem. Commun., 2022, 58, 5375–5378.
25. N. Capó, L. A. Barrios, J. Cardona, J. Ribas-Ariño, S. J. Teat, O. Roubeau and G. Aromí, Chem. Commun., 2022, 58, 10969–10972.
26. H. Casellas, A. Pevec, B. Kozlevčar, P. Gamez and J. Reedijk, Polyhedron, 2005, 24, 1549–1554.
27. S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708.
28. G. Li Manni, I. Fdez. Galván, A. Alavi, F. Aleotti, F. Aquilante, J. Autschbach, D. Avagliano, A. Baiardi, J. J. Bao, S. Battaglia, L. Birnoschi, A. Blanco-González, S. I. Bokarev, R. Broer, R. Cacciari, P. B. Calio, R. K. Carlson, R. Carvalho Couto, L. Cerdán, L. F. Chibotaru, N. F. Chilton, J. R. Church, I. Conti, S. Coriani, J. Cuéllar-Zuquin, R. E. Daoud, N. Dattani, P. Decleva, C. de Graaf, M. G. Delcey, L. De Vico, W. Dobrautz, S. S. Dong, R. Feng, N. Ferré, M. Filatov, L. Gagliardi, M. Garavelli, L. González, Y. Guan, M. Guo, M. R. Hennefarth, M. R. Hermes, C. E. Hoyer, M. Huix-Rotllant, V. K. Jaiswal, A. Kaiser, D. S. Kaliakin, M. Khamesian, D. S. King, V. Kochetov, M. Krośnicki, A. A. Kumaar, E. D. Larsson, S. Lehtola, M.-B. Lepetit, H. Lischka, P. López Ríos, M. Lundberg, D. Ma, S. Mai, P. Marquetand, I. C. D. Merritt, F. Montorsi, M. Mörchen, A. Nenov, V. H. A. Nguyen, Y. Nishimoto, M. S. Oakley, M. Olivucci, M. Oppel, D. Padula, R. Pandharkar, Q. M. Phung, F. Plasser, G. Raggi, E. Rebolini, M. Reiher, I. Rivalta, D. Roca-Sanjuán, T. Romig, A. A. Safari, A. Sánchez-Mansilla, A. M. Sand, I. Schapiro, T. R. Scott, J. Segarra-Martí, F. Segatta, D.-C. Sergentu, P. Sharma, R. Shepard, Y. Shu, J. K. Staab, T. P. Straatsma, L. K. Sørensen, B. N. C. Tenorio, D. G. Truhlar, L. Ungur, M. Vacher, V. Veryazov, T. A. Voß, O. Weser, D. Wu, X. Yang, D. Yarkony, C. Zhou, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2023, 19, 6933–6991.
29. F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432–3445.
30. S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 4300.
31. J. H. Van Vleck, Phys. Rev., 1940, 57, 426–447.
32. E. J. Verwey, Phys. Lett. A, 1968, 28, 152–153.
33. A. M. Stoneham, Proc. Phys. Soc., 1965, 86, 1163.
34. K. J. Standley and R. A. Vaughan, Electron spin relaxation phenomena in solids, Plenum Press New York, New York, 1969.
35. L. Tesi, A. Lunghi, M. Atzori, E. Lucaccini, L. Sorace, F. Totti and R. Sessoli, Dalton Trans., 2016, 45, 16635–16643.
36. K. S. Pedersen, J. Dreiser, H. Weihe, R. Sibille, H. V. Johannesen, M. A. Sørensen, B. E. Nielsen, M. Sigrist, H. Mutka, S. Rols, J. Bendix and S. Piligkos, Inorg. Chem., 2015, 54, 7600–7606.
37. K. Petukhov, S. Bahr, W. Wernsdorfer, A. L. Barra and V. Mosser, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 064408.
38. M. Bal, J. R. Friedman, W. Chen, M. T. Tuominen, C. C. Beedle, E. M. Rumberger and D. N. Hendrickson, Europhys. Lett., 2008, 82, 17005.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis, DFT crystallography, and physical measurements. CCDC 2304058 and 2304059. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00629a

---