How the spin state tunes the slow magnetic relaxation field dependence in spin crossover cobalt(II) complexes

Abstract

A novel family of cobalt(II) compounds with tridentate pyridine-2,6-diiminephenyl type ligands featuring electron-withdrawing substituents of general formula [Co(n-XPhPDI)₂](ClO₄)₂·S [n-XPhPDI = 2,6-bis(N-n-halophenylformimidoyl)pyridine with n = 4 (1–3) and 3 (4); X = I (1), Br (2 and 4) and Cl (3); S = MeCN (1 and 2) and EtOAc (3)] has been synthesised and characterised by single-crystal X-ray diffraction, electron paramagnetic resonance, and static (dc) and dynamic (ac) magnetic measurements combined with theoretical calculations. The structures of 1–4 consist of mononuclear bis(chelating) cobalt(II) complex cations, [Co^II(n-XPhPDI)₂]²⁺, perchlorate anions, and acetonitrile (1 and 2) or ethyl acetate (3) molecules of crystallisation. This unique series of mononuclear six-coordinate octahedral cobalt(II) complexes displays both thermally-induced low-spin (LS)/high-spin (HS) transition and field-induced slow magnetic relaxation in both LS and HS states. A complete LS ↔ HS transition occurs for 1 and 2, while it is incomplete for 4, one-third of the complexes being HS at low temperatures. In contrast, 3 remains HS in all the temperature range. 1 and 2 show dual spin relaxation dynamics under the presence of an applied dc magnetic field (H_dc), with the occurrence of faster- (FR) and slower-relaxing (SR) processes at lower (H_dc = 1.0 kOe) and higher fields (H_dc = 2.5 kOe), respectively. On the contrary, 3 and 4 exhibit only SR and FR relaxations, regardless of H_dc. Overall, the distinct field-dependence of the single-molecule magnet (SMM) behaviour along with this family of spin-crossover (SCO) cobalt(II)-n-XPhPDI complexes is dominated by Raman mechanisms and, occasionally, with additional temperature-independent Intra-Kramer [LS or HS (D > 0)] or Quantum Tunneling of Magnetisation mechanisms [HS (D < 0)] also contributing.

---

Introduction

Mononuclear transition metal complexes constitute the most miniature molecular magnetic units for quantum data storage and processing applications in the emerging fields of molecular spintronics and quantum computing.¹ Spin crossover (SCO) compounds^2–13 and mononuclear single-molecule magnets (SMMs),^14–27 in their excellent paradigms of addressable and stimuli-responsive magnetic materials, are bistable magnetic molecules with potential applications in molecular spintronic devices and quantum computers.^28–52

From a historical viewpoint, in the molecular magnetism field, great attention was devoted to mononuclear cobalt(II) complexes as illustrative examples of SCO compounds^53–56 or SMMs.^57–60 Now, many cobalt(II)-based SCO compounds and SMMs are known, where both high- (HS, S_Co = 3/2) and low-spin (LS, S_Co = 1/2) states are available for a 3d⁷ cobalt(II) ion depending on the metal coordination environment. To date, a few examples are known where both properties coexist in the same system, leading to a new class of multiresponsive and multifunctional SCO/SMM materials as potential candidates for multistable molecular quantum bits (qubits) for quantum information processing (QIP).^61–63 Known cobalt(II)-based SCO/SMM systems include a series of double salts whereby the SCO and SMM behaviour have been separately identified on the two components of the ion pair.^64,65 In such cases, the SCO feature occurs in cationic six-coordinate octahedral complexes, and the SMM response arises from anionic four-coordinate tetrahedral ones. More interestingly, a series of mononuclear five-coordinate cobalt(II) SCO complexes with a square-pyramidal coordination geometry exhibits a field-induced SMM behaviour in the LS state;^66,67 one of them was recently tested as a molecular qubit prototype.⁶⁸ In truth, the LS cobalt(II) ion is a genuine two-level magnetic quantum system represented by the m_S = +1/2 and −1/2 states, able to play the role of a qubit for quantum computing applications. By comparison, the HS cobalt(II) ion possesses an effective doublet or quartet ground spin state (S_eff = 1/2 or 3/2) coming from the well-isolated ground Kramers doublet resulting from a large first-order spin–orbit coupling (SOC) with either easy-plane xy- (D > 0) or easy-axis Ising-type (D < 0) magnetic anisotropy, respectively. This feature makes this effective spin state an alternative candidate for a “single” qubit. Likewise, related mononuclear octahedral cobalt(II) complexes exhibit a chemo-, electro-, or photo-switching of the SCO and SMM behaviour, being thus postulated as promising candidates for chemical sensors and switches.^69–73

Cobalt(II) complexes with bidentate 2,2′-bipyridine (bipy) or tridentate 2,2′:6′,2′′-terpyridine (terpy) ligands and related imine derivatives constitute a major class of SCO systems. In this respect, Figgins and Busch reported in 1960 the first examples of the SCO phenomenon in mononuclear octahedral cobalt(II) complexes with N-methyl substituted, pyridine-2-imine (PI) and pyridine-2,6-diimine type (PDI) ligands.^74,75 Herein, we report the synthesis, structural, and spectroscopic characterisation, as well as the static (dc) and dynamic (ac) magnetic properties for a related series of mononuclear octahedral cobalt(II) compounds of formula [Co(n-XPhPDI)₂](ClO₄)₂·S [1: X = I (n = 4), S = MeCN; 2: X = Br (n = 4), S = MeCN; 3: X = Cl (n = 4), S = MeCO₂Et; and 4: X = Br (n = 3)] (Scheme 1). This novel family of cobalt(II) complexes displays thermally-induced LS–HS transition and field-induced slow magnetic relaxation in the LS and HS states. The distinct SCO and SMM behaviours depend on the halogen substituent, the para or meta substitution, or occasionally the presence of additional crystallisation solvent molecules (acetonitrile or ethyl acetate). This study allows us to obtain appropriate magneto-structural correlations that, with the aid of ab initio and density functional theory (DFT) calculations, could be useful in designing new SCO/SMM materials as prototypes of molecular spintronic devices for QIP.

Scheme 1 General chemical formula of the [Co^II(n-XPhPDI)₂]²⁺ complex cation in 1–4.

Experimental

Materials

All chemicals were of reagent-grade quality, purchased from commercial sources, and used as received.

Preparation of the ligands

4-XPhPDI (X = I, Br, and Cl). Pyridine-2,6-diformaldehyde (0.135 g, 1.0 mmol) and 4-iodoaniline (0.438 g, 2.0 mmol), 4-bromoaniline (0.344 g, 2.0 mmol) or 4-cloroaniline (0.255 g, 2.0 mmol) were dissolved in 5.0 mL of ethanol containing 100 μL of acetic acid. The reaction mixture was refluxed for 30 min and cooled in an ice bath. The white (X = I and Cl) and brown (X = Br) crystalline solids were collected by filtration, washed with a small amount of ethanol, and dried in the open air. Yield: 94, 90 and 93% for X = I, Br and Cl, respectively. Anal. calc. for C₁₉H₁₃N₃I₂ (4-IPhPDI): C, 42.49; H, 2.44; N, 7.82. Found: C, 42.88; H, 2.54; N, 7.61%. IR (KBr, cm⁻¹): 1622(m) [ν(C=N) from 4-IPhPDI ligand]. ¹H NMR (CDCl₃; 300 MHz, ppm): δ = 8.64 (s, 2H, H_im), 8.28 (d, 2H, m-H_py, J = 7.8 Hz), 7.95 (t, 1H, p-H_py, J = 7.8 Hz), 7.75 (d, 4H, m-H_Ph, J = 8.6 Hz), 7.06 (d, 4H, o-H_Ph, J = 8.6 Hz). Anal. calc. for C₁₉H₁₃N₃Br₂ (4-BrPhPDI): C, 51.50; H, 2.96; N, 9.48. Found: C, 51.25; H, 3.12; N, 9.66%. IR (KBr, cm⁻¹): 1625(m) [ν(C=N) from 4-BrPhPDI ligand]. ¹H NMR (CDCl₃; 300 MHz, ppm): δ = 8.64 (s, 2H, H_im), 8.28 (d, 2H, m-H_py, J = 7.8 Hz), 7.95 (t, 1H, p-H_py, J = 7.8 Hz), 7.55 (d, 4H, m-H_Ph, J = 8.6 Hz), 7.19 (d, 4H, o-H_Ph, J = 8.6 Hz). Anal. calc. for C₁₉H₁₃N₃Cl₂ (4-ClPhPDI): C, 64.42; H, 3.70; N, 11.86. Found: C, 63.25; H, 3.65; N, 11.99%. IR (KBr, cm⁻¹): 1626(m) [ν(C=N) from 4-ClPhPDI ligand]. ¹H NMR (CDCl₃; 300 MHz, ppm): δ = 8.65 (s, 2H, H_im), 8.28 (d, 2H, m-H_py, J = 7.8 Hz), 7.95 (t, 1H, p-H_py, J = 7.8 Hz), 7.40 (d, 4H, m-H_Ph, J = 8.6 Hz), 7.26 (d, 4H, o-H_Ph, J = 8.6 Hz).

3-BrPhPDI. Pyridine-2,6-diformaldehyde (0.135 g, 1.0 mmol) and 3-bromoaniline (218 μL, 2 mmol) were poured into 5.0 mL of ethanol containing 100 μL of acetic acid. The reaction mixture was refluxed for 30 min, and the solution evaporated under reduced pressure to afford an oil of the crude product that was lately dried under vacuum. Yield 98%. ¹H NMR (CDCl₃; 300 MHz, ppm): δ = 8.65 (s, 2H, H_im), 8.28 (d, 2H, m-H_py, J = 7.8 Hz), 7.95 (t, 1H, p-H_py, J = 7.8 Hz), 7.40 (d, 4H, m-H_Ph, J = 8.6 Hz), 7.26 (d, 4H, o-H_Ph, J = 8.6 Hz).

Preparation of the complexes

[Co(4-IPhPDI)₂](ClO₄)₂·MeCN (1), [Co(4-BrPhPDI)₂](ClO₄)₂·MeCN (2) and [Co(4-ClPhPDI)₂](ClO₄)₂·EtOAc (3). A methanolic solution (5.0 mL) of cobalt(II) perchlorate hexahydrate (0.037 g, 0.1 mmol) was added dropwise to a suspension of 4-IPhPDI (0.107 g, 0.2 mmol), 4-BrPhPDI (0.088 g, 0.2 mmol) or 4-ClPhPDI (0.071 g, 0.2 mmol) in methanol (10.0 mL). The reaction mixtures were heated at 50 °C for 30 minutes. The resulting red precipitate was collected by filtration and washed with a small amount of methanol in all three cases. X-ray quality crystals of 1–3 were grown by slow diffusion of ethyl acetate through saturated acetonitrile/chloroform (1 : 1 v/v) solutions in glass tubes. Yield: 66 (1), 73 (2) and 62% (3). Anal. calc. for C₄₀H₂₉N₇O₈Cl₂I₄Co (1): C, 34.99; H, 2.13; N, 7.14. Found: C, 35.21; H, 2.08; N, 7.42%. IR (KBr, cm⁻¹): 2244(w) [ν(C≡N) from acetonitrile], 1580(m) [ν(C=N) from 4-IPhPDI], 1086(vs) [ν(Cl–O) from perchlorate]. UV-Vis (MeCN): ν_max (cm⁻¹) [ε (M⁻¹ cm⁻¹)] = 50 762 [114 883], 43 479 [71 901] and 28 654 [34 774]. Anal. calc. for C₄₀H₂₉N₇O₈Cl₂Br₄Co (2): C, 40.54; H, 2.47; N, 8.27. Found: C, 40.66; H, 2.45; N, 8.45%. IR (KBr, cm⁻¹): 2244(w) [ν(C≡N) from acetonitrile], 1580(m) [ν(C=N) from 4-BrPhPDI], 1086(vs) [ν(Cl–O) from perchlorate]. ν_max (cm⁻¹) [ε (M⁻¹ cm⁻¹)] = 51 282 [105 132], 43 860 [51 854] and 29 326 [26 960]. Anal. calc. for C₄₂H₃₄N₆O₁₀Cl₆Co (3): C, 47.84; H, 3.25; N, 7.97. Found: C, 47.66; H, 3.35; N, 7.92%. IR (KBr, cm⁻¹): 1730 (m) [ν(C=O) from ethyl acetate], 1580(m) [ν(C=N) from 4-ClPhPDI], 1086(vs) [ν(Cl–O) from perchlorate]. ν_max (cm⁻¹) [ε (M⁻¹ cm⁻¹)] = 51 282 [10 351], 44 053 [55 620] and 29 586 [28 428].

[Co(3-BrPhPDI)₂](ClO₄)₂ (4). Pyridine-2,6-diformaldehyde (0.027 g, 0.2 mmol) and 3-bromoaniline (44 μL, 0.4 mmol) were poured into 5.0 mL of ethanol containing 100 μL of acetic acid. Over the reaction mixture refluxed for 30 min was added dropwise a methanolic solution (5.0 mL) of cobalt(II) perchlorate hexahydrate (0.037 g, 0.1 mmol) and then heated at 50 °C for 30 minutes. The resulting red precipitate was filtered and washed with a small amount of methanol. X-ray quality crystals of 4 were grown by slow diffusion of ethyl acetate through a saturated acetonitrile/chloroform (1 : 1 v/v) solution in a glass tube. Yield 83%. Anal. calc. for C₃₈H₂₆N₆O₈Cl₂Br₄Co (4): C, 39.89; H, 2.29; N, 7.35. Found: C, 40.02; H, 2.36; N, 7.65%. IR (KBr, cm⁻¹): 1572(m) [ν(C=N) from 3-BrPhPDI], 1088(vs) [ν(Cl–O) from perchlorate]. ν_max (cm⁻¹) [ε (M⁻¹ cm⁻¹)] = 50 505 [68 630], 45 872 [61 543], and 30 395 [19 985].

Physical techniques

Elemental analyses (C, H, N) were performed at the Servicio Central de Soporte a la Investigación (SCSIE) at the Universitat de València (Spain). FTIR spectra were recorded on a Nicolet-5700 spectrophotometer as KBr pellets. Electronic absorption spectra of the ligands and complexes 1–4 (c_L = c_M = 5 × 10⁻³ mM) were carried out in acetonitrile solutions at room temperature with a Jasco UV/Vis/NIR V-670 spectrophotometer. ¹H NMR spectra were recorded at room temperature on a Bruker AC 300 (300 MHz) spectrometer. Deuterated chloroform was used as solvent and internal standard (δ = 7.26 ppm). Q-band EPR spectra of powdered samples of 1–4 were recorded at 4.0 K under non-saturating conditions with a Bruker ER 200 D spectrometer equipped with a helium-flow cryostat. PXRD data were obtained on a powder X-ray diffractometer (model Ultima IV, Rigaku, Japan) using Cu K_α radiation (λ = 1.5418 Å) at a voltage of 40 kV and a current of 30 mA with θ–2θ geometry. Data were collected using a 2θ step of 0.02° and a counting time of 0.25° 2θ min⁻¹ in the angular range from 5 to 40° (2θ).

Magnetic measurements

Variable-temperature (2.0–300 K) direct current (dc) magnetic susceptibility measurements under applied fields of 0.25 (T < 20 K) and 5.0 kOe (T > 20 K) and variable-field (0–50 kOe) magnetisation measurements at 2.0 K were carried out on crushed crystals of 1–4 with a Quantum Design SQUID magnetometer. Alternating current (ac) magnetic susceptibility measurements of 1–4 in the temperature range 0–12.0 K under ±5.0 Oe oscillating field at frequencies in the range of 0.1–10.0 kHz were performed under different applied static dc fields (0–2.5 kOe) with a Quantum Design Physical Property Measurement System (PPMS). The magnetic susceptibility data were corrected for the diamagnetism of the constituent atoms and the sample holder (a plastic bag).

Crystal structure data collection and refinement

X-ray data on single crystals of 1–4 were collected with Mo-K_α radiation (λ = 0.71073 Å) at 150 K on a Bruker APEX-II CCD (1 and 3) and an Agilent Supernova diffractometers (2 and 4), the last one equipped with an EosS2 detector. Collection, scalation, and integration of data were carried out with Bruker SAINT⁷⁶ (1 and 3) and CrysAlisPro⁷⁷ (2 and 4) software. The crystal structures were solved by intrinsic phasing methods integrated into the SHELXTL software4⁷⁸ with the Olex2 platform.⁷⁹ The models were refined by full-matrix least-squares on F² using the SHELXL-2018/3 program. Non-hydrogen atoms were anisotropically refined. Hydrogen atoms were set on geometrical positions and refined with a riding model. Two positions were found for the I2 and I7 iodine and perchlorate (Cl4) oxygen atoms of 1. The site occupancy factors (s.o.f., 0.454 and 0.546 for I2 and I2A, and 0.817 and 0.183 for I7 and I7A) of iodine atoms were refined, and constraints were applied to the bond lengths and anisotropic factors of the perchlorate oxygen atoms. Since the perchlorate Cl6 in 3 is disordered in two positions, their s.o.f. were refined considering soft restraints on the distances between oxygen atoms. Two bromophenyl groups in 4 occupy two positions connected by a rotation (ca. 180°) around the N_im–C_Ph bond; therefore, they were modelled in these positions, and their s.o.f. refined (0.484 and 0.516 for Br8 and Br8B, and 0.831 and 0.169 for Br4 and Br4B). Some constraints were also applied to the anisotropic displacements of the carbon atoms. Three perchlorate groups in 4 are also disordered into two positions; their s.o.f. were refined, and some restraints on Cl–O bond lengths and anisotropic displacements of the chlorine and oxygen atoms were applied to make more accessible the convergence of the refinement. The graphical manipulations and calculations were performed with the CRYSTALMAKER and MERCURY programs.^80,81Tables 1, S1 and S2† summarise crystallographic data, refinement conditions, and relevant structural parameters for 1–4. Crystallographic data (excluding structure factors) of 1–4 have been deposited with the Cambridge Crystallographic Data Centre as supplementary publication number CCDC 2040602 (1), 2040600 (2), 2040601 (3) and 2040599 (4).†

Table 1 Selected structural data for 1–4^a

		R 1(Co–Npy)^b (Å)	R 2(Co–Nim)^c (Å)	R 3(Co–N′im)^c (Å)	R eq ^d (Å)	R (Å)
a Structural data for each crystallographically independent cobalt atom. b Average axial cobalt to pyridyl–nitrogen bond distance from the two ligands. c Average equatorial cobalt to imine–nitrogen bond lengths from each ligand. d Average equatorial cobalt–nitrogen bond distance defined as Req = (R2 + R3)/2. e Average cobalt–nitrogen bond distance defined as R = (R1 + R2 + R3)/3.
1	Co1	1.907(2)	2.113(3)	2.126(3)	2.117(3)	2.047(3)
	Co2	1.902(2)	2.026(2)	2.209(2)	2.117(2)	2.046(2)
2	Co1	1.892(3)	2.035(3)	2.192(3)	2.114(3)	2.039(3)
	Co2	1.884(3)	2.094(3)	2.126(3)	2.110(3)	2.035(3)
3	Co1	2.0255(19)	2.185(2)	2.228(2)	2.207(2)	2.146(2)
4	Co1	1.904(5)	2.018(5)	2.245(5)	2.132(5)	2.055(5)
	Co2	1.940(5)	2.081(5)	2.194(5)	2.138(5)	2.071(5)
	Co3	2.024(5)	2.205(5)	2.214(5)	2.210(5)	2.148(5)

---

Computational details

DFT study: geometries and spin densities. Because in an SCO system the crystal structure is strongly temperature-dependent, there may be some problems in recognising a molecular geometry as one of the two competing configurations, HS and LS, from the experimental data at a given temperature. For this reason, the geometry of the mononuclear complex [Co(n-XPhXPDI)₂]²⁺ of one of the compounds, specifically 3, has been chosen and optimised in the two electronic configurations. This study was carried out by DFT-type calculations through the Gaussian 09 package using the hybrid B3LYP functional,^82,83 the quadratic convergence approach and Ahlrichs’ triple and double-zeta (TZVP) basis sets for cobalt and the rest of atoms.^84,85 A polarisable continuum model (PCM) was used with the parameters corresponding to the acetonitrile to avoid the usual electronic overdelocalisation in DFT calculations.⁸⁶ Optimised geometries were then confirmed as global minima by frequency calculations.

Ab initio calculations on the zfs tensors. The parameters that determine the axial (D) and rhombic (E) components of the local zero-field splitting (zfs), the g-tensor for the S = 3/2 state (g_3/2) and the ground Kramers doublet (g_eff) of 3 and the HS form of 4 were estimated from theoretical calculations based on a second-order N-electron valence state perturbation theory (CASSCF/NEVPT2) through an effective Hamiltonian for the spin–orbit coupling (SOC),^87–89 which often provides accurate values of the nearby excited states energies and for the zfs tensor of mononuclear first-row transition metal complexes. Experimental geometries were used in this study. Calculations were carried out on the experimental geometries with version 4.0.1 of the ORCA programme⁹⁰ using the def2-TZVP basis set proposed by Ahlrichs⁹¹ and the auxiliary TZV/C Coulomb fitting basis sets.^92–94 The contributions to zfs from 10 quartet and 20 doublet excited states generated from an active space with seven electrons in five d orbitals were included using an effective Hamiltonian. RIJCOSX method combining resolution of the identity (RI) and “chain of spheres” COSX approximations for the Coulomb and exchange terms was used.^95–97

Results and discussion

Synthesis and general characterisation

The n-XPhPDI ligands (with n-X = 4-I, 4-Br, 3-Br, 4-Cl) were synthesised from the straightforward condensation of pyridine-2,6-diformaldehyde and the corresponding para- or meta-monosubstituted aniline (1 : 2 molar stoichiometry) in acid media, as reported earlier for the parent unsubstituted PhPDI ligand.⁷⁰ All these 4-XPhPDI ligands were isolated as crystalline powders in good yields, and they were characterised by elemental analyses (C, H, N), Fourier-transform infrared (FT-IR) and proton nuclear magnetic resonance (¹H NMR) spectroscopies. In contrast, the 3-BrPhPDI ligand could not be isolated as a solid and was used as an oily crude product.

The reaction between cobalt(II) perchlorate hexahydrate and the corresponding 4-XPhPDI ligand (X = I, Br, and Cl) in the 1 : 2 molar ratio in methanol led to crystalline powders of 1–3. Compound 4 was synthesised by an in situ reaction of pyridine-2,6-diformaldehyde and 3-bromoaniline with cobalt(II) perchlorate hexahydrate. X-ray suitable single crystals of 1–4 were grown in a test tube by layering ethyl acetate on saturated acetonitrile/chloroform solutions of the crystalline powder. The experimental and calculated (from the CIF files) PXRD patterns of 1–4 (Fig. S1†) showed a remarkable coincidence of the position of all peaks, confirming the purity of the bulk materials for each sample.

Description of the structures

Compounds 1 and 2 crystallise in the P2₁/c space group of the monoclinic system; 3 and 4 do so in the P1̄ and P2₁/n space groups of triclinic and monoclinic systems (Table S1†). All structures consist of mononuclear cobalt(II) complex cations, [Co^II(n-XPhPDI)₂]²⁺ [n = 4 (1–3) and 3 (4); X = I (1), Br (2 and 4) and Cl (3)], perchlorate anions, and acetonitrile (1 and 2) or ethyl acetate (3) crystallisation solvent molecules. However, while 3 embodies a single crystallographically independent cationic complex, two coexist in 1 and 2 and even three in 4 (Fig. 1 and 2).

Fig. 1 Perspective views of the crystallographically independent mononuclear cobalt(II) units of 1–4 (a–d) with the atom numbering scheme of the coordination sphere at the cobalt atom. The ligand backbones are drawn in grey and black colours for clarity whereas the pink and green cobalt atoms correspond to the LS and HS configuration, respectively.

Fig. 2 Projection views of the crystal packing of 1–4 showing the supramolecular 3D network in 1 and 2 (a and b), 2D array of π–π stacked hexagonal grids in 3 (c) and 1D array of π-connected chains in 4 (d) through π–π stacking (dashed lines) and X⋯X contacts (brown and orange solid lines) among the mononuclear units [Symmetry operation: (i) = −x + 1, −y + 1, −z + 1 (1 and 2); (i) = x, y − 1, z (3); (i) = 1 + x, y, z (4); (ii) = 1 + x, y, z (3)].

Molecular structures. All cobalt atoms in the four compounds exhibit the same rhombically distorted, axial compressed octahedral CoN₆ environment (Fig. 1 and S2†), as reported earlier for the parent complex of formula [Co^II(PhPDI)₂](ClO₄)₂·CH₃OH.⁷⁵ The significant deviations from the ideal C_2v molecular symmetry in 3 and 4 are most likely due to the occurrence of a weak intramolecular face-to-face π–π stacking interaction between the central pyridyl and terminal phenyl rings from the ligands (Fig. 1c and d), as evidenced by the intramolecular distance between the centroids of both rings (h) and the dihedral angle (θ) between their mean planes (see Table S2†). In the coordination sphere, imine-nitrogen atoms (N_im and N′_im) from each n-XPhPDI ligand define the equatorial plane, while pyridyl-nitrogen atoms (N_py and N′_py) occupy the axial positions. Co–N bond lengths are grouped into two shorter Co–N_py and Co–N′_py [average R₁ = 1.905 (1), 1.888 (2), 2.028 (3), and 1.922 and 2.024 Å (4)], two intermediate Co–N_im [average R₂ = 2.070 (1), 2.065 (2), 2.185 (3), and 2.050 and 2.205 Å (4)], and two longer Co–N′_im bonds [average R₃ = 2.168 Å (1), 2.159 (2), 2.228 (3), and 2.200 and 2.214 Å (4)] (see Table 1). The average values of the axial bond lengths (R_ax) are rather shorter than the equatorial ones [average values: R_eq = (R₂ + R₃)/2 = 2.117 (1), 2.112 (2), 2.207 (3), and 2.125 and 2.210 Å (4)] (see Table 1).

Due to some asymmetry observed in these compounds, these bond distances are difficult to assign to a specific spin state when viewed individually. Nevertheless, the mean values [R = (2R_eq + R_ax)/3 = 2.047 (1), 2.037 (2), and 2.147 Å (3)] are typical for LS Co^II complexes in 1 and 2, but HS in 3. However, both LS and HS Co^II complexes coexist in 4 in a 2 : 1 ratio [R = 2.057 (Co1/Co2) and 2.148 Å (Co3)]. The stronger electron-withdrawing character of the p-chloro substituent (3) compared to the p-iodo- and p-bromo ones (1 and 2) should provide a weaker ligand field, explained by the HS t_2g⁵e_g² electronic configuration in 3. Since the d orbitals mainly participate in antibonding molecular orbitals and the e_g ones have their electron density better directed to the bond regions than the t_2g ones, the greater occupation of the former in the HS state (3) is responsible for its Co–N bond lengthening. However, the electronic effects induced in 4 by the weaker inductive character of the bromine substituent are partially compensated by its meta placement in the phenyl ring. Nevertheless, it is well known that the network, including the crystal packing, plays a relevant role in stabilising a particular electronic configuration of a SCO system, which is probably the case here where there are Br⋯Br strong intermolecular contacts. This circumstance is probably why the HS and LS configurations occur together in 4.

Crystal structures. Moderate and weak intermolecular face-to-face π–π stacking interactions occur in the crystal lattices of 1–4 between the halophenyl rings (only three of the four ones in 3) from neighbouring crystallographically independent [Co^II(n-XPhPDI)₂]²⁺ units, as shown in Fig. 2. The presence of these contacts, together with edge-to-face π–π interactions in 3, lead to supramolecular dimers (1 and 2), hexagonal grid (3), and double-connected chains of complex cations (4).

The springing up of intermolecular halogen–halogen interactions between neighbouring [Co^II(n-XPhPDI)₂]²⁺ units also contribute to stabilising the crystal packing of 1, 2, and 4 (Fig. 2 and S3†), but they are not present in 3 or in the HS cobalt(II) units of 4. The interhalogen distances [I⋯I = 3.858–3.964 Å (1), Br⋯Br = 3.624–3.680 Å (2), and Br⋯Br = 3.072–3.492 Å (4)] are slightly shorter than the sum of the van der Waals radii (I⋯I < 4.0 Å and Br⋯Br < 3.7 Å). Both intermolecular interactions in 1 and 2 lead to a supramolecular three-dimensional array along the crystallographic a axis (Fig. S3 and S4†), the holes being filled by perchlorate anions and acetonitrile molecules. In contrast, this situation in 4 promotes π-linked supramolecular chains of cationic mononuclear cobalt(II) complexes rather well-isolated from each by perchlorate anions placed into the interchain space (Fig. S6†). Mononuclear cobalt(II) complex cations and perchlorate anions in 3 are arranged to build a segregated layer array (Fig. S5†), where ethyl acetate molecules occupy the interlayer space establishing weak intermolecular van der Waals contacts with complex cations.

EPR spectra and theoretical calculations

Q-Band EPR spectra of crushed crystals of 1–4 at 4.0 K are in Fig. 3. All spectra show a strong predominant signal around g = 2.0 (12 000 G), typical for LS cobalt(II) complexes, split in two by the high distortion (axial and rhombic) imposed by n-XPhPDI ligands. However, two low-field signals, whose patterns are characteristic of HS cobalt(II) octahedral complexes, are also recorded for 3 and 4.⁵⁷ The presence of additional LS signatures in 3 indicates a small residual fraction of the LS phase, not inferred from crystallography and the less sensitive magnetometry techniques (see discussion below).

Fig. 3 Experimental Q-band EPR spectra of 1–4 (a–d) in the solid state at 4.0 K (black solid lines). X-band spectrum of 3 appears as inset. Red and blue solid lines are the simulated curves for S_eff = 1/2 and anisotropic S = 3/2 approaches (see text). The asterisks indicate the signals from the HS fraction.

EPR spectra of 1–4 were simulated jointly for the LS and HS fractions. LS contributions were satisfactorily simulated considering a highly axial (g_x = g_y ≠ g_z) for 3 and a rhombic octahedron (g_x ≠ g_y ≠ g_z) for the rest. Table S3† summarises the g values used in these simulations.

Based on the crystal structure, 4 is the only compound in which HS and LS configurations patently coexist. Its low-field EPR signals (g_eff = [2.39, 3.47, 6.42]), marked with an asterisk in Fig. 3d, can only correspond to the ground Kramers doublet of the HS fraction. These values are typical of an easy-plane zfs (D > 0), the most common situation in octahedral cobalt(II) complexes, and agree with those found by ab initio CASSCF/NEVPT2 calculations (g_x = 3.25, g_y = 7.21 and g_z = 2.06). A subsequent analysis considering a zfs on the quartet ground state (g_x = 2.47, g_y = 2.77, g_z = 2.13, D > 0, and E/D = 0.11) and ab initio calculations (D = +92.6 cm⁻¹ and E/D = 0.207) confirm the easy-plane zfs and a moderate rhombicity. While there is reasonable agreement between theoretical and experimental results, it is important to note that the theoretical predictions should be considered semiquantitative at best, as indicated by an abnormal g₁ value (1.91) and a large mixing of the spin components into the ground Kramers doublet, suggesting that the three spin states comprising the ⁴T₁ term in an ideal octahedral symmetry are nearly degenerate (0, 512, and 623 cm⁻¹). As a result, second-order perturbation theory may encounter challenges in its applicability.⁹⁸

However, among the four compounds, the only one exhibiting a HS configuration down to 2.0 K is 3, which shows a split signal at low fields (H < 4000 G), also occurring in the X-band spectrum. The g_i values for the two components of this signal are strongly dependent on the microwave frequency band but not their centre of gravity, which is indicative of an effect of the field-modulation amplitude, being this midpoint that provides the real g value. This signal at g_z = 7.8 is conclusive evidence of an easy-axis zfs (D < 0).^99,100 In such a situation, the two remaining g_eff components must take low values, enough so that they cannot be observed by Q-band EPR spectroscopy, but it does in X-band. Thus, the X-band spectrum shows an asymmetric signal at fields higher than those for the residual LS fraction, a consequence of the proximity between the signals at g_x = 1.43 and g_y = 1.54. According to that, the analysis of the X-band spectrum considering a zfs on a quartet spin state provided the following results: g_x = 2.25, g_y = 2.05, g_z = 2.78, D < 0, and E/D = 0.25, which are in agreement with the previous discussion and those found from ab initio calculations (g_eff = [1.19, 1.39, 8.56] or g_3/2 = [1.95, 2.15, 3.04], D = −92.1 cm⁻¹, and E/D = 0.196).

In conclusion, EPR spectroscopy allows determining the spin state and also the presence of the minor molecules undergoing a spin transition or the opposite. Supported by theoretical calculations, this spectroscopic technique has shown that this family of compounds, with unusual molecular geometries, can show both easy-axis and easy-plane anisotropies on the HS configurations. These electronic changes in a highly distorted geometry must occur by subtle geometric modifications imposed by the packing in the crystal network arising from the observation or not of a spin transition phenomenon.

Magnetic properties and theoretical calculations

The spin crossover and spin dynamics for this unique family of mononuclear cobalt(II)-n-XPhPDI complexes with electron-withdrawing substituents at the terminal phenyl rings were investigated through static (dc) and dynamic (ac) magnetic measurements in the temperature ranges 2.0–300 and 2.0–10.0 K, respectively.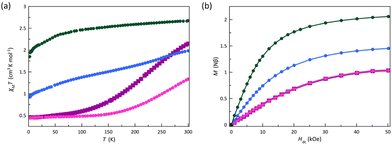

Static magnetic behaviour. The dc magnetic properties of 1–4 in the form of the χ_MT vs. T and M vs. H/T plots (χ_M and M being the molar dc magnetic susceptibility and magnetisation per mononuclear unit, T the absolute temperature, and H the applied magnetic field) are shown in Fig. 4 and S7.†

Fig. 4 (a) Temperature dependence of χ_MT and (b) field dependence of M at 2.0 K for 1 (■), 2 (●), 3 (●), and 4 (●). The solid lines are only eye guides.

The χ_MT versus T plots for 1–4 reveal a behaviour dependence on the electron-withdrawing character of the substituents and their meta or para location (Fig. 4a). At 300 K, χ_MT for 3 is 2.68 cm³ mol⁻¹ K, a value expected for a HS cobalt(II) ion with an unquenched orbital momentum contribution (2.70 cm³ mol⁻¹ K with g_Co = 2.4). However, the χ_MT values at room temperature for 1, 2, and 4 (2.15, 1.33, and 1.98 cm³ mol⁻¹ K, respectively) are much smaller. For 3, the smooth but gradual decrease in χ_MT on cooling to 1.85 cm³ mol⁻¹ K at 2.0 K reveals the occurrence of a significant zfs coming from the first-order SOC typical of an octahedral HS cobalt(II) complex (⁴T_1g term with S_Co = 3/2 and L_Co = 1). Upon cooling, a complete spin transition (with no hysteresis) occurs for 1 and 2, as reported earlier for the related complex with the electron-donating p-methoxy-substituted PDI ligand.⁷⁰ This fact is revealed by the gradual decrease of χ_MT to reach a sort of plateau [ca. 50 (1) and 150 K (2)]. The χ_MT value of 0.45 cm³ mol⁻¹ K at 2.0 K for 1 and 2 is expected for an LS cobalt(II) ion [χ_MT = (Nβ²g_Co²/3k_B)S_Co(S_Co + 1) = 0.45 cm³ mol⁻¹ K with S_Co = 1/2 and g_Co = 2.2]. In contrast, compound 4 exhibits a gradual and incomplete spin transition in agreement with the coexistence of the LS and HS signature signals observed in the EPR spectra, as reported earlier for the parent unsubstituted complex.⁷⁵ Even though the spin assignment for 4 is challenging, the χ_MT value of 0.92 cm³ mol⁻¹ K at 2.0 K agrees with that estimated for one HS and two LS cobalt(II) ions inferred from its single-crystal X-ray structure.

The M versus H plots at 2.0 K for 1–4 further conform to the aforementioned interpretation (Fig. 4b). So, the value of M at 50 kOe for 1 and 2 is 1.00Nβ, being then close to the calculated one for the saturation magnetisation of a doublet spin state of an LS cobalt(II) ion (M_s = g_CoS_CoNβ = 1.10Nβ with S_Co = 1/2 and g_Co = 2.2). Besides, for an LS octahedral cobalt(II) complex with S_Co = 1/2 on which a magnetic anisotropy does not cause any splitting, the isothermal magnetisation curves should superimpose if they are magnetically isolated, as practically occurs for 1 and 2 in the temperature range from 2.0 to 10.0 K (Fig. S7a and b†). In contrast, M at 50 kOe for 3 is 2.06Nβ, a value which agrees with the calculated one for the saturation magnetisation for an effective doublet spin state of an HS cobalt(II) ion (M_s = g_CoS_CoNβ = 2.10Nβ with S_Co = S_eff = 1/2 and g_Co = 4.2). In this case, the ground ±3/2 and excited ±1/2 Kramers doublets for D < 0, or vice versa for D > 0, are well-separated due to the sizeable zfs effects operating on the quartet ground state, recording only the magnetisation for the ground Kramers doublet. On the other hand, the value of M equal to 1.45Nβ for 4 at 50 kOe is close to that estimated for the saturation magnetisation corresponding to one HS and two LS cobalt(II) ions [M_s = (2.10 + 2 × 1.10)/3 = 1.43Nβ]. In contrast, isothermal magnetisation curves of 3 and 4 do not superimpose below 10.0 K (Fig. S7c and d†), supporting the occurrence of substantial zfs effects resulting from the significant SOC acting on their HS cobalt(II) ions. Unfortunately, all the attempts to fit the χ_MT vs. T and M vs. H/T data of 3 taking into account either a first-order spin–orbit coupling or a dominant zfs were unsuccessful, a consequence of the presence of a residual LS phase, evidenced in the EPR study (see below).

Dynamic magnetic behaviour. Ac magnetic properties of 1–4 were studied in the absence and under applied dc magnetic fields (H_dc) of 1.0 and 2.5 kOe. The in-phase (χ′_M) and out-of-phase (χ′′_M) ac molar magnetic susceptibility show frequency dependence under a H_dc (Fig. S8–S11†). However, they show neither frequency dependence of χ′_M nor a χ′′_M signal (data not shown) in the absence of a H_dc, more likely because of a fast quantum tunneling of magnetisation (QTM). Although QTM can avoid a slow magnetic relaxation, it becomes less efficient when applying a H_dc, as in 1–4. This particular field-dependent behaviour, typical of mononuclear SMMs known as field-induced SMMs, must exhibit an energy barrier governing the spin reversal arising from a easy-axis zfs (D < 0). However, this argument does not apply for LS or easy-plane HS electronic configurations in cobalt(II) complexes since both procure ground ±1/2 Kramers doublets that make a fast spin-reversal possible eluding other excited ones. Such a process is known as intra-Kramer (IK) relaxation.

Direct and IK processes may seem to be the same, but they are not. Direct relaxation can be applied to easy-axis non-Kramer or any Kramer ions, while the IK mechanism only works on easy-plane Kramer or S = 1/2 ions. Therefore, the IK contribution in our systems is related to a passage between the Zeeman-split components m_S = ±1/2 of the LS Co^II ion (S = 1/2) or the easy-plane HS Co^II ion (S = 3/2). Interestingly, both mechanisms are temperature-independent only without an external magnetic field. However, under a H_dc, the thermal dependence differs since an IK process should follow an Arrhenius law with a minimal energy barrier corresponding to the Zeeman-splitting of the ground Kramer doublet, which makes this relaxation appear temperature-independent with most common working magnetic fields.

This series of compounds reveals that the HS and LS configurations behave differently, the blocking temperature being higher for the former and intermediate for 4 (Fig. S11†), which contains both in a 2 : 1 LS/HS ratio below 150 K (see above). In this case, the presence of HS Co^II ions would affect the magnetic relaxation of the adjacent LS Co^II ions, and vice versa.

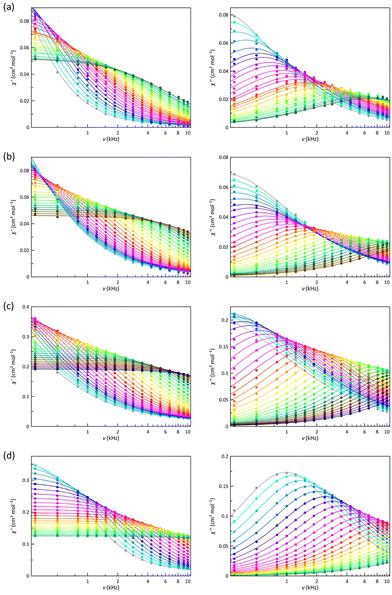
Similarly, while the blocking temperature strongly depends on H_dc for the LS configuration, it is entirely invariant for the HS one (Fig. S10†). These characteristics suggest that the mechanisms of magnetic relaxation or how they operate will be different in the two spin configurations, and they are probably strongly linked to electronic aspects such as the mixing of M_s functions by the rhombic parameter of zfs, nature of the occupied 3d orbitals, spin delocalisation on the ligands, or low-energy molecular vibrational modes. Additionally, new signals displayed as incipient or a shoulder appear in the χ′′_Mvs. T curves, mainly in 3 and under the H_dc of 2.5 kOe, allowing to discern higher (HT) and lower (LT) temperature magnetic relaxation processes.

The best way to calculate the magnetic relaxation time (τ) is the joint analysis of the χ′_M and χ′′_Mvs. ν data (Fig. 5 and 6) through the generalised Debye model, which also takes into account the static and infinite frequency magnetic susceptibility (χ_S and χ_T), and the exponential factor that describes the spectral breadth (α), as additional fitting parameters.¹⁰¹

Fig. 5 Frequency dependence of χ′_M (left) and χ′′_M (right) for 1 (a), 2 (b), 3 (c), and 4 (d) at a ± 5.0 G oscillating field in the temperature range 2.0–10 K under an applied static magnetic field of 1.0 kOe. The solid lines are the best-fit curves simulated by using the generalised Debye model (see text).

Fig. 6 Frequency dependence of χ′_M (left) and χ′′_M (right) for 1 (a), 2 (b), 3 (c), and 4 (d) at a ± 5.0 G oscillating field in the temperature range of 2.0–10 K under an applied static magnetic field of 2.5 kOe. The solid lines are the best-fit curves simulated by using the generalised Debye model (see text).

Two types of graphic representations are recommended according to the nature of the relaxation mechanisms involved. For thermally activated two-phonon Orbach-type relaxations [τ_ORB⁻¹ = τ₀⁻¹ exp(−U_eff/T)], an Arrhenius plot is preferable since they show a linear dependence where the slope directly estimates the energy barrier (U_eff) controlling the spin reversal. However, a ln τ vs. ln T plot showing linear dependencies of slope n is more appropriate for one-phonon direct or two-phonons Raman-like mechanisms (τ⁻¹ ∝ Tⁿ). When n takes values close to 2 or 8, optical or acoustic phonon-assisted Raman mechanisms dispense the fastest spin reversal.¹⁰² Instead, a direct mechanism plays the main role for n values close to unity. Nevertheless, both representations are helpful for temperature-independent relaxations, such as QTM or IK.

That being so, ln τ vs. ln T (Fig. 7) and ln τ vs. 1/T Arrhenius plots (Fig. S14†) were drawn for 1–4 at H_dc = 0.5–5.0 kOe. In all cases, there is a deviation from a linear dependence, suggesting that several relaxations coexist and compete. In the Arrhenius plots, it is not easy to distinguish straight lines, indicating that one of the mechanisms utterly prevails, which is not surprising for LS 1 and 2 since a S = 1/2 spin state cannot present an energy barrier for the spin reversal. However, the energy barrier so evaluated has sometimes been related to the energy required to reach low-lying vibrational modes that make the spin reversal easier and faster. A similar case would be that for an easy-plane HS cobalt(II) complex (D > 0), as in the HS site of 4, where the |±1/2〉 ground Kramers doublet allows fast relaxation, at least in the absence of a H_dc, being required a H_dc to observe slow magnetic relaxation effects.¹⁰³ However, 3, exhibiting a easy-axis zfs (D < 0), should be a different case where an energy barrier exists. Therefore, both representations were analysed for the four compounds. In general, a relatively high energy barrier acts at high temperatures and a significantly lower one at low temperatures. The values of this second energy barrier are too low to be related to vibrational modes and are probably a consequence of the magnetic effect on a fast IK relaxation or even competing direct or Raman mechanisms. Similarly, the energy barriers found for 3 are quite lower than that provided by the zfs. So, the fastest relaxation mechanisms must be of a different nature and probably, once again, Raman or direct type.

Fig. 7 ln τ vs. ln T plot for the calculated magnetic relaxation times (τ) of 1 (purple), 2 (pink), 3 (green), and 4 (blue) under applied dc magnetic fields of 1.0 (○) and 2.5 kOe (●). Dashed and solid lines are the best-fit curves (see text). Vertical error bars denote the standard deviation.

As with the Arrhenius plots, the ln τ vs. ln T plots for 1–4 do not usually show regions with linear dependencies. However, for 2 under a 2.5 kOe magnetic field, these features are observed at high and low temperatures. The derived n values show that Raman mechanisms assisted by optical and acoustic phonons govern the relaxation of the magnetisation at low and high temperatures, respectively. Although linear dependencies are not observed clearly under other magnetic fields or compounds, there is no reason to think that this does not occur in all of them, particularly in those that also exhibit a LS configuration. In this sense, these cases are usually described with n values intermediate between those corresponding to optical and acoustic phonons. However, good simulations are also found with values closer to what might be expected. Therefore, obtaining accurate values for n requires an extensive data range, which is not always possible, and a meticulous analysis of the experimental data to get the relaxation times. Besides, it is also essential to avoid, without physical evidence, using an oversised set of relaxation mechanisms, which will lead to additional overparameterisation problems. Considering these conclusions, we tried to carry out a similar analysis in all cases. Furthermore, a dominant temperature-independent relaxation becomes apparent under specific magnetic fields. For a LS electronic configuration, this new process can only be assigned to an IK relaxation, a direct and enabled interchange between the two M_s components of ground doublet (|+1/2〉 ⇔ |−1/2〉). The difficulties in achieving accurate relaxation times and subsequent analysis can make it challenging to establish general conclusions, but qualitative scrutiny of the ln τ vs. ln T and Arrhenius plots is often more informative.

It is worth noting that the temperature-independent relaxation in 3, due to an energy barrier arising from a negative D, is instead governed by a QTM mechanism. Thus, the relaxation times corresponding to this process prevailing at lower temperatures are greater for the QTM mechanism (3) than for the IK one (1, 2, and 4), consistent with its lower probability and wavefunctions mixing between the components of the ground Kramers doublet (Table 2). As the rhombicity of the zfs tensor (E/D) increases, so does this probability, and the QTM process becomes faster. Similarly, as expected, the relaxation rate for IK and QTM processes decreases as the magnetic field increases and, therefore, the splitting of the Kramers doublet.

Table 2 Selected parameters from the least-squares fit of the ac magnetic data of 1–4^a

	H dc (kOe)	τ IK ^b (×10^−3 s)	C 1 ^c (s^−1 K^−n)	n 1 ^c	C 2 ^c (s^−1 K^−n)	n 2 ^c
a The fits correspond to double or triple relaxation models. b Coefficient factor for the temperature-independent IK process (τ^−1 = IK). c Coefficient and polynomial factor for the Raman process (τ^−1 = CT^n).
1	1.0	—	1480 ± 50	1.98 ± 0.03	1.13 ± 0.09	5.6 ± 0.4
	2.5	1.1 ± 0.4	23 ± 2	2.4 ± 1.0	3.73 ± 0.03	4.69 ± 0.07
2	1.0	0.32 ± 0.23	900 ± 600	2.5 ± 0.4	1.3 ± 0.3	5.7 ± 0.8
	2.5	1.10 ± 0.07	58 ± 9	1.92 ± 0.10	1.15 ± 0.03	5.26 ± 0.09
3	1.0	1.39 ± 0.06	25 ± 5	2.5 ± 0.6	1.43 ± 0.19	5.16 ± 0.06
	2.5	2.4 ± 0.4	100 ± 20	2.20 ± 0.15	1.000 ± 0.016	5.30 ± 0.05
4	1.0	—	2340 ± 80	1.91 ± 0.03	0.10 ± 0.03	7.33 ± 0.13
	2.5	0.59 ± 0.09	1050 ± 60	1.95 ± 0.15	8.1 ± 1.3	5.04 ± 0.07

---

However, the two spin configurations coexist in 4, the majority being the LS form (2/3). Thus, the relaxation time for the temperature-independent process is expected to be closer to those observed for 1 and 2. A slower IK is still presumed for the HS portion even though it exhibits a |±1/2〉 ground Kramers doublet, as does the LS form. However, this Kramers doublet arises from an S = 3/2 and not an S = 1/2 state, or what is the same from an HS and not an LS form; so, this conclusion is not surprising, being also confirmed by the way it depends on H_dc, which is more like 3. However, what is the cause behind it?

An isolated electron, i.e., a single |±1/2〉 Kramers doublet, in the absence of an external magnetic field or even being moderate, must show a swift spin reversal with an oscillating field. This same doublet arising from an unpaired electron in a metal complex cannot be described as that of an isolated electron since its spin density is delocalised on the ligands. Moreover, the local spin densities caused by a spin delocalisation mechanism polarise spin densities into neighbouring atoms and even, together with the participation of magnetic orbitals in the metal centre, into some internal orbitals of the own metal ion.¹⁰⁴ In such a situation, reversing the spin density laying on the paramagnetic centre entails opposing spin densities in inner layers and also on neighbouring atoms becomes a more difficult task that requires a reversal of the overall density on the complex at once, leading to a significant slowdown in the spin reversal. On the other hand, the spin delocalisation in the HS configuration on cobalt(II) complexes is larger than in the LS form since the former one shows a larger occupation of the e_g orbitals and therefore, a less localised spin density,¹⁰⁴ as confirmed by DFT calculations (Fig. 8 and Table S4†). Hence, the relaxation of the magnetisation in a HS configuration is likely slower, as it is observed. Besides, a distinct σ- or π-type polarisation contribution in the pyridinediimine fragment is observed for the LS and HS configuration, which agrees with the different nature of the magnetic orbitals involved in each case.

Fig. 8 Spin density maps for the optimised geometries on HS (a) and LS (b) configurations of the cobalt(II) complex in 3. Isosurfaces are shown setting cut-off at 0.0002 e bohr⁻³. Colour code: dark blue, cobalt; light blue, nitrogen; brown, carbon; green, chlorine; pink, hydrogen. Positive and negative spin densities are displayed in yellow and blue colours.

How the magnetic field affects the particular dynamic magnetic behaviour of HS and LS forms is not apparent and requires a more detailed study. However, it can be argued that the most significant influence at lower temperatures observed in the LS form may be due solely to the fact that such an effect has already “saturated” under smaller magnetic fields since the Zeeman splitting is larger on a S = 3/2 than on a S = 1/2 state. In contrast, the dynamic behaviour tends to become invariant with H_dc for both HS and LS forms in the high-temperature region since a Raman mechanism governs the spin reversal relaxation,^66,67,70 which involves virtual states associated with a spin–phonon coupling or low-energy vibrations for the complex or network and they are therefore not affected by H_dc.

Conclusions

A novel series of mononuclear spin crossover cobalt(II) compounds with a field-induced single-molecule magnet behaviour has been prepared through ligand design from a series of N,N′-diphenyl-substituted pyridine-2,6-diimine (n-XPhPDI) tridentate ligands bearing electron-withdrawing iodo, bromo, or chloro substituents at the para or meta positions of the terminal N-substituted phenyl rings.

This series of compounds exhibits from complete and gradual, thermally-induced spin transition to its absence, including partial transitions. No direct correlation of the SCO phenomenology with the electron acceptor nature of the ligand substituents is observed along this series. Otherwise, the role played by the crystal lattice through its organisation assisted by covalent bonds or intermolecular interactions in the SCO phenomenon must be highlighted. Then, the effects of the intermolecular halogen⋯halogen contacts seem to be responsible for the distinct SCO behaviour. Thus, weak X⋯X interactions only concerns the LS cobalt(II) units.

These cobalt(II)-n-XPhPDI complexes show different spin relaxation dynamics under a dc magnetic field with slower- (SR) and faster-relaxing (FR) characters depending on the magnitude of the applied dc magnetic field or their LS and HS nature. This disparate field-induced SMM behaviour is dominated by IK or QTM plus Raman processes at low- and high-temperature regions. The observed Raman mechanisms are assisted by both optical and acoustic phonons, involving virtual states that can be ascribed to low-energy vibrational modes. The presence of two-phonon Raman processes at higher temperatures was confirmed by its weak or null dependence on the dc magnetic field; however, at least for the LS configuration, the strong magnetic field influence suggests that IK, QTM, or even direct mechanisms govern the spin reversal at lower temperatures. Our results and theoretical studies support that the larger spin delocalisation in the HS configuration slows down the magnetic relaxation.

Author contributions

The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Spanish MINECO (Projects PID2019-109735GB-I00 and Unidad de Excelencia María de Maeztu CEX2019-000919-M) and the Generalitat Valenciana (AICO/2020/183 and AICO/2021/295). This work has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 748921-SIMOF. R. R. thanks the Generalitat Valenciana and CAPES for the doctoral (GRISOLIAP/2017/057) and postdoctoral (88887.798611/2022-00) grants. J. P. also thanks the Cabildo de Tenerife for the Agustín de Betancourt research contract, respectively. We are indebted to Dr Gloria Agustí and José María Martínez (Universitat de València) for their assistance with the EPR measurements.

References

1. J. Ferrando-Soria, J. Vallejo, M. Castellano, J. Martínez-Lillo, E. Pardo, J. Cano, I. Castro, F. Lloret, R. Ruiz-García and M. Julve, Coord. Chem. Rev., 2017, 339, 17–103.
2. M. A. Halcrow, Chem. Soc. Rev., 2011, 40, 4119–4142.
3. M. A. Halcrow, Chem. Lett., 2014, 43, 1178–1188.
4. M. A. Halcrow, Crystals, 2016, 6, 58.
5. T. Mallah and M. Cavallini, C. R. Chim., 2018, 21, 1270–1286.
6. G. Molnár, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Adv. Mater., 2018, 30, 17003862.
7. G. Molnár, M. Mikolasek, K. Ridier, A. Fahs, W. Nicolazzi and A. Bousseksou, Ann. Phys., 2019, 531, 1900076.
8. A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313–3335.
9. C. M. Quintero, G. Félix, I. Suleimanov, J. S. Costa, G. Molnár, L. Salmon, W. Nicolazzi and A. Bousseksou, Beilstein J. Nanotechnol., 2014, 5, 2230–2239.
10. E. Ruiz, Phys. Chem. Chem. Phys., 2014, 16, 14–22.
11. R. Bertoni, M. Cammarata, M. Lorenc, S. F. Matar, J.-F. Matar, J. F. Létard, E. Lemke and H. T. Collet, Acc. Chem. Res., 2015, 48, 774–781.
12. D. J. Harding, P. Harding and W. Phonsri, Coord. Chem. Rev., 2016, 313, 38–61.
13. M. M. Khusniyarov, Chem. – Eur. J., 2016, 22, 15178–15191.
14. J. Cirera, E. Ruiz, S. Alvarez, F. Neese and J. Kortus, Chem. – Eur. J., 2009, 15, 4078–4087.
15. F. Neese and D. A. Pantazis, Faraday Discuss., 2011, 148, 229–238.
16. M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 289–290, 177–214.
17. S. Gomez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290, 379–392.
18. L. F. Chibotaru, Struct. Bonding, 2015, 164, 185–229.
19. G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147.
20. J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491.
21. A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380.
22. Y.-S. Meng, S.-D. Jiang, B.-W. Wang and S. Gao, Acc. Chem. Res., 2016, 49, 2381–2389.
23. J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491.
24. E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513.
25. E. Moreno-Pineda and W. Wernsdorfer, Nat. Rev. Phys., 2021, 3, 645–659.
26. A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984.
27. N. F. Chilton, Annu. Rev. Mater. Res., 2022, 52, 79–101.
28. J. J. Parks, A. R. Champagne, T. A. Costi, W. W. Shum, A. N. Pasupathy, E. Neuscamman, S. Flores-Torres, P. S. Cornaglia, A. A. Aligia, C. A. Balseiro, G.-K.-L. Chan, H. D. Abruña and D. C. Ralph, Science, 2010, 328, 1370–1373.
29. R. Sessoli, ACS Cent. Sci., 2015, 1, 473–474.
30. B. Doistau, L. Benda, B. Hasenknopf, V. Marvaud and G. Vives, Magnetochemistry, 2018, 4, 5.
31. Y.-S. Ding, Y.-F. Deng and Y.-Z. Zheng, Magnetochemistry, 2016, 2, 40.
32. M. Warner, S. Din, I. S. Tupitsyn, G. W. Morley, A. M. Stoneham, J. A. Gardener, Z. Wu, A. J. Fisher, S. Heutz, C. W. M. Kay and G. Aeppli, Nature, 2013, 503, 504–508.
33. M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157.
34. K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304.
35. G. D. Harzmann, R. Frisenda, H. S. J. van der Zant and M. Mayor, Angew. Chem., Int. Ed., 2015, 54, 13425–13430.
36. A. C. Aragonès, D. Aravena, J. I. Cerdá, Z. Acís-Castillo, H. Li, J. A. Real, F. Sanz, J. Hihath, E. Ruiz and I. Díez-Pérez, Nano Lett., 2016, 16, 218–226.
37. E. J. Devid, P. N. Martinho, M. V. Kamalakar, I. Salitros, U. Prendergast, J.-F. Dayen, V. Meded, T. Lemma, R. González-Prieto, F. Evers, T. E. Keyes, M. Ruben, B. Doudin and S. J. van der Molen, ACS Nano, 2015, 9, 4496–4507.
38. A. Bousseksou, G. Molnár, P. Demont and J. Menegotto, J. Mater. Chem., 2003, 13, 2069–2071.
39. Y. Hasegawa, K. Takahashi, S. Kume and H. Nishihara, Chem. Commun., 2011, 47, 6846–6848.
40. K. Takahashi, Y. Hasegawa, R. Sakamoto, M. Nishikawa, S. Kume, E. Nishibori and H. Nishihara, Inorg. Chem., 2012, 51, 5188–5198.
41. M. Milek, F. W. Heinemann and M. M. Khusniyarov, Inorg. Chem., 2013, 52, 11585–11592.
42. M. G. Cowan, J. Olguín, S. Narayanaswamy, J. L. Tallon and S. Brooker, J. Am. Chem. Soc., 2012, 134, 2892–2894.
43. D. Aravena and E. Ruiz, J. Am. Chem. Soc., 2012, 134, 777–779.
44. B. Warner, J. C. Oberg, T. G. Gill, F. El Hallak, C. F. Hirjibehedin, M. Serri, S. Heutz, M.-A. Arrio, P. Sainctavit, M. Mannini, G. Poneti, R. Sessoli and P. Rosa, J. Phys. Chem. Lett., 2013, 4, 1546–1552.
45. V. Meded, A. Bagrets, K. Fink, R. Chandrasekar, M. Ruben, F. Evers, A. Bernand-Mantel, J. S. Seldenthuis, A. Beukman and H. S. J. van der Zant, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245415.
46. B. Rösner, M. Milek, A. Witt, B. Gobaut, P. Torelli, R. H. Fink and M. M. Khusniyarov, Angew. Chem., Int. Ed., 2015, 54, 12976–12980.
47. T. Mahfoud, G. Molnár, S. Cobo, L. Salmon, C. Thibault, C. Vieu, P. Demont and A. Bouseksou, Appl. Phys. Lett., 2011, 99, 053307.
48. K. Bairagi, O. Iasco, A. Bellec, A. Kartsev, D. Li, J. Lagoute, C. Chacon, Y. Girard, S. Rousset, F. Miserque, Y. J. Dappe, A. Smogunov, C. Barreteau, M.-L. Boillot, T. Mallah and V. Repain, Nat. Commun., 2016, 7, 12212.
49. M. D. Jenkins, D. Zueco, O. Roubeau, G. Aromí, J. Majer and F. Luis, Dalton Trans., 2016, 45, 16682–16693.
50. A. C. Aragonès, D. Aravena, F. J. Valverde-Muñoz, J. A. Real, F. Sanz, J. Hihath, I. Díez-Pérez and E. Ruiz, J. Am. Chem. Soc., 2017, 139, 5768–5778.
51. T. Jasper-Toennies, M. Gruber, S. Karan, H. Jacob, F. Tuczek and R. Berndt, Nano Lett., 2017, 17, 6613–6619.
52. K. Kaushik, S. Mehta, M. Das, S. Ghosh, S. Kamilya and A. Mondal, Chem. Commun., 2023, 59, 13107–13124.
53. U. Beckmann and S. Brooker, Coord. Chem. Rev., 2003, 245, 17–29.
54. H. A. Goodwin, Top. Curr. Chem., 2004, 234, 23–47.
55. I. Krivokapic, M. Zerara, M. L. Daku, A. Vargas, C. Enachescu, C. Ambrus, P. Tregenna-Piggott, N. Amstutz, E. Krausz and A. Hauser, Coord. Chem. Rev., 2007, 251, 364–378.
56. S. Hayami, Y. Komatsu, T. Shimizu, H. Kamihata and Y. H. Lee, Coord. Chem. Rev., 2011, 255, 1981–1990.
57. M. Murrie, Chem. Soc. Rev., 2010, 39, 1986–1995.
58. X.-N. Yao, J.-Z. Du, Y.-Q. Zhang, X.-B. Leng, M.-W. Yang, S.-D. Jiang, Z.-X. Wang, Z.-W. Ouyang, L. Deng, B.-W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380.
59. P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, 7319.
60. A. Landart-Gereka, M. M. Quesada-Moreno, M. A. Palacios, I. F. Díaz-Ortega, H. Nojiri, M. Ozerov, J. Krzystek and E. Colacio, Chem. Commun., 2023, 59, 952–955.
61. X. Feng, C. Mathonière, I.-R. Jeon, M. Rouzières, A. Ozarowski, M. L. Aubrey, M. I. Gonzalez, R. Clérac and J. R. Long, J. Am. Chem. Soc., 2013, 135, 15880–15884.
62. C. Mathonière, H.-J. Lin, D. Siretanu, R. Clérac and J. M. Smith, J. Am. Chem. Soc., 2013, 135, 19083–19086.
63. A. Urtizberea and O. Roubeau, Chem. Sci., 2017, 8, 2290–2295.
64. J. Palion-Gazda, B. Machura, R. Kruszynski, T. Grancha, N. Moliner, F. Lloret and M. Julve, Inorg. Chem., 2017, 56, 6281–6296.
65. D. Shao, L.-D. Deng, L. Shi, D.-Q. Wu, X.-Q. Wei, S.-R. Yang and X.-Y. Wang, Eur. J. Inorg. Chem., 2017, 3862–3867.
66. H.-H. Cui, J. Wang, X.-T. Chen and Z.-L. Xue, Chem. Commun., 2017, 53, 9304–9307.
67. L. Chen, J. Song, W. Zhao, G. Yi, Z. Zhou, A. Yuan, Y. Song, Z. Wang and Z.-W. Ouyang, Dalton Trans., 2018, 47, 16596–16602.
68. M.-X. Xu, Z. Liu, B.-W. Dong, H.-H. Cui, Y.-X. Wang, J. Su, Z. Wang, Y. Song, X.-T. Chen, S.-D. Jiang and S. Gao, Inorg. Chem., 2019, 58, 2330–2335.
69. D. Shao, L. Shi, J. Yin, B.-L. Wang, Z.-X. Wang, Y.-Q. Zhang and X.-Y. Wang, Chem. Sci., 2018, 9, 7986–7991.
70. R. Rabelo, L. Toma, N. Moliner, M. Julve, F. Lloret, J. Pasán, C. Ruiz-Pérez, R. Ruiz-García and J. Cano, Chem. Commun., 2020, 56, 12242–12245.
71. R. Rabelo, L. Toma, N. Moliner, M. Julve, F. Lloret, M. Inclán, E. García-España, J. Pasán, R. Ruiz-García and J. Cano, Chem. Sci., 2023, 14, 8850–8859.
72. F. Kobayashi, Y. Komatsumaru, R. Akiyoshi, M. Nakamura, Y. Zhang, L. F. Lindoy and S. Hayami, Inorg. Chem., 2020, 59, 16843–16852.
73. S. E. Canton, M. Biednov, M. Pápai, F. A. Lima, T.-K. Choi, F. Otte, Y. Jiang, P. Frankenberger, M. Knoll, P. Zalden, W. Gawelda, A. Rahaman, K. B. Møller, C. Milne, D. J. Gosztola, K. Zheng, M. Retegan and D. Khakhulin, Adv. Sci., 2023, 10, 2206880.
74. P. E. Figgins and D. H. Busch, J. Am. Chem. Soc., 1960, 82, 820–824.
75. G. Juhász, S. Hayami, K. Inoue and Y. Maeda, Chem. Lett., 2003, 32, 882–883.
76. Bruker, SAINT, Bruker AXS Inc., Madison, Wisconsin, USA, 2012.
77. Agilent, CrysAlis PRO, Agilent Technologies Ltd, Yarnton, Oxfordshire, England, 2014.
78. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
79. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. J. Puschmann, Appl. Crystallogr., 2009, 42, 339–341.
80. CrystalMaker, CrystalMaker Software, Bicester, England, 2015.
81. Mercury, The Cambridge Crystallographic Data Centre, Cambridge, UK.
82. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
83. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
84. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
85. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
86. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
87. C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305.
88. C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153.
89. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264.
90. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
91. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
92. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
93. K. Eichkorn, O. Treutler, H. Ohm, M. Haser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660.
94. K. Eichkorn, F. Weigend, O. Treutler, H. Ohm and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
95. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
96. R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105.
97. R. Izsák, A. Hansen and F. Neese, Mol. Phys., 2012, 110, 2413–2417.
98. R. Boca and J. Titis, Magnetochemistry, 2023, 9, 100.
99. A. Landart-Gereka, M. M. Quesada-Moreno, I. F. Díaz-Ortega, H. Nojiri, M. Ozerov, J. Krzystek, M. A. Palacios and E. Colacio, Inorg. Chem. Front., 2022, 9, 2810–2831.
100. S. Sottini, G. Poneti, S. Ciattini, N. Levesanos, E. Ferentinos, J. Krzystek, L. Sorace and P. Kyritsis, Inorg. Chem., 2016, 55, 9537–9548.
101. K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351.
102. K. J. Stanley and R. A. Vaughan, Electronic Spin Relaxation Phenomena in Solids, Springer, 1969.
103. S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 4300.
104. J. Cano, E. Ruiz, S. Alvarez and M. Verdaguer, Comments Inorg. Chem., 1998, 20, 27–56.

---

Footnote

† Electronic supplementary information (ESI) available: Details of powder X-ray diffraction (Fig. S1), crystallographic drawings (Fig. S2–S6 and Tables S1 and S2), EPR spectroscopic (Table S3) and magnetic data of 1–4 (Fig. S7–S14), and theoretical calculations (Scheme S1 and Table S4). CCDC 2040599–2040602. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00059e

---