Carbone stabilized B₂ and B₂²⁺ – isoelectronic analogues to diborabutyne and diborabutatriene

Abstract

It has been reported that various unusual main group compounds can be stabilized by coordinating with ligands. Here, we report the use of carbone ligands in stabilizing diboron in its neutral and dicationic states by computational quantum mechanical calculations. The neutral [(L₂C)·B₂·(CL₂)] (L = CO, NHC, PMe₃, and cAAC) has singlet non-planar cumulenic-type equilibrium geometry where CL₂ groups are almost orthogonal to each other. MO analysis indicates that the [(L₂C)·B₂·(CL₂)] can be considered as formed by the interaction of the B₂ fragment in the ¹Σ_g⁺ excited state with two CL₂ ligands having σ- and π-type lone pairs. Accordingly, the π delocalization in the C–B–B–C skeleton consists of two mutually orthogonal allylic anionic-type delocalizations along the C–B–B chain. Since one of the π-delocalized MOs of allylic anionic C–B–B is majorly localized on the carbone carbon atom, the carbone ligands formally act as two-electron ligands. On the other hand, the ground state of [(L₂C)·B₂·(CL₂)]²⁺ shows a singlet planar/pseudo-planar cumulenic geometry when L = NHC and PMe₃. The MO analysis indicates that the C–B–B–C skeleton is similar to that of butatriene, viz. one localized B–B π MO, and two delocalized C–B–B–C π MOs, indicating that each carbone acts as a four-electron ligand. Since CO and cAAC are good π-acceptor ligands, [(L₂C)·B₂·(CL₂)]²⁺ ions (L = CO and cAAC) have triplet non-planar cumulenic ground states.

---

Introduction

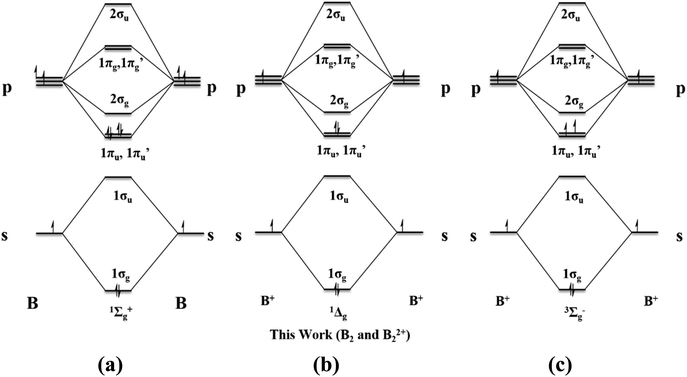
The stabilization of diboron in its neutral state and in other oxidation states is challenging for synthetic chemists.^1,2 The diboron in its ground state exists in a ³Σ_g⁻ electronic state having two half π bonds (1σ_g²1σ_u²1π_u¹π′_u¹, Scheme 1a), and this was isolated only in an argon matrix.³ The B₂ unit can accept up to eight electrons if the 1π_u, 1π′_u, 2σ_g, 1π_g and 1π′_g orbitals are susceptible to electron acceptance. This is based on the assumption that the energy difference between the 2σ_g and 1π_g type orbitals is quite low. On the other hand, the dicationic diboron system (1σ_g²1σ_u²1π_u⁰1π′_u⁰1π_g⁰1π′_g⁰) can accept up to 10 electrons. Many attempts to stabilize the neutral diboron moieties resulted in L₂B₂, L₃B₂, and L₄B₂ types of compounds where L = 2 electron donor ligands (Scheme 1b).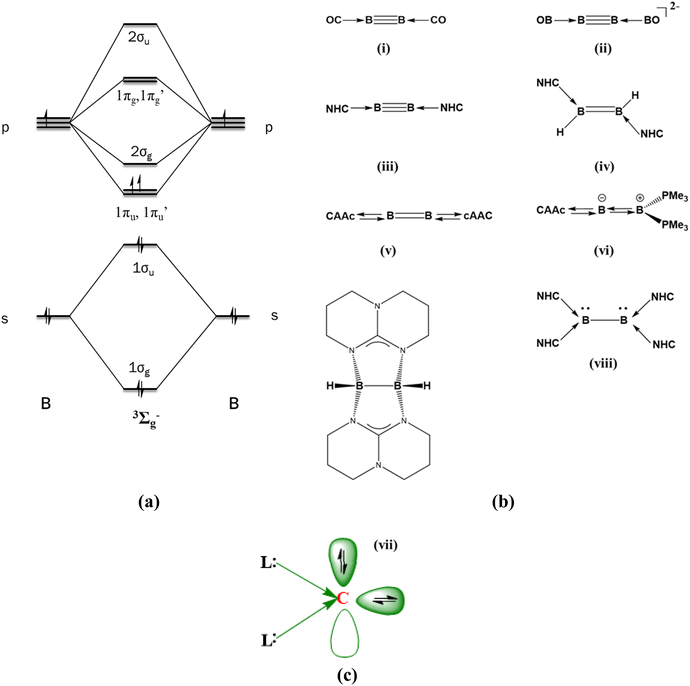

Scheme 1 (a) MO diagram of the ground state of B₂. (b) Various reported ligand-coordinated B₂ molecules. (c) Schematic representation of a bonding picture in CL₂.

The first ligand-stabilized B₂ was reported by Zhou et al. in 2002. They synthesized B₂(CO)₂ in an argon matrix at 8 K (Scheme 1b(i)).⁴ It was the first report of a triple-bonded diboron complex with a B–B bond length of 1.468 Å. Later, Mavridis et al. theoretically explored L₂B₂ compounds where the ligands were CO, CS, N₂, Ar, and Kr.⁵ They found out that B₂ acts as an acceptor group, whereas the ligand species serve as donor groups to form donor–acceptor interactions in all compounds. In another case, Li and co-workers detected [(BO)₂B₂]⁻ in the gas phase using photoelectron spectroscopy.⁶ The corresponding dianionic system resembled [(CO)₂B₂] and exhibited a triple bond between the boron atoms (Scheme 1b(ii)). Energy decomposition analysis (EDA) combined with the natural orbitals for chemical valence (NOCV) study of OCBBCO, N₂BBN₂, and [OBBBBO]²⁻ by Frenking et al. established the donor–acceptor nature of the L–B bond.⁷ The experimental breakthrough of synthesizing an isolable triple-bonded diboron stabilized by Arduengo-type N-heterocyclic carbene (NHC) units was reported in 2012 (Scheme 1b(iii)).⁸ Molecular orbital (MO) analysis showed that the two highest occupied orbitals are the orthogonal π orbitals residing in the B₂ moiety.^9,10 The boron–boron bond multiplicity in all the above systems can be considered as three viz. one σ bond and two π bonds.

The insertion of the two NHC units into the linear diborene resulted in an NHC-coordinated diborene (Scheme 1b(iv)).¹¹ Braunschweig et al. synthesized cAAC-supported diboron, and their detailed study indicates a diborabutatriene-type bonding pattern.¹² This can be attributed to the better π-accepting nature of the cAAC groups as compared to the Arduengo-type NHC.^13,14 The variation in geometrical patterns in the NHC and cAAC coordinated diboron system indicates that the electronic structure of the B₂ unit is easily tunable. Kinjo and Braunschweig reported non-planar cumulenic-type diborenes by coordinating one cAAC ligand at one terminal end and phosphene/NHC/cAAC at the other (Scheme 1b(vi)).^15–17 In these cases, the boron–boron bond multiplicity is two with one σ and one π bond. There are also reports of ligand-assisted B₂ molecules with only a boron–boron σ bond. In 2007, Himmel et al. reported a guanidine-supported diborane (Scheme 1b(vii)).¹⁸ Recently, a tetrakis NHC-supported diboron was synthesized (Scheme 1b(viii)).¹⁹ This molecule possesses a B–B single bond and a lone pair on each boron. There are also some other studies that feature the stabilization of the B–B bond.^20,21 All the above-mentioned compounds are examples of B₂ units stabilized by two-electron donor ligands, and the number of ligands varies from two to four. The number and nature of the two-electron ligand determines the geometry and bonding patterns of the resultant compounds. Even though B₂ and B₂²⁺ are, in principle, 8/10-electron acceptor groups, stabilizing these species by four-electron donor ligands such as carbones is still elusive.

Carbones (CL₂) are dicoordinate carbon compounds that coordinate to two σ-donor ligands in their ¹D state and retain all their valence electrons as two lone pairs.^22–25 In contrast to the carbenes, which possess a lone pair and a vacant orbital (singlet) or two unpaired electrons (triplet), carbones possess two lone pairs. Therefore, it can act as either a two-electron donor ligand or a four-electron donor ligand. One of the lone pairs is σ type, and the other is π type (Scheme 1c). The first class of synthesized carbones was carbodiphosphorenes, and later carbodicarbenes and other σ-donating ligand-supported CL₂ compounds were also studied.^26–30 CL₂ acting as ligands in transition metal complexes are also widely reported.³¹ The carbone-coordinated transition metals are highly active as catalysts in many reactions, such as hydrogenation of olefins, C–C coupling reactions, hydroamination, etc.^32–35 They are also suitable double Lewis donors in stabilizing many species.^36,37 Frenking and Hermann have already theoretically studied the stabilization of isoelectronic main group atoms and ions using carbones as ligands.³⁸ This study envisaged that carbone can act as a six-electron donor. The bond dissociation energy suggested that carbone coordination stabilizes the main group atoms or ions and compounds more strongly than a two-electron ligand.³⁹ Note that the phosphorous analogue P[C(NHC^Me)₂]₂³⁺ has already been reported.⁴⁰ This shows that four-electron donor carbones can act as better-stabilizing ligands than the typical two-electron ligands. However, no studies have been reported to date using two carbone ligands in stabilizing the main group diatomics. These carbone ligands are expected to stabilize the electron-deficient main group diatomics as they are capable of donating four electrons, viz. two electrons in the σ-plane and two electrons in the π-plane.

Here, we report the geometric and bonding pattern of the molecules obtained by coordinating two carbone groups with B₂ and B₂²⁺ using computational quantum mechanical calculation at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory. The studies show that the nature of the carbones and the oxidation state of B₂ determines the geometry and bonding pattern. We expect that this study will trigger experimentalists to use carbone ligands in stabilizing the electron-deficient main group diatomics.

Results and discussion

Structure and bonding analysis of doubly carbone-coordinated diboron

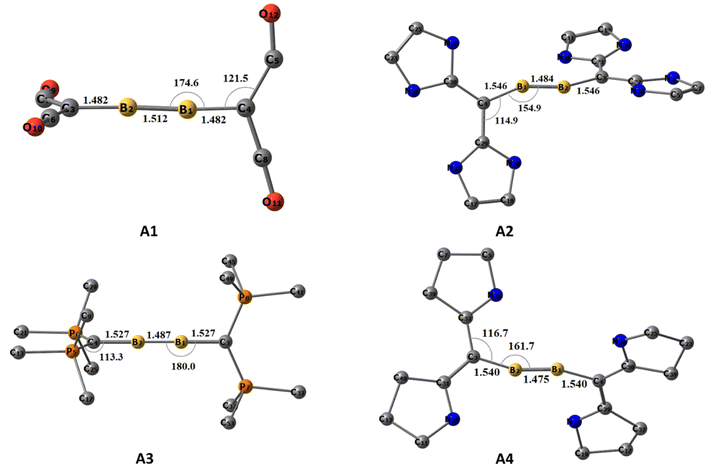
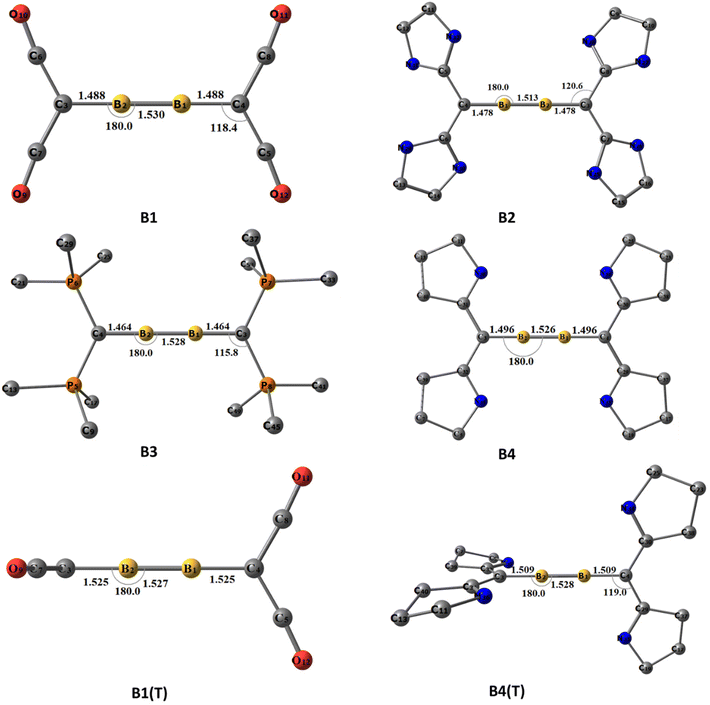
The optimized ground state geometries of [(L₂C)·B₂·(CL₂)] are shown in Fig. 1. A1–A4 denote neutral [(L₂C)·B₂·(CL₂)] compounds and the numbers 1–4 indicate the type of carbone coordinated to B₂. The number 1 indicates that the carbone coordinated to B₂ is C(CO)₂; similarly, numbers 2, 3 and 4 indicate that the carbone coordinated to B₂ is C(NHC)₂, C(PMe₃)₂ and C(cAAC)₂, respectively. The use of T in parentheses indicates the triplet state isomer of the molecule (Fig. S1†). For optimization, the initial geometries considered were the ones with the highest symmetries, viz., the non-planar cumulene-type (D_2d) structure with the CL₂ fragments perpendicular to each other and the planar cumulene-type geometry (D_2h) with two coplanar CL₂ fragments (Scheme 2). The equilibrium geometries of all the molecules in their singlet and triplet states were calculated (Fig. S1†). All compounds possess a singlet ground state consisting of a linear C–B–B–C skeleton with CL₂ fragments close to orthogonal planes. The energy difference between the singlet and triplet states lies within the 1–25 kcal mol⁻¹ range, with the energy difference for A1 (0.9 kcal mol⁻¹) being least and that for A2 (25 kcal mol⁻¹) being highest. The triplet A3(T) is not a stationary point on the potential energy surface, and all attempts to optimize the triplet A3(T) lead to the detachment of the PMe₃ ligands. The singlet A4 is more stable than the corresponding triplet state by 3.5 kcal mol⁻¹. Since the singlet state is more stable than the triplet state, we analyzed the geometries and bonding of the singlet states in detail.

Fig. 1 The equilibrium geometries and the important structural parameters of A1–A4 at the BP86/def2-TZVPP level of theory. Distances are given in Ångstroms, and angles are given in degrees. Hydrogens are omitted for a better view.

Scheme 2 Schematic representation of initial geometries considered for optimization.

A1–A4 show interesting structural variations depending on the carbones. A1 and A3 show a quasi-linear/linear C–B–B–C skeleton in which the carbone ligands are almost orthogonal (Table 1). The B1–B2 bond length in A1 (1.512 Å) is longer than the corresponding triple bond length reported in diborynes, whereas the said bond in A3 is closer to a triple bond (1.487 Å). At the same time, the B–C bond length in A1 (1.482 Å) is shorter than the corresponding single bond lengths, and the corresponding B–C bond length in A3 (1.523 Å) is closer to the single-bond length.^7,11 One of the CO groups of the carbone ligand is bent in A1, whereas the other one is coordinated linearly. The C–C_CO(bent) bond length is longer (1.449 Å) compared to that of the C–C_CO(linear) bond (1.349 Å), and both bonds are longer than the C–C_CO bond length in free C(CO)₂ (1.280 Å). Conversely, the C–P bond length (1.710 Å) in A3 is significantly elongated compared to that in the free C(PMe₃)₂ group (1.639 Å). In addition, two of the P–C_Me bonds are slightly shorter in boron-coordinated carbones than in non-coordinated carbones.

Table 1 Important bond lengths and bond angles in A1–A4 and B1–B4

	Bond lengths (Å)		Bond angle (°)
	B–B	B–C	∠BBC
A1/B1	1.512/1.530	1.482/1.488	174.6/180.0
A2/B2	1.484/1.513	1.546/1.478	154.9/180.0
A3/B3	1.487/1.528	1.527/1.464	180.0/180.0
A4/B4	1.475/1.526	1.570/1.496	161.7/180.0

---

On the other hand, both A2 and A4 has a bent C–B–B–C skeleton (∠CBBC = 143° and 160°, respectively) with geometry in between that of H₂O₂ and trans-bent Si₂H₂. The B1–B2 bond length is closer to that of the triple bond in A2 (1.483 Å) and A4 (1.475 Å). However, the B–C bond lengths are in the range of those of single bonds (1.546 and 1.540 Å). The C–C_NHC bond lengths (1.390 and 1.410 Å) are slightly longer in A2 than the respective C–C_NHC bond lengths in C(NHC)₂ (1.362 Å). In addition, the C–N bond lengths and C–C–N bond angles in A2 are reduced compared to those of the non-coordinated carbones. The same scenario is present in A4. The C–C_cAAC bond lengths (1.417 and 1.404 Å) are longer than those of the carbones (1.321 Å). Similarly, the C–N bond lengths are reduced in comparison with those of C(cAAC)₂.

MO analysis. The MOs of A1–A4 were analyzed for both linear and bent geometries. The HOMO–LUMO gaps of the neutral systems are found to be in the range of 1.70–2.58 eV, which indicates their kinetic stability (Table S1†). The HOMOs are degenerate π MOs with a maximum coefficient on boron atoms in A3 (Fig. 2a). These MOs exhibit major bonding interactions between the boron p orbitals with a slight antibonding interaction with carbon p orbitals corresponding to B–B π bonds. HOMO-1s are also degenerate MOs corresponding to the π-type lone pair on the carbone carbon atom. However, it is noteworthy that these lone-pair orbitals overlap with B π-type orbitals and P–C σ* orbitals, where the interaction with the former is significantly greater. The lone-pair orbital on the carbone carbon atom has significant back donation to the π* orbitals of CO, cAAC, and NHC as compared to the P–C σ* orbital of PMe₃. Accordingly, the π MOs of A1, A2 and A4 are quite different from that of A3. Since CO is an excellent π-acceptor with two sets of π MOs, the π* MOs are energetically low in C(CO)₂. Therefore, the carbone π-type lone-pair orbital and the B–B π orbital can overlap with the CO π* orbitals. The resulting orbitals are given in Fig. 2b. Note that NHC and cAAC have one set of π MOs as compared to the two orthogonal sets in CO. For that reason, to obtain an adequate overlap between the C–N π* MOs of two ligands attached to carbone and the B–B π MO and π-type lone pair on the carbone carbon atom, the C–B–B–C skeleton in A2 and A4 undergoes bending, resulting in geometry that is in between that of trans-Si₂H₂ and H₂O₂ (Fig. 1, 2c, d and Fig. S2†).

Fig. 2 Selected frontier π MOs of A1–A4 (A3 (a), A1 (b), A2 (c) and A4 (d)) at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory. Eigenvalues are given in eV in parentheses. The isosurface value is 0.03.

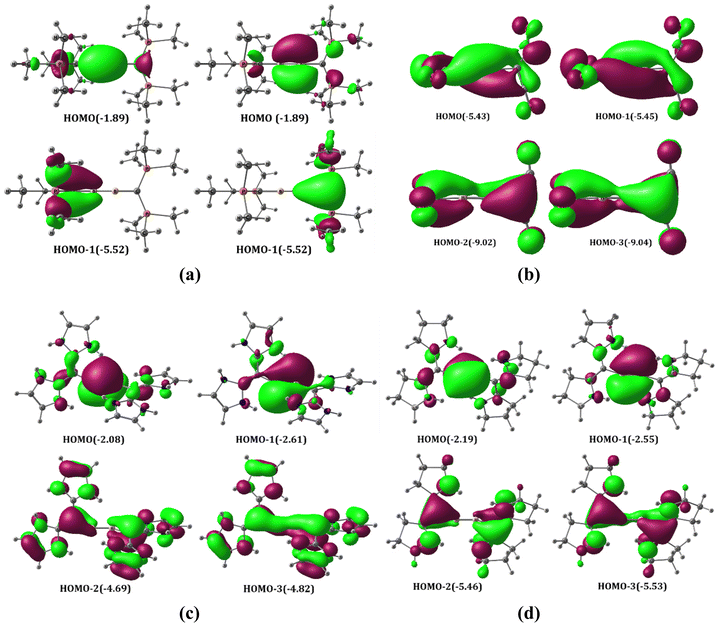
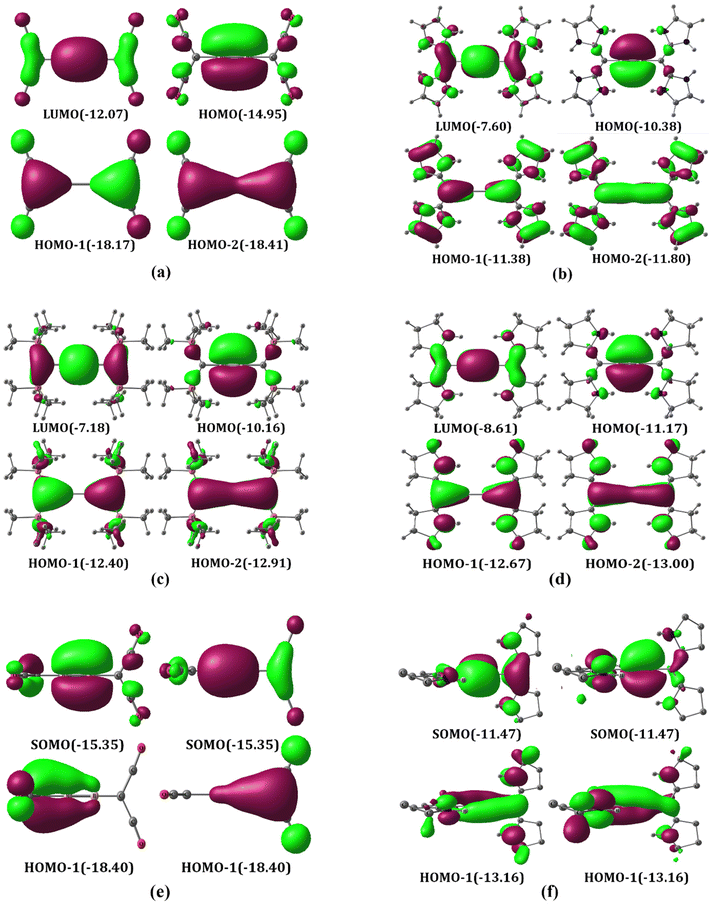
The above-discussed MOs can be considered as being generated by the interaction of the B₂ fragment with two CL₂ fragments. The ground state of B₂ is ³Σ_g⁻ with the electronic configuration 1σ_g²1σ_u²1π_u¹1π′_u¹ (Scheme 1a). To form two B–C bonds by the donation of σ lone pairs on carbones to B₂, the two electrons from 1σ_u should be excited to 1π_u and 1π′_u (Scheme 3a). This excitation results in two vacant σ-type orbitals on B₂, which has the appropriate symmetry to interact with the linear combination of the σ-type carbone lone-pair orbitals. The in-phase combination of the carbone σ-type lone pairs has the correct symmetry to interact with the 2σ_g MO of B₂. On the other hand, the out-of-phase combination of the carbone σ-type lone pairs overlap with the 1σ_u MO of B₂. Consequently, the 1σ_g, 1π_u, and 1π′_u orbitals centered on B₂ are doubly occupied, resulting in a formal B–B triple bond character (Fig. S3†).

Scheme 3 MO diagram of the various excited states of B₂ and B₂²⁺ present in the study.

It is essential to point out that the MO analysis suggests the bonding picture in the A1–A4 structures resembles the bonding scenario of a bisallylic anionic system (Fig. S4†). The HOMO and HOMO−3 constitute one allylic anionic system, and HOMO−1 and HOMO−2 constitute another orthogonal allylic anionic system for A1, A2 and A4, but for A3, one HOMO and one HOMO−1 in similar planes make up the allylic anionic MO skeleton. However, the higher electronegativity of the carbon compared to that of the boron enforces the lone pairs to be more localized on carbone carbon atoms.

NBO/NPA analysis. The above-discussed bonding pattern from MO analysis is well corroborated with the numerical values obtained from the NBO analysis (Table 2). The NBO charge analysis indicates that C(CO)₂ is a net charge acceptor compared to other carbones, indicating that C(CO)₂ is a relatively better π acceptor than the σ donor. The other carbones are better σ donors than the π acceptor with decreasing order: C(NHC)₂ > C(cAAC)₂ > C(PMe₃)₂. The Wiberg bond indices (WBIs) for the B–B bond reveal its triple bond nature for A2, A3 and A4, with values of 2.41, 2.19, and 2.42, respectively (Table 2). The lower value of the WBI for A1 (1.49) is due to the significant delocalization of the electrons from the B–B π MOs to the CO π* orbitals, which is evident from the π MOs of A1 (Fig. 2a). The occupancy data also show a significant deviation of electron density from the B1–B2 π-bonding MOs (1.15e and 1.02e) to the CO π* orbitals (2.4e) for A1. At the same time, the WBIs of B–C bonds for all the A1–A4 compounds fall within the range of single bonds with values of 0.98 (A1), 0.91 (A2), 0.92 (A3) and 0.94 (A4).

Table 2 The charge (q), Wiberg bond indices of selected bonds (P) of A1–A4 at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory

Compounds	Charge (q) (e)			WBI (P)
	C3/C4	B2	CL2	B–B	B–C
A1	−0.84	0.40	−0.20	1.49	0.98
A2	−0.53	−0.76	0.38	2.41	0.91
A3	−1.49	−0.58	0.29	2.19	0.92
A4	−0.48	−0.74	0.37	2.42	0.94

---

To understand the effect of carbone coordination on the strength of the B–B bond, we calculated the bond dissociation energy (BDE) of the B–B bond in B₂ and A1–A4 at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory (reaction (R1), Table 3). The boron atom and BCL₂ fragments are in a doublet ground state. The calculated bond dissociation energy of the neutral B₂ molecule (³Σ_g⁻) is 58.9 kcal mol⁻¹, and the corresponding BDE values in A1–A4 are very high (87–119 kcal mol⁻¹). The BDE follows the order A2 (118.9 kcal mol⁻¹) > A4 (105 kcal mol⁻¹) > A3 (94 kcal mol⁻¹) > A1 (87 kcal mol⁻¹). The dissociation energy indicates that C(NHC)₂ is better at stabilizing B≡B than the other carbones. The BDE for the B–B bond in A1–A4 is comparable to the other theoretically reported BDEs for B≡B in B₂X₂ (X = CO, N₂ and BO⁻) at the BP86/TZ2P level of theory reported by Frenking et al., which is in the range of 83–149 kcal mol⁻¹.⁷ We also calculated the complexation energy (ΔE_complex) of A1–A4 from the B₂ and 2CL₂ fragments (reaction (R2)). The complexation energy follows the order A2 (−185 kcal mol⁻¹) > A4 (−165 kcal mol⁻¹) > A3 (−152 kcal mol⁻¹) > A1 (−77 kcal mol⁻¹), indicating the same trend as that of the BDE of the B–B bond.

Table 3 The dissociation energy of the B–B bonds (D_e B–B), complexation energy of two carbones with the B₂ unit (ΔE_complex), and calculated interaction energies (ΔE_int) and preparatory energies (ΔE_prep) of the B–B bond and B–C bond of A1–A4 at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory

Compounds	D e B–B (kcal mol^−1)	ΔEcomplex (kcal mol^−1)	ΔEint (kcal mol^−1)		ΔEprep (kcal mol^−1)
			B–B	B–C	B–B	B–C
A1	87.1	−77.1	−178.3	−68.9	91.3	30.0
A2	118.9	−185.4	−184.5	−104.8	65.6	12.1
A3	93.4	−152.6	−179.3	−86.7	86.0	10.4
A4	105.3	−165.1	−177.4	−106.5	72.1	23.9

---

We calculated the intrinsic B–B and B–C bond strengths by subtracting the preparation energy of the respective fragments from the negative dissociation energy (ΔE_int = −D_e − ΔE_prep). The preparation energy (ΔE_prep) of the respective fragments is calculated by subtracting the energy of the ground state of the fragment from the energy of the fragment in the same electronic and geometric state as exists in the complex. The electronic state of the BCL₂ fragments is considered in the quartet state with three unpaired electrons, viz. one in the σ orbital and one each in the orthogonal π orbitals. The B–B triple bond is formed by the interaction of the above-mentioned BCL₂ fragments. The preparatory energies for these fragments from the respective ground geometric and electronic states of BCL₂ are 65.6–91.3 kcal mol⁻¹. The calculated intrinsic B–B bond strengths follow the order A2 (−184 kcal mol⁻¹) > A3 (−179 kcal mol⁻¹) > A1 (−178 kcal mol⁻¹) > A4 (−177 kcal mol⁻¹).

The B–C bond in A1–A4 is considered as being formed by the interaction of the B₂ fragment in the ¹Σ_g⁺ state with the two singlet CL₂ fragments. The preparatory energies for these fragment formations are quite low. As expected, the B–C bond strength (−68.9 to −106.5 kcal mol⁻¹), which is formally a single bond, is much weaker than the formal B–B triple bond.

[(L₂C)·B₂·(CL₂)]ⁿ → 2BCL₂^n/2 (n = 0/+2) (R1)

[(L₂C)·B₂·(CL₂)]ⁿ → B₂ⁿ + 2CL₂ (n = 0/+2) (R2)

QTAIM analysis. The topological analysis of the electron density of A1–A4 was performed to obtain a detailed picture of the bonding. Important parameters at the bond critical points are listed in Table 4. The Laplacian for A3 in the B1–B2–P7 plane is given in Fig. 3, and all others are given in the ESI (Fig. S5†). The Laplacian of electron densities at the bond critical points of the B–B bonds are very high negative values, whereas those at the B–C bonds are close to zero, indicating the covalent nature of the B–B bond and polar covalent coordinate nature of the B–C bond. The degree of covalence of the B–B bond and B–C bonds was calculated by using the expression H(r)/ρ(r). Interestingly, the covalence of the B–C bond is comparatively higher than that of the B–B bond. The ellipticity at the BCP can be depicted as a measure of the anisotropy of the curvature of the electron density in the directions normal to the bond, and the magnitude of this ellipticity can give insights into the multiple bonding that present. Here, close to zero ε values at the BCP match the triple-bond character of the B–B bond shown by the MO and geometry analysis. A1 and A3 with their linear C–B–B–C skeleton show bond ellipticity of the B–C bond in the range of 0.22–0.25, indicating that the π delocalization in orthogonal planes is different. This is in agreement with the geometrical and MO data. On the other hand, A2 and A4 with their bent C–B–B–C skeleton show bond ellipticity of the B–C bond close to zero, which agrees with the frontier MOs showing more delocalized MOs in orthogonal planes (HOMO−2 and HOMO−3).

Fig. 3 The Laplacian of the electron density plotted in the plane of B1–B2–P7 of A3. BCPs are marked by green dots. The wave function was generated at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory.

Table 4 Topological parameters of the electron density at the bond critical points of selected bonds of A1–A4 calculated at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory

Compounds	Bond	ρ(r)^a	∇^2ρ(r)^b	V(r)^c	G(r)^d	H(r)^e	ε	H(r)/ρ(r)
a Electron density (ρ(r), e Bohr^−3). b Laplacian of electron density (∇^2ρ(r), e Bohr^−5). c Potential energy density (V(r), Hartree Bohr^−3). d Kinetic energy density (G(r), Hartree Bohr^−3). e Total energy density (H(r), Hartree Bohr^−3). f Ellipticity (ε). H(r)/ρ(r) gives the degree of covalence.
A1	B–B	0.1900	−0.4547	−0.2142	0.0502	−0.1640	0.0	−0.86
	B–C	0.1852	0.0252	−0.3952	0.2007	−0.1944	0.26	−1.05
A2	B–B	0.1761	−0.3206	−0.2229	0.0713	−0.1515	0.06	−0.86
	B–C	0.1741	−0.0291	−0.3530	0.1728	−0.1801	0.05	−1.03
A3	B–B	0.1779	−0.3306	−0.2196	0.0685	−0.1511	0.0	−0.85
	B–C	0.1674	0.0283	−0.3421	0.1746	−0.1675	0.22	−1.00
A4	B–B	0.1811	−0.3379	−0.2328	0.0741	−0.1586	0.0	−0.88
	B–C	0.1800	−0.0489	−0.3665	0.1771	−0.1893	0.06	−1.05

---

Structure and bonding analysis of the doubly carbone-coordinated diboron dication

We also studied carbone coordination with the diboron dication, which has a different electronic structure to that of the neutral system. We calculated the equilibrium geometries of singlet and triplet states for [(L₂C)·B₂·(CL₂)]²⁺ (Fig. 4) by choosing D_2d and D_2h point group symmetric geometries as initial geometries (Scheme 2). B1–B4 denote dicationic [(L₂C)·B₂·(CL₂)]²⁺ compounds and 1–4 indicate the type of carbone coordinated to B₂²⁺. The number 1 indicates that the carbone coordinated to B₂²⁺ is C(CO)₂; similarly, numbers 2, 3 and 4 indicate that the type of carbone coordinated to B₂²⁺ is C(NHC)₂, C(PMe₃)₂ and C(cAAC)₂ respectively. The T in parentheses indicates the triplet-state isomer of the molecule (Fig. 4, Fig. S6). Both planar cumulenic (D_2h)/pseudo-planar cumulenic (D₂) and non-planar cumulenic D_2d/S₄ geometries were found to be stationary points on the potential energy surface. The singlet states converged into planar cumulenic/pseudo-planar cumulenic geometries, whereas the triplet states converged into non-planar cumulenic geometries. The ground states of B2 and B3 are singlet states with pseudo-planar cumulenic and planar cumulenic geometries, respectively. At the same time, B1 and B4 are in triplet states with non-planar cumulenic geometries. The relative energy difference between the singlet and triplet states reduces and follows the order PMe₃ (8.05) > NHC (5.49) > CO (−0.95) and cAAC (−3.53). Note that the energy differences between the singlet and triplet states of B1 and B4 are only marginal. Hence, we considered both singlet and triplet geometries of B1 and B4 for detailed study.

Fig. 4 The equilibrium geometries and the important structural parameters of B1–B4. For [((CO)₂C)·B₂·(C(CO)₂)]²⁺ and [((cAAC)₂C)·B₂·(C(cAAC)₂)]²⁺ both singlet and triplet geometries are given. T indicates a triplet state, and the rest are singlet states. Optimized at the BP86/def2-TZVPP level of theory. Distances are given in Ångstroms, and angles are given in degrees. Hydrogens are omitted for a better view.

All the B1–B4 possess a linear C–B–B–C skeleton. The B–B bond lengths in singlet cumulenic geometries are between the reported double and triple bond lengths (1.530–1.513 Å). On the other hand, the B–C bond lengths fall within the double bond length range (1.496–1.464 Å). There are no significant changes in the geometric parameters for triplet B1(T) and B4(T) as compared to the respective singlet geometries (the B–B bond lengths are 1.527 and 1.528 Å, the B–C bond lengths are 1.525 and 1.509 Å for B1 and B4, respectively). This can be attributed to the stronger π-accepting nature of CO and cAAC ligands, stabilizing both B–B π MOs through delocalization in orthogonal planes. In all B1–B4, the C–X_L (X_L = C/P) bond lengths are significantly elongated compared to those in their free carbone scenarios, which indicate the reduction of π back donation from the carbone carbon centre.

MO analysis. The MO analysis of planar/pseudo-planar cumulenic singlet B1–B4 indicates that the frontier MOs are similar to the butatriene π MOs (Fig. 5a–d). The HOMO–LUMO gaps of the dicationic systems are found to be in the range of 2.56–2.98 eV, which indicate their kinetic stability (Table S1†). The HOMOs in all cases are localized to the B–B π MO. HOMO−1 and HOMO−2 are linear combinations of π MOs having zero and one node, respectively. The nature of these MOs is similar to typical π MOs of butadiene. These MOs can be considered as formed by the interaction of B₂²⁺ with carbone ligands. The ground state of B₂²⁺ is ¹Σ_g⁺ with the electronic configuration 1σ_g²1σ_u²1π_u⁰1π′_u⁰2σ_g⁰1π_g⁰1π′_g⁰ (Scheme 3). The excitation of two electrons from 1σ_u to one of the bonding π MOs results in the ¹Δ_g state with the electronic configuration 1σ_g²1σ_u⁰1π_u²1π′_u⁰2σ_g⁰1π_g⁰1π′_g⁰. The bonding and antibonding combination of σ-type lone-pair orbitals on carbone carbons can donate to the 2σ_g and 1σ_u orbitals centered on B₂²⁺, respectively, leading to two B–C σ bonds (Fig. S7†). Similarly, the bonding and antibonding combinations of π-type lone-pair orbitals on carbone carbons can donate to the 1π′_u and 1π′_g orbitals of the B₂²⁺ moiety, resulting in two delocalized π MOs (HOMO−1 and HOMO−2, Fig. 5a–d). Accordingly, each carbone acts as a four-electron donor to B₂²⁺, resulting in a diborabutatriene system. The butadiene-type π MOs are highly stabilized when the carbone is C(CO)₂ followed by C(cAAC)₂, C(PMe₃)₂, and C(NHC)₂. These energetic orders were followed based on the π-accepting strength of ligands (L) as well as the possibility of more delocalization.

Fig. 5 Selected frontier π MOs of B1 (singlet) (a), B2 (b), B3 (c), B4 (singlet) (d), B1(T) (e) and B4(T) (f) at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory. For triplet states, low-lying alpha orbitals are given. Eigenvalues are given in eV in parentheses. The isosurface value is 0.03.

The triplet non-planar B1(T) has two sets of orthogonal allylic π MOs and resembles a bisallylic radical system. The all-in-phase combination of degenerate π MOs are doubly occupied (HOMO−1). The degenerate π MOs with one node passing through the B–C bond are singly occupied (SOMO). The π MOs of B4 are almost similar to those of B1 except for all in-phase combinations, which are delocalized through four atoms similar to that of Mobius π delocalization (Fig. 5e and f). These π MOs can be interpreted as being formed by the interaction of B₂²⁺ in the ³Σ_g⁻ state (1σ_u⁰1π_u¹, 1π′_u¹) with π-type lone pairs on the carbone carbon viz. the bonding combination results in degenerate HOMO−1 while the antibonding combination results in degenerate SOMO.

NBO/NPA analysis. The above-mentioned MO description is correlated well with the localized bonding description obtained from the NBO analysis (Table 5). The Wiberg bond indices are higher for the B–B bond than they are for the B–C bond, indicating the non-polar double-bond nature of the former bond. Since CO and cAAC are better π acceptors than NHC and PMe₃, the WBIs of the B–C bond of B1 and B4 have relatively low values. These WBI values correlate well with the diborabutatriene bonding description obtained from the MO analysis for the singlet cumulenic geometries. Note that the WBI of the B–B bond in B1–B4 is lower than that in A1–A4, indicating a delocalized B–B double-bond nature for the former and a triple bond for the latter. The charge decomposition analysis also suggests that C(NHC)₂ (0.89e) and C(PMe₃)₂ (0.83e) are relatively better donors towards B₂²⁺ as compared with C(CO)₂ (0.60e) and C(cAAC)₂ (0.81e).

Table 5 The charge (q) and Wiberg bond indices of selected bonds (P) of B1–B4 at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory. T in parentheses denotes triplet minima, and the rest are singlet minima

Compounds	Charge (q) (e)			WBI (P)
	C3/C4	B2	CL2	B–B	B–C
B1	−0.87	0.80	0.60	1.73	1.01
B2	−0.63	0.21	0.89	1.89	1.20
B3	−1.42	0.34	0.83	1.80	1.28
B4	−0.64	0.38	0.81	1.86	1.12
B1(T)	−0.86	0.84	0.58	1.40	0.90
B4(T)	−0.64	0.51	0.75	1.81	1.03

---

We further calculated the bond dissociation energy of the B–B bond by fragmenting the molecule into two [B(CL₂)]⁺ groups (reaction (R1)). The ground state of the [BCL₂]⁺ fragment is singlet with one lone pair of electrons on the boron atom and an empty p-orbital, similar to that of singlet carbene. The calculated bond dissociation energy (37.8–69.9 kcal mol⁻¹) is lower than that of the corresponding neutral system (Table 6). However, the BDE values of B2 and B4 are higher than those of B1 and B3. We also calculated the complexation energy for the formation of B1–B4 from the B₂²⁺ (triplet state) and (CL₂)₂ (singlet) fragments (reaction (R2)). The corresponding complexation energy is found to be much more exothermic compared to that of neutral systems. Even though the B–C bond in a dicationic system is much stronger than that of the B–C bond in a neutral system, as evident from geometrical and NBO analysis, this much higher negative complexation energy can be attributed to the instability of B₂²⁺ as compared to the neutral B₂.

Table 6 The dissociation energy of the B–B bonds (D_e B–B) and complexation energy of  two carbones with the B₂²⁺ unit (ΔE_complex), and calculated interaction energies (ΔE_int) and preparatory energies (ΔE_prep) of the B–B bond and B–C bond of B1–B4 at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory. T in parentheses denotes triplet minima, and the rest are singlet minima

Compounds	D e B–B (kcal mol^−1)	ΔEcomplex (kcal mol^−1)	ΔEint (kcal mol^−1)		ΔEprep (kcal mol^−1)
			B–B	B–C	B–B	B–C
B1	37.8	−311.9	−83.8	−207.2	46.0	51.3
B2	69.9	−578.7	−122.0	−335.3	52.1	46.0
B3	57.1	−564.1	−122.1	−326.3	65.0	44.3
B4	64.4	−532.5	−116.6	−326.8	52.2	60.5
B1(T)	38.8	−312.8	−84.8	−196.7	46.0	40.2
B4(T)	67.9	−536.0	−120.2	−326.8	52.3	58.8

---

We also calculated the intrinsic B–B and B–C bond strengths. The B–B bonds are considered as being formed by the interaction of two BCL₂⁺ fragments in the triplet state, viz. one electron in a σ orbital and one electron in a π orbital. Since the B–B bond is formally a double bond, the calculated intrinsic bond strength is found to be much smaller than that in A1–A4. The B–C bond is formed by the interaction of the B₂ fragment in the ¹Δ_g and ³Σ_g⁻ states (for the singlet and triplet states, respectively) with the two singlet CL₂ fragments. Note that the intrinsic bond strength is found to be higher than that in A1–A4, indicating a formal B–C double-bond nature.

QTAIM analysis. Topological analysis of the electron density of B1–B4 was carried out to acquire more details on the bonding nature using the QTAIM method (Table 7). The Laplacian of electron density in the molecular plane for B3 and B4(T) are given in Fig. 6. The corresponding plots for other molecules are given in the ESI.† The electron density and the Laplacian of electron density at the BCP of B–B and B–C have higher values as compared to those in the neutral system. We wish to point out that the electron density cannot be correlated to the strength of the bond.⁴¹ Nevertheless, the covalence of the B–B bond in the dicationic system is similar to that of the neutral system, whereas the covalence of the B–C bond in the dicationic system is slightly higher. The ellipticity (ε) values of the B–B bond in singlet cumulenic systems show significant magnitudes (0.57–0.69), which substantiate the diborabutatriene skeleton shown by MO and NBO analysis. At the same time, the triplet B1 and B4 have almost zero ε values correlating with the degenerate orthogonal half-filled π orbitals.

Fig. 6 The Laplacian of the electron density plotted in the plane of B1–B2–P7 of B3 (a) and in the plane of B1–B2–C32 of B4(T) (b). BCPs are marked by green dots. The wave function was generated at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory.

Table 7 Topological parameters of the electron density at the bond critical points of selected bonds of B1–B4 calculated at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory

Compound	Bond	ρ(r)^a	∇^2ρ(r)^b	V(r)^c	G(r)^d	H(r)^e	ε	H(r)/ρ(r)
a Electron density (ρ(r), e Bohr^−3). b Laplacian of electron density (∇^2ρ(r), e Bohr^−5). c Potential energy density (V(r), Hartree Bohr^−3). d Kinetic energy density (G(r), Hartree Bohr^−3). e Total energy density (H(r), Hartree Bohr^−3). f Ellipticity (ε). T in parentheses indicates triplet minima and the rest are singlet minima.
B1	B–B	0.1922	−0.4816	−0.2108	0.0452	−0.1656	0.69	−0.86
	B–C	0.1938	−0.0629	−0.4079	0.1961	−0.2118	0.22	−1.09
B2	B–B	0.1905	−0.4594	−0.2165	0.0508	−0.1657	0.59	−0.87
	B–C	0.2036	−0.0813	−0.4305	0.2051	−0.2254	0.05	−1.10
B3	B–B	0.1880	−0.4553	−0.2073	0.0467	−0.1606	0.57	−0.85
	B–C	0.2013	−0.0500	−0.4280	0.2077	−0.2203	0.07	−1.09
B4	B–B	0.1904	−0.4694	−0.2120	0.0473	−0.1647	0.63	−0.86
	B–C	0.2053	−0.1992	−0.4161	0.1831	−0.2330	0.10	−1.13
B1(T)	B–B	0.1880	−0.4322	−0.2102	0.0511	−0.1591	0.0	−0.85
	B–C	0.1847	−0.1432	−0.3705	0.1673	−0.2032	0.02	−1.10
B4(T)	B–B	0.1864	−0.4245	−0.2087	0.0513	−0.1574	0.0	−0.84
	B–C	0.2054	−0.2819	−0.4032	0.1664	−0.2369	0.07	−1.15

---

Conclusions

We carried out the computational study of carbone-coordinated diborons in their neutral ([(L₂C)·B₂·(CL₂)]) and dicationic ([(L₂C)·B₂·(CL₂)]²⁺) states, where L = CO, NHC, PMe₃ and cAAC. The structure and bonding analysis show that the [(L₂C)·B₂·(CL₂)] possesses a singlet non-planar cumulenic ground state independent of the ligands attached to the carbone carbon. The MO analysis depicted an orthogonal bisallylic anion-type system constituted by the two orthogonal B–B π bonds and the carbone π lone pairs, where the carbone π lone pairs are more localized on the carbons. The MOs suggest that the B₂ fragment is in a ¹Σ_g⁺ excited state and interacts with the two CL₂ fragments. NBO and QTAIM analyses confirm that the singlet non-planar cumulenic geometry exhibits a triple bond between the borons, reminiscent of the diborabutyne system. The bond dissociation energy and interaction energy indicate that carbone coordination strengthens the B–B bond and is comparable with the reported diboron complexes. On the other hand, the dicationic [(L₂C)·B₂·(CL₂)]²⁺ displays singlet planar cumulenic/pseudo-planar cumulenic and triplet non-planar cumulenic minima. Singlet cumulenic states are found to be the ground state when the carbone is C(NHC)₂ and C(PMe₃)₂, whereas for carbones C(CO)₂ and C(cAAC)₂, the triplet minima are found to be more stable. Even though the singlet–triplet energy difference is minimal, this variation can be attributed to the more π-accepting nature of CO and cAAC. The MO analysis indicates that in singlet cumulenic states, the C–B–B–C skeleton is similar to that of butatriene, viz. one localized B–B π MO, and two delocalized C–B–B–C π MOs. The NBO and QTAIM analyses support the MO picture, revealing the dual donation of CL₂ to the excited ¹Δ_g B₂²⁺ state. In the case of triplet non-planar cumulenic states, the C–B–B–C π MOs suggest a bisallylic radical-type bonding, where the carbone lone pairs are more localized on the carbons due to its higher electronegativity. The bond dissociation and interaction energies show a weaker B–B bond and stronger B–C bonds than those in the neutral analogue. This work envisages that using double donor ligands such as carbones can stabilize the diboron moiety effectively, and the careful tuning of electronic factors can alter the bonding and structure of the molecule.

Computational methodology

All calculations were carried out using the Gaussian09 programming package.⁴² Geometry optimizations were performed at the DFT level using the exchange functional of Becke in conjunction with the correlation functional of Perdew (BP86).^43–45 The basis set used was a triple zeta valence with double polarisation (def2-TZVPP), which can be notated as BP86/def2-TZVPP.⁴⁶ The analytical frequencies were calculated using the Hessian matrix to confirm the minima. Single-point calculations were carried out at the M06/def2-TZVPP level of theory.⁴⁷ Various recent studies from our group have found that the GGA functional reproduces the experimental geometries very well, whereas the meta-GGA functional gives more accurate energetics and molecular properties. The electronic energy from the M06/def2-TZVPP level of theory was added with the zero point correction from the optimization at the BP86/def2-TZVPP level of theory. Zero point correction gives the molecular energy in the lowest vibrational levels at absolute zero (0 K). The corrected energies were used to calculate the bond dissociation energies (D_e), interaction energies (ΔE_int), and preparatory energies (ΔE_prep). Natural bond orbital and natural population analyses were performed at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory using the NBO 6.0 package.⁴⁸ The electronic topological analysis was conducted using the quantum theory of atoms in molecules (QTAIM) methodology in the AIMALL package.^49–51 The wave function input for QTAIM analysis was generated using the Gaussian09 program package at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

PP thanks SERB, India, for the financial support. JS thanks UGC, India for providing the fellowship. PP and JS also thank the Centre for Computational Modelling and Simulation (CCMS) and Central Computer Center (CCC) at NITC for the computational facilities.

References

1. H. Li, G. Xu, S. Li, Y. Wu and Z. Lu, Chem. Rec., 2023, 23, e202300238.
2. Y. F. Lin and C. W. Chiu, Chem. Lett., 2017, 46, 913–922.
3. S. Tam, M. Macler, M. E. DeRose and M. E. Fajardo, J. Chem. Phys., 2000, 113, 9067–9078.
4. M. Zhou, N. Tsumori, Z. Li, K. Fan, L. Andrews and Q. Xu, J. Am. Chem. Soc., 2002, 124, 12936–12937.
5. A. Papakondylis, E. Miliordos and A. Mavridis, J. Phys. Chem. A, 2004, 108, 4335–4340.
6. S. D. Li, H. J. Zhai and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 2573–2579.
7. L. C. Ducati, N. Takagi and G. Frenking, J. Phys. Chem. A, 2009, 113, 11693–11698.
8. H. Braunschweig, R. D. Dewhurst, K. Hammond, J. Mies, K. Radacki and A. Vargas, Science, 2012, 336, 1420–1422.
9. G. Frenking and N. Holzmann, Science, 2012, 336, 1394–1395.
10. N. Holzmann, M. Hermann and G. Frenking, Chem. Sci., 2015, 6, 4089–4094.
11. Y. Wang, B. Quillian, P. Wei, C. S. Wannere, Y. Xie, R. B. King, H. F. Schaefer, P. V. R. Schleyer and G. H. Robinson, J. Am. Chem. Soc., 2007, 129, 12412–12413.
12. J. Böhnke, H. Braunschweig, W. C. Ewing, C. Hörl, T. Kramer, I. Krummenacher, J. Mies and A. Vargas, Angew. Chem., Int. Ed., 2014, 53, 9082–9085.
13. M. Soleilhavoup and G. Bertrand, Acc. Chem. Res., 2015, 48, 256–266.
14. V. Nesterov, D. Reiter, P. Bag, P. Frisch, R. Holzner, A. Porzelt and S. Inoue, Chem. Rev., 2018, 118, 9678–9842.
15. W. Lu, Y. Li and R. Kinjo, J. Am. Chem. Soc., 2019, 141, 5164–5168.
16. W. Lu, Y. Li, R. Ganguly and R. Kinjo, Angew. Chem., Int. Ed., 2017, 56, 9829–9832.
17. J. Böhnke, M. Arrowsmith and H. Braunschweig, J. Am. Chem. Soc., 2018, 140, 10368–10373.
18. O. Ciobanu, E. Kaifer, M. Enders and H. J. Himmel, Angew. Chem., Int. Ed., 2009, 48, 5538–5541.
19. J. Fan, A.-P. Koh, J. Zhou, Z.-F. Zhang, C.-S. Wu, R. D. Webster, M.-D. Su and C.-W. So, J. Am. Chem. Soc., 2023, 145, 11669–11677.
20. D. E. Trujillo-González, G. González-García, T. A. Hamlin, F. M. Bickelhaupt, H. Braunschweig, J. O. C. Jiménez-Halla and M. Solà, Eur. J. Inorg. Chem., 2023, e202200767.
21. R. Saha, S. Pan and P. K. Chattaraj, ACS Omega, 2018, 3, 13720–13730.
22. R. Tonner and G. Frenking, Chem. – Eur. J., 2008, 14, 3260–3272.
23. G. Frenking and R. Tonner, Pure Appl. Chem., 2009, 81, 597–614.
24. G. Frenking, R. Tonner, S. Klein, N. Takagi, T. Shimizu, A. Krapp, K. K. Pandey and P. Parameswaran, Chem. Soc. Rev., 2014, 43, 5106–5139.
25. A. L. Liberman-Martin, Cell Rep. Phys. Sci., 2023, 4, 101519.
26. F. Ramirez, N. B. Desai, B. Hansen and N. McKelvie, J. Am. Chem. Soc., 1961, 83, 3539–3540.
27. R. Tonner and G. Frenking, Angew. Chem., Int. Ed., 2007, 46, 8695–8698.
28. G. Frenking and R. Tonner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 869–878.
29. C. A. Dyker, V. Lavallo, B. Donnadieu and G. Bertrand, Angew. Chem., Int. Ed., 2008, 47, 3206–3209.
30. A. Fürstner, M. Alcarazo, R. Goddard and C. W. Lehmann, Angew. Chem., 2008, 120, 3254–3258.
31. L. Zhao, C. Chai, W. Petz and G. Frenking, Molecules, 2020, 25, 4943.
32. C. Pranckevicius, L. Fan and D. W. Stephan, J. Am. Chem. Soc., 2015, 137, 5582–5589.
33. Y.-C. Hsu, J.-S. Shen, B.-C. Lin, W.-C. Chen, Y.-T. Chan, W.-M. Ching, G. P. A. Yap, C.-P. Hsu and T.-G. Ong, Angew. Chem., Int. Ed., 2015, 54, 2420–2424.
34. C. C. Roberts, D. M. Matías, M. J. Goldfogel and S. J. Meek, J. Am. Chem. Soc., 2015, 137, 6488–6491.
35. M. J. Goldfogel, C. C. Roberts and S. J. Meek, J. Am. Chem. Soc., 2014, 136, 6227–6230.
36. B. Inés, M. Patil, J. Carreras, R. Goddard, W. Thiel and M. Alcarazo, Angew. Chem., Int. Ed., 2011, 50, 8400–8403.
37. W. Petz, F. Öxler, B. Neumüller, R. Tonner and G. Frenking, Eur. J. Inorg. Chem., 2009, 4507–4517.
38. M. Hermann and G. Frenking, Chem. – Eur. J., 2017, 23, 3347–3356.
39. N. Holzmann, A. Stasch, C. Jones and G. Frenking, Chem. – Eur. J., 2011, 17, 13517–13525.
40. N. Đorđević, R. Ganguly, M. Petković and D. Vidović, Chem. Commun., 2016, 52, 9789–9792.
41. L. Zhao, S. Pan and G. Frenking, J. Chem. Phys., 2022, 157, 034105.
42. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, Jr., J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc., Wallingford, CT, 2016.
43. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
44. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
45. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406–7406.
46. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
47. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
48. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
49. R. F. W. Bader and R. F. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1990.
50. The Quantum Theory of Atoms in Molecules, ed. C. F. Matta and R. J. Boyd, Wiley, 2007.
51. T. A. Keith, TK Gristmill Software, Overland Park KS, USA, 2015.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dt04358d

---