Dynamic metal-linker bonds in metal–organic frameworks

Abstract

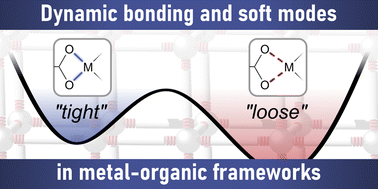
Metal-linker bonds serve as the “glue” that binds metal ions to multitopic organic ligands in the porous materials known as metal–organic frameworks (MOFs). Despite ample evidence of bond lability in molecular and polymeric coordination compounds, the metal-linker bonds of MOFs were long assumed to be rigid and static. Given the importance of ligand fields in determining the behaviour of metal species, labile bonding in MOFs would help explain outstanding questions about MOF behaviour, while providing a design tool for controlling dynamic and stimuli-responsive optoelectronic, magnetic, catalytic, and mechanical phenomena. Here, we present emerging evidence that MOF metal-linker bonds exist in dynamic equilibria between weakly and tightly bond conformations, and that these equilibria respond to guest–host chemistry, drive phase change behavior, and exhibit size-dependence in MOF nanoparticles.

---

Introduction

Metal–ligand (ML) bonds dictate the properties of metal complexes and coordination materials. Subtle differences in the geometries and energetics of ligand fields surrounding metal ions govern the optical, electronic, magnetic, and catalytic properties and overall stability of the resulting complexes.^1–3 While enthalpy favours ML bond formation, entropy drives their dissociation such that all ML bonds exist to varying degrees in dynamic equilibria between bound and unbound states. This bond lability impacts the mechanisms of transition metal catalysis^4–6 and enables the self-healing behaviour observed in coordination polymers.^7–10 Among traditional solid-state materials, the earliest examples of ferroelectric phase-change behaviour were documented to involve a special class of ML phonons,^11–13 now termed soft modes. In other words, dynamic equilibria of metal–ligand bonds exist in coordination complexes ranging from small molecules to extended solids, and yet dynamic bonding in materials bridging the gap between the molecular and solid-state divide remains an open frontier.^14,15

Metal–organic frameworks (MOFs), also termed 3D porous coordination polymers, are a compositionally tuneable class of materials. Their secondary building units (SBUs) can be altered to yield either isostructural or entirely new materials. To date, nearly 100 000 MOFs have been synthesized and over 500 000 structures have been predicted, all of which contain ML bonds.¹⁶ Considering the fundamental lability of ML bonds, it follows that MOFs and other CPs should also exhibit similar behaviour to molecules and nonporous solids. While many early reports of MOFs document phase-change behaviour, soft mode behaviour was only introduced into the MOF literature recently.^17–21 In this Frontier article we will highlight recent studies of dynamic ML bonds and their implications for the future of the MOF field.

The tension between enthalpically and entropically favoured ML bond conformations gives rise to a generic one-dimensional configurational coordinate diagram shown in Fig. 1. This free energy landscape tends towards bound ML states at low temperatures and unbound or weaker states at high temperatures. For example, magnetic spin crossover (SCO) arises from this stimulus-responsive ML bond interaction. Lower temperatures favour strong and short low-spin ML bonds, while high temperatures favour high-spin ML bonds. SCO represents an example of dynamic bonding in a phase change, which, by definition, constitutes a reversible equilibrium property. Although MOFs have been reported as phase-change materials, the underlying mechanism that makes certain MOFs susceptible to phase changes remains poorly understood. Based on the lack of investigations into MOF ML bond dynamics, we expect that phase-change behaviour represents just the beginning of MOF properties explainable by labile bonding.

Fig. 1 (a) Schematic view of metal–ligand interactions, where “tight” and “loose” bond states exist in thermodynamic equilibrium. Inserts show a metal–carboxylate interaction. (b) Illustration of the energy landscape for ensembles of “tight” and “loose” states of metal–ligand interactions and how the equilibrium may be perturbed.

From melting to magnetic and structural phase transitions, soft modes serve as the conduit for one material to transform into another. By distorting atomic positions sufficiently far from equilibrium geometries, soft modes impart their kinetic energy to the surrounding lattice as anharmonically coupled oscillators.^22,23 As a result, such lattice vibrations exhibit red-shifting frequencies as temperatures approach the critical transition temperatures.^24,25 Beyond the proposal that MOFs exist in a two-state bond equilibrium, certain dynamic bonds might fulfil the role of soft modes by serving as the mechanism for phase change behaviour. This Frontier discusses recent evidence that ML bond vibrations in MOFs behave as soft modes in cases where the phase change involves a change to the ligand sphere. In principle, by leveraging synthetic inorganic chemistry to manipulate the ML bonds, fundamental aspects of the phase change chemistry could be tailored and understood.

Beyond phase change behaviour, dynamic ML bonding in MOFs helps to explain otherwise difficult to understand phenomena. For example, the ability of MOFs to undergo replacement of their metal and linker components, commonly termed “post-synthetic exchange”,^26–29 challenges the idea of static ML bonds.^30,31 Similarly, dynamic bonding would help explain the ability of MOFs to perform catalysis at ostensibly coordinatively saturated metal sites and to melt into liquid MOFs. Whereas all semiconductors exhibit redshifting optical gaps at increased temperatures in a manner termed “Varshni behaviour”, MOF optical gaps exhibit a far greater temperature dependence explainable by dynamic bonding. This perspective, rooted in coordination chemistry, also reveals previously unnoticed aspects of MOF materials. Specifically, recent evidence indicates that MOF ML bonds become more labile for smaller MOF particle sizes. This insight implies that all MOF properties dependent on metal–ligand interactions may be tuned through particle size. Therefore, dynamic ML bonding provides a lens to see deeper into fundamental aspects of MOF chemistry, providing a tool for greater synthetic control over their performance while also uncovering behaviour distinct among any class of molecules or materials.

Dynamic bonding and soft modes

In the MOF literature, “structural dynamics” typically refers to “breathing effects”,^32–34 the transient binding of guest molecules,^26,35,36 and negative thermal expansion,^37–39 rather than ML bond dynamics. And while reversible ML bonding is attributed a key role in MOF crystallization, it is often overlooked when studying the resulting materials. As a result, little evidence attests to ML dynamics in MOFs. Whereas labile ML bonding is invoked to explain a range of molecular coordination chemistry, few studies have documented dynamic bonding in 3D materials. In a close analogy to MOFs, however, metal–ligand lability has been studied for 1D coordination polymers to such an extent that the equilibrium ratio of unbound-to-bound states, termed the formation constants K_f, have been documented for a range of metal ligand bonds, including metal–carbene,⁴⁰ metal–pyridyl,⁴¹ and metal–carboxylate bonds.⁴² These studies probe ML bond lability by measuring relative concentrations of unbound and bound ML states, but few studies have investigated the ML bonds themselves. In one example,⁴³ variable temperature (VT) Raman spectra were reported for a metallopolymer containing metal–pyridyl linkages. The data revealed that the pyridyl vibrational stretches of the bis-terpyridyl groups redshifted at higher temperatures, which the authors attributed to dynamic structural rearrangements in the metallopolymer. This work also suggests that ligand-based vibrational modes may serve as a window into ML bond dynamics without probing the bonds directly.

Given that metal–ligand vibrations occur at the low-frequency limit of common infrared spectrometers and the often-low signal intensities of Raman spectra, synchrotron techniques would likely be required to probe them in MOFs. Indeed, terahertz-based synchrotron measurements have been employed to study ligand-related dynamics in “breathing” carboxylate MOFs^44,45 and the melting behaviour of zeolitic imidazolate frameworks (ZIFs).^46–48 As an alternative, VT mid-infrared vibrational spectroscopy provides a convenient method for tracking dynamic ML MOF bonds using conventional benchtop equipment. Fig. 2a schematically depicts the justification for this strategy. Specifically, the carboxylate vibrational modes typical of most MOFs serve as a trackable spectroscopic handle during VT-diffuse-reflectance infrared Fourier transform spectroscopy (VT-DRIFTS), made possible by the fact that the ML and carboxylate bonds act as coupled oscillators. To develop VT vibrational spectroscopy as a handle for probing MOF ML dynamics, however, the temperature-dependent spectral changes must be attributable to a microscopic model of bound and unbound states. From the perspective of molecular orbital theory, the ligand-based electrons bound to metal sites also occupy anti- and non-bonding orbitals with respect to the ligand. As a consequence, this electron density shifts towards the ligand in unbound states, causing the ligand-based bonds to weaken, resulting in red-shifted vibrational modes.

Fig. 2 (a) Illustration of carboxylate vibrations (highlighted in blue) that can be probed using VT-DRIFTS, instead of the more elusive metal–oxygen interactions, as they are coupled oscillators. (b) Apparent redshift of the asymmetric carboxylate vibrational mode in HKUST-1 with increasing temperature, as extracted from Gaussian fitting to a series of experimental data. (c) Schematic illustration of tight and loose binding modes in HKUST-1. (d) Structure of HKUST-1 as viewed slightly off the crystallographic a-axis.

Evidence for dynamic ML bond equilibria in MOFs was recently reported as VT-DRIFTS spectra for a series of archetypical carboxylate MOFs.¹⁷ The observed red-shift in the vibrational frequencies of the symmetric and asymmetric C–O stretches suggested the coexistence of “tight” and “loose” states in thermal equilibrium. This nomenclature was adopted over “bound” and “unbound” because previously reported molecular dynamics simulations²⁶ revealed that MOF ML bonds dynamically fluctuate between conformations with a wide range of bond lengths and angles. Accordingly, carboxylate MOFs were interpreted to exist in an equilibrium between two shallow and wide potential energy surfaces that encompass of diverse collections of tightly or loosely bound ML states. The relative abundances of the “tight” and “loose” states can be extracted by fitting two fixed Gaussians to these data at different temperatures, permitting quantification of a “flexibility” constant (ln K_flex, K_flex = [loose]/[tight]), defined as the inverse of the familiar formation constants K_f reported for molecular complexes. In HKUST-1 (Fig. 2c and d), an ln K_flex of ∼0.3 was observed at room temperature, which compares well to values reported for discrete metal complexes such as zinc and copper benzoates/acetates in the range of 0.1–1.5.⁴² This analysis also suggests that unbound states likely comprise a significant portion of MOF structures. To gain insight into the thermodynamics of this equilibrium, Van't Hoff analysis of VT-DRIFTS data of HKUST-1 was performed to assess the temperature dependence of K_flex. This result suggests that the population of loose states is associated with a small endothermic barrier (ΔH = 5.9 ± 0.2 kJ mol⁻¹), overcome by an increase in entropy (ΔS = 22.0 ± 0.6 J mol⁻¹ K⁻¹). Interestingly, this fit required a change in specific heat capacity (ΔC_P = 37 ± 4 J mol⁻¹ K⁻¹), which is typically required for analysing phase change processes. Similar redshifts have also been observed in variable temperature spectra of an In-carboxylate MOF,⁴⁹ the catalytic activity of which is attributed to dynamic ML bonds in the material.

Dynamic bonding therefore likely plays a significant role in the phase change behaviour of MOFs.^46,50–53 As for other solids, MOF melting has been observed to follow Lindemann's law,⁵⁴ which posits that melting occurs when thermal displacements reach a critical magnitude with respect to the interatomic distances in a material. This breaking point is expressed as f = u/d, where u is the mean thermal atomic displacement (the square root of the Debye–Waller factor), d is the bond distance to the nearest-neighbour atom and f is the Lindemann ratio, which has been observed to take universal values in the range of 0.10 to 0.13.⁵⁰ Therefore, considering the degree of dynamic bonding in MOF materials, ML bond lability likely plays a critical role in the melting process and other dynamic processes, such as the negative thermal expansion often observed for MOFs, which has been shown to originate from low-frequency phonons.^55,56 Certain lattice vibrations distort equilibrium atomic positions so strongly that they cause a material to undergo a phase change. Interestingly, a hallmark feature of these phonons, termed soft modes,^22,23,57 is the redshift of their frequencies as temperatures approach the critical temperature of the phase change, where they vanish to zero. Therefore, the redshifting behaviour of MOF vibrational modes at higher temperatures bears a resemblance to soft modes.

To understand the connection between dynamic bonding, soft modes, and phase changes in MOFs, our group has studied the spin crossover (SCO) MOF Fe(1,2,3-triazolate)₂ (Fig. 3),^18,58 which possesses among the largest magnetic hysteresis windows and most abrupt magnetic transitions of any SCO molecule or material. As evidenced by VT-DRIFTS, the triazolate vibrational modes displayed temperature dependence. As was observed for the dynamic bonds in carboxylate MOFs, the shift in wavenumbers can be attributed to the coexistence of “tight” and “loose” states in equilibrium. Interestingly, an inversion in the vibrational redshift was observed at the SCO transition temperature (Fig. 4a). This phenomenon is analogous to the behaviour observed for the soft phonon modes associated with phase transitions in SrTiO₃ (Fig. 4b).⁵⁹ To further establish the presence of dynamic bonding in metal-triazolate MOFs, but to eliminate the effects of SCO, the isostructural Mn, Co, Cu, and Zn triazolates were studied. Analysis of these DRIFTS data yielded ln K_tl values ranging from 0.67–1.97.¹⁸ Interestingly, the Cu variant, which undergoes a tetragonal-to-cubic structural phase change at higher temperatures, also displayed a V-shaped inversion to its triazolate vibrational frequencies at the critical temperature. The non-phase change variants, on the other hand, only showed the smooth redshifting vibrational frequencies with heating as seen for carboxylate MOFs.

Fig. 3 Schematic illustration of the thermally induced bond expansion and apparent soft-mode coupling of the spin-crossover transition in Fe(1,2,3-triazolate)₂. A six-membered ring is shown to highlight the shape of the pore apertures in the iron triazolate structure.

Fig. 4 (a) Observation of a redshift-to-blueshift inversion of a ligand vibrational mode in iron triazolate when heated past the spin-crossover temperature. (■ = low spin, □ = high spin).¹⁸ (b) Redshifting of two soft modes in low-T tetragonal SrTiO3 upon heating, in which new phonon modes emerge and blueshift beyond the phase transition temperature.⁵⁶

For microscopic insight into the “loose” and “tight” conformations for this family of materials, electronic structure calculations predicted a large ensemble of thermodynamically stable geometries that existed within thermal energy of each other despite possessing bond lengths that differed by as much as 0.1 Å. Importantly, these same methods predicted the phase change ΔH for both the Fe and Cu variants with remarkable accuracy as compared with experimental calorimetry. Together, these results suggest that if a MOF has the potential for a phase change due to electronic aspects specific to the metal ion, the dynamic ML bonding intrinsic to MOFs serve as the soft mode. For example, in the case of SCO, where ML bonds transition from short and strong low-spin states to long and weak high-spin bonds, the “tight”–“loose” equilibrium is well suited to shuttle the material from one phase to the other.

Dynamic ML bonds also affect the electronic structures of MOFs by perturbing the ligand field of the metal sites. Early evidence of this effect was observed by VT diffuse-reflectance UV-Vis spectroscopy (VT-DRUVVis) of MUV-10(Ca), Ti₃Ca₃(μ₃-O)₃(1,3,5-benzenetricarboxylate)₄(H₂O)₆.⁶⁰ Upon heating the material, absorption tails emerged as far as 2.0 eV below the low-temperature optical gap. Despite such a large effect, these tails disappeared upon cooling, thereby ruling out irreversible thermal degradation. Instead, the absorption tailing suggests reversible structural distortions around the MOF nodes that dynamically lower the symmetry of the metal sites, creating mid-gap states. Analogously, vibronic coupling dynamically lowers the symmetry of molecular inorganic complexes. As a result, they display colour from formally forbidden optical transitions.

Guest molecules also influence the dynamic equilibria of MOF ML bonding. Whereas the above report studied MOFs under vacuum, VT-DRIFTS spectra were reported for UiO-66 (Zr₆O₄(OH)₄(1,4-benzenedicarboxylate)6)—a MOF known for its unusual stability,²¹ in the presence of solvent vapour, air, and dry N₂. For comparison, analysis of VT-DRIFTS data yielded ln K_tl (K_tl = [tight]/[loose]) values of 1.84 under vacuum. While this value, defined in analogy to K_f of molecules, is higher than previously studied carboxylate MOFs, it is smaller than coordination-based “self-healing” materials with values in the range of 9–25,^40,41 suggesting even the most “stable” MOFs exhibit bond flexibility. Introduction of air caused ln K_tl to drop to 1.7 and the introduction of Lewis-basic molecules caused it to decrease even further, with Et₃N giving a K_tl of just −0.6. Furthermore, guest molecules with larger Gutmann donor numbers—a measure of Lewis basicity—caused greater redshifts. These results suggest that the MOF ML bond equilibria involve unbound conformers to such a degree that guest molecules bind to the MOF metal sites. Given that the guest molecules could be removed by vacuum, these reproducible spectral changes hold promise for the use of MOFs in sensing technologies through rapid spectroscopic screening.

Dynamic bonding in MOF nanoparticles

Nanosizing MOFs causes ML bonding to become more labile. As a result, MOF properties sensitive to ML interactions have the potential to become size-dependent. Recent evidence was documented in a report on the temperature dependence of archetypical MOFs with particle sizes ranging from 20 nm–4 μm.²⁰ As determined by VT-DRUVVis, all materials displayed decreasing optical gaps with increasing temperatures. Although conventional semiconductors typically show this “Varshni behaviour”, the effect in MOFs was much more severe. For TiO₂, Si, and similar materials, optical gaps decrease by roughly 0.1 eV over a 300 K range, whereas the MOF nanoparticles (nanoMOFs) absorbed at photon energies nearly 1 eV below the original low-temperature optical gap. The magnitude of this effect depends on the lability of the MOF ML bonds, however. As an example, the relatively dynamic titanium–carboxylate bonds in MIL-125 (Ti₈O₈(OH)₄(terephthalate)₆) led to a large but reversible decrease of ∼600 mV over a range of 300 K, whereas ZIF-8 (Zn(2-methylimidazolate)₂), comprised of strong zinc–imidazolate bonds, shows a much smaller decrease of only ∼10 mV. For all materials, smaller particle sizes induced far larger changes to MOF optical gaps. This relationship was further evidenced by fitting the data to a model previously described by O'Donnell and Chen⁶¹ that allows extraction of the Huang–Rhys parameter S, a unitless measure of nuclear rearrangements and vibronic coupling. As with traditional quantum dots, smaller nanoMOF particles showed larger S values and they fit well to an inverse relationship with particle volume, as predicted by theory.⁶² However, whereas typical molecules and semiconductors show S < 10, while for ionic solids S > 50,^63,64 MIL-125 nanoparticles showed S ranging from 7–80 simply by decreasing particle diameters from 400–70 nm.

Size-dependent thermal shifts to optical gaps in nanoMOFs involves bond dynamics beyond the explanation typically given for “Varshni behaviour”. In conventional semiconductors, thermal shifts arise from elongation and contraction of lattice parameters with changes to thermal energy. This mechanism gives rise to rigid shifts to optical absorption profiles without altering the overall electronic structure and, hence, band shape. Such an effect could be present in MOFs, such as with ZIF-8, where higher temperatures led to rigid redshifts by decreasing the HOMO–LUMO or bandgap, (Fig. 5). Overall, a larger relative population of “loose” bonding states should lead to smaller optical gaps, given that the structural and electronic symmetry is maintained. Yet, “loose” ML bonds could also cause a loss of symmetry in the electronic structure, which could further contribute to the apparent shrinking of the optical gap at smaller crystal sizes (Fig. 5). Indeed, for smaller nanoMOFs, higher temperatures saw the emergence of additional absorption bands and significant tails extending into the infrared as if the MOFs transformed reversibly into new structures entirely.

Fig. 5 Illustration of how dynamic metal–ligand bonding affects optical and electronic band gaps, either through the population of “loose” metal–ligand bonding states or by accommodating a decrease in symmetry of the electronic structure, generating mid-gap states.

The origin of size-dependent labile bonding in MOFs remains an open research frontier, but similar observations have been reported for conventional semiconductors. For example, nano-sized metal oxide particles exhibit larger lattice parameters, alumina nanoparticles become more compressible,⁶⁵ and Si nanocrystals display lower melting point temperatures and smaller bulk moduli.⁶⁶ One proposed explanation invokes weaker Madelung fields arising simply from the absence of stabilizing electrostatic interactions at a bare nanoparticle surface.⁶⁷ Alternatively, increased bond flexibility and other forms of entropy at particle surfaces may play a critical role as has been invoked to explain size-dependent structural and phase change behaviour for SrTiO₃ and SCO nanoparticles.^68–70 With smaller sizes and greater surface-to-volume ratios, the structural and electronic effects of surface states on particle interiors should magnify, causing size-dependent functional properties.

Outlook

This article summarizes only an initial understanding of dynamic bonding in MOFs and its implications for fundamental and applied science. For example, while this discussion focuses on spectroscopic observations, diffraction and scattering techniques should provide structural insights, as has been shown in studies of MOF glasses.^48,51,71 In addition, ultra-fast spectroscopy or X-ray scattering measurements may yield information about the time-resolved dynamics of the underlying structural processes.⁷² With the available data to-date, further modelling of the redshift slopes observed by VT-DRIFTS could relate these phenomenological observations to deeper thermodynamic models of phase changes and vibronic interactions. Additionally, the size-dependent bond dynamics, although convincing, remains unexplained by models for any class of materials. Taken together, dynamic ML bonding and its size-dependence in MOFs offers a rich platform for controlling and interrogating the behaviour of coordination materials, ranging from stimuli-responsive and phase-change behaviour to catalytic activity and structural stability.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

E. S. G. acknowledges support from the Swedish Research Council (grant no. 2022-06178). C. K. B. acknowledges support from the Department of Energy through the Office of Basic Energy Sciences under Grant DE-SC0022147 and the Research Corporation for Science Advancement (Cottrell Award).

References

1. L. Guo, D. E. Ellis, B. M. Hoffman and Y. Ishikawa, Inorg. Chem., 1996, 35, 5304–5312.
2. T. Ishii, S. Tsuboi, G. Sakane, M. Yamashita and B. K. Breedlove, Dalton Trans., 2009, 680–687.
3. Z. Yang, M. Corso, R. Robles, C. Lotze, R. Fitzner, E. Mena-Osteritz, P. Bäuerle, K. J. Franke and J. I. Pascual, ACS Nano, 2014, 8, 10715–10722.
4. D. Cremer and E. Kraka, Dalton Trans., 2017, 46, 8323–8338.
5. J. Bould, O. Tok, V. Passarelli, M. G. S. Londesborough and R. Macías, Inorg. Chem., 2020, 59, 17958–17969.
6. K. Zhao, S. Liu, Y. Li, X. Wei, G. Ye, W. Zhu, Y. Su, J. Wang, H. Liu, Z. He, Z. Zhou and S. Sun, Adv. Energy Mater., 2022, 12, 2103588.
7. K. A. Williams, A. J. Boydston and C. W. Bielawski, Chem. Soc. Rev., 2007, 36, 729–744.
8. K. A. Williams, D. R. Dreyer and C. W. Bielawski, MRS Bull., 2008, 33, 759–765.
9. A. Winter and U. S. Schubert, Chem. Soc. Rev., 2016, 45, 5311–5357.
10. D.-P. Wang, J.-C. Lai, H.-Y. Lai, S.-R. Mo, K.-Y. Zeng, C.-H. Li and J.-L. Zuo, Inorg. Chem., 2018, 57, 3232–3242.
11. K. McCash, B. K. Mani, C.-M. Chang and I. Ponomareva, J. Phys.: Condens. Matter, 2014, 26, 435901.
12. M. P. Jiang, M. Trigo, I. Savić, S. Fahy, É. D. Murray, C. Bray, J. Clark, T. Henighan, M. Kozina, M. Chollet, J. M. Glownia, M. C. Hoffmann, D. Zhu, O. Delaire, A. F. May, B. C. Sales, A. M. Lindenberg, P. Zalden, T. Sato, R. Merlin and D. A. Reis, Nat. Commun., 2016, 7, 12291.
13. S. Badola, S. Mukherjee, B. Ghosh, G. Sunil, G. Vaitheeswaran, A. C. Garcia-Castro and S. Saha, Phys. Chem. Chem. Phys., 2022, 24, 20152–20163.
14. J.-C. Lai, X.-Y. Jia, D.-P. Wang, Y.-B. Deng, P. Zheng, C.-H. Li, J.-L. Zuo and Z. Bao, Nat. Commun., 2019, 10, 1164.
15. C. Li and J. Zuo, Adv. Mater., 2020, 32, 1903762.
16. C. W. Jones, JACS Au, 2022, 2, 1504–1505.
17. A. B. Andreeva, K. N. Le, L. Chen, M. E. Kellman, C. H. Hendon and C. K. Brozek, J. Am. Chem. Soc., 2020, 142, 19291–19299.
18. A. B. Andreeva, K. N. Le, K. Kadota, S. Horike, C. H. Hendon and C. K. Brozek, Chem. Mater., 2021, 33, 8534–8545.
19. M. D. Allendorf, V. Stavila, M. Witman, C. K. Brozek and C. H. Hendon, J. Am. Chem. Soc., 2021, 143, 6705–6723.
20. K. Fabrizio and C. K. Brozek, Nano Lett., 2023, 23, 925–930.
21. K. Fabrizio, A. B. Andreeva, K. Kadota, A. J. Morris and C. K. Brozek, Chem. Commun., 2023, 59, 1309–1312.
22. R. A. Cowley, Integr. Ferroelectr., 2012, 133, 109–117.
23. P. A. Fleury, Annu. Rev. Mater. Sci., 1976, 6, 157–180.
24. J. Petzelt and S. Kamba, Ferroelectrics, 2016, 503, 19–44.
25. P. Galinetto, E. Giulotto, P. Camagni, G. Samoggia, V. A. Trepakov and P. P. Syrnikov, Ferroelectrics, 2001, 254, 135–142.
26. C. K. Brozek, V. K. Michaelis, T.-C. Ong, L. Bellarosa, N. López, R. G. Griffin and M. Dincă, ACS Cent. Sci., 2015, 1, 252–260.
27. C. K. Brozek and M. Dincă, Chem. Commun., 2015, 51, 11780–11782.
28. C. K. Brozek and M. Dincă, Chem. Sci., 2012, 3, 2110–2113.
29. C. K. Brozek and M. Dincă, J. Am. Chem. Soc., 2013, 135, 12886–12891.
30. R. E. Morris and L. Brammer, Chem. Soc. Rev., 2017, 46, 5444–5462.
31. J. L. Obeso, M. T. Huxley, C. Leyva, J. Gabriel Flores, N. Martín-Guaregua, M. Viniegra, J. Aguilar-Pliego, J. Antonio De Los Reyes, I. A. Ibarra and R. A. Peralta, Coord. Chem. Rev., 2023, 496, 215403.
32. G. Férey and C. Serre, Chem. Soc. Rev., 2009, 38, 1380–1399.
33. C. R. Murdock, B. C. Hughes, Z. Lu and D. M. Jenkins, Coord. Chem. Rev., 2014, 258–259, 119–136.
34. A. Schneemann, P. Vervoorts, I. Hante, M. Tu, S. Wannapaiboon, C. Sternemann, M. Paulus, D. C. F. Wieland, S. Henke and R. A. Fischer, Chem. Mater., 2018, 30, 1667–1676.
35. V. Y. Mao, P. J. Milner, J. Lee, A. C. Forse, E. J. Kim, R. L. Siegelman, C. M. McGuirk, L. B. Zasada, J. B. Neaton, J. A. Reimer and J. R. Long, Angew. Chem., Int. Ed., 2020, 59, 19468–19477.
36. S.-H. Lo, L. Feng, K. Tan, Z. Huang, S. Yuan, K.-Y. Wang, B.-H. Li, W.-L. Liu, G. S. Day, S. Tao, C.-C. Yang, T.-T. Luo, C.-H. Lin, S.-L. Wang, S. J. L. Billinge, K.-L. Lu, Y. J. Chabal, X. Zou and H.-C. Zhou, Nat. Chem., 2020, 12, 90–97.
37. Y. Wu, A. Kobayashi, G. J. Halder, V. K. Peterson, K. W. Chapman, N. Lock, P. D. Southon and C. J. Kepert, Angew. Chem., Int. Ed., 2008, 47, 8929–8932.
38. N. Lock, M. Christensen, Y. Wu, V. K. Peterson, M. K. Thomsen, R. O. Piltz, A. J. Ramirez-Cuesta, G. J. McIntyre, K. Norén, R. Kutteh, C. J. Kepert, G. J. Kearley and B. B. Iversen, Dalton Trans., 2013, 42, 1996–2007.
39. M. J. Cliffe, J. A. Hill, C. A. Murray, F.-X. Coudert and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 11586–11592.
40. A. K. D. K. Lewis, S. Caddick, F. G. N. Cloke, N. C. Billingham, P. B. Hitchcock and J. Leonard, J. Am. Chem. Soc., 2003, 125, 10066–10073.
41. R. Dobrawa and F. Würthner, J. Polym. Sci., Part A: Polym. Chem., 2005, 43, 4981–4995.
42. J. W. Bunting and K. M. Thong, Can. J. Chem., 1970, 48, 1654–1656.
43. S. Bode, L. Zedler, F. H. Schacher, B. Dietzek, M. Schmitt, J. Popp, M. D. Hager and U. S. Schubert, Adv. Mater., 2013, 25, 1634–1638.
44. A. Krylov, A. Vtyurin, P. Petkov, I. Senkovska, M. Maliuta, V. Bon, T. Heine, S. Kaskel and E. Slyusareva, Phys. Chem. Chem. Phys., 2017, 19, 32099–32104.
45. A. E. J. Hoffman, J. Wieme, S. M. J. Rogge, L. Vanduyfhuys and V. Van Speybroeck, Z. Kristallogr. – Cryst. Mater., 2019, 234, 529–545.
46. R. Gaillac, P. Pullumbi, K. A. Beyer, K. W. Chapman, D. A. Keen, T. D. Bennett and F.-X. Coudert, Nat. Mater., 2017, 16, 1149–1154.
47. J. Hou, M. L. Ríos Gómez, A. Krajnc, A. McCaul, S. Li, A. M. Bumstead, A. F. Sapnik, Z. Deng, R. Lin, P. A. Chater, D. S. Keeble, D. A. Keen, D. Appadoo, B. Chan, V. Chen, G. Mali and T. D. Bennett, J. Am. Chem. Soc., 2020, 142, 3880–3890.
48. N. Li, Z. Shi, S. Zhai, N. Zhou, P. Zhang, A. Arramel, T. D. Bennett and Y. Yue, J. Am. Ceram. Soc., 2023, 106, 6117–6129.
49. R. A. Peralta, M. T. Huxley, P. Lyu, M. L. Díaz-Ramírez, S. H. Park, J. L. Obeso, C. Leyva, C. Y. Heo, S. Jang, J. H. Kwak, G. Maurin, I. A. Ibarra and N. C. Jeong, ACS Appl. Mater. Interfaces, 2023, 15, 1410–1417.
50. D. Umeyama, S. Horike, M. Inukai, T. Itakura and S. Kitagawa, J. Am. Chem. Soc., 2015, 137, 864–870.
51. T. D. Bennett and S. Horike, Nat. Rev. Mater., 2018, 3, 431–440.
52. L. Longley, S. M. Collins, S. Li, G. J. Smales, I. Erucar, A. Qiao, J. Hou, C. M. Doherty, A. W. Thornton, A. J. Hill, X. Yu, N. J. Terrill, A. J. Smith, S. M. Cohen, P. A. Midgley, D. A. Keen, S. G. Telfer and T. D. Bennett, Chem. Sci., 2019, 10, 3592–3601.
53. J. M. Tuffnell, C. W. Ashling, J. Hou, S. Li, L. Longley, M. L. Ríos Gómez and T. D. Bennett, Chem. Commun., 2019, 55, 8705–8715.
54. F. A. Lindemann, Phys. Z., 1910, 11, 609–612.
55. L. Wang, C. Wang, Y. Sun, K. Shi, S. Deng and H. Lu, Mater. Chem. Phys., 2016, 175, 138–145.
56. J. K. Bristow, J. M. Skelton, K. L. Svane, A. Walsh and J. D. Gale, Phys. Chem. Chem. Phys., 2016, 18, 29316–29329.
57. G. Venkataraman, Bull. Mater. Sci., 1979, 1, 129–170.
58. M. Grzywa, D. Denysenko, J. Hanss, E.-W. Scheidt, W. Scherer, M. Weil and D. Volkmer, Dalton Trans., 2012, 41, 4239–4248.
59. J. F. Scott, Rev. Mod. Phys., 1974, 46, 83–128.
60. K. Fabrizio, K. A. Lazarou, L. I. Payne, L. P. Twight, S. Golledge, C. H. Hendon and C. K. Brozek, J. Am. Chem. Soc., 2021, 143, 12609–12621.
61. K. P. O'Donnell and X. Chen, Appl. Phys. Lett., 1991, 58, 2924–2926.
62. S. Schmitt-Rink, D. A. B. Miller and D. S. Chemla, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 8113–8125.
63. K. Huang and A. Rhys, Proc. R. Soc. London, Ser. A, 1950, 204, 406–423.
64. L. D. Whalley, P. van Gerwen, J. M. Frost, S. Kim, S. N. Hood and A. Walsh, J. Am. Chem. Soc., 2021, 143, 9123–9128.
65. B. Chen, D. Penwell, L. R. Benedetti, R. Jeanloz and M. B. Kruger, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 144101.
66. B. J. Abdullah, M. S. Omar and Q. Jiang, Sādhanā, 2018, 43, 174.
67. V. Perebeinos, S.-W. Chan and F. Zhang, Solid State Commun., 2002, 123, 295–297.
68. H.-B. Neumann, U. Rütt, J. R. Schneider and G. Shirane, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 3981–3984.
69. C. Enachescu and A. Hauser, Phys. Chem. Chem. Phys., 2016, 18, 20591–20599.
70. C. Ma, N. Lin, Z. Wang, S. Zhou, H. Yu, J. Lu and H. Huang, Phys. Rev. B, 2019, 99, 115401.
71. T. D. Bennett, J.-C. Tan, Y. Yue, E. Baxter, C. Ducati, N. J. Terrill, H. H.-M. Yeung, Z. Zhou, W. Chen, S. Henke, A. K. Cheetham and G. N. Greaves, Nat. Commun., 2015, 6, 8079.
72. J. Nishida, A. Tamimi, H. Fei, S. Pullen, S. Ott, S. M. Cohen and M. D. Fayer, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18442–18447.

---