Ordering by cation replacement in the system Na_2−xLi_xGa₇

Abstract

Samples of the pseudo-binary system Na_2−xLi_xGa₇ (x ≤ 1) were synthesized from the elements at 300 °C in sealed Ta ampoules or by the reaction of Na₂Ga₇ with LiCl. The peritectic formation temperature decreases with increasing Li content from 501(2) °C (x = 0) to 489(2) °C (x = 1). The boundary compositions Na₂Ga₇ and Na₁Li₁Ga₇ crystallize with different structure types related by a group–subgroup relation. While the Na-rich compositions (x ≤ 0.5) represent a substitutional solid solution (space group Pnma), the Li-rich compositions feature an unconventional replacement mechanism in which Li atoms occupying interstitial positions induce vancancies at the Na positions (space group Cmce). The crystal structure of Na₁Li₁Ga₇ (a = 8.562(1) Å, b = 14.822(2) Å, c = 11.454(2) Å; Z = 8) was determined from X-ray single-crystal diffraction data, and reveals an anionic framework comprising 12-bonded Ga₁₂ icosahedra and 4-bonded Ga atoms, with alkali–metal atoms occupying channels and cavities. The arrangement of cations makes NaLiGa₇ a new structure type within the MgB₁₂Si₂ structure family. Band structure calculations for the composition NaLiGa₇ predict semiconducting behavior consistent with the balance [Na⁺]₂[Li⁺]₂[(Ga₁₂)²⁻][Ga^–]₂, considering closo Wade clusters [(12b)Ga₁₂]²⁻ and Zintl anions [(4b)Ga]⁻. Susceptibility measurements indicate temperature-independent diamagnetic behavior.

---

Introduction

Inorganic framework compounds composed of p-elements and encapsulated metal cations are frequently studied.^1,2 Their crystal structures show the characteristic bonding features of the framework atoms involved. While clathrate-type structures are commonly observed among frameworks based on 4-bonded group 14 elements,¹ frameworks of group 13 elements lack valence electrons to solely form two-center, two-electron bonds between all framework atoms.² They typically adopt polyhedral Wade clusters, such as closo [B₆]²⁻ in CaB₆,³ or form multiatomic bonds, like in BaAl₄,⁴ which may be considered as a framework of 2D edge-condensed nido clusters. An example of the first type is the recently discovered Na₂Ga₇,⁵ which exhibits a framework of 12-bonded [Ga₁₂]²⁻closo clusters and 4-bonded [Ga]^– Zintl anions. The electronic balance is achieved by the Na cations according to [Na⁺]₄[(Ga₁₂)²⁻][Ga^–]₂. The structure of this family can also be formed with heteroatomic frameworks and varying cation contents, as evidenced by the boride silicides MgB₁₂Si₂⁶ and Li₂B₁₂Si₂,⁷ which are composed of [B₁₂]²⁻closo clusters and 4-bonded Si atoms. In contrast to the boride silicides, the higher number of cations in Na₂Ga₇ (i.e. Na₄Ga₁₂Ga₂) leads to their disorder in the Ga channels. In this study, we investigate the pseudo-binary system Na₂Ga₇/NaLiGa₇ to determine the response of the Ga framework on the cation substitution and the possibility to obtain new members of the MgB₁₂Si₂ family.

Experimental details

Preparation

Reaction from the elements. Na (Chempur, 99.9%), Li (EVOCHEM, 99.9%) and Ga (Chempur, 5 N) were combined in a total amount of 2 g to prepare the compositions Na_2−xLi_xGa₇ (x = 0.2, 0.5, 0.8, 1.0, 1.5) and, with excess of Li, Na₁Li_1.2Ga₇. The mixtures were sealed in Ta tubes under an Ar atmosphere. For homogenization, the sample was heated to 1000 °C for 2 min using an induction furnace and then allowed to cool to room temperature by turning off the furnace. Subsequently, the Ta tube was placed in a quartz vessel and further annealed under vacuum at 300 °C for one week. After annealing, the ampoule was quenched in water. The reaction products consisted of crystalline grains with metallic luster and were sensitive to air and moisture.

Metathesis reaction. Finely ground powder mixtures of Na₂Ga₇ ⁵ and LiCl (Chempur, 99.9%) were mixed with molar ratios of 1 : 1 or 1 : 1.5. These mixtures were pressed into pellets (d = 10 mm, h = 2 mm), sealed in a Ta crucible under an Ar atmosphere, and placed in an evacuated glass vessel. The vessel was annealed at 300 °C in a tube furnace for one week and then cooled down to room temperature by switching off the furnace.

Characterization

Single-crystal X-ray diffraction. A single crystal of NaLiGa₇ was fixed on top of a glass capillary (d = 0.1 mm) with grease and sealed in another capillary (d = 0.3 mm). Room-temperature single-crystal X-ray diffraction data were collected by a Rigaku AFC7 diffractometer (Saturn 724+ CCD detector, Mo Kα radiation, λ = 0.71073 Å). Absorption correction was performed with a multi-scan procedure. The crystal structure was solved and refined by using the WinCSD program.⁸ Details about the data collection and structure refinement are listed in Table S1;† atomic coordinates and displacement parameters are shown in Table S2;† selected interatomic distances and angles are listed in Tables S3–5.† The program Diamond V4.6.8 was used for structure drawings.⁹

Powder X-ray diffraction (PXRD). All samples were characterized by the Guinier technique (Huber Image Plate Camera G670; germanium monochromator; Cu Kα1 radiation; λ = 1.54056 Å; 5.0° < 2θ < 100°; step width = 0.005°). Finely ground specimens were fixed under an Ar atmosphere on the sample holder between two polyimide foils (7.5 μm, Kapton, Chemplex), using a thin film of vacuum grease (Lithelen, Leybold). LaB₆ standard (NIST, SRM 660a) was added to the sample as a reference for the reflection positions. Lattice parameters were obtained from the least-square method, using reflection positions extracted by profile fitting.⁸

Scanning electron microscope (SEM). Compositional analysis by EDX failed as polishing of the air- and moisture-sensitive material always led to the formation of a gallium layer on the sample surface.

Thermal analysis. The thermal behaviour of the samples Na_2−xLi_xGa₇ was measured with a heat-flux DTA device (Netzsch DSC 404C). About 50 mg of a pure sample was sealed in a Nb crucible (d = 5 mm, 600 mg). The system was heated from room temperature up to 600 °C then cooled down to 100 °C with heating rate of 5 °C min⁻¹ under an Ar atmosphere. The measurements were calibrated with elemental Al measured under the same conditions. For thermal decomposition analysis, 50 mg of finely ground powder of NaLiGa₇ was filled under an Ar atmosphere in an open Ta crucible. For the heat treatment, the Ta crucible was placed in a glass tube, which was evacuated to 10⁻² mbar and closed. During the heat treatment, the decomposition is evidenced by the precipitation of a sodium mirror at the cold part of the glass vessel. After the measurement, the product was characterized by PXRD.

Magnetic susceptibility. Magnetization was measured in a SQUID magnetometer (MPMS-XL7, Quantum Design) in the temperature range 1.8–400 K. Fields μ₀H from 2 mT to 7 T were applied, the diamagnetic contribution of the sample tube was subtracted.

Calculation methods. First-principles electronic structure calculations were conducted using the all-electron full-potential local orbital (FPLO) method.¹⁰ Exchange–correlation effects were considered via the local density approximation (LDA) within the density functional theory, utilizing the Perdew and Wang parametrization.¹¹ The experimentally obtained crystal structure data were utilized. The Brillouin zone was sampled with a 15 × 15 × 15 mesh.

Results and discussion

Preparation of Na_2−xLi_xGa₇ (x ≤ 1)

When a stoichiometric mixture of the elements at composition NaLiGa₇ was melted and cooled down to room temperature within a few minutes, the resulting product predominantly consisted of NaLiGa₇, along with smaller amounts of Li₃Ga₁₄ ¹² and an unidentified phase, as determined by PXRD analysis. This behaviour notably differs from the preparation of Na₂Ga₇, which does not form directly from the melt.⁵ However, the presence of foreign phases indicates that NaLiGa₇ forms incongruently as well. Subsequent annealing at 300 °C for one week led to the formation of single-phase products for all compositions Na_2−xLi_xGa₇, with x = 0.2, 0.5, 0.8 and 1 as confirmed by PXRD analysis (Fig. 1). For the sample with x = 1.5, the majority phase was Na₁Li₁Ga₇, accompanied by foreign phases (Table 1). During annealing, the sample melted partially, indicating that the identified phases, Na₁Li₁Ga₇, Li₃Ga₁₄, LiGa₂ and LiGa₆,¹³ were not in equilibrium upon cooling. Therefore, we conclude that the upper limit for substitution of Na atoms is reached at x = 1. Furthermore, a homogeneity range Na₁Li_1+δGa₇ with a higher Li content was not detected by refinement of the lattice parameters. The product with nominal composition Na₁Li_1.2Ga₇ consisted of Na₁Li₁Ga₇ and exhibited weak reflections of an unknown phase.

Fig. 1 PXRD patterns of Na_2−xLi_xGa₇ (x = 0, 0.5, 1) after annealing at 300 °C (Cu Kα1). The calculated patterns of Na₂Ga₇ (space group Pnma, red lines) and NaLiGa₇ (space group Cmce, blue lines) are based on single-crystal diffraction data. For Na_1.5Li_0.5Ga₇ and Na₂Ga₇, some characteristic reflections breaking the C-centered lattice are indexed. In NaLiGa₇, symmetry inequivalent reflections overlap due to the hexagonal axis ratio b/a (Table 1).

Table 1 Lattice parameters of samples with the nominal compositions Na_2−xLi_xGa₇ (x = 0, 0.2, 0.5, 0.8, 1, 1.5) and NaLi_1.2Ga₇ obtained by annealing at 300 °C. PXRD patterns of samples with x ≤ 0.5 show primitive reflections breaking the Cmce symmetry. For a better comparison of the lattice parameters, samples with x = 0, 0.2, and 0.5 are listed in the non-standard setting Pmnb instead of Pnma

Nominal composition	x	Lattice parameters				Space group	b/a
		a/Å	b/Å	c/Å	V/Å^3
Na2Ga7	0	8.6766(6)	14.8580(6)	11.6105(5)	1497.1(1)	Pmnb	1.7124(1)
Na1.8Li0.2Ga7	0.2	8.646(2)	14.847(3)	11.558(3)	1483.7(6)	Pmnb	1.7172(5)
Na1.5Li0.5Ga7	0.5	8.5956(9)	14.834(1)	11.488(2)	1464.8(3)	Pmnb	1.7257(2)
Na1.2Li0.8Ga7	0.8	8.5692(9)	14.836(2)	11.466(2)	1457.7(4)	Cmce	1.7313(3)
Na1.0Li1.0Ga7	1	8.562(1)	14.822(2)	11.454(2)	1453.6(4)	Cmce	1.7311(3)
Na0.5Li1.5Ga7	1.5	8.584(7)	14.80(2)	11.444(6)	1453(4)	Cmce	1.724(3)
Na1.0Li1.2Ga7	—	8.558(1)	14.820(2)	11.453(2)	1452.6(3)	Cmce	1.7317(3)

---

Other than from direct synthesis, Na₁Li₁Ga₇ can be formed through a metathesis reaction of Na₂Ga₇ and LiCl (eqn (1)). The reaction is supported by the higher stability of NaCl compared to LiCl increasing with temperature.¹⁴ When Na₂Ga₇ and LiCl were reacted in a 1 : 1 molar ratio at 300 °C, the product consisted of Na₁Li₁Ga₇ and NaCl as confirmed by PXRD analysis (Table 2).

Table 2 Lattice parameters of NaLiGa₇ obtained from different preparation methods. Parameters were refined from the same set of non-overlapping reflections

Method	Lattice parameters				Space group
	a/Å	b/Å	c/Å	V/Å^3
Cast product	8.554(2)	14.826(3)	11.457(2)	1453.0(5)	Cmce
Annealing at 300 °C	8.562(1)	14.822(2)	11.454(2)	1453.6(4)	Cmce
1 Na2Ga7 + 1 LiCl	8.5622(9)	14.828(2)	11.458(2)	1454.7(4)	Cmce

---

No residual LiCl was detected, and the refined lattice parameter of NaCl (a = 5.6400(7) Å) matched the reported value.¹⁵ This indicates that the cation substitution was quantitative.

1 Na₂Ga₇ + 1 LiCl → 1 Na₁Li₁Ga₇ + 1 NaCl (1)

When Na₂Ga₇ was reacted with 1.5 equivalents of LiCl at 300 °C, a mixture of Na_2−xLi_xGa₇, Li₃Ga₁₄ and NaCl was observed in PXRD. The overlapping reflections lowered the precision of the lattice parameter refinement, but the obtained values are consistent with the composition NaLiGa₇. This finding confirms that Li can substitute up to one equivalent of Na in Na₂Ga₇. With an excess amount of LiCl, Na₁Li₁Ga₇ was not formed. Reacting an equimolar mixture of NaLiGa₇ and LiCl resulted in the formation of binary gallides Li₃Ga₁₄, LiGa₂ and NaGa₄.¹⁶

Thermal stability of the composition range Na_2−xLi_xGa₇

The binary phase Na₂Ga₇ forms peritectically at 501(2) °C from Na₇Ga₁₃ ¹⁷ and the melt.⁵ Regarding the ternary system Na_2−xLi_xGa₇, the thermal stability decreases with increasing Li content. A single-phase sample of Na_1.8Li_0.2Ga₇ revealed a slightly lower decomposition temperature of T = 498(2) °C. At the maximum Li-content Na₁Li₁Ga₇, the formation temperature is further reduced to T = 489(2) °C. At all compositions of Na_2−xLi_xGa₇, the presence of two signals in the DTA experiments indicates that the samples undergo incongruent melting (Table S6†).

The thermal decomposition of Na₁Li₁Ga₇ was investigated on bulk material to examine the possibility of the formation of a new ternary phase through the evaporation of Na. However, no such phase was observed. Under static vacuum conditions at 300 °C, no reaction was observed, and the initial material remained unchanged for a period of 1 week. At 400 °C, after 1 day, sodium droplets were observed in the cooler region of the glass reactor. PXRD patterns of the solid residue consisted of NaLiGa₇, minor amounts of Li₃Ga₁₄ and amorphous Ga, as indicated by its characteristic background. When the reaction time was prolonged to 3 days, only Li₃Ga₁₄ was detected along with contributions of amorphous Ga (eqn (2)).

3 Na₁Li₁Ga₇ → 1 Li₃Ga₁₄ + 7 Ga + 3 Na↑ (2)

Crystal structure of Na_2−xLi_xGa₇

Structure determination. The crystal structure of NaLiGa₇ was determined using single-crystal XRD data, revealing an orthorhombic unit cell with the space group Cmce (no. 64). The direct structure solution revealed five independent Ga positions, forming a framework consisting of icosahedral cluster units (Ga1–Ga4) and 4-bonded atoms (Ga5). A mixed occupancy of Ga and Li as it was recently detected in covalent Ge networks^18–20 was not observed. After refining the Ga positions, the cation positions were determined from the difference Fourier map. Two distinct peaks were identified, with the larger one located within the channels of the Ga framework, and a smaller peak situated in a cavity between three Ga₁₂ icosahedra. Assigning the larger peak at Wyckoff position 8e to Na and the weaker one at Wyckoff position 8f to Li, subsequent refinement cycles were performed with an anisotropic approximation of the atomic displacement parameters (ADPs). These refinement cycles resulted in full occupancy for all positions and yielded a residual value of R_F = 0.040. The ADPs of all Ga atoms and Li exhibited nearly isotropic behavior with regular U_eq values. Only for the Na atom, the ADPs showed a distinct ellipsoidal shape with a larger U_eq value (Fig. S1†). The orientation of the Na ellipsoids aligns to the walls of the channels, which run in a zig-zag pattern along the [100] direction (Fig. S2†). The disorder can be modeled by splitting the Na1 position (8e) into a 0.5-occupied Na1a position (8e) and a 0.25-occupied Na1b position (16g). In the final refinement cycle, the restraint occ(Na1a) + 2 × occ(Na1b) = 1 was applied, leading to a further reduction of the residual value R_F to 0.034. The refined unit-cell composition Na₈Li₈Ga₅₆ (Na₁Li₁Ga₇ with Z = 8) is electronically balanced according to [Na⁺]₈[Li⁺]₈[(Ga₁₂)²⁻]₄[Ga^–]₈, assuming the presence of closo Wade clusters^21,22 [(12b)Ga₁₂]²⁻ and Zintl anions^23–25 [(4b)Ga]^–. Unlike NaLiGa₇, all other compounds in the series Na_2−xLi_xGa₇ with x ≤ 0.5 crystallize with the subgroup Pnma. The lower symmetry is evident from the presence of additional reflections indexed in the PXRD patterns, e.g. (303), (231), (503) and (611), which violate the reflection conditions for space group Cmce (Fig. 1). Also, for another reason, the powder diffraction pattern of Na₂Ga₇ is more line-rich than that of NaLiGa₇. The lattice parameters a and b in NaLiGa₇ exhibit the almost ideal hexagonal ratio of √3, whereas in Na₂Ga₇, this value is not reached (Table 1). Therefore, reflections that overlap in NaLiGa₇, separate in Na₂Ga₇. The crystal structure of samples with compositions Na_2−xLi_xGa₇ (x = 0.2, 0.5, 0.8) was determined by the Rietveld method (Tables S7–S9†). In the initial structure model, the Ga positions were adopted from Na₂Ga₇ ⁵ and refined with isotropic ADPs. Subsequently, the positions of cations were determined. The partial occupancy of Na and Li positions could only be approximated.

Structure description. Compounds of the MgB₁₂Si₂ family feature a characteristic framework composed of E13 elements, which can be partially replaced by E14 elements.^5–7 The framework is built up of a face-centered arrangement of icosahedra, bonded together by exohedral bonds and 4-bonded atoms (Fig. S3†). While the overall framework topology is characteristic for all representatives, the cation positions vary depending on number and size of the cations in relation to the framework. While the anionic framework can always be described with space group Cmce, the cation arrangement in turn can lower the space group symmetry. Among the known representatives, MgB₁₂Si₂ and Na₂Ga₇ crystallize in the space group Pnma, while Li₂B₁₂Si₂ and Na₁Li₁Ga₇ crystallize in the space group Cmce (Table 3). The framework offers three distinct cation positions (Fig. 2), which are located along channels oriented in the [100] direction in the Cmce setting and in the [010] direction in the Pnma setting (Fig. 3). The potential cation positions can be visualized on a plane obtained by sectioning the three-dimensional framework perpendicular to the [001] direction (Fig. 4). The most favorable cation position seems to be the one denoted C1, which is located in the channels and the only occupied position in the compounds MgB₁₂Si₂ and Li₂B₁₂Si₂. At C1, the cations occupy hollows formed by three condensed six-membered rings (Fig. 2b).

Fig. 2 (a) Local environment of the cation positions C1, C2 and C3 in NaLiGa₇. (b) Positions C1 and C3 are alternatively occupied.

Fig. 3 Cation positions for the representatives of the MgB₁₂Si₂ family: (a) Li₂B₁₂Si₂, (b) MgB₁₂Si₂, (c) Na₂Ga₇ and (d) NaLiGa₇.

Fig. 4 Puckered hexagon layers of (a) Li₂B₁₂Si₂, (b) MgB₁₂Si₂, (c) Na₂Ga₇ and (d) NaLiGa₇. For NaLiGa₇, the mean position of the split sites Na1a/Na1b (C2 position) is shown.

Table 3 Cation arrangement in compounds of the MgB₁₂Si₂ structure family. Three cation positions are available in the B/Si or Ga framework (M = Mg, Li, Na; F = B, Si, Ga)

Compound	Occupancy (in %)			M/F	Space group
	C1	C2	C3
MgB12Si2	50	0	0	1 : 14	Pnma
Li2B12Si2	100	0	0	2 : 14	Cmce
Na2Ga7	50	100	50	4 : 14	Pnma
NaLiGa7	0	100	100	4 : 14	Cmce

---

In the boride silicide Li₂B₁₂Si₂, all C1 positions are filled by Li atoms (Fig. 3a, 4a), while in MgB₁₂Si₂ only half of them are occupied by Mg atoms (Fig. 3b, 4b). The partial occupancy manifests in such a way that in each channel half positions are removed. In this way, the partial occupancy leads to a reduction in symmetry from Cmce in Li₂B₁₂Si₂ to Pnma in MgB₁₂Si₂. The crystal structure of Na₂Ga₇ (=Na₄Ga₁₂Ga₂) contains twice as many cations as Li₂B₁₂Si₂, so that the occupation of all positions C1 is not sufficient to accommodate all Na atoms. Consequently, two additional cation positions C2 and C3 are found, which have not been observed in the boride silicides (Fig. 3c, 4c). Atoms at position C2 are also located in the channels (Fig. 2b), which creates a conflict with the spatial requirements of the atoms at C1. In Na₂Ga₇, full occupancy of C1 and C2 in the channels by Na atoms is impossible for steric reasons. The maximum filling of the channels is achieved, when 50% of the C1 positions and 100% of C2 are occupied. The replaced C1 atoms occupy C3 positions instead, located in small cavities between three Ga₁₂ icosahedra (Fig. 2b). However, only half of the available C3 positions are occupied by Na atoms. Always two C3 positions are arranged in close proximity (Fig. 5), resulting in a distance d(C3–C3) = 2.78 Å being too short if both neighboring positions were filled by Na. The half occupancy of C1 and C3 in Na₂Ga₇ along with the ordered arrangement of Na results in a symmetry reduction from Cmce to Pnma.

Fig. 5 Pair of Li atoms situated in adjacent C3 cavities having a distance of 2.78 Å.

In the crystal structure of NaLiGa₇, the smaller Li atoms fill up all C3 positions. Simultaneous occupation of the adjacent positions C1 and C3 is excluded for their short distance of ≈1.60 Å requiring the C1 positions to remain empty. The C2 positions in the channels of NaLiGa₇ are fully occupied by Na atoms (Fig. 3d, 4d), as in Na₂Ga₇. With full occupancy of C3, there is no symmetry reduction observed in NaLiGa₇ and the space group remains Cmce (Table 3). The arrangement of cations in NaLiGa₇ introduces a new structure type within the MgB₁₂Si₂ structure family.

The topology of the Ga framework in NaLiGa₇ is very similar to the one in Na₂Ga₇. The Ga₁₂ icosahedra are distorted with endohedral bond distances ranging from 2.601(1) Å to 2.817(1) Å. The distances between atoms in trans-position vary from d(Ga3–Ga3) = 4.902 Å to d(Ga2–Ga2) = 5.338 Å (Fig. S4 and S5†). As expected, the exohedral two-center, two-electron bonds (d̄_exo = 2.54 Å) are shorter than the endohedral multicenter bonds (d̄_endo = 2.67 Å). The longest Ga–Ga bond d(Ga4–Ga4) = 2.817 Å is found at the cavity position C3, which shows that the occupation of this position creates distortion in the framework. For the boride silicides, where C3 is not occupied, this distortion of the icosahedra does not occur. The 4-bonded atoms Ga5 deviate from ideal tetrahedral coordination with bond angles ranging from 97.59(1) to 123.83(4) degrees and bond distances ranging from 2.517 Å to 2.591 Å. Comparing the bond spectra of Na₁Li₁Ga₇ and Na₂Ga₇, the framework in Na₁Li₁Ga₇ shows a smaller dispersion of the Ga–Ga bond lengths (Fig. 6). The dispersion of bond lengths in Na₂Ga₇ is mainly caused by the accommodation of the larger Na atoms in 50% of the small C3 cavities. In agreement with the reduced cell volume, the mean Ga–Ga bond distance in Na₁Li₁Ga₇ of 2.62 Å is shorter than 2.66 Å in Na₂Ga₇.

Fig. 6 Distance spectra in the Ga framework of (a) NaLiGa₇ and (b) Na₂Ga₇. Blue: endohedral bonds of the Ga₁₂ icosahedra; green: exohedral bonds between icosahedra; red: exohedral bonds between the icosahedra and 4-bonded Ga atoms.

Structural evolution in the composition range Na_2−xLi_xGa₇. When Na atoms are substituted with Li atoms, the unit-cell volume decreases with increasing Li content (Fig. 7a). However, for compositions with x ≤ 0.5 (space group Pnma), the volume reduction is more pronounced than for compositions with x > 0.5 (space group Cmce). Hence, different substitution mechanisms are at work. This can be understood by considering the occupancies of the cation positions (Table S10†):

• In Na₂Ga₇, the positions C1 and C3 are half-occupied by Na.

• In NaLiGa₇, C1 is empty, while C3 is fully occupied by Li.

• In both phases, position C2 is entirely filled with Na atoms

Fig. 7 (a) Cell volume of Na_2−xLi_xGa₇ (x = 0, 0.2, 0.5, 0.8, 1) against Li content. (b) Substitution model (lines) and refined occupancies (red triangles: Na at C1; blue circles: Na at C3; black circles: Li at C3). (c) b/a ratio of the hexagon planes. (d) Na–Na distances at position C2. (e) Depths of the hollow at C1. Shaded areas show the assumed homogeneity ranges. Error bars for all figures are smaller than the symbols used.

To determine the cation site occupancies for the compositions between 0 < x < 1, only PXRD data were available (Table S11†). The accuracy of the derived structure models was further constrained by the low scattering power of Li located in proximity to the heavier Ga atoms. Despite of these experimental limitations, the substitution mechanism can be inferred: For 0 ≤ x ≤ 0.5, the Na occupancy at C1 remains constant, while the Na occupancy at C3 clearly decreases (Fig. 7b).

Consequently, starting from Na₂Ga₇, the Li atoms first replace Na atoms in the small cavities at C3. This behavior corresponds to a conventional substitution alloy (Fig. 8a). Finally, at x = 0.5, all Na atoms at C3 are substituted, so that C3 is half occupied by Li. Now, for 0.5 < x ≤ 1, the Li atoms fill up the remaining vacant C3 positions, while Na atoms at C1 evanish (Fig. 7b). This exchange mechanism is unconventional as it represents an intermediate between an interstitial and a substitution alloy. The Li atoms occupy interstitial positions but simultaneously replace Na atoms located at other positions (Fig. 8b). At x = 1, C3 is completely filled by Li and C1 is completely emptied. Deviations of the experimental results from the substitution model only occur for low Na occupancies and Li positions, as expected. Seemingly, the occupancy of the narrow C3 cavities has a stronger impact on the cell volume than the occupancy of C1, sharing the large channels with C2. This is also reflected in the distortion of the six-membered ring planes (Fig. 4). While the lattice parameters a and b in NaLiGa₇ nearly exhibit the ideal hexagonal ratio (Table 1), the value deviates significantly in Na₂Ga₇. When the Na atoms in the small C3 cavities are replaced by Li in the range of 0 ≤ x ≤ 0.5, the ratio approaches the hexagonal value (Fig. 7c). Conversely, the occupation of the C1 position by Na in the range of 0.8 ≤ x ≤ 1 has no influence on the axis ratio.

Fig. 8 (a) Scheme of a substitution alloy. (b) The unconventional intermediate of an interstitial and a substitution alloy. Green lines symbolize the Ga framework, blue spheres Na and red spheres Li.

The proposed substitution mechanism finds further support in the interatomic distances of the Na atoms at C2, located within the channels of the Ga framework. In NaLiGa₇, the Na atoms at C2 show uniform distances from each other (Fig. 4d). Conversely, in Na₂Ga₇, the channels are shared by Na atoms at C2 and C1, resulting in mutual repulsion that leads the Na atoms at C2 to form dumbbells (Fig. 4c). Therefore, the refined distance between C2 atoms is a signature of the Na occupancy at position C1. Starting from Na₂Ga₇, the experimentally determined Na–Na distances at C2 remain constant for 0 ≤ x ≤ 0.5, indicating the occupation of position C1 (Fig. 7d). For x > 0.5 the distances converge to a common value, signifying vacancies at C1. Moreover, the occupancy of C1 by Na affects the adjacent Ga atoms. The Na atoms at C1 are situated in a hollow formed by three Ga six-membered rings (Fig. 2b). As C1 becomes vacant, the depth of the hollows decreases (Fig. 7e and Fig. S6†). The decrease clearly starts for x > 0.5, in agreement with the proposed substitution model.

The X-ray results in this work suggest that the two boundary phases, Na₂Ga₇ and Na₁Li₁Ga₇, each have a homogeneity range. However, the two-phase region between both solid solutions was not detected in this study. In general, the ternary phase diagram Na–Li–Ga is unknown so far. A key challenge in determining the phase equilibria in future work will be the metallographic treatment of the air and moisture sensitive samples.

Electronic density of states

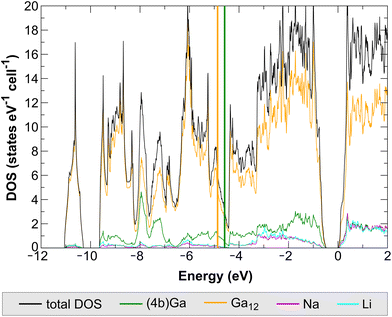
The computed electronic density of states (DOS) for NaLiGa₇ reveals a band gap of 0.47 eV (Fig. 9). This result is in line with the expectation of an electronically balanced composition for [(12b)Ga₁₂]²⁻ icosahedral closo clusters and [(4b)Ga]⁻ atoms. The Ga contributions are classified into two groups: (i) sum of the partial DOS of the Ga atoms forming the icosahedra Ga₁₂; (ii) DOS contributions of the 4-bonded Ga. These two chemically different Ga species are expected to be distinguishable in their local DOS projections.

Fig. 9 Computed electronic density of states (total DOS) for NaLiGa₇ and local DOS projections of the [(4b)Ga]⁻ species, the summed [(12b)Ga₁₂]²⁻ cluster species, and the cationic species. Thick vertical lines indicate energetical center of gravities of the [(4b)Ga]⁻ local DOS (green) and the corresponding sum for [(12b)Ga₁₂]²⁻ species (orange).

The [(4b)Ga]⁻ species do not significantly participate in the lowest-lying cluster orbital below −10 eV, containing 2 e⁻ per Ga₁₂ cluster, and the computed energetical center of gravity of the (5 + 1)-fold coordinated cluster Ga species lies energetically lower than the one for the 4-fold coordinated one (Fig. 9). All these results are in good agreement with the results previously found for Na₂Ga₇ (calculated band gap = 0.29 eV).⁵ As the DOS reveals (Fig. 9), there is no fundamental difference in the contribution of Na and Li atoms to the electronic structure of NaLiGa₇. We attribute the differences in the band gap between both compounds mainly to the larger distortions of the Ga icosahedra in Na₂Ga₇ (Fig. 6). The significant variation in the nearest neighbor distances is expected to result in a smaller intra-icosahedral band gap, which is of the bonding-antibonding type.^26,27

Physical properties

The magnetization M(T) of the sample of NaLiGa₇ was measured in the temperature range from T = 1.8 K to 400 K in magnetic fields μ₀H = 0.002 T, 0.1 T, 3.5 T and 7 T. The magnetic moment of the sample holder was subtracted from the measured data and the magnetic susceptibility χ = M/H was calculated. The magnetic susceptibility χ(T) is temperature-independent and diamagnetic (Fig. S7†) with value χ = –1.70 × 10⁻⁴ emu mol⁻¹ per formula unit, agreeing within 1% with the calculated value (−1.59 × 10⁻⁴ emu mol⁻¹) from diamagnetic increments for Na⁺, Li⁺ and elemental Ga.²⁸ The superconductivity observed below T ≈ 8 K can be attributed to the presence of elemental Ga impurities since the Meissner fraction of the signal is low (≈ 0.09%). From the reported data, the allotropes β-, γ- and δ-Ga show superconducting transitions at 5.9 K–6.2 K, 6.9 K–7.6 K and 7.85 K, respectively.²⁹ The resistivity measurements on Na_2−xLi_xGa₇ were challenging because of the tendency to form elemental Ga segregation on the surface of the sample during the measurements caused by oxidation.

Conclusions

The pseudo-binary system Na_2−xLi_xGa₇ is terminated by the compositions Na₂Ga₇ and Na₁Li₁Ga₇. Both phases show a homogeneity range with different substitution mechanisms. The crystal structure of Na₁Li₁Ga₇ belongs to the MgB₁₂Si₂ structure family, characterized by a framework of closo Ga₁₂ icosahedra and 4-bonded Ga atoms. Within the Ga framework, the alkali metal atoms occupy distinct channels and cavities. For Na₁Li₁Ga₇, the arrangement of cations is fully ordered, representing a new variant within the MgB₁₂Si₂ structure family. Na₁Li₁Ga₇ was prepared by either annealing the elements or by the quantitative metathesis reaction of Na₂Ga₇ with LiCl. Considering the electron balance [Na⁺]₈[Li⁺]₈[(12b)Ga₁₂²⁻]₄[(4b)Ga⁻]₈, the compound can be classified as a Zintl–Wade phase. The balance is consistent with the diamagnetic susceptibility and an electronic band gap, calculated to be 0.47 eV.

Author contributions

Chia-Chi Yu: investigation, formal analysis, conceptualization, methodology, writing – original draft; Yurii Prots: investigation, conceptualization, writing – review & editing; Alim Ormeci: investigation, writing – review & editing; Mitja Krnel: investigation, writing – review & editing; Marcus Schmidt: investigation; Lev Akselrud: formal analysis; Frank R. Wagner: formal analysis, writing – review & editing; Yuri Grin: formal analysis, conceptualization, methodology, writing – review & editing; Michael Baitinger: formal analysis, conceptualization, methodology, writing – original draft.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank H. Borrmann and S. Hückmann for providing PXRD data, and S. Scharsach for DTA measurements. Open Access funding provided by the Max Planck Society. C.-C. Y. acknowledges financial support by the International Max Planck Research School for Chemistry and Physics of Quantum Materials (IMPRS-CPQM).

References

1. The Physics and Chemistry of Inorganic Clathrates, ed. G. S. Nolas, Springer Series in Materials Science, 2014.
2. B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640.
3. L. Pauling and S. Weinbaum, Z. Kristallogr., 1934, 87, 181.
4. C. Zheng and R. Hoffmann, Z. Naturforsch., B: J. Chem. Sci., 1986, 41, 292.
5. C.-C. Yu, A. Ormeci, I. Veremchuk, X.-J. Feng, Yu. Prots, M. Krnel, P. Koželj, M. Schmidt, U. Burkhardt, B. Böhme, L. Akselrud, M. Baitinger and Yu. Grin, Inorg. Chem., 2023, 62, 9054.
6. T. Ludwig and H. Hillebrecht, J. Solid State Chem., 2006, 79, 1623.
7. N. Vojteer, M. Schroeder, C. Röhr and H. Hillebrecht, Chem. – Eur. J., 2008, 14, 7331.
8. L. Akselrud and Yu. Grin, J. Appl. Crystallogr., 2014, 47, 803.
9. Diamond V4.6.8, Crystal Impact, 2022.
10. K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1743.
11. J. P. Perdew and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1922, 45, 13244.
12. C. Belin and R.-G. Ling, J. Solid State Chem., 1982, 45, 290.
13. J. Sappl and C. Hoch, Inorg. Chem., 2020, 59, 6566.
14. P. W. Atkins, T. L. Overton, J. P. Rourke, M. T. Weller and F. A. Armstrong, Shriver and Atkins’ Inorganic Chemistry, W. H. Freeman and Company, New York, 5th edn, 2010.
15. W. T. Barrett and W. E. Wallace, J. Am. Chem. Soc., 1954, 76, 366.
16. G. Bruzzone, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 1206.
17. U. Frank-Cordier, G. Cordier and H. Schäfer, Z. Naturforsch., B: J. Chem. Sci., 1982, 37, 119.
18. K. Ghosh, A. Ovchinnikov, M. Baitinger, M. Krnel, U. Burkhardt, Yu. Grin and S. Bobev, Dalton Trans., 2023, 52, 10310.
19. K. Ghosh and S. Bobev, Chem. – Eur. J., 2023, 29, e20230238.
20. M. Kotsch, Yu. Prots, A. Ormeci, M. Bobnar, F. R. Wagner, A. Senyshyn and Yu. Grin, Eur. J. Inorg. Chem., 2020, 29, 2842.
21. K. Wade, J. Chem. Soc. D, 1971, 15, 792.
22. K. Wade, Adv. Inorg. Chem. Radiochem., 1976, 18, 1.
23. H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1981, 20, 33.
24. Yu. Grin, U. Schwarz and W. Steurer, Crystal Structure and Chemical Bonding. In Alloy Physics: A Comprehensive Reference, ed. W. Pfeiler, Wiley-VCH, Weinheim, 2007; pp. 19.
25. T. F. Fässler, Zintl Phases: Principles and Recent Developments, Springer, Berlin-Heidelberg, 2011.
26. H. C. Longuet-Higgins and M. De V. Roberts, Proc. R. Soc. London, Ser. A, 1955, 230, 110.
27. K. Wade, Electron Deficient Compounds, Springer, New York, 1971.
28. Diamagnetic Susceptibility and Anisotropy of Inorganic and Organometallic Compounds, ed. R. R. Gupta, Springer, Berlin-Heidelberg, 2007.
29. Y. Quan, P. J. Hirschfeld and R. G. Hennig, Phys. Rev. B, 2021, 104, 075117.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2304096 (NaLiGa₇). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3dt03628f

---