Distortion/interaction analysis via machine learning

Abstract

Machine learning (ML) models have provided a highly efficient pathway to quantum mechanical accurate reaction barrier predictions. Previous approaches have, however, stopped at prediction of these barriers instead of developing predictive capabilities in reactivity analysis tasks such as distortion/interaction–activation strain analysis. Such methods can provide insight into reactivity trends and ultimately guide rational reaction design. In this work we present the novel application of ML to the rapid and accurate prediction of distortion and interaction DFT energies across four datasets (three existing and one new dataset). We also show how our models can accurately predict on unseen, high impact literature examples where DFT-level distortion/interaction analysis has previously been used to explain reactivity trends for cycloadditions. This work thus provides support for ML to be utilised further in reactivity analysis across different reaction classes at a fraction of the cost of traditional methods such as DFT.

---

Introduction

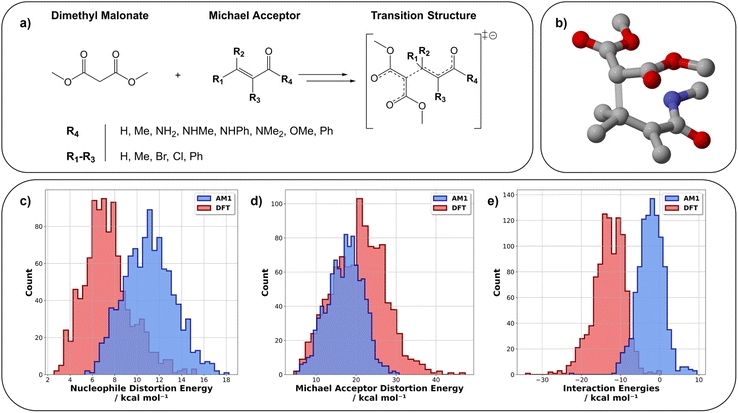
The use of machine learning (ML) across the vast catalogue of chemical problems has increased substantially in recent years given the potential for both rapid and accurate predictions with research areas including solvation effects,¹ yield predictions,^2,3 quantum chemical property prediction,^4,5 machine learned forcefields,⁶ and high-level energy predictions.^5,7–9 One area in which ML has delivered accurate and computationally efficient results is in the prediction of reaction barriers derived from, for example, density functional theory (DFT) or coupled cluster (CC) calculations.^8–15 Various ML techniques have been employed to successfully predict these reaction barriers including standard ML techniques as well as transfer learning (TL) for working in low data regimes.^8–11,13

However, these ML studies seldom go further than reaction barrier prediction. Thus, an area which remains relatively untouched by ML is reactivity analysis. To the best of our knowledge, only one paper has utilised ML in this context for energy decomposition analysis, however this work focused on minimum energy and not transition state (TS) structure analysis.¹⁶ Common computational methods used to gain insight into the origins of chemical reactivity include Natural Bond Orbital (NBO),^17,18 Non-Covalent Interaction (NCI),^18–21 and Distortion/Interaction–Activation Strain (DIAS) analysis (Fig. 1).^22–31 In the DIAS model, the reaction barrier can be decomposed into reactant distortion energies (strain) and interaction energy. The former arises from the conformational changes that occur during the reaction and the latter is the interaction between these distorted structures. The reaction barrier can therefore be considered as a balance between distortion and interaction energies. Breaking the barrier down into these energy components can provide insight into the factors that govern reactivity and is a particularly popular method of analysis in the study of cycloadditions.^{22,23,27,31–34} As an example, in a study of the reaction of cycloalkenones with various cyclic dienes,³¹ it was found that the interaction energies across the reaction series were almost identical. Therefore, the differences in reaction barrier arise from changes in dienophile and diene distortion energies. In a related study of the cycloaddition reaction of cyclopropenes with butadiene, the distortion energies of the endo and exo reactions were nearly identical, with the differences in reaction barrier (endo reactions favoured by 2–3 kcal mol⁻¹) arising from the difference in interaction energies.³⁵ This type of analysis therefore provides detailed information on reactivity trends which can aid in the rational design of new reactions.

Fig. 1 The DIAS model explained graphically. The energy required for the reactants to distort (red) into the correct geometry added to the interaction energy (green) equals the activation energy (purple).

Similar analysis has been applied to many other reactions such as: SN2/E2,^24,36 iridium-catalysed C–H borylation,²⁹ palladium-catalysed cross-coupling,³⁷ asymmetric propargylation³⁸ and allyboration,³⁹ and nickel-catalysed amide (a functional group that is ubiquitous in drug discovery) C–N bond activation.⁴⁰ However, computing accurate distortion and interaction energies requires the use of expensive quantum mechanical calculations (typically DFT) which prevents the routine use of this reactivity analysis on large datasets. ML may instead offer a rapid approach to high accuracy distortion and interaction energy predictions.

In this work, we report the first example of predicting distortion and interaction energies using ML. Models are built to predict DFT energies from rapid semi-empirical quantum mechanical (SQM) calculations for four distinct datasets (of which one is a new dimethyl malonate Michael addition dataset). The models yield high accuracy distortion and interaction energies for all four datasets with further insight available from the computed SQM TSs. Finally, we show that performance remains high when the models are applied to two unseen reaction sets from the literature.

Methodology

We utilised pre-existing datasets for three chemical reactions: nitro-Michael addition (ds1),⁸ Diels–Alder (ds2),⁹ and [3 + 2] cycloadditions (ds3).⁴¹ Ds3 geometries were available at the DFT level of theory therefore we performed SQM calculations on the reported structures (see ESI, Section 1.3† for full information). The newly created dataset is a collection of dimethyl malonate Michael addition reactions (ds4) which are a class of reactions of particular importance in polyketide biosynthesis.⁴² Reactant and TS geometries were generated for 1000 dimethyl malonate Michael addition reactions (Fig. 3a) using Schrödinger's R-group enumeration tool.⁴³ In this, we varied four positions on the α,β-unsaturated carbonyl Michael acceptor (MA) using synthetically relevant and accessible functional groups.^44–46 Once generated, Schrödinger's MacroModel⁴⁷ was used to conformationally search reactant and TSs using the OPLS3e forcefield.⁴⁸ The lowest energy conformation for every structure was then optimised with AM1 ⁴⁹ and ωB97X-D/def2-TZVP.^50,51 Single point energy (SPE) calculations at the same levels of theory were performed on these structures to account for solvent effects using the integral equation formalism of the polarisable continuum model (IEFPCM) with water.⁵² The combination of DFT and an implicit solvent model was chosen due to its good agreement with experiment as reported within the literature for this type of chemistry.^53–55 All calculations were performed with Gaussian16 (Revision A.03 ⁵⁶ and Revision C.01 ⁵⁷). Energies and quasi-harmonic free-energies (298.15 K, 1 mol l⁻¹ concentration) were calculated using GoodVibes.⁵⁸ Further details on this dataset are provided in the ESI, Section 1.4.†

For the distortion/interaction analysis, the distorted reactants at the TS must be separated to perform the necessary calculations. Whilst there is python code available for this function,⁵⁹ it requires a detailed input file about the given chemical system and does not provide a mapping of atom numbers from a TS to its respective reactant and distorted structures. We developed an approach that utilises the frequency vibrations of the TS as detailed in Fig. 2 (the code is available on GitHub (https://github.com/the-grayson-group/distortion-interaction_ML)). The main benefit of our code is that it can provide us with a mapping of atom numbers between the reactant, distorted, and TS structures regardless of the initial atom numbering. This is crucial for ML approaches that use knowledge of specific atoms. Dataset ds3 contained arbitrary atom numbering and our approach for determining the common atoms of this dataset is summarised in the ESI, Section 1.3.† After extracting the distorted structures from each TS, SPE calculations were performed at the same level of theory that the TS and reactants were calculated at and in solvent with energies then extracted with GoodVibes. The distortion and interaction energies were calculated as outlined in ESI Section 2.†

Fig. 2 How the distorted reactants at the TS were separated. In step one, the TS displacement vectors are used to generate reactant- and product-like geometries from which adjacency matrices are then created and compared. Any new bonds formed are highlighted and designated as the reaction centres. The associated atoms are then used to separate the distorted structures from the TS geometry and generate new Gaussian input files (step two).

From the SQM optimised reactants, distorted reactants, and TSs, atomic and physical organic chemical features were extracted using Morfeus⁶⁰ and cclib⁶¹ python packages. The features extracted and the entire procedure are outlined in the ESI, Section 4.1.† Features were standardised before three scikit-learn⁶² regression algorithms and two TensorFlow⁶³ neural networks (NNs) were trained. The targets were also standardised for the NNs.

The scikit learn algorithms were ridge regression, kernel ridge regression (KRR) with a radial basis function (RBF) kernel, and support vector regression (SVR) with the RBF kernel. These models were chosen due to their success in predicting reaction barriers in previous work.^8,9,64 The link between reaction barriers and distortion/interaction energies suggests that similar models may also be able to predict these new targets.

The models were hyperparameter tuned and performance was monitored on a validation set. The final model performance was evaluated on a held-out test set. For a full description of the ML procedure see ESI, Section 4.†

Results and discussion

Pre-ML metrics

Prior to training the ML models, we evaluated how closely the SQM approximated the DFT calculations. This gave us a rational, dataset specific context to consider alongside the widely accepted 1 kcal mol⁻¹ threshold typically used in evaluating reaction barrier/energy predictions.^65,66

For ds1,⁸ ds2,⁹ and ds3,⁴¹ their pre-ML SQM-DFT metrics are reported in the literature, Table 1, and in the ESI, Section 4.3.†

Table 1 Best model performance for predicting distortion and interaction energies for each dataset including test MAE as a percentage of the test set range to aid cross-dataset comparisons. These metrics are for all SVR models

Datasets		Pre-ML AM1-DFT MAE (kcal mol^−1)	Average SVR test MAE (kcal mol^−1)	Average test set range (DFT) (kcal mol^−1)	Test MAE as % of test set range
ds1	MA	4.45	1.35	2.60 to 28.26	5.3
	Nitromethane (nucleophile)	2.57	0.36	0.73 to 5.36	7.8
	Interaction	7.60	1.59	−23.11 to −0.09	6.9
ds2	Diene	2.80	0.33	12.12 to 26.54	2.3
	Dienophile	2.04	0.34	7.01 to 21.92	2.3
	Interaction	9.87	0.50	−17.40 to −3.43	3.6
ds3	Dipole	3.59	2.55	0.98 to 41.25	6.3
	Dipolarophile	3.81	2.37	0.13 to 35.33	6.7
	Interaction	20.01	2.46	−43.62 to −7.92	6.9
ds4	MA	4.07	1.27	7.30 to 39.64	3.9
	Dimethyl malonate (nucleophile)	3.70	0.54	3.43 to 13.98	5.1
	Interaction	10.83	1.23	−26.78 to −5.05	5.7

---

For ds4, the pre-ML AM1-DFT MAE for reaction barrier prediction is 10.46 kcal mol⁻¹. The spread of distortion and interaction energies are shown in Fig. 3. Fig. 3c and e highlight that AM1 significantly overestimates the dimethyl malonate distortion and interaction (pre-ML MAEs of 3.70 and 10.83 kcal mol⁻¹ respectively) energies. The interaction energy is calculated from the reaction barrier and distortion energies thus, its pre-ML AM1-DFT MAE could be impacted by the compounding of errors from the lower level of theory across multiple calculations. It could also be rationalised in part by the inability of the parent method (Hartree Fock) to account for electron correlation sufficiently and thus important interactions are not well captured.^49,67 The interaction energies are also overestimated by AM1 across the other datasets. For full information on pre-ML metrics see ESI, Section 4.3.†

Fig. 3 C–C bond forming dimethyl malonate Michael addition reaction and R groups used to generate the dataset (a), an example of a TS (b), and the spread of the dimethyl malonate nucleophile distortion (c), MA distortion (d), and interaction (e) energies (blue and red indicate AM1 and DFT energies respectively).

In this work we propose that if AM1 can provide rapid and approximate values relative to DFT, ML can be used to bridge this gap and give accurate distortion and interaction energy predictions at a fraction of the cost of DFT.

ML for ds1 and ds4 distortion energy prediction

As previously shown, SQM calculations can, when coupled with ML, provide DFT-accuracy reaction barrier predictions for ds1–3.^8,9,15 To further show the value of our hybrid SQM-ML approach, we first built models to predict the DFT reaction barriers for the new dataset (ds4). To provide a fair representation of model performance, five random seeds (RS) were tested for each model throughout this work (full results for ds1 and ds4 reaction barrier predictions are averaged and can be found in the ESI, Section 4.3, Tables S4 and S7† respectively). The best performing model for ΔG^‡ prediction on ds4 is SVR, which achieved an averaged test set MAE of 0.97 ± 0.13 kcal mol⁻¹ which is below the 1 kcal mol⁻¹ accuracy threshold.

For ds4, models were trained to predict distortion energies for the dimethyl malonate nucleophile and the MA. The best predictions were obtained once again using SVR with a test set MAE of 0.50 (RS = 23) and 1.05 kcal mol⁻¹ (RS = 14) for nucleophile and MA respectively (Fig. 4). When averaged over five random states, test set predictions were 0.54 ± 0.06 kcal mol⁻¹ and 1.27 ± 0.17 kcal mol⁻¹ for nucleophile and MA, respectively. Overall, these results are a significant improvement on the pre-ML metrics. For full metrics and figures see ESI, Section 4.3 and Table S7.†

Fig. 4 Dimethyl malonate nucleophile (top) and MA (bottom) distortion energy test set predictions from SVR on ds4. These models were chosen because they achieved the best performance on the test set for their respective targets. The dotted line indicates perfect agreement between predicted and true values. The grey region shows the 1 kcal mol⁻¹ threshold either side of this perfect agreement. Random seed = 1 (top) and 14 (bottom).

Similar performance was seen when models were built to predict the distortion energies of the nucleophile and MA of ds1 (see Table 1). The low test set MAEs seen for the ds4 but especially the ds1 nucleophiles are likely due to the minimal conformational flexibility of these species which results in fewer distorted conformations across the entire dataset thus making the task of correcting their SQM energies an easier one.

ML for ds2 and ds3 distortion energy prediction

We utilised two pre-existing datasets of Diels–Alder reactions (ds2) and [3 + 2] cycloadditions (ds3) to predict diene/dienophile and dipole/dipolarophile distortion energies, respectively.

The pre-ML MAEs for the diene and dienophile distortion energy for ds2 were 2.80 and 2.04 kcal mol⁻¹ respectively (Table 1). Across all tested models, averaged predictions of the diene distortion energies for ds2 were well below 1 kcal mol⁻¹; the best performing model was again SVR with an averaged MAE of 0.33 ± 0.08 kcal mol⁻¹ (the results of the best models are visualised in Fig. 5). Ridge regression had the highest averaged error across all predictions (0.61 kcal mol⁻¹) however, its performance is still significantly below the 1 kcal mol⁻¹ accuracy threshold that has typically been used for energy predictions.

Fig. 5 Diene (top) and dienophile (bottom) distortion energy test set predictions for SVR models for ds2. These models were chosen because they achieved the best performance on the test set for their respective targets. The dotted line indicates perfect agreement between predicted and true values. The grey region shows the 1 kcal mol⁻¹ threshold either side of this perfect agreement. Random seed for both is 14.

SVR is again the best performing model when predicting dienophile distortion energies with KRR also performing strongly (MAEs of 0.34 ± 0.05 and 0.38 ± 0.05 kcal mol⁻¹ respectively). Greater fluctuation in model performance is seen when predicting the dienophile distortion energies, however, SVR tends to perform consistently well across the diene and dienophile distortion energy prediction tasks.

Ds3 provides an interesting challenge due to the diversity and biological relevance of this bio-orthogonal dataset.⁴¹ The best reported ML predictions of the reaction barriers are between 2 and 3 kcal mol⁻¹.^68–70 These results highlight the complexity of this dataset and the difficulty in predicting barriers approaching the desired accuracy of 1 kcal mol⁻¹. A prediction limit for this dataset may have been reached.

The pre-ML AM1-DFT MAE for the dipole distortion energies was 3.59 kcal mol⁻¹ (Table 1). When predicting the distortion energy of the dipole, the best performing model again used SVR with an averaged test set MAE of 2.55 ± 0.13 kcal mol⁻¹. SVR again gave the best performing model for the dipolarophile distortion energy predictions with an averaged test MAE of 2.37 ± 0.12 kcal mol⁻¹. Across the datasets tested, prediction errors for the distortion energy models are either similar or lower than that those of the reaction barrier models. For full results on both cycloaddition datasets see ESI, Section 4.3, Tables S5 and S6.†

ML for interaction energy prediction

As previously outlined, predicting the interaction energies provides a unique challenge as the pre-ML MAEs across all datasets is significantly larger (all are greater than 7.6 kcal mol⁻¹, Table 1) than those of the distortion energies.

For ds1, the average test MAE for interaction energies was 1.59 ± 0.18 kcal mol⁻¹ (SVR) which is approaching the 1 kcal mol⁻¹ accuracy threshold and a significant improvement upon the pre-ML AM1-DFT MAE of 7.6 kcal mol⁻¹ (Table 1). Similar performance was seen for ds4 with an averaged test set MAE of 1.23 ± 0.17 kcal mol⁻¹ (SVR), improving on a pre-ML value of 10.83 kcal mol⁻¹.

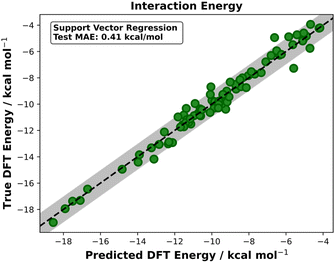
Similar success is seen with the cycloaddition datasets. Prior to ML, the interaction MAEs for ds2 and ds3 were 9.87 and 20.01 kcal mol⁻¹ respectively (Table 1). The best model built on ds2 yielded an MAE of 0.41 kcal mol⁻¹ (RS = 14) which is well below the 1 kcal mol⁻¹ accuracy threshold (Fig. 6). The averaged test MAE for ds2 was 0.50 ± 0.06 kcal mol⁻¹ (Table 1). When predicting ds3 interaction energies, the best performing model was again SVR. The best model achieved a test MAE of 2.33 kcal mol⁻¹ (RS = 1) which, when considered against the pre-ML MAE of 20.01 kcal mol⁻¹, is a striking improvement and in line with literature predictions of this dataset's reaction barriers. When averaged over five random states, the test MAE was 2.46 ± 0.12 kcal mol⁻¹. Another approach to evaluating model performance is to consider the test MAE as a percentage of the range of test values. Table 1 shows the averaged test set performances for SVR models for each distortion and interaction energy over five random states. Evaluating ds3 performance solely on MAE would lead to the conclusion that the models are above the 1 kcal mol⁻¹ accuracy threshold and thus not as accurate as other models, however, when considering the MAE as a percentage of the test set range, the performance is comparable to that of the Michael addition models (ds1 and ds4).

Fig. 6 Interaction energy test set predictions from SVR on the Diels–Alder dataset (ds2). The dotted line indicates perfect agreement between predicted and true values for the interaction energy prediction. The grey region shows the 1 kcal mol⁻¹ threshold either side of this perfect agreement. Random seed is 14.

Learning curves were also generated for models used in this work to inspect if overfitting had occurred. Across all models, there was good agreement between test and train metrics (see ESI, Section 4.5†). In addition to this, feature importances were generated for SVR models on ds2 to investigate the explainability of our models. This was done by randomly shuffling a feature at inference (full procedure can be found in the ESI, Section 4.6†). For the prediction of DFT interaction energies, the three most important features were the AM1 ΔG^‡, ΔE^‡, and ΔE_int (ESI, Fig. S48†). All these features, when randomly shuffled, resulted in a MAE above 1 kcal mol⁻¹ highlighting that they describe the target task well. Similar easily understood feature importances were also seen for the diene and dienophile distortion models. For all ds2 target feature importances see ESI, Section 4.6.†

As mentioned in the methodology section, a selection of different models were tested in this work. Across most tasks and datasets, SVR yielded the best performance, however the 2-layer NN achieved comparable accuracy (ESI, Section 4.3†). It should be noted that even with the appropriate methods to circumvent overfitting, there was a degree of this with almost every NN hence the discussion in this work primarily focussed on the use of SVR models.

External test set

To further show the value of our approach, we sought to apply the ds2 models to real examples from the cycloaddition literature given the popularity of the distortion/interaction model in this field. The papers selected examined the reaction of cyclic dienes with various cycloalkenones³¹ and cyclopropene reactions with butadiene³⁵ (Fig. 7); as detailed in the introduction, both studies use the distortion/interaction model to explain reactivity.

Fig. 7 External test sets for ds2 ML models constructed from ref. 33 and 37. The dienes in both datasets are part of ds2 thus diene distortion was not predicted. Any dienophiles that were in ds2 were removed from these external test sets.

Predictions were made using geometries that were taken from these two studies after optimising them with AM1 and DFT (see the methodology section outlined above for the full computational procedure). Model performance on ds2 was strongest using SVR thus we utilised this model for our external test set predictions (Table 2).

Table 2 External test set MAEs for cycloalkenone and cyclopropene datasets using the ds2 ML distortion and interaction models with pre-ML AM1-DFT MAEs

Dataset		Pre-ML AM1-DFT MAE (kcal mol^−1)	Average SVR test MAE (kcal mol^−1)
Cycloalkenones	Dienophile	1.93	1.58
	Interaction	12.71	1.52
Cyclopropene	Dienophile	4.27	1.62
	Interaction	6.73	1.42

---

The dienes used in the external test sets were part of ds2 therefore, diene distortion was not predicted to avoid a trained model predicting on a previously seen datapoint. Furthermore, any dienophiles that were present in ds2 were removed from the external test sets.

As before, all models were tested over five random states with results averaged. For context, three of the pre-ML AM1-DFT MAEs are large, especially for the interaction energies (Table 2). The averaged test MAEs from the ds2 ML models for each target, across both datasets, were significantly lower than the pre-ML AM1-DFT MAEs which shows that the models can make predictions close to the 1 kcal mol⁻¹ accuracy threshold on unseen datapoints. Noticeably, prediction of the interaction energies using ML resulted in a significant reduction in test MAE for both the cycloalkenone and cyclopropene datasets; the MAE on the cycloalkenone data dropped from a pre-ML value of 12.71 to 1.52 kcal mol⁻¹. As we have previously shown, SQM TSs can be a very good approximation to DFT TSs for cycloadditions.⁹ Therefore, our hybrid SQM-ML approach gives energies and mechanistic insight close to the accuracy of DFT at a fraction of the computational cost.

Conclusions

In this work, we present a hybrid SQM-ML approach for the prediction of distortion and interaction energies for four unique datasets across two reaction classes which provides a significant improvement upon the pre-ML MAEs between AM1 and DFT calculations. We have shown that predictions below the 1 kcal mol⁻¹ accuracy threshold are possible for distortion and interaction energies for the Diels–Alder dataset; Michael addition predictions are either approaching 1 kcal mol⁻¹ or are below. The accuracy of predictions for the [3 + 2] cycloaddition distortion and interaction energies are similar to barrier prediction accuracies reported in the literature (2–3 kcal mol⁻¹). We reviewed our model performances as a percentage of the test set range to better compare accuracy between datasets. This showed that while there is still room to improve model performance for the [3 + 2] cycloaddition dataset in terms of the MAE, the performance matches well with other datasets tested. Thus, our [3 + 2] models could be used to provide rapid access to accurate DFT distortion and interaction energies for these biologically relevant reactions to significantly reduce computation time in reactivity analysis.^71,72 Finally, we used our SVR models built on ds2 to accurately predict the distortion and interaction energies for two unseen, high impact literature datasets of Diels–Alder reactions that use the distortion/interaction model for reactivity analysis.

Data availability

Gaussian 16 computed output files are available in Dataset for “Distortion/Interaction Analysis via Machine Learning” in the University of Bath Research Data Archive (accessible at: https://doi.org/10.15125/BATH-01398). Code is available from https://github.com/the-grayson-group/distortion-interaction_ML.

Author Contributions

S. G. E. performed the distortion and interaction calculations, wrote the manuscript, and performed the ML analysis. S. S. A. performed the dimethyl malonate Michael addition calculations. M. N. G., S. T., and D. B. devised and supervised the project. Advice and guidance on writing of the manuscript was provided by all authors.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors gratefully acknowledge the University of Bath's Research Computing Group (https://doi.org/10.15125/b6cd-s854) for their support in this work; this research made use of the Anatra High Performance Computing (HPC) service at the University of Bath. The authors thank the EPSRC (EP/V519637/1 and EP/W003724/1), the University of Bath, and AstraZeneca for funding.

Notes and references

1. Y. Chung and W. H. Green, Chem. Sci., 2024, 15, 2410–2424.
2. R. Shi, G. Yu, X. Huo and Y. Yang, J. Cheminform., 2024, 16, 1–16.
3. M. Saebi, B. Nan, J. E. Herr, J. Wahlers, Z. Guo, A. M. Zurański, T. Kogej, P. O. Norrby, A. G. Doyle, N. V. Chawla and O. Wiest, Chem. Sci., 2023, 14, 4997–5005.
4. K. Atz, C. Isert, M. N. A. Böcker, J. Jiménez-Luna and G. Schneider, Phys. Chem. Chem. Phys., 2022, 24, 10775–10783.
5. P. van Gerwen, A. Fabrizio, M. D. Wodrich and C. Corminboeuf, Mach. Learn. Sci. Technol., 2022, 3, 045005.
6. T. A. Young, T. Johnston-Wood, V. L. Deringer and F. Duarte, Chem. Sci., 2021, 12, 10944–10955.
7. K. Jorner, T. Brinck, P.-O. Norrby and D. Buttar, Chem. Sci., 2021, 12, 1163–1175.
8. E. H. E. Farrar and M. N. Grayson, Chem. Sci., 2022, 13, 7594–7603.
9. S. G. Espley, E. H. E. Farrar, D. Buttar, S. Tomasi and M. N. Grayson, Digital Discovery, 2023, 2, 941–951.
10. S. Vargas, M. R. Hennefarth, Z. Liu and A. N. Alexandrova, J. Chem. Theory Comput., 2021, 17, 6203–6213.
11. X. García-Andrade, P. García Tahoces, J. Pérez-Ríos and E. Martínez Núñez, J. Phys. Chem. A, 2022, 127, 2274–2283.
12. K. A. Spiekermann, L. Pattanaik and W. H. Green, Sci. Data, 2022, 9, 1–12.
13. K. A. Spiekermann, L. Pattanaik and W. H. Green, J. Phys. Chem. A, 2022, 126, 3976–3986.
14. T. Lewis-Atwell, P. A. Townsend and M. N. Grayson, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1593.
15. T. Lewis-Atwell, D. Beechey, Ö. Şimşek and M. N. Grayson, ACS Catal., 2023, 13, 13506–13515.
16. T. Oestereich, R. Tonner-Zech and J. Westermayr, J. Comput. Chem., 2024, 45, 368–376.
17. E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42.
18. P. B. Momo, A. N. Leveille, E. H. E Farrar, M. N. Grayson, A. E. Mattson and A. C. B Burtoloso, Angew. Chem., Int. Ed., 2020, 132, 15684–15689.
19. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
20. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
21. E. H. E. Farrar and M. N. Grayson, J. Org. Chem., 2022, 87, 10054–10061.
22. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647.
23. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198.
24. F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128.
25. I. Fernández and F. M. Bickelhaupt, J. Comput. Chem., 2012, 33, 509–516.
26. L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324–343.
27. S. A. Lopez and K. N. Houk, J. Org. Chem., 2013, 78, 1778–1783.
28. F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086.
29. A. G. Green, P. Liu, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 4575–4583.
30. X. Hong, Y. Liang, A. K. Griffith, T. H. Lambert and K. N. Houk, Chem. Sci., 2013, 5, 471–475.
31. R. S. Paton, S. Kim, A. G. Ross, S. J. Danishefsky and K. N. Houk, Angew. Chem., Int. Ed., 2011, 50, 10366–10368.
32. A. E. Hayden and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 4084–4089.
33. P. Yu, W. Li and K. N. Houk, J. Org. Chem., 2017, 82, 6398–6402.
34. H. V. Pham, R. S. Paton, A. G. Ross, S. J. Danishefsky and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 2397–2403.
35. B. J. Levandowski and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 16731–16736.
36. J. Kubelka and F. M. Bickelhaupt, J. Phys. Chem. A, 2017, 121, 885–891.
37. C. Y. Legault, Y. Garcia, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 12664–12665.
38. P. Jain, H. Wang, K. N. Houk and J. C. Antilla, Angew. Chem., Int. Ed., 2012, 51, 1391–1394.
39. E. H. E. Farrar and M. N. Grayson, J. Org. Chem., 2020, 85, 15449–15456.
40. P. P. Xie, Z. X. Qin, S. Q. Zhang and X. Hong, ChemCatChem, 2021, 13, 3536–3542.
41. T. Stuyver, K. Jorner and C. W. Coley, Sci. Data, 2023, 10, 1–14.
42. A. Miyanaga, Nat. Prod. Rep., 2019, 36, 531–547.
43. Maestro Schrödinger, Schrödinger Release 2018-2, LLC, New York, 2018.
44. Q. Gu and S. L. You, Chem. Sci., 2011, 2, 1519–1522.
45. A. Pérez-Garrido, A. M. Helguera, F. G. Rodríguez and M. N. D. S. Cordeiro, Dent. Mater., 2010, 26, 397–415.
46. J. A. H. Schwöbel, D. Wondrousch, Y. K. Koleva, J. C. Madden, M. T. D. Cronin and G. Schüürmann, Chem. Res. Toxicol., 2010, 23, 1576–1585.
47. MacroModel Schrödinger, Schrödinger Release 2018-2, LLC, New York, 2018.
48. K. Roos, C. Wu, W. Damm, M. Reboul, J. M. Stevenson, C. Lu, M. K. Dahlgren, S. Mondal, W. Chen, L. Wang, R. Abel, R. A. Friesner and E. D. Harder, J. Chem. Theory Comput., 2019, 15, 1863–1874.
49. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909.
50. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.
51. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
52. B. Mennucci, R. Cammi and J. Tomasi, J. Chem. Phys., 1998, 109, 2798–2807.
53. J. Wu, C. M. Young, A. A. Watts, A. M. Z. Slawin, G. R. Boyce, M. Bühl and A. D. Smith, Org. Lett., 2022, 24, 4040–4045.
54. P. A. Townsend and M. N. Grayson, J. Chem. Inf. Model., 2019, 59, 5099–5103.
55. P. A. Townsend and M. N. Grayson, Chem. Res. Toxicol., 2021, 34, 179–188.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, J. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, J. C. A. Rendell, S. Burant, S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016.
57. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, J. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, J. C. A. Rendell, S. Burant, S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016.
58. G. Luchini, J. V. Alegre-Requena, I. Funes-Ardoiz and R. S. Paton, F1000Research, 2020, 9, 291.
59. D. Svatunek and K. N. Houk, J. Comput. Chem., 2019, 40, 2509–2515.
60. K. Jorner and L. Turcani, Morfeus, Zurich, 2022.
61. N. M. O'Boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845.
62. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
63. M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, R. Jozefowicz, Y. Jia, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, M. Schuster, R. Monga, S. Moore, D. Murray, C. Olah, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-scale machine learning on heterogeneous systems, 2015, https://www.tensorflow.org/about/bib.
64. H. Ji, A. Rágyanszki and R. A. Fournier, Comput. Theor. Chem., 2023, 1229, 114332.
65. K. A. Peterson, D. Feller and D. A. Dixon, Theor. Chem. Acc., 2012, 131, 1079.
66. K. N. Houk and F. Liu, Acc. Chem. Res., 2017, 50, 539–543.
67. F. Jensen, Introduction to computational chemistry, Wiley, Chichester, West Sussex, 2017.
68. T. Stuyver and C. W. Coley, Chem.–Eur. J., 2023, 29, e202300387.
69. P. van Gerwen, K. R. Briling, C. Bunne, V. R. Somnath, R. Laplaza, A. Krause and C. Corminboeuf, J. Chem. Inf. Model., 2024, 64, 5771–5785.
70. P. van Gerwen, K. R. Briling, Y. Calvino Alonso, M. Franke and C. Corminboeuf, Digital Discovery, 2024, 3, 932–943.
71. K. Sharma, A. V. Strizhak, E. Fowler, W. Xu, B. Chappell, H. F. Sore, W. R. J. D. Galloway, M. N. Grayson, Y. H. Lau, L. S. Itzhaki and D. R. Spring, ACS Omega, 2020, 5, 1157–1169.
72. C. G. Gordon, J. L. MacKey, J. C. Jewett, E. M. Sletten, K. N. Houk and C. R. Bertozzi, J. Am. Chem. Soc., 2012, 134, 9199–9208.

---

Footnote

† Electronic supplementary information (ESI) available: Additional details on generation and analysis of SQM and DFT datasets, ML procedures, and model performance evaluation. See DOI: https://doi.org/10.1039/d4dd00224e

---