Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Towards informatics-driven design of nuclear waste forms
Vinay I.
Hegde
a,
Miroslava
Peterson
b,
Sarah I.
Allec
 a,
Xiaonan
Lu
a,
Xiaonan
Lu
 b,
Thiruvillamalai
Mahadevan
c,
Thanh
Nguyen
c,
Jayani
Kalahe
c,
Jared
Oshiro
b,
Robert J.
Seffens
b,
Ethan K.
Nickerson
b,
Jincheng
Du
b,
Thiruvillamalai
Mahadevan
c,
Thanh
Nguyen
c,
Jayani
Kalahe
c,
Jared
Oshiro
b,
Robert J.
Seffens
b,
Ethan K.
Nickerson
b,
Jincheng
Du
 c,
Brian J.
Riley
c,
Brian J.
Riley
 b,
John D.
Vienna
b and
James E.
Saal
b,
John D.
Vienna
b and
James E.
Saal
 *a
*a
aCitrine Informatics, Redwood City, CA 94063, USA. E-mail: jsaal@citrine.io
bPacific Northwest National Laboratory, Richland, WA 99352, USA
cUniversity of North Texas, Denton, TX 76203, USA
First published on 9th July 2024
Abstract
Informatics-driven approaches, such as machine learning and sequential experimental design, have shown the potential to drastically impact next-generation materials discovery and design. In this perspective, we present a few guiding principles for applying informatics-based methods towards the design of novel nuclear waste forms. We advocate for adopting a system design approach, and describe the effective usage of data-driven methods in every stage of such a design process. We demonstrate how this approach can optimally leverage physics-based simulations, machine learning surrogates, and experimental synthesis and characterization, within a feedback-driven closed-loop sequential learning framework. We discuss the importance of incorporating domain knowledge into the representation of materials, the construction and curation of datasets, the development of predictive property models, and the design and execution of experiments. We illustrate the application of this approach by successfully designing and validating Na- and Nd-containing phosphate-based ceramic waste forms. Finally, we discuss open challenges in such informatics-driven workflows and present an outlook for their widespread application for the cleanup of nuclear wastes.
1 Introduction to nuclear waste forms
The United States manages large volumes of nuclear wastes generated from nuclear weapons production during World War II and the Cold War. These wastes are primarily stored at US Department of Energy sites such as Hanford (near Richland, Washington), Savannah River Site (near Aiken, South Carolina), Oak Ridge National Laboratory (ORNL; in Oak Ridge, Tennessee), Los Alamos National Laboratory (in Los Alamos, New Mexico), and the Idaho Nuclear Technical and Engineering Center (near Idaho Falls, Idaho). These wastes range from solids to sludges to liquids and contain, in broad terms, most of the elements from the periodic table. In general, the most hazardous of these wastes are high-level tank wastes at Hanford and Savannah River which will be vitrified into borosilicate glass-based waste forms and buried in disposal facilities.Recent increased interest in advanced nuclear power technologies has spurred interest in advanced nuclear fuel cycles.1 Some of those fuel cycles include the generation of unique waste streams such as molten halide salts containing fission and activation products that will need to be treated for ultimate disposal.2–6 Modern approaches that short circuit the traditional inefficient Edisonian trial-and-error style of waste form development and significantly accelerate the design of novel waste forms are in great need.
In general, options for immobilizing entire salt wastes, i.e., without any salt fraction partitioning, are limited. For such full-salt immobilization, the few demonstrated waste form options include glass-bonded sodalite and tellurite glasses,2,7 all of which exhibit low salt loading. Alternatively, rather than immobilizing the full-salt waste, the salt can be partitioned into different constituents to make waste form fabrication and/or partition recycling easier. One method for doing this is removing the halide fraction and converting the resulting salt cations (e.g., Mm+) to other chemistries (e.g., M2O, M3PO4) through a process called dehalogenation.
Dehalogenation can be accomplished through a variety of methods, including the conversion of the halide salt cation in air to oxides,8–10 conversion of halide salt cations to phosphates through reactions with NH4H2PO4,11–13, (NH4)2HPO4,12 or H3PO4,14,15 or converting fluoride-salt wastes to a different fluoride-containing compound that is environmentally stable (water insoluble), such as CaF2, for disposal.16 Any halide-containing byproducts from the dehalogenation process (e.g., H37Cl, NH374Cl) can be captured and recycled to produce new actinide halides or directly disposed (e.g., F). Since the one of the key limiters of waste loading capacity of a waste form is the halide fraction, the dehalogenated salt products (e.g., oxides, phosphates) can be immobilized at much higher salt cation loadings than the full-salt wastes prior to dehalogenation.
Different salt-based nuclear waste streams, such as alkali-based (e.g., Li/K/Na, Li/Be) and/or alkaline earth-based ones, can thus undergo a dehalogenation process with the waste cations being converted to the same anion-type compounds (e.g., oxides, phosphates). These compounds then be mixed with glass-forming compounds to create a final waste form that meets all of the necessary product criteria based on disposal requirements. Some of the primary properties of interest for each waste composition are waste loading (salt cation loading in wt%), chemical durability (e.g., aqueous solubility, leach rates), processability/manufacturability (e.g., higher melt viscosity, lower melt temperatures), mechanical durability (e.g., compressive strength), and radiation/thermal stability under expected radiation fields in the final product.
Historically, glass composition-property models have been developed to predict the properties required for efficient processing and acceptable product qualities of (mainly borosilicate) waste forms. These models have largely been empirical fits of glass composition-property data using single metal oxide concentrations as features. The model development process typically involved the production and development of painstaking, time-consuming, and empirically-created databases. There is an opportunity to leverage the large amounts of data present in existing chemical, physical, and thermodynamic databases to build machine learning (ML) models to predict the waste form properties of interest for an entirely new class of waste forms, e.g., dehalogenated phosphate ceramics or glasses. Thus, the empirical data collection process could be side-stepped entirely or be limited to incremental efforts in the novel chemistries and/or processes where there exist no prior data for the ML models to train on. Such an approach has the potential to bring about a paradigm shift in the design of different types of novel waste forms, including relatively simple single-phase systems (e.g., glasses, single-phase ceramics) or more complex multiphase systems (e.g., glass–ceramic hybrids, multiphase ceramics, and cermets).
2 AI/ML for nuclear waste immobilization: prior art
Approaches utilizing artificial intelligence (AI) or machine learning (ML) techniques have enabled significant advances in many materials science problems, ranging from the prediction of complex materials properties (e.g., superconducting critical temperatures of complex oxides,17,18 the casting size of metallic glass alloys19) to the development of self-driving labs.20,21 However, there remain certain families of materials and research questions that have not benefited as extensively from AI/ML due to their extreme complexity, of which designing new nuclear waste form materials is a prime example. In the case of nuclear waste form design, difficulties in data-driven approaches primarily arise from (1) a vast and complex design space (in terms of chemistry, phase, microstructure, processing) that spans glasses, ceramics, and glass–ceramic composites, and (2) a lack of sizeable legacy datasets for several properties a waste form must possess to be considered viable for disposal (e.g., chemical durability, radiation stability), especially for classes of materials that have not been previously explored. Further, due to the cost of performing experiments with nuclear materials and the complexity of waste form compositions, experimental data acquisition is a major bottleneck.22–24Nonetheless, there is a plethora of prior work on using AI/ML approaches to model waste forms,25,26 and we highlight a few recent reports below, including both ceramic and glass based waste forms. In terms of radiation effects, Pilania et al.27 used ML to explore the physical factors underlying amorphization resistance in pyrochlores (A2B2O7), which have been extensively investigated for use in nuclear waste forms28–37 and have been incorporated into some variants of the SYNROC waste form.38 Here, an ML model was trained to predict the critical amorphization temperature, Tc, from simple structural features and DFT energetics. Another critical property for nuclear waste forms is chemical durability, which is significantly reduced by nepheline (NaAlSiO4) precipitation during vitrification of certain waste glasses. To address this challenge, Sargin et al.39 and Lu et al.40 built ML models to predict nepheline crystallization behavior from glass composition, comparing several different algorithms and achieving a reasonable classification accuracy. However, due to the data acquisition challenge for nuclear waste forms, we note that the dataset sizes for the aforementioned models is relatively low for ML (on the order of 100–1000 data points), which may limit generalizability and extrapolability.
Similarly, several previous efforts focused on developing ML models for predicting properties relevant for glass waste forms, including glass density,41 viscosity,42 durability,43–45 glass transition temperature,46 thermal expansion,47 mechanochemical wear,48 and Young's modulus.49 While many of these models were trained to predict a single property on a specific family of glasses (e.g., silicates), a recently developed multi-task deep neural network model, GlassNet, has been trained predict 85 various glass properties on the entire SciGlass database50 with reasonable accuracy on most of the modeled properties.51
In addition to the direct modeling of waste form properties, the development of neural network interatomic potentials (NNIPs) trained on first-principles density functional theory (DFT) energetics of waste form-relevant systems has made significant strides. For example, NNIPs have been applied to the modeling of molten salts, enabling the accurate prediction of structural and dynamical properties at normal operating conditions, high-temperature–pressure conditions, and in the crystalline solid phase.52,53 Additionally, Byggmästar et al. developed a Gaussian Approximation Potential (GAP) to study radiation damage in W,54 and Ghosh et al. developed an NNIP to study Cs incorporation into hollandite (A2B8O16).55
While significant advances have been made in applying AI/ML methods toward modeling nuclear waste forms, approaches that utilize such methods for the design of entirely novel waste forms are not well established. Some recent works have explored the use of AI/ML to design optimal waste glass compositions,56,57 but a unified framework for an informatics-driven design, especially in previously-unexplored chemistries encompassing ceramics, glasses, and other types of waste forms is lacking.
In the following sections, we present a generally-applicable, closed-loop, iterative design framework that effectively combines AI/ML approaches with physics-based simulations and experiments to design novel waste forms. As a topical use-case, we present the design of new phosphate-based ceramic waste forms as part of an ongoing project under the Advanced Research Projects Agency-Energy (ARPA-E) ONWARDS program, with the following initial target properties: (1) >20% waste cation mass loading, (2) <400 cm3 waste form volume/100 g salt, and (3) >30 MPa compressive strength. For each task in the presented iterative design framework, we discuss available methods and tools, and best practices to use them, with illustrative examples from the phosphate-based waste form design problem. We also present a single end-to-end pass (i.e., the first iteration) through the design process for the same problem, resulting in successful synthesis of phosphate waste forms that satisfy all the target criteria listed above.
3 A system design view of nuclear waste forms
A system design approach primarily uses the well-established processing–structure–property–performance (PSPP) paradigm to understand the underlying materials problem.58,59 Namely, the ways in which a material is synthesized and processed (including the various steps and their respective parameters and conditions) determines its structure, both on a microscopic level (i.e., the phases that are formed, their atomistic structure, etc.) as well as on a macroscopic level (i.e., the grain structure, level of porosity and other defects, etc.). The overall structure of a material, in turn, determines its properties, which, in turn, determine its performance in the target application. This system design approach can be encapsulated in a so-called “system design chart” where individual components of the PSPP systems are connected by causal links or edges in the forward direction (i.e., from processing to structure to properties to performance), which often capture domain knowledge for the problem. Note that several processing steps can affect multiple structural features of a material, and several structural features can contribute to the properties of the overall material, and so on. Drawing up a system design chart for the materials problem at hand should therefore be the first step in any non-trivial materials design endeavor.An example system design chart for the recently-proposed phosphate glass waste forms12 is shown in Fig. 1. Here, a typical processing step can involve dehalogenation of the salt waste via reagents such as NH4H2PO4, followed by melting with glass-forming chemicals (GFCs) such as Fe2O3, and eventual quenching and/or slow cooling of the melt. The waste form resulting from such a process can be crystalline, glassy, or a mixture of both, i.e., various crystalline phases embedded in a glassy matrix. In addition, depending on other processing steps such as sintering or hot isostatic pressing (HIP), the waste form may have porosities ranging from 2% to 30%. The properties of interest of the resulting waste forms can then be obtained by direct experimental measurement during one of the processing steps (e.g., melting temperature and viscosity during the melting step) or once the processing is complete (e.g., waste salt cation loading, volume, and compressive strength of the final solid waste form). Finally, within limitations of available experimental facilities, the waste form can be tested to determine its actual performance in near-operation conditions (e.g., chemical durability in aqueous conditions).
4 A system design-informed sequential learning framework
Sequential learning (or active learning) (SL) is an iterative approach for the design of novel materials via data-driven models. A typical SL workflow consists of the following iterative loop: (1) machine learning (ML) models are trained on existing materials property data, (2) these ML models are then used to make property predictions in an as-yet unexplored design space, (3) the ML predictions, and uncertainties in such predictions, are used to identify the most-promising candidate material(s) to evaluate next, (4) the objective evaluation (via simulations and/or experiments) of the selected candidate(s) is performed, and (5) the loop iterates to augment the training data with results from the objective evaluations, retrain and/or refine the ML models, make new candidate predictions, and so on. SL workflows have been previously shown to significantly accelerate the discovery of new materials, ranging from small molecules to catalysts to semiconductors and others,60–64 as well as to rapidly optimize manufacturing and processing parameters.65,66The construction of such an SL workflow for the materials design problem at hand can greatly benefit from being informed by the underlying system design chart. An example of a system design-informed SL workflow for phosphate waste forms is shown in Fig. 2. An effective translation from the system design chart to a closed-loop SL workflow requires: (1) an initial data generation or collection effort upfront, ideally pertaining to the design spaces of interest, (2) various aspects of processing, structure, and properties to be adequately captured in the representation or schema used to store materials data, (3) physics-based simulations or ML models that can predict both (a) the mixture of phases and their structure in the final resulting waste forms based on their initial compositions and relevant processing conditions, and (b) the target waste form properties of interest, with robust uncertainty estimates, and (5) a scheme to filter and rank candidates in the target design space that takes into account model predictions and uncertainties, as well as any other application-based constraints not previously accounted for. In each of the above steps, incorporating domain knowledge and expertise can have a significant impact on the effectiveness of the SL workflow; this is further discussed in the context of each individual SL task below.
 | ||
| Fig. 2 A sample sequential learning driven workflow for the design of novel waste forms, informed by the underlying system design chart. | ||
4.1 Dataset construction
The first step in an SL workflow is dataset construction. This can involve (1) data collection from various sources such as existing materials databases, published materials property datasets, and individual or small sets of data scattered across literature, (2) data generation using relatively inexpensive physics based simulations (see Section 4.2) and/or a small set of baseline experimental measurements, and (3) data engineering of the collected and/or generated data. The latter step encompasses data curation (e.g., outlier removal, imputation of missing values), data fusion (e.g., combining data for a given set of materials from different experimental measurements or simulations), and other related post-processing.What datasets should one construct for their effective use in waste form design? The target datasets should be informed by the underlying system design chart. That is, datasets should be constructed for the target materials properties that correspond to the waste form performance criteria. This identification of materials properties data that correlates with waste form performance is non-trivial and requires significant domain knowledge integration for extracting maximum utility. We provide a sample list of openly-available datasets of materials properties and related performance criteria in Table 1, some of which were used for phosphate waste form design in this work. Note that while a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correspondence between materials property and performance metric is ideal (e.g., leach rate [property] ⇒ chemical durability [performance]), ML models can leverage indirectly-related data (e.g., cohesive energy [property] ⇔ melt temperature [property] ⇒ processability [performance]) via approaches such as transfer learning71–76 (see Section 4.3).
1 correspondence between materials property and performance metric is ideal (e.g., leach rate [property] ⇒ chemical durability [performance]), ML models can leverage indirectly-related data (e.g., cohesive energy [property] ⇔ melt temperature [property] ⇒ processability [performance]) via approaches such as transfer learning71–76 (see Section 4.3).
| Performance metric | Material property | Dataset source | Dataset size |
|---|---|---|---|
| Mass loading | Formation energy | Materials project67 | ∼140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Thermodynamic stability | Materials project67 | ∼140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
|
| Mechanical durability | Bulk modulus | Materials project67 | ∼5640 |
| Thermal stability | Melting temperature | Literature68 | ∼250 |
| Liquidus temperature | SciGlass50 | ∼45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280 280 |
|
| Processability | Glass transition temperature | SciGlass50 | ∼91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 650 |
| Viscosity | SciGlass50 | ∼6290 | |
| Chemical durability | Cohesive energy | Materials project67 | ∼140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Solubility | IUPAC-NIST69 | ∼670 | |
| Leach rate | ALTGLASS70 | ∼2400 |
Lastly, while the dataset construction task is often overlooked in favor of exploring more sophisticated ML algorithms, improving data quality and quantity is perhaps the most critical enabler of the eventual success of an informatics-driven approach to materials design. A recent “renaissance” towards data-centric AI (in contrast to model-centric AI) across several other fields is ongoing.77–79
4.2 Physics-based simulations
Physics-based simulations, such as those based on first-principles density functional theory (DFT), molecular dynamics (MD), calculation of phase diagrams (CALPHAD), and other approaches can be used to perform “computational experiments”, at various time and length scales, that can both augment datasets of materials properties as well as provide faster feedback within an SL design loop. We discuss some of the more widely-used physics-based modeling approaches below, with a focus on how they can be integrated within an SL workflow.An analysis of the convex hull of compound formation energies as a function of phase composition can be used to identify the thermodynamically stable phases in a given chemical space.80–84 Combined with linear programming approaches, a convex hull of a chemical space can rapidly predict compounds that are stable/synthesizable as well as the ground state mixture of phases that can be expected to form under thermodynamic equilibrium conditions at any given composition in that chemical space (see Fig. 3a).87
 | ||
| Fig. 3 (a) The convex hull of formation energy in a model A–B system. Blue circles indicate stable phases (“on the hull”), and red diamonds (〈u〉) indicate phases that are metastable or unstable (“above the hull”). Under perfect thermodynamic equilibrium conditions, the unstable/metastable phases will decompose into a mixture of stable phases. For example, AB is predicted to decompose into a mixture of A3B + AB3, and its distance to the convex hull (“EHD”) is an indicator of the thermodynamic drive for the decomposition (or relatedly, likelihood of its experimental synthesis85,86). (b and c) Slices of the convex hull computed using DFT-calculated formation energies in the Na–Fe–P–O chemical system, with sodium and iron phosphate (3+ and 2+, respectively) end members. | ||
The grand potential ϕ of a collection of phases in a chemical space is given by
 | (1) |
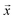 and
and  , provided the free energies Gi and the list of stable phases in the chemical system (the Ci,j terms) are defined. Typically, tools such as high-throughput DFT are used to calculate the energies of the various phases in the chemical space of interest in a self-consistent fashion, and the phase free energies are approximated by their respective 0 K formation energies. Although using 0 K energies from a computational tool such as DFT ignores finite-temperature effects, kinetic effects, and other factors, and can result in differences between predictions and experimental observations (e.g., see two slices of a DFT-computed Na–Fe–P–O convex hull in Fig. 3b and c, where two experimentally-reported phases, Na3Fe2(PO4)3 and Na6Fe3(PO4)4, are predicted to be unstable), this approach is still invaluable for estimating ground state mixture of phases with reasonable accuracy,85,86 particularly for systems that are not experimentally explored or fully described within the CALPHAD approach (see Section 4.2.3).
, provided the free energies Gi and the list of stable phases in the chemical system (the Ci,j terms) are defined. Typically, tools such as high-throughput DFT are used to calculate the energies of the various phases in the chemical space of interest in a self-consistent fashion, and the phase free energies are approximated by their respective 0 K formation energies. Although using 0 K energies from a computational tool such as DFT ignores finite-temperature effects, kinetic effects, and other factors, and can result in differences between predictions and experimental observations (e.g., see two slices of a DFT-computed Na–Fe–P–O convex hull in Fig. 3b and c, where two experimentally-reported phases, Na3Fe2(PO4)3 and Na6Fe3(PO4)4, are predicted to be unstable), this approach is still invaluable for estimating ground state mixture of phases with reasonable accuracy,85,86 particularly for systems that are not experimentally explored or fully described within the CALPHAD approach (see Section 4.2.3).
The fidelity of an MD simulation strongly depends on the type and quality of the underlying interatomic potential (IAP), making the development of an IAP and its parameterization a significant portion of the overall simulation effort. For example, the development of IAPs for the modeling of borosilicate glasses, a widely-used nuclear waste glass, has been a challenge due to the strong dependence of boron coordination on thermal history and composition, which in turn affects properties such as mechanical strength and corrosion rate. However, recent efforts in IAP development have led to successful simulations of borosilicate glasses across a wide range of compositions where boron coordination is in good agreement with experimental observations.91–93 Also, the development of efficient “reactive” potentials allow for simulations of reactions of aqueous solution with glasses.94–98
Further, these large-scale atomistic simulations enable so-called quantitative structure–property relationship (QSPR) analysis, linking properties of a material to its atomistic structural features. QSPR analysis has been applied to a wide range of properties such as glass transition temperature, dissolution rate, Young's modulus, and hardness of glass materials, correlating trends in these properties to descriptors derived from structural features such as bond angles, bond energies, coordination numbers, network connectivity (e.g., see Fig. 4a for a visualization of a iron phosphate glass, showing various Qn units, where n is the number of bridging oxygen atoms connected to network formers Q, Fe2O3 and P2O5).101 A simple statistical model (e.g., linear or multilinear regression) can then be used to identify relationships between such descriptors and the target property of interest (e.g., see Fig. 4b for an example of modeling Young's modulus as a linear function of a glass network strength descriptor, Fnet99,100).
 | ||
| Fig. 4 (a) Visualization of part of the atomic structure of a sodium iron phosphate glass with composition 5% Na2O–35% Fe2O3–60% P2O5, showing the various Qn units in the glass network (where n is the number of bridging oxygen atoms (red spheres) connected to network formers, Fe2O3 and P2O5), and (b) linear correlation between Young's modulus and QSPR-based network strength descriptor, Fnet, calculated using bond strength of diatomic cations (“BS-dc”) and a multiplicative factor (“mx”).99,100 The blue circles are MD-calculated Young's moduli values for various Na–Fe–P–O glass compositions (the error bars indicate variance in the calculated moduli across different structures at the same composition), and the solid black line shows a linear fit with an r2 score of 0.95. | ||
The CALPHAD method can be used to study the typically multicomponent, multiphase nuclear waste materials, e.g., calculate phase diagrams of the waste form systems (e.g., the Fe2O3–P2O5 iron phosphate system, shown in Fig. 5), equilibrium and non-equilibrium phase evolution during solidification of a molten salt mixture, estimating transformation temperatures between waste-relevant phases, waste salt or waste element solubility limits, and so on.
While CALPHAD-based approaches can be used to study the behavior of waste-relevant systems under non-ideal conditions (e.g., as a function of temperature, pressure, chemical potential, pH), they are often limited by the availability of fully-assessed thermodynamic databases for the systems of interest. While ab initio methods can be used to calculate the properties (e.g., formation energy) of novel phases from scratch, such data may suffer from limitations related to “ideal conditions”, as discussed in Section 4.2.1. For example, we compare the 0 K phase diagram calculated using DFT with that from CALPHAD for the Fe2O3–P2O5 system in Fig. 5. Note that two of the experimentally observed phases, Fe3PO7 and Fe4(P2O7)3, described correctly by CALPHAD are predicted to be metastable at 0 K by DFT. Further, for systems with missing or partial CALPHAD assessments, there are no currently available tools that enable a seamless integration of such ab initio data with existing thermodynamic databases to extend their capabilities to the partially assessed/unassessed system (e.g., the Na2O–Fe2O3–P2O5 system, discussed in Section 4.5).
4.3 Machine learning models
The various waste form-relevant property datasets described in Section 4.1 can be used as input to train ML models that can predict those properties of novel waste forms. While sizeable research efforts have gone into ML algorithms and models for predicting materials properties, there are a few considerations to keep in mind specifically towards their effective applicability in an SL workflow for waste forms. First, the crystal structure of a novel waste form is often unknown or yet to be characterized. Even though ML models that are built using crystal structure-based descriptors as input show higher accuracy in predicting materials properties,102 this information is often a priori unavailable. Thus, ML models that can predict waste form properties purely based on the melt composition alone tend to be of higher value than those that require crystal structure as input. Several approaches have been developed to generate physical descriptors based on chemical composition of a material (“featurization”), e.g., Magpie,103 Deml,104 Matscholar,105 MEGNet,106 including off-the-shelf software tools with implementations of such approaches, e.g., matminer,107 that can be used to featurize waste form compositions.Second, the type of AI/ML model to build, e.g., based on ensemble approaches such as random forests (RF) and gradient-boosted trees, or deep neural net (NN) approaches such as ElemNet,108 Roost,109 CrabNet,110 depends on the target property and the size of the available data. Tree-based models have been shown to generally outperform deep learning models on tabular data, especially for small-to-medium sized datasets typical of materials properties (102–103 examples).111 While NN-based models are useful for certain larger property datasets (e.g., CrabNet for predicting the formation energy, or GlassNet to predict the glass transition temperature from an input composition), we urge researchers to test “simpler” ML models using off-the-shelf tools such as scikit-learn112 and lolo,113 as these can often be more interpretable and provide superior extrapolation performance.114
Third, we underline the importance of assessing the performance of ML models using evaluation methods and metrics that are directly relevant to the task at hand. Typically, ML model accuracies are reported using metrics such as r2 values or mean absolute errors (MAEs) evaluated in random cross-validation or a random train/validation/test split of the available data, which can be informative of within-distribution generalization but not of out-of-distribution performance. For example, an ML model for predicting melt temperatures trained on chemical composition based Magpie features103 and a dataset of congruent melting temperatures of stoichiometric compounds has a reasonable accuracy (MAE of ∼200 K, consistent with prior work68) in random cross-validation (Fig. 6a). However, the model fails to capture the liquidus temperature trends in a target design space of the Fe2O3–P2O5 system, especially the two deep eutectic regions around 40% and 60% P2O5 content, where the prediction errors are higher than 400–450 K (see Fig. 6b). In short, using a test strategy (e.g., leave-one-cluster-out [LOCO] cross-validation for estimating extrapolative performance18) that is representative of the actual environment that the ML model will be eventually used in, is critical for a true assessment of its performance. Further, an accurate evaluation of a model is crucial to improving it, e.g., overcoming data scarcity with strategies such as transfer learning71–76 or prioritizing targeted data collection (see Fig. 6b, which shows how adding even a small fraction [10–20%] of data from the target design space of Fe2O3–P2O5 enables the ML model to learn the liquidus curve more effectively than from congruent melting temperatures alone).
Lastly, while most of the focus of ML-based modeling of materials properties has been towards developing more accurate models, the efficacy of an ML model within an SL workflow goes beyond simply the model accuracy.115 In other words, it is indeed possible to have performant SL workflows with lower-accuracy ML models. Further, robust uncertainty estimates along with ML model predictions are crucial not only to calibrate user confidence in the model predictions but also for ranking and selecting candidates within an SL workflow (see Section 4.4).
4.4 Candidate ranking and selection
Once ML models for target properties have been trained, the next task in the SL workflow is to rank and select candidates in a target design space for objective evaluation. The target design space is defined by the target application, and can be identified by the underlying system design chart. As discussed earlier (see Section 3), for phosphate-based nuclear waste forms, the design space is often bound by the composition of the liquid melt, which in turn is defined by the waste stream, the reagents used for dehalogenation, glass-forming chemicals (GFCs), and other additives added during the processing step. From a well-defined design space, candidates can be generated via simple enumeration (e.g., a uniform grid of compositions within a Gibbs triangle for a ternary design space). This enumerated list of candidates can be further filtered down using domain knowledge and/or outputs of simulations as an intermediate step.As illustrative examples of phosphate-based waste form design, we generate candidates in the ternary Na2O–Fe2O3–P2O5 and quaternary Na2O–Nd2O3–Fe2O3–P2O5 spaces (where Na/Nd are the waste cations, Fe2O3 acts as the GFC), using a uniform grid spacing of 2.5% along each composition axis. We then apply a combination of domain knowledge-informed rules as well as results from DFT convex hull analysis to filter out candidate compositions with the following characteristics (and are therefore unviable): (1) no salt cations in the composition, (2) unreacted elements, unreacted waste salt, or no phosphates in the ground state phase mixture predicted by the convex hull analysis, and (3) ground state phase mixtures that contain binary alkali compounds (e.g., Na3PO4) that are known to be water soluble. The resulting filtered list of viable candidate compositions is much smaller (see Fig. 7).
All the relevant target properties for each viable candidate can then be predicted using the previously trained ML models. The scoring of candidates, and the identification of candidates to prioritize for experimental validation and testing (the “acquisition function”), can be performed one of several ways depending on the design problem. For the design of waste forms in particular, it is desirable for the acquisition function to be: (1) multiobjective, to simultaneously optimize several target properties such as mass loading, waste form volume, compressive strength, and so on; (2) enable end users and domain experts to weight the different targets or success criteria differently. For example, Vienna and Kim116 used a penalty-based approach to multiattribute optimization of borosilicate glasses:
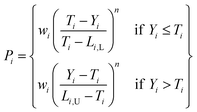 | (2) |
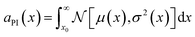 , where x is the target variable to be maximized (e.g., bulk modulus), x0 is the current baseline performance, and μ(x) and σ2(x) are the predicted value and uncertainty from the relevant ML model. For multiple objectives, a scalarizing function that combines aPI for all the targets can be defined (e.g., simply a product of aPI values for uncorrelated targets).
, where x is the target variable to be maximized (e.g., bulk modulus), x0 is the current baseline performance, and μ(x) and σ2(x) are the predicted value and uncertainty from the relevant ML model. For multiple objectives, a scalarizing function that combines aPI for all the targets can be defined (e.g., simply a product of aPI values for uncorrelated targets).
We demonstrate two different strategies for candidate selection in the two example design spaces. For the Na2O–Fe2O3–P2O5 design space, we show a single-objective optimization targeting salt cation loading in wt%, which can be estimated from DFT-based convex hull analysis without the need for ML surrogates. We choose a candidate composition from among the ones showing the highest loading (∼18%; higher than the state-of-the-art iron phosphate glasses6,12,117) for validation (e.g., “A2” in Fig. 7a). For the Na2O–Nd2O3–Fe2O3–P2O5 design space, we show a multi-objective optimization with the following three objectives as well as a hard constraint of salt cation loading >20%: (1) minimizing melt temperatures (<1173 K, the lowest liquidus temperature in the Fe2O3–P2O5 binary; see Fig. 5a), (2) minimizing the waste form volume to immobilize 100 g of salt (<100 cm3, lower than state-of-the-art phosphate glass waste forms6,12,117), and (3) maximizing bulk modulus (>48 GPa, the highest moduli reported for Fe2O3–P2O5 glasses118,119). We use the product of the individual aPI scores as a cumulative PI score [scaled to lie within 0–1 using simple min–max scaling; i.e., ascaled = (a − amin)/(amax − amin)] as the aggregate metric, representing the likelihood of improvement over all three targets simultaneously (note that the term “likelihood” is used loosely, and is not exactly equivalent to the statistical concept of likelihood), to rank candidates and choose the most promising ones for experimental synthesis and validation (e.g., “E1” and “E2” in Fig. 7b). Note that the final bulk modulus objective used here is different from the predefined project objective (>30 MPa compressive strength). This change is motivated by the lack of compressive strength data available for use in building ML models (for a discussion of this change and general guidelines on how to approach such data-scarce objectives, see Section 6).
4.5 Experimental validation
The final task in a SL workflow is the validation of selected candidates, and closing the loop by providing feedback for the refinement of next round of predictions and candidate selection tasks. Ideally, the synthesis of the target materials and any post-processing steps should mimic the final production process as closely as possible, although this is not always practical (e.g., an industrial process that is hard to replicate in a laboratory). Similarly, the characterization of the synthesized materials and measurement of properties should enable direct feedback into the earlier prediction and selection tasks in the SL workflow; note that this is not always possible, e.g., properties that are hard to measure experimentally, mismatch in target performance metrics and properties for which there exists data to train ML models.Here, we synthesize the three selected candidate waste forms (A2, E1, and E2; e.g., see Fig. 8a for an image of a quenched sample) and perform post-synthesis heat treatment to simulate a canister pour-and-cool for final disposal (see Section 7.3 for details of the heat treatment profiles used). We then characterize the heat-treated samples using X-ray diffraction (e.g., see Fig. 8b for Rietveld refinement for the as-quenched A2 candidate)—determining the phases in each sample and quantifying their distribution (Table 2). We follow up with measurements of candidate properties such as density (i.e., to validate storage volume estimation) and compressive strength.
 | ||
| Fig. 8 A2 candidate waste form: (a) picture of the as-quenched sample, (b) Rietveld refinement of the diffraction pattern of the as-quenched sample. | ||
| Phase | ICSD# | Sample A2 [SC2] | Sample E1 [SC2] | Sample E2 [SC1] | ||||
|---|---|---|---|---|---|---|---|---|
| Expt. | DFT | CALPHAD | Expt. | DFT | Expt. | DFT | ||
| NaFe3(PO4)3 | 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 696 |
33.06 | ||||||
| NaFePO4 | 193![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 244 244 |
30.97 | ||||||
| NaFeP2O7 | 237![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850 850 |
15.96 | ||||||
| Na3Fe3(PO4)4 | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 532 532 |
36.70 | 36.92 | |||||
| Na2Fe3(PO4)3 | 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238 238 |
24.41 | 11.10 | |||||
| Na3Fe2(PO4)3 | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 405 405 |
23.52 | 8.10 | 6.55 | ||||
| Na3Fe(PO4)2 | 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558 558 |
60.92 | 79.79 | 43.98 | ||||
| NaNd(PO3)4 | 401 | 9.80 | ||||||
| NdPO4 | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 750 |
10.06 | 20.21 | 11.54 | 19.10 | |||
| NaPO3 | 174![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201 201 |
11.0 | ||||||
| Na3PO4 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 718 718 |
12.45 | ||||||
| Na4P2O7 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 370 |
31.0 | ||||||
| Na5P3O10 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 837 837 |
13.0 | ||||||
| FePO4 | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 906 906 |
17.51 | 27.0 | |||||
| Fe2O3 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505 505 |
9.82 | 2.38 | 18.0 | 8.08 | 13.37 | ||
| Amorphous | 12.30 | 36.90 | 4.51 | |||||
| SUM | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |
| R wp | 6.38 | 9.29 | 7.78 | |||||
5 An end-to-end workflow run
To illustrate the end-to-end workflow of an informatics-driven framework, we consolidate and present one full SL iteration for one of the candidate waste forms discussed previously, E2, from the Na2O–Nd2O3–Fe2O3–P2O5 chemical space (with Na2O and Nd2O3 from the waste stream, Fe2O3 added as a GFC, and P2O5 from the dehalogenation process).We first generate an enumerated design space of potential candidates in the quaternary space, as a uniform grid with 2.5 mol% spacing along each composition axis, for a total of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 341 candidate compositions. For each candidate composition, we then apply DFT convex hull analysis to predict the ground state phase mixture, and apply domain knowledge filters to exclude unviable compositions, as described in Section 4.4. The E2 candidate (composition 37.5% Na2O + 5% Nd2O3 + 20% Fe2O3 + 37.5% P2O5 in mol%) passes all the domain knowledge filters, and a mixture of {50% Na3Fe(PO4)2 + 21.43% Na3Fe3(PO4)4 + 28.57% NdPO4} (mol%) is predicted to be the thermodynamic ground state at its overall composition. We then estimate (a) the salt cation loading (25.29 wt% of Na, Nd combined), (b) the waste form storage volume per 100 g of nominal waste salt (an equivalent amount of NaCl + NdCl3) as the mole fraction weighted DFT-calculated volume of the ground state phase mixture (54.36 cm3) (c) target properties (e.g., melt temperature, bulk modulus), using pretrained ML models. Note that the ML models used here are trained to predict the properties of the individual phases in the mixture, and the overall properties (and uncertainties) of the mixture are approximated as the mole fraction-weighted mean. For the E2 candidate, e.g., the predicted bulk modulus is 75.6 ± 20.1, the predicted melt temperature is 1480.7 ± 229.3. We calculate the probability of improvement for each property (e.g.,
341 candidate compositions. For each candidate composition, we then apply DFT convex hull analysis to predict the ground state phase mixture, and apply domain knowledge filters to exclude unviable compositions, as described in Section 4.4. The E2 candidate (composition 37.5% Na2O + 5% Nd2O3 + 20% Fe2O3 + 37.5% P2O5 in mol%) passes all the domain knowledge filters, and a mixture of {50% Na3Fe(PO4)2 + 21.43% Na3Fe3(PO4)4 + 28.57% NdPO4} (mol%) is predicted to be the thermodynamic ground state at its overall composition. We then estimate (a) the salt cation loading (25.29 wt% of Na, Nd combined), (b) the waste form storage volume per 100 g of nominal waste salt (an equivalent amount of NaCl + NdCl3) as the mole fraction weighted DFT-calculated volume of the ground state phase mixture (54.36 cm3) (c) target properties (e.g., melt temperature, bulk modulus), using pretrained ML models. Note that the ML models used here are trained to predict the properties of the individual phases in the mixture, and the overall properties (and uncertainties) of the mixture are approximated as the mole fraction-weighted mean. For the E2 candidate, e.g., the predicted bulk modulus is 75.6 ± 20.1, the predicted melt temperature is 1480.7 ± 229.3. We calculate the probability of improvement for each property (e.g.,  ) and aggregate the individual scores into a cumulative likelihood of improvement metric scaled to lie between 0 and 1 using a simple min–max scaling (see Fig. 7b).
) and aggregate the individual scores into a cumulative likelihood of improvement metric scaled to lie between 0 and 1 using a simple min–max scaling (see Fig. 7b).
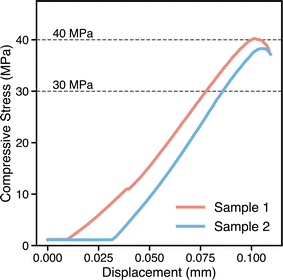
We then perform experimental synthesis and heat treatment for the target E2 composition, and characterize the phases present using X-ray diffraction (see Table 2). We measure properties such as density (3.164 g cm−3, and corresponding waste form volume) and compressive strength (38.3–40.2 MPa; see Fig. 9), with all properties surpassing the target performance criteria listed at the end of Section 2. The characterization data and measured properties are used to refine the outputs from the physics-based modeling tasks, as well as to augment existing training data and retrain ML models for the next SL iteration; these efforts will be reported in the future.
6 Discussion and outlook
While such as informatics-driven workflows are powerful tools for accelerating materials design in general, and waste form design in particular, some challenges remain and we discuss a few salient ones below.The prediction of the exact phases formed during synthesis (and their respective distributions) given the overall composition and a set of experimental conditions and post-processing steps remains an open question. Analyses based on DFT convex hull and related thermodynamic stability measures, while still extremely useful, suffer from limitations related to DFT accuracy and ideal conditions (zero temperature and, often, ambient pressure). As seen from Table 2, the mismatch between computational predictions and experimental realization is large. Some phases that have been reported experimentally are predicted to be 0 K unstable by DFT (e.g., Na2Fe3(PO4)3 found in both A2 and E1 candidates is predicted to be 60 meV per atom above the convex hull of formation energy). Some other phases are excluded from the DFT analyses due the nature of the problem set up; i.e., with the overall melt modeled as a mixture of the corresponding oxides, certain compounds with mixed elemental oxidation states (e.g., NaFe3(PO4)3 found in the E2 candidate, with two nominal Fe3+ and one nominal Fe2+) or oxidation states different from the one in the melt ingredient (e.g., NaFePO4 with Fe2+, in contrast to the GFC additive Fe2O3 in the melt) are naturally excluded. The latter problem can be mitigated by performing DFT convex hull analyses with varying elemental chemical potential (e.g., μO) but increases the computational expense and complexity of the task. While CALPHAD approaches can consider effects of variables such as temperature and chemical potential is calculating phase diagrams, they are severely limited by the lack of assessed databases, especially for compositions relevant to phosphate-based waste forms (e.g., current CALPHAD databases in FactSage do not include thermodynamic data for any quaternary phases in the Na–Fe–P–O chemical space [resulting in the mismatch for sample A2 in Table 2], and assessed databases for the Na–Nd–Fe–P–O chemical space do not exist). Further, while recent work has shown the possibility of predicting crystallization pathways from amorphous matter using a combination of ab initio methods and deep learning,120 further efforts are needed to develop a holistic framework that fully bridges the gap between computational design and experimental realization of materials.
Another general challenge is the lack of large, well-curated datasets to train ML models to predict several waste form-relevant properties of interest. For example, properties such as compressive strength are not widely reported for a large set of materials and are not trivial to calculate using ab initio techniques. Similarly, chemical durability measurements of ceramic waste forms are scattered across the literature and no centralized curated dataset exists (in contrast to traditional borosilicate glass-based waste forms, e.g.). While some of these challenges may be mitigated by using domain knowledge integration (DKI; see below) or using techniques such as transfer learning,71–76 we urge for investments into large-scale data collection and curation of waste form properties that can benefit the community as a whole.
For effective use of informatics-based approaches for the design of waste forms, especially in the context of the above-mentioned challenges, it is crucial to leverage DKI from experts in various parts of the SL workflow. Such DKI can take many forms: (1) identifying data-abundant waste form properties that are correlated with data-scarce performance metrics (e.g., cohesive energy to inform chemical durability, viscosity and liquidus temperature to inform processability, bulk modulus to compressive strength [as used in this work]), (2) defining and constraining the design spaces of interest (e.g., identifying the correct target alkali and rare-earth waste cations, and any potential pool of additives that can be used in waste form fabrication), (3) filtering undesirable candidates (e.g., excluding candidate waste form compositions that are expected to form water-soluble alkali phosphates), and so on.
In particular, while a one-to-one correspondence between target waste form properties and available datasets is ideal, such a fit can be hard to find in practice. Some approaches to tackle this challenge are to (1) perform an initial set of “data-generation” experiments, typically exploratory in nature, (2) perform physics-based simulations that can predict the target property or a close surrogate (e.g., if they are cheaper than experiments), or (3) leverage domain knowledge to identify datasets of a different property that is expected to be correlated with the target property (e.g., if neither experiments nor physics-based simulations are viable). The compressive strength of a phosphate waste form (and the related target performance of >30 MPa) is a property in the latter category. There exists no large curated dataset of compressive strength of ceramics, and generating such a database via experiments or physics-based simulations is prohibitively time-consuming and expensive. So, here we choose to rely on a relatively large dataset of DFT-calculated bulk moduli, a property we expect to be correlated with compressive strength (e.g., a relation between the two quantities has been reported in composite materials such as concrete;121 similarly, a correlation between elastic and plastic responses during deformation in aluminate spinels, oxynitrides, and nitrides has been reported,122 but a clear quantitative relationship in ceramics is unknown). For this choice of a property that is different (but expected to be correlated) to the target property, we still need to choose a suitable baseline value to improve upon in the sequential learning workflow, and we thus choose the highest moduli reported for Fe2O3–P2O5 glasses, 48 GPa. While we need more data to make a quantitative claim about the relationship between bulk modulus and compressive strength for phosphate ceramics, results presented here demonstrate that the strategy of optimizing for closely-related data-abundant property in place of a data-scarce target property is a viable one in a real-world materials design scenario.
We emphasize that the system design-informed, sequential learning-driven framework presented in this work is a general materials design framework that can be, and has been, successfully applied to designing materials for a wide variety of applications.19,44,60–63,65,74 In the context of nuclear waste disposal, the particular end-to-end workflow we demonstrate here can most readily be applied to wastes which require immobilization in glass, ceramic, or ceramic–glass composite waste forms, including LAW, HLW, and high-sodium wastes (e.g., borosilicate glass is already being used to immobilize HLW at West Valley in New York123). For other classes of materials, while the overall design framework presented here can still be applied, some of the specific tools used in this work (e.g., atomistic physics-based simulations, phase diagram calculations) may not be applicable, and alternate experimental and simulation techniques need to be identified. For instance, LAW at Savannah River Site is being immobilized in Saltstone (salt cake mixed with concrete and fly ash), geopolymers (amorphous, aluminosilicate-based inorganic polymers) have been investigated as binders for granular mineral wastes produced by fluidized bed steam reforming for LAW at Hanford, and hydroceramics have been shown to be effective for immobilizing sodium-bearing LAW at INL.123 Such systems cannot be modeled effectively using current ab initio modeling approaches, but the design framework is still applicable.
Overall, the proposed approach of using informatics-based approaches for waste form design has the potential to drastically reshape the way that these types of efforts are conducted across the world. The largest impact of this method, in contrast to the Edisonian trial and error approach, is the potential to cut the time required to find optimal solutions by an order of magnitude (or more). Tapping into crystallographic databases, thermodynamic property databases, phase diagrams, as well as other material property databases, this informatics approach can be used to design waste forms containing anywhere from high amorphous (glassy) phase fractions to high crystalline fractions as well as mixtures thereof. Finally, we note that the opportunities afforded by such approaches extend far past borosilicate and phosphate waste forms, and these techniques can be used for optimize the processing history and conditions to effectively fabricate the next generation of waste forms as well as aiding eventual scale-up efforts for promising waste forms once so identified. Some challenges related to bridging the gap between predictions and laboratory realization of waste forms exist, but current approaches already present avenues for significant acceleration of the design of novel waste forms.
7 Methods
7.1 Thermodynamic analysis
All DFT-based convex hull analysis was performed using data openly available from the Materials Project67 and the pymatgen124 software package.All CALPHAD calculations were performed using the commercial FactSage v8.1 software125 and associated databases.
7.2 Machine learning
All machine learning models reported in this work were built using the open-source lolo113 random forests library, using 128 tree estimators and all other default hyperparameters, trained on some of the open datasets listed in Table 1 (i.e., those for melting temperature and bulk modulus). The models used Magpie features generated using only the material compositions, as implemented in the matminer software package.107 The additional Fe2O3–P2O5 liquidus data used in Fig. 6 was calculated using FactSage, and the data is made available.7.3 Experimental synthesis and characterization
The raw reagents (i.e., Na2CO3 [Aldrich, 99.9% trace metals], Nd2O3, Fe2O3 [Baker, 100.4%], and NH4H2PO4 [Sigma Aldrich, ≥98.5%]) were batched using an analytical balance (Mettler Toledo ME204). The reagents were then loaded into 250 mL alumina crucibles (ACC3742, McDanel Advanced Ceramic Technologies) with a Pt/10% Rh lid and melted in a high-temperature furnace (Deltech Furnaces, Inc.) for 2 hours delay at 1250 °C, with a ramp heating rate of 5 °C min−1, followed by quenching on an Inconel plate. The quenched materials were ground to a fine particle size in a tungsten carbide milling chamber and run through slow cooling process with an aliquot of the ground material within a 10 mL alumina crucible (ACM3760, McDanel Advanced Ceramic Technologies).Two custom heat treatment profiles were employed: “SC2” for samples A2 and E1, and “SC1” for sample E2. SC2 included a ramp rate of 5 °C min−1 from room temperature to 1250 °C, a dwell for 1 hour at 1250 °C, a −5 °C min−1 cooling to 500 °C, a reheat at 5 °C min−1 to 600 °C, a dwell for 12 hours, a ramp cool at −0.03 °C min−1 to 465 °C over the course of 75 hours, and ended with a −1 °C min−1 ramp cooling rate. SC1 included a ramp rate of 5 °C min−1 from room temperature to 1250 °C at 5 °C minute−1, held for 1 hour, ramp cooled at −25 °C minute−1 to 1000 °C, and then ramp cooled to room temperature at −0.1 °C minute−1. These custom heat treatments were designed to homogenize the melt at 1250 °C, rapidly cool to above the glass transition temperature (Tg), reheat and then cool slowly to initiate crystallization.
Once the samples were cooled, vertical slides were prepared using glycol suspensions and a slow speed Buehler diamond saw. The samples were removed from their alumina crucibles, ground in a tungsten carbide milling chamber to a fine particle size and analyzed using X-ray diffraction. Then, a known amount (5 mass%) CeO2 of a NIST Standard Reference Material (SRM-674b) was added and ground for 30 additional seconds. Samples doped with CeO2 were run with a Bruker D8 Advance diffractometer in a scan range of 5–90° 2θ, with a 0.01486° 2θ step angle, with 1 second dwells per step. The diffraction patterns were analyzed using Bruker Topas (version 5) software with PDF5+ International Centre for Diffraction Data (ICDD) and Inorganic Crystal Structure Database (ICSD).
Compressive strength tests were run in duplicate on an Instron 5582 (ID 5582R1924) using a fixed rate of 0.1 mm minute−1 in accordance with ASTM C1358-18. Samples were prepared in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 geometry of height
1 geometry of height![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) width using a series of procedures from a diamond wire saw, a slow-speed diamond blade saw, and polishing processes. The preferred sample geometry is a cylinder but making cylinders from these samples proved difficult due to small sample size. Thus, rectangular prisms were made that were on the order of ∼6 mm tall by ∼3 mm wide. Samples were loaded until failure and the compressive strength was reported as the maximum uniaxial compressive stress reached when the material failed.
width using a series of procedures from a diamond wire saw, a slow-speed diamond blade saw, and polishing processes. The preferred sample geometry is a cylinder but making cylinders from these samples proved difficult due to small sample size. Thus, rectangular prisms were made that were on the order of ∼6 mm tall by ∼3 mm wide. Samples were loaded until failure and the compressive strength was reported as the maximum uniaxial compressive stress reached when the material failed.
Data availability
Associated research data has been deposited into a repository on figshare.126 The following datasets are made available: (1–3) Formation energy, cohesive energy, and bulk modulus data retrieved from the Materials Project database in September 2022. (4) Melting temperatures of solids extracted from the literature.68 (5) Liquidus temperatures of waste form-relevant binary–binary systems, calculated as part of this work using FactSage v8.1. (6) Aqueous solid solubility extracted from IUPAC-NIST Solubility Database, Version 1.1.69 (7) The Accelerated Leach Testing of GLASS (ALTGLASS) dataset of short- and long-term product consistency tests (PCT, ASTM C1285 A and B) on waste glasses.70 (8) Candidate waste form compositions generated and evaluated in this work, including ML predictions, DFT-based convex hull analysis and ground state phase predictions. In addition, sample Python scripts to train machine learning models of melting/liquidus temperatures, to perform convex hull analysis and predict ground state phases, as well as to calculate probability of improvement scores with appropriate scaling are also made available.Author contributions
Conceptualization: VIH, JES, BJR, JDV, JD; data curation: VIH, MP, SIA, XL, JO, RJS, EKN, BJR, JDV, TM, JK, TN; formal analysis: VIH, MP, JO, RJS, EKN, BJR, JDV, TM, JK, TN; funding acquisition: VIH, JES, BJR, JDV, JD; investigation: VIH, MP, JO, RJS, EKN, BJR, JD, TM, JK, TN; methodology: VIH, SIA, JES, MP, XL, RJS, EKN, BJR, JDV, TM, JK, TN; project administration: JES, JDV, JD; resources: BJR, JDV, JD; software: VIH, SIA; supervision: JES, BJR, JDV, JD; validation: VIH, BJR, TM; visualization: VIH, MP, BJR, JD, TM, JK, TN; writing – original draft: VIH, SIA, JES, MP, XL, BJR, JDV, JD, TM; writing – review and editing: all authors.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The information, data, or work presented herein was funded in part by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under Award Number DE-AR0001613. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. Pacific Northwest National Laboratory (PNNL) is operated by Battelle Memorial Institute for the DOE under contract DE-AC05-76RL01830. The authors thank Anthony Guzman (PNNL), Irving L. Brown (PNNL), and Timothy J. Roosendaal (PNNL) for help with preparing samples for compressive strength, which proved to be quite challenging, and Jarrod V. Crum (PNNL) for reviewing the manuscript.References
- D. A. Arostegui and M. Holt, Advanced nuclear reactors: technology overview and current issues, Congressional Research Service Report for Congress, Washington, DC, 2019, Technical Report R45706 Search PubMed.
- W. Ebert, Testing to evaluate the suitability of waste forms developed for electrometallurgically treated spent sodium-bonded nuclear fuel for disposal in the Yucca Mountain reporsitory, Argonne National Laboratory, Argonne, IL, 2006, Technical Report ANL-05/43 Search PubMed.
- K. Bateman, C. Knight, C. Solbrig, et al., Current status of ceramic waste form development, Idaho National Laboratory, Idaho Falls, ID, 2007, Technical Report INL/INT-06-11736, Rev. 1 Search PubMed.
- S. Frank, B. Riley, W. Ebert and J. Peterson, Literature Review of Dehalogenation Processes for Salt Wastes and Suitable Waste Forms, Idaho National Laboratory, Idaho Falls, ID, 2017, Technical Report NTRD-MRWFD-2017-000193 Search PubMed.
- B. J. Riley, J. McFarlane, G. D. DelCul, J. D. Vienna, C. I. Contescu and C. W. Forsberg, Nucl. Eng. Des., 2019, 345, 94–109 CrossRef CAS.
- B. J. Riley, Ind. Eng. Chem. Res., 2020, 59, 9760–9774 CrossRef CAS.
- B. J. Riley, J. D. Vienna, S. M. Frank, J. O. Kroll, J. A. Peterson, N. L. Canfield, Z. Zhu, J. Zhang, K. Kruska and D. K. Schreiber, et al. , J. Nucl. Mater., 2017, 489, 42–63 CrossRef CAS.
- B. J. Riley, D. A. Pierce, J. V. Crum, B. D. Williams, M. M. Snyder and J. A. Peterson, Prog. Nucl. Energy, 2018, 104, 102–108 CrossRef CAS.
- S. Chong and B. J. Riley, J. Nucl. Mater., 2022, 561, 153538 CrossRef CAS.
- Y. Dong, K. Xu, Z. Jia, C. Niu and D. Xu, J. Nucl. Mater., 2022, 567, 153833 CrossRef CAS.
- S. Donze, L. Montagne and G. Palavit, Chem. Mater., 2000, 12, 1921–1925 CrossRef CAS.
- B. J. Riley, J. A. Peterson, J. D. Vienna, W. L. Ebert and S. M. Frank, J. Nucl. Mater., 2020, 529, 151949 CrossRef CAS.
- B. J. Riley, S. Chong and C. E. Lonergan, ACS Omega, 2021, 6, 32239–32252 CrossRef CAS PubMed.
- D. D. Siemer, Nucl. Technol., 2012, 178, 341–352 CrossRef CAS.
- H.-S. Park, I.-T. Kim, Y.-Z. Cho, H.-C. Eun and H.-S. Lee, Environ. Sci. Technol., 2008, 42, 9357–9362 CrossRef CAS PubMed.
- D. J. Gregg, E. R. Vance, P. Dayal, R. Farzana, Z. Aly, R. Holmes and G. Triani, J. Am. Ceram. Soc., 2020, 103, 5454–5469 CrossRef CAS.
- V. Stanev, C. Oses, A. G. Kusne, E. Rodriguez, J. Paglione, S. Curtarolo and I. Takeuchi, npj Comput. Mater., 2018, 4, 29 CrossRef.
- B. Meredig, E. Antono, C. Church, M. Hutchinson, J. Ling, S. Paradiso, B. Blaiszik, I. Foster, B. Gibbons and J. Hattrick-Simpers, et al. , Mol. Syst. Des. Eng., 2018, 3, 819–825 RSC.
- L. Ward, S. C. O'Keeffe, J. Stevick, G. R. Jelbert, M. Aykol and C. Wolverton, Acta Mater., 2018, 159, 102–111 CrossRef CAS.
- M. Abolhasani, K. A. Brown and G. Editors, MRS Bull., 2023, 48, 134–141 CrossRef.
- N. J. Szymanski, B. Rendy, Y. Fei, R. E. Kumar, T. He, D. Milsted, M. J. McDermott, M. Gallant, E. D. Cubuk, A. Merchant, H. Kim, A. Jain, C. J. Bartel, K. Persson, Y. Zeng and G. Ceder, Nature, 2023, 624, 86–91 CrossRef CAS PubMed.
- Y. Guérin, G. S. Was and S. J. Zinkle, MRS Bull., 2009, 34, 10–19 Search PubMed.
- T. Allen, J. Busby, M. Meyer and D. Petti, Mater. Today, 2010, 13, 14–23 CrossRef CAS.
- S. J. Zinkle and G. Was, Acta Mater., 2013, 61, 735–758 CrossRef CAS.
- D. Morgan, G. Pilania, A. Couet, B. P. Uberuaga, C. Sun and J. Li, Curr. Opin. Solid State Mater. Sci., 2022, 26, 100975 CrossRef CAS.
- G. Hu and W. Pfingsten, Ann. Nucl. Energy, 2023, 180, 109452 CrossRef CAS.
- G. Pilania, K. R. Whittle, C. Jiang, R. W. Grimes, C. R. Stanek, K. E. Sickafus and B. P. Uberuaga, Chem. Mater., 2017, 29, 2574–2583 CrossRef CAS.
- K. Sickafus, L. Minervini, R. Grimes, J. Valdez, M. Ishimaru, F. Li, K. McClellan and T. Hartmann, Science, 2000, 289, 748–751 CrossRef CAS PubMed.
- B. Begg, N. Hess, D. McCready, S. Thevuthasan and W. Weber, J. Nucl. Mater., 2001, 289, 188–193 CrossRef CAS.
- J. Lian, L. Wang, J. Chen, K. Sun, R. Ewing, J. M. Farmer and L. Boatner, Acta Mater., 2003, 51, 1493–1502 CrossRef CAS.
- J. Lian, J. Chen, L. Wang, R. C. Ewing, J. M. Farmer, L. A. Boatner and K. Helean, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 134107 CrossRef.
- J. Lian, K. Helean, B. Kennedy, L. Wang, A. Navrotsky and R. Ewing, J. Phys. Chem. B, 2006, 110, 2343–2350 CrossRef CAS PubMed.
- K. Helean, S. Ushakov, C. Brown, A. Navrotsky, J. Lian, R. Ewing, J. Farmer and L. Boatner, J. Solid State Chem., 2004, 177, 1858–1866 CrossRef CAS.
- K. E. Sickafus, R. W. Grimes, J. A. Valdez, A. Cleave, M. Tang, M. Ishimaru, S. M. Corish, C. R. Stanek and B. P. Uberuaga, Nat. Mater., 2007, 6, 217–223 CrossRef CAS PubMed.
- G. R. Lumpkin, M. Pruneda, S. Rios, K. L. Smith, K. Trachenko, K. R. Whittle and N. J. Zaluzec, J. Solid State Chem., 2007, 180, 1512–1518 CrossRef CAS.
- G. Sattonnay, N. Sellami, L. Thomé, C. Legros, C. Grygiel, I. Monnet, J. Jagielski, I. Jozwik-Biala and P. Simon, Acta Mater., 2013, 61, 6492–6505 CrossRef CAS.
- Y. Li, B. Uberuaga, C. Jiang, S. Choudhury, J. Valdez, M. Patel, J. Won, Y.-Q. Wang, M. Tang and D. Safarik, et al. , Phys. Rev. Lett., 2012, 108, 195504 CrossRef CAS PubMed.
- A. E. Ringwood, S. E. Kesson, N. Ware, W. Hibberson and A. Major, Nature, 1979, 278, 219–223 CrossRef CAS.
- I. Sargin, C. E. Lonergan, J. D. Vienna, J. S. McCloy and S. P. Beckman, J. Am. Ceram. Soc., 2020, 103, 4913–4924 CrossRef CAS.
- X. Lu, I. Sargin and J. D. Vienna, J. Am. Ceram. Soc., 2021, 104, 5636–5647 CrossRef CAS.
- Y.-J. Hu, G. Zhao, M. Zhang, B. Bin, T. Del Rose, Q. Zhao, Q. Zu, Y. Chen, X. Sun and M. de Jong, et al. , npj Comput. Mater., 2020, 6, 25 CrossRef CAS.
- D. R. Cassar, Acta Mater., 2021, 206, 116602 CrossRef CAS.
- N. A. Krishnan, S. Mangalathu, M. M. Smedskjaer, A. Tandia, H. Burton and M. Bauchy, J. Non-Cryst. Solids, 2018, 487, 37–45 CrossRef.
- T. Han, N. Stone-Weiss, J. Huang, A. Goel and A. Kumar, Acta Biomater., 2020, 107, 286–298 CrossRef CAS PubMed.
- D. S. Brauer, C. Rüssel and J. Kraft, J. Non-Cryst. Solids, 2007, 353, 263–270 CrossRef CAS.
- D. R. Cassar, A. C. de Carvalho and E. D. Zanotto, Acta Mater., 2018, 159, 249–256 CrossRef CAS.
- S. M. Mastelini, D. R. Cassar, E. Alcobaça, T. Botari, A. C. de Carvalho and E. D. Zanotto, Acta Mater., 2022, 240, 118302 CrossRef CAS.
- Q. Qiao, H. He, J. Yu, Y. Zhang and H. Qi, Wear, 2021, 476, 203721 CrossRef CAS.
- K. Yang, X. Xu, B. Yang, B. Cook, H. Ramos, N. A. Krishnan, M. M. Smedskjaer, C. Hoover and M. Bauchy, Sci. Rep., 2019, 9, 8739 CrossRef PubMed.
- SciGlass Database v1.0, 2019, https://github.com/epam/SciGlass Search PubMed.
- D. R. Cassar, Ceram. Int., 2023, 49(22), 36013–36024 CrossRef CAS.
- S. T. Lam, Q.-J. Li, R. Ballinger, C. Forsberg and J. Li, ACS Appl. Mater. Interfaces, 2021, 13, 24582–24592 CrossRef CAS PubMed.
- Q.-J. Li, E. Küçükbenli, S. Lam, B. Khaykovich, E. Kaxiras and J. Li, Cell Rep. Phys. Sci., 2021, 2, 100359 CrossRef CAS.
- J. Byggmästar, A. Hamedani, K. Nordlund and F. Djurabekova, Phys. Rev. B, 2019, 100, 144105 CrossRef.
- D. B. Ghosh, B. B. Karki and J. Wang, J. Nucl. Mater., 2020, 530, 151957 CrossRef CAS.
- L. L. Gunnell, K. Manwaring, X. Lu, J. Reynolds, J. Vienna and J. Hedengren, Processes, 2022, 10, 2365 CrossRef.
- X. Lu, J. D. Vienna and J. Du, J. Am. Ceram. Soc., 2023, 107, 1603–1624 CrossRef.
- G. B. Olson, Science, 1997, 277, 1237–1242 CrossRef CAS.
- C. Kuehmann and G. Olson, Mater. Sci. Technol., 2009, 25, 472–478 CrossRef CAS.
- J. Ling, M. Hutchinson, E. Antono, S. Paradiso and B. Meredig, Integr. Mater. Manuf. Innov., 2017, 6, 207–217 CrossRef.
- D. E. Graff, E. I. Shakhnovich and C. W. Coley, Chem. Sci., 2021, 12, 7866–7881 RSC.
- E. Annevelink, R. Kurchin, E. Muckley, L. Kavalsky, V. I. Hegde, V. Sulzer, S. Zhu, J. Pu, D. Farina and M. Johnson, et al. , MRS Bull., 2022, 47, 1036–1044 CrossRef.
- E. Antono, N. N. Matsuzawa, J. Ling, J. E. Saal, H. Arai, M. Sasago and E. Fujii, J. Phys. Chem. A, 2020, 124, 8330–8340 CrossRef CAS PubMed.
- L. Kavalsky, V. I. Hegde, E. Muckley, M. S. Johnson, B. Meredig and V. Viswanathan, Digital Discovery, 2023, 2, 1112–1125 RSC.
- A. Y. Fong, L. Pellouchoud, M. Davidson, R. C. Walroth, C. Church, E. Tcareva, L. Wu, K. Peterson, B. Meredig and C. J. Tassone, J. Chem. Phys., 2021, 154, 224201 CrossRef CAS PubMed.
- J. Ling, E. Antono, S. Bajaj, S. Paradiso, M. Hutchinson, B. Meredig and B. M. Gibbons, Turbo Expo: Power for Land, Sea, and Air, 2018, p. V006T24A005 Search PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, et al. , APL Mater., 2013, 1, 011002 CrossRef.
- A. Seko, T. Maekawa, K. Tsuda and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 054303 CrossRef.
- IUPAC-NIST Solubility Database, Version 1.1, NIST Standard Reference Database 106, 2012, https://srdata.nist.gov/solubility/index.aspx.
- C. L. Trivelpiece, C. M. Jantzen and C. L. Crawford, Accelerated Leach Testing of GLASS: ALTGLASS Version 3.0, Savannah River National Laboratory, Aiken, SC, 2016 Search PubMed.
- M. L. Hutchinson, E. Antono, B. M. Gibbons, S. Paradiso, J. Ling and B. Meredig, arXiv, 2017, preprint, arXiv:1711.05099, DOI:10.48550/arXiv.1711.05099.
- H. Yamada, C. Liu, S. Wu, Y. Koyama, S. Ju, J. Shiomi, J. Morikawa and R. Yoshida, ACS Cent. Sci., 2019, 5, 1717–1730 CrossRef CAS PubMed.
- D. Jha, K. Choudhary, F. Tavazza, W.-K. Liao, A. Choudhary, C. Campbell and A. Agrawal, Nat. Commun., 2019, 10, 5316 CrossRef CAS PubMed.
- E. D. Cubuk, A. D. Sendek and E. J. Reed, J. Chem. Phys., 2019, 150, 214701 CrossRef PubMed.
- V. Gupta, K. Choudhary, F. Tavazza, C. Campbell, W.-k. Liao, A. Choudhary and A. Agrawal, Nat. Commun., 2021, 12, 6595 CrossRef CAS PubMed.
- C. Chen and S. P. Ong, npj Comput. Mater., 2021, 7, 173 CrossRef.
- D. Zha, Z. P. Bhat, K.-H. Lai, F. Yang and X. Hu, Proceedings of the 2023 SIAM International Conference on Data Mining (SDM), 2023, pp. 945–948 Search PubMed.
- O. H. Hamid, 2022 8th International Conference on Information Technology Trends (ITT), 2022, pp. 196–199 Search PubMed.
- C. J. Bartel, Patterns, 2021, 2, 100382 CrossRef CAS PubMed.
- C. B. Barber, D. P. Dobkin and H. Huhdanpaa, ACM Trans. Math. Softw., 1996, 22, 469–483 CrossRef.
- S. Kirklin, J. E. Saal, V. I. Hegde and C. Wolverton, Acta Mater., 2016, 102, 125–135 CrossRef CAS.
- D. Wang, M. Amsler, V. I. Hegde, J. E. Saal, A. Issa, B.-C. Zhou, X. Zeng and C. Wolverton, Acta Mater., 2018, 158, 65–78 CrossRef CAS.
- V. I. Hegde, M. Aykol, S. Kirklin and C. Wolverton, Sci. Adv., 2020, 6, eaay5606 CrossRef CAS PubMed.
- M. Aykol, V. I. Hegde, L. Hung, S. Suram, P. Herring, C. Wolverton and J. S. Hummelshøj, Nat. Commun., 2019, 10, 2018 CrossRef PubMed.
- G. Kim, S. Meschel, P. Nash and W. Chen, Sci. Data, 2017, 4, 1–11 Search PubMed.
- J. Ma, V. I. Hegde, K. Munira, Y. Xie, S. Keshavarz, D. T. Mildebrath, C. Wolverton, A. W. Ghosh and W. Butler, Phys. Rev. B, 2017, 95, 024411 CrossRef.
- A. R. Akbarzadeh, V. Ozoliņš and C. Wolverton, Adv. Mater., 2007, 19, 3233–3239 CrossRef CAS.
- J. Rimsza and J. Du, J. Am. Ceram. Soc., 2014, 97, 772–781 CrossRef CAS.
- M. Ren and J. Du, J. Am. Ceram. Soc., 2016, 99, 2823–2833 CrossRef CAS.
- J. Du and L. R. Corrales, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 255, 177–182 CrossRef CAS.
- L. Deng and J. Du, J. Am. Ceram. Soc., 2019, 102, 2482–2505 CrossRef CAS.
- L. Deng and J. Du, J. Non-Cryst. Solids, 2016, 453, 177–194 CrossRef CAS.
- L. Deng and J. Du, in Borosilicate and Boroaluminosilicate Glasses, 2022, ch. 8, pp. 224–260 Search PubMed.
- J. M. Rimsza, T. S. Mahadevan, L. Deng and J. Du, in Simulations of Glass–Water Interactions, 2022, ch. 15, pp. 490–521 Search PubMed.
- J. Rimsza and J. Du, J. Phys. Chem. C, 2017, 121, 11534–11543 CrossRef CAS.
- T. S. Mahadevan and J. Du, J. Am. Ceram. Soc., 2020, 103, 3676–3690 CrossRef CAS.
- T. Mahadevan, A. Baroni, M. Taron, S. Gin, J. Du and J.-M. Delaye, J. Non-Cryst. Solids, 2022, 592, 121746 CrossRef CAS.
- J. Kalahe, T. S. Mahadevan, M. Ono, K. Miyatani, S. Urata and J. Du, J. Phys. Chem. B, 2023, 127, 269–284 CrossRef CAS PubMed.
- G. Lusvardi, G. Malavasi, F. Tarsitano, L. Menabue, M. C. Menziani and A. Pedone, J. Phys. Chem. B, 2009, 113, 10331–10338 CrossRef CAS PubMed.
- J. Du, X. Lu, S. Gin, J.-M. Delaye, L. Deng, M. Taron, N. Bisbrouck, M. Bauchy and J. D. Vienna, J. Am. Ceram. Soc., 2021, 104, 4445–4458 CrossRef CAS.
- J. Kalahe, T. Mahadevan, X. Lu, J. D. Vienna, B. J. Riley and J. Du, J. Nucl. Mater., 2024, 155004 CrossRef CAS.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, npj Comput. Mater., 2020, 6, 138 CrossRef.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2, 1–7 CrossRef.
- A. M. Deml, R. O'Hayre, C. Wolverton and V. Stevanović, Phys. Rev. B, 2016, 93, 085142 CrossRef.
- L. Weston, V. Tshitoyan, J. Dagdelen, O. Kononova, A. Trewartha, K. A. Persson, G. Ceder and A. Jain, J. Chem. Inf. Model., 2019, 59, 3692–3702 CrossRef CAS PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- L. Ward, A. Dunn, A. Faghaninia, N. E. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom and M. Dylla, et al. , Comput. Mater. Sci., 2018, 152, 60–69 CrossRef.
- D. Jha, L. Ward, A. Paul, W.-K. Liao, A. Choudhary, C. Wolverton and A. Agrawal, Sci. Rep., 2018, 8, 17593 CrossRef PubMed.
- R. E. Goodall and A. A. Lee, Nat. Commun., 2020, 11, 6280 CrossRef CAS PubMed.
- A. Y.-T. Wang, S. K. Kauwe, R. J. Murdock and T. D. Sparks, npj Comput. Mater., 2021, 7, 77 CrossRef.
- L. Grinsztajn, E. Oyallon and G. Varoquaux, Adv. Neural Inf. Process. Syst., 2022, 35, 507–520 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- Lolo: a random forest-centered machine learning library in Scala, https://github.com/CitrineInformatics/lolo, [online; accessed July 5, 2024] Search PubMed.
- E. S. Muckley, J. E. Saal, B. Meredig, C. S. Roper and J. H. Martin, Digital Discovery, 2023, 2, 1425–1435 RSC.
- C. K. H. Borg, E. S. Muckley, C. Nyby, J. E. Saal, L. Ward, A. Mehta and B. Meredig, Digital Discovery, 2023, 2, 327–338 RSC.
- J. Vienna and D. Kim, Preliminary IHLW Formulation Algorithm Description, Hanford Site (HNF), Richland, WA (United States), 2023, Technical Report 24590-HLW-RPT-RT-05-001, Rev. 1 Search PubMed.
- W. Ebert and J. Fortner, Analyses of iron phosphate glasses for dehalogenated salt waste, Argonne National Laboratory (ANL), Argonne, IL (United States), 2019, Technical Report ANL/CFCT-19/5 Search PubMed.
- K. Chang, T. Lee and L. Hwa, Chin. J. Phys., 2003, 41, 414–421 CAS.
- K. Jolley and R. Smith, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 374, 8–13 CrossRef CAS.
- M. Aykol, A. Merchant, S. Batzner, J. N. Wei and E. D. Cubuk, arXiv, 2023, preprint, arXiv:2310.01117, DOI:10.48550/arXiv.2310.01117.
- T. Noguchi and K. Nemati, J. Struct. Constr. Eng., 1995, 60, 1–10 Search PubMed.
- A. M. Muller and D. J. Green, J. Am. Ceram. Soc., 2013, 96, 1263–1270 CrossRef CAS.
- N. R. Council, Waste Forms Technology and Performance: Final Report, The National Academies Press, Washington, DC, 2011 Search PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- C. W. Bale, P. Chartrand, S. Degterov, G. Eriksson, K. Hack, R. B. Mahfoud, J. Melançon, A. Pelton and S. Petersen, Calphad, 2002, 26, 189–228 CrossRef CAS.
- V. I. Hegde, Data for “Towards Informatics-Driven Design of Nuclear Waste Forms”, [figshare Collection], 2024 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |