 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Illuminating the property space in crystal structure prediction using Quality-Diversity algorithms†
Marta
Wolinska
 *a,
Aron
Walsh
*a,
Aron
Walsh
 b and
Antoine
Cully
b and
Antoine
Cully
 a
a
aAdaptive and Intelligent Robotics Lab, Imperial College London, London SW7 2AZ, UK. E-mail: a.cully@imperial.ac.uk
bThomas Young Centre and Department of Materials, Imperial College London, Exhibition Road, London SW7 2AZ, UK. E-mail: a.walsh@imperial.ac.uk
First published on 19th June 2024
Abstract
The identification of materials with exceptional properties is an essential objective to enable technological progress. We propose the application of Quality-Diversity algorithms to the field of crystal structure prediction. The objective of these algorithms is to identify a diverse set of high-performing solutions, which has been successful in a range of fields such as robotics, architecture and aeronautical engineering. As these methods rely on a high number of evaluations, we employ machine-learning surrogate models to compute the interatomic potential and material properties that are used to guide optimisation. Consequently, we also show the value of using neural networks to model crystal properties and enable the identification of novel composition–structure combinations. In this work, we specifically study the application of the MAP-Elites algorithm to predict polymorphs of TiO2. We rediscover the known ground state, in addition to a set of other polymorphs with distinct properties. We validate our method for C, SiO2 and SiC systems, where we show that the algorithm can uncover multiple local minima with distinct electronic and mechanical properties.
1 Introduction
Inorganic crystals are an important class of materials, with their application spanning a range of applications, such as photovoltaic cells,1 batteries2 and transistors.3 The computational discovery of new crystals is a promising avenue in identifying materials with the potential to augment our technological capabilities and accelerate progress in a range of fields.One of the main challenges of crystal structure prediction (CSP) is a search problem. The search space of all possible crystals increases with 10Natoms;4 this decreases to exponential if local relaxation is used.4,5 As such, techniques that explore the space efficiently and effectively are required. This can be done using both data-driven or ab initio techniques.6 Purely data-driven techniques have been successful,7 however they rely on the availability of training data,8 which becomes more limited as the complexity of systems increases. Consequently, there are advantages to techniques that do not solely rely on a base knowledge of the chemical space. One such technique is evolutionary algorithms. Thanks to their inherent randomness they can explore a highly complex search space without getting stuck in local minima. They have been shown to work effectively in CSP.9,10
Novel technological applications often require materials with a combination of optimal (but likely conflicting) properties. To access crystal structures exhibiting such unique and advanced properties, additional optimisation techniques are required. The associated computational search is constrained with limitations, such as availability of sufficient data for modelling and the size of the search space. This makes the ability to discover truly novel crystals and to select the right candidates for optimisation challenging.8 These limitations are further pronounced when optimising for multiple properties.8 One technique that considers multiple properties is multi-objective optimisation,11,12 which has been used effectively in a range of materials design studies,13,14 including a combination of an evolutionary search with multiple objectives.8 Multi-objective optimisation is typically designed to search for a set of solutions that lie at the trade-off of multiple conflicting objectives. This however can be seen as a limitation, because potentially high-performing solutions that lie outside of this condition would be discarded.15 Such techniques are also not designed to explicitly provide diverse solutions to a problem, which could aid the user in understanding the feature space of their problem. Materials properties have indeed been used to characterise organic crystal structures in the form of energy-function–structure maps, with the aim of facilitating structure selection.16 They were not however used in guiding the structure search.
To address these challenges we can use Quality-Diversity (QD) algorithms – an expanded framework built on top of evolutionary algorithms. They aim to provide a diverse set of high-performing solutions in some feature space, which effectively changes the optimisation objective. They allow the user to define a number of features of interest, which guide the optimisation to find diverse solutions while maximising overall fitness. In the context of CSP, the features could be any calculable material properties, while the fitness could be the energy function. Through optimisation they also provide the user with a better understanding of the feature space, which is why they are also referred to as illumination algorithms. These algorithms have been successfully used in a range of fields such as robotics to enable robots to learn new behaviours if they encounter damage,17 in architecture to design buildings18 or in aeronautics to design airfoils.19
Given the success of QD in other fields, in this work we will apply one such algorithm to the problem of crystal structure prediction. A requirement of these techniques is a large number of evaluations. In CSP, a first-principles approach such as density functional theory (DFT) would typically be used to predict both the energy and properties of each structure. As this approach is computationally expensive, it is not suitable for methods that require a high number of evaluations. However, in recent years machine learning surrogate models,20–23 which effectively model this energy function for a wide range of chemistries have been developed. This is also true for material properties, as recorded in the MatBench benchmark.24 The significant decrease in cost per evaluation for such surrogate models, creates an opportunity for new techniques to be tested and developed without the constraints of the number of evaluations required. This opportunity will be used in this work to demonstrate how QD algorithms can be used in crystal structure prediction. We demonstrate the capabilities of our proposed algorithm to generate a large collection of promising structures. We validated this on 4 materials to demonstrate that with minimal physical assumptions the algorithm uncovers multiple local minima with distinct electronic and mechanical properties. A high-level overview of the algorithm is visualised in Fig. 1.
2 Background
2.1 Evolutionary algorithms
Evolutionary algorithms have been successfully used for crystal structure prediction, notably in well-established packages such as USPEX9 and XtalOpt.10 They have gained popularity, not only because of their efficiency, but also because they can be based on first-principles quantum mechanical calculations. As such they are not constrained by data availability nor influenced by areas of the chemical space explored in past work.8These algorithms follow the principles of evolution. First, some random solutions, known as individuals, are generated and stored. An individual is defined by a set of genes: in the context of crystal structures those would be the position of atoms in a cell as well as the cell size. Then a number of individuals are selected and their genes are randomly updated. Such updates are called mutations; an example of a mutation in the context of crystal structures could be randomly adding Gaussian noise to the positions of atoms in a cell.25
The quality of generated individuals is evaluated using a fitness function. Based on this result individuals are either kept or discarded. This continues for a user-defined number of cycles, called generations, or until a different exit condition is met.
Evolutionary algorithms are a global optimisation technique, i.e. they aim to find the global minimum/maximum of a function. As such, they do not aim to provide an understanding search space, nor are they designed to search for multiple high-quality solutions. The need for diversity has been recognised as an important tool in ensuring the success of evolutionary algorithms. This is both in terms of (1) the starting population26 and (2) during the optimisation itself.27 QD algorithms are designed to address these challenges.
2.2 Quality-Diversity
QD algorithms are an extension of evolutionary algorithms. They provide a framework that guides optimisation to find a diverse yet high-performing set of solutions. They have a two-fold objective: to globally maximise the diversity of solutions and to locally maximise their fitness. The following discussion presents a general view of QD algorithms, with the specific case of MAP-Elites introduced in the following section and summarised in Alg. 1. As such, we will introduce the notation and reference Alg. 1 in this section to facilitate interpretation.The key difference between evolutionary algorithms and QD is that an individual (θ) is characterised not only using its fitness (p), but also using a feature vector (b). The feature vector contains any number of user-defined properties of interest. An example feature vector of a crystal structure could contain its hardness and toughness. The feature vector is used to compare individuals to each other and to determine if newly generated individuals will be added to the set of stored solutions called an archive  . There are many benefits to adding the feature vector into optimisation these include the fact that (1) they illuminate the search space thus allowing its improved understanding without the constraints of multi-objective optimisation, (2) they are intuitive to use, (3) they are agnostic to the problem statement and (4) they can also be used at initial investigation to identify promising areas for exploration.
. There are many benefits to adding the feature vector into optimisation these include the fact that (1) they illuminate the search space thus allowing its improved understanding without the constraints of multi-objective optimisation, (2) they are intuitive to use, (3) they are agnostic to the problem statement and (4) they can also be used at initial investigation to identify promising areas for exploration.
The archive is stored within a container (C), which defines how the individuals are organised within the archive (lines 12–16 in Alg. 1). A container can be as simple as a user-defined grid, where each cell is used to store an individual. When a new individual is generated, its feature vector is used to assign an individual to a cell. If the cell is empty, the individual is added to the archive (as it is more diverse), if it is not, the individual with the higher fitness is kept (line 15 Alg. 1) (as it is more fit) – thus ensuring fitness is locally maximised. In this way the diversity of an individual alters the trajectory of the search. Since individuals that are inherently different in terms of the feature vector are added to the archive, they are then available to be selected for mutation. This promotes the search space surrounding that individual. We expect that existing methods to boost diversity within the evolutionary process, such as those mentioned in section above, are orthogonal to the QD search. As such, they will continue to provide benefits if applied, for instance by promoting archives to fill more quickly. The container does not have to be discretised by the user as is the case with a grid. A container can also be unstructured and dynamically determine the local environments, for instance using a minimum distance between k-nearest neighbours.
2.3 MAP-Elites
An example of a state-of-the-art QD algorithm using a grid as the container is MAP-Elites (Multi-dimensional Archive of Phenotypic Elites).28 The goal of this algorithm is to obtain a set of solutions (archive), based on multiple dimensions defined by user-defined features (multi-dimensional phenotypes), which contains the best (elite) solutions to a problem.One of the strengths of this approach is that it can use any number of features. However, as the number of dimensions increases if a constant resolution is maintained, the number of available cells within the grid increases exponentially. To avoid the curse of dimensionality, the following variation on the MAP-Elites algorithm can be used.
CVT-MAP-Elites, uses Centroidal Vornoi Tesselation (CVT) to generate geometrically equivalent cells within any number of dimensions29,30 (line 2 Alg. 1). This allows the user to define the desired number of cells in the container, while ensuring the same resolution across each feature. Each cell within the resulting grid is referred to as a centroid. The CVT-MAP-Elites algorithm is reported in Alg. 1. We employ CVT-MAP-Elites, but the shorthand MAP-Elites will be used for convenience as the two algorithms are equivalent aside from the container definition.
To facilitate the interpretation of results a sample MAP-Elites grid is provided in Fig. 2. The x- and y-axis of the grid are described by two features, as annotated in Fig. 2a. The grid itself is defined using limits computed using CVT. A generated individual is represented using its feature vector in the grid using a scatter point. To aid visualisation the cell containing the individual is then coloured according to its fitness. For this work a known crystal system will be used, therefore cells where known structures would be positioned are marked with a red outline to aid interpretation.
 | ||
| Fig. 2 Diagramatic representation of MAP-Elites grid and optimisation process: (a) annotated MAP-Elites grid and (b) representation of evolution in MAP-Elites solutions across generations. | ||
Fig. 2b visualises what an expected change could look like over some number of generations. We start with a smaller number of lower-performing (purple) solutions. Over the course of optimisation the number of solutions increases and they become increasingly high performing (yellow).
To quantify the performance of a run, coverage and QD score can be used alongside typical metrics, such as the maximum fitness. The coverage is the proportion of cells in the grid which contain solutions, thus capturing diversity. The QD score is simply the sum of all individuals' fitness scores, which captures the global improvement in the quality of solutions.
3 Computational methods
3.1 Computational setup
This work uses the CVT-MAP-Elites algorithm augmented with open-source Python packages for materials science. Our implementation of CVT-MAP-Elites is based on the pymap-elites implementation,28,29 with some elements taken from the QDAx library.31 The starting structures were generated using the pyxtal generator.32 Strain and permutation mutation operators from the ase33 library were used with a 50/50 chance of being selected.‡ The feature vector was formed of the shear modulus and band gap of a crystal. The absolute value of the energy per atom for each crystal was used as the basis of the fitness function.§ The energy was computed using CHGNet,23 the band gap was computed using the MP-2019 model from the Materials Graph Library, matgl,20,21 and the shear modulus was computed using the MP-2018 model from MEGNET.20,22There is a range of hyperparameters that are required both from QD and CSP perspectives. The MAP-Elites grid was discretised into 200 cells, random structures were generated in batches of 20 until a minimum of 10% of the grid was populated with individuals prior to starting mutations. When an individual was generated it was relaxed for up to 100 steps with a maximum force tolerance for relaxation of 0.2 eV per atom. Then, at each generation 100 individuals were selected for mutation; this means that some individuals were mutated multiple times at each generation. We primarily used TiO2 with 24 atoms per cell. This system was selected due to its polymorphic nature and it has been used as a benchmark material.10,26,34
The cell was initialised with a volume of 450 Å, and the scaling factor between inter-atomic distances was set to 0.4. The unit cell border lengths were set to 2–60 Å, and the maximum angles were set to 0–π. Maximum angles between unit cell vector and the plane created by the other two vectors are [20°, 160°]. The CSP-driven hyperparameters were set based on previous work in the field and where relevant they were set to be less restrictive.10,25,26,33,34 The comparison against related work is provided as ESI.†
3.2 Fitness function
We introduce an additional consideration into the fitness function. To ensure that realistic and stable solutions were added to the archive, we first evaluated the maximum force acting within a structure. This is equivalent to the computation done within CHGNet during each step of relaxation.As summarised in eqn (1), if the maximum force acting on a structure was higher than the preset threshold F, the fitness was set to the negative of the maximum force. If the maximum force was lower than the threshold, then the absolute value of the energy was used. Thus, first we minimised the force to ensure realistic solutions would compete with each other to find the best absolute energy.
A key benefit of this technique is that it provided a way to filter out unrealistic solutions that exploited out-of-distribution behaviour of CHGNet resulting in unrealistic energies exceeding hundreds or thousands of eV per atom. As such thanks to the force threshold, experiments can be run more reliably. The threshold was set to 9 eV Å−1. This was determined by computing the maximum force on the reference TiO2 structures and setting a value that would capture all of them (figure available in ESI).†
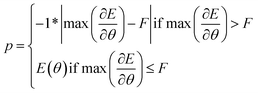 | (1) |
 is the maximum force acting on a structure, F is the value of the preset threshold.
is the maximum force acting on a structure, F is the value of the preset threshold.
3.3 Algorithm evaluation
Once the algorithm run is completed, all structures in the archive were compared against known polymorphs sourced from the Materials Project.35 The structures were evaluated using: (1) the StructureMatcher class from pymatgen;36 (2) by comparing the space group symmetry of the generated structures; (3) by computing the fingerprint distance using the ase33 implementation.Based on a combination of these metrics a confidence level was assigned if a match was found. StructureMatcher was used as the primary metric. A gold standard confidence was assigned if a match was found and it was in the right centroid within the feature space. If there was a match but the centroid did not match we assigned a high confidence. A medium confidence was assigned if the other two metrics were met or if either was met and the structure was in the same centroid as the reference. A low confidence was assigned if only one of the other two metrics was met. Otherwise, no match was assigned to a generated structure.
Here it is important to note the limitations stemming from the evaluation method and the underlying property prediction models. Firstly, let us consider the fact that the surrogate models are trained on realistic structures. As such, similar yet slightly perturbed structures could be evaluated to have different properties, thus assigning them to different centroids. Secondly, the comparison of generated structures with reference structures is limited by the tolerances used by the evaluation methods. As these were set to be quite tolerant, dissimilar structures could be evaluated to be equivalent. This means that multiple, ultimately equivalent, structures can be generated and assigned to different centroids or that the structures that are considered equivalent in this work are in fact distinct. Consequently, in this work MAP-Elites will be limited in the number of structures it can find. The final diversity of the archive could thus be improved by implementing techniques that address these constraints, such as periodically removing random individuals from the archive or fine-tuning the evaluation models.
4 Results and discussion
Three experiments are reported to attain the following objectives. Firstly, known reference structures of TiO2 were plotted within a MAP-Elites grid to validate that a wide range of structures with differing properties could be discovered. This also illustrates what a result would look like if all references available to be discovered within this resolution were found. Secondly, we demonstrate that using MAP-Elites multiple known structures of TiO2 are consistently found in a single algorithm run. Lastly, our method is applied to three other systems to demonstrate its versatility.4.1 Reference data – titanium dioxide
The known crystal structures, as sourced from the Materials Project,35 were plotted in a MAP-Elites grid in Fig. 3. To allow a wide breadth of solutions both theoretical and experimentally observed structures are included.There are 34 polymorphs which contain 24 atoms or fewer; of these 8 are reported to be experimentally observed. In Fig. 3 however, only 27 centroids are filled. Due to the resolution of the grid, some reference solutions were forced to compete and only the fitter structures (higher absolute energy) were kept. We can observe that the known reference structures are distributed across a wide range of band gap and shear modulus values, with no apparent correlation between them. The availability of a wide range of structures not correlated within the feature space validates the suitability of the system and properties for this case study.
4.2 Results – titanium dioxide
The results from the application of the MAP-Elites algorithm were averaged across 10 experiments. We observed that in all 10 experiments the global minimum was found, and that on average 10 (with a standard deviation of 2.2) other unique matches were found. On average 3 (with a standard deviation of 1.2) of the unique matches were found with a high or gold standard confidence. This demonstrates that the global minimum can be found in a reproducible manner alongside multiple other structures. To understand some of the dynamics of applying MAP-Elites to this crystal structure prediction problem, comparative statistics are plotted in Fig. 4.The increase in QD score, as shown in Fig. 4a, shows that overall the fitness of the archive is increasing, which means that there are more high-performing solutions present overtime. This can be both because centroids are populated with increasingly high-performing solutions, and that more solutions are being added to the archive. The increase in the overall number of solutions is demonstrated by the increase in coverage as shown in Fig. 4b. The increase in the median fitness of individuals is shown in Fig. 4c.
In Fig. 4d, we observe that the maximum attained fitness increases with the number of evaluations, indeed attaining the value of the ground state. The algorithm effectively explores the energy function to find its global minimum. This is expected since evolutionary algorithms have been extensively used for this application, but provides confidence in the algorithm setup, surrogate models used and hyperparameters set in this work.
These metrics do not capture whether the expected reference structures are generated, nor how different the generated structures are from each other. Therefore, a sample archive is inspected below. The archive was randomly selected from 10 experiments excluding the 2 best performing and 2 worst performing archives. Fig. 5 shows the sample MAP-Elites grid after 5000 evaluations. We can observe that the majority of the archive is populated with high-performing (yellow) individuals. Additionally, all but 2 centroids where reference structures are expected are populated. The algorithm is effectively exploring the areas of the feature space where solutions are expected.
 | ||
| Fig. 5 Sample archive after 5000 evaluations. Centroids where reference solutions are expected are marked with a red outline. | ||
 | ||
| Fig. 6 Visual analysis of behaviours within sample archive. (a) Archive with centroids containing a match to a reference structure highlighted. (b) Archive view of structures grouped by similarity using pymatgen StructureMatcher class.36 Similar solutions are represented using the same colour. (c) Unique structure matches found during optimisation. | ||
To remove the duplication of structures, Euclidean distance in the feature space between the position of the reference and generated solutions was computed, and the structure with the shortest distance was kept. The results are visualised in Fig. 6c. The centroid where the reference structure should be found is coloured using the confidence level. The positions of the reference and generated structures are indicated by the scatter points connected via the dashed line. For the majority of the structures, the position of the two structures in the feature space is similar, but it is possible for them to lie quite far apart. This can be caused by the fact that the underlying models are sensitive to the structure's definition.
The structures identified are visualised in Fig. 7. We can observe that as a whole the structures are chemically realistic and diverse in terms of connectivity in the atomic building blocks. However, some structures share common motifs. This is expected because, as highlighted above, within the tolerances used in this work, some reference structures are considered equivalent. This is the case for instance for the ground state (mp-390) and a theoretical structure mp-34688. The supporting analysis can be found in the ESI.†
 | ||
| Fig. 7 Crystallographic unit cells of the TiO2 polymorphs generated during optimisation. Structures were reduced to their primitive cell using pymatgen SpacegroupAnalyzer utility,36 visualised using VESTA.37 Each system is labelled by the corresponding Materials Project ID and confidence of the match. | ||
This enables us to understand the exploration of the algorithm. The results are plotted in Fig. 8. If the energy is higher than that of the reference this means that even if the reference structure had been discovered during optimisation, it would have been rejected due to its worse energy. This is the case for the majority of the reference centroids as shown in Fig. 8, which allows us to make three hypothesis: (1) more stable solutions could have been identified during optimisation than those present in the final archive, (2) the same base structure with small changes can be used to fool the neural networks into predicting varying property values and (3) the algorithm exploits unexplored areas of the neural network to fool it into predicting high absolute energy values. The last observation could be a powerful tool in generating structures to train more robust surrogate models for crystal structure prediction. Indeed QD methods have been used in past work exactly for this purpose38,39 and in a wider context of generating samples and exploring the latent space of machine learning models.18,40,41
4.3 Extension to other systems
To demonstrate that the method can generalise to other systems, three material systems were selected: C, SiC and SiO2. These are again known to adopt multiple polymorphs. No hyperparameter adjustments were made to improve performance on the individual systems. The only changes were the adjustment of the feature vector limits to capture the values of the corresponding references, and the allowed random symmetries used by pyxtal to generate random structures.The results are summarised in Table 1 below. For all materials tested above, between 58% (C) and 71%¶ (SiO2) of structures available to be discovered were found. The absolute number of structures identified could likely be larger, but the resolution of the grid creates a cap. For instance, the 99 reference structure of SiO2, are distributed across only 28 centroids (figure available in ESI).† Therefore, inherently due to the resolution of the grid, we are unlikely to find all reference structures. The ground state was found 7 out of 10 times for C and it was not found in any experiments for SiO2.
| Carbon | Silicon dioxide | Silicon carbide | |
|---|---|---|---|
| Unique matches (σ) | 15 (2.4) | 20 (3.4) | 6 (0.48) |
| Unique gold standard/high confidence matches (σ) | 6 (1.3) | 3 (1.4) | 3 (0) |
| Reference structures (number of filled centroids) | 44 (26) | 99 (28) | 13 (11) |
| Number of times reference ground state found | 7 | 0 | N/A |
This decreased performance as compared to TiO2 is expected, as the parameters of the experiment were not adjusted. SiC was excluded from this analysis as its ground state structure contains more than the 24 atoms available for optimisation.
5 Discussion & further work
By combining the strengths of MAP-Elites with the framework of evolutionary algorithms used in crystal structure prediction, we built a pipeline that can be used in a range of applications to identify diverse crystal structures. This work assumes almost no prior knowledge of the material system making it highly generic. Although we focused on polymorphs of single compositions, this method could be expanded to explore larger chemical spaces. Additionally, since the feature vector is defined by the user, this method can be applied out-of-the-box in a wide range of applications.The underlying evolutionary algorithm uses simple mutations and makes limited assumptions regarding the crystal system. As such, we expect that by implementing a more advanced procedure under-the-hood of MAP-Elites, such as improved starting structures, more accurate surrogate models,42,43 and tailored mutation operators, this technique could yield promising results on larger and more complex systems including artificial heterostructures.
One of the requirements of MAP-Elites is a high number of required evaluations. As evaluating thousands of structures using DFT is not feasible, surrogate models are beneficial. These, however, rely on the data available for training. To fine-tune models in particular search spaces, MAP-Elites could be used to identify structures outside of the training distribution that fool the model. We observed the ability of the algorithm to identify structures that exploit the underlying interatomic model to find structures with higher absolute energy values than expected, thus making it suitable for such an application.
Building on this work, extensions of QD techniques could also be used. For instance, multi-objective QD could be employed to enable the search for materials with conflicting objectives, while discovering large collections of structures that span across the property space.15 Alternatively, if differentiable models are used for all feature and fitness function models, gradients can be used to inform the mutations thus allowing solutions to converge faster. This is done in Differentiable Quality-Diversity.44
6 Conclusion
We presented the application of Quality-Diversity algorithms to the problem of crystal structure prediction. By using properties of materials to discretise the search space and the TiO2 system, we demonstrated that this technique can not only find the ground state structure, but also other structures with varying properties. The versatility of this algorithm was then validated on three other crystal systems, where novel structures were found for C, SiO2 and SiC. The performance of our method can benefit from improvements to the underlying algorithm to combine state-of-the-art techniques from evolutionary algorithms applied to crystal structure prediction with QD algorithms to reap the benefits of faster convergence to realistic structures with a diversity of results.Data availability
A repository containing the data and associated analysis code have been made available on Github (https://github.com/adaptive-intelligent-robotics/QD4CSP).Author contributions
M. W., A. C and A. W. designed the study. M. W. and A. C. analysed the results and discussed additional experiments from a computational perspective. M. W. and A. W. analysed results from a materials science perspective. M. W. conducted the experiments, established the methodology, wrote the software and wrote the original draft of the paper. A. C. supervised the work. A. C. and A. W. reviewed and edited the paper.Conflicts of interest
There are no conflicts to declare.References
- M. A. Green, A. Ho-Baillie and H. J. Snaith, The emergence of perovskite solar cells, Nat. Photonics, 2014, 8, 506–514 CrossRef CAS.
- K. Mizushima, P. Jones, P. Wiseman and J. Goodenough, LixCoO2 (0<x<-1): A new cathode material for batteries of high energy density, Mater. Res. Bull., 1980, 15, 783–789 CrossRef CAS.
- J. Zhou, L. Xie, X. Song, Z. Wang, C. Huo, Y. Xiong, Z. Cheng, Y. Wang, S. Zhang, X. Chen and H. Zeng, High-performance vertical field-effect transistors based on all-inorganic perovskite microplatelets, J. Mater. Chem. C, 2020, 8, 12632–12637 RSC.
- A. R. Oganov and C. W. Glass, Crystal structure prediction using ab initio evolutionary techniques: Principles and applications, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- F. H. Stillinger, Exponential multiplicity of inherent structures, Phys. Rev. E, 1999, 59, 48–51 CrossRef CAS.
- X. Yin and C. E. Gounaris, Search methods for inorganic materials crystal structure prediction, Curr. Opin. Chem. Eng., 2022, 35, 100726 CrossRef.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Scaling deep learning for materials discovery, Nature, 2023, 624, 80–85 CrossRef CAS PubMed.
- Z. Allahyari and A. R. Oganov, Coevolutionary search for optimal materials in the space of all possible compounds, npj Comput. Mater., 2020, 6, 55 CrossRef.
- C. W. Glass, A. R. Oganov and N. Hansen, USPEX—Evolutionary crystal structure prediction, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- D. C. Lonie and E. Zurek, XtalOpt: An open-source evolutionary algorithm for crystal structure prediction, Comput. Phys. Commun., 2011, 182, 372–387 CrossRef CAS.
- K. Deb and K. Deb, Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques, Springer US, Boston, MA, 2014, pp. 403–449 Search PubMed.
- Z. Allahyari and A. R. Oganov, Handbook of materials modeling: Applications: Current and emerging materials, Springer International Publishing, Cham, 2018, pp. 1–15 Search PubMed.
- S. S. Omee, L. Wei, M. Hu and J. Hu, Crystal structure prediction using neural network potential and age-fitness Pareto genetic algorithm, 2024, https://www.oaepublish.com/articles/jmi.2023.33.
- K. M. Jablonka, G. M. Jothiappan, S. Wang, B. Smit and B. Yoo, Bias free multiobjective active learning for materials design and discovery, Nat. Commun., 2021, 12, 2312 CrossRef CAS PubMed.
- T. Pierrot, G. Richard, K. Beguir and A. Cully, Proceedings of the Genetic and Evolutionary Computation Conference, 2022, pp. 139–147 Search PubMed.
- G. M. Day and A. I. Cooper, Energy–Structure–Function Maps: Cartography for Materials Discovery, Adv. Mater., 2018, 30, 1704944 CrossRef PubMed.
- A. Cully, J. Clune, D. Tarapore and J.-B. Mouret, Robots that can adapt like animals, Nature, 2015, 521, 503–507 CrossRef CAS PubMed.
- A. Hagg, M. L. Kliemank, A. Asteroth, D. Wilde, M. C. Bedrunka, H. Foysi and D. Reith, Efficient Quality Diversity Optimization of 3D Buildings through 2D Pre-optimization, Evol. Comput., 2023, 1–21 Search PubMed.
- A. Gaier, A. Asteroth and J.-B. Mouret, Proceedings of the Genetic and Evolutionary Computation Conference, Berlin Germany, 2017, pp. 99–106 Search PubMed.
- C. Chen, Y. Zuo, W. Ye, X. Li and S. P. Ong, Learning properties of ordered and disordered materials from multi-fidelity data, Nat. Comput. Sci., 2021, 1, 46–53 CrossRef PubMed.
- C. Chen and S. P. Ong, A Universal Graph Deep Learning Interatomic Potential for the Periodic Table, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling, Nat. Mach. Intell., 2023, 5, 1031–1041 CrossRef.
- J. Riebesell, R. E. A. Goodall, A. Jain, P. Benner, K. A. Persson and A. A. Lee, Matbench Discovery – An evaluation framework for machine learning crystal stability prediction, arXiv, 2023, preprint, arXiv:2308.14920 [cond-mat], DOI:10.48550/arXiv.2308.14920.
- M. Van Den Bossche, H. Grönbeck and B. Hammer, TightBinding Approximation-Enhanced Global Optimization, J. Chem. Theory Comput., 2018, 14, 2797–2807 CrossRef CAS PubMed.
- Z. Falls, P. Avery, X. Wang, K. P. Hilleke and E. Zurek, The XtalOpt Evolutionary Algorithm for Crystal Structure Prediction, J. Phys. Chem. C, 2021, 125, 1601–1620 CrossRef CAS.
- A. R. Oganov and M. Valle, How to Quantify Energy Landscapes of Solids, J. Chem. Phys., 2009, 130, 104504 CrossRef PubMed.
- J.-B. Mouret and J. Clune, Illuminating search spaces by mapping elites, arXiv, 2015, preprint, arXiv:1504.04909 [cs, q-bio], DOI:10.48550/arXiv.1504.04909.
- V. Vassiliades, K. Chatzilygeroudis and J.-B. Mouret, Using Centroidal Voronoi Tessellations to Scale Up the Multidimensional Archive of Phenotypic Elites Algorithm, IEEE Trans. Evol. Comput., 2018, 22, 623–630 Search PubMed.
- K. Chatzilygeroudis, A. Cully, V. Vassiliades and J.-B. Mouret, Quality-Diversity Optimization: a novel branch of stochastic optimization, arXiv, 2020, preprint, arXiv:2012.04322 [cs, math, stat], DOI:10.48550/arXiv.2012.04322.
- F. Chalumeau, B. Lim, R. Boige, M. Allard, L. Grillotti, M. Flageat, V. Macé, A. Flajolet, T. Pierrot and A. Cully, QDax: A Library for Quality-Diversity and Population-based Algorithms with Hardware Acceleration, 2023 Search PubMed.
- S. Fredericks, K. Parrish, D. Sayre and Q. Zhu, PyXtal: A Python library for crystal structure generation and symmetry analysis, Comput. Phys. Commun., 2021, 261, 107810 CrossRef CAS.
- A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, New developments in evolutionary structure prediction algorithm USPEX, Comput. Phys. Commun., 2013, 184, 1172–1182 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A robust, opensource python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- K. Momma and F. Izumi, VESTA: a three-dimensional visualization system for electronic and structural analysis, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- L. Grillotti and A. Cully, Unsupervised Behavior Discovery With Quality-Diversity Optimization, IEEE Trans. Evol. Comput., 2022, 26, 1539–1552 Search PubMed.
- L. Grillotti and A. Cully, Proceedings of the Genetic and Evolutionary Computation Conference, New York, NY, USA, 2022, p. 77–85 Search PubMed.
- M. C. Fontaine, R. Liu, J. Togelius, A. K. Hoover and S. Nikolaidis, AAAI Conference on Artificial Intelligence, 2021 Search PubMed.
- R. Chandra, R. I. Horne and M. Vendruscolo, Bayesian Optimization in the Latent Space of a Variational Autoencoder for the Generation of Selective FLT3 Inhibitors, J. Chem. Theory Comput., 2024, 20, 469–476 CrossRef CAS PubMed.
- K. Choudhary and B. DeCost, Atomistic Line Graph Neural Network for Improved Materials Property Predictions, npj Comput. Mater., 2021, 7, 185 CrossRef.
- S. S. Omee, S.-Y. Louis, N. Fu, L. Wei, S. Dey, R. Dong, Q. Li and J. Hu, Scalable Deeper Graph Neural Networks for HighPerformance Materials Property Prediction, Patterns, 2022, 3, 5 CrossRef PubMed.
- M. Fontaine and S. Nikolaidis, Adv. Neural Inf. Process. Syst., 2021, 10040–10052 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00054d |
| ‡ NB: for C, only the strain operator was used as only one type of atom was present in that experiment. |
| § Since typically fitness is something to be maximised, we used the absolute value of energy rather than the negative values used by convention. We will therefore refer to maximising the absolute energy, which should be taken to be equivalent to minimising the energy in standard materials science nomenclature. |
| ¶ This is computed as the ratio between unique matches over number of filled centroids. |
| This journal is © The Royal Society of Chemistry 2024 |





