Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Insights into machine learning models from chemical physics: an energy landscapes approach (EL for ML)
Maximilian P.
Niroomand
 a,
Luke
Dicks
a,
Luke
Dicks
 b,
Edward O.
Pyzer-Knapp
b,
Edward O.
Pyzer-Knapp
 *b and
David J.
Wales
*b and
David J.
Wales
 *a
*a
aUniversity of Cambridge, Department of Chemistry, Cambridge, UK. E-mail: mpn26@cam.ac.uk; dw34@cam.ac.uk
bIBM Research UK, Daresbury, UK. E-mail: EPyzerK3@uk.ibm.com
First published on 8th February 2024
Abstract
The study of energy landscapes as a conceptual framework, and a source of novel computational tools, is an active area of research in chemistry and physics. The energy landscape provides insight into structure, dynamics, and thermodynamics when combined with tools from statistical mechanics and unimolecular rate theory. This approach can also be applied to questions that arise in machine learning. Here, the loss landscape (LL) of a machine learning system is treated in the same way as the energy landscape for a molecular system. In this contribution we summarise and discuss applications of energy landscapes for machine learning (EL4ML). We will outline how various physical properties find analogues in machine learning systems, and show how these properties can be employed to both increase understanding of the machine learning ‘black-box’ and enhance the performance of machine learning models.
1 Introduction
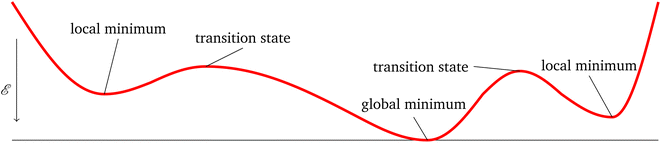
In the physical sciences, energy landscapes1 provide a computational framework to predict structure, thermodynamics, and dynamics.2 Exploring the energy landscape means computing the potential energy E for a given atomic configuration, defined by the coordinates of the individual atoms in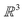 . The potential energy surface (PES) gives the energy for any combination of coordinates of the individual atoms. The PES is a continuous, non-convex function, in which local minima correspond to locally-stable states of the system, and potentially interesting configurations. The Murrell–Laidler theorem states that the lowest barrier between local minima involves a pathway mediated by index one saddle points (transition states).3 These transition states are essential to describing the dynamics of a physical system. An illustrative PES is shown in Fig. 1, where the zero-gradient transition state separates two minima. The global minimum corresponds to the lowest potential energy achievable for a given system, which corresponds to the equilibrium state at low temperature.
. The potential energy surface (PES) gives the energy for any combination of coordinates of the individual atoms. The PES is a continuous, non-convex function, in which local minima correspond to locally-stable states of the system, and potentially interesting configurations. The Murrell–Laidler theorem states that the lowest barrier between local minima involves a pathway mediated by index one saddle points (transition states).3 These transition states are essential to describing the dynamics of a physical system. An illustrative PES is shown in Fig. 1, where the zero-gradient transition state separates two minima. The global minimum corresponds to the lowest potential energy achievable for a given system, which corresponds to the equilibrium state at low temperature.
In machine learning, the problem posed is analogous to optimising atomistic arrangements in molecular systems. Given a set of variables (weights, hyperparameters etc.), a loss function is minimised to provide the best possible solution to the problem. As for molecular systems, machine learning is an optimisation problem, with the aim to minimise the cost function and identify the lowest-lying solution. In a (supervised) machine learning system, this solution is the set of weights/hyperparameters describing an arbitrary function that best fits some input data to known outputs.
In ML there is an additional consideration, requiring a model generalising well to unseen data. For a given machine learning algorithm and some data, the loss landscape describes the quality of each possible weight/hyperparameter combination. Importantly, these models are only conditioned on the training data, hence the LL cannot make a statement about generalisation to unseen testing data. Numerous loss functions exist, from simple mean squared error losses to cross-entropy, contrastive, or approximate AUC loss functions. Thus, the correlation between loss value and performance of the minimum must be viewed with caution. The global minimum of the LL is the best guess as to which set of weights may be optimal for the specific problem, but optimality cannot be guaranteed. Train-test generalisability is not the focus of this contribution, but the reader should keep this issue in mind.
To characterise the loss landscape (LL) of a machine learning system, only the training data is relevant. Hence, the global minimum is the set of weights that minimise the loss (energy) for a given cost/loss function and training data. Note that this setup implies that, for a standard loss function, overfitting the model to training data is encouraged by the formulation of the problem. Thus, ideally, the model would perfectly predict the correct output for each input, irrespective of performance on unseen data. In Table 1, we have summarised the most important features to describe an energy landscape, and what they mean when translated to a ML setting.
| Feature | Molecular PES | ML LL |
|---|---|---|
| Energy | Potential energy | Loss value |
| Temperature | Physical temperature | Fictitious parameter |
| Coordinates | Atomistic coordinates | Weights/hyperparameters |
| Local minimum | Locally-stable molecular isomer | Locally optimal weights |
| Global minimum | Energetically most favourable molecular isomer | Best weights for given loss function |
2 Motivation: EL4ML
Machine learning has become one of the most active fields in science due to its impact across a broad range of applications. These applications range from games, such as chess,4 Go,5 or the collaborative Dota 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 to autonomous driving (covered extensively in ref. 7), protein structure prediction8 mathematical proofs,9 chat bots,10,11 image generation12,13 and many more. Applications to the physical sciences, including force-field parametrisation are discussed in ref. 14. This list is far from exhaustive, and novel machine learning models are developed and open-sourced every day. The basic foundation of the machine learning approach is that, given enough data and computational resources, the fitting and prediction problem is solvable in principle. In fact, it can be shown that, given enough parameters, any dataset can be fitted perfectly by a machine learning model.15 However, we seek a deeper understanding of why and when machine learning works, and the fact that there exists a function to map given input to output does not provide understanding or interpretation of which features from the input lead the model to a given output choice.
6 to autonomous driving (covered extensively in ref. 7), protein structure prediction8 mathematical proofs,9 chat bots,10,11 image generation12,13 and many more. Applications to the physical sciences, including force-field parametrisation are discussed in ref. 14. This list is far from exhaustive, and novel machine learning models are developed and open-sourced every day. The basic foundation of the machine learning approach is that, given enough data and computational resources, the fitting and prediction problem is solvable in principle. In fact, it can be shown that, given enough parameters, any dataset can be fitted perfectly by a machine learning model.15 However, we seek a deeper understanding of why and when machine learning works, and the fact that there exists a function to map given input to output does not provide understanding or interpretation of which features from the input lead the model to a given output choice.
Interpretability in ML has received increasing attention16–18 with the realisation that in many fields, an understanding of why a certain prediction is being made, is as important as the accuracy. Unfortunately, interpreting a high-dimensional and complex function is difficult.19 Recent efforts in interpretability have been summarised in Zhang et al.16 Usually, these approaches revolve around understanding the gradients of the loss function with respect to the input, to understand how changes in the input affect the output, as in Davies et al.9 However, given the relatively high complexity of machine learning models such as neural networks, this analysis is often insufficient and does not provide a complete picture.19
To better understand the foundations of machine learning capabilities, the loss landscapes of machine learning systems20–22 can be analysed. For reasons of computational cost, it is common practice in machine learning to start from a given set of initial weights, chosen either randomly or by some initialisation scheme,23 minimise the loss as far as possible with a greedy algorithm, and accept this result for the trained weights. Perhaps unexpectedly, this procedure seems to work well, and various explanations for this fortuitous situation have been suggested.24,25 The most prominent suggestion derives from Goodfellow et al.26 They report what they call the Monotonic Linear Interpolation (MLI) property, the fact that there usually exists a monotonically decreasing path between some initial set of parameters θi and some minimum θo identified by some method such as stochastic gradient descent. The insight that this property exists, despite non-convex loss functions and non-linear training sets raises questions, but might be explained by the fact that, given enough data, many problems simply are not that difficult. These results received considerable attention in the field, and the matter is likely to be more complicated. Lucas et al.27 are able to create counterexamples to the MLI property and others have observed different results to Goodfellow et al.26 when revisiting the work on more modern architectures and data sets.28 Further doubt that ‘Machine learning may just be simple’ is cast in ref. 29 showing that the MLI does not always hold and must be considered with caution. In general, simply considering a linear interpolation from an initial set of weights to the identified minimum may be insufficient and all the aforementioned papers agree that further study and consideration of the ML-LL is of critical importance. Other work has shown that convergence to a global minimum for overparameterised networks under certain, somewhat restrictive conditions, is provable.30 These interpretability approaches share the commonality that large areas of the LL and its complex geometric features remain unexplored. In practice is not always guaranteed that the global minimum is identified, and no consideration is given to the shape of the LL or the existence of other local minima. While such results may be sufficient in terms of performance, it is not helpful in terms of interpretability. Understanding the LL has the potential to provide some of the missing understanding.31 Specifically, understanding the topography of a loss landscape can allow novel insights into the convergence process or optimiser path taken towards the global minimum.
Another suitable task for global optimisation based LL exploration is the efficient enumeration and analysis of various minima. Using generic tools, surveying large areas of the loss landscape is expensive and time consuming, while the exploration tools outlined below substantially simplify the problem.
Energy landscapes are reasonably well understood for molecules and condensed matter, and the hope exists that some of the associated methodology could help to better understand machine learning. Importantly, since a loss function is ubiquitous in any machine learning system, consideration of the LL is applicable in a broad range of fields. While most work has so far considered neural networks,20,31 LLs have also been analysed in the context of clustering methods, such as K-means32 or for Gaussian processes33 in Bayesian machine learning.34 These contributions suggest another useful property of the energy landscapes view of machine learning. Entirely different models can now be compared with each other, not just for output metrics such as accuracy, but for the solution landscapes. Understanding how many minima exist for a given model, how they are connected, their relative volumes in parameter space, and how quickly an optimiser converges for them, may provide important insights into model selection.21
3 LL exploration
There are a variety of methods developed in chemical physics for exploring potential energy landscapes. Some of these methods are commonly referred to as enhanced sampling, including meta-dynamics,35 umbrella sampling,36 and replica-exchange molecular dynamics;37 a recent review is given by ref. 38. An alternative approach suitable for both potential and loss function surfaces is the energy landscape framework.Global optimisation algorithms aim to find the lowest minimum, amongst the (possibly) many local minima and funnels. In global optimisation for physical systems popular algorithms are basin-hopping39–41 and genetic algorithms.42 In ML, it is common to simply use various random initialisations and local minimisation, which has limited use in physical systems.43 Examples of random, or pseudo-random, initialisation and minimisation are seen in K-means,44–46 Gaussian processes,47 and neural networks. All these methods rely upon minimisation algorithms to locate local minima of the cost function surfaces, and common choices are limited-memory48,49 quasi-Newton Broyden,50 Fletcher,51 Goldfarb,52 Shanno53 (L-BFGS) routine and its variants with box-constraints54,55 for bounded problems such as fitting Gaussian processes. Conjugate gradient approaches can leverage matrix multiplication tricks to address larger datasets,56,57 and stochastic gradient descent scales well with dataset size due to only considering a portion of the data.58,59 The choice of minimiser should not change the landscape, but can significantly modify the rate of exploration.
The energy landscape approach is feasible if the number of variables in the fitting space is not too large (up to perhaps 104), and the hope is to develop understanding that is transferable to the much larger problems often employed in deep learning models. To analyse the LL using the energy landscape framework, global optimisation is performed initially, the set of low-valued minima are stored, and their connected transition states are located. In a first step, the global minimum of the LL is identified, which is commonly done using basin-hopping global optimisation.39,40 Starting from any initial values for the parameters, this procedure progresses by local minimisation. Steps to new minima are accepted or rejected, commonly using a Metropolis-type60 condition, and steps are proposed by perturbing the parameters corresponding to the current minimum in the chain. Local minimisations are usually performed using the LBFGS routine. For a Metropolis accept/reject scheme, a new minimum is always accepted if its energy (loss function) is lower, and is also accepted if the energy is higher with probability
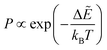 | (1) |
Local minima do not constitute a landscape. To understand the organisation of solution space, transition states, defined as saddle points with Hessian index one3 need to be located. Transition states mediate the pathways between minima with the lowest barriers according to the Murrell–Laidler theorem.3 Here, double-ended searches are usually employed to connect each selected pair of minima, using the doubly-nudged61,62 elastic band63–66 method to identify likely candidates for accurate refinement using hybrid-eigenvector following.67–69 These methods require continuous first and second derivatives, but even for loss functions without these properties, such as K-means, landscapes can still be explored using algorithmic adaptations.32 These geometry optimisation tools have been refined for a wide range of problems over several decades, and are implemented in the GMIN,70 OPTIM71 and PATHSAMPLE72 programs,73 all available for use under the GNU General Public License.
Global optimisation and subsequent transition state searches provides the foundations for a full characterisation of the energy landscape/LL of a particular system. This approach is clearly much more computationally expensive than only a single optimisation pass, but the objective here is to understand the structure of the solution space, not to seek predictions for any particular problem. The LL itself is generally unbounded from above. Regularisation methods or other constraints are usually employed to reduce overfitting problems,74,75 which tends to keep the fitting parameters within a sensible range.
4 Physical properties and analogues for ML
Machine learning loss landscapes are analogous to energy landscapes and can be interrogated to extract the analogues of thermodynamic and kinetic properties, which constitute the key observables for molecular systems. When characterising a landscape, we can loosely distinguish two sets of metrics: global and local. Global metrics characterise overall properties of the landscape, and local metrics distinguish different types of solutions (i.e. minima). The former metrics allow for a characterisation of the whole solution space for archetypal datasets, and provide a better understanding of the nature of the optimisation problem. The distinction is fuzzy and several metrics have important features in both classes. A discussion of some of the most useful properties is given below, and summarised in Table 2.| Feature | Molecular PES | ML LL |
|---|---|---|
| Basin volume | Entropic contribution to occupation probability | Connection to robustness |
| Heat capacity | Change in occupied minima as a function of temperature | Identification of minima with complementary properties |
| Frustration | Propensity for broken ergodicity | Implications for optimisation and training |
4.1 Global landscape metrics
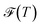 , and the Shannon entropy,77
, and the Shannon entropy,77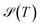 , is that
, is that 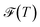 accounts for transition states and barriers, while the Shannon entropy considers only the equilibrium thermodynamic properties of local minima. The Shannon entropy is given by
accounts for transition states and barriers, while the Shannon entropy considers only the equilibrium thermodynamic properties of local minima. The Shannon entropy is given by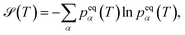 | (2) |
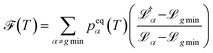 | (3) |
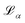 is the loss value of minimum α, and
is the loss value of minimum α, and 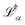 is the loss value of the highest transition state of the lowest energy path between minimum α and the global minimum. The loss value of the global minimum is denoted
is the loss value of the highest transition state of the lowest energy path between minimum α and the global minimum. The loss value of the global minimum is denoted  . To compare between systems, we can consider
. To compare between systems, we can consider 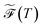 defined in terms of
defined in terms of ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) eqα(T) = peqα(T)/(1 − peqgmin(T)). As discussed above, the effective temperature T is simply a parameter to interrogate the landscape in machine learning systems. Studying
eqα(T) = peqα(T)/(1 − peqgmin(T)). As discussed above, the effective temperature T is simply a parameter to interrogate the landscape in machine learning systems. Studying 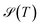 or
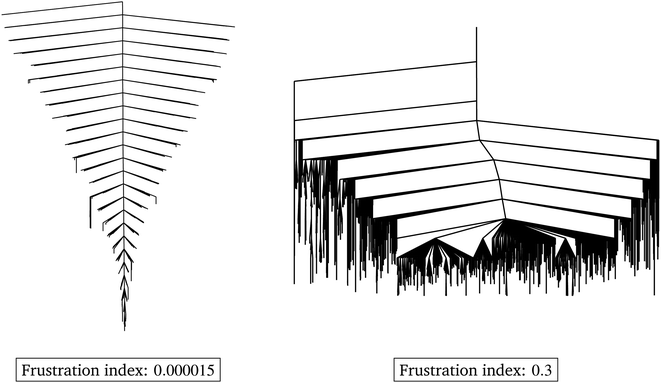
or 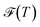 over a range of values for T at the system temperature corresponding to the peaks in heat capacity curves reveals features of the landscape comparable to the analysis of molecular and condensed matter systems in,76 where various metrics are compared. An example is given in Fig. 2. Here, the landscape on the left is an ideal single funnel, where locating the global minimum is straightforward over a wide range of temperatures. In contrast, locating the true global minimum for the landscape on the right is more difficult. However, if alternative low-lying minima provide good solutions then it will be straightforward to locate a member of this set. Importantly, the alternative minima will probably have different properties, and perhaps provide slightly different predictions. Nevertheless, this structure may be more robust to initialisation noise and multiple such minima could be combined in ensembles to improve overall accuracy. In machine learning applications,
over a range of values for T at the system temperature corresponding to the peaks in heat capacity curves reveals features of the landscape comparable to the analysis of molecular and condensed matter systems in,76 where various metrics are compared. An example is given in Fig. 2. Here, the landscape on the left is an ideal single funnel, where locating the global minimum is straightforward over a wide range of temperatures. In contrast, locating the true global minimum for the landscape on the right is more difficult. However, if alternative low-lying minima provide good solutions then it will be straightforward to locate a member of this set. Importantly, the alternative minima will probably have different properties, and perhaps provide slightly different predictions. Nevertheless, this structure may be more robust to initialisation noise and multiple such minima could be combined in ensembles to improve overall accuracy. In machine learning applications, 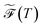 has important effects on training reproducibility and may correlate with batching effects. Since the same minimum is more likely to be found repeatedly in unfrustrated landscapes, training these systems is more reproducible and variation in output is less likely to come from initialisation noise. High-frustration surfaces may further be more prone to batch effects, or at least have increased variance with batch effects. Like above, this is due to the high likelihood of individual minima being overfit to specific aspects of the input data.
has important effects on training reproducibility and may correlate with batching effects. Since the same minimum is more likely to be found repeatedly in unfrustrated landscapes, training these systems is more reproducible and variation in output is less likely to come from initialisation noise. High-frustration surfaces may further be more prone to batch effects, or at least have increased variance with batch effects. Like above, this is due to the high likelihood of individual minima being overfit to specific aspects of the input data.
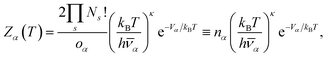 | (4) |
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) α the geometric mean normal mode vibrational frequency, a measure of basin geometry, oα the order of the molecular point group, T the temperature and Vγ the potential energy of minimum γ, the corresponding internal energy E and heat capacity CV can be derived. By defining the harmonic superposition partition function, and using some elementary identities, a novel formulation of the heat capacity can be derived.78 Peaks in the heat capacity curve can be interpreted by looking at the contribution of minima with positive and negative temperature derivatives
α the geometric mean normal mode vibrational frequency, a measure of basin geometry, oα the order of the molecular point group, T the temperature and Vγ the potential energy of minimum γ, the corresponding internal energy E and heat capacity CV can be derived. By defining the harmonic superposition partition function, and using some elementary identities, a novel formulation of the heat capacity can be derived.78 Peaks in the heat capacity curve can be interpreted by looking at the contribution of minima with positive and negative temperature derivatives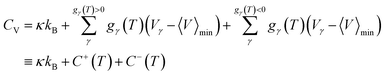 | (5) |
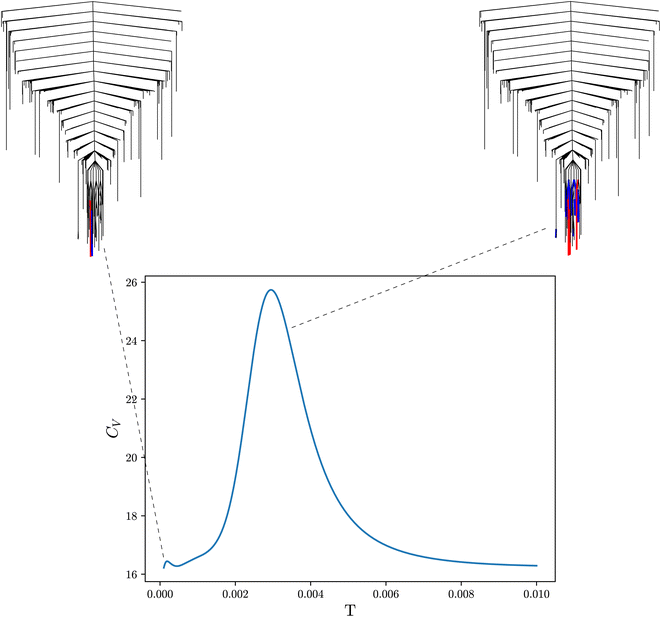
In molecular systems, peaks in the heat capacity correspond to solid–solid or solid–liquid phase transitions, where the system moves between qualitatively different sets of local minima, associated with different energy and entropy. For ML systems, the analogue of the heat capacity reveals how the occupation of minima changes with the temperature parameter. The temperature in an ML problem is fictitious (Fig. 3), but serves as a parameter to scan the properties of the landscape and report on changes that highlight qualitatively different solutions (local minima). Minima separated by a high energy barrier may be very different,79 although degenerate solutions can also exist due to symmetries of the loss function.80 In fact, it has been shown in one example that different minima may ‘specialise’ in different parts of the input data, so that better predictions can be obtained by employing alternative solutions from the LL for different input. The heat capacity provides a way to identify these ‘different’ minima with contrasting properties. In applications such as ensemble learning, this capability is highly relevant. Combining different minima enhances ensemble methods significantly beyond randomly choosing a subset of minima.80
Furthermore, the degree of each minimum, i.e. the number of direct connections to other minima via a single transition state, is a useful property. Nodes with a high degree constitute hubs, associated with small world properties. These minima are usually easy to locate during optimisation, and they are key to moving between different regions of the space. For physical systems it tends to be low-valued solutions that act as hubs, which can explain whether they are easy to locate.87,88 The degree of a node can also highlight its importance to optimisation algorithms in physical systems and abstract cost functions. Furthermore, the distribution of node degrees, which is a global property of the system, can be used to understand the organisation of the landscape.89
4.2 Local landscape metrics
In ML systems, rates have no physical analogue, but they nevertheless provide a useful estimate of the difficulty in moving between different regions of solution space. The rates, calculated with the contributions of all known solutions, account for both intervening barriers in the loss function and the number of intermediate minima. Both properties have physical meaning for understanding the solution space, and contain important additional information not present in distance calculations. Small rates indicate that two given minima are highly distinct, where interconversion requires either many, or large, changes in model parameters.
Accurate values for the analogue properties of LL minima are not required to diagnose the existence of qualitatively different solutions, and hence the harmonic value reported by the LPPHE is sufficient for diagnostic purposes. The configuration volume for a basin of attraction may also have useful interpretations in ML problems. One of the most important features of a machine learning model is that is should be robust. The LPPHE provides a harmonic measure of the basin volume31 which allows minima to be selected based on some intuition of how robust they might be, as well as training accuracy. We emphasise once again, that the value of the effective heat capacity is not important here, but peaks in this function enable us to identify local minima with distinct classification properties in an efficient manner.
4.3 Further possibilities
The machine learning community has only recently begun to explore the analogues of physically observable thermodynamic and kinetic properties for machine learning loss landscapes. In particular, little work has been done to determine whether dynamical analogues might be useful. As for thermodynamic quantities, such as the heat capacity, there could be useful insight to be gained from understanding how such quantities report on the nature of the machine learning solution space.4.4 ML model metrics
Above, we have discussed various metrics that are relevant when considering the energy landscape of an atomistic system, and how these may be applied to ML systems. We now want to briefly discuss metrics that are considered in machine learning, implicitly characterising ML LLs. As described above, the LL is at best a surrogate of quality: since it is only based on training data, the ability to generalise to testing data is not easily obtainable. The same imperfect correlation between loss function and quality is seen in unsupervised clustering methods, such as K-means, even without the presence of test data.In practice, ML models are largely scored for accuracy and robustness, i.e. test accuracy. A practitioner may be interested in how the loss value changes on training data, and perhaps also in training loss. Yet, results are usually reported on test datasets. A helpful review of machine learning evaluation can be found in ref. 99. In general, the relevant metrics in machine learning models are largely results-focused and only to a lesser degree incorporate an understanding of the system. As long as the test accuracy in terms of MSE, AUC, or top-k loss is sufficient, the practitioner rarely cares about interpretation in terms of the Hessian eigenvalues of the underlying loss landscape. Such physical quantities have a clear meaning in energy landscapes, and they are routinely analysed. We hope that by translating some of these metrics into practical machine learning understanding, more attention will be paid to these metrics in the future.
5 Applications of EL4ML
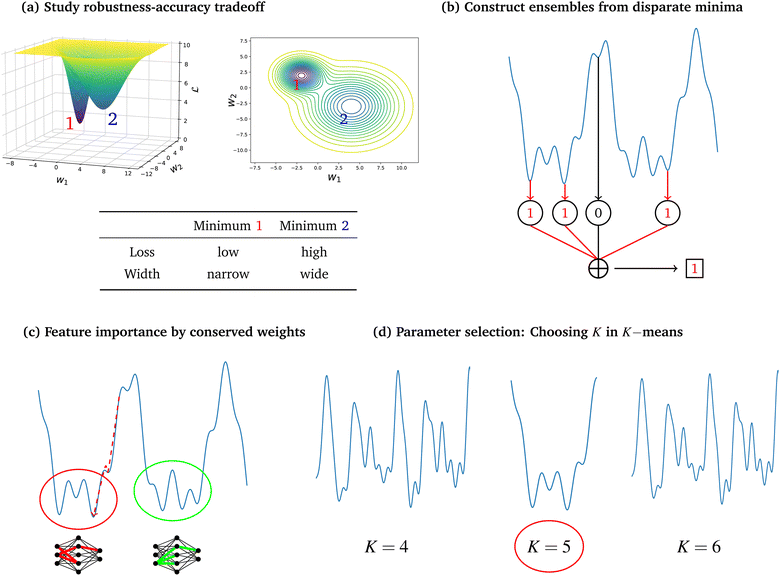
Here we will discuss applications where knowledge of the LL has been used to understand or improve machine learning. Fig. 4 provides an overview of the four application areas we consider as most promising for loss landscape methods.5.1 Robustness
Incorporating knowledge of the loss landscape has become increasingly common in machine learning. Most prominently, several new optimisation methods have been developed that include some degree of information about the gradient of the LL.100–103 Including information about the LL in optimisation seems to lead to improved robustness of the solution. Robustness in machine learning refers to the ability of a particular model to generalise well to unseen testing data. A more robust model will perform better on testing data than a model that is overfit on the training data and does not generalise well. Flatter minima, geometrically characterised by Hessian eigenvalues (curvatures) with smaller magnitudes, are expected to be more robust.104–106 This result seems intuitive, since it means that if slightly different training data displace the minimum from its given position, it will still be close to the original position for a ‘flatter’ landscape, whereas the resulting displacement may be larger when the local curvatures are greater.Mathematically, given a minimum at position P with energy/loss 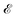 , a small displacement of P + p, caused by slightly different training data, will have an effect on
, a small displacement of P + p, caused by slightly different training data, will have an effect on 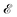 depending on the curvatures around P, i.e.
depending on the curvatures around P, i.e.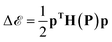 , where H(P) is the Hessian at P. Hence, if the Hessian, and more specifically its eigenvalues, are larger, the minimum is ‘narrower’ and the difference in
, where H(P) is the Hessian at P. Hence, if the Hessian, and more specifically its eigenvalues, are larger, the minimum is ‘narrower’ and the difference in 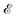 ,
, 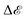 between positions P and P + p is greater, the minimum is less robust. Foret et al.101 have included knowledge about the shape of the loss function and managed to find more robust minima. Overall, robustness is one of the most important concepts in machine learning.107 A completely overfit model, one that has perfect training accuracy, but does not generalise at all to testing data, is useless in practice. Thus, considering geometric features of the loss landscape may be an important way in combating this problem.
between positions P and P + p is greater, the minimum is less robust. Foret et al.101 have included knowledge about the shape of the loss function and managed to find more robust minima. Overall, robustness is one of the most important concepts in machine learning.107 A completely overfit model, one that has perfect training accuracy, but does not generalise at all to testing data, is useless in practice. Thus, considering geometric features of the loss landscape may be an important way in combating this problem.
5.2 Ensemble methods
Knowledge of the loss landscape may help improve prediction accuracy for a given model. Ensemble methods, combining or averaging multiple predictors for a single task, is a well established approach.108–111 One reason why ensemble methods have become so important over previous years is the imperfect correlation of performance and loss resulting from limited training data. The single best minimum is often not sufficient and hence, a combination of so called weak learners is required to outperform a ‘better’ minimum. Related challenges arise in batch selection for Bayesian optimisation, where the key challenge is determining a diverse set of samples for the task of maximising an expensive ‘black-box’ function.112–116 Two of the critical design choices in ensemble learning are, which classifiers to combine, and how to combine them. Common approaches include bagging and boosting methods, which are well described in ref. 117. The possible approaches to combine predictions of different minima range from simple majority votes, to complex weighting schemes for the contribution of individual classifiers. The same methods can be applied to unsupervised learning, where clustering solutions can be combined to improve separation, without the separation into training and testing data.118 The value of ensemble learning arises when different classifiers are good at classifying different subsets of the data, or prioritise different parts of the input. Recently, the idea of combining multiple minima of the LL, obtained via energy landscapes methodology,80 has been examined. Each minimum can be viewed as an individual classifier, where all models have the same architecture, but very different parameters. Combining classifiers, all obtained from one LL, provides the distinct advantage that the classifiers are known to be qualitatively ‘different’, which is the key feature in ensemble learning. Specifically, for some LL, standard measures based on analogue properties from the physical sciences, such as the heat capacity, can be analysed to increase the likelihood that the minima are complementary. Landscape guided ensemble learning is another example of how physics-inspired machine learning can outperform common methods, and hence provide significant additional performance.5.3 Interpretability
Understanding the black box of machine learning systems is one of the greatest challenges to the field today. Various gradient and perturbation based methods exist,119 yet their usefulness and accuracy is debated, and is not generally agreed to be sufficient.120 Hence, alternative ways to improve our understanding of decision-making by a particular model are desirable. Studying individual funnels of the landscape, as seen in disconnectivity graphs, may provide a promising way to increase interpretability. This approach is commonly exploited in the molecular sciences121,122 where a multifunnelled landscape is analysed to understand which structural differences of a molecule constitute a group of solutions in a specific funnel. The machine learning analogue is that for a multi-funnelled landscape, one can compute the sets of parameters that characterise a particular funnel, as in ref. 123. These parameters, conserved across multiple minima, are therefore likely to be important in the model, and may guide interpretability.5.4 Selecting overall parameters
ML algorithms can involve choosing a parameter that is not itself part of the optimisation problem. A prominent example is the choice of cluster number, K, in K-means. Each K defines a distinct cost function surface that must be optimised to generate low-valued clustering solutions. The choice of the appropriate cluster number is usually made using one, or a small set, of solutions at each K,124–127 reviewed in ref. 128. However, it is possible to make this decision using the topography of the whole solution space, rather than a small number of solutions. The use of landscapes, composed of many solutions, increases the reproducibility, as there is less dependence on locating certain minima, amongst a vast number, when computing metrics. The presence of certain landscape structure is indicative of an appropriate number of clusters, as observed for clustering gene expression data to identify cancer subtypes.129 Such an analysis is significantly more expensive than characterising single minima, but for many applications, the quality and reproducibility of the solution are essential.6 Future work
Many applications of energy landscapes remain unexplored in the context of machine learning. In this section, we will outline a few interesting areas of future work that would build substantially on the energy landscapes methodology. Firstly, it will be interesting to see advances in understanding the physics-inspired analogues of machine learning. For example, understanding in more detail the relationship between minima contributing to the heat capacity and the importance (both in terms of accuracy and robustness) of these minima in an inference task. Furthermore, many other concepts, such as the dynamical analogues in machine learning systems, remain largely unexplored. Understanding the usefulness of such metrics may give further insights from the physical sciences to the more abstract, black-box world of machine learning. In general, physics-inspired machine learning seems to be a good candidate for improving our understanding of machine learning, by transferring knowledge from a relatively mature field, to a newer one.Another area in which the energy landscape approach may prove very helpful is Bayesian inference using Gaussian processes (GPs). An inherent challenge within these methods is identifying suitable hyperparameters. Most commonly, a loss function, usually the log marginal likelihood, is maximised and a single point estimate is taken for the hyperparameters. However, single-point estimates may be insufficient when there are multiple competing fits.130 A common method to overcome the limitations of single point estimates is Monte Carlo (MC) sampling of the hyperparameter distribution.131–133 Previous work has used sequential MC sampling,130,134 Bayesian MC sampling,135 and Hamiltonian MC sampling.136 Additionally, slice sampling,137 adaptive importance sampling,138 and entropy-based methods139 have been used within Bayesian optimisation, where there is interest in moving beyond single-point estimates to fully-Bayesian approaches.140,141 The main drawback with these methods is the high computational cost, and ideally they should only be employed when it will provide a substantial advantage over single point estimates. However, this condition cannot be known a priori. Looking at the loss landscape may provide an answer. There may be a direct relationship between the number of funnels in the landscape, perhaps characterised by monotonic sequence basins, or the frustration index, and the effect that MC sampling has on improving accuracy and generalisability over single point estimates. Thus, knowledge of the landscape, obtained via appropriate sampling, could lead to a substantial reduction in compute cost by identifying when a fully-Bayesian approach is required. Moreover, the additional information present in landscapes may extend existing variational inference methods142,143 by allowing more accurate approximate distributions to be generated and sampled.
7 Conclusions
Important relationships exist between physical molecular energy landscapes and abstract machine learning loss landscapes. In this contribution we have highlighted some of the recent work on physics-inspired machine learning and how theoretical methods from one field may be applied to the other. We have discussed how various metrics, such as the heat capacity, catchment basin volume, or frustration index can help to improve and explain robustness, accuracy, and importantly interpretability in machine learning. Many of the connections between these two fields remain to be explored and exploited.Energy landscapes provide important insight to answer questions in machine learning, irrespective of the underlying model, because they focus on the structure of the solution space. More generally, exploiting a well understood methodology is a promising approach to vastly increase the set of problems that machine learning can be applied to. The hope is that methods from the physical sciences can work in conjunction with machine learning methods to give practitioners more trust and confidence in their predictions, as well as greater understanding of what a given model is actually doing. Ultimately, this approach could facilitate further growth in the influence that machine learning has on society as a whole.
Data availability
In this review article, no novel data was analysed or studied.Conflicts of interest
There are no conflicts to declare.Acknowledgements
DJW gratefully acknowledges an International Chair at the Interdisciplinary Institute for Artificial Intelligence at 3iA Cote d'Azur, supported by the French government, with reference number ANR-19-P3IA-0002, which has provided interactions that furthered the present research project. MPN acknowledges funding from Downing College, Cambridge. LD and EOP-K would like to acknowledge this work was supported by the Hartree National Centre for Digital Innovation – a collaboration between Science and Technology Facilities Council and IBM. LD also acknowledges the financial support of the EPSRC via a knowledge transfer fellowship.Notes and references
- D. J. Wales, Energy Landscapes, Cambridge University Press, Cambridge, 2003 Search PubMed.
- J. A. Joseph, K. Röder, D. Chakraborty, R. G. Mantell and D. J. Wales, Chem. Commun., 2017, 53, 6974–6988 RSC.
- J. N. Murrell and K. J. Laidler, Trans. Faraday Soc., 1968, 64, 371–377 RSC.
- D. Silver, T. Hubert, J. Schrittwieser, I. Antonoglou, M. Lai, A. Guez, M. Lanctot, L. Sifre, D. Kumaran, T. Graepelet al., arXiv, 2017, preprint arXiv:1712.01815, DOI:10.48550/arXiv.1712.01815.
- D. Silver, J. Schrittwieser, K. Simonyan, I. Antonoglou, A. Huang, A. Guez, T. Hubert, L. Baker, M. Lai and A. Bolton, et al. , Nature, 2017, 550, 354–359 CrossRef CAS PubMed.
- C. Berner, G. Brockman, B. Chan, V. Cheung, P. Debiak, C. Dennison, D. Farhi, Q. Fischer, A. Hashme, C. Hesseet al., arXiv, 2019, preprint arXiv:1912.06680, DOI:10.48550/arXiv.1912.06680.
- S. Grigorescu, B. Trasnea, T. Cocias and G. Macesanu, J. Field Robot., 2020, 37, 362–386 CrossRef.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek and A. Potapenko, et al. , Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- A. Davies, P. Veličković, L. Buesing, S. Blackwell, D. Zheng, N. Tomašev, R. Tanburn, P. Battaglia, C. Blundell and A. Juhász, et al. , Nature, 2021, 600, 70–74 CrossRef CAS PubMed.
- P. Budzianowski and I. Vulić, arXiv, 2019, preprint arXiv:1907.05774, DOI:10.48550/arXiv.1907.05774.
- T. Brown, B. Mann, N. Ryder, M. Subbiah, J. D. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askellet al., Advances in neural information processing systems, 2020, vol. 33, pp. 1877–1901 Search PubMed.
- A. Ramesh, P. Dhariwal, A. Nichol, C. Chu and M. Chen, arXiv, 2022, preprint, arXiv:2204.06125. DOI:10.48550/arXiv.2204.06125.
- R. Gal, Y. Alaluf, Y. Atzmon, O. Patashnik, A. H. Bermano, G. Chechik and D. Cohen-Or, arXiv, 2022, preprint, arXiv:2208.01618, DOI:10.48550/arXiv.2208.01618.
- F. Noé, A. Tkatchenko, K. Müller and C. Clementi, Annu. Rev. Phys. Chem., 2020, 71, 361–390 CrossRef PubMed.
- Y. Cooper, arXiv, 2018, preprint, arXiv:1804.10200, DOI:10.48550/arXiv.1804.10200.
- Y. Zhang, P. Tiňo, A. Leonardis and K. Tang, IEEE Transactions on Emerging Topics in Computational Intelligence, 2021 Search PubMed.
- Q. Zhang and S. Zhu, Front. Inf. Technol. Electron. Eng., 2018, 19, 27–39 CrossRef.
- L. H. Gilpin, D. Bau, B. Z. Yuan, A. Bajwa, M. Specter and L. Kagal, 2018 IEEE 5th International Conference on data science and advanced analytics, DSAA, 2018, pp. 80–89 Search PubMed.
- Z. C. Lipton, Queue, 2018, 16, 31–57 CrossRef.
- A. J. Ballard, R. Das, S. Martiniani, D. Mehta, L. Sagun, J. D. Stevenson and D. J. Wales, Phys. Chem. Chem. Phys., 2017, 19, 12585–12603 RSC.
- M. P. Niroomand, C. T. Cafolla, J. W. R. Morgan and D. J. Wales, Mach. Learn.: Sci. Technol., 2022, 3, 015019 Search PubMed.
- S. R. Chitturi, P. C. Verpoort and D. J. Wales, et al. , Mach. Learn.: Sci. Technol., 2020, 1, 023002 Search PubMed.
- M. V. Narkhede, P. P. Bartakke and M. S. Sutaone, Artif. Intell. Rev., 2022, 55, 291–322 CrossRef.
- F. Draxler, K. Veschgini, M. Salmhofer and F. Hamprecht, International conference on machine learning, 2018, pp. 1309–1318 Search PubMed.
- B. Neyshabur, S. Bhojanapalli, D. McAllester and N. Srebro, Advances in neural information processing systems, 2017, vol. 30 Search PubMed.
- I. J. Goodfellow, O. Vinyals and A. M. Saxe, arXiv, 2014, preprint, arXiv:1412.6544, DOI:10.48550/arXiv.1412.6544.
- J. Lucas, J. Bae, M. R. Zhang, S. Fort, R. Zemel and R. Grosse, arXiv, 2021, preprint, arXiv:2104.11044, DOI:10.48550/arXiv.2104.11044.
- J. Frankle, arXiv, 2020, preprint, arXiv:2012.06898, DOI:10.48550/arXiv.2012.06898.
- T. J. Vlaar and J. Frankle, International Conference on Machine Learning, 2022, pp. 22325–22341 Search PubMed.
- S. Du, J. Lee, H. Li, L. Wang and X. Zhai, International conference on machine learning, 2019, pp. 1675–1685 Search PubMed.
- P. C. Verpoort, A. A. Lee and D. J. Wales, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21857–21864 CrossRef CAS PubMed.
- L. Dicks and D. J. Wales, J. Chem. Phys., 2022, 156, 054109 CrossRef CAS PubMed.
- M. Chouza, S. Roberts and S. Zohren, arXiv, 2018, preprint, arXiv:1803.09119, DOI:10.48550/arXiv.1803.09119.
- C. E. Rasmussen, Summer school on machine learning, 2003, pp. 63–71 Search PubMed.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12576 CrossRef CAS PubMed.
- G. M. Torrie and J. P. Valleau, Chem. Phys. Lett., 1974, 28, 578 CrossRef CAS.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141 CrossRef CAS.
- J. Hénin, T. Leliévre, M. R. Shirts, O. Valsson and L. Delemotte, Living J. Comput. Mol. Sci., 2022, 4, 1583 Search PubMed.
- Z. Li and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 6611–6615 CrossRef CAS PubMed.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111 CrossRef CAS.
- D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368–1372 CrossRef CAS PubMed.
- E. S. Henault, M. H. Rasmussen and J. H. Jensen, ChemRxiv, 2020 DOI:10.26434/chemrxiv.12152661.v1.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens.Matter, 2011, 23, 053201 CrossRef PubMed.
- D. Arthur and S. Vassilvitskii, Proc. of the 18th Ann. ACM-SIAM Symp. on Discrete Algorithms, 2007, pp. 1027–1035 Search PubMed.
- A. H. Mohammad, C. Vineed, S. Saeed and J. Z. Mohammed, Pattern Recognit. Lett., 2009, 30, 994–1002 CrossRef.
- O. Bachem, M. Lucic, S. H. Hassani and A. Krause, Proc. of the 30th Int. Conf. on Neural Information Processing Systems, 2016, pp. 55–63 Search PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning, MIT Press, 2005 Search PubMed.
- D. C. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528 CrossRef.
- J. Nocedal, Math. Comput., 1980, 35, 773–782 CrossRef.
- C. G. Broyden, J. Inst. Math. Its Appl., 1970, 6, 76–90 CrossRef.
- R. Fletcher, Comput. J., 1970, 13, 317–322 CrossRef.
- D. Goldfarb, Math. Comput., 1970, 24, 23–26 CrossRef.
- D. F. Shanno, Math. Comput., 1970, 24, 647–656 CrossRef.
- R. H. Byrd, P. Lu, J. Nocedal and C. Zhu, SIAM J. Sci. Comput., 1995, 16, 1190–1208 CrossRef.
- C. Zhu, R. H. Byrd, P. Lu and J. Nocedal, ACM Trans. Math. Softw., 1997, 23, 550–560 CrossRef.
- K. A. Wang, G. Pleiss, J. R. Gardner, S. Tyree, K. Q. Weinberger and A. G. Wilson, NeurIPS, 2019 Search PubMed.
- J. Wenger, G. Pleiss, P. Hennig, J. Cunningham and J. Gardner, Proc. Mach. Learn. Res., 2022, 162, 23751–23780 Search PubMed.
- D. P. Kingma and J. L. Ba, 2015, preprint, arxiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- L. Bottou, F. E. Curtis and J. Nocedal, SIAM Rev., 2018, 60, 1 CrossRef.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- S. A. Trygubenko and D. J. Wales, J. Chem. Phys., 2004, 120, 2082–2094 CrossRef CAS PubMed.
- D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 134106 CrossRef PubMed.
- G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- H. Jónsson, G. Mills and K. W. Jacobsen, Classical and quantum dynamics in condensed phase simulations, World Scientific, Singapore, 1998, ch. 16, pp. 385–404 Search PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- L. J. Munro and D. J. Wales, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 3969–3980 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- Y. Kumeda, L. J. Munro and D. J. Wales, Chem. Phys. Lett., 2001, 341, 185–194 CrossRef CAS.
- GMIN: A program for basin-hopping global optimisation, basin-sampling, and parallel tempering, http://www-wales.ch.cam.ac.uk/software.html Search PubMed.
- OPTIM: A program for geometry optimisation and pathway calculations, http://www-wales.ch.cam.ac.uk/software.html Search PubMed.
- PATHSAMPLE: A program for generating connected stationary point databases and extracting global kinetics, http://www-wales.ch.cam.ac.uk/software.html Search PubMed.
- pylfl: A Python package to survey LFLs in ML models Search PubMed.
- G. C. Cawley and N. L. C. Talbot, J. Mach. Learn. Res., 2007, 8, 841–861 Search PubMed.
- J. Chen, K. de Hoogh, J. Gulliver, B. Hoffmann, O. Hertel, M. Ketzel, M. Bauwelinck, A. Van Donkelaar, U. A. Hvidtfeldt and K. Katsouyanni, et al. , Environ. Int., 2019, 130, 104934 CrossRef CAS PubMed.
- V. K. De Souza, J. D. Stevenson, S. P. Niblett, J. D. Farrell and D. J. Wales, J. Chem. Phys., 2017, 146, 124103 CrossRef CAS PubMed.
- C. E. Shannon, Bell Syst. Tech. J., 1948, 27, 379–423 CrossRef.
- D. J. Wales, Phys. Rev. E, 2017, 95, 030105 CrossRef PubMed.
- A. V. Bradley, C. A. Gomez-Uribe and M. R. Vuyyuru, Mach. Learn.: Sci. Technol., 2022, 3, 045002 Search PubMed.
- M. P. Niroomand, J. W. R. Morgan, C. T. Cafolla and D. J. Wales, Mach. Learn.: Sci. Technol., 2022, 3, 025004 Search PubMed.
- D. J. Wales, Int. Rev. Phys. Chem., 2006, 25, 237–282 Search PubMed.
- F. Noé and S. Fischer, Curr. Opin. Struct. Biol., 2008, 18, 154–162 CrossRef PubMed.
- J. M. Carr and D. J. Wales, Phys. Chem. Chem. Phys., 2009, 11, 3341–3354 RSC.
- D. Prada-Gracia, J. Gómez-Gardenes, P. Echenique and F. Falo, PLoS Comput. Biol., 2009, 5, e1000415 CrossRef PubMed.
- C. P. Massen and J. P. K. Doye, Phys. Rev. E, 2005, 71, 046101 CrossRef PubMed.
- D. Kannan, D. J. Sharpe, T. D. Swinburne and D. J. Wales, J. Chem. Phys., 2020, 153, 244108 CrossRef CAS PubMed.
- J. P. Doye and C. P. Massen, J. Chem. Phys., 2005, 122, 084105 CrossRef PubMed.
- J. P. K. Doye and C. P. Massen, arXiv, 2007, preprint, arxiv:cond-mat/0612150, DOI:10.48550/arXiv.cond-mat/0612150.
- J. W. R. Morgan, D. Mehta and D. J. Wales, Phys. Chem. Chem. Phys., 2017, 19, 25498–25508 RSC.
- H. Eyring, Chem. Rev., 1935, 17, 65 CrossRef CAS.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875 RSC.
- S. A. Trygubenko and D. J. Wales, Mol. Phys., 2006, 104, 1497–1507 CrossRef CAS.
- S. A. Trygubenko and D. J. Wales, J. Chem. Phys., 2006, 124, 234110 CrossRef PubMed.
- A. Banerjee and D. J. Wales, Phys. Condens. Matter., 2021, 34, 034004 CrossRef PubMed.
- D. J. Sharpe and D. J. Wales, J. Chem. Phys., 2020, 153, 024121 CrossRef CAS PubMed.
- D. J. Wales, J. Phys. Chem. Lett., 2022, 13, 6349–6358 CrossRef CAS PubMed.
- D. J. Sharpe and D. J. Wales, J. Chem. Phys., 2021, 155, 140901 CrossRef CAS PubMed.
- P. G. Mezey, Potential Energy Hypersurfaces, Elsevier, Amsterdam, 1987 Search PubMed.
- S. Raschka, arXiv, 2018, preprint, arXiv:1811.12808, DOI:10.48550/arXiv.1811.12808.
- P. Chaudhari, A. Choromanska, S. Soatto, Y. LeCun, C. Baldassi, C. Borgs, J. Chayes, L. Sagun and R. Zecchina, J. Stat. Mech.: Theory Exp., 2019, 2019, 124018 CrossRef.
- P. Foret, A. Kleiner, H. Mobahi and B. Neyshabur, arXiv, 2020, preprint, arXiv:2010.01412, DOI:10.48550/arXiv.2010.01412.
- M. Andriushchenko and N. Flammarion, International Conference on Machine Learning, 2022, pp. 639–668 Search PubMed.
- F. H. Stillinger and T. A. Weber, J. Stat. Phys., 1988, 52, 1429–1445 CrossRef.
- S. Hochreiter and J. Schmidhuber, Neural Comput., 1997, 9, 1–42 CrossRef CAS PubMed.
- G. E. Hinton and D. Van Camp, Proceedings of the sixth annual conference on Computational learning theory, 1993, pp. 5–13 Search PubMed.
- Y. Zhang, A. M. Saxe, M. S. Advani and A. A. Lee, Mol. Phys., 2018, 116, 3214–3223 CrossRef CAS.
- Y. Yang, C. Rashtchian, H. Zhang, R. R. Salakhutdinov and K. Chaudhuri, Advances in neural information processing systems, 2020, vol. 33, pp. 8588–8601 Search PubMed.
- M. S. Pepe, T. Cai and G. Longton, Biometrics, 2006, 62, 221–229 CrossRef PubMed.
- S. Hashem, Neural Networks, 1997, 10, 599–614 CrossRef PubMed.
- H. Jin and Y. Lu, Stat. Probab. Lett., 2009, 79, 2321–2327 CrossRef PubMed.
- L. Breiman, Mach. Learn., 1996, 24, 123–140 Search PubMed.
- J. Azimi, A. Fern and X. Fern, Advances in Neural Information Processing Systems, 2010, vol. 23 Search PubMed.
- J. Gonazález, Z. Dai, P. Hennig and N. Lawrence, Artificial Intell. Stat., 2016, pp. 648–657 Search PubMed.
- M. Groves and E. O. Pyzer-Knapp, arXiv, 2018, preprint, arXiv:1806.01159v2, DOI:10.48550/arXiv.1806.01159.
- J. Wilson, V. Borovitskiy, A. Terenin, P. Mostowsky and M. Deisenroth, Int. Conf. Mach. Learn., 2020, pp. 10292–10302 Search PubMed.
- M. Adachi, S. Kayakawa, S. Hamid, M. J. rgensen, H. Oberhauser and M. A. Obsourne, arXiv, 2023, preprint, arxiv:2301.11832, DOI:10.48550/arXiv.2301.11832.
- M. Galar, A. Fernandez, E. Barrenechea, H. Bustince and F. Herrera, IEEE Trans. Syst. Man Cybern.: Syst. C, 2011, 42, 463–484 Search PubMed.
- M. Zhang, Pattern Recognit., 2022, 124, 108428 CrossRef.
- D. Alvarez-Melis and T. S. Jaakkola, arXiv, 2018, preprint, arXiv:1806.08049, DOI:10.48550/arXiv.1806.08049.
- S. Srinivas and F. Fleuret, arXiv, 2020, preprint, arXiv:2006.09128, DOI:10.48550/arXiv.2006.09128.
- K. Röder, G. Stirnemann, A. Dock-Bregeon, D. J. Wales and S. Pasquali, Nucleic Acids Res., 2019, 373–389 Search PubMed.
- K. Röder and D. J. Wales, Front. Mol. Biosci., 2022, 9, 820792 CrossRef PubMed.
- M. P. Niroomand and D. J. Wales, ICLR 2023 Workshop on Physics for Machine Learning, 2023 Search PubMed.
- J. C. Dunn, J. Cybersecur., 1974, 4, 95–104 Search PubMed.
- D. L. Davies and D. W. Bouldin, IEEE Trans. Pattern Anal. Mach. Intell., 1979, 1, 224–227 CAS.
- P. J. Rousseeuw, Comput. Appl. Math., 1987, 20, 53–65 CrossRef.
- R. Tibshirani, G. Walther and T. Hastie, J. R. Stat. Soc. Ser. B Methodol., 2001, 63, 411–423 CrossRef.
- E. Schubert, arXiv, 2023, preprint, arxiv:2212.12189, DOI:10.48550/arXiv.2212.12189.
- Y. Wu, L. Dicks and D. J. Wales, arXiv, 2023, preprint, arxiv:2305.17279, DOI:10.48550/arXiv.2305.17279.
- A. Svensson, J. Dahlin and T. B. Schön, 2015 IEEE 6th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, CAMSAP, 2015, pp. 477–480 Search PubMed.
- R. M. Neal, arXiv, 1997, preprint, arxiv:physics/9701026, DOI:10.48550/arXiv.physics/9701026.
- C. K. Williams and C. E. Rasmussen, Neural Information Processing Systems, NIPS, 1996 Search PubMed.
- A. Garbuno-Inigo, F. A. DiazDelaO and K. Zuev, Comput. Stat. Data Anal., 2016, 103, 367–383 CrossRef.
- P. Del Moral, A. Doucet and A. Jasra, J. R. Stat. Soc. Ser. B Methodol., 2006, 68, 411–436 CrossRef.
- M. A. Osborne, S. J. Roberts, A. Rogers, S. D. Ramchurn and N. R. Jennings, 2008 International Conference on Information Processing in Sensor Networks (ipsn 2008), 2008, pp. 109–120 Search PubMed.
- Y. Saatçi, R. D. Turner and C. E. Rasmussen, ICML-10, 2010, pp. 927–934 Search PubMed.
- D. K. Agarwal and A. E. Gelfand, Stat. Comput., 2005, 15, 61–69 CrossRef.
- D. Petelin, M. Gasperin and V. Smídl, IFAC Proc. Vol., 2014, 47, 5011–5016 CrossRef.
- J. M. Hernández-Lobato, M. W. Hoffman and Z. Ghahramani, Advances in neural information processing systems, 2014, vol. 27 Search PubMed.
- G. D. Ath, R. M. Everson and J. E. Fieldsend, Proc. Genetic. Evol. Comput. Conf. Companion, 2021, pp. 1860–1869 Search PubMed.
- Y. Saikai, arXiv, 2022, preprint, arxiv:2208.13960, DOI:10.48550/arXiv.2208.13960.
- V. Lalchand and C. E. Rasmussen, Proc. Mach. Learn. Res., 2020, 1–12 Search PubMed.
- F. Leibfried, V. Dutordoir, S. T. John and N. Durrange, arXiv, 2020, preprint, arxiv:2012.13962, DOI:10.48550/arXiv.2012.13962.
| This journal is © The Royal Society of Chemistry 2024 |