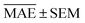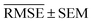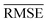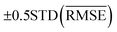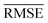Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spectroscopic constants from atomic properties: a machine learning approach
Mahmoud A. E.
Ibrahim
abc,
X.
Liu
 d and
J.
Pérez-Ríos
d and
J.
Pérez-Ríos
 *ab
*ab
aDepartment of Physics and Astronomy, Stony Brook University, Stony Brook, New York 11794, USA. E-mail: jesus.perezrios@stonybrook.edu
bInstitute for Advanced Computational Science, Stony Brook University, Stony Brook, New York 11794, USA
cDepartment of Physics, Faculty of Science, Assiut University, Assiut, 71515, Egypt
dFritz-Haber-Institut der Max-Planck-Gesellschaft, D-14195 Berlin, Germany
First published on 6th November 2023
Abstract
We present a machine-learning approach toward predicting spectroscopic constants based on atomic properties. After collecting spectroscopic information on diatomics and generating an extensive database, we employ Gaussian process regression to identify the most efficient characterization of molecules to predict the equilibrium distance, vibrational harmonic frequency, and dissociation energy. As a result, we show that it is possible to predict the equilibrium distance with an absolute error of 0.04 Å and vibrational harmonic frequency with an absolute error of 36 cm−1, including only atomic properties. These results can be improved by including prior information on molecular properties leading to an absolute error of 0.02 Å and 28 cm−1 for the equilibrium distance and vibrational harmonic frequency, respectively. In contrast, the dissociation energy is predicted with an absolute error ≲0.4 eV. Alongside these results, we prove that it is possible to predict spectroscopic constants of homonuclear molecules from the atomic and molecular properties of heteronuclears. Finally, based on our results, we present a new way to classify diatomic molecules beyond chemical bond properties.
1 Introduction
Since the beginning of molecular spectroscopy in the 1920s, the relationship between spectroscopic constants of diatomic molecules has been an intriguing and captivating matter in chemical physics. Following early attempts by Kratzer, Birge and Mecke,1–3 Morse proposed a relationship between the equilibrium distance, Re, and the harmonic vibrational frequency, ωe, as R3eωe = γ, where γ is a constant, after analyzing the spectral properties of 16 diatomic molecules.4 However, as more spectroscopic data became available, further examination of the Morse relation revealed its applicability to only a tiny number of diatomic molecules.5 Next, in a series of papers, Clark et al. generalized Morse's idea via the concept of a periodic table of diatomic molecules. Eventually, Clark's efforts translated into several relations, each limited to specific classes of molecules.5–8 Simultaneously, Badger proposed a more neat relationship, including atomic properties of the atoms constituting the molecule.9 Following Badger's proposal, multiple authors have found new relations, which have seen some utility even for polyatomic molecules.10–12 Nevertheless, Badger's relations are not generalizable to all diatomic molecules.13–15 In general, several empirical relationships between Re and ωe were proposed in the 1930s and the 1940s.7,8,16–25 In summary, from 1920 till now, the number of empirical relations published is around 70 collected by Kraka et al.10 Most of these empirical relations were tested by several authors, finding some constraints on their applicability.10,13–15,26 However, all of these relationships were based on empirical evidence rather than on a given physical or chemical principle.On the other hand, in 1939 Newing proposed a theoretical justification for observed empirical relationships between spectroscopic constants given by
| cf(Re) = μωe2 | (1) |
In the 1960s and 1970s, a number of authors devised the virial theorem, perturbation theory, and Helmann–Feynman theorem29–32 to develop a better understanding of the nature of the relationship between Re and ωevia electron densities.33–40 Most notably, Anderson and Parr were able to establish a relationship between Re, ωe, and atomic numbers Z1 and Z2, as
 | (2) |
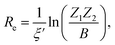 | (3) |
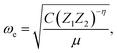 | (4) |
Alongside these developments, several authors attempted connecting the dissociation energy, D00, with ωe and Re of diatomic molecules.19,41–45 However, these received little attention due to the lack of reliable experimental data.9,41,46–48 Most of the relationships are given by
| D00 = A′μωe2Rel | (5) |
Thanks to machine learning (ML) techniques and the development of extensive spectroscopic databases,49 it has been possible to study the relationship between spectroscopic constants from a heuristic perspective, i.e., from a data-driven approach,26 find optimal potentials based on spectroscopy data50 and to improve ab initio potentials to match experimental observations.51 In particular, Gaussian process regression (GPR) models have been used on a large dataset of 256 heteronuclear diatomic molecules. As a result, it was possible to predict Re from the atomic properties of the constituent atoms. Similarly, ωe and the binding energy D00 were predicted using combinations of atomic and molecular properties. However, the work of Liu et al. only studied heteronuclear molecules. Hence, the universality of the relationship between spectroscopic constants still needs to be revised. On the other hand, ML techniques can be used to boost density functional theory approaches to larger systems with low computational costs.52–55 Hence, ML techniques are used to enlarge the capabilities of quantum chemistry methods. However, if sufficient data and information are available, could ML substitute quantum chemistry methods?
In this work, we present a novel study on the relationship between spectroscopic constants via ML models, including homonuclear molecules in a dataset of 339 molecules: the largest dataset of diatomics ever used. As a result, first, we show that it is possible to predict Re and ωe with mean absolute errors ∼0.026 Å and ∼26 cm−1, leading to an improvement of factor 2 in predicted power and accuracy concerning previous ML models. Furthermore, the dissociation energy, D00, is predicted with a mean absolute error ∼0.4 eV, in accordance with previous ML models. However, our model can benefit from having a more accurate and extensive database. Second, we show that it is possible to accurately predict the molecular properties of homonuclear molecules out of heteronuclear ones. Finally, since we use the same ML model in this work, we are in a unique situation to define similarity among molecules. Thus, we propose a data-driven classification of molecules. The paper is organized as follows: in Section 2, we introduce the database and analyze the main properties; in Section 3, we present the ML models with a particular emphasis on Gaussian process regression; in Section 4, we present our results and in Section 5, the conclusions.
2 The data set
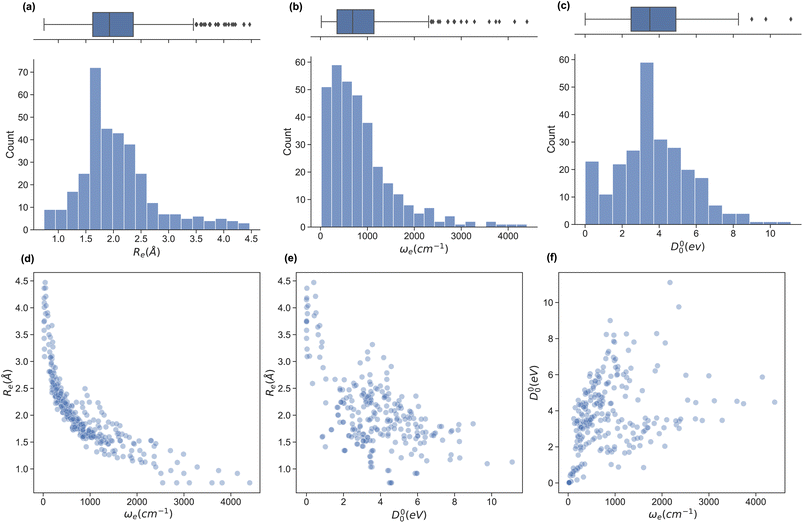
In this work, we extend the data set by Liu et al.26,49 by adding the ground state spectroscopic constants of 32 homonuclear and 54 extra heteronuclear diatomic molecules from ref. 56–127. The dataset counts 338 entries based on experimentally determined spectroscopic constants: Re is available for 338, ωe for 327, and D00 is available for 250 molecules.To assess the variation of the spectroscopic constants in the dataset, we display the histogram and box plots of Re, ωe, and D00 in Fig. 1. This Figure shows that the spectroscopic constants' histogram is nearly unimodal. However, Re and ωe show a heavy-tailed distribution. In the case of Re, the tail is due to the presence of van der Waals molecules. In contrast, light molecules are responsible for the tail in the histogram for ωe. On the other hand, the box plot of D00 shows almost no outliers and only an incipient peak for a molecule with binding energy smaller than 0.75 eV due to the presence of van der Waals molecules. On the other hand, we investigate the relationship between pairs of spectroscopic constants in panels (d)–(f) of Fig. 1. For example, panel (d) displays Reversus ωe, showing an exponential trend similar to the one suggested by eqn (2) or a power law (Morse relationship). On the contrary, by plotting Reversus D00 and D00versus ωe in panels (e) and (f), respectively, we notice a large dispersion of the points with no observed trends in both panels.
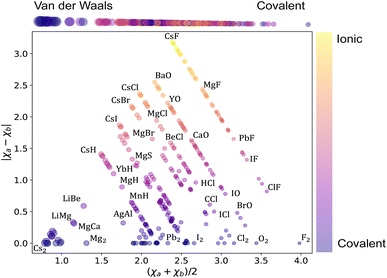
Next, we analyze the chemical properties of the molecules under consideration, employing the Arkel–Ketelaar triangle – also known as the Jensen triangle, which separates qualitatively covalent, ionic, and van der Waals molecules. The triangle plots the absolute value of the electronegativity difference between the constituent atoms |χa − χb| versus their average electronegativity, as shown in Fig. 2, where χa and χb denote the electronegativities of the molecules' constituent atoms. The average electronegativity of the constituent atoms on the x-axis quantifies the van der Waals-covalent bonding. On the contrary, the difference in electronegativity of the constituent atoms quantifies the ionic character on the y-axis. The triangle shows that the data set comprises chemically diverse diatomic molecules with bonding characters ranging from covalent to ionic with many van der Waals. This chemical diversity strongly manifests itself in the range of the ground state spectroscopic constants depicted in Fig. 1.
3 The machine learning (ML) model
Machine learning (ML) is a vast discipline that utilizes data-driven algorithms to perform specific tasks (e.g., classification, regression, clustering). Among the different ML techniques, in this work, we use Gaussian process regression (GPR), which is especially suitable for small datasets. This section briefly describes GPR and our methods to generate and evaluate models.3.1 Gaussian process regression
We define our data set D = {(xi, yi)|i = 1,⋯, n}, where xi is a feature vector of some dimension D associated with the i-th element of the dataset, yi is a scalar target label, and n is the number of observations, i.e., the number of elements in the dataset. The set of all feature vectors and corresponding labels can be grouped in the random variables X and y, respectively, where X = (x1,⋯, xn) and y = (y1,⋯, yn). Here, y consists of values of molecular properties to be learned. yi is Re, ωe, or D00 of the i-th molecule, whereas xi is a vector containing atomic or molecular properties of the same molecule.We are interested in mapping features to target labels via a regression model yi = f(xi) + εi, where f(xi) is the regression function, and εi is an additive noise. We further assume that εi follows an independent, identically distributed (i.i.d.) Gaussian distribution with variance σn2
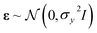 | (6) |
One approach to tackle the regression problem is to specify a functional form of f(xi). Then, set the free parameters of the regression model by fitting the data. Alternatively, one can disregard specifying a functional form of f(xi) but instead place a prior distribution over a space of functions and infer the posterior predictive distribution following a Bayesian non-parametric approach. Within this group of methods, we find Gaussian process regression (GPR), assuming a Gaussian process prior 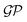 over the space of functions.128,129
over the space of functions.128,129
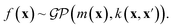 | (7) |
A Gaussian process is a collection of random variables, any finite number of which have a joint Gaussian distribution. A Gaussian process is specified by a mean function m(x) and a covariance function (kernel) k(x, x′), we will describe both shortly. A posterior distribution of the value of f(x*) at some point of interest, x*, is determined through the Bayes theorem as
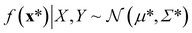 | (8) |
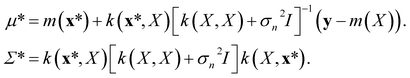 | (9) |
The mean of the resulting predictive posterior distribution, μ*, is used to obtain a point estimate of the value of f(x*), and its covariance Σ* provides a confidence interval.
In GPR, the regression model is completely specified by the kernel k(x, x′). The kernel is a similarity measure that specifies the correlation between a pair of values f(x) and f(x′) by only using the distance between a pair of feature vectors x and x′ as its input variable. Specifying a kernel, we encode high-level structural assumptions (e.g., smoothness, periodicity, etc.) about the regression function. Here, we focus on the Matérn class kernel given by given by
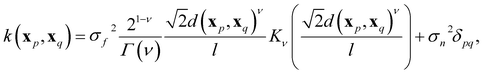 | (10) |
We can encode a physical model via the relationships between spectroscopic constants by specifying the Gaussian process prior mean function m(x). A common choice of the prior mean function is m(x) = 0. This choice is satisfactory in most cases, especially in interpolation tasks. However, selecting an appropriate prior mean function can simplify the learning process (delivering better results using fewer data). The mean function can also guide the model for better predictions as k(xp, xq) → 0; this is necessary for extrapolation and interpolation among sparse data points. Further, a model with a specified mean function is more interpretable.
3.2 Model development and performance evaluation
Its parameters and hyperparameters characterize a GPR model. Parameters involve (σn, l, σf) of eqn (10) plus additional parameters depending on the form of the prior mean function. On the contrary, hyperparameters involve selecting features, the form of the prior mean function, and the order ν of the Matérn kernel. To determine the parameters and the hyperparameters, we divide the dataset D into two subsets: Dtv and Dtest. First, Dtv is used for the training and validation stage, in which we determine the model's hyperparameters. Then, Dtest, known as the test set, is left out for model final testing and evaluation and does not take any part in determining the parameters nor the hyperparameters of the model.To design a model, we choose an X suitable to learn y through a GPR. We then choose a convenient prior mean function m(X) based on physical intuition, alongside the last hyperparameter ν ∈ {1/2, 3/2, 5/2, ∞} is determined by running four models, each with a possible value of ν, and we chose the one that performs the best on the training data to be the final model. Precisely, a cross-validation (CV) scheme is used to evaluate the performance of each model iteratively: we split Dtv into a training set Dtrain (∼90% of Dtv) and a validation set Dvalid. We use Dtrain to fit the model and determine its parameters by maximizing the log-marginal likelihood. The fitted model is then used to predict the target labels of Dvalid. We repeat the process with a different split in each iteration such that each element in Dtv has been sampled at least once in both Dtrain and Dvalid. After many iterations, we can determine the average performance of the model. We compare the average performance of the four models after the CV process. Finally, We determine the value of ν to be its value for the best-performing model.
We adopt a Monte Carlo (MC) splitting scheme to generate the CV splits. Using the MC splitting scheme, we expose the models to various data compositions, and thus, we can make more confident judgments about our models' performance and generality.26 To generate a single split, we use stratified sampling.129,130 First, we stratify the training set into smaller strata based on the target label. Stratification will be such that molecules in each stratum have values within some lower and upper bounds of the target label (spectroscopic constant) of interest. Then, we sample the validation set so that each stratum is represented. Stratified sampling minimizes the change in the proportions of the data set composition upon MC splitting, ensuring that the trained model can make predictions over the full range of the target variable. Using the Monte Carlo splitting scheme with cross-validation (MC-CV) allows our models to train on Dtv in full, as well as make predictions for each molecule in Dtv. In each iteration, Dvalid simulates the testing set; thus, by the end of the MC-CV process, it provides an evaluation of the model performance against ∼90% of the molecules in the data set before the final testing stage.
We use 1000 MC-CV iterations to evaluate each model's performance. Two estimators evaluate the models' performance at each iteration, the mean absolute error (MAE) and the root mean squared error (RMSE), given by
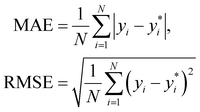 | (11) |
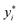 and yi are the true and predicted values, respectively, and N is the number of observations in consideration. We report the final training/validation
and yi are the true and predicted values, respectively, and N is the number of observations in consideration. We report the final training/validation 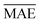 and
and 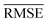 with the sample standard deviation (STD) and the standard error of the means (SEM) given by
with the sample standard deviation (STD) and the standard error of the means (SEM) given by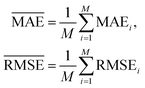 | (12) |
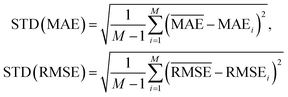 | (13) |
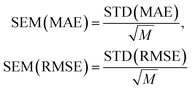 | (14) |
We use learning curves to evaluate the performance of the models as a function of the size of Dtrain. We use 500 CV splits at each training set size to generate the learning curves. The validation and training 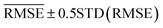 are plotted as a function of the size of Dtrain.
are plotted as a function of the size of Dtrain.
Models that have the lowest validation 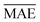 ,
, 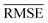 , and SEM are elected for the testing stage. In the testing stage, we fit the models to Dtv and make predictions of the target labels of Dtest. Finally, we report the validation
, and SEM are elected for the testing stage. In the testing stage, we fit the models to Dtv and make predictions of the target labels of Dtest. Finally, we report the validation 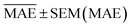 and
and 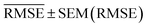 and test MAE and RMSE as our final evaluation of the model.
and test MAE and RMSE as our final evaluation of the model.
4 Results and discussion
We have developed seven new models to predict Re, ωe, and D00: r2, r3, and r4 to predict Re, models for predicting ωe are denoted w2, w3, and w4, while only one model is used to predict D00, labeled as d1. In addition, we implemented two of the best-performing models of Liu et al.26 (denoted r1 and w1) using our updated dataset and compared them with our models. All models are divided into three categories: (i) r1, r2, and w2 only employ atomic properties as features in the kernel and as variables in the prior mean function, (ii) r3 and w3 employ atomic properties as features in the kernel but use spectroscopic data in the prior mean function, and (iii) r4, w4, and d1 include spectroscopic data both in the kernel and the prior mean function.In all the seven newly developed models, we use the groups g1 and g2 and periods p1 and p2 of the molecules' constituent atoms and the square root of the reduced mass of the molecule μ1/2 as features. Therefore, the set of properties {p1, g1, p2, g2, μ1/2} uniquely defines each molecule in the dataset. On the contrary, additional spectroscopic properties are added to these five features for models within the category (iii). Furthermore, we choose the models' features and prior mean functions using physical intuition based on the discussion in the introduction and observations from the data Fig. 1, and ν was set to 3/2 using the CV scheme discussed in the last section. The models' characteristics are given in Table 1.
| Target | Model | Molecules | Features | Prior mean | ν |
|---|---|---|---|---|---|
| R e (Å) | rlr1 | 314 | p1 + p2, g1 + g2, ln(Z1Z2) | — | — |
| rlr2 | 308 | ln(ωe), p1 + p2, g1 + g2, ln(Z1Z2), ln(μ) | — | — | |
| svmr1 | 314 | p1, g1, p2, g2 | — | 3/2 | |
| svmr2 | 314 | p1, g1, p2, g2, μ1/2 | — | 3/2 | |
| svmr3 | 308 | ln(ωe), p1, g1, p2, g2, μ1/2 | — | 3/2 | |
| r1 | 314 | p1, g1, p2, g2 | m r1 | 1/2 | |
| r2 | 314 | p1, g1, p2, g2, μ1/2 | m r2 | 3/2 | |
| r3 | 308 | p1, g1, p2, g2, μ1/2 | m r3 | 3/2 | |
| r4 | 308 | ln(ωe), p1, g1, p2, g2, μ1/2 | m r3 | 3/2 | |
| ln(ωe) | wlr1 | 308 | p1 + p2, g1 + g2, ln(Z1Z2), ln(μ) | — | — |
| wlr2 | 308 | R e, p1 + p2, g1 + g2, ln(Z1Z2), ln(μ) | — | — | |
| svmw1 | 308 | p1, g1, p2, g2, μ1/2 | — | 3/2 | |
| svmw2 | 308 | R e, p1, g1, p2, g2, μ1/2 | — | 3/2 | |
| w1 | 308 | R e −1, p1, giso1, p2, giso2, ḡ | 0 | 5/2 | |
| w2 | 308 | p1, g1, p2, g2, μ1/2 | m w2 | 3/2 | |
| w3 | 308 | p1, g1, p2, g2, μ1/2 | m w3 | 3/2 | |
| w4 | 308 | R e, p1, g1, p2, g2, μ1/2 | m w4 | 3/2 | |
| ln(D00) | dlr1 | 244 ln(Re), ln(ωe), p1 + p2, g1 + g2, ln(μ) | — | — | |
| svmd1 | 244 | p1, g1, p2, g2 | — | 3/2 | |
| d1 | 244 | p1, g1, p2, g2, μ1/2 | m d1 | 3/2 |
For all the nine implemented models, we permute the groups and periods in Dtrain in the training and validation stage and in Dtv in the testing stage to impose permutational invariance.26 That is, the models should not differentiate between x = (p1, g1, p2, g2,…) and x′ = (p2, g2, p1, g1,…) upon exchanging the numbering of the two atoms in a molecule. Eight of the models use linear prior mean functions, the linear coefficients of which are determined by fitting the linear model to Dtrain in each CV iteration in the training and validation stage and by fitting to Dtv in the testing stage.
For the sake of comparison with baseline ML models we have implemented linear regression (LR) models based on eqn (3)–(5). Specifically, models rlr1 and rlr2 to predict Re, wlr1 and wlr2 to predict ln(ωe) and dlr1 to predict ln(D00). The same MC-CV scheme used to train the GPR models was used to train the LR models. Further, we train support vector machines (SVM) models for regressions tasks to predict Re, ωe and D00. The hyperparameters of the Matern 3/2 kernels for each SVM model are tuned via 1000 MC-CV steps using Bayesian optimization.131 A description of these models is given in Table 1 and a statistical summary of their performance is given in Table 2.
| Target | Model | Validation | Validation | Test MAE | Test RMSE |
|---|---|---|---|---|---|
| R e (Å) | rlr1 | 0.33 | 0.54 | — | — |
| rlr2 | 0.112 | 0.146 | — | — | |
| svmr1 | 0.043 | 0.069 | 0.044 | 0.068 | |
| svmr2 | 0.039 | 0.059 | 0.046 | 0.068 | |
| svmr3 | 0.025 | 0.038 | 0.025 | 0.037 | |
| r1 | 0.060* | 0.100* | 0.047 | 0.070 | |
| r2 | 0.041* | 0.060* | 0.046 | 0.066 | |
| r3 | 0.027* | 0.039* | 0.027 | 0.038 | |
| r4 | 0.026* | 0.038* | 0.027 | 0.040 | |
| ω e (cm−1) | wlr1 | 218 | 316 | — | — |
| wlr2 | 118 | 197 | — | — | |
| svmw1 | 39.4 | 65.2 | 36.4 | 53.7 | |
| svmw2 | 25.8 | 42.3 | 24.7 | 31.8 | |
| w1 | 33.2 ± 0.3 | 64.8 ± 1.0 | 33.5 | 61.2 | |
| w2 | 40.3 ± 0.3 | 66.3 ± 0.6 | 37.9 | 53.4 | |
| w3 | 27.7 ± 0.2 | 44.8 ± 0.4 31.3 | 39.35 | ||
| w4 | 25.9 ± 0.2 | 41.6 ± 0.3 | 26.9 | 33.6 | |
| D 00 (eV) | dlr1 | 0.98 | 1.25 | — | — |
| svmd1 | 0.36 | 0.57 | 0.79 | 0.83 | |
| d1 | 0.37 ± 0.002 | 0.52 ± 0.003 | 0.55 | 0.72 |
4.1 R e
The first spectroscopic constant under consideration is the equilibrium distance, Re. We have implemented and developed two models for predicting Re using only atomic properties: r1 and r2, as detailed in Table 1. Model r1 is the same as in Liu et al.26 using groups and periods of the constituent atoms as features. The model r2 requires an extra feature related to the reduced mass of the molecule. For both models, we explicitly express the models' prior mean functions as linear functions in the groups and periods of the diatomic molecules' constituent atoms.| mr1−r2 = β0r1−r2 + β1r1−r2(p1 + p2) + β2r1−r2(g1 + g2), | (15) |
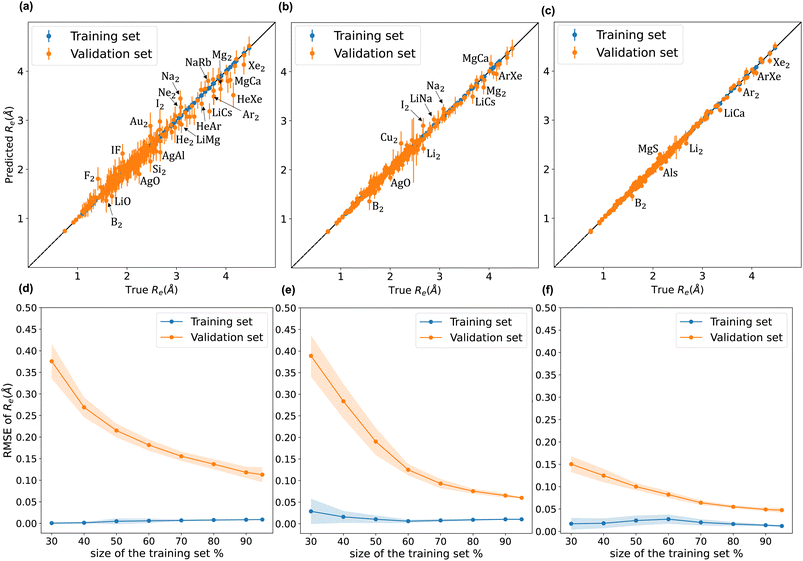
A comparison between models r1 and r2 is displayed in Fig. 3. The scatter plots show a more significant dispersion of the predictions for model r1 compared to model r2. Both models show the same outliers: homonuclear and van der Waals molecules. However, for model r2, the number of outliers is smaller than in model r1, and their dispersion from the true line is significantly suppressed. As a result, model r2 performs substantially better, especially in predicting molecules with Re ≥ 3 Å (mainly van der Waals molecules). The learning curves of models r1 and r2, displayed in panels (d) and (e) of Fig. 3, respectively, show a convergent validation curve towards the training set result as the size of the training set increases, indicative of the learning capability of the model, although, model r2 displays a faster convergence, indicating that the model learns more efficiently. Overall, model r2 shows an improvement in the prediction on Re ∼ 20% with respect r1 as shown in Table 2, leading to validation 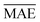 and
and 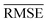 of 0.041 Å and 0.060 Å, respectively.
of 0.041 Å and 0.060 Å, respectively.
Motivated by previously proposed relationships between Re and ln(ωe), we introduce models r3 and r4. Model r3 employs the same features as model r2 but incorporates spectroscopic information in the prior mean function. On the contrary, model r4 uses ln(ωe) as a feature. Both models have a prior mean given by
mr3−r4 = β0r3−r4 + βr3−r41(p1 + p2) + βr3−r42(g1 + g2) + βr3−r43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(μ1/2) + βr3−r44 ln(μ1/2) + βr3−r44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ωe), ln(ωe), | (16) |
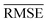 comparable to model r1 using 90% of the data set. Overall, models r3 and r4 show an improvement in the prediction on Re ∼ 40% as shown in Table 2, leading to validation
comparable to model r1 using 90% of the data set. Overall, models r3 and r4 show an improvement in the prediction on Re ∼ 40% as shown in Table 2, leading to validation 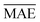 of 0.027 Å and 0.026 Å and a validation
of 0.027 Å and 0.026 Å and a validation 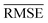 of 0.039 Å and 0.038 Å, respectively. In other words, models r3 and r4 are almost two times more precise in predicting Re than previously ML-based or empirically-derived predictions, and almost as accurate as the state-of-the-art ab initio calculations for diatomics.132,133 Furthermore, the lower panes of Fig. 3 show converging learning curves characterized by relatively narrow gaps between validation and training curves. The decaying trend of the validation curves suggests that convergence toward lower levels of errors is possible upon further training on more extensive datasets. The training MAE of r2 is ∼6 × 10−3 Å; this means that we might have the capacity to achieve an accuracy ∼0.010 Å using only atomic properties. In other words, with more data our ML models could be as accurate as state-of-the-art ab initio quantum chemistry methods.
of 0.039 Å and 0.038 Å, respectively. In other words, models r3 and r4 are almost two times more precise in predicting Re than previously ML-based or empirically-derived predictions, and almost as accurate as the state-of-the-art ab initio calculations for diatomics.132,133 Furthermore, the lower panes of Fig. 3 show converging learning curves characterized by relatively narrow gaps between validation and training curves. The decaying trend of the validation curves suggests that convergence toward lower levels of errors is possible upon further training on more extensive datasets. The training MAE of r2 is ∼6 × 10−3 Å; this means that we might have the capacity to achieve an accuracy ∼0.010 Å using only atomic properties. In other words, with more data our ML models could be as accurate as state-of-the-art ab initio quantum chemistry methods.
To highlight a few of the common outliers of the four models, we consider Li2, B2, LiCs, and LiCa. r1, r2, r3, r4 underestimate Re for Li2 by 6–10%. r1, r2, r3, r4 underestimate Re for B2 by 14%. 15%, 7%, and 8%, respectively, which could be connected to B2 being the only homonuclear molecule from group 13 in the data set. For LiCs, Re = 3.67 Å (ref. 87) and r2 predicts Re = 3.49 ± 0.15 Å; that is, the experimental value is 1.2 standard deviation away from the mean predictive posterior distribution of model r2 for LiCs, although most of the theoretical Re values of LiCs are within one standard deviation.86 For LiCa, the experimental value found by Krois et al. is Re = 3.34 Å.84 On the contrary, the r4 model predicts Re = 3.20 ± 0.05 Å, almost three standard deviations away from the experimental value. However, model r2 predicts Re = 3.33 ± 0.09 Å, with only 0.3% relative error. In addition, high-level ab initio calculations results are within one standard deviation from the mean predictive posterior distribution of model r2 for LiCa, namely CASPT2 predicts Re = 3.40 Å,134 QCISD(T) gives Re = 3.41 Å,135 MRCI leads to Re = 3.40 Å,135 and CIPI prediction is Re = 3.40 Å.136
4.2 ω e
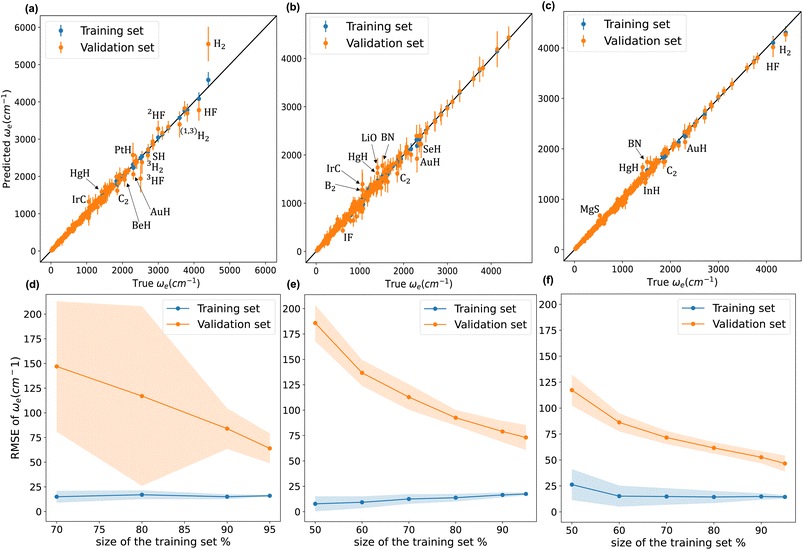
We have implemented and developed four models to predict ωe as listed in Table 1. Model w1 is the best-performing model of Liu et al.26 It is characterized by six features, including atomic and molecular properties. Namely, the groups and periods of the constituent atoms, the average group, ḡ=(giso1 + giso2)/2, and Re−1. giso encodes isotopic information, such that gisoi = 0 for deuterium, gisoi = −1 for tritium, and gisoi = gi for every other element. The prior mean function is set to zero. On the other hand, model w2 only includes groups and periods of the constituent atoms and the reduced mass of the molecule. The prior mean of model w2 is given bymw2 = β0w2 + β1w2(p1 + p2) + β2w2(g1 + g2) + β3w2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(μ1/2), ln(μ1/2), | (17) |
Motivated by the relationship between ωe and Re, both w3 and w4 use the same prior mean function
mw3−w4 = β0w3−w4 + β1w3−w4(p1 + p2) + β2w3−w4(g1 + g2) + β3w3−w4Re + β4w3−w4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(μ1/2), ln(μ1/2), | (18) |
Fig. 4 compares w1, w2, and w4 (plots of w3 are similar to those of w4). We notice from panel (a) that model w1 struggles against hydrides, and hydrogen and hydrogen fluoride isotopologues. Indeed, the model significantly overestimates ωe for H2. On the other hand, panel (b) shows that w2 performs much better against hydrides, and hydrogen and hydrogen fluoride isotopologues. w2 predictions for H2 and HF are accurate and even better than those of models w3 and w4, as shown in panel (c). Panels (a) and (b) clearly show that model w2 outperforms model w1 when considering molecules with larger values of ωe. Looking at the learning curves in panels (d) and (e), we see that model w2 is far more consistent than model w3, as indicated by the shade around the validation curves of both models. From Table 2, the validation SEM(RMSE) of models w2 and w1 show that model w2 is 40% more consistent in its performance than model w1 when both models are validated using the same 1000 MC-CV splits. Furthermore, the test RMSE of w2 is 20% lower than that of w1. Model w2 has lower dimensionality than model w1 and only implements atomic properties; nevertheless, it performs similarly to model w1.
From Table 2, we see that although model w3 has a test MAE almost equal to model w1, models w3 and w4 have validation 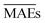 15–21% lower than that of w1, indicating an overall better average performance of the newly developed models. Furthermore, w3 and w4 have validation
15–21% lower than that of w1, indicating an overall better average performance of the newly developed models. Furthermore, w3 and w4 have validation 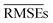 and test RMSEs 28–36% lower than w1, showing the robustness of the two new models. Panel (c) of Fig. 4 shows minimal scatter around the true line. Few hydrides, along with BN and C2, still challenge the model; however, their absolute errors are significantly suppressed compared to w1 and w2. The validation curve of model w4 in panel (f) shows a much higher learning rate than w1 and w2, with a much shallower gap between the validation and learning curves. Moreover, the shadow around the validation curve is minimal at all training sizes. From Table 2, we see that w3 and w4 are far more consistent than w1, with STD(RMSE) 60–70% lower than that of w1.
and test RMSEs 28–36% lower than w1, showing the robustness of the two new models. Panel (c) of Fig. 4 shows minimal scatter around the true line. Few hydrides, along with BN and C2, still challenge the model; however, their absolute errors are significantly suppressed compared to w1 and w2. The validation curve of model w4 in panel (f) shows a much higher learning rate than w1 and w2, with a much shallower gap between the validation and learning curves. Moreover, the shadow around the validation curve is minimal at all training sizes. From Table 2, we see that w3 and w4 are far more consistent than w1, with STD(RMSE) 60–70% lower than that of w1.
On the other hand, the lower three panels in Fig. 4 show that the validation and training curves can converge towards lower error values. Hence, all the models might benefit from training on a more extensive dataset. The training MAEs of w1, w2, w3, and w4 range between 8 to 7 cm−1, so it might be possible to reach near spectroscopic accuracy (∼10 cm−1) by training these models on larger datasets. In the case of w2, if the validation curve's decaying trend persists upon further training, near spectroscopic accuracy might be achieved only through knowledge of atomic positions in the periodic table. Similarly, these models trained in larger database could outperform the state-of-the-art ab initio quantum chemistry methods.132,133
We highlight some of the outliers that are common to some of the models. All the models overestimate ωe for HgH by at least 12%, while for IrC, w1 and w2 overestimate ωe by 30% and 25%, while w3 and w4 only overestimate it by only 4% and 7%, respectively. The observed overestimation might be because HgH and IrC are the only molecules that consist of mercury or iridium in the dataset.
We have found two values of ωe for AuF in the literature; Saenger et al. reported ωe = 560 cm−1 in 1992 (ref. 63), while Andreev et al. reported ωe = 448 cm−1 in 2000.59 All our models predict values closer to 560 cm−1: w2 predicts ωe = 529 ± 87 cm−1, while w3 and w4 are almost in exact agreement with Saenger's value with ωe = 568 ± 54 cm−1 and ωe = 565 ± 45 cm−1, respectively.† Our predictions are in agreement with relativistic density functional and ab initio methods. Namely, first-order relativistic density functional calculation predicts ωe = 491 cm−1 while Zeroth-order regular relativistic approximation within the Kohn–Sham density functional scheme ZORA(MP) predicts ωe = 526 cm−1.61 In the same line, the relativistic MP2 approach predicts ωe = 590 cm−1,138 while relativistic MR-CI predicts ωe = 525 cm−1.139 A similar situation occurs in the case of ZnBr, as shown in Table 3. For 30 years, there was a discrepancy in the value of ωe of ZnBr. Gosavi et al. reported ωe ≈ 319 cm−1 in 1971.140 Next, Givan et al. reported ωe ≈ 198 cm−1 in 1982.141 On the contrary, the MRCI calculations by Elmoussaoui and Korek predicted ωe ≈ 267 cm−1 in 2015.142 Finally, Burton et al. experimentally reported ωe = 284 cm−1 in 2019.118 Here, w2 predicts ωe = 271.2 ± 21.7 cm−1, w3 predicts ωe = 289.5 ± 15.4 cm−1 and w4 predicts ωe = 281.0 ± 12.0 cm−1. Therefore, our predicted values are in great agreement with the most recent theoretical and experimental values.
| Molecule | Models for Re, ωe | Predicted Re (Å) | Experimental Re (Å) | Predicted ωe (cm−1) | Experimental ωe (cm−1) | Ref. |
|---|---|---|---|---|---|---|
| HCl | r4, w4 | 1.267 ± 0.029 | 1.274 | 2939 ± 114 | 2990 | 56 |
| r2, w2 | 1.275 ± 0.046 | 3020 ± 209 | ||||
| 2HCl | r4, w4 | 1.286 ± 0.027 | 1.274 | 2172 ± 80.0 | 2145 | 56 |
| r2, w2 | 1.285 ± 0.0425 | 2123 ± 136 | ||||
| RuC | r4, w4 | 1.614 ± 0.039 | 1.600 | 1106 ± 59.4 | 1100 | 96 |
| r2, w2 | 1.644 ± 0.074 | 1066 ± 119 | ||||
| WO | r4, w4 | 1.667 ± 0.046 | 1.657 | 1049 ± 65.5 | 1067 | 143 and 144 |
| r2, w2 | 1.708 ± 0.088 | 994.9 ± 131 | ||||
| MoC | r4, w4 | 1.652 ± 0.037 | 1.676 | 982.5 ± 49.2 | 1008 | 96 and 97 |
| r2, w2 | 1.714 ± 0.057 | 1011 ± 106 | ||||
| WC | r4, w4 | 1.746 ± 0.0547 | 1.714 | 1065 ± 78.3 | 983.0 | 145 |
| r2, w2 | 1.645 ± 0.099 | 1097 ± 178 | ||||
| NbC | r4, w4 | 1.739 ± 0.041 | 1.700 | 1019 ± 58.3 | 980.0 | 102 |
| r2, w2 | 1.664 ± 0.057 | 967.7 ± 115 | ||||
| NiC | r4, w4 | 1.621 ± 0.048 | 1.627 | 857 ± 55.8 | 875.0 | 104 |
| r2, w2 | 1.668 ± 0.093 | 825.3 ± 114 | ||||
| PdC | r4, w4 | 1.736 ± 0.032 | 1.712 | 872.0 ± 37.9 | 847.0 | 108 |
| r2, w2 | 1.720 ± 0.057 | 866.6 ± 74.0 | ||||
| UO | r4, w4 | 1.863 ± 0.022 | 1.838 | 888.1 ± 27.2 | 846.0 | 121 |
| r2, w2 | 1.839 ± 0.033 | 893.7 ± 45.3 | ||||
| NiO | r4, w4 | 1.585 ± 0.038 | 1.627 | 785.2 ± 40.2 | 839.0 | 105 |
| r2, w2 | 1.667 ± 0.055 | 796.9 ± 82.9 | ||||
| YC | r4, w4 | 1.907 ± 0.076 | 2.050 | 649.2 ± 70.8 | 686.0 ± 20 | 122 and 123 |
| r2, w2 | 1.824 ± 0.094 | 834 ± 185 | ||||
| ZnF | r4, w4 | 1.756 ± 0.029 | 1.768 | 603 ± 24.2 | 631.0 | 146 |
| r2, w2 | 1.801 ± 0.053 | 580.4 ± 45.8 | ||||
| NiS | r4, w4 | 1.940 ± 0.044 | 1.962 | 482 ± 28.6 | 512.0 | 106 |
| r2, w2 | 1.999 ± 0.081 | 479.1 ± 58.6 | ||||
| ZnCl | r4, w4 | 2.136 ± 0.028 | 2.130 | 384.8 ± 15.4 | 390.0 | 147 |
| r2, w2 | 2.164 ± 0.053 | 371.0 ± 29.0 | ||||
| ZnBr | r4, w4 | 2.299 ± 0.029 | 2.268 | 284.9 ± 11.7 | 284.0 | 118 |
| — | — | — | 319.0 | 140 | ||
| — | — | — | 198.0 | 141 | ||
| r2, w2 | 2.321 ± 0.0542 | 271.1 ± 21.7 | ||||
| ZnI | r4, w4 | 2.499 ± 0.030 | 2.460 | 235.5 ± 10.1 | 223.0 | 56 |
| r2, w2 | 2.484 ± 0.057 | 228.0 ± 19.2 | ||||
| SnI | r4, w4 | 2.722 ± 0.035 | 2.732 | 193.3 ± 9.48 | 197.0 | 107 |
| r2, w2 | 2.725 ± 0.068 | 198.0 ± 19.9 | ||||
| PbI | r4, w4 | 2.784 ± 0.030 | 2.798 | 156.8 ± 6.54 | 160.0 | 107 |
| r2, w2 | 2.814 ± 0.056 | 154.1 ± 13.0 | ||||
| CoO | r2 | 1.543 ± 0.056 | 1.628 | — | — | 72–74 |
| CrC | r2 | 1.517 ± 0.099 | 1.630 | — | — | 77 |
| IrSi | r2 | 2.084 ± 0.171 | 2.09 | — | — | 78 |
| UF | r2 | 2.002 ± 0.081 | 2.02 | — | — | 119 |
| ZrC | r2 | 1.846 ± 0.058 | 1.740 | — | — | 124 |
4.3 D 00
Finally, we have developed model d1 to predict the dissociation energy, D00, via ln(D00) using (p1, g1, p2, g2, μ1/2) as features in a Matérn 3/2 kernel, and a prior mean function that employs both ωe and Remd1 = β0d1 + β1d1(p1 + p2) + β2d1(g1 + g2) + β3d1Re + β4d1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(μ1/2) + β5d1 ln(μ1/2) + β5d1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ωe), ln(ωe), | (19) |
During the development of this work, we have realized that, historically, uncertainties about the dissociation energy experimental values had restrained the development of empirical relations connecting them to other atomic and molecular properties and have led several authors to focus their efforts on the ωe − Re relation.9,41,47 More recently, Fu et al. used an ML model to predict dissociation energies for diatomic molecules, exploiting microscopic and macroscopic properties.150 They tested their model against CO and highlighted that the reported experimental dissociation energy in the literature had increased by 100 kcal mol−1 over the course of 78 years from 1936 to 2014 (ref. 150–152) (in Table 1 of ref. 150). The data used to train model d1 is primarily collected from Huber and Herzberg's constants of diatomic molecules, first published in 1979.56 Unlike experimental values of Re and ωe, since 1980, a significant number of D00 values have been updated.48 To name a few, MgD, MgBr, MgO, CaCl. CaO, SrI, SrO, TiS, NbO, AgF, AgBr, and BrF all have their experimental values updated with at least ±2.3 kcal mol−1 difference from their values in Huber and Herzberg.57 Moreover, for some molecules, the uncertainties in D00 experimental values are not within chemical accuracy. For instance, MgH, CaCl, CaO, CaS, SrH, BaO, BaS, ScF, Tif, NbO, and BrF have uncertainties ranging from ±1 kcal mol−1 up to ±8 kcal mol−1.48
Based on the previous discussion, we can connect the unsatisfactory performance of model d1-in comparison to our developed Re and ωe models-to noise modeling. Unlike Re and ωe, it is most likely that uncertainties around D00 experimental values drive from various systematic effects. Therefore, modeling the errors in D00 experimental values to be identically distributed as in eqn (6) might not be a proper treatment. Thus, to develop better models for predicting D00, more sophisticated techniques of error modeling might be required. To this endeavor, gathering more reliable data with experimental uncertainty within ±1 kcal mol−1 might be sufficient. Something that we are working on it, and it will be published elsewhere.
4.4 Testing ML models versus ab initio results
To further assess the accuracy of our ML models regarding Re and ωe we have exposed our models to molecules containing Fr. Indeed, our dataset does not contain any Fr-containing molecule, defining the most complicated scenario for our ML models. The results in comparison with the state-of-the-art ab initio methods are shown in Table 5, where it is noticed that our ML predictions agree well with ab initio predictions. Furthermore, more data can quickly improve ML predictions, as presented in Fig. 3 and 4. Therefore, ML predictions can be competitive with ab initio quantum chemistry methods using a larger dataset.| Molecule | Ab inito R e (Å) | r2 predicted Re (Å) | Ab inito ω e (cm−1) | w2 predicted ωe (cm−1) |
|---|---|---|---|---|
| LiFr | 3.691 | 3.709 ± 0.123 | 180.7 | 198.9 ± 35.9 |
| KFr | 4.284 | 4.483 ± 0.173 | 65.2 | 64.0 ± 16.2 |
| RbFr | 4.429 | 4.389 ± 0.145 | 46.0 | 48.8 ± 10.4 |
| CsFr | 4.646 | 4.403 ± 0.221 | 37.7 | 42.7 ± 13.7 |
4.5 Predicting homonuclear spectroscopic properties from heteronuclear data
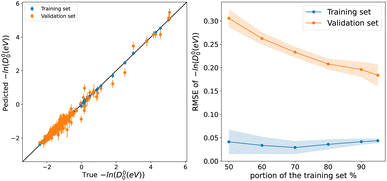
To explore the capability of our models in predicting the spectroscopic properties of homonuclear molecules from spectroscopic and atomic information of heteronuclear molecules, we train our models for predicting Re, ωe, and D00 (r3, w4, and d1) using a special split. We fit the three models to heteronuclear data in Dtv and then make predictions for the left-out homonuclear molecules. The performance of our models is displayed in Fig. 6, where we notice an outstanding performance. Only a few outliers are observed, showing a minimal deviation from the true line. In particular, we obtain MAEs of 0.08 Å, 74 cm−1, and 0.149 for models r4, w4, and d1, respectively. Hence, it is possible to predict the accurate spectroscopic properties of homonuclear molecules from heteronuclear data. Furthermore, our results indicate that expanding the data set by including homonuclear molecules yields high-performing models able to predict spectroscopic properties for both heteronuclear and homonuclear molecules.4.6 Towards a classification of diatomic molecules
For models r2, r3, w2, w3, and d1, we have achieved good results using a kernel common to all five models. That Matérn kernel given by eqn (10) with ν = 3/2, is a similarity measure. Therefore, it is possible to quantify the similarity between a pair of molecules denoted by i = p, q giving their feature vector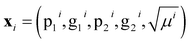 . The models are fitted to the whole dataset to determine the parameters (σn, l, σf). The kernel given by eqn (10) with ν = 3/2 and the determined parameters can be used to form a similarity matrix. Each element in the similarity matrix quantifies the similarity between a pair of molecules in the dataset. Off-diagonal elements are calculated viaeqn (10) for p ≠ q, with the diagonal representing the similarity of the molecules with themselves (p = q). A heat map representation of the similarity matrix is given in Fig. 7, while the degree of similarity from 0 to 1 is given over a greyscale as indicated by the color bar on the right side of the figure.
. The models are fitted to the whole dataset to determine the parameters (σn, l, σf). The kernel given by eqn (10) with ν = 3/2 and the determined parameters can be used to form a similarity matrix. Each element in the similarity matrix quantifies the similarity between a pair of molecules in the dataset. Off-diagonal elements are calculated viaeqn (10) for p ≠ q, with the diagonal representing the similarity of the molecules with themselves (p = q). A heat map representation of the similarity matrix is given in Fig. 7, while the degree of similarity from 0 to 1 is given over a greyscale as indicated by the color bar on the right side of the figure.
 | ||
| Fig. 7 A heat map quantifies the degree of similarity among molecules in the data set from 0 (white, not similar) to 1 (black, identical) on a grayscale. The heat map was generated by finding the matrix element of a similarity matrix. Each matrix element quantifies the similarity between a pair of molecules p (on the x-axis) and q (on the y-axis) viaeqn (10) with ν = 3/2 and parameters determined as described in the text. | ||
To further explore the quantified similarity among molecules, we consider three subsets of molecules and show their heatmaps in the upper panels of Fig. 8. The lower panels of Fig. 8 show the corresponding network representation of the similarity among these subsets of molecules. Black squares in the heat map plots of Fig. 8 indicate that a pair of molecules is highly similar, whereas white squares indicate 0% similarity. The network representation represents each molecule as a node. The similarity between two molecules is diagrammatically shown with a line joining their corresponding nodes. The networks show similarities above the 80% level. A line joins two nodes only if they are at least 80% similar. The length of a joining line indicates the degree of similarity between a pair above the 80% level. A short line indicates a high degree of similarity, and a long line indicates a lower degree of similarity.
From panel (a) of Fig. 8, we see noble gas dimers clustering around Xe2, and alkali metals-alkaline earth metals cluster around NaRb. Both clusters are isolated from each other and VF, indicating a lower degree of similarities between these clusters and VF. A similar scenario is observed in panel (b), where alkaline earth metal hydrides cluster upon themselves with tight interconnections indicating high similarity. On the other hand, ZnH is remotely connected to the cluster, indicating a lower degree of similarity. The upper right cluster shows an interconnection among diatomic reactive nonmetals, including halides and oxygen; notably, AgAl is connected to these molecules. Panel (c) displays a more involved clustering scheme involving transition metal hydrides (MnH and AgH), connected to a metalloid hydride (TlH and InH) and with a lower degree to alkaline earth metals hydrides (LiH and BeH). The right-hand side cluster consists of various transition metal diatomics, dihalides, and others, all closely related except for MgS. Note that all the molecules in the right-hand side cluster consist of atoms from the periodic table's right side. At the same time, MgS combines one atom from group 2 and one from group 16. Notably, homonuclear diatomic and heteronuclear molecules are firmly embedded within all the clusters, emphasizing the importance of including homonuclear data in our models.
Since only atomic properties are required to find elements of the matrix representation of the kernel, the similarity matrix can guide us in our data-gathering efforts. For example, we can determine which molecules can fill the gaps and connect clusters to build more robust models. More interestingly, we can systematically classify molecules based on the similarity matrix. Such classification would help develop potential energy surfaces (PES) for diatomic molecules. As pointed out by Newing, similar molecules will have similar potential energy surfaces, at least around Re.28
5 Summary and conclusion
In this work, first, we have extended the previous database of Liu et al.,26 gathering ground state spectroscopic data of 85 homonuclear and heteronuclear molecules leading to a data set of 338 molecules. Next, the database has been used to train 9 ML models to predict the main spectroscopic constants: Re, ωe, and D00. These models can be categorized into three categories:• Models in category (i) only employ information from the periodic table and thus can predict spectroscopic properties of any combination of two elements. These models can be used to systematically classify molecules made up of any two elements in the periodic table (Section 4.6). While spectroscopic data availability does not limit these models' ability to predict spectroscopic constants of any molecule, it affects the models' accuracy. These models are characterized by a relatively larger gap between validation and learning curves than models in categories (ii) and (iii). Thus, we would expect a better performance of category (i) models upon training on larger datasets.
• Models in category (ii) use spectroscopic information only in their mean function but not in the kernel, and are robust against noise in input variables. In this case, since the mean function is a linear function, we can apply standard errors-in-variables methods.153 This might be advantageous if we would like to use uncertain experimental data or predictions from (i) models or ab initio methods to train our models.
• Models in category (iii) include our most flexible, accurate, and consistent models (r4, w4). These models benefit from a high learning rate and a narrow gap between validation and learning curves. Apart from their outstanding performance, we can train these models using ground and excited states simultaneously since each state will be labeled by its spectroscopic constant values Re or ωe along with other properties that define the molecule {p1, g1, p2, g2, μ1/2}.
In summary, the newly developed models in this work showed an outstanding performance in all metrics in comparison to the previous ML models and other empirical and semiempirical models, with mean absolute errors ranging between 0.02 Å and 0.04 Å for Re, and 26 cm−1 to 40 cm−1 for ωe. We have been able to predict homonuclear spectroscopic properties with good accuracy upon training our models on heteronuclear molecules' data. Indeed, our models are almost as accurate as the state-of-the-art ab inito methods for diatomics.132,133 In addition, our models only require data, whereas ab initio quantum chemistry methods require specific knowledge by the user.
On the other hand, since we use the same kernel for all models under consideration, we are uniquely positioned to study a way to classify diatomic molecules beyond the traditional one based on the nature of the chemical bond. We expect such classification to enhance the performance and facilitate the development of ML models predicting spectroscopic and molecular properties of diatomic molecules. Further, the classification of diatomic molecules should help develop potential energy surfaces (PES).
Finally, we have shown that for molecules with large ionic character and containing heavy atoms (e.g., LiCs, LiCa, AuF, and ZnBr), our predictions are comparable to DFT and even the state-of-the-art ab initio methods. Moreover, two of our models (r2 and w2) offer a promising opportunity to predict spectroscopic properties from atomic positions in the periodic table with high accuracy. This is a stepping stone towards closing the gap between atomic and molecular information; more spectroscopy data is required to do so. More extensive, open, and user-friendly data will help the field of data-driven science to understand the chemical bonding and spectroscopy of small molecules. Indeed, that is something that we are currently working on in our group: we need more spectroscopic data in the big data era. Finally, it is worth mentioning that we are approaching a period in which machine learning techniques are as accurate as ab initio quantum chemistry methods for calculating spectroscopic constants of diatomics with almost no computational effort.
Data availability
The machine learning codes and the data employed in this work can be found on GitHub [https://github.com/Mahmoud-Ibrahim-Mamrstein/Spectroscopic-constants-from-atomic-properties]. In this repository, the user can download the folder called gpr, which contains all the codes and data employed in this paper. The data folder contains all the spectroscopic constants, including references, used as training and test sets in this work. In the same folder, the atomic properties can be found in periodictable.csv. On the contrary, the codes and performance analysis of the machine learning models can be found in each of the subfolders labeled with the model's name. For instance, folder r1 contains all the information relevant to model r1 of the paper. The folder entitled linear regression contains 5 subfolders accounting for each linear regression model employed as a baseline method. Folders labeled by svmr1, svmr2, and svmr3 correspond to support vector machine results for models r1, r2, and r3. The same holds for svmw1 and svmw2, regarding models w1 and w2, whereas the folder svmd1 is the support vector machine prediction for the d1 model. Finally, our study on the classification of molecules is found under the folder heat_maps_and_networks.Author contributions
X. L. helped with the database and the first ML models. M. A. E. I. gathered the data and performed the new ML models, whereas J. P.-R. envisioned the idea and supervised the project. M. A. E. I. and J. P.-R. wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. P.-R. acknowledges the funding of the Simons Foundation and the Lorentz Center of the University of Leiden for organizing the workshop “New directions in cold and ultracold molecules”, in which some part of this work was discussed. X. L. acknowledges the support or the the Deutsche Forschungsgemeinschaft (DFG – German Research Foundation) under the grant number PE 3477/2 – 493725479. M. A. E. I. acknowledges the funding and support of THE BINATIONAL FULBRIGHT COMMISSION and Assiut University in EGYPT. Finally, we would like to thank Rian Koots for useful suggestions to improve the GitHub repository.References
- A. Kratzer, Z. Phys., 1920, 3, 289–307 CrossRef CAS.
- R. Birge, Phys. Rev., 1925, 25, 240–254 Search PubMed.
- R. Mecke, J. Phys., 1925, 32, 823–834 CAS.
- P. M. Morse, Phys. Rev., 1929, 34, 57 CrossRef CAS.
- C. Clark, J. Sci., 1934, 18, 459–470 CAS.
- C. D. Clark, Nature, 1934, 133, 873 CrossRef CAS.
- C. D. Clark, Trans. Faraday Soc., 1941, 37, 299–302 RSC.
- C. D. Clark and K. Webb, Trans. Faraday Soc., 1941, 37, 293–298 RSC.
- R. M. Badger, J. Chem. Phys., 1934, 2, 128–131 CrossRef CAS.
- E. Kraka, J. A. Larsson and D. Cremer, Computational Spectroscopy, ed. J. Grunenberg, Wiley, New York, NY, USA, 2010, pp. 105–149 Search PubMed.
- E. Kurita, H. Matsuura and K. Ohno, Spectrochim. Acta, Part A, 2004, 60, 3013–3023 CrossRef.
- R. M. Badger, J. Chem. Phys., 1935, 3, 710–714 CrossRef CAS.
- M. Kaupp, D. Danovich and S. Shaik, Coord. Chem. Rev., 2017, 344, 355–362 CrossRef CAS.
- J. Cioslowski, G. Liu and R. A. M. Castro, Chem. Phys. Lett., 2000, 331, 497–501 CrossRef CAS.
- W. G. Penney and G. B. B. M. Sutherland, Proc. R. Soc. London, Ser. A, 1936, 156, 654–678 CAS.
- H. Allen and A. Longair, Nature, 1935, 135, 764 CrossRef CAS.
- M. L. Huggins, J. Chem. Phys., 1935, 3, 473–479 CrossRef CAS.
- M. L. Huggins, J. Chem. Phys., 1936, 4, 308–312 CrossRef CAS.
- G. B. Sutherland, Proc. Indian Acad. Sci., 1938, 341–344 CrossRef CAS.
- J. Linnett, Trans. Faraday Soc., 1940, 36, 1123–1134 RSC.
- C. Wu and C.-T. Yang, J. Phys. Chem., 1944, 48, 295–303 CrossRef CAS.
- C. Wu and S. Chao, Phys. Rev., 1947, 71, 118 CrossRef CAS.
- K. Guggenheimer, Proc. Phys. Soc., 1946, 58, 456 CrossRef CAS.
- J. Linnett, Trans. Faraday Soc., 1945, 41, 223–232 RSC.
- W. Gordy, J. Chem. Phys., 1946, 14, 305–320 CrossRef CAS.
- X. Liu, G. Meijer and J. Pérez-Ríos, RSC Adv., 2021, 11, 14552–14561 RSC.
- J. C. Slater, J. Chem. Phys., 1933, 1, 687–691 CrossRef CAS.
- R. Newing, London, Edinburgh Dublin Phil. Mag. J. Sci., 1940, 29, 298–301 CrossRef CAS.
- P. Güttinger, Z. Phys., 1932, 73, 169–184 CrossRef.
- W. Pauli, Handb. Phys., 1933, 24, 43 Search PubMed.
- H. Hellmann, Einführung in die Quantenchemie, 1937 Search PubMed.
- R. P. Feynman, Phys. Rev., 1939, 56, 340 CrossRef CAS.
- L. Salem, J. Chem. Phys., 1963, 38, 1227–1236 CrossRef CAS.
- P. Empedocles, J. Chem. Phys., 1967, 46, 4474–4481 CrossRef CAS.
- P. Empedocles, Theor. Chim. Acta, 1968, 10, 331–336 CrossRef CAS.
- A. B. Anderson, N. C. Handy and R. G. Parr, J. Chem. Phys., 1969, 50, 3634–3635 CrossRef CAS.
- A. B. Anderson and R. G. Parr, J. Chem. Phys., 1970, 53, 3375–3376 CrossRef CAS.
- A. Anderson and R. Parr, Chem. Phys. Lett., 1971, 10, 293–296 CrossRef CAS.
- G. Simons and R. G. Parr, J. Chem. Phys., 1971, 55, 4197–4202 CrossRef CAS.
- A. B. Anderson, J. Mol. Spectrosc., 1972, 44, 411–424 CrossRef CAS.
- G. B. Sutherland, J. Chem. Phys., 1940, 8, 161–164 CrossRef CAS.
- G. Somayajulu, J. Chem. Phys., 1960, 33, 1541–1553 CrossRef CAS.
- E. Lippincott, R. Schroeder and D. Steele, J. Chem. Phys., 1961, 34, 1448–1449 CrossRef.
- J. Gazquez and R. G. Parr, Chem. Phys. Lett., 1979, 66, 419–422 CrossRef CAS.
- B. J. J. Wiener, J. S. Murray, M. E. Grice and P. Politzer, Mol. Phys., 1997, 90, 425–430 CrossRef.
- H. Skinner, Dissociation Energies of Diatomic Molecules, 1954 Search PubMed.
- K. S. Jhung, I. H. Kim, K.-H. Oh, K. B. Hahn and K. H. C. Jhung, Phys. Rev. A, 1990, 42, 6497 CrossRef CAS PubMed.
- Y.-R. Luo, Comprehensive handbook of chemical bond energies, CRC press, 2007 Search PubMed.
- X. Liu, S. Truppe, G. Meijer and J. Pérez-Ríos, J. Cheminf., 2020, 12, 31 CAS.
- I. C. Stevenson and J. Pérez-Ríos, J. Phys. B: At., Mol. Opt. Phys., 2019, 52, 105002 CrossRef CAS.
- J. Fu, Z. Wan, Z. Yang, L. Liu, Q. Fan, F. Xie, Y. Zhang and J. Ma, Int. J. Quantum Chem., 2022, 122, e26953 CrossRef CAS.
- R. Pederson, B. Kalita and K. Burke, Nat. Rev. Phys., 2022, 4, 357–358 CrossRef.
- R. Nagai, R. Akashi and O. Sugino, npj Comput. Mater., 2020, 6, 43 CrossRef CAS.
- M. Gao, B. Cai, G. Liu, L. Xu, S. Zhang and H. Zeng, Phys. Chem. Chem. Phys., 2023, 25, 9123–9130 RSC.
- S. Dick and M. Fernandez-Serra, Nat. Commun., 2020, 11, 3509 CrossRef CAS PubMed.
- K.-P. Huber, Molecular spectra and molecular structure: IV. Constants of diatomic molecules, Springer Science & Business Media, 2013 Search PubMed.
- K. Huber and G. Herzberg, NIST Chemistry WebBook, NIST Standard Reference Database Number 69, 2021 Search PubMed.
- C. J. Evans and M. C. Gerry, J. Am. Chem. Soc., 2000, 122, 1560–1561 CrossRef CAS.
- S. Andreev and J. J. BelBruno, Chem. Phys. Lett., 2000, 329, 490–494 CrossRef CAS.
- D. Schröder, J. Hrušák, I. C. Tornieporth-Oetting, T. M. Klapötke and H. Schwarz, Angew. Chem., 1994, 106, 223–225 CrossRef.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244 CrossRef CAS.
- K. Saenger and C. Sun, Phys. Rev. A, 1992, 46, 670 CrossRef CAS PubMed.
- E. GharibNezhad, A. Shayesteh and P. F. Bernath, J. Mol. Spectrosc., 2012, 281, 47–50 CrossRef CAS.
- T. C. Steimle, T. Ma, A. G. Adam, W. D. Hamilton and A. J. Merer, J. Chem. Phys., 2006, 125, 064302 CrossRef.
- Q. Nadhem, S. Behere and S. Behere, Int. Lett. Chem., Phys. Astron., 2015, 58, 91 Search PubMed.
- R. Ram, P. Bernath and S. Davis, J. Chem. Phys., 1996, 104, 6949–6955 CrossRef CAS.
- A. I. Boldyrev and J. Simons, Periodic Tables of Diatomic Molecules, John Wiley & Sons, 1997 Search PubMed.
- K. P. Jensen, B. O. Roos and U. Ryde, J. Chem. Phys., 2007, 126, 014103 CrossRef PubMed.
- H. Wang, X. Zhuang and T. C. Steimle, J. Chem. Phys., 2009, 131, 114315 CrossRef.
- M. M. F. de Moraes and Y. A. Aoto, J. Mol. Spectrosc., 2022, 385, 111611 CrossRef CAS.
- M. Barnes, D. Clouthier, P. Hajigeorgiou, G. Huang, C. Kingston, A. Merer, G. Metha, J. Peers and S. Rixon, J. Mol. Spectrosc., 1997, 186, 374–402 CrossRef CAS PubMed.
- F. Liu, F.-X. Li and P. Armentrout, J. Chem. Phys., 2005, 123, 064304 CrossRef PubMed.
- S. McLamarrah, P. Sheridan and L. Ziurys, Chem. Phys. Lett., 2005, 414, 301–306 CrossRef CAS.
- O. Launila, J. Mol. Spectrosc., 1995, 169, 373–395 CrossRef CAS.
- S. Mishra, R. K. Yadav, V. Singh and S. Rai, J. Phys. Chem. Ref. Data, 2004, 33, 453–470 CrossRef CAS.
- D. J. Brugh, M. D. Morse, A. Kalemos and A. Mavridis, J. Chem. Phys., 2010, 133, 034303 CrossRef PubMed.
- M. A. Garcia, C. Vietz, F. Ruipérez, M. D. Morse and I. Infante, J. Chem. Phys., 2013, 138, 154306 CrossRef PubMed.
- R. Schlachta, I. Fischer, P. Rosmus and V. Bondybey, Chem. Phys. Lett., 1990, 170, 485–491 CrossRef CAS.
- T. D. Persinger, J. Han and M. C. Heaven, J. Phys. Chem. A, 2021, 125, 8274–8281 CrossRef CAS PubMed.
- A. Stein, M. Ivanova, A. Pashov, H. Knöckel and E. Tiemann, J. Chem. Phys., 2013, 138, 114306 CrossRef PubMed.
- C. Wu, H. Ihle and K. Gingerich, Int. J. Mass Spectrom. Ion Phys., 1983, 47, 235–238 CrossRef CAS.
- J. V. Pototschnig, R. Meyer, A. W. Hauser and W. E. Ernst, Phys. Rev. A, 2017, 95, 022501 CrossRef.
- G. Krois, J. V. Pototschnig, F. Lackner and W. E. Ernst, J. Phys. Chem. A, 2013, 117, 13719–13731 CrossRef CAS PubMed.
- A. Grochola, J. Szczepkowski, W. Jastrzebski and P. Kowalczyk, J. Quant. Spectrosc. Radiat. Transfer, 2014, 145, 147–152 CrossRef CAS.
- N. Mabrouk, H. Berriche, H. B. Ouada and F. X. Gadéa, J. Phys. Chem. A, 2010, 114, 6657–6668 CrossRef CAS PubMed.
- P. Staanum, A. Pashov, H. Knöckel and E. Tiemann, Phys. Rev. A, 2007, 75, 042513 CrossRef.
- W. Müller and W. Meyer, J. Chem. Phys., 1984, 80, 3311–3320 CrossRef.
- E. J. Breford, F. Engelke, G. Ennen and K. H. Meiwes, Faraday Discuss. Chem. Soc., 1981, 71, 233–252 RSC.
- K. F. Zmbov, C. Wu and H. Ihle, J. Chem. Phys., 1977, 67, 4603–4607 CrossRef CAS.
- T. D. Persinger, J. Han and M. C. Heaven, J. Phys. Chem. A, 2021, 125, 3653–3663 CrossRef CAS PubMed.
- F. Engelke, G. Ennen and K. Meiwes, Chem. Phys., 1982, 66, 391–402 CrossRef CAS.
- H. Atmanspacher, H. Scheingraber and C. Vidal, J. Chem. Phys., 1985, 82, 3491–3501 CrossRef CAS.
- G. C. Rizkallah, A. A. Assaf and S. N. Tohme, Chem. Phys., 2021, 550, 111316 CrossRef CAS.
- L. B. Knight Jr and W. Weltner Jr, J. Chem. Phys., 1971, 54, 3875–3884 CrossRef.
- R. S. DaBell, R. G. Meyer and M. D. Morse, J. Chem. Phys., 2001, 114, 2938–2954 CrossRef CAS.
- D. J. Brugh, T. J. Ronningen and M. D. Morse, J. Chem. Phys., 1998, 109, 7851–7862 CrossRef CAS.
- S. Leutwyler, M. Hofmann, H.-P. Harri and E. Schumacher, Chem. Phys. Lett., 1981, 77, 257–260 CrossRef CAS.
- M. Chaieb, H. Habli, L. Mejrissi, B. Oujia and F. X. Gadéa, Int. J. Quantum Chem., 2014, 114, 731–747 CrossRef CAS.
- O. Docenko, M. Tamanis, R. Ferber, A. Pashov, H. Knöckel and E. Tiemann, Phys. Rev. A, 2004, 69, 042503 CrossRef.
- N. Takahashi and H. Katô, J. Chem. Phys., 1981, 75, 4350–4356 CrossRef CAS.
- B. Simard, P. I. Presunka, H. P. Loock, A. Bérces and O. Launila, J. Chem. Phys., 1997, 107, 307–318 CrossRef CAS.
- J. Ogilvie and F. Y. Wang, J. Mol. Struct., 1992, 273, 277–290 CrossRef CAS.
- D. J. Brugh and M. D. Morse, J. Chem. Phys., 2002, 117, 10703–10714 CrossRef CAS.
- R. Ram and P. Bernath, J. Mol. Spectrosc., 1992, 155, 315–325 CrossRef CAS.
- R. Ram, S. Yu, I. Gordon and P. Bernath, J. Mol. Spectrosc., 2009, 258, 20–25 CrossRef CAS.
- C. J. Evans, L.-M. E. Needham, N. R. Walker, H. Köckert, D. P. Zaleski and S. L. Stephens, J. Chem. Phys., 2015, 143, 244309 CrossRef PubMed.
- J. D. Langenberg, L. Shao and M. D. Morse, J. Chem. Phys., 1999, 111, 4077–4086 CrossRef CAS.
- J. O. Schroeder, C. Nitsch and W. E. Ernst, J. Mol. Spectrosc., 1989, 132, 166–177 CrossRef.
- W. Ernst, J. Schröder and B. Zeller, J. Mol. Spectrosc., 1989, 135, 161–168 CrossRef CAS.
- S. Antrobus, D. Husain, J. Lei, F. Castaño and M. S. Rayo, Z. Phys. Chem., 1995, 190, 267–287 CrossRef CAS.
- A. Bernard, C. Effantin, J. d'Incan, A. Topouzkhanian and G. Wannous, J. Mol. Spectrosc., 1999, 195, 11–21 CrossRef CAS PubMed.
- M. W. Chase and N. I. S. O. (US), NIST-JANAF thermochemical tables, American Chemical SocietyWashington, DC, 1998, vol. 9 Search PubMed.
- V. Belyaev, I. Gotkis, N. Lebedeva and K. Krasnov, Russ. J. Phys. Chem., 1990, 64, 773 Search PubMed.
- T. Imajo, Y. Kobayashi, Y. Nakashima, K. Tanaka and T. Tanaka, J. Mol. Spectrosc., 2005, 230, 139–148 CrossRef CAS.
- R. Ram and P. Bernath, J. Mol. Spectrosc., 2005, 231, 165–170 CrossRef CAS.
- R. Ram, J. Peers, Y. Teng, A. Adam, A. Muntianu, P. Bernath and S. Davis, J. Mol. Spectrosc., 1997, 184, 186–201 CrossRef CAS.
- M. Burton and L. Ziurys, J. Chem. Phys., 2019, 150, 034303 CrossRef CAS PubMed.
- I. O. Antonov and M. C. Heaven, J. Phys. Chem. A, 2013, 117, 9684–9694 CrossRef CAS PubMed.
- R. Ram, P. Bernath and S. Davis, J. Chem. Phys., 2002, 116, 7035–7039 CrossRef CAS.
- L. A. Kaledin, J. E. McCord and M. C. Heaven, J. Mol. Spectrosc., 1994, 164, 27–65 CrossRef CAS.
- B. Simard, P. A. Hackett and W. J. Balfour, Chem. Phys. Lett., 1994, 230, 103–109 CrossRef CAS.
- I. Shim, M. Pelino and K. A. Gingerich, J. Chem. Phys., 1992, 97, 9240–9248 CrossRef CAS.
- M. Sievers, Y.-M. Chen and P. Armentrout, J. Chem. Phys., 1996, 105, 6322–6333 CrossRef CAS.
- M. Bobetic and J. Barker, J. Chem. Phys., 1976, 64, 2367–2369 CrossRef CAS.
- K. Tang and J. Toennies, J. Chem. Phys., 2003, 118, 4976–4983 CrossRef CAS.
- L. Piticco, F. Merkt, A. A. Cholewinski, F. R. McCourt and R. J. Le Roy, J. Mol. Spectrosc., 2010, 264, 83–93 CrossRef CAS.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, 2005 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, et al. , J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- Z. Botev and A. Ridder, Wiley statsRef: Statistics reference online, 2017, pp. 1–6 Search PubMed.
- T. Head, M. Kumar, H. Nahrstaedt, G. Louppe and I. Shcherbatyi, scikit-optimize/scikit-optimize, 2021, DOI:10.5281/zenodo.5565057.
- X. Liu, L. McKemmish and J. Pérez-Ríos, Phys. Chem. Chem. Phys., 2023, 25, 4093–4104 RSC.
- H. Ladjimi and M. Tomza, Diatomic molecules of alkali-metal and alkaline-earth-metal atoms: interaction potentials, dipole moments, and polarizabilities, 2023 Search PubMed.
- A.-R. Allouche and M. Aubert-Frécon, Chem. Phys. Lett., 1994, 222, 524–528 CrossRef CAS.
- L. Russon, G. Rothschopf, M. Morse, A. Boldyrev and J. Simons, J. Chem. Phys., 1998, 109, 6655–6665 CrossRef CAS.
- G. Gopakumar, M. Abe, M. Hada and M. Kajita, J. Chem. Phys., 2013, 138, 194307 CrossRef PubMed.
- N.-H. Cheung and T. A. Cool, J. Quant. Spectrosc. Radiat. Transfer, 1979, 21, 397–432 CrossRef CAS.
- J. K. Laerdahl, T. Saue and K. Faegri Jr, Theor. Chem. Acc., 1997, 97, 177–184 Search PubMed.
- P. Schwerdtfeger, J. S. McFeaters, R. L. Stephens, M. J. Liddell, M. Dolg and B. A. Hess, Chem. Phys. Lett., 1994, 218, 362–366 CrossRef CAS.
- R. Gosavi, G. Greig, P. Young and O. Strausz, J. Chem. Phys., 1971, 54, 983–991 CrossRef CAS.
- A. Givan and A. Loewenschuss, J. Mol. Struct., 1982, 78, 299–301 CrossRef CAS.
- S. Elmoussaoui and M. Korek, Comput. Theor. Chem., 2015, 1068, 42–46 CrossRef CAS.
- C. Krumrey, S. A. Cooke, D. K. Russell and M. C. Gerry, Can. J. Phys., 2009, 87, 567–573 CrossRef CAS.
- R. S. Ram, J. Liévin, G. Li, T. Hirao and P. F. Bernath, Chem. Phys. Lett., 2001, 343, 437–445 CrossRef CAS.
- S. M. Sickafoose, A. W. Smith and M. D. Morse, J. Chem. Phys., 2002, 116, 993–1002 CrossRef CAS.
- M. Flory, S. McLamarrah and L. Ziurys, J. Chem. Phys., 2006, 125, 194304 CrossRef CAS PubMed.
- E. Tenenbaum, M. Flory, R. Pulliam and L. Ziurys, J. Mol. Spectrosc., 2007, 244, 153–159 CrossRef CAS.
- X. Qu, D. A. Latino and J. Aires-de Sousa, J. Cheminf., 2013, 5, 34 CAS.
- A. Raza, S. Bardhan, L. Xu, S. S. R. K. C. Yamijala, C. Lian, H. Kwon and B. M. Wong, Environ. Sci. Technol. Lett., 2019, 6, 624–629 CrossRef CAS.
- J. Fu, S. Long, J. Jian, Z. Fan, Q. Fan, F. Xie, Y. Zhang and J. Ma, Spectrochim. Acta, Part A, 2020, 239, 118363 CrossRef CAS PubMed.
- (a) M. W. Wolkenstein, Molekular Optics, Moscow-Leningrad, 1951 Search PubMed; (b) The Structure and Physical Properties of Molecules, Moscow-Leningrad, 1955 Search PubMed.
- R. Kepa, M. Ostrowska-Kopeć, I. Piotrowska, M. Zachwieja, R. Hakalla, W. Szajna and P. Kolek, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 045101 CrossRef CAS.
- S. Van Huffel and P. Lemmerling, Total least squares and errors-in-variables modeling: analysis, algorithms and applications, Springer Science & Business Media, 2013 Search PubMed.
Footnote |
| † The w2, w3, and w4 predictions for AuF in the main text were predicted, including HgCl, HgI, and HgBr in the training set. To test the robustness of the models, we removed those three molecules from the training set since their Re values might be related to HgCl2, HgI2, and HgBr2.56,137 Indeed, those molecules could affect the model predictions because they are closely related to AuF since Au (group 11) and Hg (group 12) are members of the sixth period, and F, Cl, I, and Br are all halogens. However, in this case, w2, w3 and w4 predict ωe ∼ 530 cm−1, ωe ∼ 600 cm−1, and ωe ∼ 590 cm−1, respectively, in good agreement with the predicted results in the main text, experimental results and ab initio methods. |
| This journal is © The Royal Society of Chemistry 2024 |