Using natural language processing (NLP)-inspired molecular embedding approach to predict Hansen solubility parameters

Abstract

Hansen solubility parameters (HSPs) have three components, δ_d, δ_p and δ_h, accounting for dispersion forces, polar forces, and hydrogen bonding of a molecule, which were designed to better understand how molecular structure affects miscibility/solubility. HSP is widely used throughout the pipeline of pharmaceutical research and yet has not been as well studied computationally as the aqueous solubility. In the current study, we predicted HSPs using only the SMILES of molecules and utilise the molecular embedding approach inspired by Natural Language Processing (NLP). Two pre-trained deep learning models – Mol2Vec and ChemBERTa have been used to derive the embeddings. A dataset of ∼1200 organic molecules with experimentally determined HSPs was used as the labelled dataset. Upon finetuning, the ChemBERTa model “learned” relevant molecular features and shifted attention to functional groups that give rise to the relevant HSPs. The finetuned ChemBERTa model outperforms both the Mol2Vec model and the baseline Morgan fingerprint method albeit not to a significant extent. Interestingly, the embedding models can predict δ_d significantly better than δ_h and δ_p and overall, the accuracy of predicted HSPs is lower than the well-benchmarked ESOL aqueous solubility. Our study indicates that the extent of transfer learning leveraged from the pre-trained models is related to the labelled molecular properties. It also highlights how δ_p and δ_h may have large intrinsic errors in the way they are defined and therefore introduces inherent limitations to their accurate prediction using machine learning models. Our work reveals several interesting findings that will help explore the potential of BERT-based models for molecular property prediction. It may also guide the possible refinement of the Hansen solubility framework, which will generate a wide impact across the pharmaceutical industry and research.

---

Introduction

Molecular embedding

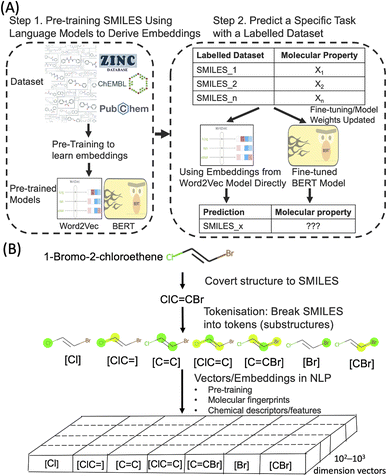
Deep learning techniques have revolutionised various fields in recent years. One of the most successful areas is Natural Language Processing (NLP) where deep learning models are applied to understand huge volumes of raw text to extract meaning and generate new content. The deep learning NLP techniques are increasingly applied to other domains where the domain data has a similarity with text. One example is SMILES (Simplified Molecular Input Line Entry System), a form of line notation to describe molecular structures using a string of chemical elements and symbols. Through SMILES, it is possible to adopt powerful NLP algorithms to process molecular structures to predict their properties and generate new molecular structures. Molecular text representation-based deep learning models are emerging as an important research tool in the ongoing data-driven revolution of chemical and biological research.^1–5

Word embedding in the field of NLP is an important technique in which the meaning of words and sentences can be captured by dense real-valued vectors. A well-established approach to obtain embeddings in NLP is pre-training (Fig. 1). In this approach, such text embeddings are obtained via learning from an extremely large set of unlabelled text sequences, in a fully unsupervised manner, to capture the semantic and syntactic meaning of words. Subsequently, when these pre-trained text embeddings are used in different downstream tasks with or without fine-tuning on smaller sets of labelled data. This concept of reusing a large general pre-trained model for many specific tasks with task-specific data annotations is known as transfer learning in machine learning and NLP. Applied to a large dataset of SMILES (such as ZINC and ChEMBL), the embedding approach could provide a new type of molecular representations that captures the physicochemical properties of molecules.

Fig. 1 (A) Illustrate pretraining of the Word2Vec and BERT models and how they are used for molecular property prediction. (B) Illustration of how a molecule is converted to SMILES, tokenised into tokens (substructures), then derived into real-valued vectors, i.e. embeddings in NLP. The vectors can come from pre-training, chemical descriptors or molecular fingerprints.

Molecular embedding approaches have been explored in the past few years as a general concept to predict molecular properties.^6–9 There is some evidence that molecular embeddings could surpass molecular descriptors and fingerprints in some tasks, but the improvement may not be significant and still lacks clear interpretability. Hence a better understanding of what the embedding models have learned of the molecular properties will help to better train and finetune them. On the other hand, earlier molecular embedding work usually required extensive coding which makes adaptation difficult for non-experts. In the past couple of years, the development of Hugging Face (https://huggingface.co/), a machine learning and data science platform has lowered the barrier for non-experts to pre-train and finetune deep learning models (transformer models to be more specific). In the present study, we explored the use of molecular embedding approaches to predict Hansen solubility parameters (HSPs) which bridge directly molecular embedding with intrinsic molecular forces. In addition, we have used pre-trained models deposited in Hugging Face for finetuning so that our approaches can be adapted more easily.

Solubility and Hansen solubility parameters

Solubility can be defined as the maximum quantity of a chemical that can be fully dissolved in a given volume of solution.¹⁰ It is applied to numerous applications in the areas of environmental chemistry, chemical process design, and pharmaceutical sciences and informs molecular design and optimisation in a wide range of tasks such as drug design and the development of lithographic materials in the semiconductor industry.¹¹

Predicting solubility can be a challenging task since it depends on various physicochemical factors. Some of the more important factors to be considered are the interactions between solute and solvent and the nature of intrinsic intermolecular forces of solute. Because of the complexity associated with the term, several types of parameters have been developed to account for different aspects of the solvating ability/miscibility of molecules. For example, the partition coefficient log P reflects a molecule's hydrophobicity and is widely used to estimate the aqueous solubility of small molecules for drug discovery. On the other hand, Hildebrand and Scott introduced the total solubility parameter δ_t in 1949, which is the square root of a solvent's cohesive energy density. The total cohesive energy can be measured by evaporating the liquid, i.e., breaking all the “cohesive interactions”. Thus, the total cohesive energy of a compound is considered to be similar to the energy of vaporization. The Hildebrand and Scott total solubility parameter usually is not sufficient to describe molecules with strong polarity and hydrogen bonds. It was further refined by Charles M. Hansen in 1967,¹² which became the widely used Hansen solubility parameters (HSPs). Hansen decomposed δ_t and introduced three variables δ_h, δ_p, δ_d as partial solubility parameters:

δ_t = sqrt(δ_d² + δ_h² + δ_p²)

where δ_d, δ_p, δ_h account for dispersion forces, polar forces, and hydrogen bonding of a molecule, respectively. HSPs were designed to better understand how the nature of intermolecular forces affect solubility, thus have vast applications in the pharmaceutical, paint and material science-related industries.¹³ While experimental methods can be used to determine HSPs, it is often not feasible when the quantity of the chemicals available is limited and costly and impossible for the vast number of hypothetical molecules that are routinely used for virtual screening. Several theoretical approaches have been developed to determine HSPs, notably the group contribution methods (GCMs)^14–16 and methods based on Quantitative Structure–Property Relationship (QSPR) and machine learning models.^17,18 In GCMs, molecules are divided into basic functional groups (UNIFAC) and polyfunctional and polycyclic groups and then linear regression models are used to determine the group contribution to the partial solubility of the molecules. GCMs are usually less accurate for large molecules with multi-functional groups that make significant positive or negative contributions to the HSPs.¹⁶ QSPR methods use molecular fingerprints and physicochemical descriptors to build regression models to predict the HSPs. These approaches are well established and often give a satisfactory prediction, but usually involve computing of the descriptors which requires expert knowledge of the molecules and can be time-consuming. There is a need to explore new ways to predict HSPs and more broadly to understand solubility from a molecular structure-based and data-driven perspective that would be more rigorous and efficient.^11,19–22

We aim to predict HSPs based on only the SMILES of the molecules and the molecular embedding approaches. In our study, two NLP embedding approaches were employed, namely Word2Vec²³ and BERT-based finetuning.²⁴ Word2Vec is a shallow, two-layer neural network to efficiently create high-dimensional vector (usually several hundred dimensions) representations of words and has been widely used since its publication in 2013. Word2Vec takes in a large corpus of text and produces a vector space, with each unique token in the corpus being assigned a corresponding vector. These vectors are positioned in the vector space such that tokens that share similar meanings are located close to one another in the vector space. In the present work, we used Mol2Vec,²⁵ a previously developed unsupervised Word2Vec-inspired chemistry model to assign the vectors. Similar to word embeddings in the Word2Vec approach, the vectors for chemically related substructures occupy the same part of vector space in Mol2Vec. The limit of Word2Vec approach is that it is “context-free” representation, where the embeddings for substructures are static (Fig. S1 in the ESI†). This means the embeddings do not depend on the context of the SMILES, i.e. the same substructure will have the same vector representation even if it is in two completely different SMILES. Static embedding limits the accuracy of the models as it is well known in chemistry that adjacent and neighbouring functional groups may have significant influence over each other's reactivity and chemical properties in molecular structures. In recent years, the power of incorporating context into text embedding learning has been demonstrated by transformer-based models, such as BERT (Bidirectional Encoder Representations from Transformers).²⁴ Similarly, applying contextual representation to SMILES could also lead to the improvement of the models. Several BERT-based models have been developed with different training objectives and strategies along with different SMILES datasets.²⁶ In the current study, we used the ChemBERTa models^27,28 as these pre-trained models are available on Hugging Face that enables more straightforward finetuning and adaptation by others. We finetuned the ChemBERTa models to make HSPs prediction.

By using and comparing our two embedding models, we aim to address the following questions relating to the prediction of HSPs: (i) Do the embedding models have an advantage over the more commonly used molecular fingerprint and descriptor-based approaches? (ii) For the embedding approach, does the BERT-based model outperform the simpler Word2Vec model? (iii) By comparing two different types of solubility parameters, namely the ESOL aqueous solubility and Hansen solubility, we will examine what the embedding models have learned of the molecular properties and how it may be related to the intrinsic molecular forces defined by HSPs.

Experimental

Datasets

Two labelled datasets were used. The first is a set of 1183 common organic molecules with experimentally determined HSPs curated by Steven Abbott.²⁹ Abbott's dataset was checked for possible duplications and the chemicals that are a mixture and do not correspond to a clearly defined molecular structure (e.g., pine oil) were removed from the dataset. The chemicals were converted into SMILES using https://cactus.nci.nih.gov/chemical/structure. This will be referred to as the Hansen dataset. The Hansen dataset has an average molecule weight of 131 g mol⁻¹ (Fig. S2 in the ESI†). δ_d ranges between 10 and 20, δ_h ranges mainly between 0 and 30 while δ_p ranges between 0 and 20 (Fig. S3 in the ESI†). As a comparison with other similar studies, we have also applied our models to the ESOL dataset to predict aqueous solubility.³⁰ ESOL is a dataset of 1143 organic molecules (Fig. S2†) and shares 117 molecules with the Hansen set. ESOL contains the experimentally determined aqueous solubility parameter log S, that comes from log P and melting point. It has an average molecular weight of 204 g mol⁻¹ and the log S values were distributed mostly between −10 and 5. For both datasets, the canonical SMILES was used for the molecules. The functional group distribution in the two datasets was analysed in a similar fashion as used by Boobier et al.²⁰ Functional groups were counted by matching their SMARTS codes to the SMILES strings using pybel/OpenBabel. The total number of occurrences of each functional group was then divided by the number of molecules in the dataset to derive the average occurrence per molecule for each functional group (Fig. S4 in the ESI† and the code available in the GitHub deposit). In addition to being lighter in average molecular weight, the Hansen dataset has fewer alkene and aromatic carbons and hydrogen-bond donor functional groups than the ESOL dataset.

Molecular fingerprints

Morgan fingerprints are fixed-length vectors that encode the presence of specific molecular functional groups. In the present study, they were generated from SMILES using RDkit³¹ where the radius was set at 8 and the vector size set to 2048. This means for each atom, molecular patterns up to a connectivity distance of 8 angstroms were identified, indexed, and hashed to a vector of size 2048.

Mol2Vec model

We have adapted the published Mol2Vec model,²⁵ which was trained using the genism implementation of Word2Vec and based on 19.9 million molecules from the ZINC and ChEMBL databases. Consistent with steps in the Mol2Vec paper, SMILES in our datasets were tokenised by the extended-connectivity fingerprints (ECFP)-based tokenisation process and the embedding size of 300 was used. Embeddings of tokens (substructures) were summed to form the molecular embedding. Subsequently, the data was trained and tested through a 6-fold cross-validation. The feed-forward neural network (FFNN) and XGBoost regression models were applied, respectively. The FFNN models were built using Pytorch. A few sets of hyperparameters were tested based on a previous study.^32,33 For the reported results, the number of hidden units used was [300, 200, 100, 10] and the dropout rates were set as 0.25, 0.1 and 0.05 at each layer with ReLU as the activation function. The learning rate was set as 0.0001, and the Adam optimizer and a batch size of 64 were used. The model was trained for between 50 and 100 epochs. The XGBoost model was used alongside Scikit-learn.³³ The performance of the models was evaluated by root-mean-squared errors (RMSEs) and Mean absolute errors (MAEs) which inform the error distribution and coefficient of determination (R²), which captures how well the predicted solubility values agree with the experimental values. The final reported RMSEs, MAEs and R² are based on the testing data (∼200 molecules per fold).

Finetuning ChemBERTa

Two ChemBERTa models were used for finetuning: the seyonec/ChemBERTa-zinc-base-v1 model²⁷ and the DeepChem/ChemBERTa-77M-MTR,²⁸ both available on the Hugging Face repository. Hugging Face is a machine learning and data science platform hosting git-based code repositories, models, and datasets under a unified API, which simplifies data transformation and coding syntax.³⁴ The Hugging Face hub stores many pre-trained transformers/BERT models for inference and finetuning in a variety of machine learning tasks. ChemBERTa-zinc-base-v1 was trained on 100k SMILES from the zinc database via the masked language model (MLM) while ChemBERTa-77M-MTR was trained using 77 million SMILES via multi-task regression (MTR). These two models appeared to give more accurate prediction after initial testing to assess the various CHEMBERTa models for solubility prediction and therefore has been used in the present study. We also aimed to compare the performance between the two models to understand the impact of the size of the BERT training datasets. The Trainer class in Hugging Face provides an API for feature-complete training in PyTorch and was used to finetune the ChemBERTa model. As before, the data was trained, and tested with a 6-fold cross-validation to ensure all data was used for testing. The performance of the models was evaluated by RMSEs, MAEs and R² from the testing data (∼200 molecules per fold). It is worth noting that tokenisation in CHEMBERTa is different from that of the Mol2Vec model. The default Byte-Pair Encoder (BPE) from the Hugging Face tokenizers library was used which finds the tokens by iteratively merging frequent pairs of characters. In addition, we used BertViz³⁵ to visualise the attention heads of the ChemBERTa model on the HSPs.

Results and discussion

We assessed the performance of the two NPL-based models against experimental values and the baseline Morgan fingerprint approach. We further compared the quality of the prediction of HSPs against aqueous solubility from the widely benchmarked ESOL dataset. Overall, five combinations of molecular representation and machine learning methods will be discussed: Morgan fingerprints with XGBoost, Mol2Vec embeddings using XGBoost and FFNN, respectively and the two ChemBERTa finetuned models. Each of them has been applied to δ_d, δ_h, and δ_p and the ESOL aqueous solubility parameters (Table 1, Fig. 2 and 3).

Table 1 Comparison of the five models in predicting HSPs and ESOL with regards to the RMSEs, MAEs and R². The errors were computed based on 6-fold cross-validation with each testing dataset containing ∼200 molecules. The model highlighted in bold gave the best prediction for that component of solubility (note: the descriptors-based result is taken from ref. 18 using a different set of 193 small organic molecules)

	Method	MAE	RMSE	R ^2
δ d
Morgan Fps	XGBoost	0.65 ± 0.04	0.91 ± 0.07	0.74 ± 0.04
Mol2Vec	XGBoost	0.60 ± 0.02	0.88 ± 0.04	0.76 ± 0.01
Mol2Vec	FFNN	0.87 ± 0.05	1.21 ± 0.08	0.53 ± 0.07
Zinc-base		0.59 ± 0.03	0.83 ± 0.04	0.73 ± 0.03
77M-MTR		0.67 ± 0.03	0.97 ± 0.09	0.64 ± 0.08
Descriptors^18	gpHSP	0.68	1.02	0.69
δ h
Morgan Fps	XGBoost	2.13 ± 0.11	3.46 ± 0.27	0.55 ± 0.04
Mol2Vec	XGBoost	2.15 ± 0.11	3.31 ± 0.23	0.59 ± 0.03
Mol2Vec	FFNN	1.92 ± 0.13	2.84 ± 0.41	0.69 ± 0.07
Zinc-base		2.03 ± 0.25	3.17 ± 0.46	0.42 ± 0.15
77M-MTR		1.79 ± 0.25	2.70 ± 0.48	0.70 ± 0.09
Descriptors^18	gpHSP	1.57	2.41	0.83
δ p
Morgan Fps	XGBoost	2.23 ± 0.09	3.02 ± 0.16	0.51 ± 0.05
Mol2Vec	XGBoost	2.26 ± 0.10	3.12 ± 0.12	0.48 ± 0.02
Mol2Vec	FFNN	2.15 ± 0.14	2.92 ± 0.21	0.54 ± 0.04
Zinc-base		2.01 ± 0.16	2.83 ± 0.27	0.41 ± 0.14
77M-MTR		2.24 ± 0.15	3.13 ± 0.21	0.42 ± 0.04
Descriptors^18	gpHSP	1.93	2.83	0.71
ESOL
Morgan Fps	XGBoost	0.86 ± 0.04	1.15 ± 0.05	0.70 ± 0.04
Mol2Vec	XGBoost	0.68 ± 0.03	0.92 ± 0.04	0.81 ± 0.02
Mol2Vec	FFNN	0.75 ± 0.03	0.98 ± 0.05	0.78 ± 0.02
Zinc-base		0.58 ± 0.02	0.79 ± 0.05	0.85 ± 0.02
77M-MTR		0.68 ± 0.04	0.79 ± 0.05	0.85 ± 0.02
Comparison with published ESOL references
Morgan Fps^25	XGBoost	0.88	1.20	0.66
Mol2Vec^25	XGBoost	0.60	0.79	0.86
Mol2Vec^32	FFNN		0.66 ± 0.01
77M-MTR^28			0.89
MolBERT^7			0.53 ± 0.04
MFBERT^6			0.42 ± 0.50

---

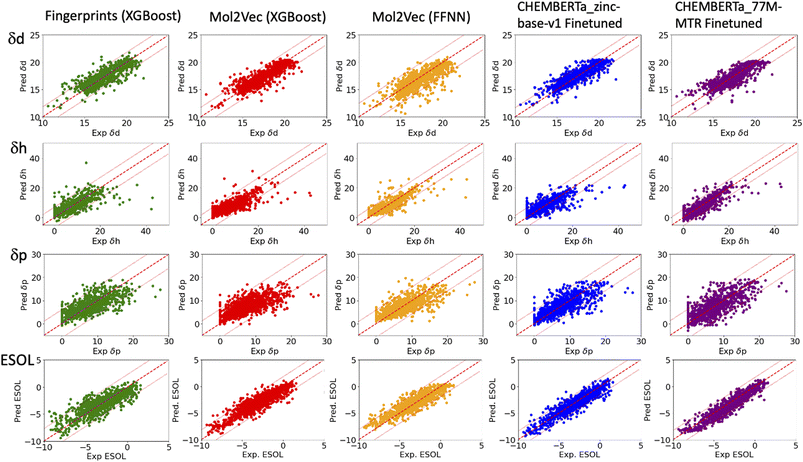Fig. 2 Plots of the predicted δ_d, δ_h and δ_p of the HSPs (top three rows) and ESOL solubility (bottom row) versus their respective experiment values. The solid red lines indicate ideal agreement between the predicted and experimental values. The dashed red lines indicate two standardised residual deviations (SRD) away from the experimental values. Molecules beyond the dashed lines are the outliers in each model and were further analysed in Fig. 4.

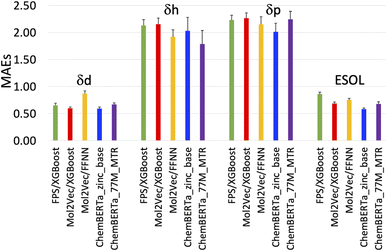Fig. 3 Plot of the mean absolute errors (MAEs) of the five models in Table 1.

Comparison with baseline Morgan fingerprints

The RMSEs, MAEs and R² of all the predicted solubility parameters are presented in Table 1. In terms of MAEs and RMSEs, both Mol2Vec and ChemBERTa finetuning models outperform the Morgan fingerprint baseline models albeit not by a significant extent and can be sensitive to ML methods (i.e., the FFNN and XGBoost of Mol2Vec embeddings tend to give varied accuracies). This is consistent with what has been observed in several previous studies³² and is expected as the embeddings derived from the two NLP models capture a latent representation of the physicochemical properties of molecules, therefore should be more informative than the simple encoding of the presence of specific molecular functional groups in the Morgan fingerprint approach.

Accuracy of the predicted HSPs

To benchmark, we compared our results with the well-studied ESOL dataset. The predicted ESOL is in excellent agreement with the published values, which validates our approaches (Table 1). There is a considerable variation of the models' prediction power over δ_d, δ_h, and δ_p. The accuracy of predicted δ_d (MAE 0.59, RMSE 0.83, and R² 0.73 for the best model) is the highest, significantly higher than δ_h, and δ_p for all models (Table 1). This is followed by predicted δ_h (MAE 1.79, RMSE 2.70, and R² 0.7) while predicted δ_p has the lowest accuracy (MAE 2.01, RMSE 2.83, and R² 0.4). The δ_d > δ_h > δ_p trend for the predicted accuracy and the range of MAEs and RMSEs are consistent with results from a previous study which used chemical descriptors and the Gaussian process, a Bayesian machine learning approach to predict the HSPs of 193 small organic molecules.¹⁸ There may be intrinsic limits to how machine learning approaches can predict this type of solubility parameters.

Outliers

In general, the models are more likely to overestimate lower-value HSPs and underestimate higher value HSPs (Fig. 2). For the lower value HSPs, this may be in part because the models failed to learn the δ_h and δ_p which are zero in value. For the higher range of HSPs, it may be because these data points are scarce and tend to be under-represented in the training set. In addition, the models were finetuned using three separate sets of labelled data (δ_d, δ_h and δ_p). It is clear that the accuracy of the predicted HSPs of the same molecule is not correlated, i.e. δ_d of the molecule may be predicted poorly while δ_h and δ_p may be predicted with good accuracy.

The predicted values two standardised residual deviations (SRDs) away from the experimental values are selected as the outliers in each model (see Table S2 in the ESI† for the list of outliers). These poorly predicted molecules were analysed to identify possible systematic limitations. The difference in the average occurrence of the functional groups between the outliers and the full dataset is presented in Fig. 4 and S5 in the ESI.† The positive values indicate the increased presence of the functional groups and the negative values indicate fewer functional groups in the outliers. For δ_d, the most frequent functional groups in the outliers are Halides (F, Cl, Br and I), and to a lesser extent nitrile, P and S. All three models (fps, Mol2Vec and ChemBERTa) performed poorly against Halides. CHEMBERTa-77M-MTR is the worst-performing one primarily because it handles Cl badly. For δ_h, consistent among all the models, the outliers tend to have more hydrogen bond donors and acceptors. However, CHEMBERTa-77M-MTR performs better than CHEMBERTa-zinc-base-v1 in general, therefore giving the best result for predicted δ_h. For δ_p, the functional groups in the outliers are more diverse and no distinct functional groups stand out. It is also interesting that the larger CHEMBERTa model performed worse than the smaller CHEMBERTa model in terms of Cl, while the smaller CHEMBERTa model tends to perform slightly poorly for carbonyl, alkene and H-bond acceptor. As a comparison, for the ESOL dataset, the outliers' functional groups are more diverse, which is similar to δ_p. In terms of the size of the molecules, outliers from predicted δ_d have similar molecular weight to the full Hansen dataset while outliners from predicted δ_h and δ_p are smaller than the full Hansen dataset (Fig. S6†). On the other hand, outliers from the ESOL set have higher average molecular weight than the full dataset. It appears that Mol2Vec and CHEMBERTa models don't have a general bias over molecular weight, but they may have some limit towards smaller or bigger molecules depending on the predicted molecular properties.

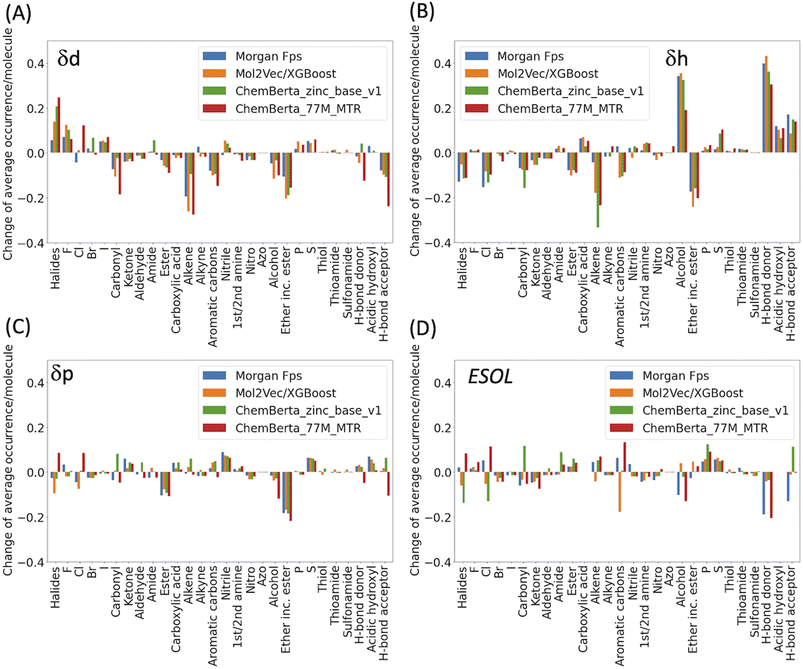Fig. 4 Functional group analysis of the outliers for (A) δ_d, (B) δ_h, (C) δ_p and (D) ESOL. Functional groups were counted by matching their SMARTS codes to the SMILES strings. The total number of each functional group was then divided by the number of molecules in the outliers to derive the average occurrence per molecule (Fig. S5†). For clarity, the difference of the average occurrence of functional groups between the outliers and the full dataset are presented in the above figures.

Attention visualisation

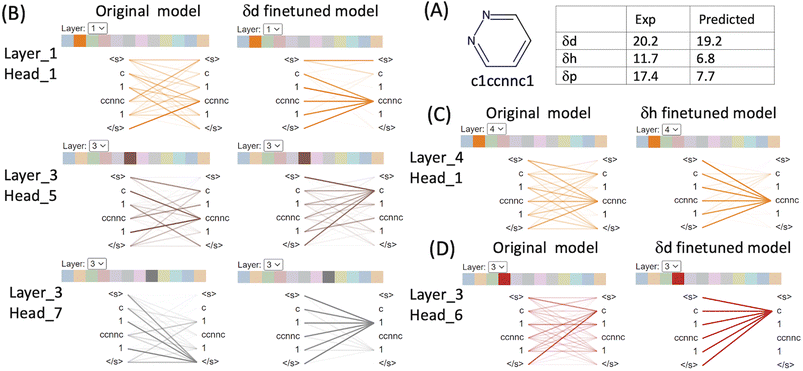
We used BertViz to visualise the attention mechanisms of outliers from the original CHEMBERTa_zinc-base-v1 model and the finetuned models to understand what they have learned from the molecular structures and their labels. The ChemBERTa model has 6 hidden layers and 12 attention heads in every layer. Since model weights are not shared between layers, the model has 72 different attention mechanisms. Attention is visualised as lines connecting the position being updated (left) with the position being attended to (right). The colours identify the corresponding attention heads while the thickness of the lines reflects the attention score. General attention patterns are present including attention to the previous/next token, attention to identical/related tokens, and attention to the delimiter token </s> when the attention head can't find anything meaningful in the input molecule to focus on (Table S1 in the ESI†).

It is clear that the attention mechanisms are different in the finetuned models compared to the original ChemBERTa model. The attention focuses more on the atoms that give rise to the HSPs in the finetuned models. For example, pyridazine (SMILES: c1ccnnc1) is an aromatic heterocyclic compound.³⁶ It contains a six-membered ring with two adjacent nitrogen atoms. The molecule has a high dipole moment with π–π stacking interactions and dual hydrogen-bonding capacity (both as hydrogen bond donor and as acceptor). Its simple structure and strong characters relating to the HSPs make it easier to interpret the attention mechanism from ChemBERTa (Fig. 5 and Table S1 in the ESI†). In the δ_d finetuned model, strong attention is distributed among c[token1], 1[token2] and ccnnc[token3]. [c] represents an aromatic carbon and [1] indicates connectivity to form an aromatic ring. [ccnnc] includes the two nitrogen – the hydrogen acceptor in the molecule. All 3 tokens contribute to δ_d because the dispersion parameter is based on the atomic forces of all the atoms in the molecule. In the δ_h finetuned model, the attention focuses more on the hydrogen bond acceptor token [ccnnc] in layer_2/(head_4), layer_3/(head_2, 5, 10 and 11), layer_4/(head_0, 1, 7) and layer_5/(head_0). In the δ_p finetuned model, there is a strong focus on the [c] token that is not seen in δ_d and δ_h. Attention to [c] is dominant in layer_1/(head_11), layer_2/(head_0, 2, 4 and 10), and layer_3/(head_1, 2, 3, 4, 5, 6, 8, and 11). The δ_d finetuned model gave an excellent prediction of 19.2 compared to the experimental value of 20.2. The δ_h finetuned model performed worse with predicted δ_h 6.8 (exp δ_h 11.7) and the δ_d finetuned model the poorest with predicted δ_p 7.7 compared to the exp δ_p 17.4.

Fig. 5 Attention analysis of pyridazine using BertViz based on the original CHEMBERTa_zinc-base-v1 model and the finetuned models. (A) Molecular structure and SMILES of pyridazine and its experimental and predicted HSPs. Selective visualisation of attention is presented for the original model and the δ_d finetuned model (B), δ_h finetuned model (C) and δ_p finetuned model (D).

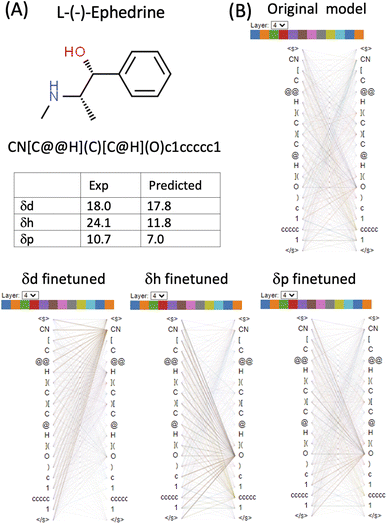
L-(−)-Ephedrine (SMILES: CN[C@@H](C)[C@H](O)c1ccccc1) has an aromatic ring, a hydroxyl (OH) and an amine (NH) functional group. The two tetrahedral centres are indicated by the chiral specification simple of @ and @@ in the SMILES (Fig. 6 and Table S1 in the ESI†). In the δ_d finetuned model, some heads (0, 1, 3, 4, 8 and 11) in layer_4 focus strongly on the [CN] token. In the δ_h finetuned model, some heads (1, 2, 3, 6, 7, 10 and 11) in layer_4 focus on the [O] token. Attention is generally more evenly distributed in the δ_p finetuned model with the focus on both [CN] and [O]. Both δ_d and δ_p are reasonably predicted (predicted 17.8 vs. exp 18.0 for δ_d and predicted 7 vs. exp 10.7 δ_p) while δ_h is significantly underestimated (predicted 11.8 vs. exp 24.1) for this molecule. Based on the visualization of attention mechanisms, it is plausible that the δ_h finetuned model only learned OH but not NH functional group as a hydrogen bond donor, therefore underestimating δ_h.

Fig. 6 Attention analysis of L-(−)-ephedrine using BertViz based on the original CHEMBERTa_zinc-base-v1 model and the finetuned models. (A) Molecular structure and SMILES of L-(−)-Ephedrine and its experimental and predicted HSPs. (B) Visualisation of attention of layer_4 is presented for the original model, and the δ_d, δ_h and δ_p finetuned models.

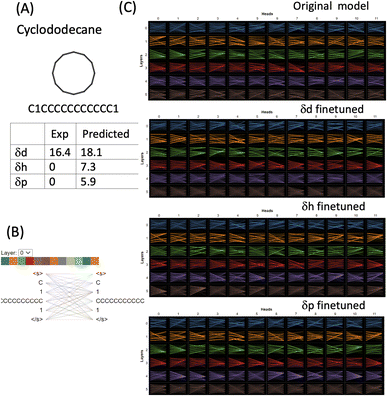
For strictly nonpolar molecules, the δ_p and δ_h terms are zeros by definition in HSPs. Cyclododecane (SMILES: C1CCCCCCCCCCC1) is such a macrocycle molecule that contains a twelve-membered ring (molecular formula (CH₂)₁₂). δ_d of cyclododecane is 16.4 while its δ_p and δ_h are both zeroes (Fig. 7). The molecule is tokenised into four tokens [C], [1], [CCCCCCCCCCC] and [1]. 11 carbons from the ring structure are grouped into one token while the two [1] and the last [C] which indicates that the connectivity is set as three separate tokens. Attention is distributed among all the tokens and although the attention mechanisms change in the finetuned models, the way the molecule is tokenised makes them difficult to interpret. The δ_d finetuned model gave a reasonable prediction of 18.1 (exp 16.4), but δ_h and δ_d were both overestimated (7.3 and 5.9). The finetuned models failed to grasp the correlation between nonpolar molecules and zero value for HSPs. However, it is important to point out that HSPs use a simplified way to define the polarity of molecules. Cyclododecane can adopt multiple conformations and has a sizable dipole moment,³⁷ therefore assigning its δ_d as 0 is a significant underestimation and does not reflect the complexity and conformational flexibility of its structure. Cyclododecane occupies a unique chemical space and has been used in drug discovery. There are several challenges for the prediction of HSPs of such unique molecules: (1) better ways to tokenise molecular structure. The 11-carbon token in our approach may be too long and will be scarce in the training set. Shorter tokens of a few carbons may account for local structural flexibility better. (2) The limit of HSPs' theoretical framework, in particular, how δ_p and δ_h terms may have large intrinsic errors for complex molecules.

Fig. 7 Attention analysis of cyclododecane using BertViz based on the original CHEMBERTa_zinc-base-v1 model and the finetuned models. (A) Molecular structure and SMILES of cyclododecane and its experimental and predicted HSPs. (B) Tokens used in the model. (C) Visualisation of attention of all layers is presented for the original model, the δ_d, δ_h and δ_p finetuned models.

General discussion

In the present study, we have predicted different components of solubility using two molecular embedding approaches. The significantly varied prediction accuracy for the three parameters of HSPs along with ESOL aqueous solubility parameters is intriguing. It raises interesting questions as to how finetuning tasks may benefit from the improvement of pretraining, e.g., increased pretraining dataset size. More importantly, it indicates that how much the pre-trained model can be leveraged for transfer learning may relate to the nature of the molecular properties in the labelled dataset, a key area to investigate further to enable more effective use of BERT-based models for molecular property prediction.

First of all, our results may be explainable by the underlying nature of these parameters and the experimental errors associated with them. The HSPs were derived from three main types of interactions in common organic molecules. The most common is the nonpolar interactions, which are usually referred to as the atomic dispersion forces (δ_d). All molecules contain this type of force, therefore δ_d is usually the predominant component of total solubility while δ_h and δ_p has relatively small contributions. δ_d can be predicted quite well with just Morgan fingerprints, indicating that it is dependent more on the molecular structure. Because the dispersion parameter is based on atomic forces, the size of the atom is important. To determine δ_d experimentally or theoretically, corrections are usually required for atoms significantly larger than carbon, such as Cl and Br but not for oxygen and nitrogen that are of similar size. The impact of the corrections is larger for small molecules.³⁸ This is consistent with our results that for δ_d, the most frequent functional groups in the outliers are the halides (F, Cl, Br and I). The fact that the models handled halides poorly could be due to a combination of two factors – the intrinsic errors in the experimental data associated with the halide atoms and the scarcity of this type of molecules in the training set.

δ _h arises from the hydrogen bonding capacity of the molecule and has been used to collect the cohesive energy component that is not included in the other two parameters. δ_h was most often found by subtracting the polar and dispersion components from the total solubility. Therefore, δ_h is less well defined physicochemically, and the experimental errors associated with δ_h are bigger than those of δ_d. This may explain why the predicted accuracy of δ_h is lower than δ_d.

δ _p arises from dipole–dipole interactions between molecules. Most molecules (except few strictly nonpolar molecules) contain these inherent molecular forces to some extent, in a way similar to the ubiquitous atomic dispersion forces in all molecules. Therefore, it is intriguing that there is a significant difference in our models' accuracy of δ_d over δ_p, despite both parameters involving all atoms of the molecules. In a previous study using descriptor-based machine learning approach,¹⁸ it was found that δ_d appeared to be more dependent on molecular structure, while δ_p depended more on the electrostatic descriptors (dipole moment, polarizability, polarity and hydrogen-bonding moments). Electrostatic properties are more complex as they are description of how atoms influence each other within a molecule. To improve model accuracy, an increased number of labelled data may be needed to finetune BERT for it to learn the more complex interactions within molecules. More labelled data can be easily generated for future studies because δ_p is well-defined and can be derived from dipole moment of molecules calculated using quantum mechanical calculations.

Comparison with the well-benchmarked ESOL aqueous solubility dataset also provided useful insights. Dissolution is a complex process that involves solute–solute, solvent–solvent and solute–solvent interactions. Aqueous solubility is dominated by solvation energy and solvent–solute interactions, due to water's high polarity and its capability for hydrogen bonding.^20,39 In contrast, HSPs mainly account for solute–solute interactions i.e. cohesive/sublimation energy, which has always been more challenging to predict.⁴⁰ Therefore the ESOL ≈ δ_d > δ_h > δ_p trend of prediction accuracy is in agreement with our understanding of the physical aspects of the dissolution process.

Finally, it is important to point out that experimental HSP values exhibit significant uncertainties. δ_p has the largest uncertainties. For example, the value derived from the dipole moment could be much smaller than values derived from the group contribution methods.^38,41 Large inconsistencies between δ_h values have been observed for compounds with strong hydrogen bonds, such as urea.⁴¹ Similarly, it has also been pointed out that experimental data quality could be a limiting factor in predicting the aqueous solubility of molecules.²²

Conclusions

In conclusion, we predicted HSPs based on only the SMILES of molecules using the so-called molecular embedding approaches. Upon finetuning, the ChemBERTa model “learned” relevant molecular features and shifted attention to functional groups that give rise to the relevant HSPs. The finetuned ChemBERTa model outperforms both the Mol2Vec model and the baseline Morgan fingerprint method and gives accuracy slightly lower or on a par with the more computing-intensive chemical descriptors-based models. In general, the embedding models can predict δ_d significantly better than δ_h and δ_p and overall, the accuracy of predicted HSPs is lower than the well-benchmarked ESOL aqueous solubility. The ESOL ≈ δ_d > δ_h > δ_p trend of prediction accuracy is in agreement with our understanding of the physical aspects of the dissolution process, i.e., HSPs mainly account for solute–solute interactions from cohesive/sublimation energy, which has always been more challenging to predict than the aqueous solubility which is dominant by solvent–solute interactions. In addition, our study indicates that the labelled molecular properties in the finetuning datasets may determine how much the pre-trained model can be leveraged for transfer learning. This is most likely due to the limit of HSPs' theoretical framework, and in particular, how the δ_p and δ_h terms may have large intrinsic errors in the way they are defined and derived, therefore introducing inherent limitation to the accuracy of their prediction from data-driven approaches. It would be worthwhile to consider refining the Hansen solubility framework using a combination of standardised experimental measurement, quantum mechanical calculations and machine learning models.

Data availability

Code repository to build models along with relevant datasets is available at https://github.com/jiayunpang/hsp_embedding.

Author contributions

J. Pang conceived and designed the study; J. Pang, A. W. R. Pine and A. Sulemana carried out the research; J. Pang wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Xinglong Wang for his helpful discussion. The work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) (grant number EP/Y004167/1) and by the University of Greenwich High Performance Computing (HPC) facility.

References

1. D. Flam-Shepherd, K. Zhu and A. Aspuru-Guzik, Nat. Commun., 2022, 13, 3293.
2. B. J. Wittmann, K. E. Johnston, Z. Wu and F. H. Arnold, Curr. Opin. Struct. Biol., 2021, 69, 11–18.
3. J. Vig, A. Madani, L. R. Varshney, C. Xiong, R. Socher and N. F. Rajani, BERTology Meets Biology: Interpreting Attention in Protein Language Models, 2020.
4. I. Lee and H. Nam, Infusing Linguistic Knowledge of SMILES into Chemical Language Models, 2022.
5. K. K. Yang, Z. Wu, C. N. Bedbrook and F. H. Arnold, Bioinformatics, 2018, 34, 2642–2648.
6. H. Abdel-Aty and I. R. Gould, J. Chem. Inf. Model., 2022, 62, 4852–4862.
7. B. Fabian, T. Edlich, H. Gaspar, M. Segler, J. Meyers, M. Fiscato and M. Ahmed, Molecular representation learning with language models and domain-relevant auxiliary tasks, arXiv, 2020, preprint, arXiv:2011.13230 [cs.LG],  DOI:10.48550/arXiv.2011.13230.
8. P. Karpov, G. Godin and I. V. Tetko, J. Cheminf., 2020, 12, 17.
9. I. Baskin, A. Epshtein and Y. Ein-Eli, J. Mol. Liq., 2022, 351, 118616.
10. A. Jouyban, Handbook of Solubility Data for Pharmaceuticals, CRC Press, 2009.
11. S. Lee, M. Lee, K.-W. Gyak, S. D. Kim, M.-J. Kim and K. Min, ACS Omega, 2022, 7, 12268–12277.
12. C. M. Hansen, The three dimensional solubility parameter and solvent diffusion coefficient: Their importance in surface coating formulation, 1967.
13. Developments and Applications in Solubility, ed. T. M. Letcher, Royal Society of Chemistry, Cambridge, 2007, pp. P007–P008.
14. E. Stefanis and C. Panayiotou, Int. J. Thermophys., 2008, 29, 568–585.
15. E. Stefanis, L. Constantinou and C. Panayiotou, Ind. Eng. Chem. Res., 2004, 43, 6253–6261.
16. M. Enekvist, X. Liang, X. Zhang, K. Dam-Johansen and G. M. Kontogeorgis, Chin. J. Chem. Eng., 2021, 31, 186–197.
17. M. Przybyłek, T. Jeliński and P. Cysewski, J. Chem., 2019, 2019, 9858371.
18. B. Sanchez-Lengeling, L. M. Roch, J. D. Perea, S. Langner, C. J. Brabec and A. Aspuru-Guzik, Adv. Theory Simul., 2019, 2, 1800069.
19. R. Han, H. Xiong, Z. Ye, Y. Yang, T. Huang, Q. Jing, J. Lu, H. Pan, F. Ren and D. Ouyang, J. Controlled Release, 2019, 311–312, 16–25.
20. S. Boobier, D. R. J. Hose, A. J. Blacker and B. N. Nguyen, Nat. Commun., 2020, 11, 5753.
21. A. D. Vassileiou, M. N. Robertson, B. G. Wareham, M. Soundaranathan, S. Ottoboni, A. J. Florence, T. Hartwig and B. F. Johnston, Digital Discovery, 2023, 2, 356–367.
22. D. S. Palmer and J. B. O. Mitchell, Mol. Pharm., 2014, 11, 2962–2972.
23. T. Mikolov, K. Chen, G. Corrado and J. Dean, Efficient Estimation of Word Representations in Vector Space, 2013.
24. J. Devlin, M.-W. Chang, K. Lee and K. Toutanova, BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding, 2018.
25. S. Jaeger, S. Fulle and S. Turk, J. Chem. Inf. Model., 2018, 58, 27–35.
26. S. Wang, Y. Guo, Y. Wang, H. Sun and J. Huang, in Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, ACM, New York, NY, USA, 2019, pp. 429–436.
27. S. Chithrananda, G. Grand and B. Ramsundar, ChemBERTa: Large-Scale Self-Supervised Pretraining for Molecular Property Prediction, 2020.
28. W. Ahmad, E. Simon, S. Chithrananda, G. Grand and B. Ramsundar, ChemBERTa-2: Towards Chemical Foundation Models, 2022.
29. https://www.stevenabbott.co.uk/practical-solubility/hsp-basics.php .
30. J. S. Delaney, J. Chem. Inf. Comput. Sci., 2004, 44, 1000–1005.
31. RDKit: Open-source cheminformatics, https://www.rdkit.org.
32. M. V. Sabando, I. Ponzoni, E. E. Milios and A. J. Soto, Briefings Bioinf., 2022, 23, bbab365.
33. F. Pedregosa, G. Varoquaux, A. Gramfort, B. Michel, V. Thirion, O. Grisel, M. Blondel, R. Prettenhofer, P. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
34. T. Wolf, L. Debut, V. Sanh, J. Chaumond, C. Delangue, A. Moi, P. Cistac, T. Rault, R. Louf, M. Funtowicz, J. Davison, S. Shleifer, P. von Platen, C. Ma, Y. Jernite, J. Plu, C. Xu, T. Le Scao, S. Gugger, M. Drame, Q. Lhoest and A. M. Rush, HuggingFace's Transformers: State-of-the-art Natural Language Processing, arXiv, 2020, preprint, arXiv:1910.03771,  DOI:10.48550/arXiv.1910.03771.
35. J. Vig, in Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics: System Demonstrations, Association for Computational Linguistics, Florence, Italy, 2019, pp. 37–42.
36. N. A. Meanwell, Med. Chem. Res., 2023, 32, 1853–1921.
37. E. Burevschi and M. E. Sanz, Molecules, 2021, 26, 5162.
38. C. M. Hansen, Hansen Solubility Parameters, CRC Press, 2007.
39. J. D. Thompson, C. J. Cramer and D. G. Truhlar, J. Chem. Phys., 2003, 119, 1661–1670.
40. I. V. Tetko, Y. Sushko, S. Novotarskyi, L. Patiny, I. Kondratov, A. E. Petrenko, L. Charochkina and A. M. Asiri, J. Chem. Inf. Model., 2014, 54, 3320–3329.
41. D. Mathieu, ACS Omega, 2018, 3, 17049–17056.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3dd00119a

---