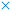Mechanistic origins for the enhanced ethanol dehydration kinetics in H-ZSM-5 by cofeeding n-butanol

Abstract

Periodic density functional theory (DFT) with dispersion corrections is used to construct a detailed reaction network for dehydration of n-butanol/ethanol mixtures in H-ZSM-5. Apart from the direct conversion of the alcohols to olefins or di-alkyl-ethers, novel mechanisms have been explored for the formation and decomposition of a cross-ether, butyl ethyl ether. Furthermore, a novel mechanism that affects the intrinsic activity of ethanol dehydration to ethene is found, the n-butanol-assisted ethanol dehydration. Thermodynamic and kinetic parameters for all elementary reaction steps were calculated and implemented in a microkinetic model capable of simulating the dehydration of (i) pure ethanol, (ii) pure n-butanol and (iii) n-butanol/ethanol mixtures over a H-ZSM-5 catalyst. The microkinetic model was able to reasonably predict the observed experimental results. A reaction path analysis shows that the mixed ether is primarily formed through an S_N2 mechanism, where the water is split off from ethanol, except at low alcohol pressure. The mixed ether decomposes predominantly to butenes and ethanol. Contrary to pure ethanol dehydration, if sufficient n-butanol is available, ethylene is primarily formed through a novel butanol-assisted mechanism for n-butanol/ethanol mixtures, indicating the intrinsic activity for ethanol dehydration is – here beneficially – altered by cofeeding of butanol. These results hint towards the possibility of cofeeding strategies to accelerate the conversion of a less reactive reagent.

---

1. Introduction

The development of a sustainable chemical industry essentially relies on shifting our dependence on petroleum towards renewable feedstocks, and this change in feedstock further stimulates the advancement of biomass-based technologies.^1–5 Light olefins are the crucial building blocks of the chemical industry, with a total production volume approaching 3.0 × 10⁸ t a⁻¹.^6–9 Therefore the conversion of biomass, such as bio-alcohols, to olefins could assist in the transition towards biomass-based technologies. As bio-alcohols are typically obtained as mixtures, e.g. acetone–butanol–ethanol (ABE) fermentation,¹⁰ CO₂ hydrogenation,…¹¹ recently efforts have been undertaken to convert them directly without prior separation.^12–14 However, the selection of a suitable catalyst and reaction conditions to process these mixtures remains a challenging task. Fundamental understanding of the associated reaction mechanisms for alcohol mixtures would allow further progression of catalyst design. Theoretical studies based on density functional theory (DFT) can aid in understanding and finding the parameters responsible for the reactivity and selectivity. Furthermore, DFT calculations allow to determine kinetic and thermodynamic parameters that can be used to develop a microkinetic model. Combining DFT with microkinetic modeling, in which the catalytic reaction is described in terms of elementary reaction steps,¹⁵ allows to unravel reaction mechanisms. By applying the microkinetic model to describe and predict experimental data, it is possible to extract insights that allow the rational design of new catalytic materials.

The dehydration of single alcohol streams has been widely investigated, both experimentally and theoretically.^16–20 For the dehydration of single alcohols, an important catalyst is H-ZSM-5,^16,20–23 which is currently also used in industrial scale ethanol dehydration plants.²⁴ The reactivity of alcohols is chain-length dependent, with higher alcohols showing higher turnover rates.^14,21 Chain branching of alcohols also leads to higher reactivity, due to the increased stability of intermediates with carbenium ion characteristics.²⁵ However, there have been considerably less studies on the effects of feedstock composition on the reaction kinetics and product selectivity.¹³ Insights into these feedstock effects could enhance the processing of bioderived alcohols.

Generally, the conversion of alcohols to their corresponding alkenes follows multiple pathways: (i) a direct pathway, essentially an intramolecular dehydration towards the corresponding alkene, (ii) an indirect pathway, where an intermediate ether is formed through an intermolecular dehydration, which can be followed by decomposition of the ether towards the alcohol and alkene, see Fig. 1. The intramolecular and intermolecular dehydration are parallel reaction pathways and the ether decomposition is consecutive to the ether formation.^16,20,26

Fig. 1 Reaction scheme for alcohol dehydration. Path A: direct dehydration to respective alkene(s), Path B: etherification reaction, Path C: ether decomposition towards respective alcohol and alkene.

In this work, a first principles based microkinetic modeling approach is utilized to investigate the dehydration reaction mechanism of n-butanol/ethanol mixtures over H-ZSM-5. For the microkinetic model, we started from an ethanol and n-butanol dehydration model for pure alcohol streams as earlier reported by our research group.^20,21,23 We then combined and extended these models to account for additional reaction pathways related to the utilization of alcohol mixtures. New reaction mechanisms are explored for the formation of a mixed ether, ethyl butyl ether (EBE). Additional mechanisms for the dehydration of n-butanol to 1-butene and ethanol to ethene are discovered, for which a new n-butanol-assisted pathway to form ethene is competitive with the mechanisms when using pure ethanol as feedstock. The additional mechanisms that were found within the direct dehydration pathways highlight the complexity of mixtures as feeds and provide some creative tools to enhance the kinetics of the dehydration of short chain alcohols in a mixture of short and slightly higher chain alcohols.

2. Methodology

2.1 Catalyst model

The H-ZSM-5 framework structure with Pnma symmetry, unit cell composition – HAlSi₉₅O₁₉₂ and unit cell as in ref. 20 and 27 is used in this study. The zeolite acid site is created by replacing a Si atom with an Al atom and adding a proton to the oxygen atom adjacent to the channel intersection (Si₃–O₂₀(H)–Al₁₂ position²⁸). The location of the Al atom in the unit cell has been experimentally found to be non-random²⁹ and dependent on zeolite synthesis conditions.³⁰ Multiple experimental studies show that typically the bulk of the Al is located at the intersection.^31,32 Furthermore, theoretical studies specify the T12 site to be the energetically preferred location for the Al atom associated with the Brønsted acid site.^33,34 When the Al atom is located at the T12 site, the Brønsted acid site is accessible to molecules located in both the straight and sinusoidal channels and could accommodate larger species. Accordingly, the T12 tetrahedral site is selected for the replacement of a Si atom with Al, while the zeolite proton is chosen to be located at the oxygen atom adjacent to the channel intersection.³⁵

2.2 Computational details

2.2.1 Electronic energy calculations. The Vienna Ab Initio Simulation Package (VASP) is used to perform dispersion-corrected periodic DFT calculations.^36–38 All calculations are performed, consistent with previous work,^20,21,39 to allow comparison and implementation in one microkinetic code framework. The calculations are performed using plane wave basis sets, the electron-ion interactions are described using the projector-augmented wave (PAW) method^40,41 with a plane-wave energy cut-off of 600 eV. The exchange correlation energies are calculated on the basis of the generalized gradient approximation (GGA) according to Perdew, Burke and Ernzerhof (PBE).⁴² Sampling of the Brillouin zone was restricted to the Γ-point. The forces in all calculations have a convergence criterion of 0.02 eV Å⁻¹ and each self-consistency loop was iterated until a convergence level of 10⁻⁸ eV was achieved. Dispersive corrections to better account for van der Waals-type of interactions were included by adding a pairwise interaction term to the Kohn–Sham energy using the DFT-D2 approach proposed by Grimme⁴³ and extended by Kerber et al.⁴⁴ for periodic PBE calculations. Although systematic deviations may be observed due to the overestimation of the dispersion interaction,^45–48 DFT-D2 has been widely applied for the theoretical investigation of adsorption^27,49–51 and reaction in zeolites^51,52 and is known to provide reasonably accurate results.^46,53 Furthermore, in recent studies by Gunst et al. and de Reviere et al. it was found that a DFT-based microkinetic model, using the PBE functional with D2-corrections could describe experimentally observed results for the n-butanol dehydration over H-ZSM-5 relatively well.^16,17,23 Despite the PBE-D2-based approach is not expected to yield electronic energies within chemical accuracy, the errors are generally systematic and will cancel out in most of the reaction and activation energies, leading to meaningful values.⁵⁴ Transition state structures are optimized using dimer^55,56 calculations, which searches for a nearby saddle point from an initial configuration close to the transition state. The initial configurations are based upon nudged elastic band calculations,⁵⁷ that are used to find an initial guess for the minimal energy path.

2.2.2 Frequency calculations. Normal mode analysis is performed using a Partial Hessian Vibrational Analysis (PHVA), relaxing the T5 cluster (HAl(SiO₄)₄) of the zeolite framework and the adsorbate molecule for the numerical Hessian calculation. Transition states are confirmed to have one imaginary frequency, strongly different from 0. Previous studies for physisorption and chemisorption in zeolites have shown that the partial Hessian approach leads to a marginal difference in the result as compared to a Full Hessian Vibrational Analysis (FHVA).⁵⁸ Furthermore, this allows comparison with earlier theoretical studies, on which this work builds upon, where PHVA were used to perform normal mode analysis. Although stringent geometry optimization (maximum force criterion of 0.02 eV Å⁻¹) and electronic convergence (10⁻⁸ eV) criteria have been used, small false imaginary frequencies were still present in very few cases. If present, these are encountered in physisorbed surface species. The low lying frequencies (<50 cm⁻¹) associated with the frustrated motions of the surface bound species (such as translation or rotation of the molecule within the zeolite pore structure) could lead to significant error in the entropy calculations.^59–62 A more accurate estimation of the entropic contributions could be obtained by accounting for anharmonicities by detailed scanning of the potential energy surface,^63,64 but this would require significant computational efforts for large systems. Another approach to treat the low lying modes is the use of a frequency cutoff.^49,59,60,65 De Moor et al.⁶⁵ studied the entropy contributions of these frequencies for alkanes and alkenes in FAU zeolite and suggested the replacement of all frequencies below 50 cm⁻¹ and spurious yet very small imaginary frequencies with 50 cm⁻¹. Therefore, in order to obtain consistent results, also in this work the small imaginary and low-lying frequencies (<50 cm⁻¹) were replaced by normal modes of 50 cm⁻¹.⁶⁵

2.2.3 Statistical thermodynamics. Standard enthalpies, entropies, Gibbs free energies, adsorption and reaction equilibrium coefficients (K) and rate constants are obtained from total canonical partition function by statistical thermodynamics calculations,⁶⁶ the calculations are shown in the ESI,† section S1 Eqn. S1 and S2.

The reaction rate coefficients of elementary reaction steps are calculated on the basis of transition state theory:

where k_B is Boltzmann constant, h is Planck constant and ΔG^0,‡ the transition state Gibbs free energy barrier. Arrhenius pre-exponential factors (A) and activation energies (E_a) are obtained by regression of eqn (1) in the temperature range of 300–800 K.

To describe quasi-equilibrated steps such as adsorption steps, a pragmatic approach as suggested in ref. 20 and 21 is utilized. Here, the rate constants of the adsorption steps are calculated as k_ads = k_BT/h, while the reaction rate coefficient for the desorption step is calculated from thermodynamic consistency as k_des= k_ads/K_ads. This will ensure adsorption/desorption is at equilibrium compared to the slower catalytic reaction steps.

2.3 Microkinetic and reactor modeling

A microkinetic model is constructed to enable the prediction of reaction rates based on the DFT-derived thermodynamic and rate coefficients, and this microkinetic model is embedded in a reactor model to allow for a dynamic interplay between reaction rate and partial pressures of the gas phase reactants and products, which allows comparison of the predictions with experimental observations. On top of this, the developed model allows to perform reaction path analysis and study the effect of operating conditions.

The model used in this work is constructed starting from previously published models for the dehydration of n-butanol over H-ZSM-5 (ref. 16) and for the dehydration of ethanol over HZSM-5.²¹ These models are evaluated, combined and extended with the newly explored reaction mechanisms of this work to cover all possible reactions that can occur during the simultaneous dehydration of ethanol and butanol. The complete microkinetic model consists of 75 reaction steps, of which all the kinetic and thermodynamic parameters were determined from first principle calculations as described in 2.2. As the thermodynamics of the global reactions from gas-phase alcohols to alkenes or ethers as determined by DFT can deviate from those reported in experimental databases, such as NIST,⁶⁷ corrections are applied to the gas phase enthalpies/entropies to ensure that the overall gas-phase thermodynamics implemented in the microkinetic model are consistent with experimental thermodynamics.

The microkinetic model is solved as a function of reaction conditions in a plug flow reactor model to predict catalytic activities and selectivities. The reactor model allows assessing the effect of a realistic build-up of product pressures, which is necessary to calculate meaningful turnover frequencies (TOFs) that can be compared with experimental results. Continuity equations are applied for the gas-phase components i and surface species k along with a site balance in order to determine individual turnover frequencies (TOFs), coverages(θ) and overall rates (R_i):

where TOF_j is the turnover frequency of elementary step j (mol mol_sites⁻¹ s⁻¹), ν_ji the stoichiometric coefficient of component i in the elementary step j, θ_k the fractional coverage of surface species k (mol mol_sites⁻¹), θ* the fractional coverage of free acid sites (mol mol_sites⁻¹), C_a the concentration of acid sites (mol_sites kg⁻¹), F_i the molar flow rate of gas-phase component i (mol s⁻¹), W the mass of the catalyst (kg) and R_i the net production rate of gas-phase species i (mol kg⁻¹ s⁻¹). This set of equations is solved transiently, using the numerical integration LSODA module of ODEPACK.⁶⁸ Microkinetic model parameters are regressed by minimizing the residual sum of squares between the model predicted flow rates and experimental flow rates.

2.4 Experiments

The catalytic experiments are performed in an isothermal plug flow reactor, where the space time is varied to obtain conversion levels between 15–80%, the inlet partial pressure of n-butanol is fixed at 29 kPa, and that of ethanol at 7.8 kPa and the studied temperatures are 503 and 513 K. The experimental procedure is reported previously,¹⁴ additional information is available in section S4.† To compare experimental and theoretical results on an active site basis, site time is calculated as:With W is the mass of catalyst (kg), C_a the density of strong acid sites of the catalyst (mol kg⁻¹) and F⁰ is the combined molar flow rate of n-butanol and ethanol. The conversion of n-butanol and ethanol (X_BuOH and X_EtOH) and selectivity to their products (S_i,j) are calculated as:With X_j the conversion of feed component j, F_j⁰ the inlet molar flowrate of component j (mol s⁻¹), F_j the outlet molar flowrate of component j (mol s⁻¹). S_i,j is the selectivity to product i, coming from reactant j. Here, c_i,j is the amount of carbon atoms in effluent i coming from reagent j, F_i is the outlet molar flowrate of component i and c_j the number of carbon atoms in feed component j. Both n-butanol and ethanol have their own product spectrum, which overlaps for the cross-ether. Therefore, in the selectivity calculation, it is necessary to account for the number of carbons coming from reactant j that end up in product i, e.g. in ethyl butyl ether, 2 carbons come from ethanol and 4 from n-butanol, hence the differentiation between c_i,j and c_j is necessary.

3. Results and discussion

3.1 Adsorbate dimer formation during BuOH–EtOH coadsorption

Alcohols can be present as a single adsorbate on an active site, the so called adsorbed monomers, or as two alcohol species adsorbed on a single site, herein referred to as alcohol dimers. The adsorption of n-butanol and ethanol as protonated alcohol monomers or as protonated butanol-butanol or ethanol–ethanol dimers on the Brønsted acid site of H-ZSM-5 has been reported in detail previously.^20,21 The adsorption of n-butanol/ethanol dimers or ethanol/n-butanol dimers on the other hand has not been studied to the best of our knowledge. For pure alcohols, the rotation for co-adsorption of the alcohol molecules to form the dimer, and towards which channel the alkyl chain is oriented, has no influence in the formation of the protonated dimer, as it is symmetrical (Fig. 2b and c). One part of the chain will end up more in the sinusoidal channel and the other in the straight channel, independent of previous adsorption configurations.

Fig. 2 Bimolecular adsorption forms of n-butanol/ethanol mixtures on the Brønsted acid site H-ZSM-5. (a) D1_BB – a protonated butanol-butanol dimer, (b) D1_BE – a protonated butanol-ethanol dimer, (c) D1_EB – a protonated ethanol–butanol dimer, (d) D1_EE – a protonated ethanol–ethanol dimer. Colour code: silicon – cyan, oxygen – red, aluminum – pink, hydrogen – white, carbon – grey, hydrogen bonds – dashed lines.

For n-butanol/ethanol mixtures, the formation of the protonated dimer is dependent on the configuration of adsorption of butanol or ethanol. The asymmetrical protonated alcohol dimer can have a different configuration in the framework and hence a different stability. To this end we report the bimolecular adsorption configurations of butanol/ethanol at the intersection of the straight and the sinusoidal channel in H-ZSM-5 (Fig. 2), with the left channel in Fig. 2 being the straight and the right channel being the sinusoidal channel. For example, in Fig. 2(b) D1_BE is displayed, meaning a protonated butanol–ethanol dimer, for which the butyl chain is located in the straight channel and the ethyl chain is in the sinusoidal channel. Similarly, for Fig. 2(c), D1_EB means a protonated ethanol–butanol dimer, with an ethyl chain in the straight and butyl chain in the sinusoidal channel. The energetics (cumulative for dimers) of these adsorption configurations are listed in Table 1. D1_BB is the most stable alcohol–alcohol dimer, followed by D1_EB and D1_BE and finally D1_EE. These differences reflect how well these dimers are confined within the zeolite framework. Logically, the stronger bonding related to a more negative adsorption enthalpy is always paired with a greater loss in entropy, reflecting the associated reduced mobility. For the conversion of pure butanol and pure ethanol, the existence of alcohol dimers on Brønsted acid sites has been reported previously,^69,70 hence butanol/ethanol dimers are likely to be present during the processing of alcohol mixtures. The presence of butanol/ethanol dimers opens up new possible reaction pathways, and their effect on the reaction kinetics needs to be assessed.

Table 1 Thermodynamics for the adsorbed alcohol monomers and alcohol–alcohol dimers of n-butanol and ethanol in H-ZSM-5. Standard adsorption enthalpy (ΔH_ads⁰ in kJ mol⁻¹), standard adsorption entropy (ΔS_ads⁰ J mol⁻¹ K⁻¹), standard adsorption Gibbs free energy (ΔG_ads⁰ in kJ mol⁻¹) and equilibrium coefficient at 500 K (K_ads^500K in bar⁻¹ and bar⁻² for one and two adsorbed molecules)

	ΔHads^0	ΔSads^0	ΔGads^0	K ads ^500K
M1B	−146	−193	−50	1.6 × 10^5
M1E	−124	−168	−40	1.5 × 10^4
D1BB	−272	−376	−84	5.6 × 10^8
D1BE	−244	−344	−72	3.2 × 10^7
D1EB	−252	−347	−78	1.4 × 10^8
D1EE	−223	−330	−58	1.0 × 10^6

---

3.2 Reaction pathways for n-butanol/ethanol mixture dehydration

The adsorbed alcohols, n-butanol or ethanol can undergo a direct dehydration producing their respective alkene (1-butene/trans-2-butene/cis-2-butene or ethene). Single n-butanol or ethanol streams can react towards their ‘unique’ ether, respectively dibutyl ether (DBE) and diethyl ether (DEE), where mixtures of these alcohols can in addition lead to the cross-ether ethyl butyl ether (EBE). All these ethers can subsequently decompose towards an alkene and alcohol, EBE can lead to either 1-butene and ethanol or n-butanol and ethene.

The possible reaction paths for conversion of n-butanol/ethanol mixtures in H-ZSM-5 are displayed in Fig. 3. The dehydration of n-butanol, respectively ethanol, to butenes and dibutyl ether, respectively ethene and diethyl ether, has been discussed in detail in previous work.^17,20,21,39 The reaction pathways are considered as the connections between the reactants and products, e.g. n-butanol can directly dehydrate to 1-butene (Path A starting from n-butanol), trans-2-butene (Path D) or cis-2-butene (Path G). Two n-butanol molecules can yield DBE (Path B starting from n-butanol), DBE can decompose to n-butanol and (i) 1-butene (Path C), or (ii) trans-2-butene (Path E) or (iii) cis-2-butene (Path H). Isomerization of the butenes is also considered: 1-butene to trans-2-butene (Path F), 1-butene to cis-2-butene (Path I), trans-2-butene to cis-2-butene (Path J). For ethanol, the pathways are similar: direct dehydration to ethene (Path A starting from ethanol), etherification to DEE (Path B) and decomposition of DEE to ethene and ethanol (Path C). The pathways utilizing both n-butanol and ethanol are: formation of EBE (Path K), but also the decomposition of the ether to either butene and ethanol (Path M) or to ethene and butanol (Path L). These pathways can consist of multiple parallel reaction mechanisms, e.g. an S_N2 or S_N1 mechanisms, which exist of multiple reaction steps. The reaction networks of n-butanol and ethanol respectively consist of 33 and 21 reaction steps and are extended here towards a complete network of 75 reaction steps for mixtures. The numbering is based on earlier work: steps 0–32 (mechanisms 1−18, Table S13†) are for n-butanol dehydration from John et al.,^20,39 the reaction steps from ethanol continue from step 33–52 (mechanisms 19–26,²¹ Table S14†) and the newly obtained reaction steps are 53–74 (mechanisms 27–36). The applied numbering is the cause why the newly found mechanisms start at mechanism 27. Further reference to a specific reaction step in the network is done as per the numbering used in Tables 2 and S10† (more extensive).

Fig. 3 Reaction scheme for n-butanol/ethanol dehydration and butene isomerization pathways in H-ZSM-5.

Table 2 Novel reaction pathways, mechanisms and elementary steps involving both n-butanol and ethanol in H-ZSM-5. Steps that are assumed to be at equilibrium are indicated in black, steps for which a transition state is present are indicated with red stoichiometric numbers. All steps listed here are schematically visualized in Fig. S1

	Path	A		K				L		M
	Mechanism	35	36	27	28	29	30	31	32	33	34
a Elementary step from the reaction network of n-butanol dehydration from ref. 20. b Elementary step from the reaction network of ethanol dehydration from ref. 21.
(R0)^a	BuOH(g) + * ⇄ M1B	1	0	1	1	0	0	0	0	0	0
(R5)^a	M1B ⇄ M2B	0	0	0	1	0	0	0	0	0	0
(R7)^a	1-Butene* ⇄ 1-butene(g) + *	0	0	0	0	0	0	1	1	0	0
(R8)^a	M2B ⇄ butoxy + H2O(g)	0	0	0		0	0	0	0	0	0
(R33)^b	EtOH(g) + * ⇄ M1E	0	1	0	0	1	1	0	0	0	0
(R34)^b	M1E ⇄ M2E	0	0	0	0	0	1	0	0	0	0
(R35)^b	M2E ⇄ ethoxy + H2O(g)	0	0	0	0	0		0	0	0	0
(R37)^b	Ethene* ⇄ ethene(g) + *	0	0	0	0	0	0	0	0	1	1
(R53)	M1B + EtOH(g) ⇄ D1BE	1	0	1	0	0	0	0	0	0	0
(R54)	D1BE ⇄ D2BE	1	0	1	0	0	0	0	0	0	0
(R55)	D2BE ⇄ BEE* + H2O(g)	0	0		0	0	0	0	0	0	0
(R56)	BEE* ⇄ EBE(g) + *	0	0	1	1	0	0	−1	−1	0	0
(R57)	M1E + BuOH(g) ⇄ D1EB	0	1	0	0	1	0	0	0	0	0
(R58)	D1EB ⇄ D2EB	0	1	0	0	1	0	0	0	0	0
(R59)	D2EB ⇄ EBE* + H2O(g)	0	0	0	0		0	0	0	0	0
(R60)	EBE* ⇄ EBE(g)	0	0	0	0	1	0	0	0	−1	−1
(R61)	Butoxy + EtOH(g) ⇄ C3BE	0	0	0	1	0	0	0	0	0	0
(R62)	C3BE ⇄ BEE*	0	0	0		0	0	0	0	0	0
(R63)	Ethoxy + BuOH(g) ⇄ C3EB	0	0	0	0	0	1	0	0	0	0
(R64)	C3EB ⇄ EBE*	0	0	0	0	0		0	0	0	0
(R65)	BEE* ⇄ C4BE	0	0	0	0	0	0		0	0	0
(R66)	C4BE ⇄ 1-butene* + EtOH(g)	0	0	0	0	0	0	1	0	0	0
(R67)	EBE* ⇄ C4EB	0	0	0	0	0	0	0	0		0
(R68)	C4EB ⇄ ethene* + BuOH(g)	0	0	0	0	0	0	0	0	1	0
(R69)	BEE* ⇄ BEE2	0	0	0	0	0	0	0	1	0	0
(R70)	BEE2 ⇄ 1-butene* + EtOH(g)	0	0	0	0	0	0	0		0	0
(R71)	EBE* ⇄ EBE2	0	0	0	0	0	0	0	0	0	1
(R72)	EBE2 ⇄ ethene* + BuOH(g)	0	0	0	0	0	0	0	0	0
(R73)	D2BE ⇄ C2E + 1-butene(g)		0	0	0	0	0	0	0	0	0
(R74)	D2EB ⇄ C2B + Ethene(g)	0		0	0	0	0	0	0	0	0
Path A	(Mechanism # 1–5, 19–23, 35–36)	n-BuOH(g) ↔ 1-butene(g) + H2O(g)
		EtOH(g) ↔ ethene(g) + H2O(g)
Path B	(Mechanism # 6–8, 24–25)	n-BuOH(g) + n-BuOH(g) ⇄ DBE(g) + H2O(g)
		EtOH(g) + EtOH(g) ⇄ DEE(g) + H2O(g)
Path C	(Mechanism # 9–10, 26)	DBE(g) ⇄ 1-butene(g) + n-BuOH(g)
		DEE(g) ⇄ ethene(g) + EtOH(g)
Path K	(Mechanism # 27–30)	n-BuOH(g) + EtOH(g) ⇄ EBE(g) + H2O(g)
Path L	(Mechanism # 31–32)	EBE(g) ⇄ 1-butene(g) + EtOH(g)
Path M	(Mechanism # 33–34)	EBE(g) ⇄ ethene(g) + BuOH(g)

---

Standard reaction enthalpy (ΔH_r°) and entropy (ΔS_r°), Arrhenius activation energies (E_a) and pre-exponential factors are tabulated in Table 3 for the new reaction pathways. The data in Table 3 has been corrected with NIST reaction enthalpies and entropies, more info on how these corrections are applied is documented in section S2, Tables S1 to S9.† All reaction steps, together with kinetic and thermodynamic parameters are encompassed in Table S11.† In Table 2, the elementary reaction steps of the new reaction pathways (EBE formation, EBE decomposition and alcohol-assisted dehydration) and mechanisms are listed. For example, four different mechanisms are found for the formation of EBE, i.e. pathway K consists of 4 different mechanisms (mechanism 27, 28, 29 and 30, more details in section 3.2.1). These mechanisms themselves consist of multiple reaction steps, e.g. mechanism 27 consists of elementary steps R0 – R53 – R54 – R55 – R56. For the decomposition of EBE (Path L and Path M), 4 mechanisms are found. Furthermore, one novel mechanism for the formation of 1-butene (leading to a total of 6 mechanisms) and one new mechanism for the formation of ethene are found, related to the processing of mixtures and are competitive with the conventional mechanisms. In Table S11† all elementary reaction steps and all reaction mechanisms are listed.

Table 3 Standard reaction enthalpy (kJ mol⁻¹), reaction entropy (J mol⁻¹ K⁻¹), activation energy (kJ mol⁻¹), pre-exponential factor (s⁻¹) and forward rate coefficient k_f (s⁻¹) at 500 K for the elementary steps (NIST-corrections on the gas-phase species have been applied)

	Elementary steps	ΔHr^0	ΔSr^0	E a(f)	A f	k f(500K)
(R0)	BuOH(g) + * ⇄ M1B	−146	−193	—	—	—
(R5)	M1B ⇄ M2B	82	−5	—	—	—
(R7)	1-Butene* ⇄ 1-butene(g) + *	77	146	—	—	—
(R8)	M2B ⇄ butoxy + H2O(g)	17	156	50	3.7 × 10^14	2.2 × 10^9
(R33)	EtOH(g) + * ⇄ M1E	−124	−168	—	—	—
(R34)	M1E ⇄ M2E	14	7	—	—	—
(R35)	M2E ⇄ ethoxy + H2O(g)	71	137	119	4.3 × 10^13	1.6 × 10^1
(R37)	Ethene* ⇄ ethene(g) + *	41	99	—	—	—
(R53)	M1B + EtOH(g) ⇄ D1BE	−99	−151	—	—	—
(R54)	D1BE ⇄ D2BE	43	20	—	—	—
(R55)	D2BE ⇄ BEE* + H2O(g)	6	113	91	2.1 × 10^12	6.1 × 10^2
(R56)	BEE* ⇄ EBE(g) + *	173	201	—	—	—
(R57)	M1E + BuOH(g) ⇄ D1EB	−128	−179	—	—	—
(R58)	D1EB ⇄ D2EB	46	19	—	—	—
(R59)	D2EB ⇄ EBE* + H2O(g)	11	116	90	2.1 × 10^12	9.2 × 10^2
(R60)	EBE* ⇄ EBE(g)	174	203	—	—	—
(R61)	Butoxy + EtOH(g) ⇄ C3BE	−41	−129	—	—	—
(R62)	C3BE ⇄ BEE*	−106	−39	30	3.8 × 10^11	3.0 × 10^8
(R63)	Ethoxy + BuOH(g) ⇄ C3EB	−71	−165	—	—	—
(R64)	C3EB ⇄ EBE*	−85	−24	42	9.4 × 10^11	3.8 × 10^7
(R65)	BEE* ⇄ C4BE	97	59	141	2.8 × 10^14	2.2 × 10^−1
(R66)	C4BE ⇄ 1-butene* + EtOH(g)	57	145	—	—	—
(R67)	EBE* ⇄ C4EB	114	62	143	5.3 × 10^13	5.9 × 10^−2
(R68)	C4EB ⇄ ethene* + BuOH(g)	86	187	—	—	—
(R69)	BEE* ⇄ BEE2	60	11	—	—	—
(R70)	BEE2 ⇄ 1-butene* + EtOH(g)	93	193	85	9.7 × 10^12	1.2 × 10^4
(R71)	EBE* ⇄ EBE2	60	0	—	—	—
(R72)	EBE2 ⇄ ethene* + BuOH(g)	140	249	96	1.5 × 10^13	1.5 × 10^3
(R73)	D2BE ⇄ C2E + 1-butene(g)	59	152	124	6.1 × 10^12	7.0 × 10^−1
(R74)	D2EB ⇄ C2B + ethene(g)	50	102	116	5.5 × 10^12	4.5 × 10^0

---

In the following sections, all additional reaction mechanisms occurring for the dehydration of alcohol mixtures are discussed, meaning the mechanisms for (i) the formation of EBE, (ii) the decomposition of EBE and (iii) alcohol-assisted dehydration. We systematically start with a section discussing the mechanistics, followed by a section discussing the energetics. Practically, the EBE formation mechanisms are discussed in 3.2.1, the energetics are compared to those for DBE and DEE formation in 3.2.2. In 3.2.3 the EBE decomposition mechanisms are reviewed, in 3.2.4 the EBE decomposition energetics in comparison to DBE and DEE decomposition energetics. Alcohol-assisted mechanisms are discussed in 3.2.5 and energetics in 3.2.6. Detailed analysis of the transition states is reported in section S3.† The effects of these mechanisms on the kinetics is discussed in section 3.3.

3.2.1 Formation of ethyl butyl ether (Path K). In previous work by de Reviere et al.,¹⁴ a significant formation of ethyl butyl ether is observed experimentally during the conversion of n-butanol/ethanol mixtures. In view of this, four possible mechanisms (mechanisms 27–30) for the formation of the ether have been studied. Mechanistically, the formation of EBE is very similar to the formation of diethyl ether and dibutyl ether formation.
Reaction mechanism 27 (butanol–ethanol dimer to ethyl butyl ether via S_N2-type reaction). Reaction mechanism 27 goes through a butanol–ethanol dimer to ether and water via S_N2-type reaction, transition state in Fig. S3.† The sequence of reaction steps is 0 – 53 – 54 – 55 – 56 (see Table 2). First n-butanol is adsorbed and protonated on the zeolite, step 0, yielding M1_B. Then, in step 53, a butanol–ethanol dimer (D1_BE) is formed, where the butyl chain is located in the straight channel and the ethyl chain in the sinusoidal channel. Subsequently, the dimer reorients to D2_BE (step 54), followed by nucleophilic substitution (step 55), leading to the protonated ether, followed by desorption (step 56). In the activated step of the mechanism (step 55, TS55 of Fig. S3†), the butyl–carbon bonded to O₁ of the protonated butanol breaks its bond with O₁ (allowing water to leave), and simultaneously forms a bond with O₂ of the physisorbed ethanol. The simultaneous formation of a new bond eases the breaking of the existing bond. For S_N2-type reactions, the nucleophile (here O₂) and leaving group (here –OH₂), are aligned directly opposing, with an angle close to 180° as in a trigonal bipyramidal structure. More elaborate transition state analyses are discussed in section S3.†
Reaction mechanism 28 (butoxide-mediated formation of ethyl butyl ether via S_N2-type reaction). Mechanisms 28 and 30 follow an alkoxy-route instead of a dimer-mediated pathway. Where mechanism 28 goes through a 1-butoxide intermediate, mechanism 30 goes through an ethoxide intermediate. The sequence of reaction steps in mechanism 28 is: 0 – 5 – 8 – 61 – 62 – 56 (Table 2 and Fig. S1†), for mechanism 30 it is: 33 – 34 – 35 – 63 – 64 – 60 (Table 2). First adsorption and protonation of the alcohol, (step 0 or step 33), followed by reorientation to either M2_B or M2_E (step 5 or step 34). The rearranged monomer undergoes a nucleophilic substitution, resulting in a surface-bound alkoxide (1-butoxide or ethoxide, step 8 or step 35), these nucleophilic substitutions leading to the alkoxides are activated, and have been discussed in detail by Alexopoulos et al. and John et al.^20,21 The alkoxide can react with another alcohol, leading to ethyl butyl ether. For mechanism 28, ethanol physisorbs next to the surface-bound 1-butoxide (step 61), followed by a nucleophilic substitution (step 62) forming the protonated ether and finally a desorption and deprotonation of ethyl butyl ether (step 56). For mechanism 30, n-butanol physisorbs next to the ethoxide (step 63), followed by nucleophilic substitution (step 64), yielding the protonated ethyl butyl ether, followed by deprotonation and desorption (step 60). For mechanism 28, step 62 is activated, in which the bond between the zeolite oxygen (O_a) and carbon of the surface butoxide is broken and concurrently a new bond is formed between the carbon and O₂ of the physisorbed ethanol. The geometry of TS62 (Fig. S3†) is in line with the stereochemical requirements for an S_N2-type mechanism.
Reaction mechanism 29 (ethanol–butanol dimer to ethyl butyl ether via S_N2-type reaction). Reaction mechanism 29 is very similar to 27, as here the ether is formed through an ethanol–butanol dimer via S_N2-type reaction. The reaction mechanism consists of steps 33 – 57 – 58 – 59 – 60 (Table 2). First ethanol (instead of butanol) is adsorbed and protonated on the zeolite, step 33, yielding M1_E. Then, following step 57, n-butanol positioned in the sinusoidal channel adsorbs next to the ethanol, forming an ethanol–butanol dimer D1_EB of which the ethyl chain is oriented to the straight channel and the butyl chain to the sinusoidal channel. Dimer D1_EB then reorients to D2_EB (step 58), followed by nucleophilic substitution, leading to the protonated ether (step 59), which is oriented differently than the ether resulting from step 55. Following desorption and deprotonation (step 60), ethyl butyl ether is generated, regenerating the zeolite Brønsted acid site. For the activated step, 59 (TS59, Fig. S3), the carbon of the protonated ethanol, bonded to O₁ is concurrently breaking the O₁–C bond and forming the C–O₂ bond with the physisorbed butanol, indicating the S_N2-type mechanism.
Reaction mechanism 30 (ethoxide-mediated formation of ethyl butyl ether via S_N2-type reaction). For mechanism 30, step 64 is activated (TS64, Fig. S3†), where the bond between the zeolite oxygen (O_a) and carbon of the surface ethoxide is broken and simultaneously a bond is forming between the carbon and O₂ of the physisorbed n-butanol, indicating an S_N2-type mechanism.

3.2.2 Comparison of ether formation mechanisms. The Gibbs free energy profile for the ethyl butyl ether formation mechanisms at 500 K are shown in Fig. 4. To allow comparison with the single n-butanol/ethanol streams, the free energy profiles for the formation of dibutyl ether and diethyl ether are also shown. In the top of Fig. 4, the free energies for S_N2-substitution of alcohol-dimer mechanisms are shown. In the bottom, the free energies for ether formation through an intermediate alkoxide are shown. The reference Gibbs free energy is the sum of the zeolite, 2 BuOH_(g), 2 EtOH_(g) and one H₂O_(g). For visual clarity, gas phase components, not participating in the pathway are omitted in Fig. 4.

Fig. 4 Standard Gibbs free energy diagrams in H-ZSM-5 for the formation of dibutyl ether (green), ethyl butyl ether (blue and red), diethyl ether (black). Straight lines indicate the mechanism is going through an alcohol-dimer (top), dotted lines indicate the mechanism is going through an alkoxide intermediate (bottom). For visual reasons, gas phase components, not consumed or formed in the mechanisms are omitted.

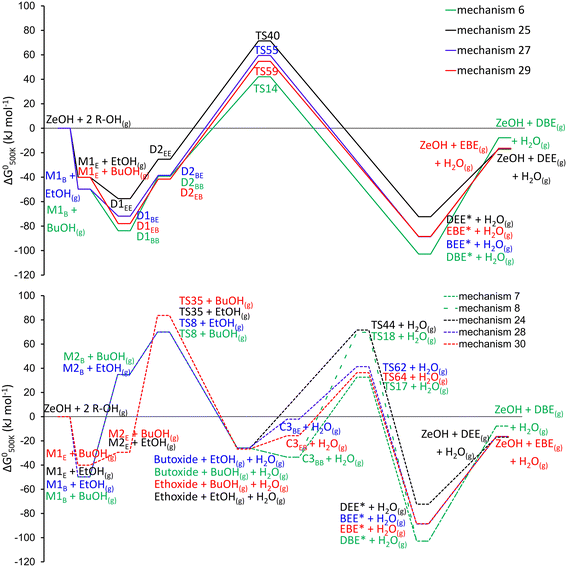
The free energy diagram for EBE formation is intermediate between those of DBE and DEE. Nevertheless, at 500 K, the formation of DBE is least favored from a thermodynamic point of view. The dimer-mediated mechanisms are energetically preferred, as they exhibit lower apparent energy barriers compared to the alkoxide-mediated mechanisms. The free energy span⁷¹ (visualized in Fig. S2†) of the dimer-mediated mechanisms is 137 kJ, 127 kJ, 132 and 127 kJ for mechanisms 6, 25, 27 and 29. Based on the energetics the lowest selectivity would be expected for DBE (Path B – BuOH) and the highest for DEE (Path B – EtOH). For the alkoxide mechanisms, the energetic spans range from 128 kJ for mechanism 7 and 24 and 109–114 kJ for mechanism 28 and 30.

Specifically, the formation of EBE through the ethoxide-mediated mechanism (mechanism 30, Fig. 4, bottom), has a drastically lower energy barrier compared to the ethoxide-mediated formation of DEE, although both start from the same ethoxide species, upon which either ethanol or butanol physisorbs and reacts to DEE or EBE. Furthermore, the alcohol dimers for which the butyl chain is in the sinusoidal channel are the most stable configurations, attributed to a favorable geometry in the channel. The butyl chain has a nearly ideal fit in the sinusoidal channel. In the straight channel, the butyl chain is more constrained, as it aligns perpendicular to the direction of the channel, leading to a more pronounced entropy compensation. Nevertheless, no clear energetic preference in EBE formation mechanism is present. The adsorption of ethanol onto the active site or onto an adsorbed n-butanol/ethanol molecule is always weaker compared to the adsorption of n-butanol. This is in agreement with the chain length dependence on adsorption strength which has been reported in literature.^72,73

3.2.3 Decomposition of ethyl butyl ether (Paths M and L). The decomposition of both dibutyl ether and diethyl ether has been reported both experimentally and theoretically,^16,20,21,23 therefore decomposition mechanisms for ethyl butyl ether are also viable and explored here. Ethyl butyl ether can decompose to either 1-butene and ethanol (Path M) or to ethene and n-butene (Path L). In view of this, two plausible mechanisms for the decomposition for both paths have been investigated. These mechanisms involve (i) either a concerted reaction step, or (ii) a reorientation of the ether followed by decomposition. Mechanistically, these decomposition reactions are very similar to those for dibutyl ether and diethyl ether. In mechanisms 31 and 32 1-butene and ethanol are formed, in mechanisms 33 and 34, ethene and n-butanol.
Reaction mechanism 31 (concerted ethyl butyl ether decomposition to 1-butene and ethanol). Mechanism 31 starts with the adsorption and protonation of ethyl butyl ether (reverse step 56), followed by steps 65, 66 and 7 (Table 2). In step 65, ethyl butyl ether undergoes a cleavage of the C–O bond, with a simultaneous abstraction of a hydrogen by the basic oxygen of the zeolite (see TS65, Fig. S4†). This step leads to a co-adsorbed 1-butene and ethanol (C4_BE) on the zeolite acid site. Further desorption steps of the ethanol (step 66) and 1-butene (step 7) regenerate the Brønsted acid site. Step 65 is activated, as shown in Fig. S4.† The C–O₂ bond of TS65 is broken to a larger extent than the C_β–H_β bond, indicating that the concerted (E₂) syn-elimination has some E₁ characteristics. TS65 is a late transition state, closely resembling the physisorbed 1-butene.
Reaction mechanism 32 (E₂ elimination of ethyl butyl ether to 1-butene and ethanol). Mechanism 32 also starts with reverse step 56, followed by a reorientation of the ether to BEE2 to an antiperiplanar adsorption configuration (step 69). Then ethanol is eliminated from the reoriented ether (step 70) to form physisorbed 1-butene and subsequently the desorption of the alkene takes place (step 7). Step 70 is activated (TS70, Fig. S4†) and similar to step 65, but instead of being syn-coplanar, here the transition state has an anti-periplanar configuration. The C_α–C_β bond is shortened, illustrating the formation of a double bond, the O_a–C bond is elongated to a greater extent than C_β–H_β, thus the extent of C–H breakage is less pronounced than the C–O breakage, however the difference is slightly less pronounced than for TS65. Nevertheless, TS70 is also considered to be a late transition state, but with an 1,2-anti-elimination configuration.
Reaction mechanism 33 (concerted syn elimination of ethyl butyl ether to ethene and n-butanol). Mechanism 33 starts with the adsorption and protonation of ethyl butyl ether (reverse step 60). In step 65, the ether heterolytically cleaves the C–O bond of the carbon of the ethyl chain and concurrently, the β-hydrogen is abstracted by the basic oxygen of the zeolite (TS67, Fig. S4†). A co-adsorbed ethene and n-butanol (C4_EB) is formed, of which butanol desorbs (step 68), followed by desorption of ethene (step 37), restoring the acid site. This mechanism is very similar to mechanism 31, however here ethene is formed instead of 1-butene. Step 67 is activated (Fig. S4†), here the β-hydrogen and n-butanol leaving group have a syn-coplanar structure. Compared to TS65, here the extent of C–H breakage is more pronounced whereas the C–O breakage less.
Reaction mechanism 34 (E₂ elimination of ethyl butyl ether to ethene and n-butanol). Mechanism 34 consists of reverse step 60, steps 71, 72 and step 37 (Table 2). In step 71, the protonated ether reorients, which is followed by the elimination of butanol, yielding physisorbed ethene, which subsequently desorbs (step 37). Mechanism 34 is similar to mechanism 32, here step 72 is activated (TS72, Fig. S4†) and similar to step 70, with an anti-elimination configuration. Similar as for TS67 compared to TS65, also here the C–O₂ bond is broken to a lesser extent compared to TS70, whilst the C_β–H_β bond breakage is more pronounced. All ethyl butyl ether decomposition mechanisms have late transition states, close to their respective products.

3.2.4 Comparison of ether decomposition mechanisms. The DFT-computed Gibbs free energy profile of the ether decomposition mechanisms are displayed in Fig. 5. The apparent energy barrier is the lowest for the concerted, syn-elimination mechanisms. Where, for the formation of EBE, there is no clear energetic preference between the different mechanisms, there is for the ether decomposition. The energetic span of the butene-forming mechanisms (127, 141, 131 and 140 kJ for mechanisms 9, 10, 31 and 32) is always lower than those for ethene (139, 136 and 154 kJ for mechanisms 26, 33 and 34). Hence, the decomposition of EBE is always preferred to yield butene and ethanol. The lower energy barrier for the butene-forming mechanisms compared to the ethene-forming mechanisms is related to the transition states being late. As they are late, they have a structure closely resembling the products of the reaction, and n-butene is more stable inside the zeolite cavity than ethene. The preferred formation of 1-butene and ethanol over ethene and n-butanol is both kinetic and thermodynamic. Consequently, the decomposition of EBE is envisaged to primarily yield 1-butene and ethanol.

Fig. 5 Gibbs free energy profile for the decomposition of DBE, EBE and DEE. For all displayed states, also water in the gas phase is present, but is omitted from the figure for clarity. Full lines indicate a concerted syn-elimination, dashed lines indicate a two-step anti-elimination mechanism. The reference energy is the same as in Fig. 4.

3.2.5 Alcohol-assisted dehydration mechanisms. Even though one could assume that the processing of alcohol mixtures only affects the formation of a cross-ether and not the direct dehydration from alcohol to alkene, however, this would imply that the direct alcohol dehydration is monomolecular. We reviewed all the mechanisms of direct alcohol dehydration in detail for ethanol and butanol and while at low alcohol partial pressures, the bimolecular pathway contribution to alcohol dehydration to alkene is negligible, at higher partial pressures it plays an important role. Therefore we studied both an n-butanol-assisted ethanol dehydration and an ethanol-assisted butanol dehydration.

Mechanism 35, the ethanol-assisted dehydration of n-butanol to 1-butene follows a sequence of elementary reaction steps, 0 – 53 – 54 – 73 – 46 and reverse step 33 (Table 2). It starts similarly as mechanism 27, with the adsorption of n-butanol, followed by adsorption of ethanol into a butanol–ethanol dimer. Then a reorientation, followed by elimination and desorption of 1-butene, leaving a protonated ethanol and water co-adsorbed on the zeolite acid site. Finally desorption of the water and protonated ethanol can take place. Step 73 is activated (TS73, Fig. S5†), here the protonated butanol of the rearranged butanol–ethanol dimer (D2_BE), breaks its C–O bond and the β-hydrogen is abstracted by the oxygen of the physisorbed ethanol molecule. The mechanism can be considered a one-step 1,2-syn-elimination with E₁ characteristics, with a late transition state.

Mechanism 36, basically the inverse of mechanism 35, the n-butanol assisted ethanol dehydration follows the elementary steps 33 – 57 – 58 – 74 – 13 and reverse step 0 (Table 2). First ethanol is protonated and adsorbed, followed by n-butanol co-adsorption to D1_EB, this is followed by rearrangement to D2_EB. The elimination and desorption of ethene, leaving protonated butanol–water co-adsorbed species is the activated step of the mechanism. Which is followed by desorption of water and n-butanol, restoring the active site. The protonated ethanol of the rearranged ethanol–butanol dimer has its C–O bond broken and the O₂ of the physisorbed butanol abstracts the β-hydrogen (TS74, Fig. S5†). The geometric features are indicative of a one-step 1,2-syn-elimination with a late transition state.

3.2.6 Comparison of direct alkene formation mechanisms. Where the other explored mechanisms lead to a new product, a mixed ether, which cannot be formed unless mixtures are processed, the newly studied mechanisms of previous paragraph assist in the formation of 1-butene and ethene. These alkenes are, depending on the reaction conditions, the main products when converting alcohols over H-ZSM-5. Consequently, these new mechanisms can influence the intrinsic activity of alcohol transformation toward its respective alkene, solely upon processing the alcohols as mixture instead of pure components. In Fig. 6, the energetics of all studied alcohol-assisted dehydration mechanisms are shown. The energetic span varies between 147 and 159 kJ, where mechanism 23 has the lowest and mechanism 36 has the highest.

Fig. 6 Standard Gibbs free energy diagram in H-ZSM-5 for the alcohol-assisted alcohol dehydration. Mechanism 5: butanol-assisted butanol dehydration, mechanism 23: ethanol-assisted ethanol dehydration, mechanism 35: ethanol-assisted butanol dehydration, mechanism 36: butanol-assisted ethanol dehydration.

The energetics of the alcohol-assisted dehydration reactions reveal that the butanol-assisted ethanol dehydration is competitive with the ethanol-assisted ethanol dehydration. The ethanol-assisted butanol dehydration seems to be of smaller importance, due to the lower stability of D1_BE compared to D1_BB, and the higher activation barrier of TS73 compared to TS12. Unravelling the exact importance of these additional dehydration mechanisms requires microkinetic modelling, where reaction conditions, surface coverages,… are accounted for.

3.3 Microkinetic modeling and reaction path analysis for n-butanol/ethanol dehydration

A detailed microkinetic model, involving 36 reaction mechanisms and consisting of 75 elementary steps in total has been implemented, without any assumptions regarding dominant reaction pathways or rate determining steps. The microkinetic model using the direct DFT-derived rate coefficients (Table S11,† including experimental correction on the gas-phase species) yields decent order-of-magnitude predictions of the activity and selectivity (see Fig. S6†), but the agreement for ethanol is quantitatively insufficient to ensure reliable conclusions from the reaction path analysis. This should also not come as a surprise, given the unique Si/Al ratio and Al site location in the simulations, and the difficulty of accurate entropy prediction of species in the confined space of a zeolite cage. Therefore, all reaction enthalpies and activation energies were allowed to vary within typical chemical accuracy, i.e. ±4 kJ mol⁻¹, in order to improve the agreement with the experiments performed at 503 and 513 K (experimental details in section S4†). It is unlikely that varying reaction enthalpies and activation energies within 4 kJ mol⁻¹ affects the qualitative behavior of the model, since most energy differences between competitive pathways are larger than 4 kJ mol⁻¹. For a quantitative agreement for the product selectivity starting from ethanol, only 1 parameter needs to be modified outside of the chemical accuracy region, i.e., the activation enthalpy for TS74, the decomposition of the DE_EB mixed dimer towards ethene (Table S11†). This is carried out using the least-square regression described in section 2.3. Table S10† lists all (unaltered) DFT-reaction parameters, Table S11† lists all reaction parameters upon variation and regression. As seen in Fig. 7, the simulated conversions of n-butanol and ethanol and the selectivities to their respective products are in reasonably good agreement at conversions below 0.99 mol mol⁻¹. Although noticeable deviation between the model simulated and experimentally observed activity is present, the selectivities are predicted rather well. Simulated activities for n-butanol or ethanol dehydration over H-ZSM-5 also deviated more from experimental results than the selectivities.^17,21 Activity is generally more difficult to predict, as the amount of active sites during the reaction is difficult to assess. Furthermore, the simulations consider only one unique active site (T12), whilst in reality there will be a range of active sites with varying activity. For the selectivity, the relative activities of the different pathways are assessed, which is, in our opinion, more important than the absolute activities. All experimentally observed trends are captured by the microkinetic model: (i) BuOH is more reactive than ethanol, (ii) EBE is the most important product coming from ethanol and its selectivity decreases quite abruptly near full BuOH conversion, (iii) the butenes approach their equilibrium composition near full conversion. This justifies further utilization of the microkinetic model for providing detailed insight into reaction condition effects.

Fig. 7 Experimental and simulated conversion of n-butanol () and ethanol () versus site time (top), catalyzed by H-ZSM-5, selectivity of products from n-butanol versus butanol conversion (X_BuOH) (middle) and selectivity of products of ethanol versus ethanol conversion (X_EtOH) (bottom). Temperature = 503 K (left) and 513 K (right), total pressure = 5 Bar, p_BuOH⁰ = 29 kPa, p_EtOH⁰ = 7.8 kPa. Full lines are simulation results.

The experimentally validated microkinetic model allows to assess the effect of each reaction condition separately. In the following subsections, reaction path analyses are performed for every varied reaction condition, i.e. 1) site time and conversion, 2) reaction temperature, 3) total alcohol pressure and 4) n-butanol–ethanol ratio.

3.3.1 Effect of site time and alcohol conversion. The influence of site time on alcohol conversion and product selectivities, TOFs and surface coverages is studied at constant reaction temperature and pressure. This effect is studied at the same conditions as experimentally, for a 6/1 n-butanol/ethanol mixture (mass based), a temperature of 500 K, and an initial alcohol total partial pressure of 36.8 kPa (BuOH = 29 kPa, EtOH = 7.8 kPa).

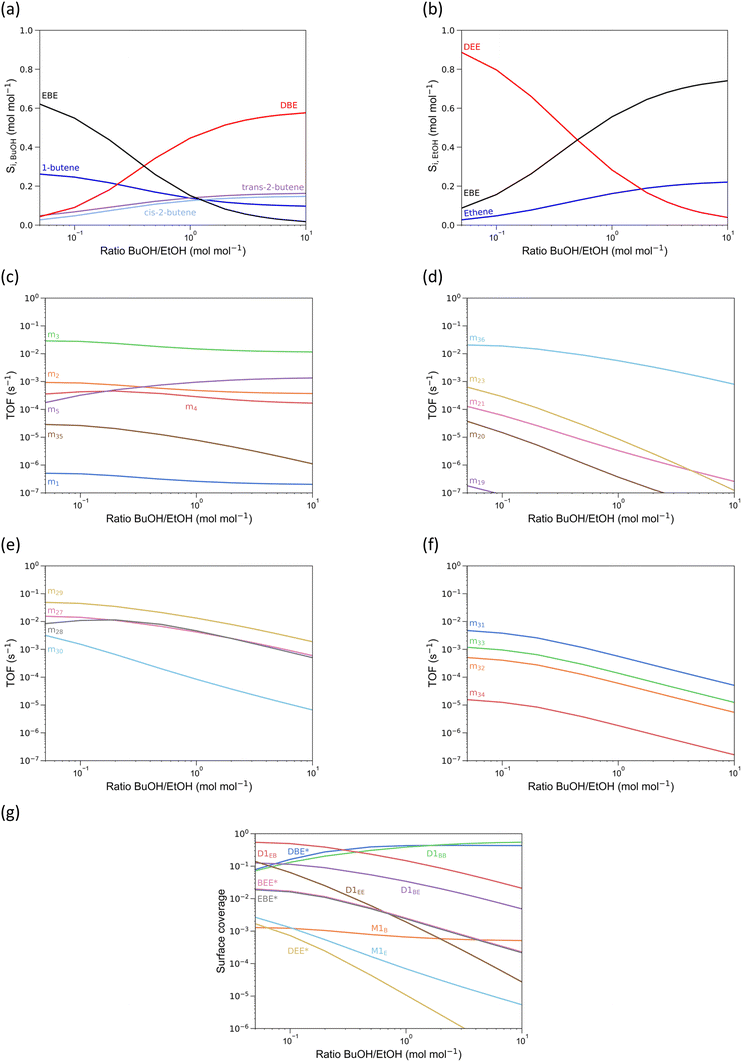
In Fig. 8(a), the conversion of n-butanol and ethanol as a function of site time is shown. Here it is clear that n-butanol is more reactive than ethanol, as per our experimental observations (see previous section). At low conversion, DBE is the most important product originating from BuOH dehydration (Fig. 8b), while for ethanol dehydration EBE is the most important product (Fig. 8c). With increasing conversion, the butenes approach equilibrium. At low conversion, mechanism 29 (alcohol-dimer D1_EB mediated, Fig. 8g) is the most dominant for the formation of EBE, but around 30% BuOH conversion mechanism 28 (butoxide-mediated) becomes the most important, with m₂₉ almost as important. The relative change in importance is related to a decrease in D1_EB surface coverage with conversion (Fig. 8d). Note that all coverages are shown as a function of BuOH conversion (even the solely ethanol-related surface species). The surface coverage of DBE goes through a maximum and occupies >90% of the active sites, as it is the most stable surface species. For pure n-butanol feeds this is also observed; for pure ethanol feeds, the same is observed for diethyl ether.²¹ At a BuOH conversion over 0.6 mol mol⁻¹, the DBE surface coverage decreases, leading to an increase in surface coverage of D1_EB, which allows m₂₉ (Fig. 8g) to become dominant again. The surface coverages of ethanol-related surface species increase with n-butanol conversion, as the partial pressure of n-butanol decreases faster than the partial pressure of ethanol due to the higher butanol reactivity. Furthermore, m₄, the butoxide-mediated formation of 1-butene²⁰ gains importance at higher conversion (Fig. 8e), which is competitive with m₂₈, partly explaining the decrease in TOF for m₂₈.

Fig. 8 Alcohol conversion as a function of site time (a), effect of n-butanol conversion on its product selectivity (b), effect of ethanol conversion on its product selectivity (c), surface coverages (d), TOF of the mechanisms of Path A involving n-butanol (e), TOF of the mechanisms of Path A involving ethanol (f), TOF of the EBE formation mechanisms (g), TOF of the EBE decomposition mechanisms (h) as function of butanol conversion. Reaction conditions: temperature = 500 K, p_BuOH⁰ = 29 kPa, p_EtOH⁰ = 7.8 kPa, total pressure = 5 Bar.

Cofeeding n-butanol and ethanol suppresses ethanol conversion TOFs (Path A, B and C), due to the low surface coverage of ethanol-related species. These paths are replaced in importance by mechanisms where n-butanol is involved in the conversion of ethanol. These results directly illustrate a pitfall of relying solely on energetic span to predict TOFs and selectivities: it does not account for surface coverages, which depend on both the catalyst, but also reaction conditions. The energetic span for EBE formation and butanol-assisted ethene formation is higher than for diethyl ether formation, yet the computed TOFs for these mechanisms is higher. Therefore, microkinetic modeling is essential to obtain accurate selectivities for complex reaction networks, as it computes surface coverages based on the reaction conditions. For the direct ethanol dehydration to ethene (path A), the novel butanol-assisted ethanol dehydration mechanism (m₃₆) has completely replaced the other mechanisms as prime contributor to path A as long as sufficient butanol is present (Fig. 8f). Remarkably, simultaneous dehydration of ethanol and butanol alters the intrinsic activity of ethanol dehydration to ethene in H-ZSM-5. At high butanol conversion, the ethanol dehydration mechanisms where no butanol is involved (m₁₈ to m₂₃) become more important, due to decrease in available butanol. TOFs related to DBE/DEE formation/decomposition and butene isomerization (mechanisms 6 to 26) are shown in section S6.†

For all EBE decomposition mechanisms, the simulations show an increase in TOF with n-butanol conversion. Beyond full n-butanol conversion (not shown), there is no more EBE present in the reactor effluent.¹⁴ Most of the EBE is decomposed through mechanism 31, the concerted decomposition to 1-butene and ethanol. This was also proposed by de Reviere et al.,¹⁴ explaining the stronger stagnation in EtOH conversion compared to BuOH as a function of site time. Yet, mechanism 33, leading to ethene and BuOH, also has a TOF of the same order of magnitude, although lower. Especially, considering the small amount of ethanol in the feed, this is a substantial fraction of the ethanol conversion route.

3.3.2 Effect of reaction temperature. The effect of temperature on activity, product selectivity, surface coverage, is investigated from 450–550 K and compared at an iso-conversion level for n-butanol of 0.10 mol mol⁻¹, in order to avoid the important effect of conversion as discussed above. The inlet partial pressures of n-butanol and ethanol are fixed at 29 and 7.8 kPa.

For the products originating from BuOH, the increase in temperature leads to an increase in linear butene selectivity and decrease in DBE selectivity (Fig. 9a). The selectivity to EBE seems to be quite unaffected (Fig. 9a and b), likely because the surface coverage of BuOH–EtOH dimers is rather unaffected by temperature, yet the coverage of BuOH–BuOH dimers decreases (Fig. 9g). The EtOH-assisted BuOH dehydration, mechanism 35, is of little importance over the complete temperature range (Fig. 9c), the BuOH-assisted EtOH dehydration, mechanism 36, on the other hand, is by far the most important contributor to the formation of ethylene from ethanol (Fig. 9d). Furthermore, based upon the TOFs of Fig. 9c, it is clear that the difference in reactivity for BuOH and EtOH conversion increases with temperature, corroborating earlier experimental observations.¹⁴ As the most important contributions to the ethanol dehydration are the formation of EBE and the butanol-assisted ethanol dehydration, this is expected. The formation of EBE also converts BuOH, hence increasing the conversion rate towards EBE increases the reactivity for both alcohols. The formation of ethene through mechanism 36 on the other hand competes with the formation of EBE through mechanism 29, hampering the increase in TOF for mechanism 36 with temperature. On the contrary, there are 4 (depending on the temperature) direct 1-butene forming mechanisms significantly contributing to the conversion rate of butanol (m₂ to m₅, Fig. 9c), having no competition from ethanol pathways whatsoever, except for surface coverage.

Fig. 9 Effect of reaction temperature on (a) the selectivity of butanol products, (b) the selectivity of ethanol-products, (c) turnover frequencies of different mechanisms of Path A for BuOH, (d) turnover frequencies for different mechanisms of Path A for EtOH, (e) turnover frequencies for EBE formation mechanisms, (f) turnover frequencies for EBE decomposition mechanisms, (g) surface coverages. Reaction conditions: P_BuOH,0 = 29 kPa, P_EtOH,0 = 7.8 kPa, X_BuOH = 10%, total pressure = 5 bar.

At temperatures below 500 K, the formation of EBE is primarily through the alcohol-dimer mediated mechanisms (m₂₇ and m₂₉, Fig. 9e), above 500 K, the butoxide-mediated formation of EBE becomes more and more dominant (m₂₈). This is partly because at higher temperatures, monomolecular pathways gain importance due to reduced adsorption, hence, more alkoxides are present on the surface, leading to a stronger contribution of alkoxide-mediated mechanisms. At all temperatures, mechanism 31 is the strongest contributor to the decomposition of EBE, followed by mechanism 33 (Fig. 9e). The surface coverages of EBE* and BEE* (Fig. 9g) are identical, the difference in EBE decomposition to 1-butene and ethanol versus ethene and n-butanol is due to the lower activation barrier for m₃₁ compared to m₃₃ (TS65 vs. TS67, Fig. 5).

3.3.3 Effect of total alcohol pressure. The effect of total alcohol pressure (P_BuOH,0 + P_EtOH,0), with a fixed mass ratio of 6/1, is investigated at total alcohol pressures ranging from 0.1 kPa to 500 kPa. Under these conditions, which allow comparison with experimental conditions, the activity, product selectivity, surface coverages are compared at a conversion of n-butanol of 0.1 mol mol⁻¹. Fig. 10(a) and (b) show the effect of inlet alcohol pressure on product selectivity for products coming from n-butanol (a) and products coming from ethanol (b). At low alcohol pressures, the selectivity of products originating from n-butanol is primarily towards 1-butene. As the formation of n-butanol to 1-butene primarily follows monomolecular mechanisms (m₁–m₄, see ref. 17, 20 and 23), these mechanisms are facilitated at low alcohol pressures (Fig. 10c). This can be rationalized by the high M1_B surface coverage (Fig. 10g) under these conditions, causing the high TOF for mechanisms 3 and 4 of path A in n-butanol conversion (Fig. 1c). As cis-2-butene is formed primarily by isomerization and from dimeric surface species (D1_BB), its formation is quite limited at low pressures, as the surface coverage of D1_BB is at its lowest. For trans-2-butene, more isomerization mechanisms were considered by John et al. in the base microkinetic model from which we started,³⁹ thus trans-2-butene is more easily formed than cis-2-butene. With increasing pressure, the selectivity towards DBE increases, as it is enabled by a higher surface coverage of D1_BB (Fig. 10g).

Fig. 10 Effect of alcohol total inlet pressure on (a and b) product selectivity, (c) turnover frequencies of different mechanisms of Path A for BuOH, (d) turnover frequencies for different mechanisms of Path A for EtOH, (e) turnover frequencies for EBE formation mechanisms, (f) turnover frequencies for EBE decomposition mechanisms, (g) surface coverages. Reaction conditions: T = 500 K, X_BuOH = 10%, total pressure = 5 bar, BuOH/EtOH = 6/1 (mass ratio).

Interestingly, the formation of ethene is slightly enhanced upon increasing the alcohol pressure. For pure ethanol dehydration on the other hand, an increase in alcohol partial pressure suppresses the formation of ethene.²¹ The opposing behavior for alcohol mixtures compared to pure ethanol is rationalized by the increase in TOF for the n-butanol-assisted ethanol dehydration, which has replaced the mechanisms of Path A as dominant contributors to ethanol dehydration to ethene (Fig. 10d). The increase in alcohol partial pressure leads to a higher surface coverage of all alcohol-dimers. The most important contributing mechanism of ethanol dehydration to ethene for BuOH/EtOH mixtures, goes through D1_EB. The higher total alcohol pressure thus enhances this mechanism, illustrating the important role of surface coverages to tune the reactivity. Although EBE is also more readily formed upon an increase in alcohol pressure, its selectivity from an ethanol point of view still decreases with alcohol pressure, as the formation of DEE and ethene vary to a larger extent with alcohol pressure than EBE formation. The TOFs of the different pathways also show that the reactivity difference between the alcohols is attenuated upon increasing the total alcohol pressure. This allows a more simultaneous conversion of both alcohols, which can be tuned by steering the surface coverages, e.g. by increasing the total pressure.

For the formation of EBE, at low pressure m₂₈, the butoxide-mediated mechanism is most important (see panel e), due to the relatively low alcohol-dimer surface coverages that are important for mechanisms m₂₇ and m₂₉ (D1_BE and D1_EB, Fig. 10 panel g). At higher pressures (>1 kPa), there is a shift in dominant mechanism towards the alcohol-dimer mediated mechanisms, m₂₇ and m₂₉, as the alcohol dimers become increasingly important surface species. The most important ethyl butyl ether decomposition mechanisms are the concerted syn-elimination mechanisms, m₃₁ and m₃₃. Most of the EBE is decomposed towards 1-butene, in line with experimental observations.¹⁴

3.3.4 Effect of molar n-butanol/ethanol ratio. The effect of the molar n-butanol/ethanol ratio of the feed is studied from 1/20 to 10/1, to simulate a broad range of experimental conditions. The alcohol total inlet partial pressure is fixed at 36.8 kPa, as in sections 3.3.1 and 3.3.2. The effects on activity, selectivity and coverages are compared at a butanol iso-conversion level of 0.10 mol mol⁻¹, even for the feeds where more ethanol is present. At low molar BuOH/EtOH ratios, the EtOH conversion increases relatively to the BuOH conversion, nevertheless, BuOH is under all studied molar ratios the most reactive alcohol.

At low BuOH/EtOH ratios, the selectivity to EBE from a BuOH point of view is maximal (Fig. 11a), while the product spectrum of EtOH (Fig. 11b) is almost identical to that of pure EtOH,²¹ apart from a limited formation of EBE of course. At high BuOH/EtOH ratios, the selectivity profile approaches the values for if pure BuOH was used as feed. This highlights that the microkinetic model is able to simulate mixtures anywhere in between pure n-butanol and pure ethanol. At low BuOH/EtOH, the direct dehydration of butanol to butenes, primarily yields 1-butene, which is formed largely through the monomolecular mechanism 3 (Fig. 11c). This is directly related to the low partial pressure of butanol under these conditions, favoring the monomolecular dehydration mechanisms. Where at low total alcohol partial pressures (see 3.3.3) the formation of 1-butene is even more pronounced, here it is suppressed due to more BuOH being on the active sites as BuOH–EtOH dimers (D1_EB and D1_BE, Fig. 11g), leading to primarily EBE being formed. Strikingly, although there is almost no BuOH present, the n-butanol-assisted ethanol dehydration is still the dominant mechanism to produce ethene, demonstrating that co-feeding small amounts of BuOH to an EtOH feed intrinsically alters the ethanol dehydration route. This is because of the high surface coverage of D1_EB, which can either lead to ethene or EBE. Even when more ethanol is in the feed than butanol (between 1/10 and 1/1 BuOH/EtOH molar ratio), the surface species related to BuOH are more abundant than those related to EtOH (Fig. 11g), illustrating the more favorable confinement of BuOH-related surface species in H-ZSM-5, partly explaining the observed reactivity difference. For all studied BuOH/EtOH ratios, mechanism 29 remains dominant for the formation of EBE (Fig. 11e). Similar for the EBE decomposition, mechanism 31 is dominant for all studied ratios here.

Fig. 11 Effect of butanol/ethanol ratio in the feed on (a and b) product selectivity, (c) TOFs of different mechanisms of Path A for BuOH, (d) TOFs for different mechanisms of Path A for EtOH, (e) TOFs for EBE formation mechanisms, (f) turnover frequencies for EBE decomposition mechanisms, (g) surface coverages. Reaction conditions: P_BuOH,0 + P_EtOH,0 = 36.8 kPa, X_BuOH = 10%, T = 500 kPa, total pressure = 5 bar.

4. Conclusions

The present study provides detailed mechanistic insights into the plausible reaction pathways for dehydration of n-butanol/ethanol mixtures in H-ZSM-5. The DFT-based microkinetic model is capable to describe the behavior of the dehydration reactions of pure n-butanol, pure ethanol and mixtures of both over H-ZSM-5. The theoretical investigation is used to explain experimental observations, but also to have a predictive guidance on the effect of reaction conditions on the observed kinetics and product yields. Dominant reaction pathways are identified, and the dependence on reaction conditions is derived through a reaction path analysis.

The reaction conditions determine the surface coverage of the key species, which in turn has a strong role in governing the dominant reaction mechanisms and thus reaction products. For the formation of EBE, alkoxide-mediated mechanisms are most important at low alcohol pressure, whilst the dominant reaction mechanism shifts to alcohol-dimer mediated mechanisms at higher alcohol pressures. Lower temperatures favor alcohol-dimers as surface species, and thus formation of ethers and olefins through dimer-mediated mechanisms. Higher temperatures favor monomolecular mechanisms, such as the butoxide-mediated formation of EBE.

Somehow counterintuitively, co-processing of n-butanol and ethanol leads to an enhanced dehydration of ethanol to ethene (albeit the formation of EBE is faster), due to a novel n-butanol-assisted ethanol dehydration mechanism. The enhanced kinetics of ethanol dehydration through the butanol-assisted mechanism occurs over the complete conversion range (as longs as n-butanol is available), over the complete studied pressure and temperature range and even for mixture consisting of primarily ethanol, highlighting the importance of this mechanism, when processing alcohol mixtures. This indicates that small amounts of butanol can be added to bio-ethanol streams to enhance the ethylene formation kinetics. These insights could be applied to other alcohol mixtures to facilitate alkene formation, and could explain promotional effects of processing alcohols as mixtures.

At a high butanol/ethanol ratio most ethanol is converted to ethyl butyl ether and most ethene is formed due to a butanol-assisted mechanism. At a low butanol/ethanol ratio, most butanol is converted to ethyl butyl ether and butenes are still primarily formed through pure n-butanol dehydration mechanisms.

To obtain high olefin yields, multiple routes are possible: converting over 90% of the alcohols will always lead to high olefin selectivity under the investigated conditions. A temperature over 500 K enhances olefin formation, yet the reactivity difference between EtOH and BuOH increases as well. Low alcohol partial pressure favors olefin production, but increases the reactivity difference between both alcohols. In case the aim is highly simultaneous dehydration with an olefin yield as high as possible, than a high temperature and high total alcohol pressure is envisaged, as a high total alcohol pressure will facilitate simultaneous conversion and a high temperature will facilitate olefin formation. Under the investigated conditions, EBE will always be the main component originating from EtOH, but if the BuOH/EtOH ratio is low EBE is the main component originating from BuOH.

The obtained insights and DFT-based microkinetic model offer a framework that can provide interesting guidelines in emerging biomass-related processes to improve the dehydration of bio-alcohols as such or as mixtures (e.g. from fermentation), avoiding the need for prior separation of the individual bio-alcohols. Consequently, it is also possible to deliberately cofeed alcohols to bio-alcohol feeds to enhance dehydration kinetics.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The computational resources (Stevin Supercomputer Infrastructure) and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by Ghent University, FWO and the Flemish Government – department EWI.

References

1. A. J. Ragauskas, C. K. Williams, B. H. Davison, G. Britovsek, J. Cairney, C. A. Eckert, W. J. Frederick, J. P. Hallett, D. J. Leak, C. L. Liotta, J. R. Mielenz, R. Murphy, R. Templer and T. Tschaplinski, The Path Forward for Biofuels and Biomaterials, Science, 2006, 311, 484–489.
2. P. A. Willems, The Biofuels Landscape Through the Lens of Industrial Chemistry, Science, 2009, 325, 707–708.
3. T. Vandevyvere, M. K. Sabbe, P. S. F. Mendes, J. W. Thybaut and J. Lauwaert, NiCu-based catalysts for the low-temperature hydrodeoxygenation of anisole: Effect of the metal ratio on SiO2 and γ-Al2O3 supports, Green Carbon, 2023, 1, 170–184.
4. A. de Reviere, B. Jacobs, I. Stals and J. De Clercq, Cross-curricular project-based laboratory learning enables hands-on interdisciplinary education for chemical engineering students, Educ. Chem. Eng., 2024, 47, 1–9.
5. T. Vandevyvere, M. K. Sabbe, A. Bouriakova, S. Saravanamurugan, J. W. Thybaut and J. Lauwaert, Impact of the incipient wetness impregnation sequence during the preparation of La or Ce promoted NiCu-Al2O3 on low-temperature hydrodeoxygenation, Catal. Commun., 2023, 181, 106734.
6. H. Zimmermann and R. Walzl, Ethylene, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 2000.
7. H. Zimmermann, Propene, Ullmann's Encyclopedia of Industrial Chemistry, 2013.
8. F. M. A. Geilen, G. Stochniol, S. Peitz and E. Schulte-Koerne, Butenes, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 2000.
9. N. V. Srinath, A. Longo, H. Poelman, R. K. Ramachandran, J.-Y. Feng, J. Dendooven, M.-F. Reyniers and V. V. Galvita, In Situ XAS/SAXS Study of Al2O3-Coated PtGa Catalysts for Propane Dehydrogenation, ACS Catal., 2021, 11320–11335.
10. I. Veza, M. F. Muhamad Said and Z. A. Latiff, Recent advances in butanol production by acetone-butanol-ethanol (ABE) fermentation, Biomass Bioenergy, 2021, 144, 105919.
11. S. Saeidi, S. Najari, F. Fazlollahi, M. K. Nikoo, F. Sefidkon, J. J. Klemeš and L. L. Baxter, Mechanisms and kinetics of CO2 hydrogenation to value-added products: A detailed review on current status and future trends, Renewable Sustainable Energy Rev., 2017, 80, 1292–1311.
12. C. P. Nash, A. Ramanathan, D. A. Ruddy, M. Behl, E. Gjersing, M. Griffin, H. Zhu, B. Subramaniam, J. A. Schaidle and J. E. Hensley, Mixed alcohol dehydration over Brønsted and Lewis acidic catalysts, Appl. Catal., A, 2016, 510, 110–124.
13. T. T. N. Nguyen, V. Belliere-Baca, P. Rey and J. M. M. Millet, Efficient catalysts for simultaneous dehydration of light alcohols in gas phase, Catal. Sci. Technol., 2015, 5, 3576–3584.
14. A. de Reviere, D. Gunst, M. Sabbe and A. Verberckmoes, Sustainable short-chain olefin production through simultaneous dehydration of mixtures of 1-butanol and ethanol over HZSM-5 and γ-Al2O3, J. Ind. Eng. Chem., 2020, 89, 257–272.
15. A. H. Motagamwala and J. A. Dumesic, Microkinetic Modeling: A Tool for Rational Catalyst Design, Chem. Rev., 2021, 121, 1049–1076.
16. D. Gunst, K. Alexopoulos, K. Van der Borght, M. John, V. Galvita, M. F. Reyniers and A. Verberckmoes, Study of butanol conversion to butenes over H-ZSM-5: Effect of chemical structure on activity, selectivity and reaction pathways, Appl. Catal., A, 2017, 539, 1–12.
17. D. Gunst, M. Sabbe, M.-F. Reyniers and A. Verberckmoes, Study of n-butanol conversion to butenes: Effect of Si/Al ratio on activity, selectivity and kinetics, Appl. Catal., A, 2019, 582, 117101.
18. T. K. Phung, L. P. Hernandez, A. Lagazzo and G. Busca, Dehydration of ethanol over zeolites, silica alumina and alumina: Lewis acidity, Bronsted acidity and confinement effects, Appl. Catal., A, 2015, 493, 77–89.
19. D. Mei and J. A. Lercher, Mechanistic insights into aqueous phase propanol dehydration in H-ZSM-5 zeolite, AIChE J., 2017, 63, 172–184.
20. M. John, K. Alexopoulos, M. F. Reyniers and G. B. Marin, Reaction path analysis for 1-butanol dehydration in H-ZSM-5 zeolite: Ab initio and microkinetic modeling, J. Catal., 2015, 330, 28–45.
21. K. Alexopoulos, M. John, K. Van der Borght, V. Galvita, M.-F. Reyniers and G. B. Marin, DFT-based microkinetic modeling of ethanol dehydration in H-ZSM-5, J. Catal., 2016, 339, 173–185.
22. A. de Reviere, T. Vandevyvere, M. Sabbe and A. Verberckmoes, Renewable Butene Production through Dehydration Reactions over Nano-HZSM-5/γ-Al2O3 Hybrid Catalysts, Catalysts, 2020, 10, 879.
23. A. de Reviere, D. Gunst, M. K. Sabbe, M.-F. Reyniers and A. Verberckmoes, Dehydration of butanol towards butenes over MFI, FAU and MOR: influence of zeolite topology, Catal. Sci. Technol., 2021, 11, 2540–2559.
24. I. S. Yakovleva, S. P. Banzaraktsaeva, E. V. Ovchinnikova, V. A. Chumachenko and L. A. Isupova, Catalytic Dehydration of Bioethanol to Ethylene, Catalysis in Industry, 2016, 8, 152–167.
25. M. J. Kang, J. F. DeWilde and A. Bhan, Kinetics and Mechanism of Alcohol Dehydration on gamma-Al2O3: Effects of Carbon Chain Length and Substitution, ACS Catal., 2015, 5, 602–612.
26. K. Van der Borght, V. V. Galvita and G. B. Marin, Ethanol to higher hydrocarbons over Ni, Ga, Fe-modified ZSM-5: Effect of metal content, Appl. Catal., A, 2015, 492, 117–126.
27. C. M. Nguyen, M. F. Reyniers and G. B. Marin, Theoretical study of the adsorption of C1-C4 primary alcohols in H-ZSM-5, Phys. Chem. Chem. Phys., 2010, 12, 9481–9493.
28. N. Hansen, T. Brüggemann, A. T. Bell and F. J. Keil, Theoretical Investigation of Benzene Alkylation with Ethene over H-ZSM-5, J. Phys. Chem. C, 2008, 112, 15402–15411.
29. D. H. Olson, N. Khosrovani, A. W. Peters and B. H. Toby, Crystal Structure of Dehydrated CsZSM-5 (5.8Al): Evidence for Nonrandom Aluminum Distribution, J. Phys. Chem. B, 2000, 104, 4844–4848.
30. J. Dedecek, V. Balgova, V. Pashkova, P. Klein and B. Wichterlova, Synthesis of ZSM-5 Zeolites with Defined Distribution of Al Atoms in the Framework and Multinuclear MAS NMR Analysis of the Control of Al Distribution, Chem. Mater., 2012, 24, 3231–3239.
31. A. Janda and A. T. Bell, Effects of Si/Al Ratio on the Distribution of Framework Al and on the Rates of Alkane Monomolecular Cracking and Dehydrogenation in H-MFI, J. Am. Chem. Soc., 2013, 135, 19193–19207.
32. M. Bernauer, E. Tabor, V. Pashkova, D. Kaucký, Z. Sobalík, B. Wichterlová and J. Dedecek, Proton proximity – New key parameter controlling adsorption, desorption and activity in propene oligomerization over H-ZSM-5 zeolites, J. Catal., 2016, 344, 157–172.
33. S. R. Lonsinger, A. K. Chakraborty, D. N. Theodorou and A. T. Bell, The Effects of Local Structural Relaxation on Aluminum Siting within H-Zsm-5, Catal. Lett., 1991, 11, 209–217.
34. B. F. Mentzen and M. Sacerdoteperonnet, Prediction of Preferred Proton Locations in Hmfi Benzene Complexes by Molecular Mechanics Calculations - Comparison with Nmr, Structural and Calorimetric Results, Mater. Res. Bull., 1994, 29, 1341–1348.
35. S. Svelle, C. Tuma, X. Rozanska, T. Kerber and J. Sauer, Quantum Chemical Modeling of Zeolite-Catalyzed Methylation Reactions: Toward Chemical Accuracy for Barriers, J. Am. Chem. Soc., 2009, 131, 816–825.
36. G. Kresse and J. Hafner, Abinitio Molecular-Dynamics for Liquid-Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
37. G. Kresse and J. Hafner, Ab-Initio Molecular-Dynamics Simulation of the Liquid-Metal Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
38. G. Kresse and J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
39. M. John, K. Alexopoulos, M. F. Reyniers and G. B. Marin, Mechanistic insights into the formation of butene isomers from 1-butanol in H-ZSM-5: DFT based microkinetic modelling, Catal. Sci. Technol., 2017, 7, 1055–1072.
40. P. E. Blochl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
41. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
42. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, Molecules, Solids, and Surfaces - Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
43. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799.
44. T. Kerber, M. Sierka and J. Sauer, Application of semiempirical long-range dispersion corrections to periodic systems in density functional theory, J. Comput. Chem., 2008, 29, 2088–2097.
45. C. Tuma and J. Sauer, Treating dispersion effects in extended systems by hybrid MP2: DFT calculations - protonation of isobutene in zeolite ferrierite, Phys. Chem. Chem. Phys., 2006, 8, 3955–3965.
46. F. Goltl, A. Gruneis, T. Bucko and J. Hafner, Van der Waals interactions between hydrocarbon molecules and zeolites: Periodic calculations at different levels of theory, from density functional theory to the random phase approximation and Moller-Plesset perturbation theory, J. Chem. Phys., 2012, 137, 114111.
47. M. V. Vener, X. Rozanska and J. Sauer, Protonation of water clusters in the cavities of acidic zeolites: (H2O)(n)center dot H-chabazite, n=1-4, Phys. Chem. Chem. Phys., 2009, 11, 1702–1712.
48. C. C. Chiu, G. N. Vayssilov, A. Genest, A. Borgna and N. Rosch, Predicting Adsorption Enthalpies on Silicalite and HZSM-5: A Benchmark Study on DFT Strategies Addressing Dispersion Interactions, J. Comput. Chem., 2014, 35, 809–819.
49. C. M. Nguyen, M. F. Reyniers and G. B. Marin, Adsorption thermodynamics of C1-C4 alcohols in H-FAU, H-MOR, H-ZSM-5, and H-ZSM-22, J. Catal., 2015, 322, 91–103.
50. C. M. Nguyen, M. F. Reyniers and G. B. Marin, Theoretical Study of the Adsorption of the Butanol Isomers in H-ZSM-5, J. Phys. Chem. C, 2011, 115, 8658–8669.
51. T. Bučko and J. Hafner, The role of spatial constraints and entropy in the adsorption and transformation of hydrocarbons catalyzed by zeolites, J. Catal., 2015, 329, 32–48.
52. F. Leydier, C. Chizallet, D. Costa and P. Raybaud, Revisiting carbenium chemistry on amorphous silica-alumina: Unraveling their milder acidity as compared to zeolites, J. Catal., 2015, 325, 35–47.
53. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
54. T. J. Goncalves, P. N. Plessow and F. Studt, On the Accuracy of Density Functional Theory in Zeolite Catalysis, ChemCatChem, 2019, 11, 4368–4376.
55. G. Henkelman and H. Jonsson, A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives, J. Chem. Phys., 1999, 111, 7010–7022.
56. A. Heyden, A. T. Bell and F. J. Keil, Efficient methods for finding transition states in chemical reactions: Comparison of improved dimer method and partitioned rational function optimization method, J. Chem. Phys., 2005, 123, 224101.
57. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904.
58. B. A. De Moor, A. Ghysels, M. F. Reyniers, V. Van Speybroeck, M. Waroquier and G. B. Marin, Normal Mode Analysis in Zeolites: Toward an Efficient Calculation of Adsorption Entropies, J. Chem. Theory Comput., 2011, 7, 1090–1101.
59. Y. Zhao and D. G. Truhlar, Computational characterization and modeling of buckyball tweezers: density functional study of concave-convex pi center dot center dot center dot pi interactions, Phys. Chem. Chem. Phys., 2008, 10, 2813–2818.
60. R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, Use of Solution-Phase Vibrational Frequencies in Continuum Models for the Free Energy of Solvation, J. Phys. Chem. B, 2011, 115, 14556–14562.
61. S. Grimme, Supramolecular Binding Thermodynamics by Dispersion-Corrected Density Functional Theory, Chem. – Eur. J., 2012, 18, 9955–9964.
62. J. H. Jensen, Predicting accurate absolute binding energies in aqueous solution: thermodynamic considerations for electronic structure methods, Phys. Chem. Chem. Phys., 2015, 17, 12441–12451.
63. G. Piccini and J. Sauer, Effect of Anharmonicity on Adsorption Thermodynamics, J. Chem. Theory Comput., 2014, 10, 2479–2487.
64. G. Piccini, M. Alessio, J. Sauer, Y. C. Zhi, Y. Liu, R. Kolvenbach, A. Jentys and J. A. Lercher, Accurate Adsorption Thermodynamics of Small Alkanes in Zeolites. Ab initio Theory and Experiment for H-Chabazite, J. Phys. Chem. C, 2015, 119, 6128–6137.
65. B. A. De Moor, M. F. Reyniers and G. B. Marin, Physisorption and chemisorption of alkanes and alkenes in H-FAU: a combined ab initio-statistical thermodynamics study, Phys. Chem. Chem. Phys., 2009, 11, 2939–2958.
66. C. J. Cramer, Essentials of computational chemistry: theories and models, Wiley, Chichester Hoboken, NJ, 2nd edn, 2004.
67. P. J. Linstrom and W. G. Mallard, The NIST Chemistry WebBook: A Chemical Data Resource on the Internet, J. Chem. Eng. Data, 2001, 46, 1059–1063.
68. A. C. Hindmarsh, ODEPACK, A Systematized Collection of ODE Solvers, in Scientific Computing, ed. R. S. Stepleman, North-Holland, Amsterdam, 1983, pp. 55–64.
69. H. Chiang and A. Bhan, Catalytic consequences of hydroxyl group location on the rate and mechanism of parallel dehydration reactions of ethanol over acidic zeolites, J. Catal., 2010, 271, 251–261.
70. J. Macht, R. T. Carr and E. Iglesia, Functional assessment of the strength of solid acid catalysts, J. Catal., 2009, 264, 54–66.
71. S. Kozuch and S. Shaik, How to Conceptualize Catalytic Cycles? The Energetic Span Model, Acc. Chem. Res., 2011, 44, 101–110.
72. F. Eder, M. Stockenhuber and J. A. Lercher, Sorption of light alkanes on H-ZSM5 and H-mordenite, in Studies in Surface Science and Catalysis, ed. L. Bonneviot and S. Kaliaguine, Elsevier, 1995, pp. 495–500.
73. B. A. De Moor, M.-F. Reyniers, O. C. Gobin, J. A. Lercher and G. B. Marin, Adsorption of C2−C8 n-Alkanes in Zeolites, J. Phys. Chem. C, 2011, 115, 1204–1219.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cy00532e

---