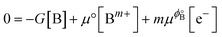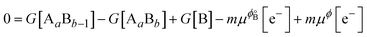Dynamic stability of Pt-based alloys for fuel-cell catalysts calculated from atomistics

Abstract

The oxygen reduction reaction (ORR) is the fundamental electron-accepting reaction in aqueous electrochemistry, and is crucial to technologies such as fuel cells and batteries. Alloys of Pt that produce a surface Pt layer under mildly compressive strain are generally the most reactive catalysts for this reaction; however, their long-term durability can vary widely with preparation. In this work, we develop atomistic models based on electronic structure calculations to compare and rationalize the stability of such electrocatalysts, focusing on contrasting face-centered tetragonal (FCT or L1₀) alloys of Fe, Ni and Co with that of their face-centered cubic (FCC or L1₂) counterparts. We first describe how the non-noble elements Ni, Fe, Co and Sc of the near-surface alloy have the driving force to undergo rapid dissolution at fuel-cell operating conditions, whereas Pt is quite stable against dissolution, leading to the well-known surface Pt enrichment. Post dissolution, we discuss the kinetics associated with diffusion of sub-surface elements through a vacancy mediated diffusion model. Through the diffusion models, we compare and discuss the effect of geometry and surface structure on an electrocatalyst's stability. We show that alloying Pt with non-noble elements results in significantly higher kinetic stability of the core as compared to pure Pt. Our calculations suggest that the diffusion energetics at the bulk can be quite different from the near-surface region; we conclude the surface rates are more essential. We find that L1₀ structures of Fe and Co could provide better stability than the L1₂ systems, especially in the presence of Pt overlayers. In contrast, for Sc-containing species, we argue that presence of Pt overlayers destabilizes the catalytic surface, as also reported by an experimental study.

---

I. Introduction

The externalities associated with the production and consumption of fossil fuels, coupled with a continuously increasing global energy demand, have created tremendous incentives to accelerate the transition to cleaner and more sustainable energy solutions. Electrochemical technologies, which facilitate the interconversion of electrical and chemical energy, are considered crucial to the electrification of several important industries.¹ This has triggered a significant increase in research activities in the field of electrochemical energy conversion and storage devices, and pathways towards large-scale commercialization of such technologies is crucial. In the past decade, several advances have been made for improving the activity of electrocatalysts for such technologies. However, a major bottleneck in scaling up such devices for industrial application is the stability of the electrocatalyst.

With the large commercial interest in developing hydrogen technologies for conversion and storage of renewable electricity, devices like hydrogen-proton exchange membrane fuel cells (PEMFCs) play a pivotal role in providing us with an ecological way to generate power by exploiting hydrogen gas.^2,3 The advancement in fuel-cell technology over the past decade, and the recent commercialization of PEMFCs in the automobile industry have drawn attention towards studies involving PEMFCs and other environmental friendly energy storage (and conversion) devices.⁴ A typical hydrogen-PEMFC consists of two half-cells separated by a proton-exchange membrane. The anodic half-cell is responsible for the hydrogen oxidation reaction (HOR) while the oxygen reduction reaction (ORR) occurs in the cathodic half-cell. In terms of activity, platinum (Pt) is known to be the best single-elemental catalyst for both HOR and ORR in acidic media. Despite that, ORR is known for being six or more orders of magnitude slower than HOR on Pt. The sluggishness of ORR is responsible for the high cathodic Pt loading (∼0.4 mg_Pt cm⁻²)^5,6versus the anode (∼0.05 mg_Pt cm⁻²).⁷ This accounts for about eight times more Pt usage in cathode, rendering the conventional hydrogen-PEMFCs economically challenging to commercialize. The overpotential, which we define as the difference between the working electrode potential and the thermodynamic equilibrium potential of a reaction, is theoretically reported to be ∼0.4–0.5 V_RHE for ORR while it is only ∼0.05 V_RHE for HOR at a current density of 1 mA cm⁻².^8–10 This high overpotential for ORR is infamous for limiting the overall performance of fuel-cells. In order to tackle the limitations of the cathodic half-cell, researchers have been devoting major resources to improving and developing ORR electrocatalysts.

Replacing Pt with other non-precious transition metals has become one of the many useful strategies in the development of ORR electrocatalysts which allows for both cost and overpotential reduction at the same time. It includes creating geometric and electronic modifications to plausible Pt-based electrocatalysts to enhance its surface activity. Some state-of-the-art Pt-based electrocatalysts include jagged Pt nanowires,¹¹ Pt–Ni nanocages,¹² Pt–Pb nanoplatelets,¹³ Pt₃Fe nanowires,¹⁴ Pt–Ni nanoframes,¹⁵ Pt₃Co nanowires,¹⁶ Mo–Pt₃Ni octahedras¹⁷ and L1₀-CoPt core–shell nanoparticles.¹⁸ In particular, core–shell type Pt–M (M = Fe, Co, Ni or Cu) nanoparticles^18–28 are one of the widely studied materials for ORR as they are known to have high surface-area-to-mass ratio and high per-site activity, rendering them very practicable for ORR activity enhancement. The increased performance of the core–shell electrocatalysts are largely attributed to the presence of a compressively strained Pt “shell” often created by acid-leaching,²⁹ dealloying³⁰ or annealing³¹ of a Pt based alloy. Computational studies have confirmed that compressive strain induced on Pt “shell” by the alloyed-core provides improved adsorbate–surface interaction resulting in higher ORR activity.^32–38 Based on the Pt shell thickness, subsurface secondary elements (the ligand effect) can further influence the binding of an adsorbate.^39,40 Descriptors like shift in d-band center,^33,41 eigenstresses,⁴² eigenforces^40,43 and coordination numbers⁴⁴ are known to predict the adsorbate interaction with a catalytic surface, making it easier for experimentalists to screen potential ORR electrocatalysts at a faster pace. The experimental evidences combined with computational predictions have proven to be a strong motivation for researchers for pursuing core–shell type Pt alloys for potential ORR electrocatalysts.⁴⁵

Despite the impressive initial activity of core–shell and other shape-controlled Pt-based alloys, the overall performance of these catalysts largely depend on their durability and long-term stability in the fuel cell environment. We get an insight from the Pourbaix diagrams that pure transition metals like Co, Ni, Fe and Cu are not stable at the fuel cell operating conditions (∼0.9–1 V_RHE; and ∼0 pH) and would readily dissolve in to the solution. In fact, dissolution or leaching of non-noble metals in the acidic environment is considered the main reason behind the poor stability of several Pt-based electrocatalysts.^{10,17,46–50} Pretreating the electrocatalyst to replace surface non-noble elements with Pt has become the most well-known strategy to avoid surface dissolution, allowing for enhanced durability and impressive activity. However, studies have shown that despite having Pt overlayers, the state-of-the-art Pt-based catalysts which showed impressive ORR activity in the laboratory designed liquid half cells, did not show much improvement over commercial Pt when tested under membrane electrode assembly (MEA) conditions.^48,51 This renders the designing of Pt-based catalysts more challenging, creating an urgent need to focus on the stability of ORR catalysts.

To improve the stability of such Pt-based alloys, strategies mainly pertaining to stabilization of the non-noble metal have been adopted. Doping of certain transition metals like Mo and Rh into Pt-based alloys have been known to improve resistance to oxidation of non-noble transition metals.^17,52–54 Core–shell structures with a protective Pt layer have also demonstrated stability against the leaching of non-noble metals, resulting in durable catalysts. However, achieving this with nanoparticles larger than 5 nm often required high Pt content, limiting Pt reduction efforts. As an alternative, researchers developed base-metal-rich random alloy nanoparticles with less than 50% Pt content, leveraging the stability of random alloys at certain compositions. This strategy was used for Au-doped Pt,⁵⁵ Mo-doped,¹⁷ and trimetallic PtPdCu nanoparticles.⁵⁶ Wang et al.⁵⁷ emphasized that precise alloy composition and atomic arrangement enhanced catalyst stability by improving resistance to dissolution and surface segregation. Furthermore, Wu et al.⁵⁶ showed that alloying PtPd with 3d-transition metals enabled realloying under operational conditions, maintaining structure and performance by healing dealloyed structures. These findings support exploring compositions with less than 50% Pt or PtPd content for durable catalysts. Another design principle that shows great potential for enhancing stability of a core–shell type Pt-based electrocatalyst is controlling its morphology and/or shape. Tian et al. fabricated Pt–Ni nanocages which showed, to the best of our knowledge, the highest ORR activity recorded from a Pt alloyed electrocatalyst in a liquid half-cell with a mass activity (MA) of 3.52 A mg_Pt⁻¹ and negligible activity decay after 50 000 cycles.¹² Similarly, Li et al. showed that face-centered tetragonal (FCT or L1₀ geometry) lattice structure resulted in superior performance than traditional face-centered cubic (FCC or A1 geometry) lattice for PtCo and PtFe catalysts in terms of both activity and stability. The core–shell L1₀-PtCo nanoparticles showed a MA of 0.56 A mg_Pt⁻¹ under MEA conditions with only 19% loss in MA after 30 000 cycles, thus surpassing the US Department of Energy (DOE) 2020 target in terms of activity and durability (0.44 A mg_Pt⁻¹ in MA and <40% loss after 30 000 cycles).^18,19 The increased stability of such L1₀ PtM structures are believed to be the consequence of high degree of order with a Pt to M ratio of 1 : 1 as compared to the disordered cubic A1 (PtM) and ordered L1₂ (Pt₃M) counterparts.

Inspired by the experimental evidences showing superior stability of L1₀-type Pt alloys, in this study we present a computational comparison on the stability between L1₀ and L1₂ structures, both in the fully ordered state. The schematic showing the disordered A1 and ordered L1₂ or L1₀ structures are shown in Fig. 1. We divided the stability analysis into three parts (Fig. 2): dissolution (thermodynamics), bulk diffusion (kinetics) and near-surface diffusion (kinetics). Firstly, we present a framework to calculate the dissolution potentials of the surface elements. Next, we present a model to analyze the kinetic stability of core (bulk) through a vacancy mediated diffusion process. Finally, we study the possibility of migration of non-noble elements to the surface by calculating “near-surface” kinetic barriers. In particular, we discuss the thermodynamic feasibility of Pt shell formation as well as its effect on kinetic stability of the alloys. In this work we consider alloys of Fe, Co, Ni and Sc. We consider Sc since computational studies has reported L1₂-Pt₃Sc to be the most stable fcc Pt-based alloy along with improved ORR activity.^58,59 However, an experimental study by Johansson et al.⁶⁰ showed that Pt-skin type structures are unstable on Pt₃Sc, creating confusion in the fuel-cell community about the usefulness of alloying early transition metals with Pt to make stable and efficient ORR electrocatalysts. As we'll show, our calculations also suggest that the presence of Pt overlayers on Pt₃Sc can destabilize the electrocatalyst surface and could promote transport of subsurface Sc atom to the dissolution-prone surface region.

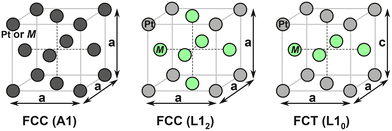Fig. 1 Schematic showing the Pt-based alloys in left: random FCC (A1) geometry, middle: ordered FCC (L1₂) geometry, and right: ordered FCT (L1₀) geometry.

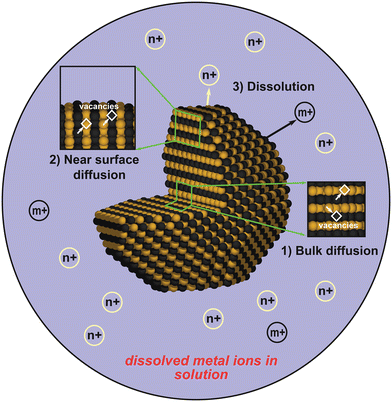Fig. 2 The three regimes studied in this work: i.e., bulk diffusion, near-surface diffusion, and dissolution.

II. Computational methods

We performed ab initio electronic structure calculations using density functional theory (DFT) by employing the GPAW (grid-based projector-augmented wave) code^61–63 with a plane wave (PW) basis set. The atomic manipulations and visualizations were handled in Atomic Simulation Environment (ASE).⁶⁴ The revised Perdew–Burke–Ernzerhof (RPBE) exchange–correlation functional⁶⁵ of Hammer, Hansen and Nørskov was employed along with a plane wave cutoff of 550 eV for all the calculations. We used the RPBE optimized bulk lattice constants listed in Table S1 of the ESI† to model the alloys. The lattice optimization was performed with a 7 × 7 × 7 k-point mesh while a 4 × 4 × 4 mesh was used for calculations involving bulk diffusion barriers and a 4 × 4 × 1 mesh for all other surface calculations. We accounted for the ferromagnetic properties of the systems containing Fe, Co and Ni by considering spin-polarization. Detail specifics pertaining to the methods employed for calculating dissolution potential, diffusion barriers in bulk and near-surface diffusion are described below.

Bulk diffusion

In order to compute and compare the relative ease of diffusion of elements in different L1₀ and L1₂ Pt alloys, we considered a vacancy mediated diffusion model similar to the one employed by Vej-Hansen et al.⁶⁶ to estimate bulk diffusion barriers in L1₂ Pt-alloy structures. Our diffusion model includes replacement of an atom (typically, a non-noble element) with a vacancy followed by movement of atoms (or the vacancy) in a fixed pattern as shown in Fig. 3 for L1₀ type Pt-based alloys. As shown in the schematic, the model includes a simple diffusive pattern comprising six steps (involving only three atoms) with configuration (a) as the start and (g) as the end. The model considers translational symmetry; i.e., the diffusive pathway from configuration (a) to (d) is a mirror image of the pathway from (d) to (g). The symmetry allowed us to break the diffusive path into half as the steps involved were pairwise mirror images of each other. Hence, we only needed to compute the first three reaction barriers (path (a) to (d)) to capture the entire bulk diffusion pathway. The overall diffusion barrier was calculated as the energy difference between the highest energy transition state along the diffusion pathway and the initial state (a). The model was employed for Pt-based alloys in L1₀, L1₂ crystal structures as well as for native/pure Pt. For L1₂ alloys the pattern is similar to that shown in Fig. 3 for L1₀ alloys, and is provided in Fig. S1 of the ESI.† All the bulk systems considered in this study were modeled using a 2 × 2 × 2 unit cell, periodic in all directions. We employed the nudged elastic band (NEB)⁶⁷ method to obtain the kinetic barriers between any two thermodynamically stable local minima. We obtained the true transition state by using the climbing image NEB (CI-NEB)⁶⁸ once the conventional NEB was optimized. The atomic force optimization criteria of 0.05 eV Å⁻¹ was used for both CI and conventional NEB. Our choice of the size of supercell was influenced by the computational intensity of calculating energy barriers using the NEB method across various systems. This complexity is further heightened by the requirement of spin-polarized calculations for systems involving Fe, Co, and Ni. The results obtained are summarized in section IIIA.

Fig. 3 Schematic showing the bulk diffusion process from configuration (a) to (g) through vacancy mediated diffusion for the L1₀ PtFe system. The squares represent a vacancy while the arrow shows the movement of an element in to the vacancy.

Near-surface diffusion

Similar to the model describing diffusion in the bulk, we considered vacancy mediated diffusion of elements to the surface from the near-surface region. In this model, we studied the diffusion of an element from the third layer below the surface to the top layer, as shown in Fig. 4. The model includes a simple diffusive pattern comprising six steps (involving only three atoms) with configuration (A) as the start and (F) being the end. The overall diffusion barrier was calculated as the energy difference between the highest energy transition state along the diffusion pathway and the initial state (A). A schematic showing a similar near-surface movement of atoms in L1₂ type Pt-based alloys is provided in Fig. S2 of the ESI.† All the surfaces were modeled using a four atomic-layer thick, 2 × 2 slab, periodic in the x–y direction and having 15 Å vacuum in the z-direction. During optimization, the bottom layer was kept fixed while the others were allowed to relax. The systems with Pt overlayers were created by replacing the non-noble elements from the top layer with Pt, while keeping the lattice constant at the same value as that of the bulk alloy. We also used the same NEB/CI-NEB procedure and parameters mentioned above for bulk diffusion. We recognize that the diffusion barrier and pathway from the subsurface to the surface layer may be influenced by the specific facet, which is particularly important when comparing absolute diffusion energetics and mechanisms across different surfaces. This is especially relevant when analyzing anisotropic surfaces in L1₀ systems compared to the cubic L1₂ systems. For simplicity, this study focuses on the 001 surface for near-surface diffusion, maintaining a consistent diffusion pathway with that of bulk diffusion. While the chosen diffusion pathway may not represent the absolute minimum energy path for the diffusion of subsurface elements to the surface, it provides a systematic method for comparing (i) bulk vs. near-surface diffusion and (ii) the relative ease of movement in the near-surface region across different alloys. This approach allows for a clear and structured comparison of diffusion behaviors, facilitating a better understanding of the kinetic stability of these systems. The results obtained are summarized in section IIIB.

Fig. 4 Schematic showing subsurface diffusion of secondary metal element (M) to the surface i.e., from configuration (A) to (F) through vacancy mediated diffusion. The squares represent a vacancy while the arrow shows the movement of an element in to the vacancy.

Dissolution

Several approaches have been reported in the literature to calculate reduction or dissolution potentials using electronic structure calculations.^46,69–71 We adopted an approach fundamentally similar to that described by Greeley et al.,⁴⁶ which they developed for calculating dissolution potentials of solute atoms embedded in the surface layers of host substrates. We started off by taking our system to be a surface region of an electrocatalyst with composition A_aB_b and considering the dissolution of element “B”:

A_aB_b(s) → A_aB_b−1(s) + B^m+_(aq) + me⁻

since the system is connected to an operating circuit, the m electrons leave the system by traveling into the circuit. We aim to find the potential ϕ at which the free-energy change of this reaction is zero:

0 = G[A_aB_b−1] − G[A_aB_b] + μ[B^m+] + mμ^ϕ[e⁻]

where we use G to denote the free energy of the system and μ for the chemical potential of species crossing the system boundary. To establish a reference potential, we compare this to the dissolution of pure B:

B_(s) ↔ B^m+ + me⁻

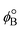which at pure B's dissolution potential has a zero free-energy change:
In this study, we took the concentration of B^m+ to be the standard ion concentration, thus μ[B^m+] = μ°[B^m+] and

where we used μ^ϕ[e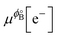⁻] − = , where e is the electron charge. The above equation allowed us to approximate the dissolution potential ϕ of the alloy. We also considered a displacement reaction, where an atom of element type B on the surface gets replaced by element A from the solution,

A_aB_b−1(s) + Aⁿ⁺_(aq) + ne⁻ → A_a+1B_b−1(s) + B^m+_(aq) + me⁻

Similar to the analysis above, the net reaction free-energy at any arbitrary potential ϕ was written as
For a situation where m = n,

The last two equations were used to calculate the change in free energy associated with replacement of a particular element with another. Note that the change in free energy (ΔG) is a function of potential when m ≠ n but is independent of potential when m = n. As in Greeley et al.,⁴⁶ we approximated G of all solids to be equivalent to E, the potential energy calculated with DFT. That is, we did not attempt to account for changes to the solids' phonon structure caused by the defect nor consider the configurational entropy of the defect. The standard reduction potentials were taken from the CRC handbook⁷² and are tabulated in Table S2 of the ESI.† The above model was used to calculate dissolution potentials of Pt, Ni, Fe, Co and Sc in L1₀ or L1₂ Pt-alloy structures. A charge of 3 was used for Sc ions and 2 for Fe, Co, Ni and Pt. The surfaces were modeled using a 3 × 4 super cell, periodic in the x–y direction with four atomic layers and 15 Å vacuum in the z-direction. During optimization of geometric structures, we fixed the bottom layer of the surface slab, while allowing the top three layers to relax until the maximum force on any unconstrained atom converged to <0.05 eV Å⁻¹. The results obtained are summarized in section IIIC.

III. Results and discussion

In this section, we report and compare the stability of Pt-based alloys of Fe, Co, Ni and Sc in two different crystal structures, L1₀ and L1₂. We divide the analysis in three parts: A) bulk diffusion, B) near-surface diffusion, and C) dissolution potential. Assuming that only atoms on the surface can dissolve into the solution, dissolution must be accompanied by internal diffusion for further degradation over time. Diffusion in solids can be broadly classified into three categories: interstitial, collective and vacancy mediated. The interstitial mechanism, as the same suggests, is known to be common in situations involving diffusion of considerably small atoms from one interstitial site to another within the host lattice. This mechanism is considered relevant for diffusion of elements like H, C, N and O in metals and alloys.⁷³ The collective mechanism involves the simultaneous movement of two (direct exchange) or more (ring exchange) atoms. In a close-packed lattice, such a diffusion process would require a large distortion for the free movement of atoms, which usually entails a high activation barrier, making this mechanism energetically unfavorable in close-packed lattices.⁷⁴ In fact, Kirkendall et al.^75,76 showed that the observed different self-diffusion rates of atoms in a substitutional binary alloy cannot be explained by collective but rather by diffusion through a vacancy. Vacancy mediated diffusion is recognized as the dominant diffusion mechanism in metals and alloys.^77,78 An atom is said to diffuse by this mechanism, when it jumps into a neighboring vacancy. In this study, we explore defect free, single-crystalline systems undergoing vacancy mediated diffusion. It is anticipated that vacancies can lower the long-term stability of an alloy due to the dissolution of diffusion-transported elements to the surface as well as by creating regions of varying metal concentrations within the bulk of a catalyst. As a descriptor of kinetic stability, we report and discuss the diffusion barriers (bulk and near-surface) for Pt-based alloys in section IIIA & IIIB. Lastly, in the discussion pertaining to diffusion near a surface, we also study the influence of Pt overlayers on the diffusion barriers. Section IIIC discusses the dissolution of Pt as well as non-noble elements considered in this study at relevant fuel-cell potentials. This provides us with a qualitative picture of the stability of individual elements at the catalyst surface. We further study the thermodynamics behind the formation of Pt overlayers, which is known to play a significant role in improving the stability of Pt-based electrocatalysts.

A. Bulk diffusion

As a descriptor of the bulk kinetic stability, we report the calculated bulk diffusion barriers in this section. Fig. 3 shows the calculated pathway for the L1₀ FePt system with an Fe vacancy; Fig. S3 in the ESI† includes the remaining systems in both the L1₀ and L1₂ configuration. As mentioned in section II, due to the translational symmetry present in our vacancy mediated diffusion model, the overall barrier can be calculated by only studying the movement from configuration (a) to (d) (i.e., from initial state (a) to the middle of the diffusion pathway (d) as shown in Fig. 3). The overall barrier is calculated as the potential energy difference between highest-energy transition state along the diffusion pathway and the lowest-energy stable state. For all the alloyed systems considered, the highest energy transition state corresponds to the transition state obtained in diffusion from configuration (c) to (d), while the lowest energy configuration was the initial state (a). Fig. 5 shows the vacancy mediated bulk diffusion barriers, plotted against the energy difference (ΔE_a–d) between the initial configuration (a) and the middle of the diffusion path (d). We note a strong correlation between ΔE_a–d and the overall diffusion barrier, E_b. Vej-Hansen et al.⁶⁶ observed a Brønsted–Evans–Polanyi (BEP) type correlation for L1₂ Pt-based alloys, and our calculations suggest that this correlation also applies to the L1₀ alloys studied here. Such correlations may be useful to efficiently estimate bulk diffusion barriers of a larger number of Pt-based alloys without actually performing NEB calculations on each of them.

Fig. 5 Plot showing a correlation between bulk diffusion barrier, E_b (eV) and the energy difference, ΔE_a–d (eV).

All of the alloys we studied have higher bulk diffusion barriers than native Pt. The diffusion barriers follow a trend Pt₃Sc > Pt₃Fe ≈ PtFe > Pt₃Co ≈ PtCo > Pt₃Ni ≈ PtNi > Pt. Among all the studied alloys, L1₂-Pt₃Sc showed the highest diffusive barrier suggesting a highly stable bulk in comparison to the other alloys considered. In fact, computational investigations have reported L1₂-Pt₃Sc to be the most stable Pt-based fct alloy along with high ORR activity, making it a plausible electrocatalyst for ORR.^58,59 Our calculations also show negligible difference between the overall bulk diffusion barriers of completely ordered L1₀ and L1₂ Pt-based alloys of Fe, Co and Ni suggesting similar bulk kinetic stability. In real-case scenarios, with the presence of vacancies, impurities, grain boundaries and curvature, the alloyed nanoparticles may not be completely ordered (in a separate study, we recently examined the influence of disorder on the bulk stability of the core⁷⁹). However, experimental studies have shown higher ORR activity and stability of ordered (L1₂) Pt-based structures in comparison with their cubic disordered (A1) counterparts. Hence, our current results can be considered as comparing the best-case scenarios while suggesting that maintaining a higher degree of orderliness may be the key to achieving higher stability.

B. Near-surface diffusion

The previous section discussed the diffusion barriers of elements within the bulk, providing us with an understanding about the kinetic stability of Pt-based alloys in the core. However, as discussed later in section IIIC, with the ease of dissolution of non-noble elements from the surface, the subsurface non-noble elements can become susceptible to dissolution upon diffusion. Hence, understanding the transport of non-noble elements to the surface becomes equally important in order to understand the overall long-term stability of an ORR electrocatalyst. In this section, we report and discuss the diffusion of non-noble elements to the surface as described by the model shown in Fig. 4. Keeping in mind the computationally expensive NEB calculations, we only study the alloys containing Sc, Fe and Co as they have the highest bulk diffusion barriers among the studied alloys.

We start off by studying diffusion of the non-noble elements from the near-surface to the surface; i.e., the total barrier required to reach from configuration A to F (as described under methods, Fig. 4). The diffusion-to-surface barriers associated with the alloys studied are reported in Fig. 6. The barriers related to diffusion-to-surface follow the trend Pt₃Sc > PtFe > Pt₃Co ≈ PtCo > Pt₃Fe. For Fe containing alloys, comparing L1₀ crystal structure to L1₂, we observe L1₀-PtFe (2.14 eV) to have a higher diffusion barrier than L1₂-Pt₃Fe (1.89 eV). However, there was no significant difference between L1₂-Pt₃Co and L1₀-PtCo, with the diffusion barriers being 1.95 eV and 1.98 eV, respectively.

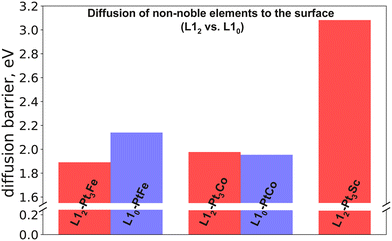Fig. 6 Diffusion barriers of transporting non-noble elements from near-surface to the surface in the absence of Pt overlayers: comparison between L1₀ and L1₂ structures.

As discussed later in section IIIC, the alloys considered favor formation of a Pt overlayer as a consequence of dissolution of non-noble elements. Hence, we incorporate the effect of presence of Pt overlayers on the diffusion barriers. This is done by replacing the non-noble elements of the top layer with Pt (as shown in Fig. 7) while maintaining the alloy lattice constant. A comparison between the diffusion barriers in the presence and absence of a Pt overlayer are reported in Fig. 8. The electronic structure calculated CI-NEB pathways for near-surface diffusion in the presence and absence of Pt overlayers for both L1₀ and L1₂ Pt-alloys are provided in Fig. S4 and S5 of the ESI.† For Fe and Co containing alloys, we observe that the presence of Pt shell increases the surface diffusion barrier, with the effect much more significantly visible for Fe containing alloys. This suggests that the presence of Pt overlayers provide kinetic stability towards transport of subsurface non-noble elements to the surface that can otherwise readily dissolve. For L1₀ crystal structure, the increase in diffusion barrier with Pt overlayer is found to be larger than for L1₂ structure suggesting influence of crystal structure and stoichiometry on the stability of an alloy. This may be the reason behind the experimentally observed higher stability of L1₂ structures with Pt overlayers compared to their disordered A1 cubic counterparts.

Fig. 7 Schematic showing subsurface diffusion of secondary metal element (M) to the surface i.e., from configuration (A) to (F) through vacancy mediated diffusion in the absence (top) and presence of Pt overlayers.

Fig. 8 Diffusion barriers of transporting non-noble elements from near-surface to the surface in the presence (and absence) of Pt overlayers: comparison between L1₀ and L1₂ structures.

Pt₃Sc, on the other hand, shows a decrease in the diffusion barrier in the presence of Pt overlayers, suggesting destabilizing of the surface in the presence of Pt overlayers. This behaviour is in agreement with Johansson et al.,⁶⁰ showing that Pt₃Sc is unstable as Pt-skin type structure. Unlike the alloys of Fe and Co considered in this study, which provide a significant compressive strain of an order of ∼2–4% on the Pt overlayer with respect to native Pt, Pt₃Sc offers a negligible bi-axial tensile strain of ∼0.9%. It well known that compressive strain is beneficial for improving ORR activity as it leads to weaker binding of ORR intermediates. On the other hand, having a tensile strain, as seen in Pt₃Sc alloys with Pt overlayers, would suggest poorer performance of ORR with respect to native Pt. Despite the presence of tensile strain, the presence of subsurface Sc (ligand effect) has been suggested to contribute to enhanced ORR activity for Pt₃Sc.⁵⁹ However, the destabilization of Pt₃Sc with the presence of Pt overlayers suggests that more Sc is prone to dissolution due to internal diffusion eventually losing the beneficial ligand effect. A computational study by Johansson et al.⁶⁰ suggested the same as the ORR activity of Pt₃Sc with 0% Sc in the second layer was obtained to be below that of native Pt. On the other hand, the increase in stability due the presence of Pt overlayers in the case Fe and Co containing alloys suggest that the presence of Pt overlayers may help in retaining the compressive strain effect required for improved ORR activity by preserving the core. To establish a similar BEP type relation, in Fig. 9 we plot the overall surface diffusion barrier (E_b) with the energy difference (ΔE_A–D). We observe that a reasonable BEP type correlation may also be applicable to near-surface diffusion allowing us to efficiently estimate diffusion barriers while limiting the number of required NEB calculations.

Fig. 9 Plot showing a correlation between near-surface diffusion barrier, E_b (eV) and the energy difference, ΔE_A–D (eV).

The overall diffusion barriers for both bulk and near-surface diffusion were further converted into rates at 80 °C and compared between different systems. While rate comparisons of all possible combinations are provided in Fig. S6 of the ESI,† we wanted to highlight the following few observations in the main text: 1) Pt-based alloys studied here may offer strong core-stability with bulk diffusion rates much slower than native Pt by a factor of 10⁷–10³⁴; 2) presence of Pt overlayers on the surface of Fe & Co containing systems slows the rate of diffusion of non-noble elements to the surface by a factor of e^3.4 (≈ 30), e^2.5 (≈ 12), e^3.6 (≈ 37) and e^5.1 (≈ 165) for L1₂-Pt₃Co, L1₂-Pt₃Fe, L1₀-PtCo and L1₀-PtFe, respectively; 3) presence of Pt overlayers on L1₂-Pt₃Sc results in a faster rate of diffusion of Sc to the surface by a factor of e¹⁴ (≈ 1.2 × 10⁶).

The current study compares the kinetic stability between ordered L1₂ and L1₀ phases, demonstrating that certain L1₀ systems with Pt overlayers may offer higher kinetic stability in retaining non-Pt elements within the catalyst. In a separate article, we examined the influence of disorder on the bulk stability of the core.⁷⁹ Using density functional theory, we attributed the enhanced durability of ordered L1₀-PtCo systems to the higher kinetic stability of Co elements in the core. Similarly, the higher average M coordination number of Pt atoms in ordered L1₂ phases compared to the disordered A1 phase has been linked to improved retention of M in ordered FCC Pt₃M and PtM₃ structures. In disordered samples, it is statistically easier to remove M from the alloy due to the weaker M–M bonds compared to M–Pt bonds.⁸⁰

Our calculations show a negligible difference between the bulk diffusion barriers for completely ordered L1₀ and L1₂ alloys. However, L1₀-PtFe and L1₀-PtCo alloys with Pt overlayers exhibit higher near-surface diffusion barriers than their L1₂ counterparts. This finding encourages the experimental research community to systematically explore the stability between L1₀ and L1₂ systems. While our study provides trends and comparisons between specific ordered L1₀ and L1₂ catalysts, it is important to note that other factors, including morphological differences, the presence of disorder or impurities, curvature, grain boundaries, reactive species on the surface, and the electrolyte environment, can influence the overall stability of the catalyst.

C. Dissolution

In this section, we report the theoretically calculated dissolution potentials of Pt and other non-noble elements, M (M = Fe, Ni, Co and Sc). To highlight the relative stability of Pt to M, Fig. 10 shows the computed dissolution potentials of Pt and M for all L1₀ and L1₂ geometries considered in this study. Pt(111) being the most studied facet for ORR, our calculations for this section were limited to 111 facet. A typical fuel cell operating potential ranges from 0.8 to 1.23 V_SHE, highlighted by the filled region in Fig. 10. If the dissolution potential, U of an element is more positive than the fuel cell operating potential, the element is expected to be stable on the catalyst surface; a less positive dissolution potential suggests dissolution. As evident from Fig. 10, our calculations suggest that Pt shall remain stable on the (111) surface while the non-noble elements (M) would readily dissolve in to the solution, consistent with the experimentally observed trends in Pt-based alloys.^{10,17,47–50} We also include the effect of varying Pt overlayers on the dissolution potential of Pt by studying systems with up to two Pt overlayers; as described in the methods, we assume that the dissolution only occurs from the top-most layer. For a slab with no Pt overlayers, both Pt and M can potentially dissolve while systems with Pt overlayers can only result in dissolution of Pt. Of course dissolution followed by internal diffusion can further cause dissolution of sub-surface elements. We discussed internal diffusion at near-surface and in bulk in sections IIIA & IIIB, respectively. While Fig. 10 shows the the relative stability of Pt to all M combined, individual dissolution potentials pertaining to each element in both L1₀ and L1₂ geometries are tabulated in Tables S3 and S4 of the ESI.†

Fig. 10 Plot showing the dissolution potentials of Pt as well as the non-noble elements (M). A circle represents dissolution of Pt while a cross represents dissolution of M. The dissolution potentials associated with each element for all the systems studied are provided in the ESI.†

The most concerning aspect of the dissolution study is the ease of dissolution of the surface elements. With removal of non-noble elements from the surface, the surface vacancies can either get replaced with Pt from the solution or can diffuse into the bulk, making elements in the near-surface region susceptible to dissolution. While we discuss the diffusion of vacancies in the next section, here, we show the change in free energy associated with replacing non-noble elements with Pt in Fig. 11 (also tabulated in Table S4 of the ESI†). Our results suggest replacement of non-noble elements with Pt is highly favorable since the free energy landscape associated with the process is exergonic in nature. For alloys containing Fe, Ni or Co, replacement with Pt does not involve any electron transfer, making this transformation potential independent; whereas replacement of Sc with Pt involves an electron transfer making it potential-dependent process. At all relevant potentials, our calculations suggest replacement of surface Sc with Pt. The free energy diagram is for a hypothetical solution with 1 M Pt²⁺; of course, with this strong of a driving force Pt will be almost absent from the solvent, but this nevertheless shows the strong driving force for that process.

Fig. 11 Free energy landscape showing the replacement of non-noble elements (M) with Pt on both L1₀ and L1₂ alloys.

It should be noted that the current study exclusively focuses on the adsorbate-free (111) facet. While the bare (111) facet of Pt seems to not readily dissolve under fuel cell operating potentials, the presence of adsorbates and/or other facets, commonly observed in practical scenarios, may influence Pt dissolution. Literature indicates that electro-oxidation of the Pt surface significantly affects the surface energy and composition of various Pt facets under fuel-cell operating conditions, highlighting the importance of adsorbed species in stability studies.^81,82 However, our study aims to provide a method to qualitatively differentiate the stability of Pt from non-noble elements, considering the strong driving forces for the dissolution of Fe, Co, Ni, and Sc. Therefore, we do not expect our conclusions to be impacted by the presence of adsorbates. It is also important to note that the adsorption of reactive species does not affect the thermodynamics of pure metal dissolution as listed in the electrochemical series.⁷² In the thermodynamic limit, this dissolution process involves only the bulk metal. However, surface adsorption of reactive species can be crucial in determining the most stable surface under electrochemical operating conditions, influencing surface dissolution and the overall stability of the catalyst.

IV. Conclusions

The need to incorporate in-depth studies on the stability of an electrocatalyst is of utmost importance given the high demand to commercialize several electrochemical energy conversion and storage devices. While durability has long been an important experimental aspect of effective catalysts, most theoretical studies have focused solely on what makes catalysts active, with comparably few studying stability; thus, the underlying principles for catalyst stability are still in development.

In this work, we analyze overall stability of Pt-based ORR electrocatalysts from both a thermodynamic (dissolution) and a kinetic (bulk diffusion) point of view. We used atomistic models to compare Pt-based alloys in two different crystal structures viz. face-centered tetragonal (L1₀) and face-centered cubic (L1₂). In terms of dissolution, our calculations agree with the literature that suggest rapid dissolution of surface non-noble elements at fuel-cell operating voltages. On the other hand, Pt(111) is expected to be stable on the surface. Of course, the presence of other facets as well as adsorbates can influence the stability of Pt on the surface. However, the loss of non-noble elements remains the major concern in terms of stability.

For the alloys of Fe, Co, Ni and Sc considered in this study, we observe that the thermodynamics favors formation of Pt overlayers as observed experimentally. Typically these overlayers are ∼2–3 atomic layers thick,^18,19 resulting in compressive strain effect which could help improve the ORR activity. The presence of Pt overlayers also provides stability towards further dissolution. However, with non-noble elements on the surface very susceptible to dissolution, their transport from the near-surface becomes a major concern while designing electrocatalysts. In order to understand the movement of elements, we studied vacancy mediated diffusion barriers in the bulk as well as surface region. We discussed a method to compute and compare bulk stability of Pt-based electrocatalysts in terms of bulk diffusion barriers. We found that the ordered L1₀ and L1₂ structures of Fe, Co and Ni showed only a negligible difference in their bulk stability. In agreement with literature, bulk Pt₃Sc was found to be the most kinetically stable among all the studied alloys. We further show that a BEP-type correlation in vacancy mediated bulk diffusion, which was originally observed by Vej-Hansen et al. also holds true for the L1₀ structures. Note that our current study only compared ordered L1₂ structures to ordered L1₀ structures. The ordered versus disordered feature that we neglected in this current study might be of more importance in studies related to diffusion.

Finally, we comment on the transport of non-noble elements to the surface of L1₀ and L1₂ alloys. For alloys containing Fe and Co, we find that presence of Pt overlayers increase the kinetic barrier for transporting sub-surface non-noble elements to the surface with L1₀ structures providing higher kinetic stability than L1₂. This provides a direction for researchers to further explore more alloys in the face-centered tetragonal geometry for ORR applications. Interestingly, Pt₃Sc was found to be destabilized with the presence of Pt overlayers. With thermodynamics favoring the formation of Pt overlayers on Pt₃Sc, eventually leading to decrease in kinetic barrier for sub-surface Sc transfer, a thicker Pt overlayer can be expected. This could lead to the loss of ligand effect reported to be beneficial for improved ORR activity in Pt₃Sc alloys. Based on our results, it can be inferred that combining dissolution with bulk as well as near-surface diffusion may be a useful methodology to screen future Pt-based ORR catalysts for their stability.

Data availability

All calculations were performed with open-source software. Atomistic manipulations were performed in the Atomic Simulation Environment (ASE),⁶⁴ which is freely available at https://wiki.fysik.dtu.dk/ase/ and in repository format at https://gitlab.com/ase/ase. Electronic structure calculations (density functional theory) was performed in GPAW,⁶¹ which is freely available at https://wiki.fysik.dtu.dk/gpaw/ and in repository format at https://gitlab.com/gpaw/gpaw. The corresponding author and his group routinely submit code to both projects. The detailed results, including reaction pathway diagrams, dissolution potentials, and optimized lattice constants are available in the ESI.†

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors are grateful to Dr Jacob Schatz Spendelow from Los Alamos National Laboratory for his guidance in the formative stages of this work, as well as to Dr. Yue Qi at Brown University for helpful insights. High-performance electronic structure calculations were performed on Brown's Center for Computation and Visualization. The authors thank the U.S. Department of Energy's Hydrogen and Fuel Cell Technologies Office (DOE-HFTO) for funding support through the project “Advanced Electrocatalysts through Crystallographic Enhancement”, as well as through Award DE-SC0019441.

References

1. S. P. S. Badwal, S. S. Giddey, C. Munnings, A. I. Bhatt and A. F. Hollenkamp, Emerging electrochemical energy conversion and storage technologies, Front. Chem., 2014, 2, 79.
2. J. O. Bockris, A Hydrogen Economy, Science, 1972, 176, 1323–1323.
3. J. O. Bockris, The Hydrogen Economy, Springer US, Boston, MA, 1977, pp. 549–582.
4. S. S. Kocha, Polymer Electrolyte Membrane (PEM) Fuel Cells: Automotive Applications, Springer, New York, NY, 2019, pp. 135–171.
5. S. Srinivasan, E. Ticianelli, C. Derouin and A. Redondo, Advances in solid polymer electrolyte fuel cell technology with low platinum loading electrodes, J. Power Sources, 1988, 22(3–4), 359–375.
6. S. Srinivasan, Electrode Kinetic and Electrocatalytic Aspects of Electrochemical Energy Conversion, Springer US, Boston, MA, 1992, pp. 577–602.
7. K. C. Neyerlin, W. Gu, J. Jorne and H. A. Gasteiger, Study of the exchange current density for the hydrogen oxidation and evolution reactions, J. Electrochem. Soc., 2007, 154(7), B631.
8. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the overpotential for oxygen reduction at a fuel-cell cathode, J. Phys. Chem. B, 2004, 108(46), 17886–17892.
9. M. K. Debe, Electrocatalyst approaches and challenges for automotive fuel cells, 2012.
10. H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Activity benchmarks and requirements for Pt, Pt-alloy, and non-Pt oxygen reduction catalysts for PEMFCs, Appl. Catal., B, 2005, 56(1–2 SPEC. ISS), 9–35.
11. M. Li, Z. Zhao, T. Cheng, A. Fortunelli, C. Y. Chen, R. Yu, Q. Zhang, L. Gu, B. V. Merinov, Z. Lin, E. Zhu, T. Yu, Q. Jia, J. Guo, L. Zhang, W. A. Goddard, Y. Huang and X. Duan, Ultrafine jagged platinum nanowires enable ultrahigh mass activity for the oxygen reduction reaction, Science, 2016, 354(6318), 1414–1419.
12. X. Tian, X. Zhao, Y. Q. Su, L. Wang, H. Wang, D. Dang, B. Chi, H. Liu, E. J. Hensen, X. W. Lou and B. Y. Xia, Engineering bunched Pt-Ni alloy nanocages for efficient oxygen reduction in practical fuel cells, Science, 2019, 366(6467), 850–856.
13. L. Bu, N. Zhang, S. Guo, X. Zhang, J. Li, J. Yao, T. Wu, G. Lu, J. Y. Ma, D. Su and X. Huang, Biaxially strained PtPb/Pt core/shell nanoplate boosts oxygen reduction catalysis, Science, 2016, 354, 1410–1414.
14. M. Luo, Y. Sun, X. Zhang, Y. Qin, M. Li, Y. Li, C. Li, Y. Yang, L. Wang, P. Gao, G. Lu and S. Guo, Stable high-index faceted Pt skin on zigzag-like PtFe nanowires enhances oxygen reduction catalysis, Adv. Mater., 2018, 30, 1705515.
15. C. Chen, Y. Kang, Z. Huo, Z. Zhu, W. Huang, H. L. Xin, J. D. Snyder, D. Li, J. A. Herron, M. Mavrikakis, M. Chi, K. L. More, Y. Li, N. M. Markovic, G. A. Somorjai, P. Yang and V. R. Stamenkovic, Highly crystalline multimetallic nanoframes with three-dimensional electrocatalytic surfaces, Science, 2014, 343, 1339.
16. L. Bu, S. Guo, X. Zhang, X. Shen, D. Su, G. Lu, X. Zhu, J. Yao, J. Guo and X. Huang, Surface engineering of hierarchical platinum-cobalt nanowires for efficient electrocatalysis, Nat. Commun., 2016, 7(1), 11850.
17. X. Huang, Z. Zhao, L. Cao, Y. Chen, E. Zhu, Z. Lin, M. Li, A. Yan, A. Zettl, Y. M. Wang, X. Duan, T. Mueller and Y. Huang, High-performance transition metal-doped Pt₃Ni octahedra for oxygen reduction reaction, Science, 2015, 348, 1230–1234.
18. J. Li, S. Sharma, X. Liu, Y. T. Pan, J. S. Spendelow, M. Chi, Y. Jia, P. Zhang, D. A. Cullen, Z. Xi, H. Lin, Z. Yin, B. Shen, M. Muzzio, C. Yu, Y. S. Kim, A. A. Peterson, K. L. More, H. Zhu and S. Sun, Hard-magnet L1₀-CoPt nanoparticles advance fuel cell catalysis, Joule, 2019, 3, 124–135.
19. J. Li, Z. Xi, Y. T. Pan, J. S. Spendelow, P. N. Duchesne, D. Su, Q. Li, C. Yu, Z. Yin, B. Shen, Y. S. Kim, P. Zhang and S. Sun, Fe stabilization by intermetallic L1₀-FePt and Pt catalysis enhancement in L1₀-FePt/Pt nanoparticles for efficient oxygen reduction reaction in fuel cells, J. Am. Chem. Soc., 2018, 140, 2926–2932.
20. T. Toda, H. Igarashi and M. Watanabe, Enhancement of the electrocatalytic O₂ reduction on Pt-Fe alloys, J. Electroanal. Chem., 1999, 460(1–2), 258–262.
21. T. Toda, Enhancement of the electroreduction of oxygen on Pt alloys with Fe, Ni, and Co, J. Electrochem. Soc., 1999, 146(10), 3750.
22. U. A. Paulus, A. Wokaun, G. G. Scherer, T. J. Schmidt, V. Stamenkovic, V. Radmilovic, N. M. Markovic and P. N. Ross, Oxygen reduction on carbon-supported Pt-Ni and Pt-Co alloy catalysts, J. Phys. Chem. B, 2002, 106, 4181–4191.
23. J. R. Salgado, E. Antolini and E. R. Gonzalez, Structure and activity of carbon-supported Pt–Co electrocatalysts for oxygen reduction, J. Phys. Chem. B, 2004, 108, 17767–17774.
24. V. R. Stamenkovic, B. Fowler, B. S. Mun, G. Wang, P. N. Ross, C. A. Lucas and N. M. Marković, Improved oxygen reduction activity on Pt₃Ni(111) via increased surface site availability, Science, 2007, 315, 493–497.
25. K. C. Neyerlin, R. Srivastava, C. Yu and P. Strasser, Electrochemical activity and stability of dealloyed Pt-Cu and Pt-Cu-Co electrocatalysts for the oxygen reduction reaction (ORR), J. Power Sources, 2009, 186, 261–267.
26. C. Wang, D. Van Der Vliet, K. L. More, N. J. Zaluzec, S. Peng, S. Sun, H. Daimon, G. Wang, J. Greeley, J. Pearson, A. P. Paulikas, G. Karapetrov, D. Strmcnik, N. M. Markovic and V. R. Stamenkovic, Multimetallic Au/FePt₃ nanoparticles as highly durable electrocatalyst, Nano Lett., 2011, 11, 919–926.
27. D. Wang, Y. Yu, H. L. Xin, R. Hovden, P. Ercius, J. A. Mundy, H. Chen, J. H. Richard, D. A. Muller, F. J. Disalvo and H. D. Abruña, Tuning oxygen reduction reaction activity via controllable dealloying: A model study of ordered Cu₃Pt/C intermetallic nanocatalysts, Nano Lett., 2012, 12, 5230–5238.
28. Y. Xiong, L. Xiao, Y. Yang, F. J. Disalvo and H. D. Abruña, High-loading intermetallic Pt₃Co/C core-shell nanoparticles as enhanced activity electrocatalysts toward the oxygen reduction reaction (ORR), Chem. Mater., 2018, 30, 1532–1539.
29. M. Escudero-Escribano, P. Malacrida, M. H. Hansen, U. G. Vej-Hansen, A. Velázquez-Palenzuela, V. Tripkovic, J. Schiøtz, J. Rossmeisl, I. E. L. Stephens and I. Chorkendorff, Tuning the activity of Pt alloy electrocatalysts by means of the lanthanide contraction, Science, 2016, 352, 73–76.
30. C. Gümeci, D. U. Cearnaigh, D. J. Casadonte and C. Korzeniewski, Synthesis of PtCu₃ bimetallic nanoparticles as oxygen reduction catalysts via a sonochemical method, J. Mater. Chem. A, 2013, 1, 2322–2330.
31. V. R. Stamenkovic, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, C. A. Lucas, G. Wang, P. N. Ross and N. M. Markovic, Trends in electrocatalysis on extended and nanoscale Pt-bimetallic alloy surfaces, Nat. Mater., 2007, 6, 241–247.
32. S. Kattel and G. Wang, Beneficial compressive strain for oxygen reduction reaction on Pt (111) surface, J. Chem. Phys., 2014, 141, 124713.
33. J. R. Kitchin, J. K. Nørskov, M. A. Barteau and J. G. Chen, Modification of the surface electronic and chemical properties of Pt(111) by subsurface 3d transition metals, J. Chem. Phys., 2004, 120, 10240–10246.
34. J. R. Kitchin, J. K. Nørskov, M. A. Barteau and J. G. Chen, Role of strain and ligand effects in the modification of the electronic and chemical properties of bimetallic surfaces, Phys. Rev. Lett., 2004, 93, 156801.
35. V. Stamenkovic, B. S. Mun, K. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Nørskov, Changing the activity of electrocatalysts for oxygen reduction by tuning the surface electronic structure, Angew. Chem., Int. Ed., 2006, 45, 2897–2901.
36. P. Strasser, S. Koh, T. Anniyev, J. Greeley, K. More, C. Yu, Z. Liu, S. Kaya, D. Nordlund, H. Ogasawara, M. F. Toney and A. Nilsson, Lattice-strain control of the activity in dealloyed core-shell fuel cell catalysts, Nat. Chem., 2010, 2, 454–460.
37. X. Zhang and G. Lu, Computational design of core/shell nanoparticles for oxygen reduction reactions, J. Phys. Chem. Lett., 2014, 5, 292–297.
38. V. A. Sethuraman, D. Vairavapandian, M. C. Lafouresse, T. A. Maark, N. Karan, S. Sun, U. Bertocci, A. A. Peterson, G. R. Stafford and P. R. Guduru, Role of elastic strain on electrocatalysis of oxygen reduction reaction on Pt, J. Phys. Chem. C, 2015, 119, 19042–19052.
39. Z. Duan and G. Wang, A first principles study of oxygen reduction reaction on a Pt(111) surface modified by a subsurface transition metal M (M = Ni, Co, or Fe), Phys. Chem. Chem. Phys., 2011, 13, 20178.
40. S. Sharma, C. Zeng and A. A. Peterson, Face-centered tetragonal (FCT) Fe and Co alloys of Pt as catalysts for the oxygen reduction reaction (ORR): A DFT study, J. Chem. Phys., 2019, 150(4), 041704.
41. B. Hammer and J. Nørskov, Electronic factors determining the reactivity of metal surfaces, Surf. Sci., 1995, 343, 211–220.
42. A. Khorshidi, J. Violet, J. Hashemi and A. A. Peterson, How strain can break the scaling relations of catalysis, Nat. Catal., 2018, 1(4), 263–268.
43. J. Li, S. Sharma, K. Wei, Z. Chen, D. Morris, H. Lin, C. Zeng, M. Chi, Z. Yin, M. Muzzio, M. Shen, P. Zhang, A. A. Peterson and S. Sun, Anisotropic strain tuning of L1₀ ternary nanoparticles for oxygen reduction, J. Am. Chem. Soc., 2020, 142(45), 19209–19216 , PMID: 33124818.
44. X. Cui, L. Gao, C.-H. Lu, R. Ma, Y. Yang and Z. Lin, Rational coordination regulation in carbon-based single-metal-atom catalysts for electrocatalytic oxygen reduction reaction, Nano Convergence, 2022, 9, 34.
45. C. E. Carlton, S. Chen, P. J. Ferreira, L. F. Allard and Y. Shao-Horn, Sub-nanometer-resolution elemental mapping of “Pt₃Co” nanoparticle catalyst degradation in proton-exchange membrane fuel cells, J. Phys. Chem. Lett., 2012, 3, 161–166.
46. J. Greeley and J. Nørskov, Electrochemical dissolution of surface alloys in acids: Thermodynamic trends from first-principles calculations, Electrochim. Acta, 2007, 52, 5829–5836.
47. E. Antolini, J. R. Salgado and E. R. Gonzalez, The stability of Pt-M (M = first row transition metal) alloy catalysts and its effect on the activity in low temperature fuel cells. A literature review and tests on a Pt-Co catalyst, J. Power Sources, 2006, 160, 957–968.
48. M. Muzzio, J. Li, Z. Yin, I. M. Delahunty, J. Xie and S. Sun, Monodisperse nanoparticles for catalysis and nanomedicine, Nanoscale, 2019, 11, 18946–18967.
49. K. Singh, E. Batsa Tetteh, H.-Y. Lee, T.-H. Kang and J.-S. Yu, Tailor-made Pt catalysts with improved oxygen reduction reaction stability/durability, ACS Catal., 2019, 9, 8622–8645.
50. M. Oezaslan, F. Hasché and P. Strasser, Pt-based core-shell catalyst architectures for oxygen fuel cell electrodes, J. Phys. Chem. Lett., 2013, 4, 3273–3291.
51. I. E. L. Stephens, J. Rossmeisl and I. Chorkendorff, Toward sustainable fuel cells, Science, 2016, 354(6318), 1378–1379.
52. V. Beermann, M. Gocyla, E. Willinger, S. Rudi, M. Heggen, R. E. Dunin-Borkowski, M. G. Willinger and P. Strasser, Rh-doped Pt-Ni octahedral nanoparticles: Understanding the correlation between elemental distribution, oxygen reduction reaction, and shape stability, Nano Lett., 2016, 16, 1719–1725.
53. Q. Jia, Z. Zhao, L. Cao, J. Li, S. Ghoshal, V. Davies, E. Stavitski, K. Attenkofer, Z. Liu, M. Li, X. Duan, S. Mukerjee, T. Mueller and Y. Huang, Roles of Mo surface dopants in enhancing the ORR performance of octahedral PtNi nanoparticles, Nano Lett., 2018, 18, 798–804.
54. L. Cao and T. Mueller, Theoretical insights into the effects of oxidation and Mo-doping on the structure and stability of Pt-Ni nanoparticles, Nano Lett., 2016, 16, 7748–7754.
55. J. Zhang, K. Sasaki, E. Sutter and R. R. Adzic, Stabilization of platinum oxygen-reduction electrocatalysts using gold clusters, Science, 2007, 315(5809), 220–222.
56. Z.-P. Wu, D. T. Caracciolo, Y. Maswadeh, J. Wen, Z. Kong, S. Shan, J. A. Vargas, S. Yan, E. Hopkins, K. Park, A. Sharma, Y. Ren, V. Petkov, L. Wang and C.-J. Zhong, Alloying-realloying enabled high durability for Pt-Pd-3d-transition metal nanoparticle fuel cell catalysts, Nat. Commun., 2021, 12, 859.
57. L. Wang, R. Ore, P. K. Jayamaha, Z.-P. Wu and C.-J. Zhong, Density functional theory based computational investigations on the stability of highly active trimetallic PtPdCu nanoalloys for electrochemical oxygen reduction, Faraday Discuss., 2023, 242, 429–442.
58. G. H. Jóhannesson, T. Bligaard, A. V. Ruban, H. L. Skriver, K. W. Jacobsen and J. K. Nørskov, Combined electronic structure and evolutionary search approach to materials design, Phys. Rev. Lett., 2002, 88(25), 255506.
59. J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Alloys of platinum and early transition metals as oxygen reduction electrocatalysts, Nat. Chem., 2009, 1, 552–556.
60. T. P. Johansson, E. T. Ulrikkeholm, P. Hernandez-Fernandez, P. Malacrida, H. A. Hansen, A. S. Bandarenka, J. K. Nørskov, J. Rossmeisl, I. E. Stephens and I. Chorkendorff, Pt skin versus Pt skeleton structures of Pt₃Sc as electrocatalysts for oxygen reduction, Top. Catal., 2014, 57(1–4), 245–254.
61. J. J. Mortensen, A. H. Larsen, M. Kuisma, A. V. Ivanov, A. Taghizadeh, A. Peterson, A. Haldar, A. O. Dohn, C. Schäfer, E. Ö. Jónsson, E. D. Hermes, F. A. Nilsson, G. Kastlunger, G. Levi, H. Jónsson, H. Häkkinen, J. Fojt, J. Kangsabanik, J. Sødequist, J. Lehtomäki, J. Heske, J. Enkovaara, K. T. Winther, M. Dulak, M. M. Melander, M. Ovesen, M. Louhivuori, M. Walter, M. Gjerding, O. Lopez-Acevedo, P. Erhart, R. Warmbier, R. Würdemann, S. Kaappa, S. Latini, T. M. Boland, T. Bligaard, T. Skovhus, T. Susi, T. Maxson, T. Rossi, X. Chen, Y. L. A. Schmerwitz, J. Schiøtz, T. Olsen, K. W. Jacobsen and K. S. Thygesen, GPAW: An open python package for electronic structure calculations, J. Chem. Phys., 2024, 160(9), 092503.
62. J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method, J. Phys.: Condens. Matter, 2010, 22, 253202.
63. J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Real-space grid implementation of the projector augmented wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109.
64. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment–a python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29(27), 273002.
65. B. Hammer, L. B. Hansen and J. K. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
66. U. G. Vej-Hansen, J. Rossmeisl, I. E. Stephens and J. Schiøtz, Correlation between diffusion barriers and alloying energy in binary alloys, Phys. Chem. Chem. Phys., 2016, 18, 3302–3307.
67. H. Jónsson, G. Mills and K. W. Jacobsen, Nudged elastic band method for finding minimum energy paths of transitions, in Classical and Quantum Dynamics in Condensed Phase Simulations, 1998, pp. 385–404.
68. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904.
69. J. Haruyama, T. Ikeshoji and M. Otani, Electrode potential from density functional theory calculations combined with implicit solvation theory, Phys. Rev. Mater., 2018, 2, 095801.
70. S. Sharma, A. Zagalskaya, S. E. Weitzner, L. Eggart, S. Cho, T. Hsu, X. Chen, J. B. Varley, V. Alexandrov, C. A. Orme, T. A. Pham and B. C. Wood, Metal dissolution from first principles: Potential-dependent kinetics and charge transfer, Electrochim. Acta, 2023, 437, 141443.
71. R. Jinnouchi, E. Toyoda, T. Hatanaka and Y. Morimoto, First principles calculations on site-dependent dissolution potentials of supported and unsupported Pt particles, J. Phys. Chem. C, 2010, 114(41), 17557–17568.
72. CRC Handbook, CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, 88th edn, 2007.
73. H. Mehrer, Diffusion mechanisms, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 95–104.
74. H. B. Huntington and F. Seitz, Mechanism for self-diffusion in metallic copper, Phys. Rev., 1942, 61, 315–325.
75. E. O. Kirkendall, Diffusion of zinc in alpha brass, Transactions of the AIME, 1942, 147, 104–110.
76. E. Kirkendall and A. Smigelskas, Zinc diffusion in alpha brass, Transactions of the AIME, 1947, 171, 130–142.
77. H. B. Huntington and F. Seitz, Mechanism for self-diffusion in metallic copper, Phys. Rev., 1942, 61, 315–325.
78. L. Gontard, L.-Y. Chang, C. Hetherington, A. Kirkland, D. Ozkaya and R. Dunin-Borkowski, Aberration-corrected imaging of active sites on industrial catalyst nanoparticles, Angew. Chem., Int. Ed., 2007, 46(20), 3683–3685.
79. Y.-T. Pan, D. Li, S. Sharma, C. Wang, M. J. Zachman, E. C. Wegener, A. J. Kropf, Y. S. Kim, D. J. Myers, A. A. Peterson, D. A. Cullen and J. S. Spendelow, Ordered CoPt oxygen reduction catalyst with high performance and durability, Chem Catal., 2022, 2(12), 3559–3572.
80. P. Jovanovič, V. S. Šelih, M. Šala, S. B. Hočevar, A. Pavlišič, M. Gatalo, M. Bele, F. Ruiz-Zepeda, M. Čekada, N. Hodnik and M. Gaberšček, Electrochemical in-situ dissolution study of structurally ordered, disordered and gold doped PtCu₃ nanoparticles on carbon composites, J. Power Sources, 2016, 327, 675–680.
81. R. Jinnouchi, K. K. T. Suzuki and Y. Morimoto, DFT calculations on electro-oxidations and dissolutions of Pt and Pt-Au nanoparticles, Catal. Today, 2016, 262, 100–109.
82. I. T. McCrum, M. A. Hickner and M. J. Janik, First-principles calculation of Pt surface energies in an electrochemical environment: Thermodynamic driving forces for surface faceting and nanoparticle reconstruction, Langmuir, 2017, 33(28), 7043–7052 , PMID: 28640641.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cy00463a

---