 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effect of molecular shape and pore structure on local and nanoscale cresol behaviour in commercial zeolite catalysts†
K. S. C.
Morton
 abc,
A. J.
Porter
abc,
A. J.
Porter
 a,
J.
Armstrong
a,
J.
Armstrong
 *c and
A. J.
O'Malley
*c and
A. J.
O'Malley
 *ab
*ab
aInstitute for sustainability, Department of Chemistry, University of Bath, UK. E-mail: a.o'malley@bath.ac.uk
bUK Catalysis Hub, Research Complex at Harwell, Science and Technology Facilities Council, Rutherford Appleton Laboratory, Oxford, UK
cISIS Pulsed Neutron and Muon Facility, Science and Technology Facilities Council, Rutherford Appleton Laboratory, Didcot, UK. E-mail: jeff.armstrong@stfc.ac.uk
First published on 3rd June 2024
Abstract
The behaviour of model lignin derivatives m- and p-cresol within commercial acidic zeolite catalysts was investigated using a combined quasielastic neutron scattering (QENS) and molecular dynamics (MD) simulation approach, to understand the diffusion mechanisms in industrial catalysts of molecules relevant to the conversion of lignocellulosic biomass into value-added fuels and chemicals, and to link such behaviours to catalytic characteristics. QENS experiments observed isotropic rotation of both isomers in H–Y and H-beta. The more linear p-cresol isomer exhibited more mobility in each catalyst, while the larger pores of H–Y allowed for greater mobile populations of both isomers over H-beta. Notably, decreased rotational rates were observed with increasing mobile populations due to increasing adsorbate–adsorbate interactions in the catalyst micropores. QENS observables calculated from MD simulations reproduced the experimental trends in mobile populations of rotating cresols with zeolite topology. Exploring cresol dynamics within the MD simulations over longer timescales saw extremely restricted diffusion and high activation energies (21–32 kJ mol−1) for all systems, with the same trends in diffusivity with pore topology and molecular shape observed as for the mobile populations observed in the experiment. Diffusivity was lower for m-cresol than p-cresol by a factor of 3.3 when confined within H-beta channels due to its propensity to form favourable 180° H-bonds with zeolite Brønsted acid sites, whereas the longer axis of p-cresol inhibits this favourable orientation, increasing its likelihood of unhindered diffusion at an orientation parallel to the zeolite channel. The agreement between the QENS experiments and simulations allowed for reliable modelling at a catalytically relevant temperature of 653 K, and we include simulation of the extensively catalytically tested H-ZSM5, revealing that the rate of reactant diffusion directly correlates with cresol conversion rates before the formation of coke, observed previously in catalytic studies. The interplay between the nature of adsorption onto acid sites, steric pore hindrance, local/nanoscale mobility, and their influence on catalytic properties is highlighted and explained for important derivatives and model monomers in the zeolite catalysed conversion of lignocellulosic biomass feedstocks.
1 Introduction
Since the 1950s, crude oil has been the primary source for producing fuels, polymers, and chemicals, but due to limited supplies and rising demands, there is a growing interest in alternative, sustainable feedstocks.1 Lignin is a promising and abundant candidate, but currently only 2% is upgraded into specialty products.2 This is due to lignin's complex structure, which contains oxygen and aromatic groups that re-polymerise and deactivate catalysts.3 Therefore, understanding how these oxygen-containing groups affect molecular behaviour is crucial for developing effective catalytic processes for lignin conversion.Several methods exist for lignin depolymerisation and upgrading, but they are not yet industrially feasible due to harsh conditions, expensive reagents, environmental issues, and low yields.4–8 Zeolite catalysts, already used in the petrochemical industry, show promise for lignin upgrading.9,10 They facilitate cracking reactions and C–C and C–O bond cleavages, converting lignin into smaller alkoxyphenols. These can then access zeolite active sites for further conversion into alkylphenols and monoaromatic hydrocarbons through deoxygenation, cracking, and oligomerisation.11
Zeolites exhibit versatile properties that make them suitable for a broad range of catalytic reactions. Their adjustable pore sizes and topologies confer shape selectivity, which is determined by the transition states and the diffusion of reactants and products through the pores. Additionally, altering the Si/Al ratio provides control over the quantity of acid sites in the pore system. The associated characteristics of these acid sites, such as their location, spacing and respective strengths, are hard to modify independently but play an important role in determining the catalytic performance of the zeolites or the nature of interactions with the adsorbate.12 Numerous studies evaluating the catalytic fast pyrolysis of lignin over zeolite catalysts of varying framework topologies and compositions with the goal of producing value-added aromatics at high rates and yields, have been conducted with promising but conflicting results.13–16 For instance, the formation of benzene, toluene and xylene (BTX) used in gasoline production was found to increase from H–Y < H-beta < H-ZSM5.17 The success of H-ZSM5 was attributed to its smaller pores, which facilitated more cracking reactions due to the confinement effect and hindered coke formation, and favoured para-species formation, whilst the large pores of H–Y lead to ineffective contact for cracking reactions. In contrast to these findings Ma et al. reported higher conversion yields in larger pore zeolites (H–Y), reasoning that larger pores enabled the adsorption and consecutive reactions of larger molecules, preventing char formation.18 Therefore, a consensus regarding the most effective methods of catalytic optimisation by changing the zeolite topology have yet to be established.17–20 The distribution, density and strengths of Brønsted acid sites (BASs) within the zeolite structure also play a crucial role in the catalytic process, where small aromatics often strongly adsorb to the acid sites, reducing the number of acid sites available for conversion reactions, subsequently leading to lower rates of conversion and overall yield, particularly over smaller-pored zeolites.21,22 Despite the previous research, the current literature lacks a comprehensive understanding of the fundamental mechanisms that limit catalytic rate, and recovery of the desired upgraded species.
To examine the effects of molecular shape on the catalytic conversion of lignin monomers, we can begin by focusing on methylphenol isomers (cresols). These isomers are some of the simplest derivatives of lignin and serve as model lignin constituents as they contain aromatic, hydroxyl and methyl functional groups commonly found in lignin based feedstocks. Cresols are frequently acquired through biomass depolymerisation methods such as pyrolysis. For instance, cresol isomers constitute approximately 8.5% wt of the pyrolysis products of soda lignin,19 16.1% wt of palm kernel shell (∼50% wt lignin) and 1.9% and 20.6% wt of the liquid products of cellulose and lignin.13 In terms of the relative production of each isomer type, almost twice the amount of m- and p-cresol have been observed to be produced from pyrolysis compared to o-cresol independent of lignin source.23
Cresols are widely used in industry as precursors for the manufacture of many chemicals including pharmaceuticals and fuel components.24–29 Common cresol-specific reactions over zeolites include isomerisation (1,2-methyl shifts), disproportionation (transalkylations into phenols and xylenols), and hydrodeoxygenation reactions (often via metal-doped zeolites).24,30 These reactions are largely dependent on the transition-state selectivity of the zeolite pores. Bi-functional metal-doped zeolites have also shown to be highly effective in cresol conversion, where a study using Lewis acidic Ni2P/H-ZSM5 zeolites with m-cresol saw high conversion (>90%) to the fuel additive methylcyclohexane.31m-Cresol conversion over Ga-modified H-beta gave BTX components as the main products, with lower yields seen with Ga/H-ZSM5.32 Further studies observing the specific reactivity of cresol isomers within zeolites29,33–35 are discussed in more detail in comparison to our results in section 3.3.
The behaviour of cresols inside the zeolite framework, both in terms of diffusion through the zeolite framework and motions local to the active site are potential rate-limiting steps in their conversion and can be expected to have significant effects on the catalytic activity and selectivity of the total process. Therefore, understanding the dynamics of cresol isomers as a function of molecular shape and zeolite catalyst framework topology and composition would be necessary to optimise and control the conversion of lignin derivatives into more desirable chemicals.
Neutron spectroscopy techniques are particularly suited to both probing the catalyst structure/active sites36 and the behaviour of adsorbed molecules in the catalyst micropores where the unique sensitivity to 1H allows for deep penetration of the neutron into the inorganic zeolite catalyst structure to interact only with the organic adsorbate.37 Quasielastic neutron scattering (QENS) allows for the detailed study of molecular motions of molecules adsorbed in porous catalysts on the timescale of 2 ps to ∼100 ns, particularly when combined with molecular dynamics (MD) simulations which probe motions over the same timescales.38,39 Direct comparison may be achieved through the reproduction of QENS observables from simulation for clear characterisation of the complex dynamical behaviour present,40–43 or MD can be applied as a method in its own right for studying dynamics in catalyst micropores.44–46 Previous studies on the simple model lignin derivatives phenol and catechol in H-beta,47,48 and benzene in H-ZSM5 (ref. 49 and 50) have employed these techniques to characterise and quantify both local rotational motions and longer range nanoscale diffusion in the zeolite channel systems and the effect of acid site interactions.
In this study, we probe the behaviour of cresol isomers in commercial zeolite catalysts H–Y and H-beta using QENS and classical MD from 340–400 K, giving us insight into the local and nanoscale dynamics of cresols in zeolite pores. We expand the study to include simulations ran at a catalytically pertinent temperature of 653 K, including H-ZSM5 owing to the extensive catalytic studies in this framework for conversion of cresols to BTX chemicals. Our combined theoretical/experimental studies uncover significant molecular shape and framework topology effects on both the cresol isomer motions local to the catalyst active site, and the nanoscale diffusivity of the cresols in each framework, and clear relationships between these mobility differences on each scale and the catalytic properties observed in previous studies.
2 Experimental
2.1 Quasielastic neutron scattering
Zeolite H–Y (Si/Al = 15, CBV-720) and NH4-beta (Si/Al = 12.5, CP814E) were obtained from Zeolyst International. NH4-beta was calcined in air by heating from room temperature to 523 K at a rate of 2 K min−1 and then to 823 K at 5 K min−1 and held for 4 hours. The zeolites were dried under vacuum at 523 K of ca. 18 hours.51 After cooling, the zeolite samples to be dosed were loaded with either 10% wt of p- or m-cresol (approximately 11 and 4 molecules per unit cell in H–Y and H-beta respectively) obtained from Sigma-Aldrich under an argon atmosphere. The cresols were applied drop-wise and the resulting physical mixtures were ground using a pestle and mortar in a glovebox under argon and transferred to an airtight container. The samples were then heated at 353 K for ca. 18 hours. Under an argon atmosphere, the empty and cresol dosed zeolite samples were loaded into annular, aluminium cans with a thickness of 2 mm to give around 10% scattering (to minimise the contributions of multiple scattering to the total signal) and sealed with indium wire to form a closed system.The QENS experiments were performed on the OSIRIS time of flight back-scattering neutron spectrometer at the ISIS Pulsed Neutron and Muon Source, Rutherford Appleton Laboratory.52 QENS spectra were obtained using the graphite 002 analyser crystal, giving an energy resolution of 24.5 μeV, and energy transfers were measured within ±0.55 meV (probing the average motions that occurred over a timescale of ∼2–54 ps) across a Q range of 0.2 to 1.8 Å−1. The measurements were taken at 340, 370 and 400 K. Differences in detector strengths were accounted for by calibrating all of the samples against a vanadium standard. Scattering from the empty zeolite samples were measured and subtracted from the loaded samples – leaving only the signal relating to the cresol isomers, which also removes any minor scattering from the aluminium sample can. Base temperature measurements (<20 K) for the H–Y samples were applied as the instrumental resolution. A vanadium standard was used as the instrumental resolution for the H-beta measurements due to time constraints, and the detectors were grouped in a way that avoided Bragg peaks due to coherent scattering from the zeolite structure. MANTID53 and DAVE54 neutron scattering analysis software packages were used to fit the QENS data.
2.2 Molecular dynamics simulations
In this section, the construction of the zeolite systems containing cresol adsorbates, the associated force-fields and the simulation procedures are described.Silicon, aluminium and oxygen atoms uninvolved in the BASs were assigned fully ionic charges,66,67 as per the ionisation potential method based on the Born model of ionic solids.68 Fractional charges were assigned to Brønsted acidic oxygen and hydrogen, all charges are listed in Table S2.† Also listed are the interatomic interactions within the zeolite, described by Buckingham potentials, while a Morse potential was used to model the interaction between the BAS oxygen hydrogen atoms.67 To model flexibility, a three-body harmonic potential was applied between O–T–O atoms, where T represents a silicon or aluminium atom.66,69 The derived potentials were bench-marked against ab initio calculations or subjected to empirical fitting procedures to reproduce experimentally observed properties.
The atomic charges and intramolecular and intermolecular potentials for cresol molecules were taken from OPLS3 (ref. 70) as detailed in our previous work,71 based on the atomic charges associated with this model being a better match to charges assigned from DFT calculations. Intramolecular cresol flexibility was modelled using the harmonic bonds and angles and triple cosine dihedral potentials listed in Table S3.† The short-range repulsion and dispersion forces calculated by non-bonding Lennard-Jones potentials, are shown in Table S4.†
The interactions between each zeolite framework and the cresol molecules were modelled using the potentials listed in Table S5.† The interaction between the cresol oxygen and the silicon and aluminium of the zeolite framework was modelled by Buckingham potentials based on previous studies, re-scaling the repulsion parameter to reproduce the results of ab initio studies.47,66,67,69,72 Lennard-Jones parameters were applied to describe the interactions of the remaining cresol atoms with the atoms involved in the zeolite BASs and framework oxygen atoms.72,73
 | (1) |
Applying the powder average expression, the atomic positions in the MD simulations can be used to calculate the rotational ISF.
 | (2) |
| Fs(Q, t) = C1(Q)exp−Γ1t + C2(Q)exp−Γ2t + B(Q) | (3) |
The mean squared displacements (MSDs) were obtained from the atom trajectories via the program MDANSE.78 The self-diffusion coefficients (Ds) were calculated using the Einstein relation (eqn (4)) from 250–1000 ps, where the log(MSD)–log(t) relationship was linear.
 | (4) |
3 Results and discussion
3.1 Quasielastic neutron scattering
QENS spectra at varying Q values are shown in Fig. 1 for p-cresol in H–Y at 370 K, with the other systems shown in Fig. S2.† The spectra were sufficiently fitted by a convolution of a delta function, a flat background and a single Lorentzian function, each convolved with the instrumental resolution, detailed in Fig. S3.†Backgrounds in the QENS spectra indicate the presence of fast motions, such as hydroxyl and methyl rotations, occurring outside the energy transfer range of the instrument and also accounts for the Debye–Waller factor.47 The delta function incorporates the signal from elastic scattering and motions taking place on timescales longer than the ∼54 ps sampled by the spectrometer, such as slow diffusion processes. As only a single broad Lorentzian function was required for sufficient fitting of the QENS spectra, this suggests that only one type of motion was dominant over the instrumental timescale. The contribution from the Lorentzian component increases with temperature, due to increased sample dynamics. Broad Lorentzians usually relate to localised dynamics but to investigate the type and rate of the motion of cresol molecules in-depth, the elastic incoherent structure factor (EISF) and the Lorentzian half-width half-maxima (HWHM) and their variance with Q were calculated from the QENS spectra and analysed by applying the models detailed herein. The EISF is defined as the ratio of the integrated elastic intensity to the total scattering intensity for a given value of Q, and is, in essence, the proportion of the QENS signal which is elastic.
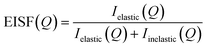 | (5) |
Many models of motion are available which can be fit to the EISF to characterise the motion of cresol molecules within zeolites, with their mathematical models discussed in section S2.1.† Illustrations of the types of motions considered for characterising cresol behaviour are illustrated in Fig. 2, including diffusion confined to a sphere of specific dimensions, isotropic rotation around any axis, methyl rotation, and uniaxial rotation of the aromatic component when anchored to a specific site.
 | ||
| Fig. 2 Motions of a p-cresol molecule: (a) confined translational motion, (b) isotropic rotation, (c) methyl rotation, and (d) uniaxial rotation. | ||
The initial fits of each model to the EISFs are shown in Fig. S4† and it was found that to obtain the best fits, it was necessary to incorporate a fraction of immobile molecules, with the improved fits shown in Fig. S5.† The best fits to the experimental EISFs for each system at 370 K are shown in Fig. 3, which were models of isotropic rotation derived by Sears79 with varying mobile components, the motion of which is depicted in Fig. 2(b). This is consistent with the model of rotation fit to the HWHM of the single Lorentzian which showed no trend with Q2, shown in Fig. S7.† As the temperature increased, decreases in the EISF values were observed, indicating an increase in the proportions of cresol molecules rotating on the instrumental timescale – though the same mode of motion is still occurring in all systems. The full set of EISFs at every temperature can be seen in Fig. S6.†
 | ||
| Fig. 3 Experimental EISFs of p- and m-cresol in H–Y and H-beta at 370 K, fit by models of isotropic rotation. Percentages of mobile molecules are shown in brackets. | ||
Table 1 lists the proportions of mobile molecules undergoing isotropic rotation for each system. The proportion of mobile cresol molecules is relatively low for all systems, with many of the molecules appearing ‘static’, possibly undergoing ‘slow’ diffusive dynamics outside of the instrument timescale. Comparing the behaviour of cresols within the two different frameworks, the mobile fractions of p- and m-cresol in H–Y are on average 2.0 and 2.4 times larger, respectively, than in H-beta. Both the larger pores of H–Y and its slightly lower acid site density (1.13 acid sites available per cresol molecule and 1.33 in H-beta) may contribute to increasing mobile populations. Framework topology has a much greater effect on the mobile populations observed compared to changes in the molecular shape, however, with only a slight increase observed for p-cresol relative to m-cresol by factors of 1.1 and 1.3 in H–Y and H-beta respectively, potentially due to the slightly more linear shape of p-cresol.
| System | 340 K mobile fraction (%) | D r (×1010 s−1) | 370 K mobile fraction (%) | D r (×1010 s−1) | 400 K mobile fraction (%) | D r (×1010 s−1) | E a (kJ mol−1) |
|---|---|---|---|---|---|---|---|
| p-Cresol in H–Y | 24.4 | 3.54 ± 0.21 | 31.0 | 4.48 ± 0.23 | 36.8 | 5.00 ± 0.21 | 6.6 ± 0.3 |
| m-Cresol in H–Y | 22.7 | 3.26 ± 0.19 | 28.2 | 3.76 ± 0.20 | 36.2 | 4.13 ± 0.18 | 4.5 ± 0.3 |
| p-Cresol in H-beta | 12.3 | 3.85 ± 0.36 | 15.1 | 4.98 ± 0.43 | 19.1 | 5.27 ± 0.33 | 6.0 ± 0.6 |
| m-Cresol in H-beta | 9.0 | 4.48 ± 0.60 | 11.8 | 5.16 ± 0.53 | 15.0 | 5.59 ± 0.50 | 4.2 ± 0.9 |
As discussed, the HWHM of the Lorentzians required to fit the quasielastic broadenings did not show a trend with Q2 and so could be fit by models of isotropic rotation consistent with the EISF model, shown in Fig. S7.† The average rates of isotropic rotation (Dr) were determined from the fitted models and are listed in Table 1 along with their corresponding activation energies for rotation. The trends in Dr values are displayed in Fig. 4, alongside the Dr trends calculated from the MD simulations, which will be discussed in section 3.2.1.
 | ||
| Fig. 4 Rotational diffusion coefficients of p- and m-cresol in H–Y and H-beta from 340–400 K, calculated from the QENS experiment and MD simulations. | ||
The rates of rotation for all systems are similar, though we note that all cresols rotate consistently faster in H-beta compared to H–Y. This could be because greater proportions of mobile molecules in H–Y allow for an increase in sorbate–sorbate interactions causing greater hindrance of their rotation, slowing their rotational rates80 – which will be explored by application of MD simulations in the next section. In H-beta, the cresol molecules have the fastest rotational rates, which could be because the rotating molecules are situated within the larger channel intersections,81 where they have room to freely rotate, but the mobile fraction is lower due to limited available intersections. In this case, the slight difference in BAS density between each framework does not seem to have a significant effect on the rotational rate of the mobile molecules.
The activation energies for isotropic rotation are listed in Table 1, ranging from 4–7 kJ mol−1 and are within error for both zeolites. However, the activation energy increases by an average factor of 1.4 from m- to p-cresol, suggesting that the isomer type has a greater impact on the energy barrier for initiating rotation.
3.2 Molecular dynamics simulations
The B(Q) component of eqn (4) is equivalent to the EISF and can therefore be analysed in the same way to characterise the modes of motion present. Due to the presence of two motions, a linear combination of two models to fit the simulated EISFs as a function of Q was required, with single models giving inadequate fits to the data, as shown in Fig. S11.† However, a model that linearly combined models of isotropic rotation with a more hindered rapid partial rotation/translation (herein referred to as ‘rapid rattling’) gave a good fit to all simulated systems, shown for the samples ran at 370 K in Fig. 5. The same dynamics were observed in simulations of catechol and phenol in H-beta investigated by Hernandez-Tamargo et al.48
The isotropic model has a radius corresponding to that of the cresol molecules (∼2.9 Å), while the model of rapid rattling is actually a model of isotropic rotation with radii shorter than the molecular dimensions, from 0.5–0.9 Å. The amplitude of the rattling motion is represented by the average molecular displacement (Δd) of the molecule away from its centre of mass, as full rotation around a 360° angle is hindered, due to factors such as strong H-bonds to acid sites and molecular crowding. Other combined models we considered, shown in Fig. S12,† failed to fit the data satisfactorily. Unlike models such as uniaxial rotation which consider rotation around a single axis, the isotropic rotation model describes this rapid rattling motion as random, as illustrated by Fig. 6. Table 2 lists the percentage of molecules undergoing each type of dynamics and the magnitude of displacement (Δd) associated with the rapid rattling motion.
 | ||
| Fig. 6 The hindered, rapid rattling of an m-cresol molecule within a H-beta channel section, showing displacement away from its centre of mass (dark blue dot). | ||
| System | 340 K isotropic rotation (%) | Rapid rattle (%) | Δd | 370 K isotropic rotation (%) | Rapid rattle (%) | Δd | 400 K isotropic rotation (%) | Rapid rattle (%) | Δd |
|---|---|---|---|---|---|---|---|---|---|
| p-Cresol in H–Y | 24.3 | 75.7 | 0.70 | 27.2 | 72.8 | 0.82 | 28.3 | 71.7 | 0.89 |
| m-Cresol in H–Y | 26.3 | 73.7 | 0.62 | 28.4 | 71.6 | 0.68 | 32.3 | 67.7 | 0.81 |
| p-Cresol in H-beta | 19.1 | 80.9 | 0.54 | 19.5 | 80.5 | 0.56 | 23.5 | 76.5 | 0.77 |
| m-Cresol in H-beta | 19.0 | 81.0 | 0.53 | 20.1 | 79.9 | 0.58 | 21.4 | 78.6 | 0.64 |
The decay constants, Γi, relating to each exponential are equivalent to the HWHM of the Lorentzian functions fit the quasielastic broadenings from the experiment. The decay constant Γ1, falls within the experimental energy transfer window of ±0.55 meV and upon analysis corresponds to isotropic rotation, showing agreement between the simulations and experiment. However, Γ2 corresponds to very high energy motions outside of the instrumental energy transfer range that would likely contribute to the flat background function and hence, in the experiment would be modelled as static, which corresponds to the static component of the isotropic rotation model applied to fit the experimental EISFs. In the simulations, the proportion of molecules undergoing isotropic rotation, which would be considered mobile on the timescale of the instrument, is only slightly greater than the experiment by an average factor of 1.1. m-Cresol and p-cresol mobile populations increase by average factors of 1.4 and 1.3 respectively going from H-beta to H–Y, showing the same trend identified by QENS but to a lesser extent. The simulations also capture the more minimal effect of molecular shape on the proportion of rotating molecules, changing by an average factor of 1.1 between isomer types in either framework. The changes in mobile populations with temperature observed a greater increase within the experiment compared to the simulations, by an average factor of 1.3.
The MD simulations provide extra insight into the modes of motions occurring, allowing observation of the rapid rattling motion that is vibrating on a timescale too fast to observe with the QENS spectrometer. The trends in the proportion of molecules undergoing rapid rattling follow the same trends as percentages of immobile molecules observed in the experiment with zeolite type. The amplitude of this rapid rattle movement, Δd, decreased in H-beta over H–Y for each isomer by an average factor of 1.2 due to less available pore space and also decreased from p- to m-cresol in each zeolite by an average factor of 1.1. The average Δd is 0.8 and 0.6 Å in H–Y and H-beta respectively, which are much smaller than the radii of the H–Y pores (5.6 Å) and the H-beta channel or channel intersections (3.0 and 3.3 Å respectively) and therefore is mostly attributed to the configuration shown in Fig. 6, when favourable bonding at a near linear angle when bound to zeolite acid sites occurs, discussed in more detail in section 3.2.2. The trends associated with this rattling motion suggest that whilst both isomer shape and zeolite pore topology impact the percentages of mobile molecules, the latter impacts it to a greater extent. Both a decreasing proportion of molecules undergoing isotropic rotation and a reduction in the displacement of molecules undergoing hindered rapid rattling motions from H–Y to H-beta lead to the conclusion of hindered local motions attributed to more/stronger H-bonding interactions and steric hindrances through confinement or crowding effects. The simulated HWHM, Γ1, for the simulated systems at 370 K are shown in Fig. S14.† The average rates of isotropic rotation were determined from the fitted models and are listed in Table 3, alongside the activation energies for rotation. The trends in Dr for each simulated system are displayed in Fig. 4, showing that the trends in rotational rates, compared to those calculated from the experiment, are slightly faster by an average factor of 1.5, but show the same trends between different zeolite frameworks, faster in H-beta than in H–Y. Faster rotational rates in the simulations could be attributed to the framework–cresol potentials applied with the rotational rate in cresol only simulations shown to under-represent the rates71 or other reasons such as the lack of zeolite defects in the models. As with the experiment, an inverse relationship is observed between the percentage of molecules undergoing isotropic rotation and the rate of such rotation. Again, this suggests that cresol–cresol interactions facilitated by the breaking of BAS–cresol H-bonds hinders the rate of isotropic rotation. Both cresol–cresol and cresol–BAS interactions within the simulations are investigated in the next section. The activation energies are within error of the QENS experiment for the H-beta samples but are less than that of the experiment for H–Y but still show the same increase from m-cresol to p-cresol in H–Y observed in the experiment.
| System | 340 K Dr (×1010 s−1) | 370 K Dr (×1010 s−1) | 400 K Dr (×1010 s−1) | E a (kJ mol−1) |
|---|---|---|---|---|
| p-Cresol in H–Y | 6.14 ± 0.12 | 6.27 ± 0.14 | 7.16 ± 0.18 | 2.8 ± 0.1 |
| m-Cresol in H–Y | 5.73 ± 0.09 | 5.95 ± 0.34 | 6.19 ± 0.09 | 1.5 ± 0.1 |
| p-Cresol in H-beta | 6.23 ± 0.06 | 6.43 ± 0.06 | 8.02 ± 0.65 | 4.6 ± 1.4 |
| m-Cresol in H-beta | 6.35 ± 0.56 | 7.92 ± 0.74 | 8.46 ± 0.52 | 5.5 ± 0.5 |
 | ||
| Fig. 7 RDFs (g(r)) between the cresol oxygen and zeolite BAS hydrogen and the associated coordination numbers (n(r)) of p- and m-cresol in (a) H–Y and (b) H-beta at 370 K. | ||
The RDF plots indicate strong H-bonding interactions between cresol molecules and the zeolite BASs across all systems from 1.4–1.5 Å. In H–Y, both isomers show similar proportions of bonding to acid sites, with each cresol approximately bonding to one acid site (one-to-one bonding) with coordination numbers of 0.83 for p-cresol and 0.89 for m-cresol. It should be noted that for each H–Y system some of the molecules remain unbonded to BASs and are free to isotropically rotate or translate, despite sufficient acid sites for one-to-one bonding (1.13 acid sites per molecule). The presence of free cresol molecules is demonstrated by the prevalence of intermolecular cresol–cresol bonding through their hydroxyl groups in Fig. S17(a).† Slightly more cresol–cresol interactions are present for the p-cresol isomers, however in both systems, the number of cresols that are free to form H-bonds and also within hydrogen bonding distance of each other is small (average n(r) of 0.06 for cresol–cresol interactions).
Conversely, in H-beta, only slightly more than half of the BASs are within H-bonding distance of a p-cresol molecule (n(r) = 0.61), compared to the m-cresol isomer (n(r) = 0.90), despite an even greater number of available acid sites (1.33 acid sites per molecule) relative to H–Y. The lower occurrence of BAS interactions with p-cresol in H-beta can be explained by examining the bonding configuration. It has been observed generally that the more a hydrogen bond deviates from a linear O–H–O angle, the weaker it becomes.82 Our simulations in H-beta, show a broader distribution of H-bonding angles for p-cresol compared to m-cresol bonded to BASs, with a mean bonding angle that is further from the optimal 180° angle, resulting in weaker bonding, as shown in Fig. S20.†
Fig. 8(a) demonstrates the steric constraints of 180° bonding due to the diameter of p-cresol being greater than that of the H-beta channels. However, we once again note that this would be highly dependent on the modelled aluminium distribution, where greater availability of acid sites in channel intersections could well reduce the diffusion of p-cresol. As a result, BAS interactions with p-cresol molecules often occur at an angle to the BAS. Weaker hydrogen bonds are more susceptible to breaking, exacerbated by cresol–cresol–BAS interactions where free cresols can disturb proximal H-bonded cresols, and can effectively ‘push’ them away from acid sites, depicted in Fig. 8(b), where the BAS–cresol bonding further lengthens and weakens upon H-bonding with other cresol molecules.
 | ||
| Fig. 8 The interactions and lengths of bonds between the BASs of H-beta and (a) p-cresol, (b) two p-cresol molecules and (c) m-cresol. | ||
The RDF plot in Fig. S17(b)† corroborates this, where a greater frequency of cresol–cresol interactions are observed for the p-isomer (n(r) = 0.09), compared to the m-isomer (n(r) = 0.05) in H-beta. However, an increase in free p-cresol molecules does not lead to an increase in rotation as confinement effects which hinder H-bonding may also hinder its full rotation, only allowing rotation in larger channel intersections. On the other hand motions such as diffusion of p-cresol may not be hindered in the same way, which will be analysed in the following section. In comparison, m-cresol molecules in H-beta (Fig. 8(c)) have sufficient space to form optimal 180° bonding interactions, and the least amount of cresol–cresol bonding is observed. For both isomers in H-beta, isotropic rotation potentially occurs most often in the zeolite channel intersections, which explains the similar proportions of molecules undergoing the aforementioned motion. Higher isotropic rotational rates observed with the m-isomer is attributed to its smaller length.
 | ||
| Fig. 9 Trajectories of a cresol molecule printed every 5 ps up to 5 ns (tracking a ring carbon atom), for (a) p-cresol and (b) m-cresol in H–Y, (c) p-cresol and (d) m-cresol in H-beta at 370 K. | ||
Despite extremely limited diffusion, approximate self-diffusion coefficients (Ds) could still be quantified using the Einstein relation due to the reasonable linearity of the calculated MSD plots displayed in Fig. S21.† The calculated self-diffusion coefficients and activation energies are listed in Table 4. The diffusion rates plotted against temperature are shown in Fig. 10.
| System | 340 K Ds (×10−11 m2 s−1) | 370 Ds (×10−11 m2 s−1) | 400 K Ds (×10−11 m2 s−1) | E a (kJ mol−1) | 653 K Ds (×10−11 m2 s−1) |
|---|---|---|---|---|---|
| p-Cresol in H–Y | 1.80 ± 0.11 | 3.08 ± 0.11 | 5.48 ± 0.25 | 20.9 ± 0.4 | 17.07 ± 0.04 |
| m-Cresol in H–Y | 0.80 ± 0.05 | 2.05 ± 0.01 | 4.25 ± 0.31 | 31.6 ± 0.1 | 17.81 ± 0.02 |
| p-Cresol in H-beta | 1.33 ± 0.06 | 2.62 ± 0.31 | 6.54 ± 0.12 | 29.9 ± 1.1 | 15.45 ± 0.02 |
| m-Cresol in H-beta | 0.40 ± 0.03 | 0.89 ± 0.08 | 1.86 ± 0.02 | 29.1 ± 1.3 | 11.06 ± 0.01 |
| p-Cresol in H-ZSM5 | 1.62 ± 0.18 | ||||
| m-Cresol in H-ZSM5 | 0.11 ± 0.03 |
 | ||
| Fig. 10 Self-diffusion coefficients of p- and m-cresol in H–Y and H-beta from 340–400 K calculated from MD simulations. | ||
When observing cresol translation in different zeolites, the self-diffusion of the m-isomer in H–Y was on average 2.2 times faster than in H-beta, while the rate of the self-diffusion of p-cresol was only faster by an average factor of 1.1 between the two zeolites, initially suggesting the steric hindrance from differing pore dimensions is less significant for the more linear p-isomer. Comparing the diffusion of different isomers within the same framework, we observed that p-cresol translated at a faster rate than m-cresol in both zeolites. In H–Y, the rate of p-cresol translation was faster than m-cresol by an average factor of 1.7, visualised by slightly more defined pore hopping in Fig. 9(a) compared to Fig. 9(b). In H-beta, the difference is even more pronounced, with an average increase in translation by a factor of 3.2. The trajectory plot of a molecule of m-cresol (Fig. 9(d)) residing in a H-beta channel intersection for the duration of the simulation highlights the difficulty that this isomer has in translating through the channels.
In contrast, the p-cresol molecule can be seen to translate through channels between BASs/channel intersections, shown in Fig. 9(c). The results suggest that cresol isomer shape has a larger impact on its self-diffusion as the zeolite pore/channel diameter approaches that of the molecule (e.g. from H–Y to H-beta), due to steric effects. Interestingly, the effect of isomer geometry on translation within the simulations is much more pronounced than its effect on the proportion of molecules undergoing rotational motions on shorter timescales, as observed in the QENS and MD experiments. Fig. 7 can help explain these observations. In all systems, there is a high probability of intermolecular interactions between the cresol hydroxyl group and zeolite BASs, explaining the limited self-diffusion. The comparably fast rate of p-cresol diffusion in H-beta can be explained by less frequent cresol–BAS interactions credited to the longer and weaker H-bonds formed, observed in Fig. S20.† This demonstrates the impact of molecular shape upon diffusion: as molecular dimension approaches the zeolite channel diameter, a decrease in the strength and frequency of acid site interactions is observed causing an increase in the number of molecules able to diffuse. Also, due to the more linear shape of p-cresol, any unbound molecules can translate relatively unhindered when at a parallel orientation to the H-beta channel. The activation energies are similar for all systems except p-cresol in H–Y, where the activation energy is lower. This may be due to the larger pores of H–Y and the more ‘streamlined’ geometry of the p-cresol molecule, resulting in lower confinement effects and a lower kinetic energy barrier for its translation. As anticipated, the activation energies for translation are much higher than the energy required to initiate local motions.
The calculated self-diffusion coefficients are observed in Table 4. The trajectory of an example p-cresol molecule in each framework at 653 K exemplifies the difference between cresol diffusion at higher temperatures compared to those run at much lower temperatures.
More significant diffusion in H–Y and H-beta at 653 K is illustrated by Fig. 11(a) and (b) and their respective Ds values. The RDF plots in Fig. 12 show that hydrogen bonding is far less significant in all systems at 653 K as the activation energy for breaking cresol to BAS H-bonds and initiating translation is overcome. A difference between the rate of diffusion in H–Y and H-beta is still observed by an average factor of 1.3, but it is less pronounced than at lower temperatures. Comparing the diffusion of the different isomers in the two larger pore zeolites, we observe that at higher temperatures molecular shape also becomes less important. A very similar rate between the two isomers is observed in H–Y and only slightly faster diffusion of p-cresol is observed in H-beta relative to m-cresol by a factor of 1.2. In contrast, cresol diffusion in the much smaller pores of H-ZSM5 is at least an order of magnitude lower, demonstrating a requirement for higher temperatures when considering the use of a H-ZSM5 catalyst. Even when compared to H-beta, the rate of diffusion decreases by a factor of 9.5 for the p-isomer, and by a factor of 100.5 for the m-isomer. Interestingly, the RDF plots in Fig. 12 show that cresol to BAS hydrogen bonds in H-ZSM5 occur with a lower probability than in the other zeolites, suggesting the slower diffusion observed is due to zeolite confinement effects rather than increased H-bonding, compounded by the presence of sinusoidal channels, unlike the other frameworks with larger straight channels. Similarly to p-cresol in H-beta, it is possible that both isomers cannot form 180° hydrogen bonds with the BASs in H-ZSM5 due to the steric restrictions imposed by its small pores. Fig. 11(c) and (d) demonstrate how the diffusion of cresols is often restricted to individual zeolite pores and as with H-beta, faster diffusion is observed with the more linear p-isomer by a factor of 14.7 relative to the m-isomer. These observations lead to the conclusion that at higher temperatures cresol diffusion is hindered greatly by the confinement effects of the zeolite framework, as opposed to hydrogen bonding interactions.
3.3 Linking dynamics to catalysis
The rate and selectivity of zeolite mediated catalysis is often limited by internal diffusion of various reactants/products throughout the zeolite framework84,85 or by kinetics at the active site,86,87 which are often dependent on fundamental characteristics of the zeolite framework (e.g. pore size, topology or Si/Al ratio dictating the concentration of acid sites) or the reactant (e.g. size, shape and functionality). Our study has focused on cresol isomer behaviour with varying molecular shapes in zeolites of differing topologies and how these properties affect their local and nanoscale mobility, where we will now correlate these changes with catalytic studies. The rate of catalysis can often be limited by conversion at the active site, but many studies looking at the conversion of similar reactants over microporous zeolites have shown that the total rate of catalysis is often controlled by mass transfer limitations, such as the acylation of m-cresol over H-beta and H-ZSM5 with high acid site densities, primarily due to product entrapment.85We have conducted simulations at the same temperature as the catalytic studies performed by Imbert et al.,33,34,88 who concluded that cresol conversion mechanisms over zeolites involve uni-molecular isomerisation via 1,2-methyl shifts, as well as bimolecular disproportionation and dealkylation reactions, where the latter becomes more likely as the zeolite pore size increases.
When measuring the percentage of transformed products against contact time with the catalyst prior to significant catalytic deactivation, all cresol isomers were converted at a higher rate by an average factor of 1.8 by H–Y (Si/Al = 2.5) compared to H-ZSM5 (Si/Al = 27). While this does not directly correlate with the magnitude of the difference in diffusivity observed between H–Y and H-ZSM5 in our MD calculations (an average increase by a factor of ∼80), differences in Si/Al ratio along with other macroscale effects may also play a role including framework defects and heterogeneity of acid site distribution, which are difficult to model on this scale and vary greatly with catalyst synthesis and treatment. More notable is the difference in molecular shape, where a higher rate of p-cresol transformation was observed relative to m-cresol by a factor of 1.2 in the larger pore H–Y and 1.7 in H-ZSM5. These findings are consistent with our trends in diffusivity and also the proportion of mobile molecules undergoing localised motions in both the experiment and in our MD simulations, with the effect of geometry on the rate being more significant as the zeolite pore size decreases in the order H–Y > H-beta > H-ZSM5.
We observed similar rates of isomer diffusion in H–Y and faster rates of p-cresol diffusion compared to m-cresol by an average factor of 3.2 (340–400 K) and 1.4 (653 K) in zeolite beta, and 14.7 in H-ZSM5 (653 K). The increasing gap in diffusivity between p- and m-cresol as the zeolite pore size decreases follows the same trends observed in the catalytic studies carried out by Imbert and colleagues, indicating that the total rate of cresol conversion, as observed in the study, is directly linked to the rate of reactant diffusion, as observed in our simulations, and hence limited by mass transport effects rather than the reaction kinetics.
However, several studies looking at the total conversion rates of cresols into products such as BTX and naphthalene over much longer timescales (where significant catalytic deactivation occurs) observed decreasing conversion as pore size increased. Kumar et al. found higher conversion of m-cresol over H-ZSM5 > H-beta > H–Y89 and To et al. found anywhere from twice to quadruple the yield of converted cresol over H-ZSM5 versus H–Y from 450–600 °C.29 This was attributed to faster rates of catalytic deactivation in the larger pore zeolites caused by the increased ability of H–Y to trap phenolics and the resulting formation of coke. Therefore, the rate of catalytic deactivation and the propensity of pore size to allow this, as well as the product distribution must be considered alongside the study of the rate of diffusion when optimising catalyst topology and composition.
As mentioned, the Si/Al ratio and distribution of acid sites has also been shown to impact the rate of cresol conversion.88,90,91 An increase in the density of the zeolite acid sites in H–Y from Si/Al = 55 to 17 to 4.5 caused an increase in the rate of cresol conversion into phenols and xylenols, showing the importance of the effect of Si/Al ratio on reactant and product selectivity. However, over longer timescales (50 minutes) the activity of H–Y with a Si/Al of 17 surpassed that of the Si/Al = 4.5 sample due to its structural stability. However, higher rates of cresol conversion were observed over Pt/H-beta zeolites with slightly lower acid site densities, which was attributed to better acid site accessibility in the dealuminated samples.35 In our study, translational diffusion and local motions were significantly hindered by a prevalence of adsorption interactions to acid sites at low temperatures, exacerbated by high Si/Al ratios.
Accurately modelling molecular diffusion and adsorption behaviour in zeolites is computationally challenging due to the complex interactions involved across a range of time and length-scales, and the large number of atoms involved in what may seem like very localised phenomena. More expensive ab initio techniques, which account for electron interactions, can more accurately model adsorbate interactions in the pore systems,92,93 such as the favourable π-complex interactions with zeolite acid sites94 which would be significant in these systems. For catalytic processes, they have been shown to model reactivity in zeolites95,96 such as the tautomerisation of phenolics in the pore systems.97 Reactive forcefield methods present a promising alternative by using machine learning to predict atomic interactions from ab initio data, enabling faster and more efficient simulations, particularly in defective systems, while maintaining high accuracy.98
Overall, our research and its relationship with the catalytic studies in the literature suggest that initial cresol transformation may be limited by internal mass-transport before coking, which is dependent on the framework topology and molecular shape of the diffusing molecule. This enables the application of classical MD models, which we have demonstrated give excellent agreement with experiments specifically probing molecular behaviour of confined reactants over the same timescales – for the relatively quick initial screening of different zeolite frameworks.
4 Conclusions
The localised motions and longer range diffusivity of m- and p-cresol was studied in commercial zeolite catalysts H–Y and H-beta using QENS experiments and classical MD simulations. In the QENS experiments, observations were limited to isotropic rotation dynamics, rotating with frequencies from 3.3–5.6 × 1010 s−1 and with activation energies falling between 4–7 kJ mol−1 from 340–400 K. A higher proportion of molecules exhibited this motion within the larger-pore H–Y zeolite compared to H-beta (by an average factor of 2.2), and with the more linear p-isomer compared to the m-isomer in the same zeolite by a factor of 1.2. This suggests that both molecular geometry and zeolite topology play pivotal roles in influencing local modes of motion, with zeolite topology exerting a more pronounced effect. We conclude that cresol molecules rotate mainly within the larger channel intersections when residing in H-beta. In general, as the proportion of mobile molecules increases from H-beta to H–Y the average rate of rotation decreases, attributed to increased cresol–cresol interactions. QENS observables describing local motions occurring within classical MD simulations were generated to assess the accuracy of the model in reproducing the experiment and aligned well with the experimental observations. Comparable proportions of mobile populations and rotational coefficients (5.7–8.5 × 1010 s−1) were noted in each system, showing the same trends and close to within error of the QENS measurements. Accessing higher energy transfer ranges in the simulations revealed a rapid rattling motion of cresols H-bonded to acid sites or partially trapped by the zeolite framework or adjacent cresols, inaccessible by the QENS instrument.Due to the excellent level of agreement between the simulation and experiment, the capability of MD simulations to explore longer timescales allowed the observation of restricted cresol diffusion through the zeolite frameworks ranging from 0.4–6.5 ×10−10 m2 s−1 at the same temperatures as the neutron experiments, impeded by substantial H-bonding interactions with the zeolite BASs. Cresol translation has higher activation energies, ranging from 20–32 kJ mol−1, compared to the energy required for initiating isotropic rotation. Greater rates of translation by an average factor of 1.7 were observed in the H–Y framework, which was attributed to reduced confinement effects. A larger than expected disparity was seen between diffusion of the two isomers in H-beta by a factor of 3.3, with the longer para-isomer unable to form many hydrogen bonds with an optimal 180° bonding angle, especially within the smaller H-beta channels. This resulted in fewer and weaker BAS interactions and increased self-diffusion. The increased O–HO bonding angle between the p-cresol hydroxyl and zeolite BAS places it in a position to translate parallel to the H-beta channel when unbound, so that any self-diffusion down the H-beta channels is far less hindered than that of m-cresol. Additional simulations operating at a catalytically relevant temperature (653 K) revealed faster diffusion, accompanied by reduced adsorption to the BASs. Incorporating the smaller pore H-ZSM5 zeolite we observed diffusion that was slower by 1–2 orders of magnitude than that of the larger pore zeolites, attributed to confinement effects rather than acid site interactions. This indicates that as the size of the diffusing molecule approaches that of the zeolite pore and as the temperature increases, confinement effects surpass H-bonding interactions as the primary determinant of diffusion rate. Consequently, to understand the internal diffusion rates of cresols throughout zeolite pores, the interplay between the molecule![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) zeolite pore diameter ratios and acid site strengths and densities must be considered. The observation of p
zeolite pore diameter ratios and acid site strengths and densities must be considered. The observation of p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m-cresol rates of diffusion increasing as the pore size decreases supports previous catalytic studies observing the same trends in the rate of total product formation,33,34 showing a strong correlation between the trends in diffusion found in our study (similar p
m-cresol rates of diffusion increasing as the pore size decreases supports previous catalytic studies observing the same trends in the rate of total product formation,33,34 showing a strong correlation between the trends in diffusion found in our study (similar p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m diffusion rates in H–Y, 1.4 in H-beta and 14.7 in H-ZSM5) and the total catalytic rate observed before significant coking in the literature (1.2 p
m diffusion rates in H–Y, 1.4 in H-beta and 14.7 in H-ZSM5) and the total catalytic rate observed before significant coking in the literature (1.2 p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m conversion rate in H–Y and 1.7 in H-ZSM5), all measured at 653 K.
m conversion rate in H–Y and 1.7 in H-ZSM5), all measured at 653 K.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) grant EP/R513155/1 and EP/T518013/1 for the University of Bath and as part of an ISIS Facilities Development studentship with the Science and Technologies Facilities Council (STFC). Experiments at the ISIS Pulsed Neutron and Muon Source were supported by a beamtime allocation from the STFC, with preliminary sample characterisation carried out with the aid of the ISIS Hydrogen and Catalysis Laboratory and Materials Characterisation Laboratory. The authors thank the STFC facilities for access to computing resources on the SCARF computer cluster. A. J. O'Malley acknowledges Roger and Sue Whorrod for the funding of a Whorrod Fellowship and IChemE for the funding of the Andrew Fellowship. The resources and support provided by the UK Catalysis Hub via membership of the UK Catalysis Hub consortium are gratefully acknowledged.References
- E. T. C. Vogt and B. M. Weckhuysen, Chem. Soc. Rev., 2015, 44, 7342–7370 RSC.
- P. Azadi, O. R. Inderwildi, R. Farnood and D. A. King, Renewable Sustainable Energy Rev., 2013, 21, 506–523 CrossRef CAS.
- C. Amen-Chen, H. Pakdel and C. Roy, Bioresour. Technol., 2001, 79, 277–299 CrossRef CAS PubMed.
- T. Belkheiri, C. Mattsson, S.-I. Andersson, L. Olausson, L.-E. Åmand, H. Theliander and L. Vamling, Energy Fuels, 2016, 30, 4916–4924 CrossRef CAS.
- C. Xu, R. A. D. Arancon, J. Labidi and R. Luque, Chem. Soc. Rev., 2014, 43, 7485–7500 RSC.
- V. M. Roberts, V. Stein, T. Reiner, A. Lemonidou, X. Li and J. A. Lercher, Chem. – Eur. J., 2011, 17, 5939–5948 CrossRef CAS PubMed.
- J. R. Gasson, D. Forchheim, T. Sutter, U. Hornung, A. Kruse and T. Barth, Ind. Eng. Chem. Res., 2012, 51, 10595–10606 CrossRef CAS.
- K. Wang, K. H. Kim and R. C. Brown, Green Chem., 2014, 16, 727–735 RSC.
- A. de Rezende Pinho, M. B. de Almeida, F. L. Mendes, L. C. Casavechia, M. S. Talmadge, C. M. Kinchin and H. L. Chum, Fuel, 2017, 188, 462–473 CrossRef.
- T. Ennaert, J. V. Aelst, J. Dijkmans, R. D. Clercq, W. Schutyser, M. Dusselier, D. Verboekend and B. F. Sels, Chem. Soc. Rev., 2016, 45, 584–611 RSC.
- J. Liang, G. Shan and Y. Sun, Renewable Sustainable Energy Rev., 2021, 139, 110707 CrossRef CAS.
- J. Dědeček, E. Tabor and S. Sklenak, ChemSusChem, 2018, 12, 556–576 CrossRef PubMed.
- P. S. Rezaei, H. Shafaghat and W. M. A. W. Daud, Green Chem., 2016, 18, 1684–1693 RSC.
- J. Jae, G. A. Tompsett, A. J. Foster, K. D. Hammond, S. M. Auerbach, R. F. Lobo and G. W. Huber, J. Catal., 2011, 279, 257–268 CrossRef CAS.
- X. Li, L. Su, Y. Wang, Y. Yu, C. Wang, X. Li and Z. Wang, Front. Environ. Sci. Eng., 2012, 6, 295–303 CrossRef CAS.
- H. Ben and A. J. Ragauskas, ACS Sustainable Chem. Eng., 2013, 1, 316–324 CrossRef CAS.
- D. J. Mihalcik, C. A. Mullen and A. A. Boateng, J. Anal. Appl. Pyrolysis, 2011, 92, 224–232 CrossRef CAS.
- Z. Ma, E. Troussard and J. A. van Bokhoven, Appl. Catal., A, 2012, 423–424, 130–136 CrossRef CAS.
- I. Kurnia, S. Karnjanakom, A. Bayu, A. Yoshida, J. Rizkiana, T. Prakoso, A. Abudula and G. Guan, Fuel Process. Technol., 2017, 167, 730–737 CrossRef CAS.
- Y. Yu, X. Li, L. Su, Y. Zhang, Y. Wang and H. Zhang, Appl. Catal., A, 2012, 447–448, 115–123 CrossRef CAS.
- A. G. Gayubo, A. T. Aguayo, A. Atutxa, R. Aguado and J. Bilbao, Ind. Eng. Chem. Res., 2004, 43, 2610–2618 CrossRef CAS.
- P. S. Rezaei, H. Shafaghat and W. M. A. W. Daud, RSC Adv., 2015, 5, 51278–51285 RSC.
- H. E. Jegers and M. T. Klein, Ind. Eng. Chem. Process Des. Dev., 1985, 24, 173–183 CrossRef CAS.
- X. Zhu, L. Nie, L. L. Lobban, R. G. Mallinson and D. E. Resasco, Energy Fuels, 2014, 28, 4104–4111 CrossRef CAS.
- G. Afreen, T. Patra and S. Upadhyayula, Mol. Catal., 2017, 441, 122–133 CrossRef CAS.
- E. Batisai, V. J. Smith, S. A. Bourne and N. B. Báthori, CrystEngComm, 2015, 17, 5134–5138 RSC.
- B. M. C. Shekara, B. S. J. Prakash and Y. S. Bhat, J. Porous Mater., 2012, 20, 827–837 CrossRef.
- A. Hellweg and C. Hättig, J. Chem. Phys., 2007, 127, 024307 CrossRef PubMed.
- A. T. To and D. E. Resasco, Appl. Catal., A, 2014, 487, 62–71 CrossRef CAS.
- Q. Sun, G. Chen, H. Wang, X. Liu, J. Han, Q. Ge and X. Zhu, ChemCatChem, 2016, 8, 551–561 CrossRef CAS.
- A. Berenguer, J. A. Bennett, J. Hunns, I. Moreno, J. M. Coronado, A. F. Lee, P. Pizarro, K. Wilson and D. P. Serrano, Catal. Today, 2018, 304, 72–79 CrossRef CAS.
- A. Ausavasukhi, Y. Huang, A. T. To, T. Sooknoi and D. E. Resasco, J. Catal., 2012, 290, 90–100 CrossRef CAS.
- F. Imbert, N. Gnep and M. Guisnet, J. Catal., 1997, 172, 307–313 CrossRef CAS.
- F. Imbert, M. Guisnet and S. Gnep, J. Catal., 2000, 195, 279–286 CrossRef CAS.
- J. Horáček, G. Št'ávová, V. Kelbichová and D. Kubička, Catal. Today, 2013, 204, 38–45 CrossRef.
- M. E. Potter, S. Chapman, A. J. O'Malley, A. Levy, M. Carravetta, T. M. Mezza, S. F. Parker and R. Raja, ChemCatChem, 2017, 9, 1897–1900 CrossRef CAS.
- A. J. O'Malley, S. F. Parker and C. R. A. Catlow, Chem. Commun., 2017, 53, 12164–12176 RSC.
- H. Jobic and D. N. Theodorou, Microporous Mesoporous Mater., 2007, 102, 21–50 CrossRef CAS.
- A. J. O'Malley and C. R. A. Catlow, in Neutron Scattering – Applications in Biology, Chemistry, and Materials Science, Elsevier, 2017, pp. 349–401 Search PubMed.
- A. J. Porter, C. H. Botchway, B. Kwakye-Awuah, C. Hernandez-Tamargo, S. K. Matam, S. L. McHugh, I. P. Silverwood, N. H. de Leeuw and A. J. O'Malley, Catal. Sci. Technol., 2022, 12, 1663–1677 RSC.
- J. Armstrong, A. J. O'Malley, M. R. Ryder and K. T. Butler, J. Phys. Commun., 2020, 4, 072001 CrossRef CAS.
- J. Armstrong, J. Phys. Commun., 2022, 6, 102002 CrossRef CAS.
- A. Porter, S. McHugh, T. Omojola, I. Silverwood and A. O'Malley, Microporous Mesoporous Mater., 2023, 348, 112391 CrossRef CAS.
- A. J. O'Malley and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2015, 17, 1943–1948 RSC.
- B. Smit and T. L. M. Maesen, Chem. Rev., 2008, 108, 4125–4184 CrossRef CAS PubMed.
- V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. G. Bell and C. R. A. Catlow, Chem. Soc. Rev., 2015, 44, 7044–7111 RSC.
- C. Hernandez-Tamargo, A. O'Malley, I. P. Silverwood and N. H. de Leeuw, Catal. Sci. Technol., 2019, 9, 6700–6713 RSC.
- C. Hernandez-Tamargo, I. P. Silverwood, A. J. O'Malley and N. H. de Leeuw, Top. Catal., 2020, 64, 707–721 CrossRef.
- S. Mitra, A. Tripathy, N. Gupta and R. Mukhopadhyay, Appl. Phys. A: Mater. Sci. Process., 2002, 74, s1308–s1310 CrossRef CAS.
- H. Jobic, M. Bée and A. J. Dianoux, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 2525 RSC.
- R. Warringham, D. Bellaire, S. F. Parker, J. Taylor, R. A. Ewings, C. M. Goodway, M. Kibble, S. R. Wakefield, M. Jura, M. P. Dudman, R. P. Tooze, P. B. Webb and D. Lennon, J. Phys.: Conf. Ser., 2014, 554, 012005 CrossRef.
- M. T. F. Telling and K. H. Andersen, The OSIRIS User Guide, STFC, ISIS neutron and Muon Source, UK, 2018 Search PubMed.
- O. Arnold, J. Bilheux, J. Borreguero, A. Buts, S. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal, M. Gigg, V. Lynch, A. Markvardsen, D. Mikkelson, R. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. Perring, P. Peterson, S. Ren, M. Reuter, A. Savici, J. Taylor, R. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341 CrossRef CAS PubMed.
- D. H. Olson, G. T. Kokotailo, S. L. Lawton and W. M. Meier, J. Phys. Chem., 1981, 85, 2238–2243 CrossRef CAS.
- W. M. Meier, D. H. Olson and C. Baerlocher, Atlas of the Zeolite Structure Types, 1996 Search PubMed.
- L. Wei, H. Yang, P. Ren, Y. Yang, Y.-W. Li, R. Li, X.-D. Wen and H. Jiao, Microporous Mesoporous Mater., 2022, 344, 112184 CrossRef CAS.
- A. R. Ruiz-Salvador, R. Grau-Crespo, A. E. Gray and D. W. Lewis, J. Solid State Chem., 2013, 198, 330–336 CrossRef CAS.
- E. Dempsey, J. Catal., 1977, 49, 115–119 CrossRef CAS.
- T. I. Korányi and J. B. Nagy, J. Phys. Chem. C, 2007, 111, 2520–2524 CrossRef.
- L. Kobera, J. Dedecek, P. Klein, E. Tabor, J. Brus, A. V. Fishchuk and S. Sklenak, J. Chem. Phys., 2022, 156, 104702 CrossRef CAS PubMed.
- X. Tang, W. Chen, W. Dong, Z. Liu, J. Yuan, H. Xia, X. Yi and A. Zheng, Catal. Today, 2022, 405–406, 101–110 CAS.
- R. E. Fletcher, S. Ling and B. Slater, Chem. Sci., 2017, 8, 7483–7491 RSC.
- K. Mlekodaj, J. Dedecek, V. Pashkova, E. Tabor, P. Klein, M. Urbanova, R. Karcz, P. Sazama, S. R. Whittleton, H. M. Thomas, A. V. Fishchuk and S. Sklenak, J. Phys. Chem. C, 2018, 123, 7968–7987 CrossRef.
- C.-L. M. Woodward, A. J. Porter, K. S. Morton and A. J. O'Malley, Catal. Commun., 2022, 164, 106415 CrossRef CAS.
- M. J. Sanders, M. Leslie and C. R. A. Catlow, J. Chem. Soc., Chem. Commun., 1984, 1271 RSC.
- K.-P. Schröder, J. Sauer, M. Leslie, C. Richard, A. Catlow and J. M. Thomas, Chem. Phys. Lett., 1992, 188, 320–325 CrossRef.
- M. Born, K. Huang and M. Lax, Am. J. Phys., 1955, 23, 474–474 CrossRef.
- C. R. A. Catlow, R. James, W. C. Mackrodt and R. F. Stewart, Phys. Rev. B, 1982, 25, 1006–1026 CrossRef CAS.
- E. Harder, W. Damm, J. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren, J. L. Knight, J. W. Kaus, D. S. Cerutti, G. Krilov, W. L. Jorgensen, R. Abel and R. A. Friesner, J. Chem. Theory Comput., 2015, 12, 281–296 CrossRef PubMed.
- K. S. C. Morton, A. M. Elena, J. Armstrong and A. J. O'Malley, J. Phys. Chem. A, 2023, 127, 3305–3316 CrossRef CAS PubMed.
- D. Mooney, F. Müller-Plathe and K. Kremer, Chem. Phys. Lett., 1998, 294, 135–142 CrossRef CAS.
- R. Vetrivel, C. R. A. Catlow and E. A. Colbourn, J. Chem. Soc., Faraday Trans. 2, 1989, 85, 497 RSC.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911 RSC.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- T. G. A. Youngs, J. Comput. Chem., 2009, 31, 639–648 CrossRef PubMed.
- G. Goret, B. Aoun and E. Pellegrini, J. Chem. Inf. Model., 2017, 57, 1–5 CrossRef CAS PubMed.
- V. F. Sears, Can. J. Phys., 1966, 44, 1279–1297 CrossRef CAS.
- S. K. Matam, C. R. A. Catlow, I. P. Silverwood and A. J. O'Malley, Top. Catal., 2021, 64, 699–706 CrossRef CAS.
- J. V. der Mynsbrugge, M. Visur, U. Olsbye, P. Beato, M. Bjørgen, V. V. Speybroeck and S. Svelle, J. Catal., 2012, 292, 201–212 CrossRef.
- D. Herschlag and M. M. Pinney, Biochemistry, 2018, 57, 3338–3352 CrossRef CAS PubMed.
- A. J. O'Malley, V. García Sakai, N. Dimitratos, W. Jones, C. Catlow and S. F. Parker, Philos. Trans. R. Soc., A, 2020, 378, 20200063 CrossRef PubMed.
- J. Aracil, M. Martinez, N. Sánchez and A. Corma, Zeolites, 1992, 12, 233–236 CrossRef CAS.
- H. K. Chau, D. E. Resasco, P. Do and S. P. Crossley, J. Catal., 2022, 406, 48–55 CrossRef CAS.
- O. Mowla, E. Kennedy and M. Stockenhuber, Renewable Energy, 2019, 135, 417–425 CrossRef CAS.
- A. M. Doyle, T. M. Albayati, A. S. Abbas and Z. T. Alismaeel, Renewable Energy, 2016, 97, 19–23 CrossRef CAS.
- F. Imbert, S. Gnep and M. Guisnet, Catal. Lett., 1997, 49, 121–128 CrossRef CAS.
- A. Kumar, A. Kumar, B. Biswas, J. Kumar, S. R. Yenumala and T. Bhaskar, Renewable Energy, 2020, 151, 687–697 CrossRef CAS.
- F. E. Imbert, N. S. Gnep, P. Ayrault and M. Guisnet, Appl. Catal., A, 2001, 215, 225–234 CrossRef CAS.
- M. Acevedo, M. Montañez-Valencia, N. Okulik, M. Sad and C. Padró, Catal. Commun., 2017, 92, 10–14 CrossRef CAS.
- F. Haase and J. Sauer, Microporous Mesoporous Mater., 2000, 35–36, 379–385 CrossRef CAS.
- A. J. O'Malley, A. J. Logsdail, A. A. Sokol and C. R. A. Catlow, Faraday Discuss., 2016, 188, 235–255 RSC.
- J. Tan, H. Liang, W. Chen, J. Yuan, W. Dong, W. Liu, X. Yu, H. Shi and A. Zheng, Microporous Mesoporous Mater., 2024, 365, 112887 CrossRef CAS.
- L. Benco, T. Demuth and F. Hutschka, Comput. Mater. Sci., 2003, 27, 87–95 CrossRef CAS.
- X. Rozanska, R. A. van Santen, T. Demuth, F. Hutschka and J. Hafner, J. Phys. Chem. B, 2003, 107, 1309–1315 CrossRef CAS.
- C. E. Hernandez-Tamargo, A. Roldan and N. H. de Leeuw, Mol. Catal., 2017, 433, 334–345 CrossRef CAS.
- A. Erlebach, M. Šípka, I. Saha, P. Nachtigall, C. J. Heard and L. Grajciar, Nat. Commun., 2024, 15, 4215 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details the MD simulation parameters, and the EISF and H-bonding analysis. See DOI: https://doi.org/10.1039/d4cy00321g |
| This journal is © The Royal Society of Chemistry 2024 |




