Cu₂O facet controlled reactivity for peroxidase-like activity

Abstract

Replicating the enzymatic surface microenvironment in vitro is challenging, but constructing an analogous model could facilitate our understanding of surface effects and aid in developing an efficient bioinspired catalytic system. In this study, we generate five unique Cu₂O morphologies: cubic (c-Cu₂O), octahedral (o-Cu₂O), rhombododecahedral (r-Cu₂O), cuboctahedral (co-Cu₂O), and spherical (s-Cu₂O) with an average edge length between 0.59 and 0.61 μm. By precisely controlling crystal growth on distinct surface planes, with surface energies in the order γ_{100} < γ_{111} < γ_{110}, we achieve a wide spectrum of shape variations during the evolution of these structures. The variations in surface morphology are a consequence of differences in the exposure of low-index facets, such as {100}, {111}, and {110}, leading to varying numbers of unsaturated copper sites at the surface. The peroxidase-like activity was investigated by altering the Cu₂O surface structures in the reduction of H₂O₂ using chromogenic substrates like TMB/ABTS. The activity catalyzed by various Cu₂O surfaces (r-Cu₂O, o-Cu₂O, and c-Cu₂O) followed the typical Michaelis–Menten kinetics, with K_m values ranging from 0.096 to 0.120 mM for TMB and 1.57 to 2.90 mM for H₂O₂ as substrates, respectively. Compared to native peroxidase enzymes (with K_m values of 0.434 mM for TMB and 3.70 mM for H₂O₂ under identical conditions), these Cu₂O catalysts exhibited a higher affinity. In general, the reactivity order observed was as follows: co-Cu₂O ≈ r-Cu₂O > o-Cu₂O > c-Cu₂O > s-Cu₂O. Mechanistically, the H₂O₂ reduction on the surface produces hydroxyl radicals that undergo H-abstraction from TMB, where the latter was found to be the rate-determining step. Both kinetic and DFT studies have unveiled that the heightened reactivity of r-Cu₂O can be attributed to its higher proportion of {110} planes, which contain a higher number of dangling (unsaturated) Cu atoms that facilitate H₂O₂ decomposition. Additionally, they exhibit sufficiently low energy barriers (TS2: 0.70 eV) that enable OH radicals to efficiently oxidize TMB molecules compared to other morphologies.

---

Introduction

PODs, which stand for peroxidases, are a crucial group of enzymes found in virtually all living organisms. These efficient metalloenzymes catalyse the reduction of peroxides which are harmful to the tissues, while also serving as crucial radical scavengers for toxin elimination in biological systems. However, due to their intrinsic limitations, such as high cost, difficulty in purification/recyclability, inadequate storage, easy inactivation, and sensitivity to solution, pH, and temperature, their catalytic activities are limited, hindering their broader usage. Peroxidase-assisted H₂O₂ reduction involves the active participation of the protein chains that provide a facile surface for the active site interaction with the substrate for enzymatic transformation. The structure of the native horse radish peroxidase (HRP) enzyme is depicted in (Fig. 1a). Specifically, the active site in HRP comprises an Fe(III)-protoporphyrin IX coordinated to a proximal His-170 and two distal His-42 and Arg-38 amino acids.¹ These amino acids have a crucial role in activating H₂O₂ towards the cleavage of the O–O bond. To approach the active site of the heme prosthetic group, H₂O₂ must diffuse from the protein surface towards the heme pocket through a fluctuating entry point located between Phe-68 and Phe-142 (Fig. 1b), subsequently traversing a channel resembling a bottle to ultimately reach the heme iron.² The reduction of H₂O₂ on the active site is only then favoured where Fe(III) (resting state) first oxidises to an Fe(IV) oxo π cation radical complex (compound I). Consequently, in the presence of two electron donor substrates (like TMB), it reduces to an Fe(IV) oxo complex (compound II) and finally completes the cycle through the generation of the resting Fe(III) enzyme (Fig. 1c).^3–6 The resplendent surface structures displayed by protein molecules provide an opulence of invaluable information for understanding the biological roles of proteins.^7,8 Proteins/enzymes and dynamic functional materials exhibit intricate interactions, and biological cells can modify the surfaces, ranging from mechanical disruption to protein excretion and enzymatic degradation.⁹ Thus, by treating proteins and material surfaces as chemical systems, it becomes possible to comprehend these complex biological reactions. Accordingly, developing chemically defined surfaces can enhance our understanding of biological systems and enable the design of biomimetic surfaces with targeted catalytic activity.

Fig. 1 (a) Native horse radish peroxidase (HRP) enzyme (PDB: 1HCH). (b) Schematic representation of the active site of HRP. (c) Peroxidase cycle for two electron donor substrates as catalyzed by HRP.

In this context, we screened chemical analogues to study peroxidase-like activity. Metal oxides emerge as an obvious choice, as they offer a range of surfaces that can be systematically tuned for facile adsorption and reduction of H₂O₂ on their surface that can generate reactive oxygen species.^10,11 Although a plethora of metal oxides such as TiO₂,^12,13 V₂O₅,¹⁴ MnO₂,¹⁵ Fe₂O₃,^16,17 Fe₃O₄,¹⁸ Co₃O₄,^19,20 NiO,²¹ Cu₂O,²² CuO,^23–25 ZnO,^26,27 RuO₂,²⁸ ZrO₂ (ref. 29) and CeO₂ (ref. 30–32) are known to exhibit peroxidase-like activity, a comprehensive study to understand the relative reactivity differences over various morphologies is still illusive. Interestingly, Cu₂O is an important p-type semiconductor with a direct band gap of 2.17 eV, which displays diverse facet-dependent electrochemical^33–38 and photocatalytic^39–43 properties. Varying the shape of ionic solids, like metal oxides with a cubic crystal structure, can regulate the exposed facets on their surface. Cu₂O can be tuned easily to generate surfaces with various exposed facets and surface energies that control their reactivity. For instance, rhombic dodecahedral Cu₂O is known to exhibit excellent photocatalytic activity towards the degradation of methyl orange.³⁹ In another study, Cu₂O with different exposed facets was investigated for electrocatalytically sensing H₂O₂, wherein the {111}-facet bound hexapod, octahedral and {110} bound rhombododecahedral Cu₂O catalysts were found to have higher reactivity than {100} bound cubic Cu₂O.⁴⁴

In one relevant computational study, Yuan et al. examined transition metal oxides such as Cu₂O and Fe₃O₄ as peroxidase mimics by analyzing their H₂O₂ adsorption energies. However, their kinetic properties still need further understanding.²² In another study, Shen et al. systematically studied POD-like reactions catalyzed by iron oxides by calculating the energy potential surface along the reaction coordinate.⁴⁵ They proposed a three-step reaction mechanism, which includes H₂O₂ dissociative adsorption on the catalyst and consecutive oxidation of TMB by two adsorbed OH radicals. However, the steps involving the H₂O₂ and substrate (TMB) adsorption were not considered, which might lead to an underestimation of the energy barriers for H₂O₂ dissociation and TMB oxidation. Additionally, solvents also influence the energy of the adsorbed species and solvated molecules within the solution. The absence of solvent effects and van der Waals (vdW) interaction corrections in both computational works could result in a significant deviation from the actual experimental conditions. Therefore, a more detailed potential energy surface is necessary for exploring the kinetics of POD-like reactions catalyzed by Cu₂O. In this work, we have synthesized Cu₂O with different morphologies such as cubic (c-Cu₂O), octahedral (o-Cu₂O), rhombododecahedral (r-Cu₂O), cuboctahedral (co-Cu₂O), and spherical (s-Cu₂O) as a surface mimic towards peroxidase activity. We employed UV-vis spectroscopy to investigate the TMB_ox production rate and utilized the Michaelis–Menten model to study steady-state kinetics. Furthermore, we conducted DFT calculations to examine the reaction mechanism on different exposed facets under more rigorous modelling conditions, including the consideration of the implicit solvent model, DFT-D3 van der Waals correction, and H₂O₂/TMB molecular adsorption steps.

Results and discussion

Synthesis and characterization

The synthesis of various shaped Cu₂O catalysts was achieved by controlling the growth of the {100}, {111}, {110} planes.^39,46,47 The facet growth of a metal oxide is driven by the increased growth of the high surface area facet, which plays a crucial role in elucidating the final morphological outcome of the metal oxides. The shape evolution of these metal oxides is predicted by the Gibbs–Curie–Wulff theorem,^48,49 which suggests that the surfaces or facets with higher surface energy have rapid perpendicular growth and are eventually eliminated from the final morphology, whereas the facets having low surface energy grow slowly and are retained in the final shape of the crystals. Therefore, to preserve the facets associated with a higher surface energy in the final morphology of a metal oxide, their growth rate is substantially reduced with the introduction of surface capping agents like polyvinylpyrrolidone (PVP) and sodium dodecyl sulphate (SDS) in the case of Cu₂O. The syntheses of five different morphologies of Cu₂O, viz., cubic (c-Cu₂O), octahedral (o-Cu₂O), rhombododecahedral (r-Cu₂O), cuboctahedral (co-Cu₂O), and spherical (s-Cu₂O) were achieved by controlling the concentration of the capping agents and reaction time.^39,47 FT-IR spectra show a characteristic Cu–O bond stretching band at around 626 cm⁻¹ for Cu₂O crystals (Fig. 2a).⁵⁰ The phase purity of the as-synthesized Cu₂O crystals was confirmed using PXRD and indexed to the cubic phase (JCPDS: 05-0667) (Fig. 2b).

Fig. 2 (a) FT-IR spectra and (b) PXRD spectra for different morphologies of Cu₂O crystals.

Here, the relative difference in the intensity of {111} and {200} peaks is indicative of the evolution of different morphologies.⁵¹ For example, due to the presence of a higher number of {111} planes on o-Cu₂O, the relative ratio of the peak intensity between {111} and {200} is very high. This was furthermore confirmed by studying the surface morphologies with SEM.

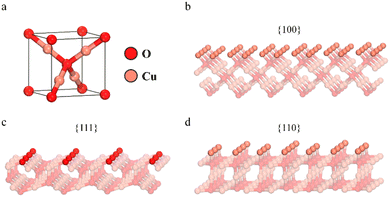
Fig. 3 and S1† show the SEM images of different as-synthesized Cu₂O crystals along with the geometric representation of the evolved facets and vertices with the change in morphology. These different shapes of Cu₂O display distinct edges and relatively uniform sizes. Each cube has six {100} facets, an octahedron has eight {111} facets, a rhombododecahedron consists of twelve {110} facets, and a cuboctahedron has 14 facets comprising six {100} and eight {111} facets (Fig. 3f). As evident from the SEM images, the shape of the Cu₂O crystal on increasing the PVP concentration evolves from cubic to octahedral. This is due to the controlled/slow growth of the high energy {111} plane in o-Cu₂O with higher PVP concentration. The average edge lengths (Fig. S2†) in c-Cu₂O and o-Cu₂O were found to be 616.68 (±78.88) nm and 595.85 (±65.40) nm, respectively. Furthermore, excessive use of capping agents resulted in the formation of s-Cu₂O with an average diameter of 603.02 (±71.62) nm. Generally, excessive use of capping agents results in indiscriminate binding around planes, resulting in the lowest energy morphology. Similarly, with the use of SDS as a capping agent and the stoichiometric concentration of NH₂OH·HCl, other morphologies, viz., r-Cu₂O and co-Cu₂O, were obtained with an average edge length of 600.75 (±73.26) nm and 615.67 (±69.32) nm, respectively (see the ESI† for details). XPS analysis show typical Cu(I) signature peaks (2P_3/2 at 931 eV and 2P_1/2 at 950.9 eV). An additional Cu 2P peak at higher binding energy centered around 933 eV and 953 eV is attributed to the partial surface oxidation to Cu (II) (Fig. S3†).⁵²

Fig. 3 SEM images and the morphological models of the exposed facets of (a) cubic (c-Cu₂O), (b) octahedral (o-Cu₂O), (c) cuboctahedral (co-Cu₂O), (d) rhombododecahedral (r-Cu₂O), and (e) spherical (s-Cu₂O) crystals, respectively. (f) Overview of the number of facets involved in the different morphologies of Cu₂O.

In a typical unit cell of Cu₂O in a cubic crystal system (Fig. 4a), each O atom is tetrahedrally coordinated to four Cu atoms, and each Cu atom is bonded to two neighbouring O atoms. It is well established that the surface energy of the low-indexed facets {100}, {111}, and {110} is closely associated with the density of the coordinatively unsaturated Cu atoms.³⁹Fig. 4b–d show the atomic arrangements along these three low-indexed facets. Generally, the {100} facets are terminated by O atoms, only making them relatively neutral, while the {111} facets have dangling coordinatively unsaturated Cu sites (Cu_CUS) perpendicular to them, making them positively charged.⁵³ Again, the {110} facets are terminated by Cu atoms in association with the dangling Cu atom perpendicular to them. As a result, the number of Cu sites in the {110} facet is found to be approximately 1.5 times higher than that found in the {111} facet.⁵³ Relatively, this makes the {110} facet more positively charged than the {111} facet. The density of these unsaturated dangling copper sites affects the surface energies of the low-indexed facets {100}, {111}, and {110}.³⁹ Likewise, the surface energies (γ) of Cu₂O follow the order: γ_{100} < γ_{111} < γ_{110}.⁴⁸ However, Su et al. reported that the presence of capping agents, such as SDS, significantly affects the surface termination of Cu₂O nanoparticles.⁵⁴ This is because the –OSO₃⁻ group in SDS tends to adsorb onto Cu sites rather than O sites. As a result, the Cu terminated surface is more favorably exposed than the O terminated surface, leading to different surface properties than initially anticipated. In terms of surface termination, the {100} and {110} surfaces have considerable dangling Cu atoms, while the {111} surface is terminated by O atoms in addition to a few dangling Cu atoms (Fig. 4).

Fig. 4 (a) Illustration of the unit cell of cuprite Cu₂O. (b–d) The arrangement of atoms in the crystal structure of Cu₂O showing the {100}, {111} and {110} facets, respectively. Orange spheres are the Cu atoms and red spheres are the O atoms.

Cu₂O as a peroxidase mimic

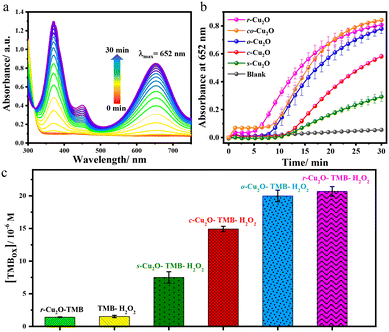
The peroxidase-like activity of the as-prepared Cu₂O with different exposed facets was first investigated by monitoring the evolution of absorption variation of the chromogenic peroxidase substrate, 3,3′,5,5′-tetramethylbenzidine (TMB), in a time scale mode at 652 nm. TMB is a two-electron donor assay used to test peroxidase-like activity for the reduction of H₂O₂. The absorption band at 652 nm may be assigned to a charge transfer complex dimer TMB_ox (ε_652nm = 39 000 M⁻¹ cm⁻¹)⁵⁵ formed between one electron oxidised radical cation and an unoxidized TMB, which is blue (Scheme 1).

Scheme 1 Oxidation of TMB catalysed by Cu₂O in the presence of H₂O₂.

Further, one electron oxidation of TMB_ox resulted in the saturation of the peak at 652 nm and evolution of the peak for the diimine complex at λ_max of 450 nm, which is yellow. As a representative case, r-Cu₂O was taken for the optimisation of pH, temperature and catalytic loading, which may affect the reactivity. Buffer solutions having a wide range of pH values (2–10) was used and the reaction was found be progressive under acidic conditions. When the reaction was initiated in a buffer solution at pH 2, the rate of reaction towards the formation of a yellow coloured 2e⁻ oxidised diimine complex (λ_max = 450 nm) was drastically fast (Fig. S4†).^56,57 Consequently, the rate of reaction for the formation of the 1e⁻ oxidised product, viz., TMB_ox (λ_max = 652 nm) was found to be optimal with the buffer solution of pH 4. The reaction was also performed in a wide range of temperatures (0–60 °C) (Fig. S5†). At 0 °C, there was no evident formation of TMB_ox and the rate of formation of the charge transfer complex (λ_max = 652 nm) was found to increase with increasing temperature. However, the formation of TMB_ox was found to be maximum at 25 °C making it an ideal temperature for the reaction. Concisely, at higher temperature the increasing reaction rate for the formation of TMB_ox and its rapid conversion to the 2e⁻ oxidised diimine complex (λ_max = 450 nm) was observed.⁵⁷ Lastly, the reaction was further optimized at various catalytic loadings ranging from 8–33 μg mL⁻¹ (Fig. S6†). A steady increase in the formation of TMB_ox was observed on increasing the Cu₂O catalytic loading from 8 to 33 μg mL⁻¹. As a result, 33 μg mL⁻¹ of Cu₂O was taken as the optimised catalytic loading for the reaction. Furthermore, under the optimised conditions, a set of commercially available metal oxides were screened towards TMB oxidation, where Cu₂O and CuO were found to have a comparatively better reactivity (Fig. S7†). Additionally, Cu₂O had a much greater reactivity than CuO as anticipated which can be attributed to the lower oxidation state of the Cu centre.²² Thus, we proceeded with 33 μg mL⁻¹ catalytic loading of various Cu₂O catalysts, H₂O₂, and TMB as a peroxidase assay at room temperature in pH = 4 acetate buffer solution as the optimised conditions. The initial reaction using Cu₂O gave the instant formation of blue coloured species along with the evolution of a peak at 652 nm showing peroxidase-like activity (Fig. 5a).¹⁸

Fig. 5 (a) Evolution of the absorbance of TMB_ox at 652 nm catalysed by Cu₂O crystals in the presence of H₂O₂. (b) Time dependent evolution of absorbance at 652 nm for TMB_ox in the presence of H₂O₂ using different morphologies of Cu₂O crystals as catalysts. (c) Concentration of TMB_ox measured at 30 min in the presence of different reaction systems viz., r-Cu₂O–TMB, TMB–H₂O₂ and different morphologies of Cu₂O in the presence of TMB and H₂O₂.

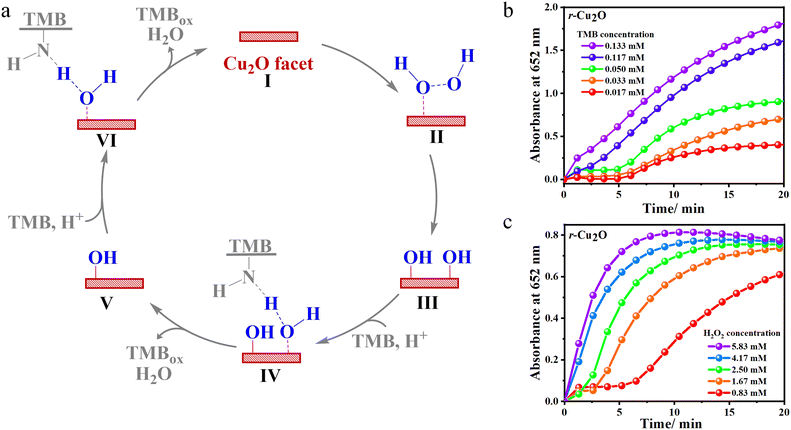
The relative temporal evolution of the 652 nm peak on different Cu₂O catalysts shows that the catalytic oxidation of TMB by H₂O₂ goes through a sedate initial phase (up to 5–10 min) due to the adsorption of the substrate on the surface of the catalyst, the phase is also referred to as the induction time.⁵⁸ After the induction time, Cu₂O with various morphologies showed different initial rate trajectories (Fig. 5b). For instance, c-Cu₂O with exposed {100} facets exhibited slow oxidation of TMB, whereas the evolution is accelerated on r-Cu₂O with exposed {110} facets. The efficiency of the different as-synthesized Cu₂O catalysts under the optimised conditions was found to follow the order: cuboctahedral (co-Cu₂O) ≈ rhombododecahedral (r-Cu₂O) > octahedral (o-Cu₂O) > cubic (c-Cu₂O) > spherical (s-Cu₂O) (Fig. 5b). Interestingly, the conversion of TMB using co-Cu₂O and r-Cu₂O was found to be comparable at 30 min. However, their induction time differed. The high reactivity of r-Cu₂O may be attributed to the presence of a higher number of dangling copper sites on the {110} facet that gives rise to the high metal density and, thereby, high surface energy.^59,60 Similar observation was found by Zhao and coworkers where the rhombododecahedral morphology of Fe₃O₄ with exposed high surface energy {110} facets showed a better catalytic activity towards TMB oxidation than the spherical morphology.⁶¹ Notably, the atomic constitutions of the facets may vary from compound to compound, but the surface reactivity depends exclusively on exposed planes and the corresponding surface energy. For example, the high energy surface is the {100} facet in the case of CeO₂ nanocubes. Therefore, CeO₂ nanocubes with exposed high surface energy {100} facets displayed higher peroxidase activity towards TMB oxidation than CeO₂ nanorods with exposed {110} facets.³¹ Furthermore, the higher reactivity of co-Cu₂O vs. c-Cu₂O may be attributed by comparing the relative reactivity of {111} and {100} facets in Cu₂O. Although both co-Cu₂O and c-Cu₂O contain 6 {100} planes, co-Cu₂O has additional 8 {111} planes. Likewise, the surface energy of the {111} facet being greater than that of {100} facet, the reactivity of o-Cu₂O was found to be greater than that of c-Cu₂O or other morphologies. The overall conversion measured at t = 30 min shows that the relative conversion with respect to a blank (without catalyst) increased up to 5, 10, 13, and 14 fold for s-Cu₂O, c-Cu₂O, o-Cu₂O, and r-Cu₂O. These results also depict the role and difference of various Cu₂O facets in peroxidase-like activity.

Furthermore, the peroxidase-like activity of Cu₂O surfaces was also investigated using 2,2′-azino-bis(3-ethylbenzothiazoline-6-sulfonic acid) diammonium salt (ABTS) as a chromogenic peroxidase assay to test the substrate versatility of the catalyst. Catalytic oxidation of the ABTS substrate in the presence of H₂O₂ generates a green coloured radical cation complex (ABTS_ox) at λ_max of 420 nm (ε_420nm = 36 000 M⁻¹ cm⁻¹, Scheme 2). Indeed, Cu₂O crystals were also found to catalyse the oxidation of ABTS, evident from the evolution of the 420 nm band (Fig. 6a).

Scheme 2 Oxidation of ABTS catalysed by Cu₂O in the presence of H₂O₂.

Fig. 6 (a) Evolution of the absorbance of ABTS_ox at 420 nm catalysed by Cu₂O crystals in the presence of H₂O₂. (b) Different reaction systems viz., r-Cu₂O–ABTS, ABTS–H₂O₂ and r-Cu₂O–ABTS–H₂O₂.

In the case of ABTS as well, the conversion of the reaction for the r-Cu₂O–ABTS–H₂O₂ system was found to be much higher than ABTS–H₂O₂ (blank) and r-Cu₂O–ABTS systems with the latter showing no significant absorbance at 420 nm even after 30 min (Fig. 6b). In fact, the relative conversion with respect to a blank (ABTS–H₂O₂) was found to be increased up to 10 fold for the r-Cu₂O–TMB–H₂O₂ system.

Steady state kinetic studies

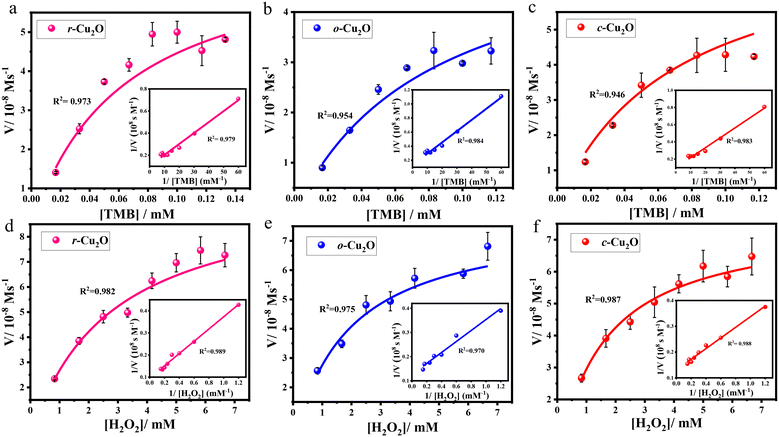
To test the reactivity of different surfaces of Cu₂O towards H₂O₂ reduction, specifically r-Cu₂O, o-Cu₂O, and c-Cu₂O, which contain unique {110}, {111}, and {100} facets, respectively, TMB as a chromogenic substrate was selected (Fig. S8–S11†). The measured initial rates vs. TMB/H₂O₂ concentrations are displayed in Fig. 7a–f; both followed a typical Michaelis–Menten behaviour in a suitable range of substrate concentrations. The kinetic parameters were calculated using the Lineweaver–Burk plots, which is a double reciprocal plot of the Michaelis–Menten equation: , where V is the initial velocity, V_max is the maximal reaction velocity, [S] is the substrate concentration, and K_m is the Michaelis constant.⁶² These parameters obtained for the different Cu₂O surfaces are highlighted in Table 1.

Fig. 7 Steady-state kinetics of r-Cu₂O (pink), o-Cu₂O (blue) and c-Cu₂O (red); 33 μg mL⁻¹ in 3 mL of 0.2 M acetate buffer (pH = 4.0) (a–c) Michaelis–Menten kinetics for the variation of the TMB concentration with a fixed H₂O₂ concentration of 0.833 mM. Inset: double reciprocal plots for affinity activity of different Cu₂O towards TMB with fixed H₂O₂ concentration. (d–f) Michaelis–Menten kinetics for the variation of the H₂O₂ concentration with a fixed TMB concentration of 0.05 mM. Inset: double reciprocal plots for affinity activity of different Cu₂O towards H₂O₂ with a fixed TMB concentration.

Table 1 Comparison of the kinetic parameters obtained for different facets of Cu₂O with HRP and commercial Cu₂O

Sl. no.	Catalyst	K m/mM		V max/10^−8 M s^−1		Ref.
		vs. TMB	vs. H2O2	vs. TMB	vs. H2O2
1	r-Cu2O {110}	0.096 ± 0.004	2.898 ± 0.060	9.64 ± 0.93	10.45 ± 0.64	This work
2	o-Cu2O {111}	0.120 ± 0.015	1.800 ± 0.001	7.51 ± 1.36	7.93 ± 0.57	This work
3	c-Cu2O {100}	0.115 ± 0.012	1.570 ± 0.012	9.95 ± 1.75	7.63 ± 0.26	This work
4	HRP	0.434	3.70	10.00	8.71	18
5	Commercial-Cu2O	—	44.4	—	4.83	22

---

The K_m values for r-Cu₂O (0.096 mM), o-Cu₂O (0.120 mM), and c-Cu₂O (0.115 mM) with TMB as a substrate were found to be 4.5, 3.6, and 3.8 times, respectively, lower than that for the natural enzyme HRP (0.434 mM) (Table 1, entries 1–3 vs. TMB). This clearly indicates that the affinity of TMB for all Cu₂O surfaces is far greater than that for native HRP. Further, r-Cu₂O exhibited the highest affinity towards TMB, as reflected in a substantially low K_m of 0.096 mM. This implies that a lower concentration of TMB is required to obtain the maximum reaction velocity for these Cu₂O catalysts over HRP.⁶² Under various H₂O₂ concentrations, the calculated K_m values for r-Cu₂O (2.898 mM), o-Cu₂O (1.800 mM), and c-Cu₂O (1.570 mM) were also found to be lower than that for the natural enzyme HRP (3.70 mM) which indicates the greater affinity of H₂O₂ for Cu₂O surfaces over the latter (Table 1, entries1–3 vs. H₂O₂).¹⁸ The role of the exposed facets may be highlighted here, wherein a recent study reported a high K_m value of 44.4 mM for commercially available Cu₂O nanoparticles with H₂O₂ as a substrate.²² Interestingly, c-Cu₂O was found to possess the highest affinity towards H₂O₂, followed by o-Cu₂O and then r-Cu₂O. This clearly reveals that for r-Cu₂O, a higher concentration of H₂O₂ is required to attain the maximum reaction velocity compared to c-Cu₂O. Precisely, the V_max values for r-Cu₂O were found to be 1.4 and 1.3 times greater than those for c-Cu₂O and o-Cu₂O, respectively. Incidentally, a higher substrate-to-product conversion was observed for r-Cu₂O (10.45 ± 0.64 × 10⁻⁸ M s⁻¹), which is higher than that for the native enzyme HRP (8.71 × 10⁻⁸ M s⁻¹).¹⁸

Mechanistic & DFT studies

Here, we conducted DFT calculations to investigate the potential energy diagram of TMB oxidation by H₂O₂ on various Cu₂O surfaces. All the optimized minima and transition states are shown in Fig. S14† (see the ESI† for details). The optimized {100}, {110}, and {111} exposed surfaces (IS), as displayed in Fig. 4, were used to calculate the potential energy diagram, as illustrated in Fig. 8. Here, the unsaturated dangling Cu sites play a crucial role in the O–O bond cleavage on the surface. These sites attract, adsorb, and dissociate H₂O₂, which distinguishes them from saturated Cu in the bulk with an oxidation number of +1. According to Bader charge analysis, these dangling Cu sites carry a positive charge of approximately +0.3 |e|. The total charge brought by dangling Cu per unit area is calculated as +2.85, +2.30, and +1.03 |e| per nm² for {100}, {110}, and {111} facets, respectively, with detailed surface properties in Table S1.† Consequently, the interaction strength of the long-range H₂O₂–Cu interaction can be estimated by comparing the electrostatic interaction between oxygen atoms from H₂O₂ and dangling Cu on the surface, following this order: {100} > {110} > {111}. This suggests that the {100} facet is the most attractive to H₂O₂ molecules near the surface, followed by {110} and then {111} facets. For the surface reaction, initially, the H₂O₂ molecule is adsorbed on the Cu₂O surface (IM1) and forms bonds with Cu_CUS (CUS: coordinatively unsaturated sites). The calculated adsorption energies are −0.43, −1.45, and −0.91 eV on {100}, {110}, and {111} surfaces, respectively. This is consistent with the observed variation in the induction time (Fig. 5b). The activation of the O–O bond in leads to subsequent dissociative adsorption. The energy barriers of the O–O bond cleavage (TS1) are 0.06, 0.15, and 0.25 eV on {100}, {110}, and {111} surfaces, respectively. The vibrational mode of imaginary frequency related to O–O bond breaking is shown in Fig. S15.† O–O bond dissociation occurs almost barrierless on the {100} surface, making it the most favorable facet for forming OH˙ radicals after H₂O₂ adsorption, followed by the {110} surface, and then the {111} surface. The formation of OH˙ radicals was established by performing the reaction with terephthalic acid (TA) in place of TMB. TA is generally used as a fluorescent probe for the detection of free hydroxyl radicals, which can generate highly fluorescent 2-hydroxyterephthalic acid upon reacting with OH radicals.^22,25,63 Indeed, when the reaction was performed in the presence of TA, H₂O₂, and Cu₂O, a strong fluorescence peak at 420 nm for 2-hydroxyterephthalic acid was observed, while a very weak fluorescence emission was detected in the absence of either H₂O₂ or Cu₂O (Fig. S13a†). Further, on increasing the concentration of H₂O₂ (Fig. S13b†), there was a significant increase in the intensity of the fluorescence peak, clearly indicating the formation of hydroxyl radical intermediates during the peroxidase-like catalytic reaction.^22,25,63

Fig. 8 The potential energy profile for TMB oxidation by H₂O₂ on Cu₂O surfaces. Red, pink, and blue colors correspond to the Cu₂O {100}, {110}, and {111} exposed facets, respectively. IS: initial state; IM: intermediate state; TS: transition state; FS: final state.

After H₂O₂ dissociation, each OH˙ radical is adsorbed on the Cu_CUS top side on {110} and {111} surfaces, while on the {100} surface, each OH˙ is adsorbed on the bridge side between two Cu_CUS (IM2). The H₂O₂ dissociation is highly exothermic, especially on the {100} surface, due to the strong O–Cu interactions resulting from the bridge site adsorption configuration. The TMB molecule was adsorbed on the Cu₂O surface in the presence of two OH˙ radicals, and a TMB molecule interacted with two OH˙ radicals via N–H⋯O hydrogen bonds between the amine group (–NH₂) of TMB and the oxygen of OH (IM3). The calculated adsorption energies are −0.66, −0.73, and −0.77 eV on {100}, {110}, and {111} surfaces, respectively. The TMB adsorption energies on {110} and {111} are comparable since the interactions between TMB and two OH˙ radicals are similar on both surfaces. However, the TMB adsorption energy on {100} is slightly smaller than that on other facets, attributed to the strongest O–Cu interactions between OH˙ and the surface, thereby weakening the hydrogen bonds between OH˙ and TMB. In the redox reactions, one OH˙ radical attracts a hydrogen radical from the amine group of TMB (TS2), forming an adsorbed water, H₂O*, and an oxidized TMB radical (FS), TMB_ox. The vibrational mode of imaginary frequency associated with H radical transfer is shown in Fig. S15.† The energy barrier of OH˙ attack is 1.51, 0.70, and 0.42 eV on {100}, {110}, and {111} surfaces, respectively. The extremely high energy barrier of 1.51 eV when OH˙ attracted one H atom from the TMB molecule on the {100} facet renders it less active in oxidizing the TMB molecule. This result is also attributed to the strongest O–Cu interactions. On the other hand, {110} and {111} surfaces exhibit moderate energy barriers in this step, which can be overcome by thermal energy at room temperature.

Discussion

The above experimental and theoretical data reveal that the catalytic oxidation of TMB in the presence of H₂O₂ proceeds via the initial adsorption of H₂O₂ over the Cu₂O facet (intermediate II in Fig. 9a).⁴⁵ At a lower substrate concentrations, the initial phase of the reaction displays a sluggish evolution of the absorbance peak at 652 nm for TMB_ox (Fig. 9b–c). This can be attributed to the adsorption of the substrate on the surface of the catalyst. With the increase in the concentration of H₂O₂, the active surface on the exposed facets of Cu₂O becomes increasingly saturated with H₂O₂. After complete saturation of the surface, the catalytic conversion of TMB to TMB_ox is highly favoured, as evident from the steeper slope of the initial phase of the reaction at a higher substrate concentration. Hence, at a higher substrate concentration, there is a drastic increase in the rate of the reaction.

Fig. 9 (a) Plausible mechanism for the oxidation of TMB using the Cu₂O catalyst in the presence of H₂O₂. Time dependent evolution of absorbance at 652 nm for TMB_ox catalysed by r-Cu₂O: (b) in the presence of different concentrations of TMB with a fixed H₂O₂ concentration of 1.67 mM and (c) in the presence of different concentrations of H₂O₂ with a fixed TMB concentration of 0.05 mM.

The dissociative adsorption of H₂O₂ over the Cu₂O facet occurs through the formation of hydroxyl radical (intermediate III, Fig. 9a).^22,64 DFT calculations add that the transition state involved in homolytic O–O cleavage over all the Cu₂O surfaces is kinetically favourable (<0.25 eV) and thermodynamically exothermic. Furthermore, relatively barrierless TS1 and the lower reactivity of the {100} surface clearly indicate the non-involvement of this process in the rate-determining step. The reduction of H₂O₂ then proceeds via the protonation-coupled hydrogen transfer from the amino group of TMB to the adsorbed hydroxyl radical, thereby facilitating the liberation of one equivalent of TMB_ox and H₂O (intermediate IV, Fig. 9a).⁴⁵ This proton-coupled H-transfer step invokes a transition state TS2 that reflects an endothermic IM3 to FS pathway in favour of r-Cu₂O ({110} facet) with a relatively lower energy barrier (0.70 eV) than that of {100} containing c-Cu₂O (1.51 eV). The lower reactivity of c-Cu₂O, lower K_m values (vs. TMB), and the observation of TMB-dependent reactivity (under limiting H₂O₂ conditions) indicates TS2 to be the rate-determining step. The reduction of the second adsorbed hydroxyl radical consequently liberates another equivalent of TMB_ox and H₂O with the recovery of the Cu₂O facet at the end of the catalytic cycle (intermediates V and VI, Fig. 9a).

Overall, the entire reactions on different Cu₂O facets are thermodynamically favorable (driving force: FS–IS = −6.18 eV, −4.37 eV and −5.36 eV for c-Cu₂O, o-Cu₂O and r-Cu₂O, respectively, Table S2†), driven largely by H₂O₂ adsorption and dissociation. Among these facets, the {100} facet exhibits the highest ability to activate the O–O bond and stabilize OH˙ radicals, while the {111} facet is the least effective. The strong O–Cu interaction between surface Cu and OH˙ leads to a high barrier for hydrogen radical transfer from TMB to OH˙, effectively suppressing the oxidation of TMB by OH˙ radicals. Furthermore, comparing the computational results from DFT calculations with measurements from the evolution of the absorbance peak, both support the conclusion that the {100} facet exhibits the lowest oxidative activity among the three facets. However, experimental observations show that {110} shows higher oxidative activity than {111}, despite the computational study indicating that {110} has a higher energy barrier in the rate-determining step (0.70 eV) compared to {111} (0.42 eV). To clarify this seemingly contradictory observation, we calculate the amount of active Cu_CUS atoms on each facet. The concentration of Cu_CUS is 10.95, 7.74, and 3.16 atoms per nm² on {100}, {110}, and {111} facets, respectively. The {110} surface has ∼2.5 times more Cu_CUS atoms than the {111} surface, which is the crucial factor that causes the {110} facet to exhibit the highest oxidative activity in dissociating H₂O₂ and producing active OH˙ radicals. Interestingly, we observed that co-Cu₂O exhibits a higher TMB conversion rate than r-Cu₂O after 20 min in absorbance evolution measurement. This strongly suggests the coexistence of {100} and {111} facets with a synergistic effect in oxidizing TMB. While modeling polycrystalline surfaces and investigating reactions between two facets remain a challenge, the experimental results suggest a cooperative effect between the two facets in co-Cu₂O crystals. In Fig. 5b, there is a rapid increase in absorbance intensity on co-Cu₂O around 9 minutes, indicating an accelerated production of TMB_ox. Since the energy barrier for TMB oxidation on {100} is significantly higher than that on {111} (1.51 eV vs. 0.42 eV), the initial overall production rate of TMB_ox on co-Cu₂O is primarily attributed to the ongoing reactions on the {111} surface. Additionally, {100} exhibits a lower activation energy (0.06 eV) for dissociation compared to {111} (0.25 eV). Consequently, the initial OH˙ generation rate on the {100} facet is higher than that on the {111} facets, leading to a more rapid increase in OH˙ concentration on the {100} facets compared to {111}. Moreover, due to the high energy barrier, the initial consumption rate of OH˙ on the {100} facet is slower than that on {111}, resulting in an accumulation of OH˙ on the {100} facet. To make an estimate of the amount of accumulated OH˙ radicals, we calculated the migration barriers of OH˙ on {100} and {111} facets, respectively, and consistently found both to be 1.19 eV (Fig. 10).

Fig. 10 a) The schematic illustration of the OH˙ migration pathway on Cu₂O {100} and {111} facets. b) The optimized configurations of the transition state of OH˙ migration on Cu₂O {100} and {111} facets. The arrows in the figures represent the vibrational modes.

It is noted that the OH˙ migration rate on each facet is dependent on the concentration of OH˙ and the concentration of active sites on the other facet. Notably, this energy barrier is lower than the energy barrier for the rate-determining step of TMB oxidation on the {100} surface, which stands at 1.51 eV. This result strongly suggests that OH˙ radicals can migrate between any two unsaturated dangling Cu sites on both {100} and {111} facets, enabling them to move towards the edge of the facet. Since the empty active sites on {100} are significantly occupied by OH˙ compared to {111}, migration from {100} to {111} is more favorable than from {111} to {100}. Ultimately, OH˙ migration from {100} to {111} increases the OH˙ concentration on {111} and converts TMB to TMB_ox efficiently. This OH˙ migration mechanism explains the accelerated production of TMB_ox around 9 minutes and the “absorbance crossover” with co-Cu₂O and r-Cu₂O around 20 minutes (Fig. S12†).

Conclusions

In this study, we examined different Cu₂O morphologies, namely r-Cu₂O, co-Cu₂O, o-Cu₂O, c-Cu₂O, and s-Cu₂O, which exhibit variations in exposed facets, for their peroxidase-like activity using TMB as a substrate. The reactivity of different Cu₂O morphologies as peroxidase mimics can be ranked as follows: co-Cu₂O ≈ r-Cu₂O > o-Cu₂O > s-Cu₂O > c-Cu₂O. This trend aligns with DFT calculations, where r-Cu₂O, o-Cu₂O, and c-Cu₂O primarily consist of {110}, {111}, and {100} facets, respectively, and the variations in reactivity are due to differences in exposed facet reactivity, with {110} > {111} > {100}.

These Cu₂O surfaces exhibit enzyme-like properties within a suitable range of substrate concentrations, with K_m values (for r-Cu₂O, o-Cu₂O, and c-Cu₂O) with both TMB and H₂O₂ as substrates being lower than those for the native enzyme (HRP). In fact, the conversion rate from the substrate to product for r-Cu₂O (10.45 ± 0.64 × 10⁻⁸ M s⁻¹) exceeded that for HRP (8.71 × 10⁻⁸ M s⁻¹). The mechanism of TMB oxidation in the presence of H₂O₂ involves the generation of hydroxyl radicals. Cu₂O plays a crucial role in activating H₂O₂ through adsorption on exposed facets, followed by the homolytic cleavage of H₂O₂. This leads to hydroxyl radical generation, a critical step in the TMB oxidation, followed by the rate-determining H-abstraction pathway. Our computational results revealed that the energy barrier for the rate-determining step of TMB oxidation on {100} facets is exceptionally high at 1.51 eV, resulting in the lowest TMB_ox production rate on the c-Cu₂O surface. In contrast, the {111} facet exhibits the smallest energy barrier of 0.42 eV for the rate-determining step, followed by the {110} facet (0.70 eV). However, the {110} facet has a higher surface Cu_CUS concentration of 7.74 atoms per nm² compared to the {111} facet (3.16 atoms per nm²), resulting in more active sites for H₂O₂ adsorption and dissociation. This leads to a higher TMB_ox production rate on the {110} facet than on the {111} facet.

Additionally, Cu₂O catalysts with specifically exposed facets outperformed commercially available Cu₂O, with significantly lower K_m values for H₂O₂ as the substrate (2.9 vs. 44.4 mM). This underscores the excellent substrate affinity of catalysts with singularly exposed facets. These findings offer insights into the facet-dependent enzymatic transformations, potentially paving the way for the future development of artificial enzymes.

Author contributions

AP and ST designed the project. SC, SR, BG and DS performed all experimental work and analyzed the data. LTW and JCJ performed the DFT calculations and analyzed the computational data. AP, JCJ, ST, RD, LTW and SC compiled, reviewed and completed the final manuscript. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

AP and ST would like to thank SERB-DST (EEQ/2016/000685), SERB-DST (EEQ/2016/000751), DST-INSPIRE (DST/INSPIRE/04/2015/002674) and SERB-DST, (EMR/2016/002505), Govt. of India for financial support. The computational work has been financially supported by the National Science and Technology Council, Taiwan (NSTC 110-2113-M-011-002-MY3). LTW and JCJ thank the Taiwan National Center of High-Performance Computing (NCHC) for computing resources. SC would like to acknowledge Sikkim University for the fellowship. We would like to thank Dr M. U. Sreekuttan, CECRI Madras Unit, CSIR-Chennai for the XPS.

Notes and references

1. M. Khajehpour, I. Rietveld, S. Vinogradov, N. V. Prabhu, K. A. Sharp and J. M. Vanderkooi, Proteins: Struct., Funct., Genet., 2003, 53, 656–666.
2. N. Mogharrab, H. Ghourchian and M. Amininasab, Biophys. J., 2007, 92, 1192–1203.
3. G. L. Kedderis and P. F. Hollenberg, J. Biol. Chem., 1983, 258, 8129–8138.
4. H. Kwon, J. Basran, C. M. Casadei, A. J. Fielding, T. E. Schrader, A. Ostermann, J. M. Devos, P. Aller, M. P. Blakeley, P. C. E. Moody and E. L. Raven, Nat. Commun., 2016, 7, 1–6.
5. M. Kathiresan and A. M. English, Chem. Sci., 2017, 8, 1152–1162.
6. G. I. Berglund, G. H. Carlsson, A. T. Smith, H. Szöke, A. Henriksen and J. Hajdu, Nature, 2002, 417, 463–468.
7. M. Ozboyaci, D. B. Kokh, S. Corni and R. C. Wade, Q. Rev. Biophys., 2016, 49, 1–45.
8. A. V. Gribenko, M. M. Patel, J. Liu, S. A. McCallum, C. Wang and G. I. Makhatadze, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 2601–2606.
9. M. D. Mager, V. Lapointe and M. M. Stevens, Nat. Chem., 2011, 3, 582–589.
10. Y. Nosaka and A. Y. Nosaka, Chem. Rev., 2017, 117, 11302–11336.
11. A. Kessler, J. Hedberg, E. Blomberg and I. Odnevall, Nanomaterials, 2022, 12, 1–24.
12. S. Lin, W. Tan, P. Han, X. Li, J. Li, Z. Nie and K. Li, Nano Res., 2022, 15, 9073–9081.
13. H. Zhao, Y. Dong, P. Jiang, G. Wang and J. Zhang, ACS Appl. Mater. Interfaces, 2015, 7, 6451–6461.
14. R. André, F. Natálio, M. Humanes, J. Leppin, K. Heinze, R. Wever, H. C. Schröder, W. E. G. Müller and W. Tremel, Adv. Funct. Mater., 2011, 21, 501–509.
15. L. Han, J. Shi, A. Liu and A. Liu, Sens. Actuators, B, 2017, 252, 919–926.
16. Y. S. Mingyun Zhu, Y. Dai, Y. Wu, K. Liu and X. Qi, Nanotechnology, 2018, 29, 0–31.
17. M. K. Masud, J. Kim, M. M. Billah, K. Wood, M. J. A. Shiddiky, N. T. Nguyen, R. K. Parsapur, Y. V. Kaneti, A. A. Alshehri, Y. G. Alghamidi, K. A. Alzahrani, M. Adharvanachari, P. Selvam, M. S. A. Hossain and Y. Yamauchi, J. Mater. Chem. B, 2019, 7, 5412–5422.
18. L. Gao, J. Zhuang, L. Nie, J. Zhang, Y. Zhang, N. Gu, T. Wang, J. Feng, D. Yang, S. Perrett and X. Yan, Nat. Nanotechnol., 2007, 2, 577–583.
19. J. Mu, Y. Wang, M. Zhao and L. Zhang, Chem. Commun., 2012, 48, 2540–2542.
20. J. Mu, L. Zhang, G. Zhao and Y. Wang, Phys. Chem. Chem. Phys., 2014, 16, 15709–15716.
21. C. Ray, S. Dutta, S. Sarkar, R. Sahoo, A. Roy and T. Pal, J. Mater. Chem. B, 2014, 2, 6097–6105.
22. B. Yuan, H. L. Chou and Y. K. Peng, ACS Appl. Mater. Interfaces, 2022, 14, 22728–22736.
23. W. Chen, J. Chen, A. L. Liu, L. M. Wang, G. W. Li and X. H. Lin, ChemCatChem, 2011, 3, 1151–1154.
24. X. Wang, Q. Han, S. Cai, T. Wang, C. Qi, R. Yang and C. Wang, Analyst, 2017, 142, 2500–2506.
25. A. P. Nagvenkar and A. Gedanken, ACS Appl. Mater. Interfaces, 2016, 8, 22301–22308.
26. A. Chakraborty, D. A. Islam and H. Acharya, Mater. Res. Bull., 2019, 120, 110592.
27. A. Hayat, W. Haider, Y. Raza and J. L. Marty, Talanta, 2015, 143, 157–161.
28. H. Li, H. Sun, J. Ding, T. Wu, S. Cai, C. Wang and R. Yang, Microchim. Acta, 2022, 189, 1–10.
29. K. Sobańska, P. Pietrzyk and Z. Sojka, ACS Catal., 2017, 7, 2935–2947.
30. X. Xiao, Q. Luan, X. Yao and K. Zhou, Biosens. Bioelectron., 2009, 24, 2447–2451.
31. Y. Yang, Z. Mao, W. Huang, L. Liu, J. Li, J. Li and Q. Wu, Sci. Rep., 2016, 6, 1–7.
32. Z. Tian, J. Li, Z. Zhang, W. Gao, X. Zhou and Y. Qu, Biomaterials, 2015, 59, 116–124.
33. Y. H. Won and L. A. Stanciu, Sensors, 2012, 12, 13019–13033.
34. Z. G. Liu, Y. F. Sun, W. K. Chen, Y. Kong, Z. Jin, X. Chen, X. Zheng, J. H. Liu, X. J. Huang and S. H. Yu, Small, 2015, 11, 2493–2498.
35. Y. Jiang, T. Xia, L. Shen, J. Ma, H. Ma, T. Sun, F. Lv and N. Zhu, ACS Catal., 2021, 11, 2949–2955.
36. Q. Ma, J. Young, S. Basuray, G. Cheng, J. Gao, N. Yao and W. Zhang, Nano Today, 2022, 101538, 1–9.
37. C. S. Tan, S. C. Hsu, W. H. Ke, L. J. Chen and M. H. Huang, Nano Lett., 2015, 15, 2155–2160.
38. B. Liu, X. Yao, Z. Zhang, C. Li, J. Zhang, P. Wang, J. Zhao, Y. Guo, J. Sun and C. Zhao, ACS Appl. Mater. Interfaces, 2021, 13, 39165–39177.
39. W. C. Huang, L. M. Lyu, Y. C. Yang and M. H. Huang, J. Am. Chem. Soc., 2012, 134, 1261–1267.
40. G. Z. Yuan, C. F. Hsia, Z. W. Lin, C. Chiang, Y. W. Chiang and M. H. Huang, Chem. – Eur. J., 2016, 22, 12548–12556.
41. C. Y. Chu and M. H. Huang, J. Mater. Chem. A, 2017, 5, 15116–15123.
42. Y. A. Wu, I. McNulty, C. Liu, K. C. Lau, Q. Liu, A. P. Paulikas, C. J. Sun, Z. Cai, J. R. Guest, Y. Ren, V. Stamenkovic, L. A. Curtiss, Y. Liu and T. Rajh, Nat. Energy, 2019, 4, 957–968.
43. H. E. Rudel, M. K. M. Lane, C. L. Muhich and J. B. Zimmerman, ACS Nano, 2020, 14, 16472–16501.
44. Y. Zhong, Y. Li, S. Li, S. Feng and Y. Zhang, RSC Adv., 2014, 4, 40638–40642.
45. X. Shen, Z. Wang, X. Gao and Y. Zhao, ACS Catal., 2020, 10, 12657–12665.
46. X. Wang, M. Chen, Y. He and J. Zhu, J. Alloys Compd., 2014, 628, 50–56.
47. D. F. Zhang, H. Zhang, L. Guo, K. Zheng, X. D. Han and Z. Zhang, J. Mater. Chem., 2009, 19, 5220–5225.
48. Y. Shang and L. Guo, Adv. Sci., 2015, 2, 1500140.
49. R. Li, X. Zhang, H. Dong, Q. Li, Z. Shuai and W. Hu, Adv. Mater., 2016, 28, 1697–1702.
50. D. Guo, L. Wang, Y. Du, Z. Ma and L. Shen, Mater. Lett., 2015, 160, 541–543.
51. Y. Sui, W. Fu, H. Yang, Y. Zeng, Y. Zhang, Q. Zhao, Y. Li, X. Zhou, Y. Leng, M. Li and G. Zou, Cryst. Growth Des., 2010, 10, 99–108.
52. M. C. Biesinger, Surf. Interface Anal., 2017, 49, 1325–1334; C. Wang, H. Tissot, C. Escudero, V. P. Dieste, D. J. Stacchiola and J. Weissenrieder, J. Phys. Chem. C, 2018, 122, 28684–28691.
53. J. Y. Ho and M. H. Huang, J. Phys. Chem. C, 2009, 113, 14159–14164.
54. Y. Su, H. Li, H. Ma, J. Robertson and A. Nathan, ACS Appl. Mater. Interfaces, 2017, 9, 8100–8106.
55. P. D. Josephy, T. Eling and R. P. Mason, J. Biol. Chem., 1982, 257, 3669–3675.
56. M. Drozd, M. Pietrzak, P. G. Parzuchowski and E. Malinowska, Anal. Bioanal. Chem., 2016, 408, 8505–8513.
57. A. Dalui, B. Pradhan, U. Thupakula, A. H. Khan, G. S. Kumar, T. Ghosh, B. Satpati and S. Acharya, Nanoscale, 2015, 7, 9062–9074.
58. A. Pariyar, S. Gopalakrishnan, J. Stansbery, R. L. Patel, X. Liang, N. Gerasimchuk and A. Choudhury, RSC Adv., 2016, 6, 38533–38540.
59. W. Huang, Acc. Chem. Res., 2016, 49, 520–527.
60. J. Paier, C. Penschke and J. Sauer, Chem. Rev., 2013, 113, 3949–3985.
61. X. L. Cheng, J. Sen Jiang, D. M. Jiang and Z. J. Zhao, J. Phys. Chem. C, 2014, 118, 12588–12598.
62. W. Chen, S. Li, J. Wang, K. Sun and Y. Si, Nanoscale, 2019, 11, 15783–15793.
63. S. Kulandaivel, C. H. Lin and Y. C. Yeh, Chem. Commun., 2022, 58, 569–572.
64. H. Wang, X. Ren, Z. Liu and B. Lv, Chem. Commun., 2022, 58, 908–924.

---

Footnotes

† Electronic supplementary information (ESI) available: All experimental details, synthesis of different Cu₂O crystals, spectral data, SEM images and computational details are included. See DOI: https://doi.org/10.1039/d3cy01399e

‡ First authors contributed equally to this work.

---