Solvation effects in the electrochemical reduction of hydrogen cyanide for ambient ammonia production on a Ni cathode

Abstract

The large-scale production of ammonia via the Haber–Bosch process is an integral part of maintaining global populations, yet it is dependent on the harsh reaction conditions and hydrogen sourced via steam reforming. The electrochemical reduction of hydrogen cyanide (HCNRR), a fixed form of nitrogen, has shown itself to be a promising route for ammonia synthesis at ambient conditions, offering a path to contribute to a circular nitrogen economy. While the HCNRR is still an understudied area of catalysis, few experimental reports have identified nickel as a promising catalyst, outperforming precious metals such as platinum. On a Ni cathode, two sets of HCNRR products have been observed, namely methylamine (major product) and ammonia/methane (minor products). Recent computational studies have rationalized this product distribution with the desorption of methylamine and hinted on the electrolyte playing a role in the selectivity towards ammonia production. Herein, we investigate the HCNRR mechanism on a Ni cathode using different solvation models in a bid to account for the influence of the electrolyte. Our findings reveal that the presence of an explicit solvent environment has indeed a drastic effect on the HCNRR, resulting in different binding modes and an unexpected metastable intermediate which ultimately leads to a different potential limiting step. These results highlight the necessity of including explicit solvent molecules for the effective modelling of physisorbed intermediates in the HCNRR process, although it may also be generalizable to other important electrochemical processes.

---

Introduction

Catalysis has served as the bedrock of most, if not all, of the luxuries available in modern society. Yet most catalytic processes rely on fossil fuels, and therefore are not sustainable. In light of the current climate crisis, it is evident that a shift to more renewable technologies is demanded, which has urged many studies on the electrocatalytic conversion of abundant constituents in the Earth's atmosphere (e.g. H₂O, CO₂, N₂) into chemical fuels and feedstocks (e.g. H₂, C_xH_y, C_xH_yO_z, and NH₃).^1,2 Although great strides have been made in this field of research, there are still many hurdles which need to be overcome.³

One of the main obstacles to the fundamental understanding of electrocatalytic processes is the accurate description of the solid–liquid interface.⁴ From a computational perspective, there are two main approaches to address this issue, namely via explicit and implicit solvation models. The former describes the electrolyte by the direct inclusion of solvent molecules in the calculation, although there are several variants within the umbrella term of explicit solvation. For example, there are reports of systems modelled with a discrete number of water molecules,^5–7 an ice-like water layer,^8,9 or with the simulation cell completely filled with water molecules.¹⁰ Regardless of the method adopted, the description of the electrolyte via explicit models is further complicated by the fact that the solid–liquid interface is dynamic; in other words, a vast number of configurations of the interface can exist. The need to capture this dynamic behavior and account for the ensemble of configurations has engendered the use of ab initio molecular dynamics (AIMD), which have shown the structure of water near the metal surface at room temperature to be quite disordered.^11,12 While this explicit description of the electrode–electrolyte interface would theoretically provide a more accurate description of the properties of and interactions between both phases, there is the added caveat of increased computational expense.¹³ For this reason, the ice-like water layer (also referred to as a water bilayer) has become a very popular model in density functional theory (DFT) studies to approximate the aqueous electrolyte and assess the thermodynamics and kinetics of electrochemical processes.^8,14–19

On the other hand, implicit solvation models serve to describe the electrolyte by encapsulating the solute in a continuum medium characterized by the dielectric constant of the bulk solvent.²⁰ Within this approach, the solvation energy is determined by the position of the solute without any explicit solvent molecules, thus significantly reducing the computational cost. However, implicit models do have some shortcomings, the most glaring of which is the neglect of site-specific interactions between the solute and solvent, such as hydrogen bonding.²¹ Furthermore, the approach whereby the solute cavity is defined can vary wildly between methods and software packages. For example, some methods mimic the solvent environment by placing Gaussian distributed plane charges within a short distance from the surface,²² while others apply a homogeneous background charge over the entire system.²³ The Poisson–Boltzmann description of the solid–liquid interface has also become increasingly popular,^13,24,25 and it has been applied to the modelling of a number of electrochemical processes, including the hydrogen evolution reaction and CO₂ electroreduction.^26–31

Hybrid solvation, or microsolvation models, serve as a compromise between purely implicit and explicit approaches. These methods involve pairing a dielectric continuum with a much smaller number of explicit solvent molecules with the intent to account for the bulk electrolyte, as well as site specific interactions, with a reduced computational cost. However, choosing the number of explicit solvent molecules that must be included has always been a matter of contention with this approach. Calle-Vallejo et al.³² developed a novel and systematic method for the determination of the number of explicit molecules by comparing adsorbate–solvent and solvent–solvent interactions. Giordano and Di Liberto³³ found that the inclusion of three explicit water molecules reported solvation energies close to that of the water bilayer model. Nevertheless, it should be noted that the addition of a discrete number of solvent molecules around an adsorbate is expected to be accompanied by an entropy penalty, which is often neglected in microsolvation methods.³⁴

The influence of the solvent has also been investigated in the electrochemical reduction of dinitrogen (N₂RR),^17,18 a process that holds promise as a greener alternative to the Haber–Bosch process for ammonia production, which currently consumes ca. 3–5% of global natural gas production and is directly responsible for over 450 Mt of CO₂ emissions per year.^35,36 However, the N₂RR is not without its challenges, specifically the activation of dinitrogen and the competition with the hydrogen evolution reaction. One promising strategy to circumvent the arduous activation of N₂, while contributing to the equilibrium of the nitrogen cycle, could be the electroreduction of fixed nitrogen sources such as NO_x and cyanide species.

Besides serving as a source of fixed nitrogen, cyanide is found in both nature and industry.^37,38 Furthermore, the electrochemical reduction of cyanide (HCNRR) offers a sustainable synthetic route towards the production of not only ammonia but methane as well.

HCN + 6H⁺ + 6e⁻ → CH₄ + NH₃ E° = +0.331 V_RHE (1)

Being a polar molecule, cyanide is also much more amenable to activation, rendering this fixed form of nitrogen particularly desirable. Notwithstanding these advantages, the literature is surprisingly devoid of studies with a focus on the HCNRR. One of the few experimental reports on this process is that by Fedurco et al.³⁹ who revealed that Ni drastically outperforms expensive noble metals such as Pd or Pt, achieving a faradaic efficiency of 71.7%. This efficiency, however, was split towards methylamine (CH₃NH₂) as the major product and NH₃/CH₄ as minor products. In light of this, we recently reported a computational mechanistic study wherein we rationalized the predominance of CH₃NH₂ with the desorption of this species from the nickel cathode and posited that solvent effects may aid in stabilizing CH₃NH₂ on the surface.⁴⁰ Additionally, the presence of several physisorbed intermediates indicates that solvent interactions may be of great importance to the HCNRR.

Herein, we present a detailed computational investigation of the HCNRR mechanism in vacuum as well as in the presence of implicit and explicit solvent. With this, we intend to compare each method and ascertain whether the aqueous electrolyte plays a role in the stabilization of key intermediates and the overall reaction kinetics. Our findings reveal key differences between the two solvation models, particularly with the introduction of an explicit aqueous environment, wherein we observe drastic effects in the stabilization of physisorbed intermediates. These results have important implications on the overall HCNRR mechanism, concluding that implicit models may not be sufficient for a good description of surface reactivity.

Computational methods

Spin-polarized DFT calculations were performed via the Vienna ab initio simulation package (VASP, version 5.4.4)^41,42 using the Bayesian error estimation functional with van der Waals corrections.⁴³ Core electrons were described by means of projector augmented wave pseudopotentials,⁴⁴ while plane waves with a kinetic cutoff of 700 eV were used to represent the valence electrons.

The Ni cathode was modelled as a 4-layer Ni(111) slab of p(3 × 3) periodicity with a vacuum spacing of at least 15 Å between periodic images in the direction perpendicular to the surface. Dipole corrections along this direction were also included in surface slab calculations. Atoms in the bottom two layers of the slab were fixed to simulate the bulk metal, while atoms in the remaining top two layers, as well as any adsorbates, were allowed to fully relax.

A surface coverage of H atoms occupying all the fcc sites was taken to be the catalyst resting state under the experimental HCNRR conditions (i.e. pH 6), as we reported elsewhere.⁴⁰ Geometry optimizations were performed with a convergence criteria of 10⁻⁶ eV and 0.01 eV Å⁻¹ for the electronic and ionic steps, respectively. A smearing width of 0.2 eV was used within the first order Methfessel–Paxton method, while the Brillouin zone was sampled with a Γ-centered 5 × 5 × 1 k-point grid.

Vibrational frequencies for the adsorbate species were computed within the harmonic approximation, fixing all the metals, coverage atoms, and explicit water molecules to reduce computational cost. Further details regarding thermodynamic test calculations can be found in the ESI.† With this information, Gibbs energy corrections were computed using the thermochemistry module in the atomic simulation environment (ASE) package⁴⁵ at ambient conditions, i.e. 298 K and 1 atm. These corrections include zero-point vibrational energy, entropy, and heat capacity contributions. Further details can be found in Table S1.†

Proton-coupled electron transfer (PCET) steps in the HCNRR mechanisms were modelled via the computational hydrogen electrode model,¹⁴ and the Gibbs adsorption energies, ΔG_ads, were calculated as:

ΔG_ads = G_surf+ads − G_surf − G_ads (2)

where G_surf+ads denotes the Gibbs energy of the slab with the adsorbate species, G_surf the energy of the slab in the resting state (all fcc sites covered with H atoms), and G_ads the Gibbs energy of the isolated adsorbate.

The influence of the applied bias was accounted for as follows:

ΔG_ads,RHE = ΔG_ads + neU (3)

where U is the applied potential referenced to the reversible hydrogen electrode (V_RHE), e the elemental charge of an electron, and n is the number of electrons involved in a reaction step. The predicted limiting potentials predicted in this work are defined as the minimum applied bias required to make each elementary step thermoneutral or downhill in energy.

The relative energies presented in this work are calculated at 0 V_RHE with the intent that a reader may amend them to any applicable reaction conditions. To connect our results with experiments,³⁹ we also present in the ESI† (Fig. S7 and S8) the relative energies calculated in vacuum, implicit solvent, and explicit solvent phases at the experimental conditions of −0.8 V_SHE and pH 6. These energies have been calculated using eqn (3) and (4).

nU_RHE = n(U_SHE + 0.059pH) (4)

where 0.059 is the Nernst slope calculated at ambient conditions, and U_RHE and U_SHE are the applied potentials relative to the reversible and standard hydrogen reference electrodes, respectively.

For relevant reaction steps, transition state (TS) structures were located through the nudged elastic band (NEB)⁴⁶ and climbing image nudged elastic band (CI-NEB)⁴⁷ methods, using a total of 8 images along the reaction coordinate. The nature of these stationary points was confirmed through vibrational frequency analysis, displaying only one imaginary frequency related to the reaction coordinate of interest. Non-covalent interactions (NCIs) were calculated using the Critic2 software.^48,49 Critical points in the reduced density gradient were established between three fragments, namely the Ni slab, the adsorbed HCN intermediate, and the explicit water bilayer. These critical points can be either attractive or repulsive. For additional details on this type of analysis we refer the reader to the ESI.†

Implicit solvent calculations were performed with the VASPsol^13,25 software using a dielectric constant of 78.4 and a Debye length of 3.0 Å. Default parameters were used to construct the solute cavity. Explicit solvent calculations were carried out by inclusion of a H-down water bilayer composed of six H-bonded waters, wherein every second molecule had a H atom pointing down towards the surface (Fig. S1a†). The ice-like neutral water layer was optimized, followed by the addition of a H atom which led to a H₃O⁺ cation in the water layer and an electron localized in the surface slab (Fig. S1b†). This H₃O⁺ cation essentially ‘caps’ a lone pair of an O atom, preventing the formation of a H-bond and consequently leading to the distortion of the water bilayer. Additionally, we note that explicit water molecules were disrupted from their ice-like structure during geometry relaxations upon the introduction of the HCNRR intermediates in the simulation cell, as we discuss below. This water bilayer was protonated via the addition of an extra H atom, i.e. a proton and an electron. Bader charge and charge density difference analyses (Table S2 and Fig. S1†) confirmed the separation of the proton and electron into the solvent molecules and surface slab, respectively. The first PCET with explicit solvent was modelled with the protonated water bilayer to allow for kinetic studies. Subsequent steps were calculated by sourcing the H atom from the bulk electrolyte (not the water bilayer).

In contrast to the implicit solvation model, the explicit solvent does not account for ionic effects. To investigate the significance of these effects on the HCNRR in implicit solvent, our investigation is detailed in Table S4.† Our results indicate that ionic effects are negligible. Consequently, any disparity between these two solvent models cannot be attributed to the absence of ionic effects in the explicit solvent.

Results and discussion

In the experimental CNRR study performed by Fedurco et al.,³⁹ cyanide was introduced into the system in the form of NaCN (0.036 M) at pH 6. Under these conditions, and given the pK_a of cyanide in water (pK_a = 9.2),⁵⁰ the predominant species in aqueous solution is expected to be HCN; as such, this was the substrate chosen for our computational investigations.

Hence, we started by adsorbing the HCN molecule on a Ni(111) surface with H atoms occupying all the fcc sites, which is predicted to be the resting state under the experimental CNRR conditions.⁴⁰ In Fig. 1, we compare the adsorption of HCN in vacuum and in the presence of implicit solvent, observing a negligible difference in the optimized geometries. In both cases, HCN remains physisorbed on the Ni(111) surface through its triple bond of 1.158 Å. The most notable difference between the two geometries is the distance of the HCN moiety from the surface, which in vacuum is 3.928 Å and in the presence of a dielectric continuum decreases to 3.904 Å. Both structures are also quite similar in terms of energetics, with HCN in vacuum being only 0.02 eV more stable than with implicit solvent.

Fig. 1 Optimized geometries of HCN adsorbed on the H-terminated Ni(111) slab in a) vacuum, b) implicit solvent, and c) the presence of an explicit water bilayer.

While the inclusion of implicit solvation does not seem to result in a radical change, treating the solvent explicitly has a much more dramatic effect on HCN adsorption. As seen in Fig. 1c, the adsorption of HCN in the presence of explicit water molecules occurs almost perpendicular to the Ni(111) surface, instead of interacting via the C≡N triple bond. To rationalize this change in orientation, we carried out a detailed NCI analysis (see ESI† for details), the results of which are summarized in Fig. 2. This analysis reveals that the lone pair of the N atom establishes a trifurcated H-bond with three solvent water molecules (labelled as a) while simultaneously repelling a water directly above it due to the clashing with the O lone pair (labelled as d). The assembly of these H-bonds is the most obvious stabilizing effect; however, it is worth noting that there are other relevant interactions, as we describe in detail below.

Fig. 2 NCI analysis of the adsorbed HCN in the presence of an explicit aqueous environment. Top: representation of the NCIs as isosurfaces (isovalue = 0.35 a.u.). Blue (red) isosurfaces denote attractive (repulsive) interactions. Color code of atoms is the same used in Fig. 1. Bottom: semi-quantitative representation of the NCIs by plotting the reduced density gradient as a function of the electron density multiplied by the sign of the second eigenvalue of the Hessian matrix (sign(λ₂)ρ), which displays the NCIs as peaks (see ESI† for details). Colder (warmer) colors represent attractive (repulsive) interactions.

Fig. 2 shows two additional interactions (labelled as b and e) involving the hydrogen coverage and the H atom of HCN. To shed light on the nature of these interactions, we performed a Bader charge analysis which revealed that hydrogens from the surface coverage exhibit a formal hydride character (q = −0.279), whereas the H atom of the HCN has a positive charge (q = +0.313). Based on these findings, we attribute the attractive interaction (labelled as b) to the sigma bond donation from the surface Ni–H bonds to the H of the HCN, while the repulsive interaction (labelled as e) can be assigned to the electronic repulsion between the surface H atoms and the H of HCN, as the H–H distances are in the range of 1.816–2.239 Å.

Upon discovering such a difference between the HCN binding modes, we modelled the full HCNRR pathway with implicit and explicit solvent and compared the energies and geometries obtained for the different reaction intermediates to those computed in vacuum.

HCNRR via implicit solvation model

The HCNRR can occur via an alternating or distal mechanisms, wherein the C or N atom is reduced completely (i.e. forming CH₄ or NH₃) or in turns. Hence, to assess the lowest energy pathway in the presence of implicit water and in vacuum, we modelled the hydrogenation of either the N or C atoms in HCN and continued from the most stable intermediate. The results of this investigation are summarized in Fig. 3, where we compare the lowest energy HCNRR mechanisms in both phases, assuming that H atoms are sourced by the electrolyte via PCET steps. Both reaction pathways follow an alternating mechanism with the intermediates varying between physisorbed and chemisorbed binding modes. In particular, the first hydrogenation of HCN results in the formation of *CHNH (* denotes a chemisorbed species), which binds on a top site of the Ni(111) surface through the C atom. Furthermore, the calculated C–N bond lengths of ca. 1.245 Å in both vacuum and implicit solvent for the *CHNH intermediate are characteristic of a C=N double bond in imines, as expected. Yet, we observe a relative energy difference of +0.17 eV across both environments, which we attribute to the slight stabilization of HCN and the slightly larger destabilization of *CHNH with implicit solvent. Further hydrogenation of this intermediate results in the imine CH₂NH, which is found to be physisorbed through the C=N double bond. This CH₂NH species is also slightly more stable in vacuum by +0.10 eV and lies at 3.900 Å from the surface compared to 3.729 Å with implicit solvation.

Fig. 3 Gibbs energy profile for the HCNRR on the resting state of Ni(111), modelled in vacuum (black) and implicit solvent (blue) at 0 V_RHE. H atoms are assumed to be sourced by the electrolyte via PCET steps. Labels of intermediates preceded by * denote chemisorbed species. The geometries of the reaction intermediates optimized with implicit solvent are shown as insets. The potential limiting step, U_PLS, for both the mechanism modelled in vacuum phase and implicit solvent are given in V_RHE. Relevant bond lengths (in Å) are also provided. The optimized structures in vacuum are available in Fig. S4.† An alternative pathway in vacuum for the evolution of the CH₃NH₂ intermediate is also shown in grey. This alternative path in vacuum and implicit solvent phases are depicted in Fig. S5.†

From the CH₂NH intermediate, the next hydrogenation favors the reduction of the N atom to give *CH₂NH₂. As with *CHNH, this species is covalently bound to Ni with distances of 2.174 and 2.332 Å in vacuum and implicit solvent, respectively. The formation of the Ni–C bond is further supported by the charge density difference analysis shown in Fig. S2† and the elongated C–N distance from ca. 1.245 Å in *CHNH to 1.350 Å.

Subsequent hydrogenation of *CH₂NH₂ favors the C atom to yield CH₃NH₂, wherein the C–N bond is reduced to a single bond with a distance of 1.473 Å. This bond undergoes a negligible elongation in the presence of the dielectric continuum, but the intermediate itself is brought closer to the surface by 0.141 Å. As we discussed in our previous study,⁴⁰ the desorption of CH₃NH₂ explains why this is the major product observed experimentally, which is unchanged by the presence of implicit solvent. Next, the reaction proceeds with the formation of CH₃NH₃, another interesting intermediate in that it is one of the two species reported in Fig. 3 to be stabilized by the dielectric continuum. The Bader charge analysis of this species in implicit solvent reveals the separation of the transferred H atom into a proton and an electron found in the molecule and on the slab, respectively (q_mol = +0.845 and q_slab = −0.845). Hence, this intermediate is better described as methylammonium, CH₃NH₃⁺. While we observe negligible differences across the C–N bond lengths and distances between this intermediate and the metal surface in both phases, the orientation of the H atoms around the C and N is markedly different. In particular, the geometry of CH₃NH₃⁺ with implicit solvation converges to a structure where one NH moiety points directly to a vacant hcp site on the surface, whereas the same intermediate in the vacuum phase does not.

The cleavage of the C–N bond in CH₃NH₃⁺ gives rise to *CH₃ and physisorbed NH₃ in a process which is endergonic both in vacuum and implicit solvent. In particular, the reaction in vacuum is uphill by only +0.08 eV, whereas in a polarizable continuum is considerably higher, i.e. 0.32 eV. Interestingly, the direct formation of *CH₃ without NH₃ in the supercell was also explored and found to be more favorable in both phases (Fig. 3 in grey and S5†), as expected due to the gain in entropy of NH₃ in the gas phase. Hence, the question arises of whether CH₃NH₂ could directly evolve into *CH₃ and NH₃(g), without going through the intermediate CH₃NH₃⁺. Based on our calculations, this is indeed the lowest energy path in vacuum but not with implicit solvation, where the formation of CH₃NH₃⁺ is slightly more favorable than *CH₃ + NH₃ and *CH₃ + NH₃(g) (i.e. 0.32 and 0.13 eV, respectively). This difference mainly stems from the stabilization of the physisorbed CH₃NH₃⁺ intermediate in the dielectric continuum. Once the methyl group is adsorbed on the surface, further hydrogenation results in CH₄ and NH₃, the experimentally observed minor products, in a process that is overall exergonic by −1.30 eV at 0 V_RHE in vacuum. This energy exhibits a notable deviation from the overall gas phase reaction energy of −1.99 eV, which is derived from the standard redox potential of +0.331 V. The observed discrepancy arises because CH₄ and NH₃ are modelled in the ‘solid state’ rather than in their gaseous form. However, when calculating the reaction energy based on gas phase reactants and products, a value of −1.55 eV is obtained, reflecting inherent errors in DFT energies of gas phase species. To address these errors, we have applied gas phase corrections following the method proposed by Calle-Vallejo et al.,⁵¹ which bring the reaction energy to −2.06 eV, aligning closely with the experimental value (Table S3†). It is important to note that, for the sake of a fair comparison between phases, we have chosen not to correct these gas phase errors due to the absence of liquid phase error corrections.

Overall, we note there is only a slight change in the optimized geometries in vacuum and implicit solvent, with relatively small differences in terms of bond lengths, both within the HCNRR intermediates and between these and the Ni(111) surface. Yet, for most of the intermediates, the inclusion of implicit solvation results in an overall energy destabilization ranging between +0.02 and +0.25 eV, which is not surprising given the dipolar nature of HCN. The largest energetic difference between pathways, however, is seen in the final intermediate CH₄ + NH₃, which we attribute to the fact that this is the only step where three solute cavities are constructed, leading to a higher energy cost. As well as this, there is a considerable decrease in entropy associated with that intermediate (i.e. the T*S term is +0.47 and +0.19 eV in vacuum and implicit solvent, respectively. See Table S1†), which results in a larger Gibbs energy correction. While these differences in energy do not change the potential limiting step for both reaction environments, that is the formation of *CHNH, it does affect their absolute values, i.e. −0.77 and −0.94 V_RHE for the vacuum and implicit solvent phases, respectively. We also note that an applied potential of −0.77 V_RHE is in better agreement with experimental studies by Fedurco et al. which show that CH₄ and NH₃ begin to form at ca. −0.8 V_RHE.^39,40 Based on all these findings, we conclude that there is a non-negligible effect of the implicit solvent, although it does not seem to provide a better description of the HCNRR process or significantly affect the overall mechanism.

HCNRR via explicit solvation model

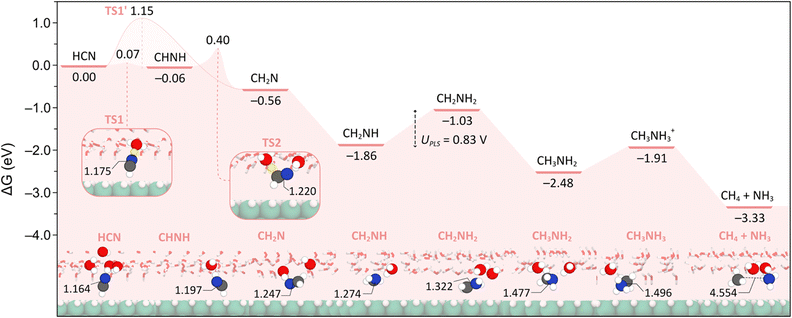
We next investigated the influence of the solvent on the HCNRR from the perspective of an explicit solvation model. A summary of the lowest energy pathway obtained in these conditions is presented in Fig. 4, along with the optimized structures of the intermediates involved and their relevant bond lengths.

Fig. 4 Gibbs energy profile for the HCNRR on the resting state of Ni(111), modelled in explicit solvent at 0 V_RHE. Gibbs energies are calculated relative to the adsorbed HCN. In the first PCET step, the H atom is sourced by the protonated water bilayer to allow for kinetic studies. In subsequent steps, hydrogen is sourced by the bulk electrolyte (not the water bilayer). The potential limiting step, U_PLS, is given in V_RHE. The geometries of the reaction intermediates and the two lowest energy TS structures optimized with explicit solvent are shown as insets. For the sake of clarity, the water molecules directly interacting with the HCNRR intermediates are depicted with a ball-and-stick representation, while the rest of waters are shown as sticks. Relevant bond lengths (in Å) are also provided.

As previously mentioned, and shown in Fig. 1, the adsorption of HCN converges to a geometry that is perpendicular to the surface. Hence, we expected that the solvent would transfer a proton to the N atom that is closer to and involved in several hydrogen bonds with the water bilayer. However, we found that the hydrogenation of the C atom to give CH₂N is instead favored by −0.50 eV compared to the formation of CHNH. In light of this unforeseen result, we investigated the reaction kinetics for the direct formation of CH₂N from HCN, motivated by the large distance between the C and the H atoms in the water layer (C–HO = 2.742 Å), as well as the interaction and shorter distance between the N atom and the water bilayer (N–HO = 1.989 Å). This analysis revealed the presence of a TS structure (TS1′, Fig. S1†) with an energy barrier of +1.15 eV (Fig. 4 and S3†), wherein the proton that is transferred from the water bilayer to the C atom is located at 1.713 Å from its parent water molecule and 2.141 Å from the C. As such, this proton has a large distance to travel, which explains the high energy barrier associated with this step.

Alternatively, the hydrogenation of the N atom yields CHNH, an intermediate that is almost thermoneutral with HCN. In this case, given the proximity of the N atom to the water bilayer, the H transfer is kinetically favored, as confirmed by the presence of a TS (TS1, Fig. 4) with an energy barrier of only +0.07 eV. In this structure, we observe that the transferred proton is midway between the aqueous environment (O–H = 1.176 Å) and the N atom (N–H = 1.297 Å), and that the resulting CHNH tilts significantly towards the water bilayer with bond angles changing from 164.8° (N–C–Ni_HCN) to 119.1° (N–C–Ni_CHNH). We also note the appearance of a radical character on the C atom in CHNH with a magnetic moment of 0.206 μ_B. It should be noted that the excess proton appears to be shuttled to the CHNH completely as evident from the net charge of the water layer decreasing from +0.626 to +0.035. Additionally, the surface slab retains some of the extra electron (q_slab = −0.230), although not the electron in its entirety (see Table S2†).

The subsequent formation of CH₂N from CHNH was found to occur via a Grotthuss-type mechanism,⁵² whereby the proton on the N atom is returned to the water bilayer, via the NH⋯O hydrogen bond, and diffuses through the network of water molecules before it is shuttled to the C atom. This proton transfer to the C atom is facilitated by the aforementioned tilting of CHNH towards the water layer, thereby reducing the distance that the proton must travel. Notably, the TS associated with this step (TS2, Fig. 4) was found to have an energy barrier of +0.40 eV, which is significantly lower than the direct hydrogenation of the C atom to form CH₂N viaTS1′ (i.e. +1.15 eV, Fig. 4 and S1†). We also note that there is a radical character on the N atom in CH₂N as evident by a magnetic moment of 0.607 μ_B. Bader charge analysis on this intermediate (Table S2†) indicates that both the surplus proton and the electron have been transferred to this species in this step. With these data in hand, we posit that the CHNH intermediate exists as a metastable state between the HCN and CH₂N intermediates.

Proceeding from the CH₂N structure, we found that the subsequent PCET step favors the hydrogenation of N to yield the imine CH₂NH. We also noted that the hydrogenation from this intermediate onwards follows the same alternating mechanism observed in vacuum and implicit solvent, depicted in Fig. 3. However, of note is the highly exergonic hydrogenation of CH₂N to CH₂NH by −1.3 eV, presumably due to the quenching of the radical character on the N atom. It is also interesting to note that this appears to be the first intermediate that is oriented almost perfectly parallel to the surface (Ni–C = 4.176 Å), implying some weak interaction through the C=N double bond. This orientation is also reminiscent of its analogue structure in the vacuum and implicit solvent phases (Fig. 3), although it also features a H-bond between the nitrogen atom and the explicit water molecules.

Further hydrogenation of the CH₂NH intermediate affords CH₂NH₂ in an endergonic process by +0.83 eV. Interestingly, this latter species acts as a H-bond donor to the solvent environment via its N–H bond, which contrasts with the H-bond acceptor interaction seen for CH₂NH. We also note that the distance between CH₂NH₂ and the surface is increased to 2.874 Å compared to 2.332 Å with implicit solvent. This illustrates the competing interactions of the CH₂NH₂ intermediate with the surface and the solvent. From this species, the formation of the 4-electron product, CH₃NH₂, occurs next. Methylamine is experimentally observed as the major product,³⁹ has a relative energy of −2.48 eV and is more stable than CH₂NH₂ by 1.45 eV. We also found that there exists a H-bond between the lone pair of the N atom and the water network (N⋯HO = 1.852 Å). While the presence of this H-bond may initially appear to act as a hindrance to desorption, it is not difficult to imagine a sequence of reorganization events within the solvent whereby CH₃NH₂ is shuttled to the bulk solvent. However, should CH₃NH₂ linger near the cathode, it may be further hydrogenated to CH₃NH₃⁺ in an endergonic process by +0.57 eV. As with implicit solvent, Bader charge analysis (Table S2†) revealed that only a proton has been shuttled across the N⋯HO to form CH₃NH₃⁺ (q_mol = +0.774), with the corresponding electron appearing to be delocalized between the water layer and the surface slab (q_water = −0.125 and q_slab = −0.649, respectively). The formation of *CH₃ + NH₃(g) from CH₃NH₂ was also investigated, rendering this intermediate +0.45 and +0.13 eV higher in energy relative to CH₃NH₃⁺ and *CH₃ + NH₃, respectively. These findings highlight the influence of explicit solvation in the stabilization of physisorbed species.

Further hydrogenation of CH₃NH₃⁺ results in the generation of CH₄ and NH₃ as the final 6-electron HCNRR products. This step is thermodynamically downhill with a relative energy of −3.33 eV, driving the overall reaction forward. As is the case with the major product, CH₃NH₂, a series of reorganization events can be imagined wherein both CH₄ and NH₃ are diffused through the solvent water molecules via hydrogen bonding.

An overall examination of the HCNRR mechanisms reveals the following key differences between the various solvation models investigated in this work. Firstly, in contrast to the reaction pathways modelled in vacuum and implicit solvent, the mechanism with explicit solvation features no chemisorbed intermediates. This is mainly due to the strong interaction of the HCNRR intermediates with the explicit solvent, which is absent in the implicit solvent and vacuum phases. The necessity of site-specific effects provided by explicit solvent molecules is further reinforced by examining the Fermi levels of the intermediates. Further discussion of this topic, including a Fermi level plot for the three different phases (Fig. S9†), can be found in the ESI.† Secondly, only when we model the solvent explicitly, we observe the formation of the metastable CHNH intermediate which rapidly evolves to the more stable CH₂N species. Thirdly, the potential limiting step predicted with explicit solvent (i.e. CH₂NH → CH₂NH₂) differs from that found in vacuum and implicit environments (i.e. HCN → *CHNH). While the values of the limiting potentials determined with the explicit solvent and vacuum models (i.e. 0.83 and 0.77 V_RHE, respectively) are in excellent agreement with experiments,³⁹ the implicit solvation model results in a larger value (i.e. 0.94 V_RHE). Hence, we conclude that, despite the water bilayer not being able to fully capture the effect of the aqueous electrolyte, the presence of explicit water molecules is essential for the accurate description of the HCNRR process. Future studies may focus on hybrid solvation models where a discrete number of explicit solvent molecules are paired with an implicit dielectric continuum to reduce computational cost, as well as the investigation of constant potential calculations. These insights may also be applicable to other electrochemical reactions which involve weakly bound intermediates.

Conclusions

In this work we have performed periodic DFT calculations to investigate and contrast the effects of implicit and explicit solvation methods on the HCNRR on a Ni(111) surface. We find that accounting for the solvent environment by means of an implicit dielectric continuum has a minimal effect overall on both the geometries of the reaction intermediates and their energies (i.e. 0.02–0.25 eV) compared to calculations in vacuum.

In contrast, the inclusion of a water bilayer to model the HCNRR process culminates in several drastic changes regarding the geometries and energetics of intermediate species. For example, we observe a very different initial binding mode of HCN which can be attributed to explicit site-specific interactions. This binding mode facilitates the unveiling of a metastable intermediate, CHNH, which subsequently undergoes fast hydrogenation via a rebound mechanism involving the water bilayer, leading to the more stable intermediate CH₂N. In addition, in the explicit phase we report a different potential limiting step compared to the HCNRR modelled in the presence of vacuum and implicit solvent phases.

Overall, the results presented in this work provide key insights into the effective modelling of the electrode–water interface in the HCNRR process. Modelling the electrochemical double layer via an implicit solvation model, while still useful at simulating the bulk effect of the solvent with a reduced computational cost, provides a poor description of the overall reaction. On the other hand, the inclusion of explicit solvent molecules has proven to be a requirement for a good representation of the HCNRR. This is due to explicit solvent–solute interactions which are neglected in the implicit and vacuum phases.

We believe these findings should compel researchers to review proposed reaction mechanisms explored in vacuum, keeping in mind that previously chemisorbed HCNRR intermediates in this work become physisorbed upon introducing the explicit solvent. In the same vein, reaction intermediates which are physisorbed in the gas phase may be more liable to undergo some interaction with the solvent. We also believe these new findings should prompt interest in the development of hybrid solvation models coupled with constant potential methods to mimic the effect of the bulk solvent without sacrificing the essential explicit interactions.

Author contributions

Kevin Brennan: investigation, formal analysis, writing – original draft. Graeme W. Watson: supervision, writing – review & editing. Max García-Melchor: supervision, writing – review & editing, project administration, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the financial support from Trinity College Dublin. Particularly, K. B. and M. G.-M. acknowledge funding from the Provost's PhD Project Awards, generously funded through alumni donations and Trinity's Commercial Revenue Unit, as well as the Science Foundation Ireland (SFI-20/FFP-P/8740). We also thank the DJEI/DES/SFI/HEA Irish Centre for High-End Computing (ICHEC) and the Supercomputing Laboratory at King Abdullah University of Science & Technology (KAUST) in Thuwal, Saudi Arabia, for the generous provision of computational resources.

Notes and references

1. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998.
2. X. Zhao, G. Hu, G. Chen, H. Zhang, S. Zhang and H. Wang, Adv. Mater., 2021, 33, 2007650.
3. S. Hammes-Schiffer and G. Galli, Nat. Energy, 2021, 6, 700–705.
4. R. Sundararaman, D. Vigil-Fowler and K. Schwarz, Chem. Rev., 2022, 122, 10651–10674.
5. S. Maheshwari, G. Rostamikia and M. J. Janik, J. Chem. Phys., 2019, 150, 041708.
6. X. Nie, M. R. Esopi, M. J. Janik and A. Asthagiri, Angew. Chem., Int. Ed., 2013, 52, 2459–2462.
7. E. Romeo, F. Illas and F. Calle-Vallejo, J. Phys. Chem. C, 2023, 127, 10134–10139.
8. C. Shi, C. P. O'Grady, A. A. Peterson, H. A. Hansen and J. K. Nørskov, Phys. Chem. Chem. Phys., 2013, 15, 7114.
9. E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250.
10. M. M. Montemore, O. Andreussi and J. W. Medlin, J. Chem. Phys., 2016, 145, 074702.
11. S. Schnur and A. Groß, New J. Phys., 2009, 11, 125003.
12. T. Roman and A. Groß, Catal. Today, 2013, 202, 183–190.
13. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106.
14. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
15. W. Schmickler and E. Santos, Interfacial Electrochemistry, Springer Berlin Heidelberg Springer e-books Imprint: Springer, Berlin, Heidelberg, 2010.
16. M. T. Tang, X. Liu, Y. Ji, J. K. Nørskov and K. Chan, J. Phys. Chem. C, 2020, 124, 28083–28092.
17. Á. B. Höskuldsson, E. Tayyebi and E. Skúlason, J. Catal., 2021, 404, 362–370.
18. E. Tayyebi, Y. Abghoui and E. Skúlason, ACS Catal., 2019, 9, 11137–11145.
19. J. A. Gauthier, C. F. Dickens, L. D. Chen, A. D. Doyle and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 11455–11463.
20. S. Ringe, N. G. Hörmann, H. Oberhofer and K. Reuter, Chem. Rev., 2022, 122, 10777–10820.
21. H. H. Heenen, J. A. Gauthier, H. H. Kristoffersen, T. Ludwig and K. Chan, J. Chem. Phys., 2020, 152, 144703.
22. Y.-H. Fang and Z.-P. Liu, J. Am. Chem. Soc., 2010, 132, 18214–18222.
23. C. D. Taylor, S. A. Wasileski, J.-S. Filhol and M. Neurock, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165402.
24. M. Garcia-Ratés and N. López, J. Chem. Theory Comput., 2016, 12, 1331–1341.
25. K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101.
26. M. Van den Bossche, E. Skúlason, C. Rose-Petruck and H. Jónsson, J. Phys. Chem. C, 2019, 123, 4116–4124.
27. M. Van den Bossche, C. Rose-Petruck and H. Jónsson, J. Phys. Chem. C, 2021, 125, 13802–13808.
28. J. D. Goodpaster, A. T. Bell and M. Head-Gordon, J. Phys. Chem. Lett., 2016, 7, 1471–1477.
29. W. Zhang, F.-L. Sun, Q.-J. Fang, Y.-F. Yu, J.-K. Pan, J.-G. Wang and G.-L. Zhuang, J. Phys. Chem. C, 2022, 126, 2349–2364.
30. C. Cui, J. Han, X. Zhu, X. Liu, H. Wang, D. Mei and Q. Ge, J. Catal., 2016, 343, 257–265.
31. Q. Zhang and A. Asthagiri, Catal. Today, 2019, 323, 35–43.
32. A. Rendón-Calle, S. Builes and F. Calle-Vallejo, Appl. Catal., B, 2020, 276, 119147.
33. G. Di Liberto and L. Giordano, Electrochem. Sci. Adv., 2023, e2100204.
34. Y. Basdogan, A. M. Maldonado and J. A. Keith, WIREs Comput. Mol. Sci., 2020, 10, e1446.
35. L. Wang, M. Xia, H. Wang, K. Huang, C. Qian, C. T. Maravelias and G. A. Ozin, Joule, 2018, 2, 1055–1074.
36. IEA, Ammonia Technology Roadmap, Paris, 2021.
37. R. R. Dash, A. Gaur and C. Balomajumder, J. Hazard. Mater., 2009, 163, 1–11.
38. M. R. Haque and J. H. Bradbury, Food Chem., 2002, 77, 107–114.
39. M. Fedurco, C. J. Sartoretti and J. Augustynski, J. Electrochem. Soc., 2001, 148, D19.
40. K. Brennan, G. W. Watson and M. García-Melchor, Catal. Sci. Technol., 2021, 11, 5633–5640.
41. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
42. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
43. J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149.
44. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
45. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
46. H. Jónsson, G. Mills and K. W. Jacobsen, in Classical and Quantum Dynamics in Condensed Phase Simulations, World Scientific, Lerici, Villa Marigola, 1998, pp. 385–404.
47. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
48. A. Otero-de-la-Roza, M. A. Blanco, A. M. Pendás and V. Luaña, Comput. Phys. Commun., 2009, 180, 157–166.
49. A. Otero-de-la-Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
50. S. Mirizadeh, S. Yaghmaei and Z. G. Nejad, J. Environ. Health Sci. Eng., 2014, 12, 85.
51. R. Urrego-Ortiz, S. Builes and F. Calle-Vallejo, ChemCatChem, 2021, 13, 2508–2516.
52. N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cy01333b

---