Intact water adsorption on Co(0001) at 100 K: transition from ordered bilayer to amorphous ice structures

Abstract

While cobalt metal is recognized as a versatile catalyst in various chemical reactions, such as Fischer–Tropsch synthesis, limited attention has been paid to understanding the detailed adsorptive interactions between water molecules and cobalt metal. In this study, we investigated the adsorption of water molecules on Co(0001) at 100 K using infrared reflection adsorption spectroscopy and low-energy electron diffraction. We experimentally revealed, for the first time, that D₂O adsorbed intact on the Co(0001) surface forms hexamer islands with coexisting D-up and D-down geometries, in line with the “ice bilayer” model. Upon completion of the first adlayer, a partially ordered (√3 × √3)R30° water bilayer structure is established, featuring coexisting D-up and D-down domains in a ratio of approximately 2 : 3. This results in a surface with mixed hydrophilic and hydrophobic regions. As a second adlayer grows, water molecules preferentially adsorb on the D-up domains before distributing onto the D-down domains. The adsorption of the second adlayer causes a partial disordering of the first water adlayer underneath, resulting in the transition from an ordered bilayer to disordered layer structures. Further increases in water coverage led to an amorphous ice structure.

---

1. Introduction

The adsorption structure of water molecules on metal surfaces significantly influences various phenomena in chemistry and materials science.¹ Factors like water molecular orientation, arrangement, and the strength of water–metal bonding dictate properties such as surface reactivity, corrosion resistance, and wetting behavior.² Experimental techniques such as scanning tunneling microscopy (STM), atomic force microscopy (AFM), infrared reflection absorption spectroscopy (IRRAS), and X-ray photoelectron spectroscopy (XPS), along with computational methods like density functional theory (DFT) and molecular dynamics simulations (MD), have been pivotal in elucidating the complex adsorption behaviors.^3,4 These advancements facilitate tailored surface engineering and the development of novel materials with superior performance and functionality.⁵

Experimentally, water monomers and small clusters (e.g., on NaCl/Au(111),^6,7 Pd(111),⁸ Ag(111) and Cu(111)⁹), 1D chains (e.g., on Ru(0001)¹⁰ and Cu(110)^11,12), 2D layers (e.g., on Au(111),¹³ Pt(111),¹⁴ and Cu(110)¹⁵), and 3D islands and films (e.g., on Pt(111)¹⁶ and Rh(111)¹⁷) have been systematically investigated. Hydrogen bonding, as a fundamental molecular interaction, plays a crucial role in determining the orientation and arrangement of water molecules on metal surfaces.^2,3 The strength and directionality of hydrogen bonds between water molecules can dictate the formation of specific adsorption configurations.¹⁵ Additionally, the interaction forces between water and metal surfaces, such as van der Waals forces,¹⁸ electrostatic interactions,^19,20 and metal–water coordination bonds,²¹ further modulate the water adsorption behavior and stability. Understanding this intricate interplay between hydrogen bonding and water–metal interactions provides insights into the mechanisms governing water adsorption on metal surfaces, thereby advancing their applications in catalysis, corrosion inhibition, and electrochemistry.²²

The catalytic importance of cobalt (Co) in reactions like Fischer–Tropsch synthesis (FTS) emphasizes the need to understand the water/Co interface, as water is a product of this process.²³ However, research on the water/Co interface has been relatively limited compared to other transition metals, especially noble metals.³ Previous studies have indicated that water adsorption on Co(0001),^24–28 Co(11–20),²⁹ and polycrystalline Co films³⁰ occurs in a molecular form at low temperatures, with slight partial decomposition being observed on Co(11–20).²⁹ For example, Heras et al. found molecular adsorption of water on Co(0001) and Co(11–20) surfaces at 100 K, with no ordered structure detected by low-energy electron diffraction (LEED).²⁵ In contrast, Xu et al. reported the formation of an intact, nonwetting, and three-dimensional water layer on Co(0001) at 130 K, exhibiting an ordered p(2 × 2) LEED pattern at low H₂O coverages.²⁴ The monolayer and multilayer of H₂O could be distinguished by XPS, which desorbed molecularly below 200 K.^24,29 At room temperature, dissociative adsorption of H₂O on Co(0001) led to the formation of chemisorbed atomic oxygen and atomic hydrogen.²⁴

The detailed adsorption structure of water on Co(0001) has been theoretically investigated.^26,27 Water monomers tend to adsorb onto the atop position of Co(0001) with a tilted configuration (8°) rather than an upright one. However, on the stepped Co(0001) surface, water monomers preferably reside on the step-top site with their molecular plane parallel to the step, and the presence of a step significantly enhances the binding strength, although the activity of water monomer dissociation does not show a noticeable improvement. Additionally, it was reported that the buckled hexamer with an H-down geometry is the most thermodynamically stable adsorption configuration on Co(0001) based on stepwise adsorption energy.²⁷

Our understanding of the water–cobalt system remains limited, and the water adsorption and reaction behaviors are still not fully comprehended, necessitating further investigation. In this study, we conducted experimental studies on the adsorption and interaction of D₂O on a Co(0001) surface at 100 K using IRRAS and LEED measurements. Our findings reveal that water adsorbs molecularly, forming partially ordered (√3 × √3)R30° bilayer structures with co-existing D-up and D-down domains. As subsequent adlayers form, the initial orderly structure becomes disturbed and transitions into a less ordered layer configuration, which further initiates the growth of amorphous ice structures.

2. Experimental section

In situ infrared reflection adsorption spectroscopy (IRRAS) experiments were conducted in a custom-built ultrahigh vacuum (UHV) system with a base pressure of better than 2 × 10⁻¹⁰ torr. The UHV system consists of a preparation chamber for sample cleaning and a measurement chamber for the IRRAS experiments. The preparation chamber is equipped with a four-grid low-energy electron diffraction (LEED) optic (OCI BDL 600IR) and a quadrupole mass spectrometer (Hiden HAL 3F/PIC). The measurement chamber features a Fourier-transform infrared spectrometer (Bruker VERTEX 70v) connected via KBr windows. The infrared beam reflects from the sample surface plane at an angle of 7°, and the signal is detected using a liquid nitrogen-cooled mercury–cadmium–telluride detector. IRRAS spectra were recorded at 100 K using p-polarized light with 256 scans and a spectral resolution of 4 cm⁻¹.

The Co(0001) single crystal (from Mateck GmbH) was spot-welded to tantalum wires at the crystal edge, which was heated by resistive heating and cooled with liquid nitrogen. Sample temperature was measured using a chromel–alumel thermocouple spot-welded at the crystal edge. The cleaning of the sample involved multiple cycles of Ar⁺ sputtering (1 kV, 10 μA) at 620 K for 20 minutes, followed by annealing in UHV at 630 K for 20 minutes.

High-purity D₂O (from Aldrich, >99.96% D) and H₂O (from Macklin) were utilized in the experiments and further purified under vacuum via freeze–thaw cycles. Their purities were verified in the preparation chamber using a quadrupole mass spectrometer. D₂O molecules were deposited in situ onto the sample surface maintained at ∼100 K through a leak valve. The exposure (or thickness of the D₂O films) was quoted in Langmuir (1 L = 1 × 10⁶ torr s), derived from integrating the pressure–time curves recorded using the pressure control software. Note that D₂O molecules were dosed in a backfilling manner, and pressure was monitored using an Agilent ion gauge (UHV-24p) without applying a gas correction factor, which is located far behind the single crystal. Thus, the exposure values are specific to our experimental setup. In our setup, an exposure of approximately 0.27 L roughly corresponds to the adsorption of one bilayer of (√3 × √3)R30° D₂O on Co(0001). This value was calibrated and confirmed using both IRRAS and LEED. Specifically, with increasing exposures, the free OD stretching mode corresponding to the water molecules adsorbed at the edges of the hexamer islands disappears at 0.27 L (as will be discussed in detail in the main text), and a clearer LEED pattern is also observed at this exposure, indicating the formation of a complete adsorbed bilayer. It is important to note that the actual surface coverage of this bilayer structure on Co(0001) is 2/3.

DFT calculations were performed using the Vienna ab initio Simulation Package (VASP)^31,32 based on the projected augmented wave (PAW) method.^33,34 The spin-polarized Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional³⁵ was employed to describe exchange and correlation. A plane-wave basis set with an energy cutoff of 400 eV and appropriate k-points was used to ensure the convergence of the total ground-state energy. All geometrical optimizations were performed until the forces acting on the relaxing atoms were less than 0.02 eV Å⁻¹. To model the adsorption of water on Co(0001) surfaces, four layers of Co(0001) slab with (√3 × √3) surface supercells were used. The slabs were separated by a 15 Å vacuum gap, with the bottom two layers fixed in the bulk structure. K-point grids of (5 × 5 × 1) were employed.

3. Results and discussion

The absorbance in IRRAS is highly sensitive to the molecular orientation due to the surface selection rules.³⁶ Monitoring the total IRRAS absorbance of the OD stretching (ν_OD) and DOD bending (δ_DOD) modes provides insights into the overall orientation of the D₂O adlayers deposited on Co(0001) at 100 K.³⁷ The integrated peak areas of the ν_OD (2800–2130 cm⁻¹) and δ_DOD (1340–1040 cm⁻¹) modes in the IRRAS spectra were analyzed for D₂O coverages ranging from 0.05 to 1.73 Langmuir (L) (Fig. 1a). In this study, an exposure of ∼0.27 L corresponds to one adsorbed layer of water on Co(0001) by assuming a sticking coefficient of unity for all coverages (refer to the Experimental section for the definition and calculation of dosage and coverage). As shown in Fig. 1a, the intensity of the ν_OD mode increased more gradually at low D₂O coverages as compared to higher coverages, whereas the opposite trend was observed for the δ_DOD mode. All data points can be fitted with two linear functions, intersecting at 0.27 L. For the ν_OD mode, the slope of the fitted line below 0.27 L is only 1/2.6 of that at higher coverages, whereas for the δ_DOD mode, the slope below 0.27 L is 1.6 times greater than at higher coverages. These findings clearly illustrate two distinct overall orientations for the water molecules adsorbed in the second adlayer and above, compared to the first adlayer on Co(0001) at 100 K.

Fig. 1 (a) Integrated peak area of the OD stretching mode (ν_OD) and DOD bending mode (δ_DOD) plotted against D₂O coverage on Co(0001). The bottom axis represents coverage in Langmuir (L), while the upper axis denotes the number of adsorbed layers. The lines alongside the data points represent linear fittings and 0.27 L corresponds to one adsorbed layer with a (√3 × √3)R30° structure, i.e., one bilayer (BL). (b) LEED patterns for D₂O adsorbed on Co(0001) at coverages of 0.27 L (1.0 BL), 0.54 L (2.0 BL), 0.90 L (3.3 BL), and 1.77 L (6.6 BL) at 100 K, with an electron energy of 84 eV. The dark blue and light blue rhombuses represent the reciprocal unit cells of (1 × 1) from the Co(0001) substrate and (√3 × √3)R30° from the adsorbed D₂O, respectively. (c) TPD spectra of 2.1 BL H₂O deposited on Co(0001) at 100 K, with a heating rate of 2 K s⁻¹.

A similar correlation between the intensity of the ν_OH mode and water coverage was previously observed by Liu et al. in their study of H₂O adsorption on Ru(0001) at 85 K.³⁷ They noted that the water adlayer exhibited IRRAS absorbance intensity seven times lower below 0.33 as a monolayer compared to higher coverages, which was attributed to the formation of a planar hexamer structure for H₂O on Ru(0001) at sub-monolayer coverage.³⁸ Although there is ongoing debate regarding the dissociation behavior of water on Ru(000), it is generally accepted that the undissociated molecules lie relatively flat on the Ru(0001) surfaces^38–41 (Fig. S1, ESI†). Therefore, the enhanced IRRAS absorbance observed at low coverage for the ν_OD mode in our study, in comparison to Ru(0001), indicates a tendency towards a relatively upright-tilted orientation of the D₂O molecular plane on Co(0001). As coverage increases beyond 0.27 L, the adsorbed water molecules further elevate their molecular plane into a more upright-tilted orientation. The observation of the intense δ_DOD mode at low coverage (<0.27 L) also supports a relatively upright-tilted orientation of the adsorbed D₂O. This is because the δ_DOD vibration occurs within the molecular plan, and it can only be detected if the molecule possesses a dipole moment perpendicular to the metal surface. At higher coverage (>0.27 L), the IRRAS absorbance per molecule for the δ_DOD mode decreased, which can be attributed to the decrease in image dipole moment as compared to that of the first adsorbed water layer.

The structures of the as-deposited water layers were examined using LEED. Fig. 1b displays LEED images of D₂O/Co(0001) at four representative coverages. At a coverage of 0.27 L, faint (√3 × √3)R30° spots are observed alongside the (1 × 1) spots of Co(0001). This (√3 × √3)R30° structure was also observed in water adsorption on Ru(0001)³⁸ and Rh(111).⁴² The diffuse thermal scattering from surface vibrations is recognized to result in relatively higher background intensity in LEED patterns of the water adlayer.⁴³ It's worth noting that previous investigations of water adsorption on Co(0001) have yielded inconsistent results. For instance, Heras et al. observed no LEED from water adlayers,²⁵ while Xu et al. observed p(2 × 2) spots.²⁴ It is important to note that electron-based techniques such as LEED and XPS can easily damage the structure of the water molecules adsorbed on metal surfaces, even with relatively low electron energy (Fig. S2, ESI†).⁴¹ The substrate temperature can also influence the adsorption behaviors, potentially leading to either reconstruction or dissociations of water molecules (Fig. S3, ESI†). Therefore, the discrepancies in previous studies may be attributed to the differences in experimental procedures. Particular care was taken in our study to capture LEED patterns. All LEED patterns were acquired within one second on fresh areas of the sample surfaces to ensure that the diffraction spots originated from the water layer structures rather than the dissociated ones.

As water coverages increased, the ordered (√3 × √3)R30° structure disappeared, and a broad ring structure emerged within the (1 × 1) spots of Co(0001), indicating disorder beginning from the second adsorbed layer (0.27–0.54 L). Further increases in water coverages resulted in the disappearance of Co(0001) spots, leaving only a distinct ring of diffuse intensity. Given the linear increase in IRRAS absorbance (Fig. 1a) and the gradual disappearance of the (1 × 1) spots of Co(0001) with increasing water coverages, we deduce that water adsorption on Co(0001) at 100 K results in complete surface wetting and follows a layer-by-layer growth mode. The amorphous character of the water layers emerges from the second adsorbed layer. The intact adsorption of water on Co(0001) at 100 K was confirmed by the temperature-programmed desorption (TPD) experiment. Two desorption peaks corresponding to the first and second water adlayers were observed, with no dissociated products (e.g., hydrogen and oxygen) detected, as shown in Fig. 1c.²⁸

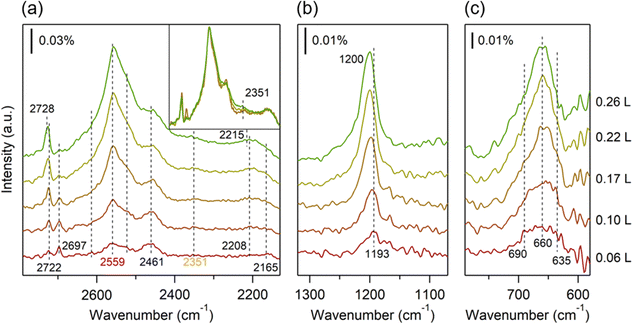
The LEED pattern mainly reflects the position of the oxygen atoms of water molecules on the Co(0001) substrate. Therefore, careful analysis of the IRRAS spectra is necessary to confirm detailed adsorption geometries and the coordination of hydrogen bond networks. We primarily focus on the ν_OD modes due to their sensitivity to hydrogen bond formation in water layers. At a very low coverage of 0.06 L (Fig. 2a), sharp peaks are observed at 2722 and 2697 cm⁻¹, accompanied by broad peaks at 2559 and 2461 cm⁻¹. Peaks around 2200 cm⁻¹, absent on other metal surfaces (e.g., on Au(111) and Ag(111), Fig. S1, ESI†), are also observed. Isotope labeling experiments further corroborate the presence of this low-frequency mode, observed at ∼2930 cm⁻¹ for H₂O/Co(0001) (Fig. S4, ESI†). With increasing D₂O coverage, the peak at 2722 cm⁻¹ rises, while the peak at 2697 cm⁻¹ disappears. Notably, between coverages of 0–0.17 L, the broad peak around 2559 cm⁻¹ exhibits a faster-increasing rate compared to the one around 2461 cm⁻¹. Within the range of 0.17–0.26 L, these broad peaks (and their shoulders), along with the lower frequency band at 2200 cm⁻¹, continue to grow consistently as shown in the inset of Fig. 2a. Additionally, the gradual emergence of a new peak at 2351 cm⁻¹ with increasing water coverage is noteworthy.

Fig. 2 IRRAS spectra of D₂O adsorbed on Co(0001) at 100 K as a function of coverage (0.06–0.26 L). (a) OD stretching mode (ν_OD), (b) bending mode (δ_DOD), and (c) librational mode. The inset in (a) shows spectra for coverages ranging from 0.17 to 0.26 L, which are normalized to the same height for clearer comparisons.

Previous DFT calculations suggest that the buckled hexamer with the H-down geometry is the most stable structure for adsorbed water molecules on the Co(0001) surface.²⁷ In our study, monomer and small cluster adsorptions are likely negligible owing to the elevated substrate temperature of 100 K during film growth. According to the LEED results, one adsorbed layer of water (i.e., 0.27 L) exhibits a (√3 × √3)R30° structure with a lattice constant of 0.433 nm,⁴⁴ smaller than that of the bulk hexagonal ice structures (0.451 nm),⁴⁵ which may cause a buckled structure on Co(0001). In the classical “ice bilayer” model, water molecules are arranged into interconnected hexamers, forming three hydrogen bonds with neighbors. Half of the water molecules are bonded to the surface through electron donation from oxygen to the metal substrate, while the remaining water molecules adsorb between them, forming the upper portion of the “ice bilayer” and completing the hydrogen-bonding network.³ Therefore, we propose that at low coverages (<0.27 L), water molecules on the Co(0001) surface organize into small buckled hexamer islands. The peaks at 2722 and 2697 cm⁻¹ correspond to the free OD stretching modes of D₂O within and at the edges of the hexamer islands (D-up bilayer), while the peaks at 2208 and 2165 cm⁻¹ represent the OD stretching modes of D₂O with an OD bond oriented toward the Co(0001) surface located within and at the edges of the hexamer islands (D-down bilayer). These OD-downward stretching modes exhibit a notably lower frequency compared to crystalline bulk ice, attributed to the elongation of the OD bond due to interaction with the metal surface.⁴⁶ As water coverage increases, the hexamer islands expand and eventually merge at one adlayer coverage (i.e., 0.27 L), leading to the disappearance of the peak at 2697 (2165) cm⁻¹. Additionally, the free OD and OD-downward stretching modes exhibit a slight blue shift of approximately 6 cm⁻¹. Estimating the size of these D-up and D-down domains is challenging in our studies. However, an average size of approximately 2.5 nm in diameter has been reported for D₂O on Rh(111) surface,⁴⁶ where both D-up and D-down domains coexist.

At one adlayer coverage, we expect that there are at least three types of water molecule species: those situated on the Co(0001) surface (lower species) and those that have free OD and OD-downward stretching modes (upper species). The DOD bending mode slightly shifts from 1193 to 1200 cm⁻¹ (Fig. 2b). In the librational region, which is sensitive to the local ordering within the water adlayer,⁴⁷ a broad peak comprising three components is observed at 690, 660, and 635 cm⁻¹, respectively (Fig. 2c). As the lower water molecule is bonded to a cobalt atom via its lone pair and forms three hydrogen bonds with surrounding water molecules, giving it the most robust hydrogen bond strength and tetrahedrality, the peak at 690 cm⁻¹ can be tentatively attributed to the librational mode of these lower species. However, the detailed assignment of the remaining two peaks to the upper species requires further investigation.⁴⁸

In perfect “ice bilayer” structures with either D-up or D-down geometries, two different hydrogen bond configurations have been identified in previous molecular dynamics simulations (Fig. 4). The lower water molecule donates two hydrogen atoms and accepts one (DDA), while the upper molecule donates one hydrogen atom and accepts two (DAA).⁴⁹ Consequently, the OD stretching mode in DDA is expected to exhibit higher vibrational energy compared to DAA. However, the difference in vibrational energies between the D-up and D-down geometries is small according to the simulations by Meng et al.⁵⁰ Many efforts have been made to clarify the components of the broad OD stretching mode observed in IRRAS experiments. Feibelman has proposed that the stretching frequency mainly reflects the O–O distance distribution in a wetting layer of water on metal, with an O–D⋯O bond in a hydrogen-bonded network.⁵¹ However, researchers are still striving to fully understand the experimentally observed peak shape. For example, the two main peaks (3430 and 3300 cm⁻¹) in H₂O/Ru(0001) were attributed to the OH stretching in DA and DA_sh H-bonded molecules,³⁷ but Yamamoto et al. assigned these peaks to the upper and lower species in the water bilayer deposited on Rh(111) without further specification.⁴²

Here, we utilize experimental data and DFT calculations to propose a possible assignment for the complex OD stretching modes. Fig. 3 presents the deconvolution of the OD stretching modes for 0.32 L D₂O/Co(0001). The small peak at 2749 cm⁻¹ is attributed to the 2-coordinated water molecules.⁵² An emerging peak at 2351 cm⁻¹ is assigned to the OD stretching mode in a molecule with DDAA hydrogen bonding (i.e., one molecule donates two hydrogen atoms and accepts two). The assignment of this component, which exhibits a noticeably wider width, is consistent with the literature.^37,53 The proportional contribution of this peak to the total peak area increases with film thickness. Fitting results indicate that the area of the OD-downward peak (2215 cm⁻¹) is more than twice the area of the free OD peak (2728 cm⁻¹). DFT calculations reveal that the main stretching modes in the hydrogen-up bilayer exhibit frequencies that are approximately 100 cm⁻¹ (12 meV) higher than those in the hydrogen-down bilayer (Table 1). This result aligns with Meng's calculations regarding water networks on noble metal surfaces.⁴⁹ In the fitted spectrum, the area of the principal peak at 2461 cm⁻¹ (with a shoulder at 2523 cm⁻¹) is slightly higher than that of the peak at 2559 cm⁻¹ (with a shoulder at 2614 cm⁻¹). We therefore tentatively assign these peaks to the OD stretching modes in DAA (DDA) bonding configurations in the D-down and D-up bilayers, respectively. Fig. 4 schematically illustrates the water adsorption structures on the Co(0001) surface.

Fig. 3 Deconvolution of the OD stretching mode into ten sub-bands for the 0.32 L D₂O/Co(0001). Green circle: raw spectra; black curve: fitting spectra; purple curve: root mean square of the fitting residuals.

Table 1 DFT calculated vibrational frequency (cm⁻¹) for the main stretching and bending modes in hydrogen-bonded water bilayers, for both hydrogen-up and hydrogen-down geometries

	H2O/Co(0001)			D2O/Co(0001)
	ν OH		δ HOH	ν OD		δ DOD
Hydrogen-up	3624	3541	1593, 1534	2617	2552	1161, 1119
Hydrogen-down	3520	3427	1800, 1569	2533	2467	1287, 1138

---

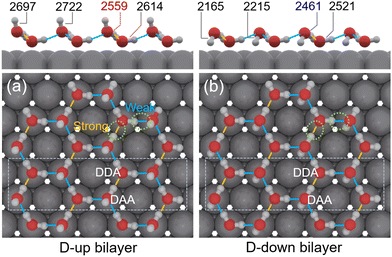Fig. 4 Schematic illustration (side and top views) of the hydrogen-bonding network for the (a) D-up and (b) D-down bilayer islands, with peak positions observed in Fig. 2a indicated. The dashed rectangle in the top view highlights the area from which the side view is taken. The hydrogen bonding configurations, including DDA and DAA, are also shown in the figure. The yellow and blue lines denote the two different types of hydrogen bonds in the bilayer structures, with their relative strengths indicated as well.

Based on the IRRAS absorbance intensity, the area of the D-down-related peaks is greater than that of the D-up-related peaks. However, it is important to note that IRRAS absorbance intensity is influenced by multiple factors, including the number and strength of hydrogen bonds, molecular orientations, and changes in intermolecular and molecule–metal interactions. In Fig. 5, we further analyze the coverage percentages of the D-up and D-down domains based on the evolution of the OD stretching mode peak areas, as well as the transitions of the ice bilayer structures. This aspect of water adsorption, particularly regarding the second adlayer, is rarely studied and provides valuable insights into the complex behavior of water–metal interactions.

Fig. 5 IRRAS spectra of the OD stretching mode for D₂O/Co(0001) adsorbed at 100 K with coverages ranging from (a) 0.28–0.56 L (1.0–2.0 BL) and (b) 0.65–1.74 L (2.4–6.4 BL). The spectra are normalized to the same height for clarity of comparison. (c) Integrated peak area of the free OD and OD-downward modes plotted against D₂O coverages on Co(0001). The bottom axis represents the number of adsorbed layers, while the upper axis denotes the coverage in Langmuir (L). (d) Schematic illustration of the growth mode for D₂O on Co(0001) at 100 K, showing the transition from ordered bilayer to amorphous ice structures, as indicated by the four growth stages (I–IV) depicted in (c) and (d).

As shown in Fig. 5a, significant changes were observed in the overall shape of the OD stretching peak when the water coverage increased to two adlayers (i.e., ∼0.54 L). The broad peaks at 2559 and 2461 cm⁻¹ merged and gradually shifted to lower frequencies. Previously, Jiang's group successfully imaged well-ordered two-bilayer structures on Au(111),¹³ Au(110), and Au(100),⁵⁴ where both the first and second bilayers are hydrogen-bonded. Stacchiola's studies suggested that the internal locking of hydrogen bonds renders the bilayer hydrophobic, resulting in the disappearance of the free OD peak in the IRRAS spectra.⁵⁵ However, in our studies on Co(0001), the intensity of the free OD peak continues to increase, reaching saturation at a coverage of 0.54 L (i.e., 2 BL) (Fig. 5c). Since the ice film becomes amorphous at a thickness of 2 BL, further increases in film thickness do not significantly change the number of free OD groups exposed on the ice film surface.

Additionally, careful examination of the OD-downward peak shows that it reaches a maximum at around 1.4 BL and then decreases continuously. It is important to note that the OD-downward stretching modes are exclusive to the first water bilayer with a D-down geometry. Therefore, we hypothesize that water molecules predominantly adsorb onto the hydrophilic D-up domains at the onset of the second adlayer growth. These newly deposited molecules adopt various orientations and form diverse hydrogen bonds with the first water bilayer, leading to partial disordering in the first bilayer. Some molecules may reorient their OD groups downward toward the Co(0001) substrate, forming structures similar to the D-down domains but with less order. This results in an increased intensity of both the free OD and OD-downward stretching modes as the thickness increases from 1.0 to 1.4 BL.

At a certain coverage, approximately 1.4 BL, the D-up domains in the first bilayer become fully occupied, leading to the adsorption of subsequent water molecules onto the D-down domains, which represent the hydrophobic surface. This indicates that 40% of the second adlayer is adsorbed on the hydrophilic regions, while the remaining 60% is adsorbed on the hydrophobic regions. Specifically, 2/5 of the initial first water bilayer comprises the D-up domain, while 3/5 consists of D-down domains. The water molecules adsorbed on the D-down domains may also disturb the structures of the underlying D-down domains. The decrease in OD-downward stretching modes beyond a thickness of 1.4 BL is attributed to partial disordering, as well as burial and attenuation by subsequent adlayers. Therefore, at 100 K, the first adlayer of water molecules adsorbs intact and wets the Co(0001) surface, while disordering occurs beyond this adlayer. Mild annealing improves the ordering of the two-bilayer structures, whereas further heating causes partial decomposition of the first adlayer. Temperature-induced reordering depends on ice film thickness and involves decomposition, dewetting, nucleation, and crystallization, which will be discussed in a separate paper.⁵⁶

Similar buckled hexamer configurations have been observed on various metal surfaces. For example, a H-down geometry is favored on Cu(111)⁹ and Rh(111),⁴⁶ while an H-up geometry is preferred on Ni(111).⁵⁷ In contrast, the planar hexamer structure is favored over the buckled one on Pd(111)⁵⁸ and Ru(0001).³⁸ Beniya et al. observed co-existing D-up and D-down geometries for water adlayers on Rh(111). By titration of Xe adsorption, they determined that the area of the D-down domains was 1.2 times greater than that of the D-up domains.⁴⁶ These differences arise from the competition between molecule–metal and hydrogen-bonding interactions among the adsorbed water molecules, leading to symmetry-breaking and bond alteration in the hexamers. However, ongoing debates persist regarding these configurations.⁴

Our findings highlight the amorphous and complex nature of the two-adlayer water structures. With further increasing D₂O coverage, a multi-layered amorphous ice structure forms.⁵⁹ As shown in the normalized spectra in Fig. 5b, the overall peak shape remains relatively stable, but subtle changes occur in the components of different hydrogen bonding configurations, including DA, DDA, DAA, and DDAA, etc.³⁷ Specifically, the main peaks shift to lower frequencies (2530 cm⁻¹), while the DDAA peak (2358 cm⁻¹) remains almost unchanged. By comparing the as-grown film (amorphous solid water, ASW) with annealed films (crystalline ice, CI) (Fig. S5 and S6, ESI†), the peak at 2463 cm⁻¹ may be attributed to the characteristic peak of the CI phase.^56,60

4. Conclusions

In summary, our investigation explored the adsorption behavior of water on the Co(0001) surface at 100 K, with a particular focus on understanding the structure of the ordered first bilayer and its transition to disordered ice films. We proposed the coexistence of D-up and D-down domains within the “ice bilayer” structure and estimated the relative percentages of these domains based on the evolution of IRRAS absorbance intensities. Our observations suggest that the second adlayer preferentially adsorbed on the D-up domains with various adsorption orientations, potentially inducing partial disordering of the underlying water bilayer. This is followed by adsorption on the D-down domains, after which further water adsorption leads to the formation of amorphous ice layers. The complex interplay between water molecules and the Co(0001) surface underscores the significance of understanding the dynamics of the water layer structures. This study lays the groundwork for further investigations into the water/cobalt system for various energy conversion and chemical synthesis applications.

Author contributions

Ping Yi: data curation, formal analysis, investigation, writing – review & editing. Yalong Jiang: data curation, formal analysis, investigation, writing – review & editing. Yitian Cao: data curation, investigation. Fangfang Liu: data curation. Yun Zhu: formal analysis. Jiayi Xu: formal analysis. Zechao Yang: funding acquisition, Resources, writing – review & editing. Chuanqi Huang: investigation, resources, writing – review & editing. Wenshao Yang: resources, writing – review & editing. Hongying Mao: formal analysis, funding acquisition, supervision, writing – review & editing. Jian-Qiang Zhong: conceptualization, formal analysis, funding acquisition, investigation, project administration, resources, supervision, writing – original draft, writing – review & editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors have no conflicts to disclose.

Acknowledgements

The authors acknowledge the financial support from the National Natural Science Foundation of China (Grant No. 22002031 and 22372053), the Natural Science Foundation of Zhejiang Province (Grant No. LGG22F010001), the startup project from Hangzhou Normal University, and the Westlake Scholar Research Program.

References

1. Y. Tian, J. Hong, D. Cao, S. You, Y. Song, B. Cheng, Z. Wang, D. Guan, X. Liu, Z. Zhao, X.-Z. Li, L.-M. Xu, J. Guo, J. Chen, E.-G. Wang and Y. Jiang, Science, 2022, 377, 315–319.
2. J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667–674.
3. A. Hodgson and S. Haq, Surf. Sci. Rep., 2009, 64, 381–451.
4. A. Groß and S. Sakong, Chem. Rev., 2022, 122, 10746–10776.
5. C. Zhu, Y. Gao, W. Zhu, J. Jiang, J. Liu, J. Wang, J. S. Francisco and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 16723–16728.
6. J. Guo, X. Meng, J. Chen, J. Peng, J. Sheng, X.-Z. Li, L. Xu, J.-R. Shi, E. Wang and Y. Jiang, Nat. Mater., 2014, 13, 184–189.
7. J. Guo, J.-T. Lü, Y. Feng, J. Chen, J. Peng, Z. Lin, X. Meng, Z. Wang, X.-Z. Li, E.-G. Wang and Y. Jiang, Science, 2016, 352, 321–325.
8. T. Mitsui, M. K. Rose, E. Fomin, D. F. Ogletree and M. Salmeron, Science, 2002, 297, 1850–1852.
9. A. Michaelides and K. Morgenstern, Nat. Mater., 2007, 6, 597–601.
10. M. Tatarkhanov, E. Fomin, M. Salmeron, K. Andersson, H. Ogasawara, L. G. M. Pettersson, A. Nilsson and J. I. Cerdá, J. Chem. Phys., 2008, 129, 154109.
11. T. Yamada, S. Tamamori, H. Okuyama and T. Aruga, Phys. Rev. Lett., 2006, 96, 036105.
12. J. Carrasco, A. Michaelides, M. Forster, S. Haq, R. Raval and A. Hodgson, Nat. Mater., 2009, 8, 427–431.
13. R. Ma, D. Cao, C. Zhu, Y. Tian, J. Peng, J. Guo, J. Chen, X.-Z. Li, J. S. Francisco, X. C. Zeng, L.-M. Xu, E.-G. Wang and Y. Jiang, Nature, 2020, 577, 60–63.
14. S. Nie, P. J. Feibelman, N. C. Bartelt and K. Thürmer, Phys. Rev. Lett., 2010, 105, 026102.
15. M. Forster, R. Raval, A. Hodgson, J. Carrasco and A. Michaelides, Phys. Rev. Lett., 2011, 106, 046103.
16. K. Thürmer and N. C. Bartelt, Phys. Rev. Lett., 2008, 100, 186101.
17. N. Kawakami, K. Iwata, A. Shiotari and Y. Sugimoto, Sci. Adv., 2020, 6, eabb7986.
18. J. Carrasco, J. Klimeš and A. Michaelides, J. Chem. Phys., 2013, 138, 024708.
19. J. I. Siepmann and M. Sprik, J. Chem. Phys., 1995, 102, 511–524.
20. S. Schnur and A. Groß, New J. Phys., 2009, 11, 125003.
21. D. T. Limmer, A. P. Willard, P. Madden and D. Chandler, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4200–4205.
22. Y. Li, Y. Sun, Y. Qin, W. Zhang, L. Wang, M. Luo, H. Yang and S. Guo, Adv. Energy Mater., 2020, 10, 1903120.
23. E. Rytter and A. Holmen, ACS Catal., 2017, 7, 5321–5328.
24. L. Xu, Y. Ma, Y. Zhang, B. Chen, Z. Wu, Z. Jiang and W. Huang, J. Phys. Chem. C, 2010, 114, 17023–17029.
25. J. M. Heras, H. Papp and W. Spiess, Surf. Sci., 1982, 117, 590–604.
26. J.-J. Ma, L.-F. Wang, S.-H. Ma and J. Yang, Eur. Phys. J. B, 2018, 91, 185.
27. M. Zhang, H. Huang and Y. Yu, Catal. Lett., 2018, 148, 3126–3133.
28. W. Jiawei, J. Chen, Q. Guo, H.-Y. Su, D. Dai and X. Yang, Surf. Sci., 2017, 663, 56–61.
29. F. Grellner, B. Klingenberg, D. Borgmann and G. Wedler, Surf. Sci., 1994, 312, 143–150.
30. J. M. Heras and E. V. Albano, Appl. Surface Sci., 1981, 7, 332–346.
31. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186.
32. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
33. P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979.
34. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
36. P. Hollins, Encyclopedia of Analytical Chemistry, 2006 DOI:10.1002/9780470027318.a5605.
37. F. Liu, J. M. Sturm, C. J. Lee and F. Bijkerk, Phys. Chem. Chem. Phys., 2017, 19, 8288–8299.
38. S. Haq, C. Clay, G. R. Darling, G. Zimbitas and A. Hodgson, Phys. Rev. B, 2006, 73, 115414.
39. P. J. Feibelman, Science, 2002, 295, 99–102.
40. M. Schilling and R. J. Behm, Surf. Sci., 2018, 674, 32–39.
41. N. S. Faradzhev, K. L. Kostov, P. Feulner, T. E. Madey and D. Menzel, Chem. Phys. Lett., 2005, 415, 165–171.
42. A. Beniya, S. Yamamoto, K. Mukai, Y. Yamashita and J. Yoshinobu, J. Chem. Phys., 2006, 125, 054717.
43. N. Materer, U. Starke, A. Barbieri, M. A. Van Hove, G. A. Somorjai, G. J. Kroes and C. Minot, Surf. Sci., 1997, 381, 190–210.
44. A. Taylor and R. W. Floyd, Acta Cryst., 1950, 3, 285–289.
45. G. A. Kimmel, J. Matthiesen, M. Baer, C. J. Mundy, N. G. Petrik, R. S. Smith, Z. Dohnálek and B. D. Kay, J. Am. Chem. Soc., 2009, 131, 12838–12844.
46. A. Beniya, Y. Sakaguchi, T. Narushima, K. Mukai, Y. Yamashita, S. Yoshimoto and J. Yoshinobu, J. Chem. Phys., 2009, 130, 034706.
47. C. Clay, S. Haq and A. Hodgson, Chem. Phys. Lett., 2004, 388, 89–93.
48. P. A. Thiel and T. E. Madey, Surf. Sci. Rep., 1987, 7, 211–385.
49. S. Meng, L. F. Xu, E. G. Wang and S. Gao, Phys. Rev. Lett., 2002, 89, 176104.
50. S. Meng, E. G. Wang and S. Gao, Phys. Rev. B, 2004, 69, 195404.
51. P. J. Feibelman, Chem. Phys. Lett., 2004, 389, 92–95.
52. S. Yamamoto, A. Beniya, K. Mukai, Y. Yamashita and J. Yoshinobu, J. Phys. Chem. B, 2005, 109, 5816–5823.
53. Q. Sun, Vib. Spectrosc., 2009, 51, 213–217.
54. P. Yang, C. Zhang, W. Sun, J. Dong, D. Cao, J. Guo and Y. Jiang, Phys. Rev. Lett., 2022, 129, 046001.
55. D. Stacchiola, J. B. Park, P. Liu, S. Ma, F. Yang, D. E. Starr, E. Muller, P. Sutter and J. Hrbek, J. Phys. Chem. C, 2009, 113, 15102–15105.
56. Y. Jiang, H. Zheng, L. Li, P. Yi, Y. Cao, Z. Yang, C. Huang, W. Yang, H. Mao and J.-Q. Zhong, in preparation, 2024.
57. A. Michaelides, Appl. Phys. A, 2006, 85, 415–425.
58. J. Cerdá, A. Michaelides, M. L. Bocquet, P. J. Feibelman, T. Mitsui, M. Rose, E. Fomin and M. Salmeron, Phys. Rev. Lett., 2004, 93, 116101.
59. L. Kringle, W. A. Thornley, B. D. Kay and G. A. Kimmel, Science, 2020, 369, 1490–1492.
60. R. S. Smith, J. Matthiesen, J. Knox and B. D. Kay, J. Phys. Chem. A, 2011, 115, 5908–5917.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03816a

‡ These authors contributed equally.

---