Helium cluster ions: coherent charge sharing and the general trimerization trend

Abstract

The coupled-monomers model views any molecular system as a coherent network of interacting monomers. Developed as a self-consistent density-matrix adaptation of the Hückel MO theory, it has been applied to various X_n^± cluster ions, where X is an inert (closed-shell) neutral monomer. Rather than keeping the bond integrals constant, the model considers their variation with the bond orders χ using a bonding function β(χ). In this work, high-level ab initio data are used to obtain the bonding function for He_n⁺. As the simplest inert species, helium is used to illustrate the general X_n^± bonding trends, using the most elementary example. Two alternative approaches to the bonding function are described. One is based on the He₂⁺ potential, the other on the “multicluster” training points obtained by analysing several special He_n⁺ structures. Each approach is tested in two regimes: by considering only the local bonds, and by including both local and remote pairwise interactions. The remote forces in He_n⁺, n ≥ 3 are destabilising and account for approximately −5% of total covalent energy. Each model variation yields similar structural results, indicating a general trend for trimer-ion formation. In the absence of geometric constraints, this appears to be a universal feature of the X_n^± covalent networks, resulting from the enthalpy-driven competition between charge sharing and localisation. Therefore, many currently unknown trimer-ions are likely to be found in cold environments, such as exoplanetary atmospheres and outer space.

---

1. Introduction

Helium is the simplest closed-shell neutral species. It is inert in the neutral state but becomes reactive with the addition of a charge, as exemplified by the formation of a >2 eV covalent bond in He₂⁺.^1–4 The reactivity is generally due to the electron (or, in this case, its opposite—the hole) acting as the elementary agent of covalent forces, the “glue” of the chemical bond.

The addition of such glue transforms helium clusters into a fundamental laboratory of chemical bonding. He_n⁺ is the simplest case of X_n^± covalent networks, where X is a closed-shell monomer.⁵ The inter-monomer (IM) couplings in such systems illuminate the competition between coherent charge sharing and localisation,^6–19 which is central to chemistry. When sterically possible,⁷ many X_n^±, n ≥ 3 clusters (including He_n⁺) form trimer-ion cores,^{1–4,6,18–26} with the rest of the monomers remaining in the neutral state, bound to the cluster by noncovalent forces.^27,28 The tendency of a charge to localise on not one, not two, but specifically three monomers is both common and intriguing.

Indeed, trimer ions have been observed or predicted in many X_n^± systems, with X ranging from rare-gas atoms (cations),^{1–4,20–22} to organic molecules (anions).^5,6,29 The diversity of these systems implies that the trimerization trend is due the universal features of covalent bonding, not the intrinsic properties of the monomers. The trimer ions emerge as the optimal outcome of two competing drives: on the one hand, extended charge sharing allows more covalent bonds to form; on the other, thinly spreading one bonding agent diminishes the strength of each bond.

To describe the universal features of charge-induced interactions, we put forth a simplified version of the molecular-orbital (MO) theory, the coupled-monomers model.⁵ The model is not intended to compete with high-level ab initio methods. Instead, it aims to provide simple descriptions of chemical bonding in supramolecular systems, focusing on fundamental insight rather than quantitative precision. The model views any molecular system as a network of coupled monomers, regardless of their intrinsic structures. The model approximations are appropriate for the X_n^± networks, where the sharing of one bonding agent results in fairly weak IM bonds with large equilibrium lengths.

These bonds are treated using a self-consistent density-matrix adaptation⁵ of the Hückel MO theory.^30–35 The original Hückel theory describes covalent bonding between all adjacent atoms in terms of constant bond integrals (β). This assumption is valid when all the bonds considered are equivalent, as is approximately the case for π electrons in conjugated hydrocarbons—the Hückel theory's original domain. However, it is unphysical for many other systems.^5,7 The coupled-monomers model,⁵ therefore, employs variable bond integrals. It considers that the equilibrium bond lengths and, therefore, the bond integrals, do vary with local Hückel (Coulson)^35,36 bond orders χ. The latter are described by a bonding function β(χ). Examples of such functions for He_n⁺ are shown in Fig. 1. A variety of β(χ) curves within the dashed boundaries were considered,⁵ but to be applicable, the bonding function must satisfy the universal boundaries plus the training point shown by the circle in the figure.

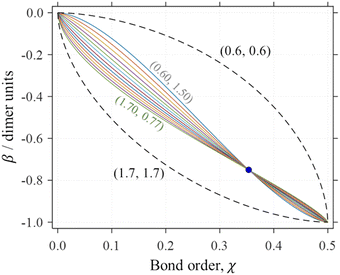Fig. 1 Examples of He_n⁺ bonding functions (solid curves in various colours). All curves are defined by eqn (6) with the training-point constraint (blue circle). Dashed curves show the boundaries of the bonding space considered, with (b₁, b₂) = (0.6, 0.6) and (1.7, 1.7).

Under realistic assumptions, the coupled-monomers model has confirmed the trimerization trend in sterically permitting X_n^± clusters. This outcome was demonstrated for several cationic and anionic systems with diverse monomer types, from rare gases to organics.⁵ In each case, the trimer prediction proved to be quite robust with respect to the exact choice of β(χ). For example, every solid curve in Fig. 1 yields a trimer-ion core in He_n⁺.

The goal of the present work is to demonstrate that the empirical form of the bonding function proposed previously⁵ is consistent with ab initio theory. We use a variety of high-level calculations to devise the bonding function for He_n⁺, but the specific case of X = He is used here to illustrate the general X_n^± bonding trends on the most elementary example. The results show that under reasonable assumptions β(χ) for He_n⁺ indeed falls within the empirical boundaries of the bonding space in Fig. 1.

The next section gives an overview of the coupled-monomers model, followed by the presentation of ab initio results for several special He_n⁺ structures in Section 3. These results power two alternative methods of deriving the bonding function in Sections 4 and 5. The first is based on the He₂⁺ potential and the second on several multicluster training points. The final section summarizes the findings and outlines future directions.

2. The coupled-monomers model

The formalism used in this work has been described previously.⁵ In short, our model relies on some of the Hückel theory's original assumptions, but includes adaptable bond and Coulomb integrals. The variability of the former is especially key in weakly bonded X_n^± systems, where the Hückel assumption of constant bond integrals does not hold, even approximately.

2.1. MMO basis set

For a system of n identical monomers, the inter-monomer orbitals (IMO) ϕ_k are described as linear combinations of the monomer orbitals (MMO) ψ_i, one per monomer: . For He_n⁺, ψ_i are the 1s orbitals of the He⁽ⁱ⁾ monomers, sketched in Fig. 2(a). Linear chains are favoured energetically for He_n⁺, so we limit modelling to such structures.⁵

Fig. 2 (a) Sketch of the 1s MMOs of the He⁽ⁱ⁾, i = 1, …, n atoms, ψ_i, comprising the basis set used to describe the linear He_n⁺ chain. All basis-pair couplings in this basis are antibonding for holes, as reflected by positive bond integrals. (b) Sketch of lowest-energy h-IMO. Only the signs of the MMO contributions are shown, not their amplitudes. This orbital is e-antibonding but h-bonding with respect to all nearest-neighbour interactions. The character of the remote forces alternates along the chain.

The {ψ_i} MMO set serves as a minimal basis for treating the interactions in He_n caused by the addition of one hole. The hole is described by an effective Hamiltonian Ĥ.⁵ Like in the Hückel theory,³⁵ we rely only on its matrix representation in the {ψ_i} basis. The diagonal elements H_i,i = 〈ψ_i|Ĥ|ψ_i〉 are the Coulomb integrals, which here we continue treating as constants. The off-diagonal elements H_i,j = 〈ψ_i|Ĥ|ψ_j〉, i ≠ j are the bond integrals.

For electrons (e), the couplings between all basis MMOs in Fig. 2(a) are attractive, described by negative bond integrals H^e_i,j < 0, for all i ≠ j. Indeed, to a chemist's eye, the MMO chain in Fig. 2(a) forms a bonding-throughout IMO. However, this holds only if the IMO is occupied by an electron. That is, the above interactions are e-bonding, rather than simply bonding. Using the same MMOs to describe a hole (h) results in an opposite, h-antibonding effect, with H^h_i,j > 0, i ≠ j.

Following Hückel,^30–35 we treat the MMO basis as orthonormal. The IMOs 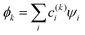and their energies E_k, k = 1, …, n are then obtained by diagonalising the Hamiltonian matrix. The solution yields n eigenvalues E_k, k = 1, …, n and eigenvectors |ϕ_k〉, which contain the c^(k)_i coefficients. Focusing on the lowest-energy IMO, ϕ = ϕ₁, we drop index k = 1 for brevity.

2.2. Charge-sharing stabilisation

IM bonding is described by the monomerization energy ΔE_M, i.e. the energy change in the X_n^± → X^± + (n − 1)X process. For a bound system, ΔE_M > 0, with bonding and antibonding interactions making positive and negative contributions, respectively.

In the general MO theory, total bond orders and stabilisation energies are defined by the combined contributions of all occupied orbitals. Here, we consider only systems bonded by a single bonding agent: one electron (in X_n⁻) or one hole (in X_n⁺). In He_n⁺, in particular, there are (2n − 1) electrons distributed among n molecular orbitals (IMOs). Such a system can be viewed as a combination of two contributions: a closed-shell 2n-electron configuration and a single hole populating the IMO in Fig. 2(b).

The first of the above contributions amounts to zero in terms of covalent bond orders and energy, as in the He_n van der Waals cluster. Therefore, instead of considering the (2n − 1) electrons in the n IMOs of He_n⁺, we can view it, equivalently, as a single-hole system with only one populated IMO. Both the stabilisation energy and all bond orders are then defined by this IMO only. With the additional assumption of constant Coulomb integrals (set arbitrarily to zero), ΔE_M is then given by the negative of the one IMO energy, i.e., the lowest energy eigenvalue of the Hamiltonian matrix. Alternatively, it can be expressed as:⁵

where h_i,j are the equilibrium values of the bond integrals, i.e., H_i,j for the relaxed cluster structure, and are the elements of the density matrix ρ = |ϕ〉〈ϕ|.^5,7 The off-diagonal ρ_i,j, i ≠ j are the Hückel (Coulson) bond orders.³⁵ The diagonal elements ρ_i,i, which do not figure in eqn (1), represent hole density on respective He⁽ⁱ⁾ monomers, i.e., the partial charges: q_i = ρ_i,i.

Under the basis set definition in Fig. 2(a), all h-bond integrals are positive, either at equilibrium (h_i,j > 0) or at an arbitrary geometry (H_i,j > 0). The resulting lowest-energy h-IMO is sketched in Fig. 2(b) (amplitudes not shown, only signs). Since the signs of c_i alternate along the chain, this IMO is e-antibonding but h-bonding throughout.

The h-bonding interactions resulting from the opposite-sign adjacent IMO coefficients correspond to negative local (nearest-neighbour) bond orders, ρ_i,i±1 < 0. All other (remote) pairwise interactions alternate, as illustrated in Fig. 2(b), between h-antibonding (ρ_i,i±s > 0) and h-bonding (ρ_i,i±s < 0) for even and odd, respectively, degrees of separation s:

s = |i − j| (2)

Since the remote (s > 1) interactions are much weaker than the local (s = 1) bonds, the latter (with h_i,i±1 > 0 and ρ_i,i±1 < 0) define the positive sign of ΔE_M, per eqn (1). That is, the chain is bound overall in its ground state.

Eqn (1) offers an intuitive perspective on the relationship between covalent bond energy and bond integrals. While ΔE_M is a sum over all IM bonds, each bond's energy is given by the magnitude of its bond integral, weighted by twice the bond order. In the valence bond theory, a single bond consists of two electrons or holes. The above weight then corresponds to the number of contributing bonding agents and each 2ρ_i,jh_i,j term can be understood as the bond integral scaled by the fractional number of electrons (holes) residing on the particular bond.

2.3. Dimer units

Most results in this work are reported in terms of dimer units (d.u.), which allow for a straightforward generalisation of the results to any X_n^± system.⁵ In this work, specifically, the dimer unit of energy is defined as the bond dissociation energy of He₂⁺: 1 d.u. = 2.446 eV. Similarly, the dimer unit of length is defined as the equilibrium bond length of He₂⁺: 1 d.u. = 1.083 Å.

2.4. Bond lengths and bond integrals

Hückel's assumption of constant bond integrals is valid only when all bonds considered can be treated as exactly or approximately equivalent. This holds for π electrons added to a framework of σ bonds in conjugated hydrocarbons—the Hückel theory's original domain, but is unphysical for most systems.^5,7 This approximation certainly cannot be used for weakly bonded clusters, such as He_n⁺ or similar. When the entirety of the bonding is due to one delocalised electron or hole, the bond lengths and, therefore, bond integrals vary significantly from bond to bond.

Instead, the local equilibrium bond lengths r_i,i±1 can be assumed to depend explicitly on the corresponding bond orders:⁵

r_i,i±1 = r(χ_i,i±1) (3)

r(χ) is a function of the absolute bond order between adjacent monomers. Here, “absolute” means independent of the basis set definition. Absolute order χ is always positive for bonds and negative for antibonds and can, therefore, differ in sign from the Hückel (Coulson) definition.^35,36 For bonding interactions, and r(χ) → ∞ for χ → 0. For antibonding, χ_i,i±1 = −|ρ_i,i±1| < 0 and r(χ) is infinite for any χ ≤ 0. The basis set in Fig. 2(a) implies that the Hückel and absolute h-bond orders are opposite in sign throughout this article:

χ_i,j = −ρ_i,j (4)

as indicated for the lowest-energy h-IMO in Fig. 2(b).

Implicit in eqn (3) is the assumption that the equilibrium geometry is defined by local interactions only. Since the bond integrals depend explicitly on the distance between the monomers, it also follows that the local equilibrium bond integrals h_i,i±1 must vary with the corresponding bond orders. We postulate that |h_i,i±1| = |β(χ_i,i±1)|, where β(χ) is no longer a Hückel constant but a negatively-valued (for χ > 0) function. We call it the bonding function.⁵ Given that all bond integrals in the this work must be positive under the basis-set definition in Fig. 2(a), we have:

h_i,i±1 = −β(χ_i,i±1) (5)

The universal (independent of the monomer identity) features of r(χ) and β(χ) were discussed previously.⁵ Both functions are expected to be well-behaved and monotonic on the χ ∈ [0, 0.5] interval. The left boundary corresponds to the nonbonding (noncovalent) limit and the right represents the largest bond order attributable to one electron or hole.

Since the stronger the bond, the shorter it is, r(χ) must be a decreasing function of χ. As shorter bonds correspond to stronger IM couplings, β(χ) is expected to increase in magnitude with increasing χ. Since the bonding function is defined to be negatively-valued or zero, it varies from β(0) = 0 (the nonbonding limit) to β(0.5) = −1 d.u. (the dimer limit).⁵ However, the above nonbonding (noncovalent) limit assumes an infinite IM separation, and this assumption will be modified in Section 3.2.

These requirements are satisfied by the empirical function

β(χ) = −[1 − (1 − 2χ)^b₂]^1/b₁ (6)

defined for χ ∈ [0, 0.5], where b₁, b₂ > 0 are parameters.⁵ For example, (b₁, b₂) = (1, 1) corresponds to the linear function β = −2χ connecting the nonbonding and dimer limits, while the dashed boundaries shown in Fig. 1 are defined by (b₁, b₂) = (0.6, 0.6) and (1.7, 1.7), as labelled. It was previously speculated⁵ that all or most relevant bonding scenarios fall within the region of the bonding space defined by eqn (6) with b₁, b₂ ∈ [0.6, 1.7], i.e., in between the two dashed curves in Fig. 1.

Indeed, the 12 solid curves shown in Fig. 1 in various colours are all defined by eqn (6) with b₁ ranging from 0.6 to 1.7 and the corresponding b₂ values determined so that each β(χ) function passes through the blue training point 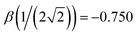.⁵ This constraint “trains” the model to reproduce the He₃⁺ energy.

2.5. Search for self-consistent solutions

As evident from eqn (1), the energy eigenvalues and hence the IMO coefficients c_i, i = 1, …, n, depend on the density matrix elements ρ_i,j. Since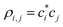 , those elements themselves represent the model solution, leading to a conundrum that the very statement of the problem to be solved depends on the solution.

This issue is resolved via an iterative search for a self-consistent solution.⁵ Given the bonding function β(χ), the search is initiated with an arbitrary set of the initial {c_i} coefficients. Each iteration then includes the following steps:

(1) From {c_i}, compute and χ_i,j = −ρ_i,j.

(2) Set all Coulomb integrals to the same constant (e.g., zero) and evaluate the local bond integrals from the bonding function and local bond orders using eqn (5). The remote integrals h_i,j, |i − j| > 1, are either set to zero (local bonding approximation) or evaluated using the method in Section 4.

(3) Find the eigenvalues and eigenvectors of matrix h from the previous step.

(4) Check for convergence and proceed to the next iteration (step 1) or exit the loop.

The convergence check is based on two criteria. The energy change must be <10⁻⁶ dimer units (2.5 μeV), compared to the previous iteration, and the norm of the eigenvector change must be <10⁻⁷. Most reported calculations involved <200 iterations.

3. Ab initio predictions for special structures

We now turn to He_n⁺ cluster ions for ab initio insight into the r(χ) and β(χ) functions. Both can be evaluated explicitly by analysing the interaction potentials for various bond orders.

3.1. Covalent interactions

In this part, we consider several He_n⁺ structures shown in Fig. 3 along with their respective IMOs. Not all of them correspond to stable clusters: (a) and (b) do, but (c)–(e) do not. These structures were chosen because they each include only equivalent (by symmetry) local bonds. That is, the local bond orders are constant within each structure but vary among them.

Fig. 3 Geometries and lowest-energy h-IMOs of special He_n⁺ structures that include only all-equivalent bonds. The structures were optimised subject to the symmetry constraints. (a) and (b) correspond to stable clusters, but (c)–(e) do not. All IMOs shown are h-bonding.

All IMOs in Fig. 3 are completely antibonding if occupied by an electron (e-antibonding) but become bonding if populated by a hole (h-bonding). In terms of the coupled-monomers model, the He₂⁺ structure in (a) has an absolute bond order of χ = 0.5. Each of the trimer bonds in (b) is described by , as obtained from the IMO coefficients dictated by the model and by the original Hückel theory, regardless of the assumed bonding function or bond length. Similarly, all bonds in square He₄⁺ (c) correspond to χ = 1/4, in hexagonal He₆⁺ (d) to 1/6, and in hendecagonal He₁₀⁺ (e) to 1/10.

Beginning with the dimer ion, its potential is represented by the blue curve in Fig. 4. The specific curve shown is a Morse-potential fit to the full-CI results for He₂⁺ by Gadea and Paidarová¹ (filled blue squares). The black open circles overlaying this curve are from our CCSD/aug-cc-pVTZ calculations using Q-Chem 5.1.³⁷ They are nearly indistinguishable from full-CI: the full-CI potential has a minimum of −2.448 eV at 1.085 Å, while our calculations yield V_min = −2.446 eV at r = 1.083 Å. Given the agreement, we will rely on our CCSD results, to be consistent with the other calculations in this work. The (r, V_min) = (1.083 Å, −2.446 eV) minimum for He₂⁺ is equivalent to (r, V_min) = (1, −1) in dimer units.⁵ It is represented by red circle ‘a’ in Fig. 4 describing a χ = 0.5 bond.

Fig. 4 Ab initio results for (a) He₂⁺ (absolute bond order χ = 1/2); (b) linear He₃⁺; (c) square He₄⁺ (χ = 1/4); (d) hexagonal He₆⁺ (χ = 1/6); (e) hendecagonal He₆⁺ (χ = 1/10); and (f) He₂ (neutral van der Waals dimer, χ = 0). The filled symbols for (a) and (f) represent the results referenced in the text. Solid blue and orange curves are the respective Morse and Lennard-Jones potential fits to these data. The series of black open circles are results of symmetry-constrained potential energy scans. Red open circles are the potential minima of the respective structures.

Turning to smaller bond orders, Fig. 4 displays additional per-bond potential minima b–e for the larger He_n⁺ structures in the respective parts of Fig. 3. In detail, black-circles ‘b’ in Fig. 4 represent the per-bond energy of He₃⁺ from a CCSD/aug-cc-pVTZ potential energy scan under the D_2h symmetry constraint. The values plotted were obtained by dividing the trimer energy relative to the He⁺ + 2He limit by the number of local bonds (2), to yield the energy attributable to each bond.

The (r, V_min) = (1.238 Å, −1.304 eV) minimum for He₃⁺ corresponds to (1.143, −0.533) in dimer units. It is indicated by red circle ‘b’ in Fig. 4. These results are in agreement with the earlier works on He₃⁺.^1,2,4,21,38 The above r = 1.238 Å compares to 1.238 Å determined by Gadea and Paidarová¹ and 1.241 Å predicted by Knowles and Murrell.⁴ The V_min value of −1.304 eV corresponds to a 2.608 eV monomerization energy, which compares to 2.598 eV calculated by Rosi and Bauschlicher² and 2.659 eV predicted by Knowles and Murrell.⁴

Datasets (c)–(e) in Fig. 4 represent the results of similar per-bond calculations for the respective structures in Fig. 3, all carried out under the appropriate symmetry constraints. To avoid clutter, Fig. 4 omits the detailed He₄⁺ (c) and He₁₀⁺ (e) scans but the (r, V_min) minima are indicated by red circles in each case.

The r and V_min values, along with the monomerization energies of these structures are summarised in Table 1. The decreasing ΔE_M for n > 3 reflect the diminishing stabilities of the constrained cyclic geometries with artificially delocalised charges. In the unconstrained ground states of He_n⁺, the charge localises on no more than three monomers, and all unconstrained n > 3 structures have ΔE_M(n) ≈ ΔE_M(3).⁵

Table 1 Results of the CCSD/aug-cc-pVTZ optimizations of the He_n⁺, n = 2, 3, 4, 6, 10 cluster structures shown in Fig. 5. The ΔE_M, bond energy, β, and equilibrium bond length r values are all in dimer units (1 d.u. of energy = 2.446 eV, 1 d.u. of length = 1.083 Å)

Case^a	Cluster^b	χ	r	ΔEM(n)	Energy per bond, −Vmin	β(local)^d	β(all)^e
a As labelled in Fig. 2–4. b Structures shown in Fig. 4. c As defined in the coupled monomers model. The exact χ values in cases a–e are 1/2, , 1/4, 1/6, and 1/10, respectively. d These β values (uncorrected for remote interactions) are calculated as β = Vmin/(2χ). e β values corrected for remote interactions, as described in the text.
a	He2^+	0.500	1	1	1	−1	−1
b	He3^+	0.354	1.143	1.066	0.533	−0.754	−0.791
c	He4^+	0.250	1.350	0.871	0.218	−0.436	−0.554
d	He6^+	0.167	1.496	0.666	0.111	−0.333	−0.375
e	He10^+	0.100	1.712	0.408	0.0408	−0.204	−0.229

---

3.2. The noncovalent limit

The orange curve in Fig. 4 is the van der Waals (vdW) potential of He₂, corresponding to a covalent bond order of zero. The specific curve shown is a Lennard-Jones potential fit to the data of Clementi and Corongiu,^39,40 shown by filled orange squares (some datapoints fall outside the graph's energy bounds). The minimum at r = 2.9 Å = 2.7 d.u. (approximately twice the vdW radius)⁴¹ is too shallow to be discerned but represented by red circle (f) in the figure.

In all χ > 0 cases (Section 3.1), we ignored noncovalent forces. If we continue to do so as χ → 0, the relaxed covalent bond length will approach infinity. This trend will cause the bond integral, i.e., the coupling between the basis functions, to vanish as well: β(χ) → 0 as χ → 0 and r → ∞.⁵

However, noncovalent interactions cannot be ignored in the χ → 0 limit: no matter how weak, they become the only remaining IM force. The very existence of van der Waals clusters implies that r remains finite even as χ vanishes. Minimum (f) in Fig. 4 sets a maximum of r, max(r) = 2.9 Å (2.7 d.u.), achieved in the χ → 0 limit. An immediate consequence of this boundary is that the bond integral for charge-induced covalent interactions cannot vanish even for χ → 0. It remains limited by the He₂⁺ potential value at the above max(r).

3.3. The bond-length function

The optimised local bond lengths for the special He_n⁺ structures a–e in Fig. 3 are plotted versus the corresponding bond orders in Fig. 5 (red circles). The discrete r(χ) data from Table 1 are supplemented with the noncovalent limit r(0) = 2.7 d.u. (point ‘f’) discussed in Section 3.2.

Fig. 5 Red circles: optimised bond lengths of the He_n⁺ structures (a)–(e) in Fig. 3 and the neutral van der Waals dimer (f), plotted versus the corresponding bond orders. Solid blue curve: a bi-exponential fit to the data, excluding (c).

The blue curve in Fig. 5 represents a bi-exponential fit to the ab initio data. It arms us with a continuous r(χ) function to use in further modelling. The fit shown was obtained excluding point ‘c’ (χ = 1/4), which deviates slightly from the general r(χ) trend.

The deviation is due to the remote interactions in square He₄⁺, which are stronger than in any other structures in Fig. 3. With the distance between the opposing monomers only times the shortest bond length, the remote integrals amount to almost half of their local counterparts. While the energetic effect of the remote forces can be estimated easily (see ESI†), the geometric effect was not pursued. Qualitatively, the strong diagonal couplings in Fig. 3(c) are h-antibonding in character and lengthen the local bonds. This results in the perceptible displacement of point ‘c’ from the general r(χ) trend in Fig. 5.

4. Dimer-based modelling

In this section, we assume that the bond integrals of any He_n⁺, n ≥ 3 cluster can be deduced from the He₂⁺ potential. This is similar to the basic idea of the diatomics-in-molecules theory⁴² proposed by Ellison in 1963.^43,44 It was used with varying success to model various polyatomic systems, including rare-gas cluster ions.^{1,3,4,18,19,23,25,45}

In a way, we aim to predict the charge-induced couplings between monomers in larger settings by observing their one-on-one interaction in the dimer ion. Despite significant quantitative errors, this approximation will allow us to reach—simply and with considerable insight—correct qualitative conclusions.

4.1. The dimer-based bonding function

Quantitatively, we assume that all X–X coupling elements—the local and remote bond integrals in any X_n^± structure, whether at equilibrium or not—depend explicitly on IM distance only. That is, H_i,j = f(R_i,j) for i ≠ j, where f is assumed to be the same for any X_n^± with a given X. Then at equilibrium (R_i,j = r_i,j, H_i,j = h_i,j), h_i,j = f(r_i,j). Note that f is defined in a different variable space than β in eqn (5).

Now apply the above to the specific case of He₂⁺. In the coupled-monomers framework, its potential energy V at any R is equal to the negative bond integral magnitude at that R (true only because the Hückel-like effective Hamiltonian and hence the bond integrals incorporate nuclear repulsion). In our basis, all bond integrals are positive, and therefore V(R) = −H_1,2(R) or, equivalently, V(R) = −f(R), where f is the function from the previous paragraph. Combined with h_i,j = f(r_i,j), this yields:

h_i,j = −V(r_i,j), i ≠ j. (7)

where V(R) is the He₂⁺ potential (the blue curve in Fig. 4).

Even though eqn (7) uses the He₂⁺ potential, it applies to all monomer pairs in any He_n⁺. This is unlike eqn (5), which is defined for local bonds only. Specifically for nearest neighbours (j = i ± 1), r_i,j in eqn (7) can be expressed in terms of the bond-length function from Fig. 5, as r_i,i±1 = r(χ_i,i±1). This results in

h_i,i±1 = −V[r(χ_i,i±1)] (8)

Together with eqn (5), this gives

β(χ) = V[r(χ)] (9)

Eqn (9) allows an explicit calculation of the local bond integrals. The corresponding bonding function is plotted by the blue curve in Fig. 6. To obtain it, r for every χ was determined using the r(χ) function in Fig. 5. The β(χ) value was then found from the corresponding V(r) value using the He₂⁺ curve in Fig. 4.

Fig. 6 Solid blue curve: the dimer-based He_n⁺ bonding function obtained using the (χ, r) → (χ, β) transform of the r(χ) curve in Fig. 5 (blue) using eqn (9) and the He₂⁺ potential V(r) in Fig. 4. Red circles (a)–(f): the respective datapoints from Fig. 5 following the same transformation. Shaded green area: the bonding space defined by the dashed boundaries in Fig. 1. Solid grey curves: the original bonding functions shown in Fig. 1 in various colours.

4.2. Local bonding approximation

Sample self-consistent solutions obtained using the above bonding function (including local couplings only) are presented in Fig. 7 and 8 (black symbols and annotations). The two figures correspond to He₃⁺ and He₁₀⁺, respectively.

Fig. 7 Sample solutions for He₃⁺ obtained using the dimer-based bonding approximation. Black symbols and annotations: only local couplings included. Red: all pairwise interactions included on an equal footing. Green asterisks: the magnitudes of the initial guess. Dashed curve: a continuous form of the Hückel (constant β) solution, shown for comparison.

Fig. 8 Sample solutions for He₁₀⁺ obtained using the dimer-based bonding approximation. See Fig. 7 caption for details. Top: The converged geometry of the monomer chain. The bond length values are indicated but the structure is not drawn to scale. Monomers shaded in red correspond to the cluster core (q_i > 0.01). Solid red lines represent covalent bonds with χ ≥ 0.1, dotted red lines bonds with 0.01 ≤ χ < 0.1.

The black circles in each figure represent the converged IMO amplitudes |c_i|, plotted vs. the monomer number i. The values plotted next to the symbols in same-colour font are the partial charges, determined as q_i = |c_i|². The monomerization energy ΔE_M in dimer units (1 d.u. = 2.446 eV) is indicated in the matching-colour (black) font in the top-right corner of each plot.

Green asterisks in each figure represent the magnitudes of the initial {c_i} guess in each calculation. Note that the guess for each calculation was chosen to contain no symmetry. This is to avoid constraining the solutions to either odd- or even-numbered cluster cores.⁵ As in the previous work,⁵ we emphasize the model divergence from the Hückel theory. To highlight the difference, a continuous form of the Hückel (constant β) solution is shown for comparison in each figure as a dashed curve that looks like the ground-state wavefunction of the particle in a box.

The original trimer-core prediction⁵ is clearly borne out in the present results. In the case of He₃⁺ (Fig. 7), with only the local interactions considered, the model charge distribution q_i = 0.250|0.500|0.250 follows the Hückel model exactly. In contrast, the He₁₀⁺ solution (Fig. 8) obtained under the same assumptions deviates significantly from the Hückel model. Even though the starting state in this example distributes the charge over the entire 10-membered chain, the converged solution is localised, placing 99.7% of the charge on three core monomers (i = 4–6 in Fig. 8). It corresponds to a He₃⁺·He₇ cluster structure.

The charge distribution within the trimer core of He₁₀⁺ (q_i = 0.250|0.497|0.250) is nearly identical to that in an isolated He₃⁺ (Fig. 7). As discussed previously, a minor charge spillage from the trimer to adjacent monomers (i = 3 and 7) is due to the bonding function trend in the χ → 0 limit.⁵ In this case, it is specifically due to the finite value of β(0).

The He₃⁺ monomerization energy (ΔE_M = 1.305 d.u.), based on the solution in Fig. 7, is >20% larger than the correct value of 1.066 d.u. (Table 1 and ref. 2 and 4). This discrepancy will be discussed shortly. The He₁₀⁺ monomerization energy is only 0.002 d.u. (5 meV) higher than that of He₃⁺. The model accounts for covalent energy only and the addition of noncovalently bonded neutral monomers does not affect ΔE_M. Its minor increase from n = 3 (Fig. 7) to n = 10 (Fig. 8) is due to the weak couplings between monomers 3–4 and 7–8 in Fig. 8, activated by the charge spillage from the trimer core to the adjacent monomers.

The top parts of Fig. 7 and 8 show the converged geometries of the He₃⁺ and He₁₀⁺ chains, respectively. The IM distances (not to scale in the figure) are indicated in dimer units (1 d.u. = 1.083 Å), with the black font corresponding to the local-bonds-only solutions discussed here. The bond lengths within the trimer core of He₁₀⁺ (Fig. 8) are essentially the same as in the isolated trimer ion (Fig. 7). The 2.696 d.u. distances between nonbonded neutral monomers correspond to the vdW separation (Section 3.2).

4.3. All pairwise interactions on an equal footing

Eqn (7) allows us to bypass the local bonding function β(χ) altogether. Instead, we can treat all bond integrals—local and remote—in a uniform fashion. To do this, at each iteration, we use the IMO coefficients c_i to calculate the local bond orders χ_i,i±1. From these, using eqn (3) with r(χ) from Fig. 5, the r_i,i±1 bond lengths are determined. Then all IM distances in the He_n⁺ chain are calculated as . The bond integrals for all i–j pairs are then determined viaeqn (7).

Sample results of this approach for He₃⁺ and He₁₀⁺, are shown in Fig. 7 and 8, respectively, in red. Since the remote interactions in the ground states of He_n⁺ are overall destabilising [Fig. 2(b)], their inclusion lowers the He₃⁺ and He₁₀⁺ monomerization energies, by 0.052 d.u. (0.127 eV) or about 4% in each case. The change is in the right direction, but ΔE_M(3) = 1.253 d.u. is still 17.5% larger than the true value, 1.066 d.u.

The inclusion of remote interactions has a minor effect on the cluster geometry and charge distribution. The antibonding nature of these interactions in the trimer core results in a slight but perceptible narrowing of the charge distribution, from q_i = 0.25|0.50|0.25 to 0.24|0.52|0.24. This redistribution helps minimize the antibonding coupling between the terminal monomers in the trimer, with little or no effect on the local bond orders.

4.4. Conclusions from the dimer-based approach

The approach tested in this section correctly predicts some key properties of He_n⁺ clusters. Among them is the key structural feature: all n ≥ 3 species possess trimer-ion cores.^2,4,21,38

The bonding function calculated using this approach (Fig. 6) does fall within the initially defined bonding space,⁵ although it comes close to its lower boundary for χ = 0.35–0.5. It is primarily due to this significant deviation from the original trimer training point (blue in Fig. 1, greyed out in Fig. 6) that this bonding function overestimates the cluster stability by 17.5%.

This discrepancy is due to the assumption that pairwise couplings are unaffected by other monomers. The performance of the model overall depends sensitively on the bonding in the trimer ion,⁵ but this approach does not use the trimer energetics as an input. Instead, it assumes that the pairwise integrals in He₃⁺ are the same as they would be at the same distance in He₂⁺. This is not strictly correct, as the effective Hamiltonians of the two systems are different. This results in the bonding function in Fig. 6 missing the original trimer training point by a lot, causing the model to miscalculate the core-ion energy.

To rectify this, next we modify how the bonding function is calculated. The model performance is improved by including not only the dimer, but also the trimer, and larger-cluster energetics.

5. Multicluster bonding function

In this section, we use the He_n⁺ structures shown in Fig. 3 plus the van der Waals dimer to parameterise the bonding function β(χ). The corresponding bond energies provide necessary data to determine β values for a discrete χ series ranging from χ = 0.5 to 0. The results are presented in Fig. 9.

Fig. 9 Black squares (a)–(f): β(χ) values determined from the respective per-bond potential minima in Fig. 4, assuming that only local bonds contribute to the overall cluster energy. Red circles (a)–(f): the same, but with the remote couplings considered. Solid blue curve: the continuous multicluster He_n⁺ bonding function obtained by fitting eqn (11) to red circles (a)–(f). Shaded green area: the bonding space defined by the dashed boundaries in Fig. 1. Solid grey curves: the original bonding functions shown in Fig. 1 in various colours.

5.1. Local bond integrals

The monomerization energy of He₂⁺ (χ = 0.5) is ΔE_M = 1 d.u., by definition of the dimer unit. On the other hand, diagonalisation of the dimer 2 × 2 Hamiltonian yields ΔE_M = h_1,2, where h_1,2 is the relaxed bond integral. It then follows from eqn (5) that β(0.5) = −1 d.u.⁵ This is included in Table 1 and represented by red circle ‘a’ in Fig. 6 and, again, symbol (a) in Fig. 9.

For He₃⁺ (χ = 0.354), the per-bond minimum (b) in Fig. 4 corresponds to V_min = −1.304 eV = −0.533 d.u. (Table 1). If only local interactions are included, then per eqn (1) and (4), it is related to the bond integral via β = V_min/(2χ) = −0.754 d.u. This value of β for χ = 0.354 is represented by black square ‘b’ in Fig. 9. It is nearly indistinguishable from the trimer training point β = −0.750 d.u. introduced previously⁵ for He_n⁺ clusters (the blue circle in Fig. 1, greyed out in Fig. 9). The miniscule difference is due to the ΔE_M(3) = 2.608 eV (1.066 d.u.) monomerization energy from the CCSD/aug-cc-pVTZ calculations used here, instead of the published^1,2,4,24 ΔE_M(3) = 2.598 eV (1.061 d.u.) result that was used to determine the original training point.⁵

Black squares c–e in Fig. 9 show the results of similar per-bond calculations for the square He₄⁺ (c), hexagonal He₆⁺ (d), and hendecagonal He₁₀⁺ (e) structures in Fig. 3. The per-bond V_min values for each structure (Table 1) were used to calculate the corresponding β(χ) values as β = V_min/(2χ).

5.2. Corrections for remote interactions

The ab initio monomerization energies in Table 1 include all IM interactions: pairwise and many-body, local and remote. In contrast, the determinations of the local bond integrals in Section 5.1 were performed as if only the first-degree (s = |i − j| = 1) couplings contributed to ΔE_M. We will continue disregarding many-body interactions but will now include the effect of remote (s > 1) pairwise couplings on ΔE_M. Since the remote interactions in He_n⁺ are overall destabilising, the analysis in Section 5.1 must have underestimated the local bonds.

A crucial distinction between the s = 1 and s > 1 interactions is that for s > 1, the corresponding specific bond orders ρ_i,j or χ_i,j have only a minor effect on the r_i,j distance, and therefore, h_i,j. For example, the r_1,3 distance in He₃⁺ [Fig. 3(b)] is twice the local bond length, r_1,3 = 2. That is, r_1,3 is determined mainly by χ_1,2, while χ_1,3 has only a small effect. For this reason, the remote couplings cannot be defined in a manner similar to eqn (5), which is used for their local counterparts. Hence, we will continue describing the remote bond integrals using the dimer-based approach expressed in eqn (7), treating these (weak) couplings as a perturbative correction for the local bonds. The latter will be described by eqn (5) with a multicluster bonding function.

We illustrate this approach on the simplest case of He₃⁺ [Fig. 3(a)]. The ab initio (CCSD) value of its monomerization energy is of ΔE_M = 1.066 d.u. (Table 1). On the other hand, per eqn (1),

ΔE_M = −2 × 2ρ_1,2h_1,2 − 2ρ_1,3h_1,3, (10)

which takes into account that ρ_1,2 = ρ_2,3 and h_1,2 = h_2,3, by symmetry. The IMO coefficients (Section 3.1) yield and 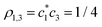. The signs of ρ_i,j reflect the fact that the IMO in Fig. 3(b) is h-bonding with respect to the local interactions (ρ_1,2, ρ_2,3 < 0), but h-antibonding for the remote 1–3 pair (ρ_1,3 > 0).

The local integrals in eqn (10) are presumed to be defined by eqn (5). Namely, h_1,2 = h_2,3 = −β(χ_1,2), with 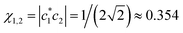, while the weaker remote interactions are described using the dimer-based eqn (7). Using r from Table 1 for the local bond length r_1,2 yields r_1,3 = 2r_1,2 = 2.286 d.u. Eqn (7) and the V(R) curve for He₂⁺ in Fig. 3 (blue) then give h_1,3 = −V(r_1,3) = 0.104 d.u. Substituting all these quantities into eqn (10), results in β(0.354) = −0.791 d.u.

This empirical β value for the trimer ion was obtained assuming that its CCSD monomerization energy is determined by a combination of the local and remote pairwise interactions. As expected, it is slightly larger in magnitude than the initial −0.754 d.u. result (Table 1), which was obtained by ignoring the slightly destabilizing remote forces. The corrected value of β = −0.791 d.u. for χ = 0.354 is included in Table 1 and indicated by red circle ‘b’ in Fig. 9.

The above estimate shows that the 1–3 remote interaction in He₃⁺ amounts to about −10% of each of the 1–2 and 2–3 bonds (ρ_1,3h_1,3/ρ_1,2h_1,2 = −0.1). That is, it is 10 times weaker and opposite in character (antibonding) compared to the local bonds. Since there are two such bonds and only one remote pair, the overall destabilising effect of the remote forces in He₃⁺ is ∼5% of ΔE_M. The relative small magnitude affirms the validity of our perturbative approach to these interactions.

Similar calculations for square He₄⁺, hexagonal He₆⁺, and hendecagonal He₁₀⁺ are detailed in ESI.† The corrected values of the bond integrals, represented by the β values for = 1/4, 1/6, and 1/10, are included in Table 1 and Fig. 9 (red circles c–e). Implicit in this analysis is the assumption underlying eqn (3): that remote interactions do not affect cluster geometry, necessitating no changes to the r(χ) datapoints in Fig. 5. The noncovalent limit of the bonding function (point ‘f’ in Fig. 9) is assumed to be the same as in Section 4: β(0) = −0.042 d.u.

5.3. Continuous multicluster bonding function

We now have six discrete β(χ) datapoints represented by red circles a–f in Fig. 9. To obtain a continuous bonding function to be used in model calculations, we performed a least-squares fit to these data using the analytical expression:

β(χ) = β₀ − (1 + β₀)[1 − (1 − 2χ)^b₂]^1/b₁ (11)

This function differs from the original⁵ expression in eqn (6) by the inclusion of β₀ to account for the finite value of β at χ = 0 (point ‘f’ in Fig. 9). This constant (not a variable parameter) equals the covalent bond integral evaluated at a vdW distance, i.e., β₀ = β(0) = −0.042 d.u. per Section 4.

The blue curve in Fig. 9 is defined by this β₀ value, with the optimal fit parameters b₁ = 0.744 and b₂ = 1.461. The resulting explicit β(χ) function was used in the following calculations.

5.4. Model results

In this section, we use the bonding function in eqn (11) with the optimal parameters determined in Section 5.3 to test our model for the He_n⁺ clusters. Similar to Section 4, we consider two approximations: (1) without and (2) with remote interactions. Since the discrete β(χ) datapoints in Fig. 9 were specifically adjusted with the second approximation in mind, more superior performance is expected in the second case. Comparing the two sets of results will allow us to draw conclusions about the quantitative effects of the remote forces on cluster structures and stabilities.

Sample self-consistent coupled-monomers solutions are presented in Fig. 10 and 11 for He₃⁺ and He₁₀⁺, respectively. The content of these figures is colour-coded and formatted similarly to Fig. 7 and 8. In each figure, the solutions shown in black result from the local interactions only, while those in red include all pairwise couplings. The local interactions in all cases shown in Fig. 10 and 11 are treated using the multicluster bonding function given by eqn (11) and plotted in Fig. 9 (blue curve). The remote couplings for the red datasets are obtained using the dimer-based approach defined by eqn (9).

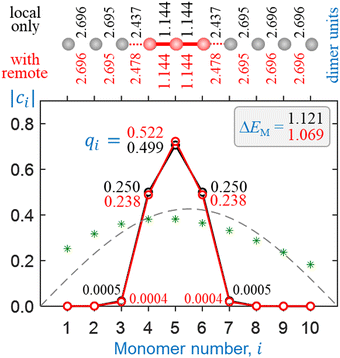
Fig. 10 Sample solutions for He₃⁺ obtained using the multicluster bonding function. Black symbols and annotations: only local couplings included. Red: all pairwise interactions included as described in the text. See Fig. 7 caption for further details.

Fig. 11 Sample solutions for He₁₀⁺ obtained using the multicluster bonding function. Black symbols and annotations: only local couplings included. Red: all pairwise interactions included as described in the text. See Fig. 7 and 8 captions for further details.

All solutions shown in Fig. 10 and 11 are structurally very similar to those in Fig. 7 and 8, despite the different bonding functions used. As predicted previously,⁵ the charge in all He_n^±, n ≥ 3 clusters localises on a core trimer ion in most chemically relevant situations. Indeed, the covalently bonded He₃⁺ structures in Fig. 10 are nearly indistinguishable from those in Fig. 7, including the very similar charge distributions. The He₁₀⁺ solution in Fig. 11, similar to Fig. 8, corresponds to a He₃⁺·He₇ cluster structure, with 99.9% of the charge localised on the trimer core.

The one significant difference between the model outcomes in Sections 4 and 5 is in the respective cluster stabilities. While the dimer-based solution for He₃⁺ including all interactions (Fig. 7) is described by a monomerizations energy that exceeds the ab initio value (1.066 d.u.) by 17.5%, the multicluster solution in Fig. 10 matches it almost exactly, provided the remote interactions are taken into account. In Fig. 11, the addition of several more He monomers to form He₁₀⁺ (with a He₃⁺·He₇ structure) results in a miniscule increase in ΔE_M. The observed increase is smaller in this case, compared to the dimer-based case Fig. 8, mirroring the smaller charge spillage off the trimer core.

6. Concluding remarks

The coupled-monomers model views any molecular system as a network of interacting monomers. We have applied this view to homogeneous X_n^± clusters, but it can be extended to heterogeneous systems with more than one monomer type. The model approximations are most appropriate for weak delocalised bonds resulting from the sharing of a single unit of charge. The model treats these bonds using a self-consistent density-matrix formalism. It considers that equilibrium bond lengths and, therefore, the bond integrals vary with local bond orders χ. This variation is described by a bonding function β(χ), which can be determined empirically based on experimental and/or ab initio data.

In this work, we relied on high-level ab initio calculations to devise the bonding function for He_n⁺ cluster ions. Helium is the simplest closed-shell monomer, allowing us to illustrate general bonding behaviours in the most elementary case. Two alternative approaches to determining the bonding function were described. The first is based on the dimer-ion potential, the other on several multicluster training points obtained by analysing a series of special, not necessarily stable equilibria with all-equivalent bonds. The bonding functions determined by either method fall within the bonding space defined in the previous work,⁵ giving extra credence to the initial predictions. Each approach was tested in two regimes: by considering only the local bonds, and by including all—local and remote—pairwise interactions.

All four model variations yielded similar structural results, consistent with the known properties of He_n⁺.^1,2,4,21,38 Under most realistic assumptions, the charge in any He_n⁺, n ≥ 3 system tends to localise on three monomers, resulting in the formation of trimer-ion cores within larger clusters. This prediction is robust with respect to an exact choice of the bonding function.

Both the dimer-based and multicluster approaches indicate that remote interactions in He_n⁺ are overall destabilising and account for approximately −5% of total covalent energy. There is, however, an important distinction between the two when it comes to cluster energetics. The dimer-based method overestimates the He_n⁺, n ≥ 3 cluster stabilities by 17.5%, even when all pairwise interactions are considered. The multicluster method, on the other hand, predicts the cluster monomerization energies almost exactly. This is because the dimer-based method is based on the He₂⁺ energetics only, while one of the multicluster training points corresponds to He₃⁺. In our previous work, we showed that the trimer training point is key to predicting any correct X_n^± energetics using the coupled-monomers model.⁵

There remains one property that our model in its present form does not reproduce, which is the exact charge distribution within the He₃⁺ trimer. High-level ab initio calculations by us and other authors^19,25 show that the charge distribution in He₃⁺ is broader than the q_i = 0.25|0.50|0.25 Hückel limit. The CCSD results for the trimer ion in Fig. 3(b) correspond to Mulliken charges of q_i = 0.267|0.466|0.267. In contrast, the coupled-monomers model in its present form, using the multicluster bonding function with all pairwise interactions accounted for, predicts a narrower distribution of q_i = 0.238|0.523|0.238 (Fig. 10).

Thus, our model predicts that the destabilising remote forces in He_n⁺ work to narrow rather than broaden the charge distribution, which is contrary to the above CCSD prediction. In the future, we will show that the answer lies with the Coulomb integrals. So far they were presumed constant, but should also vary with respect to the density elements, just like their off-diagonal counterparts (the bond integrals) do.

Finally, we reiterate the overall conclusion that in the absence of geometric constraints the charge in various X_n^± systems tends to be shared by three monomers. In this work we focused on monoatomic monomers (X = He), but the coupled-monomers approach can be and has been similarly used to treat X_n^± clusters of polyatomic species, with similar conclusions.⁵ We stress that the universal trimerization trend in such weakly-bonded covalent networks has been revealed in a purely coherent regime. It results from the enthalpy-driven competition between charge sharing and localisation and is a feature of IM covalent couplings per se, largely independent of the intrinsic properties of the monomers. Therefore, many other trimer-ion species are likely to be found, particularly in cold environments such as exoplanetary atmospheres and outer space.

Data availability

Some of the data supporting this article have been included as part of the ESI.† The code for self-consistent density-matrix calculations using the coupled-monomers model is available from the authors upon request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the U.S. National Science Foundation (grant CHE-2153986).

References

1. F. X. Gadea and I. Paidarová, Chem. Phys., 1996, 209, 281.
2. M. Rosi and C. W. Bauschlicher, Chem. Phys. Lett., 1989, 159, 479.
3. P. J. Knowles, J. N. Murrell and E. J. Hodge, Mol. Phys., 1995, 85, 243.
4. P. J. Knowles and J. N. Murrell, Mol. Phys., 1996, 87, 827.
5. L. Van Dorn and A. Sanov, Phys. Chem. Chem. Phys., 2024, 26, 5879.
6. Y. Dauletyarov and A. Sanov, Phys. Chem. Chem. Phys., 2021, 23, 11596.
7. A. Sanov, Int. Rev. Phys. Chem., 2021, 40, 495.
8. C. C. Jarrold, ACS Phys. Chem. Au, 2023, 3, 17.
9. S. H. Fleischman and K. D. Jordan, J. Phys. Chem., 1987, 91, 1300.
10. M. J. DeLuca, B. Niu and M. A. Johnson, J. Chem. Phys., 1988, 88, 5857.
11. T. Tsukuda, M. A. Johnson and T. Nagata, Chem. Phys. Lett., 1997, 268, 429.
12. M. Saeki, T. Tsukuda and T. Nagata, Chem. Phys. Lett., 2001, 348, 461.
13. M. Saeki, T. Tsukuda and T. Nagata, Chem. Phys. Lett., 2001, 340, 376.
14. R. Mabbs, E. Surber, L. Velarde and A. Sanov, J. Chem. Phys., 2004, 120, 5148.
15. P. A. Pieniazek, A. I. Krylov and S. E. Bradforth, J. Chem. Phys., 2007, 127, 044317.
16. A. A. Golubeva and A. I. Krylov, Phys. Chem. Chem. Phys., 2009, 11, 1303.
17. K. B. Bravaya, O. Kostko, M. Ahmed and A. I. Krylov, Phys. Chem. Chem. Phys., 2010, 12, 2292.
18. F. Y. Naumkin and D. J. Wales, Mol. Phys., 1998, 93, 633.
19. N. L. Doltsinis and P. J. Knowles, Mol. Phys., 1998, 94, 981.
20. K. Hiraoka and T. Mori, J. Chem. Phys., 1989, 90, 7143.
21. K. Hiraoka and T. Mori, J. Chem. Phys., 1990, 92, 4408.
22. W. R. Wadt, Appl. Phys. Lett., 1981, 38, 1030.
23. F. Y. Naumkin, P. J. Knowles and J. N. Murrell, Chem. Phys., 1995, 193, 27.
24. B. Liu, Phys. Rev. Lett., 1971, 27, 1251.
25. N. L. Doltsinis, P. J. Knowles and F. Y. Naumkin, Mol. Phys., 1999, 96, 749.
26. F. X. Gadea and M. Amarouche, Chem. Phys., 1990, 140, 385.
27. H.-J. Schneider, Angew. Chem., Int. Ed., 2009, 48, 3924.
28. A. J. Stone, The Theory of Intermolecular Forces, Oxford University Press, Oxford, 2013.
29. Y. Dauletyarov, A. A. Wallace, C. C. Blackstone and A. Sanov, J. Phys. Chem. A, 2019, 123, 4158.
30. E. Hückel, Z. Phys., 1931, 70, 204.
31. E. Hückel, Z. Phys., 1931, 72, 310.
32. E. Hückel, Z. Phys., 1932, 76, 628.
33. E. Hückel, Z. Phys., 1933, 83, 632.
34. N. C. Baird and M. A. Whitehead, Can. J. Chem., 1966, 44, 1933.
35. I. N. Levine, Quantum Chemistry, Prentice-Hall, Upper Saddle River, NJ, 2000.
36. C. A. Coulson, H. C. Longuet-Higgins and R. P. Bell, Proc. R. Soc. London, Ser. A, 1947, 191, 39.
37. E. Epifanovsky, et al. , J. Chem. Phys., 2021, 155, 084801.
38. T. González-Lezana, O. Echt, M. Gatchell, M. Bartolomei, J. Campos-Martínez and P. Scheier, Int. Rev. Phys. Chem., 2020, 39, 465.
39. E. Clementi and G. Corongiu, J. Phys. Chem. A, 2001, 105, 10379.
40. E. Clementi and G. Corongiu, J. Mol. Struct., 2001, 543, 39.
41. A. Bondi, J. Phys. Chem., 1964, 68, 441.
42. J. C. Tully, in Modern Theoretical Chemistry, ed. G. A. Segal, Plenum Press, New York, 1977, ch. 6, vol. IV-A, pp. 173–200.
43. F. O. Ellison, J. Am. Chem. Soc., 1963, 85, 3540.
44. F. O. Ellison, J. Chem. Phys., 1983, 78, 5024.
45. W. R. Wadt, J. Chem. Phys., 1980, 73, 3915.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03478c

---