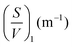Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comprehensive characterization of waterlogged archaeological wood by NMR relaxometry, diffusometry, micro-imaging and cryoporometry
Valeria
Stagno
 *ab,
Otto
Mankinen
*ab,
Otto
Mankinen
 c,
Sarah
Mailhiot
c,
Ville-Veikko
Telkki
c,
Sarah
Mailhiot
c,
Ville-Veikko
Telkki
 c and
Silvia
Capuani
b
c and
Silvia
Capuani
b
aEarth Sciences Department, Sapienza University of Rome, Piazzale Aldo Moro 5, 00185 Rome, Italy. E-mail: valeria.stagno@uniroma1.it; Tel: +39 0649913928
bNational Research Council – Institute for Complex Systems (CNR-ISC) c/o Physics Department Sapienza University of Rome, Piazzale Aldo Moro 5, 00185 Rome, Italy
cNMR Research Unit, University of Oulu, Pentti Kaiteran katu 1, 90014 Oulu, Finland
First published on 22nd October 2024
Abstract
Chemical, physical, and biological decay may partially or totally hide the historical and technological information carried by waterlogged wood. Investigation of the above-mentioned decay processes is essential to assess the wood preservation state, and it is important to find new methods for the consolidation and safeguarding of wooden archaeological heritage. A conventional method for assessing the wood preservation state is light microscopy. However, the method requires sample slicing, which is destructive and challenging when dealing with fragile and spongy submerged remains of heritage wood. To this end, a promising alternative non-destructive technique is proton nuclear magnetic resonance (1H-NMR) which considers wood as a porous system. This work aimed to perform a comprehensive analysis of structures, porosity, water distribution, decay, and possible structural inclusions of three archaeological waterlogged wood fragments of the Roman age using NMR relaxometry, micro-imaging (μ-MRI), NMR diffusometry, and NMR cryoporometry. The results were compared with a similar analysis of the three contemporary wood samples of the same species. The multimodal approach presented in this study allowed us to cover all the dimensional scales of wood, from nanometers to sub-millimeters, and reconstruct the alteration of the entire archaeological wood fragment caused by degradation.
Introduction
Archaeological wood remains are essential for understanding past human activities and raw materials technology.1 Under waterlogged conditions, the information carried by these remains may be partially hidden or lost due to physico-chemical and biological degradation, which induces an alteration of the wood structure depending on the properties of the wood species as well as environmental factors of the deposition site.2–4 Beyond physico-chemical and biological decay, tunnelling and erosion bacteria may lead to a microbial process in the presence of oxygen and anoxic conditions, respectively.4,5 Wood can also be attacked by soft-rot fungi when the oxygen level increases.2,6 Erosion bacteria produce the destruction of the cell walls and pit membranes and the filling of cell lumina with decay products from the cell wall layers.6,7 Along with the decay products, salts, and metals may be deposited within the wood depending on their concentration in water and the composition of the soil in which the object was buried.8–11 The assessment of the wood preservation state, based on the investigation of the above-mentioned degradation processes, is important for the implementation of new methods and materials to consolidate and safeguard the wooden archaeological heritage.12,13 For waterlogged archaeological wood, the main conservation practice implies the use of consolidating materials that penetrate in the wood microstructure and replace water.14–19 Sometimes, these consolidants interact with the impurities (i.e., salts and metals) stored in the archaeological wood remains, compromising their conservative effect.14 Therefore, knowledge of porosity, water distribution, decay and possible structural inclusions in the wood is crucial for the choice of an appropriate consolidating product.A conventional way for assessing the wood preservation state is light microscopy. This is an optical imaging technique classified as destructive, since it requires sampling a piece of wood20 and manually cutting it into thin sections. When dealing with the waterlogged archaeological wood, the main limitations of light microscopy are related to the sample volume21 and the fact that it is often used to provide qualitative images. The first limitation may be partially solved by selecting only one small sample in areas that would not affect the value of the object.22 However, with conventional light microscopy, even a small sample is destroyed to obtain a thin section compromising its use for further analysis. Moreover, because of the brittle and spongy texture of archaeological waterlogged wood remains, obtaining good informative images by conventional light microscopy can be a challenging task. Alternatively, reflected light microscopy and confocal laser scanning microscopy techniques23–25 may be used since they do not require a thin section but are based on the observation of the external surface of the wood remains. However, the water present within the sample and on its surface reflects light making the application of these techniques on the archaeological waterlogged wood very difficult.
In the field of heritage waterlogged wood conservation, recent works20,26–33 have shown that a promising alternative technique to light microscopy is represented by proton nuclear magnetic resonance (1H-NMR). It is based on the stimulation of nuclear spins by radiofrequency (RF) waves in the presence of a static magnetic field. Under these conditions, an electric signal (NMR signal) is received by the RF probe as an electromotive force. The NMR signal is proportional to the proton density and it decays exponentially in time because of transverse (spin–spin) relaxation processes caused by local oscillating fields due to molecular motion.34 These local oscillating fields both affect the transverse relaxation, with a time constant T2, and the longitudinal relaxation, with a time constant T1.35–39 However, because of the static magnetic field inhomogeneities, which contribute to the spins’ dephasing, the effective transverse relaxation time is known as T2*. Superimposing over the main static magnetic field time-dependent and controlled magnetic field gradients, NMR images and diffusion experiments are obtained.36 As the NMR signal depends on several parameters, such as the relaxation times T1, T2, and T2* and the diffusion coefficient D, it is possible to perform a multiparametric and multimodal investigation of the wood object acquiring both non-imaging and imaging experiments. MR images weighted on one of the above-mentioned parameters provide a semi-quantitative and direct observation of the wood structure and the measurement of these parameters, by means of NMR experiments based on the signal analysis, allows the quantitative and indirect inspection of the physico-chemical and physiological aspects of the wood. Importantly, NMR is a non-destructive technique that allows the preservation of the wood sample for further analyses. All the aforementioned NMR techniques have already been used to study ancient wood.9,26,40–44 However, magnetic resonance imaging (MRI) and diffusion NMR techniques do not allow the investigation at the sub-micrometer and nanometer scale, which is the dimensional scale characteristic of the cell wall which is the wood constituent most affected by degradation processes. With conventional diffusion techniques, the detection limit is essentially related to the diffusion length which in the Stejskal–Tanner model is set around 10 microns.45,46 Also, micro-imaging (μ-MRI), when performed using strong magnetic field gradients, allows a maximum linear resolution of about 10 μm.29 On the other hand, relaxation times may provide indirect information about the nanometer scale features but they are also sensitive to paramagnetic ions that reduce the relaxation constants and cause the appearance of unrealistic pore distributions in mathematical models used.28,47 In this scenario, NMR cryoporometry represents a non-destructive method to also investigate the cell wall scale and, combined with other NMR techniques, cover the entire wood dimensional scale.44,48
One limitation of high-field NMR and microscopic MRI is that the sample size is typically limited to a few millimeters or to a few centimeters depending on the instrument. However, surfaces of larger cultural heritage wood samples can be studied using low-field, portable single-sided NMR devices up to a couple of centimeters depth. Previous works28,49–55 have shown that it is possible to perform relaxometry and diffusometry experiments with a single-sided NMR instrument without sampling the wood artwork. Nevertheless, these mobile devices are characterized by highly inhomogeneous magnetic fields and are not equipped with either imaging gradients or a cooling system. Therefore, despite allowing studies on unlimited sample sizes outside a laboratory, portable NMR has lower resolution and does not enable micro-imaging and cryoporometry measurements.
In this work, three waterlogged archaeological wood samples (V century AD) were studied using a combination of advanced NMR techniques. The three ancient wood samples were identified as common spruce (Picea abies Karst.), sweet chestnut (Castanea sativa Mill.), and maple (Acer L.), and their preservation state was already investigated using conventional light microscopy in our previous work.28 The evaluation of decay was obtained by both normal and polarized light microscopy. A strong microbial decay was observed for spruce wood, which was associated with both cellulolytic bacteria and fungi. This decay resulted in a layer of dark-coloured substance, formed by erosion residual wood products, which appeared mainly in the secondary wall of latewood tracheids, facing the cell lumen. Polarized light microscopy highlighted the well-preserved structure of compound middle lamellae and secondary cell walls. Conversely, the inner part of the secondary walls was converted into an amorphous substance. A fungal attack was testified by the presence of hyphae passing through the cells and typical soft rot erosion tunnels. Moreover, inclusions were observed in both earlywood and latewood vessels of the chestnut wood and in some cases small vessels were completely obstructed. These black-coloured inclusions were attributed to iron–tannin precipitates.8,9 A generalized detachment and loss of fibre secondary walls was also observed in chestnut, whereas in the maple wood no complete cell wall detachment was seen. Nevertheless, the weak and spongy consistency of the maple wood indicated a significant decay, and the thinning of the fibre cell wall as well as the presence of spores and residues of fungal hyphae in the cellular lumens were observed.
This work aimed to obtain a comprehensive analysis of archaeological waterlogged wood structures, along with their porosity, water distribution, decay, and potential structural inclusions, combining four advanced NMR techniques: relaxometry, micro-imaging, diffusometry, and cryoporometry. To this end, the three archaeological wood fragments of the Roman age were compared with three contemporary wood samples of the same species. The multi-analytical approach presented in this study allowed us to cover all the dimensional scales of wood, from nanometers to millimeters, and reconstruct the state of conservation of the entire archaeological wood fragment. The results obtained from the NMR protocol presented in this work were interpreted with the support of the results obtained from decay evaluation by light microscopy carried out in our previous work.28
Experimental
Materials
Three small fragments were collected from three archaeological wood poles of a wooden pier dated to the Roman age (V century AD) and recovered in 2018 in the archaeological excavation area of the ancient harbor of Neapolis (Naples, Italy).56,57 Their botanical species were identified in previous works57–62 as common spruce (Picea abies Karst.), sweet chestnut (Castanea sativa Mill.) and maple (Acer L.). These wood samples were waterlogged and well preserved in the seawater of Naples (Mediterranean Sea). After the collection, the samples were kept in sealed containers full of distilled water. Moreover, three modern wood samples belonging to the same botanical species of the three ancient wood samples were used for comparison. All six wood samples (three ancient kinds of wood samples and three modern kinds of wood samples) had cylinder-like shapes of height 1 cm and diameter of less than 1 cm so that they could be inserted into the 10 mm NMR tube. Before starting the NMR measurements, the three modern wood samples were soaked with distilled water until complete saturation (corresponding to the sinking of the sample) and maintained in test tubes full of distilled water. During the relaxometry, diffusometry and cryoporometry experiments, all six samples were inserted without water in the NMR tube that was sealed with Parafilm to prevent the wood dehydration. Conversely, during μ-MRI acquisitions, the samples were inserted in the NMR tube with water and sealed with Parafilm to prevent water evaporation.Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000; all the echoes were collected in a single transient, TR = 8 s, and NS = 4.
000; all the echoes were collected in a single transient, TR = 8 s, and NS = 4.
| Wood sample | Ancient spruce | Ancient chestnut | Ancient maple | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Image weighting | T 2*-w | T 2-w | T 2*-w | ||||||
| Slice orientation | Transversal | Tangential | Radial | Transversal | Tangential | Radial | Transversal | Tangential | Radial |
| TE/TR (ms) | 5.5/500 | 5/1500 | 5/1500 | 2.8/2000 | 2.6/2000 | 2.6/2000 | 5/2000 | 4/2000 | 4/2000 |
| NS | 256 | 128 | 128 | 256 | 256 | 256 | 128 | 128 | 128 |
| No of slices | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| STK (μm) | 200 | 300 | 300 | 250 | 250 | 250 | 250 | 250 | 250 |
| FOV (cm) | 0.9 | 0.9 | 0.9 | 0.8 | 1.1 | 1.1 | 0.8 | 1.3 | 1.1 |
| MTX | 1024 | 512 | 512 | 512 | 512 | 512 | 512 | 512 | 512 |
| R (μm2) | 9 × 9 | 18 × 18 | 18 × 18 | 16 × 16 | 21 × 21 | 21 × 21 | 16 × 16 | 25 × 25 | 21 × 21 |
| Wood sample | Modern spruce | Modern chestnut | Modern maple | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Image weighting | T 2*-w | T 2*-w | T 2*-w | ||||||
| Slice orientation | Transversal | Tangential | Radial | Transversal | Tangential | Radial | Transversal | Tangential | Radial |
| TE/TR (ms) | 5.1/800 | 4.9/800 | 4.9/800 | 2.7/1000 | 2.6/1000 | 2.6/1000 | 2.7/1000 | 2.5/1000 | 2.7/1000 |
| NS | 100 | 128 | 128 | 256 | 256 | 256 | 256 | 256 | 256 |
| No of slices | 4 | 5 | 5 | 3 | 3 | 3 | 3 | 3 | 3 |
| STK (μm) | 300 | 250 | 250 | 300 | 300 | 300 | 300 | 300 | 300 |
| FOV (cm) | 0.8 | 1.0 | 1.0 | 0.9 | 1.2 | 1.15 | 0.9 | 1.2 | 1.2 |
| MTX | 1024 | 1024 | 1024 | 512 | 512 | 512 | 512 | 512 | 512 |
| R (μm2) | 8 × 8 | 10 × 10 | 10 × 10 | 18 × 18 | 23 × 23 | 22 × 22 | 18 × 18 | 23 × 23 | 23 × 23 |
Since wood is a complex biological system, water diffusion is restricted and shows different behaviours depending on the observation time (Δ). At short Δ, i.e. when  , where L is the length scale to probe the material structure or the typical pore size, D(Δ) depends on the surface-to-volume ratio S/V77–81 according to the following equation:
, where L is the length scale to probe the material structure or the typical pore size, D(Δ) depends on the surface-to-volume ratio S/V77–81 according to the following equation:
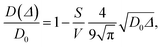 | (1) |
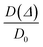 , an asymptotic value approaches
, an asymptotic value approaches| D(Δ → ∞)/D0 = 1/τ, | (2) |
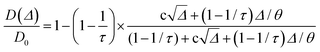 | (3) |
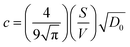 and θ is a scaling constant proportional to the pore size.78,84,85 This approximation was used to obtain the tortuosity for chestnut and maple samples. Since several diffusion components, D, were measured in each wood sample, for each D component, a tortuosity value was computed using either eqn (2) or eqn (3) and then an average tortuosity weighted on D populations was obtained.
and θ is a scaling constant proportional to the pore size.78,84,85 This approximation was used to obtain the tortuosity for chestnut and maple samples. Since several diffusion components, D, were measured in each wood sample, for each D component, a tortuosity value was computed using either eqn (2) or eqn (3) and then an average tortuosity weighted on D populations was obtained.
In NMR cryoporometry, the melting point of a substance confined to a small pore is lower than that of a bulk substance, according to the Gibbs–Thomson equation:44,86
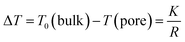 | (4) |
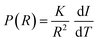 | (5) |
Results and discussion
Micro-imaging
Direct observation of the microstructure of our six wood samples was obtained by μ-MRI. Due to the finite echo time (2.5–5.5 ms, see Tables 1 and 2), the water components with the shortest T2 values (T2 ≤ TE) are filtered out from the images. Indeed, according to previous works,9,10,26,27 the contrast of μ-MR images provides important information: areas with light image voxels correspond to wood structural damages, such as holes and cavities, filled with water; areas characterized by dark image voxels indicate the accumulation of decomposed organic materials and/or heavy metals, lacking the signal due to the lack of water and fast relaxation; rounded black and large spots suggest the presence of gas bubbles due to the gas emissions of infesting microorganisms (e.g., fungi). The wood morphology is discussed separately for spruce, chestnut, and maple in the following sections.Spruce
In Fig. 1, microscopic MR images of both the modern and the ancient spruce are shown, revealing their anatomies. The upper row (a, b, and c) of Fig. 1 displays images of the modern spruce, while the lower row (d, e, and f) shows images of the ancient spruce. In Fig. 1b, the presence of a black area (light blue arrow) in the upper part of the sample is due to the incomplete water filling of the wood structure, but it is not attributable to any decay process since it disappeared during the acquisition while the sample remained immersed in water in the NMR tube. Conversely, in all the MR images of the modern spruce, many black spots (red arrows), associated with a low water content and short T2, are seen along the sample border, which are due to both the difference in the magnetic susceptibility and the presence of infest microorganisms. From the comparison among the MR images of the modern and the ancient spruce, the first thing to notice is the presence of many more artifacts and black spots (red arrows) in the ancient wood images. These are due to strongly degraded areas with bacteria, fungi, and paramagnetic inclusions.9,28 Because most of the artifacts and black spots are located along the rays and on the sample border (red arrows), as visible in the transversal and tangential sections (Fig. 1d and e), we can conclude that these structures were heavily degraded. In these areas, characterized by dark voxels, the NMR signal is weak because of the lack of water or the very short T2. Another notable difference is seen in the resin channels (green circles): those of the modern spruce appear with black image voxels and short T2, whereas those of the ancient spruce are characterized by brighter voxels and long T2. This indicates that resin was lost from the resin channels of the archaeological wood sample and replaced by water. Moreover, on average, the measured resin channels in the modern spruce have a diameter of around 75 μm and in the ancient spruce around 100 μm.Chestnut
Fig. 2 shows the MRI-based virtual histology of both modern and ancient chestnuts. The modern chestnut images are displayed in the upper row (a)–(c), while the ancient chestnut images are in the lower row (d)–(f). The MR sections acquired on the modern chestnut are characterized by a marked difference in the image contrast if compared with those acquired on the ancient chestnut. The archaeological chestnut wood exhibits a very dark contrast throughout the MR images, which hides its typical porous-ring structure60 and some regions appear with rather dark voxels associated with a low water content and short T2. Indeed, only large pores characterized by bright voxels and long T2 are fully resolved and they can be identified as vessels of the earlywood, while smaller vessels of the latewood, characterized by less bright voxels and shorter T2, are only partially visible. Conversely, in the modern chestnut image, the porous-ring structure is clearly visible and it is characterized by pores with voxels of different brightness associated with different T2 values, corresponding to vessels of different sizes, and a background with darker voxels and shorter T2, associated with parenchyma, rays and fibres. Three and four main sizes of vessels can be measured, respectively, on the transversal section of the modern and ancient chestnuts, as highlighted in Fig. 2a and d. On average, the vessel sizes, when measured along the tangential direction, are around 295 ± 31, 139 ± 33 and 60 ± 16 μm for the modern chestnut and around 355 ± 45, 263 ± 10, 170 ± 22 and 83 ± 19 μm for the ancient chestnut. Furthermore, it is worth noting that modern chestnut vessels have an elongated shape characterized by a different diameter if measured along the tangential or the radial direction; instead, the ancient chestnut vessels exhibit a more circular shape. Transversal, tangential, and radial sections of the modern chestnut (Fig. 2a–c) show the presence of regions with black voxels and very short T2 (red arrows) corresponding to the accumulation of extractives in which this wood type is naturally rich. Vessels, instead, appear almost totally free of inclusions in the modern chestnut and partially (green arrow) or totally (light blue arrow) obstructed in the ancient chestnut. The strong change in the image contrast between the modern and the ancient wood samples suggests a heavy degradation of the archaeological sample with the accumulation of inclusions and iron-impurities9 both in the parenchyma and in the vessel lumens, as already highlighted in our previous work.28 Moreover, the presence of inclusions can also be seen along the vessels in the radial section of the ancient chestnut (the yellow arrow in Fig. 2f) which, in contrast, are not present along vessels of the modern chestnut (the yellow arrow in Fig. 2c).Maple
In Fig. 3, the MRI-reflected morphology of the modern and the ancient maple wood samples can be observed. The modern maple images are displayed in the upper row (a)–(c), while the ancient maple images are in the lower row (d)–(f). According to our previous work,28 in which the assessment of the conservation state of these three archaeological wood samples was obtained by light microscopy, the ancient maple wood is better preserved than the ancient spruce and chestnut samples. Indeed, only a few black artifacts can be seen on the MR images (red arrows). For comparison, we used a piece of modern maple coming from a branch of the maple tree that for this reason has a different morphology in the center of the wood piece. However, the outermost zone well represents the typical diffuse porous-ring structure of the maple characterized by vessels with bright voxels and long T2 and a background with darker voxels and shorter T2 associated with parenchyma, rays and fibers. On average, vessels measured on the modern maple have a diameter of 36 ± 8 μm, whereas vessels of the ancient maple are characterized by two different sizes of around 86 ± 10 μm and 40 ± 4 μm. In the ancient maple, the red arrows indicate the image artifacts that are usually produced by the presence of infest microorganisms.6,9,28,47 These artifacts were not noticed in the modern maple images.Relaxometry
The results obtained from the relaxometry analysis are discussed separately for spruce, chestnut, and maple in the following sections, where the T1 and T2 peaks shown in Fig. 4 have been interpreted and assigned to different water populations associated with characteristic wood structures. Peak assignments to wood anatomical elements are summarized in Table 3. On average, the ancient wood samples include more relaxation components than their modern counterparts.| Wood specimen | T 1 (ms) | P 1 (%) | T 2 (ms) | P 2 (%) | Assignment |
|---|---|---|---|---|---|
| Modern spruce | 3000 | 9 | 200 | 4 | Water on the sample surface |
| 800 | 91 | 27 | 78 | EW tracheids | |
| 5 | 7 | LW tracheids | |||
| 0.9 | 12 | Cell walls | |||
| Ancient spruce | 6000 | 7 | — | — | Water on the sample surface |
| 1300 | 34 | 400 | 52 | Large voids due to wood decay/empty resin channels | |
| 300 | 59 | 97 | 9 | Large EW tracheids | |
| 18 | 24 | EW tracheids | |||
| 5 | 8 | LW tracheids | |||
| 1.4 | 7 | Cell walls | |||
| Modern chestnut | 1800 | 46 | 175 | 11 | Vessels ∼ 140–300 μm |
| 33 | 18 | Vessels ∼ 60 μm | |||
| 500 | 54 | 5 | 55 | Fibres, parenchyma | |
| 0.4 | 16 | Cell walls | |||
| Ancient chestnut | 3000 | 11 | 350 | 29 | Vessels ∼ 260–350 μm |
| 900 | 6 | 78 | 5 | Vessels ∼ 170 μm | |
| 26 | 3 | ||||
| 100 | 11 | 10 | 3 | Vessels ∼ 80 μm | |
| 20 | 73 | 2 | 17 | Cell walls | |
| 0.6 | 42 | Fibres, parenchyma | |||
| Modern maple | 1600 | 100 | 70 | 44 | Vessels ∼ 36 μm |
| 15 | 50 | Fibres, parenchyma | |||
| 1.5 | 6 | Cell walls | |||
| Ancient maple | 2100 | 26 | 350 | 23 | Vessels ∼ 86 μm |
| 700 | 60 | 78 | 6 | Vessels ∼ 40 μm | |
| 16 | 67 | Fibres, parenchyma | |||
| 200 | 13 | 2.3 | 4 | Cell walls |
Spruce
In Fig. 4a, the modern spruce has only two T1 components and the ancient spruce presents three different T1 components where one of the components has significantly shorter T1 than the components of the modern spruce sample. Both the modern and ancient spruce samples show a small (7–9% of the total intensity) peak at very long T1 = 3 and 6 s, respectively. These T1 peaks, along with the weak T2 component around 200 ms observed only in the modern spruce, can be attributed to excess water stored in the NMR tube outside the sample97,98 and they can be excluded from our anatomical discussions. In the modern spruce, the individual T1 component around 800 ms is a mean value over the entire wood structure and it is associated with the three different T2 components around 30, 5 and 0.9 ms (Fig. 4b). The most intense T2 peak is around 30 ms (78%) and it can be attributed to free water in earlywood (EW) tracheids with a larger lumen size, in good agreement with previous works.28,44,91,98 The small (7%) T2 peak at around 5 ms is associated with free water in latewood (LW) tracheids, which are characterized by a smaller lumen size, in agreement with the literature.28,44,91,98 The shortest T2, instead, can be attributed to bound water in cell walls, which represent the 12% of the total water signal. The observation of three T2 components and only one T1 component indicates that exchange of water between the three sites (bound water as well as EW and LW free water) is fast in the T1 time scale (τex ≪ 800 ms) but slow in the T2 time scale (τex ≥ 1–30 ms). For the ancient spruce, two different T1 peaks at around 1300 and 300 ms and five different T2 peaks at around 400, 97, 18, 5 and 1.4 ms were observed. The T1 component of 1300 ms (34%) can be associated with the T2 component of 400 ms (52%), which can be attributed to water in large voids due to wood decay and empty resin channels (i.e., full of water instead of resin), with a size of around 100 μm (as measured in the MR image of Fig. 1d). The shortest T1 peak at around 300 ms, which is also the most intense (59%), can be associated with the four shorter T2 peaks at around 97, 18, 5 and 1.4 ms. It should be noted that the peak at around 5 ms is not well-resolved and it is intermediate between the above-mentioned T2 peaks at 18 and 1.4 ms, and this suggests a continuous distribution among these three different water populations. T2 = 97 ms can be ascribed to water in large EW tracheid lumen (9%), T2 = 18 ms can be ascribed to water in the rest of EW tracheid lumen (24%) and T2 = 5 ms can be ascribed to LW tracheids (8%). Finally, T2 = 1.4 ms arises from bound water in cell walls (7%). The free and bound water peaks are closer to each other than in the case of modern spruce due to the partial decay of the cell wall structure as well as related accelerated exchange between the two sites. In conclusion, both for the modern and the ancient wood samples, earlywood tracheids occupy a greater volume than latewood tracheids. The T2 of the bound water in the ancient spruce wood is significantly longer than that in the modern spruce wood and there is a continuous distribution among the bound water, earlywood tracheids water and latewood tracheid water populations. This result denotes non-isolated water compartments and confirms the increase of the permeability of the cell wall due to its degradation,13,99 as shown by the stretching of its T2 component.Chestnut
In Fig. 4c, the modern chestnut has only two T1 components, while the ancient chestnut is characterized by four T1 components. In Fig. 4d, the modern and the ancient chestnuts exhibit similar T2 values. The ancient chestnut shows two high peaks at very long and very short T2 values, and a greater compartmentalization of water T2 populations. Conversely, the modern chestnut has a major peak at an intermediate T2 value and fewer water populations. The modern chestnut sample shows two T1 components around 1800 and 500 ms, whereas it is characterized by four T2 components around 175, 30, 5, and 0.4 ms. The T1 = 1800 ms peak (46%) can be associated with T2 = 175 and 30 ms peaks, which can be attributed to 11% of water in large vessels with a size of around 140–300 μm and to 18% of water in smaller pores with a size of around 60 μm, respectively. This agrees with the pore size measured on the respective MR image in Fig. 2a. The T1 = 500 ms peak (54%), instead, can be associated with two T2 components, 5 and 0.4 ms, that can be attributed, respectively, to water in fibres and parenchyma (55%), and to water in cell walls (16%). The three T2 peaks associated with two sizes of vessels (around 140–300 and 60 μm) and with fibres and parenchyma show a continuous distribution, whereas the T2 peak associated with cell walls is separated. The most intense T2 peak is that associated with fibres and parenchyma (55%). The archaeological chestnut shows a greater compartmentalization of both T1 and T2 with four T1 components around 3000, 900, 100 and 20 ms and six T2 components of about 350, 78, 26, 10, 2 and 0.6 ms. T1 = 3000 ms (11%) and T2 = 350 ms (29%) can be interpreted as free water in very large vessels with a size of around 260–350 μm, being in good agreement with the fact that vessels with a size of around 260–350 μm are also the most abundant in the MR image of Fig. 2b. The second T1 around 900 ms (6%) is associated with two different T2 = 78 and 26 ms (5 and 3%) and these can be attributed to water in vessels with a size of 170 μm. The third T1 peak at 100 ms (11%) is associated with the T2 peak at around 10 ms (3%) and they can be attributed to water in vessels with a size of 80 μm. Moreover, there is a continuous distribution among the peaks with T2 = 78, 26 and 10 ms that indicates the existence of not discrete relaxation populations in vessels. The last peak at very short T1 of 20 ms (73%) can be associated with the two shortest T2 peaks, at 2 and 0.6 ms (17 and 42%), and they are interpreted to arise from cell walls and fibers/parenchyma, respectively. Furthermore, the continuous distribution between the water population in fibres/parenchyma and that in cell walls suggests that there is water exchange between them. In conclusion, on average, the ancient chestnut shows a greater water compartmentalization and it is characterized by longer T2 relaxation times compared to the modern chestnut but it has two T1 components that are longer than those of the modern chestnut and two T1 components that are shorter. The shortening of these two T1 components is caused by the presence of paramagnetic inclusions, i.e., iron-tanning substances,28,99 in fibres, parenchyma, and cell walls. A strong degradation process of the wood cell wall, which has increased its water permeability and porosity, was observed, in good agreement with our previous work.28Maple
In Fig. 4e, the modern maple is characterized by only one T1 peak, whereas the ancient maple is characterized by three T1 peaks. In Fig. 4f, the modern and the ancient maple samples have a quite similar T2 distribution. However, the ancient maple shows an additional T2 component on the long side. The only one T1 component of the modern maple, around 1600 ms, can be considered a mean value over the overall structure. This T1 is associated with three different T2 at around 70, 15, and 1.5 ms that can be attributed, respectively, to water in vessels (44%) with a mean size of 36 ± 8 μm (measured on the MR image of Fig. 3a), water in fibres and parenchyma (50%), and water in cell walls (6%). There is a marked continuous distribution between the T2 peaks of vessels and fibres and the most intense peak is associated with fibres, which represent the 50% of the wood. For the ancient maple sample, the T1 component around 2100 ms and the T2 component around 350 ms indicate water in larger vessels (around 86 ± 10 μm, measured on the MR image in Fig. 3d).97,98 The second T1 = 700 ms can be associated with the two T2 = 78 and 16 ms and they are the characteristic, respectively, of water in smaller vessels (around 40 ± 4 μm, measured on the MR image in Fig. 3d) and water in fibres and parenchyma (67%), respectively. Here, a continuous distribution among vessels, fibres, and parenchyma can be observed. The last T1 = 200 ms is associated with the last T2 = 2.3 ms and they can be attributed to cell walls (4%). For the modern sample, also in the ancient sample, fibres are the most abundant element and constitute 67% of the wood.In conclusion, there is a greater compartmentalization of T1 in the ancient maple compared to the modern one. This may indicate possible structural changes in the ancient maple induced by a decay process. These changes are confirmed by the increase of T2 associated with the cell walls and the larger size of vessels in the ancient sample compared to the modern sample. However, it is worth noting that, while the specimen comes from the tree trunk for the ancient maple, the specimen was collected from a branch for the modern maple and this may be the reason of some structural differences observed in the two specimens.
Diffusion
Diffusion of water in the wood samples was measured in the tangential direction. Because in the diffusion experiments, magnetization remained in the transverse plane altogether for 10 ms before detection, and the bound water signal was filtered out due to its short T2. Altogether, three diffusion decay components were observed for all samples. However, for one of the components, the observed apparent diffusion coefficient value did not change when the observation time was increased, indicating non-restricted diffusion. Therefore, this component was interpreted to arise from bulk water on sample surfaces. For the two other diffusion components, the apparent diffusion coefficient values (D) as a function of the observation time (Δ) obtained from ILT analysis are shown in Fig. 5–7. The diffusion coefficients decrease with the increasing observation time due to restricted diffusion. The resulting surface-to-volume ratio (S/V) obtained from eqn (1) and the pore diameter (d), calculated from S/V, with the ratio between the weights (p1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p2) of the two d components are reported in Table 4, along with the average tortuosity (τ) obtained respectively from eqn (2) for spruce samples and from eqn (3) for chestnut and maple samples.
p2) of the two d components are reported in Table 4, along with the average tortuosity (τ) obtained respectively from eqn (2) for spruce samples and from eqn (3) for chestnut and maple samples.
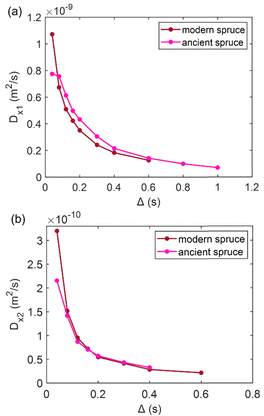 | ||
Fig. 5 (a) The first component (Dx1) and (b) the second component (Dx2) of the diffusion coefficient (D) measured along the x-axis (perpendicular to the wood grain) as a function of the observation time (Δ) and calculated using the ILT method76 for modern and ancient spruce samples. The intensity ratio between Dx1 and Dx2 components is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 and 1 0.10 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.26 for the modern spruce and the ancient spruce, respectively. 0.26 for the modern spruce and the ancient spruce, respectively. | ||
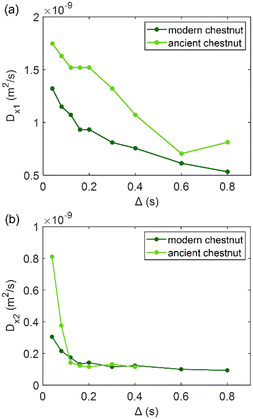 | ||
Fig. 6 (a) The first component (Dx1) and (b) the second component (Dx2) of the diffusion coefficient (D) measured along the x-axis (perpendicular to the wood grain) as a function of the observation time (Δ) and calculated using the ILT method76 for modern and ancient chestnut samples. The intensity ration ratio between Dx1 and Dx2 components is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.30 and 1 0.30 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.47 for the modern chestnut and the ancient chestnut, respectively. 0.47 for the modern chestnut and the ancient chestnut, respectively. | ||
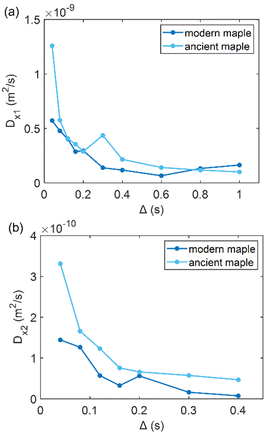 | ||
Fig. 7 (a) The first component (Dx1) and (b) the second component (Dx2) of the diffusion coefficient (D) measured along the x-axis (perpendicular to the wood grain) as function of the observation time (Δ) and calculated using the ILT method76 for modern and ancient maple samples. The intensity ratio between Dx1 and Dx2 components is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.38 and 1 0.38 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.06 for the modern maple and the ancient maple, respectively. 0.06 for the modern maple and the ancient maple, respectively. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p2), and mean tortuosity (τ) calculated as the weighted average between the tortuosity obtained for the two diffusion populations from eqn (2) for spruce samples and from eqn (3) for chestnut and maple samples
p2), and mean tortuosity (τ) calculated as the weighted average between the tortuosity obtained for the two diffusion populations from eqn (2) for spruce samples and from eqn (3) for chestnut and maple samples
| d 1 (μm) | d 2 (μm) |
p
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p2 p2 |
τ | |||
|---|---|---|---|---|---|---|
| Modern spruce | (1.9 ± 0.1) × 105 | (2.5 ± 0.3) × 105 | 31.7 ± 1.6 | 24.4 ± 2.8 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 0.10 |
16.9 ± 1.1 |
| Ancient spruce | (1.7 ± 0.1) × 105 | (2.5 ± 0.3) × 105 | 35.7 ± 1.8 | 24.2 ± 2.9 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.26 0.26 |
23.3 ± 1.3 |
| Modern chestnut | (1.3 ± 0.1) × 105 | (2.4 ± 0.3) × 105 | 45.2 ± 2.9 | 25.1 ± 3.0 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.30 0.30 |
7.2 ± 2.0 |
| Ancient chestnut | (7.4 ± 0.4) × 104 | (2.3 ± 0.1) × 105 | 81.5 ± 4.5 | 26.5 ± 1.6 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.47 0.47 |
23.9 ± 0.2 |
| Modern maple | (2.1 ± 0.2) × 105 | (2.5 ± 0.3) × 105 | 28.1 ± 2.9 | 23.7 ± 3.0 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.38 0.38 |
65.2 ± 0.7 |
| Ancient maple | (1.9 ± 0.1) × 105 | (2.4 ± 0.3) × 105 | 30.8 ± 1.5 | 24.6 ± 2.8 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.06 0.06 |
87.5 ± 0.6 |
It is worth noting that the major weakness of NMR diffusion is that the maximum length scale covered by this technique (on the order of  , where D0 = 2.2 × 10−9 m2 s−1 is the bulk water diffusion coefficient) is intrinsically limited by the characteristic T1 of the wood material, which limits the maximum diffusion delay (Δ < T1).
, where D0 = 2.2 × 10−9 m2 s−1 is the bulk water diffusion coefficient) is intrinsically limited by the characteristic T1 of the wood material, which limits the maximum diffusion delay (Δ < T1).
The results obtained from diffusion analyses are discussed separately for spruce, chestnut and maple in the following sections.
Spruce
In Fig. 5, the water diffusion measured perpendicular to the wood grain is quite similar both in the modern and in the ancient spruce samples. The two diffusion components, Dx1 and Dx2, are associated with water inside pores of sizes d1 = 31.7 ± 1.6 μm and d2 = 24.4 ± 2.8 μm in the modern spruce and with pores of sizes d1 = 35.7 ± 1.8 μm and d2 = 24.2 ± 2.9 μm in the ancient spruce, respectively. The pore size d1 can be attributed to the lumen size of earlywood tracheids, whereas the pore size d2 can be attributed to the lumen size of latewood tracheids, in good agreement with results reported in the literature.100 Both Dx1 and d1 are a bit higher in the ancient spruce indicating that their earlywood tracheids have a bit larger lumen size than those of the modern spruce. The relative intensity of the earlywood component was about 10 times higher than that of the latewood component, being in good agreement with the relaxation experiments. The mean tortuosity is higher in the ancient spruce (τ = 23.3 ± 1.3) than in the modern spruce (τ = 16.9 ± 1.1). This result suggests that on average water motion in the archaeological sample is more tangled than in the modern sample.Chestnut
Fig. 6 shows that on average the first component Dx1 of the diffusion coefficient in the archaeological chestnut is higher than that in the modern chestnut. Conversely, the component Dx2 is similar in both samples. The two derived pore sizes d1 and d2 can be associated with small vessels and with fibers and parenchyma, respectively. For the ancient chestnut, d1 = 81.5 ± 4.5 μm, whereas for the modern chestnut d1 = 45.2 ± 2.9 μm. This result indicates that vessels are smaller in the modern chestnut compared to the ancient one. Indeed, this pore size can be attributed to the smallest size of vessels that were measured on the μ-MR image for both wood samples (Fig. 2a and d). μ-MRI showed that the smallest size of vessels in the ancient chestnut (∼80 μm) was larger than that in the modern chestnut (∼60 μm). The pore size d2 = 26.5 ± 1.6 for the ancient chestnut and d2 = 25.1 ± 3.0 for the modern chestnut suggests that fibres and parenchyma have a similar size in both wood samples. The mean tortuosity is three times greater in the archaeological sample (τ = 23.9 ± 0.2) than that in the modern sample (τ = 7.2 ± 2.0) indicating that water motion is less easy in the archaeological sample. This result can be explained considering the high content of inclusions (i.e. iron-tanning substances28,99) stored in the structure of the ancient wood, as observed in the MR images (Fig. 2d–f). The inclusions lead to the formation of new compartments and water pools that make the ancient wood structure more complex.Maple
Fig. 7 shows that the two diffusion components, Dx1 and Dx2, are quite similar in the modern maple and ancient maple. These two water diffusion components are associated with two different pore sizes, d1 and d2, that are = 28.1 ± 2.9 and 23.7 ± 3.0 μm for the modern maple and 30.8 ± 1.5 and 24.6 ± 2.8 μm for the ancient maple, respectively. The intrinsic limitation due to the T1 only allowed us to probe water diffusion in small vessels (quantified by the diameter d1) of the ancient maple but not in the large vessels (with a size of around 86 μm) measured instead on the MR image (Fig. 3d). From diffusion, both the vessels size (d1) and the size of fibres and parenchyma (d2) are quite similar for both the ancient and modern samples. Moreover, it seems that vessels and fibers have a similar size in the modern sample. However, the mean tortuosity is greater in the ancient maple (τ = 87.5 ± 0.6) than that in the modern one (τ = 65.2 ± 0.7). This result suggests that on average water moves hardly in the archaeological wood.Cryoporometry
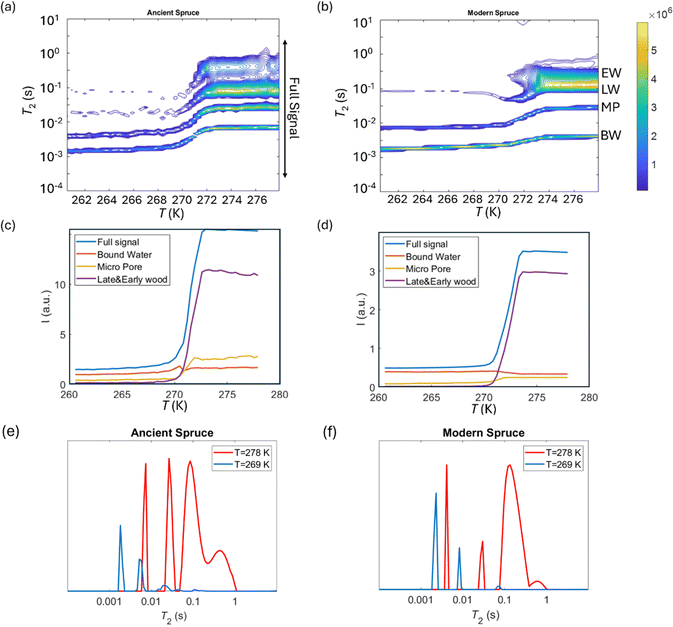
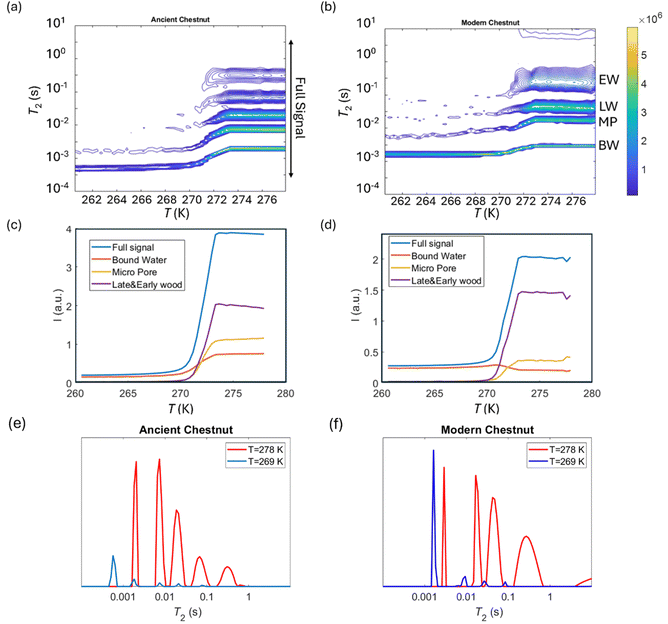
T 2 relaxation distributions and signal intensities are both plotted versus temperature for ancient and modern spruce, chestnut, and maple in Fig. 8–10, respectively. Moreover, as an example, the T2 distribution at two different temperatures, one above (T = 278 K) and one below (T = 269 K), and a melting point of 273 K are reported. Different signal contributions were separated, such as earlywood (EW), latewood (LW), micropore (MP) and bound water (BW). The two components observed below 273 K can be associated with two populations of bound water in the cell wall: BW has the shorter T2 and arises from water molecules hydrogen bonded to the hydroxyl groups and between the cellulose chains, whereas MP water has the longer T2 component and originates from water in cell wall micropores.48,101 It can be seen that, in all modern samples, the bound water signal intensity decreases after the bulk melting point, most probably because the bound water and free water signals are partially mixed due to molecular exchange.48,102 We note that the exchange cannot take place below the bulk melting point, as free water is frozen. A similar trend was not observed in the ancient counterparts, suggesting differences in the structure and dynamics. Furthermore, in all cases, water associated with tracheid/vessel lumens is frozen, as no clear signal is observed corresponding to those at lower temperatures, and as these structures are bigger in nature, the main melting point of these structures coincides with the bulk melting point of water (T = 273 K). In all the modern wood samples, the EW and LW signals constitute most of the full signal, while in the ancient counterparts, the relative amount of EW and LW water is significantly smaller, and other components (i.e., cell walls) also play crucial role in the total signal, in good agreement with relaxometry results showing an increased T2 peak associated with water in cell walls. All ancient wood samples have MP water signals greater than that of their modern counterparts, indicating an increase of the micropore water content in the ancient wood samples. This result confirms the degradation suffered by the cell wall, corresponding to an increased permeability, which was already detected by relaxometry, diffusometry and micro-imaging. In the case of the ancient chestnut, also an extra signal is present (Fig. 9a), behaving similarly as the LW and EW signals, which is therefore likely attributed to similar bigger pore structures (i.e., vessels) associated with the wood structure. This is in agreement with the increased compartmentalization of vessels in the ancient chestnut, characterized by three main relaxation components belonging to three different vessel sizes of around 260–350 μm, 170 μm and 80 μm detected from relaxation measurements and observed in μ-MR images.The relative amounts of water in pores with a size of below 8 nm, corresponding to the ratio of the signal intensities measured at 265 K and above 273 K, are shown in Fig. 11. The main result is that in all ancient wood samples it is smaller than in modern wood samples. The decrease of water portion in small pores corresponds to the decreased amount of bound water in the archaeological wood samples due to decay of cell wall structures.30,103–105
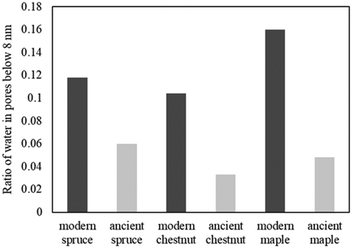 | ||
| Fig. 11 The amount of water in pores with a diameter of below 8 nm, corresponding to the ratio of the signal intensities measured at 265 K and above 273 K. | ||
Overall porosity
The combination of μ-MRI, relaxometry, diffusometry, and cryoporometry allowed us to cover several dimensional scales of wood samples, from cell wall cavities to sub-millimeter pores. In the following sections, we summarize the characteristics of the overall porosity and the different water distributions in each species of wood obtained by combining all the NMR techniques and we explain how these characteristics change as a result of the decay process.Spruce
Both the modern spruce and the ancient spruce are characterized by at least three water populations corresponding to three different pore sizes: earlywood tracheids, latewood tracheids and cell walls. In addition, the ancient spruce also shows a fourth population of water in the resin canals with a size of around 100 μm, which was not seen for the modern spruce where the resin canals, having a size of about 75 μm, are still full of resin rather than water. The earlywood tracheids in the ancient spruce have a larger diameter (∼36 μm) than in the modern spruce (∼32 μm). The similar T1 and T2 values along with the close diffusion coefficient (Dx2) and pore size (d2) indicate that LW tracheids have similar sizes in both the modern spruce and the ancient spruce. The increase of T2 associated with water in cell walls and the decrease of the water amount in pores smaller than 8 nm indicate that the cell walls of the archaeological wood can retain less bound water. This is most probably due to the decay of the cell walls, and it may be possible that bigger pores appeared in the cell walls of the ancient wood samples. The decay process of the wood cell wall was also observed in the MR images in Fig. 1 and in the optical microscopy images reported in our previous work.28 Moreover, the non-isolated water compartments in EW tracheids, LW tracheids and cell walls, along with the increased signal of MP water, confirm the increase of the cell wall permeability due to its degradation. The higher tortuosity measured for the ancient spruce is in agreement with the greater number of components of the relaxation times T1 and T2 indicating the increase of water compartmentalization in the structure of the archaeological wood. This increased compartmentalization is due to the presence of inclusions, spores, and residues of fungal hyphae,28 and to the overall structural decay that led to the formation of new pores and water pools.Chestnut
The modern and the ancient chestnut belong to the hardwood group that is characterized by structures with different sizes that correspond to several water populations. The modern chestnut has three mean vessel sizes of around 300, 140, and 60 μm, whereas the ancient chestnut has four vessels sizes of about 350, 260, 170, and 80 μm. In the ancient chestnut, the vessels with sizes in the range of 260–350 μm are the most abundant. On average, the ancient chestnut is characterized by larger vessels compared to the modern chestnut and it shows a greater water compartmentalization, as indicated by its greater number of T1 and T2 components and by its higher mean tortuosity. The shortening of the T1 components in the ancient chestnut is caused by the significant presence of paramagnetic inclusions, i.e., iron-tanning substances,28,99 in fibres, parenchyma and cell walls. Paramagnetic inclusions, that totally or partially obstruct vessels in the ancient sample, are also responsible for the formation of new compartments throughout the wood structure. Moreover, it is worth noting that, in the ancient wood, the T2 associated with water in vessels of size = 80 μm and with fibers/parenchyma is shorter than the T2 associated with water in vessels of size = 60 μm and fibers/parenchyma in the modern wood. This indicates that also the T2 may be shortened by the effect of paramagnetic substances. The decrease of the bound water amount in small pores (<8 nm) of the cell wall and the increased intensity of the MP water signal and of the T1 and T2 peaks associated with water in the cell walls of the ancient chestnut suggest a strong degradation process of the wood cell wall, which shows higher permeability and porosity, in good agreement with our previous work.28Maple
Three different water populations, corresponding to vessels, fibres and parenchyma, were detected for both the modern maple and the ancient maple. The modern maple is characterized by only one size of vessels, around 36 μm, whereas the ancient maple is characterized by two sizes, around 86 and 40 μm. Water is mostly stored in fibres and parenchyma, with a similar mean size of 25 μm in both the modern maple and the ancient maple. The similar size of fibres and parenchyma in both the wood samples is also confirmed by their close T2 values. The increase of T2 of water stored in cell walls in the archaeological maple suggests the increase of their size. Moreover, the decrease of the water content in pores below 8 nm of the cell walls along with the increase of the MP water signal in the ancient maple suggest a greater permeability of the cell walls. Again, the tortuosity is higher in the archaeological sample than in the modern sample, implying a more complex structure in the ancient wood. Indeed, the higher number of T1 and T2 components in the ancient sample indicates its greater structural compartmentalization that is induced by the decay process and the presence of spores and residues of fungal hyphae.28 However, the aforementioned results must be taken with care because the specimen comes from the tree trunk for the ancient maple and the specimen was collected from a branch for the modern maple. It may be that the total porosity and anatomical structures in the modern maple are not yet well developed compared to those in the ancient maple, due to their different growth stages.Conclusions
Research in the field of conservation sciences is constantly engaged in the search for innovative non-destructive techniques for the investigation of archaeological submerged wood. Ideal alternative techniques should allow obtaining information complementary or similar to that provided by conventional optical microscopy. This requirement has led to the advancement of the micro-imaging NMR technique with the optimization of its resolution such that it can resolve anatomical elements of wood with minimum dimensions around 10 micrometers. Additionally, wood anatomical features and water dynamics can also be characterized indirectly using techniques such as NMR relaxometry, NMR diffusometry, and NMR cryoporometry, which provide the characterization of both static and dynamic systems, e.g., MR imaging vs. diffusion-weighted imaging (DWI). Specifically, NMR cryoporometry overcomes the resolution limit of MRI and diffusion and the paramagnetic bias of relaxometry, allowing us to go below 10 microns and investigate wood structures on the nanometric scale (i.e., cell walls). Combining the above-mentioned NMR techniques and using appropriate mathematical models, it was possible to implement an innovative NMR protocol to obtain a comprehensive analysis of the porous wood structure. This work laid the foundation for the application of the new NMR protocol to the archaeological waterlogged wood. The multi-modal approach allowed us to detect the incipient cell wall decay, the accumulation of inclusions (black areas in MR images) and the biological infestations in the three archaeological wood samples studied in this work. Decay, inclusions, fungal spores, and hyphae have increased the structural complexity (corresponding to a higher tortuosity) of the ancient wood with the formation of new populations of water, identified by new T1 and T2 components, compared to the modern wood samples. All three ancient wood samples are characterized by a lower amount of water inside pores with a size of below 8 nm compared to the modern wood samples, indicating that the cell walls in the ancient wood hold more water in bigger pores and increase their permeability. To the best of our knowledge, this is the first study to jointly apply four different NMR techniques to encompass all the relevant length scales of wood. In future work, the protocol needs to be tested on a higher number of samples to verify its validity on several wood species. It would be preferable to develop two separate protocols, one for the characterization of softwood and the other for hardwood. Wood samples can have quite different structures depending on the individual, the age of the wood, and the location of the sample in the trunk/branch. Therefore, the differences between modern and ancient wood samples will require careful evaluation and correct interpretation.Data availability
Data for this article are available at “STAGNO 2024” at 10.6084/m9.figshare.26196911.Conflicts of interest
There are no conflicts to declare.Acknowledgements
V. Stagno acknowledges the funding of Lazio Region under the Torno Subito 2018 program of the Department of Education, Research, School, University, and the Regional Body for the Right to Study and Knowledge (DiSCo). O. Mankinen acknowledges the Research Council of Finland (grant number 355001), KAUTE foundation and Finnish Cultural Foundation-Kalle and Dagmar Välimaan Fund. V.-V. Telkki acknowledges European Research Council (grant number 772110), the Research Council of Finland (grant number 340099) and Kvantum institute (University of Oulu) for financial support. Part of this work was carried out with the support of the Centre for Material Analysis, the University of Oulu, Finland. The authors thank the national Italian agreement between CRUI-CARE and Royal Society of Chemistry (RSC) for funding the article processing charge (APC).Notes and references
- W. H. Schoch, G. Bigga, U. Böhner, P. Richter and T. Terberger, New insights on the wooden weapons from the Paleolithic site of Schöningen, J. Hum. Evol., 2015, 89, 214–225 CrossRef PubMed.
- C. G. Björdal, T. Nilsson and G. Daniel, Microbial decay of waterlogged archaeological wood found in Sweden. Applicable to archaeology and conservation, Int. Biodeterior. Biodegrad., 1999, 43, 63–73 CrossRef.
- N. B. Pedersen, J. J. Łucejko, F. Modugno and C. Björdal, Correlation between bacterial decay and chemical changes in waterlogged archaeological wood analysed by light microscopy and Py-GC/MS, Holzforschung, 2021, 75, 635–645 CrossRef CAS.
- N. B. Pedersen, C. G. Björdal, P. Jensen and C. Felby, in Stability of Complex Carbohydrate Structures: Biofuels, Foods, Vaccines and Shipwrecks, ed. S. E. Harding, The Royal Society of Chemistry, 2012, pp. 160–187 Search PubMed.
- R. A. Blanchette, A review of microbial deterioration found in archaeological wood from different environments, Int. Biodeterior. Biodegrad., 2000, 46, 189–204 CrossRef.
- C. Gjelstrup Björdal, Microbial degradation of waterlogged archaeological wood, J. Cult. Herit., 2012, 13, S118–S122 CrossRef.
- K. E. High and K. E. H. Penkman, A review of analytical methods for assessing preservation in waterlogged archaeological wood and their application in practice, Heritage Sci., 2020, 8, 83 CrossRef.
- Å. Henrik-Klemens, F. Bengtsson and C. G. Björdal, Raman Spectroscopic Investigation of Iron-Tannin Precipitates in Waterlogged Archaeological Oak, Stud. Conserv., 2022, 67, 237–247 CrossRef.
- D. Cole Hamilton, B. Kaye, J. A. Chudek and G. Hunter, Nuclear magnetic resonance imaging of waterlogged wood, Stud. Conserv., 1995, 40, 41–50 CrossRef.
- D. J. Cole-Hamilton, J. A. Chudek, G. Hunter and C. J. M. Martin, N.M.R. imaging of water in wood including water-logged archaeological artefacts, J. Inst. Wood Sci., 1990, 12, 111–113 Search PubMed.
- J. I. Hedges, The Chemistry of Archaeological Wood, 1989 Search PubMed.
- R. Brunning and J. Watson, Waterlogged wood Guidelines on the recording, sampling, conservation and curation of waterlogged wood, English Heritage, 2010.
- N. Macchioni, Encyclopedia of Global Archaeology, 2020 Search PubMed.
- M. Broda and C. A. S. Hill, Conservation of waterlogged wood—past, present and future perspectives, Forests, 2021, 12, 1193 CrossRef.
- M. N. Mortensen, H. Egsgaard, S. Hvilsted, Y. Shashoua and J. Glastrup, Characterisation of the polyethylene glycol impregnation of the Swedish warship Vasa and one of the Danish Skuldelev Viking ships, J. Archaeol. Sci., 2007, 34, 1211–1218 CrossRef.
- Conservation of cultural heritage. Guidelines for the management of waterlogged wood on archaeological terrestrial sites, Europe, 2016.
- M. Bardet, G. Gerbaud, Q. K. Trân and S. Hediger, Study of interactions between polyethylene glycol and archaeological wood components by 13C high-resolution solid-state CP-MAS NMR, J. Archaeol. Sci., 2007, 34, 1670–1676 CrossRef.
- J. Stelzner, I. Stelzner, J. Martinez-Garcia, D. Gwerder, M. Wittköpper, W. Muskalla, A. Cramer, G. Heinz, M. Egg and P. Schuetz, Stabilisation of waterlogged archaeological wood: the application of structured-light 3D scanning and micro computed tomography for analysing dimensional changes, Heritage Sci., 2022, 10, 60 CrossRef CAS PubMed.
- Z. Walsh, E. R. Janeček, M. Jones and O. A. Scherman, Natural polymers as alternative consolidants for the preservation of waterlogged archaeological wood, Stud. Conserv., 2017, 62, 173–183 CrossRef CAS.
- V. Stagno, C. Moricca, L. Sadori, E. Dell’Aglio, R. Reale and S. Capuani, Evaluation of the efficacy of micro-Magnetic Resonance Imaging compared with light microscopy to investigate the anatomy of modern and ancient waterlogged wood, Magn. Reson. Imaging, 2023, 102, 164–178 CrossRef PubMed.
- J. L. Silva, C. S. Barata and J. Pissarra, Limitations and Obstacles on Wood Identification From Sculptures - Analysis of A Set of Gilded and Polychromed Flemish Artworks From The 15thCentury, Int. J. Conserv. Sci., 2021, 12, 349–360 Search PubMed.
- R. Bruzzone and M. C. Galassi, Studying old master paintings: technology and practice: the National Gallery Technical Bulletin 30th anniversary conference postprints, 2011, pp. 253–259 Search PubMed.
- K. Čufar, A. Balzano, L. Krže and M. Merela, Wood identification using non-destructive confocal laser scanning microscopy, Les/Wood, 2019, 68, 19–29 CrossRef.
- F. Ruffinatto, N. Macchioni, G. Boetto, P. Baas and R. Zanuttini, Reflected light microscopy as a non-invasive identification tool for wooden artefacts, IAWA J., 2010, 31, 317–331 Search PubMed.
- F. Ruffinatto, C. Cremonini, N. Macchioni and R. Zanuttini, Application of reflected light microscopy for non-invasive wood identification of marquetry furniture and small wood carvings, J. Cult. Herit., 2014, 15, 614–620 CrossRef.
- S. Capuani, V. Stagno, M. Missori, L. Sadori and S. Longo, High-resolution multiparametric MRI of contemporary and waterlogged archaeological wood, Magn. Reson. Chem., 2020, 58, 860–869 CrossRef CAS PubMed.
- S. Longo, F. Egizi, V. Stagno, M. G. Di Trani, G. Marchelletta, T. Gili, E. Fazio, G. Favero and S. Capuani, A Multi-Parametric Investigation on Waterlogged Wood Using a Magnetic Resonance Imaging Clinical Scanner, Forests, 2023, 14, 276 CrossRef.
- V. Stagno, S. Mailhiot, S. Capuani, G. Galotta and V. V. Telkki, Testing 1D and 2D single-sided NMR on Roman age waterlogged woods, J. Cult. Herit., 2021, 50, 95–105 CrossRef.
- C. Moricca, V. Stagno, N. M. Hamza, G. Favero, L. Sadori and S. Capuani, The High Potential of Micro-Magnetic Resonance Imaging for the Identification of Archaeological Reeds: The Case Study of Tutankhamun, Heritage, 2023, 6, 7170–7180 CrossRef.
- J. Guo, L. Xiao, L. Han, H. Wu, T. Yang, S. Wu, Y. Yin and L. A. Donaldson, Deterioration of the cell wall in waterlogged wooden archeological artifacts, 2400 years old, IAWA J., 2019, 40, 820–844 Search PubMed.
- J. Kowalczuk, A. Rachocki, M. Broda, B. Mazela, G. A. Ormondroyd and J. Tritt-Goc, Conservation process of archaeological waterlogged wood studied by spectroscopy and gradient NMR methods, Wood Sci. Technol., 2019, 53, 1207–1222 CrossRef CAS.
- P. M. Kekkonen, V. V. Telkki and J. Jokisaari, Determining the highly anisotropic cell structures of Pinus sylvestris in three orthogonal directions by PGSTE NMR of absorbed water and methane, J. Phys. Chem. B, 2009, 113, 1080 CrossRef CAS PubMed.
- Ö. Gezici-Koç, S. J. F. Erich, H. P. Huinink, L. G. J. van der Ven and O. C. G. Adan, Bound and free water distribution in wood during water uptake and drying as measured by 1D magnetic resonance imaging, Cellulose, 2017, 24, 535–553 CrossRef.
- P. T. Callaghan, Principle of Nuclear Magnetic Resonance Microscopy, 1994 Search PubMed.
- D. Shaw, Fourier transform NMR spectroscopy, Elsevier Scientific Pub Co, 1976 Search PubMed.
- C. L. Partain, Nuclear Magnetic Resonance NMR Imaging, Saunders College Publishing, 1983 Search PubMed.
- C. L. Maini, G. Valle, M. G. Bonetti and M. A. Macrì, Principi di tomografia a risonanza magnetica nucleare, I.S.U. Università Cattolica Milano, 1987.
- E. L. Hahn, An accurate nuclear magnetic resonance method for measuring spin-lattice relaxation times, Phys. Rev., 1949, 76, 145 CrossRef CAS.
- J. Keeler, Understanding NMR Spectroscopy, 2nd edn, Wiley, 2010 Search PubMed.
- U. Mikac, M. Merela, P. Oven, A. Sepe and I. Serša, Mr study of water distribution in a beech (Fagus sylvatica) branch using relaxometry methods, Molecules, 2021, 26, 4305 CrossRef CAS PubMed.
- R. E. Hernández and C. B. Cáceres, Magnetic resonance microimaging of liquid water distribution in sugar maple wood below fiber saturation point, Wood Fiber Sci., 2010, 42, 259–272 Search PubMed.
- C. Cai, M. A. Javed, S. Komulainen, V. V. Telkki, A. Haapala and H. Heräjärvi, Effect of natural weathering on water absorption and pore size distribution in thermally modified wood determined by nuclear magnetic resonance, Cellulose, 2020, 27, 4235–4247 CrossRef CAS.
- S. Hiltunen, A. Mankinen, M. A. Javed, S. Ahola, M. Venäläinen and V. V. Telkki, Characterization of the decay process of Scots pine caused by Coniophora puteana using NMR and MRI, Holzforschung, 2020, 74, 1021–1032 CAS.
- V. V. Telkki, Wood characterization by NMR & MRI of fluids, eMagRes, 2012, 1, 1 Search PubMed.
- G. Costantini, S. Capuani, F. A. Farrelly and A. Taloni, A new perspective of molecular diffusion by nuclear magnetic resonance, Sci. Rep., 2023, 13, 1–19 CrossRef PubMed.
- V. Stagno, F. Egizi, F. Corticelli, V. Morandi, F. Valle, G. Costantini, S. Longo and S. Capuani, Microstructural features assessment of different waterlogged wood species by NMR diffusion validated with complementary techniques, Magn. Reson. Imaging, 2021, 83, 139–151 CrossRef CAS PubMed.
- V. Stagno and S. Capuani, Decay of a Roman age pine wood studied by micro magnetic resonance imaging, diffusion nuclear magnetic resonance and portable nuclear magnetic resonance, Acta IMEKO, 2022, 11, 1–10 CrossRef.
- P. M. Kekkonen, A. Ylisassi and V. V. Telkki, Absorption of water in thermally modified pine wood as studied by nuclear magnetic resonance, J. Phys. Chem. C, 2014, 118, 2146–2153 CrossRef CAS.
- B. Blümich, M. Baias, C. Rehorn, V. Gabrielli, D. Jaschtschuk, C. Harrison, C. Invernizzi and M. Malagodi, Comparison of historical violins by non-destructive MRI depth profiling, Microchem. J., 2020, 158, 105219 CrossRef.
- N. Proietti, D. Capitani and V. Di Tullio, Applications of nuclear magnetic resonance sensors to cultural heritage, Sensors, 2014, 14(4), 6977–6997 CrossRef CAS PubMed.
- S. Viel, D. Capitani, N. Proietti, F. Ziarelli and A. L. Segre, NMR spectroscopy applied to the Cultural Heritage: A preliminary study on ancient wood characterisation, Appl. Phys. A: Mater. Sci. Process., 2004, 79, 357–361 CrossRef CAS.
- V. Di Tullio, D. Capitani, A. Atrei, F. Benetti, G. Perra, F. Presciutti, N. Proietti and N. Marchettini, Advanced NMR methodologies and micro-analytical techniques to investigate the stratigraphy and materials of 14th century Sienese wooden paintings, Microchem. J., 2016, 125, 208–218 CrossRef CAS.
- C. Casieri, L. Senni, M. Romagnoli, U. Santamaria and F. De Luca, Determination of moisture fraction in wood by mobile NMR device, J. Magn. Reson., 2004, 171(2), 364–372 CrossRef CAS PubMed.
- B. Blümich, L. Ciobanu and S. Haber-Pohlmeier, Magnetic resonance microscopy: instrumentation and applications in engineering, life science and energy research, John Wiley & Sons, Inc., Hoboken, NJ, 2022 Search PubMed.
- B. J. Balcom and M. Zhang, Magn. Reson. Microsc., 2022, 337–353 Search PubMed.
- V. Di Donato, M. R. Ruello, V. Liuzza, V. Carsana, D. Giampaola, M. A. Di Vito, C. Morhange, A. Cinque and E. Russo Ermolli, Development and decline of the ancient harbor of Neapolis, Geoarchaeology, 2018, 33, 542–557 CrossRef.
- D. Giampaola, V. Carsena, G. Boetto, F. Crema, C. Florio, D. Panza, B. Pizzo, C. Capretti, G. Galotta, G. Giachi, N. Macchioni, M. P. Nugari and M. Bartolini, Archaeol. maritima Mediterr. Int. J. Underwater Archaeol., 2005, 2, 1–216 Search PubMed.
- E. A. Wheeler, InsideWood - A web resource for hardwood anatomy.
- P. Baas, N. Blokhina, T. Fujii, P. E. Gasson, D. Grosser, I. Heinz, J. Ilic, J. Xiaomei, R. Miller, L. A. Newsom, S. Noshiro, H. G. Richter, M. Suzuki, T. Terrazas, E. Wheeler and A. Wiedenhoeft, IAWA List of microscopic features for softwood identification, IAWA J., 2004, 25, 1–70 Search PubMed.
- D. J. B. White, E. A. Wheeler, P. Baas and P. E. Gasson, IAWA List of Microscopic Features for Hardwood Identification by an IAWA Committee, IAWA J., 1991, 10, 219–332 Search PubMed.
- F. Ruffinatto, A. Crivellaro and A. C. Wiedenhoeft, Review of macroscopic features for hardwood and softwood identification and a proposal for a new character list, IAWA J., 2015, 36, 208–241 Search PubMed.
- D. Capitani, V. Di Tullio and N. Proietti, Nuclear magnetic resonance to characterize and monitor cultural heritage, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 64, 29–69 CrossRef CAS PubMed.
- E. D. Becker, J. A. Ferretti, R. K. Gupta and G. H. Weiss, The choice of optimal parameters for measurement of spin-lattice relaxation times. II. Comparison of saturation recovery, inversion recovery, and fast inversion recovery experiments, J. Magn. Reson., 1980, 37, 381–394 CAS.
- R. L. Vold, J. S. Waugh, M. P. Klein and D. E. Phelps, Measurement of spin relaxation in complex systems, J. Chem. Phys., 1968, 48, 3831–3832 CrossRef CAS.
- V. V. Krishnan and N. Murali, Radiation damping in modern NMR experiments: Progress and challenges, Prog. Nucl. Magn. Reson. Spectrosc., 2013, 68, 41–57 CrossRef CAS PubMed.
- S. Meiboom and D. Gill, Modified spin-echo method for measuring nuclear relaxation times, Rev. Sci. Instrum., 1958, 29, 688–691 CrossRef CAS.
- R. Amador-Baheza, E. Sacristan-Rock and A. O. Rodríguez, Dual Frequency Coil Array for MR Imaging, AIP Conf. Proc., 2002, 630, 153–163 CrossRef.
- A. Haase, Principles and applications of FLASH NMR imaging, Magn. Reson. Mater. Phys., Biol. Med., 1994, 2, 157–160 CrossRef.
- H. T. Edzes, D. van Dusschoten and H. Van As, Quantitative T2 imaging of plant tissues by means of multi-echo MRI microscopy, Magn. Reson. Imaging, 1998, 16, 185–196 CrossRef CAS PubMed.
- J. E. Tanner, Use of the stimulated echo in nmr diffusion studies, J. Chem. Phys., 1970, 52, 2523–2526 CrossRef CAS.
- D. A. Faux and P. J. McDonald, Nuclear-magnetic-resonance relaxation rates for fluid confined to closed, channel, or planar pores, Phys. Rev. E, 2018, 98, 063110 CrossRef CAS.
- M. Urbańczyk, A. Shchukina, D. Gołowicz and K. Kazimierczuk, TReNDS—Software for reaction monitoring with time-resolved non-uniform sampling, Magn. Reson. Chem., 2019, 57, 4–12 CrossRef PubMed.
- P. Galvosas and P. T. Callaghan, Multi-dimensional inverse Laplace spectroscopy in the NMR of porous media, C. R. Phys., 2010, 11, 172–180 CrossRef CAS.
- L. Venkataramanan, Y. Q. Song and M. D. Hürlimann, Solving Fredholm integrals of the first kind with tensor product structure in 2 and 2.5 dimensions, IEEE Trans. Signal Process., 2002, 50, 1017–1026 CrossRef.
- P. Berman, O. Levi, Y. Parmet, M. Saunders and Z. Wiesman, Laplace inversion of low-resolution NMR relaxometry data using sparse representation methods, Concepts Magn. Reson., Part A: Bridging Educ. Res., 2013, 42, 72–88 CrossRef PubMed.
- M. Urbańczyk, D. Bernin, W. Koźmiński and K. Kazimierczuk, Iterative thresholding algorithm for multiexponential decay applied to PGSE NMR data, Anal. Chem., 2013, 85, 1828–1833 CrossRef PubMed.
- A. V. Anisimov, N. Y. Sorokina and N. R. Dautova, Water diffusion in biological porous systems: A NMR approach, Magn. Reson. Imaging, 1998, 16, 565 CrossRef CAS PubMed.
- L. L. Latour, P. P. Mitra, R. L. Kleinberg and C. H. Sotak, Time-Dependent Diffusion Coefficient of Fluids in Porous Media as a Probe of Surface-to-Volume Ratio, J. Magn. Reson., Ser. A, 1993, 101, 342–346 CrossRef CAS.
- P. P. Mitra, P. N. Sen, L. M. Schwartz and P. Le Doussal, Diffusion propagator as a probe of the structure of porous media, Phys. Rev. Lett., 1992, 68, 3555 CrossRef CAS PubMed.
- R. W. Mair, P. N. Sen, M. D. Hürlimann, S. Patz, D. G. Cory and R. L. Walsworth, The narrow pulse approximation and long length scale determination in xenon gas diffusion NMR studies of model porous media, J. Magn. Reson., 2002, 156, 202–212 CrossRef CAS PubMed.
- P. N. Sen, Time-dependent diffusion coefficient as a probe of geometry, Concepts Magn. Reson., Part A: Bridging Educ. Res., 2004, 23A, 1–21 CrossRef.
- F. A. L. Dullien, Porous media: fluid transport and pore structure, Academic press, 1st edn, 1979 Search PubMed.
- M. Zecca, S. J. Vogt, P. R. J. Connolly, E. F. May and M. L. Johns, NMR Measurements of Tortuosity in Partially Saturated Porous Media, Transp. Porous Media, 2018, 125, 271–288 CrossRef.
- M. Urbańczyk, Y. Kharbanda, O. Mankinen and V. V. Telkki, Accelerating Restricted Diffusion NMR Studies with Time-Resolved and Ultrafast Methods, Anal. Chem., 2020, 92, 9948–9955 CrossRef PubMed.
- C. R. Brodersen, Visualizing wood anatomy in three dimensions with high-resolution X-ray micro-tomography (MCT) – A review, IAWA J., 2013, 34, 408–424 Search PubMed.
- J. Mitchell, J. B. W. Webber and J. H. Strange, Nuclear magnetic resonance cryoporometry, Phys. Rep., 2008, 461, 1–36 CrossRef CAS.
- O. Petrov and I. Furó, Curvature-dependent metastability of the solid phase and the freezing-melting hysteresis in pores, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 11608 CrossRef PubMed.
- J. H. Strange, M. Rahman and E. G. Smith, Characterization of porous solids by NMR, Phys. Rev. Lett., 1993, 71, 3589 CrossRef CAS PubMed.
- B. Cowan, Nuclear Magnetic Resonance and Relaxation, 1997 Search PubMed.
- Y. Kharbanda, M. Urbańczyk, O. Laitinen, K. Kling, S. Pallaspuro, S. Komulainen, H. Liimatainen and V.-V. Telkki, Comprehensive NMR Analysis of Pore Structures in Superabsorbing Cellulose Nanofiber Aerogels, J. Phys. Chem. C, 2019, 123, 30986–30995 CrossRef CAS PubMed.
- V. V. Telkki, M. Yliniemi and J. Jokisaari, Moisture in softwoods: Fiber saturation point, hydroxyl site content, and the amount of micropores as determined from NMR relaxation time distributions, Holzforschung, 2013, 67, 291–300 CrossRef CAS.
- R. S. Menon, A. L. MaCkay, J. R. T. Hailey, M. Bloom, A. E. Burgess and J. S. Swanson, An NMR determination of the physiological water distribution in wood during drying, J. Appl. Polym. Sci., 1987, 33, 1141–1155 CrossRef CAS.
- N. Labbé, B. De Jéso, J. C. Lartigue, G. Daudé, M. Pétraud and M. Ratier, Time-domain 1H NMR characterization of the liquid phase in greenwood, Holzforschung, 2006, 60, 265–270 Search PubMed.
- S. Flibotte, R. S. Menon and A. L. MacKay, and J. R. T. Hailey, Proton Magnetic Resonance of Western Red Cedar, Wood Fiber Sci., 2007, 22, 362–376 Search PubMed.
- K. R. Brownstein, Diffusion as an explanation of observed NMR behavior of water absorbed on wood, J. Magn. Reson., 1980, 40, 505–510 CAS.
- C. Cai, F. Zhou and J. Cai, Bound water content and pore size distribution of thermally modified wood studied by nmr, Forests, 2020, 11, 1279 CrossRef.
- M. Fredriksson and P. Johansson, A Method for Determination of Absorption Isotherms at High Relative Humidity Levels: Measurements on Lime-Silica Brick and Norway Spruce (Picea abies (L.) Karst, Dry. Technol., 2016, 34, 132–141 CrossRef CAS.
- M. Fredriksson and L. G. Thygesen, The states of water in Norway spruce (Picea abies (L.) Karst.) studied by low-field nuclear magnetic resonance (LFNMR) relaxometry: Assignment of free-water populations based on quantitative wood anatomy, Holzforschung, 2017, 71, 77–90 CrossRef CAS.
- C. Capretti, N. Macchioni, B. Pizzo, G. Galotta, G. Giachi and D. Giampaola, The characterization of waterlogged archaeological wood: The three roman ships found in Naples (Italy), Archaeometry, 2008, 50, 855–876 CrossRef.
- P. O. Kettunen, Wood Structure and Properties, Trans Tech Publications, Uetikon-Zuerich, 2006 Search PubMed.
- R. S. Menon, A. L. Mackay, S. Flibotte and J. R. T. Hailey, Quantitative separation of NMR images of water in wood on the basis of T2, J. Magn. Reson., 1989, 82, 205–210 CAS.
- K. R. Brownstein and C. E. Tarr, Importance of classical diffusion in NMR studies of water in biological cells, Phys. Rev. A, 1979, 19, 2446 CrossRef.
- L. Han, X. Tian, T. Keplinger, H. Zhou, R. Li, K. Svedström, I. Burgert, Y. Yin and J. Guo, Even visually intact cell walls in waterlogged archaeological wood are chemically deteriorated and mechanically fragile: A case of a 170 year-old shipwreck, Molecules, 2020, 25, 1113 CrossRef CAS PubMed.
- J. Guo, J. Chen, R. Li, J. Liu, R. Luo, L. Jiao and Y. Yin, Thermoporometry of waterlogged archaeological wood: Insights into the change of pore traits after the water-removal by supercritical drying, Thermochim. Acta, 2022, 715, 179297 CrossRef CAS.
- H. Cao, X. Gao, J. Chen, G. Xi, Y. Yin and J. Guo, Changes in Moisture Characteristics of Waterlogged Archaeological Wood Owing to Microbial Degradation, Forests, 2023, 14, 9 CrossRef.
| This journal is © the Owner Societies 2024 |