Heteroatom-vacancy centres in molecular nanodiamonds: a computational study of organic molecules possessing triplet ground states through σ-overlap

Abstract

Small molecules possessing a triplet ground state are fundamentally intriguing but also in high demand for applications such as quantum sensing and quantum computing. Such molecules are rare, and most examples involve extended π-systems. Topology and shape of the spin density will be very different for molecules where the triplet state arises from σ-overlap. Drawing inspiration from NV⁻ (anionic nitrogen-vacancy) centres in a diamond crystal, which possess triplet ground states that are robust due to the distortion-preventing crystal lattice, we investigate hetero-atom substituted diamondoids (molecular nanodiamonds) as molecular mimics for NV⁻ centres. It is found that even in these small systems, distortions that stabilize singlet states are energetically costly, and the triplet states are more stable than the singlets. The stabilization of the triplet over the singlet is 13, 16, and 18 kcal mol⁻¹, in anionic C_3v-C₃₃H₃₆N⁻ and in the charge-neutral molecules C_3v-C₃₃H₃₆O and C_3v-C₃₃H₃₆S, respectively, using CAM-B3LYP-D3(BJ)/Def2-QZVPP. Comparable numbers are obtained with other density functional theory (DFT) methods, including double-hybrids. Wavefunction-based approaches on the other hand disagree in their predictions: While the MP2 method applied with the DLPNO approximation predicts a preference for the singlet, density matrix renormalization group (DMRG) calculations qualitatively agree with DFT in their prediction of a triplet ground state, although by a small margin, for C_3v-C₃₃H₃₆N⁻ and C_3v-C₃₃H₃₆O, but not for C_3v-C₃₃H₃₆S. Weighing the evidence, we conclude, with reasonable confidence for C_3v-C₃₃H₃₆N⁻ and C_3v-C₃₃H₃₆O and lesser confidence for C_3v-C₃₃H₃₆S, that the ground state for the molecular nanodiamonds studied is a triplet state.

---

Introduction

Organic molecular systems that possess a triplet ground state are very rare. However, such systems are in high demand due to their applications in organic magnets, memory devices, spintronics, and many other emerging technologies like quantum sensing and quantum computing.¹ Generally, π-conjugated systems are used to create a triplet ground state, and most research has focused on such systems.² Topology and shape of the spin density will be very different for molecules where the triplet state arises from σ-overlap.³ Here we study computationally organic molecular systems that lack π-bonds yet are ground-state triplets, by taking inspiration from defect centres in diamond.

The NV⁻ (anionic nitrogen-vacancy) centre in a diamond crystal lattice has a triplet ground state.⁴ NV⁻ centres are produced from the perfect crystal lattice by nitrogen doping/irradiation and suitable annealing. The NV⁻ centre can be understood if its formation is formally broken down into three steps (Fig. 1). An arbitrary carbon atom is removed from its T_d-symmetric environment inside the diamond crystal lattice, thereby generating a hole surrounded by four “dangling bonds”. Fig. 1a depicts a molecular orbital (MO) scheme for the vacancy centre thus formed. This analysis is closely based on the classic work by Loubser and van Wyk.⁵ Four valence electrons and four basis functions are in a T_d arrangement, resulting in one A₁ MO plus a T₂ set. Replacement of one of the four carbon atoms adjacent to the hole by nitrogen (Fig. 1b) lowers the symmetry from T_d to C_3v (T₂ → E + A₁) and creates a charge-neutral NV centre (NV⁰).⁶ Since N has one additional valence electron compared to carbon, the centre will now contain five valence electrons. The low-lying A₁ MO would be, due to the higher electronegativity of nitrogen compared to carbon, best described as a localized lone pair at nitrogen. Opposite to N resides a system of three carbon-based atomic orbitals directed toward a common point (the central vacancy) in C_3v symmetry, which contains the remaining three electrons. Thus, the simple scheme predicts for the NV⁰ centre that three electrons are delocalized in a three-carbon ring, in a C-based A₁ orbital (the higher one of the two A₁ MOs) and a C-based E set (Fig. 1b). Not strictly in a geometrical sense but in a topological (Hückel) sense, the situation is analogous to three hydrogen s-orbitals in a ring or to the cyclopropenyl π-system. While NV⁰ is a radical (spin doublet), NV⁺ is a closed-shell singlet⁷ (just as the σ-aromatic H₃⁺ or the aromatic cyclopropenium cation). Reduction of NV⁰ to NV⁻ is possible in the solid state, and the ground state of NV⁻, where the E set of orbitals is occupied by two electrons, will be a triplet (Fig. 1c). The triplet nature follows from orbital degeneracy, due to the threefold symmetry. Significant distortions destroying the threefold symmetry could lift the degeneracy of the E set to the extent that a distorted singlet state could become more stable – but this is prevented by the rigidity of the diamond lattice.

Fig. 1 Generation of an NV⁻ centre through a formal stepwise process: (a) carbon removal, (b) nitrogen substitution, (c) reduction.

The NV⁻ centre in crystalline diamond is a localized defect in a periodic diamond lattice.^4–8 The question arises of whether such a spin triplet-bearing centre could be incorporated into a small molecule and whether it still would be stable against distortion and singlet state formation.⁹ A molecular nanodiamond (diamondoid) could host such a centre. To mimic diamond, the molecule should have one central carbon that is surrounded by four tertiary carbon atoms in initial T_d symmetry. The smallest diamondoid with this property is T_d-decamantane or (“superadamantane”).¹⁰

If the central carbon atom is removed, one of the four tertiary carbon atoms is replaced by a nitrogen atom, and the molecule is reduced by an extra electron, a molecular anion is obtained that should be the smallest possible diamondoid that can realistically model a diamond NV⁻ centre: C_3v-C₃₃H₃₆N⁻. This molecule will here be referred to as NV⁻ (in bold). Since a charge-neutral oxygen or sulfur atom has the same number of valence electrons as N⁻, charge-neutral OV (C_3v-C₃₃H₃₆O) and SV (C_3v-C₃₃H₃₆S) will also be considered as alternative molecular candidates. Here we investigate and report the singlet–triplet energy gaps and possible distortions for NV⁻, OV, and SV (Fig. 2).

Fig. 2 General structure of the decamantane heteroatom-vacancy systems (NV⁻, OV, SV) studied in this work. The central cavity (decamantane would have a central carbon atom at this position) is surrounded by one heteroatom and, in a three-fold symmetric fashion (in the absence of distortion), by three tertiary carbon atoms labelled here as ‘a’, ‘b’, and ‘c’.

Computational methods

The molecules NV⁻, OV, and SV were computationally optimized as both spin singlet and spin triplet. Starting geometries were constructed manually using the Avogadro¹¹ program. Symmetry was not used as a constraint but was rather the result of an unconstrained geometry optimization (C_3v resulted for all triplet structures, C_s for all singlet structures). The starting geometries were subjected to geometry optimization, to the next local minimum, using the Gaussian¹² software package. These computations were run using 32 processors (2× Intel E5-2683 v4 Broadwell @ 2.1GHz CPU) on the Graham high-performance computing cluster of the Digital Resource Alliance of Canada. In order to not miss a low-lying local minimum, starting geometries were distorted in both an acute and an obtuse fashion (see Fig. 3) and allowed to relax from each. The quantum-chemical method used was the CAM-B3LYP¹³ density functional with Def2-QZVPP basis set¹⁴ and the D3¹⁵ dispersion correction scheme using Becke–Johnson¹⁶ (BJ) damping, i.e., CAM-B3LYP-D3(BJ)/Def2-QZVPP level of theory. CAM-B3LYP is a range-separated functional that minimizes the delocalization error and expected to predict reliable singlet–triplet energy gaps.¹⁷ A frequency calculation was performed for each minimum to ensure that true minima were found. In Gaussian, all calculations were performed in the gas-phase and employed a self-consistent field (SCF) convergence criterion of 10⁻⁸ hartrees (default), ultrafine integration grid, and tight optimization convergence criteria (maximum force  =  1.5  ×  10⁻⁵ hartrees bohr⁻¹, RMS force  =  1 × 10⁻⁵ hartrees bohr⁻¹, maximum displacement  =  6 × 10⁻⁵ bohr, RMS displacement  =  4 × 10⁻⁵ bohr). Spin contamination was found to be negligible for all triplets (2.00 < (〈S²〉) < 2.03). CAM-B3LYP-D3(BJ)/Def2-QZVPP optimized geometries were then used for all other electronic structure computations including single-point energy calculations with density functionals (with dispersion correction wherever appropriate) such as PBEPBE¹⁸, BP86¹⁹, M06-2X²⁰, LC-ωPBE²¹, ωB97xD.²² Further single-point energy calculations for double-hybrid density functionals with the DLPNO approximation i.e., DLPNO-B2PLYP²³ and DLPNO-DSD-PBEP86²⁴ were carried out with the Orca program.²⁵ Spin density plots (Fig. 4) were created with the visual molecular dynamics (VMD)²⁶ software using an isosurface value of 0.005 a.u. The spin-flip TDDFT calculations and SCF orbital and MO integral calculations in the Def2-QZVPP basis for DMRG have been performed using the Orca program at the Czech National Supercomputer centre IT4I in Ostrava. The DMRG calculations were performed using the MOLMPS program²⁷ at the computer cluster of the Heyrovsky Institute in Prague (32 nodes with Intel Xeon Gold 6226R nodes running at 2.9 GHz).

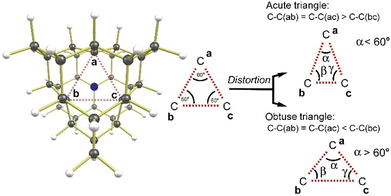Fig. 3 Possible Jahn–Teller distortions for the singlet states of NV⁻, OV, SV. View of the molecule is along the three-fold axis, through the cavity, with the heteroatom at the back of the molecule. The tertiary carbons a, b, and c (compare Fig. 2 for an alternative view) are involved in the distortion. The unique angle α (angle at unique tertiary carbon a) provides a measure of the distortion, and so does the difference between the C–C distances C–C(bc) and C–C(ab).

Fig. 4 Spin density plots for the triplet states of NV⁻, OV, and SV (using CAM-B3LYP-D3(BJ)/Def2-QZVPP). Each structure is viewed along the three-fold axis with the heteroatom in the back, similar to the view in Fig. 3. Isosurface value is 0.005 a.u.

Results and discussion

All spin triplet structures optimized, with CAM-B3LYP-D3(BJ)/Def2-QZVPP, to be C_3v-symmetric, as expected from MO arguments (Fig. 1). In contrast, spin singlet structures were found to distort, which is also expected: any significant distortion destroying the initially threefold symmetry will lift degeneracy in the initially doubly degenerate (E) set of orbitals to an extent that may be sufficient to stabilize a singlet state. This broadly Jahn–Teller-like distortion is similar to symmetry lowering and bond localization that stabilizes formally antiaromatic molecules. There are two possible Jahn–Teller distortions in a triangle: the equilateral triangle formed by the three quaternary carbons C(a), C(b), and C(c) might become either acute or obtuse (Fig. 3).

The undistorted structure, which we found for all spin triplets, consists of all three carbons (a, b, c) forming an equilateral triangle. In the distorted structures (all spin singlets we found), the unique carbon will be labelled ‘a’, with the corresponding angle denoted as ‘α’. Acute distortion is most easily seen in an angle α that is smaller than 60°, while obtuse distortion implies α > 60°. Alternatively, the C–C distances can be used. The distance C–C(bc) will be smaller than C–C(ab) in an acute triangle and larger in an obtuse triangle. For each of the molecules NV⁻, OV, and SV, we found indeed two spin singlet structures, one distorted in an acute fashion, the other one in an obtuse fashion. Energies, angles, and distances can be found in Table 1. Although the distorted singlets are true minima, they are energetically higher than the corresponding symmetrical spin triplet. Thus, DFT predicts that all molecules studied are true ground state triplets, enabled by the rigid polycyclic structure that makes distortions energetically costly. The singlet–triplet energy separation computes with CAM-B3LYP-D3(BJ)/Def2-QZVPP (Table 1) to be 17.8 kcal mol⁻¹ for SV and 15.6 and 12.8 kcal mol⁻¹ for OV and NV⁻, respectively, with the triplet most stable. Zero-point vibrational energy corrections lead to only minor changes in the exact values and do not change the relative ordering (Table 1). The predicted energetic separation between singlet and triplet will be sensitive to the specific density functional used. However, the qualitative result, the triplet is more stable than the singlet for all three species, is observed for all functionals we tried: CAM-B3LYP, PBEPBE, BP86, M06-2X, LC-ωPBE, ωB97XD, DLPNO-B2PLYP-D3BJ, DLPNO-DSDPBEP86-D3BJ, see ESI,† Table S2. It is particularly noteworthy that even the PBE functional, which is known to over-stabilize the lower spin state,²⁸ predicts the triplet to be more stable in all cases. The most stable singlets are predicted by PBEPBE to be higher than the triplet by 8.44 kcal mol⁻¹ for SV and 12.62 and 11.35 kcal mol⁻¹ for OV and NV⁻, respectively. Because of the known bias of PBEPBE, these numbers may serve as a lower bound for the true energy gap, and the fact that even PBEPBE (and also BP86) predicts a triplet ground state for all three species is a strong indication that this qualitative ordering – triplet more stable than singlet – is real. In addition to “energy-difference” DFT calculations, we also performed spin-flip TDDFT calculations, where the singlet state is computed by the TDDFT method from a triplet reference. We employed the CAM-B3LYP-D3(BJ) in Def2-QZVPP basis (with Def2/J auxiliary basis set) in the Orca program for these calculations. Except for distorted OV, and acute SV, where we were not able to converge the triplet KS DFT calculations for the distorted geometries, the results were in agreement with previous DFT calculations, confirming triplet ground states (ESI,† Table S2). For our conclusion about the ground state, it is safe to ignore spin–orbit coupling (SOC). We computed the SOC coupling vectors between the lowest singlet and triplet states for the NV⁻ and SV species at their acute geometries at the TDDFT/Def2-QZVPP level using Orca. For the former, the magnitude of the SOC vector was below 1 cm⁻¹ (<0.003 kcal mol⁻¹), while for the latter it was about 5 cm⁻¹ (0.015 kcal mol⁻¹) and we thus consider the effects of SOC on the singlet–triplet gap negligible.

Table 1 Summary of computational results obtained with the CAM-B3LYP-D3(BJ) density functional. For each molecule, the energy of the most stable spin state, triplet, is defined as zero, with values for the singlet spin states given relative to it. α, β, γ, C–C(bc), C–C(ab), C–C(ac) are defined as in Fig. 3

Molecule	Distortion	ΔES–T^a (kcal mol^−1)		α (°)	β (°)	γ (°)	C–C(bc) (Å) (base–base)	C–C(ab) (Å) (base–apex)	C–C(ac) (Å) (base–apex)
a ΔES–T is defined as the difference between the total energy obtained at CAM-B3LYP-D3(BJ)/Def2-QZVPP level of theory for singlet and triplet state. b is defined as the difference between the sum of the total energy obtained at CAM-B3LYP-D3(BJ)/Def2-QZVPP level of theory and zero-point energy correction obtained at CAM-B3LYP-D3(BJ)/Def2-TZVPP level of theory for singlet and triplet state.
NV ^− singlet	Acute	+12.8	+14.8	37.5	71.3	71.3	1.83	2.84	2.84
	Obtuse	+24.3	+24.2	69.8	55.1	55.1	2.98	2.60	2.60
NV ^− triplet	Undistorted	0.0	0.0	60.0	60.0	60.0	2.89	2.89	2.89
OV singlet	Acute	+15.6	+17.1	38.0	71.0	71.0	1.84	2.83	2.83
	Obtuse	+25.7	+25.5	70.2	54.9	54.9	2.97	2.59	2.59
OV triplet	Undistorted	0.00	0.0	60.0	60.0	60.0	2.88	2.88	2.88
SV singlet	Acute	+17.8	+20.0	39.2	70.4	70.4	1.89	2.81	2.81
	Obtuse	+23.3	+23.6	66.5	56.8	56.8	3.01	2.74	2.74
SV triplet	Undistorted	0.0	0.0	60.0	60.0	60.0	2.92	2.92	2.92

---

One still may wish to confirm the prediction of a ground state triplet using a post-Hartree–Fock wavefunction-based method of suitable accuracy. However, the size of our molecules precludes the use of many methods such as DLPNO-CCSD and CCSD(T) which are not feasible. Given these severe limitations imposed by the size of the system, we performed DLPNO-MP2 energy calculations in the Def2-TZVPP basis set (RI with Def2-TZVPP/C). Unlike the DFT results, DLPNO-MP2 favours the singlet states (by 5.5 kcal mol⁻¹ for NV⁻, 2.5 kcal mol⁻¹ for OV, 22.3 kcal mol⁻¹ for SV, see ESI,† Table S2). These data do not sway us to re-consider the predictions from DFT. A computational study on the ground state energetics, singlet or triplet, of various carbenes has recently concluded that “MP2 methods do not match the performance of double hybrid functionals, and are surprisingly challenged even by a functional such as BLYP”.²⁹ In order to test whether our molecules have multiconfigurational character in the states of interest, we performed DMRG computations in the (22,37) active space with a modest bond dimension 512 and basis set Def2-QZVPP. This active space should be large enough to include the important orbitals around the “active site”. We found that the DMRG energies strongly depend on the orbitals employed (ROHF triplet or RHF singlet orbitals), since the active space is much smaller than the orbital space and DMRG cannot compensate orbital relaxation effects. Unfortunately, DMRG-SCF calculations were computationally too demanding. We found out that the triplet state at the symmetric geometry is dominated by the HF determinant in the ROHF orbitals, while it has modest multireference character (the coefficient of the leading determinant about 0.8) when the DMRG is based on RHF singlet orbitals (orbital entropies confirming this conclusion). The singlet states have a degenerate two-determinantal character at the symmetric geometry, while at the distorted geometries they were also dominated by a single determinant in DMRG based on the RHF orbitals. One can thus conclude that at their respective optimum geometries, both singlet and triplet states do not exhibit strong static correlation and can be treated by a single-reference wavefunction method that capture the dynamic correlation. One potential weakness of DFT, lack of static correlation, is thus not a significant problem here. We decided to compare the DMRG energies and took the ones based on RHF singlet orbitals, with a bias favouring the singlet state. The adiabatic singlet–triplet energy gap computes with this method to be −3.37 kcal mol⁻¹ for SV (singlet more stable) while it is positive, 1.12 and 0.50 kcal mol⁻¹ for OV and NV⁻, respectively (triplet more stable). Weighing the evidence, our conclusion is that the ground state for the molecular nanodiamonds studied is a triplet, where our confidence is higher for OV and NV⁻ and lesser for SV.

The shape of the spin density is also worth commenting on. Most stable triplet molecules involve extended π-systems, but spins in π-systems are easily perturbed by the environment, such as solvent molecules interacting or other aromatics stacking closely. In contrast, spin density plots (CAM-B3LYP-D3(BJ)/Def2-QZVPP) for NV⁻, OV, and SV (Fig. 4) show that the spin density of the triplet spin state is mostly confined to the interior of the molecule, quite in line with what is predicted from simple MO arguments, with little extending to the surface through spin polarization. The spin density is carbon-based and is largely independent of the heteroatom used here (N⁻ or O or S). Based on the localization of the spin density in the interior, we would anticipate excellent chemical stability for these molecules. If the small spin density at the exterior hydrogens should become problematic, the hydrogen substituents could be replaced by alkyl substituents. The synthesis of molecular NV⁻, OV, and SV will be a challenging but worthwhile goal.

Conclusions

The superadamantane heteroatom-vacancy system successfully takes diamond heteroatom-vacancy centres into the molecular realm. All three molecular systems studied (NV⁻, OV, and SV) have a triplet ground state, as judged by DFT. We are reasonably confident in this prediction to be correct, at least for NV⁻ and OV, where DMRG computations also predict a triplet ground state (a singlet ground state is predicted for SV). The spin density is largely confined to the interior of the molecule and is mostly carbon based. Both features may be useful for creating very long-lived spin states in a molecular system – use of ¹²C could eliminate interaction with nuclear spins. We anticipate that these molecules are challenging but realistic targets for synthesis.

Author contributions

UF conceived and designed the project. CMM performed the geometry optimizations of singlets and triplets with CAM-B3LYP-D3(BJ)/Def2-QZVPP. VKP assisted with the computations, overseeing the research progress, and added single-point computations with additional functionals and with DLPNO-MP2. JP added TD-DFT as well as DMRG and SOC computations. All authors contributed to writing the paper.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

U. F. and C. M. M. would like to thank the Natural Sciences and Engineering Research Council of Canada for providing generous financial support, through a Discovery Grant to UF and an Undergraduate Student Research Award to C. M. M. V. K. P. was funded by the Data Sciences Institute (DSI) at the University of Toronto and the University of Toronto Mississauga through a DSI Catalyst Grant to UF and Hans-Arno Jacobsen (Electrical and Computer Engineering). Computational resource support was provided by the University of Toronto Mississauga and the Digital Research Alliance of Canada. J. P. acknowledges the assistance provided by the Advanced Multiscale Materials for Key Enabling Technologies project, supported by the Ministry of Education, Youth, and Sports of the Czech Republic. Project No. CZ.02.01.01/00/22_008/0004558, Co-funded by the EU. Part of the CPU time was supported by the IT4Innovations Centre of Excellence project (CZ.1.05/1.1.00/02.0070), funded by the European Regional Development Fund and the national budget of the Czech Republic via the Research and Development for Innovations Operational Programme, as well as Czech Ministry of Education, Youth and Sports via the project Large Research, Development and Innovations Infrastructures (LM2011033).

References

1. (a) A. Rajca, Chem. Rev., 1994, 94, 871–893; (b) S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336–3355; (c) I. Ratera and J. Veciana, Chem. Soc. Rev., 2012, 41, 303–349.
2. (a) L. C. Bush, R. B. Heath, X. W. Feng, P. A. Wang, L. Maksimovic, A. I. Song, W.-S. Chung, A. B. Berinstain, J. C. Scaiano and J. A. Berson, J. Am. Chem. Soc., 1997, 119, 1406–1415; (b) C. Herrmann, G. C. Solomon and M. A. Ratner, J. Am. Chem. Soc., 2010, 132, 3682–3684; (c) C. P. Constantinides, T. A. Ioannou and P. A. Koutentis, Polyhedron, 2013, 64, 172–180; (d) N. M. Gallagher, A. Olankitwanit and A. Rajca, J. Org. Chem., 2015, 80, 1291–1298; (e) W. Wang, C. Chen, C. Shu, S. Rajca, X. Wang and A. Rajca, J. Am. Chem. Soc., 2018, 140, 7820–7826; (f) N. Gallagher, H. Zhang, T. Junghoefer, E. Giangrisostomi, R. Ovsyannikov, M. Pink, S. Rajca, M. B. Casu and A. Rajca, J. Am. Chem. Soc., 2019, 141, 4764–4774.
3. X. Bao, X. Zhou, C. F. Lovitt, A. Venkatraman, D. A. Hrovat, R. Gleiter, R. Hoffmann and W. T. Borden, J. Am. Chem. Soc., 2012, 134, 10259.
4. (a) Á. Gali, Nanophotonics, 2019, 8, 1907–1943; (b) N. Savage, Nature, 2021, 591, S38–S39; (c) J. Wrachtrup and F. Jelezko, J. Phys.: Condens. Matter, 2006, 18, S807; (d) F. Casola, T. van der Sar and A. Yacoby, Nat. Rev. Mater., 2018, 3, 17088; (e) C. E. Bradley, J. Randall, M. H. Abobeih, R. C. Berrevoets, M. J. Degen, M. A. Bakker, M. Markham, D. J. Twitchen and T. H. Taminiau, Phys. Rev. X, 2019, 9, 031045.
5. J. H. N. Loubser and J. A. van Wyk, Rep. Prog. Phys., 1978, 41, 1201.
6. S. Baier, C. E. Bradley, T. Middelburg, V. V. Dobrovitski, T. H. Taminiau and R. Hanson, Phys. Rev. Lett., 2020, 125, 193601.
7. A. Karim, I. Lyskov, S. P. Russo and A. Peruzzo, J. Appl. Phys., 2021, 130, 234402.
8. (a) Y. G. Zhang, Z. Tang, X. G. Zhao, G. D. Cheng, Y. Tu, W. T. Cong, W. Peng, Z. Q. Zhu and J. H. Chu, Appl. Phys. Lett., 2014, 105, 052107; (b) R. Löfgren, R. Pawar, S. Öberg and J. A. Larsson, New J. Phys., 2018, 20, 023002.
9. NV⁻ centres in diamondoids were computed with DFT before, as models for the corresponding defect centres in diamond. Since they were not studied as molecules in their own right, they were assumed to be triplets, and the question of stability with regard to (possibly distorted) singlet states was not addressed: (a) V. A. Pushkarchuk, S. Y. Kilin, A. P. Nizovtsev, A. L. Pushkarchuk, A. B. Filonov and V. E. Borisenko, J. Appl. Spectrosc., 2007, 74, 95; (b) V. A. Pushkarchuk, A. B. Filonov, V. L. Shaposhnikov, A. P. Nizovtsev, A. L. Pushkarchuk and S. A. Kuten, in Physics, Chemistry and Application of Nanostructures, ed. V. E. Borisenko, S. V. Gaponenko, and V. S. Gurin, World Scientific, New Jersey, 2007, p. 22.
10. M. Shen, H. F. I. Schaefer, C. Liang, J. H. Lii, N. L. Allinger and P. V. R. Schleyer, J. Am. Chem. Soc., 1992, 114, 497–505.
11. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
12. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
13. (a) T. Yanai, P. D. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57; (b) S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211; (c) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100; (d) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789; (e) A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377; (f) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (g) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
14. F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753.
15. (a) S. Grimme, J. Anthony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
16. E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104.
17. (a) E. R. Johnson, A. Otero-de-la-Roza and S. G. Dale, J. Chem. Phys., 2013, 139, 184116; (b) H. Sun, C. Zhong and J.-L. Brédas, J. Chem. Theory Comput., 2015, 11, 3851; (c) A.-A. Farcas and A. Bende, AIP Conf. Proc., 2020, 2206, 030001.
18. (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
19. (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
20. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
21. (a) O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109; (b) O. A. Vydrov, J. Heyd, A. Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106; (c) O. A. Vydrov, G. E. Scuseria and J. P. Perdew, J. Chem. Phys., 2007, 126, 154109.
22. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
23. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
24. S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2011, 13, 20104–20107.
25. F. Neese, WIREs Comp. Mol. Sci., 2022, 12, 1.
26. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38.
27. J. Brabec, J. Brandejs, K. Kowalski, S. Xantheas, O. Legeza and L. Veis, J. Comp. Chem., 2021, 42, 534.
28. L. A. Mariano, B. Vlaisavljevich and R. Poloni, J. Chem. Theory Comput., 2020, 16, 6755–6762.
29. R. G. Shirazi, D. A. Pantazis and F. Neese, Mol. Phys., 2020, 118, e1764644.

---

Footnote

† Electronic supplementary information (ESI) available: XYZ coordinates and absolute as well as relative energies. See DOI: https://doi.org/10.1039/d4cp02667e

---