Effect of ion to ligand ratio on the aqueous to organic relative solubility of a lanthanide–ligand complex

Abstract

In the solvent extraction of rare earth elements, mechanistic aspects remain unclear regarding where and how extractant molecules coordinate metal ions and transport them from the aqueous phase into the organic phase. Molecular dynamics simulations were used to examine how unprotonated di(2-ethylhexyl)phosphoric acid (DEHP⁻) ligands that coordinate the Gd³⁺ ion can transfer the ion across the water–organic interface. Using the umbrella sampling technique, potential of mean force profiles were constructed to quantify the relative solubility of the Gd³⁺ ion coordinated to 0–3 DEHP⁻ ligands in either water, 1-octanol, or hexane solvents and at the water–organic interfaces. The simulations show the Gd–DEHP⁻ complexes, at varying Ln–ligand ratios, preferentially solvate on water–organic interfaces. While the Gd(DEHP⁻)₃ complex will diffuse past the aqueous–organic interface into the octanol solvent, it is thermodynamically preferred for the Gd(DEHP⁻)₃ complex to remain in the water–hexane interface when there is no amphiphilic layer of excess ligand.

---

Introduction

For several decades, there has been a rapid development of modern technologies that incorporate rare earth elements for their unique catalytic, magnetic, electrical, and optical properties. As a result, there has been great interest in improving the extraction and separation of rare earths from their ores and recycled electronics, particularly by increasing separation efficiency and reducing waste.^1,2 The predominant, scalable rare earth separation approach continues to be solvent extraction.³

The solvent extraction of lanthanide (Ln³⁺) ions involves placing an aqueous solution containing Ln³⁺ ions in contact with a diluent (typically an organic solution) that contains dissolved extractant molecules (ligands) that bind the Ln³⁺ ions and transfer them from the aqueous to organic phase.⁴ Multiple classes of complexing ligands have been employed as extractants, including diglycolamides, bis-trazinylpyridines, and organophosphorous compounds.^5,6 The extraction efficiency and selectivity for these ligands is expectedly dependent on the interplaying thermodynamic and kinetic factors related to both the immediate Ln–extractant complex and the extraction conditions. For example, the Ln–ligand interaction strength, complex coordination structure, presence and identity of counterions, and acidity of the system all impact the thermodynamic stability of the complex formed within the two layers.⁴ Likewise, the supramolecular and nanoscale fluid organization (particularly at the liquid–liquid interface) also influence the kinetics of the Ln–extractant complex to assembly and transfer between the two layers, similarly impacting solvent extraction efficiency.^7,8 Many studies have probed into where and how extractant aggregation, complexation, reverse micelle formation, and phase splitting occurs using X-ray reflectometry, fluorescence and kinetics experiments, X-ray spectroscopy, and other techniques.^8–13

Classical molecular dynamics (MD) simulations can examine liquid–liquid interfaces in atomic resolution with models comprising tens of thousands of atoms. With such sizeable systems, the solvent organization in bulk and interfacial regions can be modeled and provide atomic-level details into the effects of both solvent and ligand.^14,15 Moreover, rare event simulation techniques such as umbrella sampling may be used to drive the simulation along the biphasic transfer coordinate and quantify a free energy difference (i.e., relative solubility) between the two solvent layers.^16,17 Molecular dynamics simulations with rare event simulation techniques can provide quantitatively accurate predictions for octanol–water partition coefficients¹⁸ and has recently provided insights into the solubility of different lanthanide and actinide extraction complexes.^19–22

In this work, we model the liquid–liquid extraction of the Gd³⁺ ion with di(2-ethylhexyl)phosphoric acid (HDEHP, also called DEHPA; Fig. 1A) using MD umbrella sampling simulations. HDEHP was chosen given its common use as an organophosphorous extractant both independently and synergistically with other additives.^5,23,24 The amphiphilic character of HDEHP and similar extractants is known to lead to accumulation of the compounds at the aqueous–organic interface,^25,26 where it is then expected that Ln–ligand complexation and transfer to the organic phase occurs.^10,11,27 However, several studies have suggested an additional path can occur where the extractant diffuses into the bulk aqueous phase and complexes with the metal ions before reentry into the organic layer.^12,28–31 This path provides a target for kinetics-based separations since the crossing of aqueous phase complexes can be inhibited by excess extractant at the water–organic interface while complexes assembled at the interface continue to transfer to the organic phase.^12,32

Fig. 1 (A) Structure of HDEHP. (B) Biphasic model illustrating the aqueous layer (left; oxygen spheres colored red and hydrogen colored white) and organic hexane layer (right; orange sticks with hydrogens excluded for clarity).

This work describes a series of umbrella sampling MD simulations in a simplified structural model of the Gd–HDEHP complex in an aqueous–organic interface in order to characterize the relative solubility of Ln–ligand complexes across aqueous–organic interfaces. The simulations do not consider that higher HDEHP concentrations would form a monolayer in the aqueous–organic interface. The number of DEHP⁻ ligands (HDEHP with the phosphate deprotonated) coordinating Gd is varied from 0 to 3 to examine the impact of coordination structure on which phase (aqueous, interface, organic) the complex will preferentially solvate. The difference between having a polar or non-polar organic solvent is also evaluated with 1-octanol and hexane representing the organic phase.

Methodology

Molecular dynamics modeling

Models of the liquid–liquid interface comprising a water box (3500–4850 molecules) adjacent to an organic box of either 1-octanol or hexane (500–775 molecules) were constructed within an elongated Z-axis box with periodic boundary conditions (Fig. 1B). The molecule of interest (solute) was solvated within the bulk water layer along with Na⁺ or Cl⁻ counterions if necessary to maintain a net neutral charge. The MD simulations were modeled with OPLS-AA force field using previously published parameters for the solvents, ions, and molecules.^33–36 The OPLS force field was chosen to model the organic phase as it has been optimized to replicate liquid properties of organic molecules.³³ Also, the OPLS force field has been used to determine physical properties of alcohols and alkanes,³⁷ free energies of solvation of solutes in alcohols and alkanes,³⁸ and partitioning of solutes between water and octanol.³⁹ Parameters of the DEHP⁻ molecule, the box xy dimensions, as well as specific details on the number of solvent/ions present in each of the models are provided in the (ESI†) Table S1. While there are some known limitations in the OPLS-AA parameters towards modeling Ln³⁺ ions, and the development of improved forcefields and corrections continue to advance,^40–42 the forcefield is sufficient for this case study based on our previous work: we simulated the Gd³⁺ aqua ion and Gd–DTPA complexes with the OPLS-AA force field and demonstrated accuracy in determining the Gd coordination structures by verifying with extended X-ray absorption fine structure spectroscopy.⁴³

The systems were first minimized, followed by 3.5 ns of NPT simulation to equilibrate the box dimensions size using a 0.5 fs timestep (Fig. S1 and S2, ESI†). Temperature and pressure conditions were maintained at 298 K and 1 bar via the velocity-rescaling thermostat and Berendsen barostats, respectively.^44,45 Nonbonded interactions were cutoff at 9 Å and long-range electrostatics interactions were treated using a particle-mesh Ewald scheme.⁴⁶ During the NPT simulation, the molecule of interest (and any accompanying counterions) was restrained to their initial positions to prevent premature changing of solvent layers while the unrestrained solvent molecules equilibrated. All simulation computations were performed using the GROMACS v2021 software.⁴⁷

Umbrella sampling

To generate the initial configurations for the umbrella sampling simulations,¹⁷ a pulling simulation was conducted that translated the molecule of interest along the Z-axis from the bulk water into the organic layer. Continuing from the previous equilibrated NPT simulation, the center of mass of the molecule was pulled away from the center of mass of a random nearby water molecule within the aqueous phase whose position is restrained for an immobile distance reference. A pull rate of 0.1 Å ps⁻¹ and spring constant of 1000 kJ mol⁻¹ nm⁻² were used over a simulation time of at least 800 ps with a 1 fs timestep. Temperatures and pressure conditions were maintained at 298 K and 1 bar via the Nosé–Hoover thermostat and Parrinello–Rahman barostat.^48–51

The pulling simulation modeled a path for the molecule to traverse through the liquid–liquid interface along the Z-axis from the aqueous phase into the organic phase. The molecule was only constrained along the Z-axis and was freely permitted to translate in the xy plane. Structures along this path were collected every ∼0.2 nm, with additional configurations collected particularly near the interfacial interchange. The collected configurations were used as inputs for umbrella sampling simulations. The simulations began with a brief 50 ps NPT equilibration step which was then passed into a 10 ns NVT umbrella simulation to generate the ensemble. Once all the umbrella sampling simulations completed, a histogram of the energy distributions was constructed to verify the distributions were overlapping along the path (Fig. S3, ESI†), and additional samplings were conducted when needed. The potential of mean force (PMF) for each molecule over the course of their path was calculated by combining the local free energy segments calculated from the probability distribution functions of the position of the molecule via the weighted histogram analysis method (WHAM).⁵² As a measure of the statistical uncertainty in the obtained PMF, the difference in the PMF computed from sampling only the initial half of the NVT umbrella simulation versus the latter half of the simulation are also plotted to provide an upper and lower bounds to the computed PMF.

Computing partition coefficients

The partition coefficient K_OW measures the equilibrium ratio of concentrations of a solute within a two-phase system of water and 1-octanol:

From partition coefficients, the free energy difference between aqueous and organic phases (ΔG) can be calculated:

where R is the molar gas constant and T is the temperature.^18,53,54 Because the umbrella sampling simulations are performed in the NVT ensemble, Helmholtz free energies are obtained from simulation; however due to the very small differential volumes between each position in the umbrella sampling simulations, the free energies in the potential of mean force are essentially Gibbs free energy differences (ΔG_comp) that can be directly compared to the experimental free energy difference between aqueous and organic phases (ΔG_exp) calculated with eqn (2) from experimentally measured K_OW values. Indeed, computing solvation energy differences using the OPLS-AA forcefield has already demonstrated reasonable accuracy for drug-like organic molecules, with some overestimation on the hydrophobicity noted for some cases.^55,56 To confirm our approach, we first calculate the free energy difference between aqueous and organic phases from potentials of mean force for three solute molecules (ethylbenzene, acetonitrile, formamide) and compare to ΔG_exp values from known water octanol partition coefficients.

Results and discussion

Approach validation

Before modeling ion–ligand complexes across water–organic interfaces, we first conducted simulations of the transfer of acetonitrile, ethylbenzene, and formamide to validate the methods chosen for this study. The molecules are suitable as proof-of-concept tests because the molecules have known experimental octanol–water partition coefficients (log K_OW), and they have differing octanol–water solubilities as ethylbenzene is lipophilic, formamide is hydrophilic, and acetonitrile is slightly hydrophilic. Classical MD umbrella sampling simulations of the transfer of each of the three molecules from bulk water into either octanol or hexane solvent was conducted, and potentials of mean force (i.e., free energy profiles) were constructed (Fig. S4–S6, ESI†).

The main energetic features of the graphs are summarized in Table 1 and indicate there is qualitative agreement to the known hydrophilicities of the molecules. Using experimental log K_OW values of 3.2 to 3.6 for ethylbenzene,^57,58 −0.82 to −1.51 for formamide,⁵⁹ and −0.34 to −0.54 for acetonitrile,^60,61 values of experimental free energy difference between aqueous and organic phases (ΔG_exp) can be computed viaeqn (2) for a quantitative evaluation of accuracies for the octanol–water system. The results show excellent agreement between computation and experiment, confirming a quantitative accuracy for the umbrella sampling classical MD approach (Table 1).

Table 1 Free energy differences (kJ mol⁻¹) between aqueous and organic phases computed from the potentials of mean force (ΔG_comp) and compared to the experimental values (ΔG_exp) from known water–octanol partition coefficients

Solute	ΔGcomp water–hexane	ΔGcomp water–octanol	ΔGexp water–octanol
Ethylbenzene	−18.3	−19.1	−18.3, −20.5
Formamide	23.7	5.0	4.7, 8.6
Acetonitrile	14.8	3.2	1.9, 3.1

---

It is also of interest to examine the structural conformations of the molecules as they pass through the different layers. Octanol forms an ordered layer of molecules perpendicular to the plane of the interface with their polar alcohol groups hydrogen bonding with the water.⁶² This arrangement creates a barrier for individual molecules passing through the interface as the hydrogen bonding network occurring between water and octanol at the interface must be disrupted. While disrupting this ordered interface is shown to be unfavorable for both formamide and acetonitrile, the PMF curve for ethylbenzene shows a plateauing as the ethylbenzene passes through the polar headgroups of octanol followed by a small local minimum once beyond that corresponds to a small interfacial solvation energy (relative to bulk octanol) of −2.0 kJ mol⁻¹ (Table 1 and Fig. S4–S6, ESI†). With hexane as the organic solvent, the interfacial layer is comparably less ordered, and all three molecules show a slight preference to reside at the water–hexane interface relative to their most soluble bulk solvent. Formamide and acetonitrile, which are both polar organic molecules, are slightly more stabilized at this hexane–water interface (both −4.9 kJ mol⁻¹) compared to the nonpolar organic ethylbenzene (−3.3 kJ mol⁻¹).

Unbound Gd³⁺ and DEHP⁻ across water–organic interfaces

With the modeling protocol validated for both qualitative and quantitative accuracy, we now establish a baseline for how the individual components of the Gd–DEHP assembly behave as they pass through two aqueous–organic interfaces. Within bulk water, the Gd³⁺ cation preferably formed a stable nona-aquo complex though octa-aquo complexes were also occasionally observed (Fig. S9, ESI†); experimental results indicate the structure fluctuates between 8 and 9-coordinate, indicating a slight bias in the forcefield towards the upper hydration number, although the average Gd–O bond lengths (2.45 Å) remain comparable to experiment (2.415–2.455 Å).^63–66 Unsurprisingly, the Gd³⁺ ion thermodynamically prefers the aqueous phase, with the computed free energy rapidly increasing without plateau as the Gd³⁺ aqua ion is pulled from water into either octanol or hexane, see ESI† and Fig. S7 for additional discussion.

The simulations of the lone DEHP⁻ molecule passing from aqueous to organic solvents have several similar features to the Gd³⁺ models. As the DEHP⁻ molecule is in its unprotonated state, there is a persistent cluster of water molecules encapsulating the charged phosphate head group as the molecule changes solvent layers (Fig. 2). The free energy begins to plateau near 11.4 kJ mol⁻¹ relative to the aqueous phase within octanol; this differs from the results with hexane which show the free energy continuously increasing until ∼200 kJ mol⁻¹ relative to the aqueous phase.

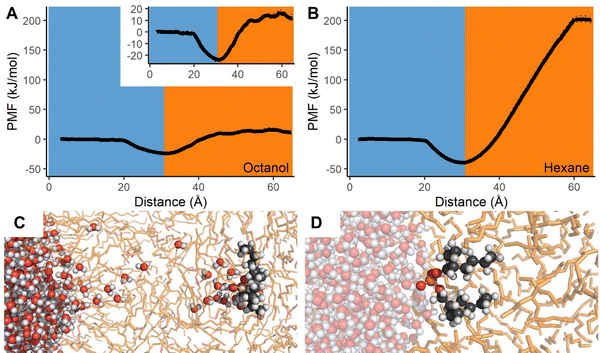Fig. 2 (A) and (B) Potential of mean force as DEHP⁻ transfers from aqueous to either octanol or hexane layers. Dotted lines indicate statistical upper and lower bounds of the PMF. (C) Chain of waters present as DEHP⁻ enters bulk octanol. (D) DEHP⁻ at water–hexane interface. Coloring is same as Fig. 1 with DEHP⁻ shown as spheres with grey carbon and orange phosphorous atoms.

The findings also indicate that while DEHP⁻ is more soluble within water than octanol or hexane, it strongly prefers remaining at the water–organic interface due to its amphiphilic character with the phosphate head group facing the water and the hydrocarbon within the organic layer (Fig. 2D). The stabilization of DEHP⁻ at the interface is much stronger than the effect previously noted for ethylbenzene, formamide, or acetonitrile, with relative free energies to bulk water of −23.9 kJ mol⁻¹ at the water–octanol interface and −39.2 kJ mol⁻¹ for water–hexane. The significant stabilization of DEHP⁻ at the interface suggests that, at least in the absence of an extensive DEHP⁻ interfacial monolayer, aqueous DEHP⁻ will preferentially populate the water–organic interface, which is in agreement with computations done with other organophosphorous solutes.⁶⁷ Simulations with the DEHP⁻ molecule unconstrained also typically lead to the molecule readily migrating to, and remaining at, the interface, see ESI† and Fig. S8 for additional discussion. In experiment, HDEHP molecules could form dimers that solvate in the organic phase. The free energy comparison of the charged DEHP⁻ molecule between the interface and the organic phase is of the theoretical system that was simulated and unlikely to be observed in experiment.

Gd–HDEHP complexes across water–organic interfaces

The previous results affirm the amphiphilicity of DEHP⁻ and that Gd³⁺ will not readily diffuse on its own into the organic phase. We now examine the effect that Gd complexation with one to three DEHP⁻ molecules in the aqueous phase will have on the transport of the complex into the organic phase. Beginning with a 1 : 1 ratio of Gd to DEHP⁻, the DEHP⁻ displaces one of the coordinating waters of the Gd aqua ion⁶⁸ to form a 9-coordinate [Gd³⁺(DEHP⁻)(H₂O)₈]²⁺ complex with the phosphate group of DEHP⁻ coordinating in a monodentate configuration. Similar to the free Gd³⁺ ion, the 9-coordinate geometry is favored, but an 8-coordinate complex, with one less water coordinated, is also observed (Fig. S9, ESI†). As the ion–ligand complex approaches the water–organic interface (Fig. 3A and B), the hydrocarbon tails of DEHP⁻ orient and incorporate into the organic partition with the Gd remaining on the aqueous side. The complex is stabilized at the interface with relative free energies to bulk water of −16.3 kJ mol⁻¹ at the water–octanol interface and −40.9 kJ mol⁻¹ for water–hexane. The interfacial stabilization effect is smaller than for the free DEHP⁻ molecule, but it flips the trend for the free Gd ion which strongly prefers remaining in bulk solvent. When the complex enters the organic layer, water molecules surrounding the Gd³⁺ ion also enter, and the free energies monotonically increase over the simulated distance. Altogether, the simulations indicate the 1 : 1 Ln–ligand ratio complex is not sufficient to carry the Gd³⁺ into the organic solvent.

Fig. 3 (A) and (B) Potential of mean force as a Gd(DEHP⁻) complex transfers from aqueous to either octanol or hexane layers. Dotted lines indicate statistical upper and lower bounds of the PMF. (C) and (D) Potential of mean force as a Gd(DEHP⁻)₂ complex transfers from aqueous to either octanol or hexane layers.

Adding a second DEHP⁻ ligand for a 1 : 2 ratio of Gd to DEHP⁻ leads to the formation of a 9-coordinate [Gd³⁺(DEHP⁻)₂(H₂O)₇]⁺ complex with both DEHP⁻ ligands in a monodentate configuration. Similar to the single ligand complex, [Gd³⁺(DEHP⁻)₂(H₂O)₇]⁺ prefers remaining at the water–organic interface (Fig. 3C and D). The stability of the bi-ligand complex relative to bulk water are −30.8 kJ mol⁻¹ at the water–octanol interface and −72.1 kJ mol⁻¹ at the water–hexane interface, both of which are greater than the stabilization effect observed for the lone ligand and the single ligand complex. When the complex passes into the layer of octanol, it is accompanied by a cluster of second-sphere water molecules around the Gd³⁺ ion similar to that seen for the lone DEHP⁻ molecule (Fig. 2C). When the organic layer is hexane, a microdroplet forms composed of the [Gd³⁺(DEHP⁻)₂(H₂O)₇]⁺ complex and 26 non-coordinating water molecules; the separation of this microdroplet from the water–hexane interface is noted by the beginning of a plateau in the free energy curve. Having the Gd complex within this microdroplet remains significantly unstable relative to both bulk water and interfacial environments, indicating that a Ln–ligand ratio of 1 : 2 is not suitable for transporting the Gd³⁺ into either organic solvents even though the additional DEHP⁻ ligand does help stabilize the transport into the organic layer compared to the single ligand complex.

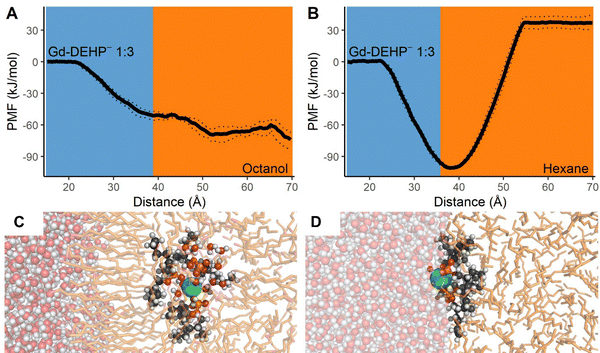
Lastly, simulations with a 1 : 3 ratio of Gd to DEHP⁻ were conducted. This Ln–ligand ratio would be consistent with X-ray absorption spectroscopy experiments on Eu³⁺ extracted by HDHP (dihexylphosphoric acid)⁶⁹ and DHDP (dihexadecylphosphate)¹⁰ that characterize the extracted coordination structure in a 1 : 3 Ln–ligand ratio. In the aqueous solvent, a neutral 9-coordinate [Gd³⁺(DEHP⁻)₃(H₂O)₆]⁰ aqueous complex formed with all three HDEHP ligands coordinated to the Gd in a monodentate configuration. As the complex approached the water–octanol interface, the [Gd³⁺(DEHP⁻)₃(H₂O)₆]⁰ complex readily passes through into the bulk octanol accompanied by 21 non-coordinating second-shell water molecules. This passage through the ordered octanol membrane is effectively barrierless, and the stability of the complex within the octanol relative to bulk water is −66.4 kJ mol⁻¹ (Fig. 4). These results indicate the complex is more soluble in octanol than water and represent the lowest ion–ligand ratio where the complex is lipophilic enough for Gd to effectively be transported into the bulk octanol layer. Interestingly, this ratio remains insufficient for transport into hexane as the complex is thermodynamically favored to remain at the water–hexane interface (free energy minimum relative to bulk water of −101.0 kJ mol⁻¹, Fig. 4). The tri-ligand complex does dramatically alter the transport behavior, though, as the complex enters hexane alongside 15 non-coordinating water molecules to rapidly form a microdroplet; further, the relative stability of this system is now only 37.0 kJ mol⁻¹, an approximately five-fold improvement in stabilization. Coordination of additional HDEHP molecules is expected to further shift the thermodynamics to favor the exchange of Gd³⁺ from aqueous to hexane layer, as other studies report Ln³⁺(DEHP⁻)₃(HDEHP)₃ coordination structures in the organic phase.^9,70–72

Fig. 4 (A) and (B) Potential of mean force as a Gd(DEHP⁻)₃ complex transfers from aqueous to either octanol or hexane layers. Dotted lines indicate statistical upper and lower bounds of the PMF. (C) Gd(DEHP⁻)₃ complex in octanol just beyond the ordered interfacial octanol molecules. (D) Gd(DEHP⁻)₃ complex at water–hexane interface.

In experimental solvent extractions, with a hexane-like diluent and an excess of extractant (HDEHP), a thin film of amphiphilic DEHP⁻ molecules would form at the aqueous–organic interface. This monolayer was excluded from our simulations in order to focus on the relative solubility of Gd–HDEHP complexes from the aqueous phase to the interface and organic phase, along with isolating the impact of the different organic solvents and number of coordinated DEHP⁻ molecules. Identifying how the presence of extractant monolayer and other surfactants influence ion transfer remains an active point of research.^{10,12,32,73–75}

The relative free energies from the Gd–ligand simulations are compiled in Table 2 to highlight the changing Gd relative energies across aqueous–organic interfaces with different coordination complexes and organic solvents. As the Gd: DEHP⁻ ratio increases from 0 to 3, the Gd–DEHP⁻ complexes become more soluble in the aqueous–organic interface. The charge neutral Gd(DEHP)₃ complex becomes more soluble in the octanol phase but prefers the aqueous–organic interface when the organic solvent is hexane and there is no amphiphilic layer in the interface.

Table 2 Free energies (kJ mol⁻¹) of the interface and organic phase relative to the aqueous phase, computed from the potentials of mean force. Interface values indicate relative energetic maxima or minima if present

Solute	Water	Interfacewat–oct	Octanol	Interfacewat–hex	Hexane
[Gd]^3+	0	—	>146	—	>226
[DEHP]^−	0	−23.9	11.4	−39.2	>201
[Gd(DEHP)]^2+	0	−16.3	>89	−40.9	>278
[Gd(DEHP)2]^+	0	−30.8	>20	−72.1	183.3
[Gd(DEHP)3]^0	0	—	−66.4	−101.0	37.0

---

It should be noted that multiple PMFs do not plateau in the organic phase, mostly those of highly charged solutes (Table 2). Umbrella sampling simulations with larger time and length scales would be required for the PMFs of charged solutes to plateau in the organic phase, and the lack of plateau in the organic phase observed in the PMFs with highly charged solutes is a result of bulk conditions not being reached. This supports the aqueous solubility of charged solutes in contrast to the favorable organic solubility of Gd(DEHP)₃. A plateau in the organic phase is clearly observed for the PMFs in Table 1 and in that of the neutral Gd(DEHP)₃ complex solute. To keep the simulation box neutral, counterions are added to the simulation box with charged solutes, and the counterions remain in the aqueous phase (Fig. S10, ESI†), resulting in an electric field between the aqueous counterions and the charged solute which contributes to the aqueous preference of charged species.

Conclusions

Molecular dynamics simulations with umbrella sampling were used to characterize the relative energies of Gd³⁺, DEHP⁻, and Gd–DEHP complexes across water–octanol and water–hexane interfaces. The free Gd³⁺ ion readily remains in the bulk aqueous environment. The unprotonated DEHP⁻ ligand is thermodynamically favored to reside in the water–organic interface. The complexation of one or more DEHP⁻ molecules to Gd³⁺ in the bulk water is shown to change the relative solubility for Gd³⁺ and facilitate its solvation on the water–organic interface, with increasing numbers of coordinated DEHP⁻ molecules leading to greater stability at the interface. It is energetically favored for the complex to transfer from the aqueous phase into the octanol phase when three DEHP⁻ molecules coordinate the Gd³⁺ ion. With hexane as the organic solvent, the [Gd³⁺(DEHP⁻)₃]⁰ complex prefers remaining on the aqueous–organic interface, though an excess of DEHP⁻ ligands forming an amphiphilic layer at the aqueous–organic interface would result in the [Gd³⁺(DEHP⁻)₃]⁰ complex to transfer into the organic phase.

Author contributions

Conceptualization (TJS, DCC), formal analysis (TJS, JDS), funding acquisition (DCC), investigation (TJS, JDS), methodology (TJS, JDS, DCC), writing – original draft (TJS), writing – review & editing (TJS, JDS, DCC)

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Support from the National Science Foundation (award 2041914).

References

1. T. Liu and J. Chen, Sep. Purif. Technol., 2021, 276, 119263.
2. N. Swain and S. Mishra, J. Clean. Prod., 2019, 220, 884–898.
3. K. L. Nash, Solvent Extr. Ion Exch., 2015, 33, 1–55.
4. A. Matthew Wilson, P. J. Bailey, P. A. Tasker, J. R. Turkington, R. A. Grant and J. B. Love, Chem. Soc. Rev., 2014, 43, 123–134.
5. A. Leoncini, J. Huskens and W. Verboom, Chem. Soc. Rev., 2017, 46, 7229–7273.
6. D. Stamberga, M. R. Healy, V. S. Bryantsev, C. Albisser, Y. Karslyan, B. Reinhart, A. Paulenova, M. Foster, I. Popovs, K. Lyon, B. A. Moyer and S. Jansone-Popova, Inorg. Chem., 2020, 59, 17620–17630.
7. S. Nayak, K. Lovering and A. Uysal, Nanoscale, 2020, 12, 20202–20210.
8. B. L. Bonnett, D. Sheyfer, P. N. Wimalasiri, S. Nayak, J. Lal, Q. Zhang, S. Seifert, G. Brian Stephenson and M. J. Servis, Phys. Chem. Chem. Phys., 2023, 25, 16389–16403.
9. T. S. Grimes, M. P. Jensen, L. Debeer-Schmidt, K. Littrell and K. L. Nash, J. Phys. Chem. B, 2012, 116, 13722–13730.
10. W. Bu, H. Yu, G. Luo, M. K. Bera, B. Hou, A. W. Schuman, B. Lin, M. Meron, I. Kuzmenko, M. R. Antonio, L. Soderholm and M. L. Schlossman, J. Phys. Chem. B, 2014, 118, 10662–10674.
11. R. J. Ellis, M. Audras and M. R. Antonio, Langmuir, 2012, 28, 15498–15504.
12. P. Sun, E. A. Binter, Z. Liang, M. A. Brown, A. V. Gelis, I. Benjamin, M. K. Bera, B. Lin, W. Bu and M. L. Schlossman, ACS Cent. Sci., 2021, 7, 1908–1918.
13. D. Sheyfer, M. J. Servis, Q. Zhang, J. Lal, T. Loeffler, E. M. Dufresne, A. R. Sandy, S. Narayanan, S. K. R. S. Sankaranarayanan, R. Szczygiel, P. Maj, L. Soderholm, M. R. Antonio and G. B. Stephenson, J. Phys. Chem. B, 2022, 126, 2420–2429.
14. M. J. Servis, A. McCue, A. J. Casella and A. E. Clark, Fluid Phase Equilib., 2020, 511, 112497.
15. M. J. Servis, B. Sadhu, L. Soderholm and A. E. Clark, J. Mol. Liq., 2022, 345, 117743.
16. J. Kästner, WIREs Comput. Mol. Sci., 2011, 1, 932–942.
17. C. Jarzynski, Phys. Rev. E, 1997, 56, 5018–5035.
18. R. E. Skyner, J. L. McDonagh, C. R. Groom, T. van Mourik and J. B. O. Mitchell, Phys. Chem. Chem. Phys., 2015, 17, 6174–6191.
19. T. Mangin, R. Schurhammer and G. Wipff, J. Phys. Chem. B, 2022, 126, 2876–2890.
20. G. Benay and G. Wipff, J. Phys. Chem. B, 2013, 117, 1110–1122.
21. Z. Liu, X. Ren, R. Tan, Z. Chai and D. Wang, J. Phys. Chem. B, 2020, 124, 1751–1766.
22. X. Wang, S. Nayak, R. E. Wilson, L. Soderholm and M. J. Servis, arXiv, 2023, preprint, arXiv:2309.14578 DOI:10.4855/arXiv.2309.14578.
23. X. Huang, J. Dong, L. Wang, Z. Feng, Q. Xue and X. Meng, Green Chem., 2017, 19, 1345–1352.
24. X. Wang, W. Li, S. Meng and D. Li, J. Chem. Technol. Biotechnol., 2006, 81, 761–766.
25. K. Prochaska, Adv. Colloid Interface Sci., 2002, 95, 51–72.
26. A. G. Gaonkar and R. D. Neuman, J. Colloid Interface Sci., 1987, 119, 251–261.
27. A. U. Chowdhury, L. Lin and B. Doughty, ACS Appl. Mater. Interfaces, 2020, 12, 32119–32130.
28. D. B. Drelsinger and U. C. Cooper, Solvent Extr. Ion Exch., 1986, 4, 317–344.
29. M. A. Hughes and V. Rod, Faraday Discuss. Chem. Soc., 1984, 77, 75–84.
30. P. Sun, E. A. Binter, T. Vo, I. Benjamin, M. K. Bera, B. Lin, W. Bu and M. L. Schlossman, J. Phys. Chem. B, 2023, 127, 3505–3515.
31. W. Su, J. Chen and Y. Jing, Ind. Eng. Chem. Res., 2016, 55, 8424–8431.
32. U. I. Premadasa, V. Bocharova, L. Lin, A.-C. Genix, W. T. Heller, R. L. Sacci, Y.-Z. Ma, N. A. Thiele and B. Doughty, J. Phys. Chem. B, 2023, 127, 4886–4895.
33. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
34. S. Pothoczki and L. Pusztai, J. Mol. Liq., 2017, 225, 160–166.
35. B. Doherty, X. Zhong, S. Gathiaka, B. Li and O. Acevedo, J. Chem. Theory Comput., 2017, 13, 6131–6145.
36. F. C. J. M. van Veggel and D. N. Reinhoudt, Chem. – Eur. J., 1999, 5, 90–95.
37. R. Zangi, ACS Omega, 2018, 3, 18089–18099.
38. E. M. Duffy and W. L. Jorgensen, J. Am. Chem. Soc., 2000, 122, 2878–2888.
39. B. Chen and J. I. Siepmann, J. Am. Chem. Soc., 2000, 122, 6464–6467.
40. M. Baaden, F. Berny, C. Madic and G. Wipff, J. Phys. Chem. A, 2000, 104, 7659–7671.
41. P. Li, L. F. Song and K. M. Merz, J. Phys. Chem. B, 2015, 119, 883–895.
42. G. Sormani, A. Korde, A. Rodriguez, M. Denecke and A. Hassanali, ACS Omega, 2023, 8, 36032–36042.
43. T. J. Summers, R. D. O’Brien, J. A. Sobrinho, A. de Bettencourt-Dias and D. C. Cantu, Eur. J. Inorg. Chem., 2024, 27, e202300507.
44. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
45. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
46. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
47. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25.
48. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
49. S. Nosé and M. L. Klein, Mol. Phys., 1983, 50, 1055–1076.
50. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
51. S. Nosé, Mol. Phys., 1984, 52, 255–268.
52. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021.
53. S. Hossain, A. Kabedev, A. Parrow, C. A. S. Bergström and P. Larsson, Eur. J. Pharm. Biopharm., 2019, 137, 46–55.
54. N. Bhatnagar, G. Kamath, I. Chelst and J. J. Potoff, J. Chem. Phys., 2012, 137, 014502.
55. S. Fan, B. I. Iorga and O. Beckstein, J. Comput. Aided Mol. Des., 2020, 34, 543–560.
56. D. Vassetti, M. Pagliai and P. Procacci, J. Chem. Theory Comput., 2019, 15, 1983–1995.
57. Sigma-Aldrich. Safety Data Sheet: Ethylbenzene. 2023.
58. ThermoFisher Scientific. Safety Data Sheet: Ethylbenzene. 2021.
59. Roche. Safety Data Sheet: Formamide. 2021.
60. ThermoFisher Scientific. Safety Data Sheet: Acetonitrile. 2021.
61. Sigma-Aldrich. Safety Data Sheet: Aceotonitrile. 2023.
62. R. L. Napoleon and P. B. Moore, J. Phys. Chem. B, 2006, 110, 3666–3673.
63. R. C. Shiery, J. L. Fulton, M. Balasubramanian, M.-T. Nguyen, J.-B. Lu, J. Li, R. Rousseau, V.-A. Glezakou and D. C. Cantu, Inorg. Chem., 2021, 60, 3117–3130.
64. I. Persson, Pure Appl. Chem., 2010, 82, 1901–1917.
65. I. Persson, P. D’Angelo, S. De Panfilis, M. Sandström and L. Eriksson, Chem. – Eur. J., 2008, 14, 3056–3066.
66. P. D’Angelo, A. Zitolo, V. Migliorati, G. Chillemi, M. Duvail, P. Vitorge, S. Abadie and R. Spezia, Inorg. Chem., 2011, 50, 4572–4579.
67. Y. Ghadar, P. Parmar, A. C. Samuels and A. E. Clark, J. Chem. Phys., 2015, 142, 104707.
68. Z. Liang, T. Vo, K. J. Schweighofer, I. Benjamin and M. L. Schlossman, J. Chem. Phys., 2023, 158, 134715.
69. B. Gannaz, M. R. Antonio, R. Chiarizia, C. Hill and G. Cote, Dalton Trans., 2006, 4553–4562.
70. T. B. Pierce and P. F. Peck, Analyst, 1963, 88, 217–221.
71. J. Luo, C. Wang, J. Lan, Q. Wu, Y. Zhao, Z. Chai, C. Nie and W. Shi, Sci. China: Chem., 2016, 59, 324–331.
72. C. Marie, B. Hiscox and K. L. Nash, Dalton Trans., 2011, 41, 1054–1064.
73. B. Qiao, J. V. Muntean, M. Olvera de la Cruz and R. J. Ellis, Langmuir, 2017, 33, 6135–6142.
74. R. Kusaka and M. Watanabe, J. Phys. Chem. B, 2021, 125, 6727–6731.
75. M. Špadina, K. Bohinc, T. Zemb and J.-F. Dufrêche, Langmuir, 2019, 35, 3215–3230.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02586e

‡ Present address: Los Alamos National Laboratory, Los Alamos, NM, USA.

---