Statistical accuracy of molecular dynamics-based methods for sampling conformational ensembles of disordered proteins

Abstract

The characterization of the statistical ensemble of conformations of intrinsically disordered regions (IDRs) is a great challenge both from experimental and computational points of view. In this respect, a number of protocols have been developed using molecular dynamics (MD) simulations to sample the huge conformational space of the molecule. In this work, we consider one of the best methods available, replica exchange solute tempering (REST), as a reference to compare the results obtained using this method with the results obtained using other methods, in terms of experimentally measurable quantities. Along with the methods assessed, we propose here a novel protocol called probabilistic MD chain growth (PMD-CG), which combines the flexible-meccano and hierarchical chain growth methods with the statistical data obtained from tripeptide MD trajectories as the starting point. The system chosen for testing is a 20-residue region from the C-terminal domain of the p53 tumor suppressor protein (p53-CTD). Our results show that PMD-CG provides an ensemble of conformations extremely quickly, after suitable computation of the conformational pool for all peptide triplets of the IDR sequence. The measurable quantities computed on the ensemble of conformations agree well with those based on the REST conformational ensemble.

---

1 Introduction

The prevalence of proteins with intrinsically disordered regions (IDRs) in eukaryotic genomes¹ and the increasing evidence of their important role in different biological processes,^2–4 despite lacking a folded three-dimensional structure, explain why their study is nowadays an active research field.^1,2,5–8 IDRs dynamically explore their huge conformational space replete with local minima separated by small free energy barriers that can be overpass under physiological conditions. The image of a unique native structure must then be replaced in IDRs by a conformational ensemble. Consequently, the paradigms successfully applied over decades to describe the functionality of structured proteins (structures encoded in the amino acid sequence, lock-and-key mechanism, effect of mutations, …) are basically useless in describing the function and biological evolution of IDRs and make it necessary to rework the experimental^9,10 and theoretical^11,12 methods applied.

On the experimental side, nuclear magnetic resonance (NMR) spectroscopy is the most widely used tool for probing the properties of proteins with IDRs at atomic resolution.^9,10 Chemical shifts (CSs), scalar couplings (SCs), and residual dipolar couplings (RDCs) provide averaged information about the backbone dihedral angle distributions and/or the long-range contacts between distant parts of the molecule. NMR data can be complemented by small angle X-ray scattering (SAXS) or small angle neutron scattering (SANS),¹³ which probe the apparent size of proteins in solution. Other techniques¹⁰ such as Förster resonance energy transfer (FRET) and nuclear paramagnetic relaxation enhancements (PREs) have been used much less extensively. In practice, the number of experimental observables is always many orders of magnitude smaller than the size of the conformational ensemble, so the IDR ensemble reconstruction from the measured data^14,15 is a task full of uncertainties complicated by the fact that different ensembles may provide the same experimental results within the error resulting after averaging.^{10,14,16–19}

On the theoretical side, molecular dynamics (MD) simulations are the standard tool to simulate the dynamics of a protein with IDRs. Their limitations are mainly concentrated on two independent factors,^20–22 which are the inaccuracies of the force field and the difficulties in achieving statistical convergence of the structural sampling of the IDR. The recent optimizations of force fields specifically for IDRs have proved their reliability to reproduce accurately experimental structural data when the statistical sampling of the simulations is adequate.¹⁸ Therefore, the most important challenge currently facing MD is to achieve the statistical convergence of the generated conformational ensembles.

In this work, we compare the reliability and computational efficiency of different MD-based methods to build conformational ensembles, using as a quality criterion their ability to converge the NMR and SAXS variables. We selected these particular descriptors since they represent the true linkage with the experimental information of IDRs.^18,22–26 As other collective variables, NMR and SAXS variables reduce the dimension of the conformational ensemble while keeping some representative structural information of the IDRs (see the Methods section 2.1). Extensive comparative analysis of these descriptors with other structural variables allows us to determine in this work the degeneracy of the conformational states and the loss of structural information associated with their employment.

In order to suppress the force field accuracy factor from our comparative study, we use as references the computational results for NMR and SAXS data obtained from replica exchange solute tempering (REST)²⁷ simulations, since they provide at present the most accurate statistical sampling in IDRs.^18,28,29 The other MD-based methods evaluated in this work are standard MD simulations, the Markov state model approach (MSM),^30,31 and a novel method, called probabilistic MD chain growth (PMD-CG), both based on the flexible-meccano^23,32–34 and the hierarchical chain growth^24,26,35 approaches. Likewise, we have discarded in our comparative study coil libraries-based approaches since the force field accuracy as well as the statistical robustness of the coil libraries for certain amino acid triplets would hinder the direct comparison between the method performances and accuracy.

The IDR selected in this work is a 20-aa region (364–383) from the C-terminal domain of p53 tumor suppressor protein (p53-CTD). This region has been extensively studied^36–39 due to its essential role in the functionality of p53 as a transcription factor. Nevertheless, the regulation mechanisms of p53-CTD are still a work-in-progress because of its structural versatility in adopting different secondary motifs when bound to receptors, while its structure remains disordered in solution.^37,38

Overall, our work aims to be a practical guide for researchers who need to interpret experimental NMR and SAXS data of proteins with IDRs, assess the quality of the force fields used, analyze the effect of mutations in the protein chain or predict the presence of particular motifs in conformational ensembles, among other possible applications.

2 Methods

2.1 Dimensionality reduction of conformational ensembles in IDRs

MD simulations are severely restricted by the computational effort needed to guarantee the complete exploration of the conformational space of the molecule. To illustrate this point, let us make the following simple but reliable estimation. Let us consider an IDR with N residues, each adopting different C_i conformations. The total number of molecular conformations is then . Even if we assume a coarse grained description of the conformational space of each residue, for instance by defining three regions such as the typical helix, the extended and other conformations, so that C_i = 3, and a relative short peptide with 20 residues, the total number of molecular conformations⁴⁰ is of the order of 10⁹ (see Fig. 1a). It is true that some molecular conformations may not be viable due to the presence of clashes, but our tests show that this is only a fraction of the total that does not modify the order of magnitude of the number of conformations.

Fig. 1 (a) Virtual number of conformations on the basis of the number of residues of the IDR if just three conformational regions (helix, extended and others) are defined in the Ramachandran map of each residue's backbone dihedral angles. (b) Graphical representation of the 20-aa region (364–383) from the C-terminal domain of p53 tumor suppressor protein (p53-CTD).

Our simulations also show that the averaged time required for at least one residue to change its conformation, is of the order of tens of picoseconds. Accordingly, the hypothetical simulation time required to visit at least once each molecular conformation is of the order of milliseconds. Considering that each conformation would have to be visited many times to obtain reasonable statistics, since the molecular conformations are not equiprobables, we conclude that generating a complete conformational ensemble of IDRs is computationally prohibitive.

The alternative is to perform a dimensionality reduction, i.e. to generate reduced conformational ensembles representative of the whole conformational ensemble and able to reproduce a given set of properties. The choice of the experimental observables described in the introduction as the average values to be reproduced seems a practical option. In fact this strategy has been used to evaluate the quality of conformational ensembles generated using different approximations.^18,22–26

2.2 MD-Based methods to generate conformational ensembles

The first MD-based method considered is a new method but was largely inspired by two groups from earlier works. In the first group,^23,32–34 that we will refer to as flexible-meccano methods, the molecular conformational ensembles are built using the conformational data of individual residues extracted from the so-called coil libraries (see ref. 41 and references therein), which include residue-specific (ϕ, ϕ) dihedral angle distributions from fragments of experimental protein structures that do not form well-defined secondary structures. In the second group,^24,26,35 a hierarchical chain growth (HCG) approach is used to build conformational ensembles by assembling the structures of fragments with 3–6 residues previously obtained through independent MD simulations into full-length IDRs. We merge both methods by taking advantage of our recent work⁴⁰ in which we showed that the probability of an IDR molecular conformation can be described properly as the product of conformational probabilities of each residue, conditioned to the identity of the residue neighbours. As a result, we can obtain the conformational probabilities of the central residue of every triad in the IDR molecule from independent MD simulations of the corresponding tripeptides. Basically, this method, which we refer to as probabilistic MD chain growth (PMD-CG), is identical to the flexible-meccano methods but uses the results from MD simulations of the tripeptides instead of the coil libraries as the source of the statistical distributionst. The main difference with respect to the HGC method is that we do not store a pool of structures of the fragments to be later assembled since only statistical information is transferred from the MD simulations of the tripeptides.

The second MD-based method is simply to perform standard MD simulations of the IDR molecule. We are aware that the accumulated simulation time (2 μs) employed for every approach for the sake of comparison in this work, may not be long enough to obtain an accurate statistical sampling^18,29 in certain physical variables. However, this circumstance will allow us to verify the influence of two important factors on the sampling of the conformational space of the IDRs which are the choice of the initial configurations of the molecule²⁴ and the time length of the individual trajectories.^22,42 From a computational point of view, performing many short simulations instead of fewer longer ones is always advantageous since the calculations can be straightforwardly distributed without any lack of computational performance.

The third MD-based method considered is a Markov state model (MSM).^30,31 MSMs have been used to describe conformational ensembles in earlier studies^29,43–48 following a similar strategy. First, a long MD trajectory is carried out using an enhanced sampling MD simulation, and then the structures generated are clustered to create a MSM using some collective variables (CVs) from which the weights of each cluster of structures is evaluated. Of course, the success of this methodology strongly depends on the ability of the initial MD simulation to extensively explore the molecular conformational space, which is always questionable in proteins with IDRs. In this work we prefer to use the initial formulations of the MSMs based on the exploration of the conformational space using short simulations,^49–51 where the collective variables are chosen a priori and an adaptive sampling method⁵² is used to force the system to visit conformational regions with low probabilities, that would be rarely visited in an unrestricted MD simulation.

The fourth MD-based method consists of using an enhanced sampling MD approach. In this case we focus on replica exchange solute tempering (REST) simulations, which have already been used to successfully generate conformational ensembles of IDRs.^18,28,29,44 The REST method has been used^27,53 as an efficient alternative to the more traditional replica exchange (or parallel tempering) MD (REMD) approach,⁵⁴ in which the simulation of several replicas of the same system although at different temperatures is performed in parallel. After a certain period, the exchange between the coordinates of neighboring replicas is attempted with a Monte Carlo procedure. A known issue of the REMD method²⁷ is that the number of replicas necessary to cover a certain range of temperatures grows with the system size (including the solvent), since the whole system is being accelerated by increasing the temperature. In the REST approach, only the protein–protein and protein–water interactions are scaled, so that the mimicked temperature is increased only on the protein while the temperature of the solvent is maintained. Accordingly, the replica with the lowest temperature (the unbiased replica in which protein and solvent have the same temperature) is the only one that provides a correct statistical distribution.

2.3 Computational details

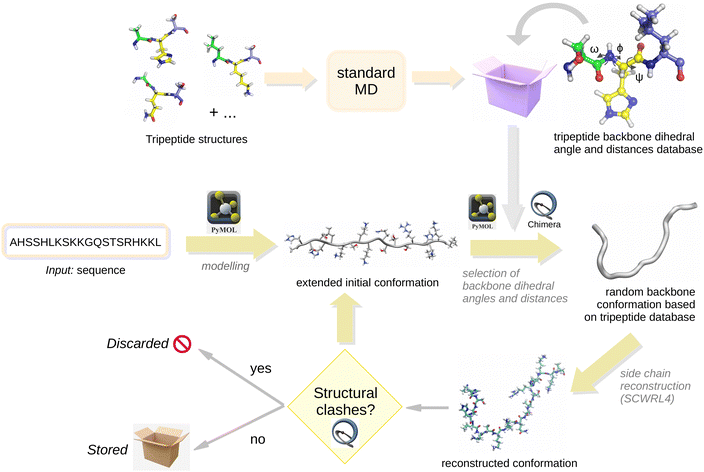
MD simulations of the A³⁶⁴HSSHLKSKKGQSTSRHKKL³⁸³ peptide (see Fig. 1), which has a sequence taken from the C-terminal IDR domain of p53³⁷ (p53-CTD), were carried out in order to test the reliability of the molecular conformational ensembles provided by the different approximations described below. This peptide with an heterogeneous sequence has been previously used as a test system in our previous study on the characterization of IDR ensembles through probabilistic expressions.⁴⁰ In addition, MD simulations of the 18 tripeptides encoded in the peptide sequence (AHS, HSS, …, HKK, KKL) were performed. All molecules were blocked using acetyl and N-methyl groups.

MD simulations were carried out with the molecules dissolved in water using the GROMACS package v2021.2.^55,56 Each solute molecule was surrounded by a number of water molecules ranging from 900 to 12000 (depending on the length of the peptide) and placed in a cubic box of a size chosen to reproduce the experimental density of the liquid at room temperature. All the molecules were described using the CHARMM36m⁵⁷ force field and the flexible TIP3P model was used for the solvent water molecules. This force field has been shown^58,59 to provide a good representation of proteins with IDRs. Periodic boundary conditions were imposed in the simulations using the Particle–Mesh Ewald method to treat the long-range electrostatic interactions. All H–X bonds were kept fixed using the LINCS algorithm.⁶⁰ The equations of motion were integrated using a time step of 2 fs. All simulations were carried out in a NVT ensemble by coupling to a thermal bath using the stochastic velocity rescaling method by Bussi et al.⁶¹

2.3.1 MD simulations of tripeptides. Every system was equilibrated following a two-step method. In the first step, the system was propagated during 1 ns at 500 K to allow extensive exploration of the molecular conformational space. In the second step, the system was equilibrated at 298 K during 1 ns. This procedure was repeated 100 times for every molecule. Each of these 100 initial configurations were propagated during 10 ns generating the same number of trajectories. During these production runs, the values of the dihedral angles were written every 10 fs. From these data we computed the 2D histograms of the (ϕ, ψ) dihedral angles, the 1D histograms for the ω dihedral angle and the 1D histogram of the C–N, C_α–C and N–C_α interatomic distances of the backbone chain. The resolutions of the histograms were 1° and 0.02 Å for the angles and distances respectively.

2.3.2 Probabilistic MD chain growth (PMD-CG). Molecular conformations of the peptide were built using a protocol similar to that employed in the flexible-meccano methods. In particular, we basically followed the steps detailed in the DIPEND tool,³³ the main of them being:

• An extended initial conformation was built using open-source Pymol v2.3.0.⁶²

• Values of the ϕ, ψ and ω dihedral angles and the C–N, C_α–C and N–C_α distances were randomly selected from the corresponding histograms of the tripeptides taking into account the identity of the nearest neighbour residues. Angles and distances were modified using Pymol⁶² and Chimera v1.16,⁶³ respectively.

• Non-backbone atoms were erased and the side chains were placed again using SCWRL4.⁶⁴ Some tests were also performed using FASPR,⁶⁵ showing that the results were largely unaffected by the choice of either of the two packages.

• The resulting molecular structures were tested for the presence of steric clashes using Chimera with default parameters. If a clash was detected, the structure was discarded. Approximately one third of the structures was found to pass the clash test.

These steps were repeated until generating 40 000 molecular conformations. A summary work-flow is shown in Fig. 2 to help understand how the PMD-CG method works in practice.

Fig. 2 Work-flow of the PMD-CG method.

2.3.3 MD equilibration. Two different sets of equilibrated systems were calculated. The first one was generated from a common extended conformation of the peptide. To facilitate the exploration of the conformational space, we followed a two-step method as in the case of tripeptides. In the first step, the system was propagated during 2 ns at 500 K to allow exploration of the molecular conformational space. In the second step, the system was equilibrated at 298 K during 5 ns. These structures were simply referred to as standard MD (S-MD) structures. The second set took as starting point one of the conformations generated using the PMD-CG method chosen randomly. Since these structures were already generated to explore the conformational space of the peptide, the high-temperature step was not necessary and the system was equilibrated only at 298 K during 0.5 ns. These structures were referred to as PMD-CG-MD structures. These two procedures were repeated to generate as many equilibrated structures as required.

2.3.4 Standard MD production runs. Each initial equilibrated configuration was propagated during 1, 10 or 100 ns, exporting the results every 1 ps for further analysis. In every case, the total number of trajectories was that necessary to reach an accumulated propagation time of 2 μs, leading to 2000, 200 and 20 trajectories, respectively. For the 10 ns runs, two independent production sets were carried out using the equilibrated trajectories from the S-MD and PMD-CG-MD structures as starting points. 1 ns and 100 ns trajectories were only generated from the PMD-CG-MD structures.

2.3.5 Markov state models. Each MSM trajectory was composed of 200 segments corresponding to short MD simulations of 50 ps. The initial conformations of each segment were chosen from one previously visited using the adaptive sampling method⁵² in order to force the system to visit conformational regions with low probabilities that would be rarely visited in an unrestricted MD simulation. The time length of the segments was chosen as a compromise between two factors. It must be long enough to allow conformational changes of the molecule which places its value in the order of tens of picoseconds at least. Simultaneously it must be short enough to allow an efficient exploration of the collective variables space through the adaptive sampling method. Three independent sets of MSM simulations were carried out using two collective variables (CVs) to map the conformational space to be chosen among the radius of giration (R_g), the end-to-end distance (d_ee) and the sphericity (γ). The corresponding intervals were R_g ∈ (0.5 nm, 2.0 nm), d_ee ∈ (0 nm, 7.5 nm) and γ ∈ (0, 1), which were divided into 50 bins. For the R_g–γ MSM calculations, two independent production sets were carried out using the equilibrated trajectories from the S-MD and PMD-CG-MD structures as the starting point, and for the R_g–d_ee and d_ee–γ MSM calculations only the initial PMD-CG structures were considered. 200 independent trajectories were thus run in every case to reach an accumulated propagation time of 2 μs exporting the results every 1 ps for further analysis. Equilibrium populations were obtained using standard procedures and the maximun likehood estimate method⁶⁶ was applied to assure detailed balance.

2.3.6 REST. We employed the replica exchange with solute tempering 2 method (REST2)⁵³ as implemented in GROMACS (v.2021.7)⁶⁷ patched with PLUMED (v.2.9.0).^68,69 All p53-CTD atoms were selected for the scaling of the solute–solute and solute–solvent interactions. Eight replicas of p53-CTD in water at the effective solute temperatures of 298, 310.8, 324.1, 338.1, 352.6, 367.7, 383.5 and 400 K were run in order to ensure an exchange probability of approximately 0.3 between all replicas. The coordinate exchange was attempted every 500 steps. Two REST simulations at constant NVT for 1.1 μs were performed. The first 100 ns were considered an equilibration period and therefore discarded from all production runs. For analysis, only the unscaled replica at T = 298 K was employed. Snapshots of the system were saved every 10 ps during the production phase.

2.3.7 Calculation of experimental magnitudes. We used standard tools to evaluate the J-couplings,^10,33 the chemical shifts,^24,26,41 the residual dipolar couplings (RDCs),^26,33 and the SAXS profiles⁴¹ from the IDR ensembles generated using the different MD-based methods. The J-couplings were evaluated using parametrized Karplus^70,71 equations included in the chi module of GROMACS.^55,56 The NMR chemical shifts were calculated with SPARTA+,⁷² the RDCs with PALES,⁷³ and the SAXS profiles with CRYSOL.⁷⁴ In order to compare the results from the different MD-based methods we have fixed the total accumulated propagation time equal to 2 μs. In order to measure the statistical confidence of the results for every magnitude, we evaluated their standard deviations using a block averaging approach in which the conformations generated in every MD-based method were split into four groups of the same size.

3 Results and discussion

The performance of three validated MD-based sampling methods, i.e. MD, R_g–γ MSM and REST with the initial S-MD structures, was first evaluated in an IDR system by comparing the different NMR and SAXS variables obtained from their trajectories (see the Methods section 2.3.7). Since the three approaches employ the same force field, system and conditions, our first analysis focused on the evaluation efficiency of each sampling method to provide statistically converged conformational ensembles for these variables at equal (computationally accessible) simulation length times.

In principle, it is expected that the conformational ensembles from the three methods are equivalent at infinite simulation times but they may reach convergence at completely different time scales. The average values of J-couplings, chemical shifts, RDC and SAXS intensities obtained from each method are shown in Fig. 3. For the sake of clarity, the standard deviation bars are hidden for each average value in Fig. 3, while the average standard deviations of each experimental-based variable are shown in Fig. 4a for all three methods.

Fig. 3 NMR and SAXS variables obtained from REST, MD and R_g–γ MSM using the S-MD structures and PMD-CG conformational ensembles of p53-CTD. Average values of (a)–(e) J-couplings, (f) SAXS intensities, (g)–(i) chemical shifts and (j) RDC couplings.

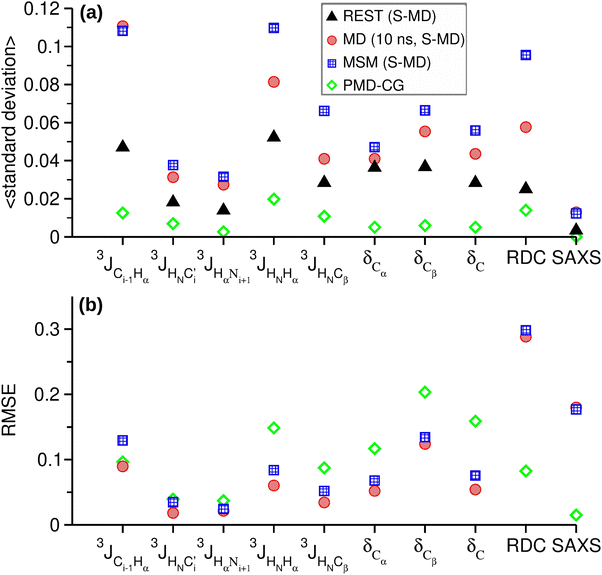Fig. 4 (a) Average standard deviations, and (b) root mean square errors (RMSE) of the NMR and SAXS variables obtained from REST, MD and R_g–γ MSM using the S-MD structures and PMD-CG approaches. RMSE values have been calculated with respect to the REST results. The standard deviation and RMSE units are the same as each variable unit as given in Fig. 3. The corresponding values for RDC have been divided by 10 and those for SAXS have been multiplied by 500.

The variables studied plotted in Fig. 3 show, in general, similar profiles for the three different approaches. However, significant differences are found in some variables, such as the RDC and the SAXS intensities (Fig. 3f and j), in which the REST data clearly differ from those obtained from MD and MSM trajectories. The standard deviation calculated by block analysis is an indicator of the convergence of the associated average value.²⁰ Comparison of the standard deviations associated with these (and indeed for all) variables in Fig. 4a shows that the REST results have the lowest values. This agrees with previous computational works in IDRs that demonstrate the high efficiency of the REST method to provide accurate conformational ensembles in affordable computational times.^18,29,44 Also, the poor convergence obtained in other variables extracted from MD trajectories is expected, in agreement with the same previous works already showing that longer simulation times (from 5–30 μs) are needed to obtain convergent results from standard MD trajectories for IDRs of similar length. MSM methods have the highest average standard deviations in most of the variables.

We therefore conclude that the conformational ensembles of p53-CDT obtained from REST trajectories can be considered as the reference for the comparison with the other MD-based approaches. Accordingly, the results obtained from REST trajectories were used as a reference to calculate the root mean squared error (RMSE) for all the NMR and SAXS variables obtained from MD and MSM trajectories (see Fig. 4b).

³ J-Couplings measure the spin–spin interaction between atoms at a distance of 3 bonds, and they can offer local structural information via Karplus equations. Four backbone and one side-chain ³J-couplings have been evaluated from our trajectories. Certain J-coupling variables show higher differences than others. In particular, the ³J_Ci−1Hα, which involves the peptide bond between two residues, are those who show the highest RMSE among all J-couplings. The differences between the RMSE values of the MD and MSM results are small and not significant as accounted for by their standard deviations.

Chemical shifts from ¹³C NMR spectra have been used extensively in the structural studies of proteins. Their dependence on the protein structure is very sensitive and complex. Many structural factors, such as the backbone and the side-chain angles, the identity of neighboring residues, the interaction with aromatic groups, the hydrogen bonding, the solvent exposure or the geometric distortions, affect the chemical shift values. Among the ¹³C chemical shifts analyzed, the highest differences are found in C_β where the values extracted from MD and MSM trajectories are consistently lower than those obtained with REST trajectories. Also, in this case the differences between the RMSE values extracted from the MD and MSM results are not significant.

The dipolar couplings between nuclear spins are typically averaged to zero by molecular tumbling in isotropic media. In weakly orientating media or as an effect of the molecular magnetic susceptibility anisotropy, residual dipolar couplings (RDC) can be present and measured in specific NMR experiments. Also, software based on the molecular geometry is available to predict the RDC measured for the weakly aligned molecule. The interesting feature of the RDCs, similar to that of the SAXS intensities, is that they depend on non-local conformational features, in contrast with the chemical shifts and the J-couplings, which depend mostly on the local conformation. The RMSE values are similar for both methods and both underestimate the RDC values, although the shifts are more erratic for those from the MSM values.

The scattering intensity obtained from the small angle X-ray scattering (SAXS) method provides information about the overall shape and size of the proteins. The SAXS profiles obtained from MD and MSM are very similar, although both differ from the reference REST results at low values of the scattering vector. The curve profile in this region is related to the globular, partially or completely unfolded shape of the protein. The Kratki representation of the data in Fig. S1 (ESI†) is generally used to better understand the folding state and flexibility of the proteins.⁷⁵ The profiles obtained from MD and MSM correspond to pure unfolded protein profiles. On the other hand, the shallow maximum before the plateau in the REST profile may indicate that in these trajectories the peptide has explored certain folded conformations with higher probability.

In order to assess the significance of the errors affecting the predicted NMR observables, we considered the median of the experimental errors of the same observables as stated by the authors of entries deposited in the biological magnetic resonance database (BMRD).⁷⁶ All entries were downloaded and the statistics of the stated errors in the relevant quantities were assessed. Apparently wrong – very large or non-numeric – values were removed from the list of stated errors and their mean and median were computed. Although the median and the mean were very close in all cases, the average is reported here as it is the most representative of the majority of frequently declared errors. These results are given in Table 1.

Table 1 The median of the experimental errors of the principal NMR observables obtained from the biological magnetic resonance database⁷⁶

Exptl. quantity	Error
^3 J Ci−1Hα	0.35 Hz
^3 J HNC	0.35 Hz
^3 J HαNi+1	0.25 Hz
^3 J HNHα	0.5 Hz
^3 J HNCβ	0.35 Hz
δ Cα	0.2 ppm
δ Cβ	0.2 ppm
δ C	0.2 ppm
RDC (HN-N)	1 Hz

---

It is apparent that for the J-couplings, the RMSEs behave well with respect to the REST results, within the mean experimental errors, which means that all the approaches reproduce experimentally the distribution of the intervening torsion angles. Similarly, the RMSE of the selected carbon chemical shifts are within the median error (0.2 ppm). For the RDCs the RMSE of MSM and MD methods are circa three times larger than the median error value of BMRB entities, showing that the differences are significant. As for the SAXS measurements, the estimation of the experimental error is complex and many mathematical models have been proposed for this task. A recent model⁷⁷ that takes into account the measurement process and the setup geometry, estimates the experimental relative error under different measurement conditions to always be less than 1% for small scattering angles, i.e. where our results show the largest differences. The SAXS RMSE values of MD and MSM methods show significantly highest values (4 × 10⁻⁴ a.u.) than the 1% of the intensity values obtained at q < 0.2 Å.

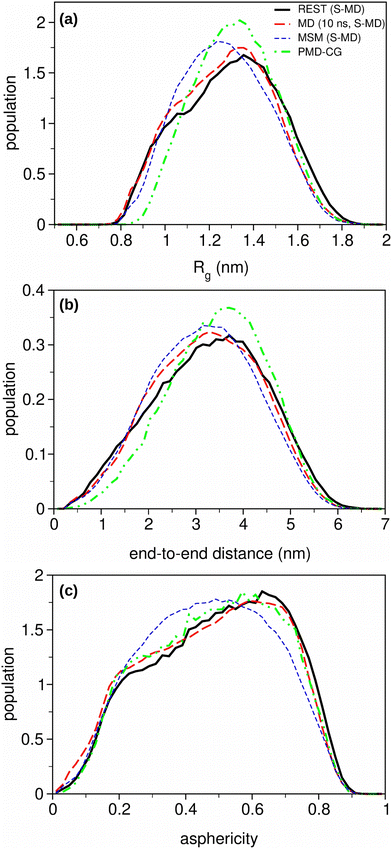
To better understand the relationship between the NMR and SAXS variables and the structural ensembles provided by the MD-based trajectories, three structural collective variables, the radius of gyration (R_g), the end-to-end distance and the asphericity, are depicted in Fig. 5.

Fig. 5 Structural variables obtained from REST (solid black), MD (long dashed red), MSM (short dashed blue) and PMD-CG (dash-dotted green) conformational ensembles of p53-CTD. Histrogram profiles of the (a) radius of gyration (R_g), (b) end-to-end distance, and (c) asphericity.

The results obtained for the R_g and the asphericity contrast with the general trend observed for the NMR and SAXS variables, which show similar RMSE results for the MD and MSM trajectories. The curves extracted from the MD trajectories show a shoulder at low R_g values while achieving their maxima at higher values than the curves provided by MSM trajectories. This profile is similar to that obtained from the reference REST simulations. A similar behaviour is found for the asphericity curves. Both variables provide slightly different structural information. R_g focuses on the compactness of the molecule, with 0 corresponding to the maximum of compactness, while the asphericity indicates how much the protein deviates from the spherical shape, with 0 corresponding to a perfect sphere and 1 corresponding to a thin rod. Therefore, the population of extended structures seems to be significantly higher in the conformation ensembles obtained from MD and REST trajectories than the one obtained using the MSM method. Moreover, the maxima of the end-to-end distance curves show a shift towards higher distances for the REST curve, as compared with those from the other methods, indicating that there are certain differences in the conformations explored via the different methods.

In order to complete our analysis, three additional structural descriptors, i.e. the solvent-accessible surface area (SASA), the number of H-bonds and the secondary structure content (helix and strand), were evaluated along the trajectories for each method (see Fig. S2, ESI†). A comparison of the distribution of the solvent-exposed surface values among the three protocols is complementary to the end-to-end distance results, in which the maxima of MD and MSM curves are shifted with respect to the reference one (REST). The distribution of the number of H-bonds and the secondary structure content give specific, meaningful information about the probability of the formation of compact, structured conformations inside the conformational ensembles generated with each MD-based protocol. Both descriptors show the higher probability of secondary structures containing a high number of H-bonds (4–6) in the REST conformational ensemble with respect to those obtained from MD and MSM.

Overall, the MD and MSM results provide similar descriptions of the variables considered, with reasonable estimates of the J-couplings and the chemical shifts which are related to local structural information, whereas the RDCs and SAXS profiles, which are related more to the global shape and orientation of the disordered peptide, show significant deviations from the reference REST results.

3.1 Evaluation of the PMD-CG method

We next analyze the performance of the PMD-CG method. Forty thousand different conformations were generated for this purpose using a flexible-meccano protocol (see the Methods section 2.3.2 for details), and then the NMR and SAXS variables were calculated. The resulting values are shown in Fig. 3, while their standard deviations and the RMSE values with respect to the REST results are displayed in Fig. 4. The average standard deviations included in Fig. 4a just confirm the robustness of the average values obtained from the constructed conformational ensemble.

As observed in Fig. 4, the backbone J-coupling RMSE values are similar to those from the other methods. However, for two J-couplings, the RMSE values are higher than those obtained from the MD and MSM trajectories. As for the chemical shifts, the RMSE values are greater for the 3 C atoms. Moreover, Fig. 3 shows a general shift towards higher values in δ_Cβ, while the shift occurs towards lower values in δ_C. There are also shifts in δ_Cα with respect to the reference values but without any clear trend. The overall differences in chemical shifts and J-couplings are consistent with lesser sampling of compact conformations, such as alpha-helix structures. For the RDC and the SAXS variables, the PMD-CG conformational ensemble is significantly more accurate than the ensembles obtained from MD and MSM.

Likewise, we have calculated the three structural variables from the PMD-CG conformational ensemble, with their curves included in Fig. 5. For the R_g and end-to-end curves, their maxima are located at similar values compared with the reference maxima in the REST method. However, significant differences are found in the shape of the curves, with the narrower PMD-CG curves showing a significantly lower population for the compacted conformations, in consonance with the differences observed in the chemical shifts and the J-couplings. The same behavior appears in the SASA distribution curves in Fig. S2 (ESI†), in which the lowest values of SASA correspond to the compacted conformations. The analysis of the distribution of H-bonds and secondary structure content probability in the PMD-CG ensembles (Fig. S2b and c, ESI†) just indicates the very low H-bond formation probability. This result is expected due to the stochastic nature during the construction of the IDR conformation in the PMD-CG protocol, since the creation of specific H-bonds between residues within the distance and angle cut-offs would require the support of post hoc, refinement protocols, such as energetic minimizations, or short MD simulations. In contrast, the asphericity data show that the shape distribution is similar to those from the REST and MD trajectories.

It should be highlighted that the differences between the PMD-CG and REST results are not due to convergence issues (as seen in Fig. 4a), as partially occurs with MD and MSM results, but rather to the accuracy of the PMD-CG approach. Two different factors can mainly influence the quality of the results, the prediction of the backbone conformational distribution from the tripeptide library, and the prediction of the side-chain distribution by a side-chain predictor, i.e. Scwrl4. To evaluate separately both factors, we have analyzed the distribution of the dihedral angles ϕ, ψ, and χ₁ of the peptide in the different conformational ensembles. In Fig. 6 we depict the Pearson correlation of the Ramachandran histograms and the χ₁ histograms from MD, MSM, REST and PMD-CG ensembles with respect to the tripeptide histograms. These results show that the backbone dihedral distribution of the tripeptides and the p53-CTD obtained from the 4 methods are similar (Fig. 6a), in agreement with our previous work.⁴⁰ Therefore, the lower representation of more compacted conformations in the conformational ensemble obtained from the PMD-CG seems to be uncorrelated with possible inaccuracies to predict the backbone conformational ensemble of the peptide.

Fig. 6 Pearson correlation coefficients for the (a) Ramachandran (ϕ, ψ dihedral angles) and (b) χ₁ dihedral angle histograms obtained from REST (triangle black), MD (circle red), MSM (square blue) and PMD-CG (diamond green) conformational ensembles of p53-CTD with respect to the histograms obtained from the MD conformational ensembles of the equivalent tripeptides.

The correlations of the χ₁ distributions obtained from MD, MSM and REST with respect to the tripeptide distributions are also very high (Fig. 6b). However, the distribution obtained from the PMD-CG method shows very low correlations for all the p53-CTD residues, indicating that the side-chain dihedral distributions obtained from the Scwrl4 are significantly different compared with the distributions obtained from the other methods and also of those calculated with the tripeptides. Direct comparison between the χ₁ distributions from the REST and PMD-CG conformational ensembles in Fig. S3 (ESI†) shows that for both distributions the maxima of the curves are located in similar χ₁ values, but the curve widths of the PMD-CG ensemble are significantly narrower than those obtained from the REST method, as a consequence of building side chains from a library of rotamers. A similar conclusion holds for independent molecular dynamics simulations when side-chains are reconstructed on a set of 55 diverse proteins⁷⁸ and the predicted side-chain dihedral angles are compared with the experimental values. The distributions for the χ₁ angles of the Scwrl4 side-chain peaks at about the same values as the original distributions, although with a significantly lower dispersion (see Fig. S4, ESI†).

The differences in the conformational distribution of the amino acid side-chains may certainly affect the accuracy of the J-coupling and chemical shift results, which take into account the local structural environment. However, the lower population for the compacted conformations observed in the end-to-end descriptor only depends on the backbone of the conformational distribution. This behavior could be related to the rejection of locally clashing compact conformations in the peptide building phase of the PMD-CG method (see the Methods section 2.3.2). To confirm this, we have performed further analysis of the distances between the backbone C_α atoms of residues separated by a gap of 2 amino acids (i.e. between ith and ith + 3 residues). The probability distribution of interatomic distances in Fig. S5 (ESI†) indeed shows high similarities between the REST and the PMD-CG ensembles except for the lowest values, associated with compacted peptide structures, for which the REST ensemble shows probabilities slightly higher than those from the PMD-CG curves. These results confirm the under-population of the most compacted peptide structures in the PMD-CG method, due to their rejection during the clashing test phase. When assembling the fragments, we note that very small variations – of a few units of degrees – in the local geometry can lead to significant displacements along the peptide chain, and therefore to clashes. This issue is enhanced when constructing compact conformations, such as the α-helix structure, in which the interatomic distance windows are significantly narrow.

3.2 PMD-CG conformation ensemble as a pool for MD starting structures

Despite its limitations, the PMD-CG method provides, in principle, a good statistical accuracy for certain collective variables, such as SAXS intensities or RDC. Therefore, we propose the use of the PMD-CG conformational ensemble as a pool for the selection of the starting structures of the MD-based approaches. In Fig. 7 we compare the standard deviation and the RMSE values of the NMR and SAXS variables obtained from new MD conformational ensembles extracted from the PMD-CG conformations as starting structures, with the previous data.

Fig. 7 Influence of the use of the PMD-CG ensemble as the starting structure pool for MD-based simulations. (a) Average standard deviations, and (b) root mean square errors (RMSE) of the NMR and SAXS variables obtained from REST (black triangle), MD (red circle) and MSM (blue square). Comparison of (c) average standard deviations, and (d) RMSE of the NMR and SAXS variables obtained from MD trajectories at different time lengths: 100 ns (maroon diamond), 10 ns (red circle) and 1 ns (orange triangle). RMSE values have been calculated with respect to the REST results. For the MD and MSM results the filled symbols correspond to trajectories starting from the PMD-CG structures while empty symbols are the standard protocol trajectories. The standard deviation and RMSE units are the same as each variable unit. The corresponding values for RDC have been divided by 10 and those for SAXS have been multiplied by 500.

First, we observe that the standard deviations of the MD and MSM results obtained using the PMD-CG structures are smaller than those coming from the S-MD ones, that is, there is an improvement in the convergence. And more importantly, the RMSE values for the RDC and SAXS magnitudes are substantially reduced when employing the PMD-CG conformational ensemble as a pool of MD starting structures and are now similar to the mean experimental errors. Indeed, the curves of the three structural variables obtained from MD and MSM trajectories starting from the PMD-CG conformations (see Fig. S6, ESI†) are more similar to those from the REST trajectories than the values obtained from the original MD and MSM trajectories starting from the S-MD structures. On the other hand, J-couplings and chemical shifts, which account for local structural information, show, in general, minor variations in their performance. Nevertheless, the RMSE values of those variables previously showing the highest values, such as ³J_Ci−1Hα and δ_Cβ, now decrease. We have also observed (results not shown) that the use of PMD-CG starting structures, instead of the S-MD ones, in the REST method barely affects the results as expected from the ability of the method to explore large regions of the conformational space independently of the initial structures of the replicas.

Other parameters that can be explored to optimize the performance of the MD simulations in IDRs are the number of trajectories and the trajectory lengths, while keeping constant the accumulative simulation time (2 μs). The use of many independent short MD simulations rather than few long-time trajectories in biomolecular systems has already been recommended.²² Nevertheless, the employment of very long MD time lengths in IDRs is still common practice.^18,29 Accordingly, two additional sets of MD simulations, i.e. 20 trajectories at 100 ns and 2000 trajectories at 1 ns, have been performed. Likewise, both MD sets have used the PMD-CG conformational ensemble as a selection pool of starting structures. The statistical sampling evaluation of the NMR and SAXS variables have been added to Fig. 7c and d. These results show that the different time length of the trajectories indeed influences the sampling quality of NMR and SAXS variables. The standard deviations obtained from the 100 ns trajectory set are clearly the highest. On the other hand, the 1 ns trajectory set has the lowest standard deviation values in all calculated variables. This confirms that the use of a larger number of different initial structures favors the exploration of the conformational space and therefore accelerates the convergence of the results. The comparison with the reference average values (Fig. 7d) shows that the accuracy of certain variables to reproduce the reference values are more sensitive than others from the different simulation time lengths. Thus, RDC and SAXS intensities show again the greatest differences among all the different conformational ensembles, following the same trend of the standard deviations, i.e. the shortest the time length and the highest the number of independent trajectories the lowest the RMSE values with respect to the REST values. Regarding the NMR variables offering local structural information, the influence of the time length is just minor, since similar RMSE values are obtained in all J-couplings and chemical shifts for the 10 and 1 ns trajectories. Nevertheless, δ_Cβ shows again certain differences, since the RMSE obtained from 100 ns trajectories is higher than the other two.

As far as the MSM approach is concerned, the employment of different pairs of collective variables to map the conformational space has also been explored to optimize the statistical sampling of the MSM conformational ensembles. Thus, two additional sets of MSM trajectories have been performed by using the pairs of CVs R_g–d_ee and d_ee–γ, respectively. The resulting convergence study of the NMR and SAXS variables depicted in Fig. S7 (ESI†) shows that the employment of different CVs in the MSM approach barely affects the accuracy of the analyzed variables.

3.3 Computational effort

Considering the computational times of each method, the total computational time of the PMD-CG method, t_PMD-CG, is spent mainly in the calculation of the tripeptide conformational ensemble library to generate ultimately the structures of p53-CTD. For the molecule with 20 residues considered in this work, MD and MSM approaches require both 1.4 × t_PMD-CG, which is not enough for certain variables to obtain accurate values (unless the PMD-CG structures are used as starting points). The REST approach requires 1.4 × R × t_PMD-CG, where R is the number of employed replicas in the simulation.

We note that the computational effort of the PMD-CG method increases linearly with the number of residues in the molecule, while the computational effort required in MD-based simulations increases much faster,⁷⁹ so the 1.4 factor increases with the length of the peptide. We also recall that running many short-time trajectories instead of fewer long-time trajectories allows us a more effective distribution of the computational effort in any multicore system.

The great potential of the PMD-CG method performance is apparent when considered under the scenario of mutagenesis studies: a single point mutation in p53-CTD implies, in MD, MSM and REST approaches, the simulation re-run of the p53-CTD mutant (the same computational times for each mutation). However, a single-point mutation involved in the PMD-CG method requires the re-run of only three new tripeptides, i.e. 0.17 × t_PMD-CG. Moreover, if a MD conformational ensemble database of all the 800 possible tripeptides was available for the community, a complete mutagenesis study of an IDR could be done in a number of hours. IDRs can tolerate, in general, a high number of mutations without substantial loss of flexibility and function. However, there are certain molecular recognition features within IDR sequences that are highly conserved and seem essential for the correct function of the protein.³⁷ The complexity of the problem could be addressed using an exhaustive computational mutagenesis approach enabling fast identification of pathogenic mutations.

4 Conclusions

In this work, we have assessed the performance of different molecular dynamics approaches to compute accurately NMR and SAXS descriptors for intrinsically disordered regions of proteins. The convergence evaluation of the structural or energetic descriptors calculated from MD-based simulations is, in general, an issue under active investigation. As far as we know, there is not a convergence evaluation method that could guarantee that the MD-based trajectories accurately explore the whole conformational space of a given collective variable. For this reason, the employment of enhanced sampling methods aims to completely explore the conformational phase space, and have become the reference methods to study many biophysical systems. Nevertheless, each enhanced method has its own disadvantages and the lack of a “gold standard” results in the continued exploration of new sampling methods and the current use of the most traditional ones. A representative example of this scenario has been the challenging characterization of the structural ensembles in IDRs in recent years.

Using the 20-residue region from the C-terminal domain of p53 tumor suppressor protein as a reference system, the results obtained from standard MD and MSM protocols provide reasonable values for the J-couplings and chemical shifts, although fail to describe the RDC and SAXS profiles. The PMD-CG method provides a good representation of the calculated RDC and SAXS observables but lower quality values for two ³J-couplings and especially for the chemical shifts. The origin of this failure is the limited representativity of the distributions of the χ₁ dihedral angles provided by the libraries used during the side-chain construction, and the generation of clashes during the chain building procedure that decrease the relative presence of more compact structures. In future work we intend to address the above limitations of the approach by employing structural minimization and/or short MD simulations that can correct the possible inaccuracies of the method for building the chains leading to misrepresentations of more compact conformations. Moreover, additional non-homologous IDR sequences with different lengths should be tested in future to prove that our conclusions have validity for IDRs with different structural features and functionalities.

The choice of the PMD-CG structures as the starting point in the MD and MSM calculations is shown to be a good strategy that greatly improves the results, especially for the RDC and SAXS profiles, as previously argued by Hummer and collaborators.²⁴ Moreover, the use of many short-time trajectories in MD simulations is advantageous with respect to the use of fewer long-time ones, since they provide a wider exploration of the conformational space. Under these circumstances, the employment of a representative conformational ensemble as a pool of starting structures for many short MD simulations should become the “best practice”, rather than the run of few, very long MD simulations. Being aware of the computational cost required to construct the conformational ensemble pool, the use of the PMD-CG method, as proposed in this work, would greatly enhance the study of IDRs, due to its efficient performance.

Data availability

The inputs and scripts used to produce the PMD-CG conformational ensembles presented in this publication are provided at https://github.com/abastidap/PMD-CG as a tagged release (1.0.0).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the computational assistance provided by J. F. Hidalgo of the Servicio de Infraestructuras TIC de ATICA.

References

1. R. Van Der Lee, M. Buljan, B. Lang, R. Weatheritt, G. Daughdrill, A. Dunker, M. Fuxreiter, J. Gough, J. Gsponer and D. Jones, et al., Classification of intrinsically disordered regions and proteins, Chem. Rev., 2014, 114, 6589–6631.
2. P. Wright and H. Dyson, Intrinsically disordered proteins in cellular signalling and regulation, Nat. Rev. Mol. Cell Biol., 2015, 16, 18–29.
3. A.-S. Hsiao, Plant Protein Disorder: Spatial Regulation, Broad Specificity, Switch of Signaling and Physiological Status, Front. Plant Sci., 2022, 13, 904446.
4. K. Zhu, I. J. Celwyn, D. Guan, Y. Xiao, X. Wang, W. Hu, C. Jiang, L. Cheng, R. Casellas and M. A. Lazar, An intrinsically disordered region controlling condensation of a circadian clock component and rhythmic transcription in the liver, Mol. Cell, 2023, 83, 3457–3469.e7.
5. V. Uversky, Introduction to intrinsically disordered proteins (IDPs), Chem. Rev., 2014, 114, 6557–6560.
6. V. Uversky, Intrinsically disordered proteins and their “Mysterious” (meta)physics, Front. Phys., 2019, 7, 00010.
7. H. Dyson, Making Sense of Intrinsically Disordered Proteins, Biophys. J., 2016, 110, 1013–1016.
8. A. Dishman and B. Volkman, Unfolding the Mysteries of Protein Metamorphosis, ACS Chem. Biol., 2018, 13, 1438–1446.
9. M. R. Jensen, M. Zweckstetter, J.-R. Huang and M. Blackledge, Exploring Free-Energy Landscapes of Intrinsically Disordered Proteins at Atomic Resolution Using NMR Spectroscopy, Chem. Rev., 2014, 114, 6632–6660.
10. N. Salvi, in Intrinsically Disordered Proteins, ed. N. Salvi, Academic Press, 2019, pp. 37–64.
11. S.-H. Chong and S. Ham, Folding Free Energy Landscape of Ordered and Intrinsically Disordered Proteins, Sci. Rep., 2019, 9, 14927.
12. P. Robustelli, S. Piana, D. Shaw and D. Shaw, Mechanism of Coupled Folding-upon-Binding of an Intrinsically Disordered Protein, J. Am. Chem. Soc., 2020, 142, 11092–11101.
13. T. N. Cordeiro, F. Herranz-Trillo, A. Urbanek, A. Estaña, J. Cortés, N. Sibille and P. Bernadó, in Biological Small Angle Scattering: Techniques, Strategies and Tips, ed. B. Chaudhuri, I. G. Muñoz, S. Qian and V. S. Urban, Springer Singapore, Singapore, 2017, pp. 107–129.
14. E. Ravera, L. Sgheri, G. Parigi and C. Luchinat, A critical assessment of methods to recover information from averaged data, Phys. Chem. Chem. Phys., 2016, 18, 5686–5701.
15. A. Carlon, L. Gigli, E. Ravera, G. Parigi, A. M. Gronenborn and C. Luchinat, Assessing Structural Preferences of Unstructured Protein Regions by NMR, Biophys. J., 2019, 117, 1948–1953.
16. D. Boehr, R. Nussinov and P. Wright, The role of dynamic conformational ensembles in biomolecular recognition, Nat. Chem. Biol., 2009, 5, 789–796 , cited By 1182.
17. J. Mittal, T. H. Yoo, G. Georgiou and T. M. Truskett, Structural Ensemble of an Intrinsically Disordered Polypeptide, J. Phys. Chem. B, 2013, 117, 118–124.
18. U. R. Shrestha, J. C. Smith and L. Petridis, Full structural ensembles of intrinsically disordered proteins from unbiased molecular dynamics simulations, Commun. Biol., 2021, 4, 243.
19. T. Lazar, E. Martinez-Perez, F. Quaglia, A. Hatos, L. B. Chemes, J. A. Iserte, N. A. Mendez, N. A. Garrone, T. E. Saldano and J. Marchetti, et al., PED in 2021: a major update of the protein ensemble database for intrinsically disordered proteins, Nucleic Acids Res., 2021, 49, D404–D411.
20. A. Grossfield and D. M. Zuckerman, in Quantifying Uncertainty and Sampling Quality in Biomolecular Simulations, ed. R. A. Wheeler, Annual Reports in Computational Chemistry, Elsevier, 2009, ch. 2, vol. 5, pp. 23–48.
21. S.-H. Chong, P. Chatterjee and S. Ham, Computer Simulations of Intrinsically Disordered Proteins, Annu. Rev. Phys. Chem., 2017, 68, 117–134.
22. M. C. Childers and V. Daggett, Validating Molecular Dynamics Simulations against Experimental Observables in Light of Underlying Conformational Ensembles, J. Phys. Chem. B, 2018, 122, 6673–6689.
23. P. Bernadó, C. Bertoncini, C. Griesinger, M. Zweckstetter and M. Blackledge, Defining long-range order and local disorder in native α-synuclein using residual dipolar couplings, JACS, 2005, 127, 17968–17969.
24. L. M. Pietrek, L. S. Stelzl and G. Hummer, Hierarchical Ensembles of Intrinsically Disordered Proteins at Atomic Resolution in Molecular Dynamics Simulations, J. Chem. Theory Comput., 2020, 16, 725–737.
25. A. Estaña, A. Barozet, A. Mouhand, M. Vaisset, C. Zanon, P. Fauret, N. Sibille, P. Bernadó and J. Cortés, Predicting Secondary Structure Propensities in IDPs Using Simple Statistics from Three-Residue Fragments, J. Mol. Biol., 2020, 432, 5447–5459.
26. L. S. Stelzl, L. M. Pietrek, A. Holla, J. Oroz, M. Sikora, J. Koefinger, B. Schuler, M. Zweckstetter and G. Hummer, Global Structure of the Intrinsically Disordered Protein Tau Emerges from Its Local Structure, JACS AU, 2022, 2, 673–686.
27. P. Liu, B. Kim, R. A. Friesner and B. J. Berne, Replica exchange with solute tempering: a method for sampling biological systems in explicit water, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13749–13754.
28. A. K. Smith, C. Lockhart and D. K. Klimov, Does Replica Exchange with Solute Tempering Efficiently Sample Aβ Peptide Conformational Ensembles?, J. Chem. Theory Comput., 2016, 12, 5201–5214.
29. A. Hicks and H.-X. Zhou, Temperature-induced collapse of a disordered peptide observed by three sampling methods in molecular dynamics simulations, J. Chem. Phys., 2018, 149, 072313.
30. B. E. Husic and V. S. Pande, Markov State Models: From an Art to a Science, JACS, 2018, 140, 2386–2396.
31. F. Noe and E. Rosta, Markov Models of Molecular Kinetics, J. Chem. Phys., 2019, 151, 174105.
32. V. Ozenne, F. Bauer, L. Salmon, J.-R. Huang, M. R. Jensen, S. Segard, P. Bernado, C. Charavay and M. Blackledge, Flexible-meccano: a tool for the generation of explicit ensemble descriptions of intrinsically disordered proteins and their associated experimental observables, Bioinformatics, 2012, 28, 1463–1470.
33. Z. Harmat, D. Dudola and Z. Gaspari, DIPEND: An Open-Source Pipeline to Generate Ensembles of Disordered Segments Using Neighbor-Dependent Backbone Preferences, Biomolecules, 2021, 11, 1505.
34. J. M. C. Teixeira, Z. H. Liu, A. Namini, J. Li, R. M. Vernon, M. Krzeminski, A. A. Shamandy, O. Zhang, M. Haghighatlari and L. Yu, et al., Idpconformergenerator: a flexible software suite for sampling the conformational space of disordered protein states, Biophys. J., 2023, 122, 204A.
35. L. M. Pietrek, L. S. Stelzl and G. Hummer, Structural ensembles of disordered proteins from hierarchical chain growth and simulation, Curr. Opin. Struct. Biol., 2023, 78, 102501.
36. J. Ahn and C. Prives, The C-terminus of p53: the more you learn the less you know, Nat. Struct. Biol., 2001, 8, 730–732.
37. O. Laptenko, D. R. Tong, J. Manfredi and C. Prives, The Tail That Wags the Dog: How the Disordered C-Terminal Domain Controls the Transcriptional Activities of the p53 Tumor-Suppressor Protein, Trends Biochem. Sci., 2016, 41, 1022–1034.
38. E. Fadda and M. G. Nixon, The transient manifold structure of the p53 extreme C-terminal domain: insight into disorder, recognition, and binding promiscuity by molecular dynamics simulations, Phys. Chem. Chem. Phys., 2017, 19, 21287–21296.
39. A. Kumar, P. Kumar, S. Kumari, V. N. Uversky and R. Giri, Folding and structural polymorphism of p53 C-terminal domain: one peptide with many conformations, Arch. Biochem. Biophys., 2020, 684, 108342.
40. A. Bastida, J. Zuniga, B. Miguel and M. A. Soler, Description of conformational ensembles of disordered proteins by residue-local probabilities, Phys. Chem. Chem. Phys., 2023, 25, 10512–10524.
41. A. Estaña, N. Sibille, E. Delaforge, M. Vaisset, J. Cortés and P. Bernadó, Realistic Ensemble Models of Intrinsically Disordered Proteins Using a Structure-Encoding Coil Database, Structure, 2019, 27, 381–391.
42. A. D. J. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack Jr., J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo and S. Ha, et al., All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins, J. Phys. Chem. B, 1998, 102, 3586–3616.
43. Q. Qiao, G. R. Bowman and X. Huang, Dynamics of an Intrinsically Disordered Protein Reveal Metastable Conformations That Potentially Seed Aggregation, JACS, 2013, 135, 16092–16101.
44. U. R. Shrestha, P. Juneja, Q. Zhang, V. Gurumoorthy, J. M. Borreguero, V. Urban, X. Cheng, S. V. Pingali, J. C. Smith and H. M. O'Neill, et al., Generation of the configurational ensemble of an intrinsically disordered protein from unbiased molecular dynamics simulation, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 20446–20452.
45. P. Herrera-Nieto, A. Perez and G. De Fabritiis, Characterization of partially ordered states in the intrinsically disordered N-terminal domain of p53 using millisecond molecular dynamics simulations, Sci. Rep., 2020, 10, 12402.
46. A. Paul, S. Samantray, M. Anteghini, M. Khaled and B. Strodel, Thermodynamics and kinetics of the amyloid-beta peptide revealed by Markov state models based on MD data in agreement with experiment, Chem. Sci., 2021, 12, 6652–6669.
47. B. Strodel, Energy Landscapes of Protein Aggregation and Conformation Switching in Intrinsically Disordered Proteins, J. Mol. Biol., 2021, 433, 167182.
48. M. U. Rahman, K. Song, L.-T. Da and H.-F. Chen, Early aggregation mechanism of Aβ_16–22 revealed by Markov state models, Imt. J. Biol. Macromol., 2022, 204, 606–616.
49. F. Noe, C. Schuette, E. Vanden-Eijnden, L. Reich and T. R. Weikl, Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19011–19016.
50. J.-H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schuette and F. Noe, Markov models of molecular kinetics: generation and validation, J. Chem. Phys., 2011, 134, 174105.
51. F. Nueske, H. Wu, J.-H. Prinz, C. Wehmeyer, C. Clementi and F. Noe, Markov state models from short non-equilibrium simulations-Analysis and correction of estimation bias, J. Chem. Phys., 2017, 146, 094104.
52. E. Hruska, J. R. Abella, F. Nuske, L. E. Kavraki and C. Clementi, Quantitative comparison of adaptive sampling methods for protein dynamics, J. Chem. Phys., 2018, 149, 244119.
53. L. Wang, R. A. Friesner and B. J. Berne, Replica Exchange with Solute Scaling: A More Efficient Version of Replica Exchange with Solute Tempering (REST2), J. Phys. Chem. B, 2011, 115, 9431–9438.
54. Y. Sugita and Y. Okamoto, Replica-Exchange Molecular Dynamics Method for Protein Folding, Chem. Phys. Lett., 1999, 314, 141–151.
55. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4, 435–447.
56. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson and D. van der Spoel, et al., GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit, Bioinformatics, 2013, 29, 845–854.
57. J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmueller and A. D. MacKerell, Jr., CHARMM36m: an improved force field for folded and intrinsically disordered proteins, Nat. Methods, 2017, 14, 71–73.
58. J. Huang and A. D. MacKerell, Force field development and simulations of intrinsically disordered proteins, Curr. Opin. Struct. Biol., 2018, 48, 40–48.
59. P. Robustelli, S. Piana and D. Shaw, Developing a molecular dynamics force field for both folded and disordered protein states, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4758–E4766.
60. B. Hess, P-LINCS: a parallel linear constraint solver for molecular simulation, JCTC, 2008, 4, 116–122.
61. G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, JCP, 2007, 126, 014101.
62. L. Schrödinger and W. DeLano, PyMOL, https://www.pymol.org/pymol.
63. E. F. Pettersen, T. D. Goddard, C. C. Huang, E. C. Meng, G. S. Couch, T. I. Croll, J. H. Morris and T. E. Ferrin, UCSF ChimeraX: structure visualization for researchers, educators, and developers, Protein Sci., 2021, 30, 70–82.
64. G. G. Krivov, M. V. Shapovalov and R. L. Dunbrack, Jr., Improved prediction of protein side-chain conformations with SCWRL4, Proteins: Struct., Funct., Bioinf., 2009, 77, 778–795.
65. X. Huang, R. Pearce and Y. Zhang, FASPR: an open-source tool for fast and accurate protein side-chain packing, Biofinformatics, 2020, 36, 3758–3765.
66. G. R. Bowman, K. A. Beauchamp, G. Boxer and V. S. Pande, Progress and challenges in the automated construction of Markov state models for full protein systems, J. Chem. Phys., 2009, 131, 124101.
67. B. Hess, D. van der Spoel, M. J. Abraham and E. Lindahl, GROMACS 2021.7 Source code, version 2021.7, 2023 DOI:10.5281/zenodo.7586728.
68. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, PLUMED 2: new feathers for an old bird, Comput. Phys. Commun., 2014, 185, 604–613.
69. G. Bussi, Hamiltonian replica exchange in GROMACS: a flexible implementation, Mol. Phys., 2014, 112, 379–384.
70. G. Vuister and A. Bax, Quantitative J correlation – A new approach for measuring homonuclear 3-bond J(H(N)H(ALPHA)) coupling-constants in N15-enriched proteins, JACS, 1993, 115, 7772–7777.
71. A. Wang and A. Bax, Determination of the backbone dihedral angles phi in human ubiquitin from reparametrized empirical Karplus equations, JACS, 1996, 118, 2483–2494.
72. Y. Shen and A. Bax, SPARTA plus: a modest improvement in empirical NMR chemical shift prediction by means of an artificial neural network, J. Biomol. NMR, 2010, 48, 13–22.
73. M. Zweckstetter and A. Bax, Prediction of sterically induced alignment in a dilute liquid crystalline phase: aid to protein structure determination by NMR, JACS, 2000, 122, 3791–3792.
74. D. Svergun, C. Barberato and M. Koch, CRYSOL – A program to evaluate x-ray solution scattering of biological macromolecules from atomic coordinates, J. Appl. Crystallogr., 1995, 28, 768–773.
75. A. G. Kikhney and D. I. Svergun, A practical guide to small angle X-ray scattering (SAXS) of flexible and intrinsically disordered proteins, FEBS Lett., 2015, 589, 2570–2577.
76. J. C. Hoch, K. Baskaran, H. Burr, J. Chin, H. R. Eghbalnia, T. Fujiwara, M. R. Gryk, T. Iwata, C. Kojima and G. Kurisu, et al., Biological Magnetic Resonance Data Bank, Nucleic Acids Res., 2023, 51, D368–D376.
77. S. M. Sedlak, L. K. Bruetzel and J. Lipfert, Quantitative evaluation of statistical errors in small-angle X-ray scattering measurements, J. Appl. Crystallogr., 2017, 50, 621–630.
78. H. Tjong and H. X. Zhou, GBr⁶: a parametrization free, accurate, analytical generalized Born method, J. Phys. Chem., 2007, 111, 3055–3061.
79. D. Jones, J. E. Allen, Y. Yang, W. F. D. Bennett, M. Gokhale, N. Moshiri and T. S. Rosing, Accelerators for Classical Molecular Dynamics Simulations of Biomolecules, J. Chem. Theory Comput., 2022, 4047–4069.

---

Footnote

† Electronic supplementary information (ESI) available: Kratky plot obtained from REST, MD, MSM and PMD-CG conformational ensembles (Fig. S1), distribution of SASA, number of H-bonds and secondary structural elements obtained from REST, MD, MSM and PMD-CG conformational ensembles (Fig. S2), histograms of χ₁ dihedral angles obtained from REST and PMD-CG conformational ensembles (Fig. S3), histogram of χ₁ angles of all amino acids obtained from the experimental 55 protein structures and after side-chain reconstruction using Scwrl4 (Fig. S4), distribution of C_α–C_α interatomic distances obtained from REST and PMD-CG conformational ensembles (Fig. S5), structural variables obtained from REST, MD and MSM trajectories starting from PMD-CG structures (Fig. S6), and comparison of the average standard deviations and RMSE of the NMR and SAXS variables obtained from MSM trajectories that employ different pairs of collective variables (Fig. S7). See DOI: https://doi.org/10.1039/d4cp02564d

---