Elucidating gas–surface interactions relevant to atmospheric particle growth using combined temperature programmed desorption and temperature-dependent uptake†
Kristen N.
Johnson
 ,
Yixin
Li‡
,
Michael J.
Ezell
,
Yixin
Li‡
,
Michael J.
Ezell
 ,
Pascale S. J.
Lakey
,
Pascale S. J.
Lakey
 ,
Manabu
Shiraiwa
,
Manabu
Shiraiwa
 and
Barbara J.
Finlayson-Pitts
and
Barbara J.
Finlayson-Pitts
 *
*
Department of Chemistry, University of California, Irvine, CA 92697-2025, USA. E-mail: bjfinlay@uci.edu
First published on 28th August 2024
Abstract
Understanding growth mechanisms for particles in air is fundamental to developing a predictive capability for their impacts on human health, visibility, and climate. In the case of highly viscous semi-solid or solid particles, the likelihood of impinging gases being taken up to grow the particle will be influenced by the initial uptake coefficient and by the residence time of the adsorbed gas on the surface. Here, a new approach that combines Knudsen cell capabilities for gas uptake measurements with temperature programmed desorption (TPD) for binding energy measurements of gases is described. The application of this unique capability to the uptake of organic gases on silica demonstrates its utility and the combination of thermodynamic and kinetic data that can be obtained. Lower limits to the initial net uptake coefficients at 170 K are (3.0 ± 0.6) × 10−3, (4.9 ± 0.6) × 10−3 and (4.3 ± 0.8) × 10−3 for benzene, 1-chloropentane, and methanol, respectively, and are reported here for the first time. The uptake data demonstrated that the ideal gas lattice model was appropriate, which informed the analysis of the TPD data. From the thermal desorption measurements, desorption energies of 34.6 ± 2.5, 45.8 ± 5.5, and 40.0 ± 5.6 kJ mol−1 (errors are 1σ) are obtained for benzene, 1-chloropentane, and methanol, respectively, and show good agreement with previously reported measurements. A multiphase kinetics model was applied to quantify uptake, desorption, and diffusion through the particle multilayers and hence extract desorption kinetics. Implications for uptake of organics on silica surfaces in the atmosphere and the utility of this system for determining relationships between residence times of organic gases and particle surfaces of varying composition are discussed in the context of developing quantitative predictions for growth of aerosol particles in air.
Introduction
Exchange between the gas phase and the condensed phase of airborne particles is important as it determines concentrations of species in both phases.1,2 The growth of particles via net uptake from the gas phase is of particular importance. This is because particle size determines their impacts on light scattering and visibility,3–5 ability to alter cloud formation and properties,6–17 and the region of the lung they reach, which impacts health.18–25When a gas interacts with the surface of a particle in the atmosphere, its fate involves a number of potential pathways: (1) inelastic collisions of the gas with the surface in which the gas adsorbs to the surface rather than elastically scattering; (2) desorption back to the gas phase; (3) reaction on the surface; (4) diffusion into the condensed phase; and (5) reaction in the bulk. A number of approaches have been developed that treat these interactions in different ways to quantify experimental measurements of net gas uptake and particle growth, and to provide predictive capabilities for these processes on scales from molecular to global.26–42
Steps (1) and (2) depend on the interactions between the adsorbate and the surface which are determined by the intermolecular forces between the adsorbed gas molecule and the surface functional groups.43–45 Adsorbates are often described on a molecular basis as a 2D ideal gas or as a 2D ideal lattice gas.44,45 In the former case, the energy barrier for diffusion on the surface is much smaller than the thermal energy, kBT (kB is the Boltzmann constant, T is the temperature), and molecules move relatively freely in the x,y directions parallel to the surface. In the case of the 2D ideal lattice gas, the energy barrier for diffusion is significantly greater than the available thermal energy so that the adsorbates are immobile and are treated as harmonic oscillators with no translational degrees of freedom. The intermediate case where the energy barrier and thermal energy are comparable is described as a hindered translator.44
The stronger the adsorbate–surface interaction, the longer the residence time on the surface, providing increased opportunities for diffusion into the bulk, reaction on the surface, or the adsorbed species becoming “buried” by incoming molecules from the gas phase. While there is experimental evidence for such a “burying mechanism” of particle growth,46–48 quantifying its contribution requires a detailed molecular-level understanding of the residence time of species on the surface and hence the factors that contribute to the binding energies between the gas and surface.
Diffusion into the bulk, step (4), is dependent on the phase state of the particles and competes with desorption. The phase state of airborne particles is highly variable, depending on their source, reactions in air, temperature and relative humidity.49–59 Their phase can vary from low viscosity liquids to high viscosity semi-solids and solids, with the corresponding diffusion coefficients varying from high (∼10−5 cm2 s−1) to extremely low (<10−20 cm2 s−1).60 Furthermore, regions of very different viscosity can exist within one particle due to phase separation.61 While diffusion into liquids is relatively fast, this is not the case for solids and semi-solids,60 and other processes such as desorption back into the gas phase or burying by incoming gases can be competitive.
We describe here an approach to study the interaction of gases with surfaces in non-reactive systems that combines temperature programmed desorption (TPD)62 measurements to obtain binding energies, with a Knudsen cell1,63 for uptake measurements. The latter was very useful in identifying the appropriate gas adsorption model to use (ideal gas lattice model). The Knudsen cell portion of this apparatus was used to measure reactive gas uptake and has been recently described for the temperature dependent uptake of n-butylamine on various solid diacids.64 In that case, an irreversible acid–base reaction occurs to form an ionic liquid layer, and desorption of the amine back into the gas phase is not important. Application to non-reactive systems is a more challenging problem since desorption competes with uptake. We report here adsorption and desorption from silica particles of benzene,65 1-chloropentane,66 and methanol.67 These gases have desorption energies spanning a range of values and different intermolecular forces such as hydrogen bonding, halogen bonding68,69 and dispersion forces. Silica is a well-studied surface due to its stability and widespread use. It is also relevant to the atmosphere as silica is the main component of suspended mineral dust particles,1,70 which can be transported over long distances. Organic coatings have been observed on such particles, making them a sink for volatile organic compounds, VOC.71 In addition, glass surfaces which have a high silica content are known to play a key role in the partitioning of organics indoors.72,73
Experimental
Apparatus design
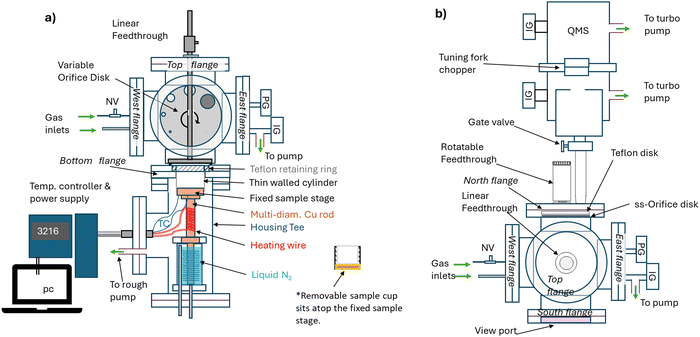
The apparatus design is based on the Knudsen cell designs of Caloz et al.74 and of Mønster et al.75 modified to incorporate TPD capabilities (Fig. 1). A detailed description is found in the ESI.† Briefly, the main chamber consists of a stainless steel six way cross with total volume of 5260 cm3 and an estimated interior surface area of 2360 cm2. The bottom flange holds the removable sample cup and separates the cross from the cryogenic/heating parts of the apparatus. Temperature control of the sample from 100 K to 400 K is provided by balancing heating and cooling with liquid nitrogen of a copper part that terminates in a fixed sample stage that is in contact with the bottom of the sample cup (Fig. S1, ESI†). The top flange of the main chamber holds a linear feedthrough (Fig. 1a) that controls the position of the sample cover for uptake experiments or the gas doser (Fig. S2, ESI†) for TPD experiments. A rotatable feedthrough (Fig. S3, ESI†) allows for the selection of orifices of different diameters (0.5, 1, 2, 4, 8, 11 and 14 mm) which control the gas flow rate to the quadrupole mass spectrometer (QMS, Extrel Core Mass Spectrometer equipped with an electron impact ionization source). One flange has a hinged easy access viewport to insert or remove the sample cup. It also provides a line-of-sight to view the selected orifice and ensure it is centered over the opening to the mass spectrometer. Gas escape rates were measured experimentally to define the effective orifice diameters (Table S2, ESI†).Materials and methods
Sample preparation
A suspension of fumed silica powder (Cabosil® Grade 5, Cabot Corp.) (particle size ∼ 100 nm) was made in either toluene or water, and 1–5 mg of silica was deposited on an argon plasma-cleaned silicon wafer. After the solvent had evaporated, the sample was placed in the vacuum chamber (P = 1 × 10−7 torr) and heated for at least 8 hours at 380 K to remove excess solvent and adsorbed water. The main gas phase contaminant at 10−7 torr is water vapor from the chamber walls. Considering the water impingement rate at 10−7 torr and 298 K is 3.6 × 1013 collisions cm−2 s−1, the time before the entire sample surface (∼200 cm2) is coated with a layer of water is on the order of hours, longer than the time for each sample run. Gases used in the experiments were prepared by adding liquid benzene (99.7%, EMD Chemicals), methanol (ACS Grade 99.8%, Fisher Chemical), or 1-chloropentane (99%, Sigma-Aldrich) to a 50 mL glass bulb attached to a vacuum manifold. Each underwent 3 freeze–pump–thaw cycles before use. | (1) |
Results & discussion
Uptake of organics onto silica particles
Representative time profiles for uptake at 170 K are shown in Fig. 2. Concentration dependent initial uptake coefficients were measured from the minimum in the signal immediately after opening the sample cup lid and are shown in Fig. 2. Uptake on the sample cup alone was negligible and experiments with the silicon wafer but no added silica particles (surface area 18 cm2) showed less than 5% reduction in the I0 after opening the lid. Initial values of the net uptake coefficients (γ0) are summarized in Table 1. Although the data are somewhat scattered at the lowest pressures, an estimate for the zero-pressure limit can be obtained from linear fits to the data (Fig. 3). The decrease in the initial uptake coefficients at higher gas phase concentrations may be due to the gas-substrate collision rates at higher pressures being fast enough to quickly decrease the numbers of available surface sites, while simultaneously increasing desorption. Thus, the measured values are lower limits, since increased desorption rates can reduce apparent uptake coefficients even at the shortest times when it is typically assumed the desorption rate is zero. By extrapolating to the zero-pressure limit, the influences of desorption as well as limitations in the response time are minimized in the reported value of the initial uptake coefficient.A significant source of uncertainty in uptake measurements is determination of the effective available sample area. One way to address this is to use a single layer (or less) of particles evenly distributed across the sample holder in such a way that the adjacent particles do not touch.64,82 In the case of Cabosil, the particles do not spread out evenly over the surface of the silicon wafer (Fig. S7, ESI†) so that this approach could not be used.
Consequently, an alternative approach was developed where we used TPD profiles that showed both the multilayer and monolayer peaks to estimate that there are ∼5–10 multilayers of the gas initially adsorbed. The multilayer desorption peak that occurs at lower temperatures has a zero-order line shape and is narrower than the monolayer peak that occurs at higher temperatures. The profiles could be deconvoluted to determine the total signal associated with the monolayer signal (Fig. S4, ESI†). By calibrating the mass spectrometer signal using known pressures and escape rates (Fig. S8 and Table S2, ESI†), the monolayer signal can be converted to a total number of molecules. From the cross-sectional areas of each of the three molecules,83 the available surface area was found to be ∼10% of the BET surface area of the same sample determined using N2 adsorption. This is similar to the observation by Seisel et al.84 who found that the effective surface area was roughly 1/20th of the BET surface area in uptake experiments of water on mineral dust. In that case they assumed that the total number of adsorbed molecules during the uptake experiments corresponded to one monolayer. A significant advantage of our approach is that the combination of uptake and desorption measurements on the same sample provides a way to experimentally determine the available surface area of powdered samples. The kinetic multilayer modeling results point to a possible explanation for the apparent surface area of ∼10% of the BET surface area. The model shows that during the first few seconds of exposure and uptake, the adsorbed molecules only reside in the top layers of the bed of particles (Fig. S6, ESI†).
In the uptake time profiles shown in Fig. 2, the signal does not recover to the initial signal (I0) but rather to a smaller value where the rate of net uptake (i.e., the difference of adsorption and desorption fluxes) is constant. We assume that the uptake has reached a steady-state at the end of the exposure. Note that this assumption may not be fully correct as the system can be limited by diffusion through silica particles and the time-dependent uptake may not be captured as discussed in the modeling section. The number of molecules that have been adsorbed are determined by numeric integration of the difference in the uptake profile signal with the lid closed and with the lid open. By measuring the number of adsorbed molecules at the steady state at various gas-phase concentrations, an effective adsorption isotherm can be obtained by neglecting bulk diffusion. These are shown in Fig. 4 with a Langmuir isotherm fit to the data. In the Langmuir model, it is assumed that each adsorbate is immobile on the surface and that they do not interact with neighboring molecules. The surface coverage can then be expressed as eqn (2),
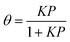 | (2) |
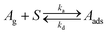 | (I) |
In reaction (I)Ag is the molecule in the gas phase, S is an available surface site, and Aads is the adsorbed molecule. Langmuir isotherm plots as well as values of the equilibrium constants are shown in Fig. 4. The equilibrium constants were determined by linear regression of plots of θ/(1 − θ) against the gas phase concentration which has a slope equal to K (Fig. S9, ESI†). It should be noted that K measured here is an effective value for the steady state Langmuir isotherm which may or may not be a true equilibrium due to possible gradients in the concentration of adsorbed molecules within the bed of particles. Nevertheless, the experimentally determined values of the Langmuir constant (Kbenzene = (8.6 ± 2.9) × 10−12 cm3 molecule−1, Kmethanol = (3.0 ± 0.2) × 10−11 cm3 molecule−1, and K1-chloropentane = (1.6 ± 1.1) × 10−10 cm3 molecule−1) are in good agreement with those calculated with the kinetic model (Kbenzene = 7.7 × 10−12 cm3 molecule−1, Kmethanol = 4.4 × 10−11 cm3 molecule−1, and K1-chloropentane = 1.8 × 10−10 cm3 molecule−1). The K's from the kinetic model are calculated from the expression K = σ (ka/kd) taking ka = αs,0·(vT/4) where σ is the cross-sectional area of the molecule, αs,0 is the initial surface accommodation coefficient and vT is the mean thermal velocity of the molecule in the gas phase (Table S3, ESI†).76 Measurement of Langmuir isotherms along with uptake and desorption described below demonstrate the versatility of this apparatus in providing both kinetics and steady-state data simultaneously.
 | (3) |
 | (4) |
The coverage dependent desorption energy can be extracted from the experimental desorption curves. This desorption energy is then used in eqn (3) to simulate desorption curves at initial coverages smaller than the curve with the highest initial coverage that is used as a starting point. This involves integrating eqn (3) to determine the change in coverage with temperature (time). The simulated TPD curves are then compared with the experimentally measured desorption rates and the sum of the squared residuals is calculated. The process is then repeated, treating the preexponential factor as a variational parameter until the error between the experimental and simulated TPD curves is minimized as shown in Fig. 5d–f, giving best-fit values for the preexponential factors. As discussed below, while the measured preexponential factor is affected by diffusion and adsorption/readsorption processes, these do not affect the desorption energies derived from this approach.87
Fig. 6 shows desorption energies as a function of coverage from a typical TPD experiment. Extrapolation of the linear portion of the curves in Fig. 6 to the zero-coverage limit corresponds to the desorption energy of an isolated molecule that is not on a unique type of site e.g., a defect site, or subject to adsorbate-adsorbate interactions.85 These are summarized in Table 2. For comparison, Table 2 also shows results from Abelard et al.65,66 whose experimental approach and data analysis are similar to those in the present studies. Both the desorption energies and preexponential factors are in good agreement. However, the preexponential factors in both sets of studies (106–9 s−1) are much smaller than expected for desorption kinetics, where values ∼1013 s−1 are often taken as typical.43,45,62
 | ||
| Fig. 6 Dependence of desorption energy on surface coverage for typical experiments by inversion of the Polanyi–Wigner equation, eqn (3), using a preexponential factor that corresponds to the minimum error for each molecule: benzene ν = 106.5, 1-chloropentane ν = 109.4, and methanol ν = 106.7. The linear part of each curve was fit to a first order polynomial. The y-intercept corresponds to the desorption energy for an isolated molecule from a terrace site and is reported in Table 2. | ||
Unexpectedly small preexponential factors have been observed in studies of desorption from porous catalysts and attributed to readsorption of the gas as it moves through the solid.87–92 In the current experiments, the silica powder formed irregular mounds (Fig. S7, ESI†) across the surface of the silicon wafer. An estimate of ∼22 layers of particles is obtained by assuming hexagonal close packing and uniform distribution of 1 mg of particles within a cylindrical bed of particles with 2 cm diameter. As discussed above, the number of molecules in a monolayer desorbed during TPD suggested that about 10% of the total particle surface area measured by BET adsorption of nitrogen was involved in the organic gas uptake, some of which will be subsurface layers. Therefore, the adsorbates are desorbing but have an opportunity to readsorb as they travel through the silica before ultimately escaping into the gas phase. While this affects the measured preexponential factor, it does not alter the measured desorption energies87 which are the parameters of interest here. Readsorption can also broaden the TPD peaks for powdered samples when compared to TPD from single crystal samples. Sneh and George reported methanol desorption from silicon wafers with the native SiO2 layer and comparing the shape of the TPD curves in to those presented here shows that the monolayer peak broadens for the powdered sample and the maximum desorption rate shifts from 180 K to 200 K.67 Using thin layers of powders has been shown to minimize the readsorption effects. For example, in the case of water desorption from TiO2, shifts of up to 40 K compared to the single crystal counterpart have been observed, but did not change the peak assignments.88,91
It is clear from the gas uptake data and the Langmuir-type behavior that the 2D ideal lattice gas model is the most appropriate representation of adsorbates on silica. Evidence for the applicability of this model is the surface saturation observed in the gas uptake experiments (Fig. 2). In this case, adsorbates have higher rates of desorption at higher surface coverages. This can be seen experimentally in Fig. 7 where the desorption rate increases nonlinearly with coverage, especially at high surface coverage. From transition state theory, the desorption rate (Rdes) for a 2D lattice gas can be expressed as eqn (5) (Campbell et al.44 equation 70),
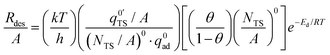 | (5) |
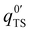 and q0ad are partition functions for the molecule in the transition and adsorbed state respectively, (NTS/A)0 is the standard surface concentration for molecules in the transition state, θ is the surface coverage, and Ed is the desorption energy. This equation holds for any choice of standard state. eqn (5) is similar in form to the Polanyi–Wigner equation used in the inversion analysis of the data (eqn (3)), where ν is defined as eqn (6),
and q0ad are partition functions for the molecule in the transition and adsorbed state respectively, (NTS/A)0 is the standard surface concentration for molecules in the transition state, θ is the surface coverage, and Ed is the desorption energy. This equation holds for any choice of standard state. eqn (5) is similar in form to the Polanyi–Wigner equation used in the inversion analysis of the data (eqn (3)), where ν is defined as eqn (6), | (6) |
However, eqn (5) explicitly recognizes that for a 2D ideal lattice gas, the surface coverage dependence of the desorption rate depends on θ/(1 − θ), rather than θn (eqn (3)), so that desorption rates increase with coverage. This is consistent with the data in Fig. 7 that clearly show this strong dependence of desorption rates on surface coverage. At small surface coverages, θ ≪ 1 eqn (5) predicts desorption rates that are first order in θ. In terms of atmospheric relevance, it is these lower surface coverages that are of most interest.
From eqn (5), the slope of a line of ln[(Rdes)/(θ/1 − θ)] versus 1/T is equal to Ed/R if Ed is not a function of the coverage. The data in Fig. 6 show only a weak dependence on coverage for θ from 0.2 to 0.8. Therefore, assuming the coverage dependent contribution is small in this region, the slope was used to determine Ed. The plots for benzene, 1-chloropentane, and methanol are shown in Fig. 8. The desorption energies obtained in this manner (Table 3) agree within experimental error with those determined through inversion analysis (Table 2). Note that these desorption energies are similar to those calculated for benzene on silica by Fang et al.93 (28 kJ mol−1) or on quartz by Budi et al.94 (34 kJ mol−1). However, our measured methanol value is significantly smaller than that calculated by Budi et al.94 (61 kJ mol−1) for adsorption on quartz.
| Gases | E d (kJ mol−1) |
|---|---|
| Benzene | 34.5 ± 5.0 |
| Methanol | 33.7 ± 4.0 |
| 1-Chloropentane | 40.1 ± 5.6 |
The desorption energy is lowest for benzene, followed by methanol, and finally is highest for 1-chloropentane. Hydrogen bonding between the –OH groups of methanol and of the silica will be the major intermolecular force in that case, while for benzene, hydrogen bonding occurs between the –OH group and the π-system on the benzene ring.65,93 In the case of 1-chloropentane, dispersion forces and possibly halogen bonding69 play a role.
 | ||
| Fig. 9 Measurements (black) and kinetic multilayer model simulations (blue) of benzene uptake on silica particles for different initial benzene pressures. | ||
The best fits to the experimental data for different gases are compared in Fig. 10 and in Table 4. The model shows that the fit value for the diffusion coefficient for diffusion within the pores between particles is approximately the same for all the gases. The desorption rate constant (kd) on the other hand is around 10 times greater for benzene (3 s−1) than for 1-chloropentane (0.1 s−1) or methanol (0.4 s−1). These calculated desorption rate constants can be used to calculate preexponential factors, via ν = kd/exp(Ed/RT) which are summarized in Table 4. These are much closer to the typical values of ∼1013 expected for such processes.43,45,62
| Molecule | D p (cm2 s−1)a | k d (s−1)b | ν (s−1)c |
|---|---|---|---|
| a Diffusion coefficient through gas phase pores. b Desorption rate coefficient of molecules from the silica surface. c ν = kd/exp(Ed/RT), T = 170 K and Ed was determined by inversion analysis of TPD measurements. | |||
| Benzene | 0.001 | 3 | 1.3 × 1011 |
| Methanol | 0.0012 | 0.4 | 7.8 × 1011 |
| 1-Chloropentane | 0.0015 | 0.1 | 1.2 × 1013 |
Both the uptake and desorption of gases on silica surfaces are determined by the specific intermolecular forces involved in the particular gas-surface combination, as discussed in detail by Knopf et al.43 These include hydrogen-bonding, dipole–dipole and London dispersion forces. Benzene has been shown in MD simulations to hydrogen-bond to the Si-OH group through its π electron cloud,93 and methanol of course also hydrogen-bonds to the surface –OH groups.95 In the case of the larger chloropentane molecule, both London dispersion forces as well as halogen bonding69 between the chlorine and surface-OH groups contribute. It is therefore not surprising that the Langmuir equilibrium constants and desorption energies follow similar trends in that chloropentane is the most strongly bound, followed by methanol and benzene. An additional factor for uptake is that the portion of the gas phase molecule that binds to the surface –OH groups need to be appropriately oriented as it initially interacts with the surface if uptake is to occur, i.e. steric factors also play a role.
Summary and conclusions
Application of this new approach that combines Knudsen cell and TPD capabilities in the same system to study both adsorption and desorption processes, including for non-reactive gas–surface interactions, provides both thermodynamic and kinetics data. This approach provides desorption data and binding energies for benzene, 1-chloropentane and methanol on silica that are in good agreement with previous studies. The combination of uptake with TPD experiments clearly shows that sub-monolayer coverages of benzene, 1-chloropentane and methanol on silica can be described by Langmuir, 2D lattice gas, type adsorption. The combination of TPD and uptake measurements also allows for experimental determination of the effective available surface area of a powdered sample, which is a major source of uncertainty in typical uptake experiments. The kinetic modeling results provide a deeper understanding of the desorption mechanism and kinetics in this system where diffusion and readsorption onto the particles occurs. The combination of the Knudsen cell uptake measurements, TPD profiles, and kinetic multilayer modeling is more powerful than any of the individual parts.In the atmosphere, reversible adsorption is a key process for gas condensed-phase interactions as it is a determining factor in aerosol particle growth. A large component of airborne particles is organic, formed by oxidation of organic gases that generate secondary organic aerosol (SOA) particles through new particle formation and growth.96 Predicting growth rates requires knowledge of uptake coefficients as well as desorption energies, and how they are determined by the structural features of particle surfaces and the gases. Thus, based on an understanding of the relationship between binding energies and the gas and surface compositions, a predictive model can be developed that can be used to quantify particle growth mechanisms in the atmosphere. Future studies will use self-assembled monolayers having selected terminal groups in order to probe the reversible adsorption/desorption of gases of known structures on particles coated with various organic functionalities. This will provide insights into the relationships between gas-surface interactions and provide the basis of a predictive capability for growth mechanisms of highly viscous organic particles in air.
Data availability
All relevant data are included in the manuscript or ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation (Grant no. 2030175). PL and MS thank Alfred P. Sloan Foundation for funding (G-2020-13912). We thank Mark Steinborn and Shane Embleton for their assistance with the design and construction of the Knudsen-TPD apparatus. We would also like to thank Wilson Ho, John Hemminger, and Cyril McCormick for helpful discussions and assistance with technical design of the apparatus. Finally, we thank Professor Charlie Campbell for reviewing the manuscript and providing insightful comments and suggestions.References
- B. J. Finlayson-Pitts and J. N. Pitts, Jr., Chemistry of the Upper and Lower Atmosphere - Theory, Experiments, and Applications, Academic Press, San Diego, 2000 Search PubMed.
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, Wiley, New York, 2006 Search PubMed.
- W. C. Hinds, Aerosol Technology: Properties, Behavior and Measurement of Airborne Particles, John Wiley & Sons Inc, New York, 1999 Search PubMed.
- M. Kanakidou, J. H. Seinfeld, S. N. Pandis, I. Barnes, F. J. Dentener, M. C. Facchini, R. Van Dingenen, B. Ervens, A. Nenes, C. J. Nielsen, E. Swietlicki, J. P. Putaud, Y. Balkanski, S. Fuzzi, J. Horth, G. K. Moortgat, R. Winterhalter, C. E. L. Myhre, K. Tsigaridis, E. Vignati, E. G. Stephanou and J. Wilson, Atmos. Chem. Phys., 2005, 5, 1053–1123 CrossRef CAS.
- A. Singh, W. J. Bloss and F. D. Pope, Atmos. Chem. Phys., 2017, 17, 2085–2101 CrossRef CAS.
- A. S. Ackerman, O. B. Toon, J. P. Taylor, D. W. Johnson, P. V. Hobbs and R. J. Ferek, J. Atmos. Sci., 2000, 57, 2684–2695 CrossRef.
- Y. C. Chen, M. W. Christensen, L. Xue, A. Sorooshian, G. L. Stephens, R. M. Rasmussen and J. H. Seinfeld, Atmos. Chem. Phys., 2012, 12, 8223–8235 CrossRef CAS.
- D. K. Farmer, C. D. Cappa and S. M. Kreidenweis, Chem. Rev., 2015, 115, 4199–4217 CrossRef CAS PubMed.
- E. A. Fofie, N. M. Donahue and A. Asa-Awuku, Aerosol Sci. Technol., 2018, 52, 242–251 CrossRef CAS.
- V. M. Kerminen, M. Paramonov, T. Anttila, I. Riipinen, C. Fountoukis, H. Korhonen, E. Asmi, L. Laakso, H. Lihavainen, E. Swietlicki, B. Svenningsson, A. Asmi, S. N. Pandis, M. Kulmala and T. Petaja, Atmos. Chem. Phys., 2012, 12, 12037–12059 CrossRef CAS.
- S. J. Lowe, D. G. Partridge, J. F. Davies, K. R. Wilson, D. Topping and I. Riipinen, Nat. Commun., 2019, 10 Search PubMed.
- A. Nenes, R. J. Charlson, M. C. Facchini, M. Kulmala, A. Laaksonen and J. H. Seinfeld, Geophys. Res. Lett., 2002, 29, 29-1–29-4 CrossRef.
- D. Rosenfeld, Science, 2006, 312, 1323–1324 CrossRef CAS PubMed.
- J. Schmale, S. Henning, S. Decesari, B. Henzing, H. Keskinen, K. Sellegri, J. Ovadnevaite, M. L. Pohlker, J. Brito, A. Bougiatioti, A. Kristensson, N. Kalivitis, I. Stavroulas, S. Carbone, A. Jefferson, M. Park, P. Schlag, Y. Iwamoto, P. Aalto, M. Aijala, N. Bukowiecki, M. Ehn, G. Frank, R. Frohlich, A. Frumau, E. Herrmann, H. Herrmann, R. Holzinger, G. Kos, M. Kulmala, N. Mihalopoulos, A. Nenes, C. O'Dowd, T. Petaja, D. Picard, C. Pohlker, U. Poschl, L. Poulain, A. S. H. Prevot, E. Swietlicki, M. O. Andreae, P. Artaxo, A. Wiedensohler, J. Ogren, A. Matsuki, S. S. Yum, F. Stratmann, U. Baltensperger and M. Gysel, Atmos. Chem. Phys., 2018, 18, 2853–2881 CrossRef CAS.
- S. Twomey, Atmos. Environ., 1991, 25A, 2435–2442 CrossRef CAS.
- D. M. Westervelt, J. R. Pierce, I. Riipinen, W. Trivitayanurak, A. Hamed, M. Kulmala, A. Laaksonen, S. Decesari and P. J. Adams, Atmos. Chem. Phys., 2013, 13, 7645–7663 CrossRef.
- V. F. McNeill, Annu. Rev. Chem. Biomol. Eng., 2017, 8, 427–444 CrossRef CAS PubMed.
- D. W. Dockery, C. A. Pope, X. P. Xu, J. D. Spengler, J. H. Ware, M. E. Fay, B. G. Ferris and F. E. Speizer, New Engl. J. Med., 1993, 329, 1753–1759 CrossRef CAS PubMed.
- P. J. Landrigan, R. Fuller, N. J. R. Acosta, O. Adeyi, R. Arnold, N. Basu, A. B. Balde, R. Bertollini, S. Bose-O'Reilly, J. I. Boufford, P. N. Breysse, T. Chiles, C. Mahidol, A. M. Coll-Seck, M. L. Cropper, J. Fobil, V. Fuster, M. Greenstone, A. Haines, D. Hanrahan, D. Hunter, M. Khare, A. Krupnick, B. Lanphear, B. Lohani, K. Martin, K. V. Mathiasen, M. A. McTeer, C. J. L. Murray, J. D. Ndahimananjara, F. Perera, J. Potocnik, A. S. Preker, J. Ramesh, J. Rockstrom, C. Salinas, L. D. Samson, K. Sandilya, P. D. Sly, K. R. Smith, A. Steiner, R. B. Stewart, W. A. Suk, O. C. P. van Schayck, G. N. Yadama, K. Yumkella and M. Zhong, Lancet, 2018, 391, 462–512 CrossRef PubMed.
- P. J. Landrigan, R. Fuller, H. Hu, J. Caravanos, M. L. Cropper, D. Hanrahan, K. Sandilya, T. C. Chiles, P. Kumar and W. A. Suk, Environ. Health Persp., 2018, 126 Search PubMed.
- J. Lelieveld, J. S. Evans, M. Fnais, D. Giannadaki and A. Pozzer, Nature, 2015, 525, 367–374 CrossRef CAS PubMed.
- P. M. Mannucci, S. Harari, I. Martinelli and M. Franchini, Intern. Emerg. Med., 2015, 10, 657–662 CrossRef PubMed.
- C. A. Pope III and D. W. Dockery, J. Air Waste Manage. Assoc., 2006, 56, 709–742 CrossRef PubMed.
- M. Shiraiwa, K. Ueda, A. Pozzer, G. Lammel, C. J. Kampf, A. Fushimi, S. Enami, A. M. Arangio, J. Frohlich-Nowoisky, Y. Fujitani, A. Furuyama, P. S. J. Lakey, J. Lelieveld, K. Lucas, Y. Morino, U. Poschl, S. Takaharna, A. Takami, H. J. Tong, B. Weber, A. Yoshino and K. Sato, Environ. Sci. Technol., 2017, 51, 13545–13567 CrossRef CAS PubMed.
- J. E. Thompson, J. Occup. Environ. Med., 2018, 60, 392–423 CrossRef CAS PubMed.
- J. A. Faust and G. M. Nathanson, Chem. Soc. Rev., 2016, 45, 3609–3620 RSC.
- J. F. Pankow, Atmos. Environ., 1994, 28, 185–188 CrossRef CAS.
- J. F. Pankow, Atmos. Environ., 1987, 21, 2275–2283 CrossRef CAS.
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. H. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. S. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Y. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, A. M. Middlebrook, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Science, 2009, 326, 1525–1529 CrossRef CAS PubMed.
- V. Perraud, E. A. Bruns, M. J. Ezell, S. N. Johnson, Y. Yu, M. L. Alexander, A. Zelenyuk, D. Imre, W. L. Chang, D. Dabdub, J. F. Pankow and B. J. Finlayson-Pitts, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 2836–2841 CrossRef CAS PubMed.
- M. Ammann and U. Pöschl, Atmos. Chem. Phys., 2007, 7, 6025–6045 CrossRef CAS.
- T. Berkemeier, A. J. Huisman, M. Ammann, M. Shiraiwa, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2013, 13, 6663–6686 CrossRef.
- J. P. Abbatt, A. K. Lee and J. A. Thornton, Chem. Soc. Rev., 2012, 41, 6555–6581 RSC.
- N. M. Donahue, W. Chuang, S. A. Epstein, J. H. Kroll, D. R. Worsnop, A. L. Robinson, P. J. Adams and S. N. Pandis, Environ. Chem., 2013, 10, 151–157 CrossRef CAS.
- I. Riipinen, J. R. Pierce, T. Yli-Juuti, T. Nieminen, S. Hakkinen, M. Ehn, H. Junninen, K. Lehtipalo, T. Petaja, J. Slowik, R. Chang, N. C. Shantz, J. Abbatt, W. R. Leaitch, V. M. Kerminen, D. R. Worsnop, S. N. Pandis, N. M. Donahue and M. Kulmala, Atmos. Chem. Phys., 2011, 11, 3865–3878 CrossRef CAS.
- P. Roldin, A. C. Eriksson, E. Z. Nordin, E. Hermansson, D. Mogensen, A. Rusanen, M. Boy, E. Swietlicki, B. Svenningsson, A. Zelenyuk and J. Pagels, Atmos. Chem. Phys., 2014, 14, 7953–7993 CrossRef.
- M. Shiraiwa, C. Pfrang, T. Koop and U. Poschl, Atmos. Chem. Phys., 2012, 12, 2777–2794 CrossRef CAS.
- R. A. Zaveri, J. E. Shilling, A. Zelenyuk, J. M. Liu, D. M. Bell, E. L. D'Ambro, C. Gaston, J. A. Thornton, A. Laskin, P. Lin, J. Wilson, R. C. Easter, J. Wang, A. K. Bertram, S. T. Martin, J. H. Seinfeld and D. R. Worsnop, Environ. Sci. Technol., 2018, 52, 1191–1199 CrossRef CAS.
- V. Lannuque, M. Camredon, F. Couvidat, A. Hodzic, R. Valorso, S. Madronich, B. Bessagnet and B. Aumont, Atmos. Chem. Phys., 2018, 18, 13411–13428 CrossRef CAS.
- M. Shrivastava, C. D. Cappa, J. W. Fan, A. H. Goldstein, A. B. Guenther, J. L. Jimenez, C. Kuang, A. Laskin, S. T. Martin, N. L. Ng, T. Petaja, J. R. Pierce, P. J. Rasch, P. Roldin, J. H. Seinfeld, J. Shilling, J. N. Smith, J. A. Thornton, R. Volkamer, J. Wang, D. R. Worsnop, R. A. Zaveri, A. Zelenyuk and Q. Zhang, Rev. Geophys., 2017, 55, 509–559 CrossRef.
- S. Tuovinen, J. Kontkanen, R. Cai and M. Kulmala, Environ. Sci. Atmos, 2021, 1, 543–557 CAS.
- C. E. Kolb, R. A. Cox, J. P. D. Abbatt, M. Ammann, E. J. Davis, D. J. Donaldson, B. C. Garrett, C. George, P. T. Griffiths, D. R. Hanson, M. Kulmala, G. McFiggans, U. Pöschl, I. Riipinen, M. J. Rossi, Y. Rudich, P. E. Wagner, P. M. Winkler, D. R. Worsnop and C. D. O' Dowd, Atmos. Chem. Phys., 2010, 10, 10561–10605 CrossRef CAS.
- D. A. Knopf, M. Ammann, T. Berkemeier, U. Pöschl and M. Shiraiwa, Atmos. Chem. Phys., 2024, 24, 3445–3528 CrossRef CAS.
- C. T. Campbell, L. H. Sprowl and L. Arnadottir, J. Phys. Chem. C, 2016, 120, 10283–10297 CrossRef CAS.
- D. A. Knopf and M. Ammann, Atmos. Chem. Phys., 2021, 21, 15725–15753 CrossRef CAS.
- A. C. van der Waals, P. S. J. Lakey, E. Rossich Molina, V. Perraud, L. M. Wingen, J. Xu, D. Soulsby, R. B. Gerber, M. Shiraiwa and B. J. Finlayson-Pitts, Environ. Sci.: Processes Impacts, 2018, 20, 1593–1610 RSC.
- A. C. van der Waals, V. Perraud, L. M. Wingen and B. J. Finlayson-Pitts, Environ. Sci.: Processes Impacts, 2020, 22, 66–83 RSC.
- A. C. van der Waals, L. M. Wingen, V. Perraud, Y. Zhao and B. J. Finlayson-Pitts, ACS Earth Space Chem., 2020, 4, 1435–1447 CrossRef.
- E. Saukko, A. T. Lambe, P. Massoli, T. Koop, J. P. Wright, D. R. Croasdale, D. A. Pedernera, T. B. Onasch, A. Laaksonen, P. Davidovits, D. R. Worsnop and A. Virtanen, Atmos. Chem. Phys., 2012, 12, 7517–7529 CrossRef CAS.
- A. Virtanen, J. Joutsensaari, T. Koop, J. Kannosto, P. Yli-Pirila, J. Leskinen, J. M. Makela, J. K. Holopainen, U. Poschl, M. Kulmala, D. R. Worsnop and A. Laaksonen, Nature, 2010, 467, 824–827 CrossRef CAS PubMed.
- A. Virtanen, J. Kannosto, H. Kuuluvainen, A. Arffman, J. Joutsensaari, E. Saukko, L. Hao, P. Yli-Pirila, P. Tiitta, J. K. Holopainen, J. Keskinen, D. R. Worsnop, J. N. Smith and A. Laaksonen, Atmos. Chem. Phys., 2011, 11, 8759–8766 CrossRef CAS.
- C. Kidd, V. Perraud, L. M. Wingen and B. J. Finlayson-Pitts, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 7552–7557 CrossRef CAS PubMed.
- A. P. Bateman, A. K. Bertram and S. T. Martin, J. Phys. Chem. A, 2015, 119, 4386–4395 CrossRef CAS PubMed.
- M. Kuwata and S. T. Martin, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17354–17359 CrossRef CAS PubMed.
- L. Renbaum-Wolff, J. W. Grayson, A. P. Bateman, M. Kuwata, M. Sellier, B. J. Murray, J. E. Shilling, S. T. Martin and A. K. Bertram, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8014–8019 CrossRef CAS PubMed.
- M. Shiraiwa, Y. Li, A. P. Tsimpidi, V. A. Karydis, T. Berkemeier, S. N. Pandis, J. Lelieveld, T. Koop and U. Poschl, Nat. Commun., 2017, 15002 CrossRef PubMed.
- J. P. Reid, A. K. Bertram, D. O. Topping, A. Laskin, S. T. Martin, M. D. Petters, F. D. Pope and G. Rovelli, Nat. Commun., 2018, 9 Search PubMed.
- Y. M. Han, Z. H. Gong, J. H. Ye, P. F. Liu, K. A. McKinney and S. T. Martin, Environ. Sci. Technol., 2019, 53, 13209–13218 CrossRef CAS PubMed.
- A. M. Maclean, N. R. Smith, Y. Li, Y. Z. Huang, A. P. S. Hettiyadura, G. V. Crescenzo, M. Shiraiwa, A. Laskin, S. A. Nizkorodov and A. K. Bertram, ACS Earth Space Chem., 2021, 5, 305–318 CrossRef CAS.
- T. Koop, J. Bookhold, M. Shiraiwa and U. Poschl, Phys. Chem. Chem. Phys., 2011, 13, 19238–19255 RSC.
- M. A. Freedman, Acc. Chem. Res., 2020, 53, 1102–1110 CrossRef CAS PubMed.
- R. I. Masel, Principles of Adsorption and Reaction on Solid Surfaces, Wiley-Interscience, 1st edn, 1996 Search PubMed.
- D. M. Golden, G. N. Spokes and S. W. Benson, Angew. Chem., Int. Ed. Engl., 1973, 12, 534–546 CrossRef.
- Y. Li, P. S. J. Lakey, M. J. Ezell, K. N. Johnson, M. Shiraiwa and B. J. Finlayson-Pitts, ACS ES&T Air, 2023, 1, 52–61 Search PubMed.
- J. Abelard, A. R. Wilmsmeyer, A. C. Edwards, W. O. Gordon, E. M. Durke, C. J. Karwacki, D. Troya and J. R. Morris, J. Phys. Chem. C, 2016, 120, 13024–13031 CrossRef CAS.
- J. Abelard, A. R. Wilmsmeyer, A. C. Edwards, W. O. Gordon, E. M. Durke, C. J. Karwacki, D. Troya and J. R. Morris, J. Phys. Chem. C, 2014, 119, 365–372 CrossRef.
- O. Sneh and S. M. George, J. Phys. Chem., 1995, 99, 4639–4647 CrossRef CAS.
- J. A. Ganske, L. M. Wingen, V. Perraud and B. J. Finlayson-Pitts, ACS Earth Space Chem., 2019, 3, 1315–1328 CrossRef CAS.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- C. R. Usher, A. E. Michel and V. H. Grassian, Chem. Rev., 2003, 103, 4883–4940 CrossRef CAS PubMed.
- O. A. Choobari, P. Zawar-Reza and A. Sturman, Atmos. Res., 2014, 138, 152–165 CrossRef CAS.
- A. P. Ault, V. H. Grassian, N. Carslaw, D. B. Collins, H. Destaillats, D. J. Donaldson, D. K. Farmer, J. L. Jimenez, V. F. McNeill, G. C. Morrison, R. E. O'Brien, M. Shiraiwa, M. E. Vance, J. R. Wells and W. Xiong, Chem, 2020, 6, 3203–3218 CAS.
- J. M. Mattila, C. Arata, A. Abeleira, Y. Zhou, C. Wang, E. F. Katz, A. H. Goldstein, J. P. D. Abbatt, P. F. DeCarlo, M. E. Vance and D. K. Farmer, Environ. Sci. Technol., 2022, 56, 109–118 CrossRef CAS PubMed.
- F. Caloz, F. F. Fenter, K. D. Tabor and M. J. Rossi, Rev. Sci. Instrum., 1997, 68, 3172–3179 CrossRef CAS.
- J. Mønster, T. Rosenørn, O. J. Nielsen and M. S. Johnson, Environ. Sci. Pollut. Res. Int., 2002, 1, 63–67 CrossRef PubMed.
- M. Shiraiwa, R. M. Garland and U. Pöschl, Atmos. Chem. Phys., 2009, 9, 9571–9586 CrossRef CAS.
- P. S. J. Lakey, G. C. Morrison, Y. Won, K. M. Parry, M. von Domaros, D. J. Tobias, D. Rim and M. Shiraiwa, Commun. Chem., 2019, 2, 56–63 CrossRef.
- H. Y. Fan, E. S. Frank, P. S. J. Lakey, M. Shiraiwa, D. J. Tobias and V. H. Grassian, J. Phys. Chem. C, 2022, 126, 6267–6279 CrossRef CAS.
- Y. Fang, P. S. J. Lakey, S. Riahi, A. T. McDonald, M. Shrestha, D. J. Tobias, M. Shiraiwa and V. H. Grassian, Chem. Sci., 2019, 10, 2906–2914 RSC.
- L. B. Huang, E. S. Frank, S. Riahi, D. J. Tobias and V. H. Grassian, J. Chem. Phys., 2021, 154 Search PubMed.
- M. von Domaros, P. S. J. Lakey, M. Shiraiwa and D. J. Tobias, J. Phys. Chem. B, 2020, 124, 3836–3843 CrossRef CAS PubMed.
- R. C. Hoffman, M. E. Gebel, B. S. Fox and B. J. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2003, 5, 1780–1789 RSC.
- K. S. W. Sing, in Adsorption by Powders and Porous Solids, ed. F. Rouquerol, J. Rouquerol, K. S. W. Sing, P. Llewellyn and G. Maurin, Academic Press, 2nd edn, 2014, pp. 237–268 DOI:10.1016/b978-0-08-097035-6.00007-3.
- S. Seisel, Y. Lian, T. Keil, M. E. Trukhin and R. Zellner, Phys. Chem. Chem. Phys., 2004, 6, 1926–1932 RSC.
- S. L. Tait, Z. Dohnalek, C. T. Campbell and B. D. Kay, J. Chem. Phys., 2005, 122, 164707 CrossRef PubMed.
- P. A. Redhead, Vacuum, 1962, 12, 203–211 CrossRef CAS.
- R. J. Gorte, J. Catal., 1982, 75, 164–174 CrossRef CAS.
- D. D. Beck, J. M. White and C. T. Ratcliffe, J. Phys. Chem., 1986, 90, 3123–3131 CrossRef CAS.
- R. J. Cvetanović and Y. Amenomiya, Catal. Rev., 1972, 6, 21–48 CrossRef.
- J. L. Falconer and J. A. Schwarz, Catal. Rev., 2007, 25, 141–227 CrossRef.
- M. B. Hugenschmidt, L. Gamble and C. T. Campbell, Surf. Sci., 1994, 302, 329–340 CrossRef CAS.
- A. R. Wilmsmeyer, J. Uzarski, P. J. Barrie and J. R. Morris, Langmuir, 2012, 10962–10967, DOI:10.1021/la301938f.
- Y. Fang, S. Riahi, A. T. McDonald, M. Shrestha, D. J. Tobias and V. H. Grassian, J. Phys. Chem. Lett., 2019, 10, 468–473 CrossRef CAS PubMed.
- A. Budi, S. L. S. Stipp and M. P. Andersson, J. Phys. Chem. C, 2018, 122, 8236–8243 CrossRef CAS.
- H. Noller and G. Ritter, J. Chem. Soc., Faraday Trans., 1984, 80, 275–283 RSC.
- P. J. Ziemann and R. Atkinson, Chem. Soc. Rev., 2012, 41, 6582–6605 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02528h |
| ‡ Current address: Department of Atmospheric Sciences, Texas A&M University, College Station, TX 77843. |
| This journal is © the Owner Societies 2024 |