Resolving heterogeneous particle mobility in deeply quenched liquid iron: an ultra-fast assembly-free two-step nucleation mechanism

Abstract

Despite intensive research, little is known about the intermediate state of phase transforming materials, which may form the missing link between e.g. liquids and solids on the nanoscale. The unraveling of the nanoscale interplay between the structure and dynamics of the intermediate state of phase transformations (through which e.g. crystal nucleation proceeds) is one of the biggest challenges and unsolved problems of materials science. Here we show using unbiased molecular dynamics simulations and spatially resolved atomic displacement maps (d-maps) that upon deep quenching the solidification of undercooled liquid iron proceeds through the formation of metastable pre-nucleation clusters (PNCs). We also reveal that the hitherto hidden PNCs are nearly immobile (dynamically arrested) and the related heterogeneity in atomic mobilities becomes clearly visible on atomic displacement-maps (d-maps) when atomic jumps are referenced to the final crystalline positions. However, this is in contrast to PNCs found in molecular solutions, in which PNCs tend to aggregate, move and crystallize via an activated process. Coordination filtered d-maps resolved in real space directly demonstrate that previously unseen highly ramified intermediate atomic clusters with a short lifetime emerge after incubation of undercooled liquid iron. The supercooled liquid iron is neither a spinodal system nor a liquid and undergoes a transition into a specific state called a quasi-liquid state within the temperature regime of 700–1250 K (0.5T_m > 0.7T_m, where the melting point is T_m ≈ 1811 K). Below 700 K the supercooled system is spinodal-like and above 1300 K it behaves like an ordinary liquid with long incubation times. A two-step process is proposed to explain the anomalous drop in the incubation time in the temperature regime of 700–1250 K. The 1st step is activated aggregation of small atomic clusters followed by assembly-free nearly barrierless ultrafast growth of early ramified prenucleation clusters called germs. The display and characterization of the hidden PNCs in computer simulations could provide new perspectives on the deeper understanding of the long-standing problem of precursor development during crystal nucleation following deep quenching.

---

I. Introduction

Crystal nucleation and other phase transitions (PTs) in liquids (such as vitrification or solid to solid transitions mediated by a liquid) are some of the most fundamental phenomena in Nature; however, the underlying mechanism of these phenomena is still elusive so far despite tremendous research efforts.^1–21 In particular, how and through what nanoscale intermediate structural phases liquids transform at the atomistic level into solid phases and vice versa is poorly understood yet.^{5–9,11,19,20,22}

Molecular dynamics (MD) simulations have intensively been used to reveal the possible mechanism of crystal nucleation in liquid iron.^16,23–26 It has been shown that the local heterogeneity in the distribution of grains is caused by the local accumulation of the icosahedral structure in the undercooled melt near the previously formed grains.¹⁶ The heterogeneities in homogeneous nucleation are also studied by large scale MD simulations of pure melts.²⁶ The simulation results showed that abundant types of atomic clusters with short range order, mainly including the icosahedral-like (ICO-like) and fcc-like clusters, were predominant in undercooled iron melts.²⁵ Phase-field approaches have also been utilized for understanding nucleation.²⁷

The multistep (MST) nucleation scenario (including the two-step mechanism^15,18) has been drawing considerable interest, with successful application to crystallization from solutions.^{7–9,28–36} Single-step models, such as classical nucleation theory (CNT, see ref. 30, 31, 35 and 36), were challenged by the studies on MST nucleation. MST nucleation has also been addressed in the solid state.^19,20,37,38 The presence of a liquid-like intermediate has been pointed out in solid-to-solid PTs.^19,20 The stable form of liquid-like intermediate pre-nucleation clusters (PNCs) during the formation of CaCO₃ in solution has also been reported,^6–10,34 which suggests that the otherwise metastable intermediate can be captured under specific conditions. Recently, real time liquid-phase transmission electron microscopy (TEM) and advances in cryogenic TEM have also provided an interesting insight into the mechanism of MST nucleation.¹⁴

In this paper we would like to show using brute-force molecular dynamics (MD) simulations that a nearly barrierless multistage nucleation is the dominant mechanism in a relatively deeply (>20%) quenched liquid of molten iron. According to the explored mechanism, structurally and dynamically arrested¹³ metastable prenucleation hidden clusters^29,34 play an essential role in prenucleation.

We identify randomly generated early-stage and nearly immobile arrangement of atoms (initial PNCs) together with a disordered network character,^30,31,34 which further rapidly transform into a highly ramified precursor state. This pre-nucleus state is clearly not visible by standard display approaches (Voronoi's tesselation,³⁹ bond orientation order,⁴⁰ radial distribution function, etc.) because the underlying symmetries are broken, which prevents the real-space recognition of preordering during the pre-nucleus regime, which therefore remains hidden for explicit analysis. More sensitive structural and order descriptors are needed for the appropriate resolution of the pre-nucleus state (PNS).⁴¹

We find that above glass transition temperature but still in deep quenching of undercooled liquid iron (ULI, T ≈ 900–1250 K, 0.5T_m < T < 0.7T_m, where the melting point is T_m ≈ 1811 K for pure iron⁴²), the prenucleating system is neither spinodal nor an ordinary liquid. This specific state of the phase transforming supercooled liquid is termed as a quasi liquid state (QLS). The most notable feature of the QLS is the anomalous drop in the incubation time of nucleation (the time needed for the onset of nucleation) within a narrow regime of 700–1250 K in ULI. During the QLS the prenucleating system undergoes an assembly-free and nearly barrierless ultrafast phase transition. We argue that the QLS is a specific state of undercooled liquids different from ordinary liquids with dynamically self-induced disorder or even from glassy and spinodal systems in many respects. The QLS potentially undergoes an ultrafast nucleation (∼100–150 ps) within the narrow temperature regime of 700–1250 K (0.5T_m < T < 0.7T_m) with a very short incubation time (t_inc < 200 ps). Outside this temperature regime, nucleation begins after a long incubation period (see the inset in Fig. 2(s)). Understanding the structural, energetic and dynamical details of the QLS as a distinct state of phase transforming materials upon deep quenching might provide a deeper insight into material transformations even closer to the melting point. There are a few arguments in favor of the finding that the QLS at least in deep quenching (above the glass transition temperature and below the temperature at which an exponential increase of the incubation time sets in) can be characterized by spatial and dynamic heterogeneity (DH) and particle mobility heterogeneity (MH) similar to glassy systems,^12,13,43 however, even with more complex heterogeneity. We also find that the QLS can also be characterized by growing hidden order as well as by medium to long range correlations together with competing hidden phases with different atomic mobilities.⁴⁴ For unraveling the hidden order of the QLS, we propose using simple atomic displacement maps with appropriately chosen reference states.^{25,43,45–47} We are able to localize PNCs taking advantage of the fact that atomic motion slows down in them while coordination is at its highest in PNCs with respect to the liquid environment. The simple basic question what we would like to answer using the d-maps is that how far and from where the atoms came from the liquid state to their final crystalline positions during solidification. We are attempting to at least partly answer these questions supported by molecular dynamics (MD) simulations and via visualizing heterogeneity in the QLS. We see well behind the usual scenes of nucleation using specific displacement maps (d-maps) going backward in time with respect to the final crystalline reference configuration: the hitherto hidden structures are revealed in the pre-nucleus state.

II. Results and discussion

The immobility of the pre-nucleation clusters in deep quenching

Our primary focus is to discuss the possible role of the PNC concept developed by Gebauer et al.^7–9,34 in the nucleation process of undercooled liquid iron (ULI). This is a non-classical pathway of nucleation originally suggested for molecular solutions.^7–9,34 However, we would like to extend the probable range of the modified version of the PNC concept of nucleation to ULI (and perhaps to other liquid metals). The basic feature of the PNC concept is that the PNCs are relatively stable to have enough time for aggregation in molecular solutions. We argue, however, that with decreasing stability the PNCs undergo ultrafast decomposition and/or growth instead of aggregation in ULI. Moreover, the robust immobility of ramified PNCs has also been explored, which hinders their aggregation in ULI. Although apparently a fundamentally different situation develops in molecular solutions and in supercooled liquid metals, we also argue that the two cases might not be that different in all respects. This is because the two basic parameters of the concept, the stability and dynamics of PNCs, can vary system by system. Even within the same system these parameters can be different under different external conditions. We find that decreasing stability, together with particle immobility, however, opens up an assembly-free barrierless pathway of nucleation instead of the thermally activated one. This is essentially a diffusionless pathway of subdiffusive particles during the prenucleation state similar to that found in charged colloids.³ Barrierless growth kinetics without activated control has also been suggested in deeply quenched pure metal melts.⁴ The early-stage lack of mobility in the precursor state is due perhaps to kind of a dynamical arrest¹³ of the forming ramified nanoclusters.

It must also be noted that the exploration of PNCs in the ULI is perhaps more challenging than that in molecular solutions. This is because the solute PNCs can relatively easily be separated from the solvent molecules,^9,10,34 while in single component liquid metals the early stage PNCs notoriously remain hidden when using standard descriptors (such as PTM or Voronoi's tesselation^39,48), not to mention the difficulty in their experimental observation, e.g., in liquid metals. Moreover, it is challenging yet to explore computationally the earliest PNCs with below a few nanometer diameter due to the likely increasing mobility with decreasing size in the ULI, which makes it difficult to identify the tiny PNCs using displacement maps. At the present stage of the resolution of various descriptors (even with d-maps) the early stage tiny mobile PNCs are not detectable yet. These PNCs perhaps undergo aggregation forming the earliest detectable nearly immobile germs, which once formed grow into nuclei rapidly up to the temperature at which germs more frequently decompose rather than growing. Above this critical temperature (∼1300 K) it is likely that the assembly-free mechanism is inhibited.

The quasi liquid state

Our aim also goes beyond this level and we would like to demonstrate that a modified version of the PNC concept is realized in the specific state of the liquid-like phase called the quasi liquid state. The short lived PNC (its lifetime is on the order of 0.1 ns or less) is the precursor state of nucleation including also the earliest nuclei in deep quenching. We would like to stress that the QLS is not simply the phase separation of different liquid–liquid phases^9,32 with one of those phases containing the PNCs but a unique complex state with specific intrinsic features not characteristic of ordinary liquids. Briefly the QLS can be described by two separated phases without a definite phase boundary (the interface is somewhat blurred), among which one of them contains mobile individual particles and/or tiny PNCs, while the other contains nearly immobile clusters of slowed-down particles. However, the situation is even more complicated and the dynamic liquid-like phase is dynamically also weakly heterogeneous similar to glassy systems^12,13 (background DH).

Among the intriguing features of the QLS in particular, first we recognize the robust immobility of the computationally extracted PNCs based on spatially resolved displacement maps (d-maps, Fig. 1(c)) referenced to the final bcc state (in fact the recognition and extraction of the PNCs is based on their immobility). We would like to show that contrary to original suggestions,⁹ the mobility of PNCs is not necessarily essential for nucleation in that particular case if the aggregation of the PNCs will be omitted due to the localization of the PNCs. Instead, the forming PNCs rapidly grow into nuclei and then into grains while remaining meanwhile nearly immobile (see Fig. 1(c), (d), (l) and 2(f), (r); only ultrafast front propagation and growth takes place (rapid assembly-free PNC mechanism). The primary reason could be that the dense heterogeneous phase of the QLS in ULI anchors the PNCs to their place of formation. Individual particles of the liquid phase of the QLS are dynamical; however, the PNCs as whole entities are localized only. Therefore presumably the situation is somewhat different than in e.g. aqueous solutions in which the solvent environment allows the nanoscale dynamics of PNCs in the less dense liquid medium than in the ULI.^9,10,34 Moreover, since we are able to identify PNCs in d-maps due to their immobility, mobile, perhaps, small PNCs (below a few nanometer diameter) if they exist at all, will remain, however, hidden (early stage mobile PNCs or subgerms).

Fig. 1 The quasi-liquid state (QLS) of phase transformations. (a) A simple schematic diagram for introducing the concept of QLS of supercooled liquids. S and L denote solid and liquid phases, respectively. The arrows show the corresponding phase transitions, melting (S to L) and solidification (L to S). (b) A dynamically arrested PNC is shown in the QLS as a surface mesh plot at 1150 K. The location of the PNC is shown in (c) and (d) by a circle. The PNC is extracted from the full system using a specific filtering process (dc-filter). (c) Spatially resolved d-map of the QLS for a large pre-nucleating system: the blue spots are the fingerprints of PNCs. The simulation cell: 12.8 million atoms, 116.7 × 117.3 × 11.7 nm³. (d) A typical spatially resolved filtered coordination heat map, here deep blue and yellow-to-red spots are the liquid and immobile regions, respectively, of the heterogeneous QLS is shown within a thin slab. Yellow-to-red spots correspond to particles that are mostly coordinated with immobile first neighbor atoms (PNCs). A few PNCs (red spots) are seen within a large area of 116.7 × 117.3 nm². (e) The cross-linked network-disordered-like QLS. (f) The filtered coordination map of the QLS with another contrast to highlight network interconnections. (g)–(k) The time development of PNCs in a large system (88 × 88 × 29 nm³, the full system includes 18 million atoms). (l) The average atomic displacement/particle displacement (d_ave or d̄) with respect to the previous step within a PNC with different radii at 1150 K (the full system includes 18 M atoms). The sudden drop in d̄ (Å) indicates the abrupt slow down of particles within the forming PNC below 100 ps. Note the much later drop in d̄ for the liquid environment (black curve) of the PNC. (m)–(o) The PTM-bcc atoms in the PNCs at 50 ps (m), 70 ps (n) and 100 ps (o) as characterized by PTM for the same systems in (i)–(k). (p) The time evolution of the position of the center of mass (COM) of a PNC (marked by an ellipse in (g)) as a function of the simulation time (the color code). (q) The bcc content as a function of the diameter of various PNCs. The vertical red dashed line denotes the approximate borderline of the onset of the rapid crystal growth (RCG) or the end of the QLS. PNS: pre-nucleus state. N stands for the early nucleus state and marks the end of the QLS. Error bars are associated with the scatter in determining the diameter of PNCs. The vertical bar is due to scatter in bcc content event by event. (r) The mean square of displacements (MSD) for the system with 18 M atoms at 1150 K (the reference system is the initial as-quenched state). The MSD is calculated for the entire system (liquid) and for the PNC marked in (g) within a sphere with various radii (the radius in Å is shown in the figure).

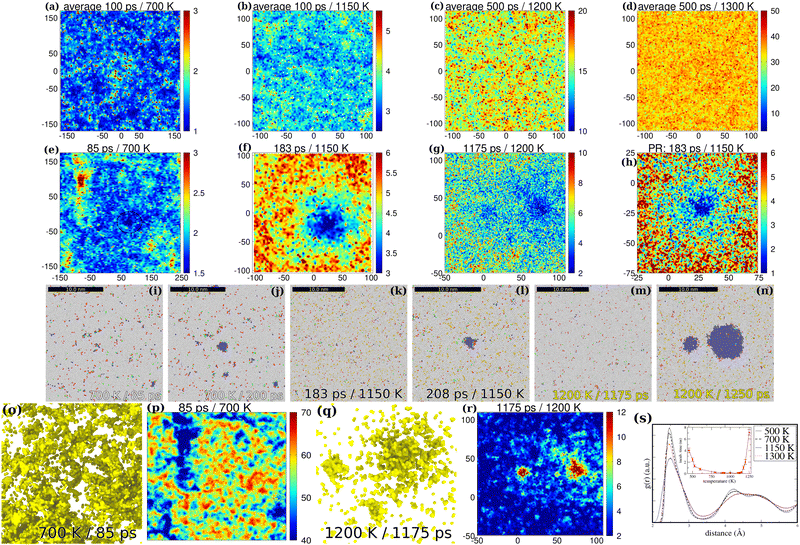Fig. 2 Spatially resolved maps of mobility heterogeneity. The temperature dependence of spatially resolved inhomogeneity of displacement maps (d-maps) directly related to mobility heterogeneity (MH, 1st row maps) and to pre-nucleation (2nd row maps) depicted in the xy-plane within a thin cross-sectional slab of the simulation cell in the central region of the simulation cell (the axis assignment is in Å). MH is proportional to atomic displacements: blue regions correspond to regions with low mobility, while yellow to red colors correspond to mobile regions. First row panels: the reference configuration is the initial quenched disordered supercooled liquid ((a): 500 K, (b) 700 K, (c) 1150 K, (d) 1300 K). Displacements d(r,t) averaged over some time are shown for various temperatures (a): 700 K (100 ps), (b) 1150 K (100 ps), (c) 1200 K (500 ps) and (d) 1300 K (500 ps). (e)–(h) The d-maps of the pre-nucleus (pre-PTM nucleus) state at 700 (e), 1150 (f) and 1200 K (g). The reference configuration is the final bcc crystal. For the 2nd row maps instantaneous structures were used (no time averaging is employed). The “spreading” blue spot is the signature of the pre-nucleation cluster (PNC). (h) The zoomed spatial map of (f) (the right bottom region) in order to highlight fluctuations in the quasi-liquid environment of the detected pre-nucleus (blue spot). (i)–(n) The PTM images directly correspond to the 2nd row images (a)–(c). (i) and (j) PTM maps at 700 K in the pre-nucleus (i) and in the nucleus (N) states (j). (k) and (l) PTM maps at 1150 K (PR (k) at 183 ps, N (l) at 208 ps). (m) The PNS by PTM at 1200 K at 1175 ps. (n) The nuclei are at 1200 ps. (o) Disordered-network-like (DNL) PNC at 700 K below glass transition depicted as a 3D mesh using a Gaussian surface construction method^49,50 (a 2-step filtering process is applied). The cross-linked DNL-PNC can be taken as the rigid inner frame of the pre-nucleating glassy system. (p) Spinodal-like pattern shown by the coordination map for the DNL-PNC at 700 K within a thin slab (with an enhanced cut-off of r_c = 6 Å, d-filtering used: d ≤ 2.5 Å). (q) PNCs with satellite clusters at 1200 K (at 1175 ps) depicted as a 3D mesh. (r) Reduced coordination map as obtained using a d-filtering process for the PNC at 1200 K (1175 ps). Within the thin slab plotted for the PNC shown in (q) the 3rd small cluster is not visible (it is outside the thin slab). (s) The pair distribution function (g(r), RDF) is also shown for the system shown in (a) and (d) together with a system at 500 K. The g(r) plots are calculated over the time averaged structures. Inset: Incubation time (ns) for spontaneous homogeneous nucleation as a function of temperature (K). Error bars denote fluctuations in values due to sampling in various 5–7 events.

The spatially resolved d-map of the pre-nucleating QLS is shown in Fig. 1(c) (the displacement of particles d_i is with respect to the final bcc state, d_i(t) is the distance what atom i in the QLS yet to be displaced to take its final position in the bcc crystal at t instantaneous time). The blue spots in Fig. 1(c) are the fingerprints of PNCs (localized atomic clusters) in the QLS when bcc atoms are absent yet. These spots once appeared in the d-map do not move in the rest of the nucleation process. This is a surprising result at first sight because the standard Brownian-like motion of small atomic clusters (with a diameter below a few nanometers) is assumed even in a dense medium such as the supercooled liquid of iron.⁹ However, we indeed find using MD simulations that pre-formed small bcc (with the diameter of 1–2 nm) clusters are fairly immobile in the ULI below ∼1300 K. Further details of cluster mobility are provided in the ESI.‡ What is surprising, however, is that the loosely bound immobile PNCs survive the QLS without dissolution and even further grow rapidly without moving from their place where they are formed. This is also the case for pre-formed bcc clusters below ∼1300 K. Therefore it seems quite likely that cluster mobility is suppressed due to its ramified nature. We are able to capture PNCs up to ∼1200 K where incubation takes place in a nanosecond time range (see Fig. 2(g) and (r)). The main differences between the QLS and the normal liquid state (NLS) are summarized in S1 (ESI‡).

Further evidence for the immobility of PNCs

It is important to know precisely the magnitude of immobility of PNCs; therefore, we present further evidence. Fig. 1(l) further corroborates the sudden drop in average atomic mobility d̄_ave before the onset of nucleation within the forming PNC core (green curve). The drop in d̄_ave occurs much later for the liquid environment (black curve). We find that once a PNC (see Fig. 1(b)) is formed the cluster remains nearly localized at the site of the first formation. This has been further evidenced by plotting the center of mass (COM) of a typical PNC shown in Fig. 1(g)–(j) as a function of the elapsed time in Fig. 1(q). The displacement of the COM of a typical PNC remains below ∼2 Å, which is within the error bar due to the scatter of particle positions in the rapidly growing PNC. Particles eventually can exchange positions within the PNC (intrinsic dynamics is not fully frozen); however, the PNC as a whole remains fairly localized. By plotting the mean square of atomic displacements (MSD) with respect to the initial configuration, we even further evidence that the particles within the PNC marked in Fig. 1(g) slow down (Fig. 1(r)). In the PNC core (r = 10 Å) the MSD turns into the plateau phase as soon as ∼50 ps when we are still in the early QLS and PNS with a vanishingly small bcc content (see Fig. 1(m)). Similar features are seen for the other PNCs. Inspecting visually (Fig. 1(g)–(k)) one can also see that most of the early-stage tiny PNCs remain surprisingly localized in their original as-quenched positions (in this particular case the original sources (seeds) of the later grains are rooted in the quenched disordered initial state (0 ps)). Based on various independent methods (d-maps, average mobility d̄, immobility of the COM, the MSD with respect to the initial quench disordered state) we conclude that PNCs are fairly immobile from the early stages of development and this finding is thus the basis of their characterization.

The underlying reason of the immobility of PNCs is although somewhat unclear yet; however, we find that the core of the PNCs contains strongly correlated atoms that mostly bind to immobile atoms (see red spots with enhanced coordination in long-range coodination maps, Fig. 1(d) and (f)). On top of that the ramified nearly also immobile exterior might hinder rotation and translation of the forming PNCs. Moreover the PNCs are interconnected with each other increasingly as time progresses forming an evolving cross-linked network (CLN) of localized clusters (see Fig. 1(e) and (f)). It is likely that the pre-nuclei become dynamically arrested¹³ due to kind of a cage effect⁵¹ provided by the CLN. This disordered network-like nearly immobile “skeleton” of the QLS (see Fig. 1(e)), which roughly fills only 5–10% of the space, likely further hinders rotation and/or translation of its constituent clusters. Therefore we argue that deeply undercooled pre-nucleating liquids can be described by an intrinsic hidden network-like nearly immobile although flexible frame, which promotes nucleation. We also find that the large active ramified and rough surface of a PNC (Fig. 1(b)) and the entire network of PNCs (Fig. 1(e)) rapidly adsorb liquid particles, which explains the calculated ultrafast growth rates^3,4 (see also Fig. S9(a), ESI‡).

The exploration of the metastable and immobile PNCs

The unfolding of the hidden clusters (PNCs) is mainly based on the recognition of the immobility of prenucleation clusters in the undercooled molten iron within the narrow critical temperature regime of 700–1250 K. Within this narrow T-regime, incubation time nearly vanished or reduced. Using displacement maps we are able to resolve the immobile regions. Using additional coordination filters (CFs) we are able to further specify the probable shape of the PNC. CFs are based on the recognition that immobile atoms tend to coordinate with each other and force out of themselves mobile atoms. In this way PNC cores can be resolved in great detail (see e.g. the 3rd row in Fig. 3 and 5(g) and the 3rd row in Fig. S1, ESI‡). Other methods that use order parameters (e.g. bond order analysis) are unable to resolve PNCs. These methods indicate phase evolution in a later stage when ordered regimes (bcc phases) occur. The earlier stages of prenucleation remain almost fully unresolved, however, by them.

Fig. 3 A schematic diagram of the expected mechanism of multistage nucleation and pre-nucleation clusters. L, SL, G, PR, N and S denote liquid, supercooled liquid, germ, precursor, nucleus and solid phases, respectively. The arrows show the corresponding phase transformation. 2nd row panels: Pre-nucleation and nucleation clusters in the MST mechanism. The 3-step filtered 3D views of intermediate stages (depicted as smooth surface meshes) of the MST nucleation in supercooled liquid iron at 1150 K. The PNC stage (PN state/QLS) is sampled at 4 time points (G1 at 50 ps, G2 at 100 ps, G3 at 133 ps and PR at 183 ps) during the QLS. The pre-nucleus PR (183 ps) state can be considered as the precursor of MST nucleation (not seen by PTM or Voronoi). The nucleus state is sampled in two stages (N at 208 ps and N2 at 245 ps). The details of the filtering process are shown in extended Data Fig. 5 and further details are discussed in the Methods section. Polyhedral surface mesh around atomic clusters is shown (the geometric surface reconstruction method has been employed with the Gaussian density method together with a smoothing procedure).^49,50 3rd row panels: The various clusters are cut in the middle and color-coded with respect to the reduced coordination in the cross-section in order to highlight the development of the PNC core as well as the bcc phase in the nuclei. For N and N2 the cross-section is color-coded according to PTM (the blue atoms are recognized as bcc).

Practically the extraction of PNCs can be done using a fairly simple double-filtering process in the QLS (dc-filter, details are given in the Methods section). Using d-maps we are able to d-filter nearly localized particles that are already very close to their final crystalline positions in the QLS. In order to further enhance the visibility of the otherwise hidden PNCs a coordination map can also be seen (Fig. 1(d) and (f)). Herein, the coordination of the d-filtered system is used (reduced coordination, RC, for details see the Methods section). The PNCs in solutions also have no definite phase boundary.⁸ In aqueous solution the outer hydration shell is also embedded into the solute environment. A similar feature can be expected in the QLS of ULI, which makes even more difficult the extraction of the PNCs. Applying then the c-filter PNCs are shown in Fig. 1(b) and (g)–(k) (only those particles are kept which are above a reasonably selected coordination threshold value). The initial PNCs at 0 ps (Fig. 1(g)) are those small clusters with a 2–4 nm diameter, which are detected in the d-map right after the quenching process of the liquid at 1150 K and which can be taken as seeds of pre-nucleation (details of seeded vs. spontaneous nucleation are provided in the ESI‡ in Section S3). Such hidden seeds randomly appear in various samples as detected by d-maps regardless of the length of equilibration of liquid iron before the quenching process (see the subsection Melting conditions in the Methods section).

The extraction of a typical PNC denoted by a circle in Fig. 1(c) and (d) can be done by applying a dc-filtering process and an additional radial c-filter. Particles with a higher coordination number are kept (yellow to red atoms). The resulting PNC is shown in Fig. 1(b), which is non-crystalline according to the radial density function g(r) (5th row panel S1(a), ESI‡) and to polyhedral template matching (PTM,⁴⁸ the 4th row panel in Fig. S1(d)–(g) (ESI‡). It shows no sign of any amorphous character, which excludes the role of the amorphous precursor mechanism (liquid-like g(r) is found for the PNCs).^27,30–34 The PNCs are also shown in 4th row in S1(c) (ESI‡) at 60 ps. Most of them are hidden yet at 60 ps, not detected by PTM (seethe 4th row in S1(e), ESI‡).

In an even larger system including 18 million atoms we further demonstrate the process of pre-nucleation in Fig. 1(g)–(k). Only the PNCs are shown, with the liquid-like rest of the system filtered using a dc-filter (details are given in the Methods section). In Fig. 1(m)–(p) the bcc atoms are shown within the PNCs detected by PTM.⁴⁸ A notable feature of those PNCs is that they already have a small bcc core compared to the entire cluster (compare Fig. 1(h)–(j) and (m)–(o)) that rapidly grows at the onset of the rapid crystal growth (RCG, see Fig. 1(q)) period.

We extract PNCs embedded into the liquid environment taking advantage of the explored basic rule that the PNCs are the clusters of nearly immobile particles, which mostly are coordinated with each other excluding mobile particles from the cluster core. Although the exterior part of the PNC is under-coordinated with localized atoms, by filtering mobile particles we are able to approximately find its most probable shape. Such typical PNCs are shown in Fig. 1(b) and (g)–(k) (also in Fig. 3). Therefore we find the unexpected persistence of PNCs, which suggests their relative stability with respect to the liquid environment.

Long range correlation effects and PNCs

Among the specific features of the QLS long range effects (LREs) are likely essential for the formation of growing PNCs. This has been evidenced by a few probes, which will be discussed in this subsection. During the prenucleation period spontaneously appearing coherent particles perform coordinated movement and form the early seeds of dynamic PNCs driven by LREs. These very early tiny PNCs (their diameter is expected to be in the range of d_PNC < 1 nm) are perhaps not detectable on dc-maps due to their mobility, which degrades the spatiotemporal resolution of the d-maps in this early stage of phase evolution.

Simple radial density functions (g(r)) reflect LREs: the 2nd, 3rd and 4th neighbor prominent peaks responsible for the 2nd, 3rd or 4th next nearest neighbors are definitely visible only for PNCs when compared to the g(r) of the as-quenched disordered liquid or to liquid states at 2000 K (5th row S1(a), ESI‡). The higher g(r) peaks reflect the presence of enhanced long-range coordination (ELRC) in PNCs relative to the pre-QLS state (as-quenched undercooled liquid) or to the self-disordered liquid phase at 2000 K. ELRC in turn implicitly is proportional to long range correlations between slowed down particles with concerted motion. The role of LREs has also been demonstrated in the 3rd row panels of the ESI,‡ Fig. S1(a)–(c). Increasing the cut-off radius of coordination in the range of r_c = [3, 12] Å using reasonably chosen coordination intervals the robust spread of the PNC exterior is seen together with the broadening of the core as well (see the 3rd row in S1(a)–(c), ESI‡). No such broadening is seen in the liquid environment, in ordinary self-disordered liquids or in as-quenched ULI. The broadening of the PNC in the coordination map with respect to r_c is expected to be due to robust LREs, which are much weaker in the quasi liquid environment of the PNC (background heterogeneity). In the liquid state no such correlations can be seen as expected (see S8(c), ESI‡).

The experienced intriguing long range correlations in PNCs can also be even further supported by coordination histograms. In the 5th row panels in S1(b) (ESI‡), the distribution of the reduced coordination (RC, the coordination of the filtered system) is shown for PNCs and compared to that of their liquid environment. While in the liquid medium typically a nearly Gaussian distribution can be seen (inset), the PNCs exhibit a non-Gaussian tailed decay. The deviation from the normal distribution indicates that PNCs cannot be described by the statistics of ordinary liquids. Instead pre-nucleation centers (the cores of the PNCs) occur with increased coordination leading to asymmetric distribution and to the coordination tail in the histogram. The fat-tailed distribution is the signature of ELRC within the PNC cores: high coordination numbers occur typical of the full (unfiltered) system in the PNC cores in which immobile and/or subdiffusive particles interact mostly with each other. Mobile (liquid) particles are pushed out of the cluster core of the PNCs and the liduid-like phase of the QLS fills the inter-PNC space.

The experienced robust long range effects, which manifest itself in enhanced long range coordination in the PNCs, could be among the revealed peculiar features of the QLS together with the immobility of the PNCs and the revealed heterogeneity in mobility in the entire supercooled system. Another notable important feature is the ability of the QLS to undergo concerted association processes of particles mostly in the early stage of the PNS, which leads to the formation of PNCs. These features are lacking in self-disordered liquids, in as-quenched supercooled liquids, and in stable glasses, which remain seedless for a long time.¹² The unraveled intriguing new features of the QLS further strengthen our view that the QLS is a specific state of matter in deep quenching that has not been sufficiently taken into account until now. Although the QLS is regularly a short-lived intermediate state of undercooled liquid-like matter (its lifetime t_QLS 0.1 < t_QLS < 1 ns), under certain specific and yet poorly understood conditions it can also be captured and stabilized presumably for a longer time.^8,34,38

An attempt is made using MD simulations to stabilize the QLS by cooling down abruptly the QLS from 1150 K down to 500 K, where incubation slows down and the QLS can in principle be captured. Indeed we were able to stabilize the QLS at least for ∼1 ns at 500 K (the simulation was interrupted at 1 ns). The captured amorphous QLS once prepared as a real matter can also be probed hopefully experimentally and its fascinating features can be reproduced and verified. The QLS is thus neither a pure liquid nor a solid-like state of matter or spinodal, as well as nor an amorphous and/or a glassy state, but instead a specific state that is yet to be fully understood. Therefore we argue that the QLS is not simply the transition state of phase transitions but a series of multistage intermediates smoothly transforming from one to the other. The multistage QLS pathway then allows the energetically often unfavorable single-step barrier of CNT to be bypassed via the concerted motion of coherent pre-nucleating particles. The presumably arising strong long range correlations between the pre-nucleating particles moving in concert within the PNC in incubated ULI likely enables the QLS to become energetically favorable with respect to the single-step mechanism in which existing small PNCs undergo activated aggregation processes.

Double dynamic heterogeneity in the QLS

Another important related feature of the QLS is the spatial inhomogeneity of particle motion. The first row figures in Fig. 2 illustrate the presence of mobility heterogeneity in incubated ULI at various temperatures before the nucleation has started. The corresponding d-maps are calculated as time averaged d-maps: the reference system is here the initial as-quenched ULI in this particular case (details are given in the figure caption as well as in the Methods section). The spatial modulation of mobility heterogeneity progressively damps with increasing temperature and becomes practically not visible above 1200 K. In ESI,‡ S8(a) the d-map of typical liquid iron is shown at 2100 K after 300 ps following the onset of melting. Note the obvious homogeneity with vanishing heterogeneity also in the q̄₆ map (S8(b), ESI‡). The modulation of MH is in the range of a few nanometers at 1150 K, which is in accordance with the range of dynamic heterogeneity observed in other metallic glasses¹⁷ and which goes into the sub-nm regime above 1200 K. With decreasing temperature the wavelength of MH peaks is at 8–10 nm at 500 K (the corresponding image is shown in the ESI,‡ Fig. S3(a)). Below this temperature the system transforms into frozen amorphous: the mobility of particles drastically slows down and the incubation time of the liquid-like system increases abruptly (Fig. 2(s) inset). Interestingly, the decay of MH above 1200 K conincides with the sudden jump of the incubation time for nucleation (estimated to be a few tens of nano-seconds at 1300 K, see the Fig. 2(s) inset). We argue then that the drop in incubation time for nucleation in the temperature range of 700–1250 K might be associated with the presence of MH in this regime, although the microscopic details are still unclear (perhaps MH somehow promotes transient nucleation).^1,12,13,52

In the 2nd row panels of Fig. 2 the PNS is shown at various temperatures in d-maps for a smaller system (512k atoms) as obtained by MD simulations. In particular now the reference system is again the final bcc crystal (as it was for Fig. 1(c)) at various temperatures and sampling in the MD movie file is taken at the elapsed time after quenching (marked at the top of the panels). The d-maps also reveal the occurrence of immobile PNCs (blue spots again, right in the position of the bcc nucleus) otherwise not visible by standard approaches such as PTM⁴⁸ or VoroTop³⁹ (see the 3rd row PTM panels in Fig. 2). Note that the pre-nucleus is embedded in an environment that can be described by a “background” MH (see the color fluctuations in the d-map). Therefore, the pre-nucleating system can be characterized by double-inhomogeneity: the coexistence of the MH in the quasi-liquid environment and the MH between the pre-nuclei and the bulk of the liquid-like system. Double-MH (DMH), typical of the QLS presumably, is also a novel feature of pre-nucleating systems perhaps not reported yet. We also find that with vanishing double-MH nucleation slows down e.g. above 1200 K where the background MH decays.

The pair distribution g(r) and MH (Fig. 2(s))

The split of the 2nd peak in the radial density function g(r) also shows the presence of a glassy (amorphous) state at 500 and 700 K (up to 900 K, shown in the ESI,‡ Fig. S3(c)).^1,53 The lack of peak splitting at 1150 and 1300 K can also be found because perhaps they are above the glass transition temperature (estimated T_g ≈ 900 K⁵⁴). Indeed g(r) is unable to resolve MH at 1150 K, which could be due to the lack of a glassy state. Above 900 K we see no 2nd peak splitting at all (see Fig. S3(c), ESI‡). However, the visible short-wavelength fluctuations and MH at 1150 and 1200 K in the time-lapsed d-maps (in Fig. 2(b) and (c)) indicate that a weak MH could persist above T_g (weak MH regime) for which g(r) is not sensitive enough to resolve. D-maps for nucleating phases in Fig. 2(f)–(h) also show that MH persists above T_g: see the short-wavelength inhomogeneity of red regions around the blue pre-nucleus in Fig. 2(f) and (h).

The schematic description of the expected mechanism of nucleation

Although we propose basically a 2-step process (will be outlined below), the 2nd step can further be divided, at least, schematically into a few other stages. This multistage mechanism is based on various maps as shown in Fig. 1 and 2. The first major step is the stochastic and spontaneous formation of a germ or seed (germination, the conversion of the supercooled liquid to G at the end of the incubation period). The germ (G) is an early-stage seedless loosely bound hidden PNC, which is already relatively localized and therefore is at least weakly visible in d-maps. The germ state has been sampled in 3 elapsed-time positions of 50 (G1), 100 (G2) and 133 (G3) ps. The corresponding PNCs can be seen in the 2nd row in Fig. 3. The germ rapidly transforms into the precursor state (PR) via the expected concerted motion of the coherent particles of the PNCs. The G to PR step is an ultrafast growth process via particle additions. G and PR states are hidden since they are not visible by standard display approaches (such as PTM, VoroTop or q̄₆, see Fig. 6(a)). The separation of the G and PR states is justified by the following expected mechanism: the G state can be characterized by loosely bound ramified cluster(s) (embedded in a liquid environment decorated by a background MH below 1250 K) with a nearly complete lack of a definite core and a considerable order of the clustered atoms. G turns into the PR state, and a weak order sets in, in the hidden cluster core (e.g. stacking and/or packing order with many defects such as e.g. misorientations and/or mixed packing). The PR state can also be characterized as a highly ramified cluster with a weakly ordered hidden core (see the corresponding PNCs shown in Fig. 3, 2nd and 3rd row panels). The PR then rapidly develops into the nucleus (N), which is already detectable and visible by standard approaches (Voronoi, PTM, bond orders etc.), and can be taken as a relatively ordered and nearly spherical cluster more or less free of defects. The states G, PR and early stage N are the various forms of the QLS free of translational and rotational order, however, different from ordinary liquids. Finally the rapid solidification (crystal growth) takes place from the N state into the solid crystal (S).

Nucleation as a two-step process

It is well established from MD simulations (see the inset in Fig. S9(a), ESI‡) that the length of the incubation period is anomalously temperature (T) dependent.^16,23–26 Although it has already been known in the literature that nucleation can spontaneously be induced in deep quenching (<0.7T_m), the details of this anomalous T-dependence have not been well established yet. The experienced anomalous T-dependency of the incubation period in deep quenching can be attributed to the probable temperature dependence of the association process of early-stage dynamic PNCs, which remains hidden unfortunately in our d-maps. These metastable mobile small PNCs, however, likely differ from those found by Gebauer et al. in molecular solutions in many respects. The small dynamic PNCs (a few tens of clustering atoms) that are formed easily as well as decompose into smaller parts are likely present in the undercooled liquid. However, their diffusion and aggregation must certainly be an activated process. This is because incubation takes a long time with increasing temperature due to the change in cluster mobility. In pure systems, in which cohesion is very strong even between liquid particles such as in liquid iron, the detection of mobile atomic clusters is challenging. The formation and aggregation of these small mobile atomic clusters must indeed be a rare event above ∼1250 K. This must be the primary reason for the exponential increase of the incubation time. In the narrow T-regime of 700–1250 K, in which incubation time drops (see the inset in Fig. 2(s) and its enlarged inset in the ESI,‡ Fig. S9(a), the mobility of the initial dynamic PNCs in the incubation period, however, perhaps also anomalously drops.

The anomalous temperature dependence of prenucleation (incubation vanishes within the narrow T-regime of 700–1250 K) can be understood by the assumpation of a 1st activated step, in which initial germs (highly ramified PNCs) are formed. We see only the appearance of these germs in the d-maps; however, we are unable to resolve their formation yet. Perhaps, tiny mobile PNCs aggregate to form the immobile germs. The concentration of these small mobile PNCs in the NLS likely depends on the temperature and on a few other yet unknown parameters. It is also likely that in the NLS these germs dissociate too frequently to initialize prenucleation. Once a critical size germ is formed rapid growth sets in by ultrafast serial particle addition and/or by the adsorption of small mobile atomic clusters. We can resolve in detail the 2nd nearly barrierless step, the ultrafast growth of immobile PNCs, by following the time development of d-maps.

The strong correlation between the incubation time and PNC mobility is expected although the atomistic details of this dependence are unclear yet, however. Perhaps, the formation and the specific features of the QLS are responsible mostly for the anomalous drop in the incubation time in the T-regime of 700–1250 K. The possible influence of a temporary spinodal phase on particle mobility may also be a consideration. It is outlined below in detail that no definite spinodal phase has been found at >700 K.

In the 700–1250 K regime, however, the already localized highly ramified PNCs (germs) are formed from small dynamic PNCs after short incubation (∼100 ps). Unfortunately we are able to detect at the earliest only the germs (nearly immobile loosely bound small PNC clusters) in the d-maps (see the 2nd row clusters G1, G2 and G3 in Fig. 3). The formation of the germs due to the aggregation of the dynamic PNCs is certainly an activated process. However, once a germ is formed it rapidly adsorbs particles, followed by assembly-free nearly barrierless growth to form a nucleus. In this sense nucleation is a two-step process: the germination of the small dynamic PNCs during incubation is the 1st activated step and the remaining part of nucleation is nearly barrierrless with a vanishingly small barrier. The activated 1st step is responsible mostly for the strong T-dependence of the incubation time above the critical temperature (T_c) of ∼1250 K. An important consequence of the 2-step mechanism outlined above is that the 2nd ultrafast barrierless step is nearly T-independent (athermal) and as such must remain nearly invariant in the entire temperature range up to the melting point. Therefore, the QLS (the prenucleation of the germs) could survive a critical temperature of T_c > 1250 K up to the melting point, although no direct evidence is available for now. Approaching the T_m germs will dissociate more and more frequently and nucleation becomes inhibited.

This simple 2-step mechanism seems to be consistent with most of the available experimental and theoretical findings. A few details of the proposed mechanism remain, however, still not fully understood. One of them is that why the mobility of the incubated PNCs is anomalously T-dependent and why it drops in the narrow T-regime of 700–1250 K. Another issue is that to what extent spinodals play a role below the glass temperature.⁵⁵ Nevertheless we assume that the occurrence of the glassy state below ∼700–900 K is responsible for the slow down of nucleation.

Most of the MD studies detect bcc-like precursors using standard methods (PTM, Voronoi, etc.). However, we are able to detect earlier hidden ramified atomic clusters not revealed before. We can look back earlier in prenucleation using filtered dc-maps than using standard descriptors (Voronoi's tesselation, PTM, CNA, bond order, etc.).

It could also be the case that under deep quenching a different mechanism works for nucleation than at temperatures closer to the melting point. According to classical nucleation theory (CNT), nucleation is a single activated step process. Our 2-step mechanism can easily be transformed into a single step mechanism approaching the melting point, e.g. the role of the 2nd step diminishes and only the 1st activated step survives the temperature increase. In this case nucleation takes place by a simple activated process of aggregation of the dynamic PNCs (no germination takes place). This paper focuses on the details of the deeply undercooled regime (T < 0.7T_m), which is accessible for MD simulations. In this article we try to understand mainly the mechanism of this ultrafast nucleation regime. Using a simple approach (d-maps) we follow the atomic movements and unravel the heterogeneity of the mobility of particles. We also find that in the narrow temperature regime of 900–1250 K (0.5T_m < T < 0.7T_m) the system is neither spinodal nor an ordinary liquid, nor a glassy system, but something different in many respects. This is what we call the QLS (quasi liquid state). It is a kind of a transition regime between the spinodal and ordinary liquid state (quasi spinodal or quasi liquid in this sense).

Single event d-maps

The spatiotemporal development of the pre-nucleus is shown in d-maps in the 1st row panels of Fig. 4 in a smaller system with a single nucleation event (the time values are the elapsed time after the quenching of the melt). The time development of atomic displacements d_i(r,t) shows us the spread of regions with lower mobility in the entire system in agreement with the dashed red curve in Fig. 4(j) (the decay of the curve in the quasi-liquid environment). The detected spreading blue-spots (low-displacement regions) are directly related to slow particle mobility as before. Surprisingly, the spread of these spots can be seen from the blue spot center towards the entire area (Fig. 4(c) and (d)). Therefore we conclude that the nonlocal nature of “preordering” (the spatial spread of blue spots) can be seen long before the onset of bcc nucleation.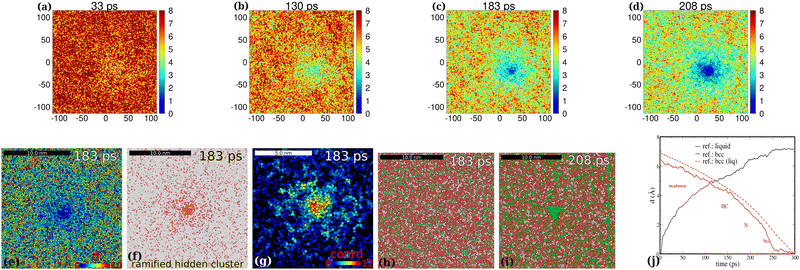

Fig. 4 D-maps at 1150 K: the developed localized PNCs made visible. 1st row: spatio-temporal heat overview d-maps with respect to the final atomic bcc positions within a thin cross-sectional slab of the simulation cell at various elapsed times after melting ((a)–(d), 33, 130, 183 and 208 ps). 2nd row: (e) d-map at 183 ps. (f) The ramified hidden cluster (red atoms for which d < 2.5 Å) surrounded by liquid atoms (white) for which d ≥ 2.5 Å at 183 ps (the colors here nothing to do with the PTM colors, mobile atoms: white, frozen atoms: red). (g) The ramified hidden cluster in the d-filtered system color-coded with the reduced coordination: atoms are excluded for which d_i ≥ 2.5 Å in the d-filtered system. The atomic coordination is then calculated for this reduced system (cut off at 2.8 Å). A PNC is more visible with reduced coordination marked. Cross-sectional slabs are shown with the thickness of 10 Å. NPT simulation: 1150 K, 512k atoms. (h) and (i) Color-coding consistent with Tanaka's notation with respect to q̄₆: red 0.28 < q̄₆ < 0.4, green q̄₆ ≥ 0.4, white q̄₆ ≤ 0.28. Red corresponds to MRCO atoms (medium range crystalline order²). q₆ is cut off at 2.8 Å. (j) The average time-dependent atomic displacement (“order parameter”) 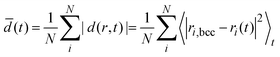(equivalent to the mean square of atomic displacements averaged over elapsed time t) as calculated with respect to different reference states within a sphere with 10 Å radius pointing to the bcc center shown in the 2nd row panel (e): The two reference states are the initial supercooled liquid (black) and the final bcc crystal (red). The dashed red curve is calculated for the system outside the nucleus sphere (liquid-like regions). This is just to show that the liquid region in general behaves in a different way than the dedicated bcc center where nucleation takes place. The rectangular simulation cell: 512 000 atoms, 23.39 × 11.61 × 23.62 nm³.

At 183 ps PTM still indicates the lack of a nucleus (see the corresponding PTM maps in the 3rd row in Fig. 2(k)). Note that although at 208 ps still we have only very few nucleating bcc atoms according to PTM (see the corresponding PTM maps in Fig. 2(l)), the blue regions spread far outside the nucleation center in the d-map (Fig. 2(f)–(h)). Therefore d-maps localize the forming nucleus in great detail in a much larger area than that indicated by PTM. The ramified nature of the forming PNC is further demonstrated in the 2nd row in Fig. 4(a)–(c) using different approaches. In Fig. 4(e) a simple d-map is used, while in Fig. 4(f) subdiffusive atoms (d_i < 2.5 Å) are shown in red and the rest (mobile atoms) are shown in white. In Fig. 4(g) in the d-filtered system color coding is according to reduced coordination (RC). These figures clearly demonstrate that the hidden pre-nucleus is deeply embedded in its quasi-liquid environment covering an area (volume) nearly twice or more as extended as the pre-nucleus core. This peculiar nonlocal intrinsic feature of the diffuse precursor is especially visible in Fig. 4(g) or Fig. 5(b) and is reminiscent of the growing correlation length in the QLS. The RC highlights those atoms that are clustering with more localized atoms rather than those undercoordinated atoms in the outer regions that have less 1st neighbor “frozen” atoms. Although the mobile (liquid) atoms are excluded from d-filtered plots, using color-coding with respect to RC the network-like character of the pre-nucleus is revealed. In fact these plots show us the coordination between frozen (slow) atoms whose particles are the basic elements of the pre-nucleation process. The filtered mobile particles would overshadow otherwise the visibility of the ramified hidden cluster (see S1(a), ESI‡). Sufficient coordination-contrast can only be seen for d-filtered maps (see details in the ESI,‡ Fig. S1).

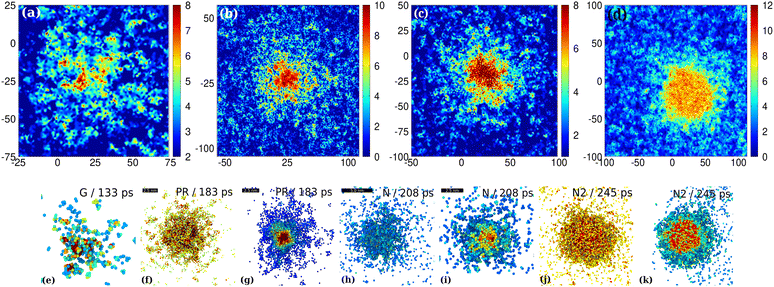Fig. 5 Spatially resolved coordination maps at various stages of the QLS. Ramified pre-nucleation and nucleation clusters are shown on zoomed d-filtered coordination maps at 133 (a), 183 (b), 208 ps (c) and 245 ps (d) for the G, PR, N and later N states, respectively at 1150 K. The d-filtered systems are shown in coordination maps (color coded with respect to the reduced coordination (RC) of subdiffusive atoms). The d-filtered maps exclude mobile atoms, only localized (immobile) atoms are kept in the map (d_i ≤ 0.25 nm). Reduced coordination is calculated for the d-filtered systems cut off at 0.28 nm. Further details of d-filtered maps and RC are given in the Methods section. The scale is in Å. (e)–(k) 3D view of the PNCs of the MST nucleation at various stages (G (e), PR (f) and (g), N (h) and (i), N2 (j) and (k)). The clusters are displayed after a 3-step filtering process: according to d < 2.5 Å and additional filterings are applied with respect to the reduced coordination (RC < 4) to get rid of unnecessary undercoordinated atoms that limit the visibility of PNCs. Color coding is with respect to RC. (g), (i) and (k) Slices cut in the middle of PR (g), N (i) and N2 (k). The further details of the multistage filtering process are shown in the ESI,‡ Fig. S1.

Disordered network in the QLS in coordination maps

In Fig. 5 the further details of the disordered network character of various intermediates of the multistage pathway are resolved on d-filtered coordination maps. In Fig. 5(a) the seedless (spinodal-like) germ state is shown, which precedes the expected precursor (PR) state (see also G1–G3 PNCs in Fig. 3 and 5(e)). Although the ramified PNCs looks like spinodal nanoparticles (see Fig. 5(a) and (b)), the entire volume of the QLS including the liquid environment cannot be regarded as spinodal somewhere above the glass transition temperature (>900 K). A full volume spinodal-like pattern is seen e.g. at 700 K (see Fig. 2(o) and (p)). In Fig. 5(b) the elaborate network-like spreading of the outer part of the PNC in the PR state with a ramified pattern is also seen (see also the PNC of the PR state in Fig. 3 and 5(f)). Fig. 5(c) reveals that the early-stage nucleus is also ramified as found for the pre-nucleus (Fig. 5(b)). Fig. 5(b)–(d) provide an especially enhanced visibility of the ramified outer region of the nucleus resolved at high quality using the coordination maps. We find that even the small nucleus (Fig. 5(c)) cannot be considered as a compact spherical-like arrangement of particles (Fig. 5(h) and (i)), although it has a compact nearly crystalline core (see the 3rd row in Fig. 3 and 5(i)). The diffuse yellow-to-red “cloud” around the nearly spherical nucleus core in Fig. 5(d) comprises immobile atoms, which already are at their final bcc positions at 245 ps; however, still at 245 ps they are deeply embedded in a liquid-like environment. Therefore, despite being deeply embedded in the liquid-like environment the ramified outer region is immobile. In principle it goes against what can be assumed about oridnary liquids in which these deeply embedded particles should intermix with their liquid neighborhood. The reason for this apparent contradiction perhaps is that the prenucleation process is so fast that there is no time for interdiffusion, which occurs on a much longer timescale. The strong tendency of the enrichment of immobile atoms within the disordered network of PNCs during the precursor state could be a strong driving force of crystal growth.

The bond orientational order (BOO, q̄₆) maps are also shown in Fig. 6(a) and (b) for the PR and N states. It can clearly be seen that the q̄₆ map is featureless for the pre-nucleus state at 183 ps (Fig. 6(a)) and shows the modulation of the background MH.⁵² Even for the N state (Fig. 6(b), at 208 ps) it indicates a similar extent of the nucleus as found for the PTM map (Fig. 2(l)). Therefore the q̄₆ map seems to be unable to account for the PNCs as well as the highly ramified nature of the nucleus (compare Fig. 6(b) with Fig. 5(c)). It is likely that medium range crystalline order (MRCO⁵²), which is accounted for by q̄₆ maps, does not play an essential role in the pre-nucleation process, instead perhaps long-range correlations (e.g. the formation of long ramified atomic chains or “arms” in the PNC exterior, LREs) are the main driving forces of the growing hidden order during the QLS. The 3D network-like long range interaction of these atomic chains with the liquid-like environment could robustly promote (speed up) pre-nucleation.

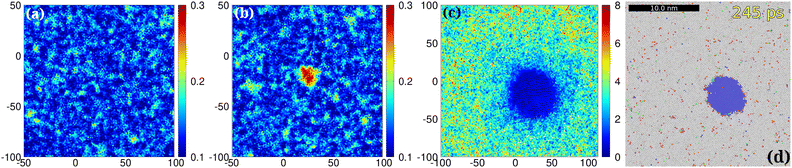Fig. 6 Bond orientational order (BOO) on spatial maps. BOO (q̄₆) spatial maps (nearest neighbors are cut off at 0.4 nm) at 183 ps (a) and at 208 ps (b) (PR and N states, respectively). (c) and (d) The nucleus at 245 ps plotted as a d-map (c), and the corresponding ptm map (d). The maps are calculated for the same thin slabs used for coordination and d-maps in Fig. 4 and 5. q̄₆ has been calculated for the fully coordinated system; no d-filtering is used. The Lechner–Dellago-type averaged q̄₆ was used for the calculations.⁴⁰

Conclusions

We find that the incubation time (t_inc) of spontaneous homogeneous nucleation is strongly temperature dependent in the case of undercooled liquid iron. Moreover in the narrow temperature regime of 700–1200 K t_inc falls below 1 ns. Above 1250 K t_inc grows exponentially, which challenges brute force molecular dynamics simulations.

We are able to trace back prenucleation to an early phase in which standard descriptors (e.g. Voronoi's tesselation) indicate an ordinary liquid. We are able to localize immobile early phases called germs (small metastable ramified prenucleation clusters), which undergo assembly-free growth to form nuclei rapidly within 100–150 ps. The details of the formation of the germs (germination) remain, however, unexplored yet. Nevertheless, we expect that during incubation small dynamic prenucleation clusters, including likely a few tens of atoms undergo an activated aggregation process forming finally the germs. The nearly immobile germs once formed undergo assembly-free nearly barrierless growth to form nuclei rapidly.

The undercooled liquid in the anomalous T-regime of 700–1250 K is neither a spinodal nor a glassy system and nor an ordinary liquid, according to our analysis (quasi liquid state, QLS). This specific state of matter can be described by a few interesting features such as its intriguing heterogeneity: ramified prenucleation clusters are embedded into a liquid-like environment, which is also dynamically heterogeneous. Moreover the entire system can be described by long range effects via forming network-like interconnections, which are, however, different from a spinodal phase in which the full volume decomposes into well defined separate phases entangled in each other.⁵⁵ In the QLS the decomposition of the PNC phase from the liquid-like environment is much less well defined (with blurred boundaries). Typical spinodal-like phases are found below 700 K where nucleation slows down and incubation time increases exponentially with temperature. On top of that the rapidly growing PNCs in the QLS are highly immobile (localized): this particular feature makes it possible to identify them easily on displacement maps. The immobility and the subsequent assembly-free growth represent an important difference with respect to PNCs found by Gebauer et al. in aqueous solutions,^7–9 in which the activated aggregation of mobile PNCs is the basis of nucleation.

We argue then that nucleation following deep quenching of molten iron is essentially a two-step process. The 1st step is the activated aggregation of small prenucleation clusters leading to the germs. The 2nd step is the ultrafast nearly barrierless growth of the nearly localized germs without aggregation between them. The 1st step can be very long (incubation), while the 2nd athermal step is a transient process (100–150 ps). The transient width of the 2nd step is nearly temperature independent up to 1250 K. No data are available for higher temperatures, although it can be expected that it remains nearly athermal up to nearly the melting point. The 1st activated step is strongly temperature dependent. Approaching the melting point it cannot be ruled out though that the 2nd step diminishes (germs decompose into dynamic PNCs regularly) and the 2-step mechanism turns into a single step process (classical nucleation theory). In the latter case the aggregation of dynamic PNCs of various sizes becomes the dominant step instead of the germination and subsequent assembly-free ultrafast athermal growth.

III. Methods

A. Molecular dynamics

The simulations were performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS) code⁵⁶ and NPT (Nose–Hoover⁵⁷ thermostat and the Parrinello–Rahman algorithm for the barostat) simulations with periodic boundary conditions in all three directions. The velocity-Verlet algorithm is used to integrate the classical equation of motion with a time step (dt) of 0.1–1 fs. A periodic cubic simulation box filled with bcc Fe atoms (the initial lattice constant a₀ = 2.87 Å) is melted in a few hundreds of steps over a melting temperature of 3200 K and then the system is cooled down to the target temperature at a fast cooling rate of 185 K ps⁻¹ (quenching). The variations of the quenching rate in the 7–740 K ps⁻¹ regime do not alter considerably the final conclusions of the present work (see Fig. S6(a) for details, ESI‡). The slowest cooling rate is τ = 7 K ps⁻¹ at which nucleation is still initialized at 1150 K. The target temperature of 1150 K cannot be reached before the onset of nucleation if τ < 7 K ps⁻¹. Even with this or somewhat higher rates (7 < τ < 100 K ps⁻¹), however, the average temperature exceeds the target temperature during the incubation period and/or leads to moderate short wavelength temperature oscillations (see Fig. S6(a), ESI‡). The d-map shown in the ESI,‡ Fig. S6(c) reveals, however, that even at the slowest cooling rate tested in this work (τ = 7 K ps⁻¹) we also find local hidden ordering (LHO) before nucleation. The phenomenon LHO is therefore robust against cooling rate selection. Throughout the paper we employ the fast cooling rate of τ ≈ 185 K ps⁻¹ in order to ensure stable isothermal conditions both for incubation and for nucleation and to avoid the onset of prenucleation during the quenching process. However, it is also important to avoid vitrification, which can happen at extremely high cooling rates.¹ The lack of peak splitting in the 2nd g(r) peak is found above the glass transition temperature in ULI (T_g ≈ 900 K⁵⁴), which does not support vitrification. Therefore it is unlikely that in the simulations with an ultrafast quenching rate we are faced with vitrification induced fast nucleation.

Our experience shows that nucleation is the fastest within the temperature regime of 700–1200 K (see Fig. S9(a), ESI‡) and therefore it is relatively easy to induce spontaneous nucleation with the shortest incubation time (less than a few hundred picoseconds). We have shown both for homogeneous spontaneous and for heterogeneous nucleation with a reflecting wall that the growth speed peaks and the incubation time takes its minimum value at around 1150 K (Fig. S9(a), ESI‡). Spontaneous nucleation has been realized via keeping the system at various constant temperatures. Snapshots were saved at every 1–10 ps for analyzing the atomic scale ordering process during nucleation/solidification. Incubation time increases abruptly below 700 K or above 1200 K, which makes it challenging to follow the time development of heterogeneity in the supercooled liquid (see the inset in Fig. 2(s)).

The equations of motion used are those of Shinoda et al. in ref. 58, which combine the hydrostatic equations of Martyna, Tobias and Klein in ref. 59 with the barostat proposed by Parrinello and Rahman in ref. 60. The time integration schemes closely follow the time-reversible measure-preserving Verlet and rRESPA integrators derived by Tuckerman et al.⁶¹ Previously we used MD simulations for various other systems.^62–66

Empirical potential. Following previous work on iron, we used the embedded atom method (EAM)⁶⁷ to describe the atomic interactions. In the present work, the potential proposed by Ackland et al.^68,69 was used, which provides a reasonably accurate melting temperature for Fe (∼1791 K), as opposed to the experimental value of 1811 K.⁴² This potential was also used to address crystal nucleation recently^70–72 and tested in detail, which showed accurate prediction of solid–liquid coexistence properties (e.g. melting point, solid–liquid interfacial energy, specific heat, critical nucleus, cohesion, etc.). Other state-of-the-art empirical potentials, such as the second nearest-neighbor modified-embedded atomic method (2NN-MEAM), given by Asadi et al.^73,74 and the one recently reported by Starikov et al.⁷⁵ (angular dependent potential, ADP) have also been used to compare results with those of obtained by the Ackland EAM potential.^68,69 The force field of Asadi et al. accurately reproduces various properties of liquid iron (e.g. the melting point, in different solid/liquid interface systems).⁷³ This potential is mainly developed for high-temperature applications, which makes it a suitable empirical potential for simulations of the quasi liquid state of iron (e.g. nearly fully molten phases, incubated undercooled liquid iron). However, the use of this angular-dependent 2NN-MEAM potential is rather time-consuming, and therefore we used it only for a few smaller test systems. Nevertheless, it is important to point out that the conceptually less accurate simple EAM potential of Ackland et al. provides similar features of the QSL state (e.g., the extent of inhomogeneity, early-stage local hidden order, and hidden precursor development) to those calculated by the more accurate but computationally more demanding 2NN-MEAM approach. The main advantages of the 2NN-MEAM approach are that it is able to account for directional bonding, which is important in bcc metals, as well as the second neighbor shell has also been taken into account (long range effects). A very similar spatial distribution of inhomogeneity, however, is found by the 2NN-MEAM approach (the cut-off distance r_c = 5.0 Å) and by a recently parameterized angular dependent potential (ADP⁷⁵) in incubated undercooled liquid iron (at 1150 K) as compared with simple EAM as shown in the ESI,‡ Fig. S7. The ADP EAM potential⁷⁵ implicitly accounts for angular forces, which is related to directional bonding. It is worth mentioning that the force field is fitted to ab initio density functional theory (DFT) data using the force matching method.⁷⁴ One of the most important features of these empirical potentials (EAM,^68,69 MEAM^73,74 and ADP⁷⁵) is that they relatively accurately reproduce melting temperature (EAM: 1791 K,^68,69 MEAM: 1807 K,⁷³ and ADP: 1770 K⁷⁵vs. the experimental 1811 K⁴²).

Melting conditions. The initial configuration of the periodic simulation box was prepared by heating up a cubic bcc crystal of iron of various sizes up to 3000 K and was maintained at this temperature for 300 ps until reaching thermal equilibrium. Then, the melt was cooled down to 2500 K and kept at this temperature up to further 200 ps. Subsequently, the melt was quenched to the target temperature at an ultrafast cooling rate of 185 K ps⁻¹ (the effect of the cooling rate on nucleation has been discussed in detail in the ESI,‡ Fig. S6(a) and in the Methods section). The undercooled liquid was kept at the target temperature until full solidification was obtained. bcc nuclei of size 1 nm (diameter of the nearly spherical nucleus) spontaneously grow within 150–200 ps (5% of the cell is bcc at 1150 K). Nearly the whole simulation cell transforms into the bcc phase within 300 ps (>95% of the cell atoms are bcc) at 1150 K. At higher temperatures, such as at 1200 K, the incubation period takes a much longer time of nanoseconds or more. The main computations were carried out on a GPU cluster and/or on supercomputers with Intel Xeon Phi coprocessors.

The effect of the cooling rate on the temperature is also shown in the ESI,‡ Fig. S6(a). We find that the 185 K ps⁻¹ cooling rate is the best possible choice because we can avoid spurious fluctuations in the temperature at the beginning of the cooling process and we can provide stable isothermal conditions during incubation. The latter is especially important in order to study the onset of pre-nucleation under temperature fluctuation-free (isothermal) conditions. Nevertheless, we find that even when applying a much slower cooling rate (7 K ps⁻¹) the calculated d-map reveals a localized pre-nucleation cluster, which suggests that the process is robust against the cooling rate.

More gentle conditions can also be applied and tested during the quenching process. The cooling process can be divided into a few steps in order to reach the target temperature slowly and to avoid spurious temperature fluctuations. Starting from 3000 K, in a few steps we reach 1300 K, the temperature at which we keep the system for a few nanoseconds without the onset of nucleation. Up to 20 ns we find no sign of nucleation at 1300 K. Then using a subsequent fast cooling process we can reach the target temperature finally. Even when varying the cooling rate (0.5 < τ < 200 K ps⁻¹) when cooling down from 1300 K to the target temperature, the outlined ultrafast nucleation mechanism is robust against τ.

However, even when using such gentle conditions, the conclusions remain invariant.

B. The calculation of displacement maps based on single-atomic movements

In principle, ensemble or time-averages are needed for statistical analysis of stochastic processes such as nucleation.⁴⁶ Unfortunately the plot of statistically resolved spatial maps (displacement maps) for nucleation is challenging. This is because nucleation can be initialized at random positions and at random elapsed time within a simulation cell with a nearly equal probability in different independent simulation runs, which makes ensemble averages difficult to consider. The highly stochastic nature of the spatio-temporal distribution of nucleation ensemble averaged real-space maps could unravel the interplay between structure and dynamics. Therefore instead of probing spatial averages of isoconfigurational runs, which are indeed useful for glassy systems,⁴⁶ we focus on spatial maps based on unique runs time averaged over the lifetime of the quasi-liquid state in order to get rid of short wavelength fluctuations as well as to average out lattice vibrations. We also reveal, however, that even without time-lapsing simple instantaneous displacement-maps (d-maps) are sufficiently informative to unravel the hitherto hidden details of pre-nucleation. Event to event during sampling various pre-nucleations the same multistage mechanism is explored robustly regardless of the system size and the applied reasonable empirical potentials.

In particular, it is possible to display atomic displacements as a color-coded (heat overview) spatial map (d-map) relative to stable atomic configurations in order to reveal phase transformations and/or phase development between the initial and final states. Therefore the relative atomic instantaneous displacements d_i(t) for an arbitrary atom i are calculated with respect to a reference state (RS, which can be selected as the initial, intermediate or final state). The local quantity d_i(x,y) = d(r) is plotted against x,y lateral positions as a color coded map (d-map) for thin slabs cut in the middle of the simulation cell or in those slabs where nucleation appears for the first time. For melting and for crystal growth the reference configurations are the initial and final bcc crystals, respectively. Therefore, in the case of crystal growth we have to go backward in time in the movie file of the MD simulation during sampling the phase development when an atomic displacement is calculated at elapsed time t as d_i = 〈|r_i(t) − r_i,fin|²〉, where r_i(t) and r_i,fin are the atomic positions of atom i at time t and in the final position in the bcc crystal or in other reference states. The color coded d-maps are then used to follow the time development of local hidden order and inhomogeneity. We are able to display early-stage occurrence of phase development (e.g. prenucleation) in incubated undercooled liquids of molten iron using d-maps. The calculation of d-maps is performed using OVITO⁴⁹ ensuring the appropriate mapping between atomic indices, which requires the appropriate sorting of atomic IDs during LAMMPS simulations.

C. d-maps with various reference states and sampling backwards in time in the movie file

Our experience shows that the displayability of heterogeneity in the prenucleation state is strongly sensitive to the appropriate choice of the reference system (RS). The reference configuration for the atomic displacement (AD) calculations can be placed at various positions (initial (I), final (II), and intermediate (III) in the liquid-to-solid pathway) within the movie file of MD simulations. Also there can be a difference in the direction of sampling. Logically in the case of RS_final (II) one has to go backward in time under sampling the movie file. When using the initial state for the RS, sampling moves forward in time. When using the intermediate RS, e.g. at the nucleus, backward or forward movement in time is possible. To gain sufficiently visible contrast in d-maps (d-heterogeneity, dHE) it is important to have a well developed double-mobility heterogeneity (MH) in the system. The lack of inhomogeneity in the mobility of particles can be seen e.g. in Fig. 2(d) at 1300 K. Below 1200 K, however, double-MH (DMH) develops due to the localization of immobile particles (PNCs). DMH is not detectable on d-maps for case I due to the lack of visible contrast of d-maps. The most visible contrast is seen for case II.

The appearance of sufficient contrast in the d-map as a basic condition for making visible the otherwise hidden PNCs is satisfied only by two positions of the RS: the final state with naturally moving backward in time (case II) and the intermediate position with moving forward in time at sampling (case III forward). The two other possible RS positions (initial and intermediate with moving backward) do not give sufficient contrast for d-maps. This could be the reason that the role of d-maps in displaying PN is overlooked in the past. The underlying reason for the weak contrast is the following: particles are displaced at least a few times until reaching the QLS under deep quenching. In the QLS pre-nucleating particles slow down and d-heterogeneity rapidly develops. Reaching the pre-nucleus regime particles in the PNC do not move beyond their vibrations around their equilibrium positions any more; however, particles around the forming PNC still hop a few times to reach their final positions in the final crystal. The ultrafast assembly-free growth takes place via particle addition: liquid particles hop into the rough surface of the PNCs. The localized (rigid) feature of the PNC is what allows us to isolate the localized metastable PNC from its environment using the multistage d and c-filtering process (dc-filter, see Fig. S1, ESI‡). However, the time required for the development of visible d-heterogeneity in atomic displacements exceeds the short lifetime of the QLS (τ_QLS < 100 ps). When the pre-critical nucleus is formed its more remote environment still contains mobile particles in significant numbers, while the nucleus and its immediate ramified hidden neighborhood are already immobile during the QLS. This is what basically leads to the development of a visible d-heterogeneity when the reference configuration is the final bcc state. Particles in general move a lot with respect to the initial state (case I, even the slowing down particles hop at least once, see Fig. 1(r)), while particles that make up the localized PNCs do not nearly move with respect to the final state from the QLS (starting from the end of the incubation period). Therefore in the case of II d-heterogeneity is robust, while for case I it will be weak and no traces of the PNCs will be seen, and they will continue to be hidden on the d-maps regardless of the time of sampling.

RS positions II and III (forward) satisfy the main condition of contrast visibility; however, a sufficient period of time is required for the occurrence of d-heterogeneity. In the cases of I and III (backward) dHE remains insufficiently small throughout the pathway of liquid-to-QLS. For case III (backward) see results plotted in the ESI,‡ Fig. S4, in which traces of PNCs (blue spots in the d-map) can be seen only weakly. If we continue sampling for I after the QLS, dHE does not develop to the sufficient level, not even in the final bcc crystal. This is because particle mobility persists for the entire simulation cell until the onset of the QLS and with respect to the initial state dHE does not develop to the visible level until the final crystal. Particles move a lot with respect to the initial state, and no visible contrast develops for case I (the contrast is blurred).

Another reason is that for the mean mobility of liquid-like particles for RS I and II it holds that d̄^I_m < d̄^II_m for the QLS-to-bcc period where I and II denote the RS. In Fig. 4(j) the time development of d̄ can be seen for cases I and II. Indeed, it is obvious on the basis of Fig. 4(j) that d̄ changes more rapidly for case II after the QLS than that for case I (compare the red curve vs. the black one from 125 ps onwards: d̄^I_m ≈ 2.0 Å, d̄^II_m ≈ 4.5 Å). A rapid phase transition takes place: mobile particles are displaced much more with respect to the final state compared to the initial one (while PNC particles are immobile). Therefore, when dHE is calculated for the same simulation run with respect to the final crystal (case II) dHE is robust when sampling takes place in the QLS. Also, in this case sampling takes place directly in the QLS, while in case I even if sampling takes place in the final state dHE will be weak. Therefore there is a kind of an anisotropy in the magnitude of dHE with respect to the direction of sampling and to the choice of the RS. The direct evidence of this is that double-MH is robust for the QLS-to-final crystal period (somewhere in the nucleation regime), while there is no double-MH at all for the initial state-to-QLS period (see Fig. 4(a)–(d)).

CaseIII forward: in this particular case, it is worth sampling in the final bcc solid and only the remnant of the pre-nucleus can be detected (Fig. S4, ESI‡). These remnant atoms originating from the PNS were immobile in the QLS-to-bcc pathway, giving a considerable contrast in the d-map with respect to the rest of the particles, which were more or less mobile. Therefore, in terms of displayability, visible d-heterogeneity develops well after the QLS in the final crystal if the RS is selected in the QLS and sampling is moving forward in time (case III forward) (see Fig. S4, ESI‡). Case II provides the only possibility of direct sampling in the QLS when going backward in time. This setup is used therefore mainly in this paper for constructing d-maps (also called reversed d-maps).

It must also be noted that case I is the most widespread in the literature e.g. for displaying a dynamic propensity on spatial maps for glassy systems.^{12,25,45–47} In this particular case, indeed it is a suitable choice to place the RS in the initial quenched configuration to sample MH (as we used it for displaying “background” MH in Fig. 2 in the 1st row panels). For nucleation, however, case I (and case III-backward) does not work unfortunately due to the reasons mentioned above.

Other global quantities such as the average time-dependent atomic displacement (the mean square of atomic displacements with respect to the RS) (equivalent to the average atomic displacements with respect to the reference atomic positions) are also calculated, where N is the number of particles, in order to monitor the time development of d̄(t). The d̄(t) could be a useful indicator of phase development during phase transitions, e.g. a sudden drop in d̄(t) indicates the presence of crystal growth,¹² see Fig. 4(j).

D. The definition of the quasi-liquid state in deep quenching

The QLS is a specific state of undercooled liquid (UL) when incubation time of nucleation is anomalously short and other states to be considered in UL such as vitrification or spinodal decomposition as well as ordinary liquid behavior can clearly be excluded. Vitrification induced glassy systems exhibit the split of the 2nd peak in the radial density function g(r). No such splitting is seen in undercooled liquid iron above the glass transition temperature T_g ≈ 900 K⁵⁸ (see Fig. S3(c), ESI‡). A spinodal-like pattern in this pure metal system is difficult to identify and apparent phase separation is observed, which we find in deep quenching at 700 K. Using filtered coordination maps we are able characterize spinodals at 700 K (see Fig. 2(p)). In this case a network-like “skeleton” weaves through the entire volume. No such features (amorphous phase, glass, and spinodal) are seen, however, above 900 K in the QLS. The incubation time for nucleation increases abruptly above 1250 K, and therefore we argue that the ULI turns into a liquid at around the critical temperature of T_c ≈ 1300 K. The specific state of the QLS exists in the narrow regime of 900–1250 K.

According to our understanding the QLS can be described by local hidden order (LHO), by a certain amount of spatial and DH (MH) and by growing long range correlations (LRCs), which manisfests e.g. itself in the formation of ramified atomic clusters in network-like cross-linked nanostructures.³⁴ Moreover we find that the PNCs are surrounded by satellite small hidden clusters (HCs) directly not always bound to the PNC cluster core. These small HCs are surprisingly immobile, which could be due to some hidden cage effect not fully understood yet. The “cage effect” describes the transient dynamical confinement of atomic clusters or molecule by its neighbouring atoms.^13,51 We find that the immobility of these loosely bound satellite HCs robustly persists during the QLS. We also argue that the prenucleation state can be explained by a relatively flat potential energy surface (PES) in supercooled molten iron. This is supported by our calculated potential energy curves shown in ESI,‡ Fig. S9(b), which display a nearly flat PES before the phase transition.

The QLS is also similar in many respects to simple liquids. Standard approaches and metrics such as e.g. radial distribution functions (RDF or g(r)), Voronoi's methods or calculations based on spherical harmonics (bond-orientation order, e.g. q̄₆) fail to clearly differentiate between the QSL and liquid states, see Fig. 6(a) and (b). It should also be checked whether the appearance of the QLS is more widespread and for instance it can also play a role in liquid intermediate phases that occur in certain solid-to-solid phase transitions.^19,20,38

One important aspect, perhaps overlooked until now, is that the role of medium to long range correlations (MROs and beyond) in phase development becomes increasingly important in the QLS.^12,52 In particular, local quasi-ordered nanoscale atomic clusters occur in the QLS, which show unexpected localization and can be described by a highly ramified outer region. During the course of the incubation period nanoscale atomic clusters (small PNCs) thermally aggregate forming the early-stage nearly immobile germs. Therefore, once a germ is formed, it becomes nearly localized besides the vibrations around the equilibrium positions of the constituent atoms within a liquid environment. We define germs as nanoscale nearly localized loosely bound ramified atomic clusters embedded in their liquid environment. These germs below T_c ≈ 1300 K grow rapidly into larger PNCs, which are decorated by partial stacking and packing order of layers together with mixed packing of various phases as well as with a considerable amount of defects such as stacking faults, vacancies and/or various misorientations. Germs can be displayed and highlighted by reduced coordination in dc-filtered maps (see PNCs in the 2nd row figures in Fig. 3, 4(g), 5(e)–(g)). This is because in d-filtered d-maps we are able to detect PNCs and it is possible to highlight the increased coordination between the subdiffusive atoms in the hidden cluster core. In d-filtered d-maps only those atoms are shown, which moved less than a threshold value (e.g. a ≈ 2.5 Å) with respect to the reference state. a is in the range of the maximum amplitude of vibrations in the nearly equilibrium positions. In principle the localized atoms form a disordered network-like “frozen” frame within the quasi-liquid system, which is especially visible below glass transition temperature (see Fig. 2(o)). This frame rapidly adsorbs further atoms and/or small mobile PNCs from the liquid environment and undergoes an ultrafast phase evolution towards nucleation. The further details of this process remain, however, somewhat unclear and go beyond the scope of the present work.

Structural snalysis: the atomic configurations obtained from simulations were analyzed by the OVITO code.⁴⁹ VoroTop (Voronoi)³⁹ and PTM (polyhedral template matching)⁴⁸ analyses were used to identify the bcc and other atom types.³⁹ The displacement of each atoms (d_i(t) where i is the atomic index, t is the instantaneous time) with respect to the corresponding reference configurations (melting: initial liquid and solidification: the final crystal) were calculated within the OVITO code. As far as solidification is concerned d_i(t) is the distance what atom i yet to be displaced to take its final position in the bcc crystal at t instantaneous time. The appropriate indexing (sorting) of atoms during MD simulation was ensured by the specific “dump_modify” command in LAMMPS. The local averaged bond order parameter q̄₆ based on spherical harmonics was also used to describe ordering.⁴⁰

Multistage filtering and the unfolding of PNCs. The main purpose of multistage filtering is to extract hidden PNCs seen in d-maps (e.g. the structure corresponding to the blue spot in Fig. 2(f)–(h)). Coordination maps display the PNCs in more detail (see e.g.Fig. 1(d) and 5(b)). The enhanced coordination (red and yellow spots) allows the appropriate selection of PNC atoms using a coordination filter (c-filter). In order to unfold the hidden clusters of pre-nucleation (PNC) embedded in the quasi-liquid environment a multistage filtering process based on displacement and coordination filtering (dc-filter) must be applied. A 2 or 3-step filtering process is required for enhanced visibility of localized hidden clusters. The basic physical rules for extracting PNCs are the following: it is a reasonable assumption based on Fig. 1–4 that PNCs are robustly localized (immobile) and strongly coordinated with other localized atoms (with each other) and much less with liquid (mobile) atoms. These two main features allow us to effectively select those atoms which belong to the immobile PNCs. The rest of the system can be taken as a “wetting” mobile (liquid) environment of the PNC in the QLS.

First step is d-filtering: (quasi)localized particles are selected in this way, which are not displaced with respect to the final state after the QLS. The filtering cut-off parameter of d_loc ≈ 2.5 Å is proved to be a suitable choice (this is roughly proportional to the Lindemann parameter of melting). However, other choices of d_loc ≤ 8 Å could also be effective when combined with a sufficient c-filter. Particles with atomic displacements of d_i > 2.5 Å can be taken as liquid-like atoms, which hop at least once or more from their original quenched disordered position. The next nearest neighbor (NNN) coordination map (CM) applied for the d-filtered system (DFS) shows already a highly coordinated core of the PNC (see the 2nd row in Fig. S1(c), ESI‡). We introduce the phrase of reduced coordination (RC) for NNN coordinations if calculated for d-filtered systems. In this case inter-localized atomic coordination is calculated. In particular, d-filtering reduces the number of liquid particles and therefore RC provides artificially smaller coordination mostly outside the cluster core (reduced coordination number, N_RC). RC can be a powerful tool for highlighting otherwise not or only weakly visible localized hidden cluster cores and their ramified neighborhood. We also use the phrase virtual coordination (VC) when the coordination cut-off is r_c ≫ d_loc = 2.5 Å. Using a much longer-cut-off (e.g. r_c = 6 Å or even longer) at coordination one can take into account long range effects up to e.g. the 2nd, 3rd or more nearest neighbors. Our experience shows that VC further highlights the visibility of PNCs (see the 3rd row panels of ESI,‡ S1(a)–(c)). The second step is c-filtering: coordination filtering (c-filter) is applied in the next step to the previously DFS using the RC or VC calculated for the DFS (see Fig. S5(d), ESI‡). One can play with the “strength” of the applied c-filter. The cut-off in the atomic coordination number (n_c) is another adjustable parameter in unfolding PNCs.

In the 2nd row panels of the ESI,‡ Fig. S1, the filtering process is shown with d_loc ≈ 8 Å. In this particular case a much larger number of particles are kept including liquid-like atoms. Roughly more than a half of the particles is filtered out in this way. Then applying a c-filter together with an additional radial filter a nearly spherical-like PNC is found. Radial filtering selects those atoms that are within the sphere around the center of the PNC (the center is taken from sliced CMs; the sphere radius is ∼50 Å). This process effectively allows us to highlight various localized quasi-ordered hidden structures otherwise not visible. The adjustable parameters in the filtering process (d_loc,r_c,n_c) allow us to extract the otherwise hidden “building blocks” of pre-nucleation. Although the different setup of the parameters leads to somewhat different PNCs (see Fig. S1, ESI‡), the reasonable choice of the parameters gives a converging result. Note e.g. that starting with d_loc ≈ 8 Å a very similar PNC is unfolded at end of the process compared to that of the process with d_loc ≈ 2.5 Å. The process is only weakly sensitive compared to the choice of d_loc. However, for d_loc > 8 Å, the c-filter looses its effectiveness, because the average 1st neighbor coordination of the particles becomes homogeneous (featureless), as shown in the full system (see Fig. S1(a), ESI‡). Therefore, at least a minimal d-filter is required to highlight localized or weakly mobile particles.

In the 3rd row panels of the ESI,‡ Fig. S1(d)–(g) the filtering process is compared for d_loc ≈ 3 Å and d_loc ≈ 8 Å without applying radial filtering. The process ends up finally with a very similar irregulary shaped PNC as shown in the 2nd row panel (f). Therefore we find that although different filtering conditions lead to somewhat different morphological parameters of PNCs (shape, roughness of the surface, etc.), the basic features remain very similar (comparable size, irregular shape, rough ramified surface, highly coordinated core, and localized immobile particles).

For displaying PNCs the polyhedral surface mesh around atomic clusters is shown (the geometric surface reconstruction method has been employed with the Gaussian density method together with an additional fine smoothing procedure).^49,50

Author contributions

P. S. designed the theoretical model, performed the simulations and wrote the manuscript.

Data availability

The data that support the findings of this study and custom gnuplot codes for image processing of d-maps as well as the scripts for LAMMPS MD simulations or OVITO settings are available from the corresponding author upon request.

Conflicts of interest

The author declares no competing interests.

Acknowledgements

The author acknowledges many helpful discussions with L. Gránásy, M. Tegze and T. Pusztai. This work is supported by the National Science Foundation of Hungary grant no. KKP-126749, KKP-138144, K-134258, and FK-142985. The simulations were performed on the GPU cluster of Institute ELKH-Wigner as well as on the National HPC resources of KIFÜ. In Memoriam L. Gránásy.

References

1. L. Zhong, J. Wang, H. Sheng, Z. Zhang and S. X. Mao, Nature, 2014, 512, 177–180.
2. T. Kawasaki and H. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14036–14041.
3. Q. Gao, J. Ai, S. Tang, M. Li, Y. Chen, J. Huang, H. Tong, L. Xu, L. Xu, H. Tanaka and P. Tan, Nat. Mater., 2021, 20, 1431–1439.
4. G. Sun, J. Xu and P. Harrowell, Nat. Mater., 2018, 17, 881–886.
5. J. Baumgartner, A. Dey and P. Bomans, et al. , Nat. Mater., 2013, 12, 310–314.
6. E. M. Pouget, P. H. H. Bomans, J. A. C. M. Goos, P. M. Frederik, G. de With and N. A. J. M. Sommerdijk, Science, 2009, 323, 1455–1458.
7. D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819–1822.
8. D. Gebauer and S. E. Wolf, J. Am. Chem. Soc., 2019, 141, 4490.
9. D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348–2371.
10. J. Anwar, S. Khan and L. Lindfors, Angew. Chem., Int. Ed., 2015, 54, 14681.
11. G. D. Leines, R. Drautz and J. Rogal, J. Chem. Phys., 2017, 146, 154702.
12. L. Berthier and G. Biroli, Rev. Mod. Phys., 2011, 3, 587–633.
13. C. P. Royall and S. R. Williams, Phys. Rep., 2015, 560, 1–75.
14. J. J. De Yoreo and N. A. J. M. Sommerdijk, Nat. Rev. Mater., 2016, 1, 16035–16044.
15. H. J. Schöpe, G. Bryant and W. van Megen, Phys. Rev. Lett., 2006, 96, 175701–175705.
16. Y. Shibuta, S. Sakane, E. Miyoshi, S. Okita, T. Takaki and M. Ohno, Nat. Commun., 2017, 8, 10–19.
17. P. Zhang, J. J. Maldonis, Z. Liu, J. Schroers and P. M. Voyles, Nat. Commun., 2018, 9, 1129–1136.
18. P. G. Vekilov, Nanoscale, 2010, 2, 2346–2357.
19. Y. Peng, F. Wang, Z. Wang, A. M. Alsaved, Z. Zhang, A. G. Yodh and Y. Han, Nat. Mater., 2015, 14, 101–108.
20. S. Pogatscher, D. Leutenegger, J. E. K. Schawe, P. J. Uggowitzer and J. F. Löffer, Nat. Commun., 2016, 7, 1113–1119.
21. J. Zhou, Y. Yang and Y. Yang, et al. , Nature, 2019, 570, 500–503.
22. L. Sun, Y.-X. Zhou, X.-D. Wang, Y.-H. Chen, V. L. Deringer, R. Mazzarello and W. Zhang, npj Comput. Mater., 2021, 7, 29–37.
23. Y. Shibuta, K. Oguchi, T. Takaki and M. Ohno, Sci. Rep., 2015, 5, 13534–13543.
24. Y. Shibuta, K. Oguchi and M. Ohno, Scr. Mater., 2014, 20, 86–95.
25. Q. Zhang, J. Wang, S. Tang, Y. Wang, J. Li, W. Zhou and Z. Wang, Phys. Chem. Chem. Phys., 2018, 21, 4122–4135.
26. A. Mahata, T. Mukhopadhyay and M. A. Zaeem, J. Mater. Sci. Technol., 2022, 106, 77–85.
27. G. I. Tóth, T. Pusztai, G. Tegze, G. Tóth and L. Gránásy, Phys. Rev. Lett., 2011, 107, 175702.
28. N. Loh, S. Se and M. Bosman, et al. , Nat. Chem., 2017, 9, 77–82.
29. K. Z. Takahashi, T. Aoyagi and J. Fukuda, Nat. Commun., 2021, 12, 5278–5287.
30. J. De Yoreo, Nat. Mater., 2013, 12, 284–285.
31. J. De Yoreo, in Crystallization via Nonclassical Pathways: Nucleation, Assembly, Observation & Application, ed. X. Zhang, ACS Publications, 2020, vol. 1, pp. 1–17.
32. A. F. Wallace, et al. , Science, 2013, 341, 885–889.
33. M. H. Nielsen, S. Aloni and J. J. De Yoreo, Science, 2014, 345, 1158–1162.
34. R. Demichelis, P. Raiteri and J. Gale, et al. , Nat. Commun., 2011, 2, 590–598.
35. P. G. Vekilov, Nucleation, Cryst. Growth Des., 2010, 10, 5007–5019.
36. G. C. Sosso, J. Chen, S. J. Cox, M. Fitzner, P. Pedevilla, A. Zen and A. Michaelides, Chem. Rev., 2016, 116, 7078–7116.
37. L. Fei, X. Gan, S. M. Ng, H. Wang, M. Xu, W. Lu, Y. Zhou, C. W. Leung, C.-L. Mak and Y. Wang, ACS Nano, 2019, 13, 688–695.
38. X. Fu, X. D. Wang and B. Zhao, et al. , Nat. Mater., 2022, 21, 290–296.
39. E. A. Lazar, Modell. Simul. Mater. Sci. Eng., 2018, 26, 015011.
40. W. Lechner and C. Dellago, J. Chem. Phys., 2008, 129, 114707.
41. H. Tanaka, H. Tong, R. Shi and J. Russo, Nat. Rev. Phys., 2019, 1, 333–339.
42. A. T. Dinsdale, Calphad, 1991, 15, 317–322.
43. G. D. Leines, A. Michaelides and J. Rogal, Faraday Discuss., 2022, 235, 406–410.
44. P. Tan, N. Xu and L. Xu, Nat. Phys., 2014, 10, 73–80.
45. G. C. Sosso, J. Colombo, J. Behler, E. D. Gado and M. Bernasconi, J. Phys. Chem. B, 2014, 118, 13621–13628.
46. A. Widmer-Cooper and P. Harowell, Phys. Rev. Lett., 2006, 96, 185701.
47. K. H. Pham and T. T. Giap, RSC Adv., 2021, 11, 32435–32440.
48. P. M. Larsen, S. Schmidt and J. Schiotz, Modell. Simul. Mater. Sci. Eng., 2016, 24, 055007.
49. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012–015017.
50. A. Stukowski, JOM, 2014, 66, 399–407.
51. W. van Megen and H. J. Schöpe, J. Chem. Phys., 2017, 146, 104503.
52. T. Kawasaki, T. Araki and H. Tanaka, Phys. Rev. Lett., 2007, 99, 215701.
53. B. O’Malley and I. Snook, J. Chem. Phys., 2005, 123, 054511.
54. A. K. Gangopadhyay and K. F. Kelton, J. Non-Cryst. Solids: X, 2019, 2, 100016.
55. R. Alert, P. Tierno and J. Casademunt, Nat. Commun., 2016, 7, 13067–13075.
56. S. J. Plimpton and A. P. Thompson, MRS Bull., 2012, 37, 513–523.
57. S. Nosé, J. Chem. Phys., 1984, 81, 511–515; W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1705.
58. W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134103.
59. G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4185.
60. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
61. M. E. Tuckerman, J. Alejandre, R. Lopez-Rendon, A. L. Jochim and G. J. Martyna, J. Phys. A: Math. Gen., 2006, 39, 5629–5633.
62. P. Süle, M. Szendrö, G. Z. Magda, C. Hwang and L. Tapasztó, Nano Lett., 2015, 15, 8295–8299.
63. G. Dobrik, P. Nemes-Incze, B. Majérus, P. Süle, P. Vancsó, G. Piszter, M. Menyhárd, B. Kalas, P. Petrik, L. Henrard and L. Tapasztó, Nat. Nanotechnol., 2022, 17, 61–66.
64. P. Süle, M. Szendrö, C. Hwang and L. Tapasztó, Carbon, 2014, 77, 1082–1089.
65. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
66. G. Simonelli, R. Pasianot and E. J. Savino, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 727–734.
67. M. S. Daw, S. M. Foiles and M. I. Baskes, Mater. Sci. Rep., 1993, 9, 251–285.
68. M. I. Mendelev, S. Han, D. J. Srolovitz, G. J. Ackland, D. Y. Sun and M. Asta, Philos. Mag., 2003, 83, 3977–3987.
69. G. J. Ackland, M. I. Mendelev, D. J. Srolovitz, S. Han and A. V. Barashev, J. Phys.: Condens. Matter, 2004, 16, S2629–S2635.
70. J. Liu and H. B. Dong, IOP Conf. Ser.: Mater. Sci. Eng., 2012, 33, 012113.
71. J. Liu, R. L. Davidchack and H. B. Dong, Comput. Mater. Sci., 2013, 74, 92–99.
72. Q. Zhang, J. Wang, S. Tang, Y. Wang, J. Li, W. Zhou and Z. Wang, Phys. Chem. Chem. Phys., 2019, 21, 4122–4128.
73. E. Asadi, M. A. Zaeem, S. Nouranian and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 024105.
74. B.-J. Lee and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8564–8573; B.-J. Lee, M. I. Baskes, H. Kim and Y. K. Cho, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 184102.
75. S. V. Starikov, D. E. Smimova, T. Pradhan and Y. V. Lysogororskiy, Phys. Rev. Mater., 2021, 5, 06307–06314.

---

Footnotes

† The author dedicates this work in memoriam of L. Gránásy.

‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02526a

---