Simulation of the non-adiabatic dynamics of an enone-Lewis acid complex in an explicit solvent

Abstract

Unlocking the full potential of Lewis acid catalysis for photochemical transformations requires a comprehensive understanding of the ultrafast dynamics of substrate-Lewis acid complexes. In a previous article [Peschel et al., Angew. Chem. Int. Ed., 2021, 60, 10155], time-resolved spectroscopy supported by static calculations revealed that the Lewis acid remains attached during the relaxation of the model complex cyclohexenone-BF₃. In contrast to the experimental observation, surface-hopping dynamics in the gas phase predicted ultrafast heterolytic dissociation. We attributed the discrepancy to missing solvent interactions. Thus, in this work, we present an interface between the SHARC and FermiONs++ program packages, which enables us to investigate the ultrafast dynamics of cyclohexenone-BF₃ in an explicit solvent environment. Our simulations demonstrate that the solvent prevents the dissociation of the complex, leading to an intriguing dissociation–reassociation mechanism. Comparing the dynamics with and without triplet states highlights their role in the relaxation process and shows that the Lewis acid inhibits intersystem crossing. These findings provide a clear picture of the relaxation process, which may aid in designing future Lewis acid catalysts for photochemical applications. They underscore that an explicit solvent model is required to describe relaxation processes in weakly bound states, as energy transfer to the solvent is crucial for the system to reach its minimum geometries.

---

1 Introduction

In the last decades, trajectory surface hopping (TSH) has become a powerful and widely applied tool to investigate non-adiabatic ultrafast relaxation processes of photoexcited molecules.^1–5 However, most of these investigations are performed in the gas phase, even though the investigated processes take place in solution. Implicit solvent models, which are frequently used to describe the influence of a solvent on the electronic structure, cannot capture the non-equilibrium forces exerted on the molecule by the solvent cage. In contrast, explicit solvent models correctly describe these effects and are thus becoming increasingly common as an ingredient for a successful TSH simulation.^6–14 We use this methodology to systematically investigate the ultrafast dynamics of the enone-Lewis acid complex cyclohex-2-enone-BF₃ and show how confinement by the solvent cage leads to qualitatively different relaxation behavior compared to the gas phase.

We focus on the photorelaxation of enone-Lewis acid complexes because chiral Lewis acids enable enantioselective [2+2] photocycloadditions of 2-enones.^15–21 Cyclohex-2-enone-BF₃ serves as a small, achiral model system.

The excited state structure and dynamics of free 2-enones are well explored and a consistent picture of a pathway leading to a [2+2] photocycloaddition product has emerged.^22–26 2-Enones can be excited either in the strong S₂ band (ππ*, ≈225 nm) or in the weak S₁ band (nπ*, ≈330 nm). Usually, in synthetic applications, direct excitation into the weak S₁ (nπ*) is chosen to avoid side reactions. In this case, the dominant relaxation pathway is intersystem crossing (ISC) into the triplet states.^22,27 This occurs via a S₁ (nπ*) → T₂ (ππ*) → T₁ (ππ*) relaxation cascade. In the Franck–Condon (FC) region of the enone, the S₁ (nπ*) state is energetically close to the T₂ (ππ*). After facile ISC according to El-Sayed's rule,²⁸ the T₂ population passes within a few femtoseconds through a conical intersection (CoIn) with the T₁ state, still in the FC region. This passage occurs such that the ππ* character of the active state is preserved. The triplet state minimum is characterized by a 90° twist of the H–C=C–H dihedral and has a lifetime of 25 ns for cyclohexenone in cyclohexane.²⁹ The [2+2] photocycloaddition then occurs from this minimum via the formation of a 1,4-triplet biradical intermediate.²³

When the enone binds to the Lewis acid its excited states are shifted significantly. The ππ* states are redshifted due to an enhanced charge transfer to the carbonyl moiety caused by the electron-withdrawing effect of the Lewis acid. The nπ* states are blueshifted because the n orbital is lowered in energy by the formation of the dative bond. In 2,3-dihydropyridinones and coumarins, this leads to an inversion of the state ordering such that the excited state dynamics in the singlet manifold are solely determined by the ππ* state.^30,31 However, in simple α,β-enones, such as cyclohexenone, the order of the states is not inverted. Instead, S₂ (ππ*) and S₁ (nπ*) are now close in energy, and vibrational intensity borrowing can be observed, such that S₁ (nπ*) increases significantly in brightness.

Previously, some of us investigated the ultrafast dynamics of the cyclohexenone-BF₃ complex from a theoretical and experimental perspective.³² However, disagreements between experiment and theory prevailed. When cyclohexenone-BF₃ is excited at 285 nm the S₁ (nπ*) state is populated. Starting there, static calculations indicated two possible ultrafast processes; (1) the dissociation of the BF₃ group, which occurs in the S₁ (nπ*) state due to a weakening of the coordinative O–B bond; (2) ISC into the T₁ (ππ*) state, where the BF₃ group is more strongly bound and a twist of the H–C=C–H dihedral is observed. Dynamic TSH simulations in the gas phase with only singlet states showed (1) as the only significant pathway. However, neither time-resolved spectra nor synthetic studies showed direct evidence for this dissociation. Instead, strong evidence for ISC into the triplet states and pathway (2) was presented experimentally and supported by static calculations of transient spectra at critical geometries. Only relaxation towards the T₁ (ππ*) minimum would allow follow-up reactions, like the observed [2+2] cycloaddition, and would explain the enantioselectivity of this reaction in complexes with chiral Lewis acids.¹⁹ The measured transient absorption signal after a few picoseconds matched the intact complex in the T₁ (ππ*) state.

In the free enone, for the ISC process, a time constant of 746 fs was observed in TSH simulations. Although there is evidence that this process is faster in complexes with Lewis acids that contain heavy atoms,³⁰ there is no reason to expect such a speedup in cyclohexenone-BF₃. Thus, dissociation of the complex in S₁, occurring on a timescale of fewer than 200 fs, is expected to be faster than ISC in the gas phase. A reasonable mechanism explaining a slowdown of the dissociation would be a caging effect of the surrounding solvent. This would allow ISC to compete with dissociation in solution.

In our present work, we focus on resolving these discrepancies between experiment and theory. Therefore, we perform TSH simulations of the cyclohexenone-BF₃ complex in an explicit solvent environment, which show that caging effects slow down the dissociation in the singlet states significantly and even prevent it in most cases. If triplet states are included in the simulation this leads to ISC in the intact complex and relaxation to the T₁ (ππ*) minimum, the starting point for follow-up reactions such as [2+2] photocycloadditions. These simulations are performed with a novel interface between the SHARC^33–36 and FermiONs++^37–39 programs, that enables rapid non-adiabatic quantum mechanics/molecular mechanics (QM/MM) simulations with large QM regions.

2 Methods

2.1 The FermiONs++–SHARC interface

Today, quite a few program interfaces enable TSH simulations with QM/MM gradients.^40–42 Some of the existing interfaces of the SHARC program suite^33–36 also support QM/MM calculations and have been used to study a variety of photodynamical processes.^11,43,44 SHARC has also been interfaced with the COBRAMM package⁴⁵ to allow the automated simulation of time-resolved transient absorption spectra.^46,47 In this work, we want to leverage the speed of the FermiONs++ ab initio program package for the simulation of the QM region.^37–39 The MM part of the calculation is performed internally by FermiONs++ via the OpenMM library.⁴⁸

Both SHARC and FermiONs++ provide a Python3-based interface (PySHARC,⁴⁹ PyFermiONs). Thus, file-based communication between SHARC and FermiONs++ can be avoided. However, since PySHARC does not currently offer all the features of conventional SHARC, the interface can default to file-based communication, if necessary. In both cases, FermiONs++ is run in a server-like fashion, which avoids setting up an entirely new quantum chemistry calculation at each simulation time step and allows us to transfer relevant information between successive time steps. Currently, the interface only supports calculations using the Tamm–Dancoff approximation (TDA). However, expansion to orbital-optimized methods is planned. To perform the local diabatization implemented in SHARC, overlaps between the different TDA states are required. These are calculated highly efficiently by the freely available cis_nto program which expands the configuration interaction singles (CIS)-like⁵⁰ for each state in terms of excitations between natural transition orbitals.^51,52 This efficient expansion avoids truncation to the most significant contributing coefficients, which is often necessary with other approaches. However, transferring TDA coefficients between the SHARC–FermiONs++ interface and the cis_nto program still relies on writing the coefficients to files on disk. In total, the following properties can be requested via the SHARC–FermiONs++ interface: energies, gradients, state overlaps (via cis_nto), state dipole moments, transition dipole moments, and spin–orbit couplings.

2.2 Choice of quantum-chemical method

While a short-time simulation of cyclohexenone-BF₃ using XMS-CASPT2⁵³/cc-pVDZ⁵⁴ is possible,³² the extended simulation times necessary to equilibrate the QM/MM system and to reach the triplet states after excitation make an XMS-CASPT2 simulation of the dynamics in solution not feasible. Because the primary ultrafast processes in cyclohexenone-BF₃ do not involve relaxation through a CoIn with the ground state or homolytic dissociation processes, they are described by time-dependent density functional theory (TDDFT) correctly and cost-effectively.

Simulating the singlet state dynamics of cyclohexenone-BF₃ in solution is a complex task. To adequately describe the slowdown of the dissociation, multiple shells of the solvent dichloromethane (DCM) need to be included in the simulation, which amounts to several hundred solvent molecules. Obtaining the excited state gradients for such an extensive system using a QM model is prohibitively expensive. Since all excitations are localized on the chromophore, a description of the solvent by classical MM is sufficient. Hence, a QM/MM approach is chosen, where the cyclohexenone-BF₃ complex constitutes the central QM region and the DCM shells form the MM region around it. The OPLS/AA force field was chosen to describe the MM region, which is specifically designed for the simulation of organic liquids and describes the properties of DCM reasonably well.^55–57 The use of this fixed charge force field neglects the role of rapid electronic polarization of the DCM solvent due to the changes in the electronic structure of the cyclohexenone-BF₃ complex upon excitation.^58,59 In future studies, such an effect could be included through polarizable force fields, which have recently been successfully employed in non-adiabatic simulations.^60,61 A suitable functional for the TDDFT calculations was chosen, reproducing benchmark XMS-CASPT2/cc-pVQZ S₁ excited state gradients at selected geometries encountered during the simulation. After an extensive screening including all hybrid functional available in LibXC,⁶² we chose the functional PBE-MOL0,⁶³ a non-empirically improved version of PBE0 for molecular properties with the def2-TZVP basis set.⁶⁴ Apart from S₁ gradients it also performed well for the S₀S₁ and S₁S₂ energy gaps. Likely, this good performance of the global hybrid PBE-MOL0 is due to the charge-local nature of the S₁ (nπ*) state. For properties of higher lying singlet states, such as the S₂ (ππ*) gradients, range-seperated hybrids would be more suitable, as especially their optimally tuned variants have been successful in this regard.^65,66 A detailed explanation of the benchmarking and evaluation procedure can be found in the ESI.†

2.3 System setup and simulation parameters

Two equilibration steps were performed to set up the simulations. Firstly, a classical molecular dynamics (MD) simulation with the OPLS/AA force field was carried out, followed by ab initio ground state MD at the PBE-MOL0/def2-TZVP//OPLS/AA QM/MM level. The first step aims to pre-equilibrate the solvent, such that long equilibration times in the ab initio MD can be avoided. The second step leads to full equilibration. No parameters are available for the interactions of BF₃ with cyclohexenone in OPLS/AA. Thus, in the first step of the equilibration, cyclohex-2-enone-BF₃ was replaced by the isoelectronic N-(trifluoromethyl)cyclohex-2-enimine for which MM parameters were obtained using LigParGen.⁶⁷ The molecule was placed in a cubic box with 511 molecules of DCM and equilibrated at 298 K and 1 atm. Then, the system was propagated for 50 ns in an NPT ensemble. From this simulation, 200 snapshots were taken. The procedure was repeated for both conformers of cyclohexenone-BF₃ (which are nearly isoenergetic, see Scheme 1 in ref. 32) for a total of 400 snapshots.

For the second step, the 268 DCM molecules closest to the center mass of cyclohexenone-BF₃ were retained, and the others were discarded. For each snapshot, the system was then confined inside a sphere with a radius of 20 Å, which keeps the density approximately equal to the equilibrium density of the classical MD simulation. C1 of cyclohex-2-enone-BF₃ was kept approximately stationary at its initial position by a weak harmonic constraint to keep the molecule of interest close to the center of the confining sphere. Then, ab initio ground state MD simulations were performed for 5 ps in an NVT ensemble to equilibrate the system. An exemplary result for one of the snapshots is shown in Fig. 1. The cyclohex-2-enone-BF₃ complex can be seen in the center, surrounded by multiple shells of DCM.

Fig. 1 Equilibrated cyclohexenone-BF₃ complex in DCM.

Transition dipole moments for the lowest three excited states were calculated for each final geometry of the previous step. Systems were randomly transferred to the excited state, with the total probability for each state proportional to its total oscillator strength in the range 0 eV to 5 eV, which corresponds to the red edge of the absorption spectrum. This resulted in 60 trajectories in S₁ and no trajectories in other excited states. Then, QM/MM TSH simulations were run for 1 ps with 4 singlet states only and for 2 ps including 4 additional triplet states. As a reference, 0.5 ps long gas-phase TSH simulations were also run for the same initial conditions including only singlet states. In all cases, an integration time-step of 0.5 fs was chosen and an energy-based decoherence correction was employed.⁶⁸

3 Results and discussion

We compare the excited state dynamics of the cyclohexenone-BF₃ complex in the gas phase and in DCM solution. In solution, we compare the dynamics including triplet states with a hypothetical case where ISC to the triplet states is disabled.

We do not observe non-adiabatic transitions in simulations without triplet states, neither with nor without a solvent. If ISC is included, transitions to the triplet manifold are observed (Fig. 2a). All dynamics occur in the lowest three excited states, the S₁ which is of nπ* character, and the T₁ and T₂ states which are of ππ* and nπ* character, respectively, but change character depending on the geometry of the molecule (Fig. 2b and c).

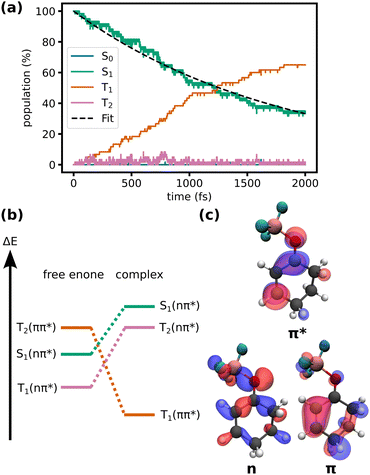Fig. 2 (a) Energy-adiabatic, spin-diabatic populations during the TSH simulations of the complex in DCM including triplet states. Exponential fit of the S₁ population (τ = 1.8 ± 0.3 ps, error determined by bootstrapping⁶⁹). (b) Qualitative changes in energy of the relevant states upon complexation (adapted from ref. 32). (c) Natural transition orbitals characterizing the states (isovalue: 0.05).

During the first picosecond, the population flux from the singlet to the triplet manifold is approximately constant. After the first picosecond, the population flux decreases. At the end of the simulation (2 ps), 40 out of 60 trajectories have relaxed to the triplet states. While the relaxation can be roughly described by a single exponential (τ = 1.8 ± 0.3 ps, as determined by bootstrapping⁶⁹), small deviations from monoexponential behavior at the beginning of the simulation might hint at faster processes that modulate the ISC rate. In Fig. 2a, a small, but near-constant population in T₂ is apparent. This shows, that the relaxation mechanism occurs in large parts analogously to the uncomplexed cyclohexenone (S₁ (nπ*) → T₂ → T₁ (ππ*) relaxation cascade with a T₂ lifetime of only a few femtoseconds). However, at the FC point of the complex, the energetic alignment of the states in the complex is less favorable compared to the free enone (Fig. 2b). Complexation by the Lewis acid increases the energy gap between the nπ* singlet and ππ* triplet and slightly decreases the energy gap between nπ* singlet and nπ* triplet. Crossing between the first pair of states is favored while crossing between the second pair of states is disfavoured according to El-Sayed's rule.²⁸ Thus, ISC is inhibited in the FC region of the complex. The energy gap changes as the complex relaxes in S₁, a process associated with an increase of the O–B bond length (vide infra). This suggests, that the ISC rate is coupled to the O–B bond length, which might explain slight deviations from an exponential decay in Fig. 2a at the beginning of the simulation. Overall, we can roughly compare the slower ISC rate of the complex in solution (1.8 ps) to the faster rate for the free enone in the gas phase (0.75 ps)³² although some of that difference might be due to different methodologies.

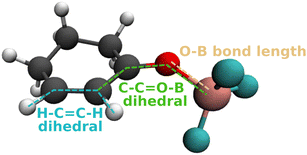
We monitor several geometric parameters throughout the dynamics (Fig. 3). In addition to the O–B bond length, we include the C–C=O–B twist angle, since the minima of the S₁ state are characterized by a rotation of the BF₃ above or below the plane of the cyclohexene ring. As a third parameter, we include the H–C=C–H dihedral, since a twist of the C=C double bond indicates relaxation into the T₁ (ππ*) minima.

Fig. 3 Internal coordinates monitored throughout the trajectories.

The time evolution of these parameters is depicted in Fig. 4. As evident in Fig. 4a, there is rapid, irreversible, heterolytic dissociation of the complex in the gas phase on a timescale of 100–200 fs. The reason for this dissociation is the removal of an electron from the n orbital of the oxygen, to which the BF₃ binds, by the excitation. This weakens the bond between the Lewis acid and the substrate. At the minimum structures of the S₁ state this bond is elongated and the BF₃ group is situated above or below the molecular plane. The excess energy of the complex is too high to allow for relaxation into these shallow minima. Accordingly, the C–C=O–B dihedral, shown in Fig. 4b, which starts at 0° or 180° (the two ground-state conformers of the complex), becomes nearly uniformly distributed during dissociation (Fig. 4b).

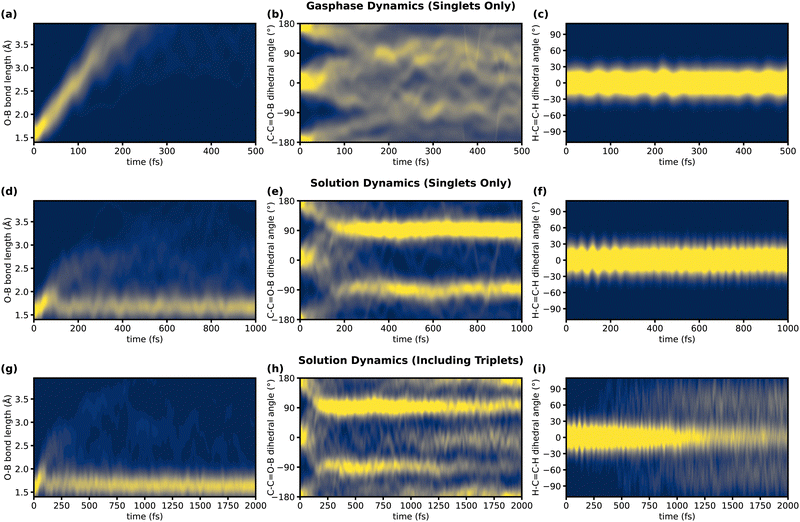Fig. 4 Evolution of three key geometric features during TSH simulations of the complex and comparison of these between a simulation in the gas phase (first row), a simulation in the explicit solvent including only singlet states (second row), and a simulation in the explicit solvent including triplet states (third row). The chosen geometric features (see Fig. 3) are the O–B bond length (first column, characteristic for dissociation), the C–C=O–B dihedral (second column, characteristic for relaxation in S₁), and the H–C=C–H dihedral (third column, characteristic for relaxation in T₁). A high probability that a certain trajectory displays a specific value for the given geometric parameter is indicated in yellow, and a low probability is indicated in blue. To obtain the probability densities displayed in these figures, the well-defined geometric parameters were broadened by Gaussians (σ = 0.15 Å for the first column, σ = 15° for the second and third column) and summed over all trajectories.

The situation is remarkably different in solution (Fig. 4d) where excess energy can be efficiently dissipated. After an initial elongation of the O–B bond, during the first 50 fs, the dissociating BF₃ collides with the solvent cage. This prevents full dissociation and leads to reassociation for 42 out of 60 trajectories within the next 50 fs. Whether a trajectory dissociates or reassociates depends on the configuration of the solvent cage. Seven of these dissociating trajectories reassociate during the remaining simulation time. After the complex has lost excess energy to the environment (between 100 and 250 fs), relaxation to the S₁ minima takes place. This can be seen in Fig. 4e, by a clustering of the C–C=O–B dihedral around 90° and −90°, indicating that BF₃ has moved above or below the molecular plane. This shows, how cooling by the solvent enables the system to relax into the shallow S₁ minima. In this configuration, the O–B bond is still elongated (1.7 Å) compared to the FC point (1.6 Å), due to the nπ* character of the S₁. However, this elongation is considerably smaller than in the optimized S₁ gas-phase minimum (1.9 Å), meaning that the complex is significantly compressed by the pressure of the surrounding solvent.

If triplet states are included in the dynamics, O–B bond length and C–C=O–B dihedral behave similarly at the beginning of the simulation. However, as trajectories cross into the triplet manifold (Fig. 2), two additional geometric changes are observed. As Fig. 4h shows, the population at a C–C=O–B dihedral of 90° and −90° decreases during the simulation if triplet states are included, shifting again towards 0° and 180°. Simultaneously, the H–C=C–H dihedral twists towards 90° and −90° (Fig. 4i). However, most trajectories do not reach the gas-phase T₁ minimum at 90° and −90°. This might be because of interactions with the solvent or large anharmonicity in the T₁ potential energy surface along the H–C=C–H twist. Structures from an exemplary trajectory are given in Fig. 5a, showing a full rotation of the C–C=O–B dihedral and the twist of the H–C=C–H dihedral. Fig. 5b shows the initial rise in dissociated and C–C=O–B twisted trajectories. As the trajectories cross into the triplet state, the C–C=O–B dihedral untwists, while the population with H–C=C–H twist increases.

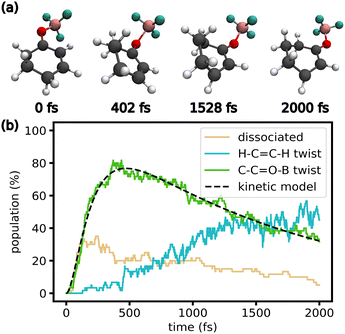Fig. 5 (a) Snapshots of an exemplary trajectory displaying the geometric changes discussed in the main text (solvent not shown for clarity). (b) Fraction of trajectories displaying certain key geometric features during the TSH simulations of the complex including triplet states. A trajectory is classified as dissociated with an O–B bond > 2 Å. A trajectory is classified as C–C=O–B twist if the dihedral is in [60°, 120°] or [−120°, −60°]. A trajectory is classified as H–C=C–H twist if the dihedral is not in [−45°, 45°]. Details on the kinetic model can be found in the ESI.†

We now compare simulated timescales to the experimentally observed ones. A time-resolved transient absorption experiment yielded three different time constants in a time window that might be observed in our simulation. A fast component (0.10–0.16 ps) that is associated with a large quantitative change in the visible part of the transient spectrum, a medium component (0.30–0.45 ps) and a slow component (4.4–4.8 ps), both of which are associated with smaller changes in the ultraviolet (UV) part of the transient spectrum, mainly a loss of absorption intensity.³²

We can confidently assign the fast component to the relaxation of the S₁ state in the solvent, including the fast dissociation reassociation dynamics and the twist of the C–C=O–B dihedral. Fitting a kinetic model to the data in Fig. 5 yields a time constant of 0.16 ps for the description of this twisting motion (see ESI† for details on the kinetic model). Interestingly, our calculated ISC time lies with 1.8 ps between the medium and slow experimental components. This might be due to shortcomings in our TDDFT-based model or due to difficulties disentangling the UV part of the transient absorption spectrum into components directly arising from ISC and components arising from vibrational cooling. Thus, we calculated the transient absorption spectrum at the TD-PBEmol0/def2-TZVP level (see ESI†). A quantitative analysis of this spectrum and the associated time scales would require a much larger number of trajectories and is inherently limited by the ability of TDDFT to describe the high-lying excited states involved in the transient absorption. Nevertheless, we observe a faster loss of intensity in the visible part (≈500 nm) and a slower loss of intensity in the UV (≈300 nm) which is in qualitative agreement with the experimental observations.³² While trajectories in S₁ show absorption peaks in both the visible and the UV, trajectories in T₁ show a broader, much weaker absorption with only a peak in the UV. Relaxation in S₁ leads to a strong reduction in intensity, ISC and the accompanying H–C=C–H twist lead to further loss of intensity and a slight redshift of the UV absorption. Thus, it is likely that the observed medium and slow components contain contributions from both ISC and vibrational cooling.

4 Conclusion

In summary, we have performed QM/MM TSH of cyclohex-2-enone-BF₃ in DCM solution using a new interface between the SHARC and FermiONs++ program packages. By benchmarking against XMS-CASPT2/cc-pVQZ gradients, a TDDFT functional was found that is well suited for the excited state dynamics. The simulations revealed that the fast heterolytic dissociation, occurring in the gas phase, is prevented by the solvent cage. Instead, vibrational cooling leads to the population of shallow minima in the S₁ state, where the BF₃ group lies above and below the molecular plane. This rearrangement occurs with a time constant of 0.16 ps matching a previously experimentally observed relaxation time. From there, ISC into the triplet states and relaxation into the T₁ (ππ*) minima occurs with a time constant of 1.8 ps, the state which is responsible for the further photoreactivity of the complex. This is accompanied by a motion of the BF₃ group back into the molecular plane and a twist of the H–C=C–H dihedral. We observe that the presence of the Lewis acid hinders ISC because it increases the energy gap for the El-Sayed-allowed transition.

These findings suggest two points that should be kept in mind when designing future Lewis acid catalysts for photochemical applications. (1) Care must be taken that spectral shifts induced by the Lewis acid are not too large, otherwise ISC might become unfavorable, especially if the Lewis acid does not contain heavy atoms.³⁰ This might favor side reactions on the singlet surface. (2) If the lowest singlet state of the complex is of nπ* character, it should be kept in mind that excitation will temporarily weaken the bond to the catalyst and might lead to a rotation of the substrate at the catalytic site. This might lead to reduced enantioselectivity for reactions catalyzed by chiral Lewis acids. Thus, these catalysts should be designed to prevent dissociation or twisting of the substrate through steric or dispersive effects.

Author contributions

Martin T. Peschel: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review & editing; Jörg Kussmann: methodology, resources, software, validation, project administration, supervision, writing – original draft, writing – review & editing; Christian Ochsenfeld – funding acquisition, supervision, resources, writing – review & editing; Regina de Vivie-Riedle – conceptualization, funding acquisition, project administration, resources, supervision.

Data availability

TDDFT Benchmarks, details regarding the kinetic model, time-resolved spectra, and references to software used for visualization and plotting are provided in the ESI.† The SHARC trajectory data for this article are available at ZENODO (DOI: https://doi.org/10.5281/zenodo.12204483). The modified SHARC code including the SHARC–FermiONs++ interface can be found at https://github.com/ochsenfeld-lab/sharc.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support by the “Deutsche Forschungsgemeinschaft” (DFG, German Research Foundation) via the Collaborative Research Centre 325-444632635 (“Assembly Controlled Chemical Photocatalysis”) and via Germany's Excellence Strategy-EXC 2089/1-390776260 (“e-conversion”). C. O. further acknowledges financial support as Max-Planck-Fellow at the MPI-FKF Stuttgart. M. T. P. thanks Yannick Lemke for help with the PyFermiONs API.

Notes and references

1. M. Barbatti, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 620–633.
2. R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068.
3. L. Wang, J. Qiu, X. Bai and J. Xu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1435.
4. A. Jain and A. Sindhu, ACS Omega, 2022, 7, 45810–45824.
5. S. Mai, P. Marquetand and L. González, Surface Hopping Molecular Dynamics, John Wiley & Sons, Ltd, 2020, ch. 16, pp. 499–530.
6. P. Cattaneo and M. Persico, J. Am. Chem. Soc., 2001, 123, 7638–7645.
7. Z. Lan, Y. Lu, E. Fabiano and W. Thiel, ChemPhysChem, 2011, 12, 1989–1998.
8. N. O. Carstensen, Phys. Chem. Chem. Phys., 2013, 15, 15017–15026.
9. P. Mondal, G. Granucci, D. Rastädter, M. Persico and I. Burghardt, Chem. Sci., 2018, 9, 4671–4681.
10. F. Siddique, M. Barbatti, Z. Cui, H. Lischka and A. J. A. Aquino, J. Phys. Chem. A, 2020, 124, 3347–3357.
11. D. Valverde, S. Mai, S. Canuto, A. C. Borin and L. González, JACS Au, 2022, 2, 1699–1711.
12. A. J. Coffman, Z. Jin, J. Chen, J. E. Subotnik and D. V. Cofer-Shabica, J. Chem. Theory Comput., 2023, 19, 7136–7150.
13. J. Wen, S. Mai and L. González, J. Phys. Chem. A, 2023, 127, 9520–9529.
14. M. Huix-Rotllant, K. Schwinn, V. Pomogaev, M. Farmani, N. Ferré, S. Lee and C. H. Choi, J. Chem. Theory Comput., 2023, 19, 147–156.
15. R. Brimioulle and T. Bach, Science, 2013, 342, 840–843.
16. R. Brimioulle, A. Bauer and T. Bach, J. Am. Chem. Soc., 2015, 137, 5170–5176.
17. T. P. Yoon, Acc. Chem. Res., 2016, 49, 2307–2315.
18. T. R. Blum, Z. D. Miller, D. M. Bates, I. A. Guzei and T. P. Yoon, Science, 2016, 354, 1391–1395.
19. S. Poplata and T. Bach, J. Am. Chem. Soc., 2018, 140, 3228–3231.
20. S. Poplata, A. Bauer, G. Storch and T. Bach, Chem. – Eur. J., 2019, 25, 8135–8148.
21. D. P. Schwinger and T. Bach, Acc. Chem. Res., 2020, 53, 1933–1943.
22. E. García-Expósito, M. J. Bearpark, R. M. Ortuño, V. Branchadell, M. A. Robb and S. Wilsey, J. Org. Chem., 2001, 66, 8811–8814.
23. E. García-Expósito, M. J. Bearpark, R. M. Ortuño, M. A. Robb and V. Branchadell, J. Org. Chem., 2002, 67, 6070–6077.
24. A. M. Lee, J. D. Coe, S. Ullrich, M.-L. Ho, S.-J. Lee, B. M. Cheng, M. Z. Zgierski, I.-C. Chen, T. J. Martínez and A. Stolow, J. Phys. Chem. A, 2007, 111, 11948–11960.
25. O. Schalk, M. S. Schuurman, G. Wu, P. Lang, M. Mucke, R. Feifel and A. Stolow, J. Phys. Chem. A, 2014, 118, 2279–2287.
26. J. Cao and Z.-Z. Xie, Phys. Chem. Chem. Phys., 2016, 18, 6931–6945.
27. R. Bonneau, J. Am. Chem. Soc., 1980, 102, 3816–3822.
28. M. A. El-Sayed, Acc. Chem. Res., 1968, 1, 8–16.
29. D. I. Schuster, D. A. Dunn, G. E. Heibel, P. B. Brown, J. M. Rao, J. Woning and R. Bonneau, J. Am. Chem. Soc., 1991, 113, 6245–6255.
30. H. Wang, X. Cao, X. Chen, W. Fang and M. Dolg, Angew. Chem., Int. Ed., 2015, 57, 14593–14596.
31. H. Wang, W.-H. Fang and X. Chen, J. Org. Chem., 2016, 81, 7093–7101.
32. M. T. Peschel, P. Kabaciński, D. P. Schwinger, E. Thyrhaug, G. Cerullo, T. Bach, J. Hauer and R. de Vivie-Riedle, Angew. Chem., Int. Ed., 2021, 60, 10155–10163.
33. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Chem. Theory Comput., 2011, 7, 1253–1258.
34. S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231.
35. S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370.
36. S. Mai, D. Avagliano, M. Heindl, P. Marquetand, M. F. S. J. Menger, M. Oppel, F. Plasser, S. Polonius, M. Ruckenbauer, Y. Shu, D. G. Truhlar, L. Zhang, P. Zobel and L. González, SHARC3.0: Surface Hopping Including Arbitrary Couplings – Program Package for Non-Adiabatic Dynamics, https://sharc-md.org/, 2023.
37. J. Kussmann and C. Ochsenfeld, J. Chem. Phys., 2013, 138, 134114.
38. J. Kussmann and C. Ochsenfeld, J. Chem. Theory Comput., 2015, 11, 918–922.
39. L. D. M. Peters, J. Kussmann and C. Ochsenfeld, J. Chem. Theory Comput., 2019, 15, 6647–6659.
40. D. A. Tracy, S. Fernandez-Alberti, S. Tretiak and A. E. Roitberg, J. Chem. Theory Comput., 2022, 18, 5213–5220.
41. D. V. Cofer-Shabica, M. F. S. J. Menger, Q. Ou, Y. Shao, J. E. Subotnik and S. Faraji, J. Chem. Theory Comput., 2022, 18, 4601–4614.
42. H. Huang, J. Peng, Y. Zhang, F. L. Gu, Z. Lan and C. Xu, J. Chem. Phys., 2024, 160, 234101.
43. J. Wen, S. Mai and L. González, J. Phys. Chem. A, 2023, 127, 9520–9529.
44. L. M. Ibele, P. A. Sánchez-Murcia, S. Mai, J. J. Nogueira and L. González, J. Phys. Chem. Lett., 2020, 11, 7483–7488.
45. O. Weingart, A. Nenov, P. Altoè, I. Rivalta, J. Segarra-Martí, I. Dokukina and M. Garavelli, J. Mol. Model., 2018, 24, 271.
46. D. Avagliano, M. Bonfanti, M. Garavelli and L. González, J. Chem. Theory Comput., 2021, 17, 4639–4647.
47. D. Avagliano, M. Bonfanti, A. Nenov and M. Garavelli, J. Comput. Chem., 2022, 43, 1641–1655.
48. P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, e1005659.
49. F. Plasser, S. Gómez, M. F. S. J. Menger, S. Mai and L. González, Phys. Chem. Chem. Phys., 2019, 21, 57–69.
50. I. Tavernelli, B. F. E. Curchod, A. Laktionov and U. Rothlisberger, J. Chem. Phys., 2010, 133, 194104.
51. M. Sapunar, T. Piteša, D. Davidović and N. Došlić, J. Chem. Theory Comput., 2019, 15, 3461–3469.
52. P. Alonso-Jordá, D. Davidović, M. Sapunar, J. R. Herrero and E. S. Quintana-Ortí, Comput. Phys. Commun., 2021, 258, 107521.
53. T. Shiozaki, W. Győrffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106.
54. T. H. Dunning, Jr, J. Chem. Phys., 1989, 90, 1007–1023.
55. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
56. W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670.
57. C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, J. Chem. Theory Comput., 2012, 8, 61–74.
58. K. Sneskov, T. Schwabe, O. Christiansen and J. Kongsted, Phys. Chem. Chem. Phys., 2011, 13, 18551–18560.
59. B. F. E. Curchod and T. J. Martínez, Chem. Rev., 2018, 118, 3305–3336.
60. M. Bondanza, B. Demoulin, F. Lipparini, M. Barbatti and B. Mennucci, J. Phys. Chem. A, 2022, 126, 6780–6789.
61. C. Song, J. Chem. Phys., 2023, 158, 014101.
62. S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, SoftwareX, 2018, 7, 1–5.
63. J. M. del Campo, J. L. Gázquez, S. B. Trickey and A. Vela, J. Chem. Phys., 2012, 136, 104108.
64. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
65. N. Kuritz, T. Stein, R. Baer and L. Kronik, J. Chem. Theory Comput., 2011, 7, 2408–2415.
66. T. Izadkhast and M. Alipour, J. Chem. Phys., 2023, 159, 024304.
67. L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336.
68. G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111.
69. B. Efron, Ann. Stat., 1979, 7, 1–26.

---

Footnote

† Electronic supplementary information (ESI) available: TDDFT benchmarks, details of the kinetic model, time-resolved spectra, software for visualization and plotting. See DOI: https://doi.org/10.1039/d4cp02492c

---