Unraveling the influence of organic cations on tuning electronic structures and spin-splitting in two-dimensional layered organic–inorganic tin-iodine perovskites†
Abdesslem
Jedidi
 *a,
Shatha M.
Alamri
a,
Norah O.
Alotaibi
a,
Souraya
Goumri-Said
*a,
Shatha M.
Alamri
a,
Norah O.
Alotaibi
a,
Souraya
Goumri-Said
 *b and
Mohammed Benali
Kanoun
*b and
Mohammed Benali
Kanoun
 *c
*c
aChemistry Department, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia. E-mail: ajedidi@kau.edu.sa
bPhysics Department, College of Science and General Studies, Alfaisal University, P.O. Box 50927, Riyadh 11533, Saudi Arabia. E-mail: sosaid@alfaisal.edu
cDepartment of Mathematics and Sciences, College of Humanities and Sciences, Prince Sultan University, P.O. Box 66833, Riyadh 11586, Saudi Arabia. E-mail: mkanoun@psu.edu.sa
First published on 1st August 2024
Abstract
The solar cell and light-emitting device research community is currently focusing on investigating two-dimensional (2D) hybrid perovskite materials owing to their remarkable stability and intriguing optoelectronic characteristics, which hold significant promise for various applications. In general, the introduction of chirality in hybrid perovskites arises from symmetry breaking within their inorganic frameworks. Nevertheless, despite this understanding, the specific factors driving the observed increase in splitting remain obscure due to a lack of comprehensive investigations. Our research delves into the electronic properties of 2D layered hybrid perovskites, considering their behavior with and without spin–orbit coupling. We specifically focus on effect of Rashba splitting and the impact of electronic structure variation across a range of chiral perovskites by introducing chiral organic cations with differing degrees of π-conjugation, resulting in significant changes in spin-splitting magnitude. Systematic first principles investigations confirm that the distortion of the cage and d-spacing of chiral perovskites are crucial design parameters for achieving strong spin-splitting in 2D layered perovskites. Furthermore, our investigation reveals that these systems exhibit remarkable absorption capabilities in the visible light spectrum, as demonstrated by their computed optoelectronic characteristics. The chiral perovskites described in this study, which exhibit substantial spin-splitting, present a distinctive prototype with potential implications for spintronics and photovoltaics.
1. Introduction
In recent years, there has been a notable surge in interest surrounding two-dimensional (2D) layered perovskites, primarily due to their significant improvements in stability compared to conventional bulk hybrid halide perovskites.1–7 These advancements have spurred exploration into their promising applications across various fields, including light-emitting diodes (LEDs), photodetectors, and solar cells.8,9 Two-dimensional perovskites typically adhere to the formula A2BX4, featuring a bulky ammonium cation positioned between octahedral (BX6)4− metal-halide inorganic frameworks. In these 2D hybrid perovskites, the disruption of the crystal structure demands increased energy, attributed to the substantial van der Waals (vdW) interactions between organic cations and inorganic anions. This phenomenon contributes to their remarkable stability, setting them apart from their 3D counterparts.10,11 Due to their exceptional structural tunability, 2D layered metal-halide perovskites have garnered rapid interest for applications where the interaction between the organic and inorganic layers determines the achievable functionality.12 Moreover, the helical arrangement of organic cations within the organic layer induces deformations in the inorganic layer, fostering the development of properties essential for spintronics applications.13Numerous studies14–19 have enriched the field of chiral metal halides, with the majority centered on Pb systems and employing specific chiral organic linkers.16–21 The necessity of eliminating toxic lead has driven the shift towards utilizing alternative metals such as Cu, Bi, Sb, and Sn in the synthesis of lead-free chiral metal halides,13,15,19–25 unveiling a variety of intriguing properties. Substituting tin for lead presents a common strategy aimed at creating less toxic materials, simultaneously narrowing the band gap towards the optimum25 in accordance with the Shockley–Queisser limit.26 Chiral tin halide perovskites, notably (R/S-MBA)2SnI4, have garnered significant interest, initially investigated by Lu et al.27 Their study introduced layered tin iodine perovskites characterized by highly distorted octahedra, influenced by specific hydrogen bonding arrangements. Furthermore, they demonstrated that the presence of chiral MBA cations induces circularly polarized absorption from the inorganic Sn–I sublattice, showcasing chiroptical activity.
Recent studies have employed chiral molecules in Sn-based 2D halide perovskites to fabricate field-effect transistor28 and solar cell devices,29 showcasing enhanced charge injection and greater stability of the inorganic perovskite layers. Very recently, F. De Angelis and colleagues utilized the chiral Cl-MBA to design chiral pairs, Cl-MBA2SnI4.30 Their research unveiled a novel low-bandgap Sn-based 2D chiral perovskite capable of tuning chiroptical properties through Cl-MBA ligand inclusion. This innovation induced Rashba band splitting, resulting in significant spin splitting values observed for the R- and S-enantiomers. These studies have convincingly illustrated the promising capabilities of 2D tin halide perovskite materials.
The advancement of novel lead-free chiral metal halide systems serves as a platform for elucidating the intricate structure–property relationships, particularly regarding Rashba spin splitting, aimed at facilitating efficient spin manipulation. It is noteworthy that the 2D tin halide perovskites have received comparatively less attention than their lead-based counterparts. It is established that organic molecules, serving to facilitate charge transport, can be incorporated into the semiconducting inorganic framework.31 Moreover, chiral organic cations serve dual roles as encapsulating layers, offering potential to enhance the stability of perovskite materials.31 Additionally, by varying the organic cation sites, it is possible to manipulate the characteristics of the Sn iodide framework, thereby allowing for the modulation of optical, spin, and electronic properties. Recent experimental observations suggest that chiral perovskites containing a large π-conjugated organic spacer exhibit the most substantial circular dichroism signals ever reported in chiral perovskites.32,33 However, the influence of chiral organic size and the presence of π bonds remains unexplored in relation to the spintronic properties of chiral perovskites.
To address the concerns raised earlier, we present an in-depth theoretical analysis delving into the stability, crystal structures, and electronic properties of two distinct 2D tin halide perovskite systems: S-cyclohexylethylamine (CYHEA) and S-methylbenzylamine (MBA), as depicted in Scheme 1. Our investigation aims to shed light on their versatile tunable optoelectronic and spintronic attributes. We have harnessed density functional theory calculations to offer a deeper understanding of impact of organic spacers on the intricate interplay between structure and property within 2D hybrid tin halide perovskites. These insights hold the potential to govern and finely tune the optoelectronic properties of these materials. Furthermore, we explore the effect of spacer organic cation on the electronic structures and optical properties of the materials. Through first-principles computations incorporating spin–orbit coupling and considering broken inversion symmetry, we elucidate the potential role of Rashba band splitting in 2D hybrid perovskites. This phenomenon has implications for tailoring their electronic and optical absorption properties, making them suitable for applications in optoelectronics, spintronics. Our findings highlight the significant role of structural distortions in driving the observed Rashba effect.
2. Computational methods
Density functional theory (DFT) calculations were carried out to optimize the crystal structure and analyze the Rashba splitting of 2D (S-MBA)2SnI4, and (b) (S-CYHEA)2SnI4 systems using the Vienna Ab Initio Simulation Package (VASP, version 5.4).34 The projector augmented wave (PAW) pseudopotential method35 is employed to address the interaction between valence electrons and ion cores. The exchange and correlation potential were handled using the generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE).36 Considering the influence of intermolecular forces on the calculation, the Tkatchenko–Scheffler (TS) correction was applied to address van der Waals (vdW) interactions.37 The geometry structures are completely relaxed when the force acting on every atom is less than 0.01 eV Å−1. The energy cutoff was defined as 500 eV and 10−5 eV total energy convergence threshold was applied in calculation. The Brillouin zone is sampled using a 4 × 2 × 4 mesh for –(MBA)2SnI4 and a 4 × 4 × 2 mesh for S-(CYHEA)2SnI4. We take spin–orbit coupling (SOC) impact into account owing to the relativistic effects in heavy elements. The hybrid functional based on Heyd–Scuseria–Ernzerhof (HSE06)38,39 is applied to achieve more accurate electronic and optical properties, where the standard mixture of 25% Hartree–Fock and 75% PBE was considered for short-range interactions. VESTA used for visualization, VASPKIT used for KPOINTS and K-PATH generation, and SUMO was used to visualize and analyze DOS and BAND structures.To further quantify the distortion of inorganic [SnI6]2− octahedra, we calculated the bond angle variances and bond length distortion
 | (1) |
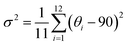 | (2) |
To examine the energetic stability of (S-MBA)2SnI4 and (S-CYHEA)2SnI4, the formation energy, Ef, is calculated, defined as follows:
| ET((MBA/CYHEA)2SnI4) = ET((MBA/CYHEA)2SnI4) − 2ET(MBA/CYHEAI) − ET(SnI2) | (3) |
To investigate the optical properties of the 2D tin halide perovskite systems, the optical absorption coefficient, α(ω), are computed using the following equation:
 | (4) |
3. Results and discussion
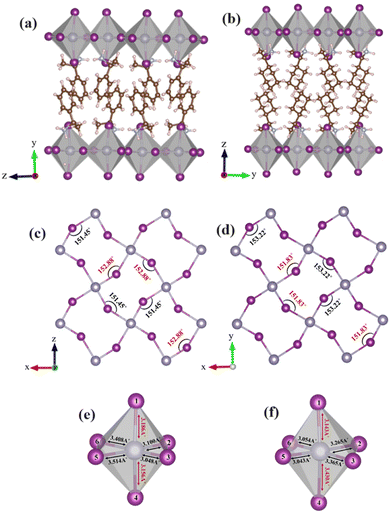
It is well-established that chiral molecules exist in two forms, which are mirror images of each other (i.e., enantiomers S/R-(MBA/CYHEA)2SnI4). Typically, their chemical composition and physical properties are identical, and the only method to differentiate between them is by their spatial geometry. In this study, we examined the structural characteristics of two 2D layered hybrid organic–inorganic tin-iodine perovskite systems, specifically enantiomer S-based (MBA)2SnI4 and (CYHEA)2SnI4. These systems incorporate two distinct spacer cations. (MBA)2SnI4 and (CYHEA)2SnI4 crystallize in the orthorhombic and monoclinic crystal systems,24 respectively, with chiral space groups of P21212 and P21, respectively, as shown in Fig. 1a. Both crystals display a 2D perovskite structure composed of corner-sharing SnI6 octahedra, with organic cations (MBA/CYHEA) bridging the 2D layer framework. However, the crystallographic packing direction is along the y-direction for (S-MBA)2SnI4, whereas it is along the z-direction for (S-CYHEA)2SnI4. Additionally, the unit-cell volume of (S-MBA)2SnI4 is 45% larger than that of the (S-CYHEA)2SnI4 system. These structures were optimized using GGA-PBE + TS, yielding results in close agreement with experimental results. The lattice constants of (S-MBA)2SnI4 (a = 8.793 Å and c = 9.148 Å) are slightly smaller than the experimental values (a = 8.910 Å and c = 9.357 Å).27 For (S-CYHEA)2SnI4, the lattice constants (a = 8.816 Å and c = 8.669 Å) are slightly larger than those of (R/S-CYHEA)2PbI4 (a = 8.612 Å, b = 7.954 Å).40 The analysis of crystal structure depicted in Fig. S1 (ESI†), shows that the tin atoms of MBA are staggered in each adjacent inorganic layer, leading to a staggered conformation characteristic of the orthorhombic unit cell. Conversely, S-CYHEA adopts an eclipsed conformation, where the tin atoms are aligned from layer to layer. We also examined the bond length and equatorial Sn–I–Sn bond angle, which reflect the distortions of inorganic layer, as summarized in Tables S1 and S2 (ESI†). The average Sn–I bond length in the (S-MBA)2SnI4 is calculated to be 3.235 Å with the minimum value being 3.048 Å and the maximum value being 3.514 Å. For (S-CYHEA)2SnI4, the Sn–I bond lengths are in the range of 3.043–3.430 Å, which is slightly shorter than those in (S-MBA)2SnI4 (Fig. 1c and d). Through calculation based on eqn (1) and (2), the distortion, Δd and σ2 of [SnI6]2− octahedron are determined to be 2.701 × 10−3 and 9.10 respectively for (S-MBA)2SnI4 and 2.124 × 10−3 and 10.79 respectively for (S-CYHEA)2SnI4. Additionally, the 2D layered tin halide perovskites demonstrate two closely similar Sn–I–Sn angles, measuring 152.88° and 151.45° in the structure of (S-MBA)2SnI4, and 153.22° and 151.83° in the structure of (S-CYHEA)2SnI4, as illustrated in Fig. 1e and f. The calculated Sn–I bond lengths and their corresponding average distortions are collected in Table S1 (ESI†). In the organic layers, the cyclohexane rings are arranged in the chair configuration.Each CYHEA spacer cation is hydrogen-bonded to the distorted SnI6 octahedrons through three hydrogen bonds, adopting an axial configuration. The hydrogen bond distances to the bridging halides measure longer at 2.85 Å and 2.69 Å compared to the axial halides at 2.45 Å and 2.60 Å, and 2.57 Å and 2.41 Å, respectively, for two adjacent cations. Similarly, in CYHEA-based 2D perovskite, each ordered MBA spacer cation is linked to the [SnI6]2− octahedron by three hydrogen bonds with an axial configuration, as illustrated in Fig. 2 and summarized in Table S3 (ESI†). Furthermore, chiral organic cations in both 2D chiral halide perovskites engage in van der Waals interactions with adjacent cations. These non-covalent interactions contribute to the stabilization of the crystal packing in the 2D systems. The energetically stable configuration was investigated by computing the formation energy, Ef, of the two structures, using eqn (3). The computed values for the formation energies of (S-MBA)2SnI4 and (S-CYHEA)2SnI4 are −9.55 eV and −14.92 eV, respectively. Additionally, the greater negative formation energy observed for (S-CYHEA)2SnI4 suggests enhanced stability.
 | ||
| Fig. 2 Hydrogen bonding interaction between iodide atoms and the hydrogen on the organic cation. (a) (S-MBA)2SnI4, and (b) (S-CYHEA)2SnI4. | ||
Next, the electronic properties of the (S-MBA)2SnI4 and (S-CYHEA)2SnI4 are explored by calculating the electronic band structure at GGA-PBE levels of approximation in Fig. 3. Both materials manifest a direct band gap characteristic, observed precisely at the high symmetry Γ-point within the Brillouin zone (BZ). The calculated band gap values for this feature are 1.63 eV for (S-MBA)2SnI4 and 1.56 eV for (S-CYHEA)2SnI4.
 | ||
| Fig. 3 Calculated band structure of (a) (S-MBA)2SnI4 and (b) (S-CYHEA)2SnI4 by GGA GGA-PBE without SOC. | ||
To enhance the accuracy of band gap determination while managing computational resources efficiently, we focused our HSE06 functional calculations on the total and partial densities of states (DOS) for both studied materials. The resulting DOS features are presented in Fig. 4a and b, offering a detailed view of the electronic state distributions and a more reliable estimation of the band gap.
The computed band gap values have increased to 2.1 eV and 2.0 eV for (S-MBA)2SnI4 and (S-CYHEA)2SnI4, respectively. Notably, there were no significant alterations observed in the contributions of atomic orbitals at the top of the valence band (VB) and the bottom of the conduction band (CB). However, the calculated band gap value of (S-MBA)2SnI4 aligns well with the values reported in the literature of 2.02 eV.27 Analysis of the DOS (refer to Fig. 4a and b) for (S-MBA)2SnI4 and (S-CYHEA)2SnI4, reveals that in both systems, the occupied band of edge of VB predominantly arises from contributions of I-p states, with a supplementary minor contribution from C p and Sn p states whereas the first unoccupied band is mainly influenced by Sn-p and I p states. In Fig. 4c and d, we present the isosurface of the electron charge density at the boundary between the valence and conduction bands of both 2D layered halide perovskites. Corresponding to the DOS characteristics, the lower of CB of the 2D chiral perovskite mainly consists of Sn p states with a small contribution of I p states, while the higher of VB is mostly composed of I-p, demonstrating excellent concordance with theoretical studies.22,24,27 These findings suggest that both materials show significant promise for electron transport, particularly since the lower of CB involves the p-states of the Sn-site atoms.
Furthermore, our investigation delved into the effective masses of charge carriers in 2D layered halide perovskite systems, shedding light on how the choice of organic spacer cations influences carrier mobilities.41 Specifically, we conducted calculations to determine the electron (me) and hole (mh) effective masses along the Γ direction of the Brillouin zone. For (S-MBA)2SnI4 and (S-CYHEA)2SnI4, we found the electron effective masses to be me = 0.241 m0 and me = 0.195 m0, respectively, while the hole effective masses are mh = 0.251 m0 and mh = 0.206 m0, respectively (m0 is a free electron mass). Moreover, we calculate the corresponding reduced mass of charges carriers using the following equation;  . The estimated reduced masses are found to be 0.123 and 0.100 for (S-MBA)2SnI4 and (S-CYHEA)2SnI4, respectively. The exciton stands as one of the most critical physical entities influencing the performance of optoelectronic and photovoltaic devices. Utilizing the effective-mass approximation and the hydrogen-like model, the exciton binding energy can be computed using the expression41,42;
. The estimated reduced masses are found to be 0.123 and 0.100 for (S-MBA)2SnI4 and (S-CYHEA)2SnI4, respectively. The exciton stands as one of the most critical physical entities influencing the performance of optoelectronic and photovoltaic devices. Utilizing the effective-mass approximation and the hydrogen-like model, the exciton binding energy can be computed using the expression41,42; 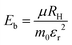 , where the symbol RH (equal to 13.6 eV) represents the Rydberg constant, which signifies the binding energy of an electron in the ground-state 1s orbital of the hydrogen (H) atom and εr denotes the relative dielectric function. The εr represents the value of the real part of the dielectric function when it reaches its maximum, which is 2.1 for S-(MBA)2SnI4 and 2.07 for (S-CYHEA)2SnI4 (see Fig. S2, ESI†). The estimated exciton binding energy values for the (S-MBA)2SnI4 and (S-CYHEA)2SnI4 are found to be 379 and 317 meV, respectively. It is found that the Eb of (S-MBA)2SnI4 is greater than that of the 2D perovskite (S-CYHEA)2SnI4. Based on the findings, 2D layered perovskites exhibit high exciton binding energies, making them promising candidates for optoelectronic applications.
, where the symbol RH (equal to 13.6 eV) represents the Rydberg constant, which signifies the binding energy of an electron in the ground-state 1s orbital of the hydrogen (H) atom and εr denotes the relative dielectric function. The εr represents the value of the real part of the dielectric function when it reaches its maximum, which is 2.1 for S-(MBA)2SnI4 and 2.07 for (S-CYHEA)2SnI4 (see Fig. S2, ESI†). The estimated exciton binding energy values for the (S-MBA)2SnI4 and (S-CYHEA)2SnI4 are found to be 379 and 317 meV, respectively. It is found that the Eb of (S-MBA)2SnI4 is greater than that of the 2D perovskite (S-CYHEA)2SnI4. Based on the findings, 2D layered perovskites exhibit high exciton binding energies, making them promising candidates for optoelectronic applications.
To investigate the optical absorption characteristics, we computed absorption spectra for (S-MBA)2SnI4 and (S-CYHEA)2SnI4 using the HSE06 functional across the photon energy that varies from 0 to 5 eV, as depicted in the Fig. 5. Interestingly, both 2D layered perovskites exhibit excellent visible light absorption capabilities, with a prominent absorption peak exceeding 105 cm−1 located around 2.9 eV. Notably, the absorption coefficient of (S-CYHEA)2SnI4 in the visible region and ultraviolet surpasses that of (S-MBA)2SnI4 perovskite. These findings underscore the potential application of the studied systems in photovoltaic cells.
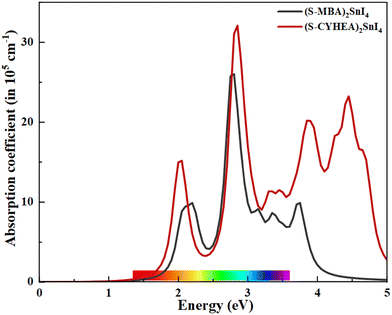 | ||
| Fig. 5 Calculated absorption coefficient spectra of (S-MBA)2SnI4 and (b) (S-CYHEA)2SnI4 systems using the HSE06 functional without SOC. | ||
The inclusion of heavy elements such as tin within the crystal structure triggers a significant SOC effect, potentially resulting in the Rashba effect in noncentrosymmetric systems. This effect could render the fundamental bandgap indirect, impacting the behavior of charge carriers. Consequently, it may lead to reduced recombination rates and an extended lifetime for charge carriers.31 To investigate the impact of chirality-induced inversion asymmetry, π-conjugated and the size of organic cations on the electronic band structures of chiral (S-MBA)2SnI4 and (S-CYHEA)2SnI4, we conducted electronic band structure calculations using DFT within GGA-PBE with SOC contribution, as plotted in Fig. 6. The inclusion of SOC significantly underestimates the band gap, yielding values of 1.48 eV and 1.39 eV for (S-MBA)2SnI4 and (S-CYHEA)2SnI4, respectively. This reduction can be attributed to the influence of heavy elements, present in the systems. In the band structure analysis of (S-MBA)2SnI4, the Rashba effect manifests by breaking the spin degeneracy present in both the valence and conduction bands. This leads to the formation of unique parabolic band minima, distinctly observed in the plane the Γ–Z path high-symmetry points of the Brillouin zone.
 | ||
| Fig. 6 Band structure of chiral (a) (S-MBA)2SnI4 (b) (S-CYHEA)2SnI4 along the high symmetry directions of Brillouin zone. Light purple and black curves for CB and VB band, respectively. | ||
The expression can be identified in the Rashba Hamiltonian43,44 that describes the linear-in-k space with effective SOC interaction in quasi-two-dimensional (2D) systems:
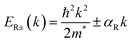 | (5) |
 , where, ER represents the energy splitting, and kR denotes the distance in k-space between the band extremum and the band crossing point. Based on our calculations, for the conduction band, we observe a splitting with an energy ER = 2.6 meV and a corresponding distance in k-space of ER = 0.0265 Å−1, resulting in a Rashba coupling parameter magnitude of 0.196 eV Å. For the valence band, we find an energy splitting of ER = 3 meV and a distance of kR = 0.029 Å−1, leading to a Rashba coupling parameter magnitude of 0.207 eV Å. Notably, (S-MBA)2SnI4 demonstrates a small value of α, and consequently, a minor band splitting.39 In the spacer cation-based system (S-CYHEA)2SnI4, characterized by the absence of π bonds within its molecular framework, an intriguing discovery emerges: the spin splitting values at both the valence and conduction band edges along the Γ–A points exhibit significant enhancements. Remarkably, they are measured at 0.388 eV Å for the VB and 0.339 eV Å for the CB, respectively, showcasing a notable increase when compared to those observed in MBA.
, where, ER represents the energy splitting, and kR denotes the distance in k-space between the band extremum and the band crossing point. Based on our calculations, for the conduction band, we observe a splitting with an energy ER = 2.6 meV and a corresponding distance in k-space of ER = 0.0265 Å−1, resulting in a Rashba coupling parameter magnitude of 0.196 eV Å. For the valence band, we find an energy splitting of ER = 3 meV and a distance of kR = 0.029 Å−1, leading to a Rashba coupling parameter magnitude of 0.207 eV Å. Notably, (S-MBA)2SnI4 demonstrates a small value of α, and consequently, a minor band splitting.39 In the spacer cation-based system (S-CYHEA)2SnI4, characterized by the absence of π bonds within its molecular framework, an intriguing discovery emerges: the spin splitting values at both the valence and conduction band edges along the Γ–A points exhibit significant enhancements. Remarkably, they are measured at 0.388 eV Å for the VB and 0.339 eV Å for the CB, respectively, showcasing a notable increase when compared to those observed in MBA.
Our findings reveal a fascinating trend: the dramatic increase in spin-splitting observed from (S-MBA)2SnI4 to (S-CYHEA)2SnI4 cannot solely be ascribed to alterations in π-conjugation. Hence, it suggests that besides π-conjugation, another factor may play a significant role in influencing the splitting of chiral hybrid halide perovskites. As it is known, a large helical distortion of the octahedral cages generates a significant Rashba splitting. A comprehensive understanding of helical distortion is gained by comparing the cage distortions of (S-MBA)2SnI4 and S-(CYHEA)2SnI4 with that of (S-NEA = naphthylethylamine)2SnI4.12 As shown in Fig. S3 (ESI†), the cage of (S-NEA)2SnI4 significantly deviates from the ideal 180°, characteristic of an undistorted perovskite layer. This deviation may be attributed to the substantial π-conjugation in NEA cations, leading to strong interactions with neighboring organic cations. Additionally, the cage displays two distinct Sn–I–Sn angles: 149.88° on one side of the inorganic layer and 138.88° on the opposite side, resulting in distortions that propagate helically parallel to the y-axis. In contrast, the perovskites (S-MBA)2SnI4 and (S-CYHEA)2SnI4 demonstrate two very similar Sn–I–Sn angles, yielding nearly flat perovskite layers, as depicted in Fig. S3 (ESI†). Given that a larger helical distortion correlates with increased spin-splitting, these findings confirm that (S-NEA)2SnI4 cation exhibits (αR ≈ 0.707 eV Å) the largest Rashba splitting compared to perovskites based on CYHEA and MBA. However, despite the similar distortion of the octahedral cage between (S-MBA)2SnI4 and (S-CYHEA)2SnI4, the difference in splitting between these two 2D layered perovskites cannot be solely explained by cage distortion. Additionally, we explored another factor that could influence spin splitting in 2D layered perovskites: the d-spacing between inorganic layers. Surprisingly, we found that the estimated d-spacing of the chiral hybrid halide perovskites follows the order of 19.2 Å (S-NEA)2SnI4 > 16.7 Å (S-CYHEA)2SnI4 > 14.4 Å (S-MBA)2SnI4, which aligns with the magnitude of splitting, as depicted in Fig. S4 (ESI†). Remarkably, the observed spin-splitting is also linked to the d-spacing of chiral perovskites, where increasing distortion and d-spacing lead to a larger splitting size.
4. Conclusion
In conclusion, our study sheds light on the intricate electronic properties and potential design considerations for chiral hybrid perovskites, (S-MBA)2SnI4 and (S-CYHEA)2SnI4. The study of electronic structures and DOSs using first principles computational techniques indicates that contributions from I-p states, and Sn-p and I p states, respectively, have a major impact on the edge of valence and conduction bands. Effective mass calculations indicate promising electron transport properties for both materials. Additionally, exciton binding energy calculations suggest high values for both perovskites, making them suitable for optoelectronic applications. Moreover, the exceptional visible light absorption capabilities exhibited by these materials hold promising implications for optoelectronic applications Through comprehensive investigations into electronic structures with and without spin–orbit coupling, we highlight the significance of Rashba spin–orbit coupling effect. In addition, our investigation of various chiral perovskite systems highlights the significance of organic cations with different π-conjugation levels in controlling spin-splitting magnitude. Our findings emphasize that the distortion of the perovskite cage and d-spacing between layers serve as pivotal design parameters for achieving robust spin-splitting in 2D layered perovskite structures. Overall, our study provides valuable insights into the electronic behavior and potential engineering strategies for 2D hybrid tin halide perovskites, paving the way for further advancements in this interestingly developing area.Data availability
All data were communicated in the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under grant no. KEP-PhD:83-130-1443. The authors, therefore, acknowledge with thanks DSR for technical and financial support. The authors are also grateful to the HPCC (Aziz Supercomputer) for the resources. A. J. is grateful to the KAUST Supercomputing Laboratory (Shaheen II) for the provided resources.References
- F. Zhang, H. Lu, J. Tong, J. J. Berry, M. C. Beard and K. Zhu, Advances in Two-Dimensional Organic-Inorganic Hybrid Perovskites, Energy Environ. Sci., 2020, 13, 1154–1186 RSC.
- W. Zheng, X. Wang, X. Zhang, B. Chen, H. Suo, Z. Xing, Y. Wang, H. Wei, J. Chen, Y. Guo and F. Wang, Emerging Halide Perovskite Ferroelectrics, Adv. Mater., 2023, 35, 2205410 CrossRef CAS PubMed.
- N. Ali, N. Shehzad, S. Uddin, R. Ahmed, M. Jabeen, A. Kalam, A. G. Al-Sehemi, H. Alrobei, M. B. Kanoun, A. Khesro and S. Goumri-Said, A review on perovskite materials with solar cell prospective, Int. J. Energy Res., 2021, 45, 19729–19745 CrossRef CAS.
- D. H. Cao, C. C. Stoumpos, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, 2D Homologous Perovskites as Light-Absorbing Materials for Solar Cell Applications, J. Am. Chem. Soc., 2015, 137, 7843–7850 CrossRef CAS PubMed.
- H. Zhang, J.-W. Lee, G. Nasti, R. Handy, A. Abate, M. Gratzel and N.-G. Park, Lead Immobilization for Environmentally Sustainable Perovskite Solar Cells, Nature, 2023, 617, 687–695 CrossRef CAS PubMed.
- S. Liu, M. Kepenekian, S. Bodnar, S. Feldmann, M. W. Heindl, N. Fehn, J. Zerhoch, A. Shcherbakov, A. Pothig, Y. Li, U. W. Paetzold, A. Kartouzian, I. D. Sharp, C. Katan, J. Even and F. Deschler, Bright circularly polarized photoluminescence in chiral layered hybrid lead-halide perovskites, Sci. Adv., 2023, 9, eadh5083 CrossRef CAS PubMed.
- R. Das, M. Hossain, A. Mahata, D. Swain, F. De Angelis, P. K. Santra and D. D. Sarma, Unique Chiro-optical Properties of the Weakly-2D (R-/S-MBA)2CuBr4 Hybrid Material, ACS Mater. Lett., 2023, 5, 1556–1564 CrossRef CAS.
- L. Mao, C. C. Stoumpos and M. G. Kanatzidis, Two-Dimensional Hybrid Halide Perovskites: Principles and Promises, J. Am. Chem. Soc., 2019, 141, 1171–1190 CrossRef PubMed.
- Y. Jiang, K. Wei, C. Sun, Y. Feng, L. Zhang, M. Cui, S. Li, W.-D. Li, J. T. Kim, C. Qin and M. Yuan, Unraveling Size-Dependent Ion-Migration for Stable Mixed-Halide Perovskite Light-Emitting Diodes, Adv. Mater., 2023, 35(39), 2304094 CrossRef CAS PubMed.
- B. Cheng, T.-Y. Li, P.-C. Wei, J. Yin, K.-T. Ho, J. R. D. Retamal, O. F. Mohammed and J.-H. He, Layer-edge device of twodimensional hybrid perovskites, Nat. Commun., 2018, 9, 5196 CrossRef PubMed.
- Y. Shao, W. Gao, H. Yan, R. Li, I. Abdelwahab, X. Chi, L. Rogee, L. Zhuang, W. Fu, S. P. Lau, S. F. Yu, Y. Cai, K. P. Loh and K. Leng, Unlocking surface octahedral tilt in two-dimensional Ruddlesden-Popper perovskites, Nat. Commun., 2022, 13, 138 CrossRef CAS PubMed.
- M. P. Arciniegas and L. Manna, Designing Ruddlesden–Popper Layered Perovskites through Their Organic Cations, ACS Energy Lett., 2022, 7, 2944–2953 CrossRef CAS.
- J. Yin, P. Maity, L. Xu, A. M. El-Zohry, H. Li, O. M. Bakr, J.-L. Brédas and O. F. Mohammed, Layer-Dependent Rashba Band Splitting in 2D Hybrid Perovskites, Chem. Mater., 2018, 30(23), 8538–8545 CrossRef CAS.
- D. G. Billing and A. Lemmerer, Synthesis and Crystal Structures of Inorganic-Organic Hybrids Incorporating an Aromatic Amine with a Chiral Functional Group, CrystEngComm, 2006, 8(9), 686–695 RSC.
- J. Ahn, E. Lee, J. Tan, W. Yang, B. Kim and J. Moon, A New Class of Chiral Semiconductors: Chiral-Organic-Molecule-Incorporating Organic-Inorganic Hybrid Perovskites, Mater. Horiz., 2017, 4(5), 851–856 RSC.
- C. Chen, L. Gao, W. Gao, C. Ge, X. Du, Z. Li, Y. Yang, G. Niu and J. Tang, Circularly polarized light detection using chiral hybrid perovskite, Nat. Commun., 2019, 10(1), 1927 CrossRef PubMed.
- L. Wang, Y. Xue, M. Cui, Y. Huang, H. Xu, C. Qin, J. Yang, H. Dai and M. Yuan, A Chiral Reduced-Dimension Perovskite for an Efficient Flexible Circularly Polarized Light Photodetector, Angew. Chem., Int. Ed., 2020, 59(16), 6442–6450 CrossRef CAS PubMed.
- D. R. Kripalani, Y. Cai, J. Lou and K. Zhou, Strong Edge Stress in Molecularly Thin Organic–Inorganic Hybrid Ruddlesden–Popper Perovskites and Modulations of Their Edge Electronic Properties, ACS Nano, 2022, 16(1), 261–270 CrossRef CAS PubMed.
- T. Liu, W. Shi, W. Tang, Z. Liu, B. C. Schroeder, O. Fenwick and M. J. Fuchter, High Responsivity Circular Polarized Light Detectors based on Quasi Two-Dimensional Chiral Perovskite Films, ACS Nano, 2022, 16(2), 2682–2689 CrossRef CAS PubMed.
- T. Yin, H. Yan, I. Abdelwahab, Y. Lekina, X. Lu, W. Yang, H. Sun, K. Leng, K. Cai, Z. X. Shen and K. P. Loh, Pressure driven rotational isomerism in 2D hybrid perovskites, Nat. Commun., 2023, 14, 411 CrossRef CAS PubMed.
- E. A. Morais, N. A. M. S. Caturello, M. A. Lemes, H. Ferreira, F. F. Ferreira, J. J. S. Acuña, S. Brochsztain, G. M. Dalpian and J. A. Souza, Rashba Spin Splitting Limiting the Application of 2D Halide Perovskites for UV-Emitting Devices, ACS Appl. Mater. Interfaces, 2024, 16(3), 4261–4270 CrossRef CAS PubMed.
- A. Dibenedetto, C. Coccia, M. Boiocchi, M. Moroni, C. Milanese and L. Malavasi, Synthesis and Characterization of Cu-Containing Chiral Metal Halides and Role of Halogenation of the Organic Ligand, J. Phys. Chem. C, 2024, 128, 4803–4808 CrossRef CAS.
- A. Azmy, D. M. Konovalova, L. Lepore, A. Fyffe, D. Kim, L. Wojtas, Q. Tu, M. T. Trinh, N. Zibouche and I. Spanopoulos, Synthesis and Optical Properties of One Year Air-Stable Chiral Sb(III) Halide Semiconductors, Inorg. Chem., 2023, 62, 20142–20152 CrossRef CAS PubMed.
- T. Li, X. Chen, X. Wang, H. Lu, Y. Yan, M. C. Beard and D. B. Mitzi, Origin of Broad-Band Emission and Impact of Structural Dimensionality in Tin-Alloyed Ruddlesden–Popper Hybrid Lead Iodide Perovskites, ACS Energy Lett., 2020, 5, 347–352 CrossRef CAS.
- C. T. Triggs, R. D. Ross, W. Mihalyi-Koch, C. F. M. Clewett, K. M. Sanders, I. A. Guzei and S. Jin, Spacer Cation Design Motifs for Enhanced Air Stability in Lead-Free 2D Tin Halide, Perovskites, ACS Energy Lett., 2024, 9, 1835–1843 CrossRef CAS.
- J. Cao and F. Yan, Recent progress in tin-based perovskite solar cells, Energy Environ. Sci., 2021, 14, 1286–1325 RSC.
- H. Lu, C. Xiao, R. Song, T. Li, A. E. Maughan, A. Levin, R. Brunecky, J. J. Berry, D. B. Mitzi, V. Blum and M. C. Beard, Highly Distorted Chiral Two-Dimensional Tin Iodide Perovskites for Spin Polarized Charge Transport, J. Am. Chem. Soc., 2020, 142, 13030–13040 CrossRef CAS PubMed.
- Y. Gao, Z. Wei, P. Yoo, E. Shi, M. Zeller, C. Zhu, P. Liao and L. Dou, Highly Stable Lead-Free Perovskite Field-Effect Transistors Incorporating Linear π-Conjugated Organic Ligands, J. Am. Chem. Soc., 2019, 141(39), 15577–15585 CrossRef CAS PubMed.
- M. Konstantakou and T. Stergiopoulos, A Critical Review on Tin Halide Perovskite Solar Cells, J. Mater. Chem. A, 2017, 5, 11518–11549 RSC.
- C. Coccia, M. Morana, A. Mahata, W. Kaiser, M. Moroni, B. Albini, P. Galinetto, C. Milanese, A. Porta, E. Mosconi, F. De Angelis and L. Malavasi, Ligand-Induced Chirality in Novel 2D Tin Iodide Perovskite Cl-MBA2SnI4, Angew. Chem., Int. Ed., 2024, 63, e202318557 CrossRef CAS PubMed.
- Z. Ding, Q. Chen, Y. Jiang and M. Yuan, Structure-Guided Approaches for Enhanced Spin-Splitting in Chiral Perovskite, JACS Au, 2024, 4, 1263–1277 CrossRef CAS PubMed.
- A. Ishii and T. Miyasaka, Direct detection of circular polarized light in helical 1D perovskite-based photodiode, Sci. Adv., 2020, 6, eabd3274 CrossRef CAS PubMed.
- J. Son, S. Ma, Y.-K. Jung, J. Tan, G. Jang, H. Lee, C. U. Lee, J. Lee, S. Moon, W. Jeong, A. Walsh and J. Moon, Unraveling chirality transfer mechanism by structural isomer-derived hydrogen bonding interaction in 2D chiral perovskite, Nat. Commun., 2023, 14, 3124 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blochl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Accurate Molecular van der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- J. Heyd, G. F. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- N. Kanoun-Bouayed, M. B. Kanoun, A.-A. Kanoun and S. Goumri-Said, Insights into the impact of metal tin substitution on methylammonium lead bromide perovskite performance for photovoltaic application, Sol. Energy, 2021, 224, 76–81 CrossRef CAS.
- Y. Hu, F. Florio, Z. Chen, W. A. Phelan, M. A. Siegler, Z. Zhou, Y. Guo, R. Hawks, J. Jiang and J. Feng, et al., A chiral switchable photovoltaic ferroelectric 1D perovskite, Sci. Adv., 2020, 6, 9 Search PubMed.
- H. M. Jang, J. S. Kim, J. M. Heo and T. W. Lee, Enhancing Photoluminescence Quantum Efficiency of Metal Halide Perovskites by Examining Luminescence-Limiting Factors, APL Mater., 2020, 8, 020904 CrossRef CAS.
- R. I. Biega, M. R. Filip, L. Leppert and J. B. Neaton, Chemically Localized Resonant Excitons in Silver-Pnictogen Halide Double Perovskites, J. Phys. Chem. Lett., 2021, 12(8), 2057–2063 CrossRef CAS PubMed.
- J. Chen, K. Wu, W. Hu and J. Yang, Spin–Orbit Coupling in 2D Semiconductors: A Theoretical Perspective, J. Phys. Chem. Lett., 2021, 12, 12256–12268 CrossRef CAS PubMed.
- Y. A. Bychkov and E. Rashba, Properties of a 2D electron gas with spectral degeneracies lifted, JETP Lett., 1984, 39, 78–81 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02426e |
| This journal is © the Owner Societies 2024 |