Theoretical infrared spectroscopy of protonated methane isotopologues

Abstract

The vibrational spectroscopy of protonated methane and its mixed hydrogen/deuterium isotopologues remains a challenge to both experimental and computational spectroscopy due to the iconic floppiness of CH₅⁺. Here, we compute the finite-temperature broadband infrared spectra of CH₅⁺ and all its isotopologues, i.e. CH_nD_5−n⁺ up to CD₅⁺, from path integral molecular dynamics in conjunction with interactions and dipoles computed consistently at CCSD(T) coupled cluster accuracy. The potential energy and dipole moment surfaces have been accurately represented in full dimensionality in terms of high-dimensional neural networks. The resulting computational efficiency allows us to establish CCSD(T) accuracy at the level of converged path integral simulations. For all six isotopologues, the computed broadband spectra compare very favorably to the available experimental broadband spectra obtained from laser induced reactions action vibrational spectroscopy. The current approach is found to consistently and significantly improve on previous calculations of these broadband vibrational spectra and defines the new cutting-edge for what has been dubbed the “enfant terrible” of molecular spectroscopy in view of its pronounced large-amplitude motion that involves all intramolecular degrees of freedom.

---

Protonated methane, CH₅⁺, the prototype of hypercoordinate non-classical carbocations with outstanding relevance to chemistry,¹ persists as an enduring challenge to both experiment and theory, even after decades of inquiry.^2–4 The underlying cause of these difficulties is the unusually flat potential energy surface (PES) of CH₅⁺ which allows for large-amplitude motion in terms of pseudorotational dynamics. This leads to structural fluxionality called hydrogen scrambling that involves the many equivalent minima separated by only tiny energy barriers.^5–8 For these reasons CH₅⁺ has been considered the archetypical floppy molecule³ for a long time. It has been dubbed more recently “the enfant terrible of chemical structures”, given that even “the very concept of molecular structure becomes problematic”.⁴ Yet, after a period of confusion, it has been established that despite its fluxionality⁵ even in the quantum ground state,⁷ CH₅⁺ can structurally be described in terms of a “CH₃ tripod” to which an “H₂ moiety” is attached via a three-center two-electron bond⁹ that constantly exchange their constituting protons due to hydrogen scambling. Despite enormous experimental difficulties, infrared (IR) spectroscopy of many different flavors is – so far – the only experimental probe to tackle the structural dynamics of CH₅⁺.^10–16 This includes high-resolution spectroscopy in narrow frequency windows carried out at cryogenic conditions as well as broadband spectra recorded at much higher temperatures spanning the entire mid-IR range.

Systematic isotope substitution, where all five protons are replaced stepwise by deuterons yielding a total of six CH_nD_5−n⁺ isotopologues, does not merely imprint structural differences¹⁷ but turned out to be a most powerful tool to unfold the spectral richness of protonated methane^14,18–20 as proposed earlier.²¹ The pronounced nuclear quantum delocalization effects on the flat PES, different for heavy deuterons versus light protons, have been shown to lead to preferential, noncombinatorial populations of the different isotopomers within a given isotopologue^14,20 as anticipated.²¹ This leads to drastic changes in the overall IR lineshape of the isotopologues CH_nD_5−n⁺ compared to the CH₅⁺ ref. 14 and 18–20 in stark contrast to simple frequency shifts as they are well known from stiff, quasi-rigid molecules.

When it comes to computing IR spectra of protonated methane and its isotopologues while including full anharmonicity and possibly also temperature effects, an array of complementary methods has been deployed to tackle that challenge for such floppy molecules.^{12–14,18,20,22–36} Out of these, path integral-based simulations^37,38 rigorously tackle large-amplitude motion, hydrogen scrambling dynamics, and permutations of identical particles.^36,39 In conjunction with spectral decomposition,³⁹ this approach has been demonstrated to be particularly successful in accurately assigning the peaks, shoulders, and other features of all isotopologue IR spectra to the underlying molecular motion in terms of generalized normal coordinates,^14,20 as reviewed some time ago.²⁹ Yet, these previous path integral simulations were limited along multiple computational dimensions as outlined in the following. First of all, they either relied on a quantum-reweighting technique of classical IR spectra or on path integral centroid molecular dynamics (CMD)⁴⁰ to seamlessly generate the approximate quantum time-evolution of the different isotopologues. While the first approach is quasiclassical by construction, the CMD method has been shown by us to be plagued by increasingly pronounced artifical frequency red-shifts and peak broadenings due to the curvature problem when lowering the temperature;⁴¹ see ref. 42 and 43 for lucid reviews of approximate path integral dynamics methods including recent advances. Furthermore, the electronic structure has been computed earlier^14,20 on-the-fly along the finite-temperature path integral simulations using density functional theory (DFT). Although the previously chosen density functional has been repeatedly shown to perform very well for CH₅⁺, the pronounced computational demand of on-the-fly electronic structure evaluation in the framework of path integral simulations³⁸ hampered both path integral and statistical convergence of the IR spectra.

Today, methodological advances offer unprecedented access to converged path integral simulations down to ultralow temperatures at the level of CCSD(T) coupled cluster electronic structure theory. This applies not only to interactions and thus the PES, but also the DMS (dipole moment surface) can be obtained from machine learning (ML) representations at coupled cluster quality;^44–49 see ref. 50 for a Perspective on converged path integral simulations combined with neural network techniques. The IR spectroscopic accuracy of our consistent coupled cluster-based ML approach to PES + DMS representations has been demonstrated recently for small molecules when combined with quasiexact wavefunction-based variational and quantum dynamics techniques to compute rovibrational energy levels and IR spectra.^51,52 Unfortunately, it is still impossible to rigorously compute finite-temperature IR spectra (and not merely a limited set of rovibrational states) of very floppy molecules such as protonated methane and its isotopologues using quasiexact quantum techniques. This arises from the intricacies of the large-amplitude motion of the fluxional CH₅⁺ species, leading to hydrogen scrambling that involves all internal degrees of freedom and entangled rovibrational states.^31,33–35 As shown in the following, revisiting approximate path integral dynamics with our latest methodological improvements offers a viable path to achieve progress. In contrast to practical quasiexact wavefunction-based techniques, large-amplitude motion of all coupled degrees of freedom of fluxional molecules such as protonated methane are readily included in path integral-based techniques when computing broadband IR spectra at finite temperatures. Despite their virtues, finite-temperature path integral simulations are known to be unable to provide high-resolution IR spectra, thus offering no insight into rovibrational energy levels and couplings. Computing such state-resolved spectra, however, is the domain of quasiexact wavefunction-based techniques^26,31,34 where nuclear spin statistics of all identical particles are imposed to filter out the low-lying Pauli-allowed rovibrational states as required for high-resolution IR spectra close to the ground state. Incidentally, this complementary situation as to path integral-based versus wavefunction-based techniques is similar in experimental spectroscopy: those spectroscopic methods that provide broadband spectra at elevated temperatures^12,14,16,53 and those that yield high-resolution state-resolved spectra at low temperatures^11,13,15 are very different in nature. Our present focus clearly is on computing as accurately as possible the broadband IR spectra of all isotopologues of protonated methane at an elevated temperature of 100 K as obtained from laser induced reactions (LIR) action vibrational spectroscopy.^12,14

In this short note, we apply converged path integral simulations^37,38 in the framework of ring polymer molecular dynamics (RPMD)⁵⁴ to compute the broadband IR spectra of all six CH_nD_5−n⁺ isotopologues at 100 K close to the experimental temperature using ML-based potential energies and dipole moments at CCSD(T) accuracy; we refer to the “Computational methods and details” section at the end of the main text for the details of the underlying explicitly correlated CCSD(T*)–F12a/aug-cc-pVTZ and DF–CCSD(T*)–F12a/aug-cc-pVDZ reference calculations of potential energies and dipole moments, respectively, abbreviated by “CCSD(T)” throughout this text, and to the ESI† for the neural network parameterization. Based on our results, we demonstrate that this approach currently provides the most accurate broadband IR spectra of protonated methane and its isotopologues as judged by comparing to the experimental broadband spectra.

We start the discussion connecting back to our earlier work²⁰ by comparing in panel (a) of Fig. 1 the IR spectrum of CH₅⁺ obtained from CMD to the experimental LIR (laser induced reactions) action vibrational spectrum¹² recorded at roughly 110 K. At variance with our earlier work, we can first of all now improve the path integral convergence (using 150 Trotter slices to discretize the path integral at 200 K versus only 32 beads more than a decade ago and a total of 8 ns CMD trajectories versus 162.5 ps earlier to compute the spectrum). Secondly, we used DFT earlier to compute on-the-fly the interactions that govern the path integral time evolution as well as the dipole moments required to compute the IR spectrum from its auto-correlation function. Here, we now use CCSD(T) theory to describe both, the PES and DMS. Whereas the first improvement merely provides more thoroughly converged data, the latter enables one to clearly see the red-shift of the CMD spectrum in the C–H stretching window relative to LIR, which is an artifact due to the curvature problem;⁴¹ we note in passing that 200 K is roughly the lowest temperature in the “linear regime”⁴¹ in the case of CH₅⁺ before CMD fully breaks down. Earlier,²⁰ we clearly discussed this caveat while lacking at that time any means to quantify the CMD-shift: the CMD spectrum obtained from DFT matched LIR very well but only fortuitously since the CMD-induced red-shift perfectly compensated the DFT-induced blue-shift of the C–H stretches. In addition, the splitting of the bending peak around 1200 cm⁻¹ as observed with DFT but not seen in experiment vanishes when using CCSD(T) in conjunction with CMD and, thus, is not a CMD artifact.

Fig. 1 Infrared spectra of CH₅⁺ and its deuterated isotopologues up to CD₅⁺ computed from RPMD (blue) and CMD (green) path integral simulations at CCSD(T) accuracy, see text. The corresponding experimental reference spectra (gray) were obtained from laser induced reactions (LIR) action vibrational spectroscopy as published in ref. 14 the arbitary intensity scale of the LIR spectra has been adjusted individually to allow for easy comparison to the computed IR spectra.

As opposed to CMD, RPMD does not feature any curvature problem by construction and thus no artifical red-shifts of vibrational spectra, yet artificial resonances between physical and fictitious modes⁴¹ might appear depending on the specific system and simulation parameters; see ref. 42 and 43 for reviews on deep analyses of this phenomenon and possible remedies. For CH₅⁺, we did not encounter such interferences at the relevant temperature and, thus, refrained from using thermostats⁵⁵ or applying other modifications of bare RPMD propagation.^42,43 Indeed, the CCSD(T)-based RPMD spectrum of CH₅⁺ turns out to be very close to the LIR ref. 12 at the experimental temperature, see Fig. 1(a). In this context, we recall that LIR⁵⁶ is an intricate variant of action spectroscopy where an IR excitation, ħω, induces a bimolecular reaction of a mass–selected parent molecule, here CH₅⁺, with a reactant, CO₂ in this case, to generate CH₄ + HCO₂⁺ in a variable-temperature ion trap according to the reaction rate of the excited ion.⁵³ The amount of HCO₂⁺ generated by the reaction is a measure of the absorption intensity as a function of the IR laser excitation wavelength ω, thus yielding the LIR action spectrum. This implies in the first place that the LIR intensities are not directly governed by the oscillator strength of rovibrational transitions as is the case for linear IR absorption spectra. In addition, the LIR signal is proportional to the product of the linear absorption cross section, α(ω), and the rate coefficient 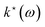. While the former is directly computed in theoretical spectroscopy, the frequency-dependence of the latter is unknown but is estimated for the above laser induced reaction to decrease significantly below 1000 cm⁻¹ and to quickly drop toward zero according to approximate modeling.^12,53 In consequence, these LIR spectra are known to significantly lose sensitivity at frequencies below roughly 1000 cm⁻¹; we note in passing a recent proposal⁵⁷ of an empirical approach to approximately correct for this experimental phenomenon (see Section 4.4.2 and the Appendix in ref. 57). Yet, in view of all inherent uncertainties, we refrain from applying such ad hoc models of to the computed linear absorption cross section, α(ω).

At this stage, we conclude that converged RPMD simulations using CCSD(T)-quality interactions and dipole moments satisfactorily reproduce the broadband IR spectrum of CH₅⁺ without any further adjustments.

Given that favorable situation, we now turn to the deuterated isotopologues including the fully deuterated CD₅⁺ species as well, see Fig. 1(b)–(f). The partially deuterated species have been shown earlier to provide deep insights into the assignment of the IR peak structure of protonated methane.¹⁴ This can be achieved in terms of generalized normal coordinates³⁹ by decomposing the IR spectra of all individual isotopomers underlying the fully scrambling CH_nD_5−n⁺ isotopologues (which provide the observable IR spectra) into molecular motions in real space.^14,20 The current simulations provide overall a very convincing match with the LIR spectra¹⁴ which outperforms the earlier comparisons obtained from path integral-based methods^14,20 as analyzed in the following (see Fig. 7 in ref. 29 for one-to-one comparisons to experiment offered by the previous calculations including the DMC/VCI IR spectra^18,19 which (i) do not reproduce the clearly observed bimodal bending band of CH₂D₃⁺ and CHD₄⁺ and (ii) provide artificially symmetric lineshapes of the prominent stretching band of these two isotopologues that are very asymmetric according to experiment).

At first glance it may be surprising that the rather high intensity of the blue-wing part of the tripod stretching band of CD₅⁺ depicted in Fig. 1 appears to visibly distort the peak structure. This most intense peak of the CD₅⁺ spectrum has been assigned previously¹⁴ to consist (from lower to higher frequencies) of the in-plane, symmetric out-of-plane and antisymmetric out-of-plane C–D stretching modes within the CD₃ tripod fragment of the perdeuterated species (labelled by tⁱ_D, t^s_D and t^a_D, respectively, and visualized in Fig. S1 of ref. 14). The lineshape of that peak computed from RPMD reflects (but overemphasizes) the significant skewness of the tripod stretching band that is clearly seen in the experimental LIR spectrum of CD₅⁺, whereas the corresponding peak of CH₅⁺ (spanned by the tⁱ_H, t^s_H and t^a_H modes) is very symmetric according to both, experiment and simulation according to Fig. 1(a). We therefore assign the experimentally observed skewness of the tripod C–D stretching band of CD₅⁺, unseen in previous calculations of that IR spectrum (see Fig. 7 in ref. 29), to the antisymmetric out-of-plane C–D stretching mode t^a_D.

The present RPMD simulations that are entirely based on CCSD(T) quality electronic structure theory moreover reproduce perfectly the unimodal bending band (in the range of roughly 1000 to 1550 cm⁻¹) for CH₅⁺, CH₄D⁺, CH₃D₂⁺ and CD₅⁺ as well as the rather symmetric bimodal peak structure in case of the CH₂D₃⁺ and CHD₄⁺ isotopologues in full accord with experiment, see Fig. 1. This systematic agreement greatly improves previous calculations where, depending on the approach, the unimodal peak in LIR is found computationally to split into a greatly asymmetric dublet structure or the bimodal peak in LIR is confluent and yields a single maximum (see the IR spectra of all isotopologues in the original literature^14,18–20 or compiled in Fig. 7 of the review²⁹). Last but not least, the relative intensities of the different mode contributions to the significantly modulated lineshape functions of the CH_nD_5−n⁺ species are found to closely match the experimental peak heights, which is another noteworthy improvement with respect to all previous calculations.²⁹

In conclusion, our results demonstrate that path integral molecular dynamics simulations at CCSD(T) accuracy provide the most accurate set of theoretical broadband IR spectra for protonated methane and its partially deuterated isotopologues up to the perdeuterated species as judged by directly comparing to the respective experimental spectra at the same temperature of about 100 K. This is promising progress given the remaining lack of quasiexact methods that would be able to ultimately provide accurate IR spectra of extremely floppy molecules such as protonated methane, while this route has been successfully demonstrated recently for much less demanding species.^51,52 Moving away from practical path integral molecular dynamics simulations with all their inherent difficulties and limitations in systematically approximating exact quantum dynamics,^42,43 our finding provides the perfect basis for future work on high-resolution rather than broadband vibrational spectroscopy of protonated methane. The goal in this case would be to assign in terms of state-to-state transitions the entangled rovibrational states^31,33–35 that have been measured¹⁵ a decade ago with utmost accuracy – and yet await assignment! The necessary methodological advances in theoretical vibrational spectroscopy might come from improvements in multi-configurational time-dependent Hartree (MCDTH), vibrational matrix product state (MPS) or tree tensor networks state (TTNS) techniques^51,58 to eventually enable quasiexact calculations of IR spectra even of floppy molecular systems such as protonated methane.

Computational methods and details

All reported path integral simulations were carried out using the CP2k software package^59,60 in conjunction with the RubNNet4MD interface⁶¹ to high-dimensional neural network (NN) representations.⁶² We use our published NN-PES of CH₅⁺ trained on CCSD(T) energies computed from an augmented correlation-consistent basis set up to triple zeta functions^63,64 (aug-cc-pVTZ or AVTZ) in combination with the explicitly correlated F12a method^65,66 and an adequate scaling (*) of the triples,⁶⁶ thus providing CCSD(T*)–F12a/AVTZ accuracy for our NN-PES of CH₅⁺ as validated and benchmarked in detail in ref. 67. This potential energy surface is combined with a neural network-based dipole moment surface (NN-DMS), developed for this study (see below), to compute the reported IR spectra as usual from the Fourier transform of the dipole time-autocorrelation function generated from either RPMD⁵⁴ or CMD⁴⁰ path integral trajectories;^42,43 all reported IR spectra have been smoothed to a minimal extent by applying a Hann window that is identical to the length of the underlying RPMD or CMD trajectories. To correctly sample the quantum canonical ensemble each system was propagated using path integral Langevin equation (PILE) thermostatting⁶⁸ at T = 100 as well as 200 K with the time constant τ = 200 fs and friction coefficient λ = 0.5; Trotter discretizations in terms of P = 300 and 150 beads were used at 100 and 200 K, respectively. After an equilibration period of 20 ps, path integral positions and velocities were recorded every 500 fs and used to start both, RPMD and CMD simulations at 100 and 200 K, respectively; in case of CMD we used a centroid adiabatic decoupling parameter of γ = 16 in accordance with the definition provided in ref. 41 corresponding to a decrease in the non-centroid bead masses by a factor of γ² = 256. To correctly integrate the resulting fast dynamics, a timestep of Δt = 0.1 fs was chosen for the RPMD simulations, whereas CMD was carried out with Δt = 0.01 fs at this level of adiabatic decoupling. In total, 400 such RPMD and CMD trajectories were generated for each of the six isotopologues and propagated for 20 ps, generating a total of 8 ns per isotopologue for both, RPMD and CMD sampling in order to compute the respective dipole time-autocorrelation functions.^42,43 For the newly parameterized NN-DMS of CH₅⁺ we refer to the ESI† where we compile all NN parameters and also report our validation tests to support the quality. The dipole moment vectors underlying this NN-DMS have been computed based on CCSD(T) data computed from an augmented correlation-consistent basis set up to double zeta functions^63,64 (aug-cc-pVDZ or AVDZ) in combination with the explicitly correlated F12a method^65,66 and an adequate scaling (*) of the triples⁶⁶ within the density fitting (DF) approximation⁶⁹ thus providing DF–CCSD(T*)–F12a/AVDZ accuracy for our NN-DMS of CH₅⁺ which is consistent in quality with the NN-PES. In ref. 49 we show for a large data set of 10 000 structures of the Zundel cation that the AVDZ basis set results in a negligible mean absolute error of 0.003 D compared to the AVTZ basis set when computing dipole moments from DF–CCSD(T*)–F12a/AVDZ theory. The Molpro software package^70,71 has been used to compute these dipole moments for which reference input is also provided in the ESI.†

Data availability

All CC calculations were performed using the Molpro quantum chemistry package.^70,71 The NN-DMS has been constructed using the RubNNet4MD package,⁶¹ while the NN-PES used is available within the ESI† of ref. 67 The data used to train and validate the NN-DMS presented in this paper together with the final NN-DMS paremeterization have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Harald Forbert (Bochum) not only for insightful discussions but for providing us with a program to efficiently and accurately compute IR spectra from molecular dynamics trajectories. R. B. acknowledges funding from the Studienstiftung des deutschen Volkes and C. S. acknowledges partial financial support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) project number 500244608. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV as well as by the individual DFG grant MA 1547/19 to D. M. This work is supported by the “Center for Solvation Science ZEMOS” funded by the German Federal Ministry of Education and Research and by the Ministry of Culture and Research of North Rhine-Westphalia. The computational resources were provided by HPC@ZEMOS, HPC-RESOLV, and BoViLab@RUB.

References

1. G. A. Olah, My Search for Carbocations and Their Role in Chemistry (Nobel Lecture), Angew. Chem., Int. Ed. Engl., 1995, 34, 1393–1405.
2. R. J. Saykally, Infrared Laser Spectroscopy of Molecular Ions, Science, 1988, 239, 157–161.
3. G. E. Scuseria, The elusive signature of CH₅⁺, Nature, 1993, 366(6455), 512–513.
4. T. Oka, Taming CH₅⁺, the “enfant terrible” of chemical structures, Science, 2015, 347, 1313.
5. V. Dyczmons and W. Kutzelnigg, Ab initio Calculation of small Hydrides Including Electron Correlation, Theor. Chim. Acta, 1974, 33, 239.
6. P. R. Schreiner, S. J. Kim, H. F. Schaefer III and P. V. R. Schleyer., CH₅⁺: The never ending story or the final word?, J. Chem. Phys., 1993, 99(5), 3716.
7. D. Marx and M. Parrinello, Structural quantum effects and three-centre two-electron bonding in CH₅⁺, Nature, 1995, 375(6528), 216–218.
8. P. R. Schreiner, Does CH₅⁺ Have (a) “Structure?” A Tough Test for Experiment and Theory, Angew. Chem., 2000, 39(18), 3239–3241.
9. D. Marx and A. Savin, Topological Bifurcation Analysis: Electronic Structure of CH₅⁺, Angew. Chem., Int. Ed. Engl., 1997, 36, 2077.
10. D. W. Boo, Z. F. Liu, A. G. Suits, J. S. Tse and Y. T. Lee, Dynamics of Carbonium Ions Solvated by Molecular Hydrogen: CH₅⁺ (H₂)_n (n = 1,2,3), Science, 1995, 269, 57.
11. E. T. White, J. Tang and T. Oka, CH₅⁺: The infrared spectrum observed, Science, 1999, 284, 135.
12. O. Asvany, P. P. Kumar, P. B. Redlich, I. Hegemann, S. Schlemmer and D. Marx, Understanding the Infrared Spectrum of Bare CH₅⁺, Science, 2005, 309, 1219.
13. X. Huang, A. B. McCoy, J. M. Bowman, L. M. Johnson, C. Savage and F. Dong, et al., Quantum Deconstruction of the Infrared Spectrum of CH₅⁺, Science, 2006, 311, 60.
14. S. D. Ivanov, O. Asvany, A. Witt, E. Hugo, G. Mathias and B. Redlich, et al., Quantum-induced symmetry breaking explains infrared spectra of CH₅⁺ isotopologues, Nat. Chem., 2010, 2(4), 298–302.
15. O. Asvany, K. M. T. Yamada, S. Brünken, A. Potapov and S. Schlemmer, Experimental ground-state combination differences of CH₅⁺, Science, 2015, 347, 1346.
16. J. A. Davies, S. Yang and A. M. Ellis, Infrared spectra of carbocations and CH₄⁺ in helium, Phys. Chem. Chem. Phys., 2021, 23, 27449–27459.
17. A. B. McCoy, B. J. Braams, A. Brown, X. Huang, Z. Jin and J. M. Bowman, Ab initio diffusion Monte Carlo calculations of the quantum behavior of CH₅⁺ in full dimensionality, J. Phys. Chem. Soc., 2004, 108, 4991.
18. X. Huang, L. M. Johnson, J. M. Bowman and A. B. McCoy, Deuteration effects on the structure and infrared spectrum of CH₅⁺, J. Am. Chem. Soc., 2006, 128, 3478.
19. L. M. Johnson and A. B. McCoy, Evolution of structure in CH₅⁺ and its deuterated analogues, J. Phys. Chem. A, 2006, 110, 8213.
20. A. Witt, D. S. Ivanov, G. Mathias and D. Marx, Quantum Molecular Dynamics Calculations of Ultrafast Time Scales and Infrared Spectra of Protonated Methane: Quantifying Isotope-Specific Lifetimes, J. Phys. Chem. Lett., 2011, 2, 1377.
21. D. Marx and M. Parrinello, CH₅⁺ Stability and Mass Spectrometry, Science, 1999, 286, 1051.
22. A. L. L. East, M. Kolbuszewski and P. R. Bunker, Ab Initio Calculation of the Rotational Spectrum of CH₅⁺ and CD₅⁺, J. Phys. Chem. A, 1997, 101, 6746–6752.
23. A. Brown, A. B. McCoy, B. J. Braams, Z. Jin and J. M. Bowman, Quantum and classical studies of vibrational motion of CH₅⁺ on a global potential energy surface obtained from a novel ab initio direct dynamics approach, J. Chem. Phys., 2004, 121, 4105.
24. P. Kumar and D. Marx, Understanding hydrogen scrambling and infrared spectrum of bare CH₅⁺ based on ab initio simulation, Phys. Chem. Chem. Phys., 2006, 8, 573.
25. A. B. McCoy, Diffusion Monte Carlo approaches for investigating the structure and vibrational spectra of fluxional systems, Int. Rev. Phys. Chem., 2006, 25, 77–107.
26. X. G. Wang and T. Carrington Jr, Vibrational energy levels of CH₅⁺, J. Chem. Phys., 2008, 129, 234102.
27. M. P. Deskevich, A. B. McCoy, J. M. Hutson and D. J. Nesbitt, Large-Amplitude Quantum Mechanics in Polyatomic Hydrides. II. A Particle-on-a-Sphere Model for XH_n (n = 4,5), J. Chem. Phys., 2008, 128, 094306.
28. C. E. Hinkle, A. S. Petit and A. B. McCoy, Diffusion Monte Carlo studies of low energy ro-vibrational states of CH₅⁺ and its deuterated isotopologues, J. Mol. Spectrosc., 2011, 268, 189.
29. S. D. Ivanov, A. Witt and D. Marx, Theoretical spectroscopy using molecular dynamics: theory and application to CH₅⁺ and its isotopologues, Phys. Chem. Chem. Phys., 2013, 15, 10270.
30. F. Uhl, L. Walewski, H. Forbert and D. Marx, Adding flexibility to the “particles-on-a-sphere” model for large-amplitude motion: POSflex force field for protonated methane, J. Chem. Phys., 2014, 141, 104110.
31. R. Wodraszka and U. Manthe, CH₅⁺: Symmetry and the Entangled Rovibrational Quantum States of a Fluxional Molecule, J. Phys. Chem. Lett., 2015, 6, 4229.
32. H. Schmiedt, S. Schlemmer and P. Jensen, Symmetry of extremely floppy molecules: Molecular states beyond rotation-vibration separation, J. Chem. Phys., 2015, 143, 154302.
33. H. Schmiedt, P. Jensen and S. Schlemmer, Collective Molecular Superrotation: A Model for Extremely Flexible Molecules Applied to Protonated Methane, Phys. Rev. Lett., 2016, 117, 223002.
34. X. G. Wang and T. Carrington, Jr, Calculated rotation-bending energy levels of CH₅⁺ and a comparison with experiment, J. Chem. Phys., 2016, 144, 204304.
35. H. Schmiedt, P. Jensen and S. Schlemmer, Rotation-vibration motion of extremely flexible molecules - The molecular superrotor, Chem. Phys. Lett., 2017, 672, 34–46.
36. A. Esser, H. Forbert and D. Marx, Tagging effects on the mid-infrared spectrum of microsolvated protonated methane, Chem. Sci., 2018, 9, 1560–1573.
37. M. E. Tuckerman, Statistical Mechanics and Molecular Simulations, Oxford Graduate Texts, Oxford University Press, UK, 2008.
38. D. Marx and J. Hutter, Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge University Press, 2009.
39. G. Mathias, S. D. Ivanov, A. Witt, M. D. Baer and D. Marx, Infrared Spectroscopy of Fluxional Molecules from (ab initio) Molecular Dynamics: Resolving Large-Amplitude Motion, Multiple Conformations, and Permutational Symmetries, J. Chem. Theory Comput., 2012, 8, 224.
40. J. Cao and G. A. Voth, A new perspective on quantum time correlation functions, J. Chem. Phys., 1993, 99, 10070–10073.
41. A. Witt, S. D. Ivanov, M. Shiga, H. Forbert and D. Marx, On the applicability of centroid and ring polymer path integral molecular dynamics for vibrational spectroscopy, J. Chem. Phys., 2009, 130, 194510.
42. S. C. Althorpe, Path-integral approximations to quantum dynamics, Eur. Phys. J., 2021, 94, 155.
43. S. C. Althorpe, Path Integral Simulations of Condensed-Phase Vibrational Spectroscopy, Annu. Rev. Phys. Chem., 2024, 75, 397–420.
44. C. Schran, F. Uhl, J. Behler and D. Marx, High-dimensional neural network potentials for solvation: The case of protonated water clusters in helium, J. Chem. Phys., 2018, 148(10), 102310.
45. C. Schran, F. Brieuc and D. Marx, Converged Colored Noise Path Integral Molecular Dynamics Study of the Zundel Cation down to Ultralow Temperatures at Coupled Cluster Accuracy, J. Chem. Theory Comput., 2018, 14, 5068–5078.
46. C. Schran, J. Behler and D. Marx, Automated Fitting of Neural Network Potentials at Coupled Cluster Accuracy: Protonated Water Clusters as Testing Ground, J. Chem. Theory Comput., 2020, 16(1), 88–99.
47. C. Schran, K. Brezina and O. Marsalek, Committee neural network potentials control generalization errors and enable active learning, J. Chem. Phys., 2020, 153(10), 104105.
48. C. Schran, F. Brieuc and D. Marx, Transferability of machine learning potentials: Protonated water neural network potential applied to the protonated water hexamer, J. Chem. Phys., 2021, 154(5), 051101.
49. R. Beckmann, F. Brieuc, C. Schran and D. Marx, Infrared Spectra at Coupled Cluster Accuracy from Neural Network Representations, J. Chem. Theory Comput., 2022, 18(9), 5492–5501.
50. F. Brieuc, C. Schran, F. Uhl, H. Forbert and D. Marx, Converged quantum simulations of reactive solutes in superfluid helium: The Bochum perspective, J. Chem. Phys., 2020, 152, 1–22.
51. H. R. Larsson, M. Schröder, R. Beckmann, F. Brieuc, C. Schran and D. Marx, et al., State-resolved infrared spectrum of the protonated water dimer: revisiting the characteristic proton transfer doublet peak, Chem. Sci., 2022, 13(37), 11119–11125.
52. I. Simkó, C. Schran, F. Brieuc, C. Fábri, O. Asvany and S. Schlemmer, et al., Quantum Nuclear Delocalization and its Rovibrational Fingerprints, Angew. Chem., Int. Ed., 2023, 62, e202306744.
53. S. Schlemmer and O. Asvany, Laser induced reactions in a 22-pole ion trap, J. Phys.: Conf. Ser., 2005, 4, 134–141.
54. I. R. Craig and D. E. Manolopoulos, Quantum statistics and classical mechanics: Real time correlation functions from ring polymer molecular dynamics, J. Chem. Phys., 2004, 121(8), 3368–3373.
55. M. Rossi, M. Ceriotti and D. E. Manolopoulos, How to remove the spurious resonances from ring polymer molecular dynamics, J. Chem. Phys., 2014, 140(23), 234116.
56. S. Schlemmer, T. Kuhn, E. Lescop and D. Gerlich, Laser excited N₂⁺ in a 22-pole ion trap: experimental studies of rotational relaxation processes, Int. J. Mass Spectrom., 1999, 185, 589.
57. D. S. Tikhonov and Y. V. Vishnevskiy, Describing nuclear quantum effects in vibrational properties using molecular dynamics with Wigner sampling, Phys. Chem. Chem. Phys., 2023, 25, 18406.
58. H. R. Larsson, Computing vibrational eigenstates with tree tensor network states (TTNS), J. Chem. Phys., 2019, 151, 204102.
59. CP2K: Open Source Molecular Dynamics; https://www.cp2k.org/.
60. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, CP2K: atomistic simulations of condensed matter systems, WIRE Comput. Mol. Sci., 2014, 4(1), 15–25.
61. F. Brieuc, C. Schran, H. Forbert and D. Marx, RubNNet4MD: The RUB Neural Network for Molecular Dynamics Software Package Version 2, 2021, https://www.theochem.rub.de/go/rubnnet4md.html.
62. J. Behler, Four Generations of High-Dimensional Neural Network Potentials, Chem. Rev., 2021, 121(16), 10037–10072.
63. R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96(9), 6796–6806.
64. D. E. Woon and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. IV. Calculation of static electrical response properties, J. Chem. Phys., 1994, 100(4), 2975–2988.
65. T. B. Adler, G. Knizia and H. J. Werner, A simple and efficient CCSD(T)-F12 approximation, J. Chem. Phys., 2007, 127(22), 221106.
66. G. Knizia, T. B. Adler and H. J. Werner, Simplified CCSD(T)-F12 methods: Theory and benchmarks, J. Chem. Phys., 2009, 130(5), 54104.
67. F. Brieuc, C. Schran and D. Marx, Manifestations of local supersolidity of He4 around a charged molecular impurity, Phys. Rev. Res., 2023, 5(4), 043083.
68. M. Ceriotti, M. Parrinello, T. E. Markland and D. E. Manolopoulos, Efficient stochastic thermostatting of path integral molecular dynamics, J. Chem. Phys., 2010, 133(12), 124104.
69. W. Györffy and H. J. Werner, Analytical energy gradients for explicitly correlated wave functions. II. Explicitly correlated coupled cluster singles and doubles with perturbative triples corrections: CCSD(T)-F12, J. Chem. Phys., 2018, 148(11), 114104.
70. H. J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll and A. Heßelmann, et al., The Molpro quantum chemistry package, J. Chem. Phys., 2020, 152(14), 144107.
71. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz and P. Celani, et al., Molpro, version 2019.1, a package of ab initio programs, 2019.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02295e

‡ Present address: Cavendish Laboratory, Department of Physics, University of Cambridge, Cambridge, CB3 0HE, UK.

§ Present address: Laboratoire Matière en Conditions Extrêmes, Université Paris-Saclay, CEA, 91680 Bruyères-le-Châtel; CEA, DAM, DIF, F-91297 Arpajon, France.

---