Grazing incidence fast atom diffraction: general considerations, semiclassical perturbation theory and experimental implications
Received
27th May 2024
, Accepted 10th September 2024
First published on 18th September 2024
Abstract
Using semiclassical methods, an analytical approach to describe grazing incidence scattering of fast atoms (GIFAD) from surfaces is described. First, we consider a model with a surface corrugated in the scattering plane, which includes the surface normal and the incidence direction. The treatment uses a realistic, Morse potential, within a perturbation approach, and correctly reproduces the basic GIFAD phenomenology, whereby the scattering is directed primarily in the specular direction. Second, we treat the more general case of scattering from a surface corrugated in two-dimensions. Using time averaging along the direction of fast motion in the incidence direction, we derive a time dependent potential for the GIFAD scattering away from a low index direction. The results correctly describe the observation that diffraction is seen only when the scattering plane is aligned close to a low-index direction in the surface plane. For the case of helium scattering from LiF(001) we demonstrate that the resulting theoretical predictions agree well with experiment and show that the analysis provides new information on the scattering time and the length scale of the interaction. The analysis also gives insights into the validity of the axial surface channeling approximation (ASCA) and shows that within first order perturbation theory, along a low-index direction, the full 3-dimensional problem can be represented accurately by an equivalent 2-dimensional problem with a potential averaged along the third dimension. In contrast, away from low-index directions, the effective 2-dimensional potential in the projectile frame is time-dependent.
1 Introduction
Grazing incidence, fast-atom diffraction (GIFAD) has emerged as a tool with a particular sensitivity to both the structural corrugation of electron density at the surface (see e.g. ref. 1 and 2 for reviews) and to the details of the van der Waals forces between the incident particle and the surface.3–5 The information provided by these experiments is complementary to that obtained from thermal-energy experiments6,7 as, in both cases, the classical turning point occurs above the outermost atomic layer. The similarity between the two different scattering approaches arises from the particular scattering geometry in GIFAD, and especially a high incident energy along a direction close to grazing incidence, which leads to a separation of the dynamics into a fast-direction, parallel to the surface, and a slow-direction, normal to the surface. Motion in the fast-direction leads to averaging of the interaction where the dynamics in the slow-direction can be treated using methods developed for thermal energy scattering,8–12 or alternatively by treating the coupling between fast and slow variables as one of quasi-resonance.13 In experiment, similar effects have been seen when scattering molecular hydrogen at large angles of incidence;14,15 however, experiments close to grazing incidence show that averaging leads to extinction of in-plane diffraction in almost every case, though counter examples have been observed.16,17
In the scattering plane, defined to include the surface normal and the incidence direction, the transition from fast to slow atom diffraction has been addressed with quantum techniques9,11 confirming the suppression of in-plane diffraction. The presence of strong out of plane diffraction is observed only when a low-index direction in the surface plane is closely parallel to the scattering plane giving rise to the typical, high-symmetry diffraction pattern recorded at once and responsible for the initial interest into the GIFAD method.18,19 However, in the general case of arbitrary surface orientation, only the specular peak is present and the rapid attenuation of the diffraction when the scattering plane is at an angle with the crystal axis has also been investigated with quantum theory.10,20 In this manuscript we present a general description of both characteristics of GIFAD quoted above; the disappearance of in-plane diffraction at grazing incidence and the rapid attenuation of out of plane diffraction when the angle between the low-index direction and the scattering plane increases. We quantify these effects using a semi-classical approach, which offers a number of advantages in understanding the basic phenomenology and has been used widely to describe GIFAD scattering.8,12,21,22 Not only are classical trajectories relatively easy to determine, the essential aspects of the quantum behaviour are included through interference effects between the relevant classical trajectories. The method becomes particularly advantageous when combined with perturbation methods and a Morse-type potential23,24 as analytic results can then be derived. One key result of this general analysis is that when the scattering plane is parallel to a low-index direction of the surface the three-dimensional scattering potential is reduced to a two-dimensional effective potential, the well known axial surface channeling approximation (ASCA),1,9,25 while away from low-index directions, diffraction is suppressed and the effective potential becomes time-dependent.
Fig. 1 illustrates the scattering geometry for the case when the scattering plane is misaligned by a small angle, ϕ, with respect to a low index direction of the surface (y in Fig. 1). The scattering plane itself is defined by the incident direction and the surface normal, z. By definition it also includes the specularly scattered beam (shown red). Other directions for elastic scattering lie on the Ewald sphere, of constant wavevector modulus (shaded green) at points corresponding to changes in wavevector ΔK = Gjk, where Gjk are the reciprocal lattice vectors. Fig. 1 indicates the projection of the reciprocal lattice through lines of constant j and k, where the intersections define the G-vectors. In grazing incidence fast atom diffraction (GIFAD), the basic phenomenology is that diffraction in the scattering plane is suppressed compared with diffraction out of the scattering plane. Furthermore, diffraction out of the plane is only observed when a low index direction is closely aligned with the scattering plane. In the latter case, as sketched in Fig. 1, diffraction peaks with k = 0 and j ≠ 0 are observed, as shown by the dots in the figure. These two aspects of the phenomenology are the subject of the present work, where we derive analytic results within a semi-classical analysis using a scattering potential of Morse form, coupled with first-order perturbation theory. The validity of our approach is confirmed by comparison with experimental results for the scattering of He from LiF(001).
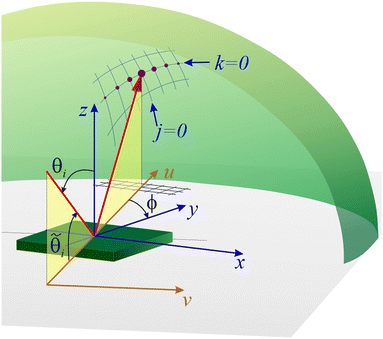 |
| | Fig. 1 Schematic diagram showing the scattering geometry, and defining some of the variables used in the text. The incident direction for scattering is in the plane containing the laboratory coordinate, u, and the surface normal, z. It is conventionally referred to as the scattering plane. In the diagram, the specularly scattered beam (red line) is the only scattered component that lies entirely in the scattering plane (lightly shaded). Other directions for elastically scattered particles lie on the Ewald sphere (green shading) according to the projection of the reciprocal lattice, Gj,k, (indicated by blue lines of constant j and k) onto the sphere. The scattering geometry shown corresponds to a rotation, ϕ, of the surface about its normal, z. Angles in the diagram have been exaggerated for clarity; for example, the grazing angle of incidence ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i is typically a few milli-radians. i is typically a few milli-radians. | |
2 Semiclassical perturbation theory. Grazing incidence and specular scattering
One of the features of grazing incidence scattering along a low index direction is that, in the scattering plane, one observes only a single elastic scattering peak. There are no observable Bragg peaks other than the specular one. With high incident energies, the extremely fast motion along the incident direction underlies this phenomenon. The purpose of this Section is to demonstrate qualitatively and quantitatively how this comes about, using a semi-classical scattering theory within a framework of time-dependent perturbation theory.
For this purpose we first define the conditions of the “standard” scattering experiment in three degrees of freedom. One is the vertical coordinate z (with conjugate momentum pz) describing the distance of the atom from the surface, the other two are the horizontal coordinates x and y (with conjugate momenta px and py) for motion parallel to the surface. The Hamiltonian for an atom of mass M colliding with a corrugated surface is
| |  | (1) |
Assuming that the symmetry axes of the surface are along the horizontal
x and
y coordinates, and that the potential is periodic along these coordinates with periods
lx and
ly allows us to write the potential as
| |  | (2) |
where the prime in the sum implies that the summation does not include the case that
j =
k = 0. We have introduced the “corrugation heights”
hjk which are assumed to be much smaller than the respective lattice lengths and so play the role of the perturbation parameters. At a later stage we will compare the theory with experiments involving LiF(001) and, for that purpose, we set
Vjk(
z) =
Vkj(
z) and
lx =
ly and, in the spirit of earlier work,
26 we take the

. The
hjk parameters are typically unequal and define the corrugation of the potential.
For the zero-th order dynamics, the only potential governing the dynamics is the vertical potential V00(z). In the general scattering case, the particle is initiated at the time −t0 with initial vertical (negative) momentum pzi and horizontal momenta pxi and pyi. To zero-th order, at t = 0 the particle impacts the surface. We are then interested in the final momenta of the particle at the time +t0, which is taken to be sufficiently large to assure that the scattering event is over. In the analytical formalism developed below, we then take the limit t0 → ∞.
At this point we identify the GIFAD direction to be along the y axis. The scattering plane is then defined by the y and z coordinates. The angle of incidence
| |  | (3) |
is close to −π/2 since the central property of GIFAD scattering is that the incident momentum
pyi along the horizontal
y direction is much larger than the magnitude of the (negative) momentum
pzi in the vertical direction. Most often, in GIFAD the small complementary angle
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i
i = π/2 −
θi is used to describe the grazing angle of incidence referred to the surface plane.
The exact quantum final momentum distribution for an initial state characterized by the initial momenta pyi, pzi and ending with the final momenta pyf, pzf with amplitude Wk for a transition to the k-th Bragg channel is
| |  | (4) |
where in the argument of the second delta function we have used the notation
| |  | (5) |
to express the Bragg condition and
k is referred to as the Bragg index. The final angular distribution is obtained by integrating the momentum probability over all final momenta subject to the condition that

.
The central purpose of this Section is to use semiclassical perturbation theory to understand why one observes experimentally only the k = 0 (specular) Bragg peak. For this purpose, we summarize the first and second-order semiclassical perturbation theory results derived previously,24,27,28 for a single sine corrugation function such that h10 ≡ h and all other corrugation amplitudes vanish. This implies that the effective two dimensional GIFAD Hamiltonian, takes the form
| |  | (6) |
where the corrugation height
h is assumed to be much smaller than
ly.
The first-order expression for the probability of observing the k-th Bragg peak is24
| |  | (7) |
where
Jk denotes the
k-th order Bessel function, the action
Ay being
| | 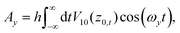 | (8) |
where
z0,t is the zero-th order trajectory in the vertical direction that hits the turning point at the time
t = 0. The central object for our purpose is the horizontal frequency
ωy defined as
| |  | (9) |
Due to the fast GIFAD motion along
y (also following the spirit of ASCA), this frequency is much larger than the inverse of the collision time, implying that many cycles along
y are traversed during the collision. In other words, as we shall also see below, the time averaging implied in
eqn (8) causes the action
Ay to essentially vanish, leaving a contribution in
eqn (7) only for
k = 0. The term in the pre-factor,
X1, is
| | 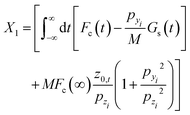 | (10) |
with
| |  | (11) |
and
| |  | (12) |
Here too, due to the fast GIFAD motion, we expect
X1 to be extremely small.
2.1 First order perturbation theory treatment for a Morse potential model
Beyond the general observation that the fast oscillation due to ωy causes all quantities to vanish, it is of interest to understand analytically, the (small) magnitudes involved in the various parameters. It is possible to do this analytically if one specifies the interaction potential to have the Morse form| | ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) M(z) = D[(exp(−αz) − 1)2 − 1], M(z) = D[(exp(−αz) − 1)2 − 1], | (13) |
which is defined through the physisorption well depth D and the stiffness parameter α. In order to simplify the final expressions, the following notations are used| | 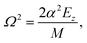 | (14) |
| |  | (15) |
and| |  | (16) |
where Ez = pzi2/2M and θi is the (negative) angle of incidence.
When applied to GIFAD, the first order treatment leads to the following analytical results:
| |  | (17) |
| |  | (18) |
| | 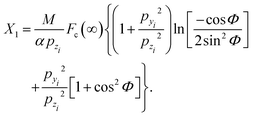 | (19) |
The GIFAD limit, in which the horizontal incident momentum is much larger than the vertical implies that the “frequency”
| | ![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) ≫ 1. ≫ 1. | (20) |
In this limit then
| |  | (21) |
Since the angle
Φ is always less than π (see
eqn (15)) we find that
Fc(∞) is exponentially small in the GIFAD limit and the same will be the case for the parameter
X1 which has the dimensions of length. In this limit, the action appearing in the expression for the scattering amplitude is
| |  | (22) |
and it is also exponentially small. Noting the series expansion of the Bessel functions
| |  | (23) |
one finds that the first non-zero diffraction peaks will be given approximately by
| |  | (24) |
while the specular peak will be given by
| |  | (25) |
we then note from
eqn (22) that
| | 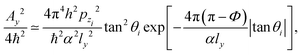 | (26) |
while from
eqn (19) and (21)| | 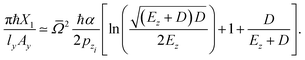 | (27) |
The non-zero Bragg components are truly exponentially small. Interestingly, in the GIFAD limit, irrespective of the value of the energy in the vertical (
z) direction, the reduced prefactor (
X1/
l) is larger than the reduced action (
Ay/
ħ); however, it is also exponentially small.
The second order treatment for a Morse potential model is presented in Appendix A, the conclusions are the same.
2.2 First order perturbation treatment for a repulsive potential model
These results may be even further simplified by assuming that the central contribution to the action comes from motion close to the turning point of the unperturbed vertical trajectory. If we ignore the well and only assume an exponential wall| | V(z) = Ve![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2αz), exp(−2αz), | (28) |
then we readily find that| | 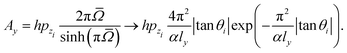 | (29) |
the Morse potential result for Ay reduces to the same in the limit that the vertical momentum is much larger than the well-depth, since in this limit the angle Φ → π/2. We also find that| |  | (30) |
and the prefactor term, X1, is no longer important. However, this will be the case only if| |  | (31) |
so that for most physical cases, it is the prefactor (X1) that will dominate. This is important since most implementations of semiclassical theory ignore this prefactor.
Finally, let us compare with the result (eqn (38)) derived by Henkel et al.,29 for cold atoms reflected/diffracted on an evanescent standing light-wave and recently adapted to GIFAD.30 In their notation,
| |  | (32) |
where
| |  | (33) |
the identification of their notation with ours is that
| | 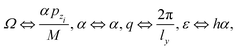 | (34) |
so that
| |  | (35) |
| |  | (36) |
As commented above, their theory does not take the prefactor into consideration. However, qualitatively the result is the same, the ratio of the lowest diffraction peaks to the specular one is exponentially small.
3 General theory for GIFAD
The purpose of this Section is to understand what the implications of a GIFAD scattering experiment are for theoretical analysis. We will distinguish between a GIFAD experiment in which the GIFAD direction is along one of the low-index directions in the surface and when it is at an angle (necessarily small) to it. To simplify, we will assume a surface with a square unit-cell so that lx = ly ≡ l, but the same considerations are applicable to other geometries.
In the GIFAD experiment, there is a direction in which the momentum parallel to the surface is very large. We thus transform from the x, y coordinates which characterize the surface to the coordinates u and v where by construction the fast GIFAD direction is along u
In the GIFAD experiment, the velocity in the GIFAD direction is extremely fast, such that it creates an effective Hamiltonian for the other two degrees of freedom. This assumption of fast motion implies that one could first time average over the fast motion, and this leads to the following relations
| |  | (39) |
| |  | (40) |
where
δk,j is the Kronecker delta function. The averaging is such that the motion along the two degrees of freedom
v,
z perpendicular to the GIFAD direction
u is much slower than the GIFAD motion, so the time average implied by the brackets is identical to a spatial averaging over the GIFAD coordinate.
The potential as given in eqn (2) in terms of the three coordinates x, y, z is also rewritten in terms of the coordinates u, v, z as
| | 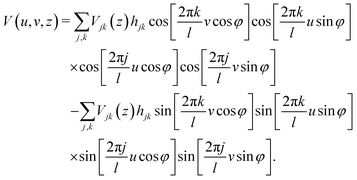 | (41) |
to implement the necessary averaging we note, using the standard trigonometric identities
31 that the averaging as in
eqn (39) and (40) implies that
| | 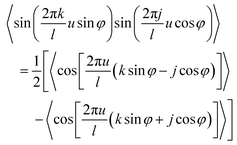 | (42) |
and
| |  | (43) |
From these results, one readily deduces that, with the exception of the specular channel, j = k = 0, the averages vanish unless tanφ = ±j/k. The most important cases are the low index directions with φ = 0, ±π/2, ±π/4, corresponding to j, k ∈ {0,±1}, which we discuss below. The scattering is particularly interesting near to these low index directions as we show.
3.1 Scattering along a low-index direction
Having in mind a surface such as LiF(001), and a square unit cell, we consider the two low directions namely: [110] and [100]. For the [110] case, we may assume that the GIFAD coordinate u = y so that time averaging of the GIFAD fast motion over the full potential as in eqn (2) one readily finds that the dynamics is reduced to two degrees of freedom.| |  | (44) |
The 100 case would then correspond to the choice φ = π/4 so that from eqn (42) and (43) we have| |  | (45) |
and| |  | (46) |
This implies that after averaging over the GIFAD coordinate| |  | (47) |
Eqn (44) and (47) have two consequences. One is that the uncoupled component of the vertical potential (V00(z)) must be the same for scattering in both the [110] and [100] directions. Secondly, the potentials Vk0(z), which determine the diffraction along [110] are, in general, different from the Vkk(z), which affect scattering along [100]. The two azimuths provide complimentary information and, as we shall see in the next subsection, knowing these potentials puts some clear limitations on the effective equations of motion when the GIFAD axis is no longer a low-index direction.
3.2 Scattering close to a low-index direction
Here we consider scattering when the incident azimuth is close to, but not exactly parallel with, a low-index direction in the crystal plane. Our analysis shows that the magnitude of the deviation from the low-index direction, as expressed in the angle δϕ is critical. As already discussed above, if it is too large, then one remains only with specular scattering from the zero-th order scattering potential V00(z). It follows that measurements of the diffraction pattern as a function of the angle δϕ will provide information on the surface averaged potential potential V00(z). The two lowest index directions, 〈100〉 and 〈110〉, are considered separately.
3.2.1 Close to the 〈100〉 direction.
Let us consider first when the GIFAD direction is close to the 100 direction, such that| |  | (48) |
It is then a matter of straightforward algebra to show that the potential as in eqn (41) is rewritten as| |  | (49) |
In Appendix B, the angular average over the GIFAD motion is carried out. The interaction potential is then written in terms of the v and z variables, leading to the conclusion that V(v, z) is a time-dependent effective potential with two degrees of freedom.
3.2.2 Close to the 〈110〉 direction.
Here we assume that the azimuthal angle of incidence is δϕ so that following the same kind of derivation, one finds after some algebra that the GIFAD averaged potential is| |  | (50) |
and here too the scattering problem is reduced to two degrees of freedom but with a time-dependent potential.
4 Perturbation theory for scattering close to low-index directions
Here we make a connection between the time-dependent potentials, derived in the previous section, and experiments that reveal the dependence of the diffraction pattern on the deviation in angle from the the low-index directions.5 For this purpose, we calculate the distributions of diffraction intensities using first-order perturbation theory. We then use the second-moment of that distribution, its variance, as a measure of the width of the pattern in order to make a direct comparison with experiment.5
Analytic results may be obtained if we restrict the potential to the first term in each Fourier series giving
| |  | (51) |
for incidence close to the 〈100〉 direction and
| |  | (52) |
for incidence close to 〈110〉.
In the zeroth order motion, the particle moves only along the GIFAD direction u so that the perpendicular surface coordinate v is static. Without loss of generality, we may set it as v = 0. From eqn (44) and (45) we then conclude that xt = ut![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δϕ. The free motion along u, is
δϕ. The free motion along u, is
| |  | (53) |
so that the velocity along the
x direction is (
pu/
M)sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
δ
ϕ and this identifies the frequency in the
x direction
ωx (see
eqn (9)) as
| |  | (54) |
The significance of the lateral frequency ωx is the same as in Section 2. Note that ωx establishes a connection to the simplified ASCA formalism where the angle δϕ is reduced to an initial momentum px = pu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δϕ in an approximate stationary Hamiltonian.10 Ignoring the prefactor, the k-th diffraction peak is given within first order perturbation theory, as before, by
δϕ in an approximate stationary Hamiltonian.10 Ignoring the prefactor, the k-th diffraction peak is given within first order perturbation theory, as before, by
| |  | (55) |
where
Jk is the integer Bessel function and the action,
Ax, is
| |  | (56) |
for the 〈100〉 direction and
| |  | (57) |
for the 〈110〉 direction, which we evaluate below. When the incident direction is a low-index direction, δ
ϕ = 0, we have
ωx = 0 so that
![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif)
= 0 and the action is 2
hpzi. The diffraction pattern along the
x direction will be symmetric and its width will depend on the incident vertical momentum. Well away from a low-index direction, when the offset angle is such that
![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif)
≫ 1, the action will be exponentially small and only specular scattering is possible. This condition implies that (
vzi = |
pzi/
M| is the magnitude of the incident velocity in the vertical direction)
| |  | (58) |
if 2π/
lα is of the order of unity, the inequality is satisfied when δ
ϕ ≫
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif)
, the grazing angle of incidence, since
vzi =
vG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif)
.
Between these two limits (i.e. when δϕ ∼ ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ), the action is a decreasing function of the offset angle δϕ and we expect the width of the diffraction pattern to decrease as a function of increasing offset angle δϕ.
), the action is a decreasing function of the offset angle δϕ and we expect the width of the diffraction pattern to decrease as a function of increasing offset angle δϕ.
The manner in which the diffraction shrinks towards the specular peak offers a direct point of comparison between the predictions of first-order perturbation theory and the measure of the angular width of the diffraction pattern obtained in experiment.5
For a measure of the “width” of the diffraction pattern we use the second moment, or variance, of the diffraction intensities, which within the first order perturbation theory, is given by
| | σ2 = Σk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2Ik = Σk k2Ik = Σk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2Jk(Ax)2 = (Ax)2/2, k2Jk(Ax)2 = (Ax)2/2, | (59) |
where the final equality comes from a standard result.
32
The variance, σ2 is readily converted to an experimental, angular width σϕ using σϕ = ϕBσ, where the Bragg angle, ϕB = arctan(G⊥/py), is that for the respective low-index scattering geometry and is given by G⊥ = 2π/a⊥. The linear distance, a⊥, is that separating identical atomic rows, more commonly known as the width of the scattering channel (see, for example ref. 2, 9 and 22).
For a potential of the Morse form (see Section 2.1), values for the action follow from eqn (56) and (57), which lead to expressions identical to eqn (18). The angular standard deviation (σϕ = σϕB) is then
| |  | (60) |
The first term describes the scattering width in the well-aligned condition (δ
ϕ = 0 giving
![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif)
= 0) while the second term can be considered as the oblique incidence factor,
β(π
![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif)
). It has a value of 1 for
![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif)
= 0 and governs the evolution with δ
ϕ. It can be written in a form directly adapted to GIFAD coordinates by noting that close to a low index direction (δ
ϕ ≪ 1),
![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif)
= (
G⊥/
α)·(sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
δ
ϕ)/(sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i
i) ≃ (
G⊥/
α)·(δ
ϕ/
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i
i). Values for
ϕB and
h depend on the relevant low-index direction, while
D and
α define the mean planar potential (
eqn (13)).
5 Comparison with experiment
The results of the previous section make the general phenomenology clear: when aligned with a low index direction, ωx = 0 and the action Ax, given by eqn (56) and (57) is maximal. As the misalignment increases, so does ωx and oscillation of the cos(ωxt) terms reduces the value of the action leading to weaker diffraction as seen earlier in eqn (22).
We now compare the expression for the angular width of the diffraction pattern using eqn (60) with experiment at a quantitative level. Results from the helium LiF(001) system, recorded by Debiossac and Alarćon20 provide what is required. The experiment employed helium atoms whose incident energy is E0 = 460 eV with a grazing angle of incidence of ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i = 0.9° where the azimuth δϕ was varied in steps of 0.08° around the [100] and [110] directions using a setup described in ref. 33. As in the theory, the angular spread of the experimental diffraction pattern is obtained from the variance of the diffracted intensities
i = 0.9° where the azimuth δϕ was varied in steps of 0.08° around the [100] and [110] directions using a setup described in ref. 33. As in the theory, the angular spread of the experimental diffraction pattern is obtained from the variance of the diffracted intensities
| | σ2 = ΣkIk(k − ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )2 with )2 with ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) = ΣkkIk. = ΣkkIk. | (61) |
Note that the experimental variance is calculated without assuming symmetry of the diffraction pattern,
Ik =
I−k, which is implicit in first-order perturbation theory in
eqn (55). For each value of δ
ϕ, diffracted intensities have been evaluated after correction for inelastic and Debye–Waller effects, as detailed in ref.
34.
Fig. 2 and 3 show the experimental behaviour (discrete data points), compared with the results of first-order perturbation theory (solid and dashed lines). The diffraction width, shown in Fig. 2, decreases as the azimuthal misalignment, δϕ, increases, while the corresponding changes to the specularly scattered intensity can be seen in Fig. 3. In both azimuths, the diffraction width decreases uniformly towards zero and the specular intensity increases towards unity, though not monotonically in the case of the [110] azimuth, where the behaviour can be related to the supernumerary rainbow structure.35
 |
| | Fig. 2 Evolution of the relative scattering width σϕ/θi (eqn (61)) with the azimuthal misalignment angle δϕ around the [100] ( ) and [110] ( ) and [110] ( ) directions.20 The red lines result from eqn (60)i.e. without use of the Bessel function. The corrugations h11 and h10 are derived at δϕ = 0 while α and D are taken from literature and reported in Table 1. The inset shows a ϕ-scan taken from ref. 5 where both peaks appear at their absolute location. ) directions.20 The red lines result from eqn (60)i.e. without use of the Bessel function. The corrugations h11 and h10 are derived at δϕ = 0 while α and D are taken from literature and reported in Table 1. The inset shows a ϕ-scan taken from ref. 5 where both peaks appear at their absolute location. | |
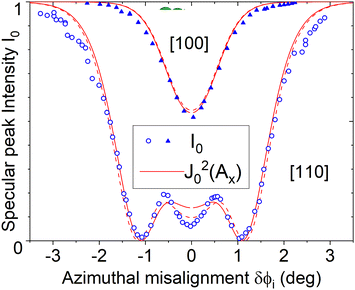 |
| | Fig. 3 Evolution of the specular beam intensity I0 for the azimuthal direction close to the [100] and [110] directions. The red lines are for J0(Ax) with Ax given in eqn (60) and h measured at δϕ = 0°. The full line corresponds to h derived from σ (eqn (61)) as in Fig. 2 and Table 1. The dotted lines correspond to h′ derived from the fit of all the measured intensities Ik by Bessel functions in eqn (54) giving 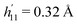 and and  . . | |
In the calculations we use eqn (60) to generate the curves in Fig. 2, and eqn (55) to generate the curves in Fig. 3. To illustrate the robustness of the perturbation analysis, we choose parameters close to ones derived from earlier work (see Table 1), rather than simply fitting eqn (55) and (60) to the experimental data.
Table 1 Parameter values used in the calculation shown in Fig. 2 and 3. The values for h are within a few percent from those measured in ref. 1, 2 and 36, D is consistent with precise measurements via bound state resonances3,6 while values of α are rarely reported (see text)
| Direction |
a
⊥/Å |
h/Å |
D/meV |
α/Å−1 |
| 100 |
2.01 |
0.07 |
8.6 |
1.95 |
| 110 |
2.86 |
0.28 |
8.6 |
1.95 |
In Fig. 3, the experimental data for the [110] azimuth, shows the specular intensity having local maxima and minima. These correspond to interference effects due to the surface corrugation and, as expected, they are sensitive to the precise value of the parameters h11 and h10, corresponding to the [110] and [100] directions respectively. The solid curve in Fig. 3 corresponds to h11 = 0.28 Å, the same value as in Fig. 2, while the dashed line corresponds to a value of  . The 12% greater corrugation of the dashed curve illustrates the sensitivity of the diffraction intensities to the precise value of the corrugation.
. The 12% greater corrugation of the dashed curve illustrates the sensitivity of the diffraction intensities to the precise value of the corrugation.
Our analysis shows that the theory and experiment are in close agreement throughout, demonstrating that first-order perturbation theory provides a useful and quantitative description of GIFAD scattering.37,38 In addition, the analysis confirms the origin of the phenomena in terms of the time averaging of the potential over the collision time along the grazing incidence trajectory.
6 Discussion and conclusions
In the present manuscript we have demonstrated that semi-classical perturbation theory provides a semi-quantitative description of fast atom diffraction near grazing incidence (GIFAD). We have considered two related situations. In the first case (Section 2), the surface corrugation is restricted to lie in the scattering plane and we showed that first-order perturbation theory correctly reproduces the basic phenomenology of GIFAD, whereby the scattering is directed exclusively into the specular channel. The effect is well known and arises from time averaging, of the corrugation in the surface potential during the interaction. Our model describes the averaging in the classical action (eqn (8)) in terms of a horizontal frequency (eqn (9)), which is zero at normal incidence, and increases with the angle of incidence θi, which is to say as grazing incidence is approached. The derivation also provides a prefactor, which was absent in previous work.29
Our analysis of the more general case where the potential, V(x, y, z), is fully 3-dimensional (Section 3) shows that, along low-index directions, the 3D potential reduces to a static 2D potential V(x, z), where x is the coordinate perpendicular to the plane of the incident motion. Our derivation provides an origin for ASCA,9 which was developed initially using classical mechanics as an evolution of the axial channeling approximation in crystals39 and has been verified quantum mechanically.10
When the scattering plane is not aligned exactly with a low-index direction, an attempt to reduce the 3D potential to an effective 2D case is only possible if the 2D potential has a time dependence (eqn (89) and (50)). That time dependence implies another horizontal frequency, in this case along a direction perpendicular to the low-index direction. The phenomenology, and the quantitative estimates of changes to the scattering, are closely related to those discussed above. The horizontal frequency (eqn (54)) is zero when δϕ = 0 and the scattering plane is aligned exactly with a low-index direction. The alignment maximises the action (eqn (56)) and the out-of-plane diffraction. Increasing the value of δϕ leads to an increase in the horizontal frequency, ωx, and reduced diffraction. Eventually all of the scattering is directed into the specular peak, as illustrated in Fig. 2 and 3, as observed in experiment.40 In effect, the corrugations in the surface plane are averaged in both directions and the surface appears as a perfect mirror.
It is remarkable how well the first-order theory reproduces the experimental observations in Fig. 2 and 3. Also, we note that the numerical values used for the parameters are similar to those found in earlier work.20,22,37,40 For example, the corrugation amplitudes h10 and h11 are close to those obtained from an analysis of the relevant low-index diffraction.1,2,36 The well-depth, D, is taken from the best theoretical estimates41–43 using bound-state resonance measurements in the thermal energy regime. The range of the potential, as measured by the Morse parameter, α, is more difficult to pin down and it may be that the analysis we describe here offers a more direct route to obtain experimental values for this quantity. Theoretical estimates for α can be extracted from the same work that gives the well-depth. The Fowler, Hutson potential,42 for example, is consistent with a value of α = 1.4 Å−1, which is 28% less than the value used in Fig. 2 and 3. Second-order perturbation theory corrections may contribute to these differences in α. However, we also note that the theoretical potentials are optimised in the low energy regime (Ez = Ei![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi ≤ 50 meV), rather than being specifically tuned to the normal-energies in GIFAD, which may be an order of magnitude greater.
θi ≤ 50 meV), rather than being specifically tuned to the normal-energies in GIFAD, which may be an order of magnitude greater.
Fig. 3 shows that measurements of the specular intensity are well reproduced by first-order theory. As we have noted, first-order theory generates a scattering distribution that is symmetrical, whereas the experimental distribution shows some asymmetry. The first-order theory also reproduces the width of the scattering distribution extremely well, as can be seen in Fig. 2. Second order perturbation theory, as shown for example in Pollak and Miret-Artés,24 is required to reproduce the observed asymmetry in the diffraction pattern.
Our analysis in Fig. 2 and 3 illustrates the sensitivity of such measurements to the range of the repulsive potential as defined by α and suggests a new avenue to extract such information from experiment. For example, the width of the bell-shaped peaks, in Fig. 2 is directly related to the range of the potential as can be seen by evaluating the variance of the incidence factor, β(π![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) ), in eqn (60). Considering the case where E ≫ D, so that Φ = π/2, the width of the obliquity function is analytic by noting that
), in eqn (60). Considering the case where E ≫ D, so that Φ = π/2, the width of the obliquity function is analytic by noting that  so that in the GIFAD coordinates, the width takes a remarkably compact form.
so that in the GIFAD coordinates, the width takes a remarkably compact form.
| |  | (62) |
Notice that the width scales with α/G⊥ and that is precisely what is seen in Fig. 2 when the widths of the two azimuths are compared, since α is defined from the mean planar potential, V00, and is identical in both azimuths (eqn (51) and (52)).
We have given a general derivation of the GIFAD Hamiltonian, which turns out to be time dependent. To gain a more intimate understanding of the processes involved we limited ourselves, in the present work, to first order perturbation theory. In principle, the diffraction patterns for the resulting time dependent Hamiltonian may be computed numerically exactly. There is no need to limit oneself to perturbation theory. However, it is gratifying to see that first order perturbation theory does account for the main experimental features, especially away from the symmetry axis.
The theoretical analysis presented in this paper is based on some assumptions. One is a Morse potential interaction along the vertical direction. The Morse potential captures two important effects – the short range repulsion and the existence of a physisorption well. It does not have the very long range attractive properties of the vdW potential. For the phenomena considered here, it is these first two factors which significantly affect the measured diffraction pattern. Only at very low energy should one expect that the exact shape of vdW long range attractive potential becomes important. Secondly, we assumed that the next order vertical interaction terms are given by the derivative of the Morse potential  . Thirdly, we limited ourselves to first order perturbation theory. All of these limitations may be relaxed but perhaps most prominently is the fact that second order perturbation theory can account for the asymmetry in the diffraction pattern when measured away from the symmetry direction. This remains a topic for future consideration.
. Thirdly, we limited ourselves to first order perturbation theory. All of these limitations may be relaxed but perhaps most prominently is the fact that second order perturbation theory can account for the asymmetry in the diffraction pattern when measured away from the symmetry direction. This remains a topic for future consideration.
In summary, the present work reinforces the value of perturbation theory, combined with a semi-classical analysis, as a quantitative description of GIFAD scattering.38 Our methods emphasise the origin of the averaging of the lateral potential that takes place, through expressions for the classical action such as eqn (8), (55) and (56). The first-order theory provides simple analytic expressions, which provide an excellent, quantitative description of the width σϕ of the azimuthal diffraction pattern and its evolution with the angular deviation δϕ away from the low symmetry direction. It gives the triangulation technique a quantitative basis. The widths measured during a ϕ-scan (see inset in Fig. 2 and ref. 44 and 45) show peaks indicating low-index directions, where their height and width are given by  and σT/
and σT/![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i = α/G⊥π (eqn (60) and (62)) respectively. The analysis outlines, as simply as possible, the role of the corrugation amplitude h and stiffness α. We note that second-order theory, which we describe in Appendix A, allows the discussion to be extended to the observed asymmetries in the diffraction pattern.46 Perturbation theory can also address more complex forms of the interaction potential allowing, for instance the investigation of the effect of the location of the attractive well.12
i = α/G⊥π (eqn (60) and (62)) respectively. The analysis outlines, as simply as possible, the role of the corrugation amplitude h and stiffness α. We note that second-order theory, which we describe in Appendix A, allows the discussion to be extended to the observed asymmetries in the diffraction pattern.46 Perturbation theory can also address more complex forms of the interaction potential allowing, for instance the investigation of the effect of the location of the attractive well.12
Author contributions
All authors contributed equally to this work.
Data availability
All data supporting the findings of this study are included within the article.
Conflicts of interest
There are no conflicts to declare.
Appendices
A review of semiclassical second order perturbation treatment. Application to a Morse potential model
The second-order expression for the diffraction intensities24 is similar in form to eqn (7):| | 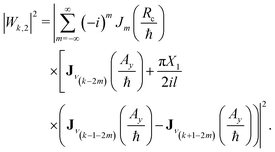 | (63) |
Here, Jν(x) is no longer the Bessel function but the Anger function of order ν. The argument Rc is| |  | (64) |
with| |  | (65) |
we also used the notation| | 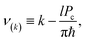 | (66) |
with| |  | (67) |
and| |  | (68) |
| |  | (69) |
For the Morse potential model, one finds the explicit expressions
| | 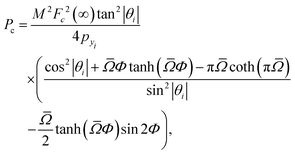 | (70) |
and
| | 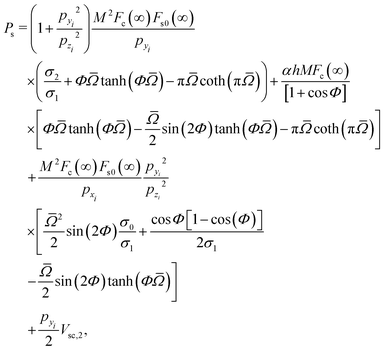 | (71) |
and
| |  | (72) |
Compared to the first order treatment, one finds the same conclusion when considering the second-order perturbation theory results. In the GIFAD limit one readily finds that
| |  | (73) |
| | Ax = 2hpziπ![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(π − Φ) exp[−(π − Φ)![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) ] ] | (74) |
| |  | (75) |
| |  | (76) |
with
| |  | (77) |
and
| |  | (78) |
and
| |  | (79) |
| | 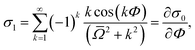 | (80) |
| |  | (81) |
Since
Pc is exponentially smaller than
Fc(∞) it can be set to 0, and in this limit
| |  | (82) |
and the Anger function becomes the integer Bessel function
| |  | (83) |
The second-order expression is then
| |  | (84) |
and perhaps as might be expected, this leading order term is precisely the same as in the first-order perturbation theory.
To summarise this Appendix, we have shown that the very fast motion in the GIFAD direction leads to an exponentially small probability for measuring a nonzero diffraction peak in this direction, as also observed experimentally. From the analysis above, it is clear that adding in the second horizontal coordinate y which is perpendicular to the GIFAD plane will not change this conclusion. The very large frequency ωx leads to the same physics.
The principal difference between the second and first order theories is that away from the GIFAD direction, the second order theory diffraction pattern is not necessarily symmetric about the elastic peak, in qualitative agreement with experimental observations.
B Angular averaging
In this Appendix we detail some of the derivation leading to the time dependent GIFAD Hamiltonian. To perform the average over the fast GIFAD motion, let us consider the various terms| | 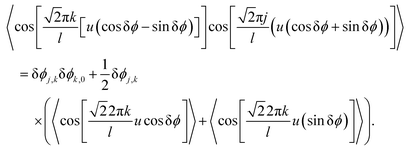 | (85) |
Similarly, one has that
| |  | (86) |
and
| | 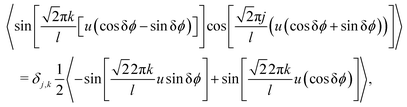 | (87) |
and finally
| |  | (88) |
As before, since cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
δ
ϕ ≃ 1 the averaging of the terms

and

will make them vanish. However, the averaging over terms such as

is no longer clear due to the small magnitude of δ
ϕ. Due to the fast GIFAD motion, one could assume that the time dependence of the GIFAD coordinate is known. So, if the scattering process starts at the time −
t0 we know that the motion along the GIFAD direction is the free particle motion as given in
eqn (53). and therefore averaging over the fast motion will leave us with
| |  | (89) |
leading to a time-dependent effective potential with two degrees of freedom.
Acknowledgements
EP thanks the Israel Science Foundation for its generous support. WA acknowledges support from the Cambridge Atom Scattering Facility (https://atomscattering.phy.cam.ac.uk) and EPSRC award EP/T00634X/1. SMA acknowledges support of a grant from the Ministery of Science, Innovation and Universities with Ref. PID2023-149406NB-I00.
Notes and references
- H. Winter and A. Schüller, Prog. Surf. Sci., 2011, 86, 169–221 CrossRef CAS.
- M. Debiossac, P. Pan and P. Roncin, Phys. Chem. Chem. Phys., 2021, 23, 7615 RSC.
- M. Debiossac, A. Zugarramurdi, P. Lunca-Popa, A. Momeni, H. Khemliche, A. Borisov and P. Roncin, Phys. Rev. Lett., 2014, 112, 023203 CrossRef CAS PubMed.
- G. A. Bocan, H. Breiss, S. Szilasi, A. Momeni, E. M. Casagrande, M. S. Gravielle, E. A. Sánchez and H. Khemliche, Phys. Rev. Lett., 2020, 125, 096101 CrossRef CAS PubMed.
- M. Debiossac, P. Roncin and A. G. Borisov, J. Phys. Chem. Lett., 2020, 11, 4564–4569 CrossRef CAS PubMed.
- A. P. Jardine, S. Dworski, P. Fouquet, G. Alexandrowicz, D. J. Riley, G. Y. Lee, J. Ellis and W. Allison, Science, 2004, 304, 1790–1793 CrossRef CAS PubMed.
- B. Holst, G. Alexandrowicz, N. Avidor, G. Benedek, G. Bracco, W. E. Ernst, D. Faras, A. P. Jardine, K. Lefmann and J. R. Manson,
et al.
, Phys. Chem. Chem. Phys., 2021, 23, 7653–7672 RSC.
- J. Manson, H. Khemliche and P. Roncin, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 155408 CrossRef.
- A. Zugarramurdi and A. G. Borisov, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 062903 CrossRef.
- A. Zugarramurdi and A. G. Borisov, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 062902 CrossRef.
- A. Muzas, F. Gatti, F. Martín and C. Díaz, NIM-B, 2016, 382, 49–53 CrossRef CAS.
- W. Allison, S. Miret-Artés and E. Pollak, Phys. Chem. Chem. Phys., 2022, 24, 15851–15859 RSC.
- A. Ruiz, J. P. Palao and E. J. Heller, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 052901 CrossRef.
- D. Farías, C. Díaz, P. Rivière, H. F. Busnengo, P. Nieto, M. F. Somers, G. J. Kroes, A. Salin and F. Martín, Phys. Rev. Lett., 2004, 93, 246104 CrossRef PubMed.
- P. Nieto, D. Barredo, D. Farías and R. Miranda, J. Phys. Chem. A, 2011, 115, 7283–7290 CrossRef CAS PubMed.
- M. Busch, J. Seifert, E. Meyer and H. Winter, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 241402 CrossRef.
- Note that the result observed in ref. 16 corresponds to specific conditions where ly ≫ lx and only with δϕ ≫
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i and comparatively low total energy. This is not in contradiction with the present paper as discussed in ref. 10 but would deserve a specific treatment beyond the general situation presented here.
i and comparatively low total energy. This is not in contradiction with the present paper as discussed in ref. 10 but would deserve a specific treatment beyond the general situation presented here.
- P. Rousseau, H. Khemliche, A. G. Borisov and P. Roncin, Phys. Rev. Lett., 2007, 98, 016104 CrossRef CAS PubMed.
- A. Schüller, S. Wethekam and H. Winter, Phys. Rev. Lett., 2007, 98, 016103 CrossRef PubMed.
- A. Zugarramurdi, M. Debiossac, P. Lunca-Popa, L. Alarcón, A. Momeni, H. Khemliche, P. Roncin and A. Borisov, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 012904 CrossRef.
- M. Gravielle, A. Schüller, H. Winter and J. Miraglia, NIM-B, 2011, 269, 1208–1211 CrossRef CAS.
- G. A. Bocan, H. Breiss, S. Szilasi, A. Momeni, E. M. S. Casagrande, E. A. Sánchez, M. S. Gravielle and H. Khemliche, Phys. Rev. B, 2021, 104, 235401 CrossRef CAS.
- S. Miret-Artés, S. Daon and E. Pollak, J. Chem. Phys., 2012, 136, 204707 CrossRef PubMed.
- E. Pollak and S. Miret-Artés, J. Phys. Chem. C, 2015, 119, 14532–14541 CrossRef CAS.
- R. Pfandzelter and M. Schuster, Nucl. Instrum. Methods Phys. Res., Sect. B, 1988, 33, 898–904 CrossRef.
- S. Miret-Artés and E. Pollak, Surf. Sci. Rep., 2012, 67, 161–200 CrossRef.
- L. M. Hubbard and W. H. Miller, J. Chem. Phys., 1983, 78, 1801 CrossRef CAS.
- L. M. Hubbard and W. H. Miller, J. Chem. Phys., 1984, 80, 5827–5831 CrossRef CAS.
- C. Henkel, J.-Y. Courtois and A. Aspect, J. Phys. II, 1994, 4, 1955–1974 CrossRef CAS.
- M. Debiossac and P. Roncin, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 054701 CrossRef.
-
M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, 1965, vol. 361 Search PubMed.
-
I. S. Gradshteyn and I. M. Ryzhik, Table of integrals, series, and products, Academic Press, 2014 Search PubMed.
- P. Pan, J. N. Rad and P. Roncin, Rev. Sci. Instrum., 2022, 93, 093305 CrossRef CAS PubMed.
- P. Pan, C. Kanitz, M. Debiossac, A. Le-Guen, J. N. Rad and P. Roncin, Phys. Rev. B, 2023, 108, 035413 CrossRef CAS.
- G. Boato, P. Cantini, U. Garibaldi, A. Levi, L. Mattera, R. Spadacini and G. Tommei, J. Phys. C: Solid State Phys., 1973, 6, L394 CrossRef CAS.
- A. Momeni, P. Soulisse, P. Rousseau, H. Khemliche and P. Roncin, e-J. Surf. Sci. Nanotechnol., 2010, 8, 101–104 CrossRef CAS.
- G. A. Bocan, H. Breiss, S. Szilasi, A. Momeni, E. M. S. Casagrande, E. A. Sánchez, M. S. Gravielle and H. Khemliche, Phys. Chem. Chem. Phys., 2023, 25, 33193–33197 RSC.
- W. Allison, S. Miret-Artés and E. Pollak, Phys. Chem. Chem. Phys., 2023, 25, 33198–33202 RSC.
- H. Krause, S. Datz, P. Dittner, J. G. del Campo, P. Miller, C. Moak, N. Nesković and P. Pepmiller, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 6036 CrossRef CAS PubMed.
- J. Seifert, A. Schüller, H. Winter and K. Gärtner, NIM-B, 2011, 269, 1212–1215 CrossRef CAS.
- V. Celli, D. Eichenauer, A. Kaufhold and J. P. Toennies, J. Chem. Phys., 1985, 83, 2504–2521 CrossRef CAS.
- P. W. Fowler and J. M. Hutson, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 3724 CrossRef CAS PubMed.
- D. J. Riley, A. P. Jardine, S. Dworski, G. Alexandrowicz, P. Fouquet, J. Ellis and W. Allison, J. Chem. Phys., 2007, 126, 104702 CrossRef CAS PubMed.
- N. Kalashnyk, H. Khemliche and P. Roncin, Appl. Surf. Sci., 2016, 364, 235–240 CrossRef CAS.
- F. E. Feiten, J. Seifert, J. Paier, H. Kuhlenbeck, H. Winter, J. Sauer and H.-J. Freund, Phys. Rev. Lett., 2015, 114, 216101 CrossRef PubMed.
- E. Pollak and S. Miret-Artés, J. Phys. Chem. C, 2015, 119, 14532–14541 CrossRef CAS.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
P.
Roncin
a,
P.
Roncin
 b,
W.
Allison
b,
W.
Allison
 c and
S.
Miret-Artés
c and
S.
Miret-Artés
 *d
*d


 . The hjk parameters are typically unequal and define the corrugation of the potential.
. The hjk parameters are typically unequal and define the corrugation of the potential.

![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i = π/2 − θi is used to describe the grazing angle of incidence referred to the surface plane.
i = π/2 − θi is used to describe the grazing angle of incidence referred to the surface plane.


 .
.


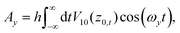

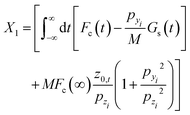


![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) M(z) = D[(exp(−αz) − 1)2 − 1],
M(z) = D[(exp(−αz) − 1)2 − 1],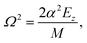




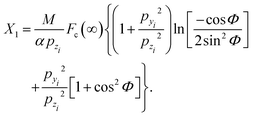
![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) ≫ 1.
≫ 1.




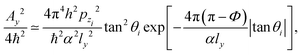
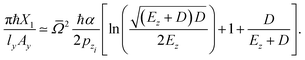
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2αz),
exp(−2αz),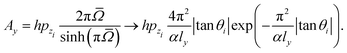




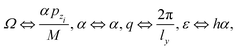


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ + y
φ + y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ,
φ,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ − y
φ − y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ.
φ.

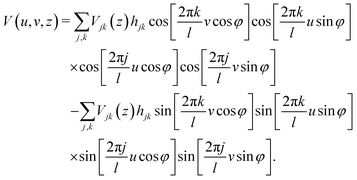
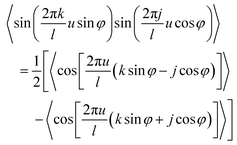










![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δϕ. The free motion along u, is
δϕ. The free motion along u, is
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δϕ and this identifies the frequency in the x direction ωx (see eqn (9)) as
δϕ and this identifies the frequency in the x direction ωx (see eqn (9)) as
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δϕ in an approximate stationary Hamiltonian.10 Ignoring the prefactor, the k-th diffraction peak is given within first order perturbation theory, as before, by
δϕ in an approximate stationary Hamiltonian.10 Ignoring the prefactor, the k-th diffraction peak is given within first order perturbation theory, as before, by


![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) = 0 and the action is 2hpzi. The diffraction pattern along the x direction will be symmetric and its width will depend on the incident vertical momentum. Well away from a low-index direction, when the offset angle is such that
= 0 and the action is 2hpzi. The diffraction pattern along the x direction will be symmetric and its width will depend on the incident vertical momentum. Well away from a low-index direction, when the offset angle is such that ![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) ≫ 1, the action will be exponentially small and only specular scattering is possible. This condition implies that (vzi = |pzi/M| is the magnitude of the incident velocity in the vertical direction)
≫ 1, the action will be exponentially small and only specular scattering is possible. This condition implies that (vzi = |pzi/M| is the magnitude of the incident velocity in the vertical direction)
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) , the grazing angle of incidence, since vzi = vG
, the grazing angle of incidence, since vzi = vG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) .
.
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ), the action is a decreasing function of the offset angle δϕ and we expect the width of the diffraction pattern to decrease as a function of increasing offset angle δϕ.
), the action is a decreasing function of the offset angle δϕ and we expect the width of the diffraction pattern to decrease as a function of increasing offset angle δϕ.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2Ik = Σk
k2Ik = Σk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2Jk(Ax)2 = (Ax)2/2,
k2Jk(Ax)2 = (Ax)2/2,
![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) = 0) while the second term can be considered as the oblique incidence factor, β(π
= 0) while the second term can be considered as the oblique incidence factor, β(π![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) ). It has a value of 1 for
). It has a value of 1 for ![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) = 0 and governs the evolution with δϕ. It can be written in a form directly adapted to GIFAD coordinates by noting that close to a low index direction (δϕ ≪ 1),
= 0 and governs the evolution with δϕ. It can be written in a form directly adapted to GIFAD coordinates by noting that close to a low index direction (δϕ ≪ 1), ![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) = (G⊥/α)·(sin
= (G⊥/α)·(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δϕ)/(sin
δϕ)/(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i) ≃ (G⊥/α)·(δϕ/
i) ≃ (G⊥/α)·(δϕ/![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i). Values for ϕB and h depend on the relevant low-index direction, while D and α define the mean planar potential (eqn (13)).
i). Values for ϕB and h depend on the relevant low-index direction, while D and α define the mean planar potential (eqn (13)).
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i = 0.9° where the azimuth δϕ was varied in steps of 0.08° around the [100] and [110] directions using a setup described in ref. 33. As in the theory, the angular spread of the experimental diffraction pattern is obtained from the variance of the diffracted intensities
i = 0.9° where the azimuth δϕ was varied in steps of 0.08° around the [100] and [110] directions using a setup described in ref. 33. As in the theory, the angular spread of the experimental diffraction pattern is obtained from the variance of the diffracted intensities![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) )2 with
)2 with ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) = ΣkkIk.
= ΣkkIk.
 ) and [110] (
) and [110] ( ) directions.20 The red lines result from eqn (60)i.e. without use of the Bessel function. The corrugations h11 and h10 are derived at δϕ = 0 while α and D are taken from literature and reported in Table 1. The inset shows a ϕ-scan taken from ref. 5 where both peaks appear at their absolute location.
) directions.20 The red lines result from eqn (60)i.e. without use of the Bessel function. The corrugations h11 and h10 are derived at δϕ = 0 while α and D are taken from literature and reported in Table 1. The inset shows a ϕ-scan taken from ref. 5 where both peaks appear at their absolute location.
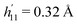 and
and  .
. . The 12% greater corrugation of the dashed curve illustrates the sensitivity of the diffraction intensities to the precise value of the corrugation.
. The 12% greater corrugation of the dashed curve illustrates the sensitivity of the diffraction intensities to the precise value of the corrugation.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi ≤ 50 meV), rather than being specifically tuned to the normal-energies in GIFAD, which may be an order of magnitude greater.
θi ≤ 50 meV), rather than being specifically tuned to the normal-energies in GIFAD, which may be an order of magnitude greater.![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) ), in eqn (60). Considering the case where E ≫ D, so that Φ = π/2, the width of the obliquity function is analytic by noting that
), in eqn (60). Considering the case where E ≫ D, so that Φ = π/2, the width of the obliquity function is analytic by noting that  so that in the GIFAD coordinates, the width takes a remarkably compact form.
so that in the GIFAD coordinates, the width takes a remarkably compact form.
 . Thirdly, we limited ourselves to first order perturbation theory. All of these limitations may be relaxed but perhaps most prominently is the fact that second order perturbation theory can account for the asymmetry in the diffraction pattern when measured away from the symmetry direction. This remains a topic for future consideration.
. Thirdly, we limited ourselves to first order perturbation theory. All of these limitations may be relaxed but perhaps most prominently is the fact that second order perturbation theory can account for the asymmetry in the diffraction pattern when measured away from the symmetry direction. This remains a topic for future consideration. and σT/
and σT/![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i = α/G⊥π (eqn (60) and (62)) respectively. The analysis outlines, as simply as possible, the role of the corrugation amplitude h and stiffness α. We note that second-order theory, which we describe in Appendix A, allows the discussion to be extended to the observed asymmetries in the diffraction pattern.46 Perturbation theory can also address more complex forms of the interaction potential allowing, for instance the investigation of the effect of the location of the attractive well.12
i = α/G⊥π (eqn (60) and (62)) respectively. The analysis outlines, as simply as possible, the role of the corrugation amplitude h and stiffness α. We note that second-order theory, which we describe in Appendix A, allows the discussion to be extended to the observed asymmetries in the diffraction pattern.46 Perturbation theory can also address more complex forms of the interaction potential allowing, for instance the investigation of the effect of the location of the attractive well.12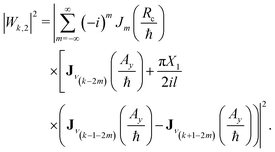


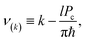



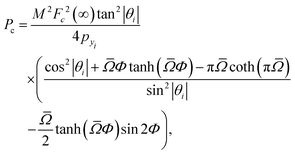
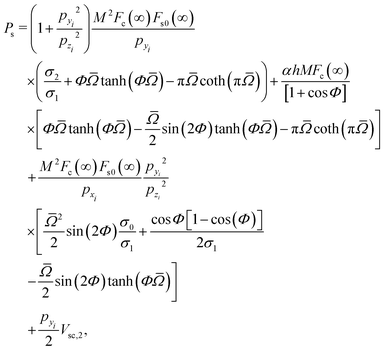


![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(π − Φ)
exp[−(π − Φ)![[capital Omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c0.gif) ]
]




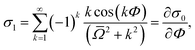




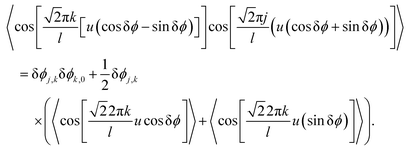

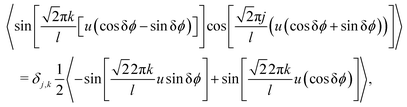

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δϕ ≃ 1 the averaging of the terms
δϕ ≃ 1 the averaging of the terms  and
and  will make them vanish. However, the averaging over terms such as
will make them vanish. However, the averaging over terms such as  is no longer clear due to the small magnitude of δϕ. Due to the fast GIFAD motion, one could assume that the time dependence of the GIFAD coordinate is known. So, if the scattering process starts at the time −t0 we know that the motion along the GIFAD direction is the free particle motion as given in eqn (53). and therefore averaging over the fast motion will leave us with
is no longer clear due to the small magnitude of δϕ. Due to the fast GIFAD motion, one could assume that the time dependence of the GIFAD coordinate is known. So, if the scattering process starts at the time −t0 we know that the motion along the GIFAD direction is the free particle motion as given in eqn (53). and therefore averaging over the fast motion will leave us with
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i and comparatively low total energy. This is not in contradiction with the present paper as discussed in ref. 10 but would deserve a specific treatment beyond the general situation presented here.
i and comparatively low total energy. This is not in contradiction with the present paper as discussed in ref. 10 but would deserve a specific treatment beyond the general situation presented here.
