Urocanic acid as a novel scaffold for next-gen nature-inspired sunscreens: I. electronic laser spectroscopy under isolated conditions

Abstract

Urocanic acid is a naturally occurring UV-A and UV-B absorbing compound found in the skin. Its use in artificial sunscreens has been abandoned because of health risks associated with the cis isomer. Here we report laser spectroscopic studies on urocanic acid and various substituted derivatives under supersonically cooled conditions. We find that the spectroscopy and excited-state dynamics of urocanic acid are dominantly determined by the nearly degenerate ¹nπ* and ¹ππ* electronically excited states. These properties are only affected to a minor extent by esterification of the carboxylic acid group or NH alkylation of the N₃H tautomer. Tautomerization, on the other hand, has a much more profound influence and leads-from a photoprotective point of view-to more favorable excited-state dynamics. The approach presented here paves the way to tailoring the photoactive properties of urocanic acid for specific applications amongst which their use as safe UV filters.

---

Introduction

While solar radiation is essential to all lifeforms on our planet, exposure is also potentially harmful to all forms of life. Adverse health effects in humans include various types of skin cancer, photoaging and photoallergic reactions.^1–4 In order to prevent such effects a range of artificial sunscreens has been developed and incorporated into skincare cosmetics.⁵ However, the use of these filters has recently come under considerable debate as concerns have risen on their potential adverse effects on health and environment.^6–10 At the moment there is therefore a strong demand for better, safer and more efficient sunscreen agents. Nature has developed a finely balanced inventory of screening agents to protect against UV radiation damage¹¹ which have been found to provide powerful leads for the further development and optimization of novel sunscreens. Examples of chemical motifs that in the recent past have been used as a starting point include cinnamic acids^12–15 and mycosporine-like amino acids.¹⁶

Urocanic acid (UA) (Fig. 1) is another example of such a natural sunscreen. It is formed as the trans isomer in the epidermal layer of the human skin where it is one of the primary UV absorbing chromophores. It has therefore for a long time been assumed that it served as a UV filter to prevent DNA damage. As such, it was initially added to sunscreen formulations until it was discovered that the cis isomer produced upon irradiation of trans-UA has immunosuppressive properties.¹⁷

Fig. 1 Molecular structure of urocanic acid and derivatives studied in the present work (methyl urocanate, N₃-methyl methyl urocanate, and N₁-methyl methyl urocanate). Structures of urocanic acid and its methyl ester are drawn for the N₃H tautomer which is the dominating tautomer under the employed experimental conditions. In the article conformers of these compounds are labeled according to the trans/cis configuration of the C₅–C₆, C₆=C₇, and C₇–C₈ bonds. The conformer drawn here for urocanic acid is thus labeled as the N₃H-TTC conformer.

Considered purely from a sunscreen point of view, urocanic acid offers a number of favourable photophysical and photochemical features starting with the fact that it has a strong absorption in the relevant UV regions. A priori one would expect the C₆=C₇ bond to give rise to (near-)conical intersections of the electronically excited singlet states with the ground state leading to an ultrafast decay of these states and thereby to an ultrafast conversion of harmful UV radiation into harmless heat. The imidazole ring, on the other hand, can be present in two different tautomeric forms (the N₃H and N₁H tautomers) with potentially different spectroscopic properties. As such, it is a highly promising starting point for the development of novel sunscreens¹⁸ albeit that one has to ensure that the immunosuppressive properties of cis-UA are reduced to an acceptable level.

The molecular pathway by which cis-UA mediates immune suppression has for a long time remained elusive, but nowadays it is commonly accepted that it involves binding of cis-UA to the serotonin [5-hydroxytryptamine (5-HT)] receptor¹⁹ which then becomes activated. Important to notice is that the underlying reason for the relatively high affinity of cis-UA-as opposed to trans-UA-is the similarity of the ring structure of the former with the molecular structure of serotonin. A further factor to take into account is that the cis isomer of the N₁H tautomer is stabilized by a relatively strong intramolecular hydrogen bond. Chemical substitutions at strategic positions in UA thus seems to be a promising approach to reduce the binding affinity of cis-UA. In the present work we consider to this purpose methyl urocanate, N₃-methyl methyl urocanate and N₁-methyl methyl urocanate (Fig. 1). These are compounds in which the possibility to form intramolecular hydrogen bonds is reduced or absent, and for which steric interactions can reasonably be expected to lead to a reduced binding to the serotonin receptor. It should be emphasized that the methyl substituents used here are just the first step towards a further optimization with other substituents. What is important at this stage is to determine how the spectroscopic properties and excited-state dynamics of the UA core chromophore are affected by such substitutions.

The photophysical and photochemical properties of UA have attracted considerable attention from experimentalists and theoreticians alike and continue to do so.^20–22 One of particularly intriguing observations in experimental studies-which have predominantly been performed in aqueous solutions-has been the unusual wavelength dependence of the photoisomerization quantum yield of trans-UA.^23–26 Excitation in the red tail of the absorption band leads to a quantum yield near 0.5, while for excitation at the maximum of this band it is reduced to a few percent. Concurrently with these observations it has been concluded that the opposite happens for the triplet quantum yield: a high triplet quantum yield is observed for excitation near the absorption maximum while for excitation at longer wavelengths no evidence is found for the presence of a long-lived triplet state.^27–29

Theoretical studies have shown that for both the trans and cis isomers the manifold of the lower-lying electronically excited singlet states is formed by an ¹n_Oπ* state associated with excitation of an electron from the lone pair orbital on the carbonyl oxygen to the antibonding π* LUMO (which from now on will be referred to as the ¹nπ* state) and a ¹ππ* state associated with the HOMO → LUMO excitation.^30–34 Interestingly, it has been found that these states are nearly degenerate with an ordering that is strongly dependent on which particular tautomer is considered. For the N₃H tautomer the strongly absorbing ¹nπ* state is vertically the lowest excited singlet state with the ¹ππ* state at slightly higher energies, while for the N₁H tautomer the reverse is found. The calculations show moreover that the energy separation between these two states is critically dependent on which particular conformer is considered.

This manifold of excited states has been the starting point for theoretical studies seeking to rationalize the experimentally observed wavelength dependence of photoisomerization and triplet formation but so far no unambiguous consensus has been reached on the underlying mechanisms.^33–36 Apart from the experimental results obtained for UA under solvated conditions, these theoretical studies were also benchmarked by what was observed in fluorescence excitation and emission studies of UA under molecular beam conditions, that is, under isolated and internally cold conditions.³⁷ These studies revealed three distinct regions in the excitation region from which conclusions were drawn on the energy separation of the S₁ and S₂ states and the presence of a barrier for isomerization in S₁. However, subsequent rotational spectroscopic studies on the N₁H and N₃H tautomers of 4-vinylimidazole generated in situ by thermal decarboxylation of UA³⁸ indicated that the results of the molecular beam studies should be considered with caution as also in the molecular beam studies UA was heated to obtain sufficient vapor pressure.

It is clear that studies under isolated molecule conditions are the ideal starting point for a further understanding of the photochemical and photophysical properties of UA in solution as well as the development of UA derivatives for sunscreen applications. To this purpose we report here on molecular beam studies of (substituted) UA compounds using Resonance Enhanced MultiPhoton Ionization (REMPI) spectroscopic techniques. In contrast to the previous gas phase studies, we use laser desorption techniques³⁹ to seed these compounds into a supersonic expansion, thereby avoiding detrimental thermal reactions. As will be shown, such an approach indeed leads to excitation spectra of UA that differ from previously reported spectra. Our studies provide for the first time (i) a detailed view on the electronically excited states of UA, (ii) how these are modified by substitutions of the carboxylic acid part as well as on the NH group of the imidazole part of the molecule, and (iii) to what extent the N₃H and N₁H tautomers give rise to different spectroscopic and dynamic properties. They thereby provide a solid basis for a further interpretation of the photoactivity of UA and pave the way for a rational design of novel UA-based sunscreens.

Results and discussion

In the following we will first discuss in detail the spectroscopic and dynamic properties of bare UA as determined in the present REMPI experiments and consider them in the light of quantum chemical calculations on its lower electronically excited states. Subsequently, the excitation spectra and dynamics of the substituted compounds will be discussed and compared with those of UA. From this comparison we aim to obtain a detailed view on how the electronically excited states of UA and their decay pathways can be tuned by judicious substitutions.

Urocanic acid

Fig. 2 displays the (1 + 1′) Resonance Enhanced Two-Photon Ionization (R2PI) excitation spectrum of UA in the 31 500–32 850 cm⁻¹ region. A coarse inspection of this spectrum leads to the conclusion that it appears to consist of contributions of two different excitation spectra, the first one starting at 31 577.4 cm⁻¹ and consisting of bands with a relatively narrow width while starting at 32 350 cm⁻¹ a second set of bands appear with a significantly larger width. Comparison with the previously reported fluorescence excitation spectrum of UA³⁷ shows that the two spectra differ significantly. In view of the conclusion from previous rotational spectroscopic studies that thermal decarboxylation of UA already occurs quite efficiently at 220 °C,³⁸ and the fact that in the fluorescence excitation, spectroscopic studies the sample was heated up to 270 °C leads us to conclude that UA is not the carrier of the previously reported excitation spectrum. It should be emphasized that in the present experiments in which UA is seeded by laser desorption no thermal heating occurs of the compound. Thermal side reactions can thus definitely be excluded.

Fig. 2 (1 + 1′) R2PI excitation spectrum of urocanic acid (black trace). The inset provides a blow-up of the initial part of the spectrum where a band system starting at 31 577.4 cm⁻¹ with relatively narrow resonances is present. The red trace displays the vibrationally resolved excitation spectrum predicted for the ¹nπ* ← S₀ transition using TD-DFT calculations at the wB97XD/cc-pVDZ level taking vibronic coupling into account and using a scaling factor of 0.953 for the calculated vibrational frequencies.

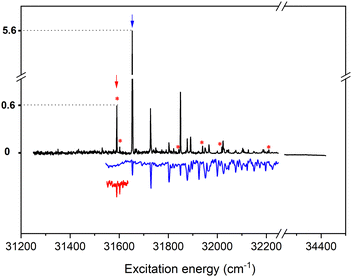
Focusing in first instance on the excitation spectrum with the narrow resonances, we observe that the lowest-energy band occurs at 31 577.4 cm⁻¹ and has a width of 1.8 cm⁻¹. A more detailed inspection of the shape of the band leads to the conclusion that it actually reflects an unresolved rotational contour, thus suggesting that the electronic state that is excited has a relatively long lifetime which does not give rise to lifetime broadening. Although only a qualitative statement can be made, comparison with excitation spectra of similarly sized compounds with long-lived electronically excited states^40–43 leads us to conclude that in our laser desorption experiments UA is quite effectively cooled to rotational temperatures below 10 K. The absence of hot bands similarly suggests that also vibrational cooling occurs quite efficiently.

Up to 32 350 cm⁻¹ extensive vibronic activity is observed in the R2PI excitation spectrum for which the detailed assignment will be discussed later. What is at this point more relevant is that starting from 32 350 cm⁻¹ a clear progression of broader features appears. Noticeably, these features are not single bands but consist of a broad main band with a width of roughly 20–30 cm⁻¹ on which sharper bands are superimposed with widths as small as of those of the sharp resonances discussed above (see Fig. S1 in the ESI† for an expanded view of the region above 32 350 cm⁻¹). The integrated intensity of each of these bands is at least two orders of magnitude larger than those of the sharp bands and one thus rapidly comes to the conclusion that they are associated with a transition with a much larger oscillator strength than the transition giving rise to the sharp bands. In order to account for these observations two possible explanations, come to mind: (i) the two excitation spectra are associated with different conformers or tautomers of UA, or (ii) the two excitation spectra are associated with two different electronically excited singlet states.

Previous calculations have shown that UA has a number of conformers and tautomers with relatively small ground-state energy differences.³³ More quantitatively, our calculations performed at the wB97XD/cc-pVDZ level (vide infra) predict-in agreement with those previous calculations-that the N₃H-TTC is the lowest-energy C=C trans structure with the N₁H-TTC, N₃H-TTT and N₁H-TTT structures at 151, 267, and 345 cm⁻¹ (see caption Fig. 1 for labelling convention and Fig. S3(a), ESI† for explicitly drawn conformers). In view of these small energy differences and the fact that the excited-state manifold of different tautomers might differ significantly, it could thus be that the sharp and broad excitation spectra are associated with different conformers or tautomers. Whether this is indeed the case might in principle be determined by depletion spectroscopy as will indeed be shown for the case of N₁-methyl methyl urocanate. However, for UA the intrinsic much lower signal-to-noise ratio of laser desorption experiments prevented us to come to such an unambiguous conclusion.

A number of arguments favour assigning both band systems to the same species. Firstly, if the two band systems originate from two different conformers, these would be the N₃H-TTC and N₁H-TTC conformers. Based on their energies and band intensities, one would then need to conclude that the N₁H-TTC conformer would be the carrier of the band system with the narrow resonances. Inspection of the vertical and adiabatic excitation energies in Table 1 predicted for these conformers shows that for the latter conformer the ¹ππ* state is the lowest excited singlet state for which no stable minimum is found. Geometry optimization instead brings the molecule barrierless to a conical intersection with the ground state. Such characteristics would be incompatible with the widths of the sharp bands. Secondly, if the two band systems would arise from two different conformers, one would expect that changing expansion conditions would change their relative intensities. However, spectra recorded in experiments under different cooling conditions show the same intensity distributions as in Fig. 2. Finally, for methyl urocanate, similar energy differences between the different conformations are predicted, but for this compound, the excitation spectrum consists of a single band system. Taken together these observations strongly suggest that both the sharp and broad resonances derive from the same species which we assign to the N₃H-TTC conformer.

Table 1 TD-DFT vertical and adiabatic energies (eV) of the most stable trans conformer of UA and its methylated derivatives calculated at the wB97XD/cc-pVDZ level. Oscillator strengths are given in parentheses

	Singlet excited states
	State	Vertical	Adiabatic
a Excitation energy obtained for geometry optimization under Cs symmetry restrictions. Nonplanar geometry optimization of the state leads to root switching with S1.b Excitation energy obtained for geometry optimization under Cs symmetry restrictions. Harmonic force field at optimized minimum features an imaginary frequency of 83.4 cm^−1 for an out-of-plane torsional mode involving the C5–C6 and C6=C7 bonds. Nonplanar geometry optimization of the state leads to a conical intersection with S0.c Excitation energy obtained for geometry optimization under Cs symmetry restrictions. Harmonic force field at optimized minimum features an imaginary frequency of 20.8 cm^−1 for a C5–C6 torsional mode. Nonplanar geometry optimization of the state leads to root switching with S1.d Excitation energy obtained for geometry optimization under Cs symmetry restrictions. Harmonic force field at optimized minimum features imaginary frequencies of 94.5 and 72.5 cm^−1 for a C5–C6=C7 in-plane bending mode and rotation of the methyl group, respectively.e Excitation energy obtained under non-constrained geometry optimization conditions.
Urocanic acid (N3H-TTC)	S1	4.99 (0)	4.30 (0)
	S2	5.04 (0.65)	4.70 (0.66)^a
Urocanic acid (N1H-TTC)	S1	4.67 (0.70)	4.40 (0.68)^b
	S2	4.96 (0)	4.27 (0)
Methyl urocanate (N3H-TTC)	S1	5.00 (0)	4.35 (0)
	S2	5.04 (0.72)	4.69 (0.73)^a
N3-Methyl methyl urocanate (N3H-TTC)	S1	4.96 (0.8)	4.35 (0)
	S2	5.00 (0)	4.61 (0.81)^a
N1-Methyl methyl urocanate (N1H-CTC)	S1	4.46 (0.64)	4.16 (0.59)
	S2	4.96 (0)	4.30 (0)^c
N1-Methyl methyl urocanate (N1H-TTC)	S1	4.67 (0.73)	4.41 (0.75)^d
			4.09 (0.03)^e
	S2	5.00 (0)	4.36 (0)

---

The concurrent conclusion that needs to be drawn, namely that the two spectra should be assigned to two different electronically excited singlet states, finds strong support from quantum chemical calculations. Previous calculations at the CASPT2 and CC2 levels^34,35 have reported that for vertical excitation the lowest ¹nπ* and ¹ππ* states are nearly degenerate with either the ¹nπ* or the ¹ππ* state being the lower one depending on the level of calculation. Our TD-DFT calculations at the wB97XD/cc-pVDZ level (Table 1) similarly find that the ¹nπ* state is vertically the lowest excited singlet state at 4.99 eV with the HOMO → LUMO ¹ππ* state only slightly higher in energy (5.04 eV), excitation energies that are in excellent agreement with the CASPT2 and CC2 calculations. Above it was noticed that the two spectra are associated with transitions with oscillator strengths that differ at least two orders in magnitude. This observation is indeed in line with the quantum chemical calculations as the transition to the ¹nπ* state has an oscillator strength which for all practical purposes is zero while the transition to the ¹ππ* state is strongly allowed.

Further information on the properties of these two electronic states can in principle be obtained from the vibrational activity in the two excitation spectra. To this purpose we have performed geometry optimizations of the ¹nπ* and ¹ππ* states in order to subsequently obtain harmonic force fields which can then be used to predict their vibrationally-resolved excitation spectra. It turns out that such a geometry optimization is well possible for the ¹nπ* state, leading to an adiabatic excitation energy of 4.30 eV and a spectrum depicted as the red trace in Fig. 2. Geometry optimization of the ¹ππ* state under planar geometry restrictions, on the other hand, leads to a structure with a ¹ππ* excitation energy of 4.70 eV but with an harmonic force field that has an imaginary frequency for an out-of-plane mode characterized by pyramidalization of C₇. Releasing the planarity conditions and optimizing the structure along out-of-plane coordinates rapidly brings the structure, however, to a structure where the lower two electronically excited states become nearly degenerate after which root switching occurs and the ¹nπ* state is once again optimized. This observation strongly suggests that there is a conical intersection between the ¹nπ* and ¹ππ* states at slightly higher energies than the minimum of the ¹nπ* state. Such a conclusion is fully in line with the results of the CASPT2 calculations in which such conical intersections have indeed been identified.³⁴

In view of small oscillator strength of the ¹nπ* ← S₀ transition and the nearby presence of the strongly dipole-allowed ¹ππ* state, it is to be expected that vibronic coupling between the ¹nπ* and ¹ππ* states will play an important role. Calculations in which Herzberg–Teller coupling has been taken into account indeed predict vibronic transition intensities that are at least an order of magnitude larger than when merely Franck–Condon factors are considered (see Fig. S2, ESI†). This observation therefore strongly suggests that that the band at 31 577.4 cm⁻¹ is not the 0⁰₀ band of the ¹nπ* ← S₀ transition but should be assigned to a false origin associated with one of the a” vibrational modes. Inspection of the intensities predicted for the (ν_a′′)¹₀ false origins lead to the conclusion that the 31 577.4 cm⁻¹ band should be assigned as (42)¹₀ with ν₄₂ being the lowest-frequency mode of a” symmetry, an out-of-plane torsion of the imidazole and carboxyl groups.⁴⁴ Further support for such an assignment is found in the presence of a very weak band at 31 518.6 cm⁻¹, which-taking into account a predicted scaled frequency of ν₄₂ of 58.5 cm⁻¹-nicely coincides with the expected transition energy of the 0⁰₀ transition. Based on these assignments, tentative assignments are provided in Table S1 (ESI†) for bands observed in the initial part of the spectrum of Fig. 2. It is clear, however, that already quite rapidly such assignments are very hard to make once levels are accessed with higher vibrational energies, not only because of the multitude of bands that are observed but also because of the degeneracy with levels of the ¹ππ* state, which strongly influences their intensities and leads to significant differences between the experimentally observed and theoretically predicted spectrum.

As mentioned before, starting from 32 350 cm⁻¹ a second band system emerges that we assign to the excitation spectrum of the ¹ππ* state. A further inspection of this band system leads to the conclusion that it is basically built up from an extended progression of a mode with an exited-state frequency of about 100 cm⁻¹ and the same progression combined with excitation of a mode with a frequency of about 220 cm⁻¹. These frequencies nicely match the frequencies obtained for the two lowest frequency a′ modes ν₂₉ (an in-plane C₅–C₆=C₇ bending mode) and ν₂₈ (a scissoring mode) at the planar geometry of the ¹ππ* state for which scaled frequencies of 100 and 218 cm⁻¹ are calculated. We thus conclude that along these two normal modes-and in particular along the in-plane bending mode-significant geometry changes occur upon excitation. Such changes are in line with a priori expectations since the ¹ππ* state is characterized by excitation from an orbital with bonding character between C₆ and C₇ to an orbital with an antibonding character between these two atoms.

Fig. 3a and b show pump–probe traces obtained at 31 577 (the false origin of the ¹nπ* state) and 32 350 cm⁻¹ (the 0-0 transition to the ¹ππ* state). Interestingly, it is observed that at both energies the same decay is found which can be fitted nicely with the convolution of a Gaussian profile with a mono-exponential decay of 28 ns. As far as the decay from the ¹ππ* state is concerned, this observation suggests that after excitation of the ¹ππ* state internal conversion to the ¹nπ* state occurs on a time scale faster than the nanosecond timescale of the present experiments. An estimate of the actual timescale on which this internal conversion takes place can be obtained from the width of the 0-0 band, which is found to be about 20 cm⁻¹ and thus suggests a rate of (270 fs)⁻¹.

Fig. 3 Pump–probe traces obtained for excitation of (a) urocanic acid excited at 31 577.4 cm⁻¹, (b) urocanic acid excited at 32 350.0 cm⁻¹, (c) methyl urocanate excited at 32 631.8 cm⁻¹, (d) N₃-methyl methyl urocanate excited at 33 250.5 cm⁻¹ and (e) N₁-methyl methyl urocanate excited at 31 653.1 cm⁻¹. In (a) the false origin band of the ¹nπ* state is excited while in (b)–(e) excitation takes place via the origin band of the ¹ππ* state.

The decay time of 28 ns observed for the ¹nπ* state is in line with expectations for internal conversion rates from an ¹nπ* state to the electronic ground state, and is also not at odds with the observed linewidth of the narrow resonances. Nevertheless, at the same time the present experiments cannot exclude that a decay mechanism similar to what has been observed for cinnamates might occur.⁴⁵ For the latter compounds it has been concluded that a pathway involving intersystem crossing to the triplet manifold followed by decay to the electronic ground state mediated by a minimum energy seam of crossings (MESXs) between the lowest excited triplet state and the ground state, and characterized by perpendicular geometries of the C=C double bond also leads to very similar decay times as observed here. In that case the observed decay of the pump–probe signal would thus not be associated with the decay of the ¹nπ* state but of the lowest excited triplet state. Considering that the ¹nπ* state is the lowest electronically excited singlet state and that the El-Sayed rules⁴⁶ predict significant spin–orbit coupling matrix elements with the lowest excited triplet state T₁(ππ*) such a scenario is on forehand not unlikely. Further information on the relative importance of these two decay pathways (direct ¹nπ* ← S₀ internal conversion vs. triplet-mediated conversion) can in principle be obtained from experiments in which the photoionization efficiency is determined in wavelength regions corresponding to vertical ionization from T₁⁴⁵ or by (1 + 1′) photoelectron spectroscopy using high-energy photons for the ionization step. Such experiments will shortly be performed in our labs.

Methyl urocanate

In the past, it has been concluded that the immunosuppressive effects of urocanic acid arise from the similarity of the cis isomer of urocanic acid-produced upon sunlight exposure and serotonin leading to competitive binding of this isomer to the serotonin receptor.¹⁹ Alkylation of the carboxylic acid part of the molecule disables the formation of a strong intramolecular hydrogen bond between the imidazole ring and carboxylic acid part in the cis isomer and thereby decreases the stability of the cis isomer. In order to determine the influence of such an alkylation on the spectroscopic properties and excited-state dynamics of the parent compound, we have performed similar studies as described above for urocanic acid for methyl urocanate. Fig. 4 displays to this purpose the (1 + 1′) R2PI excitation spectrum of this compound which shows an extensive series of broad bands with the first band appearing at 32 632 cm⁻¹. In view of the similarity of this spectrum with the system of broad bands in the excitation spectrum of UA, it seems reasonable to assign it to the excitation spectrum of the ¹ππ* state of methyl urocanate, implying a blue shift of this state by about 300 cm⁻¹. Quantum chemical calculations of the ground-state energies of the various trans conformers find analogous to UA that N₃H-TTC is the lowest-energy trans conformation with the N₁H-TTC, N₃H-TTT and N₃H-CTC structures at 219, 396, and 548 cm⁻¹ (see Fig. S3(b), ESI†), that is, the energy difference between the two lower-energy conformations is even larger than in UA. We can thus safely assume that the spectrum in Fig. 4 originates from the N₃H-TTC conformer.

Fig. 4 (1 + 1′) R2PI excitation spectrum of methyl urocanate.

Important to notice is that the excitation spectrum of methyl urocanate does not give any indication for the presence of a system of narrow bands-which we associated with transitions to the ¹nπ* state-as was observed for the parent compound. Quantum chemical calculations of vertical excitation energies and consideration of the excited-state dynamics that will be discussed further on give us reason to believe that both vertically as well as adiabatically the ¹nπ* state is still below the ¹ππ* state. One would thus need to conclude that for methyl urocanate transitions to the ¹nπ* state are so much less intense than the transitions to the ¹ππ* state that they cannot be detected in the present experiments.

Similar to UA, we find that TD-DFT calculations of the ¹nπ* state lead to a minimum with an adiabatic excitation energy that is slightly higher (0.05 eV) than in UA (Table 1) while the ¹ππ* state has a planar minimum with the same excitation energy as in UA. Once again, however, the harmonic force field shows at this minimum an out-of-plane normal coordinate with an imaginary frequency. Non-planar geometry optimizations lead to a switch with the ¹nπ* state, indicating the presence of a conical intersection between the two states.

Inspection of the vibronic activity in the excitation spectrum displayed in Fig. 4 leads to the conclusion that it is dominated by an extensive progression of a mode with a frequency of 82 cm⁻¹ in combination with activity of a mode at 201 cm⁻¹. These frequencies perfectly match scaled frequencies calculated for the lower-frequency a’ modes at the planar minimum of the ¹ππ* state which-similar to UA-are associated with an in-plane C₅–C₆=C₇ bending mode and a scissoring mode. We thus conclude that regarding the spectroscopic properties only minor changes occur upon alkylation, the absence of observable transitions to the ¹nπ* state being the most noticeable one.

As far as the excited-state dynamics are concerned, similar conclusions can be drawn. Firstly, we notice that the width of the 0-0 band in the excitation spectrum is similar to that of UA, albeit slightly smaller (16 vs. 20 cm⁻¹). Interestingly, we find that for methyl urocanate the band at 201 cm⁻¹ and combination bands of this mode with the 82 cm⁻¹ progression appear to have a smaller width (12 cm⁻¹) than the other bands, indicating a slower decay of these particular excited-state vibrational levels. Fig. 3c shows the decay trace obtained after excitation at vibrationless origin (32 632 cm⁻¹) with similar traces being obtained (not shown) for higher excitation energies. Fits of the decay to the convolution of a Gaussian profile with an exponential decay lead to a decay time of 31 ns, which is very similar to what was observed for UA (28 ns). Taking into account the widths of the resonances in the excitation spectrum-which indicate a decay of excited-state levels on the order of hundreds of femtoseconds-and the presently observed decay on a nanosecond timescale, it seems reasonable to conclude that also for methyl urocanate the decay of electronically excited ¹ππ* levels initially proceeds via internal conversion to a lower-lying electronically excited state, which in view of the analogies with UA would be the ¹nπ* state. From this state the ground state is repopulated either via direct internal conversion or possibly via a triplet-mediated conversion pathway.

N₃-Methyl methyl urocanate

A further means to influence the immunosuppressive properties of UA is to alkylate the NH group in the imidazole ring. While alkylation of the carboxylic acid part of UA has been found to affect the electronic structure of UA only to a minor extent, alkylation of this nitrogen atom is expected to have a much larger impact on the electronically excited states of the bare chromophore. This is indeed borne out in the experiments as can be concluded from Fig. 5 where the (1 + 1′) R2PI excitation spectrum of N₃-methyl methyl urocanate is depicted. The spectrum displays an apparent origin band at 33 250 cm⁻¹ with a bandwidth of about 500 cm⁻¹ followed by a series of bands for more than 3000 cm⁻¹. Quantum chemical calculations predict-similar to the two compounds discussed previously-that the TTC conformer is the most stable conformer with the TTT, CTC and CTT conformers having relative energies of 396, 521, and 712 cm⁻¹ (see Fig. S3(c), ESI†). We thus expect only one conformer to be present in our molecular beam expansion as is indeed confirmed by depletion experiments that reproduce the R2PI excitation spectrum.

Fig. 5 (1 + 1′) R2PI excitation spectrum of N₃-methyl methyl urocanate.

In view of the computational results, it is reasonable to assume that the excitation spectrum depicted in Fig. 5 is associated with the ¹ππ* ← S₀ transition. While for UA and methyl urocanate the excitation spectrum of the ¹ππ* state displayed vibrationally resolved progressions of low-frequency a’ modes, this is not the case for N₃-methyl methyl urocanate. Since the calculations predict for all three compounds similar properties of the lower electronically excited states, this observation suggests that for N₃-methyl methyl urocanate vibrational resolution is lacking because of lifetime broadening, and thus that ¹ππ* → ¹nπ* internal conversion is significantly accelerated upon N₃-methylation. We notice that vibrational resolution might in principle also be washed out because of extensive Frank–Condon activity of a vibrational mode with a lower frequency than the a′ in-plane C₅–C₆=C₇ bending mode-which for N₃-methyl methyl urocanate is predicted to have a scaled frequency of 71 cm⁻¹ in the ¹ππ* state-but no such modes are present. Assuming that this 71 cm⁻¹ mode is the non-resolved carrier of the broad band around 33 250 cm⁻¹ would lead to a rough estimate of the ¹ππ* → ¹nπ* internal conversion rate on the order of higher than 10¹³ s⁻¹.

Fig. 3d shows the pump–probe trace of the ion signal obtained at 33 250 cm⁻¹. Because of the weakness of the signal, some caution needs to be taken when interpreting this trace. What is nevertheless clear is that there is an asymmetry in the trace (compare with Fig. 3e) which suggests the presence of a decay on a nanosecond time scale. Fits of a Gaussian profile with a mono-exponential decay then lead to a decay time of about 14 ns, which is about twice as fast as observed for UA and methyl urocanate. Once again it is noticed that with the present experiments, it is not possible to decide whether this 14 ns is associated with the decay of the ¹nπ* state or from T₁. Overall, it can thus be concluded that N₃-methylation does not have far-reaching consequences for the spectroscopic and dynamics properties of the lower electronically excited singlet state, the major change being that internal conversion from the ¹ππ* state is enhanced as a result of which vibrational resolution is absent in the excitation spectrum of this state.

N₁-Methyl methyl urocanate

The compounds studied up till now have an N₃H tautomer configuration. In view of assessing further possibilities to address the immunosuppressive properties of urocanic acid but also to modulate its spectroscopic properties, it is of considerable interest to study compounds based on the N₁H tautomer. Fig. 6 shows to this purpose the (1 + 1′) R2PI spectrum of N₁-methyl methyl urocanate. A first inspection of this spectrum rapidly leads to the conclusion that methylation of N₁ drastically changes the properties of the lower electronically excited states. The spectrum displays a series of well-resolved bands with widths of about 2 cm⁻¹, while a system of broad bands as observed for the N₃H tautomers is completely absent. Depletion spectroscopy studies (Fig. 6) demonstrate that the spectrum is actually built up from the contributions of two conformers. One of these conformers gives rise to a spectrum with a 0-0 transition at 31 653.1 cm⁻¹, while a much weaker spectrum with a 0-0 transition at 31 590.1 cm⁻¹ is associated with a second conformer. It is gratifying to find that our quantum chemical calculations find in agreement with experiment that for this compound the CTC and TTC conformers have nearly the same energy with the former one being slightly more stable (12 cm⁻¹), while the TTT and CTT conformers are predicted to have much higher energies (337 and 491 cm⁻¹, respectively, Fig. S3(d), ESI†). We therefore assign the dominant spectrum to the CTC conformer and the weaker one to the TTC conformer.

Fig. 6 (1 + 1′) R2PI excitation spectrum of N₁-methyl methyl urocanate (black trace). The blue trace depicts the depletion spectrum obtained for excitation at 31 653.1 cm⁻¹ indicated by the blue arrow in the black trace. The red trace depicts the depletion spectrum obtained for excitation at 31 590.1 cm⁻¹ indicated by the red arrow in the black trace. Because of the low intensities only the indicated small part has been scanned. The red stars indicate bands that are concluded to belong to the conformer associated with the red trace on the basis of their absence in the blue trace.

Table 1 reports the results of TD-DFT calculations on these two conformers. Focusing in first instance on the CTC conformer, it is observed that in this case the HOMO → LUMO ¹ππ* state is both for vertical as well as adiabatic excitation the lowest electronically excited singlet state, and energetically well separated from the ¹nπ* state. Such an ordering was also found for the N₁H tautomer of urocanic acid conformers.³⁴ It therefore seems reasonable to assign the observed excitation spectrum to the ¹ππ* state, which would imply a red shift compared to the ¹ππ* state of methyl urocanate by about 0.12 eV. Such a shift is in fair agreement with the calculations that find a redshift of 0.19 eV. The red trace in Fig. 7 displays the Franck–Condon spectrum predicted for excitation of the ¹ππ* state from the vibrationless level of the ground state, which is characterized by extensive vibrational activity of the in-plane C₅–C₆=C₇ bending mode. This spectrum is in excellent agreement with the experimental depletion spectrum of this conformer (black trace), albeit that the experimental spectrum also displays activity of a scissoring mode at 197 cm⁻¹ and a C₅–N₁–Me bending mode at 235 cm⁻¹ for which the calculations predict significantly less activity.

Fig. 7 Comparison of the depletion spectrum of N₁-methyl methyl urocanate excited at 31 653.1 cm⁻¹ (see Fig. 6) with the Franck–Condon spectrum predicted for the ¹ππ* ← S₀ transition as obtained from TD-DFT calculations at the wB97XD/cc-pVDZ level and employing a scaling factor of 0.953 for the calculated vibrational frequencies.

What is, however, more striking to observe is that the Franck–Condon progression as manifested in the depletion spectrum is in stark contrast with what is seen in the R2PI excitation spectrum of Fig. 6, the latter being dominated by the strong 0-0 transition. Intensities in depletion spectra are in first instance only dependent on absorption cross sections, while in the excitation spectrum intensities also depend on the dynamic processes occurring after excitation. We therefore conclude that slightly above the vibrationless level of the ¹ππ* state of the CTC conformer of N₁-methyl methyl urocanate an additional decay channel opens up as a result of which intensities of transitions to ¹ππ* vibrational levels are significantly reduced.

Fig. 3e shows the pump–probe trace obtained at the 0-0 transition of the CTC conformer. This trace can be nicely fitted by the convolution of the two laser pulses and, in contrast to the previously discussed compounds, does not show any indication of a decay occurring on an ns timescale. Such an observation is in line with the conclusion that the ¹ππ* is the lowest excited singlet state and thus that no internal conversion to the ¹nπ* state occurs. We thus conclude that the excited-state dynamics of the lowest excited singlet state of N₁-methyl methyl urocanate do not involve other electronically excited states and are governed by internal conversion to the electronic ground state. The present experiments do not provide a definite answer on the time scale on which this internal conversion takes place, only that it is faster than about 5 ns (the convolution of the two laser pulses) and slower than about 3 ps (the bandwidth of the observed resonances). Neither do the experiments provide information on whether this internal conversion pathway involves a conical intersection with the ground state, and what the nature of the pathway is that is responsible for an enhancement of this rate for vibrationally excited levels in the electronically excited state. Analogous experiments as performed here on a ps time scale^47,48 or time-resolved ion yield and photoelectron spectroscopies⁴⁹ could in this respect provide further insight into these decay channels.

As discussed above, we identified with depletion spectroscopy a set of significantly weaker bands as being associated with the TTC conformer. TD-DFT calculations on this conformer indicate that also in this conformer the ¹ππ* state is both vertically as well as adiabatically the lowest excited singlet state (Table 1), although the geometry optimization of the molecule in the excited state gives rise to some unexpected observations. Firstly, optimization of the ¹ππ* state under C_s restrictions lead to a structure for which the harmonic force field has an imaginary frequency for an out-of-plane vibrational mode involving rotation of the methyl group but also for the C₅–C₆=C₇ bending mode. Attempts to optimize the molecule to a structure with only an imaginary frequency for an a′′ mode were, however, not successful. Secondly, geometry optimizations without symmetry restrictions lead to a stable minimum characterized by a nearly perpendicular geometry of the imidazole part (N₁–C₅–C₆=C₇ dihedral angle of 88.7°) for which the oscillator strength of the ¹ππ* ← S₀ transition is considerably reduced. Such large geometry changes would be expected to lead to extensive Franck–Condon activity in the excitation spectrum, but this is not what is observed experimentally. We are therefore hesitant to assign the experimentally observed spectrum to such a structure. Further theoretical studies would be needed to resolve this issue.

We close the discussion on the TTC conformer by noticing that in the depletion spectrum of this conformer the intensities of the 31 590.1 cm⁻¹ origin band and the first vibrational band at 31 602.1 cm⁻¹ do not reflect the intensity ratio as observed in the excitation spectrum. This is quite similar to what was observed for the CTC conformer, and suggests that also for this conformer an additional decay channel becomes accessible once it is vibrationally excited in the electronically excited state.

Conclusions

In the present studies high-resolution laser spectroscopy in combination with Resonance Enhanced MultiPhoton Ionization techniques has been applied to come to a fundamental understanding of the spectroscopy and decay pathways of electronically excited states of urocanic acid, and determine how these properties are modified in substituted derivatives. It has been shown that for these experiments it is crucial to employ laser desorption to seed the investigated compounds into supersonic expansions instead of heating them to obtain sufficient vapor pressure. Using such an approach has enabled us to record for the first time excitation spectra of urocanic acid. They also have led to the conclusion that previously reported studies suffered from thermal decarboxylation reactions, leading to spectra that should be assigned to decomposition products.

In combination with quantum chemical calculations, it has been shown that the spectroscopy and excited-state dynamics of urocanic acid are determined by two very close-lying electronically excited states. The lower one of these two is an ¹nπ* state which intrinsically has a very small oscillator strength but which becomes ‘visible’ in excitation spectra because of vibronic coupling with a strongly allowed ¹ππ* state at slightly higher energies. As a result, the excitation spectrum of the ¹nπ* state is dominated by false origins of a” symmetry and features extensive vibrational activity. The excitation spectrum of the ¹ππ* state, on the other hand, is dominated by Franck–Condon activity of modes reflecting the geometry changes associated with excitation from a bonding C₆=C₇ orbital to an antibonding orbital. Nanosecond pump–probe studies in combination with what is observed for the bandwidths of ¹nπ* and ¹ππ* resonances lead to the conclusion that the decay of the ¹ππ* state is dominated by internal conversion to the ¹nπ* state, quite probably mediated by a conical intersection between the two states. The latter state has an apparent decay on a tens of nanosecond time scale which in first instance would seem to be in line expectations for direct internal conversion of such a state to the electronic ground state. However, it cannot be excluded that repopulation of the ground state might also occur via an indirect pathway in which the triplet manifold is involved.

Similar studies on methyl-substituted derivatives have shown that esterification of urocanic acid does not lead to major changes in the photophysical properties of the parent compound, albeit that in this case resonances involving the ¹nπ* state are not observed in the excitation spectra which only features the broad-band system associated with excitation of the ¹ππ* state. Time-resolved experiments in combination with TD-DFT calculations of vertical and adiabatic excitation energies lead to the conclusion that the decay of this ¹ππ* state once again involves internal conversion to the ¹nπ* state from which subsequently the ground state is recovered.

While urocanic acid and its methyl ester are from a spectroscopic point of view quite similar, much more dramatic changes occur upon methylation of NH in the imidazole ring. Methylation of the N₃H tautomer leads to an excitation spectrum that no longer displays vibrationally resolved bands, but which retains the ordering and dynamics observed for urocanic acid and its methyl ester, that is, an-in this case not observable-¹nπ* state as adiabatically the lowest excited singlet state with at slightly higher energies a strongly allowed ¹ππ* state. As far as the excited-state dynamics are concerned, the present experiments have shown that that the decay rates of the relevant states are enhanced but not by orders of magnitude. The N₁–Me tautomer, on the other hand, shows significantly different properties, the underlying reason being that in this case the ¹ππ* state is vertically as well as adiabatically the lowest excited singlet state. For this compound well-resolved vibrational bands are observed in the ¹ππ* ← S₀ excitation spectrum with bandwidths that indicate that the decay of these ¹ππ* levels occurs on a much slower time scale than for ¹ππ* levels of the N₃H tautomers. A further difference between this compound and the N₃H tautomers is that in the latter the TTC conformer is by far the most stable conformer at room temperature, while in the former both the TTC and CTC conformers are present. Intriguingly, it is found that the decay of the ¹ππ* state is significantly faster for vibrationally excited levels than from the vibrationless level, indicating that close to the minimum of the excited-state potential an additional decay channel is present that can be accessed by vibrational excitation of the ¹ππ* state.

From a point of view of potential detrimental excited-state reactions the present experiments indicate that the N₁H tautomers appear to have more favourable characteristics. For the N₃H tautomers, the excited-state dynamics involve at least in part a state that decays on tens of nanosecond timescale, and might even involve the triplet manifold. Such characteristics are clearly unfavourable from a photochemical reaction point of view. Energy dissipation in the N₁H tautomer, on the other hand, does not involve other long-lived electronically excited states. Having said this, it should at the same time also be kept in mind that under the conditions in which such compounds would be employed also interactions with the environment need to be taken into account. In view of the small energy differences between the ¹nπ* and ¹ππ* states in the N₃H tautomers and knowing that these two states are differently affected by an environment it is clear that one needs to be cautious to directly transfer conclusions drawn from the present isolated-molecule experiments to experiments under ‘as-used’ conditions. Nevertheless, it is also clear that the present experiments are a prerequisite for obtaining a solid framework to interpret observations under non-isolated conditions.

Urocanic acid has for a long time remained an enigma for experimental spectroscopists and theoretical chemists alike. The present studies have in this sense revolutionized the field by getting for the first-time access to knowledge on its intrinsic photochemical and photophysical properties. At the same time, these studies have also paved the way for a rational design of derivatives in which (i) the immunosuppressive properties of cis-urocanic acid are significantly reduced or even absent and (ii) excited-state decay pathways are optimized to dissipate the energy of the absorbed UV photons harmlessly. We therefore expect that the present studies will incite a renewed interest in the photoactive properties of this class of molecules that ultimately will lead to novel sunscreen filters but also to novel applications in areas in which photothermal materials are employed for other purposes.

Author contributions

H. S. synthesized, purified and characterized substituted UA derivatives. J. F. A. K. L., M. H. and W. R. carried out the spectroscopic experiments. J. F. and W. J. B. performed the quantum chemical calculations. J. F. and W. J. B. conceived the study and analysed the data. W. J. B. supervised the work. All authors contributed to writing the manuscript.

Data availability

Data for this article, including Fig. 2–7, are available at Zenodo at https://doi.org/10.5281/zenodo.12593199.

Conflicts of interest

There are no conflicts to declare.

Note added after first publication

This version of the article replaces the previous version published on 8th July 2024.

Acknowledgements

This project has received funding from the European Union's Horizon 2020 research and innovation programme under the grant agreement No. 828753. Jiayun Fan acknowledges a doctoral fellowship from the China Scholarship Council (No. 201808440365).

Notes and references

1. G. J. Fisher, Z. Q. Wang, S. C. Datta, J. Varani, S. Kang and J. J. Voorhees, N. Engl. J. Med., 1997, 337, 1419–1429.
2. M. Ichihashi, M. Ueda, A. Budiyanto, T. Bito, M. Oka, M. Fukunaga, K. Tsuru and T. Horikawa, Toxicology, 2003, 189, 21–39.
3. L. Marrot and J. Meunier, J. Am. Acad. Dermatol., 2008, 200858, S139–S148.
4. J. J. Bernard, R. L. Gallo and J. Krutmann, Nat. Rev. Immunol., 2019, 19, 688–701.
5. L. L. Guan, H. W. Lim and T. F. Mohammad, Am. J. Clin. Dermatol., 2021, 22, 819–828.
6. R. B. Raffa Jr., J. V. Pergolizzi Jr., R. Taylor and J. M. Kitzen, J. Clin. Pharm. Ther., 2019, 44, 134–139.
7. S. L. Schneider and H. W. Lim, J. Am. Acad. Dermatol., 2019, 80, 266–271.
8. M. K. Matta, R. Zusterzeel, N. R. Pilli, V. Patel, D. A. Volpe, J. Florian, L. Oh, E. Bashaw, I. Zineh, C. Sanabria., S. Kemp, A. Godfrey, S. Adah, S. Coelho, J. Wang, L.-A. Furlong, C. Ganley, T. Michele and D. G. Strauss, J. Am. Acad. Dermatol., 2019, 321, 2082–2091.
9. M. K. Matta, J. Florian, R. Zusterzeel, N. R. Pilli, V. Patel, D. A. Volpe, Y. Yang, L. Oh, E. Bashaw, I. Zineh, C. Sanabria, S. Kemp, A. Godfrey, S. Adah, S. Coelho, J. Wang, L.-A. Furlong, C. Ganley, T. Michele and D. G. Strauss, J. Am. Acad. Dermatol., 2020, 323, 256–267.
10. I. B. Miller, S. Pawlowski, M. Y. Kellermann, M. Petersen-Thiery, M. Moeller, S. Nietzer and P. J. Schupp, Environ. Sci. Eur., 2021, 33(1), 1–13.
11. C. S. Cockell and J. Knowland, Biol. Rev., 1999, 74, 311–345.
12. E. M. M. Tan, M. Hilbers and W. J. Buma, J. Phys. Chem. Lett., 2014, 5, 2464–2468.
13. T. T. Abiola, N. d N. Rodrigues, C. Ho, D. J. L. Coxon, M. D. Horbury, J. M. Toldo, M. T. Do Casal, B. Rioux, C. Peyrot, M. M. Mention, P. Balaguer, M. Barbatti, F. Allais and V. G. Stavros, J. Phys. Chem. Lett., 2020, 12, 337–344.
14. T. T. Abiola, B. Rioux, J. M. Toldo, J. Alarcan, J. M. Woolley, M. A. P. Turner, D. J. L. Coxon, M. T. Do Casal, C. Peyrot, M. M. Mention, W. J. Buma, M. N. R. Ashfold, A. Braeuning, M. Barbatti, V. G. Stavros and F. Allais, Chem. Sci., 2021, 12, 15239–15252.
15. S. Kinoshita, Y. Harabuchi, Y. Inokuchi, S. Maeda, M. Ehara, K. Yamazaki and T. Ebata, Phys. Chem. Chem. Phys., 2021, 23, 834–845.
16. R. Losantos, I. Funes-Ardoiz, J. Aguilera, E. Herrera-Ceballos, C. García-Iriepa, P. J. Campos and D. Sampedro, Angew. Chem., Int. Ed., 2017, 129, 2676–2679.
17. E. C. De Fabo and F. P. Noonan, J. Exp. Med., 1983, 158, 84–98.
18. F. X. Ji, X. Y. Zhao, Y. R. Guo, Z. B. Wu, M. Q. Wang, Y. N. Shi and G. J. Zhao, J. Lumin., 2021, 238, 118215.
19. J. P. Walterscheid, D. X. Nghiem, N. Kazimi, L. K. Nutt, D. J. McConkey, M. Norval and S. E. Ullrich, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 17420–17425.
20. T. Mohammad, H. Morrison and H. HogenEsch., Photochem. Photobiol., 1999, 69, 115–135.
21. J. D. Simon, Acc. Chem. Res., 2000, 33, 307–313.
22. N. K. Gibbs, J. Tye and M. Norva, Photochem. Photobiol. Sci., 2008, 7, 655–667.
23. H. Morrison, D. Avnir, C. Bernasconi and G. Fagan, Photochem. Photobiol., 1980, 32, 711–714.
24. H. Morrison, C. Bernasconi and G. Pandey, Photochem. Photobiol., 1984, 40, 549–550.
25. B. L. Li, K. M. Hanson and J. D. Simon, J. Phys. Chem. A, 1997, 101, 969–972.
26. J. Brookman, J. N. Chacón and R. S. Sinclair, Photochem. Photobiol. Sci., 2002, 1, 327–332.
27. K. M. Hanson, B. L. Li and J. D. Simon, J. Am. Chem. Soc., 1997, 119, 2715–2721.
28. K. M. Hanson and J. D. Simon, Photochem. Photobiol., 1998, 67, 538–540.
29. N. Haralampus-Grynaviski, C. Ransom, T. Ye, M. Rôżanowska, M. Wrona, T. Sarna and J. D. Simon, J. Am. Chem. Soc., 2002, 124, 3461–3468.
30. C. S. Page, M. Merchán, L. Serrano-Andrés and M. Olivucci, J. Phys. Chem. A, 1999, 103, 9864–9871.
31. J. Danielsson, J. Uličný and A. Laaksonen, J. Am. Chem. Soc., 2001, 123, 9817–9821.
32. J. Danielsson and A. Laaksonen, Chem. Phys. Lett., 2003, 370, 625–630.
33. M. Barbatti, Phys. Chem. Chem. Phys., 2011, 13, 4686–4692.
34. D. Tuna, A. L. Sobolewski and W. Domcke, J. Phys. Chem. B, 2014, 118, 976–985.
35. L. Zhao, P. W. Zhou and G. J. Zhao, J. Chem. Phys., 2016, 145, 044316.
36. D. Tuna, L. Spörkel, M. Barbatti and W. Thiel, Chem. Phys., 2018, 515, 521–534.
37. W. L. Ryan and D. H. Levy, J. Am. Chem. Soc., 2001, 123, 961–966.
38. P. D. Godfrey and E. G. Robertson, J. Chem. Phys., 2012, 137, 064306.
39. G. Meijer, M. S. De Vries, H. E. Hunziker and H. R. Wendt, Appl. Phys. B: Lasers Opt., 1990, 51, 395–403.
40. S. Smolarek, A. Vdovin, A. M. Rijs, C. A. van Walree, M. Zgierski and W. J. Buma, J. Phys. Chem. A, 2011, 115, 9399–9410.
41. E. M. M. Tan, S. Amirjalayer, S. Smolarek, A. Vdovin, F. Zerbetto and W. J. Buma, Nat. Commun., 2015, 6, 5860.
42. E. Maltseva, S. Amirjalayer and W. J. Buma, Phys. Chem. Chem. Phys., 2017, 19, 5861–5869.
43. J. Fan, W. Roeterdink and W. J. Buma, Mol. Phys., 2021, 119, e1825850.
44. The normal modes of urocanic acid are divided into modes 1-29 of a’ symmetry and modes 30-42 of a” symmetry using a standard mode numbering with decreasing frequencies.
45. K. Yamazaki, Y. Miyazaki, Y. Harabuchi, T. Taketsugu, S. Maeda, Y. Inokuchi, S. Kinoshita, M. Sumida, Y. Onitsuka, H. Kohguchi, M. Ehara and T. Ebata, J. Phys. Chem. Lett., 2016, 7, 4001–4007.
46. M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838.
47. M. A. Trachsel, T. Wiedmer, S. Blaser, H. Frey, Q. S. Li, S. Ruiz-Barragan, L. Blancafort and S. Leutwyler, J. Chem. Phys., 2016, 145, 134307.
48. F. M. Siouri, S. Boldissar, J. A. Berenbeim and M. S. de Vries, J. Phys. Chem. A, 2017, 121, 5257–5266.
49. E. L. Holt and V. G. Stavros, Int. Rev. Phys. Chem., 2019, 38, 243–285.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and theoretical procedures, synthesis and characterization, additional figures and table. See DOI: https://doi.org/10.1039/d4cp02087a

---