Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical terahertz spectroscopy of free radical solutes in solution: an EPR spin probe in water
Bikramjit
Sharma
 *a,
Philipp
Schienbein
*a,
Philipp
Schienbein
 bc,
Harald
Forbert
bc,
Harald
Forbert
 d and
Dominik
Marx
a
d and
Dominik
Marx
a
aLehrstuhl für Theoretische Chemie, Ruhr-Universität Bochum, 44780 Bochum, Germany. E-mail: dominik.marx@theochem.rub.de
bLehrstuhl für Theoretische Chemie II, Ruhr-Universität Bochum, 44780 Bochum, Germany
cResearch Center Chemical Sciences and Sustainability, Research Alliance Ruhr, 44780 Bochum, Germany
dCenter for Solvation Science ZEMOS, Ruhr-Universität Bochum, 44780 Bochum, Germany
First published on 25th September 2024
Abstract
Free radical species are used as spin labels in electron paramagnetic resonance (EPR) spectroscopy of biomolecular systems in water, for instance in the frame of Overhauser dynamic nuclear polarization (ODNP) relaxometry to probe the local hydration water dynamics close to protein surfaces in aqueous environments. Widely used in this context are nitroxide spin probes such as TEMPO, PROXYL or MTSL derivatives. Here, we study the THz spectroscopy of HMI (2,2,3,4,5,5-HexaMethylImidazolidin-1-oxyl) in water at ambient conditions which has been recently investigated as to how its EPR properties depend on its solvation pattern in water. To enable theoretical THz spectroscopy of molecular radicals in solution, we have generalized well-established methodologies for THz spectral decomposition of closed-shell systems, namely the supermolecular solvation complex (SSC) and cross-correlation analysis (CCA) techniques, to open-shell polyatomic solute species in water. Based on this methodological advance, we have decomposed and assigned the THz response of HMI including its solvation shell by employing the generalized SSC and CCA methods to cope with the open-shell character of this free radical solute, in particular its unpaired electron localized at the nitroxy group. We reveal that the main modulations of the far-IR spectrum of HMI are dominated by the low-frequency intramolecular modes of the spin probe molecule itself while the solvation of its two hydrogen bonding sites contribute much less intensely in this spectral window. Finally, we have computed THz spectra of HMI with its local solvation water with an aim to provide a theoretical analogue of experimental THz difference spectroscopy. Beyond the specific case, our decomposition methodology that now is able to include open shells can be applied in future work to analyze the low-frequency vibrational response of the solvation shell of other free radicals in solution.
1 Introduction
Organic free radicals are complex chemical species with great importance from atmospheric science1,2 to chemistry,3,4 biology,5,6 materials science and technology.7,8 Ever since stable nitroxide containing organic free radicals have been synthesized,9–12 their applications have widely spread to the fields of polymerization,13–15 organic synthesis,16 and solvation dynamics.17–20 Particularly, the realm of electron paramagnetic resonance spectroscopy (EPR) experiments have seen a paradigm shift thanks to the tremendous utility of stable nitroxide radicals as site directed spin label21–23 and as EPR spin probes in general.24 Progress in more sophisticated experiments using nitroxide radicals as a source of so-called unpaired electrons, e.g. Overhauser dynamic nuclear polarization (ODNP) spectroscopy where the electron spin couples with the water protons to investigate hydration dynamics17–20 or 17O hyperfine spectroscopy to reveal properties of solvation water25,26 has opened the whole avenue of importance of such radicals in solvation science. The results of these sophisticated experiments are ideally complemented by investigations of the solvation of the spin probe molecules themselves, to deepen our insights of the intermolecular nitroxide radical–water interactions. Furthermore, since water is the universal solvent, the microscopic understanding of the solvation properties of nitroxide containing free radicals is of utmost importance not only from the perspective of these experiments but much beyond.The solvation properties of nitroxide based organic free radicals have been investigated since long by computing statistical structural correlation functions and hydrogen-bonding properties.27–32 Such studies revealed important microscopic information and provided spatially averaged local solvation information. For instance, detailed insights into the spatial distribution of water molecules around the nitroxide's oxygen atom containing the EPR probe were revealed by 17O hyperfine spectroscopic experiments in conjunction with force field molecular dynamics simulations.26 Earlier experiments aided by static quantum chemical calculations have attempted to understand properties of microsolvated nitroxide radicals by probing only the water vibrations.33–35
Going beyond water-only vibrations, an orthogonal but complementary experimental technique, namely terahertz (THz) spectroscopy, has been shown to be a useful approach to understand intermolecular solute–solvent interactions36–41 by directly probing the low frequency vibrational modes in the far-IR region. THz resonances have been theoretically resolved in space42 to interpret THz spectra of liquid water, and later of closed-shell solutes species, in terms of distance-dependent solvation shell contributions. On the other hand, time-resolved THz modes have been interpreted43 in terms of dynamical properties by employing wavelet transform techniques. Experimental THz spectroscopy coupled with theoretical insights has become immensely successful in investigating solvation phenomena, in particularly at the molecular level of deciphering the noncovalent interactions between solute and solvent molecules. Although existing THz studies have primarily dealt with solvation of solutes without unpaired electrons, it is highly desirable to utilize this technique for studying the solvation properties of free radicals more broadly.
In the current work, we therefore set out to compute and systematically decompose the theoretical THz spectrum of an important nitroxide containing organic free radical in bulk water based on ab initio molecular dynamics (AIMD) simulations.44 Our aim is to devise a theoretical approach and computational protocol which can be exploited seamlessly in future assignments of THz spectra of free radicals in solution. Hence, our goal is to generalize well-established THz analysis techniques for closed-shell systems to open-shell cases. Earlier, we developed two complementary methodologies, namely the supermolecular solvation complex (SSC) and cross-correlation analysis (CCA) approaches, (see Sections 3.1 and 3.2 for background and references) and applied them successfully to various closed-shell solute species in aqueous solution. In the present paper, we generalize these methodologies for systems containing free radicals as solutes. Furthermore, we are interested in computing the local THz response of an open-shell solute molecule and its solvation water which can serve as theoretical reference for difference THz spectroscopy experiments.
We have chosen a pH-sensitive EPR probe, namely HMI (C9H19N2O: (2,2,3,4,5,5-hexamethylimidazolidin-1-oxyl as depicted in Fig. 1) as the prototype, given the purpose of our study. Such pH-sensitive nitroxide probes, including HMI in particular, have greatly expanded the horizon of EPR spectroscopy by enabling pH-sensitive imaging,45,46 determining local pH,47 acid–base properties,48–50 as well as dielectric and electrostatic properties.51 Previously we already studied the EPR response of HMI in aqueous solution30,32 as well as in the gas phase,52 due to the broad interest in such pH-sensitive EPR probes. In particular, HMI in water is an interesting representative case for establishing theoretical THz spectroscopy in the territory of free radical solvation in aqueous environments. Herein, we have performed extensive AIMD simulations of HMI in bulk water to sample the solvation space of HMI and decomposed the total THz spectrum in terms of customized molecular fragment and intermolecular interaction contributions. The unpaired electron – leading to non-zero spin density – is localized on the nitroxide group of the HMI molecule (Fig. 1) which then provides the EPR-active site in spin labeling, causing the suitability of HMI as an EPR probe. In contrast, the ring nitrogen (Nring) does not feature any non-zero spin density but contributes instead the pH-sensitivity of HMI since that site can be protonated. When solvated in water, the nitroxide oxygen (ON) as well as Nring provide two distinct solvation sites for hydrogen bonding to the surrounding solvent molecules which are separated from each other (Fig. 1). Thus, the total THz spectrum of solvated HMI is expected to be a combination of responses coming from different intermolecular modes associated with these two solvation sites. This observation suggests a divide-and-conquer approach to decompose the global THz response. Using AIMD, the THz response of HMI has been studied by employing the complementary SSC and CCA methodologies. Moreover, in contrast to closed-shell solutes in water, AIMD simulations of free radical solute species must consider their open-shell character by treating these solutions in a spin-polarized manner. This not only roughly doubles the computational effort but also adds complexity in the context of breaking up the global THz response into localized contributions based on Wannier decomposition to be discussed below. Moreover, standard GGA density functionals suffer from self-interaction errors which leads to spurious delocalization of spin density that might also include the aqueous environment. This needs to be taken care of as pioneered long ago based on applying an explicit self-interaction correction scheme.53 Today, spin-polarized hybrid density functionals are much used to cure the problem which is the route we follow here as explained in Section 2. The price to pay compared to applying corrections to GGA functionals is an increase of the computational effort by an order of magnitude. Overall, simulating an EPR spin probe such as HMI in aqueous solution by AIMD introduces a substantial computational overhead compared to investigating seemingly similar solutions of closed-shell species.
2 Computational details
Before launching AIMD sampling of the system, constant pressure (NpT) force field molecular dynamics (FFMD) simulations of 1 HMI in 128 water molecules were performed at 1 bar and 300 K from which the box length of 15.9581 Å was computed by averaging over the fluctuating volumes to fix the periodic cubic supercell for subsequent constant volume simulations. The initial configuration for AIMD was generated by pre-equilibration based on NVT simulations using the same FFMD protocol as for NpT. We carried out the subsequent AIMD simulations using the CP2K package54,55 and its QUICKSTEP module56 at NVT conditions to sample the solvation configurations of HMI in water at ambient conditions. We refer the reader to our earlier publication30 for further details of FFMD and AIMD. Nevertheless, we summarize important aspects of the AIMD simulations for the sake of completeness. We employed a plane wave basis with a kinetic energy cutoff of 500 Ry and the atom-centered TZV2P Gaussian basis set in conjunction with Goedecker–Teter–Hutter pseudopotentials57–59 to represent the total electron density and Kohn–Sham orbitals, respectively, within Quickstep. Due to the open-shell nature of the system we have expressed the exchange–correlation contribution in terms of the spin-polarized revPBE0 density functional60,61 together with the D3 dispersion correction62 thus providing revPBE0-D3. Computation of the demanding Fock exchange terms of the hybrid functional was accelerated by the auxiliary density matrix method (ADMM)63 with the cpFIT3 auxiliary basis. The constant average temperature during the NVT simulation was maintained using massive Nosé–Hoover chain thermostatting64 where each Cartesian degree of freedom is thermostatted separately. A time step of 0.5 fs was used to generate a 200 ps long NVT trajectory after careful equilibration.In order to generate the dipole moment trajectory required for rigorously computing the THz response from the time auto-correlation function, we have extracted independent phase space snapshots after every 10 ps from the 200 ps long canonical (NVT) AIMD trajectory. Starting from those snapshots, we launched microcanonical (NVE) AIMD simulations to properly generate the real-time dynamics in the microcanonical ensemble that is free from any thermostatting artifacts. Each of the NVE runs produced 20 ps long trajectories making a total of 400 ps of NVE trajectories. For the calculations of the dipole moment,44 the Wannier function center (WFC) associated with each electron (in either spin up or spin down polarization thus adding up to an odd total number of such spin-WFCs) was computed by localization of the full set of alpha (spin up) and beta (spin down) Kohn–Sham spin orbitals to obtain 20 independent dipole moment trajectories and subsequently the total or partial THz spectra by averaging the 20 individual NVE spectra, thus providing the desired NVT averages.
3 Methodology for computation and decomposition of THz spectra
We briefly discuss here the general frameworks of the two (SSC and CCA) approaches employed in the current decomposition of the THz response of HMI in water. The total THz spectrum (or IR spectra in general) is obtained by Fourier transformation of the dipole moment auto-correlation function as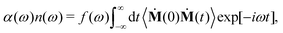 | (1) |
3.1 Supermolecular solvation complex (SSC)
The SSC method36 has been developed in-house to successfully assign the low frequency vibrational modes to atomic motions within strongly coupled solute–solvent complexes. As a first step, SSC relies on extracting sufficiently stable solute–solvent solvation complexes as the system dynamically evolves for which the dipole moment is computed from the WFCs obtained in solution (thus avoiding artifacts due to microsolvation of the solute in vacuum or continuum solvent). This amounts to studying the partial THz spectra of tailor-made subsystems with distinct supermolecular identities that include the solute and a specific subset of solvent molecules which, thus, provides a microscopic picture of the corresponding spectral response.To this end, the dipole velocity cross-correlation matrix is constructed between charge-weighted Cartesian velocity components ξ of center i and χ of center j in the molecular frame as
 | (2) |
 | (3) |
After this rough sketch of the SSC approach, we refer the interested reader to ref. 36 for further details of SSC analysis of THz spectra in the realm of solutions that contain only closed-shell solutes.
3.2 Cross-correlation analysis (CCA)
In the CCA approach,38 the system is divided into groups of particles (e.g. molecules in solution or specific sites within molecules) and group relations (e.g. hydrogen-bonding or coordinating) between the associated particles are defined. The group and relation selectors are defined as time-dependent Heaviside step functions as | (4) |
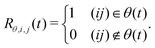 | (5) |
 | (6) |
The key difference between the results obtained from SSC and CCA is that the former decomposes the spectra into mode specific spectral contributions due to all modes within user-defined SSCs while the later decomposes the total spectrum in terms of spectral contributions of groups of particles within the system without providing a mode picture. Thus, SSC requires the existence of sufficiently long-lived solvation complexes in the solution, while CCA can be applied to cases where such complexes cannot be defined due to their fleeting existence or ill-defined nature. Akin to SSC, the existing CCA technique has been applied to far-IR to analyze closed-shell solute species in solutions.
3.3 Dimensionality reduction through coarse-graining of degrees of freedom
We now address our strategy to generalize the existing SSC and CCA techniques to open-shell solute species. To this end, we adopted a coarse-grained representation of certain degrees of freedoms to reduce both, the number of the explicitly treated atoms of the system and the complexity of the electronic structure of open-shell solutes to efficiently carry out our SSC or CCA analyses as described in the following (while this is not required to compute total THz spectra). Firstly, the methyl groups can rotate essentially without hindrance in the solution due to negligible methyl–water interactions. Thus, it is reasonable to assume that an average THz response will be coming from the methyl hydrogen atoms, HMe. Hence, we represented the three HMe atoms of each methyl group as a single effective atom with three times the mass of a hydrogen atom (Fig. 2) obtained by averaging the coordinate vectors in each dimension. Similarly, the overall six singly occupied spin-WFCs corresponding to the three covalent C–H bonds within every methyl group are converted to one effective WFC with a charge of −6e in order to represent the electronic structure of each coarse-grained methyl group. | ||
| Fig. 2 Representative snapshot of HMI showing the coarse-graining of the methyl groups. The coarse-grained Wannier function centers, see text, are not shown for the sake of clarity. | ||
In addition, all those pairs of spin-WFCs (which are singly occupied and thus carry a charge of −1e each) which correspond to alpha and beta spin orbitals describing two-center two-electron covalent bonds are well localized within molecules and, thus, can be vectorially averaged into one effective doubly occupied WFC (thus with charge −2e) as in case of usual Wannier localization of closed-shell systems. For HMI in water, this applies to all those spin-WFCs that are associated to the water molecules in which all pair up in space, providing two pairs of alpha and beta Wannier spin orbitals between the O and H sites since they are associated with the covalent O–H bonds, as well as two such pairs describing the two lone pair electrons in accord with the Lewis structure of water molecules. The situation within the HMI molecule is much more complex due to the presence of an unpaired electron that provides non-zero spin density being localized at the nitroxy group (and providing the EPR spin probe site). But even for HMI, it turns out that most of the centers of the Wannier spin orbitals are well-localized in terms of alpha/beta pairs and remain close in space within the quasi-rigid molecular skeleton that fluctuates along the generated AIMD trajectories. These spin-WFCs are associated with all C–C, C–H and C–N covalent bonds in the HMI heteroring, which are thus also paired into localized alpha+ beta WFCs carrying a charge of −2e each (while the electron pairs of the methyl C–H bonds have already been coarse-grained together with the methyl hydrogens, see above). Yet, there are several spin-WFCs within HMI that cannot be paired – as expected based on the open-shell character of HMI. All of them, except for three spin-WFCs at the oxygen terminus of the nitroxy group, remain well-localized and are thus treated in the analysis as individual electronic degrees of freedom. In contrast, the three spin-WFCs at the O site (on its solvent-facing side) turn out to be not well-localized in space since they change dynamically their positioning along the AIMD trajectories. We thus coarse-grained them into one effective WFC of charge −3e. Such system-adapted complexity reduction of the electronic structure enabled us to now generalize the SSC and CCA spectral decomposition methodologies – introduced and applied so far exclusively to closed-shell systems – to free radicals in solution as applied here to dissect and assign the total THz spectrum of the HMI spin probe in water as explained below.
4 Results and discussions
4.1 Structural solvation properties
Before dealing with the theoretical THz analysis, we present here key solvation structural properties around the two sites of HMI that strongly interact with nearby water molecules, namely ON and Nring (Fig. 3(a)). Earlier we already studied30,32 the water structure around ON of HMI in detail due to the importance of that group for EPR spectroscopy and only summarize the findings here. The ON atom of HMI primarily exists in three types of hydrogen bonding states with water, namely by accepting one, two or three hydrogen bonds. The two and three hydrogen bonding states are predominant with approximately 60 and 27% of the population, respectively. Apart from these hydrogen bonded water molecules (abbreviated here by HB), the existence of non-hydrogen bonded water molecules within the first solvation shell (i.e. interstitial water, IW) was found around ON in earlier work on EPR properties of HMI in aqueous solution.32 Note that the first solvation shell of ON is formed by water molecules whose oxygen (OW) atoms reside within a distance that is given by the first minimum (3.6 Å) of the corresponding ON–OW radial distribution function30 (RDF) and will be referred to as OsolvN throughout this paper. In the current study, we have further deciphered the contributions of the HB and IW molecules to the ON–OW RDF by calculating the incremental RDF (IRDF).71 Such IRDF reveals information about the contribution of the nth nearest water molecule from the ON atom to the overall RDF. The IRDF (Fig. 3(a)) clearly shows that the first and second nearest water molecules contribute only to the first solvation shell of ON while the third and fourth nearest water molecule IRDFs extend beyond, meaning that these water molecules span the exchange pathway toward the second solvation shell. From the fifth nearest water molecule onward (Fig. 3(a)), no contributions to the first solvation shell occurs. We further unveil here the contributions in terms of coordinated, HB and IW molecules (Fig. 3(c)). To this end, we have used the same hydrogen bonding criterion established in our earlier study.32 The HB molecules offer the maximum contribution to the total ON–OW RDF. Diminished contributions of the IW molecules start from a larger distance compared to that of HB molecules. As expected, the coordinating water component which is a combination of HB and IW molecules overlaps with the total ON–OW RDF validating the accuracy of the decomposition. Note that the frequent interchange between the HB and IW molecules makes the solvation environment of ON, i.e., OsolvN, very labile. These frequent interchanges do not permit use of the SSC method (see Section 3.1) and hence we instead employ the complementary CCA analysis (see Section 3.2) for OsolvN as detailed below. The CCA analysis can rigorously handle all transient structures, even though they are frequently interchanging, at the expense of mode vectors as available in SSC for sufficiently stable solvation complexes (see Section 3.1). Note that the nitrogen atom of the nitroxy group is shielded from the solvent molecule by the methyl groups and hence does not form any hydrogen bonds with water. Next, the RDF of OW with respect to Nring (Fig. 3(b)) is characterized by a probability density of close to zero in its first minimum, thus implying a very well-defined first coordination shell. In fact, only the first nearest water molecule (Fig. 3(b)) and the HB water molecule (Fig. 3(d)) contribute to the first solvation shell peak of the Nring–OW RDF. Inspection of the trajectory also shows that the identity of the water molecule initially hydrogen bonded to Nring does not change during the course of the simulation. This gives rise to a very strong and thus long-lived solute–solvent solvation complex that is perfectly suited for mode decomposition using the SSC methodology.4.2 THz response of HMI itself and its hydrogen bonded NW-solvation complex
The SSC analysis can be readily performed on HMI molecule itself (dubbed “HMI-only”) and, given its stability, of the HMI-solvent complex formed by water molecules that are hydrogen-bonded to the Nring atom (denoted as “NW-complex”). Hence as a first step, a meaningful “average solute structure” (Fig. 4(a)) and average HMI-solvent complex structure (Fig. 4(b)) were extracted from all NVE trajectories by proper translational and rotational coordinate transformation from the lab-fixed to the molecular frame of “HMI-only” and the “NW-complex”, respectively. Note that the impact of the surrounding solvation environment is imprinted in the average structures of “HMI-only” due to that averaging in the liquid environment. We refer to ref. 36 for details of these transformations. | ||
| Fig. 4 Average structures of (a) “HMI-only” and of the (b) “NW-complex” computed for THz mode decomposition using the SSC analysis, see text. | ||
Having access to these two reference structures, we performed the SSC analysis and thus obtain the THz mode assignment with respect to the average HMI structure “HMI-only” as well as the average HMI-solvent complex structure “NW-complex” and compare their THz spectra in Fig. 5. The difference between the two spectra is insignificant which means very weak impact of the hydrogen bonding water of Nring on the overall THz response of the “NW-complex”. The “HMI-only” spectrum is characterized by a broad peak in the range of about 100–200 cm−1, a sharp peak at ≈400 cm−1 and smaller peaks at ≈310, 350 and 460 cm−1. The full mode decomposition in terms of atomic displacement patterns corresponding to these THz resonances of HMI itself is presented in Fig. 6 and the corresponding mode decomposed THz spectra in Fig. 7.
 | ||
| Fig. 6 Atomic displacement vectors and their assignment in terms of intramolecular motion of the THz modes corresponding to low frequency vibrations of “HMI-only” obtained from SSC analysis; the corresponding average frequencies are reported in parentheses. See Fig. 7 for the mode decomposed THz spectra. | ||
 | ||
| Fig. 7 THz spectra corresponding to the vibrations of HMI itself: (a) combination of collective motion of methyl groups with wagging of ON; (b) complex rocking motion of the methyl groups; (c) twisting motion of the ring atoms of the HMI molecule; (d) scissoring motion of the methyl groups with wagging of the nitroxy oxygen (pink), collective motion of the methyl groups plus wagging of the nitroxy oxygen (indigo) and collective motion of the methyl groups (dotted cyan); (e) complex wagging and scissoring motion of the methyl groups (violet) and scissoring motion of methyl groups (turquoise broken line); (f) out-of-plane motion of the nitroxy oxygen (dark green) and torsional motion about the C–Nring in the inset. See Fig. 6 for the corresponding mode displacement patterns. | ||
The low frequency intramolecular modes of HMI in water can be assigned as follows based on the SSC decomposition of the “HMI-only” THz spectrum. The peak at ≈400 cm−1 stems from a combination of collective motion of methyl groups with wagging of ON (Fig. 6(a) and 7(a)) and complex rocking motion of the methyl groups (Fig. 6(b) and 7(b)). However, the maximum contribution comes from the mode corresponding to collective motion of methyl groups with wagging of ON as evident from the intensities of the corresponding spectra (Fig. 7(a) and (b)). The peak at ≈460 cm−1 is due to twisting motion of the ring atoms of the HMI molecule (Fig. 6(c) and 7(c))). The peak at ≈350 cm−1 encompasses three SSC modes corresponding to scissoring motion of the methyl groups coupled to wagging of the nitroxy oxygen (Fig. 6(d)), collective motion of the methyl groups and wagging of nitroxy oxygen (Fig. 6(e)) as well as a third type of collective motion of the methyl groups (Fig. 6(f)). The intensities of the partial THz spectra corresponding to these three modes (Fig. 7(d)) are very comparable meaning quite equal contributions to the peak at 350 cm−1. Two normal modes corresponding to complex wagging with scissoring motion of the methyl groups (Fig. 6(g)) and another scissoring motion of methyl groups (Fig. 6(h)) contribute comparably in THz intensity (Fig. 7(e)) to the peak at ≈310 cm−1. Finally, the broad frequency range from ≈100–200 cm−1 (where hydrogen bonded water contributions are also expected in case of the “NW-complex”) is found to have contributions from two intramolecular solute modes due to out-of-plane motion of the nitroxy oxygen (Fig. 6(i)) and torsional motion about the C–Nring bond although the intensity of the later is very small as shown in the inset of Fig. 7(j). The modes discussed so far are found to be originating exclusively from the motion of the solute at THz frequencies without direct intervention of the water molecules that are hydrogen bonded to Nring. Note that as these modes are common in both “HMI-only” and “NW-complex” as stressed above, it suffices to discuss only the former case. Another interesting aspect revealed by the SSC dissection of the THz response of HMI in water is the non-existence of any spectral mode feature with reasonable intensity arising mainly due to electronic motion as encoded in the dynamics of the WFCs; recall that the WFCs are treated as pseudo-atoms in the SSC approach (Section 3.1) and motion of those at THz frequencies would be captured as modes. Hence, there is no mode specifically emerging due to the unpaired electron that is localized at the nitroxy group which could significantly impact the THz spectrum of HMI in water for instance as a result of local polarization fluctuations.
The contribution to the THz response that comes from the firmly hydrogen bonded water molecule at the NH-group as obtained from the “NW-complex” is found to be localized in the characteristic broad peak from ≈100–200 cm−1. Three normal modes corresponding to motion of the hydrogen bonded water molecule at THz frequencies are identified as follows. The vibration of the hydrogen bond (Fig. 8(a)) and two orthogonal rattling motions of the water molecule, namely rattling motion I of water (Fig. 8(b)) and rattling motion II of water (Fig. 8(b)) contribute to the broad peak in the spectra. It is to be noted the intensities of the water modes (Fig. 9) are very low compared to those of the solute itself and, hence, the corresponding contributions are buried in that broad intramolecular low frequency peak of HMI itself (Fig. 7(f)) without any distinct additional features. Secondly, the mode decomposed THz spectra due to the water modes (Fig. 9) are very broad due the heterogeneous environment provided by the rest of the water molecules. The THz contributions of intramolecular HMI modes are much narrower as this quasi-rigid solute species is affected only slightly by the dynamically fluctuating solvent environment.
 | ||
| Fig. 8 Atomic displacement vectors and their assignment in terms of intermolecular motion of the THz modes corresponding to low frequency vibrations of the “NW-complex” obtained from SSC analysis; the corresponding average frequencies are reported in parentheses. See Fig. 9 for the mode decomposed THz spectra. | ||
 | ||
| Fig. 9 THz spectra corresponding to the intermolecular vibrations of the “NW-complex”: (a) vibration of the hydrogen bond; (b) two orthogonal modes corresponding to rattling motion I and II of the water molecule. See Fig. 8 for the corresponding mode displacement patterns. | ||
4.3 THz response from the solvation shell around the nitroxy–oxygen
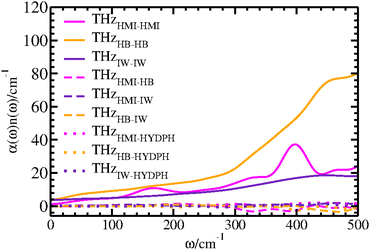
The nitroxy group of HMI hosts the free electron and its ON atom interacts with the surrounding water molecules via hydrogen bonding. Thus, the intermolecular modes in the solvation shell of the ON site are potentially affected by the unpaired electron of this spin probe molecule. Extracting the THz spectra for the solvation shell water will inherently carry any effect of the cumulative electronic structure of the solute (nitroxy group in particular) on the intermolecular interaction between water molecules and ON atom. We have applied the CCA methodology to compute the THz spectra for different groups and group relations between ON and surrounding water molecules. Hence this approach generates THz spectra for different subensembles corresponding to auto- and cross-correlations between the molecules within a defined group or group relations which rigorously adds up to give the total spectrum of the system (Fig. 10, see THzTotal(CCA)). Before going to the definition of the different groups and the group relations that we introduced in order to specifically decipher the THz activity of the nitroxy group (see below), we have validated the CCA decomposition accordingly by comparing the total CCA spectrum THzTotal(CCA) to the standard one that is directly computed from the auto-correlation function of the dipole moment of the total system, THzDipole. We find excellent agreement between the THzTotal(CCA) and THzDipole spectra (Fig. 10) where the CCA method has been applied for the first time to an open-shell system.The THz response due to the presence of the solute interacting with the solvent can be divided into responses from auto- and cross-correlations of HMI and the solvation shell water molecules around ON. Thus, we have defined two groups consisting of the HMI molecule and solvation shell water which will be referred as OsolvN. The solvation shell itself consists of HB and IW molecules as described in Section 4.1. Thus, we have defined group relations as HB and IW corresponding to water molecules that are either hydrogen bonded to the ON atom or remain interstitial within the first coordination shell as defined above for the structural analyses. The CCA-based THz responses arising from the dipole moment auto-correlations of the HMI (THzHMI–HMI), HB (THzHB–HB) and IW (THzIW–IW) components are presented in Fig. 11 to decipher the respective contributions to the total THz response of the solution.
From the intensities of these self terms (Fig. 11), it is clear that the HB component dominates among all three auto-correlation contributions followed by the HMI contribution which primarily carries the features of the intramolecular THz modes of the solute. Note, that the average numbers of HB and IW water molecules are ≈2.16 and ≈0.69 according to earlier work,32 respectively, which is the main cause of the difference in intensities of auto-correlations involving the two types of water molecules (Fig. 11, THzHB–HBvs. THzIW–IW) within OsolvN. Importantly, the THzHMI–HMI recovers the main features already obtained and assigned based on the SSC analysis of HMI itself as depicted by the black line in Fig. 5, albeit all peaks are broadened in the CCA decomposition. The former single-molecule contribution, i.e. THzHB–HB, is mainly due to the librational motion of the individual water molecules that are hydrogen bonded to ON and results into a prominent but featureless absorption that decays from the maximum of the librational band from about 500 cm−1 to zero frequency. The auto-correlation contribution due to the IW molecules to the THz spectrum turns out to be broad, featureless, and rather small on the scale set by the HB waters but follows that general shape since it is also due to single-particle librations, this time of the interstitial water molecules around the oxygen site of the nitroxy group. Next, we have examined the dipolar cross-correlation contributions (Fig. 11) of HMI and HB (THzHMI–HB), HMI and IW (THzHMI–IW) as well as HB and IW (THzHB–IW). Interestingly, the cross-correlation contributions from the components of OsolvN are found to be very small in comparison to the auto-correlation contributions. Thus, the auto-correlations dominate the THz response due to the solvation of OsolvN and thus of the entire nitroxy group that carries the unpaired electron of this spin probe molecule.
The hydrophobic water molecules72 which interact with the methyl groups of HMI are significant components of the full solvation shell of HMI in water which may impact the THz response of OsolvN. That impact can be revealed in terms of the corresponding cross-correlation analysis by introducing an additional CCA group, HYDPH. For this analysis, we have defined hydrophobic water molecules as those ones where the nearest methyl carbon with respect to the oxygen atom of a given water molecule lies within a distance of at most 4 Å thus following earlier work.72 The cross-correlation calculations between hydrophobic water and HMI (THzHMI–HYDPH) as well as HB (THzHB–HYDPH) and IW (THzIW–HYDPH) water show negligible intensity meaning that hydrophobic water does not have any appreciable impact on the THz response of the nitroxy group according to the respective CCA contributions compiled in Fig. 11.
The CCA analysis also reveals that the hydrophobic water molecules around the methyl groups and the ON site and thus the nitroxy group are independent entities in the solvation shell of HMI and retain their own identity. This also rules out the possibility of significant cooperative solvation effects involving water molecules close to the nitroxy group, and thus nearby the unpaired electron, and the methyl groups of this spin probe molecule.
Having the all types of correlations at hand, we have reconstructed the total THz spectrum of the solvated ON site (see Fig. 12 providing the  ) by adding the auto- and cross-correlation contributions involving the solute itself as well as the hydrogen bonded and interstitial water molecules. In experimental THz experiments, the selective response due to the presence of solute species with their associated solvation shell is obtained in terms of difference spectra between the pure solvent and the solution. In the current case, the selective response can come from HMI and close by water molecules. Since we have shown above that both, hydrogen bonded water at the Nring site in the ring and hydrophobic water around the methyl groups do not contribute much to the total THz response of HMI in liquid water on the relevant intensity scale, we can now conclude that the reconstructed
) by adding the auto- and cross-correlation contributions involving the solute itself as well as the hydrogen bonded and interstitial water molecules. In experimental THz experiments, the selective response due to the presence of solute species with their associated solvation shell is obtained in terms of difference spectra between the pure solvent and the solution. In the current case, the selective response can come from HMI and close by water molecules. Since we have shown above that both, hydrogen bonded water at the Nring site in the ring and hydrophobic water around the methyl groups do not contribute much to the total THz response of HMI in liquid water on the relevant intensity scale, we can now conclude that the reconstructed  spectrum presented in Fig. 12 can serve as a reference for assigning experimental difference spectra.
spectrum presented in Fig. 12 can serve as a reference for assigning experimental difference spectra.
One intriguing feature revealed by the CCA analysis depicted in Fig. 11 is the negligible cross-correlation between the ON group of HMI and the surrounding water molecules. We have observed such behavior before39 and it is reminiscent of only weak interactions between the solute and the solvent molecules. In the current scenario, the negligible cross-correlation is found, although hydrogen bonds are formed with the ON group thus yielding OsolvN. The exchange between HW and IW water within OsolvN as already analyzed and discussed previously (see Section 4.2.1 in ref. 32) allows the ON–water hydrogen bonds to exist only fleetingly. Consequently, the cross-correlations between the HB or IW water and HMI within OsolvN become negligible. This is also the main reason why we could not apply the SSC analysis to extract the intermolecular water–ON vibrations as explained above, which is consistent with the finding of negligible cross-correlations by CCA decomposition. Notably, this behavior of OsolvN is in stark contrast to the “NW-complex” of the HMI molecule, where a long-lived hydrogen bond is formed between the ring nitrogen and the adjacent water molecule thus allowing for SSC analysis, see Fig. 8 and 9.
5 Conclusions and outlook
We have computed, decomposed and assigned the THz spectrum of a typical nitroxide EPR spin label, namely HMI in liquid water at ambient conditions based on ab initio molecular dynamics simulations. Two complementary decomposition methods have been used to assign the far-IR response of HMI in water which involves both, intra- and intermolecular motion at THz frequencies. The supermolecular solvation complex (SSC) approach is well-suited to extract those signals that result from water molecules, including their coupling to the solute, that are persistently hydrogen bonded to the solute at specific molecular sites allowing one to compute mode-specific THz absorption coefficients with proper intensities including the atomic displacement vectors of these modes. The cross-correlation analysis (CCA) technique does not require such long-lived hydrogen bonds but instead probes signals that arise from distinct classes of solvent molecules, such as hydrophobic or interstitial water, in the vicinity of specific sites or fragments of the solute species, thus including also fleetingly changing solvation patterns. In the specific case of spin probe solutes such as HMI, the open-shell character of these free radical molecules in solution implies an odd total number of electrons and, in particular, non-zero spin density that is accumulated at the EPR-active site. Transcending the earlier THz studies of closed-shell solutes in water, we introduce here a coarse-graining approach to the electronic degrees of freedom, represented in terms of singly-occupied Wannier spin orbitals, to cope with the spin density that is localized at the nitroxy group due to the presence of an unpaired electron. This generalization allows us to decompose and thus assign the THz spectrum also of solvated free radical species, such as HMI, including the hydration shell using the SSC and CCA techniques in concert.Having introduced this open-shell machinery, we find that the THz response of the nitrogen group within the HMI ring, Nring, which accepts one rather long-lived hydrogen bond on average, contributes localized THz intensity from about 100–200 cm−1 which is about two orders of magnitude weaker than the strongest intramolecular THz signal of HMI itself at ≈400 cm−1 as inferred by comparing the respective mode-specific THz absorption coefficients provided by SSC decomposition. Such behavior is not specific to HMI but has been found previously in similar cases where water molecules are quite rigidly attached to very hydrophilic groups.72 In these cases, it is the intramolecular covalent OH bond of such water molecules that donate the intermolecular hydrogen bond to the solute that is found to be strongly red-shifted, which provides their signature in the mid-IR range. Next, we find that the nitroxy group, which hosts the localized spin density and thus carries the so-called unpaired electron, features a first coordination shell around its oxygen site ON with predominantly two, but sometimes also three accepted hydrogen bonds. In addition, there are interstitial water molecules present in that first shell which vividly exchange with hydrogen bonded waters, thus leading overall to short-lived hydrogen bonds around ON. Perhaps surprisingly, the solvation shell of the entire nitroxy group does not contribute intensity modulations to the THz response of HMI in water, except for the trivial contribution that comes from the smoothly decaying low-frequency wing of the usual librational band which is due to single-particle motion of the individual water molecules in the first coordination shell of ON. Unsurprisingly, however, the hydrophobic water around the six bulky methyl groups of HMI also do not contribute to the solute-induced THz response on the relevant intensity scale that is set by the total THz absorption coefficient. Importantly, we note that we did not find any specific features in the THz response that could be related to the unpaired electron that is localized at the nitroxy group of HMI.
Overall, the intensity modulations of the THz spectrum of the HMI spin label in water at ambient conditions is dominated by the low-frequency intramolecular modes of the spin probe molecule itself, which are localized in the far-IR regime. Most notable here is a prominent peak at roughly 400 cm−1 as a result of correlated intramolecular motion within HMI itself involving the nitroxy oxygen, ON, and the methyl groups. The bottom line outcome of our investigation is that HMI is essentially insensitive to its local solvation environment as probed by vibrational far-IR (THz) spectroscopy, whereas it is an excellent local probe molecule for EPR spectroscopy that features sensitivity to the specific solvation pattern of the nitroxy oxygen site as we have demonstrated recently. We conclude therefore that HMI does not qualify as a dual-readout EPR + THz probe to investigate local solvation effects in aqueous solutions. This result serves as a guideline for future research to design novel dual-probe molecules. They should carry different functional groups which are individually sensitive to local solvation effects as probed orthogonally by EPR and THz spectroscopy given their complementary probe mechanism.
Data availability
The data that support the results of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are very grateful to Aman Jindal for helpful discussions. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV as well as by the individual DFG grant MA 1547/11-2 to DM. This work was further supported by an individual postdoctoral grant to PS funded by the DFG under Project No. 519139248 (Walter Benjamin Programme). Computing resources have been provided by LRZ (SuperMUC-NG) as well as by HPC@ZEMOS, HPC-RESOLV, and BOVILAB@RUB.Notes and references
- C. L. Heald and J. Kroll, Sci. Adv., 2020, 6, eaay8967 CrossRef CAS PubMed.
- J. G. Anderson, Annu. Rev. Phys. Chem., 1987, 38, 489–520 CrossRef CAS.
- A. Studer and D. P. Curran, Angew. Chem., Int. Ed., 2016, 55, 58–102 CrossRef CAS PubMed.
- A. Bhunia and A. Studer, Chem, 2021, 7, 2060–2100 CAS.
- W. Dröge, Physiol. Rev., 2002, 82, 47–95 CrossRef PubMed.
- W. A. Pryor, K. N. Houk, C. S. Foote, J. M. Fukuto, L. J. Ignarro, G. L. Squadrito and K. J. Davies, Am. J. Physiol.: Regul., Integr. Comp. Physiol., 2006, 291, R491–R511 CrossRef CAS PubMed.
- S. Kumar, Y. Kumar, S. K. Keshri and P. Mukhopadhyay, Magnetochemistry, 2016, 2, 42 CrossRef.
- L. Ji, J. Shi, J. Wei, T. Yu and W. Huang, Adv. Mater., 2020, 32, 1908015 CrossRef CAS PubMed.
- A. K. Hoffmann and A. T. Henderson, J. Am. Chem. Soc., 1961, 83, 4671–4672 CrossRef CAS.
- M. Neiman, É. Rozantzev and Y. G. Mamedova, Nature, 1962, 196, 472–474 CrossRef CAS.
- A. R. Forrester and R. H. Thomson, Nature, 1964, 203, 74–75 CrossRef CAS.
- L. B. Volodarsky, V. A. Reznikov and V. I. Ovcharenko, Synthetic chemistry of stable nitroxides, CRC Press, 2017 Search PubMed.
- D. Bertin, D. Gigmes, S. R. A. Marque and P. Tordo, Chem. Soc. Rev., 2011, 40, 2189–2198 RSC.
- H. R. Lamontagne and B. H. Lessard, ACS Appl. Polym. Mater., 2020, 2, 5327–5344 CrossRef CAS.
- J. Nicolas, Y. Guillaneuf, C. Lefay, D. Bertin, D. Gigmes and B. Charleux, Prog. Polym. Sci., 2013, 38, 63–235 CrossRef CAS.
- D. Leifert and A. Studer, Chem. Rev., 2023, 123, 10302–10380 CrossRef CAS PubMed.
- J. Song, J. Franck, P. Pincus, M. W. Kim and S. Han, J. Am. Chem. Soc., 2014, 136, 2642–2649 CrossRef CAS PubMed.
- B. D. Armstrong and S. Han, J. Am. Chem. Soc., 2009, 131, 4641–4647 CrossRef CAS PubMed.
- P. J. Stals, C.-Y. Cheng, L. van Beek, A. C. Wauters, A. R. Palmans, S. Han and E. Meijer, Chem. Sci., 2016, 7, 2011–2015 RSC.
- O. Fisette, C. Päslack, R. Barnes, J. M. Isas, R. Langen, M. Heyden, S. Han and L. V. Schäfer, J. Am. Chem. Soc., 2016, 138, 11526–11535 CrossRef CAS PubMed.
- O. H. Griffith and H. M. McConnell, Proc. Natl. Acad. Sci. U. S. A., 1966, 55, 8–11 CrossRef CAS PubMed.
- S. A. Sundberg and W. L. Hubbell, Biophys. J., 1986, 49, 553–562 CrossRef CAS PubMed.
- C. Altenbach, W. Froncisz, J. S. Hyde and W. L. Hubbell, Biophys. J., 1989, 56, 1183–1191 CrossRef CAS PubMed.
- E. Bordignon, EPR spectroscopy of nitroxide spin probes, John Wiley & Sons, Ltd, 2017, vol. 6 Search PubMed.
- F. Hecker, J. Stubbe and M. Bennati, J. Am. Chem. Soc., 2021, 143, 7237–7241 CrossRef CAS PubMed.
- F. Hecker, L. Fries, M. Hiller, M. Chiesa and M. Bennati, Angew. Chem., Int. Ed., 2023, 62, e202213700 CrossRef CAS PubMed.
- M. Pavone, A. Sillanpä, P. Cimino, O. Crescenzi and V. Barone, J. Phys. Chem. B, 2006, 110, 16189–16192 CrossRef CAS PubMed.
- D. Sezer, Phys. Chem. Chem. Phys., 2014, 16, 1022–1032 RSC.
- J. Hunold, J. Eisermann, M. Brehm and D. Hinderberger, J. Phys. Chem. B, 2020, 124, 8601–8609 CrossRef CAS PubMed.
- B. Sharma, V. A. Tran, T. Pongratz, L. Galazzo, I. Zhurko, E. Bordignon, S. M. Kast, F. Neese and D. Marx, J. Chem. Theory Comput., 2021, 17, 6366–6386 CrossRef CAS PubMed.
- E. Falbo, M. Fusè, F. Lazzari, G. Mancini and V. Barone, J. Chem. Theory Comput., 2022, 18, 6203–6216 CrossRef CAS PubMed.
- V. A. Tran, M. Teucher, L. Galazzo, B. Sharma, T. Pongratz, S. M. Kast, D. Marx, E. Bordignon, A. Schnegg and F. Neese, J. Phys. Chem. A, 2023, 127, 6447–6466 CrossRef CAS PubMed.
- E. M. Brás, T. L. Fischer and M. A. Suhm, Angew. Chem., Int. Ed., 2021, 60, 19013–19017 CrossRef PubMed.
- T. L. Fischer, M. Bödecker, A. Zehnacker-Rentien, R. A. Mata and M. A. Suhm, Phys. Chem. Chem. Phys., 2022, 24, 11442–11454 RSC.
- E. M. Brás, C. Zimmermann, R. Fausto and M. A. Suhm, Phys. Chem. Chem. Phys., 2024, 26, 5822–5829 RSC.
- J. Sun, G. Niehues, H. Forbert, D. Decka, G. Schwaab, D. Marx and M. Havenith, J. Am. Chem. Soc., 2014, 136, 5031–5038 CrossRef CAS PubMed.
- M. Śmiechowski, J. Sun, H. Forbert and D. Marx, Phys. Chem. Chem. Phys., 2015, 17, 8323–8329 RSC.
- P. Schienbein, G. Schwaab, H. Forbert, M. Havenith and D. Marx, J. Phys. Chem. Lett., 2017, 8, 2373–2380 CrossRef CAS PubMed.
- A. Esser, H. Forbert, F. Sebastiani, G. Schwaab, M. Havenith and D. Marx, J. Phys. Chem. B, 2018, 122, 1453–1459 CrossRef CAS PubMed.
- G. Schwaab, F. Sebastiani and M. Havenith, Angew. Chem., Int. Ed., 2019, 58, 3000–3013 CrossRef CAS PubMed.
- P. K. Gupta, A. Esser, H. Forbert and D. Marx, Phys. Chem. Chem. Phys., 2019, 21, 4975–4987 RSC.
- M. Heyden, J. Sun, S. Funkner, G. Mathias, H. Forbert, M. Havenith and D. Marx, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12068–12073 CrossRef CAS PubMed.
- A. Petrone, G. Donati, P. Caruso and N. Rega, J. Am. Chem. Soc., 2014, 136, 14866–14874 CrossRef CAS PubMed.
- D. Marx and J. Hutter, Ab initio molecular dynamics: basic theory and advanced methods, Cambridge University Press, 2009 Search PubMed.
- A. Sotgiu, K. Mäder, G. Placidi, S. Colacicchi, C. L. Ursini and M. Alecci, Phys. Med. Biol., 1998, 43, 1921 CrossRef CAS PubMed.
- T. Yoshitomi, R. Suzuki, T. Mamiya, H. Matsui, A. Hirayama and Y. Nagasaki, Bioconjugate Chem., 2009, 20, 1792–1798 CrossRef CAS PubMed.
- M. A. Voinov and A. I. Smirnov, Spin labels and spin probes for measurements of local pH and electrostatics by EPR, The Royal Society of Chemistry, 2010 Search PubMed.
- E. G. Kovaleva, L. S. Molochnikov, U. Venkatesan, A. Marek, D. P. Stepanova, K. V. Kozhikhova, M. A. Mironov and A. I. Smirnov, J. Phys. Chem. C, 2016, 120, 2703–2711 CrossRef CAS.
- K. Margita, M. A. Voinov and A. I. Smirnov, Cell Biochem. Biophys., 2017, 75, 185–193 CrossRef CAS PubMed.
- E. G. Kovaleva, L. S. Molochnikov, D. O. Antonov, D. P. Tambasova Stepanova, M. Hartmann, A. N. Tsmokalyuk, A. Marek and A. I. Smirnov, J. Phys. Chem. C, 2018, 122, 20527–20538 CrossRef CAS.
- V. Perelygin, M. A. Voinov, A. Marek, E. Ou, J. Krim, D. Brenner, T. I. Smirnova and A. I. Smirnov, J. Phys. Chem. C, 2019, 123, 29972–29985 CrossRef CAS.
- A. A. Auer, V. A. Tran, B. Sharma, G. L. Stoychev, D. Marx and F. Neese, Mol. Phys., 2020, 118, e1797916 CrossRef.
- J. VandeVondele and M. Sprik, Phys. Chem. Chem. Phys., 2005, 7, 1363–1367 RSC.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, et al. , J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641 CrossRef CAS.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348–2364 CrossRef CAS PubMed.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- R. Ramírez, T. López-Ciudad, P. P. Kumar and D. Marx, J. Chem. Phys., 2004, 121, 3973–3983 CrossRef PubMed.
- C. Apostolidou, Adv. Theory Simul., 2020, 3, 2000174 CrossRef CAS.
- A. Strachan, J. Chem. Phys., 2004, 120, 1–4 CrossRef CAS PubMed.
- N. Rega, Theor. Chem. Acc., 2006, 116, 347–354 Search PubMed.
- G. Mathias and M. D. Baer, J. Chem. Theory Comput., 2011, 7, 2028–2039 CrossRef CAS PubMed.
- G. Donati, A. Petrone and N. Rega, Phys. Chem. Chem. Phys., 2020, 22, 22645–22661 RSC.
- T. T. Duignan, S. M. Kathmann, G. K. Schenter and C. J. Mundy, Acc. Chem. Res., 2021, 54, 2833–2843 CrossRef CAS PubMed.
- S. Imoto, H. Forbert and D. Marx, Phys. Chem. Chem. Phys., 2018, 20, 6146–6158 RSC.
| This journal is © the Owner Societies 2024 |