Reaction kinetics of lithium–sulfur batteries with a polar Li-ion electrolyte: modeling of liquid phase and solid phase processes

Abstract

The present investigation fits the reaction kinetics of a lithium–sulfur (Li–S) battery with polar electrolyte employing a novel two-phase continuum multipore model. The continuum two-phase model considers processes in both the liquid electrolyte phase and the solid precipitates phase, where the diffusion coefficients of the Li⁺ ions in a solvent-softened solid state are determined from molecular dynamics simulations. Solubility experiments yield the saturation concentration of sulfur and lithium sulfides in the polar electrolyte employed in this study. The model describes the transport of dissolved molecular and ion species in pores of different size in solvated or desolvated form, depending on pore size. The Li–S reaction model in this study is validated for electrolyte 1 M LiPF₆ in EC/DMC. It includes seven redox reactions and two cyclic non-electrochemical reactions in the cathode, and the lithium redox reaction at the anode. Electrochemical reactions are assumed to take place in the electrolyte solution or the solid state and cyclic reactions are assumed to take place in the liquid electrolyte phase only. The determination of the reaction kinetics parameters takes place via fitting the model predictions with experimental data of a cyclic voltammetry cycle with in operando UV-vis spectroscopy.

---

Introduction

Enormous research effort has been invested worldwide on Li–S batteries but there are still challenges to overcome to realize the high theoretical capacity and energy density at cell level and ensure good cyclability and long lifetime.¹ Cathode host materials are targeted to accommodate maximum amount of sulfur and its expansion while soluble polysulfides are trapped from moving to the anode by physical restriction,^2–4 high tortuosity in 2D materials^5–7 or functional groups that may also act as electrocatalysts.^8,9 Further research has focused on the development of separators and interlayers to eliminate the shuttling of soluble polysulfides and protect the anode^10–12 and on the optimization of the electrolyte.¹³ In order to design the microstructure and chemical structure of these materials for Li–S batteries challenged by complex and competing processes, multipore continuum models are needed beyond the classical zero-dimensional (0-d) models encountered in the literature which are used to fit electrochemical reaction kinetics, usually two-step reactions for Li–S batteries.^14,15

One-dimensional (1-d) models have been proposed for Li–S batteries^16–18 and many incorporate multistage reactions. However, the fitted reaction kinetics parameters of such models are microstructure dependent and functional groups dependent with regards to the specific cathode and separator which were used in the associated experimental study. Such reaction kinetics parameters cannot be used universally for the design of materials and schedule optimization of Li–S batteries with different materials microstructure and functionalities.

Following the continuum multipore model developed and validated for electrochemical double layer capacitors (EDLCs) by our group,^19,20 this model has been extended to Li–S batteries²¹ including a multistep reaction mechanism in the liquid electrolyte phase only. A recent study employed this model to determine the electrochemical reaction kinetics parameters of a six-step electrochemical reaction chain for a Li–S battery with a porous carbon cathode host and electrolyte 1 M LiTFSI in DOL : DME 1 : 1 v/v.²² This reaction chain followed the order in discharge²³: from S₈, to Li₂S₈, to Li₂S₆, to Li₂S₄, to Li₂S₂ and to Li₂S, also from S₄ to Li₂S₄ in ultramicropores, with the reverse reactions and reaction chain during charge. No physical and chemical processes were considered in solid state, although there is a considerable amount of precipitated sulfur or sulfides in Li–S battery cells and a considerable amount of undissolved sulfur was predicted till the end of slow discharge at 0.05C.^21,22

From a broader viewpoint, a typical electrolyte for Li-ion batteries such as 1 M LiPF₆ in EC : DMC 1 : 1 v/v is of much lower cost than the electrolyte 1 M LiTFSI in DOL : DME 1 : 1 v/v, given the lower commercial cost of salt (500 US$ per kg for LiPF₆versus 650 US$ per kg by BASF²⁴) and the fact that LiPF₆ has 1.9 times lower molecular weight than LiTFSI, which combined with the slightly lower cost of the EC and DMC solvents compared to DOL and DME result in 2.7 times lower cost for the 1 M LiPF₆ in EC : DMC 1 : 1 v/v electrolyte. The high dielectric constant of EC may offer higher sulfur solubility in EC:DMC which would favor lean electrolyte battery cells,²⁵ a major requirement in the targeted metrics of Li–S batteries.²⁶ In fact, this may be seen from the difference of the Hansen solubility parameter δ between sulfur and solvent:^27–29 where δ_sulfur = 33.1 MPa^1/2 (ref. 30) is closer to δ_{EC : DMC 1 : 1 v/v} = 22.9 MPa^1/2 (with δ_EC = 29.6 MPa^1/2 and δ_DMC = 18.7 MPa^1/2) rather than δ_{DOL : DME 1 : 1 v/v} = 19.0 MPa^1/2.³¹ Another advantage of the carbonate-based electrolytes for Li–S batteries is their low flammability due to the low volatility of these solvents compared to DOL and DME.

A major disadvantage of carbonate solvents is their irreversible reaction with polysulfide intermediates to form a sulfide carbonate complex^32,33 which consumes active material at the expense of battery capacity and cycling life. Considering a Li–S battery with a 50 wt% sulfur in Ketjenblack EC 600 JD based cathode, cells with electrolyte 1 M LiTFSI in TEGDME were compared to cells with electrolyte 1 M LiTFSI in EC : EMC 1 : 1 v/v.³³ The comparison revealed that whereas the cell with the ether electrolyte exhibited a discharge capacity from 1280 to 800 mA h g_S⁻¹ after 10 cycles at 0.1C, the cell with the carbonate electrolyte started with a low discharge capacity of 380 mA h g_S⁻¹ which fell to negligible capacity in the second cycle at 0.1C and remained so after 10 cycles.³³

However, this might be controlled and reduced: in a study of Li–S battery with microporous carbon cathode host using electrolyte 1 M LiPF₆ in EC/DMC,⁴ sulfides were formed inside the ultramicropores limiting their side reactions with the carbonate solvents as well as their shuttling effects. This improved the discharge capacity from an initial 1900 mA h g_S⁻¹ to 1000 mA h g_S⁻¹ after 20 cycles at 0.05C for the electrolyte 1 M LiPF₆ in EC/DMC compared to an initial capacity of 1250 mA h g_S⁻¹ falling to 470 mA h g_S⁻¹ after 20 cycles at 0.05C for the electrolyte 1 M LiTFSI in DOL/DME.⁴ Furthermore, researchers considering carbonate electrolytes for Li–S batteries have been investigating solid-state reactions, such as conversion from solid S₈ to precipitate Li₂S₄ and further conversion to precipitates Li₂S₂ and Li₂S targeting the solid–solid reactions on the surface of each precipitate,³⁴ or even direct conversion from S₈ to Li₂S.³⁴ The latter was revealed in Li–S cell with 65 wt% S in Ketjenblack EC 600 JD based cathode with a 30 nm layer of alucone coating and electrolyte 1 M LiPF₆ in EC : DEC 1 : 1 v/v which exhibited a single voltage plateau around 1.8 V in discharge with a discharge capacity to 1 V of 650 mA h g_S⁻¹ in first discharge falling to 400 mA h g_S⁻¹ after 100 cycles.³⁵ Trapping sulfur and sulfides in the microporous cathode host and using a carbonate electrolyte yielded a single plateau discharge at low voltage, while in operando XANES revealed direct conversion of S₈ to Li₂S in assumed solid-state reaction.³⁵ An alternative Li–S cell with cathode based on BP2000 (black pearl carbon 2000) with a high proportion of micropores of 0.7 nm (size of S₈ allotrope) and 1M LiPF₆ in EC/DEC electrolyte exhibited a discharge curve falling from 2 to 1 V with an initial capacity of 1200 mA h g_S⁻¹ falling to 800 mA h g_S⁻¹ after 100 cycles.³⁵ These studies demonstrate the need for optimized design of the cathode microstructure in Li–S battery cells with carbonate electrolytes to maximize the rate of Li⁺ ion diffusion and redox reactions in semisolid or solid state and avoid the parasitic reactions of sulfides with the carbonate solvents in the liquid phase. Simulations based on a physicochemical model would be very valuable for such optimization, and hence, a physicochemical multipore continuum model is needed taking into account processes in both the liquid electrolyte phase and the solid (or semisolid) precipitate state.

For the analysis and modeling of these reactions, data of sulfur and sulfides solubility in carbonate solvents is needed. Unfortunately, such data is missing from the literature. Hence, the first task in this study is to detemine the saturation concentration of sulfur and sulfides in a typical carbonate solvent system employed for Li-ion electrolytes. Furthermore, for the model to consider both reactions with Li⁺ ions at solid precipitate surface or in the bulk of the solid precipitate, molecular dynamics (MD) simulations will be conducted to determine the diffusion coefficient of Li⁺ ions in solid or semisolid, since semisolid sulfur or sulfides have been encountered in solubility studies from the diffusion of DME or DOL solvents in the solid phase.^36,37

As we have already determined the electrochemical reaction kinetics for Li–S batteries with electrolyte 1 M LiTFSI in DOL/DME using a multipore continuum model,²² this study focuses on the determination of the reaction kinetics in Li–S batteries using the higher dielectric constant electrolyte 1 M LiPF₆ in EC : DMC 1 : 1 v/v. For such highly polar electrolyte solvent system, cyclic (non-electrochemical) polysulfide reactions between S₈²⁻ sulfides, to S₆²⁻ and S₈, and S₃˙⁻ radical anion (from S₆²⁻) take place in the liquid electrolyte phase at the first plateau during discharge, rather than the gradual change from S₈²⁻ to S₆²⁻ to S₄²⁻ in the DOL/DME solution.²³ Furthermore, there is speculation on whether the electrochemical reactions progress directly to S²⁻ bypassing S₂²⁻ or not, for either liquid or solid phase reactions. Considering the solubility data of sulfur and all above sulfides in carbonate solvent mixture to be collected as the first task in this study, and also inputting the diffusion coefficients of Li⁺ ions in solid or semisolid phase from MD simulations to be conducted in this study, reactions will be considered in both liquid and solid phase in the novel model to be developed in this study. Overall, we shall investigate the reaction chain in this study for a carbonaceous cathode host (without the presence of any electrocatalysts) via monitoring the evolution of sulfides during the cyclic voltammetry (CV) of a Li–S battery using in operando UV-vis spectroscopy. We shall then employ our multipore continuum model,^21,22 after novel modifications to include the new reactions for the electrolyte 1 M LiPF₆ in EC/DMC and physicochemical processes in solid and semisolid phase, in simulations of the CV test to fit the kinetics of these electrochemical and cyclic reactions on the basis of experimental CV data and in operando UV-vis data.

MD simulations

ReaxFF molecular dynamics (MD) simulations using software of the Ansterdam modeling suite (AMS) were carried out employing the ReaxFF force field for the system of S and Li atoms.³⁸ A model of α-S₈ allotrope of 128 S atoms was created in a slit pore of slit size (‘a’ dimension) of 0.91 nm. This pore was considered sufficiently large to accommodate the formation of S₈ during sulfur infiltration of the cathode host in a microporous carbon host. Li diffusion was considered in this sulfur structure by inserting 43 Li atoms (equivalent to the stoichiometry of Li₂S₆). The procedure of MD simulations in the AMS software comprised the following steps: The model was inported in the AMS software and the structure's geometry was optimized involving lattice relaxation under the LiS.ff parameters of the Reaxff force field. Simulated annealing was conducted to generate an amorphous system by heating from 300 K to 1600 K over 5000 fs, followed by simulated cooling of 1250 fs from 1600 K to 300 K. The amorphous system was optimized as earlier by lattice relaxation. The diffusion coefficient of the Li atoms was computed by the AMS software via the velocity autocorrelation function, over a period of 27 500 fs with a sampling frequency of 5. Diffusion coefficients were computed for several temperatures from which an Arrhenius plot was constructed to extrapolate diffusion coefficients for different temperatures, including room temperature at 21 °C. The procedure was repeated for slit pore sizes of 0.85 nm (Fig. 1) and 0.75 nm. For smaller slit pores, the γ-S₈ allotrope crystal was used in the initial model, and the procedure of MD simulations were repeated for slit pores of 0.69 and 0.63 nm. Furthermore, the procedure was repeated to also determine the diffusion coefficient of Li in the Li₂S, cubic Fm̄3m crystal structure in all slit pore sizes of 0.91, 0.85, 0.75, 0.69 and 0.63 nm. The values of the so determined diffusion coefficients of lithium at 21 °C were in the range of 10⁻³¹ (pore of 0.91 nm) to 10⁻¹¹⁰ m² s⁻¹ (pore of 0.63 nm). This renders impossible diffusion of Li⁺ ions in the bulk of solid sulfur or solid sulfides during the cycling of the Li–S battery, even at the slow rate of 0.05C.

Fig. 1 Snapshots of the 128 S – 43 Li system in the 0.85 nm slit pore during the 1600 K MD simulations.

The next step was to consider the diffusion of Li⁺ ions in “softened” solids, i.e. semisolid state. Considering solvent diffusion coefficients in solid sulfur or lithium sulfides in the range of 10⁻¹² to 10⁻⁹ m² s⁻¹,³⁷ DMC solvent molecules were inserted into the above sulfur and lithium sulfide structures at a molecular ratio of 50 : 50, and the same type of MD simulations were repeated. This yielded a Li⁺ ion diffusion coefficient of (8.6 ± 0.2) × 10⁻⁷ m² s⁻¹ of one Li⁺ ion in “soft” S₈, (3.8 ± 0.5) × 10⁻¹¹ m² s⁻¹ in the “soft” 43 Li – 128 S system (equivalent to Li₂S₆) and (3.4 ± 0.4) × 10⁻¹² m² s⁻¹ in “soft” Li₂S. These values have been averaged over all the examined slit pore sizes (0.91, 0.85, 0.75, 0.69 and 0.63 nm).

Physicochemical model

On the basis of the findings via the MD simulations, a two-phase reaction model is presented, covering: (a) reactions in the liquid electrolyte phase with electron transfer in electrochemical reactions occurring at the solid–electrolyte interface; and (b) solid-state reactions in the “soft” precipitate layer covering the pore walls. A continuum multipore model is adopted based on the volume-averaged species transport equations in the transverse direction through the cell thickness for a Li–S battery cell as in the schematic diagram in Fig. 2.

Fig. 2 Schematic diagram of the Li–S battery cell and the boundary conditions for the numerical solution, where N_s is the flux of species s and I_app is the applied current density.

Each pore of size p from the local discretized pore size distribution (PSD) contains a liquid electrolyte phase and a solid precipitates phase. Every pair of point x through the battery cell thickness and pore size p is characterized by the cathode host or separator volume fraction, ε_host,p, the liquid electrolyte volume fraction which is equal to the pore fraction, ε_p, assuming electrolyte saturated porous medium,³⁹ and the solid precipitates volume fraction, ε_{precipitate,p}, where

ε_host,p + ε_p + ε_{precipitate,p} = 1 (1)

Each phase may contain any of the species s, where these species are molecules S₈ or S₄ depending on pore size, sulfide ions S²⁻, S₂²⁻, S₄²⁻, S₆²⁻, S₈²⁻, radical anion S₃˙⁻, and electrolyte ions Li⁺ and PF₆⁻. These are defined by species concentrations C_s,l,p and C_s,s,p in the liquid and solid phase, respectively, and corresponding species volume fractions, α_s,l,p, and α_s,s,p, which are related via the equations:

α_s,l,p = C_s,l,pN_AV_s (2)

α_s,s,p = C_s,s,pN_AV_s (3)

where V_s is the volume of ion or molecule of species s and N_A is the Avogadro number.

The following volume-averaged equations describe all species transport, production or consumption in the liquid electrolyte phase, the Li⁺ ion transport,^21,22 production or consumption in the solid precipitates phase (in fact, assumed to be semisolid phase), and the solid species (other than Li⁺) production or consumption in the solid precipitates phase at each position x through the cell and pore size p from the PSD (indicated by subscript p in the different variables and terms):

The transport eqn (4) of any species s in the liquid electrolyte phase includes the drift current term where i_e is the current density in the liquid electrolyte phase, z_s is the number of transferred electrons for species s and F is the Faraday constant; the diffusion term, where D_s,l,p is the diffusivity of species s in the liquid electrolyte phase, given by a modified Stokes–Einstein relation as a function of the species size, pore p tortuosity and constrictivity relating the species s size to the pore size p^6,19–21 and the electrolyte viscosity (see ref. 40 for viscosity value of electrolyte 1 M LiPF₆ in EC : DMC 1 : 1 v/v, changing during the electrochemical cycle as in ref. 21), and t_s,l,p is the transference number of species s in the liquid electrolyte phase; the interpore fluxes I_s,p−1/p − I_s,p/p+1^19,20 assuming a hierarchical PSD. The species s size is that of the solvated species s⁴¹ or for smaller pores it is the size of the desolvated species s.⁴¹ If the pore size p is even smaller than the size of desolvated species s, no s species exists in this pore size, in either the liquid or the solid phase. F_s,decay is a decay factor applied to all flux terms in eqn (4) for each desolvated species s, expressing the probability of desolvation depending on whether there is sufficient electrochemical energy to overcome the desolvation energy required.^6,19,20r_{s,p,liq.elect} is the rate of all the electrochemical reactions related with species s in the liquid electrolyte phase, and r_{s,p,liq.cyclic} is the rate of all the cyclic chemical reactions related to species s in the liquid electrolyte phase.

Only Li⁺ ion transport may take place in the solid phase according to eqn (5). The Li⁺ ion transport eqn (5) in the solid state considers transport of Li⁺ ions through the y-direction (transverse direction) of the solid precipitate layer lining the slit pore walls (flat walls). It includes the drift current term, where i_Li+,sol is the current density of Li⁺ ions in the solid phase, and the diffusion term, where D_Li+,s,p is the diffusivity of Li⁺ ions in the solid phase (assumed as semisolid phase in this study) determined by the MD simulations.

Eqn (6) describes the production or consumption rate of any other species s apart from Li⁺ in the solid phase due to R_s,p which is the net rate of species s precipitation or dissolution, respectively (also appearing in the liquid electrolyte phase in eqn (4)), and to r_{s,p,sol,elect} which is the rate of the electrochemical reactions involving species s in the solid phase. r_{s,p,sol,elect} also appears in eqn (5) regarding all electrochemical reactions involving Li⁺ ions in the solid phase. R_s,p is a function of the concentration difference between C_s,l,p and the saturation concentration of species s, C_sat,s, in the liquid electrolyte.^21,22 Data of C_sat,s for each species s considered in this study in electrolyte solvent system EC/DMC 1 : 1 v/v is presented in Table 1 as results of the solubility experiments conducted in this study.

Table 1 Saturation concentration, C_sat,s data at 21 °C in EC/DMC 1 : 1 v/v, in the format of molar concentrations (M) in S-mol L⁻¹, and comparison with C_sat,s data in DOL/DME 1 : 1 v/v^36,37

Solute	C sat,s, in EC/DMC (S mol L^−1)	C sat,s, in DOL/DME (S mol L^−1)
S8	0.01	0.11
Li2S8	0.044	6
Li2S6	0.037	5.5
Li2S4	0.033	5
Li2S3	0.027
Li2S2	0.012	0.5
Li2S	0.005	0.060

---

The walls of each pore are assumed to be lined with a solid layer of sulfur or sulfides precipitates of volume fraction ε_{precipitate,p}. ε_p, ε_{precipitate,p} and the thickness of the precipitate layer, H_sol.layer,p, change as a function of the rate of dissolution or precipitation of species according to the equations:

Fig. 3 presents the reaction scheme adopted in the model of this study according to the findings and proposed schemes by Lu et al.²³ The reaction scheme comprises the lithium redox reaction at the anode, 7 redox reactions in the cathode and 2 cyclic reactions without any electron transfer. It is assumed that the cyclic reactions take place in the liquid electrolyte solution only, excluding any chance for reaction in the solid state of any precipitated species s. The electrochemical reactions are assumed to take place in the liquid electrolyte phase and in the solid phase, depending on the local reactant concentrations in each phase.

Fig. 3 Scheme of electrochemical reactions j and chemical reactions i (without any electron transfer) considered in the model of this study. Reactions i = 1 and 2 occur only in the liquid electrolyte phase; the electrochemical reactions may occur in the liquid or the solid phase.

r _{s,p,liq.cyclic} in eqn (4) denotes the rate of cyclic reactions i = 1,2 that take place only in the liquid electrolyte phase as follows:

where k_i,f and k_i,b are the constants of forward and backward reactions i, m_s,i is the stoichiometric coefficient of species s in reaction i, P_s,i = −m_s,i and Q_s,j = m_s,j.

r _s,p,elect denotes the rate of all the electrochemical reactions j occurring in the liquid electrolyte phase or the solid phase, r_{s,p,liq.elect} and r_{s,p,sol.elect}, respectively:

where A_p is the specific area of the porous cathode in pore size p and n_j is the number of electrons transferred in reaction j. i_j,p is the current density due to electrochemical reaction j given by the Butler–Volmer equation^16,21,22 as a function of i_o,jref (to be determined via fitting in this study), the concentration of species C_s,p in the liquid electrolyte phase, C_s,l,p, or in the solid phase, C_s,s,p (including the Li⁺ ion concentration C_Li+,s,p), and the overpotential η_j for reaction j which is given by:

η_j = ϕ_sol − ϕe − U_j,_ref (12)

where ϕ_sol and ϕ_e are the potential of the solid and liquid phase, respectively, and U_j,ref is the open-circuit potential (OCP) for reaction j at a reference concentration c_s,ref:¹⁶where R is the gas constant and T is the absolute temperature.

The system of equations is solved using the time implicit finite volume/finite difference numerical method,^42,43 with boundary conditions as presented in Fig. 2, where I_app varies during the simulation of a CV test and is inputted from the experimental data as in ref. 22.

Experimental

Solubility experiments

The first experimental stage was to determine the saturation concentration values of sulfur and sulfides Li₂S₈, Li₂S₆, Li₂S₄, Li₂S₃, Li₂S₂ and Li₂S in the EC : DMC 50 : 50 v/v solution. Sulfides Li₂S_x, x = 2, 3, 4, 6, 8 were prepared as a stoichiometric mixture of Li₂S and sulfur in the EC/DMC solvent system in test tubes. After manual shaking (repeated periodically), the test tubes were left at 21 °C in a BINDER environmental chamber and monitored for solubility after the first 24 h and periodically every few hours up to seven days for low solubility compounds. The saturation concentration was thus determined as the concentration above which precipitation started.

Fabrication

Activated carbon fabric (ACF) Kynol® ACC-507-15 (Kynol Europe GmbH, Hamburg, Germany) of 0.6 mm thickness, areal density of 12 mg cm⁻² and specific surface area SSA_BET = 1461 m² g⁻¹(ref. 44–46) was used as the cathode host. Following the technique described in ref. 44 and 45 sulfur was impregnated in the ACF by heating over its melting point to 33 wt% sulfur in the composite S-ACF cathode. The discretized PSDs of the ACF host (from experimental data²⁰) and 33 wt% S-ACF cathode as fabricated (from simulations in ref. 44 and 45, given in ref. 22) were employed as initial condition of the cathode microstructure in the current simulations.

The Li–S battery cell comprised a 5 × 5 mm S-ACF cathode, an aluminium current collector (on the cathode side) with a small central hole, Celgard 3500 separator, a 5 × 5 mm lithium foil anode and electrolyte 1 M LiPF₆ in EC : DMC (50 : 50 v/v). The assembly was housed in a three-part case with a quartz glass window on the side of the cathode, by the hole of the aluminium current collector on the cathode as shown in Fig. 4(a).

Fig. 4 Experimental set up for the Li–S battery testing: (a) three-part cell case with o-ring and top with a small hole in the middle under which a 25 × 25 mm square quartz glass plate is placed over the battery cathode; (b) schematic diagram of the in operando UV-vis system monitoring a Li–S battery cell.

Cell testing

Electrochemical testing of the Li–S cell was conducted using a Gamry Interface 1010E potentiostat and involved a CV test of one cycle of discharge/charge at a scan rate of 0.041 mV s⁻¹. In operando UV-vis spectroscopy was conducted during this CV cycle on the cathode window using a portable StellarNet system presented in Fig. 4(b), which comprised a SL1-SL3 Combo deuterium and halogen light source of 200–2300 nm range, a BLK CXR UV-VIS spectrometer of 273–900 nm range and a R600-8-UVVIS-SR reflectance probe. The reflectance spectra were recorded every 10 minutes.

Results and discussion

Solubility data

The obtained saturation concentration, C_sat,s, data in the carbonate system EC/DMC at 21 °C are presented in Table 1, together with a comparison of the corresponding data for the DOL/DME solvent system.^36,37 It is clear that the sulfur and sulfides are almost insoluble in the EC/DMC solvent system, with all solubilities even lower than the solubility of Li₂S in DOL/DME. Hence, it might be assumed that any reactions occur either at the surface of the solid precipitates (sulfur or sulfides) or in the bulk of the precipitates with Li⁺ ions that may diffuse through the solid bulk or a semisolid bulk, comprising a softened precipitate with diffused solvent.

It is well known that each solution may contain a mixture of sulfides in addition to the main sulfides. Cyclic reactions between soluble sulfides²³ would ultimately lead to the production of sulfur precipitates, which might explain the seemingly negligible solubility of all sulfides in EC/DMC. Reactions of the sulfides with the carbonate solvents also create precipitates of irreversible side products^32,33 and this is another reason to explain the low solubility values in EC/DMC displayed in Table 1. On the other hand, the EC/DMC mixture might well be a poor solvent system at least for the sulfides. It is surprising that it is also a poorer solvent for sulfur than the DOL/DME system, despite its estimated Hansen solubility parameter being closer to that of sulfur than the estimated Hansen solubility parameter of DOL/DME.

Electrochemical and in operando UV-vis test data of Li–S cell

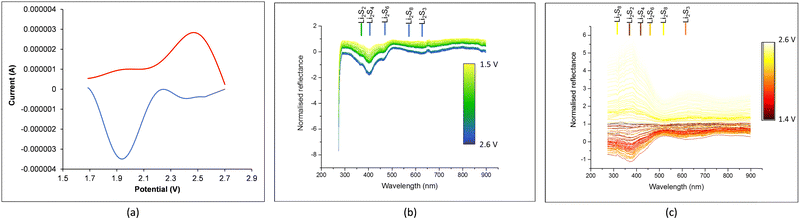
Fig. 5 presents the experimental CV curves (Fig. 5(a)) and the reflectance spectra from the in operando UV-vis monitoring during the first CV cycle of the Li–S battery cell, including the expected wavelength position for the absorbance peaks of the lithium sulfides from experimental data in the literature.⁴⁷

Fig. 5 Electrochemical test data from the first CV cycle of a Li–S battery cell: (a) CV curves in discharge (blue) and charge (red) at 0.041 mV s⁻¹. In operando UV-vis spectra during (b) discharge and (c) charge, including the expected position for the absorbance peaks of the lithium sulfides.

The color of each spectrum in Fig. 5(b) and (c) corresponds to the appropriate voltage according to the voltage color scale in each plot. The intensity of the reflectance valley (i.e. the intensity of absorbance) is assumed to be proportional to the concentration of the corresponding lithium sulfide identified by its wavelength, with the wavelength positions of each sulfide indicated in Fig. 5(b) and (c) as follows: Li₂S₈ at 560 nm; L₂S₆ at 460 nm; Li₂S₄ at 405 nm; Li₂S₃ at 630 nm; and Li₂S₂ at 365 nm. A small gap in the reflectance spectra in Fig. 5(b) (between a blue and a green spectrum) is due to an interruption in the automatic saving of the in operando UV-vis spectra (while the CV test was still going on and the CV data were being saved), with the in operando UV-vis periodic recording restarted by the operator and the time gap (translated to voltage gap) of the interruption taken into account in plotting the data in Fig. 5(b).

Fig. 6(a) and (b) display the in operando profiles of the UV-vis absorbance peaks related to Li₂S₂, Li₂S₃, Li₂S₄, Li₂S₆ and Li₂S₈ concentrations, superimposed with the corresponding CV curves during discharge and charge, respectively. The presence of Li₂S₂ in the UV-vis spectra clarifies that the step of Li₂S₂ formation is part of the reaction chain.²³

Fig. 6 In operando profiles of the absorbance peaks related to lithium sulfides detected from the UV-vis spectra, superimposed with the corresponding CV curves during (a) discharge and (b) charge from the first CV cycle of a Li–S battery cell.

In Fig. 5(b) and 6(a), at the start of discharge, there is very little amount of Li₂S₈, some Li₂S₆ and substantial Li₂S₄. There are two reasons that might explain this. From the results of the simulation of sulfur infiltration under heat into the ACF during cathode fabrication,^44,45 a considerable amount of sulfur has infiltrated pore sizes 0.46 and 0.58 nm in the form of S₄ and pore size 0.69 nm in the form of S₆. Pores greater than 0.7 nm up to 1.3 nm contain S₈. When electrolyte is added, some amount of these sulfur allotropes dissolve in the electrolyte and appear in the UV-vis spectrum in Fig. 5(b) and 6(a) at the start of discharge at 2.6 V. Cyclic reactions also occur at this stage, as will be explained shortly. At the end of discharge, the absorbance peaks of these sulfides have been reduced as expected due to the formation and precipitation of Li₂S. Another reason might be that the reactions in the semisolid state bypass the formation of high order sulfides Li₂S₈ and Li₂S₆, and instead form directly low order sulfides.^33,35

Fig. 5(c) and 6(b) present the reflectance UV-spectra during charge: they depict the continuous decrease of the Li₂S₂ and Li₂S₄ through their absorbance peak (increase of its reflectance) and formation of Li₂S₈, specially towards the end.

Fitting the reaction kinetics model

The first step of fitting the reaction kinetics parameters was to use the UV-vis profiles in Fig. 6 to fit the parameters of chemical reactions i = 1,2 (independently from the electrochemical reactions j) as:

k_1,f = 0.091 s⁻¹ k_1,b = 9 × 10⁻⁵ m^0.75 mol^−0.25 s⁻¹

k_2,f = 0.0119 m^1.5 mol^−0.5 s⁻¹ k_2,b = 4.767 × 10⁻⁴ s⁻¹

and these values were used as initial guess in the trial-and-error procedure of fitting the reaction kinetics parameters. The trial-and-error procedure was conducted manually, determining the relative error between predictions and experimental data of the CV test at the end of each trial on the basis of the least squares method, until the average relative error fell below 1%.

Fig. 7 depicts the predictions from the simulation of the first CV cycle, with the inputted best fitted parameter values presented in Table 2, against the corresponding experimental data. The good agreement between simulation and experiment justifies the use of the 10-reaction model in the volume-averaged continuum multipore model of Li–S batteries with Li-ion electrolyte in the EC/DMC solvent system.

Fig. 7 Results of first CV cycle: predictions versus experimental data.

Table 2 Values of the parameters of electrochemical reactions (j) and chemical reactions (i) after the best fitting of the CV predictions to the CV experimental data

Electrochemical reaction j		U j ^o (V)	i o,jref (A m^−2)
j = 1	Li ↔ Li^+ + e^−	0	0.394
j = 2	½ S8 + e^− ↔ ½ S8^2−	2.56	1.972
j = 3	½ S4 + e^− ↔ ½ S4^2−	2.41	1.9 × 10^−3
j = 4	S6^2− + e^− ↔ 1.5 S4^2−	2.35	24.0
j = 5	½ S8^2− + e^− ↔ S4^2−	2.14	1.9 × 10^2
j = 6	½ S4^2− + e^− ↔ S2^2−	1.93	1.97 × 10^−2
j = 7	⅓ S3*^− + e^− ↔ ⅓ S2^2− + ⅓ S^2−	1.85	1.97 × 10^−2
j = 8	½ S2^2− + e^− ↔ S^2−	1.80	1.97 × 10^−2

---

Chemical reaction i		k i,f	k i,b
i = 1	S8^2− ↔ S6^2− + ¼ S8	9.1 × 10^−3 s^−1	9 × 10^−5 m^0.75 mol^−0.25 s^−1
i = 2	½ S6^2− ↔ S3*^−	0.0119 m^1.5 mol^−0.5 s^−1	4.767 × 10^−4 s^−1

---

Fig. 8 presents the predicted concentration profiles of sulfides in the liquid electrolyte solution and in the precipitated solid phase during discharge and charge of the first CV cycle, averaged over all pore sizes. After checking the predicted concentration profiles at different positions in the cathode, no significant variation was observed through the cathode thickness, indicating that the low solubility of sulfur and lithium sulfides in EC/DMC eliminated the migration of sulfides through and away from the cathode, unlikely what is usually observed in an DOL/DME-based electrolyte and predicted in ref. 22 for the same cathode, where DOL/DME is a much better solvent system than the EC/DMC system as demonstrated in Table 1.

Fig. 8 Predicted concentration profiles of the lithium sulfides in the cathode during (a) and (b) CV discharge and (c) and (d) CV charge of the first CV cycle of Li–S battery cell; (a) and (c) concentration profiles in liquid electrolyte phase, (b) and (c) concentration profiles in the solid phase.

The next step is a comparison between the predicted concentration profiles of Fig. 8 and the experimental UV vis absorbance peak profiles in Fig. 6. One might conclude that the experimental profiles represent the sulfides in the solution in the macropores and any precipitated sulfides in the solid phase on or near the surface of the AC fibers of cathode and have missed any species in the pores deeply in the AC fibers. Hence, the experimental data do not represent the full picture of the predicted results.

Fig. 8 illustrates the importance of the solid phase in the Li–S battery cathode with Li-ion electrolyte in EC/DMC solvent system, where in fact the model assumes this phase to be a semisolid phase in terms of the Li⁺ ion diffusivity values employed. Species concentrations are of several orders of magnitude higher in the “solid” phase (Fig. 8(b) and (d)) than in the liquid electrolyte solution (Fig. 8(a) and (c)), where the species concentration is limited by the saturation concentration given in Table 1, and precipitation occurs for concentrations above the saturation concentration. Electrochemical reactions also occur in this “solid” phase, with local concentration of the transported Li⁺ ions steadily around 7700 mol m⁻³ during discharge, about 10 times lower than the Li⁺ ion concentration in the liquid phase.

During discharge electrochemical and mainly cyclic reactions create a constant presence of Li₂S₈, Li₂S₆ and Li₂S₃ in the liquid electrolyte phase in Fig. 8(a) which is up to their saturation concentration, with precipitation to the solid phase thereafter. However, the solid phase with no upper concentration limit illustrates the progress of the electrochemical reactions in the production and consumption of Li₂S₈ and Li₂S₄. The model does not include any cyclic reactions in the solid phase which explains the absence of Li₂S₆ and Li₂S₃ in the predicted concentration profiles in the solid phase during discharge. Li₂S₂ production is predicted to a small extent due to cyclic reactions in the liquid phase during discharge, from the beginning of discharge. However, there is clearly a peak in the concentration of Li₂S₂ in the liquid electrolyte phase just after the low voltage CV valley and in the solid phase during the whole width of the low voltage CV valley during discharge in Fig. 8(a) and (b) attributed to the electrochemical reactions. A small amount of Li₂S production is also predicted in the liquid electrolyte phase at low voltages during discharge in Fig. 8(a). The experimental data of Fig. 6(a) may be seen as a combination of the predicted corresponding species concentrations in the liquid and solid phases in Fig. 8(a) and (b) during CV discharge.

Similar mechanisms in terms of the predicted effects of cyclic reactions are observed in the predicted concentration profiles of Li₂S₈, Li₂S₆ and Li₂S₃ in the liquid electrolyte phase during charge in Fig. 8(c), with a low amount of precipitated Li₂S₃ in Fig. 8(d). The small amount of Li₂S in the liquid phase is predicted to be converted to Li₂S₂, with the predicted Li₂S₂ concentration profile in the liquid phase during charge reflecting the Li₂S₂ profile predicted in discharge (Fig. 8(a)), although maintaining higher predicted concentration levels during charge. Net Li₂S₄ production is predicted in the liquid electrolyte phase during charge with a concentration peak at the high voltage plateau. The solid phase in Fig. 8(d) displays predicted Li₂S₂ production around only the low voltage peak during CV charge and predicted concentration plateaus for Li₂S₃, Li₂S₄, Li₂S₆ and Li₂S₈ attributed to continuous precipitation from the liquid phase (electrochemical and cyclic reactions) and selected electrochemical reactions in the solid phase. The predicted Li₂S₈ concentration profile in the solid phase curves down towards the end of charge due to its consumption in the electrochemical reaction for the production of S₈.

Conclusions

This study fitted the parameters of a multiple reaction model of Li–S battery with a polar Li-ion electrolyte, which is of interest to Li–S batteries due to its lower cost and flammability compared with the typical electrolyte of 1 M LiTFSI in DOL : DME 1 : 1 v/v. The first stage of investigations concluded that sulfur and sulfides exhibited much lower solubility in this Li-ion electrolyte in the polar solvent system EC : DMC 1 : 1 v/v, which directed the research efforts in the development of a novel continuum multipore model for metal–sulfur batteries with physical and chemical processes taking place in both the liquid electrolyte phase and the solid phase of precipitates. MD simulations yielded reasonable values for the diffusion coefficient of Li⁺ ions in semisolid precipitate state of sulfur and lithium sulfides, where the solid phase has softened by the presence of solvent molecules which are assumed to have diffused in the solid state according to the values of solvent diffusion coefficients in the solid sulfur and sulfide state determined in previous experimental study.³⁷ Hence, these values of the diffusion coefficient of Li⁺ ions were inputted in the simulations, assuming that the “solid” phase is in fact in semisolid state.

Simulations of the first CV cycle of a Li–S battery cell with ACF cathode host revealed very little transport of sulfur and sulfides away from the cathode, which was attributed to the low solubility of sulfur and sulfides in the polar electrolyte, which has proven beneficial in almost eliminating the “shuttling” effect.

According to past studies of Li–S batteries with polar electrolyte and evidence of the presence of different sulfides from in operando UV-vis characterization during the CV test in this study, a reaction model of 8 electrochemical reactions in both the liquid electrolyte phase and the solid phase, and 2 cyclic reactions in the liquid electrolyte phase only was constructed. The two cyclic reactions observed in electrolytes with carbonate solvents in Li–S batteries are generally considered parasitic consuming active material. The liquid–solid phase continuum model of this study predicted the positive role of the high precipitation rate in this electrolyte which limited the degree of such reactions.

The reaction kinetics parameters determined from the fitting of the CV simulation predictions to experimental data are most valuable as they are valid for Li-ion electrolyte in carbonate solvents, such as EC : DMC 1 : 1 v/v, and any cathode host without any functional groups, as the liquid–solid phase, continuum model of this study takes into account the PSD of the cathode host and the cathode. The benefit of this model is that the electrochemical and chemical reaction constants and parameters fitted in this study can be used universally for the design of the microstructure and geometry of cathode and separator materials of Li–S batteries with a polar electrolyte, or for the optimization of the operating schedule of this type of Li–S batteries. This may encourage the further development of Li–S batteries with low cost polar electrolytes beyond the currently typical electrolyte 1 M LiTFSI in DOL/DME.

Author contributions

Simon Bacon: methodology, formal analysis, investigation, data curation, visualization. Shumaila Babar: methodology, software. Matthew Dent: methodology, formal analysis, investigation. Joseph Paul Baboo: methodology, investigation, supervision. Allan Foster: methodology, software, formal analysis, investigation, writing – review & editing, visualization. Teng Zhang: methodology, supervision. John F. Watts: methodology, supervision. Constantina Lekakou: conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing – original draft, supervision, funding acquisition.

Data availability

Data is available after reasonable request to the corresponding author.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge funding by the Faraday Institute under the LiSTAR project (EP/S003053/1, Grant FIRG014) and by EPSRC under the HiPoBat project (EP/R022852/1).

References

1. K. Zhu, C. Wang, Z. Chi, F. Ke, Y. Yang, A. Wang, W. Wang and L. Miao, Front. Energy Res., 2019, 7, 123.
2. X. Ji, K. T. Lee and L. F. Nazar, Nat. Mater., 2009, 8, 500.
3. G. Xu, B. Ding, P. Nie, L. Shen, H. Dou and X. Zhang, ACS Appl. Mater. Interfaces, 2014, 6, 194.
4. M. Helen, T. Diemant, S. Schindler, R. J. Behm, M. Danzer, U. Kaiser, M. Fichtner and M. A. Reddy, ACS Omega, 2018, 3, 11290.
5. Y. Cao, Y. Lin, J. Wu, X. Huang, Z. Pei, J. Zhou and G. Wang, ChemSusChem, 2020, 13, 1392.
6. J. P. Baboo, S. Babar, D. Kale, C. Lekakou and G. M. Laudone, Nanomaterials, 2021, 11, 2899.
7. E. C. Vermisoglou, T. Giannakopoulou, G. Romanos, N. Boukos, V. Psycharis, C. Lei, C. Lekakou, D. Petridis and C. Trapalis, Appl. Surf. Sci., 2017, 392, 244.
8. E. I. Andritsos, C. Lekakou and Q. Cai, J. Phys. Chem. C, 2021, 125, 18108.
9. E. Hojaji, E. I. Andritsos, Z. Li, M. Chhowalla, C. Lekakou and Q. Cai, Int. J. Mol. Sci., 2022, 23, 15608.
10. X. Wu, L. Fan, Y. Qiu, M. Wang, J. Cheng, B. Guan, Z. Guo, N. Zhang and K. Sun, ChemSusChem, 2018, 11, 3345.
11. Y. Chen, G. Zhou, W. Zong, Y. Ouyang, K. Chen, Y. Lv, Y. E. Miao and T. Liu, Comp. Commun., 2021, 25, 100679.
12. A. K. Murugesh, A. Uthayanan and C. Lekakou, Appl. Phys. A, 2010, 100, 135.
13. A. Gupta, A. Bhargav and A. Manthiram, Adv. Energy Mater., 2019, 9, 1803096.
14. Y. V. Mikhaylik and J. R. Akridge, J. Electrochem. Soc., 2004, 151, A1969.
15. M. Marinescu, T. Zhang and G. J. Offer, Phys. Chem. Chem. Phys., 2016, 18, 584.
16. K. Kumaresan, Y. Mikhaylik and R. E. White, J. Electrochem. Soc., 2008, 155, A576.
17. A. F. Hofmann, D. N. Fronczek and W. G. Bessler, J. Power Sources, 2014, 259, 300.
18. T. Danner, G. Zhu, A. F. Hofmann and A. Latz, Electrochim. Acta, 2015, 184, 124.
19. F. Markoulidis, J. Bates, C. Lekakou, R. Slade and G. M. Laudone, Carbon, 2020, 164, 422.
20. J. Bates, F. Markoulidis, C. Lekakou and G. M. Laudone, C, 2021, 7, 15.
21. S. Grabe, M. Dent, T. Zhang, S. Tennison and C. Lekakou, J. Power Sources, 2023, 580, 233470.
22. S. Grabe, T. Zhang, S. Tennison and C. Lekakou, J. Electrochem. Soc., 2023, 170, 020527.
23. Y.-C. Lu, Q. He and H. A. Gasteiger, J. Phys. Chem. C, 2014, 118, 5733.
24. R. Younesi, G. M. Veith, P. Johansson, de K. Edstrombe and T. Vegge, Energy Environ. Sci., 2015, 8, 1905.
25. C. Luo, E. Hu, K. J. Gaskell, X. Fan, T. Gao, C. Cui, S. Ghose, X.-Q. Yang and C. Wang, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14712.
26. A. Bhargav, J. He, A. Gupta and A. Manthiram, Joule, 2020, 4, 285.
27. E. M. Kampouris, C. D. Papaspyrides and C. N. Lekakou, Conserv. Recycl., 1987, 10, 315.
28. E. M. Kampouris, C. D. Papaspyrides and C. N. Lekakou, Polym. Eng. Sci., 1988, 28, 534.
29. E. C. Vermisoglou, M. Giannouri, N. Todorova, T. Giannakopoulou, C. Lekakou and C. Trapalis, Waste Manage. Res., 2016, 34, 337.
30. R. Guo, A. G. Talma, R. N. Datta, W. K. Dierkes and J. W. M. Noordermeer, Macromol. Mater. Eng., 2009, 294, 330.
31. C. M. Hansen, Hansen solubility parameters, a users’ handbook, CRC Press, London, 1999.
32. R. Dominko, A. Vizintin, G. Aquilanti, L. Stievano, M. J. Helen, A. R. Munnangi, M. Fichtner and I. Arcon, J. Electrochem. Soc., 2018, 165, A5014.
33. T. Yim, M.-S. Park, J.-S. Yu, K. J. Kim, K. Y. Im, J.-H. Kim, G. Jeong, Y. N. Jo, S.-G. Woo, K. S. Kang, I. Lee and Y.-J. Kim, Electrochim. Acta, 2013, 107, 454.
34. A. Rafie, J. W. Kim, K. K. Sarode and V. Kalra, Energy Storage Mater., 2022, 50, 197.
35. X. Li, M. Banis, A. Lushington, X. Yang, Q. Sun, Y. Zhao, C. Liu, Q. Li, B. Wang, W. Xiao, C. Wang, M. Li, J. Liang, R. Li, Y. Hu, L. Goncharova, H. Zhang, T.-K. Sham and X. Sun, Nat. Commun., 2018, 9, 4509.
36. M. Dent, E. Jakubczyk, T. Zhang and C. Lekakou, J. Phys. Energy, 2022, 4, 024001.
37. H. A. Adeoye, M. Dent, J. F. Watts, S. Tennison and C. Lekakou, J. Chem. Phys., 2023, 158, 6.
38. M. M. Islam, A. Ostadhossein, O. Borodin, T. Yeates, W. W. Tipton, R. G. Hennig, N. Kumarf and A. C. T. van Duin, Phys. Chem. Chem. Phys., 2015, 17, 3383.
39. M. Dent, S. Grabe and C. Lekakou, Batteries Supercaps, 2024, 7, e202300327.
40. A. Celeste, L. Silvestri, M. Agostini, M. Sadd, S. Palumbo, J. K. Panda, A. Matic, V. Pellegrini and S. Brutti, Batteries Supercaps, 2020, 3, 1059.
41. S. Babar and C. Lekakou, Ionics, 2021, 27, 635.
42. A. D. Gosman, C. Lekakou, S. Politis, R. I. Issa and M. K. Looney, AIChE J., 1992, 38, 1946.
43. Y. Elsayed, C. Lekakou and P. Tomlins, Biotechnol. Bioeng., 2019, 116, 1509.
44. S. Grabe, J. P. Baboo, S. Tennison, T. Zhang, C. Lekakou, E. I. Andritsos, Q. Cai, S. Downes, S. Hinder and J. F. Watts, AIChE J., 2022, 68, e17638.
45. K. Lasetta, J. P. Baboo and C. Lekakou, J. Compos. Sci., 2021, 5, 65.
46. F. Markoulidis, C. Lei and C. Lekakou, Electrochim. Acta, 2017, 249, 122.
47. G. Bieker, J. Wellmann, M. Kolek, K. Jalkanen, M. Winter and P. Bieker, Phys. Chem. Chem. Phys., 2017, 19, 11152.

---