Valence photoelectron imaging of molecular oxybenzone

Abstract

An oxybenzone molecule in the gas phase was characterized by mass spectrometry and angle-resolved photoelectron spectroscopy, using both single and multiphoton ionization schemes. A tabletop high harmonic generation source with a monochromator was used for single-photon ionization of oxybenzone with photon energies of up to 35.7 eV. From this, vertical ionization and appearance energies, as well as energy-dependent anisotropy parameters were retrieved and compared with the results from DFT calculations. For two-photon ionization using 4.7 eV light, we found a higher appearance energy than in the extreme ultraviolet (EUV) case, highlighting the possible influence of an intermediate state on the photoionization process. We found no differences in the mass spectra when ionizing oxybenzone by single-photons between 17.2 and 35.7 eV. However, for the multiphoton ionization, the fragmentation process was found to be sensitive to the photoionization order and laser intensity. The “softest” method was found to be two-photon ionization using 4.7 eV light, which led to no measurable fragmentation up to an intensity of 5 × 10¹² W cm⁻².

---

1. Introduction

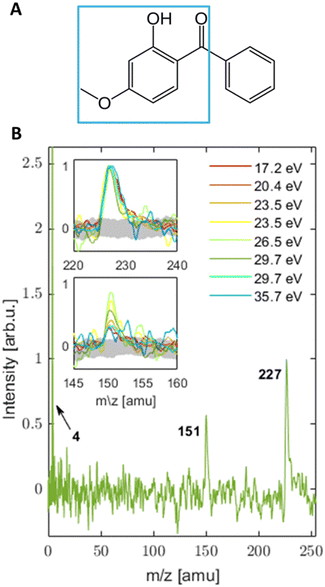
Oxybenzone (OB, C₁₄H₁₂O₃, 2′-hydroxy-4′-methoxy-benzophenone, see panel A in Fig. 1) is an efficient photosensitizer that is one of the most commonly used chemicals in sunscreens where it serves as an ultraviolet filter.¹ Coming off the swimmers’ skin, it can be found in marine environments where its impact is less beneficial. Recent studies^2,3 showed that aqueous OB in the presence of 290–370 nm light activates a toxic metabolic pathway in sea organisms and is one of the causes of reef bleaching. It is modified within corals’ cells by the attachment of glucose that turns it into a potent photosensitizer. Possibly, this modification involves the excited-state proton transfer in OB.² The latter is the main energy-dissipation mechanism of OB and similar sunscreen molecules in solutions, as shown by Baker et al. (see ref. 4 and 5 and references therein). OB has been extensively studied in solution.^4,6–14 Relatively few studies have taken a bottom-up approach^15–20 and investigated OB in an isolated form or small mixed clusters.^15,21–23 Its structure and excited-state absorption were determined by static spectroscopic approaches,^24–26 while to the best of our knowledge the only work focusing on excited-state dynamics of gas phase OB has been theoretical.²⁷ However, a detailed understanding of the electronic properties of isolated OB in its ground and excited states is still missing and will be the focus of this work.

Fig. 1 (A) Structure of OB in its enol form with an indication (blue square) of the suggested structure for the m/z = 151 amu fragment. (B) MS (normalized to the peak centred at 227 amu) collected upon ionization with a series of photon energies in the EUV range. Insets are zoomed to the mass fragments of OB seen in the MS with the noise level indicated in gray. The helium peak is also indicated in the main MS. The mass accuracy of the fragments is estimated to be ±1 amu.

Here, we present a photoelectron imaging study of isolated, gas-phase OB following single- and multiphoton ionization. With this approach, we characterized the valence electronic structure of ground state OB in the gas phase and found first experimental indications of its ultrafast excited-state dynamics. This study was performed with our tabletop EUV setup,^28–31 which delivers femtosecond pulses (∼100 fs) with tunable photon energy. In combination with a velocity map imaging spectrometer, we gain simultaneous and direct (single-photon ionization) access to ionization energies (IEs) and photoelectron angular distributions (PADs).^32–44

The quality of the measurements and the broad range of photon energies they cover (∼3–36 eV) demonstrate the readily available capabilities of laboratory measurements using table-top high harmonic generation (HHG) in comparison with the limited user access offered by dedicated facilities. Photon energies well above the threshold were used to provide accurate ionization energies and information on orbital symmetries. The latter can be derived from the PAD that for single-photon ionization with linearly polarized light is described by an anisotropy parameter β following eqn (1):

θ is the angle between the linear polarization of light field's electric field and the ejection direction of the photoelectrons, and I(θ) is the electron signal detected at that angle. The anisotropy parameter β (sometimes referred to as β₂) ranges between −1 (when photoelectrons are preferentially ejected perpendicular to the polarization of light) and 2 (when photoelectrons are preferentially ejected parallel to the polarization of light). β takes the value of 0 in the case of isotropic distribution.

2. Experimental and computational methods

The measurements were made on a molecular beam (MB) of OB in our velocity-map imaging (VMI) spectrometer that was previously described in more detail.^{28–31,45,46} Briefly, the spectrometer consists of three vacuum chambers: (i) the “source chamber” where the MB is formed; (ii) a differential pumping chamber where a physical barrier in the form of a retractable metal plate can “block” the MB in order for background images to be recorded; and (iii) the “detection chamber” for electron\ion detection with the VMI and mass spectrometer.

Neat OB powder was purchased from Sigma Aldrich and heated in a “bubbler” (in-line container) to a temperature of 195–200 °C and seeded in helium (He) carrier gas, with a backing pressure of 2–4 bar. The mixture was supersonically expanded through a heated, pulsed Even–Lavie (EL) valve,⁴⁷ that was operated at a repetition rate of 500 Hz, to form the MB. To ascertain that there was no thermal decomposition, the OB sample was analyzed by GC–MS after several heating cycles. After formation, the MB traversed a pair of skimmers before entering the VMI spectrometer.

Photoelectrons were produced between the repeller and extractor plates of the VMI extraction optics by single-photon ionization with femtosecond EUV light from our table-top, home-built HHG source with a time-preserving monochromator.^28–31 The EUV was generated by focusing ∼3–4 mJ per pulse of 800 nm, 1 kHz, ∼35 fs laser (Coherent, Astrella) output in an argon filled cell and the single harmonic was selected in a time-preserving monochromator based on the design by Poletto and coworkers^48,49 (see Fig. S2 and Table ST2 in the ESI† for a representative HHG spectrum). The second line of 800 nm light from the Astrella, 37 fs, was used to generate 266 nm (UV) and 400 nm (VIS) light. Both the second harmonic (VIS) and the third harmonic (UV) were generated in BBO crystals as configured in a commercially available Femtokit (EKSMA). The resulting pulses of VIS light were ∼70 fs (at FWHM) with a pulse energy of up to 300 μJ, while the UV pulses were ∼100 fs long (at FWHM) with a pulse energy of up to ∼100 μJ. Both the UV and VIS were used in multiphoton ionization experiments.

The VMI spectrometer was operated in two modes – time-of-flight cation mass spectrometry or photoelectron VMI by using the appropriate polarity and voltage ratios on the electrodes.^50,51 VMI photoelectron images were recorded with a microchannel plate/phosphor screen assembly (MCP/PS) and a CCD camera. The MCP was operated at 500 Hz, while the camera was operated in a long exposure mode (at 20 Hz with 50 millisecond exposure time). Background images were recorded when the MB was blocked as described above and subsequently subtracted from OB photoelectron images. Every image was averaged over ∼4.5 × 10⁶ laser shots. Photoelectron images, photoelectron spectra and anisotropy parameters β were recovered from the background-subtracted data using the pBASEX image inversion algorithm⁵² (examples of images and corresponding reconstruction can be seen in Fig. 3).

In addition to the experiments, we performed time dependent (TD-)DFT calculations. The optimized ground state structure of OB (more stable enol tautomer) was taken from the work of Cui and co-workers.²⁷ We approximated the vertical ionization energies (VIEs) using two approaches: (i) by using the negative Kohn–Sham orbital energies of the neutrals^53,54 and (ii) from the excitation spectrum of the ionized OB calculated with TD-DFT.^54–56 For approach (i), we used DFT (B3LYP with the 6-311++G(d,p) basis set) to calculate total energies of the neutral and ionized OB at the geometry of the neutral. Orbital energies of the neutral were obtained from the population analysis. For method (ii), we used TD-DFT to calculate the excitation spectrum of the ionized OB at the neutral geometry and included up to 60 excited states. We used two functionals (B3LYP and CAM-B3LYP) to assess the quality of the excited state calculations. These functionals were previously used for excited state calculations of a wide range of organic molecules,⁵⁷ with the CAM-B3LYP often showing better agreement with the experiments. The same basis set as that for the DFT calculations was used. The photoelectron spectra were simulated by convoluting the obtained stick spectra with a Gaussian representing the typical bandwidth (0.71 eV) of our photoionization pulses (based on a Gaussian fit to the He peak, as shown in Table ST3 in the ESI†). Finally, we calculated the adiabatic ionization energy (AIE) as the energy difference between the neutral OB to the geometry-optimized OB cation.

3. Results and discussion

3.1 Mass spectra (MS)

MS were collected for a broad range of photon energies (3.1–35.7 eV). The MS from UV and VIS light are a product of multi-photon ionization (MPI), while photon energies in the EUV range produce single-photon ionization spectra.

3.1.1 Single-photon EUV ionization. In the MS recorded following EUV ionization (Fig. 1, panel B) we see only three peaks, corresponding to the molecular ion, either intact (228 amu) or after elimination of hydrogen atom (227 amu), and a fragment (151 amu) that can be assigned to the product of phenyl cleavage (C₆H₅, 77 amu), connected by the longest, and weakest bond²³ (228 − 77 = 151 amu), and a peak of the carrier gas (He) at 4 amu. Within experimental uncertainty, it is not possible to conclusively determine whether the molecular ion lost a hydrogen atom. A similar fragmentation channel was found to be dominant in the case of benzophenone (BP),⁵⁸ which can be viewed as a simpler analogue of OB. As a function of the photon energy (see insets in Fig. 1), we see a change in the ratio between the parent and the fragment ion however we do not observe a systematic dependence on photon energy. In view of the low signal to noise ratio, we refrain from a quantitative analysis of the photon-energy dependent fragmentation.

3.1.2 Multi-photon ionization (MPI). In the cases of 266 nm (UV, 4.7 eV, I ∼ 5 × 10¹² W cm⁻²) and 400 nm (VIS, 3.1 eV, intensities of either I ∼ 6 × 10¹² W cm⁻² or I ∼ 2 × 10¹³ W cm⁻²) light the energy of a single photon is not sufficient for ionization of OB, thus the MS is a product of MPI. Comparison of UV-MPI (2 photons with a total energy of 9.3 eV) and VIS-MPI (3 photons with the same total energy of 9.3 eV) shows that while VIS-MPI leads to an MS similar to EUV-MS, UV-MPI results in a single peak (Fig. 2).

Fig. 2 MPI-MS spectra recorded with: (A) 266 nm with an intensity of 5 × 10¹² W cm⁻²; (B) 400 nm with a relatively low intensity of I ∼ 6 × 10¹² W cm⁻² (C) 400 nm with a relatively high intensity of I ∼ 2 × 10¹³ W cm⁻². The masses of the observed fragments are indicated in the figure with an accuracy of ±1 amu.

3.1.3 Discussion and summary. Based on the data presented in Fig. 1 and 2, we conclude that the fragmentation pattern of OB is very sensitive to the ionization pathway and laser intensity, though rather insensitive to available single photon energy in the range between 17.2 eV and 35.7 eV. Both 2-photon UV-MPI and 3-photon VIS-MPI have the same total energy of 9.3 eV, yet we observe a difference in the fragmentation pattern. Low-intensity VIS excitation (Fig. 2(B)), with a similar intensity as that used for UV excitation (resulting in a similar height of the molecular peak), results in a fragmentation pattern similar to that of EUV excitation (Fig. 1(B)). High-intensity VIS excitation, by contrast, produced additional fragments. To get a better insight into the energy balance, fragment appearance energies for two fragmentation channels were retrieved from DFT calculations (using B3LYP with the 6-311++G(d,p) basis set). The calculated adiabatic appearance energy for the molecular ion is 7.9 eV (see Section 3.2.2). The first fragmentation channel leads to a neutral phenyl fragment and the m/z = 151 amu charged fragment, and the second to a phenyl cation (m/z = 77 amu) and a neutral second fragment. The calculations predict adiabatic ionization energies of 10.35 eV and 12.3 eV, respectively. On the basis of the calculations, we find two scenarios that explain the dependence of the observed fragmentation patterns on the excitation pathways (Fig. 1 and 2).

Scenario 1 assumes that the ordering of the ionic states obtained in the calculations is correct, but the absolute energies of the two states of that fragment are calculated to be too high, by at least 1 eV. In this scenario the excitation energy of 9.3 eV in the 2-photon UV and the 3-photon VIS would both be sufficient to produce the m/z = 151 amu fragment. The fact that this fragment is not observed in the 2-photon UV could be ascribed to a very fast relaxation of the resonant 1-photon intermediate state in the UV case, so that the photon energy would no longer suffice to produce the m/z =151 amu fragment. In the non-resonant 3-photon VIS ionization, there is no such relaxation to prevent fragmentation, so that the m/z = 151 amu ion fragment can be formed. Neither the 2-photon UV nor the 3-photon VIS excitations can reach the next higher ionic state that fragments to the phenyl cation (m/z = 77 amu). When the VIS intensity is increased, 4 photon ionization starts to contribute, which corresponds to an excitation energy of 12.4 eV. This is sufficient to produce the phenyl cation and its further fragmentation product m/z = 51 amu ([C₄H₃]⁺, assignment based on ref. 59). These two fragments are not seen in the 1-photon EUV spectra, not because the energy would not be sufficient, but because of a particularly low cross section for this channel. This could be rationalized by the major change of geometry of the phenyl fragment upon ionization. The neutral phenyl ring is planar while the phenyl cation is non-planar. If we assume that the ionic state that leads to that fragmentation channel also features such a large geometry change in the phenyl ring, one would expect correspondingly small Franck–Condon factors and correspondingly low cross sections for the excitation. As a result, the fragmentation channel producing the phenyl cation would not be observable in the 1 photon EUV excitation. In the case of high-intensity 4-photon VIS excitation (or higher order MPI), the intermediate states might offer a bypass around this Franck–Condon gap.

Scenario 2 assumes that the calculated absolute energies of the two fragmenting states are essentially correct. In this scenario an excitation energy of 9.3 eV in the 2 photon UV and 3 photon VIS would not be enough to produce any fragmentation at all. The low-intensity VIS excitation would then have to involve a significant contribution of 4-photon excitation (total photon energy of 12.4 eV) to produce the m/z = 151 amu fragment. The additional fragments (phenyl cation and its fragment) observed in the high-intensity VIS excitation would then have to be the result of 5-photon contributions to the excitation (15.5 eV). The energy provided by 4-photon excitation would be too close to the calculated appearance energy of 12.3 eV (neglecting potential barriers) to justify the observed signal height. We note that it is possible that strong field effects start playing a role in the high-intensity VIS case. Intensities in the 10¹³ W cm⁻² range were previously shown to result in unexpectedly strong fragmentation.^60,61 The absence of the phenyl cation and its fragment in the EUV would be explained in the same way as in scenario 1.

Both scenarios explain the observations, but both have aspects that appear at least unusual: for scenario 1, the overestimation of the adiabatic ionization energies of the two excited ion states by more than 1 eV would appear rather large given that the calculated AIE for the ionic ground state (7.9 eV) lies only 0.2 eV above the observed appearance energy (see Table 2). Moreover, the same level of calculation predicts an adiabatic appearance energy of 10.13 eV for the phenyl cleavage of the BP cation, which lies in fact 0.9 eV below its experimental appearance potential (11.04 eV⁵⁸). For scenario 2, it might be difficult to rationalize why the same intensity in the UV and the low-intensity VIS experiments leads to significant 4-photon excitation in the latter while the former remains strictly 2-photon ionization. If a 4-photon process contributes then this should show up in the 3-photon spectrum as a low-energy tail in the binding energy spectrum (see Fig. 4). The spectrum indeed shows a very weak tail, but its weakness is not easily reconciled with the signal strengths of the fragments in the mass spectra. At the current stage, we cannot give a clear preference to either scenario. In the context of complex ion fragmentation dynamics, we note a similar situation for BP which also showed unexpected fragmentation behavior upon ionization,⁵⁸ in that case tentatively explained by autoionization of doubly excited Rydberg states.

3.2 PE images and ionization energies

3.2.1 EUV images and spectra – vertical binding (ionization) energies. Vertical binding energies, VBE (or equivalently vertical ionization energies, VIE) are essential characteristics of a molecular electronic structure and important for the evaluation of different calculation methods. VBEs however cannot be reliably determined with MPI. Instead we used photon energies in the EUV range well above the threshold provided by a home-built HHG source described above. PE images were recorded in a broad EUV energy range (17–36 eV) and reconstructed to retrieve photoelectron spectra (PES) and associated anisotropy parameters β (see Section 3.4 on PADs below). Two of the recorded PE images are shown in Fig. 3. The kinetic energy (KE) of the electrons increases from the centre of the images (zero kinetic energy) with increasing radius, while the binding energy (BE) decreases. At a higher photon energy, above the ionization threshold of He, the image is dominated by the signal of He which is present in excess (Fig. 3(A)). However, the higher kinetic energy (i.e. larger radius) signal originating from OB can be clearly identified. At photon energies below the BE of He, only the OB signal is visible (Fig. 3(B)).

Fig. 3 (A) and (B) examples of two photoelectron images taken at different photon energies and their corresponding reconstructions (as indicated). E⃑ indicates the polarization direction of light in the experiment; (C) EUV PES and calculated spectrum (using method (i)^53,54 (indicated as “DFT”) convoluted with Gaussian of FWHM = 0.71 eV). Bands (as assigned in Table 1) are marked in gray with their corresponding band index. Data from the center of the image (KE < 0.1 eV) has been excluded from these traces.

Reconstructed PES are shown in Fig. 3(C). PES measured with photon energies above the VBE of He show the expected carrier gas contribution at VBE = 24.7 eV. Of interest for the current work are the pronounced bands with BE < 16 eV. We also note that for the highest photon energy (35.7 eV) leaking of the adjacent lower order harmonic from the HHG source leads to the spurious signal at 3 eV higher BE, but its contribution of ∼8% does not significantly affect the PES of OB as can be seen from its resemblance to other spectra (see also peak VBE in Table 1). The uncertainty that stems from the experimental system is 0.3 eV (see Section B in the ESI†). We identify 3 dominant PE bands labelled as bands 0, 1, and 2 in Fig. 3(C). For a quantitative analysis we performed a multi-component Gaussian fit to the experimental spectra (see the ESI† for details). A summary of these fits for the abovementioned bands is shown in Table 1. The obtained VBEs (determined from the maxima of the respective Gaussian peaks and averaged over all photon energies) are 9.2, 12.2 and 14.4 eV, respectively (the widths of the fits can be found in ST4 in the ESI†). Here as well, we can compare the PES of OB with that of a simpler analogue BP and notice that PES of BP in the energy range of BE < 16 eV (see Fig. 1 in ref. 62) is indeed very similar to that of OB with 3 main valence bands that can be indentified.^58,62

Table 1 Summary of the VBE of the three lowest valence bands as retrieved from Gaussian fits. The indicated error is the standard deviation (STD) in the presented values. The experimental uncertainty is ±0.3 eV as explained in Section B in the ESI

Photon energy [eV]	VBE of band 0 [eV]	VBE of band 1 [eV]	VBE of band 2 [eV]
17.2	9.2	12.2	14.3
20.4	9.1	12.3	14.5
23.5	9.2	12.2	14.5
26.5	9.0	12.0	14.3
29.7	9.2	12.3	14.6
32.7	9.4	12.3	14.6
35.7	9.1	12.2	14.3
Average ± STD	9.2 ± 0.1	12.2 ± 0.1	14.4 ± 0.1

---

These first three valence bands are indicated in gray in Fig. 3(C), where the box indicates regions over which the β trace was integrated (see section on PADs below). This range corresponds to 80% of FWHM of the Gaussian that was fitted for each of the bands (see Table 1). The sum of all Gaussians fitted to the PES is shown in the ESI,† Fig. S3. The fitted spectra show that best energy resolution is achieved with the two lowest photon energies, thus we compare the spectrum calculated from orbital energies^53,54 (see Section 3.3) to PES taken at 20.35 eV. While the VBEs are rather stable for different photon energies, we observe band broadening with increasing photon energy. This broadening is directly related to the bandwidth of the EUV light and is also visible in the He peak (see Section B in the ESI†).

3.2.2 Appearance energy and implication for future pump–probe studies. Here we determine the appearance energies (AE, the ionization onset in the experimental PES) from the EUV spectra discussed above, as well as from the UV-MPI and VIS-MPI spectra. The AE values were approximated (as in similar cases^63–65) from the intersection between linear fits to the rising edge of the signal and the baseline (indicated with dotted lines in the inset of Fig. 4 and in Fig. S4, ESI†). The value approximated from the EUV spectra, is the average of those retrieved from the intersection between the linear fits to the fitted spectra of the sharpest harmonics (see Fig. S4 and Table ST5 in the ESI†). The appearance energy is then compared with the calculated adiabatic ionization energy (AIE) value as the PES was taken for vibrationally cold MB. The AIE plays an important role in the characterization of a molecule, e.g. for identifying effects of geometry relaxation of the ionized molecule and of any intermediate state dynamics.

Fig. 4 Comparison of PES taken with VIS (400 nm), UV (266 nm) and EUV (20.4 eV) photon energies (PES present data from KE > 0.1 eV). Dotted black lines in the inset are linear fits to the onset of the 20.4 eV and 266 nm signals and the noise level. Dashed magenta spectrum as calculated by method (i) and convoluted with a Gaussian (FWHM = 0.71 eV).

Qualitative assessment of the traces measured with different techniques (MPI vs. single photon ionization) shows a better signal to noise ratio (SNR) in the MPI case. Because of the latter, MPI is sometimes used for a more precise determination of the appearance energy, especially in aqueous environments, however with the drawback of possible distortions by the excited state dynamics if the excitation is resonant.⁶⁶ In the current study, we do not see a clear benefit over the EUV data for the determination of the appearance energy as the signal to noise ratio for the latter was sufficient (see Fig. 4 and Fig. S4 in the ESI†).

The obtained AE for the EUV, UV and VIS ionization methods and the calculated AIE are summarized in Table 2. In the case of EUV, experimental uncertainty was taken from the bandwidth of the harmonics used for ionization and was quantified by measuring the width of the He peak by photoelectron VMI (see Table ST3 and Section B in the ESI†). The uncertainty was defined to be half of the 80% of FWHM of the fitted Gaussians of the He peak. The uncertainty in the VIS and UV cases is based on the measured spectral profile of the 800 nm light.

Table 2 Summary of experimental appearance energies (AE)/ionization onset and the calculated adiabatic ionization (AIE)

Method\measurement	Appearance energy [eV]
EUV	7.7 ± 0.3
VIS	7.7 ± 0.1
UV	8.0 ± 0.1
DFT	7.9

---

We see that the VIS value agrees with the EUV result within estimated uncertainties. In the VIS case an onset for 3 photons is clearly visible at 7.7 eV. These values are also in excellent agreement with the calculated AIE. The estimated AE from the linear fit to the sharp rise in the VIS PES indicates that no significant intermediate state dynamics takes place. This is consistent with the short “effective” pulse duration of ∼40 fs used in MPI. It is worth noting that while no resonance is expected from the first 3.1 eV photon, 2 photons with this energy can reach a resonant state, whose fast relaxation might be responsible for the shoulder at BE∼8.2 eV. Also, the tail at BE < 7.7 eV might contain contributions from a higher MPI order (four 400 nm photons). The measured values are lower than the AIE of BP (which is 8.9 eV), while the first band is centered at a similar value.⁵⁸ This could indicate a larger geometry relaxation in the ion which would mean that the geometry change is more significant upon ionization in the case of OB. In turn, it would indicate that the cation of OB is stabilized by the additional methoxy and hydroxy electron donating functional groups (a similar trend in other BP derivatives can be seen in Fig. 2 of ref. 62 and is discussed regarding the difference in the VBE of BP and hydroxyphenone⁶⁷).

The noticeably higher AE of 8.0 ± 0.1 eV in the UV case suggests the importance of ultrafast excited state dynamics in the intermediate state of resonant excitation^24,26,27 and will be the topic of future work. This resonant state can also play a role in a barrierless hydrogen transfer that was shown to happen in solution within ∼100 fs following 325 nm photoexcitation,⁴ and on a calculated time scale of the same order in the gas phase²⁷ with relaxation channels^24,27 that are in line with the measured energy gap between the determined AE in the UV and VIS\EUV cases. The resonant state that is accessed only in the UV case, but not the VIS or EUV cases, could also explain the difference in the MS shown in Fig. 1 and 2, where UV-MS shows the softest ionization and a mass spectrum free of photofragments. The lack of fragments in the UV case could possibly be attributed to excited state driven tautomerization which results in a reduction of the total energy available for ionization²⁷ with the parent ion trapped in a potential energy well, from which phenyl loss is not accessible.

3.3 DFT calculations – VBEs and AIE

VBEs and AIE were calculated using 2 approaches: (i) by using the negative Kohn–Sham orbital energies^53,54 and (ii) from the excitation spectrum of the ionized OB calculated with TD-DFT.^54–56 We find that both methods show reasonable qualitative agreement with the experiment in terms of peak positions. The calculated intensity envelope using method (i) is compared with the experimental result in Fig. 3 (see also Fig. 4), while the comparison with method (ii) is shown in the ESI† (Fig. S1). A photoelectron spectrum calculated by method (i) leads to better agreement with the experiment. However, since no information on the transition probabilities is available from either of the methods and the calculated intensities simply reflect the density of states/transitions, this observation is likely coincidental and depends strongly on the quality of the functional and basis set (especially for the TD-DFT) employed.

The calculations show that each experimentally assigned band (see above) consists of many individual electronic transitions (see Fig. S1 and Table ST1 in the ESI†). Detailed assignment is therefore complicated, but some qualitative features emerge. Transitions contributing to the first VBE band (band 0) originate from the removal of electrons from the highest five molecular orbitals in method (i) and four in method (ii). Visualization of electron densities corresponding to these orbitals in the case of method (i) is shown in Fig. 5. These are all lone-pair orbitals with dominant π-character (either pure or >60% contribution for mixed orbitals). This seems to agree with previous work on similar aromatic systems where the first VBE band below 10 eV was typically assigned to π-type and non-bonding lone pair ionization.^{36,62,68–72} Already in the second VBE band (band 1), we find that electrons originate from lower-lying lone-pair orbitals that are either mixed with stronger s-character (e.g. HOMO−5) or core orbitals of a pure s-character (e.g. HOMO−6). Detailed assignment based on method (ii) is complicated by increasingly more orbital transitions contributing to a single excitation of the cation.

Fig. 5 Visualization of the 7 energetically highest lying occupied orbitals of neutral oxybenzone as obtained by method (i). The 5 energetically highest lying occupied orbitals contribute to the first VBE band (band 0) and exhibit predominantly π-character while orbitals lying lower in energy (separated by dashed line) exhibit mostly s-character.

Calculated AIE (after geometry optimization of the cation) is in very good agreement with the experimental AE obtained by EUV ionization (see Table 2). Although slightly higher, the calculated AIE lies within the experimental uncertainty. A relatively small energy gain calculated from the geometry relaxation of the cation (∼0.3 eV) therefore suggests that the EUV appearance energy is a good estimate of the AIE. A similar value is obtained from the VIS data, as expected from a non-resonant process. In contrast, the AE in the UV case is higher than the calculated AIE (though still within experimental uncertainties) and other experimental values (AE measured in VIS and EUV schemes). This suggests that dynamics in the resonantly excited intermediate state may play an important role (see above).

3.4 Photoelectron angular distributions (PADs)

One goal in this study and a benefit of angle resolved photoelectron spectroscopy is that it enables the determination of photoemission anisotropy parameters (e.g. β), and their energy-dependence thus providing information about the orbital symmetry of the molecule. The experimentally determined β parameters for the first 3 valence bands are presented in Fig. 6. They show an increase of β with kinetic energy for all 3 bands. β increases more rapidly with kinetic energy for the lowest band (band 0) while the change is much less pronounced for the other 2 bands (from 0.2 to 1.2 for band 0 and from ∼0.2 to ∼0.6 for the other 2 bands in the same kinetic energy range).

Fig. 6 Evolution of the β-parameter as a function of electron kinetic energy for the first 3 valence bands. The shaded area indicates the uncertainty.

This behaviour was previously observed for other aromatic moleclules.^68,70,71,73 It was also found that an increase in β with kinetic energy is observed for ionization from dominantly π and non-bonding lone pair orbitals, while β stays almost constant in ionization from σ orbitals.^36,68–72 Based on this, we can conclude that in the case of isolated OB, band 0 is dominated by ionization from π-type orbitals, while for band 1 and band 2 the contributions from σ type orbitals become more important. This is supported by our analysis of the DFT calculations (see Fig. 5 and the discussion above).

These findings can again be compared with the case of BP as a simpler analogue of OB. In the case of BP, the binding energy range of 8–10 eV is also attributed to the π-type electrons from the benzene rings along with the non-bonding lone pair of the carbonyl oxygen.⁶²

4. Conclusions

The primary aim of this study was to experimentally characterize the electronic structure of OB in the gas phase as this information was missing, but is crucial for understanding more complex phenomena (e.g. its metabolic pathways). We achieved this aim with an in-house photoelectron imaging spectrometer coupled to either a UV (4.7 eV), VIS (3.1 eV) or a table-top EUV laser providing photon energies in the 17–36 eV range.

The comparison of the single photon ionization in the EUV with multi-photon ionization in the UV and VIS revealed fragmentation patterns that are sensitive to the method of ionization and laser intensity, but insensitive to the photon energy between 17.2 and 35.7 eV in the single photon EUV ionization. The high intensity of VIS light causes extensive fragmentation with main features comparable to 70 eV electron ionization (the industry standard in GC–MS, available online from NIST Chemistry WebBook⁷⁴). The 2-photon UV excitation, by contrast, yields a fragment free mass spectrum, making it a particularly soft ionization pathway for OB. Quantum chemical calculations (DFT) offer plausible explanations for the dependence of the fragmentation patterns on the excitation pathways. The insensitivity of the fragmentation pattern to the photon energy in the EUV could be explained by a Franck–Condon gap due to the large geometry change of the phenyl cation. This would reduce the ionization cross-sections for the corresponding fragmentation channel below our detection limit. In the case of multi-photon excitation, the explanation is less clear cut. We propose two scenarios. Scenario 2 explains the absence of any fragments in the UV by insufficient excitation energy. The fragmentation upon excitation in the VIS would then have to be the result of 4-photon excitation at low intensity and at least 5-photon excitation at higher intensity. Alternatively (scenario 1), the available photon energy would in principle be sufficient to cause fragmentation of the ion both in the UV and for low-intensity VIS. In the UV, however, fast relaxation of the intermediate resonant state could cause a loss of energy available for ionization, so that the fragment channel can no longer be reached. The different fragmentation patterns in the VIS depending on the light intensity could be readily explained by 3- and 4-photon excitation, respectively. For future work, examining ion signal intensity as a function of laser power could be helpful to determine the number of photons required for ionization.

The appearance energy of gas phase OB derived from multiphoton ionization in the VIS agrees well with that determined from single photon ionization in the EUV, yielding a value of 7.7 eV in agreement with the calculated adiabatic ionization energy of 7.9 eV. Multiphoton ionization with UV light results in a slightly higher value of 8.0 eV. This might be ascribed to ultrafast intermediate state dynamics during the ionization pulse of about 100 fs, consistent with the ultrafast relaxation pathways via excited state hydrogen transfer predicted in the gas phase.^24,27 Such intermediate state dynamics can be an issue when using MPI for the determination of appearance energies – an issue that is avoided by using single photon EUV ionization.

Another advantage of single photon EUV ionization is the broad accessibility of vertical binding energies (VBE) including excited ionic states. We identified three pronounced bands, with VBEs of 9.2, 12.2 and 14.4 ± 0.3 eV, in good agreement with the results from DFT calculations. These bands show a different energy-dependence of photoelectron anisotropy (β parameter). While β increases with energy in all three bands, this increase is much more pronounced for the lowest BE band. The (TD-) DFT analysis of the transitions contributing to these bands suggests that the lowest band (band 0) is dominated by the removal of electrons from lone-pair orbitals of π character. This explains the high value and pronounced energy-dependence of the corresponding β parameter. The larger contributions from s-type orbitals to the higher bands (bands 1 and 2) is consistent with the experimentally observed slower increase of β with increasing KE.

Future work will elucidate the excited state dynamics in the UV range and investigate the effect of solvation in systems of mixed clusters, with particular attention to the internal C=O⋯H hydrogen bond, and its role in the excitation process and excited/ionic state dynamics.

Data availability

Data required to reproduce the results presented in the paper can be found in the open access data collection of ETHZ at doi: https://doi.org/10.3929/ethz-b-000677638.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Evangelos Miliordos for advice regarding the calculations, as well as David Stapfer, Daniel Zindel and Markus Steger for technical support. Financial support was provided by the NCCR MUST, funded by the Swiss National Science Foundation (SNSF), through ETH-FAST, and through SNSF project no. 200020_200306, the FP-RESOMUS (founded by European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 801459), the ESKAS Scholarship, and the European Union Horizon 2020 research and innovation program from the European Research Council under grant agreement no. 786636.

References

1. A. Scheele, K. Sutter, O. Karatum, A. A. Danley-Thomson and L. K. Redfern, Environmental impacts of the ultraviolet filter oxybenzone, Sci. Total Environ., 2023, 863, 160966.
2. D. Vuckovic, A. I. Tinoco, L. Ling, C. Renicke, J. R. Pringle and W. A. Mitch, Conversion of oxybenzone sunscreen to phototoxic glucoside conjugates by sea anemones and corals, Science, 2022, 376, 644–648.
3. C. A. Downs, E. Kramarsky-Winter, R. Segal, J. Fauth, S. Knutson, O. Bronstein, F. R. Ciner, R. Jeger, Y. Lichtenfeld, C. M. Woodley, P. Pennington, K. Cadenas, A. Kushmaro and Y. Loya, Toxicopathological Effects of the Sunscreen UV Filter, Oxybenzone (Benzophenone-3), on Coral Planulae and Cultured Primary Cells and Its Environmental Contamination in Hawaii and the U.S. Virgin Islands, Arch. Environ. Contam. Toxicol., 2016, 70, 265–288.
4. L. A. Baker, M. D. Horbury, S. E. Greenough, P. M. Coulter, T. N. V. Karsili, G. M. Roberts, A. J. Orr-Ewing, M. N. R. Ashfold and V. G. Stavros, Probing the Ultrafast Energy Dissipation Mechanism of the Sunscreen Oxybenzone after UVA Irradiation, J. Phys. Chem. Lett., 2015, 6, 1363–1368.
5. L. A. Baker, B. Marchetti, T. N. V. Karsili, V. G. Stavros and M. N. R. Ashfold, Photoprotection: Extending lessons learned from studying natural sunscreens to the design of artificial sunscreen constituents, Chem. Soc. Rev., 2017, 46, 3770–3791.
6. L. A. Baker, L. C. Grosvenor, M. N. R. Ashfold and V. G. Stavros, Ultrafast photophysical studies of a multicomponent sunscreen: Oxybenzone–titanium dioxide mixtures, Chem. Phys. Lett., 2016, 664, 39–43.
7. B. M. Baughman, E. Stennett, R. E. Lipner, A. C. Rudawsky and S. J. Schmidtke, Structural and Spectroscopic Studies of the Photophysical Properties of Benzophenone Derivatives, J. Phys. Chem. A, 2009, 113, 8011–8019.
8. L. A. Baker, M. D. Horbury, S. E. Greenough, M. N. R. Ashfold and V. G. Stavros, Broadband ultrafast photoprotection by oxybenzone across the UVB and UVC spectral regions, Photochem. Photobiol. Sci., 2015, 14, 1814–1820.
9. A. César-Razquin, B. Snijder, T. Frappier-Brinton, R. Isserlin, G. Gyimesi, X. Bai, R. A. Reithmeier, D. Hepworth, M. A. Hediger, A. M. Edwards and G. Superti-Furga, A Call for Systematic Research on Solute Carriers, Cell, 2015, 162, 478–487.
10. L. Beyere, S. Yarasi and G. R. Loppnow, Solvent effects on sunscreen active ingredients using Raman spectroscopy, J. Raman Spectrosc., 2003, 34, 743–750.
11. M. T. Ignasiak, C. Houée-Levin, G. Kciuk, B. Marciniak and T. Pedzinski, A Reevaluation of the Photolytic Properties of 2-Hydroxybenzophenone-Based UV Sunscreens: Are Chemical Sunscreens Inoffensive?, ChemPhysChem, 2015, 16, 628–633.
12. Y. Li, X. Qiao, C. Zhou, Y. Nan Zhang, Z. Fu and J. Chen, Photochemical transformation of sunscreen agent benzophenone-3 and its metabolite in surface freshwater and seawater, Chemosphere, 2016, 153, 494–499.
13. Z. Deng, J. Pang, Z. Situ, L. Yin, L. Dang and M. De Li, Revealing how proton transfer process of 2-hydroxylbenzophenones affected by the intermolecular hydrogen bond with different para-substituted groups, J. Photochem. Photobiol., A, 2022, 422, 113553.
14. R. Kumasaka, A. Kikuchi and M. Yagi, Photoexcited States of UV Absorbers, Benzophenone Derivatives, Photochem. Photobiol., 2014, 90, 727–733.
15. N. G. K. Wong and C. E. H. Dessent, Illuminating the Effect of the Local Environment on the Performance of Organic Sunscreens: Insights From Laser Spectroscopy of Isolated Molecules and Complexes, Front. Chem., 2022, 9, 1222.
16. E. L. Holt and V. G. Stavros, Applications of ultrafast spectroscopy to sunscreen development, from first principles to complex mixtures, Int. Rev. Phys. Chem., 2019, 38, 243–285.
17. A. L. Whittock, T. T. Abiola and V. G. Stavros, A Perspective on Femtosecond Pump-Probe Spectroscopy in the Development of Future Sunscreens, J. Phys. Chem. A, 2022, 126, 2299–2308.
18. N. D. N. Rodrigues, M. Staniforth and V. G. Stavros, Photophysics of sunscreen molecules in the gas phase: a stepwise approach towards understanding and developing next-generation sunscreens, Proc. R. Soc. A, 2016, 472, 20160677.
19. N. D. N. Rodrigues and V. G. Stavros, From fundamental science to product: A bottom-up approach to sunscreen development, Sci. Prog., 2018, 101, 8–31.
20. L. A. Baker and V. G. Stavros, Observing and understanding the ultrafast photochemistry in small molecules: Applications to sunscreens, Sci. Prog., 2016, 99, 282–311.
21. N. G. K. Wong, J. A. Berenbeim, M. Hawkridge, E. Matthews and C. E. H. Dessent, Mapping the intrinsic absorption properties and photodegradation pathways of the protonated and deprotonated forms of the sunscreen oxybenzone †, Phys. Chem. Chem. Phys., 2019, 21, 14311.
22. J. A. Berenbeim, N. G. K. Wong, M. C. R. Cockett, G. Berden, J. Oomens, A. M. Rijs and C. E. H. Dessent, Sodium cationization can disrupt the intramolecular hydrogen bond that mediates the sunscreen activity of oxybenzone, Phys. Chem. Chem. Phys., 1952, 22, 19522.
23. S. R. Domingos and M. Schnell, Wet Sunscreens in the Gas Phase: Structures of Isolated and Microsolvated Oxybenzone, J. Phys. Chem. Lett., 2018, 9, 4963–4968.
24. T. N. V. V. Karsili, B. Marchetti, M. N. R. R. Ashfold and W. Domcke, Ab Initio Study of Potential Ultrafast Internal Conversion Routes in Oxybenzone, Caffeic Acid, and Ferulic Acid: Implications for Sunscreens, J. Phys. Chem. A, 2014, 118, 11999–12010.
25. L. Joseph, D. Sajan, K. Chaitanya, T. Suthan, N. P. Rajesh and J. Isac, Molecular structure, NBO analysis, electronic absorption and vibrational spectral analysis of 2-Hydroxy-4-Methoxybenzophenone: Reassignment of fundamental modes, Spectrochim. Acta, Part A, 2014, 120, 216–227.
26. B. Bin Xie, X. F. Tang, X. Y. Liu, X. P. Chang and G. Cui, Mechanistic photophysics and photochemistry of unnatural bases and sunscreen molecules: insights from electronic structure calculations, Phys. Chem. Chem. Phys., 2021, 23, 27124–27149.
27. C. X. Li, W. W. Guo, B. Bin Xie and G. Cui, Photodynamics of oxybenzone sunscreen: Nonadiabatic dynamics simulations, J. Chem. Phys., 2016, 145, 74308.
28. T. E. Gartmann, S. Hartweg, L. Ban, E. Chasovskikh, B. L. Yoder and R. Signorell, Electron scattering in large water clusters from photoelectron imaging with high harmonic radiation, Phys. Chem. Chem. Phys., 2018, 20, 16364–16371.
29. L. Ban, C. W. West, E. Chasovskikh, T. E. Gartmann, B. L. Yoder and R. Signorell, Below Band Gap Formation of Solvated Electrons in Neutral Water Clusters?, J. Phys. Chem. A, 2020, 124, 7959–7965.
30. T. E. Gartmann, L. Ban, B. L. Yoder, S. Hartweg, E. Chasovskikh and R. Signorell, Relaxation dynamics and genuine properties of the solvated electron in neutral water Clusters, J. Phys. Chem. Lett., 2019, 10, 4777–4782.
31. L. Ban, B. L. Yoder and R. Signorell, Size-Resolved Electron Solvation in Neutral Water Clusters, J. Phys. Chem. A, 2021, 125, 5326–5334.
32. R. Signorell, M. Goldmann, B. L. Yoder, A. Bodi, E. Chasovskikh, L. Lang and D. Luckhaus, Nanofocusing, shadowing, and electron mean free path in the photoemission from aerosol droplets, Chem. Phys. Lett., 2016, 658, 1–6.
33. K. R. Wilson, Z. Shengli, S. Jinian, E. Rühl, S. R. Leone, G. C. Schatz and M. Ahmed, Size-dependent angular distributions of low-energy photoelectrons emitted from NaCI nanoparticles, Nano Lett., 2007, 7, 2014–2019.
34. J. Shu, K. R. Wilson, M. Ahmed and S. R. Leone, Coupling a versatile aerosol apparatus to a synchrotron: Vacuum ultraviolet light scattering, photoelectron imaging, and fragment free mass spectrometry, Rev. Sci. Instrum., 2006, 77, 43106.
35. R. Signorell and B. Winter, Photoionization of the aqueous phase: clusters, droplets and liquid jets, Phys. Chem. Chem. Phys., 2022, 24, 13438–13460.
36. D. M. P. Holland, I. Powis, A. B. Trofimov, I. L. Bodzuk, D. Y. Soshnikov, A. W. Potts and L. Karlsson, A study of the valence shell electronic structure and photoionisation dynamics of ortho-dichlorobenzene, ortho-bromochlorobenzene and trichlorobenzene, Chem. Phys., 2015, 448, 61–75.
37. S. Arnold and N. Hessel, Photoemission from single electrodynamically levitated microparticles, Rev. Sci. Instrum., 1985, 56, 2066–2069.
38. K. R. Wilson, D. S. Peterka, M. Jimenez-Cruz, S. R. Leone and M. Ahmed, VUV photoelectron imaging of biological nanoparticles: Ionization energy determination of nanophase glycine and phenylalanine-glycine-glycine, Phys. Chem. Chem. Phys., 2006, 8, 1884–1890.
39. E. Antonsson, H. Bresch, R. Lewinski, B. Wassermann, T. Leisner, C. Graf, B. Langer and E. Rühl, Free nanoparticles studied by soft X-rays, Chem. Phys. Lett., 2013, 559, 1–11.
40. C. C. Su, Y. Yu, P. C. Chang, Y. W. Chen, I. Y. Chen, Y. Y. Lee and C. C. Wang, VUV photoelectron spectroscopy of cysteine aqueous aerosols: A microscopic view of its nucleophilicity at varying pH conditions, J. Phys. Chem. Lett., 2015, 6, 817–823.
41. O. Kostko, B. Xu, M. I. Jacobs and M. Ahmed, Soft X-ray spectroscopy of nanoparticles by velocity map imaging, J. Chem. Phys., 2017, 147, 13931.
42. S. Tigrine, N. Carrasco, D. K. Bozanic, G. A. Garcia and L. Nahon, FUV Photoionization of Titan Atmospheric Aerosols, Astrophys. J., 2018, 867, 164.
43. P. C. Chang, Y. Yu, Z. H. Wu, P. C. Lin, W. R. Chen, C. C. Su, M. S. Chen, Y. L. Li, T. P. Huang, Y. Y. Lee and C. C. Wang, Molecular Basis of the Antioxidant Capability of Glutathione Unraveled via Aerosol VUV Photoelectron Spectroscopy, J. Phys. Chem. B, 2016, 120, 10181–10191.
44. I. Fischer and S. T. Pratt, Perspective Photoelectron Spectroscopy in Molecular Physical Chemistry, Phys. Chem. Chem. Phys., 2013, 00, 1–3.
45. T. E. Gartmann, B. L. Yoder, E. Chasovskikh and R. Signorell, Lifetimes and energetics of the first electronically excited states of NaH₂O from time-resolved photoelectron imaging, Chem. Phys. Lett., 2017, 683, 515–520.
46. L. Ban, T. E. Gartmann, B. L. Yoder and R. Signorell, Low-Energy Electron Escape from Liquid Interfaces: Charge and Quantum Effects, Phys. Rev. Lett., 2020, 124, 013402.
47. U. Even, The Even-Lavie valve as a source for high intensity supersonic beam, EPJ Tech. Instrum., 2015, 2, 17.
48. F. Frassetto, C. Cacho, C. A. Froud, I. C. E. Turcu, P. Villoresi, W. A. Bryan, E. Springate and L. Poletto, Single-grating monochromator for extreme-ultraviolet ultrashort pulses, Opt. Express, 2011, 19, 19169.
49. F. Frassetto, P. Miotti and L. Poletto, Grating Configurations for the Spectral Selection of Coherent Ultrashort Pulses in the Extreme-Ultraviolet, Photonics, 2014, 1, 442–454.
50. A. T. J. B. Eppink and D. H. Parker, Velocity map imaging of ions and electrons using electrostatic lenses: Application in photoelectron and photofragment ion imaging of molecular oxygen, Rev. Sci. Instrum., 1997, 68, 3477–3484.
51. D. W. Chandler and P. L. Houston, Two-dimensional imaging of state-selected photodissociation products detected by multiphoton ionization, J. Chem. Phys., 1987, 87, 1445–1447.
52. G. A. Garcia, L. Nahon and I. Powis, Two-dimensional charged particle image inversion using a polar basis function expansion, Rev. Sci. Instrum., 2004, 75, 4989–4996.
53. D. P. Chong, O. V. Gritsenko and E. J. Baerends, Interpretation of the Kohn-Sham orbital energies as approximate vertical ionization potentials, J. Chem. Phys., 2002, 116, 1760–1772.
54. V. Lemierre, A. Chrostowska, A. Dargelos and H. Chermette, Calculation of ionization potentials of small molecules: A comparative study of different methods, J. Phys. Chem. A, 2005, 109, 8348–8355.
55. D. A. Horke and J. R. R. Verlet, Photoelectron spectroscopy of the model GFP chromophore anion, Phys. Chem. Chem. Phys., 2012, 14, 8511–8515.
56. O. Tau, A. Henley, A. N. Boichenko, N. N. Kleshchina, R. Riley, B. Wang, D. Winning, R. Lewin, I. P. Parkin, J. M. Ward, H. C. Hailes, A. V. Bochenkova and H. H. Fielding, Liquid-microjet photoelectron spectroscopy of the green fluorescent protein chromophore, Nat. Commun., 2022, 13, 1–7.
57. A. D. Laurent and D. Jacquemin, TD-DFT benchmarks: A review, Int. J. Quantum Chem., 2013, 113, 2019–2039.
58. Z. Gouid, A. Röder, B. K. Cunha De Miranda, M. A. Gaveau, M. Briant, B. Soep, J. M. Mestdagh, M. Hochlaf and L. Poisson, Energetics and ionization dynamics of two diarylketone molecules: Benzophenone and fluorenone, Phys. Chem. Chem. Phys., 2019, 21, 14453–14464.
59. N. C. Cole-Filipiak, M. Shapero, B. Negru and D. M. Neumark, Revisiting the photodissociation dynamics of the phenyl radical, J. Chem. Phys., 2014, 141(10), 104307.
60. T. D. Scarborough, J. Strohaber, D. B. Foote, C. J. McAcy and C. J. G. J. Uiterwaal, Ultrafast REMPI in benzene and the monohalobenzenes without the focal volume effect, Phys. Chem. Chem. Phys., 2011, 13, 13783–13790.
61. J. Strohaber, T. Mohamed, N. Hart, F. Zhu, R. Nava, F. Pham, A. A. Kolomenskii, H. Schroeder, G. G. Paulus and H. A. Schuessler, Intensity-resolved ionization yields of aniline with femtosecond laser pulses, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 063414.
62. L. Klasinc, I. Novak, A. Sabljic and S. P. McGlynn, Photoelectron spectroscopy of biologically active molecules. XVI. Benzophenone derivatives, Int. J. Quantum Chem., 1988, 34, 259–266.
63. A. S. Chatterley, A. S. Johns, V. G. Stavros and J. R. R. Verlet, Base-specific ionization of deprotonated nucleotides by resonance enhanced two-photon detachment, J. Phys. Chem. A, 2013, 117, 5299–5305.
64. X. Yang, X. Bin Wang, E. R. Vorpagel and L. S. Wang, Direct experimental observation of the low ionization potentials of guanine in free oligonucleotides by using photoelectron spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17588–17592.
65. M. V. Ivanov, D. Wang, D. Zhang, R. Rathore and S. A. Reid, Vertical vs. adiabatic ionization energies in solution and gas-phase: Probing ionization-induced reorganization in conformationally-mobile bichromophoric actuators using photoelectron spectroscopy, electrochemistry and theory, Phys. Chem. Chem. Phys., 2018, 20, 25615–25622.
66. A. Roy, R. Seidel, G. Kumar and S. E. Bradforth, Exploring Redox Properties of Aromatic Amino Acids in Water: Contrasting Single Photon vs Resonant Multiphoton Ionization in Aqueous Solutions, J. Phys. Chem. B, 2018, 122, 3723–3733.
67. E. J. McAlduff and D. L. Bunbury, Photoelectron spectra of some aromatic mono- and di-ketones, J. Electron Spectrosc. Relat. Phenom., 1979, 17, 81–89.
68. Y. Suzuki and T. Suzuki, Photoelectron Angular Distribution in Valence Shell Ionization of Heteroaromatic Molecules Studied by the Continuum Multiple Scattering Xα Method, J. Phys. Chem. A, 2008, 112, 402–411.
69. D. M. P. Holland, L. Karlsson and W. Von Niessen, Identification of the outer valence shell π-photoelectron bands in furan, pyrrole and thiophene, J. Electron Spectrosc. Relat. Phenom., 2001, 113, 221–239.
70. P. R. Keller, J. W. Taylor, T. A. Carlson and F. A. Grimm, A systematic angle-resolved photoelectron study of π orbitals in unsaturated organic molecules, J. Electron Spectrosc. Relat. Phenom., 1984, 33, 333–345.
71. I. Powis, D. M. P. Holland, E. Antonsson, M. Patanen, C. Nicolas, C. Miron, M. Schneider, D. Y. Soshnikov, A. Dreuw and A. B. Trofimov, The influence of the bromine atom Cooper minimum on the photoelectron angular distributions and branching ratios of the four outermost bands of bromobenzene, J. Chem. Phys., 2015, 143, 144304.
72. A. W. Potts, D. M. P. Holland, A. B. Trofimov, J. Schirmer, L. Karlsson and K. Siegbahn, An experimental and theoretical study of the valence shell photoelectron spectra of purine and pyrimidine molecules, J. Phys. B: At., Mol. Opt. Phys., 2003, 36, 3129–3141.
73. P. R. Keller, J. W. Taylor, F. A. Grimm and T. A. Carlson, Angle-resolved photoelectron spectroscopy of formaldehyde and methanol, Chem. Phys., 1984, 90, 147–153.
74. National Institute of Standards and Technology, https://www.nist.gov/, (accessed 9 May 2016).

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06224d

---