ANI neural network potentials for small molecule pK_a prediction

Abstract

The pK_a value of a molecule is of interest to chemists across a broad spectrum of fields including pharmacology, environmental chemistry and theoretical chemistry. Determination of pK_a values can be accomplished through several experimental methods such as NMR techniques and titration together with computational techniques such as DFT calculations. However, all of these methods remain time consuming and computationally expensive. In this work we develop a method for the rapid calculation of pK_a values of small molecules which utilises a combination of neural network potentials, low energy conformer searches and thermodynamic cycles. We show that neural network potentials trained on different phase and charge states can be employed in tandem to predict the full thermodynamic energy cycle of molecules. Focusing here on imidazolium derived carbene species, the method utilised can easily be extended to other functional groups of interest such as amines with further training.

---

1 Introduction

Acids ionise in solution by the association or dissociation of a proton. The acid dissociation constant, K_a, describes the strength of an acid in solution and is defined by the equilibrium between the dissociated, A⁺ and H⁺, and associated state, HA, of the acid. Consequently, the pK_a can be derived as the negative log of the dissociation constant, eqn (1), which can subsequently be related to pH through the Henderson–Hasselbalch equation for dilute acids in aqueous solutions, eqn (2).

Many factors are understood to affect the pK_a value of a molecule. These factors include solvent present,¹ the temperature of the system,² and the local chemistry present³ within a molecule. Crucially, the understanding of pK_a values is important for several branches of chemistry including drug discovery,⁴ coordination chemistry, and environmental chemistry.

Often determined experimentally through techniques such as titration,^5,6 spectrometry⁶ and NMR,⁷ several methods have been developed regarding the calculation of pK_a theoretically.

Among these include methods such as machine learning (ML), density functional theory (DFT) and constant pH molecular dynamics. In 2004, Yates et al.¹ demonstrated the calculation of pK_a values for a set of imidazolium derived carbene molecules using a mixture of ab initio and DFT methods in conjunction with the Conductor-like Polarisable Continuum Model (CPCM) for modelling of the aqueous phase. Yates studied a series of imidadzole carbenes in dimethyl sulfoxide and acetonitrile to good accuracy versus available data from experimental pK_a values. The study goes on to highlight the importance of conformation within pK_a calculations by examining the energies of conformers of the studied carbenes extensively, utilising only the conformers with the lowest energy in each case. The method used by Yates echoes earlier work by Liptak and Shields⁸ surrounding the use of a thermodynamic cycle for calculation of the relevant thermodynamic properties. This has been visualised in Scheme 1 which shows the deprotonation of a molecule, or in the context of this paper, an imidazolium salt, HA⁺, resulting in the products, A, a carbene, and H⁺, a proton.

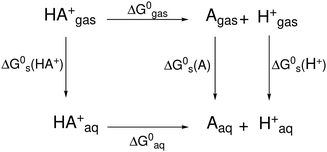Scheme 1 Thermodynamic cycle for the deprotonation of an acid (A). These thermodynamic cycles can be used to calculate pK_a values more accurately than by direct calculation of ΔG⁰_aq.

Where ΔG⁰_gas and ΔG⁰_aq are the free energies of deprotonation of the gas and aqueous phase, respectively, and the solvation free energy is represented by ΔG⁰_s(X) where X = HA⁺, A and H. The pK_a can then be calculated for a molecule by application of eqn (3)–(5), requiring the free energy of deprotonation for the species in the gaseous and aqueous phase alongside the solvation free energy for each species.

ΔG⁰_aq = −2.303RT log K_a (3)

pK_a = ΔG⁰_aq/2.303RT (4)

where,

ΔG⁰_aq = G⁰(A_aq) + G⁰(H⁺_aq) − G⁰(HA⁺_aq) = G⁰(A_gas) + ΔG⁰_s(A) + G⁰(H⁺_gas) + ΔG⁰_s(H⁺) − G⁰(HA⁺_gas) − ΔG⁰_s(HA⁺) (5)

Liptak and Shields also drew attention to the demanding nature of theoretical pK_a calculations as an energy difference of just 1.36 kcal mol⁻¹ is equal to a change in pK_a of 1 unit.⁸ This naturally requires energies and structures to be calculated with high degree of accuracy. If such an approach as that shown in eqn (5) is used then there are four sources of potential error even when literature values regarding the proton are employed.

Theoretical approaches to calculating pK_a have continued to be explored since the work of Yates with studies determining the pK_a of molecules such as phenols⁹ and thiols.¹⁰ Studies have also been undertaken to explore the accuracy of methods in the calculation of pK_a, with Dutra et al.¹¹ reporting that results via DFT methods are highly dependent on the basis set employed and the number of explicit water molecules in the system. One study by Ho and Coote¹² set out to determine if there could be a universal method to be applied to pK_a calculations. The study examined four different calculation methods and several different solvent models, concluding that using a proton exchange scheme, wherein a reference acid is employed to conserve charge on both sides of a reaction, gave the most promising results. It was found that for a universal approach, the exchange scheme was much less sensitive to a change in reference than the direct continuum model approaches which are more sensitive to the species upon which the model was parameterised with. Thus methods for calculation of pK_a tend to fall within the realms of absolute calculations such as those that employ DFT to calculate thermodynamic cycles like those described above or within the realms of relative methods such as the proton exchange scheme approach.

There have been attempts at pK_a prediction using methods other than thermodynamic cycles, one of which includes predicting pK_a values by drawing linear correlations between the vibrational frequencies of H–X bonds in hydrogen halides before extrapolating the insights to carboxylic acids.¹³ The method proved to predict the pK_a of a set of aliphatic carboxylic acids to within 0.3 pK_a units of their experimental values.

As mentioned above, approaches to pK_a calculations like those described above incur many associated errors which need to be minimised in order to achieve any degree of accuracy versus experimental techniques. Amongst these is the value of the solvation free energy of a proton, ΔG⁰_s(H⁺), a value which is much debated in literature with reported values as high as −254.30 kcal mol^−1 14 and as low as −265.77 kcal mol⁻¹.¹⁵ Indeed, the uncertainty surrounding the value of ΔG⁰_s(H⁺) has led to the popularity of calculating pK_a in a relative manner as mentioned above.

Machine learning (ML) has also been employed in the determination of pK_a values to good effect. Williams et al. employed ML algorithms including support vector machines, deep neural networks (DNN) and extreme gradient boosting (XGBoost) on a dataset of over 7900 chemicals.¹⁶ The best models were capable of producing a coefficient of determination (R² value) as high as 0.80 and root mean square error (RMSE) values as low as 1.5 pK_a units. A 2020 paper by Baltruschat and Czodrowski¹⁷ found that a five-fold cross validation random forest model performed best, producing an R² of 0.82 and RMSE of 1.03 when trained on a compilation of monoprotic compounds assembled from DataWarrior¹⁸ and the ChEMBL databases.¹⁹ Roszak et al.²⁰ developed a graph neural network for the prediction of pK_a values of C–H groups in non-aqueous solvents, with results showing a mean absolute error (MAE) of 2.1 pK_a units. The authors reported that the use of descriptors for the chemical properties of the chemical environment alongside topological descriptors led to the low errors in the method when validated on synthetic problems.

ML methods have continued to expand in recent years with efforts at pK_a prediction including areas such as proteins²¹ and drug-like molecules.²² Another area which is developing simultaneously alongside ML models is that of data availability. Datasets of increasing size and quality are becoming available to help drive the training of ML models without which the continued improvements of such models to perform well would suffer. Within the realm of pK_a prediction, datasets such as those from DataWarrior¹⁸ and ChEMBL,¹⁹ allow for access to experimental pK_a data, albeit via premium access. Datasets containing theoretical pK_a values such as PHMD549²³ are also available.

Indeed, there have been papers in recent years which make use of published datasets for pK_a prediction. Mayr et al. published a graph NN based method capable of enumerating protonatable sites and predicting their pK_a based on training comprised of experimental pK_a values and molecules from the ChEMBL dataset. Providing code in both commercial and free-to-use format, the published models show a RMSE of less than 1 pK_a unit.²⁴

One of the key requirements to accurate calculation of pK_a values is accurate representation of the chemical environment of the molecule/protonatable site of interest. One such way to capture the information computationally is through the use of atomic environment vectors (AEVs), versions of modified symmetry functions that are suited to provide a description of molecular environments on an atomic basis. One of the benefits of describing molecules in such a way is that AEVs are specifically concerned with individual atoms and their local environments rather than molecules as a whole. This allows exact chemical environments to be encoded within them.

Neural network potentials (NNPs), such as ANI,²⁵ SchNet^26,27 MACE^28,29 and AIMNet³⁰ are able to map chemical information like that within AEVs to the energy of molecules. NNPs use reference data, often from quantum mechanical calculations such as DFT, to build a representation of the potential energy surface to be learning by ML techniques like DNNs. The ANAKIN-ME (ANI) suite of models were first released in 2017. Developed by Smith et al., ANI-1²⁵ is an NNP capable of <1.0 kcal mol⁻¹ RMSE values versus DFT calculations at a fraction of the cost. Initially limited to only molecules containing H, C, N and O, the ANI models have since expanded through models ANI-1x,³¹ ANI-1ccx³² and ANI-2x³³ to include H, C, N, O, F, S and Cl alongside also introducing active learning and coupled cluster training data.³² In its latest form, ANI-2x³³ is capable of performing 10⁶ times faster than DFT and produces sub-chemical accuracy on test datasets. ANI-2x³³ also included improved parameterisation for bulk water, molecular force training (analytical derivatives of the molecular energies) and sampling of torsion angles and chemical space all aimed at improving the accuracy of the model. Much of the success of the ANI suite can be attributed to the development of AEVs. Based on Behler–Parrinello symmetry functions,³⁴ AEVs provide additional terms in order to capture more distinct molecular features allowing the NNP to be capable of better distinguishing between atom types, functional groups, and rings amongst other molecular features. Within the ANI models, the AEVs of a molecule are split up by atom type and fed through separate DNNs to yield an atomic energy which is consequently summed to produce the energy of the conformer (additional information regarding the ANI architecture can be found in the ESI†). ANI-2x³³ has also been utilised in the development of pK_a-ANI,³⁵ a ML tool that builds upon the existing ANI-2x architecture to predict pK_a values for all five titrable amino acid residues within input proteins. pK_a-ANI uses the AEVs for each atom type as well as layers from the atomic neural networks as descriptors within the model. The model, based on deep representation learning, performed better than PROPKA,³⁶ a widely used semi-empirical modelling tool, with mean absolute error (MAE) values below 0.5 pK_a units for the titrable amino acid residues.

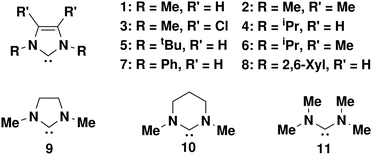
In this study, we evaluate a weighted Boltzmann approach to pK_a calculation. Utilising an ensemble of conformers we are better able to consider the molecules under study by including non-equilibrium structures, which is more similar to ensembles of molecules being measured by experimental approaches. A subset of previously investigated carbenes,¹Fig. 1, were studied. Most of the carbenes contain an imidazole core. Imidazole-derived carbenes are well known as versatile ligands due to their highly tuneable electronic nature and as such are of great interest in areas such as catalysis.^37,38 The previous results by Yates et al.,¹ have been studied at multiple levels of theory and provide useful reference points for evaluation of the methods developed within this work. We develop and apply a set of datasets that presents evidence that ANI architecture NNPs can be trained on species in charged and/or aqueous phase so long as the dataset each model is trained on does not overlap in respect to charge/phase and provides a method by which this method of pK_a prediction could be extended to any class of small molecules given the appropriate training data.

Fig. 1 Subset of carbenes studied in this work for pK_a prediction.

2 Results and discussion

Calculation of pK_a values with DFT at the ωB97X-D4/Def2-SVP level of theory, DFT global minima (GM) (Table 1), gave good comparison to Yates literature values, Yates GM (Table 1), when calculated for carbenes 1–11, Fig. 1. There are of course expected differences between the values owed to a change in level of theory and software package. The Yates values were reported via gas phase calculation optimisation and frequency calculations at B3LYP, CBSB7 level of theory. The solvent phase calculations were completed using CPCM solvent at B3LYP and HF with 6-31+G(d) and 6-31+G(d,p) levels of theory. The carbenes studied here also have the potential to minimise at different conformers. This is noted by Yates et al. in their work and an effort was made in this work to optimise single conformation (GM) reference DFT calculations to the same conformational minima. This is particularly prevalent for structures 7 and 8 where the aromatic R-groups can rotate relative to the imidazole centre of the molecule.

Table 1 Value of carbene pK_a by method

Carbene	Yates GM^a	DFT GM^b	DFT ensemble^c	ML ensemble^d
a pKa values reported by Yates et al.^1 b pKa values calculated from the Yates optimised structure, optimised at ωB97X-D4/Def2-SVP level of theory and calculated using the direct aqueous method as detailed in Section 3.7. c pKa values calculated using the DFT optimised (ωB97X-D4/Def2-SVP) geometries of generated crest conformers as detailed in Sections 3.6 and 3.7. d pKa values as predicted by ML models, as detailed in Sections 3.6 and 3.7.
1	27.40 ± 0.4	28.01	28.12	29.30
2	29.50 ± 0.3	29.94	29.98	31.16
3	23.40 ± 0.2	23.13	23.56	22.97
4	28.20 ± 0.3	28.12	28.03	27.18
5	28.30 ± 0.1	29.33	29.36	28.60
6	30.40 ± 0.3	29.97	30.90	29.13
7	22.00 ± 0.1	23.26	23.08	28.44
8	22.60 ± 0.1	24.32	25.65	26.48
9	28.50 ± 0.4	28.69	27.93	25.54
10	33.70 ± 0.3	32.40	32.75	31.63
11	34.00 ± 0.3	34.68	34.29	35.11

---

Initial attempts at pK_a calculation through direct interface with ANI-2x were unsuccessful. Optimisation from DFT output geometries (Yates et al. ESI¹) with ANI as well as optimisation of carbene molecules explicitly solvated with water, Fig. 2, followed by extraction of the relevant carbene AEVs all resulted in large errors. With explicit solvation, the conformational changes to the carbene induced by the water molecules were expected to establish the aqueous structure, facilitating AEV extraction and subsequent summation of atomic energies in order to determine the aqueous energy of the molecule. Despite additional attempts to predict the Gibbs free energy using ANI-2x and ASE's vibrations module, these efforts proved unsuccessful as well. It was thought that the training of ANI on potential energies and not on Gibbs energies could contribute to the large errors when calculating pK_a. The Gibbs energy is essential when calculating the pK_a through the full thermodynamic cycle. As such it was deemed that ANI-2x was unsuitable for the nature of these calculations.

Fig. 2 Carbene molecule with explicitly solvated water. The AEV's of the molecule being investigated capture the surrounding water molecules without including the atomic energies of the water.

Upon close examination of the ANI-2x dataset, it was found that while it does contain carbene molecules, they comprise a very small amount (247 structures out of 9 651 712 total, 0.0026%) of the total dataset. Further, the handling of charged states and solvent phase calculations are unavailable within the ANI family of models to date. As such, the development of extensive carbene datasets, both protonated and deprotonated as well as in the gas and aqueous phases have been undertaken in this work, Section 3.4.

There are two routes to calculate the value of ΔG⁰_aq as shown in eqn (5). The first involves the full thermodynamic cycle (the full cycle approach), Fig. 1, which includes calculating gas and aqueous phase energies in order to give the solvation energies. The second involves calculating the aqueous phase directly (the direct aqueous approach), which avoids calculating the gas phase energies. Both routes follow the workflow laid out in Section 3.7, utilising a Boltzmann distribution and weighted average. The direct aqueous approach, while being slightly less accurate, results in a reduction of half the processing time which is the main objective in this study. Indeed, a difference in RMSE of only 0.05 pK_a units (1.94 on the full cycle vs. 1.99 direct aqueous) separated using the full cycle versus the direct calculation. Due to the extended time required to compute the full cycle, even if it provides a slight increase in prediction accuracy, results moving forward will be taken from aqueous phase prediction only.

Development of DNN models based on the ANI architecture and calculation of pK_a values when carried out on DFT-optimised structures afforded very good results compared to Yates et al.¹ Direct calculation via the aqueous phase (GM approach) afforded a RMSE and MAE of 2.03 and 1.19 pK_a units respectively. This highlights that our models are capable of calculating pK_a values with good accuracy for the studied carbene species. It further indicates that the models have a good grasp of the energetics of carbene species at minima and can reliably predict the pK_a of such species. However, using the pre-optimised structures from a DFT calculation doesn't provide any information on whether the models can arrive at the minima when provided with higher energy structures, i.e. those drawn by hand in Avogadro.³⁹

As such, attempts were then made to calculate pK_a values from non-ground state structures. The structures were drawn in Avogadro³⁹ and then optimised by the universal force field⁴⁰ to give a reasonable starting structure for DFT calculations. These structures were then directly used to calculate the pK_a of the carbene. As mentioned in Section 1, calculating pK_a values is demanding owing to the sensitive nature of the energies involved in their calculation. As such, the structures given as output from Avogadro were not optimised fully to their minima and the trained models struggled to accurately predict pK_a values. This led to large errors with an RMSE value of 14.75 and an MAE value of 12.69.

As a result the workflow detailed in Sections 3.6 and 3.7 were developed. First, calculations were completed on the optimised geometries from the ESI of Yates et al.¹ at the ωB97X-D4/Def2-SVP level of theory and the pK_a calculated via the direct aqueous approach, DFT GM (Table 1). Secondly, conformers for each carbene in both gaseous and aqueous states were generated with Crest (Section 3.6) as detailed below and the Gibbs energy calculated with DFT for each structure. These energies were then used in calculating Boltzmann populations and thus pK_a values as detailed in Section 3.7, DFT ensemble (Table 1). Lastly, Crest generated conformers were optimised with the models trained herein and pK_a values calculated similarly through Boltzmann populations, ML ensemble (Table 1). More information about the ensemble including the number of conformers generated for each method and analysis of conformer energy and structure can be found in the ESI† (pages S3–S8).

Isayev and Gockan took a different approach to using the ANI DNN potential for pK_a predictions by developing the pK_a-ANI application.³⁵ The pK_a-ANI model provides excellent and efficient computation of pK_a values for titrable residues in large proteins due to the calculation of pK_a directly from the AEVs without explicit energy calculation. Further, the pK_a-ANI model is comprised of five independent models, one for each titrable amino acid residue (His, Asp, Glu, Lys, Tyr). This provides an efficient way to calculate the pK_a eliminating compounding errors associated with calculating via thermodynamic cycles. However, this results in the model being limited to protein side chains and their individual pK_a ranges. This is in contrast to the model presented here which is more generalisable (though restricted to smaller molecules) due to its use of thermodynamic cycles and global optimisation schemes. As such, in contrast to the pK_a-ANI paper, which directly utilises AEVs as features for representation learning, the method employed here only uses AEVs as neural network inputs to predict atomic energies. AEVs are not incorporated directly into the pK_a calculation within this workflow. The scope of this model produces higher error measurements by virtue of being able to predict a larger range of pK_a values (22–34 pK_a units).

pK_a-ANI has a range of around ±2 pK_a units for each independent residue model. This results in a low RMSE range of between 0.49 and 0.88 units due to the smaller prediction range for each residue. This is reflected in the results of the reported null model which showed that using the mean value as the prediction results in an error of less than 1.5 pK_a units. Due to the larger range of pK_a values evaluated by our model we report a larger RMSE value of 1.99 pK_a units. Although individual predictions generally align well with DFT Ensemble values, Fig. 3, for each carbene, the normalised RMSE (NRMSE) becomes pertinent, calculated by dividing the RMSE by the prediction range. This yields a NRMSE of 0.166 for our model compared to 0.180 for pK_a-ANI, indicating comparable performance despite differing prediction ranges.

Fig. 3 Predicted pK_a results of ML Ensemble method vs. reference methods of pK_a calculation. We score our model primarily against the DFT ensemble as the DNN was trained on data at the same level of theory as the DFT and used an ensemble of conformers to make its predictions.

When exploring the conformations of carbenes, Yates et al. found that the minima for carbene 8 was found when the xylene R-groups were orthogonal to the core imidazole ring.¹ This was due to the methyl groups present at the 2 and 6 positions on the ring of the xylene. Such methyl groups are not present in carbene 7 which gives more rotational freedom to the structure around the C–N bonds connecting the R-groups to the central imidazole. Shown below in Fig. 4(b), the overlap of a conformer of carbenes 1 and 7 highlights the difference between the optimised structures by DFT (blue atoms) and the structure as optimised by the trained models (red atoms). It can be seen that the conformer of carbene 7, as optimised by the models, struggles to match the DFT geometry. This potentially is the cause of the larger error seen in prediction of carbene 7. Conversely, the structure of carbene 8 is modelled well by both methods and this is reflected in the improved prediction of pK_a. This could be due to the aforementioned forced conformation of xylene R-groups as orthogonal to the core imidazolium.

Fig. 4 (a) Carbene 1 showing a very close optimisation with an RMSD of 0.08 Å vs. the DFT optimised structure. (b) Carbene 7 showing an overlap of optimised DFT conformer (blue) and conformer optimised with ANI charged aqueous model (red) with an RMSD of 0.81 Å.

Previous studies have reported that the ANI architecture cannot handle charged molecules, however we find that this is only true when trying to mix different charge states into the same training model. This is due to the lack of knowledge of the number of electrons in a system which results in an inability to differentiate between the same conformers with different charge states.³³ In this study, we have found that by training separate neural networks based on charge and gas/aqueous phase that the ANI architecture is able to accurately predict energies for charged and/or aqueous phase molecules as long as that was exclusively the type of data it was trained on.

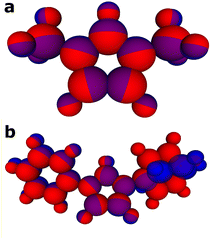
To further examine the internal representation of molecules in the charged vs. neutral models we comparatively analyse the protonated carbenes in both models (neutral and charged). As ANI potentials work by using Atomic Environment Vectors (AEVs) as inputs for neural networks which output the atomic contributions, or absolute energies for each atom, we can thus determine the energy associated to each atom in a molecule by the trained models. This allows us to scrutinise the disparities in energy allocations across atomic components between the neutral and charge models. It should be noted that atomic contributions to the energy are directly outputs of the neural networks within the ML models and do not stem from DFT. It is difficult to infer any understanding of neural network intermediate states between input and final output, however in ANI potentials, the output of a neural network is the atomic energy associated with specific atoms which are in turn summed to give the total molecular energy. We note that the difference between predicted Gibbs energy for a molecule between charged and uncharged models (G^Z=+1 − G^Z=0) aligns with the expected charge distribution difference. It was found that for protonated carbenes the charged model assigns a greater contribution to the total molecular energy from the ylidine carbon and nitrogen atoms. Moreover, the discrepancy in energetic contributions depends on the N-substituents (Fig. 5). This aligns with the expectation that charge delocalisation increases with the presence of more electronegative N-substituents, as exemplified by the comparison between xylene and methyl substituents (Fig. 5(a)vs.Fig. 5(b)). Within molecules, where greater electron density is present it follows that the electronic energy will be lower due to minimised electrostatic and coulombic repulsion. It is important to note that although there is an approximate correlation between the models energy contribution difference and the difference in charge distribution, it cannot be stated that the ANI potential has explicitly learned how to infer charge distribution.

Fig. 5 The difference in atomic contributions to the molecular energy derived from the neutral gaseous ANI and charged gaseous ANI models indicates varying degrees of charge delocalisation. These differences are represented as a shift from orange to blue. In the case of carbene 11 (a), the variation is confined to the protonated ylidine carbon and to a lesser extent the bonded nitrogens, representing localised charge distribution on the ylidine carbon. Conversely, in carbene 8 (b), the variation extends further, with the biggest difference being the nitrogen atoms and to a lesser extent encompassing the N-xylene R-groups, indicating an increase of charge delocalisation.

Despite the neural network not being informed of electrons or atomic charge whilst training, the models implicitly capture where the difference in the molecule is located (Fig. 5). This is important as it highlights that, through structure and energies alone, ANI models can infer other chemical properties within its hidden representation. This accounts for the ability of the separate ANI models developed herein to accurately predict pK_a values, as charge plays a significant part in the free energy associated with the direct calculation.

3 Methodology

3.1 Level of theory and thermodynamic parameters

DFT calculations were carried out in ORCA V5.0.4⁴¹ at the ωB97X⁴²/Def2-SVP⁴³ level of theory. Additionally, Grimme's D4 dispersion correction⁴⁴ was employed alongside RIJCOSX algorithm⁴⁵ and the Def2/J auxiliary basis set.⁴⁶ The integration grid was set to DefGrid2 whilst SCF convergence tolerance was set to TightSCF. Orca's DFT module was utilised for geometry optimisations, vibrational analysis, and single point calculations. Implicit water solvation was modelled by the conductor-like polarizable continuum model (CPCM).⁴⁷

In this work, we use benchmark results from Yates et al.¹ As such, the value of the proton in the gas phase (G_gas(H⁺)) has been taken as −4.39 kcal mol⁻¹, a value derived from the Sackur–Tetrode equation but has accounted for a state change into moles per litre from atmospheres. We acknowledge however, that the value of free energy of solvation of the hydrogen atom (ΔG⁰_s(H⁺)) can contribute as a source of error due to the range in reported values differing significantly.^14,15 As the value of the free energy of solvation of the proton in this work we adopt a value of −261.85 kcal mol⁻¹ in accordance with the value used by Yates et al.¹ Another source of error in the determination of ΔG⁰_s(H⁺) is the choice of quantum mechanical method. Although we are not determining the value of the solvation energy of the proton in this work we do utilise a range-separated hybrid functional with additional dispersion corrections. It has been noted that such functionals are suitable for application to such calculations.⁴⁸

3.2 Calculation with the ANI-2x potential

Calculation of pK_a values with the ANI-2x³³ potential was carried out in Python via the PyTorch framework.⁴⁹ The ANI-2x model and parameters were obtained through the torchani module.⁵⁰ Through interface with the atomic simulation environment (ASE)⁵¹ molecules were optimised with the LBFGS⁵² optimisation algorithm to an maximum force of 0.01. In order to calculate the pK_a value, four values were needed. These were the protonated and deprotonated carbene molecules in both the gaseous and aqueous phase.

Carbene geometries were generated in Avogadro.³⁹ Gas phase energies were then obtained by optimising with the ANI-2x potential and retrieving the molecular energy. In order to gain access to solvation phase geometries, the isolated carbene molecules were solvated in GROMACS⁵³ with single point charge water within the General Amber Force Field.⁵⁴ Topology files were generated with the ACPYPE web server.^55,56 Boxes of size 3 × 3 × 3 nm with the carbene centred and surrounded with water molecules were then written to XYZ files. The XYZ files were then used as the input for ASE to optimise with the ANI-2x potential. The AEVs corresponding to the water molecules were then extracted and the atomic energies for each of the atoms present in the carbene summed to give the solvation phase energy of the protonated and deprotonated carbene forms. Explicit solvent is utilised only here, in conjunction with the pre-trained ANI-2x model in order to attempt to access the solvation phase structure and energy. Explicit solvent is not used again within this paper.

3.3 Calculation of reference pK_a values

ORCA calculations were carried out as described in Section 3.1, upon reference carbene structures. The structures, Fig. 1, were selected to allow comparison between published results by Yates et al.,¹ DFT and the developed models. The value of G⁰_aq can be directly calculated from aqueous phase energies, as shown in eqn (5), negating potential error from two additional gas phase calculations (G⁰(A_gas) and G⁰(HA⁺_gas)).

3.4 Development of datasets

Although the original paper by Yates et al.¹ calculated the value of 12 carbenes, in this paper, only 11 were studied as we have not extended our models to sulphur due to the large computational effort required to do so. As such our models cover elements H, C, N, O and Cl.

As mentioned in Section 3.2, there are four energies required for calculation of pK_a, protonated and deprotonated carbene energies in the gaseous and aqueous phase. As such, four different datasets were developed for training of subsequent models. For each distinct molecule there were two optimisation and frequency calculations completed, one in the gas phase and one with implicit CPCM water solvation. Once collated, the coordinates, energies and species of each job were stored in HDF5 format through the H5py python module.⁵⁷

It is worth noting that as aqueous models were trained on DFT data calculated in the aqueous phase (with implicit CPCM solvation), that when trained, the aqueous models will predict the aqueous structure and energy. The opposite is true for gas state models. This means that there is no solvent present, either implicit or explicit, when predicting energies for pK_a calculation with the developed models as it is embedded within the developed models.

Structures under consideration for calculation were limited to contain only H, C, N, O and Cl atoms. This gave a great deal of flexibility in searching for structures to add to datasets whilst also limiting to structures that would have a sizeable impact on what each model could learn. With ANI architecture models scaling in cost in relation to the number of individual atomic networks that have to be trained this also ensured reasonably quick training of each model.

Initial calculations for deprotonated models involved recalculation of the ANI-1 dataset⁵⁸ at the level of theory indicated in Section 3.1. Further, the calculated geometries were subsequently protonated through RDKit⁵⁹ and then calculated as before. These calculations, in both gaseous and aqueous phases formed the initial data space. Next, molecules from the QMSpin dataset⁶⁰ were similarly calculated in the singlet state and in both gas and aqueous phases, both deprotonated and protonated on the -ylidene carbon. Within structures from the QMSpin dataset, any fluorine atoms were replaced by chlorine atoms via RDKit.

Further calculations were completed in order to fine-tune the dataset to be sensitive to energy changes arising from any changes in bond angle and length. To do so, a molecule was scanned to find all connections which returned all bonds, angles and dihedral angles. Each connection was then adjusted over a range and stationary frequency calculations were completed to obtain the Gibbs energy of the structure. For angles and dihedrals, the connection was altered over a range of ±20 degrees. For bonds, alterations were made between a minimum and maximum distance. Maximum distances were calculated using van der Waals radii as reported by Alvarez.⁶¹ The radii of both atoms in the bond were summed and then divided by two to obtain the maximum distance the bond should be at. Subsequently the minimum distance was taken as the maximum distance divided by 1.75. For example, for a C–H bond, maximum distance would be the radius of a C atom (1.77 Å) summed with the radius of the H atom (1.2 Å) divided by two, 1.485 Å. The minimum distance would then be 1.485/1.75, or 0.845 Å.

The collected data were also screened to ensure that none of the validation data (Structures 1–11, Fig. 1) appeared within the training and testing datasets. This was achieved by removing all structures that contained the same amount and type of atoms and were within a root mean squared distance (RMSD) of 2.0 Å from any of the validation structures. Unreasonable structures were also removed based on features such as unbound hydrogen atoms present within a structure.

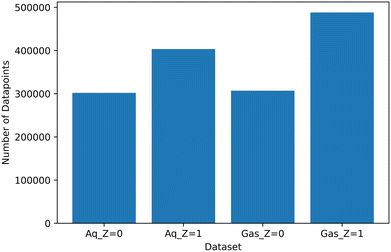
Following data collation, the final dataset sizes can be seen in Fig. 6 and is expanded upon in the ESI† (Table S3). As a result of the fine tuning calculations, the charged datasets have a higher number of data points due to the increased number of calculations associated with fine-tuning the additional proton present in molecules.

Fig. 6 Bar chart depicting the number of distinct data points within each developed dataset.

3.5 Development of auxiliary neural network potential models

The way in which the newly developed models were trained does not differ significantly from the parameters used to train the ANI-2x model. A neural network is defined for each atomic AEV type and default settings were utilised for the AEV parameters. When utilising the ANI-2x model through ASE,⁵¹ the generated outputs are the result of a combination of models rather than just one. In line with developers recommendations,⁵⁰ for each individual model-subset we have trained six models that differ only in batch size with batches of size 256, 512, 1024, 2048, 4096, and 8192. Batch sizes were scaled as powers of 2 in order to generate a wide array of trained models. Training of the models was carried out by applying the PyTorch⁴⁹ and TorchANI⁵⁰ Python modules.

Models were trained with a decay learning rate on plateau with an MSE loss function until the learning rate reached 1 × 10⁻⁵, then training switched to an MAE loss function until the loss plateaued again. This was done to generate a model where the errors were concordant with each other. As mentioned previously, pK_a calculations cancel out errors if protonated and deprotonated states have the same sign, i.e. are both positive, but compound the error in pK_a value if the errors have different signs. The introduction of the second loss training function works to actively produce errors of the same direction, i.e. both positive.

3.6 Generation, optimisation and filtering of conformers

The workflow for conformer generation and pK_a calculation can be seen in Scheme 2, below. Using Avogadro,³⁹ carbene structures were drawn and minimised using the Universal Force Field (UFF).⁴⁰ The structures were then saved as an XYZ file and used as the input to CREST⁶² for conformer generation. Through CREST, conformers were generated from the input XYZ using the GFN2-XTB method.⁶³ Generalised Born and solvent accessible surface area implicit solvation (GBSA) available within CREST was used for water solvation for aqueous conformer generation.⁶² Using the conformers generated by Crest these were then converted into ASE⁵¹ and optimised to the default fmax value of 0.05 eV Å⁻¹. Here, the calculators were set to the trained models as described in Section 3.5 and the optimisation algorithm set to FIRE.⁶⁴

Scheme 2 Flowchart detailing the workflow of the pK_a prediction.

Conformers were filtered twice during the workflow. On both occasions, the energy of each conformer was obtained and used to calculate a weighted Boltzmann average for each molecule. From the weighted average filtering was completed to retain ∼99% of the Boltzmann population. When the modelled number of conformers is low, this can result in some conformers being filtered out and thus, in this instance, slightly less than 99% of the Boltzmann population was retained. This corresponded to an energy threshold of 3.5 kcal mol⁻¹.⁶⁵ However, as the filtering was to occur twice, once after CREST conformer generation and once after optimisation, the first threshold was set to a less stringent threshold of 5.0 kcal mol⁻¹ in order to filter any high energy conformers (details of the conformers generated for each structure is provided in the ESI,† pages S3–S6).

3.7 Calculation of pK_a values

As shown in eqn (4) and (5), it is possible to calculate the pK_a of a compound using Gibbs energy values of different protonation and solvation states as detailed in Fig. 1. In order to calculate ΔG⁰_aq through eqn (5), four values must be calculated. Using each of the newly generated NNP models, for a carbene, A, the values for the deprotonated gas (ΔG(A)) and aqueous phase (ΔG_aq(A)) as well as for the protonated gas (ΔG(AH⁺)) and aqueous phase (ΔG_solv(AH⁺)) can be obtained. These species are consistent with the thermodynamic cycle shown in Fig. 1. The Gibbs energy of solvation for all species can be calculated as shown in eqn (6). Once the ΔG_gas has been calculated as shown in eqn (7), the value of ΔG⁰_aq can be calculated as shown in eqn (8).

ΔG⁰_solv = G_aq − G_gas (6)

ΔG_gas = (G(A) + G(H⁺) − G(AH⁺)) (7)

ΔG⁰_aq = ΔG⁰_gas + ΔG⁰_solv(A) + ΔG⁰_solv(H⁺) − ΔG⁰_solv(HA⁺) (8)

As mentioned in Section 3.1, the Gibbs energy values associated with the proton are taken from literature. Once calculated, ΔG⁰_aq can be used in eqn (4) to calculate the pK_a value.

Once filtering of optimised conformers was completed as shown in Section 3.6, the pK_a was calculated. For every combination of conformers of a molecule, both protonated and deprotonated, the pK_a is calculated and then weighted based on the combined Boltzmann probabilities of the protonated and deprotonated conformer used in the calculation. The final pK_a for the molecule is then calculated by taking the weighted average of all calculated pK_a values, eqn 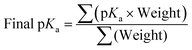(9).

4 Conclusion

We have describe a robust method for the determination of imidazolium-derived carbene pK_a values. The method involves a conformer search that ensures the molecule's Boltzmann population is taken into account when calculating pK_a. Further, we show that the architecture developed by the ANI family of models can be extended past the neutral singlet gaseous state structures detailed thus far. We show that when trained on aqueous phase energies and/or charged molecules, the models can retain their accuracy, which we demonstrate in this study the prediction of energies and subsequent accurate calculation of pK_a values, a problem which is very sensitive to subtle changes in energies and structure.

In future, by expanding our models to other functional groups we can overcome some of the limitations with the current developed workflow. Preliminary modelling of butylamine with trained ML models produced a result of 12.79 versus a literature value of 10.70.⁶⁶ This prediction is almost in line with the results presented in this paper as such, extension to other cationic species is possible with current methods. It should be noted due to the development of charged datasets for this paper, there may be some overlap within the chemical space with protonated amine molecules. However, to better represent this chemical space further calculations may be necessary with emphasis placed on expanding the coverage of amines within the training data.

For expansion to functional groups that include anions within their pK_a calculation, e.g. carboxylic acids, there would need to be significant computational effort put towards development of an anionic dataset for accurate modelling of such species. The current level of theory may also need to be reworked as accurate modelling of anionic species often requires diffuse functions, e.g. aug-cc-pVDZ.

Author contributions

Ross Urquhart: methodology, validation, software, investigation, data curation, writing. Alexander van Teijlingen: methodology, validation, software, investigation, writing. Tell Tuttle: conceptualization, methodology, supervision and manuscript editing.

Data availability

Relevant files and data underpinning this publication are openly available from the University of Strathclyde KnowledgeBase at: https://doi.org/10.15129/8e3a4b33-c787-43d6-afbb-0c1a9a975af8. All code relevant to this publication can be accessed openly at https://github.com/Tuttlelab/DeepSolv. Other additional data including a description of files and data types have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Results were obtained using the EPSRC-funded ARCHIE-WeSt High Performance Computer based at the University of Strathclyde (https://www.archie-west.ac.uk; EPSRC grant no. EP/K000586/1).

Notes and references

1. A. M. Magill, K. J. Cavell and B. F. Yates, J. Am. Chem. Soc., 2004, 126, 8717–8724.
2. L. Samuelsen, R. Holm, A. Lathuile and C. Schönbeck, Int. J. Pharm., 2019, 560, 357–364.
3. K. C. Gross and P. G. Seybold, Int. J. Quantum Chem., 2000, 80, 1107–1115.
4. G. Cruciani, F. Milletti, L. Storchi, G. Sforna and L. Goracci, Chem. Biodiversity, 2009, 6, 1812–1821.
5. D. J. Adams, L. M. Mullen, M. Berta, L. Chen and W. J. Frith, Soft Matter, 2010, 6, 1971–1980.
6. J. H. Berkhout and H. N. Aswatha Ram, Indian J. Pharm. Educ. Res., 2019, 53, S475–S480.
7. J. Reijenga, A. Van Hoof, A. Van Loon and B. Teunissen, Anal. Chem. Insights, 2013, 8, 53–71,  DOI:10.4137/ACI.S12304.
8. M. D. Liptak and G. C. Shields, J. Am. Chem. Soc., 2001, 123, 7314–7319.
9. S. Pezzola, S. Tarallo, A. Iannini, M. Venanzi, P. Galloni, V. Conte and F. Sabuzi, Molecules, 2022, 27, 8590.
10. B. Thapa and H. B. Schlegel, J. Phys. Chem. A, 2016, 120, 5726–5735.
11. F. R. Dutra, C. D. S. Silva and R. Custodio, J. Phys. Chem. A, 2021, 125, 65–73.
12. J. Ho and M. L. Coote, Theor. Chem. Acc., 2010, 125, 3–21.
13. M. Quintano and E. Kraka, Chem. Phys. Lett., 2022, 803, 139746.
14. M. D. Tissandier, K. A. Cowen, W. Y. Feng, E. Gundlach, M. H. Cohen, A. D. Earhart, J. V. Coe and T. R. Tuttle, J. Phys. Chem. A, 1998, 102, 7787–7794.
15. Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 2995–2999.
16. K. Mansouri, N. F. Cariello, A. Korotcov, V. Tkachenko, C. M. Grulke, C. S. Sprankle, D. Allen, W. M. Casey, N. C. Kleinstreuer and A. J. Williams, J. Cheminf., 2019, 11, 60.
17. M. Baltruschat and P. Czodrowski, F1000Res., 2020, 9, 113.
18. T. Sander, J. Freyss, M. Von Korff and C. Rufener, J. Chem. Inf. Model., 2015, 55, 460–473.
19. D. Mendez, A. Gaulton, A. P. Bento, J. Chambers, M. De Veij, E. Félix, M. Magariños, J. Mosquera, P. Mutowo, M. Nowotka, M. Gordillo-Marañón, F. Hunter, L. Junco, G. Mugumbate, M. Rodriguez-Lopez, F. Atkinson, N. Bosc, C. Radoux, A. Segura-Cabrera, A. Hersey and A. Leach, Nucleic Acids Res., 2018, 47, D930–D940.
20. R. Roszak, W. Beker, K. Molga and B. A. Grzybowski, J. Am. Chem. Soc., 2019, 141, 17142–17149.
21. Z. Cai, F. Luo, Y. Wang, E. Li and Y. Huang, ACS Omega, 2021, 6, 34823–34831.
22. R. C. Johnston, K. Yao, Z. Kaplan, M. Chelliah, K. Leswing, S. Seekins, S. Watts, D. Calkins, J. Chief Elk and S. V. Jerome, et al. , J. Chem. Theory Comput., 2023, 19, 2380–2388.
23. Z. Cai, T. Liu, Q. Lin, J. He, X. Lei, F. Luo and Y. Huang, J. Chem. Inf. Model., 2023, 63, 2936–2947.
24. F. Mayr, M. Wieder, O. Weider and T. Langer, Front. Chem., 2022, 10, 866585.
25. J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203.
26. K. Schütt, P.-J. Kindermans, H. Sauceda, S. Chmiela, A. Tkatchenko and K.-R. Müller, Advances in Neural Information Processing Systems, 2017, pp. 992–1002.
27. K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 13890.
28. I. Batatia, D. P. Kovacs, G. N. C. Simm, C. Ortner and G. Csanyi, Advances in Neural Information Processing Systems, 2022.
29. E. Gelžinytė, M. Öeren, M. D. Segall and G. Csányi, J. Chem. Theory Comput., 2024, 20, 164–177.
30. R. Zubatyuk, J. S. Smith, J. Leszczynski and O. Isayev, Sci. Adv., 2019, 5, eaav6490.
31. J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733.
32. J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 2903.
33. C. Devereux, J. S. Smith, K. K. Huddleston, K. Barros, R. Zubatyuk, O. Isayev and A. E. Roitberg, J. Chem. Theory Comput., 2020, 16, 4192–4202.
34. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
35. H. Gokcan and O. Isayev, Chem. Sci., 2022, 13, 2462–2474.
36. M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537.
37. F. Nahra, D. J. Nelson and S. P. Nolan, Trends Chem., 2020, 2, 1096–1113.
38. D. V. Pasyukov, M. A. Shevchenko, A. V. Astakhov, M. E. Minyaev, Y. Zhang, V. M. Chernyshev and V. P. Ananikov, Dalton Trans., 2023, 52, 12067–12086.
39. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
40. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
41. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
42. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
43. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
44. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
45. B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109.
46. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
47. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
48. T. Matsui, Y. Shigeta and K. Morihashi, J. Chem. Theory Comput., 2017, 13, 4791–4803.
49. A. Paszke, S. Gross, S. Chintala, G. Chanan, E. Yang, Z. DeVito, Z. Lin, A. Desmaison, L. Antiga and A. Lerer, NIPS-W, 2017.
50. X. Gao, F. Ramezanghorbani, O. Isayev, J. S. Smith and A. E. Roitberg, J. Chem. Inf. Model., 2020, 60, 3408–3415.
51. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
52. D. C. Liu and J. Nocedal, Math. Prog., 1989, 45, 503–528.
53. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
54. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
55. A. W. Sousa Da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 367.
56. L. Kagami, A. Wilter, A. Diaz and W. Vranken, Bioinformatics, 2023, 39, btad350.
57. A. Collette, Python and HDF5, O’Reilly, 2013.
58. J. S. Smith, O. Isayev and A. Roitberg, ANI-1: A data set of 20M off-equilibrium DFT calculations for organic molecules, 2017, https://springernature.figshare.com/collections/ANI-1_A_data_set_of_20M_off-equilibrium_DFT_calculations_for_organic_molecules/3846712/1.
59. G. Landrum, RDKit: Open-Source Cheminformatics Software, 2016, https://www.rdkit.org.
60. The QMspin data set: Several thousand carbene singlet and triplet state structures and vertical spin gaps computed at MRCISD + Q-F12/cc-pVDZ-F12 level of theory, 2020.
61. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.
62. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
63. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
64. E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Phys. Rev. Lett., 2006, 97, 170201.
65. I. Iribarren and C. Trujillo, J. Chem. Inf. Model., 2022, 62, 5568–5580.
66. M. Morgenthaler, E. Schweizer, A. Hoffmann-Röder, F. Benini, R. Martin, G. Jaeschke, B. Wagner, H. Fischer, S. Bendels, D. Zimmerli, J. Schneider, F. Diederich, M. Kansy and K. Müller, ChemMedChem, 2007, 2, 1100–1115.

---

Footnote

† Electronic supplementary information (ESI) available: All computational data described in this publication are openly available from the University of Strathclyde knowledge base at https://doi.org/10.15129/8e3a4b33-c787-43d6-afbb-0c1a9a975af8. The code from this paper is available at https://github.com/Tuttlelab/DeepSolv. See DOI: https://doi.org/10.1039/d4cp01982b

---