View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/D4CP01916D (Paper) Phys. Chem. Chem. Phys., 2024, 26, 19795-19811

Microwave spectroscopic and computational analyses of the phenylacetylene⋯methanol complex: insights into intermolecular interactions†

Surabhi Gupta a, Charlotte N. Cummings b, Nicholas R. Walker b and Elangannan Arunan *a
aDepartment of Inorganic and Physical Chemistry, Indian Institute of Science, Bangalore, 560012, India. E-mail: arunan@iisc.ac.in
bChemistry-School of Natural and Environmental Sciences, Newcastle University, Bedson Building, Newcastle-upon-Tyne NE1 7RU, UK

Received 8th May 2024 , Accepted 3rd July 2024

First published on 4th July 2024

Abstract

The microwave spectra of five isotopologues of phenylacetylene⋯methanol complex, C6H5CCH⋯CH3OH, C6H5CCH⋯CH3OD, C6H5CCH⋯CD3OD, C6H5CCD⋯CH3OH and C6H5CCH⋯13CH3OH, have been observed through Fourier transform microwave spectroscopy. Rotational spectra unambiguously unveil a specific structural arrangement characterised by dual interactions between the phenylacetylene and methanol. CH3OH serves as a hydrogen bond donor to the acetylenic π-cloud while concurrently accepting a hydrogen bond from the ortho C–H group of the PhAc moiety. The fitted rotational constants align closely with the structural configuration computed at the B3LYP-D3/aug-cc-pVDZ level of theory. The transitions of all isotopologues exhibit doublets owing to the methyl group's internal rotation within the methanol molecule. Comprehensive computational analyses, including natural bond orbital (NBO) analysis, atoms in molecules (AIM) theory, and non-covalent interactions (NCI) index plots, reveal the coexistence of both O–H⋯π and C–H⋯O hydrogen bonds within the complex. Symmetry adapted perturbation theory with density functional theory (SAPT-DFT) calculations performed on the experimentally determined geometry provide an insight into the prominent role of electrostatic interactions in stabilising the overall structural arrangement.

Introduction

Phenylacetylene (PhAc) displays a wide range of binding behaviour, which is characterised by the presence of three potential docking sites. The specific docking sites that are utilised by PhAc are dependent on the type of solvent and the environmental conditions present.1 One of the ways in which PhAc interacts with other molecules is by acting as a hydrogen bond donor. This is facilitated through the presence of its acetylenic CH group. Additionally, PhAc can accept hydrogen bonds through the π-clouds in acetylene and benzene moieties. In the gas phase, studies have shown that all three binding sites of PhAc can be identified in its interactions with some molecules.2–13 Furthermore, PhAc has been extensively investigated in complexation studies with various molecules. Some examples of these binding molecules include argon,11,12 water,7,10,13 methanol,2–4 ammonia,3 methylamine,3 hydrogen sulphide,9 trifluoroethanol1 and itself.5 In order to investigate these complexes, researchers have utilised techniques such as matrix isolation infrared spectroscopy, low-temperature supersonic jet studies involving IR/UV double resonance and microwave spectroscopy, and high-level quantum chemical calculations. The identification of higher energy structures alongside global minima has been made possible using matrix isolation techniques. On the other hand, studies utilizing molecular beam with IR/UV double resonance and microwave techniques have primarily detected the global minima of these complexes.

For the PhAc⋯H2O complex, it is evident that there is a clear preference for water to bind with the acetylenic moiety (rather than the phenyl ring) while acting as a hydrogen bond donor, as proposed by IR/UV double resonance experiment and confirmed by microwave experiment.7,10 This interaction is accompanied by a secondary interaction involving the ortho C–H group of PhAc and the oxygen atom of water. In contrast, in the PhAc⋯H2S complex, microwave spectroscopic experiment showed a structure in which, hydrogen sulphide is located above the phenyl ring and donates a hydrogen bond to the π-cloud of the phenyl ring.9 In order to obtain a deeper understanding of the effects of replacing water with alcohols as the donor molecule in the complexes formed with PhAc, an IR-UV double resonance spectroscopic method was utilized.3,4

During their investigations using the IR-UV double resonance spectroscopic technique, Singh et al. reported some intriguing differences in hydrogen bonding tendencies exhibited by H2O and CH3OH when interacting with PhAc.4 H2O showed a preference for forming hydrogen bonds with the acetylenic π-cloud of PhAc, while CH3OH donated hydrogen bonds to the phenyl π-system. These observations were derived from fluorescence dip infrared (FDIR) spectra obtained for H2O and CH3OH complexes with PhAc. To further substantiate the intriguing methyl group-induced hydrogen bond switching phenomenon, they conducted energy decomposition analyses employing symmetry-adapted perturbation theory (SAPT). The SAPT calculations brought to light a disparity in energy contributions between the PhAc⋯H2O and PhAc⋯CH3OH complexes. In contrast to the predominantly electrostatic energy component characterizing the PhAc⋯H2O complex, the PhAc⋯CH3OH complex exhibited dispersion as its primary energy-driving force. Given the similarity in mass between CH3OH and H2S, it was inferred that dispersion plays a dominant role in both PhAc⋯CH3OH and PhAc⋯H2S complexes. A delicate balance of interactions, which encompasses a range of forces such as electrostatic interactions between permanent multipoles, induction, dispersion, and exchange-repulsion, plays an important role in regulating intricate molecular recognition events that occur in chemical and biological systems. Consequently, critical significance lies in the experimental investigation and accurate estimation of the structures of these complexes at their respective global minima.

Surprisingly, nearly a decade later, Karir et al. conducted a study utilizing the slit-jet molecular beam with FTIR detection of the PhAc⋯H2O and PhAc⋯CH3OH complexes, which yielded some conflicting results compared to the earlier findings.2 While the structure of the PhAc⋯H2O complex remained consistent with the previous observations, a discrepancy emerged in the structure of the complex formed between PhAc and CH3OH. Analysis of Fourier-transform infrared (FTIR) spectra obtained from these experiments indicated that methanol also donates hydrogen bonds to the acetylenic π-cloud, a result supported by density functional theory (DFT) calculations, which identified the acetylene-bound structure as the global minimum.

The discrepancy in results for the PhAc⋯CH3OH complex that arises from the combination of molecular beam with IR-UV double resonance spectroscopic and FTIR spectroscopic experimental results can potentially be resolved using microwave spectroscopy. Microwave spectroscopy offers the advantage of providing an unambiguous structure for the complex. A significant amount of research has been carried out on different complexes involving methanol, with microwave spectroscopy being used in many of these studies. Specifically, the barrier height to internal rotation of CH3OH and CH3OH-containing complexes, including the CH3OH dimer, has been a topic of great interest and investigation.14–34 In the case of CH3OH, it has been reported that this barrier height is 373 cm−1, which is the result of the interactions between the internal rotation of the methyl group and the large amplitude motion of the OH group.14 There are reports that suggest that the binding of CH3OH to another molecule can influence (change the barrier height of) the internal rotation of the methyl group in the methanol molecule. Given these findings, it would be of interest to explore the barrier to internal rotation of the methyl group in the PhAc⋯CH3OH complex.

This study presents a comprehensive analysis of the microwave spectrum exhibited by five isotopologues of the PhAc⋯CH3OH complex. In order to delve deeper into the intricate nature of the interactions within the complex, the study employs techniques such as atoms in molecules (AIM) theory, natural bond orbital (NBO) analysis and non-covalent interactions (NCI) index analysis. Through these methods, the molecular interactions present in the complex are explored. The results of this analysis provide valuable insights into the intricate and complex nature of the PhAc⋯CH3OH compound.

Methods

Computational details

The Gaussian 09 package35 was employed for the optimization of the PhAc⋯CH3OH complex structures, utilizing DFT and ab initio quantum chemical calculations. Two alternative methods were used in this study to optimize the structures: the harmonic hybrid functional36–38 of Becke, Lee, Yang, and Parr (B3LYP), which was combined with Grimme's dispersion correction effects,39 and the MP2 method.40,41 These methods were used with Dunning's augmented double-ζ aug-cc-pVDZ basis sets.42–45 The initial guess geometries were taken from the previous reports.2,4 Harmonic frequency calculations were performed to ascertain that the structures obtained were minima on the potential energy surface. The freq = vibrot keyword was used to calculate the centrifugal distortion constants for all isotopologues. The binding energies for the complexes were calculated using the supermolecule approach. The binding energies were corrected for the basis set superposition error (BSSE) using Boys and Bernardi's counterpoise method.46 To understand the internal rotation of the methyl group, the relaxed potential energy scan was performed using the opt = modredundant keyword. The barriers obtained from this scan would help to determine the feasible pathways for internal rotation that lead to the splitting of the observed spectra. The electron density topologies for the optimized structures have been calculated to understand the nature of interactions present using the AIMAll software.47 Noncovalent interactions index (NCI) analysis48 and natural bond orbital (NBO) analysis49 were also performed to characterize and visualize the intermolecular interactions. The NCI plots were computed using Multiwfn software,50 and NBO calculations were performed using NBO 6.0 as implemented in Gaussian 09.51 The energy decomposition analyses (SAPT2 + 3 and SAPT-DFT) were carried out using the PSI4 program.52,53 The wavefunctions for these calculations were obtained from Gaussian 09 calculations at B3LYP-D3/aug-cc-pVDZ level of theory.

Experimental details

The spectrum of the most naturally abundant isotopologue of PhAc⋯CH3OH, hereafter referred to as the parent isotopologue, was obtained over a frequency range of 2.0–8.0 GHz using a chirped pulse Fourier transform microwave (CP-FTMW) spectrometer at Newcastle University, and over a range of 8.0–14.0 GHz using a Balle–Flygare type pulsed-nozzle Fourier transform microwave (PN-FTMW) spectrometer at the Indian Institute of Science Bangalore. The PhAc⋯CH3OH complex was formed through the pulsed supersonic expansion of a gaseous mixture comprising helium (99.999%) or neon (BOC, CP grade) as carrier gases. Pure samples of phenylacetylene (98%), phenylacetylene-D (99%), methanol (99.9%), methanol-D (99%), methanol-D4 (99.8%) and methanol-13C (99%) were obtained from Sigma Aldrich and used without further purification.

For the experiments conducted at Newcastle University, the introduction of PhAc into a neon flow was executed under a backing pressure of 5 bar. Owing to the low vapour pressure, the PhAc was heated to 50 °C, facilitated by a modified general valve,54 in order to produce the mixture with the carrier gas. A second reservoir containing CH3OH (or isotopic variants) was positioned downstream of the modified general valve allowing the introduction of low concentrations of CH3OH into the neon carrier gas. A detailed description of the spectrometer can be found elsewhere.55,56 To capture the broadband spectrum, a chirped pulse was generated by an Arbitrary Waveform Generator (Tektronix AWG7102) with a frequency range from 2.0 GHz to 8.0 GHz and a duration of 1 μs, was sent directly to a 450 W traveling-wave tube amplifier (TWTA) (Applied Systems Engineering), before transmission to the vacuum chamber. The polarization of the molecules within the sample was achieved following the introduction of the chirp from the horn antenna to the vacuum chamber. The microwave radiation and the expanding gas jet exhibit a mutually perpendicular orientation. Subsequently, the free induction decay (FID) of a 20 μs duration was recorded using a second horn antenna after the microwave pulse interaction. The FID's were then digitised by employing a 100 GS s−1 oscilloscope (Tektronix DPO72304XS). The utilization of a gas pulse lasting approximately 200 μs facilitates the acquisition of eight FID's per gas pulse, which was achieved through the implementation of the ‘fast frame’ operational mode of the oscilloscope. Subsequently, the FID's were co-added in the time domain and then Fourier transformed using either a Kaiser-Bessel or High Resolution Window function. Individual lines in the frequency domain spectrum have a full width at half-maximum of approximately 100 kHz allowing line centres to be measured with an estimated precision of 10 kHz. The arbitrary waveform generator (AWG) and the oscilloscope were referenced to a 10 MHz local oscillator obtained from an Analog Signal Generator (Agilent MXG N5183A) or an Rb-clock (SRS FS725) to guarantee phase coherence within the temporal domain and precision in the transition frequencies.

The pulsed nozzle Fourier transform microwave spectrometer (PN-FTMW) was utilized to acquire experimental data at the Indian Institute of Science Bangalore. A comprehensive description of the spectrometer can be found elsewhere.57 The PhAc and CH3OH both were kept in two different bubblers at ambient conditions. The most optimal signal intensity was achieved by allowing helium to flow through the PhAc and CH3OH bubblers at a rate of approximately 20 SCCM (standard cubic centimetre per minute) and 2 SCCM, respectively. At a four-way junction, the samples were mixed with a bath of helium (about 200 SCCM), and the mixture was then sent to the nozzle. The mixture underwent expansion via a 0.8 mm nozzle after being subjected to a backing pressure of 1.5–2.0 bar. A microwave pulse duration of 0.4 μs was found to be optimal for inducing a- and c-dipole transitions, while a duration of 1.0 μs was found to yield the highest intensity signals for b-dipole transitions. The Doppler doubling phenomenon observed in the spectra is a consequence of the molecular beam's colinear arrangement relative to the cavity axis. The spectra were recorded utilizing a sampling frequency of 5 MHz, and during the scanning for the transitions, 256 points were collected. To obtain the high-resolution spectra, the observed rotational lines were subsequently averaged at 512 points.

Results

Optimized structures

The structural elucidation of the PhAc monomer has been well-established through microwave spectroscopy.58,59 For optimizing the structure of the PhAc⋯CH3OH complex, initial structural approximations were drawn from previous IR/UV double resonance and FTIR spectroscopic studies.2,4 Subsequently, the structures were optimised using ab initio MP2 and DFT calculations with B3LYP-D3 functionals employing aug-cc-pVDZ basis set. The optimized structures of PhAc⋯CH3OH complex are shown in Fig. 1. Our nomenclature of the complexes lists the donor molecule abbreviation (P for PhAc and M for CH3OH) connected by a dash to the acceptor molecule abbreviation, adding the acceptor docking site (Ac for acetylenic, Ph for phenyl and OH for hydroxyl preference) as an index. For example, the phenyl-bound complex of CH3OH with PhAc is denoted as (M–P)Ph. Within the scope of our investigation, two distinct scenarios were considered: one where CH3OH serves as the hydrogen bond donor and PhAc acts as the hydrogen bond acceptor, and the other where the roles are reversed. Notably, the configuration in which CH3OH donates a hydrogen bond to the phenyl ring of PhAc is found to have the same interactions at both MP2 and DFT computational levels. However, variations emerge when CH3OH acts as the hydrogen bond donor to the acetylenic π-bond moiety (Fig. 1). In the (M–P)Ac configuration optimized using the MP2 method, CH3OH donates a hydrogen bond to the acetylenic moiety, while the methyl group interacts with the π-cloud of the phenyl ring. In contrast, in the structure optimized using DFT methods, CH3OH donates a hydrogen bond to the acetylenic moiety, and the ortho hydrogen of PhAc interacts with the oxygen of CH3OH.
image file: d4cp01916d-f1.tif
Fig. 1 Structures of the PhAc⋯CH3OH complex and their relative energies (kJ mol−1) optimized at MP2/aug-cc-pVDZ (top panel) and B3LYP-D3/aug-cc-pVDZ (bottom panel) level of theories.

The energy landscape reveals interesting details. At the MP2 level of theory, the (M–P)Ph structure is the lowest energy configuration, with a marginal 0.4 kJ mol−1 difference from the (M–P)Ac structure. Furthermore, their rotational constants exhibit a high degree of similarity. Discrimination between these two configurations based on their rotational spectra becomes feasible by considering their c-dipole moments. The (M–P)Ph configuration possesses a zero c-dipole moment, rendering it devoid of c-type transitions in its microwave spectrum. In contrast, at the B3LYP-D3/aug-cc-pVDZ level of theory, the (M–P)Ac is the global minimum, exhibiting a 3.0 kJ mol−1 energy difference from the (M–P)Ph configuration. The structures optimized using the B3LYP-D3/aug-cc-pVDZ level of theory exhibit markedly distinct rotational constants and dipole moment components, facilitating their obvious differentiation in rotational spectra analysis. The structure where PhAc acts as the hydrogen bond donor and CH3OH as the acceptor has higher energy at both MP2 and DFT levels of theory. Detailed molecular properties such as rotational constants, dipole moment components and binding energies, corrected for basis set superposition error (BSSE) are presented in Table 1. Calculated atomic coordinates of each structure presented in Fig. 1 are provided in the Tables S6–S11 (ESI†).

Table 1 Rotational constants (MHz), electric dipole moment (Debye), second moments, the binding energies (ΔE), and BSSE corrected binding energies (ΔEBSSE) (kJ mol−1) calculated at MP2/aug-cc-pVDZ and B3LYP-D3/aug-cc-pVDZ level of theories
Parameters MP2/aug-cc-pVDZ B3LYP-D3/aug-cc-pVDZ
(M–P)Ph (M–P)Ac (P–M)OH (M–P)Ph (M–P)Ac (P–M)OH
P cc is the second moment given by: image file: d4cp01916d-t1.tif.
A e 1469.97 1564.70 4193.61 1380.46 2004.82 4252.43
B e 1121.38 1041.56 364.67 1136.82 802.76 369.14
C e 828.30 817.29 348.24 803.93 621.78 347.38
μ a −0.8 −1.8 −1.5 −0.6 −1.6 −1.3
μ b −1.7 1.0 1.0 −1.7 0.6 1.2
μ c 0.0 0.8 0.8 −0.0 1.2 0.0
P cc (μÅ2) 92.17 94.92 27.56 91.00 34.42 16.54
ΔE 31.8 30.8 18.3 21.3 23.6 15.9
ΔEBSSE 16.9 16.5 12.9 18.2 21.2 14.0

Observations and spectral analysis

The broadband rotational spectrum, obtained from a mixture of PhAc and CH3OH with neon as the carrier gas, is depicted in Fig. 2 (upper trace). The spectral data were acquired over the frequency range of 2.0 to 8.0 GHz and the displayed spectrum is an average over 1.11 million FID's (approximately 18.5 hours of data collection).
image file: d4cp01916d-f2.tif
Fig. 2 (Top panel) The broadband rotational spectrum of PhAc⋯CH3OH complex recorded in 2.0–8.0 GHz region using CP-FTMW spectrometer. (Bottom panels) Experimentally observed transitions of the PhAc⋯CH3OH complex are shown (black) above the simulated spectrum (red and green colour for A- and E-states, respectively).

Notably, the spectrum reveals the presence of CH3OH dimer and parent and six 13C isotopologues of the PhAc monomer, all of these have been subjects of prior investigation.20,22,59 In particular, the CH3OH dimer exhibits line splitting attributable to internal motions of the methyl group. Each of the two possible structures of PhAc⋯CH3OH (as shown in Fig. 1) displays the feature of a nearly prolate asymmetric top. Computational calculations, as outlined earlier, were employed to anticipate the rotational constants (Ae, Be, and Ce) as well as five distortion constants (DJ, DJK, DK, d1, d2) for the equilibrium configuration of both isomers. Subsequently, based on these computational predictions, the observed spectral transitions were fitted, and the experimental rotational constants agree with the structure optimised at B3LYP-D3/aug-cc-pVDZ level of theory, in which the CH3OH donates the hydrogen bond to the acetylenic π-cloud, and there is a secondary interaction between the ortho hydrogen with the oxygen atom of the CH3OH ((M–P)Ac). We also optimized the structure at B3LYP-D3(BJ)/aug-cc-pVDZ level of theory, which has been found to give accurate structures for chiral tag complexes.60 However, for the PhAc⋯CH3OH complex, the agreement with experimental rotational constants did not improve with B3LYP-D3(BJ)/aug-cc-pVDZ level of theory. The results from this calculation are given in ESI,† Table S17. This fitted structure of the PhAc⋯CH3OH complex is consistent with the structure reported by Karir et al.2 The lower trace of Fig. 2 presents a small section of the broadband spectrum, spanning from 4190 to 4206 MHz and from 4338 to 4348 MHz, showing selected transitions.

For the PhAc⋯CH3OH parent complex, a total of 59 transitions were successfully fitted to Watson's S-reduced asymmetric rotor Hamiltonian61 within the Ir representation using Western's PGOPHER62 program. Notably, most of the assigned transitions in the PhAc⋯CH3OH complex were part of a doublet splitting pattern, indicative of a methyl rotor-type large amplitude motion. The complete list of transitions for both states is given in the ESI,† in Table S1. The assignment includes strong a- and c-type transitions, alongside weaker b-type transitions. The fitted parameters determined by fitting to the frequencies of A-state transitions are shown in Table 2. Notably, in this fit, d2 distortion constant is not determinable. The experimentally determined rotational constants and distortion constants closely match those calculated for the (M–P)Ac isomer using DFT methods. Additionally, E-state transitions, arising from the internal rotation of the methyl group, were identified in the spectra, and subsequently assigned using the XIAM14 program to obtain a global fit. The details of the global fit are provided in Section 4.1. Successively, utilizing the fitted rotational constants, the spectral predictions were regenerated within the 8.0 to 14.0 GHz frequency range, and the predicted transitions were searched using a PN-FTMW spectrometer in IISc Bangalore. Both the A- and E-state transitions were measured. A representative portion of the recorded spectra, displaying A and E-state transitions, is presented in Fig. 3. All the transitions were further split into Doppler doublets.

Table 2 Experimental rotational constants (MHz), centrifugal distortion constants (kHz) and second moment of A-state for PhAc⋯CH3OH complex, fitted using ASFIT program (fit includes the transitions obtained from both the CP-FTMW spectrometer and the PN-FTMW spectrometer) and PGOPHER program (fit includes transitions obtained from the CP-FTMW spectrometer only)
Constants ASFIT PGOPHER B3LYP-D3/aug-cc-pVDZ
P cc is the second moment given by: image file: d4cp01916d-t5.tif.
image file: d4cp01916d-t2.tif 1955.3325(9) 1955.3331(8) 2004.82
image file: d4cp01916d-t3.tif 796.5840(3) 796.5836(4) 802.76
image file: d4cp01916d-t4.tif 626.0865(3) 626.0858(4) 621.78
D J 1.157(3) 1.134(4) 0.49
D JK −6.04(2) −6.01(2) −2.37
D K 17.5(1) 17.53(8) 8.83
d 1 −0.142(1) −0.144(1) −0.09
d 2 — — −0.001
P cc (μÅ2) 42.85 42.85 34.41
N A 72 58 —
σ (kHz) 7.1 5.1 —


image file: d4cp01916d-f3.tif
Fig. 3 The 422 → 312 transition of PhAc⋯CH3OH complex (recorded using PN-FTMW spectrometer) showing A and E-states. The transitions are further split due to the Doppler effect.

The observed A-state transitions using the PN-FTMW spectrometer were further fitted alongside transitions observed using the CP-FTMW spectrometer utilizing the ASFIT25 program (fitted parameters are given in Table 2). This fit was found to be more accurate than that performed to the CP-FTMW data alone because it was possible to include a greater number of higher frequency transitions. Fits performed using ASFIT and PGOPHER while using only the CP-FTMW data alone were found to be consistent (see Table S18 of the ESI†). As previously highlighted, the results consistently support the conclusion that the observed spectra correspond to the isomeric configuration where CH3OH is bound to the acetylenic moiety of PhAc, and the ortho-hydrogen of PhAc interacts with the oxygen of CH3OH. It is noteworthy that despite rigorous search, spectral data for the complex in which CH3OH donates a hydrogen bond to the π-cloud of the phenyl ring, as well as the isomer where CH3OH donates a hydrogen bond to the acetylenic moiety, while the methyl group interacts with the π-cloud of the phenyl ring, remained elusive.

Rotational constants, distortion constants, and second moment calculated at B3LYP-D3/aug-cc-pVDZ level of theory are taken from Table 1.

Isotopic substitution

The spectra for isotopologues of the PhAc⋯CH3OH complex were recorded to ascertain the geometry of the observed structure and to better comprehend the motions that lead to the spectral splitting. The results of the spectroscopic fitting for (M–P)Ac enabled the identification and fitting of transitions for four more isotopologues, including PhAc⋯CH3OD, PhAc⋯CD3OD, PhAc-D⋯CH3OH, and PhAc⋯13CH3OH. The CP-FTMW spectrometer at Newcastle University was used to detect and assign transitions for each isotopologue. The spectroscopic parameters were determined by fitting the observed transitions using Western's PGOPHER62 program. Transition frequencies and their assignments for all the isotopologues are given in the ESI,† in Tables S2–S5. Intriguingly, all the isotopologues exhibited distinct spectral splitting in the transition frequencies due to the large amplitude motion of the methyl group. Subsequently, a global fit analysis was conducted for all the isotopologues, excluding the PhAc⋯CD3OD complex. In the case of PhAc⋯CD3OD, substantial overlap between A and E-state transitions, coupled with reduced signal intensity precluded the global fit. Additionally, hyperfine structures (caused by the deuterium nucleus which has I = 1) could not be resolved for the PhAc⋯CH3OD, PhAc⋯CD3OD, and PhAc-D⋯CH3OH complexes. For each isotopologue, the fitted rotational constants and centrifugal distortion constants of A-state transitions are presented in Table 3. The rotational constants and centrifugal distortion constants determined from the global fit are presented in Table 4.
Table 3 Experimental rotational constants (MHz), centrifugal distortion constants (kHz) and second moment of the A-state transitions (fit includes transitions obtained from the CP-FTMW spectrometer only) of observed isotopologues of PhAc⋯CH3OH complex
Constants PhAc⋯CH3OD PhAc⋯CD3OD PhAc–D⋯CH3OH PhAc⋯13CH3OH
P cc is the second moment given by: image file: d4cp01916d-t9.tif.
image file: d4cp01916d-t6.tif 1962.828(5) 1874.215(6) 1891.361(3) 1935.976(1)
image file: d4cp01916d-t7.tif 786.004(2) 750.849(2) 789.244(1) 785.5191(5)
image file: d4cp01916d-t8.tif 619.382(2) 595.750(2) 615.3129(9) 618.7176(4)
D J 1.060(2) 0.79(2) 1.051(2) 1.172(9)
D JK −5.483(9) −5.8(1) −4.97(1) −6.31(5)
D K 52.6(7) 29.0(7) 18.9(5) 18.1(1)
d 1 −0.186(2) −0.216(9) −0.140(1) −0.172(2)
P cc (μÅ2) 42.25 47.21 43.10 43.80
N lines 31 23 29 44
σ (kHz) 10.2 13.1 7.6 5.7

Table 4 Experimental rotational constants (MHz), centrifugal distortion constants (kHz) and second moment obtained from the global fit containing A- and E-state transitions (fit includes transitions obtained from the CP-FTMW spectrometer) of PhAc⋯CH3OH complex and its isotopologues
Constants PhAc⋯CH3OH PhAc⋯CH3OD PhAc–D⋯CH3OH PhAc⋯13CH3OH
P cc is the second moment given by: image file: d4cp01916d-t10.tif.a The corresponding F values for PhAc⋯CH3OH, PhAc⋯CH3OD, PhAc–D⋯CH3OH, and PhAc⋯13CH3OH are 6.18, 6.15, 6.20, and 6.22 cm−1, while the ρ value is approximately 0.004 for all isotopologues.
A 0 1955.321(1) 1962.819(6) 1891.348(3) 1935.967(2)
B 0 796.5629(6) 785.989(2) 789.224(1) 785.4982(8)
C 0 626.0072(7) 619.323(2) 615.237(1) 618.6409(8)
D J 1.153(3) 1.06(2) 1.046(6) 1.16(1)
D JK −6.06(3) (−5.518) −4.91(8) −6.36(6)
D K 17.4(1) 52.5(6) 18.7(4) 18.32(2)
d 1 −0.142(2) −0.18(2) −0.135(8) −0.172(2)
D π2J −322(3) −274(1) −315(5) −327(3)
D π2K 844(5) 760(5) 787(10) 858(7)
V 3 (cm−1) 235(1) 255(8) 236(4) 237.0(2)
F 0 (cm−1) 6.16(5)a 6.1(2)a 6.2(1)a 6.20(6)a
∠(i, a) (degree) 68.1(1) 69.0(6) 68.3(2) 68.0(1)
∠(i, b) (degree) 22.9(2) 21.8(6) 22.8(2) 22.8(1)
∠(i, c) (degree) 96.155(6) 95.66(2) 96.777(8) 95.750(6)
P cc (μÅ2) 42.80 42.22 43.06 43.77
N A/NE 72/48 31/25 29/24 44/38
σ (kHz) 10.4 12.4 8.8 9.7

Discussions: structure and dynamics

Internal rotation and large amplitude motion

Observation of both A- and E-state transitions allows for an analysis of large amplitude motions within the PhAc⋯CH3OH complex. It will be shown that it is possible to fit the frequencies of both A- and E-state transitions to the predictions of a Hamiltonian that includes parameters to describe the internal rotation of the methyl group within the complex. These include V3, the height of the potential energy barrier to the internal rotation that has three-fold symmetry about the rotor axis; F, which is equal to h/[8π2Iα(1 − ρa)] where ρa = Iα/Ia and Iα is the moment of inertia for rotation of the CH3 group about the internal rotor axis; ∠(i, a), ∠(i, b), and ∠(i, c) which represent the angles between the rotor axis and each of the principal inertial axes, a, b and c respectively; and Dπ2J, Dπ2K and Dπ2− terms which represent the effects of centrifugal distortion. However, it is important first to review the extent to which a Hamiltonian containing these terms is appropriate for modelling the large amplitude motions present within PhAc⋯CH3OH.

It is possible to separately determine F and V3 where a sufficient number of rotational transitions are recorded for multiple torsional states as achieved by De Lucia et al. for the CH3OH monomer.14 However, in general, studies of CH3OH-containing complexes performed by microwave spectroscopy tend to probe rotational transitions of only the ground torsional state and this is also true of the present work. It is not possible to separately determine F and V3 with high precision through fits performed to rotational spectra recorded only for the ground torsional state. An approach often taken by microwave spectroscopists involves fixing F at an assumed value such that a fitted value of V3 can be obtained. Many studies have sought to explore changes in V3 as a function of the substitution position of a CH3 group on a rigid molecular framework (for example, at different substitution positions on an aromatic ring). In such examples, it is well-established that Iα and F0 (where F0 is equal to F for the limiting case where ρa = 0) can respectively be approximated as ∼3.2 μÅ2 and ∼157.9 GHz and this knowledge was exploited by two authors of the present work during recent analyses of internal rotation within isomers of the monohydrate complexes of methylthiazole and methylimidazole.63,64 However, the CH3 group is not bound to a rigid molecular framework within CH3OH so the value of F0 cannot a priori be assumed to be reliable in such cases. In fact, as long ago as the 1980's, papers by Lovas et al. and Suenram et al. analysed large amplitude motions within hydrogen-bonded complexes containing CH3OH while highlighting that their analyses would not reliably distinguish the effects of CH3 internal rotation from vibrational motions of the O–H group.24,25 Authors were careful to report only “effective” V3 barriers which they did not intend to be used in direct comparisons with V3 determined for other molecules and complexes. A recent study of the diphenyl ether⋯CH3OH complex highlighted this continuing constraint.23 The results of two alternative approaches were presented when the spectrum of diphenyl ether⋯CH3OH was analysed: (1) a fit was performed to determine both V3 and F0 even while it was explained that these parameters are unavoidably correlated in the fit that was performed and (2) a fit was performed to determine V3 while assuming a fixed value of F0. To facilitate broad comparisons of data sets which may follow in future works, the same approach will be taken towards the reporting of results for internal rotation parameters herein. The results presented in Table 4 employed the first of the approaches described above while the results obtained by the alternative approach are presented in the ESI† (Table S14).

To gain insight into the V3 barrier within the context of the PhAc⋯CH3OH complex, we conduct a relaxed potential energy scan for the rotation of the CH3 group within the CH3OH monomer and (M–P)Ac structure. These potential energy scans are carried out at the B3LYP-D3/aug-cc-pVDZ level of theory. The resulting potential energy curves for these relaxed scans are shown in Fig. 4, in which the barrier to CH3 rotation is found to be 385.5 cm−1 (solid line) for methanol monomer and 312.8 cm−1 (dashed line) for PhAc⋯CH3OH complex. The experimentally observed (373 cm−1) and computed barrier height (385.5 cm−1) for CH3 rotation in the methanol monomer are in good agreement with each other. The computed barrier height of the PhAc⋯CH3OH complex, when compared to the computed barrier in the methanol monomer, suggests that the methyl (CH3) group within the (M–P)Ac complex is not significantly engaged in intermolecular interactions with PhAc. Analysis of the experimental spectra is facilitated by the XIAM program, which can be used to perform a “global” fit of both A- and E-state transitions to determine parameters in a rotational Hamiltonian, which includes terms to describe the effects of centrifugal distortion and internal rotation. The XIAM program utilizes a Hamiltonian that is formulated within the principal axis system. The program uses a “local” approach, treating each torsional state individually without taking into account any interactions between different torsional states. The analysis yields the values shown in Table 4 for the F0, V3, ∠(i, a), ∠(i, b), ∠(i, c), Dπ2J and Dπ2K parameters (defined within the opening paragraph of this section) for each of four isotopologues of the PhAc⋯CH3OH complex.


image file: d4cp01916d-f4.tif
Fig. 4 The potential energy curve for the internal rotation of the CH3 group in the CH3OH monomer (solid line) and PhAc⋯CH3OH complex (dashed line).

Table 5 presents a comparison of results reported for F and V3 for the series of CH3OH-containing complexes studied to date where analyses of internal rotation have been reported. As noted earlier, F0 and V3 cannot be independently determined from rotational spectra reported for only a single torsional state. On the other hand, the value of the reduced barrier, s = 4V3/9F (a dimensionless quantity), is also sensitive to the splitting between A- and E-state transitions and provides an interesting perspective on the results shown. The complexes featured in Table 5 are presented in order of decreasing s. Many previous works assumed a fixed value of F0 to allow the determination of an “effective” V3. It is immediately apparent from Table 5 that the results for V3 cannot easily be rationalised with any trend in molecular properties or geometry across this set of complexes. For example, the V3 reported for Ar⋯CH3OH and HCl⋯CH3OH are significantly higher than that for the CH3OH monomer for reasons that do not obviously connect with any aspect of the properties of these complexes.14,25,26 In any case, as noted by the authors of the original works, the V3 of these species almost certainly differ because accurate values of F0 were not available when the fits to determine V3 for each of Ar⋯CH3OH and HCl⋯CH3OH were performed, and unreliable assumptions were therefore made. An alternative and more insightful perspective on the underpinning molecular physics is provided by the trend in s as a function of molecular geometry and bonding across the series of complexes featured in Table 5.

Table 5 Barrier heights V3 for methyl rotation in the previously studied methanol-containing complexes. Except as indicated by footnotes (a,b), the original works performed fits to determine V3 while fixing the values for F at the results shown
Molecule V 3 (cm−1) F (cm−1) s Ref.
a The original works fixed F0 rather than F, so the value for F0 is quoted in this table. For the heavier complexes (phenyl vinyl ether⋯CH3OH, diphenyl ether⋯CH3OH), it can reliably be assumed that the value of F0 will be very similar to (within a few percent of) that of F. This will not necessarily be true for complexes of CH3OH with lighter molecules such as HCl, Ar or formamide. b Allowed to float during the fitting procedure. c Mon I and Mon II are the two CH3OH monomers within the (CH3OH)2 dimer, where Mon I is the hydrogen bond donor whereas Mon II is hydrogen bond acceptor.
CH 3 OH [double bond, length as m-dash]H-bond donor
Phenyl vinyl ether⋯CH3OH 261.8 5.3a 21.95 34
Diphenyl ether⋯CH3OH 480 10.16ab 21.00 23
Diphenyl ether⋯CH3OH 250.74 5.3a 21.03 23
Formamide⋯CH3OH 231.01 5.26a 19.52 24
Aniline⋯CH3OH 215 5.28 18.10 29
H2CO⋯CH3OH 240.5 6.17 17.32 31
PhAc⋯CH3OH 200.0 5.24 16.96 Present work
PhAc⋯CH3OH 235 6.16b 16.96 Present work
CH3OH dimer (Mon I)c 201c 5.4b 16.54 20
Trimethylamine⋯CH3OH 174 5.30 14.59 28
CO⋯CH3OH 183 5.76 14.12 30
Other molecules and complexes
Phenol⋯CH3OH 170 5.27 14.34 65
CO2⋯CH3OH 174.8 5.45 14.25 31
SO2⋯CH3OH 128.7 5.3 10.79 27
CH3OH dimer (Mon II)c 118.7c 5.16b 10.22 20
HCl⋯CH3OH 74.0 5.3a 6.21 26
CH3OH monomer 373 27.63b 6.00 14
Ar⋯CH3OH 68.5 5.3a 5.74 66

CH3OH-containing complexes where the O of CH3OH acts as hydrogen bond acceptor (HCl⋯CH3OH or monomer II of (CH3OH)2) or where the complex is bound by another form of weak interaction (e.g. SO2⋯CH3OH, Ar⋯CH3OH) have values of s which are very similar to that determined (s = 6.0) for the isolated CH3OH monomer.14,21,22,25,27 Those complexes where the O–H of CH3OH acts as a hydrogen bond donor have significantly higher s that range from 14.12 for CO⋯CH3OH to 21.95 for phenyl vinyl ether⋯CH3OH.30,34 There also appears to be a correlation between the relative strength of the hydrogen bond(s) formed within each complex and the value of s. Where a complex contains only a single hydrogen bond, and especially where this bond can be expected to be weak, the s for the complex appears to lie at the lower end of the range. Complexes with stronger hydrogen bonds generally associate with higher values of s and those at the high end of the range are held together by multiple interactions. For example, formamide⋯CH3OH contains multiple intermolecular hydrogen bonds whereas the diphenyl ether and CH3OH monomers interact via dispersion interactions in addition to the hydrogen bond present within the diphenyl ether⋯CH3OH complex. An important confirmation of the described relationship is provided by the s values attributed to each of the CH3OH monomers present within the CH3OH dimer. This complex is primarily the result of a hydrogen bond formed between the O−H of one monomer and the oxygen atom of the second. That monomer which acts as hydrogen bond donor within the CH3OH dimer has a value for s that is consistent with its role. The other, which acts as the hydrogen bond acceptor, has an s value similar to that seen for the isolated CH3OH monomer.

Structural analysis

Analysis of the fitted rotational constants reveals a very close agreement between the experimentally determined values and those computed for the (M–P)Ac structure using DFT (B3LYP-D3/aug-cc-pVDZ). The structural characteristics observed in the PhAc⋯CH3OH complex exhibit similarities to those observed in the PhAc⋯H2O complex.10

The findings of the IR/UV double resonance experiments conducted on the PhAc⋯H2O and PhAc⋯CH3OH complexes have been previously reported, with the determination of their structures relying on the analysis of the fluorescence dip infrared (FDIR) spectra in the O–H and C–H stretching regions.4 The vibrational frequencies corresponding to the O–H stretch (νO–H) of the H2O and CH3OH complexes of PhAc, both calculated and experimentally obtained (as cited in ref. 2), are given in Table S15 of the ESI.† In the case of the PhAc⋯H2O complex, the experimentally recorded νO–H value for the PhAc⋯H2O complex was identified at 3629 cm−1 for the hydrogen bonded O–H and 3724 cm−1 for the free OH. The predicted values for the hydrogen bonded νO–H in acetylenic and phenyl bound structures were 3587 and 3621 cm−1, respectively. Clearly, the observed value of 3629 cm−1 is larger than what is predicted for both conformers, though closer to the phenyl-bound structure. Still, the acetylenic bound structure was favoured for the following reasons. The resonant ion-dip infrared spectra of the benzene⋯H2O π hydrogen bonded complex in the O–H stretch region exhibit over six transitions, attributed to the large amplitudes tumbling motion of the H2O molecule.67 As previously mentioned, the FDIR spectrum of the PhAc⋯H2O complex displays two distinctive transitions corresponding to the hydrogen bonded and the free O–H vibrations. Consequently, it was deduced that, unlike benzene⋯H2O, the H2O molecule forms a strong bond with the PhAc in the PhAc⋯H2O complex. Given that the acetylenic bound structure involves O–H⋯π and C–H⋯O hydrogen bonds leading to a cyclic structure, it suggests the plausibility of the acetylenic bound configuration. More importantly, the FDIR spectra in the C–H stretch region were utilized to gain more comprehensive insights. In the PhAc monomer, peaks at 3325 cm−1 and 3343 cm−1 were detected, indicating the occurrence of Fermi resonance. This Fermi resonance entails the vibration of C–H stretching and a combination band of one quantum of C[triple bond, length as m-dash]C stretch and two quanta of out-of-plane acetylenic C–H bend. Disturbances impacting the C[triple bond, length as m-dash]C bond stretching vibration, such as intermolecular bonding, lead to the disappearance of Fermi resonance bands and the appearance of a single band corresponding to the free C–H oscillator. The FDIR spectrum of the PhAc⋯H2O complex reveals a single band at 3331 cm−1, which further confirms the interaction of the O–H group with the π electron density of the acetylenic group.

As for the PhAc⋯CH3OH complex, the experimental νO–H for the hydrogen bonded O–H was identified at 3615 cm−1. The theoretically predicted νO–H for the acetylenic (3633 cm−1) and phenyl bound (3637 cm−1) structures of the PhAc⋯CH3OH complex were very similar, with a marginal difference of only 4 cm−1. Consequently, these slight infrared band shifts observed in the weak O–H⋯π complexes do not offer sufficient evidence for definitive structural determinations. In the C–H stretch region of the FDIR spectrum, two bands were observed at 3323 cm−1 and 3334 cm−1, indicating the presence of Fermi resonance. Hence, based on the Fermi resonance bands, it was deduced that the PhAc⋯H2O complex involves O–H⋯π interactions through the acetylenic-π, while the PhAc⋯CH3OH complex exhibits O–H⋯π interactions through the phenyl π-system. The PhAc⋯H2O complex has already been previously investigated by microwave spectroscopy and has confirmed the unambiguous structure of the complex to the acetylenic bound conformer.10

Karir et al. explored the docking preference of CH3OH in the PhAc and its mono-methylated derivative (3-methylphenylacetylene) using FTIR spectroscopy of supersonic jet expansions.2 The FTIR jet spectra of the 3-methylphenylacetylene⋯CH3OH complex displayed two additional peaks at 3620 cm−1 and 3639 cm−1 in the O–H stretch region (see Fig. S7 of ref. 1, ESI†) compared to the spectrum of bare methanol (3686 cm−1), therefore these new bands were attributed to the acetylene and phenyl docking of the CH3OH. It is well-established that deuteration strengthens the hydrogen bond due to reduction of zero point vibrational energy (ZPVE). The observed spectrum of 3-methylphenylacetylene⋯CH3OD complex was very similar (OD stretch region was scaled to the OH stretch region by using a scaling factor of 1.356) with a reduction in intensity noted for the less shifted band (Fig. 4 of ref. 1). Thus, the band at 3620 cm−1 was assigned to the acetylenic bound whereas the band at 3639 cm−1 was assigned to the phenyl bound structure. The observation of both the phenyl and acetylene bound structure in 3-methylphenylacetylene⋯CH3OH complex is possible if the barriers between the docking sites are too high to be overcome. The DFT calculations (refer to Table 1 of ref. 1) also suggested that the acetylenic bound structure is the more favourable case in 3-methylphenylacetylene⋯CH3OH complex therefore the binding preference in this complex is shifted towards the acetylenic coordination by deuteration and also shifted in the same direction in the PhAc⋯CH3OH complex. In the FTIR jet spectra of the PhAc⋯CH3OH complex, a vibrational frequency associated with hydrogen bonded O–H stretching was detected only at 3622 cm−1. This value notably deviates from that previously reported by Singh et al. (3615 cm−1 for CH3OH complex). This disparity in the experimentally obtained vibrational frequencies within the same complex are attributed to inaccuracies in calibration during the laser experiment. Additionally, there is a notable discrepancy between the result of 3622 cm−1 and the measured vO–H of 3613 cm−1 for the PhAc⋯H2O complex, for which no explanation was provided. The DFT-predicted and experimentally observed vibrational frequencies (taken from ref. 1) are given in Table S15 of the ESI,† for the hydrogen bonded O–H in the acetylenic and phenyl bound conformations for PhAc⋯H2O, PhAc⋯CH3OH and 3-methylphenylacetylene⋯CH3OH. As described above, the assignments for PhAc⋯CH3OH complexes were based on consistent deviations between DFT predictions and experimental results across various systems, further supported by isotope effects in the methylated derivative of PhAc.

The second moment, Pcc, calculated from the optimized structures at the DFT and MP2 levels of theories are presented in Table 1. It is apparent that the Pcc values for the (M–P)Ac structure optimized at MP2 and DFT exhibit substantial discrepancies. This discrepancy can be attributed to the presence of a secondary interaction in the DFT-optimized (M–P)Ac structure, which significantly impacts the overall configuration, despite both structures involving CH3OH donating a hydrogen bond to the acetylenic moiety. The experimentally-determined values of Pcc for the parent and other isotopologues are provided in Tables 2–4, obtained during A-state only fits and global fitting containing both A- and E-state transitions. The experimental second moments closely align with the DFT-calculated (M–P)Ac structure. The replacement of a bonded hydrogen atom of CH3OH causes minimal changes to the Pcc value, whereas the substitution of all four hydrogen atoms of the CH3OH moiety results in a notable increase.

By using the Kraitchman approach,68 the singly substituted isotopologues enable a direct structural examination of the complex. These equations could be used to find the position of the substituted atom from the centre of mass. For a non-planar asymmetric top molecule, the coordinate (rs) of the substituted atom is given as follows:

image file: d4cp01916d-t11.tif
where, Pa, Pb and Pc represent the planar moment of inertia. The Kraitchman analysis operates under the assumption that bond distances and angles remain constant upon isotopic substitution. While this assumption generally holds for heavier atoms, the substitution of hydrogen (H) with deuterium (D) can lead to significant alterations in zero-point average positions. Consequently, H/D substitution may not always yield accurate positions for the substituted atoms. The KRA program,69 developed by Kisiel and available on the PROSPE70 website, was employed for this analysis. In this context, the PhAc⋯CH3OH complex served as the parent isotopologue.

In Fig. 6, we present the labelling of atoms within the molecular complex, along with an approximate orientation of the inertial axis framework. The rotational constants obtained using XIAM fitting approach, which contains both A- and E-species transitions, were utilised for the derivation of rs coordinates for the acetylenic H atom (H14) and the carbon atom of CH3OH (C15).


image file: d4cp01916d-f5.tif
Fig. 5 Labelling of the atoms used in the structural analysis for the PhAc⋯CH3OH complex. The approximate location of the principal axes is shown.

image file: d4cp01916d-f6.tif
Fig. 6 Atoms in Molecules (AIM) topology study for the PhAc⋯CH3OH and PhAc⋯H2O complexes. The green dots and red dots refer to the bond critical point and ring critical points respectively.

These coordinates, along with associated Costain errors,71 are provided in Table 6. It is noteworthy that the Kraitchman method does not yield the signs of atomic coordinates, which have been inferred from the outcomes of DFT calculations. The rs coordinate of the bonding hydrogen atom (H20) of the CH3OH sub-unit was found to deviate from the corresponding coordinate in the calculated structural model. This discrepancy can be attributed to the interplay between the methyl internal rotation and the large amplitude motion of the OH group in the CH3OH.

Table 6 Kraitchman substitution coordinates (rs) for the substituted atoms of the PhAc⋯CH3OH complex. The coordinates are given in Å. Labelling of the atoms is shown in Fig. 5. Theoretical values correspond to the (M–P)Ac structure
Atom number Method Coordinates
a b c
H14 Theory 2.4776 2.9328 −0.2894
Experiment 2.3578(7) 2.9401(6) −0.492(3)
C15 Theory 2.8611 −1.2257 0.9626
Experiment 2.8282(5) −1.296(1) 0.986(2)

Following a rigorous examination of the spectra of all five isotopologues, the structural configuration where CH3OH forms a hydrogen bond with the phenyl π system could not be observed. Since the spectral assignment in the case of results obtained by Singh et al. was exclusively based on the presence and absence of Fermi resonance, one possibility is that the PhAc⋯CH3OH complex has a structure (CH3OH is interacting with acetylenic-π system) that is observed by both FTIR spectroscopic study and the present study by microwave spectroscopy, while the Fermi resonance is unaffected. If this is the case, then all three experimental results give a consistent structure. The current study using microwave spectroscopy provides an unambiguous structure for PhAc⋯CH3OH complex, wherein MeOH is forming hydrogen bond with the acetylenic π-system followed by a secondary weak C–H⋯O interaction. The present study further supports the conclusions drawn through FTIR spectroscopic results.2

Atoms in molecules (AIM) analysis

The present study employs the atoms in molecules (AIM)47 topological analysis to perform a comparative assessment of the bonding characteristics between PhAc⋯CH3OH and PhAc⋯H2O complexes. It is noteworthy that the AIM analysis for the PhAc⋯H2O complex has been previously reported.9 The wavefunctions for PhAc⋯CH3OH were obtained at the B3LYP-D3/aug-cc-pVDZ level of theory, whereas, for PhAc⋯H2O, they were derived from previously reported coordinates optimized at the MP2/aug-cc-pVDZ level of theory.10

The molecular graph for the PhAc⋯CH3OH complex closely resembles that of the PhAc⋯H2O complex except for the one additional bond critical point (BCP) and ring critical point (RCP) found in the PhAc⋯CH3OH complex. The first BCP occurs between the hydroxyl hydrogen atom of CH3OH/H2O and the midpoint of the π-bond in PhAc, while the second BCP is situated between the oxygen atom of CH3OH/H2O and the ortho-hydrogen atom of PhAc. The third BCP in case of PhAc⋯CH3OH complex is present between one of the hydrogen atoms of the methyl group to the ortho-carbon atom of the PhAc. The electron densities (ρ) and Laplacian (∇2ρ) values for all BCPs are provided in Table 7. The molecular graphs showing BCP's and RCP's are given in Fig. 6. These ρ and ∇2ρ values for both complexes fall within the range defined by Koch and Popelier for C–H⋯O hydrogen bonds.72 A comparison of the electron densities at the BCP for O–H⋯π and C–H⋯O interactions in PhAc⋯CH3OH and PhAc⋯H2O complexes reveals that both interactions contribute equally to the stability of the observed geometries. Consistent with the findings in the PhAc⋯H2O complex, the C–H⋯O interaction in the PhAc⋯CH3OH complex is as strong as the O–H⋯π interaction.

Table 7 Electron density (ρ) and the Laplacian of the electron density (∇2ρ) of the PhAc⋯CH3OH and PhAc⋯H2O complexes
Interactions PhAc⋯CH3OH Interactions PhAc⋯H2O
ρ (a.u) ∇2ρ (a.u) ρ (a.u) ∇2ρ (a.u)
O19–H20⋯π 0.013 +0.033 O15–H16⋯π 0.013 +0.036
C6–H11⋯O19 0.011 +0.031 C3–H11⋯O15 0.011 +0.032
C15–H17⋯C6 0.005 +0.020 — — —

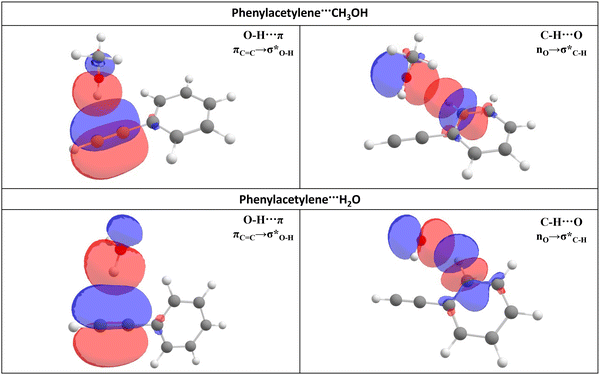
Natural bond orbital analysis

In this study, a natural bond orbital (NBO)51,73 analysis was performed utilizing NBO 6.0 at the B3LYP-D3/aug-cc-pVDZ level of theory to assess the intermolecular orbital interactions within the PhAc⋯CH3OH and PhAc⋯H2O complexes. The Cartesian coordinates for the PhAc⋯CH3OH complex were derived from the optimized structure at the B3LYP-D3/aug-cc-pVDZ level of theory, while for the PhAc⋯H2O complex, the Cartesian coordinates were obtained from the previously reported structure optimized at MP2/aug-cc-pVDZ method.10 The second-order perturbation energy (E(2)) was utilized as a quantitative measure of the strength of delocalization interactions. The computed E(2) values for O–H⋯π and C–H⋯O interactions are provided in Table 8 for both the complexes and shown in Fig. 7. Similar to the PhAc⋯H2O system, for the PhAc⋯CH3OH complex also, the NBO analysis reveals two significant stabilization interactions. The first interaction involves the delocalization between the π-cloud of PhAc and the σ* antibonding orbital of the CH3OH/H2O hydroxyl (OH), denoted as πC[double bond, length as m-dash]C → σO–H*. The second interaction is characterized by the interaction between the lone pair of electrons on the oxygen atom of CH3OH/H2O and the σ* antibonding orbital of the C–H group located at the ortho position in PhAc, represented as nO → σC–H*. Our findings indicate that for the PhAc⋯CH3OH complex, the E(2) value for the πC[double bond, length as m-dash]C → σO–H* interaction is 10.8 kJ mol−1 and for nO → σC–H* interaction it is 7.1 kJ mol−1. Whereas, for PhAc⋯H2O complex, E(2) value for the πC[double bond, length as m-dash]C → σO–H* interaction is 13.3 kJ mol−1 and for nO → σC–H* interaction it is 10.0 kJ mol−1. These results highlight that the O–H⋯π interaction makes the most substantial contribution to the overall interaction strength.
Table 8 Second-order perturbation energies (E(2)) for interacting orbitals shown in Fig. 7, calculated at B3LYP-D3/aug-cc-pVDZ level of theory
Interaction E (2) (kJ mol−1)
PhAc⋯CH3OH PhAc⋯H2O
πC[double bond, length as m-dash]C → σO–H* 10.8 13.3
nO → σC–H* 7.1 10.0


image file: d4cp01916d-f7.tif
Fig. 7 Interacting natural orbitals in PhAc⋯CH3OH and PhAc⋯H2O complexes.

Non-covalent interactions (NCI) index analysis

The analysis of the non-covalent interactions (NCI) index48,74–76 was also conducted to gain an understanding of the interactions found in the PhAc⋯CH3OH complex. The NCI plots were acquired using the Multiwfn 3.6 software.50Fig. 8 shows the plots depicting the product of the sign of the second eigenvalue (λ2) of the electron density Hessian matrix and the electron density (ρ) in relation to the reduced density gradient (RDG). The sign of λ2*ρ holds significance, as negative values of this quantity indicate attractive interactions (such as hydrogen bonds or van der Waals interactions), while positive values indicate non-bonded interactions (such as steric repulsion). The NCI plots exhibit spikes in both positive and negative directions, which can be regarded as an approximate indication of the critical points obtained from the AIM analysis. Similar to AIM analysis, the presence of O–H⋯π, C–H⋯O and C–H⋯C interactions are indicated by the observed three green isosurfaces.
image file: d4cp01916d-f8.tif
Fig. 8 Non-covalent interactions (NCI) index plots for PhAc⋯CH3OH complex.

Symmetry-adapted perturbation theory (SAPT) analysis

In order to elucidate the primary forces responsible for stabilizing the acetylene-bound structure, we conducted symmetry adapted perturbation theory (SAPT)52 calculations. All the SAPT Analysis were performed using PSI4 software.53 As previously discussed in Section 3.1, there exists a notable disparity between the acetylene-bound structures optimized using the B3LYP-D3/aug-cc-pVDZ and MP2/aug-cc-pVDZ levels of theory. To shed light on the experimental observations, we employed SAPT-DFT and SAPT2+3 approaches, utilizing the aug-cc-pVDZ basis set. Specifically, SAPT-DFT was applied to the structures optimized at the B3LYP-D3/aug-cc-pVDZ level of theory, while SAPT2+3 was performed on the structures optimized at the MP2/aug-cc-pVDZ level. The outcomes of the SAPT calculations are summarized in Table 9, and visual representations of the energy components are presented in Fig. 9. A consistent trend emerges from both SAPT-DFT and SAPT-‘2 + 3’ analyses, revealing that the phenyl-bound structure exhibits similar energy component patterns, with the highest contribution stemming from dispersion forces. However, for acetylene-bound structures, SAPT-DFT and SAPT2+3 gave different results. SAPT-DFT results highlight the predominance of electrostatic forces, while SAPT2+3 identifies dispersion interactions as the dominant component. This discrepancy can be attributed to the distinct structural characteristics of acetylene-bound complexes at different levels of theory. As, in the structure optimized at the MP2/aug-cc-pVDZ level of theory, the methyl group is positioned atop the phenyl ring. In contrast, the structure optimized at the B3LYP-D3/aug-cc-pVDZ level of theory situates the methyl group away from the phenyl ring, accompanied by the presence of a secondary interaction between the lone pair of oxygen and the ortho C–H group of PhAc. This additional interaction contributes to the electrostatic energy component, accounting for the variation in SAPT results between the two acetylene-bound structures. Therefore, the observed structure demonstrates that electrostatics plays a significant role, contributing 48.4% to the total attractive component. Previous investigations on the PhAc⋯H2O complex have revealed that electrostatics is the dominant force responsible for stabilizing the complex.1 Conversely, in the case of the PhAc⋯H2S complex, dispersion emerges as the prevailing force. The Table S16 ESI,† provides the SAPT‘2 + 3’ calculations for both the PhAc⋯H2O and PhAc⋯H2S systems.
Table 9 SAPT‘2 + 3’ and SAPT-DFT interaction energy decomposition (kJ mol−1) for PhAc⋯CH3OH complex calculated at MP2/aug-cc-pVDZ and B3LYP-D3/aug-cc-pVDZ level of theories respectively
Method Structures E Electrostatics E Induction E Dispersion E Exchange E Interaction
SAPT‘2 + 3’ OH⋯πPh −17.6 −6.8 −29.7 37.8 −16.3
MP2/aug-cc-pVDZ OH⋯πAc −20.2 −7.0 −29.1 39.4 −16.9
SAPT‘DFT’ OH⋯πPh −12.7 −4.1 −20.4 21.7 −15.5
B3LYP-D3/aug-cc-pVDZ OH⋯πAc −25.6 −7.5 −19.8 35.8 −17.1


image file: d4cp01916d-f9.tif
Fig. 9 Bar charts depicting the energy decomposition using the SAPT2+3 and SAPT-DFT calculations for the PhAc⋯CH3OH complex calculated at MP2/aug-cc-pVDZ and B3LYP-D3/au-cc-pVDZ level of theories respectively.

Conclusions

The rotational spectra of a complex formed between PhAc and CH3OH, as well as its isotopologues PhAc⋯CH3OD, PhAc⋯CD3OD, PhAc-D⋯CH3OH, and PhAc⋯13CH3OH, were recorded and analysed. These findings indicate that the structure of the complex observed during the present work is consistent with that previously reported by Karir et al. In the proposed structure, CH3OH donates a hydrogen bond to the acetylenic π-cloud, while the ortho C–H group of the PhAc complex forms a C–H⋯O hydrogen bond with the oxygen atom of the CH3OH moiety. Notably, the observed structure is consistent with the acetylenic bound structure calculated using the B3LYP-D3/aug-cc-pVDZ level of theory. The (V3) barrier to internal rotation of the CH3 group within the complex was determined to be 235 cm−1 in fits, where F0 was also floated and determined to be 6.16(6) cm−1. The result thus obtained for V3 is in reasonable agreement with the barrier height calculated at the B3LYP-D3/aug-cc-pVDZ level of theory. However, as discussed in Section 4, tabulations of the reduced barrier height, s = 4V3/9F suggest that the value of this parameter may provide a more direct perspective on patterns of intramolecular bonding within CH3OH-containing complexes. The result of s = 16.96 for PhAc⋯CH3OH is similar to the values reported for several other complexes in which CH3OH acts as a hydrogen bond donor, providing additional support to the structure determined. The SAPT-DFT analysis suggests that the electrostatic energy component plays a significant role in stabilizing the experimentally observed structure. These findings provide valuable insights into the structural and energetic aspects of the observed PhAc⋯CH3OH complex.

It should be noted that Singh et al.'s conclusion that PhAc⋯CH3OH contains a hydrogen bond donated by the O–H group of CH3OH to the phenyl π-cloud has been very well supported by IR/UV double resonance spectroscopic experiments and ab initio computations. However, the evidence of the CH3OH donating hydrogen bond to the phenyl π-system was concluded based on the presence or absence of the Fermi resonance in the FDIR spectra of the C–H stretch region. The Fermi resonance bands which involve the acetylenic π-cloud, was not affected in the PhAc⋯CH3OH complex, whereas in the PhAc⋯H2O complex, the Fermi resonance disappeared and gave only one peak corresponding to the C–H oscillator. In case, the interaction in PhAc⋯CH3OH complex having similar structure as PhAc⋯H2O complex does not affect the Fermi resonance, it is likely that there is no discrepancy in the experimental results about the global minimum structure.

There is clearly a need for further investigation which might rationalise all the observations made during this and previous works. One possible explanation can be immediately stated: it is possible that the isomer of PhAc⋯CH3OH complex observed by Singh et al. authentically has a different structure from that observed during the present work. However, given the extensive similarities between the experimental conditions of this work and those used by Singh et al., which each involved co-expansion of the PhAc and CH3OH precursors within a buffer gas of helium, this seems very unlikely.

Author contributions

SG: investigations, formal analysis, validation and writing-original draft. CNC: investigations, formal analysis, validation and writing – review and editing. NRW: supervision, funding acquisition, and writing – review and editing. EA: conceptualization, supervision, funding acquisition, and writing – review and editing.

Data availability

All the data have been presented in the manuscript and the ESI† available in the journal website. Readers requiring any more information may contact the corresponding author whose email is given.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Scheme for Promotion of Academic and Research Collaboration (SPARC) Ministry of Human Resources Development, Project code P311 for financial support which helped this collaborative effort. The authors acknowledge the Engineering and Physical Sciences Research Council for a DTA studentship awarded to C. N. C. and the European Research Council for project funding (Grant No. CPFTMW-307000). E. A. and S. G. acknowledge financial support from the Indian Institute of Science and Department of Science and Technology, India. S. G. thanks the Inorganic and Physical Chemistry Department, IISc, and Prof. Sai. G. Ramesh for the use of Computational facilities.

References

  1. S. Maity, M. Guin, P. C. Singh and G. N. Patwari, Phenylacetylene: A hydrogen bonding chameleon, ChemPhysChem, 2011, 12, 26–46 CrossRef CAS PubMed.
  2. G. Karir, N. O. B. Lüttschwager and M. A. Suhm, Phenylacetylene as a gas phase sliding balance for solvating alcohols, Phys. Chem. Chem. Phys., 2019, 21, 7831–7840 RSC.
  3. R. Sedlak, P. Hobza and G. N. Patwari, Hydrogen-bonded complexes of phenylacetylene with water, methanol, ammonia, and methylamine. the origin of methyl group-induced hydrogen bond switching, J. Phys. Chem. A, 2009, 113, 6620–6625 CrossRef CAS PubMed.
  4. P. C. Singh and G. N. Patwari, IR-UV double resonance spectroscopic investigation of phenylacetylene-alcohol complexes. Alkyl group induced hydrogen bond switching, J. Phys. Chem. A, 2008, 112, 5121–5125 CrossRef CAS PubMed.
  5. S. Maity, G. N. Patwari, R. Sedlak and P. Hobza, A π-stacked phenylacetylene dimer, Phys. Chem. Chem. Phys., 2011, 13, 16706–16712 RSC.
  6. S. Maity, D. K. Maity and G. N. Patwari, Interaction of Alcohols with 2-Fluoro- and 4-Fluorophenylacetylenes: Infrared-Optical Double Resonance Spectroscopic and Computational Investigation, J. Phys. Chem. A, 2011, 115, 11229–11237 CrossRef CAS PubMed.
  7. P. C. Singh, B. Bandyopadhyay and G. N. Patwari, Structure of the phenylacetylene-Water complex as revealed by infrared-ultraviolet double resonance spectroscopy, J. Phys. Chem. A, 2008, 112, 3360–3363 CrossRef CAS PubMed.
  8. S. Islam Mondal, A. Dey, S. Sen, G. Naresh Patwari and D. Ghosh, Spectroscopic and ab initio investigation of 2,6-difluorophenylacetylene–amine complexes: coexistence of C–H⋯N and lone-pair⋯π complexes and intermolecular coulombic decay, Phys. Chem. Chem. Phys., 2015, 17, 434–443 RSC.
  9. M. Goswami and E. Arunan, Microwave spectrum and structure of C6H5CCH⋯H2S complex, J. Mol. Spectrosc., 2011, 268, 147–156 CrossRef CAS.
  10. M. Goswami and E. Arunan, Microwave Spectroscopic and Theoretical Studies on Phenylacetylene⋯H2O Complex: C–H⋯O and O–H⋯π Hydrogen Bonds as Equal Partners, Phys. Chem. Chem. Phys., 2011, 13, 14153–14162 RSC.
  11. K. Siglow and H. J. Neusser, Rotationally resolved UV spectroscopy of weakly bound complexes: structure and van der Waals vibronic bands of phenylacetylene·Ar, Chem. Phys. Lett., 2001, 343, 475–481 CrossRef CAS.
  12. H. Dreizler, B. Hartke and H. Dieter Rudolph, A contribution to the structure of the van-der-Waals complex phenylacetylene-argon by microwave spectroscopy and quantum chemistry, J. Mol. Struct., 2006, 825, 1–19 CrossRef CAS.
  13. G. Karir and K. S. Viswanathan, Phenylacetylene–water complex: Is it n⋯σ or H⋯π in the matrix?, J. Mol. Struct., 2016, 1107, 145–156 CrossRef CAS.
  14. F. C. De Lucia, E. Herbst, T. Anderson and P. Helminger, The Analysis of the Rotational Spectrum of Methanol to Microwave Accuracy, J. Mol. Spectrosc., 1989, 134, 395–411 CrossRef CAS.
  15. R. M. Lees, Torsion-vibration-rotation interactions in methanol. II Microwave spectrum of CD3OD, J. Chem. Phys., 1972, 56, 5887–5890 CrossRef CAS.
  16. R. M. Lees and J. G. Baker, Torsion-vibration-rotation interactions in methanol. I. Millimeter wave spectrum, J. Chem. Phys., 1968, 48, 5299–5318 CrossRef CAS.
  17. M. Ndao, F. Kwabia Tchana, L. H. Coudert, R. A. Motiyenko, L. Margulès, J. Barros, L. Manceron and P. Roy, The torsional and rotation–torsion spectra of CD2HOH, J. Mol. Spectrosc., 2016, 326, 136–143 CrossRef CAS.
  18. Y. B. Duan and A. B. McCoy, Global Fit of Torsion-Rotational Transitions in the First Three Torsional States of CH3OD, J. Mol. Spectrosc., 2000, 199, 302–306 CrossRef CAS PubMed.
  19. A. El Hilali, L. H. Coudert, I. Konov and S. Klee, Analysis of the torsional spectrum of monodeuterated methanol CH2DOH, J. Chem. Phys., 2011, 135, 194309 CrossRef CAS PubMed.
  20. F. J. Lovas and H. Hartwig, The Microwave Spectrum of the Methanol Dimer for K = 0 and 1 States, J. Mol. Spectrosc., 1997, 185, 98–109 CrossRef CAS PubMed.
  21. C. L. Lugez, F. J. Lovas, J. T. Hougen and N. Ohashi, Global Analysis of a-, b-, and c-Type Transitions Involving Tunneling Components of K = 0 and 1 States of the Methanol Dimer, J. Mol. Spectrosc., 1999, 194, 95–112 CrossRef CAS PubMed.
  22. N. Ohashi and J. T. Hougen, Analysis and Global Fit of Tunneling Splittings in the K = 0 a-Type Microwave Spectrum of the Methanol Dimer, J. Mol. Spectrosc., 1995, 170, 493–505 CrossRef CAS.
  23. C. Medcraft, S. Zinn, M. Schnell, A. Poblotzki, J. Altnöder, M. Heger, M. A. Suhm, D. Bernhard, A. Stamm, F. Dietrich and M. Gerhards, Aromatic embedding wins over classical hydrogen bonding-a multi-spectroscopic approach for the diphenyl ether-methanol complex, Phys. Chem. Chem. Phys., 2016, 18, 26975–26983 RSC.
  24. F. J. Lovas, R. D. Suenram, G. T. Fraser, C. W. Gillies and J. Zozom, The microwave spectrum of formamide-water and formamide-methanol complexes, J. Chem. Phys., 1988, 88, 722–729 CrossRef CAS.
  25. R. D. Suenram, F. J. Lovas, G. T. Fraser, J. Z. Gillies, C. W. Gillies and M. Onda, Microwave Spectrum, Structure, and Electric Dipole Moment of Ar–CH3OH, J. Mol. Spectrosc., 1989, 137, 127–137 CrossRef CAS.
  26. X.-Q. Tan, I. I. Ioannou and R. L. Kuczkowski, The methanol·HCl complex: structure and methyl group internal rotation barrier, J. Mol. Struct., 1995, 356, 105–115 CrossRef CAS.
  27. L. Sun, X. Q. Tan, J. J. Oh and R. L. Kuczkowski, The microwave spectrum and structure of the methanol·SO2 complex, J. Chem. Phys., 1995, 103, 6440–6449 CrossRef CAS.
  28. X.-Q. Tan, I. I. Ioannou, K. B. Foltz and R. L. Kuczkowski, The Methanol·Trimethylamine Complex: Structure and Large Amplitude Motions, J. Mol. Spectrosc., 1996, 177, 181–193 CrossRef CAS.
  29. M. Haeckel and W. Stahl, The Microwave Spectrum and Molecular Structure of the Hydrogen-Bonded Aniline-Methanol Complex, J. Mol. Spectrosc., 1999, 198, 263–277 CrossRef CAS PubMed.
  30. F. J. Lovas, S. P. Belov, M. Y. Tretyakov, J. Ortigoso and R. D. Suenram, The Microwave Spectrum and Structure of the CH3OH·CO Dimer, J. Mol. Spectrosc., 1994, 167, 191–204 CrossRef CAS.
  31. V. V. Ilyushin, F. J. Lovas and D. F. Plusquellic, Microwave spectrum of the heterodimers: CH3OH–CO2 and CH3OH–H2CO, J. Mol. Spectrosc., 2006, 239, 94–100 CrossRef CAS.
  32. A. Westphal, C. Jacoby, C. Ratzer, A. Reichelt and M. Schmitt, Determination of the intermolecular geometry of the phenol–methanol cluster, Phys. Chem. Chem. Phys., 2003, 5, 4114–4122 RSC.
  33. H. C. Gottschalk, A. Poblotzki, M. Fatima, D. A. Obenchain, C. Pérez, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, M. Krasowska, L. C. Kröger, K. Leonhard, M. Mogren Al-Mogren, H. Mouhib, F. Neese, M. N. Pereira, M. Prakash, I. S. Ulusoy, R. A. Mata, M. A. Suhm and M. Schnell, The first microsolvation step for furans: new experiments and benchmarking strategies, J. Chem. Phys., 2020, 152, 164303 CrossRef CAS PubMed.
  34. D. Bernhard, F. Dietrich, M. Fatima, C. Pérez, H. C. Gottschalk, A. Wuttke, R. A. Mata, M. A. Suhm, M. Schnell and M. Gerhards, The phenyl vinyl ether–methanol complex: a model system for quantum chemistry benchmarking, Beilstein J. Org. Chem., 2018, 14, 1642–1654 CrossRef CAS PubMed.
  35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
  36. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Results obtained with the correlation energy density functionals of becke and Lee, Yang and Parr, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
  37. S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
  38. A. D. Becke, Density-functional thermochemistry. I. The effect of the exchange-only gradient correction, J. Chem. Phys., 1992, 96, 2155–2160 CrossRef CAS.
  39. S. Grimme and M. Steinmetz, Effects of London dispersion correction in density functional theory on the structures of organic molecules in the gas phase, Phys. Chem. Chem. Phys., 2013, 15, 16031 RSC.
  40. C. Møller and M. S. Plesset, Note on an Approximation Treatment for Many-Electron Systems, Phys. Rev., 1934, 46, 618–622 CrossRef.
  41. J. S. Binkley and J. A. Pople, Møller-Plesset theory for atomic ground state energies, Int. J. Quantum Chem., 1975, 9, 229–236 CrossRef CAS.
  42. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
  43. A. Schäfer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
  44. T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
  45. R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
  46. S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
  47. R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon Press; Oxford University Press, Oxford [England]: New York, 1994 Search PubMed.
  48. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, NCIPLOT: A Program for Plotting Noncovalent Interaction Regions, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
  49. F. Weinhold, C. R. Landis and E. D. Glendening, What is NBO analysis and how is it useful?, Int. Rev. Phys. Chem., 2016, 35, 399–440 Search PubMed.
  50. T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
  51. E. D. Glendening, C. R. Landis and F. Weinhold, NBO 6.0: Natural bond orbital analysis program, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
  52. T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, Levels of symmetry adapted perturbation theory (SAPT). I. Efficiency and performance for interaction energies, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
  53. R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
  54. D. Loru, M. A. Bermúdez and M. E. Sanz, Structure of fenchone by broadband rotational spectroscopy, J. Chem. Phys., 2016, 145, 074311 CrossRef PubMed.
  55. D. P. Zaleski, S. L. Stephens and N. R. Walker, A perspective on chemistry in transient plasma from broadband rotational spectroscopy, Phys. Chem. Chem. Phys., 2014, 16, 25221–25228 RSC.
  56. G. A. Cooper, C. Medcraft, J. D. Littlefair, T. J. Penfold and N. R. Walker, Halogen bonding properties of 4-iodopyrazole and 4-bromopyrazole explored by rotational spectroscopy and ab initio calculations, J. Chem. Phys., 2017, 147, 214303 CrossRef PubMed.
  57. E. Arunan, A. P. Tiwari, P. K. Mandal and P. C. Mathias, Pulsed nozzle Fourier transform microwave spectrometer: Ideal to define hydrogen bond radius, Curr. Sci., 2002, 82, 533–540 CAS.
  58. A. P. Cox, I. C. Ewart and W. M. Stigliani, Microwave Spectrum, Structure and Dipole Moment of PhenyIacetylene, J. Chem. Soc., Faraday Trans. 2, 1975, 71, 504–514 RSC.
  59. H. Dreizler, H. D. Rudolph and B. Hartke, A contribution to the microwave spectrum and structure of phenylacetylene, J. Mol. Struct., 2004, 698, 1–24 CrossRef CAS.
  60. K. Mayer, C. West, F. E. Marshall, G. Sedo, G. S. Grubbs, L. Evangelisti and B. H. Pate, Accuracy of quantum chemistry structures of chiral tag complexes and the assignment of absolute configuration, Phys. Chem. Chem. Phys., 2022, 24, 27705–27721 RSC.
  61. J. K. G. Watson, Determination of Centrifugal Distortion Coefficients of Asymmetric-Top Molecules. III. Sextic Coefficients, J. Chem. Phys., 1968, 48, 4517–4524 CrossRef CAS.
  62. C. M. Western, PGOPHER: A program for simulating rotational, vibrational and electronic spectra, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221–242 CrossRef CAS.
  63. E. Gougoula, C. N. Cummings, C. Medcraft, J. Heitkämper and N. R. Walker, Microwave spectra, molecular geometries, and internal rotation of CH3 in N-methylimidazole⋯H2O and 2-methylimidazole⋯H2O Complexes, Phys. Chem. Chem. Phys., 2022, 24, 12354–12362 RSC.
  64. C. N. Cummings, I. Kleiner and N. R. Walker, Noncovalent Interactions in the Molecular Geometries of 4-Methylthiazole⋯H2O and 5-Methylthiazole⋯H2O Revealed by Microwave Spectroscopy, J. Phys. Chem. A, 2023, 127, 8133–8145 CrossRef CAS PubMed.
  65. M. Schmitt, J. Küpper, D. Spangenberg and A. Westphal, Determination of the structures and barriers to hindered internal rotation of the phenol-methanol cluster in the S0 and S1 states, Chem. Phys., 2000, 254, 349–361 CrossRef CAS.
  66. X. Q. Tan, L. H. Sun and R. L. Kuczkowski, The Methanol·Ar Complex: Apparent Reduction of the Methyl Group Internal Rotation Barrier, J. Mol. Spectrosc., 1995, 171, 248–264 CrossRef CAS.
  67. R. N. Pribble, A. W. Garrett, K. Haber and T. S. Zwier, Resonant ion-dip infrared spectroscopy of benzene–H2O and benzene–HOD, J. Chem. Phys., 1995, 103, 531–544 CrossRef CAS.
  68. J. Kraitchman, Determination of Molecular Structure from Microwave Spectroscopic Data, Am. J. Phys., 1953, 21, 17–24 CrossRef CAS.
  69. Structural Calculations, https://info.ifpan.edu.pl/~kisiel/struct/struct.htm#kra, (accessed August 30, 2023).
  70. PROSPE-ProgramsforROtationalSPEctroscopy, https://info.ifpan.edu.pl/~kisiel/prospe.htm#table_of_programs, (accessed August 30, 2023).
  71. C. C. Costain, Determination of Molecular Structures from Ground State Rotational Constants, J. Chem. Phys., 1958, 29, 864–874 CrossRef CAS.
  72. U. Koch and P. L. A. Popelier, Characterization of C–H–O Hydrogen Bonds on the Basis of the Charge Density, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
  73. A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
  74. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
  75. J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, Are Bond Critical Points Really Critical for Hydrogen Bonding?, J. Chem. Theory Comput., 2013, 9, 3263–3266 CrossRef CAS PubMed.
  76. J. Contreras-García, W. Yang and E. R. Johnson, Analysis of Hydrogen-Bond Interaction Potentials from the Electron Density: Integration of Noncovalent Interaction Regions, J. Phys. Chem. A, 2011, 115, 12983–12990 CrossRef PubMed.

Footnote

† Electronic supplementary information (ESI) available: Tables of microwave transitions measured for parent and five isotopologues of the title complex (Tables S1–S6), equilibrium geometries of the complex optimized at various levels (Tables S7–S11), normal mode vibrational wave numbers at two different levels (Tables S12–S13), experimental rotational constants from the global fit (Table S14), experimental and computed C–H/O–H stretching wavenumbers from ref. 1 and 2 (Table S15) and results from SAPT energy decomposition analysis (Table S16) are available online as ESI. See DOI: https://doi.org/10.1039/d4cp01916d
This journal is © the Owner Societies 2024
Click here to see how this site uses Cookies. View our privacy policy here.