Open Access Article
Open Access ArticleAb initio electronic structure analysis of ground and excited states of HfN0,+†
Isuru R.
Ariyarathna
 *
*
Physics and Chemistry of Materials (T-1), Los Alamos National Laboratory, Los Alamos, NM 87545, USA. E-mail: isuru@lanl.gov
First published on 16th July 2024
Abstract
High-level ab initio electronic structure analysis of third-row transition metal (TM)-based diatomic species is challenging and has been perpetually lagging. In this work, fourteen and eighteen electronic states of HfN and HfN+ respectively are studied, employing multireference configuration interaction (MRCI) and coupled cluster singles doubles and perturbative triples [CCSD(T)] theories under larger correlation-consistent basis sets. Their potential energy curves (PECs), energetics, and spectroscopic parameters are reported. Core electron correlation effects on their properties are also investigated. Chemical bonding patterns of several low-lying electronic states are introduced based on the equilibrium electron configurations. The ground state of HfN (X2Σ+) has the 1σ22σ23σ11π4 electronic configuration, and the ionization of the 3σ1 electron produces the ground state of HfN+ (X1Σ+). Ground states of both HfN and HfN+ are triple bonded in nature and bear 124.86 and 109.10 kcal mol−1 binding energies with respect to their ground state fragments. The findings of this work agree well with the limited experimental literature available and provide useful reference values for future experimental analysis of HfN and HfN+.
I. Introduction
Today, scientists are making great advances in synthesizing and characterizing a variety of TM-based molecular systems with novel or improved chemicophysical properties for applications in electronics, catalysis, pharmaceutics, and many other industrial fields. Indeed, chemical bonding is the basis that allows for a particular molecular structure to exist and permits geometrical manipulations to synthesize desired complexes. Hence, understanding the nature of the chemical bonding is vital. Utilization of high-level theoretical tools for gaining insight on electronic structures and bonding of molecular systems is rather common. However, such theoretical studies of TM-based systems are challenging due to their complicated electronic structures. Especially, bonding analysis of TM-based diatomic species is demanding owing to their many closely lying electronic structures, multireference characteristics of the states, and the dependence of results on the level of theory utilized.1,2Over the years, several attempts have been made to demystify the chemical bonding of TM monoxides primarily aiming to investigate the oxidation process of TM surfaces and to understand and predict catalytic properties of TM oxides.1,3–7 Of course, investigation of TM nitrides (or TM–N bond) is equally important because of their applications in various fields. For example, TM nitride systems are being applied as electrochemical energy storage materials,8 coating materials,9,10 dielectrics, semiconductors, and electrical conductors.11 Furthermore, they are potential electrocatalysts for water splitting reactions12,13 and are also being tested as photocatalysts.14,15 So far, ab initio electronic structure analysis of ground and excited states of all first-row (Sc–Cu)1 and several second-row TMs mononitrides (Y–Rh)16–23 have been reported. Relatively, such studies are scarce for third-row TM mononitrides and hence this work is devoted to high-level ab initio analysis of the third-row TM mononitride HfN and its cation.
The first bonding analysis of HfN goes back to Karl Gingerich's work in 1968 of analyzing bond energies of HfN.24 This study estimated a 141 kcal mol−1D0 for HfN. In 1973, Kohl and Stearns identified HfN by a molecular beam mass spectrometric study and reported a D0 of 126.83(7.15) kcal mol−1 for HfN.25 Six years later, DeVore and Gallaher performed a vibrational infrared spectroscopic analysis for HfN and determined its harmonic vibrational frequency (ωe) and bond distance (re) to be 919.5(20) cm−1 and 1.69(30) Å, respectively.26 Furthermore, based on the spectral features, they predicted a 2Σ+ ground state for the molecule.26 In 1997, Ram and Bernath carried out a Fourier transform infrared spectroscopic analysis to investigate the electronic emission spectrum of HfN and observed a set of bands in the 5500–6800 cm−1 region that corresponds to the [6.7]2Σ+–X2Σ+ transition.27 Furthermore, they reported a re of 1.724678(36) Å, ωe of 932.7164(15) cm−1, and anharmonicity (ωexe) of 4.41299(65) cm−1 for HfN.27 Importantly, they highlighted the fact that more experimental and theoretical analyses are necessary to understand low-lying states of HfN, but twenty-seven years since their discovery, this system still remains poorly understood. In 1999 Kushto et al.28 performed density functional theory (DFT) BP86 calculations for HfN, and their re (1.734 Å) and ωe (942 cm−1) values are in reasonable agreement with the findings of Ram and Bernath.27 Another DFT/B3LYP study carried out by Hong et al.,29 reported a dissociation energy (De) of 113.92 kcal mol−1, ωe of 940 cm−1, re of 1.764 Å, ionization energy (IE) of 7.7 eV, and dipole moment (μ) of 5.70 D for HfN. Furthermore, under the same level of theory, they reported corresponding values for HfN+ (i.e., De of 91.55 kcal mol−1, ωe of 994 cm−1, re of 1.720 Å, and μ of 6.18 D).29 The most recent work on HfN is reported by the Morse group.30 They measured the D0 of HfN to be 123.93(9) kcal mol−1 using resonant two-photon ionization spectroscopy.30 Furthermore, they performed CCSD(T) analysis for HfN and the calculated D0 value at the complete basis set (CBS) limit is 127.99 kcal mol−1.30
In the present work, ground and excited electronic states of HfN and HfN+ were studied utilizing the ab initio MRCI, MRCI+Q, and CCSD(T) theories to shed light on their PECs, equilibrium electronic configurations, chemical bonding patterns, and De, re, Te, ωe, ωexe, and μ values. The basis set effects, core electron correlation effects, spin–orbit effects on the energy related properties and spectroscopic parameters are also reported.
II. Computational details
The MOLPRO 2023.2 quantum chemistry package was utilized for all calculations.31–33 In all cases, C2v Abelian sub point group of the original C∞v non-Abelian symmetries of HfN and HfN+ was used. First, full PECs of fourteen and eighteen low-lying electronic states of HfN and HfN+ respectively were produced at the internally contracted MRCI34–36 level using the correlation consistent aug-cc-pVQZ of N37 and cc-pVQZ-PP of Hf38 basis set. For Hf, the Stuttgart relativistic pseudopotential that substitutes 1s22s22p63s23p64s23d104p64d104f14 electrons was used (ECP60).38 Complete active space self-consistent field (CASSCF)39–42 reference wavefunctions (WFs) were provided for MRCI calculations. Specifically, the CAS(7,12) (7 electrons in 12 orbitals) and CAS(6,12) (6 electrons in 12 orbitals) active spaces were used for HfN and HfN+, respectively. When the fragments are well separated (>10 Å), the CASSCF active orbitals are pure 6s, 6p, and 5d atomic orbitals of Hf and the 2p atomic orbitals of N. Under the utilized C2v symmetry, they are 5a1 (6s, 5dz2, 5dx2−y2, and 6pz of Hf and 2pz of N), 3b1 (5dxz and 6px of Hf and 2px of N), 3b2 (5dyz and 6py of Hf and 2py of N), and 1a2 (5dxy of Hf). The doubly occupied 2s atomic orbital of N is excluded from the CASSCF active space to achieve proper convergences. At the MRCI level, all valence electrons including the 2s2 of N were correlated. The Davidson correction (MRCI+Q) was used to reduce the size extensivity errors. The produced MRCI and MRCI+Q PECs of electronic states were used to calculate each of their De, re, and Te values. Furthermore, by solving the ro-vibrational Schrödinger equation numerically, ωe and ωexe values of the electronic states were calculated. The MRCI dipole moment curves (DMCs) of several low-lying states of HfN and HfN+ are also reported. Note that the negative μ values indicate that the positive and negative dipoles of the molecule are aligned with the negative and positive sides of the z-axis of the Cartesian coordinate plane. Spin–orbit coupling effects were evaluated at the MRCI level under the same basis set using the Breit–Pauli Hamiltonian as implemented in MOLPRO.The CCSD(T)43 potential energy scans were performed around the equilibrium bond distance regions of several low-lying single-reference electronic states of HfN and HfN+ using the same aug-cc-pVQZ of N37 and cc-pVQZ-PP (60ECP) of Hf38 basis set to obtain their De, re, Te, ωe and ωexe values. To evaluate the effect of core electron correlation on the aforementioned properties of HfN and HfN+, another set of coupled cluster energy scans were carried out by correlating 5s25p6 core electrons of Hf with the aug-cc-pVXZ of N37 and cc-pwCVXZ-PP38 (60ECP) of Hf basis set (X = Q, 5). Hereafter, these calculations are labelled as QZ-C-CCSD(T) or 5Z-C-CCSD(T). Similar C-CCSD(T) calculations were performed for the ground states of HfN and HfN+ at X = T of aug-cc-pVXZ of N and cc-pwCVXZ-PP (60ECP) basis set [TZ-C-CCSD(T)], then the X = T, X = Q, and X = 5 PECs were extrapolated to the CBS limit to calculate CBS De, re, Te, ωe and ωexe of HfN and HfN+. From now on the CBS extrapolated C-CCSD(T) approach is denoted by CBS-C-CCSD(T). The IE of HfN was also calculated under these coupled cluster methods. Coupled cluster, μ values of several single-reference electronic states of HfN and HfN+ were calculated using the finite-field method embedded in MOLPRO by applying a field of 0.01 a.u. Hartree–Fock wavefunctions were used for all coupled cluster calculations.
III. Results and discussion
III.A. HfN
The MRCI level of theory is ideal for calculating full PECs of highly correlated TM-based diatomic systems because of its ability to represent both single-reference and multireference electronic states accurately. Hence to study the electronic states of HfN, MRCI PECs originating from several low energy fragments of Hf + N were considered.The ground state of Hf is an a3F that carries [Xe]4f145d26s2 electronic configuration.44 The 4f14 electrons of Hf are inert in nature but the four valence electrons (5d26s2 in ground state) and their excited configurations are known to readily participate in chemical reactions.7,45,46 The electron rearrangement within the 5d shell yields the first and second excited electronic states for Hf atom (i.e., a3P and a1D) that lie ∼16–26 kcal mol−1 and ∼16 kcal mol−1 above, respectively.44 The same 5d26s2 electronic configuration is carried by its fourth excited state (i.e., a1G) that rests at ∼30 kcal mol−1.44 The promotion of an electron from the 5d shell to the valence 6p orbitals creates its third and fifth excited state (i.e., z1D; ∼30 kcal mol−1 and z3D; ∼40–53 kcal mol−1, respectively) with the 5d16s26p1 configuration.44 Due to these diverse-types of low energy electronic states, we can expect the Hf + N reaction to produce a plethora of stable molecular electronic structures. In the present work, all the molecular electronic states arising from the interactions between the aforementioned states of Hf with the ground state of N (4S; [He]2s22p3) were considered. The interaction between the excited electronic states of N versus the states of Hf were not studied since the excitation energies of N atom are relatively high. For example, the first excited state of N(2D) lies ∼54 kcal mol−1 high in energy which is even higher than the fifth excited state of Hf(z3D).44 The reactions between the Hf(a3F) + N(4S), Hf(a3P) + N(4S), Hf(a1D) + N(4S), Hf(z1D) + N(4S), Hf(a1G) + N(4S), and Hf(z3D) + N(4S) produce 2,4,6(Σ+, Π, Δ, Φ), 2,4,6(Σ+, Π), 4(Σ−, Π, Δ), 4(Σ+, Π, Δ), 4(Σ−, Π, Δ, Φ, Γ), and 2,4,6(Σ+, Π, Δ) states, respectively. In this work, all these electronic states for HfN were studied at the CASSCF level to identify the most stable electronic states of HfN. Then, the fourteen most stable electronic states of HfN were investigated under the MRCI level of theory and are given in Fig. 1.
The right end of the potential energy profile of Fig. 1 represents the Hf + N fragments (a, b, c, d, e, and f). The PECs arising from the d- and e-fragments are not among the most stable fourteen electronic states of HfN and hence are not available in Fig. 1. Notice that at the MRCI level the Hf(a1D) + N(4S) is slightly stabilized over the Hf(a3P) + N(4S) (by ∼3 kcal mol−1) even though we expect the opposite based on the experimental excitation energies of Hf atom, where a3P and a1D are very closely lying first and second excited states of Hf, respectively.44 All PECs produce minima around 1.7–1.9 Å and are with ∼60–128 kcal mol−1De with respect to the ground state fragments. The ground state of HfN is a X2Σ+ which dissociates to Hf(a3F) + N(4S) ground state fragments. On the other hand, the first excited state of HfN(22Σ+) dissociates to Hf(a3P) + N(4S). The second excited state, 12Π, lies closer to the 22Σ+ in energy (less than 5 kcal mol−1) and originates from the ground state fragments. The first three electronic states of HfN lie well separated from the rest that are congested within the 60–90 kcal mol−1 energy range.
The equilibrium electronic configurations of the studied fourteen electronic states of HfN are reported in Table 1 and the corresponding state average CASSCF molecular orbitals are given in Fig. 2. The 1σ orbital (Fig. 2) is dominantly the polarized 2s of N atom (∼87%) which is doubly occupied in all the studied electronic states. The 2σ bonding molecular orbital is a result of the hybridization of the atomic orbitals 6s(Hf), 5dz2(Hf), with a larger contribution from the 2pz(N). Specifically, the % contributions of the aforementioned atomic orbitals on the 2σ are approximately 17%, 18%, and 64%, respectively. The 3σ is predominantly the 6s(Hf) (∼72%) with a minor fraction of 5dz2(Hf) (∼15%). The hybridization of the 5dyz(Hf) + 2py(N) and 5dxz(Hf) + 2px(N) produces the 1πy and 1πx bonding molecular orbitals, respectively. On the other hand, the 5dyz(Hf) − 2py(N) − 6py(Hf) and 5dxz(Hf) − 2px(N) − 6px(Hf) give rise to the 2πy and 2πx orbitals, respectively. See ESI,† Table S1 for % atomic orbitals contribution on these molecular orbitals. The 1δx2−y2 and 1δxy orbitals do not mix with the atomic orbitals of N atoms and are purely the 5dx2−y2 and 5dxy atomic orbitals of Hf.
| Statea | Coefficientb | Configurationc |
|---|---|---|
| a Only one component under C2v symmetry is listed for Π, Δ, and Φ states. The respective irreducible representations are provided in parentheses. b All the configuration interaction coefficients that are larger than 0.30 of the corresponding natural orbital representations are listed. c β and α-spin electrons are specified with and without bars over the spatial orbital, respectively. | ||
| X2Σ+ | 0.93 | 1σ22σ23σ1πx21πy2 |
| 22Σ+ | 0.93 | 1σ22σ3σ21πx21πy2 |
| 12Π (B1) | 0.91 | 1σ22σ23σ21πx1πy2 |
| 12Δ (A2) | 0.69 | 1σ22σ21πx21πy21δxy |
| −0.49 |

|
|
| 0.31 |
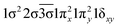
|
|
| 14Δ (A1) | 0.95 | 1σ22σ3σ1πx21πy2(1δx2−y2) |
| 14Π (B1) | −0.66 | 1σ22σ23σ1πx1πy2(1δx2−y2) |
| 0.66 | 1σ22σ23σ1πx21πy1δxy | |
| 14Φ (B1) | 0.67 | 1σ22σ23σ1πx1πy2(1δx2−y2) |
| 0.67 | 1σ22σ23σ1πx21πy1δxy | |
| 12Φ (B1) | 0.54 |

|
| 0.54 |

|
|
| 22Π (B1) | 0.53 |
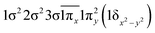
|
| −0.53 |
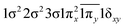
|
|
| 22Δ (A1) | −0.42 | 1σ22σ21πx21πy2(1δx2−y2) |
| 0.60 |

|
|
| −0.54 |
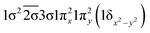
|
|
| 32Π (B1) | 0.60 | 1σ22σ21πx22πx1πy2 |
| −0.53 |

|
|
| 0.31 |

|
|
| 14Σ+ | 0.64 | 1σ22σ23σ1πx2πx1πy2 |
| 0.64 | 1σ22σ23σ1πx21πy2πy | |
| 24Π (B1) | 0.93 | 1σ22σ3σ1πx22πx1πy2 |
| 24Δ (A2) | 0.63 | 1σ22σ23σ1πx22πx1πy |
| −0.63 | 1σ22σ23σ1πx1πy22πy | |
 | ||
| Fig. 2 Select CASSCF state average molecular orbitals of HfN. The Hf and N atoms are depicted in green and blue, respectively. The 90° rotation of 1πy and 2πy orbitals along the principal axis yields 1πx and 2πx orbitals, respectively, whereas the 45° rotation of 1δx2−y2 produces 1δxy orbital. The contours were produced using the IboView software.47 The molecular orbitals of HfN+ have similar shapes. | ||
The ground state of the HfN has the 1σ22σ23σ11π4 electron configuration. Based on this electron arrangement and the contours of the occupying molecular orbitals, we can expect triple-bonded nature for the ground state of HfN. The promotion of an electron from the 2σ to 3σ produces its first excited electronic state (22Σ+). On the other hand, moving an electron from 1πx to 3σ from the X2Σ+ gives rise to the 12Π state of HfN. The destabilization of the 22Σ+ and 12Π compared to the X2Σ+ is expected due to the replacement of an electron from a bonding orbital of X2Σ+ (2σ or 1πx) to a non-bonding 3σ orbital. Note that all three of these electronic states of HfN are single-reference in nature and the proceeding 12Δ is the lowest energy multireference state of HfN. Furthermore, this is the first electronic state of HfN that carries populated δ orbitals (Table 1). The 12Δ is followed by the first quartet-spin electronic state of HfN (14Δ) which also possesses an electron in δ orbitals. The 14Δ is a single-reference state and all the proceeding electronic states except for 24Π are multireference in nature (Table 1). Based on the dominant electron configurations and the shapes of the occupying molecular orbitals, the valence-bond-Lewis (vbL) diagrams were proposed for the first five electronic states of HfN (Fig. 3).
 | ||
| Fig. 3 Proposed vbL diagrams for the five lowest energy electronic states of HfN. In all cases, the 2s orbital of nitrogen is doubly occupied and not shown for clarity. The dominant configuration of the 12Δ state is shown in the bottom-left vbL diagram, whereas its two minor components that bear similar electron arrangements are shown in the bottom-right diagram. See Table 1 for their exact electronic configurations. | ||
The spin–orbit effects of the heavier third-row TM species are significant. Hence, we have investigated the spin–orbit effects of a few low-lying electronic states of HfN at the MRCI level. Here, to construct the spin–orbit matrix, the X2Σ+, 22Σ+, 12Π, and 12Δ states were used. The spin–orbit coupling produces the Ω = 1/2 (X2Σ+), Ω = 1/2 (22Σ+), Ω = 3/2 and 1/2 (12Π), Ω = 5/2 and 3/2 (12Δ) components. The MRCI spin–orbit PECs with respect to the Hf⋯N distance are given in Fig. 4. The Ω = 1/2 ground state spin–orbit curve is mildly affected by the high-lying Ω = 1/2 states. The excited Ω = 1/2 components of each 22Σ+ and 12Π show an avoided crossing around the 1.85 Å. Similarly, the Ω = 3/2 products of the 12Π and 12Δ undergo an avoided crossing at ∼1.6 Å. Overall, among the studied states, the ordering of the Ω states of HfN are 1/2, 1/2, 3/2, 1/2, 3/2, 5/2 (Fig. 4). More information on the spin–orbit effects on the ground and excited states of HfN are given in Table 2, ESI,† Table S2, and in the upcoming paragraphs of the paper.
 | ||
| Fig. 4 MRCI spin–orbit coupling curves resulting from X2Σ+, 22Σ+, 12Π, and 12Δ electronic states of HfN as a function of Hf⋯N distance [r(Hf⋯N), Å]. The relative energies are referenced to the lowest energy spin–orbit curve at r = 12 Å, which is set to 0 kcal mol−1. The Ω = 1/2, Ω = 3/2, and Ω = 5/2 curves are shown in blue, green, and red, respectively. See Fig. 1 for the PECs of their parent X2Σ+, 22Σ+, 12Π, and 12Δ states. | ||
| State | Methoda | D e | r e | T e | ω e | ω e x e |
|---|---|---|---|---|---|---|
| a Davidson corrected MRCI is denoted by MRCI+Q. For all MRCI, MRCI+Q, and CCSD(T) calculations cc-pVQZ-PP (60ECP) of Hf and aug-cc-pVQZ of N basis set was applied. The 5s25p6 (of Hf) core electrons correlated CCSD(T) calculations are labeled as XZ-C-CCSD(T) and the appropriate weighted-core cc-pwCVXZ-PP (60ECP) basis set of Hf was used (X = Q, 5). The MRCI findings of Ω states of the four lowest electronic states of HfN are listed in the MRCI-SOC rows. b CCSD(T) results of the single-reference 22Σ+ state are not included due to convergence issues. | ||||||
| X2Σ+ | MRCI | 127.90 | 1.736 | — | 924 | 4.9 |
| MRCI-SOC (Ω = 1/2) | 126.17 | 1.736 | — | 916 | 4.9 | |
| MRCI+Q | 131.06 | 1.739 | — | 915 | 4.7 | |
| CCSD(T) | 130.88 | 1.735 | — | 937 | 4.0 | |
| QZ-C-CCSD(T) | 132.69 | 1.718 | — | 953 | 3.6 | |
| 5Z-C-CCSD(T) | 134.39 | 1.715 | — | 958 | 3.5 | |
| CBS-C-CCSD(T) | 135.31 | 1.714 | — | 961 | 3.4 | |
| CBS-CCSD(T)30 | D 0 = 127.99 | — | ||||
| DFT/BP8628 | 1.734 | — | 942 | |||
| DFT/B3LYP29 | 113.92 | 1.764 | — | 940 | ||
| Experiment | D 0 = 123.93(9)30 | 1.69(30)26 | — | 919.5(20)26 | 4.41299(65)27 | |
| D 0 = 14124 | 1.724678(36)27 | 932.7164(15)27 | ||||
| D 0 = 126.83(7.15)25 | ||||||
| 22Σ+b | MRCI | 109.77 | 1.780 | 6343 | 993 | 5.0 |
| MRCI-SOC (Ω = 1/2) | 108.26 | 1.781 | 6264 | 862 | 18.4 | |
| MRCI+Q | 112.48 | 1.786 | 6498 | 981 | 4.8 | |
| 12Π | MRCI | 106.70 | 1.867 | 7417 | 927 | 5.4 |
| MRCI-SOC (Ω = 3/2) | 105.54 | 1.866 | 7216 | 939 | 12.6 | |
| MRCI-SOC (Ω = 1/2) | 103.25 | 1.847 | 8015 | 1095 | 7.9 | |
| MRCI+Q | 108.61 | 1.871 | 7851 | 927 | 3.7 | |
| CCSD(T) | 107.55 | 1.867 | 8161 | 835 | 3.3 | |
| QZ-C-CCSD(T) | 108.56 | 1.846 | 8439 | 848 | 3.2 | |
| 5Z-C-CCSD(T) | 109.64 | 1.844 | 8657 | 851 | 3.4 | |
| 12Δ | MRCI | 86.25 | 1.822 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567 567 |
768 | 4.8 |
| MRCI-SOC (Ω = 3/2) | 87.58 | 1.825 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 498 498 |
795 | 1.9 | |
| MRCI-SOC (Ω = 5/2) | 81.01 | 1.825 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796 796 |
797 | 2.0 | |
| MRCI+Q | 88.90 | 1.823 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 744 744 |
736 | 6.1 | |
| 14Δ | MRCI | 79.93 | 1.806 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 777 777 |
873 | 4.3 |
| MRCI+Q | 82.50 | 1.810 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 982 982 |
873 | 5.5 | |
| CCSD(T) | 82.27 | 1.809 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002 002 |
869 | 3.2 | |
| 14Π | MRCI | 78.97 | 1.895 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113 113 |
750 | 4.0 |
| MRCI+Q | 80.94 | 1.896 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528 528 |
750 | 4.3 | |
| 14Φ | MRCI | 78.31 | 1.896 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 345 345 |
749 | 4.0 |
| MRCI+Q | 80.27 | 1.897 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765 765 |
749 | 4.1 | |
| 12Φ | MRCI | 76.82 | 1.898 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 865 865 |
759 | 3.9 |
| MRCI+Q | 78.95 | 1.900 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 226 226 |
758 | 4.0 | |
| 22Π | MRCI | 73.25 | 1.898 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 116 116 |
800 | 22.6 |
| MRCI+Q | 75.55 | 1.900 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 415 |
840 | 24.7 | |
| 22Δ | MRCI | 72.82 | 1.772 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 267 267 |
856 | 8.5 |
| MRCI+Q | 76.07 | 1.777 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231 231 |
856 | 9.6 | |
| 32Π | MRCI | 67.94 | 1.824 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972 972 |
881 | 9.2 |
| MRCI+Q | 70.60 | 1.826 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147 147 |
889 | 8.2 | |
| 14Σ+ | MRCI | 66.24 | 1.894 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565 565 |
753 | 7.3 |
| MRCI+Q | 67.94 | 1.899 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075 075 |
733 | 6.1 | |
| 24Π | MRCI | 65.45 | 1.809 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 842 842 |
887 | 11.6 |
| MRCI+Q | 67.79 | 1.814 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 128 |
864 | 11.5 | |
| 24Δ | MRCI | 60.14 | 1.888 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
724 | 46.8 |
| MRCI+Q | 61.91 | 1.892 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187 187 |
682 | 39.7 | |
We have exploited several single-reference electronic states of HfN to perform CCSD(T) calculations. Furthermore, due to the relatively less expensive nature of CCSD(T) compared to MRCI, at the CCSD(T) level core electron correlation effects and the basis set effects were tested. The calculated multireference and coupled cluster results of the HfN are listed in Table 2. The De of HfN(X2Σ+) is 127.90 kcal mol−1 at the MRCI level, which is 3.2 kcal mol−1 lower compared to the MRCI+Q De (Table 2). Our MRCI De is only slightly lower compared to the CBS-CCSD(T) D0 reported by Merriles et al., (i.e., 127.99 kcal mol−1).30 The CCSD(T) De of the HfN(X2Σ+) calculated in the present work with the aug-cc-pVQZ(N) cc-pVQZ-PP(Hf) basis set is nearly identical to the MRCI+Q value (130.88 versus 131.06 kcal mol−1). The 5s25p6 core electrons of Hf correlation [i.e., QZ-C-CCSD(T)] increased the De of the HfN(X2Σ+) by 1.81 kcal mol−1. Moving to the larger aug-cc-pV5Z(N) cc-pwCV5Z-PP(Hf) basis set [i.e., 5Z-C-CCSD(T)] further increased the De of HfN(X2Σ+), which is a common observation in the literature.7,46 The CBS-C-CCSD(T) only increased the De by 0.92 kcal mol−1 compared to the 5Z-C-CCSD(T) De. The zero-point energy corrected CBS-C-CCSD(T) D0 is 133.94 kcal mol−1 which is almost identical to the upper limit of the D0 reported by the Kohl and Stearns in 1973 [i.e., 126.83(7.15) kcal mol−1].25 The experimental D0 value reported by Merriles et al., for the HfN(X2Σ+) [i.e., 5.374(4) eV or ∼124 kcal mol−1] is ∼4 kcal mol−1 lower than the smallest De (127.90 kcal mol−1 at MRCI) reported in this work (Table 2).30 The inclusion of spin–orbit effects at the MRCI level decreased our De of HfN (X2Σ+1/2) to 126.17 kcal mol−1. Furthermore, with the inclusion of zero-point energy, this value dropped further to 124.86 kcal mol−1 (D0), which is in perfect harmony with the Merriles et al.'s value. A better agreement between CCSD(T) versus MRCI+Q was also observed for the De of 12Π and 14Δ. Similar to the ground state, these CCSD(T) values are slightly smaller compared to the MRCI+Q values. The increment of De moving from CCSD(T) to QZ-C-CCSD(T) and QZ-C-CCSD(T) to 5Z-C-CCSD(T) was also observed for the 12Π state. Overall, for all fourteen states the MRCI+Q De are 1.7–3.3 kcal mol−1 higher compared to the MRCI De.
For all the states, the MRCI+Q predicted re values are slightly longer compared to the MRCI re (by 0.001–0.006 Å). Similarly, the MRCI+Q re values are longer than the coupled cluster re values (Table 2). According to the available QZ-C-CCSD(T) and CCSD(T) results, the core electron correlation tends to shorten the bond distance (by ∼0.02 Å), which we have seen in our earlier studies.48,49 The re of the spin–orbit ground state X2Σ+1/2 is identical to the spin–orbit effect neglected MRCI value of the ground state (i.e., 1.736 Å). Since the spin–orbit effects are insignificant for the re of the X2Σ+, a direct comparison between coupled cluster versus experiment can be made. Our coupled cluster re values under QZ-C-CCSD(T), 5Z-C-CCSD(T), and CBS-C-CCSD(T) for the X2Σ+ are 1.718, 1.715, and 1.714 Å, respectively which align well with the experimental re reported by Ram and Bernath which is 1.724678(36) Å.27 Furthermore, upon comparison with the literature theoretical analysis, the DFT/BP86 re reported by Kushto et al.,28 (i.e., 1.734 Å) for the ground state is in harmony with our MRCI and CCSD(T) value, whereas the DFT/B3LYP re by Hong et al.,29 (1.764 Å) is longer compared to all the re values reported in the present work (Table 2).
The first excitation energy with the spin–orbit effects is 6264 cm−1 which is only 79 cm−1 lower compared to the spin–orbit untreated excitation energy (Table 2). The 0-0 band of the [6.7]2Σ+–X2Σ+ transition of the HfN reported by Ram and Bernath is 6668 cm−1 which is 404 cm−1 higher than our spin–orbit treated first excitation energy of HfN.27 Upon comparison of spin–orbit untreated MRCI+Q Te with MRCI Te values, the MRCI+Q Te values are higher (by 155–510 cm−1) compared to the MRCI except for the 22Δ state that predicted 36 cm−1 lower Te by MRCI+Q compared to the MRCI value.
The experimental ωe and ωexe values reported by Ram and Bernath for the X2Σ+ are 932.7164(15) cm−1 and 4.41299(65) cm−1, respectively.27 The CCSD(T) predicted the closest ωe value (i.e., 937 cm−1) to their finding by underestimating the ωexe by ∼0.4 cm−1 (Table 2). However, the CBS extrapolation increases the ωe value to 961 cm−1, while decreasing the ωexe to 3.4 cm−1. Interestingly, the CCSD(T) ωe and ωexe values are in better agreement with the values of Ram and Bernath compared to our spin–orbit treated MRCI ωe (916 cm−1) and ωexe (4.9 cm−1) values of the ground state X2Σ+1/2 (Table 2).
The μ values can be used to predict spectra, opacities, and radiative properties of molecular species and hence are often calculated using ab initio techniques.50–53 The MRCI DMCs of the first five electronic states of HfN are given in Fig. 5. The μ of HfN(X2Σ+) calculated under the DFT/B3LYP with aug-cc-pVQZ(N) aug-cc-pVQZ-PP(Hf) basis set by Merriles et al., is 5.50 D.30 This value is in reasonable agreement with the μ of HfN(X2Σ+) obtained at the finite-field approach with CCSD(T) (i.e., −5.37 D). Since Hf is placed to the left of the coordinate point zero of the z-axis in our calculations, the negative μ value implies that the μ vector points to Hf. Under the same approach, μ values calculated at the QZ-C-CCSD(T) and 5Z-C-CCSD(T) are identical (i.e., −5.35 D). Similarly, the CCSD(T) μ values of single-reference 12Π and 14Δ were also calculated and are −3.59 and −4.60 D, respectively. The MRCI μ values calculated at the equilibrium bond distances for these electronic states deviate from the CCSD(T) by 0.2–0.5 D (Fig. 5).
III.B. HfN+
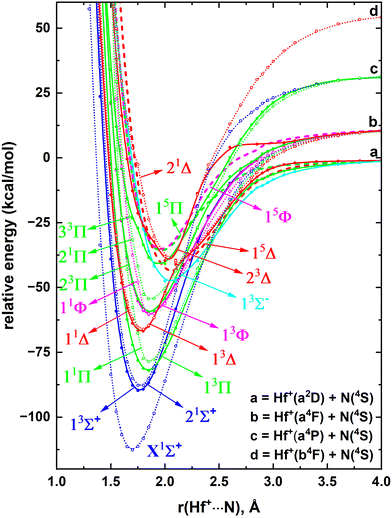
The removal of an electron from the 5d shell of the ground state of Hf(a3F; 5d26s2) yields the ground state of Hf+(a2D; 5d16s2).44 The experimental IE of this process is 6.82507 eV.54 Under the implemented CCSD(T), QZ-C-CCSD(T), 5Z-C-CCSD(T), and CBS-C-CCSD(T) levels in this work, the IE of Hf is 6.531, 6.735, 6.757, and 6.762 eV respectively. Notice that the discrepancy between the CCSD(T) IE versus experimental IE is 0.294 eV, whereas it is 0.09 eV between QZ-C-CCSD(T) versus experiment. This displays the importance of the core electron correlation on gaining more accurate IE values. Indeed, as expected the more expensive 5Z-C-CCSD(T) and CBS-C-CCSD(T) predicted IE values are in better agreement with the experiment. The first excited state of Hf+(a4F) lies ∼10–24 kcal mol−1 above the ground state and carries the 5d26s1 valence electron configuration.44 Similarly, the next five excited states of Hf+ (i.e., a4P, a2F, b2D, a2P, a2G) that span between ∼34–51 kcal mol−1 have 5d26s1 configuration.44 The seventh excited state of Hf+(b4F) is the first state of Hf+ with a vacant 6s orbital which carries three electrons in the 5d shell (∼54–67 kcal mol−1).44The first IE of the N atom (i.e., 14.5341 eV) is more than twice high compared to that of Hf.54 Hence, in this work, the reactions between the low-lying electronic states of Hf+versus the ground state of N(4S) were selected to study the PECs of HfN+. Specifically, all the PECs arising from the Hf+(a2D) + N(4S), Hf+(a4F) + N(4S), and Hf+(a4P) + N(4S) fragments and the singlet-spin molecular states generating from Hf+(b4F) + N(4S) were studied. The first three combinations give rise to 5(quintet + triplet), 7(septet + quintet + triplet + singlet), and 3(septet + quintet + triplet + singlet) states. The union of high energy Hf+(b4F) + N(4S) gives out 7(septet + quintet + triplet + singlet) states but in our CASSCF calculations only the seven singlet-spin PECs of this channel were included. Of course, we expect a series of quintet- and triplet-spin electronic states to be produced from the Hf+(a2F) + N(4S), Hf+(b2D) + N(4S), Hf+(a2P) + N(4S), and Hf+(a2G) + N(4S) fragments. However, according to our preliminary analysis these quintet- and triplet-spin states are not among the most stable states of HfN+. However, the high energy Hf+(b4F) + N(4S) produces a reasonably stable singlet-spin states and hence here they were studied. Overall, at the CASSCF level 57 states were studied and the lowest eighteen electronic states of HfN+ were identified to investigate under the MRCI level. The MRCI PECs HfN+ are given in Fig. 6.
The ground state of the HfN+ is a X1Σ+ with an equilibrium distance of ∼1.7 Å (Fig. 6). It is originating from the second lowest energy fragments [i.e., Hf+(a4F) + N(4S)] and lies well separated from its first excited state (i.e., 13Σ+). Similar to X1Σ+, 13Σ+ dissociates to Hf+(a4F) + N(4S). The second excited state of HfN+(21Σ+) is very close in energy to the 13Σ+ (energy difference is less than 2 kcal mol−1) and is originating from Hf+(a4P) + N(4S). This state is followed by several Π, Δ, Φ, and Σ− electronic states and the spectrum becomes rather complicated around the 35–50 kcal mol−1 region (Fig. 6). Furthermore, in this region we see avoided crossings between the 13Δ versus 23Δ and 11Δ versus 21Δ PECs.
The ground state of HfN+(X1Σ+) can be created by detaching an electron from the 3σ orbital of the HfN(X2Σ+) (compare the electronic configurations listed in Tables 1 and 3). This process requires 7.207 eV at the CCSD(T). At the QZ-C-CCSD(T), 5Z-C-CCSD(T), and CBS-C-CCSD(T) levels they are 7.408, 7.405 eV, and 7.401 respectively. Excitation of an electron from the HfN+(X1Σ+) 2σ to 3σ creates the electron configuration of the first excited state of HfN+ (i.e., 13Σ+). Both X1Σ+ and 13Σ+ states are dominantly single-reference in nature. The next state of HfN+ (i.e., 21Σ+) is the corresponding multireference open-shell singlet of the 13Σ+ state. Notice that an ionization of a 3σ electron from the HfN(22Σ+) gives rise to 13Σ+ and 21Σ+ states of HfN+. By a similar electron ionization from the HfN(12Π), the third and fourth excited states of HfN+ (13Π and 11Π) can be created. The next state of HfN+ is a single-reference 13Δ which is followed by a series of multireference states (i.e., 11Δ, 13Φ, 11Φ, 23Π, 21Π, 13Σ−). The first quintet-spin electronic state of HfN+ (i.e., 15Δ) falls just above the 13Σ−. The proposed vbL diagrams based on the electron arrangements of the seven most stable electronic states of HfN+ are given in Fig. 7.
| Statea | Coefficientb | Configurationc |
|---|---|---|
| a Only one component under C2v symmetry is listed for Π, Δ, and Φ states. The respective irreducible representations are provided in parentheses. b All the configuration interaction coefficients that are larger than 0.30 of corresponding natural orbital representations are listed. c β and α-spin electrons are specified with and without bars over the spatial orbital. | ||
| X1Σ+ | 0.95 | 1σ22σ21πx21πy2 |
| 13Σ+ | 0.91 | 1σ22σ3σ1πx21πy2 |
| 21Σ+ | −0.65 |

|
| 0.65 |

|
|
| 13Π (B1) | 0.88 | 1σ22σ23σ1πx1πy2 |
| 11Π (B1) | 0.63 |

|
| −0.63 |
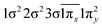
|
|
| 13Δ (A2) | 0.92 | 1σ22σ1πx21πy21δxy |
| 11Δ (A2) | 0.65 |
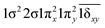
|
| −0.65 |

|
|
| 13Φ (B1) | 0.65 | 1σ22σ21πx1πy2(1δx2−y2) |
| 0.65 | 1σ22σ21πx21πy1δxy | |
| 11Φ (B1) | −0.45 |

|
| 0.45 |

|
|
| 0.45 |

|
|
| −0.45 |
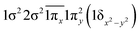
|
|
| 23Π (B1) | −0.62 | 1σ22σ21πx1πy2(1δx2−y2) |
| 0.62 | 1σ22σ21πx21πy1δxy | |
| 21Π (B1) | −0.46 |

|
| 0.46 |

|
|
| 0.46 |

|
|
| −0.46 |

|
|
| 13Σ− | −0.47 |

|
| −0.47 |
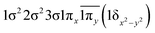
|
|
| 0.47 |
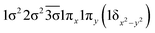
|
|
| 0.47 |
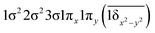
|
|
| 15Δ (A1) | 0.95 | 1σ22σ23σ1πx1πy1δxy |
| 33Π (B1) | 0.80 | 1σ22σ3σ21πx1πy2 |
| 23Δ (A2) | 0.82 | 1σ22σ1πx21πy21δxy |
| 21Δ (A2) | −0.58 |

|
| 0.58 |

|
|
| 15Π (B1) | −0.64 | 1σ22σ3σ1πx1πy2(1δx2−y2) |
| 0.64 | 1σ22σ3σ1πx21πy1δxy | |
| 15Φ (B1) | 0.66 | 1σ22σ3σ1πx1πy2(1δx2−y2) |
| 0.66 | 1σ22σ3σ1πx21πy1δxy | |
 | ||
| Fig. 7 Proposed vbL diagrams for the seven lowest energy electronic states of HfN+. In all cases, the 2s orbital of nitrogen is doubly occupied and not shown for clarity. See Table 3 for their exact electronic configurations. | ||
In this work, the low-lying X1Σ+, 13Σ+, 21Σ+, 13Π, 11Π electronic states of HfN+ were used to construct a spin–orbit matrix and study their corresponding spin–orbit components. The spin–orbit coupling produces the Ω = 0+ (X1Σ+), Ω = 0− and 1 (13Σ+), Ω = 0+ (21Σ+), Ω = 2, 1, 0+, and 0− (13Π), and Ω = 1 (11Π) products and they are depicted in Fig. 8. The energy difference between the Ω = 0− and 1 components of 13Σ+ are minor and similarly the Ω = 2, 1, 0+, and 0− products of the 13Π are also energetically closely arranged. The spectroscopic constants and compositions of the spin–orbit states are listed in Table 4 and ESI,† Table S4.
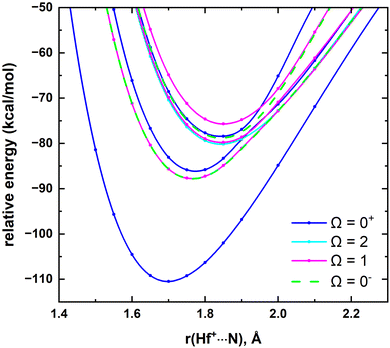 | ||
| Fig. 8 MRCI spin–orbit coupling curves resulting from X1Σ+, 13Σ+, 21Σ+, 13Π, and 11Π electronic states of HfN+ as a function of Hf+⋯N distance [r(Hf+⋯N), Å]. The relative energies are referenced to the lowest energy spin–orbit curve at r = 12 Å, which is set to 0 kcal mol−1. The Ω = 0+, Ω = 2, Ω = 1, and Ω = 0− curves are shown in blue, cyan, pink, and green, respectively. See Fig. 6 for the PECs of their parent X1Σ+, 13Σ+, 21Σ+, 13Π, and 11Π states. | ||
| State | Methoda | D e | r e | T e | ω e | ω e x e |
|---|---|---|---|---|---|---|
| a Davidson corrected MRCI is denoted by MRCI+Q. For all MRCI, MRCI+Q, and CCSD(T) calculations cc-pVQZ-PP (60ECP) of Hf and aug-cc-pVQZ of N basis set was applied. The 5s25p6 (of Hf) core electrons correlated CCSD(T) calculations are labeled as XZ-C-CCSD(T) and the appropriate weighted-core cc-pwCVXZ-PP (60ECP) basis set of Hf was used (X = Q, 5). The MRCI findings of Ω states of five lowest electronic states of HfN+ are listed in the MRCI-SOC rows. | ||||||
| X1Σ+ | MRCI | 112.45 | 1.697 | — | 965 | 6.6 |
| MRCI-SOC (Ω = 0+) | 110.48 | 1.698 | — | 955 | 6.5 | |
| MRCI+Q | 115.71 | 1.695 | — | 982 | 5.8 | |
| CCSD(T) | 115.29 | 1.693 | — | 992 | 5.5 | |
| QZ-C-CCSD(T) | 117.18 | 1.674 | — | 1007 | 6.3 | |
| 5Z-C-CCSD(T) | 119.47 | 1.672 | — | 1013 | 6.2 | |
| CBS-C-CCSD(T) | 120.56 | 1.671 | — | 1017 | 6.2 | |
| DFT/B3LYP29 | 91.55 | 1.720 | — | 994 | ||
| 13Σ+ | MRCI | 89.63 | 1.764 | 7984 | 921 | 3.8 |
| MRCI-SOC (Ω = 0−) | 87.78 | 1.766 | 7939 | 920 | 7.0 | |
| MRCI-SOC (Ω = 1) | 87.75 | 1.765 | 7950 | 922 | 6.8 | |
| MRCI+Q | 92.29 | 1.762 | 8191 | 934 | 4.0 | |
| CCSD(T) | 91.24 | 1.761 | 8410 | 954 | 3.7 | |
| QZ-C-CCSD(T) | 95.19 | 1.739 | 7690 | 975 | 3.6 | |
| 5Z-C-CCSD(T) | 96.79 | 1.737 | 7932 | 978 | 3.6 | |
| 21Σ+ | MRCI | 87.89 | 1.774 | 8591 | 985 | 3.5 |
| MRCI-SOC (Ω = 0+) | 86.13 | 1.774 | 8517 | 928 | 11.7 | |
| MRCI+Q | 90.71 | 1.773 | 8745 | 990 | 3.3 | |
| 13Π | MRCI | 81.86 | 1.845 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
836 | 5.1 |
| MRCI-SOC (Ω = 2) | 80.16 | 1.843 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605 605 |
839 | 5.0 | |
| MRCI-SOC (Ω = 1) | 79.75 | 1.845 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 749 749 |
866 | 4.1 | |
| MRCI-SOC (Ω = 0−) | 78.76 | 1.843 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 094 094 |
904 | 1.1 | |
| MRCI-SOC (Ω = 0+) | 78.42 | 1.842 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 215 215 |
911 | 4.4 | |
| MRCI+Q | 83.64 | 1.845 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 216 |
841 | 5.2 | |
| CCSD(T) | 81.95 | 1.840 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 661 661 |
852 | 3.6 | |
| QZ-C-CCSD(T) | 84.70 | 1.820 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 360 |
862 | 3.6 | |
| 5Z-C-CCSD(T) | 86.24 | 1.818 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622 622 |
866 | 3.5 | |
| 11Π | MRCI | 78.62 | 1.829 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 834 834 |
875 | 6.7 |
| MRCI-SOC (Ω = 1) | 75.68 | 1.850 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171 171 |
890 | 1.2 | |
| MRCI+Q | 80.55 | 1.829 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 295 295 |
891 | 6.6 | |
| 13Δ | MRCI | 66.80 | 1.783 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 968 968 |
903 | 5.9 |
| MRCI+Q | 69.11 | 1.779 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298 298 |
901 | 4.3 | |
| CCSD(T) | 68.49 | 1.775 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 366 366 |
916 | 3.5 | |
| QZ-C-CCSD(T) | 72.01 | 1.751 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 799 799 |
936 | 3.4 | |
| 5Z-C-CCSD(T) | 73.92 | 1.749 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 929 929 |
939 | 3.4 | |
| 11Δ | MRCI | 65.92 | 1.791 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 274 274 |
901 | 5.9 |
| MRCI+Q | 68.19 | 1.787 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 619 619 |
894 | 4.7 | |
| 13Φ | MRCI | 60.27 | 1.865 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
766 | 3.3 |
| MRCI+Q | 61.86 | 1.864 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 834 834 |
772 | 3.9 | |
| 11Φ | MRCI | 60.10 | 1.833 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 310 |
718 | 11.2 |
| MRCI+Q | 61.74 | 1.833 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 876 876 |
732 | 11.5 | |
| 23Π | MRCI | 59.27 | 1.861 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601 601 |
780 | 3.2 |
| MRCI+Q | 60.98 | 1.861 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 142 142 |
784 | 3.7 | |
| 21Π | MRCI | 54.32 | 1.833 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 334 334 |
724 | 2.8 |
| MRCI+Q | 56.16 | 1.833 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825 825 |
735 | 2.8 | |
| 13Σ− | MRCI | 47.99 | 2.054 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 545 545 |
614 | 3.3 |
| MRCI+Q | 50.76 | 2.051 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 716 716 |
618 | 3.0 | |
| 15Δ | MRCI | 44.15 | 2.068 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889 889 |
600 | 2.9 |
| MRCI+Q | 45.26 | 2.068 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 638 |
601 | 3.0 | |
| 33Π | MRCI | 41.38 | 1.947 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 860 |
728 | 2.2 |
| MRCI+Q | 44.68 | 1.946 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 842 842 |
733 | 2.5 | |
| 23Δ | MRCI | 40.82 | 2.050 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053 |
874 | 10.1 |
| MRCI+Q | 42.16 | 2.061 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 724 724 |
894 | 9.7 | |
| 21Δ | MRCI | 40.04 | 2.072 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 327 |
989 | 18.5 |
| MRCI+Q | 41.20 | 2.072 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 059 059 |
982 | 18.7 | |
| 15Π | MRCI | 36.25 | 1.965 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654 654 |
709 | 4.1 |
| MRCI+Q | 37.70 | 1.966 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 283 283 |
702 | 4.3 | |
| 15Φ | MRCI | 35.76 | 1.965 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 824 824 |
708 | 4.1 |
| MRCI+Q | 37.20 | 1.966 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 460 |
702 | 4.0 | |
Under the utilized methods, the De of HfN+(X1Σ+) varied between 112–121 kcal mol−1 (Table 4). Specifically, the highest level of coupled cluster approach, CBS-C-CCSD(T), predicted the largest De (i.e., 120.56 kcal mol−1). These De values calculated in the present work are significantly higher than the previously reported DFT/B3LYP value by Hong et al. (i.e., 91.55 kcal mol−1).29 The spin–orbit corrected MRCI De of HfN+(X1Σ+) is 110.48 kcal mol−1. The zero-point energy correction decreases the D0 of HfN+(X1Σ+) to 109.10 kcal mol−1. Compared to the De of the HfN(X2Σ+), the De of HfN+(X1Σ+) is ∼15 kcal mol−1 lower under all levels of theory (Table 2 and Table 4). Similar to HfN, the De increased in the order of CCSD(T) < QZ-C-CCSD(T) < 5Z-C-CCSD(T) for HfN+ (see the De of X1Σ+, 13Σ+, 13Π, and 13Δ in Table 4). Furthermore, for all the states, the MRCI predicted De are slightly smaller (by 1.1–3.3 kcal mol−1) compared to the MRCI+Q values, which is a consistent observation with the De of HfN.
Due to the electrostatic attraction between Hf+ and N, we can expect a shorter re value for HfN+ compared to HfN. Indeed, this is true where the re of HfN+(X1Σ+) is ∼0.04 Å shorter than that of HfN(X2Σ+) at all the utilized theoretical approaches (Tables 2 and 4). Among all the studied electronic states of HfN+ the X1Σ+ ground state has the shortest re (Table 4). Notice that in the X1Σ+ state the 2σ, 1πx, and 1πy bonding orbitals host six electrons in total which accounts for its triple bonded character. In all excited electronic states of HfN+ these three bonding orbitals carry either five or four electrons, which rationalizes the comparatively longer re of excited states compared to the X1Σ+. Recall that for all the states of HfN, MRCI+Q predicted re are longer than the MRCI values. This trend does not translate to the states of HfN+, where the MRCI+Q re of HfN+ are either longer, shorter, or identical to the MRCI re (Table 4). Similar to the HfN(X2Σ+), the spin–orbit mixing of the HfN+(X1Σ+) is minor (ESI,† Table S4) and the re of the HfN+(X1Σ+) is almost identical to the re of  . Similarly, the re values of the parent electronic states 13Σ+, 21Σ+, and 13Π are either the same or nearly identical to their spin–orbit products (Table 4). For all states, the MRCI+Q predicted Te are ∼150–750 cm−1 higher than the MRCI Te except for the 33Π state which has an 18 cm−1 lower MRCI+Q Te compared to the MRCI Te (Table 4). Importantly, this trend was also maintained by all but one excited state of HfN (Table 2). The spin–orbit effects decreased the first Te value of HfN+ by 45 cm−1 (i.e., 7984 versus 7939 cm−1). The energy difference between Ω = 0− and 1 products of the 13Σ+ is only 11 cm−1. Similar to the 13Σ+ case, the spin–orbit couplings decreased Te of the 21Σ+ (8591 versus 8517 cm−1; see Table 4). The Ω = 2, 1, 0−, and 0− components of the 13Π span between 10
. Similarly, the re values of the parent electronic states 13Σ+, 21Σ+, and 13Π are either the same or nearly identical to their spin–orbit products (Table 4). For all states, the MRCI+Q predicted Te are ∼150–750 cm−1 higher than the MRCI Te except for the 33Π state which has an 18 cm−1 lower MRCI+Q Te compared to the MRCI Te (Table 4). Importantly, this trend was also maintained by all but one excited state of HfN (Table 2). The spin–orbit effects decreased the first Te value of HfN+ by 45 cm−1 (i.e., 7984 versus 7939 cm−1). The energy difference between Ω = 0− and 1 products of the 13Σ+ is only 11 cm−1. Similar to the 13Σ+ case, the spin–orbit couplings decreased Te of the 21Σ+ (8591 versus 8517 cm−1; see Table 4). The Ω = 2, 1, 0−, and 0− components of the 13Π span between 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605–11
605–11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 215 cm−1, where the Te of only Ω = 2 state is lower compared to the Te of the original 13Π (Table 4).
215 cm−1, where the Te of only Ω = 2 state is lower compared to the Te of the original 13Π (Table 4).
The DFT/B3LYP ωe = 994 cm−1 value of the Hong et al., is in better harmony with our ground state ωe values and is almost identical to the CCSD(T) ωe.29 For all single-reference states the coupled cluster approaches predicted slightly larger ωe values compared to the MRCI and MRCI+Q ωe values (Table 4). For the ground state, the CBS extrapolation only increased the ωe by 4 cm−1 compared to the 5Z-C-CCSD(T). The ωexe of the CBS-C-CCSD(T) and 5Z-C-CCSD(T) are identical (6.2 cm−1). The ωe and ωexe values of several low-lying spin–orbit curves are listed in Table 4.
The MRCI DMCs of the five most stable electronic states of HfN+ are given in ESI,† Fig. S1. The μ values of the single-reference X1Σ+, 13Π, and 13Σ+ at the CCSD(T) level are −6.20, −4.23, and −3.51 D, respectively. Similar to HfN, the CCSD(T) μ values of HfN+ were calculated at the CCSD(T) re values (Table 4). These values are in excellent agreement with the corresponding MRCI μ values. Specifically, the discrepancies between MRCI versus CCSD(T) values are less than 0.08 D. For the ground state, the DFT/B3LYP μ has been reported before as 6.18 D, which is in perfect harmony with our MRCI and CCSD(T) values.29
IV. Conclusions
In conclusion, the current work reports PECs, electronic configurations, and De, Te, ωe, and ωexe values of fourteen and eighteen electronic states of HfN and HfN+ respectively at the MRCI and MRCI+Q levels of theory. Single-reference electronic states were also analyzed under the CCSD(T) method. At CCSD(T) the effects of the basis set and core electrons on the predictions were also tested. The ground state of HfN is a X2Σ+ with 1σ22σ23σ11π4 electron configuration. At the MRCI level, the spin–orbit effect accounted D0 of HfN(X2Σ+) is 124.86 kcal mol−1 which is in harmony with the recently reported D0 of HfN by Merriles et al. [i.e., 123.93(9) kcal mol−1].30 Unlike HfN(X2Σ+), the ground state of HfN+(X1Σ+) dissociates to excited state fragments [i.e., Hf+(a4F) + N(4S)] and bears a D0 of 109.10 kcal mol−1 with respect to the ground state fragments. By detaching an electron from the 3σ orbital of the HfN(X2Σ+), the ground state of HfN+(X1Σ+) can be created and this IE is 7.401 eV at the CBS-C-CCSD(T) level. Similar single electron ionization from the 3σ2 of the first excited state of HfN(22Σ+) produces the first two excited states of HfN+(13Σ+ and 21Σ+), whereas that of HfN(12Π) creates the third and fourth excited states of HfN+ (i.e., 13Π and 11Π). The De increased in the order of CCSD(T) < QZ-C-CCSD(T) < 5Z-C-CCSD(T) for both HfN and HfN+. The core electron correlation was found to shorten the bond distances. The ground state of each HfN(X2Σ+) and HfN+(X1Σ+) is triple bonded in nature and carries the shortest bond lengths compared to their excited states which carry bond orders less than 3. The CCSD(T) μ versus MRCI μ values vary by 0.2–0.5 D for the states of HfN but the discrepancies between the two levels for the states of HfN+ are less than 0.08 D. Overall, the results of this study are in harmony with the previously reported experimental values and are expected to serve as a guide for future experimental studies on HfN and HfN+.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The support of the Los Alamos National Laboratory (LANL) Laboratory Directed Research and Development program Project No. 20240737PRD1 is acknowledged. This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001. Dr. Nuno M. S. Almeida is thanked for the useful discussions about spin–orbit coupling effects.References
- J. F. Harrison, Chem. Rev., 2000, 100, 679–716 CrossRef CAS PubMed.
- E. E. Claveau and E. Miliordos, Phys. Chem. Chem. Phys., 2021, 23, 21172–21182 RSC.
- I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2018, 20, 12278–12287 RSC.
- N. M. S. Almeida, I. R. Ariyarathna and E. Miliordos, J. Phys. Chem. A, 2019, 123, 9336–9344 CrossRef CAS PubMed.
- I. R. Ariyarathna, N. M. S. Almeida and E. Miliordos, Phys. Chem. Chem. Phys., 2020, 22, 16072–16079 RSC.
- I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2021, 23, 1437–1442 RSC.
- I. R. Ariyarathna, C. Duan and H. J. Kulik, J. Chem. Phys., 2022, 156, 184113 CrossRef CAS PubMed.
- B. Gao, X. Li, K. Ding, C. Huang, Q. Li, P. K. Chu and K. Huo, J. Mater. Chem. A, 2019, 7, 14–37 RSC.
- D. D. Kumar, N. Kumar, S. Kalaiselvam, S. Dash and R. Jayavel, Surf. Interfaces, 2017, 7, 74–82 CrossRef CAS.
- M. Kommer, T. Sube, A. Richter, M. Fenker, W. Schulz, B. Hader and J. Albrecht, Surf. Coat. Technol., 2018, 333, 1–12 CrossRef CAS.
- J. Peng and R. Zierold, Encyclopedia of Condensed Matter Physics, 2024, pp. 716–728 DOI:10.1016/b978-0-323-90800-9.00206-7.
- X. Peng, C. Pi, X. Zhang, S. Li, K. Huo and P. K. Chu, Sustainable Energy Fuels, 2019, 3, 366–381 RSC.
- Z. Meng, S. Zheng, R. Luo, H. Tang, R. Wang, R. Zhang, T. Tian and H. Tang, Nanomater., 2022, 12, 2660 CrossRef CAS PubMed.
- W. Qi, Z. Cheng, S. Liu and M. Yang, Catal. Sci. Technol., 2023, 13, 6864–6877 RSC.
- Z. Cheng, W. Qi, C. H. Pang, T. Thomas, T. Wu, S. Liu and M. Yang, Adv. Funct. Mater., 2021, 31, 2100553 CrossRef CAS.
- X. Dou, H. Han, G. Zhai and B. Suo, Int. J. Quantum Chem., 2011, 111, 3378–3384 CrossRef CAS.
- A. Farhat and S. N. Abdul-Al, J. Comput. Chem., 2015, 36, 1252–1258 CrossRef CAS PubMed.
- S. R. Langhoff and C. W. Bauschlicher, J. Mol. Spectrosc., 1990, 143, 169–179 CrossRef CAS.
- A. Nils and M. Boris, Phys. Scr., 2000, 62, 417 CrossRef.
- I. Shim and K. A. Gingerich, J. Mol. Struct., 1999, 460, 123–136 CrossRef CAS.
- A. C. Borin and J. P. Gobbo, J. Phys. Chem. A, 2009, 113, 12421–12426 CrossRef CAS PubMed.
- R. S. Ram, J. Liévin and P. F. Bernath, J. Chem. Phys., 1998, 109, 6329–6337 CrossRef CAS.
- R. Du, B. Suo, H. Han, Y. Lei and G. Zhai, Int. J. Quantum Chem., 2013, 113, 2464–2470 CrossRef CAS.
- K. A. Gingerich, J. Chem. Phys., 1968, 49, 19–24 CrossRef CAS.
- F. J. Kohl and C. A. Stearns, J. Phys. Chem., 1973, 78, 273–274 CrossRef.
- T. C. Devore and T. N. Gallaher, J. Chem. Phys., 1979, 70, 3497–3501 CrossRef CAS.
- R. S. Ram and P. F. Bernath, J. Mol. Spectrosc., 1997, 184, 401–412 CrossRef CAS.
- G. P. Kushto, P. F. Souter, G. V. Chertihin and L. Andrews, J. Chem. Phys., 1999, 110, 9020–9031 CrossRef CAS.
- B. Hong, L. Cheng, M. Y. Wang and Z. J. Wu, Mol. Phys., 2010, 108, 25–33 CrossRef CAS.
- D. M. Merriles, A. S. Knapp, Y. Barrera-Casas, A. Sevy, J. J. Sorensen and M. D. Morse, J. Chem. Phys., 2023, 158, 084308 CrossRef CAS PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 242–253 Search PubMed.
- H. J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Hesselmann, D. Kats, A. Kohn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, 3rd, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- H.-J. Werner and P. J. Knowles, et al., MOLPRO, version 2023.2, a package of ab initio programs, see https://www.molpro.net Search PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- K. R. Shamasundar, G. Knizia and H. J. Werner, J. Chem. Phys., 2011, 135, 054101 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, J. Chem. Phys., 2009, 130, 164108 CrossRef PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- D. A. Kreplin, P. J. Knowles and H. J. Werner, J. Chem. Phys., 2019, 150, 194106 CrossRef PubMed.
- D. A. Kreplin, P. J. Knowles and H. J. Werner, J. Chem. Phys., 2020, 152, 074102 CrossRef CAS PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- A. Kramida, Y. Ralchenko and J. Reader, NIST Atomic Spectra Database (Version 5.3), National Institute of Standards and Technology, Gaithersburg, MD, 2015, https://physics.nist.gov/asd Search PubMed.
- S. Bhattacharyya and J. F. Harrison, Comput. Theor. Chem., 2022, 1216, 113853 CrossRef CAS.
- I. R. Ariyarathna, Y. Cho, C. Duan and H. J. Kulik, Phys. Chem. Chem. Phys., 2023, 25, 26632–26639 RSC.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS PubMed.
- I. R. Ariyarathna and E. Miliordos, J. Quant. Spectrosc. Radiat. Transfer, 2020, 255, 107265 CrossRef CAS.
- N. M. S. Almeida, I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2018, 20, 14578–14586 RSC.
- M. C. Zammit, J. A. Leiding, J. Colgan, W. Even, C. J. Fontes and E. Timmermans, J. Phys. B: At., Mol. Opt. Phys., 2022, 55, 184002 CrossRef CAS.
- E. Gharib-Nezhad, A. R. Iyer, M. R. Line, R. S. Freedman, M. S. Marley and N. E. Batalha, Astrophys. J., Suppl. Ser., 2021, 254, 34 CrossRef CAS.
- J. Tennyson and S. N. Yurchenko, Atoms, 2018, 6, 26 CrossRef.
- S. N. Yurchenko, in Chemical Modelling: Applications and Theory, ed. M. Springborg and J.-O. Joswig, The Royal Society of Chemistry, 2013, ch. 7, pp. 183–228 10.1039/9781849737241-00183.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, New York, 93rd edn, 2012 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Table S1 lists the molecular orbital compositions of HfN; Table S2 lists spectroscopic constants and compositions of low-lying spin–orbit state of HfN; Table S3 lists the De, re, ωe, and ωexe values of the HfN(X2Σ+) and HfN+(X1Σ+) at the TZ-C-CCSD(T) level; Table S4 lists spectroscopic constants and compositions of low-lying spin–orbit state of HfN+; Fig. S1 illustrates the DMCs of low-lying electronic states of HfN+. See DOI: https://doi.org/10.1039/d4cp01847h |
| This journal is © the Owner Societies 2024 |