 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Methodological and force field effects in the molecular dynamics-based prediction of binding free energies of host–guest systems
Zhaoxi
Sun
 a and
Piero
Procacci
a and
Piero
Procacci
 *b
*b
aChangping Laboratory, Beijing 102206, China
bDipartimento di Chimica “Ugo Schiff”, Università degli Studi di Firenze, Via della Lastruccia 3, 50019 Sesto Fiorentino, Italy. E-mail: piero.procacci@unifi.it
First published on 2nd July 2024
Abstract
As a contribution to the understanding and rationalization of methodological and modeling effects in recent host–guest SAMPL challenges, using an alchemical molecular dynamics technique we have examined the impact of force field parameterization and ionic strength in connection with guest charge neutralization on computed dissociation free energies in two typical SAMPL heavily charged macrocyclic hosts encapsulating small protonated amines with disparate binding affinities. We have shown that the methodological treatment for host neutralization, with explicit ions or with the background neutralizing plasma in the context of alchemical calculations under periodic boundary conditions, has a moderate effect on the calculated affinities. On the other hand, we have shown that seemingly small differences in the force field parameterization in highly symmetric hosts can produce systematic effects on the structural features that can have a significant impact on the predicted binding affinities.
1 Introduction
The SAMPL challenge (statistical assessment of the modeling of proteins and ligands) is a long-standing international initiative, started in 2008, aimed at innovating and advancing reliable predictive tools for drug design.1–7 The challenges over the last decade have been mostly focused on host–guest systems as “widely accepted model systems to validate computational binding affinity methods and to gain insight into the physical chemistry of molecular recognition.”2 Typical SAMPL hosts, such as cyclodextrins, octa-acid cavitands,8 or pillar[n]arenes,9,10 are characterized by a concave binding surface able to accommodate drug-size molecules with a wide range of affinities in aqueous solution. The latest SAMPL9 challenge overview7 reported on the results of the challenge for 8 cyclodextrin–phenothiazine systems and 13 ligands of the WP6 pillar[6]arene host. It was observed that “methods applying force fields [and molecular dynamics (MD) techniques] achieved in general better correlation with experiments for WP6 [as] opposed to the machine learning and docking models”. This outcome is important as it justifies the use of such computationally intensive simulation techniques as the last screening step in a high-throughput virtual screening funnel-shaped pipeline for drug design. Nonetheless, MD-based alchemical methodologies11–13 for absolute dissociation free energy (ADFE) calculations yielded predictions with significant discrepancies, even when using the same force field for the host and guest models.7,14 According to organizers, the “origins of such differences remain unclear”'.Most of the recent SAMPL9 host–guest systems, despite being designed as an effective sketch in modeling the essential features of the protein–ligand recognition mechanism, present some additional challenges due to their peculiar chemical–physical characteristics that are not common in protein–ligand interactions. The WP6 cavitand used in SAMPL9, for example, is a heavily charged host with the symmetry-related upper and lower rim (see Fig. 1) decorated by six deprotonated carboxylate moieties at the experimental pH where binding affinity measurements are taken. The quasi-D6h symmetry makes this system extremely sensitive to tiny differences in the force field parameterization, whether related to electrostatics, dispersive–repulsive, or bonded terms. Indeed, the effect of a small error in a single symmetry-related parameter can be amplified in the modelization of the bound states, with a systematic impact on the calculated ADFEs.
MD-based approaches are also strongly affected by the way charge neutralization is imposed in the system. Finite-size artifacts in alchemical simulations due to the mainstream use of periodic boundary conditions are deemed to be an important source of systematic errors for free-energy calculations in systems that involve charge changes.15,16 Ionic strength modelization, whether imposed using explicit counter ions or a uniform neutralizing background plasma,17 may also be an important source of systematic errors in pillar[6]arenes such as WP6 bearing-12 charges, especially when MD boxes are relatively small as performed in most of the MD-based SAMPL9 submissions.14,18–22
In this study, as a contribution to the understanding and rationalization of methodological and modeling effects in host–guest SAMPL challenge outcomes, we examine the impact of force field differences and ionic strength in connection with charge neutralization on computed dissociation free energies using the recently proposed virtual double system single box approach23,24 (vDSSB) in two typical SAMPL systems, namely, those involving the heavily charged WP6 host and the strictly related pillar[6]MaxQ25 (SP6) system (see Fig. 1), with acetyl groups being replaced by sulfonic moieties, a modification that has yet to be featured in a SAMPL challenge. The latter choice was dictated by the fact that force field-based methods in SAMPL show particularly severe errors for sulfur-containing compounds.7
For the SP6 system, we show that, contrary to expectations, using a uniform neutralizing background or explicit ions for host-neutralization in the bound state has little effect on the calculated ADFEs. ADFEs computed with ions or a uniform background are found to be very well mutually correlated and in decent and similar agreement with the experimental counterparts, despite the presence of sulfur atoms on the host.
In the case of WP6, we show that the systematic overestimation of the ADFEs in the vDSSB ranked submission,26 originally attributed to artifacts27 due to the uniform neutralizing background in the bound-state leg of the alchemical cycle, can be notably reduced by using the GAFF force field28 for the WP6 host which differ significantly from those obtained using the GAFF2 in the original submission in the modelization of a “single” torsional potential involving the phenoxyacetic moieties of the rim. We show that this apparently tiny difference, with the rest of the force field involving electrostatics, dispersive–repulsion and bonded terms remaining largely unchanged, is responsible for most of the systematic overestimation observed in ref. 26.
2 Electrostatics in the MD alchemical simulation of highly charged systems
2.1 Ionic strength under periodic boundary conditions
In most of the host–guest SAMPL challenges, participants using MD-based methods relying on the alchemical protocol12 (often scoring the best performance) adopted periodic boundary conditions with lattice sums29–31 (PBC-LS) for the treatment of electrostatic interactions. Limiting ourselves to the host–guest challenges SAMPL7, SAMPL8, and SAMPL9, where participants were obliged to submit just one ranked prediction “intended to be the single entry each participant expects to be best performing”',32 we note that all MD-based submissions were done using the PBC-LS protocol in combination with the particle mesh Ewald (PME) with tinfoil boundary conditions.31 The merits and virtues of PBC-LS compared to other methods such as those based on spherical boundary conditions (SBCs) and the reaction field have been authoritatively discussed by Sagui and coworkers in a seminal 2014 review paper.33 Tinfoil (i.e. zero surface dipole29) PBC-LS/PME has become de facto a standard in the MD simulation of biological systems, supported in all the most popular MD packages such as GROMACS,34 AMBER,35 CHARMM,36 NAMD,37 LAMMPS,38 and OPENMM.39For highly charged hosts, such as SP6 and WP6 examined in this study, a non-secondary methodological issue is related to how charge neutralization in the bound state of the host–guest system is handled. When using PBC-LS with PME, charge neutralization can be enforced either using explicit ions or using the uniform neutralizing background plasma implied in the Ewald Sum. The two approaches yield a significant difference in the nominal ionic strength of the MD box. Experimental measurements in SAMPL host–guest challenges are done in general in PBS buffer at pH = 7.4 with an ionic strength of the order of 0.2 M,7,40 neglecting the contributions of the host salt whose concentration is at least 3 orders of magnitude smaller than that of the buffer.
The MD simulation of a single molecular system using PBC-LS, whether the guest, the host or the host–guest complex, is aimed at mimicking the conditions of an infinitely dilute solution, irrespective of the nominal concentration set by the (cubic) box of volume L3, provided that L is chosen large enough. This is because the use of PBC, by design, sets a minimal “invariant” distance L between the images in the lattice and no molecular encounter between images is allowed, while L is chosen large enough so that the local solvent density ρ(r) at L/2 from any atom of the single-molecule system is approximately equal to the solvent density ρ. As a consequence of this fact, for “uncharged” small molecules, hydration energies computed using alchemical techniques in explicit solvents are found to be remarkably stable with varying box sizes even when using boxes with a small L (i.e. ≃12–15 Å),41 quickly reaching the limiting (infinite dilution) value for a large L.
The infinite dilution assumption and the negligible effect of the box size on solvation free energy still hold when the molecular system bears a net charge, provided that finite-size corrections due to the extra charge are accounted for ref. 17, 42 and 43 as we shall discuss further on.
The “effective ionic strength” (EIS) in an MD simulation under PBC-LS of a single molecular system is hence mainly due to the explicit ions included in the simulation box. In general, for n ions of a unitary charge in a cubic box with a side-length L (expressed in Å), the ionic strength (in M units) is given by:
 | (1) |
Most of the MD-based submissions in the latest SAMPL7-9 challenges are done using alchemical techniques (see ref. 12 for a review on alchemical methods for ADFE calculations), whereby the guest is decoupled in a bulk solvent with the volume Lu3 and in the solvated bound state with the volume Lb3. As the two decoupling processes should be done under the same thermodynamic conditions, the EIS in the two legs of the alchemical thermodynamic cycle should be the same, a fact that is often overlooked in SAMPL submissions of highly charged hosts. If the volume in the bulk simulation of the guest is Lg3, then the corresponding number ng of unitary positive and negative charge pairs that must be inserted in the MD box in the bulk state to approximately match the ionic strength of the bound state for WP6 and SP6 with L = Lhg is given by:
 | (2) |
When the neutralization of the highly charged host is imposed using the uniform background, the EIS
 | (3) |
2.2 Finite size effects in the decoupling of charged guests in alchemical simulations with LS-PBC
In alchemical simulations of charged guests as those shown in Fig. 1, the formal total charge of the MD box at the initial and final end states differs. In reality, when using LS-PBC/PME, neutralization holds at any stage of the discharging or recharging process if the uniform neutralizing background is correctly accounted for (ref. 42) in the PME implementation, regardless of whether explicit ions have been included or not. As a consequence of this fact, as discussed in ref. 17 “the ion charging free energy is remarkably invariant to the system size”. In ref. 42 it was shown that “even for systems with only 16 water molecules, it is possible to obtain accurate estimates of the solvation free energy of the sodium ion [via alchemical simulations].” This is because during the alchemical process, the changing uniform background is interacting with the guest as well as with the solvent molecules and with explicit ions (if present). The effect of the background on the guest is hence screened by the dielectric environment and the finite size effects on the solvation free energy are small provided that L is large enough and solvent polarization is strong.46Finite-size effects in the discharging of charged molecules or ions during alchemical simulations under PBC-LS have been thoroughly discussed in several seminal papers from the end of the past century.17,30,42,43,46 Briefly, the energy (in kcal mol−1) computed in PBC-LS/PME of a single ion to bring its charge (in e units) from qbeg to qend in a cubic MD box with side-length L (in Å) is given by the so-called Wigner energy:17
 | (4) |
In PME, this size-dependent Wigner energy is given by a reciprocal lattice contribution and a direct lattice contribution. The former, ΔGrecpr, is automatically included in the standard PME implementation17 while the latter is sometimes added a posteriori19,20 and is given by
 | (5) |
The free energy of discharging or recharging an ion in vacuo, however, must be equal to zero. To account for this fact, Figuerido et al.43 and Hummer et al.46 proposed to add an empirical “thermodynamic” size-dependent correction when computing the ion solvation free energy in an explicit solvent of a dielectric constant ε such that
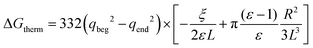 | (6) |
 | (7) |
The problem of the finite-size effects to the calculation of the charging free energy in the context of alchemical simulations of complex host–guest or ligand–protein systems (rather than simple monoatomic ions) has been re-examined in many instances in the past decades,15,16,47–50 proposing a plethora of L-dependent correction terms based again on the continuum model, sometimes requiring costly extra calculations. Strikingly, in the latest of these series of studies,16 dealing with alchemical MD simulations for systems as complex as water-solvated buckyball derivatives hosting charged molecular guests, finite size free energy corrections in charged simulation boxes with or without explicit salt ions were found to be systematically small (less than 1 kcal mol−1) even for small boxes (i.e. with a minimal distance of any solute atom from the wall box of the order of 10 Å). The L-invariance of alchemical free energies under PBC-LS including only the Wigner term eqn (4) in host–guest systems involving charge changes was also numerically verified in SAMPL submissions.19,21
3 Force field effects on the ADFE of host–guest systems
The force field effect on ADFE calculations using alchemical simulations is a long-standing and complicated issue not only in host–guest SAMPL challenges7 but in general in computational drug design.51–54 Limiting ourselves on the host–guest MD-based modelization, the commonly adopted force fields by participants28,39,55–57 are based on an analytical expression of the form: | (8) |
With a few exceptions, the atomic charges in the MD-based SAMPL submissions are fixed, derived using a variety of ab initio or empirical schemes.61–63 In the real world, the electron density on a molecule is constantly modulated by charge reorganization due to the conformational activity of the host, guest, their mutual polarization and the polarization of the solvent. Fixed atomic charges are meant to account for the environment polarizability and for the charge reorganization due to conformational changes in a mean-field spirit.64,65 This approach in modeling electrostatic interactions is widely considered a decent compromise between accuracy and efficiency as the explicit accounts for atomic charge modulation would imply the use of polarizable force fields involving many-body effects. In some cases,21,22,66 the polarizable force field AMOEBA67 has been used in SAMPL challenges, often with remarkable results.5,7 However, polarizable force fields and charge fluctuating simulations are much more demanding than the fixed charge MD protocol, casting doubts on the benefit–cost ratio of these techniques as the last screening stage in the HTVS pipeline for drug design.
4 Methods
4.1 Simulation setup and parameters
The SP6 host has yet to be examined in SAMPL challenges. SP6 guests are shown in Fig. 1. We applied the GAFF2 force field for the host and guest modelization, using the PrimaDORAC online interface68 for atomic type assignment. Atomic RESP62,63 charges on the host and guests were computed using the Antechamber AMBER suite.69 MD simulations were conducted in the NPT ensemble under standard conditions using an isotropic Parrinello–Rahman Lagrangian70 and a series of Nosé thermostats71 for pressure and temperature control, respectively. For the simulation of the bound (host–guest complex) and unbound (guest in bulk) states, cubic boxes of a standard size were used with L ≃ 38 Å3 and L ≃ 25 Å3 (after equilibration of 100 ps), respectively, filled with OPC372 water molecules. Bond constraints were imposed on X–H bonds only, where X is a heavy atom. Charge neutralization was imposed using the PBC/LS/PME neutralizing background (zero EIS) and using explicit ions (EIS = 0.2 M). In the latter case, in the bound state, we added 12 Na+ to neutralize the charge of the host, while in the unbound state two Na+ ions and two Cl− ions were added to approximately match the same EIS as that of the bound state (see Section 2.1). The mass of the ions, irrespective of their type, was set to 4 amu to enhance the passive diffusion of the ions with the scope of accelerating the convergence of the ionic distribution in the bound and unbound states.For the WP6 host–guest system, we selected the guests (reported in Fig. 1) that gave the largest systematic overestimation compared to the experimental ADFEs in our SAMPL9 submission.26 We used GAFF255 with AM1-BCC charges for the guests as in ref. 26. For the WP6 host, we used instead the GAFF parameterization as obtained from PrimaDORAC68 with AM1-BCC charges. Both GAFF and GAFF2 for the WP6 host are based on eqn (8) and have identical AM1-BCC charges, atom types, and very similar bonded and non-bonded parameters. They differ significantly only in the parameters of the O–C–C–O torsion involving the quadruplet connecting the –CH2COO− charged groups to the phenyl rings73 (see Fig. 2). In GAFF, this torsion is zero, while in GAFF2 this torsion has three non-zero terms with multiplicity 1, 2, and 3. The resulting torsional potentials for GAFF and GAFF2 are shown in Fig. 2. For each O–C–C–O, there are two O–C–C–O combinations and the total number (12) of –CH2COO− groups lead to 24 O–C–C–O combinations. The two combinations for a given –CH2COO− group differ by a phase factor of 180°. The torsional energy resulting from the combination of the two O–C–C–O GAFF2 torsions is shown in green in the plot of Fig. 2 with a barrier of 2.5 kcal mol−1 between the two minima at 0 and 180°. We hence expect the distribution of the host O–C–C–O dihedral angle in GAFF2 to be markedly different compared to that observed with GAFF where the O–C–C–O rotation is unrestrained.
 | ||
| Fig. 2 Left: Highlighted quadruplets for the O–C–C–O torsions in WP6. Right: Torsional energy for the O–C–C–O torsions in GAFF, GAFF2, and in the GAFF2 combination (see the text). | ||
The MD protocol (equilibration, thermodynamic conditions, constraints, and water model) is the same as that used for SP6 host–guest batch.
4.2 The vDSSB approach for absolute dissociation free energies
The vDSSB methodology has been thoroughly described in ref. 23, 24, 26 and 74. Briefly, the method consists of two massively parallel computational steps independently applied to the two legs of the alchemical cycle, namely the HREM stage and the nonequilibrium alchemical stage. The HREM stage is aimed at collecting the equilibrium enhanced sampling of the host–guest bound state (with the ligand at full coupling). The initial configurations for the unbound state are obtained by combining the HREM-sampled gas-phase (decoupled) ligand configurations with a pre-equilibrated box filled with explicit water. The HREM technical specification is identical to those adopted in ref. 26. For the NE stage, starting from the HREM sampling of the end states, we launched independently two swarms of 500 and 250 NE alchemical trajectories where the ligand was decoupled in the bound state and recoupled in the unbound state, respectively. The bound state and unbound state annihilation trajectories lasted for 720 ps and 360 ps, respectively. The resulting NE work distributions were combined to produce a sample of 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 work values, yielding the final highly resolved vDSSB convolution of the two bound and unbound distributions. The vDSSB work convolution refers to a NE “unidirectional” process, corresponding to the host–guest dissociation, where the ligand is annihilated in the bound state while materializing in the far distant bulk solvent, with the possibility, by design, of calculating independently the decoupling and recoupling contributions. The dissociation free energy is recovered from the work distribution produced by the convolution using well-known nonequilibrium theorems.75,76
000 work values, yielding the final highly resolved vDSSB convolution of the two bound and unbound distributions. The vDSSB work convolution refers to a NE “unidirectional” process, corresponding to the host–guest dissociation, where the ligand is annihilated in the bound state while materializing in the far distant bulk solvent, with the possibility, by design, of calculating independently the decoupling and recoupling contributions. The dissociation free energy is recovered from the work distribution produced by the convolution using well-known nonequilibrium theorems.75,76
4.3 Further technical details
All calculations were done using the open-source ORAC program,77 freely available at the site https://www.chim1.unifi.it/orac. All data, including MD input parameters for the HREM and NE computational stages, enhanced sampling PDB trajectories, work distributions, and software for input preparation and for post-processing the work data, along with essential documentation, are available at the general-purpose open-access repository Zenodo (https://zenodo.org/records/11074240) to enable anyone willing to do so to reproduce our data.5 Results and discussion
5.1 The SP6 host–guest system: ionic strength effects
In this host–guest batch, all guests have a single positive charge on the amino moiety (see Fig. 1) with the host bearing 12 negative charges. We hence expect the finite size effects due to the treatment of the electrostatic interactions and ionic strength to be remarkable when using MD boxes of standard sizes (i.e. with L = ≃38 and L = ≃25 for the bound and unbound state, respectively). To ascertain the effect of the ionic strength, possibly intertwined with finite-size effects related to charge annihilation or creation, we performed two full vDSSB calculations with and without explicit ions. In the first calculation, no counter ions were inserted in both the bound and unbound states, with the neutralizing PME background plasma yielding an EIS of zero (see eqn (3)) irrespective of the total nominal charge in the MD box. In the second calculation, we inserted 12 Na+ host-neutralizing ions in the bound state and two Na+ and Cl− ions in the unbound state to match the ionic strength (see eqn (1)) in the two legs of the alchemical thermodynamic cycle.Unlike in the WP6 batch, for the SP6 system, we noticed from the preliminary unrestrained HREM simulations of the Vina-prepared bound state that bulky guests tend to significantly populate poses where the center of mass (COM) of the guest molecule is mostly lingering outside the host toroidal cavity. To allow for the sampling of these poses (that are in any case included in a SAMPL isothermal titration calorimetry measurement40), in the bound state, we used a weak harmonic restraint potential with a force constant of K = 0.05 kcal mol−1 Å−2 between the COM of the host and the guest, with a guest allowance volume of Vrestr = (2πRT/K)3/2≃ 600 Å3. We then computed standardly the free energy correction to the annihilation free energy of the bound guest due to the restraint78,79 as ΔGrest = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vrestr/V0 for all guests, as done in most of the recent alchemy-based SAMPL submissions.32,80,81
Vrestr/V0 for all guests, as done in most of the recent alchemy-based SAMPL submissions.32,80,81
Host charge neutralization with or without ions has profound and troubling implications in the electrostatic potential at the host center. In Fig. 3, we report the ionic radial distribution function from the COM of the host of the bound state of the SP6 host–guest systems, obtained from the HREM simulations with explicit ions and with the background (no counter ions). We note that ≃9 explicit ions on average are found within a sphere of radius 18 Å (and volume ≃L3/2) centered on the COM of the host, with a high local density near the outer side of the SO3-decorated rim (with a radius of ≃5.5 Å). The g(r) of the neutralizing background (magenta lines) is equivalent to a uniform distribution of −12 charges and is equal to 1 everywhere, with an integral reaching 6 units at r = 18 ≃ L/2 Å.
 | ||
Fig. 3 Ionic radial distribution, g(r), from the COM of the SP6 host in the equilibrium bound state for all 11 SP6-guest systems of Fig. 1 with explicit ions. Dashed lines are the integral  of the g(r). The thick black lines refer to the average g(r) and n(r) for all host–guest systems with explicit ions. The magenta line is the result obtained with the background only. of the g(r). The thick black lines refer to the average g(r) and n(r) for all host–guest systems with explicit ions. The magenta line is the result obtained with the background only. | ||
These striking differences in the ionic distribution in the two approaches for host neutralization (with ions or with the background) can indeed translate into significant discrepancies in the discharging free energy of the ligand in the bound state. In Table 1, we show the finite-size corrections calculated for the bound and unbound states according to eqn (4) (Wigner energy), eqn (5) (direct lattice Wigner correction) and eqn (6) (Hummer–Figuerido correction) with explicit ions and with the background. The latter correction was calculated with a mean gyration of the guest of R = 3.4 ± 0.3 Å, and ε = 80. Taking into account that the reciprocal lattice contribution to the Wigner energy ΔGew is automatically included in vDSSB calculations when using PME and need not to be considered,17 the finite-size correction to the bound and unbound states for SP6 includes the a posteriori Wigner corrections in the direct lattice ΔGdir, eqn (5), and the thermodynamic corrections ΔGtherm, eqn (6), in the two legs of the alchemical cycle, the latter leading to a negligible correction for the ADFE when explicit ions are included.
| 〈L〉 | α | Grid | N ions | ΔGew | ΔGdir | 〈ΔGtherm〉 | |
|---|---|---|---|---|---|---|---|
| With ions | |||||||
| Bound | 37.0 | 0.37 | 1.17 | 12 | 12.40 | 0.06 | 0.0 |
| Bulk | 24.8 | 0.38 | 1.03 | 4 | 18.84 | 0.21 | 0.0 |
| Total | n/a | n/a | n/a | — | −6.44 | −0.15 | 0.0 |
| With background | |||||||
| Bound | 37.8 | 0.37 | 1.17 | — | −285.1 | −1.37 | 1.9 ± 0.3 |
| Bulk | 24.9 | 0.38 | 1.03 | — | 18.84 | 0.21 | 0.0 ± 0.04 |
| Total | n/a | n/a | n/a | — | 266.26 | −1.16 | 1.9 ± 0.3 |
When neutralization is handled via the background (i.e. without explicit ions), due to a charge change for all ligands of Fig. 1 from −11 to −12e in the bound state, the total direct lattice term is negative (as with explicit ions) and equal to ≃−1.2 kcal mol−1, whereas the total thermodynamic term yields an average “positive” correction term of 1.9 ± 0.3 kcal mol to the ADFE. Had one used this correction in the SAMPL9 vDSSB submission26 where a systematic overestimation of ≃3 kcal mol−1 of the binding strength was observed, such systematic overestimation would have increased, significantly worsening the accuracy of the method. In ref. 26 it was hypothesized that the observed overestimation of the ADFE was due to the fact that the uniform background charge ρBG artificially causes27 the guest with charge qg to favor the lower dielectric environment region inside the toroidal cavity with dielectric constant εl. Probably, this effect could be related to the observed significant improvement of the calculated binding affinity of continuum model approaches when adjusting the cavity dielectric εin in host–guest systems.82 Hub et al.27 provided a simplified negative correction to the ADFE, based on the Poisson–Boltzmann model, for the free energy difference in the two dielectrics (low dielectric environment and bulk water), proportional to qgρBGR2/εl. Additional and subtle corrections within PBC-LS/PME due to the finite size and shape of the ionic system in the final and initial states of the alchemical transitions16 may hence cancel out, in light of the remarkable insensitiveness of solvation free energies observed in a strongly polar solvent for both uncharged41 and charged species, whether monatomic or molecular ions,16,22,42,46 without any other correction but the Wigner energy eqn (4).
Therefore, in computing the host–guest ADFE for the SP6 system, as done in our study and other successful SAMPL submissions,19–21,26 we only included the direct lattice finite-size Ewald corrections (eqn (5)) shown in bold in Table 1, neglecting altogether the thermodynamic empirical correction (eqn (6)) and other continuum-model corrections.15,27,48,50
In Table 2, we report the results for the calculated ADFEs of the host–guest SP6 system obtained with the two vDSSB calculations, namely with counter ions and with the background. In Fig. 4, we show the corresponding correlation plots for the calculated vDSSB dissociation free energies with the experimental counterpart,25 obtained with and without counter ions, and their mutual correlation. In general, we note that the correlation with the experiment, as measured by the Pearson correlation coefficient R and by the Kendall rank coefficient τ, is better when using explicit ions.
| Guest | ΔGexp | With counter ions | With background |
|---|---|---|---|
| ΔGvDSSB | ΔGvDSSB | ||
| L24 | 9.5 | 11.5 ± 0.5 | 11.3 ± 0.8 |
| L25 | 10.9 | 10.5 ± 0.9 | 9.3 ± 1.1 |
| L26 | 8.5 | 9.5 ± 0.6 | 8.1 ± 0.3 |
| L27 | 7.0 | 7.8 ± 0.9 | 7.8 ± 1.3 |
| L28 | 10.6 | 8.9 ± 0.9 | 7.8 ± 0.7 |
| L29 | 8.3 | 6.2 ± 0.6 | 4.9 ± 0.7 |
| L30 | 8.3 | 5.8 ± 1.8 | 4.4 ± 1.0 |
| L31 | 6.8 | 4.5 ± 0.6 | 4.6 ± 0.8 |
| L32 | 7.8 | 6.8 ± 1.3 | 3.5 ± 0.8 |
| L33 | 9.9 | 11.1 ± 0.7 | 10.8 ± 1.0 |
| L34 | 10.3 | 10.9 ± 0.7 | 11.6 ± 0.7 |
In both cases, vDSSB tends to underestimate the host–guest dissociation free energy, yielding mean signed errors (MSEs) of 1.26 and 0.50 kcal mol−1 when using the uniform background and with counter ions, respectively. Strikingly, the mutual correlation of the two vDSSB free energies (see Fig. 4(c)) is excellent, resulting in R = 0.94, τ = 0.74, and an MSE of 1.0 kcal, possibly due to unaccounted (and small) finite-size effects when using the uniform background. Incidentally, we note that the inclusion of the thermodynamic correction of ≃1.9 kcal mol−1 when using the background plasma would have brought the ADFEs of the four bulky ligands L28–L32 closer to the experimental data, while further worsening the results for all the other ligands, yielding a correlation coefficient with the experiment of R = 0.65 and an MSE in the opposite direction of −0.6 kcal mol−1.
We were indeed surprised at the small differences, often within the confidence interval, between the two calculations with zero EIS (the background) and realistic EIS set by the explicit counter ions, notwithstanding the notable differences in the ionic distributions in the two cases (see Fig. 3). The small effect, on the dissociation free energies of host–guest systems computed with alchemical techniques, of the insertion of explicit counter ions with moderate EIS in lieu of the uniform background in host–guest systems was also recently observed in ref. 16, 21 and 22.
The results shown in Fig. 4 and Table 2, as well those reported in recent studies,16,21,22 can have important implications in the practical application of the alchemical simulation in drug design. Charge changes in ligand–protein systems, even when using the simple background plasma and no counter ions, are much less pronounced than those in the bound state of the SP6 or other SAMPL host–guest systems and MD boxes are significantly larger, so that finite-size effects account for corrections to the ADFE well below 1 kcal mol−1.16 MD simulations in PBC-LS/PME for computing ADFEs are, after all, only a model for the real system where many physical effects are not and cannot be included if not devising corrections based on crude approximations (such as the continuum model) relying on a multitude of arbitrary and system-dependent parameters. The goodness of the model should be judged, in the spirit of the SAMPL challenge, by the quality of its predictions in connection with the computational cost, and by the simplicity and smoothness of its application.
5.2 The WP6 host–guest system: force field effects
We have seen in the previous section that the imposition of a realistic EIS in the SP6 host–guest system through explicit ions, while somewhat improving the agreement with the experiment, does not entail dramatic changes in the computed dissociation free energies (see Fig. 4(c)). The latter is found higher by ≃1 kcal mol−1 when ions are included. It is not clear why binding, on average, is more favorable in the SP6 system when ions are included. Based on Tables 1 and 2 referring to SP6, we may nonetheless infer that adding explicit ions to the strictly related WP6 host–guest system, where dissociation free energies computed with the background were systematically overestimated,26 would likely further worsen the accuracy of the method.In ref. 73 it was shown that the structural and dynamical behaviors of the –CH2COO− tails in the apo form of WP6 was dramatically altered when switching from the GAFF force field to the GAFF2 force field. As discussed in ref. 73 and in the “Methods” section, the only significant difference between the GAFF and GAFF2 modelization for the WP6 host involves just one torsion, i.e. the O–C–C–O torsion with the two terminal atoms referring to carbonyl and esteric oxygen atoms (see Fig. 2). Such a seemingly minor difference in the two WP6 parameterizations, amplified by the presence of twelve equivalent –CH2COO− moieties, yielded a much open average configuration of the –CH2COO− tails with the GAFF force field compared to GAFF2, which is attributed73 to the host–solvent and host–explicit ion interactions.
In Fig. 5, we show the effect of this difference on the overall distribution of the 24 O–C–C–O dihedral angles obtained with GAFF and GAFF2 from the HREM simulations of the apo form of WP6 under standard conditions without including explicit ions, i.e. using the same host neutralization protocol of the original vDSSB SAMPL9 submission.26 The GAFF2 distribution exhibits peaks at 0° and ±180°, whereas the GAFF distribution has maxima at ±100°. The maxima of the GAFF2 dihedral probability density are in full accordance with the potential energy of the GAFF2 torsion reported in Fig. 2 exhibiting minima at 0° and ±180°. In GAFF, the O–C–C–O torsional potential is zero and the unhindered rotation about the C–C bond is modulated by the other interacting terms inside the system resulting in a more uniform and spread-out distribution.
 | ||
| Fig. 5 o-c-ct-os torsional distribution obtained with the GAFF and GAFF2 force fields from the HREM simulation of the apo form of WP6 in water. | ||
As observed in ref. 73 where WP6 was simulated including explicit ions, the absence of the O–C–C–O torsional potential in GAFF translates in a more open and disordered behavior of the –CH2COO− tails compared to GAFF2. This can be appreciated in Fig. 6 where we show the probability distribution of the distances between opposite oxygen atoms in the upper and lower rims obtained with the two force fields. The maximum of the distribution in GAFF2 occurs at a shorter distance (of ≃2 Å) than in GAFF. Correspondingly, by aligning the HREM sampled structures on the six connecting carbon atoms of the ring methylene groups of one of the rims, the resulting distribution of the –CH2COO− tails (shown in the circles of Fig. 6) is much more disordered and stretched out in GAFF than that obtained with the GAFF2 force field.
 | ||
| Fig. 6 OO-distance distribution obtained with GAFF and GAFF2 force fields from the HREM simulation of the apo form of WP6 in water. | ||
This strikingly different behavior produced by the O–C–C–O torsion in GAFF and GAFF2 must likely give rise to a systematic impact on the calculated binding free energy. When the hydrophobic scaffold of a WP6 guest (see Fig. 1) enters the host cavity, we might infer that the inward and more rigid configuration of the –CH2COO− tails in GAFF2 could entail a decrease in the koff, due to the stronger interaction between the carboxylate and the protonated amino groups of the guest pointing outside the WP6 torus. As the binding poses for most of the 11 guests are characterized by non-polar moieties trapped into the WP6 cavity and exposed amino groups interacting with the –CH2COO− tails of the rim, this structural feature in GAFF2, with a tightly restrained guest, could eventually translate into higher dissociation free energies compared to GAFF.
To verify this hypothesis, we repeated here the vDSSB calculations presented in the SAMPL9 challenge7,26 on WP6 with the only difference that we adopted the GAFF force field for the host, while maintaining the GAFF2 force field for the guests and the OPC3 model for water. We emphasize that the atomic (AM1-BCC) charges for the host and the guests are identical in the present calculation and that of ref. 26 as well as the other methodological parameters connected to the use of the background neutralizing plasma, the standard volume correction, the HREM protocol for the bound state, the duration and decoupling/recoupling of the NE trajectories. The comparison of the two vDSSB ADFEs for the host–guest WP6 system is hence aimed at singling out the effect of the O–C–C–O torsion on the computed vDSSB dissociation free energy.
The results are collected in Table 3. We notice that in general the ADFEs computed with GAFF for the host are smaller than those computed with GAFF2.
| Guest | ΔGexp | ΔGvDSSB (GAFF2) | ΔGvDSSB (GAFF) |
|---|---|---|---|
| G02 | 10.59 | 17.0 ± 0.4 | 14.0 ± 1.3 |
| G03 | 8.03 | 11.5 ± 0.6 | 12.1 ± 0.6 |
| G06 | 8.08 | 10.4 ± 1.3 | 11.5 ± 1.1 |
| G07 | 7.07 | 12.2 ± 1.7 | 11.2 ± 1.6 |
| G08 | 6.04 | 12.2 ± 1.6 | 9.4 ± 1.1 |
| G09 | 6.32 | 12.5 ± 0.6 | 10.7 ± 1.1 |
| G10 | 9.96 | 13.5 ± 1.1 | 12.9 ± 0.7 |
| G14 | 9.68 | 17.2 ± 0.4 | 11.8 ± 0.4 |
| G15 | 8.37 | 11.2 ± 1.6 | 8.0 ± 0.8 |
| G16 | 10.59 | 14.5 ± 1.5 | 10.5 ± 0.9 |
| G17 | 6.48 | 7.9 ± 0.8 | 7.1 ± 0.9 |
In Fig. 7, we show the corresponding correlation plots with the experimental data and the mutual correlation between the two vDSSB estimates. As inferred, the rigidity of the host –CH2COO− tails with GAFF2 appears to favor binding in most of the cases. The size of the resulting overestimation is nearly halved, passing from −4.44 kcal mol−1 with GAFF2 MSE to −2.54 kcal mol with GAFF. Ranking agreement with GAFF as measured by τ also increases, while we see a degradation of the R Pearson coefficient. Overall, these results neatly show that seemingly small differences in the force field parameters for highly symmetric hosts, like those referring to the single O–C–C–O WP6 torsion in GAFF and GAFF2 (see Fig. 2), may produce systematic errors in the estimates that are far larger than the errors related to methodological issues such as those examined in the preceding section for SP6.
6 Conclusions
We have analyzed the effect of the ionic strength and of the force field parameterization in the calculations of the absolute dissociation free energies of the highly charged host–guest systems (see Fig. 1), typically adopted in the SAMPL challenges, via an MD-based alchemical technique. We have shown that the methodological treatment for host neutralization (with explicit ions or with the background neutralizing plasma in the context of PBC-LS/PME) has a moderate effect on the calculated ADFEs, irrespective of whether finite-size corrections derived from continuum models and related to charge change of the guests are included or not. On the other hand, we have shown that seemingly small differences in the force field parameterization in some cases might be quite significant. In this regard, the systematic overestimation of ADFEs observed in ref. 26 for the WP6 host–guest system can be attributed in large part to a single torsional potential involving the –CH2COO− moieties of the host alone. Atomic charge parameterization may also play an important role, showing better agreement with those in the experiments observed in SP6, where we used RESP charges, compared to WP6, where we used AM1-BCC charges.This study, in accordance with other SAMPL predictions, shows that the confidence intervals of MD-based alchemical ADFE estimates in host–guest systems, if judiciously implemented, are of the order of 2 kcal mol−1 and this is probably the best that we can currently perform with standard force fields of the form of eqn (8) adopted in most SAMPL submissions throughout the years. Explicit ions matching the ionic strength of the system should certainly be considered for improving the estimates. However, such a consensus on the methodological protocol does not appear as a decisive factor even in critical/pathological systems such as highly charged SP6 and WP6. The 2 kcal mol−1 uncertainty in the MD-based free energy translates into 1.5 pKd units, with a correlation (R > 0.5) that is in general higher than that obtained with end point, docking, and machine learning approaches. However, this uncertainty and correlation are still not optimal for reliably using MD-based alchemical methodologies as the last screening step in the HTVS pipeline in industrial settings for drug design.
Our study, as well as the bulk of SAMPL challenge submissions in the last decade, shows that efforts should be focused on improving the force field parameterization. In ligand–protein systems, apparently minor deficiencies in the force field, even when connected with mismatches in the assignment and handling of the parameters from force field databases in automatic procedures,87 can make big differences in the calculated ADFEs, most likely larger than those related to methodological aspects such as the imposition of the ionic strength via counter ions and/or finite-size correction in the PBC-LS context. Concerning this point, it should be noted that, in the latest SAMPL challenges, the “polarizable” AMOEBA force field67 in combination with a standard MD-based alchemical methodology was consistently found among the top-performing methods. In AMOEBA, electrostatic interactions explicitly include polarization effects via distributed atomic polarizabilities. Polarization effects, related to induction phenomena or molecular charge reorganization due to conformational changes, can indeed be decisive in shaping the binding affinity, especially in highly charged host–guest systems such as WP6 and SP6. The computational burden of the AMOEBA many-body protocol is still too high compared to the standard approach with fixed atomic charges, making the method unfit in HTVS pipelines for the time being. However, AMOEBA's success in SAMPL challenges shows, in our view, that the future endeavor in MD-based methodologies for improving the reliability of ADFE estimates in ligand–receptor systems should be mostly devoted to the development of efficient atomic charge fluctuating techniques that account in a realistic fashion for the polarizability feedback between drugs, receptors and solvents in the process of molecular recognition and induced fit.
Data availability
All data for reproducing the results presented in this study, including trajectory files, starting structures, force field parameters, template input files, and ancillary software for preparing the HREM and NE stages on HPC platforms are available at the public repository Zenodo https://zenodo.org/records/11074240.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computing resources and the related technical support used for this work have been mostly provided by CRESCO/ENEAGRID High Performance Computing infrastructure and its staff. The CRESCO/ENEAGRID High Performance Computing infrastructure is funded by ENEA, the Italian National Agency for New Technologies, Energy and Sustainable Economic Development and by the Italian and European research programmes (see https://www.cresco.enea.it for information). Part of the calculations were performed on the LEONARDO HPC cluster, for which we acknowledge the CINECA award under the ISCRA initiative (HP10CV2G9I), for the availability of high-performance computing resources and support. PP acknowledges the National Recovery and Resilience Plan, Mission 4 Component 2 - Investment 1.4 - NATIONAL CENTER FOR HPC, BIG DATA AND QUANTUM COMPUTING - funded by the European Union - NextGenerationEU - CUP B83C22002830001.References
- https://www.samplchallenges.org, accessed 21 March 2024.
- H. S. Muddana, A. T. Fenley, D. L. Mobley and M. K. Gilson, The SAMPL4 host–guest blind prediction challenge: an overview, J. Comput.-Aided Mol. Des., 2014, 28, 305–317 CrossRef CAS PubMed.
- J. Yin, N. M. Henriksen, D. R. Slochower, M. R. Shirts, M. W. Chiu, D. L. Mobley and M. K. Gilson, Overview of the SAMPL5 host–guest challenge: Are we doing better?, J. Comput.-Aided Mol. Des., 2016, 1–19 Search PubMed.
- A. Rizzi, S. Murkli, J. N. McNeill, W. Yao, M. Sullivan, M. K. Gilson, M. W. Chiu, L. Isaacs, B. C. Gibb, D. L. Mobley and J. D. Chodera, Overview of the SAMPL6 host–guest binding affinity prediction challenge, J. Comput.-Aided Mol. Des., 2018, 32, 937–963 CrossRef CAS PubMed.
- M. Amezcua, L. El Khoury and D. L. Mobley, SAMPL7 Host-Guest Challenge Overview: assessing the reliability of polarizable and non-polarizable methods for binding free energy calculations, J. Comput.-Aided Mol. Des., 2021, 35, 1–35 CrossRef CAS PubMed.
- M. Amezcua, J. Setiadi, Y. Ge and D. L. Mobley, An overview of the SAMPL8 host-guest binding challenge, J. Comput.-Aided Mol. Des., 2022, 36, 707–734 CrossRef CAS PubMed.
- M. Amezcua, J. Setiadi and D. L. Mobley, The SAMPL9 hostguest blind challenge: an overview of binding free energy predictive accuracy, Phys. Chem. Chem. Phys., 2024, 26, 9207–9225 RSC.
- C. L. D. Gibb and B. C. Gibb, Binding of cyclic carboxylates to octa-acid deep-cavity cavitand, J. Comput.-Aided Mol. Des., 2014, 28, 319–325 CrossRef CAS PubMed.
- G. Yu, X. Zhou, Z. Zhang, C. Han, Z. Mao, C. Gao and F. Huang, Pillar[6]arene/Paraquat Molecular Recognition in Water: High Binding Strength, pH Responsiveness, and Application in Controllable Self-Assembly, Controlled Release, and Treatment of Paraquat Poisoning, J. Am. Chem. Soc., 2012, 134, 19489–19497 CrossRef CAS PubMed.
- W. Xue, P. Y. Zavalij and L. Isaacs, Pillar[n]MaxQ: A New High Affinity Host Family for Sequestration in Water, Angew. Chem., Int. Ed., 2020, 59, 13313–13319 CrossRef CAS PubMed.
- W. L. Jorgensen, J. K. Buckner, S. Boudon and J. TiradoRives, Efficient computation of absolute free energies of binding by computer simulations. Application to the methane dimer in water, J. Chem. Phys., 1988, 89, 3742–3746 CrossRef CAS.
- A. Pohorille, C. Jarzynski and C. Chipot, Good Practices in Free-Energy Calculations, J. Phys. Chem. B, 2010, 114, 10235–10253 CrossRef CAS PubMed.
- P. Procacci, Alchemical determination of drug-receptor binding free energy: Where we stand and where we could move to, J. Mol. Graphics Modell., 2017, 71, 233–241 CrossRef CAS PubMed.
- M. F. D. Hurley, R. M. Raddi, J. G. Pattis and V. A. Voelz, Expanded ensemble predictions of absolute binding free energies in the SAMPL9 host-guest challenge, Phys. Chem. Chem. Phys., 2023, 25, 32393–32406 RSC.
- G. J. Rocklin, D. L. Mobley, K. A. Dill and P. H. Hnenberger, Calculating the binding free energies of charged species based on explicit-solvent simulations employing lattice-sum methods: An accurate correction scheme for electrostatic finite-size effects, J. Chem. Phys., 2013, 139, 184103 CrossRef PubMed.
- D. Petrov, J. W. Perthold, C. Oostenbrink, B. L. de Groot and V. Gapsys, Guidelines for Free-Energy Calculations Involving Charge Changes, J. Chem. Theory Comput., 2024, 20, 914–925 CrossRef CAS PubMed , PMID: 38164763.
- T. Darden, D. Pearlman and L. G. Pedersen, Ionic charging free energies: Spherical versus periodic boundary conditions, J. Chem. Phys., 1998, 109, 10921–10935 CrossRef CAS.
- S. Khuttan, S. Azimi, J. Z. Wu, S. Dick, C. Wu, H. Xu and E. Gallicchio, Taming multiple binding poses in alchemical binding free energy prediction: the β-cyclodextrin hostguest SAMPL9 blinded challenge, Phys. Chem. Chem. Phys., 2023, 25, 24364–24376 RSC.
- P. Procacci, M. Guarrasi and G. Guarnieri, SAMPL6 host–guest blind predictions using a non equilibrium alchemical approach, J. Comput.-Aided Mol. Des., 2018, 32, 965–982 CrossRef CAS PubMed.
- P. Procacci and G. Guarnieri, SAMPL7 blind predictions using nonequilibrium alchemical approaches, J. Comput.-Aided Mol. Des., 2021, 35, 37–47 CrossRef CAS PubMed.
- Y. Shi, M. L. Laury, Z. Wang and J. W. Ponder, AMOEBA binding free energies for the SAMPL7 TrimerTrip host-guest challenge, J. Comput.-Aided Mol. Des., 2021, 35, 79–93 CrossRef CAS PubMed.
- M. K. J. Chung, R. J. Miller, B. Novak, Z. Wang and J. W. Ponder, Accurate HostGuest Binding Free Energies Using the AMOEBA Polarizable Force Field, J. Chem. Inf. Model., 2023, 63, 2769–2782 CrossRef CAS PubMed , PMID: 37075788.
- M. Macchiagodena, M. Pagliai, M. Karrenbrock, G. Guarnieri, F. Iannone and P. Procacci, Virtual Double-System Single-Box: A Nonequilibrium Alchemical Technique for Absolute Binding Free Energy Calculations: Application to Ligands of the SARSCoV-2 Main Protease, J. Chem. Theory Comput., 2020, 16, 7160–7172 CrossRef CAS PubMed.
- M. Macchiagodena, M. Karrenbrock, M. Pagliai and P. Procacci, Virtual Double-System Single-Box for Absolute Dissociation Free Energy Calculations in GROMACS, J. Chem. Inf. Model., 2021, 61, 5320–5326 CrossRef CAS PubMed.
- A. T. Brockett, W. Xue, D. King, C.-L. Deng, C. Zhai, M. Shuster, S. Rastogi, V. Briken, M. R. Roesch and L. Isaacs, Pillar[6]MaxQ: A potent supramolecular host for invivo sequestration of methamphetamine and fentanyl, Chemistry, 2023, 9, 881–900 CrossRef CAS PubMed.
- P. Procacci and G. Guarnieri, SAMPL9 blind predictions using nonequilibrium alchemical approaches, J. Chem. Phys., 2022, 156, 164104 CrossRef CAS PubMed.
- J. S. Hub, B. L. de Groot, H. Grubmller and G. Groenhof, Quantifying Artifacts in Ewald Simulations of Inhomogeneous Systems with a Net Charge, J. Chem. Theory Comput., 2014, 10, 381–390 CrossRef CAS PubMed , PMID: 26579917.
- J. Wang, R. Wolf, J. Caldwell, P. Kollman and D. Case, Development and testing of a general AMBER force field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- S. W. de Leeuw, J. W. Perram and E. R. Smith, Simulation of electrostatic systems in periodic boundary conditions. I. Lattice sums and dielectric constants, Proc. R. Soc. London, Ser. A, 1980, 373, 27–66 CAS.
- F. Figueirido, G. S. Del Buono and R. M. Levy, On finite-size effects in computer simulations using the Ewald potential, J. Chem. Phys., 1995, 103, 6133–6142 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- SAMPL submissions and evaluation Goals of SAMPL. https://samplchallenges.github.io/roadmap/submissions/, accessed 23 March 2024.
- G. A. Cisneros, M. Karttunen, P. Ren and C. Sagui, Classical Electrostatics for Biomolecular Simulations, Chem. Rev., 2014, 114, 779–814 CrossRef CAS PubMed , PMID: 23981057.
- M. J. Abraham, T. Murtola, R. Schulz, S. Pll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, An overview of the Amber biomolecular simulation package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CAS.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-Mc Carthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wirkiewicz-Kuczera, D. Yin and M. Karplus, All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed , PMID: 24889800.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kal and K. Schulten, Scalable molecular dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS–a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, OpenMM 7: Rapid development of high performance algorithms for molecular dynamics, PLoS Comput. Biol., 2017, 13, 1–17 CrossRef PubMed.
- C.-L. Deng, M. Cheng, P. Y. Zavalij and L. Isaacs, Thermodynamics of pillararene-guest complexation: blinded dataset for the SAMPL9 challenge, New J. Chem., 2022, 46, 995–1002 RSC.
- S. Parameswaran and D. L. Mobley, Box size effects are negligible for solvation free energies of neutral solutes, J. Comput.-Aided Mol. Des., 2014, 28, 825–829 CrossRef CAS PubMed.
- G. Hummer, L. R. Pratt, A. E. Garcia, B. J. Berne and S. W. Rick, Electrostatic Potentials and Free Energies of Solvation of Polar and Charged Molecules, J. Phys. Chem. B, 1997, 101, 3017–3020 CrossRef CAS.
- F. Figueirido, G. S. Del Buono and R. M. Levy, On Finite-Size Corrections to the Free Energy of Ionic Hydration, J. Phys. Chem. B, 1997, 101, 5622–5623 CrossRef CAS.
- W. Chen, Y. Deng, E. Russell, Y. Wu, R. Abel and L. Wang, Accurate Calculation of Relative Binding Free Energies between Ligands with Different Net Charges, J. Chem. Theory Comput., 2018, 14, 6346–6358 CrossRef CAS PubMed , PMID: 30375870.
- W. R. Fawcett and A. C. Tikanen, Role of Solvent Permittivity in Estimation of Electrolyte Activity Coefficients on the Basis of the Mean Spherical Approximation, J. Phys. Chem., 1996, 100, 4251–4255 CrossRef CAS.
- G. Hummer, L. R. Pratt and A. E. Garca, Ion sizes and finite-size corrections for ionicsolvation free energies, J. Chem. Phys., 1997, 107, 9275–9277 CrossRef CAS.
- M. A. Kastenholz and P. H. Hünenberger, Computation of methodology-independent ionic solvation free energies from molecular simulations. II. The hydration free energy of the sodium cation, J. Chem. Phys., 2006, 124, 224501 CrossRef PubMed.
- M. M. Reif and P. H. Hünenberger, Computation of methodology-independent single-ion solvation properties from molecular simulations. III. Correction terms for the solvation free energies, enthalpies, entropies, heat capacities, volumes, compressibilities, and expansivities of solvated ions, J. Chem. Phys., 2011, 134, 144103 CrossRef PubMed.
- C. Ohlknecht, J. W. Perthold, B. Lier and C. Oostenbrink, Charge-Changing Perturbations and Path Sampling via Classical Molecular Dynamic Simulations of Simple GuestHost Systems, J. Chem. Theory Comput., 2020, 16, 7721–7734 CrossRef PubMed , PMID: 33136389.
- C. Ohlknecht, B. Lier, D. Petrov, J. Fuchs and C. Oostenbrink, Correcting electrostatic artifacts due to net-charge changes in the calculation of ligand binding free energies, J. Comput. Chem., 2020, 41, 986–999 CrossRef PubMed.
- C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, Force Field Benchmark of Organic Liquids: Density, Enthalpy of Vaporization, Heat Capacities, Surface Tension, Isothermal Compressibility, Volumetric Expansion Coefficient, and Dielectric Constant, J. Chem. Theory Comput., 2012, 8, 61–74 CrossRef CAS PubMed.
- H. Zhang, C. Yin, Y. Jiang and D. van der Spoel, Force Field Benchmark of Amino Acids: I. Hydration and Diffusion in Different Water Models, J. Chem. Inf. Model., 2018, 58, 1037–1052 CrossRef CAS PubMed.
- D. L. Mobley, C. C. Bannan, A. Rizzi, C. I. Bayly, J. D. Chodera, V. T. Lim, N. M. Lim, K. A. Beauchamp, D. R. Slochower, M. R. Shirts, M. K. Gilson and P. K. Eastman, Escaping Atom Types in Force Fields Using Direct Chemical Perception, J. Chem. Theory Comput., 2018, 14, 6076–6092 CrossRef CAS PubMed , PMID: 30351006.
- Y. Qiu, D. G. A. Smith, S. Boothroyd, H. Jang, D. F. Hahn, J. Wagner, C. C. Bannan, T. Gokey, V. T. Lim, C. D. Stern, A. Rizzi, B. Tjanaka, G. Tresadern, X. Lucas, M. R. Shirts, M. K. Gilson, J. D. Chodera, C. I. Bayly, D. L. Mobley and L.-P. Wang, Development and Benchmarking of Open Force Field v1.0.0-the Parsley Small-Molecule Force Field, J. Chem. Theory Comput., 2021, 17, 6262–6280 CrossRef CAS PubMed , PMID: 34551262.
- GAFF and GAFF2 are public domain force fields and are part of the AmberTools distribution, available for download at https://amber.org internet address (accessed April 20, 2024). According to the AMBER development team, the improved version of GAFF, GAFF2, is an ongoing poject aimed at “reproducing both the high quality interaction energies and key liquid properties such as density, heat of vaporization and hydration free energy”. GAFF2 is expected “to be an even more successful general purpose force field and that GAFF2-based scoring functions will significantly improve the successful rate of virtual screenings.”.
- K. Vanommeslaeghe and A. D. MacKerell, Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing, J. Chem. Inf. Model., 2012, 52, 3144–3154 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. P. Raman and A. D. MacKerell, Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges, J. Chem. Inf. Model., 2012, 52, 3155–3168 CrossRef CAS PubMed , PMID: 23145473.
- D. van der Spoel, Systematic design of biomolecular force fields, Curr. Opin. Struct. Biol., 2021, 67, 18–24 CrossRef CAS PubMed.
- S. Boothroyd, P. K. Behara, O. C. Madin, D. F. Hahn, H. Jang, V. Gapsys, J. R. Wagner, J. T. Horton, D. L. Dotson, M. W. Thompson, J. Maat, T. Gokey, L.-P. Wang, D. J. Cole, M. K. Gilson, J. D. Chodera, C. I. Bayly, M. R. Shirts and D. L. Mobley, Development and Benchmarking of Open Force Field 2.0.0: The Sage Small Molecule Force Field, J. Chem. Theory Comput., 2023, 19, 3251–3275 CrossRef CAS PubMed.
- E. Gelzinyte, M. Oeren, M. D. Segall and G. Csanyi, Transferable Machine Learning Interatomic Potential for Bond Dissociation Energy Prediction of Drug-like Molecules, J. Chem. Theory Comput., 2024, 20, 164–177 CrossRef CAS PubMed , PMID: 38108269.
- A. Jakalian, D. B. Jack and C. I. Bayly, Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- X. Wang, Z. Huai and Z. Sun, Host Dynamics under General-Purpose Force Fields, Molecules, 2023, 28, 5940 CrossRef CAS PubMed.
- Z. Sun, Z. Huai, Q. He and Z. Liu, A General Picture of Cucurbit[8]uril HostGuest Binding, J. Chem. Inf. Model., 2021, 61, 6107–6134 CrossRef CAS PubMed , PMID: 34818004.
- X. Wang, M. Wang and Z. Sun, Comprehensive Evaluation of End-Point Free Energy echniques in Carboxylated-Pillar[6]arene Host-Guest Binding: IV. The QM Treatment, GB Models and the Multi-Trajectory Extension, Liquids, 2023, 3, 426–439 CrossRef CAS.
- M. L. Laury, Z. Wang, A. S. Gordon and J. W. Ponder, Absolute binding free energies for the SAMPL6 cucurbit[8]uril host-guest challenge via the AMOEBA polarizable force field, J. Comput.-Aided Mol. Des., 2018, 32, 1087–1095 CrossRef CAS PubMed.
- C. Zhang, C. Lu, Z. Jing, C. Wu, J.-P. Piquemal, J. W. Ponder and P. Ren, AMOEBA Polarizable Atomic Multipole Force Field for Nucleic Acids, J. Chem. Theory Comput., 2018, 14, 2084–2108 CrossRef CAS PubMed.
- P. Procacci, PrimaDORAC: A Free Web Interface for the Assignment of Partial Charges, Chemical Topology, and Bonded Parameters in Organic or Drug Molecules, J. Chem. Inf. Model., 2017, 57, 1240–1245 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, Automatic Atom Type and Bond Type Perception in Molecular Mechanical Calculations, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- M. Parrinello and A. Rahman, Crystal Structure and Pair Potentials: A MolecularDynamics Study, Phys. Rev. Lett., 1980, 45, 1196–1199 CrossRef CAS.
- S. Nośe, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- S. Izadi and A. V. Onufriev, Accuracy limit of rigid 3-point water models, J. Chem. Phys., 2016, 145, 074501 CrossRef PubMed.
- X. Liu, L. Zheng, C. Qin, Y. Cong, J. Z. H. Zhang and Z. Sun, Comprehensive Evaluation of End-Point Free Energy Techniques in Carboxylated-Pillar[6]arene HostGuest Binding: III. Force-Field Comparison, Three-Trajectory Realization and Further Dielectric Augmentation, Molecules, 2023, 28, 2767 CrossRef CAS PubMed.
- M. Macchiagodena, M. Karrenbrock, M. Pagliai, G. Guarnieri, F. Iannone and P. Procacci, Methods in Pharmacology and Toxicology, Springer Nature, New York, NY, 2021, pp. 1–41 Search PubMed.
- G. E. Crooks, Nonequilibrium measurements of free energy differences for microscopically reversible Markovian systems, J. Stat. Phys., 1998, 90, 1481–1487 CrossRef.
- C. Jarzynski, Nonequilibrium equality for Free energy differences, Phys. Rev. Lett., 1997, 78, 2690–2693 CrossRef CAS.
- P. Procacci, Hybrid MPI/OpenMP Implementation of the ORAC Molecular Dynamics Program for Generalized Ensemble and Fast Switching Alchemical Simulations, J. Chem. Inf. Model., 2016, 56, 1117–1121 CrossRef CAS PubMed.
- M. K. Gilson, J. A. Given, B. L. Bush and J. A. McCammon, The StatisticalThermodynamic Basis for Computation of Binding Affinities: A Critical Review, Biophys. J., 1997, 72, 1047–1069 CrossRef CAS PubMed.
- P. Procacci and R. Chelli, Statistical Mechanics of Ligand-Receptor Noncovalent Association, Revisited: Binding Site and Standard State Volumes in Modern Alchemical Theories, J. Chem. Theory Comput., 2017, 13, 1924–1933 CrossRef CAS PubMed.
- The SAMPL8 Blind Prediction Challenges for Computational Chemistry. https://github.com/samplchallenges/SAMPL8, accessed 13 April 2024.
- SAMPL9: Original submission txt files for host–guest systems. https://github.com/samplchallenges/SAMPL9/tree/main/hostguest/Analysis/Submissions, accessed 13 April 2024.
- X. Liu, L. Zheng, Y. Cong, Z. Gong, Z. Yin, J. Z. H. Zhang, Z. Liu and Z. Sun, Comprehensive evaluation of end-point free energy techniques in carboxylated-pillar[6]arene host-guest binding: II. regression and dielectric constant, J. Comput.-Aided Mol. Des., 2022, 36, 879–894 CrossRef CAS PubMed.
- C.-L. Deng, M. Cheng, P. Y. Zavalij and L. Isaacs, Thermodynamics of pillararene-guest complexation: blinded dataset for the SAMPL9 challenge, New J. Chem., 2022, 46, 995–1002 RSC.
- K. Yang, J. Wen, S. Chao, J. Liu, K. Yang, Y. Pei and Z. Pei, A supramolecular photosensitizer system based on the hostguest complexation between water-soluble pillar[6]arene and methylene blue for durable photodynamic therapy, Chem. Commun., 2018, 54, 5911–5914 RSC.
- D. Hessz, S. Bádogos, M. Bojtar, I. Bitter, L. Drahos and M. Kubinyi, Complexes of carboxylato pillar[6]arene with Brooker-type merocyanines: Spectral properties, pKa shifts and the design of a displacement assay for trimethyl lysine, Spectrochim. Acta, Part A, 2021, 252, 119455 CrossRef CAS PubMed.
- B. Hua, L. Shao, Z. Zhang, J. Sun and J. Yang, Pillar[6]arene/acridine orange hostguest complexes as colorimetric and fluorescence sensors for choline compounds and further application in monitring enzymatic reactions, Sens. Actuators, B, 2018, 255, 1430–1435 CrossRef CAS.
- Y. Khalak, G. Tresadern, B. L. de Groot and V. Gapsys, Non-equilibrium approach for binding free energies in cyclodextrins in SAMPL7: force fields and software, J. Comput.-Aided Mol. Des., 2021, 35, 49–61 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2024 |



