High-level ab initio characterization of the OH + CH₃NH₂ reaction

Abstract

The complex multichannel OH + CH₃NH₂ reaction is investigated using high-level ab initio methods considering not just the abstraction, but the substitution pathways, too. The H-abstraction channels are proven to be exothermic with classical(adiabatic) relative energies of −25.58(−26.23) and −17.93(−19.32) kcal mol⁻¹ for the methyl- and amino-H-abstraction processes resulting in H₂O + CH₂NH₂ and CH₃NH, respectively. There is another reaction path that is thermodynamically favored: the amino-substitution leading to NH₂ + CH₃OH with a classical(adiabatic) reaction energy of −6.43(−7.76) kcal mol⁻¹. The H- and methyl-substitution reactions, which provide H + HOCH₂NH₂/CH₃NHOH and CH₃ + NH₂OH, respectively, have higher energies relative to the reactants making them endothermic. The entrance channel of the reaction is studied using one-dimensional energy curves where the reactants are frozen in their equilibrium structures and they approach each other from different directions. The geometry optimization of the stationary points, including the reactants, transition states, post-reaction complexes and products, is carried out by the MP2 and CCSD(T)-F12b methods using the aug-cc-pVDZ and aug-cc-pVTZ basis sets. To reach higher chemical accuracy we perform single-point energy calculations at the CCSD(T)-F12b/aug-cc-pVQZ level of theory that are augmented with different energy corrections accounting for post-CCSD(T) correlation, core correlation, scalar relativistic effect, spin–orbit coupling and zero-point energy. Rate coefficients are computed using transition-state theory with Wigner tunneling correction and compared with previous theoretical and experimental data.

---

I. Introduction

The OH radical and the CH₃NH₂ molecule have been detected in the interstellar medium and their combined participation may lead to the formation of the simplest amino acid, glycine that is one of the building blocks of life.^1–6 Furthermore, the reaction between the OH radical and CH₃NH₂ may be relevant to combustion chemistry, especially for blended combustion of ammonia and hydrocarbon fuels.^7,8 However, the mechanism and energetics of the OH + CH₃NH₂ reaction are not well characterized, therefore we would take the opportunity and describe in detail the topology of the potential energy surface (PES) of this reaction with the help of high-level ab initio methods. The new benchmark results open the possibility of theoretical kinetic investigations which can be directly comparable with the experimental results^9,10 and later can give a great platform for PES developments and can contribute to future reaction-dynamics simulations. The reaction of NH₃ with the OH radical was studied by Espinosa-Garcia and his group theoretically and this previous work can help to understand what can happen at the amino-side of the CH₃NH₂ molecule in the title reaction.¹¹ As a starting point in the current investigation, we have tried to utilize the former results of our research group. The experiences with the OH + CH₄/C₂H₆ and F/Cl/Br/I + C₂H₆ systems can be useful for considering the possibilities of other reaction channels such as the H-substitution and the methyl-substitution that have not been investigated yet for the title reaction.^12,13 From the methylamine point of view, the reactions of CH₃NH₂ with F and Cl also serve as a good pre-knowledge since the F and Cl atoms are isoelectronic with the OH radical considering their valence shells.^14,15

In the literature, mainly the H-abstraction reaction pathway is studied, which is considered as the main channel of the title reaction. H-abstraction can happen in two parts of the CH₃NH₂ molecule: at the amino group or at the methyl group forming H₂O and CH₃NH or CH₂NH₂, respectively. These two competitive reaction channels were investigated using theoretical methods by Tian and coworkers in 2009.¹⁶ They determined the geometries and frequencies of the reactants, pre-reaction minima, transition states, post-reaction complexes and the products at the CCSD/6-31G(d) level of theory. Furthermore, using the obtained structures, they performed single-point energy calculations at the CCSD(T)/6-311++G(2d,2p) level of theory providing the relative energies of the stationary points. In 2013, the H-abstraction pathway of the title reaction was investigated by Onel and coworkers who optimized the geometries of the stationary points with the MP2 method utilizing the aug-cc-pVDZ and aug-cc-pVTZ basis sets.¹⁷ They also carried out energy calculations at higher levels using the CCSD(T) and CCSD(T)-F12a methods.

In the present study we go beyond previous work by preforming high-level ab initio computations considering energy contributions beyond the gold-standard frozen-core CCSD(T) level of theory as detailed in Section II. Furthermore, we compute rate coefficients using transition-state theory and reveal several novel pathways and product channels for the title reaction as described in Section III. Finally, the paper ends with summary and conclusions in Section IV.

II. Computational details

To identify the structures and obtain the corresponding energies and harmonic vibrational frequencies of the stationary points of the title reaction we use the second-order Møller–Plesset¹⁸ perturbation theory with the correlation-consistent aug-cc-pVDZ basis set.¹⁹ In order to reach higher accuracy, we use the restricted open-shell Hartree–Fock (ROHF)-based unrestricted explicitly-correlated coupled-cluster singles, doubles and perturbative triples method (CCSD(T)-F12b)²⁰ associated with aug-cc-pVDZ and aug-cc-pVTZ¹⁹ basis sets utilizing the previously-obtained MP2/aug-cc-pVDZ geometries. In some cases, the standard Hartree–Fock (HF) process failed to converge. To resolve this problem we carry out computations that are based on the ManyHF method,²¹ which was recently developed in our group. The algorithm tries to determine the lowest-energy HF solution utilizing numerous sets of initial orbitals before the correlation methods are applied.

To refine the energies of the stationary points we perform single-point energy calculations at the CCSD(T)-F12b/aug-cc-pVQZ^19,20 level of theory using the most accurate optimized structures. Five different energy corrections are considered in order to increase the accuracy utilizing the best structures. The post-CCSD(T) correlation corrections are calculated with the CCSD(T),²² CCSDT²³ and CCSDT(Q)²⁴ methods using the cc-pVDZ basis set, which are determined using the following expressions:

δ[T] = CCSDT/cc-pVDZ − CCSD(T)/cc-pVDZ (1)

δ[(Q)] = CCSDT(Q)/cc-pVDZ − CCSDT/cc-pVDZ (2)

We carry out all-electron (AE) and frozen-core (FC) computations at the CCSD(T)-F12b/cc-pCVTZ-F12²⁵ level of theory. The core-correlation originates from the difference between the AE and FC calculations as:

Δ_core = AE-CCSD(T)-F12b/cc-pCVTZ-F12 – FC-CCSD(T)-F12b/cc-pCVTZ-F12 (3)

To take into account the scalar relativistic effect, we use the second-order Douglas–Kroll (DK)²⁶ relativistic energies that are computed at the AE-CCSD(T)/aug-cc-pwCVTZ-DK level of theory and non-relativistic computations are performed at the AE-CCSD(T)/aug-cc-pwCVTZ level of theory. The following equation defines the scalar relativistic correction as the difference between the two energies:^22,27

Δ_rel = DK-AE-CCSD(T)/aug-cc-pwCVTZ-DK − AE-CCSD(T)/aug-cc-pwCVTZ (4)

Spin–orbit (SO) coupling effects are computed using the Breit–Pauli Hamiltonian in the interacting-states approach²⁸ utilizing the Davidson-corrected²⁹ multi-reference configuration interaction³⁰ (MRCI+Q) method with the aug-cc-pVTZ basis set.³¹ In the MRCI computations an active space consisting of 21 valence electrons distributed among 11 spatial orbitals (HOMO, HOMO−1, …, HOMO−10) is employed with all 3 doubly-occupied 1s-like core orbitals of the C, N, and O atoms (HOMO−11, HOMO−12, and HOMO−13) kept closed. The spin–orbit correction is determined as the difference between the SO₁-ground-state and the non-SO₁-ground-state energies as:

Δ_SO = SO₁(MRCI+Q/aug-cc-pVTZ) – non-SO₁(MRCI+Q/aug-cc-pVTZ) (5)

For a better understanding of the entrance channel, we perform one-dimensional scans at the levels of ManyHF-based MP2/aug-cc-pVDZ and MRCI/aug-cc-pVDZ where the reactants are kept frozen in their equilibrium geometries and only one distance is varied between the OH and CH₃NH₂ molecules.

The benchmark relative classical energies are determined using the most accurate single-point energies and all of the above mentioned corrections. The following sum provides the benchmark relative classical energies:

E_c = CCSD(T)-F12b/aug-cc-pVQZ + δ[T] + δ[(Q)] + Δ_core + Δ_rel + Δ_SO (6)

The benchmark relative adiabatic energies are obtained with the following expression:

E_a = E_c + Δ_ZPE (7)

where Δ_ZPE means the zero-point energy corrections obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory. In cases where harmonic frequencies computed at the CCSD(T)-F12b/aug-cc-pVTZ theoretical level are unavailable, we add the zero-point energy obtained at the most accurate level (MP2/aug-cc-pVDZ or CCSD(T)-F12b/aug-cc-pVDZ) to the classical energies.

The computations of the MP2, CCSD(T)-F12b, AE, DK, MRCI and SO data are performed using the Molpro program package.³² The frozen-core CCSD(T), CCSDT and CCSDT(Q) calculations are carried out with MRCC^33,34 interfaced to Molpro.

Thermal rate coefficients are determined using standard transition-state theory (TST) as

where k_B is the Boltzmann constant, T is the temperature, h is the Planck constant, ΔE_a is the adiabatic barrier height, R is the gas constant, and Q_TS, Q_OH, and Q_CH3NH2 denote the partition functions of TS, OH, and CH₃NH₂, respectively. The partition functions are obtained as the product of the translational (Q_trans), rotational (Q_rot), vibrational (Q_vib), and electronic (Q_elec) contributions. These factors are calculated using standard expressions, utilizing rigid rotor and harmonic oscillator approximations for Q_rot and Q_vib, respectively. The Wigner formula is used to estimate a multiplicative tunneling correction aswhere v_TS is the imaginary frequency of the TS.

III. Results and discussion

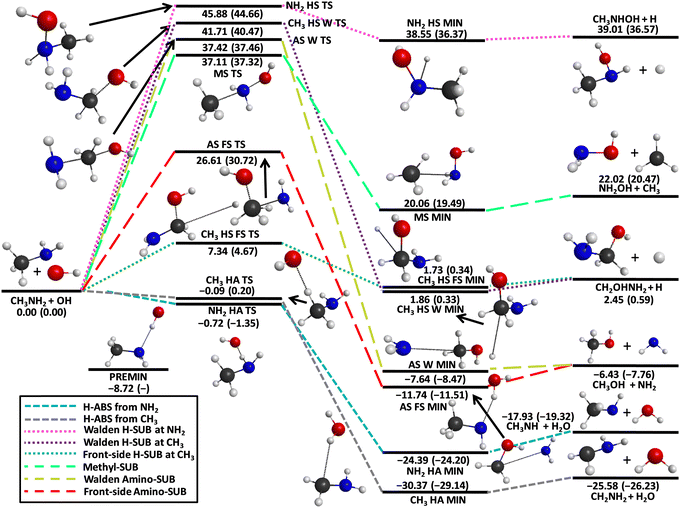
For the entrance channel, we present one-dimensional energy curves at 11 different orientations utilizing the ManyHF-based MP2/aug-cc-pVDZ and MRCI/aug-cc-pVDZ levels of theory, as shown in Fig. 1. We examine 4 cases where the OH molecule goes toward CH₃NH₂ with its H-side, because it has the possibility to form a H-bond where OH is the donor, and there are 7 cases where CH₃NH₂ is approached by the O-side of the OH molecule. All of the potentials show a minimum except one case: where the OH molecule attacks the N atom of CH₃NH₂ with its O-side perpendicular to the C–N bond. This phenomenon can be explained by the repulsion between the non-bonding electrons of the N and O atoms. The positions of the minima are typically between 2.0 and 2.5 Å that can be interpreted as the range of the H-bond length. The depths of these minima are shallow except one case, characteristically the maximum depths are around 2 kcal mol⁻¹. The exception, where we experience a deeper (8 kcal mol⁻¹) minimum, is the case where the C–N bond is approached perpendicularly at the N atom by the H-side of the OH molecule. The difference between the performance of the two applied methods (MP2 and MRCI) is slight, the behavior of the curves and the positions of the minima are very similar.

Fig. 1 Potential energy curves determined in different directions for the entrance channel at the levels of MP2/aug-cc-pVDZ (black) and MRCI/aug-cc-pVDZ (red) theory where the OH and CH₃NH₂ molecules are kept frozen at their equilibrium structures and only one distance (dotted bond) is varied.

The schematic potential energy surface of the OH + CH₃NH₂ reaction with the optimized geometries, the classical as well as the adiabatic relative energies, is shown in Fig. 2. Basically, the reaction of these two species can lead to 6 different product channels depending on what the orientation of the molecules is and how much energy they have during the collision. The most favored reaction path is the hydrogen abstraction, where a hydrogen atom is ripped off from the CH₃NH₂ molecule by the OH radical. There are two ways of passing this process since it can happen at the C and N atom, too. According to this separation we can differentiate between amino-(H-ABS from NH₂)- and methyl-(H-ABS from CH₃)-H-abstractions. The abstraction from the amino group is less beneficial thermodynamically compared to that from the CH₃ group. Furthermore, both of them are exothermic since the classical (adiabatic) reaction enthalpies are −17.93(−19.32) kcal mol⁻¹ in the case of the amino H-abstraction and −25.58(−26.23) kcal mol⁻¹ with respect to the CH₃–H-abstraction. Both pathways are barrierless and the energy order of the submerged transition states is opposite as in case of the reaction enthalpies, i.e., −0.72(−1.35) and −0.09(0.20) kcal mol⁻¹, respectively. However, in the exit channel, the post-reaction complex of the CH₃–H-abstraction reaction channel has lower energy, where we can observe a larger energy gap than in the case of the transition states and a smaller one than in the case of the products. With the increasing energy of the system, the substitution can open up. During this type of mechanism, a part of CH₃NH₂ is replaced by OH. According to which atoms or groups leave, we can differentiate between hydrogen-(H-SUB from NH₂ and H-SUB from CH₃), amino-(Walden amino-SUB and front-side amino-SUB) and methyl-substitutions (methyl-SUB). The substitution process can happen via two mechanisms: Walden inversion and front-side attack. In the case of Walden inversion, the attacking OH approaches CH₃NH₂ from the opposite side of the leaving group and an inversion happens, while during the front-side mechanism the attacking and leaving processes take place next to each other and the configuration of the product molecule remains the same as in the reactant CH₃NH₂. The H-substitution at the CH₃ group with front-side mechanism possesses the lowest energy barrier among the H-substitutions followed by H-substitution from the CH₃ group via Walden inversion and the kinetically most unfavored one is the H-substitution from the amino group. The classical (adiabatic) energy barriers are 7.34(4.67), 41.71(40.47) and 45.88(44.66) kcal mol⁻¹, respectively. The energy of the transition state of the H-substitution at the NH₂ group is not just the highest among the H-substitutions, but among all of the possible reaction channels, too. It is important to note that the finding that CH₃ HS FS TS is below CH₃ HS W TS is somewhat surprising, because in the case of similar reactions, like halogen + C₂H₆,¹³ Cl + CH₃NH₂/CH₃CN,^15,35 and OH + C₂H₆,¹² the Walden pathway was found to be favored (see more discussion on this result below). The energy order of the post-reaction minima with respect to the H-substitution channels is the same as in case of the transition states considering the adiabatic energies, but the energy gap between the Walden- (CH₃ HS W MIN) and front-side (CH₃ HS FS MIN)-type minima of the H-substitution at the CH₃ group is much smaller. However, if we neglect the zero-point energies, the post-reaction complex of the front-side attack mechanism has lower energy. The post-reaction minimum of the H-substitution at the amino group has the highest classical (adiabatic) energy of 38.55(36.37) kcal mol⁻¹ considering all reaction channels. The H-substitution process at the CH₃ group creates a CH₂OHNH₂ molecule and a hydrogen atom, meanwhile if it happens at the amino group the products are CH₃NHOH + H. The classical (adiabatic) reaction enthalpies are 2.45(0.59) and 39.01(36.57) kcal mol⁻¹, respectively. Functional groups can also exchange with the OH molecule via substitution such as the NH₂(amino-substitution) and CH₃(methyl-substitution). In the case of the methyl-substitution there is only one possible way for the reaction to take place while the amino-substitution can occur through two types of mechanism: Walden inversion and front-side attack. The front-side amino-substitution has the lowest classical (adiabatic) energy barrier out of the three reaction channels, i.e., 26.61(30.72) kcal mol⁻¹. This is followed by the methyl-substitution with a 37.11(37.32) kcal mol⁻¹ classical (adiabatic) energy barrier and the kinetically most hindered pathway is the amino-substitution via Walden inversion with a barrier height of 37.42(37.46) kcal mol⁻¹. The fact that amino-substitution with front-side attack is more favored than Walden inversion is consistent with the finding for the CH₃ HS channel. In the case of the title reaction, the preference of the front-side TSs may be explained by steric considerations and/or H-bond interactions, which cannot occur at the Walden configurations. In the case of the post-reaction complexes the energy order is different: the minimum with the highest energy corresponds to the complex of the methyl substitution with 20.06(19.49) kcal mol⁻¹ classical (adiabatic) energy. The energy levels of the minima of the amino-substitutions with Walden inversion and front-side attack are relatively close to each other with classical (adiabatic) energies of −7.64(−8.47) and −11.74(−11.51) kcal mol⁻¹, respectively. The amino-substitution is an exothermic reaction path with a classical (adiabatic) energy of −6.43(−7.76) kcal mol⁻¹ forming CH₃OH and NH₂ molecules while the methyl-substitution produces NH₂OH and CH₃ molecules and has a higher classical (adiabatic) energy level of 22.02(20.47) kcal mol⁻¹ making this reaction path endothermic.

Fig. 2 Schematic potential energy surface of the OH + CH₃NH₂ reaction visualizing the most accurate optimized geometries and classical (adiabatic) benchmark energies, in kcal mol⁻¹, of the lowest-energy conformers relative to the reactants.

During our investigation, we successfully identify several conformers of the transition states, post-reaction complexes and products as it is represented in Fig. 3–5 with the most accurate optimized geometries as well as classical and adiabatic energies. Considering the transition states 3 conformers for the NH₂–H-abstraction and 5 conformers for the CH₃–H-abstraction reaction channel are revealed. The conformers of the amino H-abstraction are very close to each other in energy since the lowest-energy transition state has a −0.72(−1.35) kcal mol⁻¹ classical (adiabatic) relative energy and the highest-energy conformer possesses a classical (adiabatic) relative energy level of −0.78(−1.30) kcal mol⁻¹. In the case of the H-abstraction from the CH₃ group there are no large differences in energy between the three lower-energy conformers. However, the two highest-energy conformers have significantly greater energy levels with classical (adiabatic) values of 15.90(12.58) and 16.69(14.16) kcal mol⁻¹. All in all, for the H-substitution reaction channel 5 conformers of the transition states are identified, 2 for the H-substitution from the CH₃ group with the front-side attack mechanism, 2 for the H-substitution from the amino group and 1 for the H-substitution from the CH₃ group with Walden inversion. There is a major gap in energy between the two conformers of the front-side CH₃ H-substitution. The difference between them is 14.63(16.40) kcal mol⁻¹ classically (adiabatically). There is one more reaction channel where more than one conformer is determined: the amino-substitution with the front-side attack mechanism. In this case the higher-energy conformer is more than twice as large as the lower one in energy. For the amino-substitution with Walden inversion and methyl-substitution reactions only one structure is obtained. Considering the geometries of the post-reaction complexes, 2 conformers are revealed for every reaction channel except one case: the H-abstraction from the amino group. Characteristically the energy difference between the two conformers is relatively small in every case, whereas there is an increasing tendency in the gaps as the energies of the conformers grow. The energy differences of the post-reaction conformers are under 1 kcal mol⁻¹ except for the two reaction channels with the highest relative energies: the methyl-substitution and the H-substitution at the amino group. Furthermore, conformers are obtained for the two highest-energy product channels: the methyl-substitution and H-substitution at the amino group. In the case of the methyl-substitution, we can separate the cis and trans conformer of the NH₂OH molecule where the cis structure has a higher energy. In the case of the product geometries of the H-substitution at the amino group, the orientation of the CH₃ group and the OH part can be different, which means a 3.49(3.38) kcal mol⁻¹ difference in energy classically (adiabatically).

Fig. 3 Different transition state structures for the OH + CH₃NH₂ reaction illustrating the benchmark classical and adiabatic energies relative to the reactants.

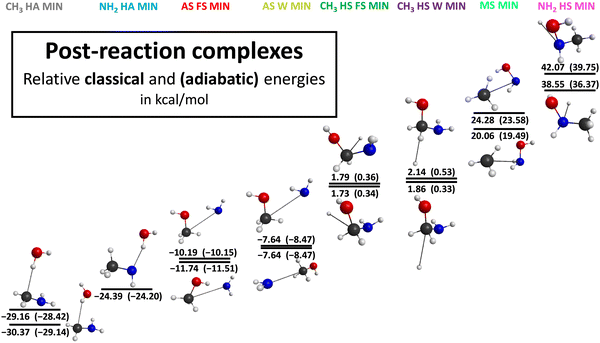Fig. 4 Different post-reaction complex structures for the OH + CH₃NH₂ reaction illustrating the benchmark classical and adiabatic energies relative to the reactants.

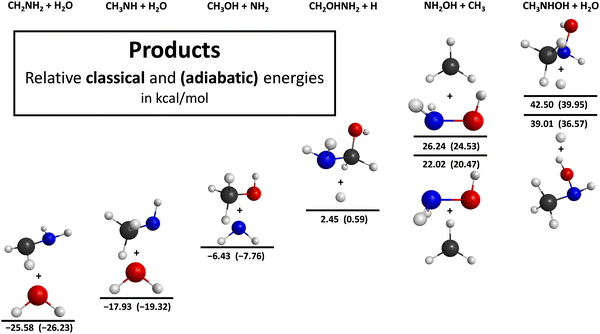Fig. 5 Different product structures for the OH + CH₃NH₂ reaction illustrating the benchmark classical and adiabatic energies relative to the reactants.

The determined energies of the stationary points are summarized in Table 1. The optimizations of the structures, the energy and frequency calculations for the optimized geometries are executed at three different levels of theory: MP2/aug-cc-pVDZ, CCSD(T)-F12b/aug-cc-pVDZ and CCSD(T)-F12b/aug-cc-pVTZ. At the MP2/aug-cc-pVDZ level of theory the energies and frequencies are obtained and the geometries are optimized successfully for all of the stationary points. The calculations are not converged in three cases using the CCSD(T)-F12b method with aug-cc-pVDZ basis set: CH₃ HA TS 4, CH₃ HA TS 5 and CH₃ HS W TS. For the CCSD(T)-F12b/aug-cc-pVDZ computations the previously-obtained geometries are utilized as initial points. In six cases (CH₃ HA TS 3, NH₂ HA TS 1, NH₂ HA TS 2, NH₂ HA TS 3, AS W MIN 1 and PREMIN) we use the ManyHF method to overcome the convergence problems. The structures determined at the CCSD(T)-F12b/aug-cc-pVDZ level of theory are used as initial geometries for the highest level (CCSD(T)-F12b/aug-cc-pVTZ) of the optimizations and frequency calculations. The computations failed because of convergence issues in the same cases as those using the CCSD(T)-F12b method with the aug-cc-pVDZ basis set plus five situations: CH₃ HA TS 1, CH₃ HA TS 3, NH₂ HA TS 1, NH₂ HA TS 2 and NH₂ HA TS 3. The utilization of the ManyHF method helps in the case of the following stationary points: CH₃ HS FS TS 1, PREMIN, CH₃ HA MIN 2, CH₃ HS FS MIN 1, CH₃ HS FS MIN 2, CH₃ HS W MIN 1, CH₃ HS W MIN 2 and AS FS MIN 1. For further single-point calculations including the CCSD(T)-F12b/aug-cc-pVQZ computations and the determination of the five energy corrections the best previously-obtained geometries are used. In the case of seven stationary points convergence issues have occurred using the standard HF method: CH₃ HA TS 1, CH₃ HA TS 3, NH₂ HA TS 1, NH₂ HA TS 2, NH₂ HA TS 3, PREMIN and CH₃ HA MIN 2. To resolve this issue, the single-point energies are successfully determined in all cases using the ManyHF method. Moving from the MP2/aug-cc-pVDZ to the CCSD(T)-F12b/aug-cc-pVTZ level of theory the energy differences relative to CCSD(T)-F12b/aug-cc-pVQZ become smaller. The deviations between the CCSD(T)-F12b/aug-cc-pVTZ and CCSD(T)-F12b/aug-cc-pVQZ energies are typically a few hundredths of kcal mol⁻¹ showing the excellent basis convergence of the method.

Table 1 Energies (kcal mol⁻¹) and auxiliary energy contributions (kcal mol⁻¹) of the stationary points including the products of the OH + CH₃NH₂ reaction relative to the reactants at different levels of theory

Stationary point	MP2	CCSD(T)-F12b			δ[T]^e	δ[(Q)]^f	Δ core	Δ rel	Δ SO	Classical^j	Δ ZPE	Adiabatic^l
	DZ^a	DZ^b	TZ^c	QZ^d
a MP2/aug-cc-pVDZ relative energies determined at MP2/aug-cc-pVDZ geometries. b CCSD(T)-F12b/aug-cc-pVDZ relative energies determined at CCSD(T)-F12b/aug-cc-pVDZ geometries. c CCSD(T)-F12b/aug-cc-pVTZ relative energies determined at CCSD(T)-F12b/aug-cc-pVTZ geometries. d CCSD(T)-F12b/aug-cc-pVQZ relative energies determined at the most accurate geometries. e CCSDT – CCSD(T) determined using the cc-pVDZ basis set at the most accurate geometries. f CCSDT(Q) – CCSDT determined using the cc-pVDZ basis set at the most accurate geometries. g Core-correlation correction determined as the difference between all-electron and frozen-core CCSD(T)-F12b/cc-pCVTZ-F12 relative energies at the most accurate geometries. h Scalar relativistic effect determined as the difference between DK-AE-CCSD(T)/aug-cc-pwCVTZ-DK and non-relativistic AE-CCSD(T)/aug-cc-pwCVTZ relative energies at the most accurate geometries. i Spin–orbit (SO) corrections determined as the difference between the SO and non-SO ground-state MRCI+Q/aug-cc-pVTZ relative energies at the most accurate geometries. j Benchmark classical relative energy determined as CCSD(T)-F12b/aug-cc-pVQZ + δ[T] + δ[(Q)] + Δcore + Δrel + ΔSO. k ZPE corrections determined at the most accurate level of theory at which geometry optimizations converged. l Benchmark adiabatic relative energy determined as Classical + ΔZPE. m The ManyHF method is used.
CH3 HA TS 1	3.69	−0.35	—	−0.10^m	−0.14^m	−0.06^m	0.01^m	0.01^m	0.19	−0.09	0.29	0.20
CH3 HA TS 2	4.37	1.07	1.25	1.29	−0.17	−0.15	−0.03	0.03	0.19	1.16	−0.71	0.45
CH3 HA TS 3	−0.34	−0.57^m	—	−0.31^m	−0.01^m	−0.02^m	−0.08^m	0.07^m	0.12	−0.23	0.85	0.62
CH3 HA TS 4	14.83	—	—	16.48	−0.21	−0.58	−0.04	0.06	0.19	15.90	−3.32	12.58
CH3 HA TS 5	15.50	—	—	17.24	−0.19	−0.58	−0.03	0.06	0.19	16.69	−2.53	14.16
CH3 HS FS TS 1	0.88	6.56	7.24^m	7.23	0.10	−0.20	−0.15	0.17	0.19	7.34	−2.67	4.67
CH3 HS FS TS 2	18.53	21.31	21.99	22.09	−0.03	−0.33	0.01	0.04	0.19	21.97	−0.90	21.07
CH3 HS W TS	43.18	—	—	41.82	−0.20	−0.36	0.22	0.04	0.19	41.71	−1.24	40.47
AS W TS	43.83	37.97	38.03	38.15	−0.76	−0.57	0.48	−0.07	0.19	37.42	0.04	37.46
AS FS TS 1	27.23	26.55	26.57	26.60	−0.11	−0.15	−0.05	0.13	0.19	26.61	4.11	30.72
AS FS TS 2	70.29	58.25	58.01	58.49	−1.55	−0.70	0.55	−0.08	0.19	56.90	−0.63	56.27
MS TS	44.66	37.91	37.69	37.76	−0.66	−0.55	0.44	−0.07	0.19	37.11	0.21	37.32
NH2 HA TS 1	−2.17	−0.76^m	—	−0.37^m	−0.31^m	−0.27^m	0.03^m	0.01^m	0.19	−0.72	−0.63	−1.35
NH2 HA TS 2	−2.09	−0.85^m	—	−0.43^m	−0.33^m	−0.27^m	0.04^m	0.01^m	0.19	−0.79	−0.52	−1.31
NH2 HA TS 3	−2.09	−0.85^m	—	−0.42^m	−0.33^m	−0.27^m	0.04^m	0.01^m	0.19	−0.78	−0.52	−1.30
NH2 HS TS 1	46.45	45.68	46.01	46.10	−0.15	−0.52	0.28	−0.02	0.19	45.88	−1.22	44.66
NH2 HS TS 2	51.06	51.16	51.51	51.60	−0.11	−0.54	0.31	−0.04	0.19	51.41	−1.58	49.83
PREMIN	−8.98^m	−8.71^m	−8.61^m	−8.47^m	−0.12^m	−0.10^m	−0.04^m	0.01^m	0.01	−8.71	—	—
CH3 HA MIN 1	−32.20	−30.28	−30.22	−30.25	−0.04	−0.17	−0.25	0.15	0.19	−30.37	1.23	−29.14
CH3 HA MIN 2	−30.94	−29.10	−29.00^m	−29.03	−0.04^m	−0.17^m	−0.26	0.15	0.19	−29.16	0.74	−28.42
CH3 HS FS MIN 1	−4.77	0.94	1.56^m	1.56	0.10	−0.22	−0.03	0.13	0.19	1.73	−1.39	0.34
CH3 HS FS MIN 2	−4.72	1.00	1.62^m	1.62	0.10	−0.22	−0.03	0.13	0.19	1.79	−1.43	0.36
CH3 HS W MIN 1	−4.68	1.07	1.69^m	1.69	0.10	−0.22	−0.03	0.13	0.19	1.86	−1.53	0.33
CH3 HS W MIN 2	−4.46	1.35	1.98^m	1.97	0.10	−0.21	−0.04	0.13	0.19	2.14	−1.61	0.53
AS W MIN 1	−8.59	−8.10^m	−7.95^m	−7.90	−0.06	−0.07	0.17	0.03	0.19	−7.64	−0.83	−8.47
AS W MIN 2	−8.57	−8.09	−7.94	−7.90	−0.06	−0.07	0.17	0.03	0.19	−7.64	−0.83	−8.47
AS FS MIN 1	−12.69	−12.24	−12.06^m	−11.98	−0.06	−0.08	0.14	0.05	0.19	−11.74	0.23	−11.51
AS FS MIN 2	−11.12	−10.60	−10.48	−10.42	−0.06	−0.08	0.14	0.04	0.19	−10.19	0.04	−10.15
MS MIN 1	19.54	19.87	19.92	19.96	−0.05	−0.22	0.13	0.05	0.19	20.06	−0.57	19.49
MS MIN 2	23.89	24.05	24.12	24.16	−0.05	−0.21	0.15	0.04	0.19	24.28	−0.70	23.58
NH2 HA MIN	−25.25	−24.63	−24.46	−24.43	−0.10	−0.09	−0.02	0.06	0.19	−24.39	0.19	−24.20
NH2 HS MIN 1	33.25	37.78	38.39	38.45	0.08	−0.32	0.09	0.06	0.19	38.55	−2.18	36.37
NH2 HS MIN 2	36.91	41.24	41.89	41.94	0.09	−0.31	0.10	0.06	0.19	42.07	−2.32	39.75
CH3NHOH(1) + H	37.20	41.66	42.32	42.37	0.09	−0.31	0.10	0.06	0.19	42.50	−2.55	39.95
CH3NHOH(2) + H	33.51	38.21	38.85	38.90	0.09	−0.31	0.08	0.06	0.19	39.01	−2.44	36.57
NH2OH(1) + CH3	26.12	26.24	26.15	26.09	−0.04	−0.19	0.15	0.04	0.19	26.24	−1.71	24.53
NH2OH(2) + CH3	21.69	22.04	21.94	21.88	−0.04	−0.20	0.14	0.05	0.19	22.02	−1.55	20.47
CH2OHNH2 + H	−4.26	1.64	2.29	2.28	0.10	−0.21	−0.04	0.13	0.19	2.45	−1.86	0.59
CH3OH + NH2	−7.07	−6.72	−6.70	−6.71	−0.05	−0.06	0.17	0.03	0.19	−6.43	−1.33	−7.76
CH3NH + H2O	−18.49	−18.03	−17.97	−18.03	−0.09	−0.07	0.03	0.04	0.19	−17.93	−1.39	−19.32
CH2NH2 + H2O	−27.04	−25.27	−25.36	−25.50	−0.03	−0.14	−0.24	0.14	0.19	−25.58	−0.65	−26.23

---

To provide the best possible energies it is fundamental to count in the post-CCSD(T) correlation corrections, especially in the case of the transition states, because the difference between these geometries and the equilibrium structures is the most significant, thus electron correlation may play a major role at the transition states. In most cases the δ[CCSDT] and δ[CCSDT(Q)] values are negative and the absolute sums of these energy contributions are usually small. The core correlation contributions (Δ_core) do not go above 0.30 kcal mol⁻¹ in absolute value except for the cases of the AS W TS, AS FS TS 2, MS TS and NH₂ HS TS transition states, where the core correlation energies are found to be 0.48, 0.55, 0.44 and 0.31 kcal mol⁻¹, respectively. The scalar relativistic effects (Δ_rel) are usually positive, but in a few cases there are some negative values, and they are typically small at around 0.00–0.15 kcal mol⁻¹. The largest Δ_rel value of 0.17 kcal mol⁻¹ is obtained for the CH₃ HS FS TS 1 transition state. The non-relativistic ground-state of the OH radical splits into a higher and a lower energy level because of the spin–orbit interaction, thereby the energy of the reactants decreases while increasing all of the relative energies by 0.19 kcal mol⁻¹ SO correction (Δ_SO), except for the case of the CH₃ HA TS 2 and PREMIN stationary points, where Δ_SO is only 0.12 and 0.01 kcal mol⁻¹, respectively. This phenomenon can be explained by the reactant-like structure of these stationary points, where the OH is located relatively far from the CH₃NH₂ molecule, thus the effect of the spin–orbit interaction is also significant in these geometries lowering the magnitude of the increase in the relative energy. For calculating the zero-point energies (Δ_ZPE) we use the model of the harmonic oscillator and the values are determined with the help of the geometries optimized at the highest possible level of theory. The ZPE corrections are typically negative values in the range of 0.0 and −2.5 kcal mol⁻¹. The largest ZPE correction is found for the AS FS TS 1 transition state with a value of 4.11 kcal mol⁻¹.

In order to compare the adiabatic reaction enthalpies calculated by us with experimental data, we determine the 0 K-referenced reaction enthalpies for various product channels (except for the H-substitution reaction pathways, as experimental data are not available for CH₂OHNH₂ and CH₃NHOH) from the heats of formation found in the Active Thermochemical Tables (ATcT)³⁶ using Hess's law. We refer to the heats of formation found in the ATcT database as “experimental”, although it is worth mentioning that the values therein are derived from weighted averages of many experimental and theoretical results. In Table 2, we summarize the reaction enthalpies determined by us and those calculated based on ATcT. It can be concluded that reaction enthalpies calculated based on the ATcT heats of formation exhibit excellent agreement with our benchmark adiabatic energies, and in fact, in three cases, these reaction enthalpies coincide within the margin of error.

Table 2 Comparison of the reaction enthalphies obtained from the ATcT database with our calculated benchmark adiabatic energies at 0 K (in kcal mol⁻¹) for the OH + CH₃NH₂ reactions

Reaction	Theory^a	ATcT^b
a Benchmark adiabatic 0 K reaction enthalphies obtained from this work. b Reference data obtained from the most recent version (1.130) of the Active Thermochemical Tables (ATcT).^36 Uncertainties are calculated based on the uncertainties associated with each enthalpy of formation at 0 K as provided in ATcT employing the Gaussian error propagation law.
OH + CH3NH2 → CH2NH2 + H2O	−26.23	−26.35 ± 0.14
OH + CH3NH2 → CH3NH + H2O	−19.32	−19.53 ± 0.11
OH + CH3NH2 → CH3OH + NH2	−7.76	−7.63 ± 0.07
OH + CH3NH2 → NH2OH (trans) + CH3	20.47	20.53 ± 0.11
OH + CH3NH2 → NH2OH (cis) + CH3	24.53	24.76 ± 0.34

---

The computed rate coefficients, obtained by utilizing our best benchmark ab initio results, in the temperature range of 295–3000 K and their comparison with previous theoretical and experimental data are given in Table 3. By directly comparing the rate coefficients computed solely based on TST by us and by Tian and co-workers,¹⁶ a difference of more than an order of magnitude can be observed. At this point, it is worth mentioning that the rate coefficients provided by Tian and co-workers may not be reliable as the data presented in their article are not consistent with those shown in the figures and found in the tables. When the tunneling effect is considered in our calculation of the rate coefficients, a relatively close match can be observed between our theoretical predictions and the experimental values. Additionally, it can be seen that the decreasing trend of the data measured by Atkinson and co-workers⁹ in the temperature range of 299–426.1 K is reflected in our computed rate coefficients, although our results indicate a more pronounced decrease.

Table 3 Computed and measured rate coefficients (in cm³ × molecule⁻¹ × s⁻¹) at different temperatures for the OH + CH₃NH₂ reaction

T/K	This work		Tian et al.^a			Atkinson et al.^b	Carl and Crowley^c	Butkovskaya and Setzer^d	Onel et al.^e
	TST	TST + tunneling^f	TST	ICVT	ICVT/SCT
a Computed results taken from ref. 16. b Experimental data taken from ref. 9. c Experimental data taken from ref. 10. d Experimental data taken from ref. 37. e Experimental data taken from ref. 17. f TST with Wigner tunneling corrections obtained as κ(T)k(T) using eqn (8) and (9).
295	6.71 × 10^−12	1.03 × 10^−11					(1.73 ± 0.11) × 10^−11
298	6.61 × 10^−12	1.01 × 10^−11						(2.00 ± 0.40) × 10^−11	(1.97 ± 0.11) × 10^−11
299	6.58 × 10^−12	1.00 × 10^−11	2.15 × 10^−10	1.36 × 10^−11	2.98 × 10^−11	(2.20 ± 0.22) × 10^−11
300	6.55 × 10^−12	9.95 × 10^−12	2.14 × 10^−10	1.37 × 10^−11	2.96 × 10^−11
353.9	5.56 × 10^−12	7.45 × 10^−12	1.87 × 10^−10	1.39 × 10^−11	2.56 × 10^−11	(1.94 ± 0.20) × 10^−11
400	5.26 × 10^−12	6.56 × 10^−12	1.80 × 10^−10	1.42 × 10^−11	2.40 × 10^−11
426.1	5.22 × 10^−12	6.31 × 10^−12	1.75 × 10^−10	1.42 × 10^−11	2.28 × 10^−11	(1.75 ± 0.18) × 10^−11
500	5.39 × 10^−12	6.13 × 10^−12	1.78 × 10^−10	1.48 × 10^−11	2.16 × 10^−11
550	5.68 × 10^−12	6.29 × 10^−12	1.84 × 10^−10	1.54 × 10^−11	2.14 × 10^−11
600	6.07 × 10^−12	6.59 × 10^−12	1.94 × 10^−10	1.61 × 10^−11	2.16 × 10^−11
650	6.55 × 10^−12	7.00 × 10^−12	2.06 × 10^−10	1.70 × 10^−11	2.21 × 10^−11
700	7.11 × 10^−12	7.51 × 10^−12	2.21 × 10^−10	1.80 × 10^−11	2.28 × 10^−11
800	8.43 × 10^−12	8.77 × 10^−12	2.56 × 10^−10	2.05 × 10^−11	2.49 × 10^−11
900	1.00 × 10^−11	1.03 × 10^−11	3.00 × 10^−10	2.37 × 10^−11	2.78 × 10^−11
1000	1.19 × 10^−11	1.22 × 10^−11	3.55 × 10^−10	2.76 × 10^−11	3.17 × 10^−11
1050	1.30 × 10^−11	1.33 × 10^−11	3.81 × 10^−10	2.94 × 10^−11	3.35 × 10^−11
1250	1.81 × 10^−11	1.83 × 10^−11	5.19 × 10^−10	3.93 × 10^−11	4.33 × 10^−11
1500	2.64 × 10^−11	2.66 × 10^−11	7.46 × 10^−10	4.41 × 10^−11	4.67 × 10^−11
1750	3.73 × 10^−11	3.75 × 10^−11	1.04 × 10^−9	5.94 × 10^−11	6.17 × 10^−11
2000	5.11 × 10^−11	5.14 × 10^−11	1.40 × 10^−9	7.81 × 10^−11	8.05 × 10^−11
2200	6.45 × 10^−11	6.47 × 10^−11	1.74 × 10^−9	9.56 × 10^−11	9.81 × 10^−11
2400	8.01 × 10^−11	8.04 × 10^−11	2.15 × 10^−9	1.12 × 10^−10	1.14 × 10^−10
2500	8.88 × 10^−11	8.91 × 10^−11	2.36 × 10^−9	1.20 × 10^−10	1.22 × 10^−10
2800	1.19 × 10^−10	1.19 × 10^−10	3.10 × 10^−9	1.45 × 10^−10	1.47 × 10^−10
3000	1.42 × 10^−10	1.42 × 10^−10	3.67 × 10^−9	1.65 × 10^−10	1.67 × 10^−10

---

Table 4 presents a comparison of the branching ratios calculated by us and those determined by Tian and co-workers¹⁶ specifically showing how much the reactions occurring at the methyl and amino groups contribute to the overall rate coefficient of the H-abstraction. When comparing the results obtained solely from TST with those that incorporate the tunneling effect, it becomes clear that the differences are generally small. Additionally, as the temperature increases, the gap between the two values diminishes. This trend is expected since the tunneling effect plays a significant role at lower temperatures, while at higher temperatures, the increased energy of molecules enhances the chance of overcoming the barrier of the reaction. Comparing our branching ratios with those presented in the work of Tian and co-workers leads to opposing conclusions. While our results indicate that H-abstraction from the amino group plays a more significant role in the H-abstraction process, Tian and co-workers emphasize the greater contribution of H-abstraction from the methyl group. This can be attributed to the fact that, in our case, the H-abstraction at the amino group has a lower energy barrier than that occurring at the methyl group, while the situation is reversed for Tian and co-workers.

Table 4 Branching ratios at different temperatures for the OH + CH₃NH₂ → H₂O + CH₂NH₂ (k_C) and H₂O + CH₃NH (k_N) reactions, where k denotes the total rate coefficients (k_C + k_N)

T/K	k C/k			k N/k
	This work		Tian et al.^b	This work		Tian et al.^b
	TST	TST + tunneling^a		TST	TST + tunneling^a
a TST with Wigner tunneling corrections. b Computed results taken from ref. 16.
299	0.190	0.130	0.738	0.810	0.870	0.262
353.9	0.268	0.206	0.739	0.732	0.794	0.261
426.1	0.355	0.300	0.733	0.645	0.700	0.267
500	0.426	0.380	0.722	0.574	0.620	0.278
550	0.465	0.425	0.714	0.535	0.575	0.286
600	0.497	0.463	0.706	0.503	0.437	0.294
650	0.524	0.495	0.697	0.476	0.505	0.303
700	0.547	0.521	0.689	0.453	0.479	0.311
800	0.583	0.564	0.673	0.417	0.436	0.327
900	0.611	0.595	0.659	0.389	0.405	0.341
1050	0.640	0.629	0.640	0.360	0.371	0.360
1250	0.665	0.658	0.621	0.335	0.342	0.379
1500	0.686	0.681	0.769	0.314	0.319	0.231
1750	0.699	0.695	0.758	0.301	0.305	0.242
2200	0.713	0.711	0.749	0.287	0.289	0.251
2400	0.717	0.715	0.744	0.283	0.285	0.256
2500	0.719	0.717	0.766	0.281	0.283	0.224
2800	0.724	0.722	0.821	0.276	0.278	0.179
3000	0.726	0.725	0.843	0.274	0.275	0.157

---

IV. Summary and conclusions

We have described all the important reaction channels that are possible in the OH + CH₃NH₂ system with high-level ab initio methods considering five different energy contributions that provide higher accuracy. We have moved beyond the so far investigated H-abstraction pathway and taken into account the H-, amino- and methyl-substitutions, which can proceed via two types of mechanisms: Walden inversion and front-side attack. The entrance channel is examined using MP2 and MRCI methods with aug-cc-pVDZ basis set by one-dimensional potential energy curves in this study at eleven different orientations. In most cases the depths of the wells are approximately 0–2 kcal mol⁻¹. When the OH radical approaches CH₃NH₂ with its O-side at the N atom perpendicularly to the C–N bond we cannot experience any minimum in the potential curve. Moreover, the orientation gives a relatively deeper well (around 8 kcal mol⁻¹) when the OH molecule goes with the same alignment as before, just with its H-side pointing toward CH₃NH₂. This structure, featuring a deeper 8 kcal mol⁻¹ minimum, is similar to the pre-complex identified by both Tian and co-workers,¹⁶ as well as Onel and partners.¹⁷ In our research, we successfully optimized this geometry as well, but this was only achievable with the ManyHF method as the standard HF method failed to converge. It is also worth mentioning that we could not definitively confirm the nature of this stationary point, specifically whether it is a minimum on the potential energy surface, as the ManyHF method cannot be employed for frequency computations. Irrespective of the side of the CH₃NH₂ molecule from which the separation of the H atom happens, the H-abstraction reaction path is kinetically favored. The transition state of the methyl-H-abstraction has a −0.09(0.20) kcal mol⁻¹ classical (adiabatic) energy, which is a little higher than the barrier height of the amino-H-abstraction, which has −0.72(−1.35) kcal mol⁻¹ classical (adiabatic) energy relative to the reactants. In this current study, considering the former literature, we report a transition state with deeper relative energy for the amino-H-abstraction making this reaction pathway barrierless.¹⁶ In the exit channel referring to the H-abstraction the energy order of the minima changes with respect to the transition states. We find two different post-reaction complexes for the methyl-H-abstraction channel, where the lower-energy structure matches the one found by Onel and partners.¹⁷ We were unable to locate the structure described by Tian and co-workers.¹⁶ This minimum has such a structure where the abstracted H atom from the methyl group is near the amino group. It is worth noting that Onel and co-workers also did not identify this structure, despite the fact that their work was similarly informed by the article from Tian and co-workers. The reason they could identify that minimum in the exit channel may be that they used a smaller basis set for their computations. Both the H-abstraction channels from the methyl and the amino group are exothermic with classical (adiabatic) relative energies of −25.58(−26.23) and −17.93(−19.32) kcal mol⁻¹, respectively. These results are in good agreement with the previous findings.^16,17 For the H-abstraction reaction pathway, we estimated the rate coefficients using transition-state theory and applied the Wigner correction to account for the tunneling effect. Our computed rate coefficients considering the tunneling effect are consistent with the experimental data.

Within the framework of this investigation, the H-, amino- and methyl substitution reactions are also taken into account. The substitution, just like the abstraction, can happen from the sides of the CH₃NH₂ molecule and it can proceed via two different mechanisms: Walden inversion and front-side attack. In this study, we have moved beyond the H-abstraction and revealed the complex mechanisms of the substitution channels considering their transition states, post-reaction complexes and products. Furthermore, for the H-substitution at the methyl group and the amino-substitution, we could separate the Walden-inversion and front-side attack processes. The refinement of the previous results and the exploration of the substitution pathways may give a better understanding of the title reaction and can guide future potential energy surface developments opening the possibility of investigating the dynamics of the reaction even at hyper-thermal collision energies, where the high-energy substitution channels may also open.

Data availability

The main data supporting this article have been included in Tables 1–4 and additional data are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors thank the National Research, Development and Innovation Office−NKFIH, K-146759; Project no. TKP2021-NVA-19, provided by the Ministry of Culture and Innovation of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme; and the Momentum (Lendület) Program of the Hungarian Academy of Sciences for the financial support.

References

1. D. González, B. Ballesteros, A. Canosa, J. Albaladejo and E. Jiménez, Front. Astron. Space Sci., 2022, 8, 2021.
2. A. Ali, A. Canosa and D. Leisawitz, Front. Astron. Space Sci., 2022, 9, 2022.
3. S. A. Sanford, M. Nuevo, P. P. Bera and T. J. Lee, Chem. Rev., 2020, 120, 4616.
4. D. E. Woon, Astrophys. J., 2002, 571, L177.
5. M. Ohishi, T. Suzuki, T. Hirota, M. Saito and N. Kaifu, Publ. Astron. Soc. Jpn., 2019, 71, 86.
6. T. Suzuki, L. Majumdar, P. F. Goldsmith, K. Tokuda, H. Minamoto, M. Ohishi, M. Saito, T. Hirota, H. Nomura and Y. Oya, Astrophys. J., 2023, 954, 189.
7. L. Marrodán, T. Pérez and M. U. Alzueta, Combust. Flame, 2024, 259, 113130.
8. M. U. Alzueta, T. Pérez and L. Marrodán, Proc. Combust. Inst., 2024, 40, 105456.
9. R. Atkinson, R. A. Perry and J. N. Pitts Jr., J. Chem. Phys., 1977, 66, 1578.
10. S. A. Carl and J. N. Crowley, J. Phys. Chem. A, 1998, 102, 8131.
11. M. Monge-Palacios, C. Rangel and J. Espinosa-Garcia, J. Chem. Phys., 2013, 138, 084305.
12. B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2020, 22, 14560.
13. D. Papp, B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 396.
14. T. Szűcs and G. Czakó, Phys. Chem. Chem. Phys., 2022, 24, 20249.
15. T. Szűcs and G. Czakó, Phys. Chem. Chem. Phys., 2021, 23, 10347.
16. W. Tian, W. Wang, Y. Zhang and W. Wang, Int. J. Quantum Chem., 2009, 109, 1566.
17. L. Onel, L. Thonger, M. A. Blitz, P. W. Seakins, A. J. C. Bunkan, M. Solimannejad and C. J. Nielsen, J. Phys. Chem. A, 2013, 117, 10736.
18. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
19. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007.
20. T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106.
21. T. Győri and G. Czakó, J. Chem. Phys., 2022, 156, 071101.
22. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
23. J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041.
24. M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105.
25. J. G. Hill, S. Mazumder and K. A. Peterson, J. Chem. Phys., 2010, 132, 054108.
26. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89.
27. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48.
28. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
29. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61.
30. K. R. Shamasundar, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 135, 054101.
31. K. A. Peterson and T. H. Dunning, Jr., J. Chem. Phys., 2002, 117, 10548.
32. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see https://www.molpro.net.
33. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, B. P. Szabó, L. Gyevi-Nagy and B. Hégely, et al., MRCC, a quantum chemical program suite, see https://www.mrcc.hu.
34. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy and B. Hégely, et al. , J. Chem. Phys., 2020, 152, 074107.
35. P. Tóth, T. Szűcs and G. Czakó, J. Phys. Chem. A, 2022, 126, 2802.
36. B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.130 of the Thermochemical Network, Argonne National Laboratory, 2019, available at https://ATcT.anl.gov.
37. N. I. Butkovskaya and D. W. Setser, J. Phys. Chem. A, 2016, 120, 6698.

---