Local force constants and charges of the nitrosyl ligand in photoinduced NO linkage isomers in a prototypical ruthenium nitrosyl complex

Abstract

Photoinduced linkage isomers (PLI) of the NO ligand in transition-metal nitrosyl compounds can be identified by vibrational spectroscopy due to the large shifts of the [small nu, Greek, tilde](NO) stretching vibration. We present a detailed experimental and theoretical study of the prototypical compound K₂[RuCl₅NO], where [small nu, Greek, tilde](NO) shifts by ≈150 cm⁻¹ when going from the N-bound (κN) ground state (GS) to the oxygen-bound (κO) metastable linkage isomer MS1, and by ≈360 cm⁻¹ when going to the side-on (κ²N,O) metastable linkage isomer MS2. We show that the experimentally observed N–O stretching modes of the GS, MS1, and MS2 exhibit strong coupling with the Ru–N and Ru–O stretching modes, which can be decoupled using the local mode vibrational theory formalism. From the resulting decoupled pure two-atomic harmonic oscillators the local force constants are determined, which all follow the same quadratic behavior on the wavenumber. A Bader charge analysis shows that the total charge on the NO ligand is not correlated to the observed frequency shift of [small nu, Greek, tilde](NO).

---

1. Introduction

Photo-induced linkage isomers (PLI) have been reported both in the crystalline phase and in solution for a large number of metal–nitrosyl complexes with varying chemical composition.^1–6 These materials are of importance in medicine and biology because, e.g., NO acts as a signaling molecule in the nervous system^7,8 but might also find applications in optical technologies due to the photochromic and photorefractive changes induced by the PLI generation.^9,10 Upon irradiation with appropriate wavelengths, the NO ligand changes its bonding configuration with the transition metal, and can thus adopt different structural geometries. For mono- and dinitrosyl complexes {M(NO)_m}ⁿ (in the Enemark–Feltham notation with m = 1, 2 and n = number of metal d electrons if NO⁺ is considered the ligand) with different transition metals M, various geometries of the MNO group have been reported, exhibiting linear or bent configurations of the NO ligand depending on the number of metal d electrons, n = 6–10 (see Scheme 1 and corresponding discussion in ref. 11). For the {MNO}⁶ octahedrally sixfold coordinated complexes three such structural configurations have been reported, the linear nitrogen bound (κN) ground state (GS), and two metastable states (MS), a side-on bound M–NO configuration (κ²N,O; MS2) where the M–N–O angle is of the order of 80°–90° and an inverted linear oxygen-bound isonitrosyl configuration M–O–N (κO, MS1). The reorganization of the NO ligand from GS to MS1 can thus be pictured as the rotation along a polar angle by 180° with MS2 as an intermediate step. The thermal stability of the photoinduced NO configurations MS1 and MS2 depends notably on the nature of the ligand in position trans to NO.^12,13 The complex trans-[Ru(py)₄(NO)F]²⁺ shows one of the most long-lived MS1 isomers,¹⁴ with a decay temperature of T_d = 290 K, while the highest T_d of 313 K was found in trans-[Ru(NH₃)₄(NO)F](ClO₄)Cl¹⁵ (T_d is defined as the temperature where the decay constant is k = 10⁻³ s⁻¹). In paramagnetic complexes of the type [FeCl₃(NO)]⁻, the PLI exhibit a much lower thermal stability (T_d < 50 K).¹⁶ The concentration of PLI that can be induced varies from 1–100%, depending on the chemical composition of the complex or crystal. The origin of this large variation lies in the absorption properties of the different PLI, most of the time the absorption bands of GS and MS1,2 overlap and thus a photostationary state is built up equilibrating forward and backward processes at the given irradiation wavelength, depending on the ratio of the corresponding cross sections.^17,18 Inspecting the dynamics of the PLI generation, it was reported that MS2 is reached within approximately 300 fs,¹⁹ followed by vibrational relaxation into its minimum within a few picoseconds.²⁰ TD-DFT calculations indicate that two channels contribute to the PLI formation, a combination of fast intersystem crossings to a triplet state within 80–160 fs followed by internal conversions through the conical intersections at the transition states resulting in the relaxation into the singlet MS potentials or, alternatively, a purely internal conversion via the singlet states and the corresponding transition states.²¹

In most of the nitrosyl complexes, the ν(NO) stretching vibration shifts to lower wavenumbers when going from GS to MS1 and MS2.² The only reported exception to this observation for sixfold coordination are the {PtNO}⁸ complexes [Pt(NH₃)₄Cl(NO)]Cl₂, [Pt(NH₃)₄(NO₃)NO](NO₃)₂ and [Pt(NH₃)₄(SO₄)NO]HSO₄·CH₃CN, for which a shift to higher wavenumbers was observed upon generation of PLI.^22,23 Note, however, that for these PtNO complexes, the nitrogen-bound GS is already in a bent configuration with Pt–N–O angles of the order of 110–120°, and only one PLI has been detected, an oxygen bound bent configuration with slightly larger (calculated) Pt–O–N angles of the order of 120–130°. In most cases the generation of the PLI is triggered by a metal-to-ligand charge transfer (MLCT) excitation from the occupied metal-d orbitals to the empty antibonding π*(NO) orbitals.¹⁸ Therefore, sometimes, the downshift of the ν(NO) stretching vibration has been interpreted as due to an increase of the charge on the NO ligand,²⁴ resulting in a change of the formally NO⁺ towards NO⁰ in the MS, an interpretation that would be in line with the known ν(NO) stretching vibrations of free NO, 2387 cm⁻¹ for NO⁺ and 1876 cm⁻¹ for NO⁰.²⁵ This simplified picture is sometimes applied as a shortcut to the deduction of the NO angle and its formal charge from the observed frequency of the stretching vibration. This should be however handled with precaution as already Enemark and Feltham pointed out in their seminal 1974 review that “it is very tenuous to infer M–N–O angles from ν(NO)”.²⁶ Fundamental insight into these questions and, especially, also with respect to the oxidation state of the “non-innocent” ligand NO, has been given in the recent work by Klüfers and co-workers.^27,28 Through detailed structure analysis combined with DFT calculations and the determination of the charges on the NO, it was shown that the M–N–O angle is not a reliable indicator to derive bond strengths or ligand charges.

In the framework of this fundamental discussion we present a detailed experimental and theoretical study of the PLI in K₂[RuCl₅NO], which already earlier has served as a prototypical {MNO}⁶ complex for DFT calculations.^29,30 Starting from an accurate single-crystal structure determination of GS we use infrared spectroscopy, including ¹⁵N isotope substitution, to unambiguously identify the ν(RuN) and ν(NO) stretching and δ(RuNO) deformation vibrations for GS, MS1 and MS2. A solid-state DFT calculation is performed and its quality is assessed by comparison with the experimental structural, infrared as well as NMR data of the GS. Since MS1 and MS2 populations are too low to allow for experimental structure determination, their structures are calculated and the corresponding calculated vibrational spectra are compared to the experimental results. A Bader³¹ analysis is performed in order to determine the charges on the relevant atoms and atom groups for GS, MS1, and MS2. Finally, we use the local mode vibrational theory as developed by Konkoli, Cremer and Kraka³² in order to calculate the decoupled ν(RuN) and ν(NO) stretching vibrations and determine the corresponding local force constants. The implications of these results on the interpretation of the downshift of the ν(NO) stretching vibration upon PLI generation are discussed.

2. Material and methods

2.1. Synthesis

K₂[RuCl₅NO] was synthesized according to a previously reported procedure.³³ The ¹⁵NO labelled complex was synthesized by using Na¹⁵NO₂. Single crystals suitable for XRD were obtained by slow evaporation of a water solution of the complex.

2.2. Single crystal X-ray diffraction

Single crystal X-ray diffraction (XRD) data for K₂[RuCl₅NO] were collected on a Bruker Apex Duo diffractometer with CCDs using graphite-monochromated MoKα radiation (λ = 0.71073 Å) via 0.5° ω- and φ-scan techniques. Reduction of the experimental data was performed using the APEX2 suite. The structure was solved using SHELXT and refined by the full-matrix least-squares technique SHELXL³⁴ assisted by Olex2 GUI.³⁵ The atomic displacement parameters of the atoms were refined using an anisotropic approximation. The crystallographic characteristics, experimental data, and structure refinements are listed in Table S1 (ESI†). The structure of K₂[RuCl₅NO] has been deposited with the CCDC with deposition number 2336093.†

2.3. NMR

¹⁵N NMR analysis was performed on a high-field Bruker NMR AVANCE III spectrometer operating at 14 T (¹H NMR frequency, 600 MHz) with a Bruker 2.5 mm MAS HX probe. The signal was acquired at 10 kHz MAS frequency using a single pulse excitation optimized at 6.5 μs. Interscan recovery time was set to 50 s and 512 scans were accumulated. The ¹⁵N chemical shifts have been referenced with respect to CH₃NO₂.

2.4. UV-Vis spectroscopy

UV-Vis measurements were performed using a Cary 4000 spectrometer with a resolution of 2 nm at room temperature. Polycrystalline samples were either prepared as KBr pellets like for IR spectroscopy for measuring solid-state spectra in transmission mode, or solved in water in different concentrations for the solution spectra. In accordance with previously published solution spectra^36,37 (in acidic solutions) a broad absorption band is detected in the visible range, which can be deconvoluted into two bands at 480 nm (20 800 cm⁻¹) and 525 nm (19 050 cm⁻¹), which we assign to the transitions d_xy → π*(NO) and d_xz,yz → π*(NO). The occupied d-orbitals are thus separated by less than 2000 cm⁻¹. Consequently, we used irradiation wavelengths in the spectral range 450–590 nm for the generation of the PLI in the IR experiments.

2.5. Infrared spectroscopy

IR measurements were performed using a Nicolet 5700 FT-IR spectrometer with a resolution of 2 cm⁻¹ and 1 cm⁻¹ at temperature T = 10 K. Samples were ground, mixed with KBr and pressed into pellets. The KBr pellets were bonded onto the cold finger of the Oxford Optistat cryostat using silver paste, and irradiated through KBr windows with LED light and diode-lasers in the wavelength range of 450–1310 nm. Specifically, in a first step the generation of the PLI was performed at 10 K using 455 nm (LED), 505 nm (LED), 520 nm (LED), 526.5 nm (LASER), 530 nm (LED), 556 nm (LASER), 586 nm (LASER). In this manner both MS1 and MS2 (in smaller amounts) can be produced with a maximum for MS1 using 520 nm. In an effort to unambiguously identify the Ru–N stretching vibration related to MS2, the sample in the MS1 state was irradiated using wavelengths in the infrared spectrum, in particular using a LASER diode at 1310 nm. Using 660 nm (LED), both MS1 and MS2 can be transferred back to GS.

2.6. Raman spectroscopy

Raman spectra were recorded on a LabRAM Horiba (Japan) single-stage spectrometer with a CCD Symphony detector (Jobin Yvon, France) having 2048 horizontal pixels. The laser power at the sample surface was typically 1 mW for the 633 nm line of a He–Ne laser and 0.1 mW for the 514 nm line of an Ar+ laser. A spectral resolution was 3.0 cm⁻¹. The spectra were measured in 180° backscattering collection geometry with a Raman microscope. For low-temperature measurements (5 K), the crystals were wrapped in indium foil for better thermal contact and fixed on the cold finger of the He cryostat.

2.7. DFT

The crystal structure, NMR parameters, charge density, as well as infrared spectra were calculated using density functional theory with the first principle quantum mechanical code CASTEP19.11^38,39 and using the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE),⁴⁰ with ZORA relativistic treatment.⁴¹ The structures were described as extended solids using periodic boundary conditions. The wavefunctions were expanded using a planewave (PW) basis set with a kinetic energy cutoff and Brillouin zone k-point spacing chosen to produce converged results. In a first step, geometry optimization of all atoms was performed, as already successfully applied in a previous paper.⁴² For geometry optimization, IR spectra, and charge density calculations, the Norm Conserving pseudopotentials CASTEP 19.0 (NCP19) were used to describe the interaction of the valence electrons with the nuclei and core electrons. The wavefunctions were expanded using a PW basis set with a kinetic energy cutoff of 900 eV and integration over the Brillouin zone with k-point spacing <0.04 Å⁻¹ on the Monkhorst–Pack (MP) mesh.⁴³ The sizes of the standard and fine grids were set to 2 and 3 respectively. The self-consistent field calculations were considered to be converged when the total energy of the system was stable within 10⁻¹⁰ eV. Geometry optimization was performed with semi-empirical dispersion correction using the Tkatchenko–Scheffler scheme.⁴⁴ The geometry optimization was performed with strict convergence tolerance criteria (10⁻⁷ eV per atom total energy convergence; 5 × 10⁻³ eV per Å max ionic force; and 5 × 10⁻⁴ Å max ionic displacement). Coordinates of optimized structures are listed in Tables S2–S5 (ESI†). The IR spectra were simulated using the PDielec package⁴⁵ applied to the output of CASTEP calculations, for a powder of spherical particles diluted in KBr and applying a Lorentzian width of 0.5 cm⁻¹. In order to obtain the decoupled force constants from the DFT calculated vibrational spectra, the verbosity of the CASTEP output was set to 3, and the Cremer–Kraka transformation, as provided by the PyMOL plugin LmodeA-nano,⁴⁶ was used. For the charge density calculations, spin–orbit couplings were included in the calculations. After applying the den2vasp utility to convert the CASTEP charge density to the VASP CHGCAR format, the Bader analysis program was used to perform Bader charge analysis.⁴⁷ NMR calculations were performed with “on the fly” generated pseudopotentials (OTFG C19). In order to compare the GIPAW-calculated ¹⁵N shielding values directly with the experimentally measured isotropic chemical shift values, the following expression was used δ^calc_iso = σ_ref − σ_iso where σ_ref = −178.9 ppm as in our previously published study.⁴⁸

3. Results

3.1. Ground state (GS)

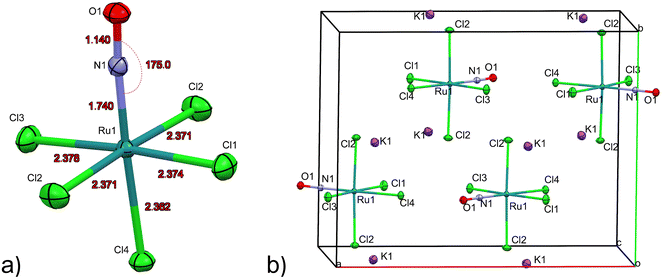
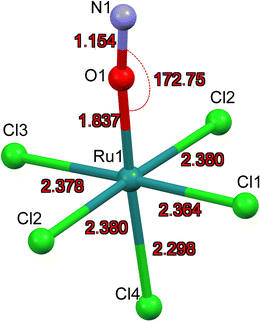
The first structure analysis of K₂[RuCl₅NO] had been performed by Khodashova and Bokii⁴⁹ in 1960 and reexamined by the same authors in 1964.⁵⁰ The structure was refined in the orthorhombic space group Pnma with Z = 4, yielding atomic distances of d(N–O) = 1.25(5) Å, d(Ru–N) = 1.70(4) Å, and d(Ru–Cl) = 2.35(1) Å. In 1972 Veal and Hodgson reinvestigated the compound,⁵¹ based on additional reflections they refined the structure in the non-centrosymmetric space group P2₁2₁2₁ with atomic distances according to the labelling given in Fig. 1a: d(N–O) = 1.112(7) Å, d(Ru–N) = 1.747(6) Å, d(Ru–Cl1) = 2.363(7) Å, d(Ru–Cl2) = 2.371(2)/2.377(2) Å, d(Ru–Cl3) = 2.375(8) Å and d(Ru–Cl4) = 2.359(2) Å. This study resulted thus in an improved determination of the N–O distance and revealed a trans influence, at the origin of the shorter Ru–CI bond trans to the nitrosyl group compared to the average Ru–Cl1 bond cis to the nitrosyl. However, the space group determination was not unambiguous, so that Zarhloul et al.⁵² proceeded to a structural reinvestigation within the whole series of K₂Ru(NO)X₅ complexes, with X = Cl, Br, I, concluding that Pnma should be considered the correct space group, based on a comparative analysis of the resulting refined bond lengths and overall better agreement statistics. Contrary to Veal and Hodgson, these authors interpreted the fact that the trans-to-NO Ru–Cl bond is longer than the average equatorial Ru–Cl bond as in fact being an elongation indicating a weaker σ bonding for Cl⁻ than for NO when compared in a larger series of complexes with differing axial ligands. A temperature dependent neutron powder diffraction study of Rüdlinger et al.⁵³ in 1993 confirmed the Pnma space group and reported on a significant dependence of the bond lengths on the temperature. Since we aim for a detailed analysis of charges on the RuNO group, we need very accurate information on the structure. We therefore redetermined the structure of K₂[RuCl₅NO] at T = 100 K using MoKα radiation, on a single crystal exhibiting grown faces, allowing for a precise absorption correction. The refinement is performed in the Pnma space group, and the resulting atomic distances are given in Table 1 and Fig. 1a. The Ru–Cl4 bond length is about 0.010(1) Å shorter than the equatorial Ru–Cl bond lengths. The polar Ru–N–O angle amounts to θ = 175.0(1)°, whereby the oxygen is bent towards the Cl1 atom.

Fig. 1 (a) [RuCl₅NO]²⁻ anion and bond lengths in the Ru–N–O ground state (GS) structure. (b) Unit cell view along the c-axis depicting layers of K⁺ cations and antiparallel alignment of Ru–NO groups. Atomic displacement ellipsoids are given at the 80% probability level.

Table 1 Atomic distances (Å) and angles (°) from XRD measurements, solid-state DFT calculations (CASTEP) and the differences between these experimental and calculated values for GS

Distances/angles	XRD	DFT	Δ(exp − calc)
N–O	1.140(1)	1.152	−0.012
Ru–N	1.740(1)	1.727	+0.013
Ru–Cl4trans	2.362(1)	2.355	+0.007
Ru–Cl1	2.374(1)	2.384	−0.010
Ru–Cl2	2.371(1)	2.380	−0.009
Ru–Cl3	2.378(1)	2.369	+0.009
K–Cl4trans	3.327(1)/3.455(1)	3.246/3.478	+0.081/−0.023
K–Cl1	3.283(1)/3.527(1)	3.178/3.562	+0.105/−0.035
K–Cl2	3.206(1)/3.240(1)	3.087/3.133	+0.119/+0.107
	3.581(1)/3.666(1)	3.465/3.572	+0.116/+0.094
K–Cl3	3.307(1)/3.448(1)	3.253/3.349	+0.054/+0.099
K–O	4.015(1)/4.279(1)	3.953/4.385	+0.062/−0.106
K–N	3.987(1)/4.042(1)	3.932/4.054	+0.055/−0.012
O–Cl2	2.929(1)	2.890	+0.039
N–Cl1	2.929(1)	2.902	+0.027
∠Ru–N–O	175.0(1)	172.5	+2.5

---

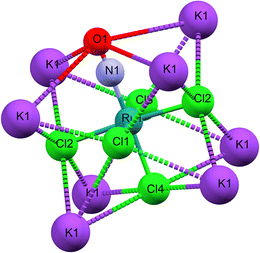
As illustrated in Fig. 1b, the mirror plane m perpendicular to the b-axis contains the Cl4–Ru–N–O axis of the molecule as well as the ligands Cl1 and Cl3, and therefore also the polar angle θ describing the Ru–N–O bending. Notably, we observe a rectangular arrangement of four K⁺ cations around each Cl ligand (Fig. 2). The corresponding distances are listed in Table 1. This peculiar embedding of the [RuCl₅NO]²⁻ anions in the K⁺ cation lattice, with d(K–Cl) distances of 3.2 to 3.7 Å, and the resulting strong coupling is the reason for the temperature dependence of the bond lengths reported in ref. 53. The excellent quality of our structure determination can be assessed from the residual Fourier-difference maps, where the empty e_g and the filled t_2g-orbitals of the Ru central atom are clearly visible as electron deficient and enriched zones (see Fig. S1 in ESI†).

Fig. 2 Cationic K⁺ environment for the [RuCl₅NO]²⁻ anion.

Table 1 lists also the bond lengths obtained with geometry optimization in the solid state using the CASTEP DFT code, along with the resulting differences compared to the experimentally obtained values. The intramolecular distances agree very well, the largest difference of 0.013 Å is found for the Ru–N bond. Contrary to that, the cation–anion distances match far less, one of the K–Cl1 distances is overestimated by 0.035 Å and one of the K–Cl2 distances is underestimated by 0.119 Å in the calculation. The Ru–N–O angle is underestimated by 2.5° in the calculation, but the oxygen atom is bent towards the Cl1 atom in the mirror plane, as found experimentally.

In a first step, in order to evaluate the quality of the solid-state DFT calculations based on the XRD structure, we measured the ¹⁵N chemical shift tensor and compared the results with our calculations. Table 2 presents the results for GS. Consistently with XRD measurements, only one ¹⁵N site is observed with an experimental isotropic chemical shift of δ_iso = −38.6 ppm with respect to CH₃NO₂ (see Fig. S2, ESI†). When referencing the DFT calculations to σ_ref = −178.9 ppm, the value used in our precedent NMR study of [Ru(¹⁵NO)(py)₄¹⁹F](ClO₄)₂,⁴⁸ we find a difference of −5.9 ppm in the range of what was found in our earlier study. These values of the ¹⁵N chemical shift are in the range of known values for linear Ru–N–O geometries^33,54–56 considering the corresponding reference. Regarding chemical shift anisotropy, the difference between experimental and calculated value are small since the values of the asymmetry parameter η match within experimental error margin, and the reduced anisotropy Δ_δ (expressed using the Haeberlen convention) shows a deviation of 6%. Due to the polar Ru–N–O angle of θ = 172.5° the calculation yields a small value of η = 0.03, which however could not be detected experimentally, as it is probably too small.

Table 2 Experimental and DFT calculated chemical shift of ¹⁵N (ppm). Δ_δ is the reduced anisotropy according to Haeberlen convention

	Experiment	DFT
δ iso	−38.6	−32.7
η	0.00	0.03
Δ δ	−393	−368.7

---

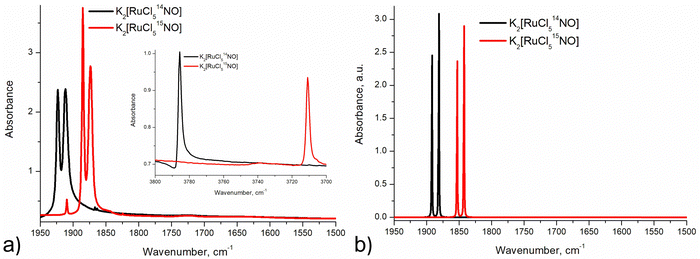
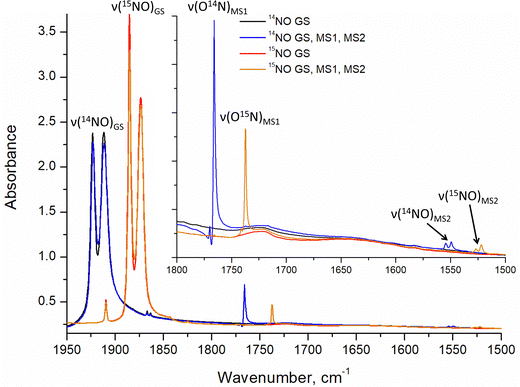
Infrared and Raman spectroscopy allow for the detection of changes in bonding due to excitation of PLI even at low populations. Despite the high sensitivity of Raman spectroscopy, only the GS and MS1 configurations were studied by this method since there is no irradiation wavelength for which MS2 is stable with sufficient population (see ref. 57 and Fig. S3, ESI†). Nevertheless, these two methods enable the investigation of local changes both in the molecular ion and the crystal. Using isotopic substitution of ¹⁴N for ¹⁵N, an unambiguous assignment of the detected vibrational bands is possible. For this reason, IR- and Raman spectroscopy have been applied from the early days for the characterization of NO complexes and their linkage isomers.^57–64 Infrared and Raman spectra were collected for GS by Tosi⁶³ and for MS1 and MS2 by Güida et al.⁶⁴ The latter have also performed DFT calculations for the quasi-free molecule in order to assign the measured vibrational bands. In (idealized) 4m symmetry 18 vibrations are expected for the [RuCl₅NO]²⁻ anion, which distribute according to Γ = 5A₁ + 2B₁ + B₂ + 5E. Fig. 3 shows the measured and calculated infrared spectra of GS in the range 1950–1500 cm⁻¹.

Fig. 3 Infrared spectra: (a) experimental spectra (KBr pellet at 10 K) of ¹⁴NO (black line) and ¹⁵NO (red line) samples in GS in the range 1950–1500 cm⁻¹ with an insert showing overtones of [small nu, Greek, tilde](NO) vibrations; (b) calculated (CASTEP) spectra of ¹⁴NO (black line) and ¹⁵NO (red line) complexes in GS in the range 1950–1500 cm⁻¹.

In GS, [small nu, Greek, tilde](NO) is split by 11 cm⁻¹ into two bands at 1923 cm⁻¹ and 1912 cm⁻¹. Upon cooling from 296 K to 10 K these two bands shift by 8/9 cm⁻¹ to higher wavenumbers. The first overtone at 3786 cm⁻¹ shows no splitting. Since for the transition 0 → 2 there is only a small concentration in the n = 2 level, this splitting might thus depend on the concentration. For a sample with 96% isotopic substitution of ¹⁵N the splitting remains and both [small nu, Greek, tilde](NO) bands shift by 38 cm⁻¹. We note however, that for the remaining 4% of ¹⁴N there is no observable splitting. There is no observable splitting either in the ¹⁵N band (0.38% natural abundance (NA)) of the original ¹⁴N spectrum. The two low-concentration bands without splitting are found at [small nu, Greek, tilde](¹⁴N¹⁶O) = 1910 cm⁻¹ and [small nu, Greek, tilde](¹⁵N¹⁶O) = 1867 cm⁻¹, respectively. Upon decreasing concentrations, the bands thus shift by 2 cm⁻¹ and 7 cm⁻¹ to lower wavenumbers, respectively. Hence, the band at 1923 cm⁻¹ appears due to correlation through concentration, and is thus clearly a solid-state effect. Moreover, the vibrations involving ¹⁸O (NA of 0.205%) could be detected at [small nu, Greek, tilde](¹⁴N¹⁸O) = 1863 cm⁻¹ and [small nu, Greek, tilde](¹⁵N¹⁸O) = 1825 cm⁻¹, their difference being 38 cm⁻¹ as expected, and again, no split can be observed. This type of splitting of the ν(NO) stretching mode into two bands was already measured and discussed by Piro et al.⁶⁵ in Na₂[Fe(CN)₅NO]·2H₂O (SNP) single crystals using reflectance spectroscopy. As a matter of fact, when considering the vibrational modes in the space group Pnnm of SNP and Pnma for the K₂[RuCl₅NO] crystal structure, the ν(NO) correlates into the two infrared active optic modes B_2u and B_3u so that two bands can be expected for a crystalline material.

The anharmonicity of the NO potential with respect to the fundamental 1912 cm⁻¹ is 38 cm⁻¹ for the first and 95 cm⁻¹ for the second overtone. Furthermore, the isotopic substitution with ¹⁵N allows to unambiguously assign the ν(RuN) stretching and δ(RuNO) deformation vibrations (see Fig. S3, ESI†). For [small nu, Greek, tilde](RuN) the isotopic shift is only 8 cm⁻¹ (from 609 to 601 cm⁻¹) while for δ(RuNO) it is 16/14 cm⁻¹ (from 590/585 to 574/571 cm⁻¹), so that the larger shift can be used to assign the deformation vibration also for MS1 and MS2. For GS this technique was already used by Miki^59–61 through application of a linear three-body model for Ru–N–O. Table 3 summarizes the experimental data and DFT-calculated vibrations for the solid state, along with the differences between experiment and calculation. Overall the agreement between experiment and calculation is good, the largest deviation is found for the [small nu, Greek, tilde](NO) with 41/43 cm⁻¹ for ¹⁴N. Note however, that in relative terms the deviation for the [small nu, Greek, tilde](RuN) is with −33/32 cm⁻¹ much higher. The splitting of the deformation mode can be observed also in the first overtone at 1179/1165 cm⁻¹, indicating an influence of the local environment, supported by the fact that the lower energy band is broad.

Table 3 Experimental (T = 10 K) and DFT solid state calculated vibrations for ¹⁴N and ¹⁵N in GS. br = broad, Δ¹⁴N(exp − calc) is the difference between measured and calculated ¹⁴N vibrations

Mode	GS-^14N	GS-^15N	Δ(Iso)	DFT-^14N	DFT-^15N	Δ(Isoto)	Δ ^14N(exp − calc)
3 × [small nu, Greek, tilde](NO)	5641	5527	114	—	—	—	—
2 × [small nu, Greek, tilde](NO)	3786	3711	75	—	—	—	—
[small nu, Greek, tilde](NO)	1923	1885	38	1882	1844	38	41
	1912	1874	38	1869	1831	38	43
2 × [small nu, Greek, tilde](RuN)	1213	1196	17	—	—	—	—
2 × δ(RuNO)	1179	1147	32	—	—	—	—
2 × δ(RuNO)	1165	1139	26	—	—	—	—
[small nu, Greek, tilde](RuN)	609	601	8	642/641	635/633	7/8	−33/−32
δ(RuNO)	590	574	16	577	561	16	13
	585 br	571 br	14	573/569	558/554	15/15	12/16
[small nu, Greek, tilde](RuCl)	349	349	0	339	339	0	10
[small nu, Greek, tilde](RuCl)	343	343	0	335/334	335/333	0/1	8/9
[small nu, Greek, tilde](RuCl)	332	332	0	330	330	0	2
[small nu, Greek, tilde](RuCl)	324	324	0	328	328	0	−4

---

3.2. Metastable state MS2

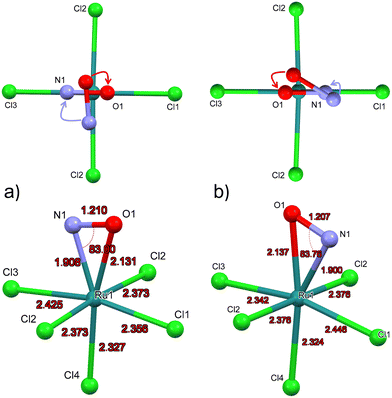
Due to the space group Pnma in GS the Cl4-Ru–N–O axis lies in the mirror plane m. Since DFT geometry optimization provides local energy minima, different positions of the NO ligand are chosen as a starting point for the energy minimization, in order to find out whether the mirror plane is conserved in MS2. For the calculation of the structural model of MS2, we used as starting position the polar Ru–N–O angle θ as 90° and chose an azimuthal position of φ = 90°, i.e. the NO ligand is oriented along the direction of Ru–Cl2 bonds, the so-called eclipsed geometry of MS2⁶⁶ (see Fig. 4a, top). DFT Geometry optimization was then performed and in the course of the convergence of the calculation, the NO ligand did rotate stepwise so that in the end this azimuthal angle φ amounts to 0°, i.e. the O atom of N-O ligand is oriented in direction to the Ru–Cl1 and Ru-Cl3 bonds. Another projection of the converged structure is shown in Fig. 4a, bottom.

Fig. 4 Calculated structural model of [RuCl₅NO]²⁻ in MS2: (a) Initial and converged structure of MS2 converging O atom of NO towards Cl1 ligand; (b) initial and converged structure of MS2 converging O atom of NO towards Cl3 ligand.

In order to verify the azimuthal position of the NO in MS2, we performed calculations with several starting geometries of the NO group, choosing the azimuthal position of φ = 45°, i.e. the NO ligand is oriented along the direction between Ru–Cl1 and Ru–Cl2 bonds, the so-called staggered geometry of MS2 (Fig. 4b, top). For the latter, the converged position of the O atom is pointing towards the Cl3 ligand (see Fig. 4b, top). The energy of the NO position where O is closer to Cl3 is 0.12 eV higher than that for the direction towards Cl1, so that the latter corresponds to the global minimum of MS2 (Fig. 4a). In GS the symmetry related distances Ru–Cl2 and Ru–Cl2′ are identical with 2.371(1) Å. According to the calculations the NO remains in the mirror plane and the Ru–Cl2 and Ru–Cl2′ distances are identical (see Fig. 4), independent whether the final position of the O atom is towards Cl1 or Cl3. These two configurations lead to different Ru–Cl1 distances. When the oxygen atom of NO is in the direction of Cl1, the bond lengths of Ru–Cl1 is shorter than that of Ru–Cl3. The calculations were performed in space groups with lower symmetry (P2₁/c and P1) in order to avoid symmetry-induced preferential orientations for NO, especially due to the mentioned mirror plane. Table 4 summarizes the calculated structural data for GS and MS2 and the corresponding differences. The pairs of values correspond to the two configurations where the O atom is in direction of Ru–Cl3/Ru–Cl1.

Table 4 Structural parameters for MS2: atomic distances (Å), angles (°) and differences with respect to GS. The pairs of values correspond to O–Cl3/O–Cl1 geometry (Fig. 4a and b)

Distances/angles	MS2 (DFT)	GS (DFT)	Δ(MS2-GS)
Ru–N	1.900/1.908	1.727	+0.173/+0.181
Ru–O	2.137/2.131	—	—
N–O	1.207/1.210	1.152	+0.055/+0.058
Ru–Cl4trans	2.324/2.327	2.355	−0.031/−0.028
Ru–Cl1	2.446/2.356	2.384	+0.062/−0.028
Ru–Cl2	2.376/2.373	2.380	−0.004/−0.007
Ru–Cl3	2.342/2.425	2.369	−0.027/+0.056
∠Ru–N–O	83.8/83.0	172.5	−88.7/−89.5

---

Due to the fact that experimentally achievable populations of MS2 and MS1 in K₂[RuCl₅NO] are rather low, infrared spectroscopy is the best tool to obtain structural information on these linkage isomers. The side-on geometry of MS2 leads to a pronounced downshift of [small nu, Greek, tilde](NO) by 369/362 cm⁻¹ with respect to GS. The observed splitting in MS2 is three times smaller than the one observed in GS. Since the population of MS2 is very low (only 2–3%), the origin of the splitting in MS2 is most probably due to the local environment and not a consequence of a coupling to the lattice.

As for GS, we performed solid-state DFT calculations of the IR vibrations on the structural model obtained in 4a, which corresponds to the minimum-energy configuration. As listed in Table 5, the difference between calculated and experimental [small nu, Greek, tilde](NO) values are 63/66 cm⁻¹ and thus about 20 cm⁻¹ larger than in GS. Fig. 5 and Fig. S4, S5 (ESI†) illustrate the experimental and solid-state DFT-calculated infrared spectra, respectively. Surprisingly, we observe a shift by 18 cm⁻¹ to higher wavenumbers for the δ(Ru–O–N) deformation mode, even though atomic distances increase in MS2 with respect to GS. The assignment of the band to the deformation mode is based on the larger isotopic shift compared to the [small nu, Greek, tilde](Ru–N) stretching mode. The latter is hidden by the Ru–Cl vibrational modes, and the calculation shows that it has a small cross section. Possibly, the detected intensity changes in the band at 349 cm⁻¹ after transferring MS1 to MS2 through 1310 nm irradiation, are due to the appearance of the ν(Ru–N) stretching mode of MS2, but the change is too small to unambiguously assign it. For all the other bands, the agreement between calculated and experimentally observed isotope shift is excellent, so that their assignment is unambiguous, even though the absolute value of the upshift of the δ(Ru–O–N) deformation mode is largely overestimated by the calculation (+99 cm⁻¹) compared to the observed +18 cm⁻¹. The calculated downshift of [small nu, Greek, tilde](Ru–N) is -219 cm⁻¹, possibly much to large. However, the direction of the shift of these two bands is opposite and in agreement with experiment. Similar trends were reported earlier.^29,30

Table 5 Experimental (T = 10 K) and calculated vibrations in MS2 and differences between isotopes Δ(Iso) and between experimental and calculated ¹⁴N vibrations Δ(¹⁴N)

Mode	MS2-^14N	MS2-^15N	Δ(Iso)	DFT-^14N	DFT-^15N	Δ(Iso)	Δ(^14N)
[small nu, Greek, tilde](NO)	1554/1550	1527/1522	27/28	1491/1484	1464/1457	27/27	+63/+66
δ(RuNO)	608/603	593/588	15/15	676/673	658/654	18/19	−68/−70
[small nu, Greek, tilde](RuN)	—	—	—	423/422	421/419	2/3	—
[small nu, Greek, tilde](RuCl)	349	349	0	342	342	0	7
[small nu, Greek, tilde](RuCl)	343	343	0	340	340	0	3
[small nu, Greek, tilde](RuCl)	338	338	0	328	328	0	10
[small nu, Greek, tilde](RuCl)	332	332	0	325/324	325/324	0	7

---

Fig. 5 Comparison of the experimentally observed vibrations of GS, MS1 and MS2 in the spectral range of 1950–1500 cm⁻¹. The spectra were measured at 10 K, MS1 and MS2 were photogenerated by irradiation at 520 nm.

3.3. Metastable state MS1

As for MS2, the experimentally achievable population of MS1 is too low to perform X-ray crystallography. Hence, we present the geometry-optimized model where we used as a starting point the structure of GS where O and N have been interchanged. The resulting DFT-calculated structural model is shown in Fig. 6.

Fig. 6 DFT calculated structural model of [RuCl₅(ON)]²⁻ in MS1.

Table 6 summarizes the most important structural changes between GS and MS1, notably the increased Ru–O distance of 1.837 Å compared to GS Ru–N distance of 1.727 Å and the significantly shortened Ru–Cl4 bond (Cl4 = trans to NO) of 2.298 Å compared to 2.355 Å in GS. The N–O distance remains almost the same in the inverted MS1 geometry and the polar Ru–O–N angle points again toward Cl1. The Ru–Cl1 distance decreases by 0.02 Å.

Table 6 Atomic distances (Å), RuNO angles (°) and differences Δ between MS1(calc)–GS(calc)

Distances/angles	MS1(DFT)	GS(DFT)	Δ(MS1-GS)
Ru–O/N	1.837	1.727	+0.110
N–O	1.154	1.152	+0.002
Ru–Cl4trans	2.298	2.355	−0.057
Ru–Cl1	2.364	2.384	−0.020
Ru–Cl2	2.380	2.380	0
Ru–Cl3	2.378	2.369	+0.009
∠Ru–O–N/Ru–N–O	172.8	172.5	+0.3

---

With respect to the vibrational bands, the increase or decrease of atomic distances is expected to lead to a corresponding decrease or increase of the vibrational frequency. We note immediately that especially for the case of the [small nu, Greek, tilde] (NO) stretching vibration the large downshift of 153/146 cm⁻¹ in MS1 with respect to GS cannot be explained in this manner.

As for the other isomers, we performed solid-state DFT calculations of the IR vibrations. Table 7 lists the experimental and calculated vibrations for ¹⁴N and ¹⁵N in MS1, and the corresponding spectra are shown in Fig. 5. The [small nu, Greek, tilde](Ru–Cl) vibrations do not exhibit any change when going from GS to MS1. For [small nu, Greek, tilde](NO) we observe again a splitting as in GS, for the NA sample the two ¹⁴N bands are found at 1770/1766 cm⁻¹ and for the 96% ¹⁵N the two bands at 1741/1737 cm⁻¹, thus an isotopic shift of 29 cm⁻¹. The ¹⁴N band (4%) in the ¹⁵N sample is found as a single band at 1766 cm⁻¹, analogous to the GS case we interpret thus the splitting as due to coupling to the lattice, and the correlation-free band is the one found for low concentrations at 1766 cm⁻¹. The assignment of the [small nu, Greek, tilde](RuO) band at 467 (465) cm⁻¹ and δ(RuON) band at 454 (449) cm⁻¹ can be made by the smaller/larger isotope shift. We note that the [small nu, Greek, tilde](RuO) band remains the higher frequency band in MS1 as in GS, even after rotation of the NO ligand. The rather important downshift for [small nu, Greek, tilde](RuO) and δ(RuON) of 142 and 136 cm⁻¹, respectively, is compatible with the significant change in Ru–O bond length of +0.11 Å compared to the Ru–N GS configuration, which is in line with the previous report.⁴² While the [small nu, Greek, tilde](NO) in MS1 are well reproduced by the calculations, the [small nu, Greek, tilde](RuO) and δ(RuON) are overestimated and hence the downshift with respect to GS is underestimated. Moreover, the calculation indicates a splitting of 1 cm⁻¹ for the δ(RuON), which was not detected experimentally (resolution of 1 cm⁻¹), since these bands are weak and broad.

Table 7 Experimental (T = 10 K) and DFT calculated vibrations in MS1, differences Δ(Iso) between isotopes and Δ(¹⁴N) between measured/calculated ¹⁴N values

Mode	MS1-^14N	MS1-^15N	Δ(Iso)	DFT-^14N	DFT-^15N	Δ(Iso)	Δ(^14N)
2 × [small nu, Greek, tilde](NO)	3499	3443	56	—	—	—	—
[small nu, Greek, tilde](NO)	1770/1766	1741/1737	29/29	1778/1772	1749/1743	29/29	8/6
[small nu, Greek, tilde](RuO)	467	465	2	486/484/482	485/480/479	1/4/3	−19/−17/−15
δ(RuON)	454	449	5	506/505	500/499	6/6	−52/−45
[small nu, Greek, tilde](RuCl)	349	349	0	346	346	0	3
[small nu, Greek, tilde](RuCl)	343	343	0	344	344	0	1
[small nu, Greek, tilde](RuCl)	332	332	0	325	325	0	7
[small nu, Greek, tilde](RuCl)	324	324	0	318/316	318/316	0	6/8

---

4. Discussion

Due to the strong coupling between the [RuCl₅NO]²⁻ anion and the K⁺ cation sublattices, a solid-state calculation is necessary to assess correctly the structures of GS, MS2 and MS1. Since the performed solid-state CASTEP calculations show good agreement with all atomic distances, the positions of the vibrational bands and the chemical shifts in GS, we used this calculation to perform a Bader analysis to determine the charges on the atoms (see Table 8). In this manner the charge redistribution upon generation of the two PLI MS1 and MS2 with respect to GS can be investigated.

Table 8 Atomic charge distribution obtained from Bader analysis of the CASTEP DFT charge density calculation. The +/− sign for Δq indicates increase/decrease of the charge compared to GS (GS–MS)

	GS		MS2			MS1
	Total	charge q	Total	charge q	Δq	Total	charge q	Δq
O	6.32	−0.32	6.37	−0.37	+0.05	6.46	−0.46	+0.14
N	4.83	+0.17	4.88	+0.12	+0.05	4.62	+0.38	−0.21
Ru	14.73	+1.27	14.78	+1.22	+0.05	14.78	+1.22	+0.05
Cl1	7.55	−0.55	7.55	−0.55	±0.00	7.56	−0.56	+0.01
Cl2	7.57	−0.57	7.56	−0.56	−0.01	7.59	−0.59	+0.02
Cl3	7.56	−0.56	7.50	−0.50	−0.06	7.57	−0.57	+0.01
Cl4trans	7.57	−0.57	7.50	−0.50	−0.07	7.52	−0.52	−0.05
K	8.15	+0.85	8.15	+0.85	±0.00	8.15	+0.85	±0.00
∑(RuNO)	25.88	+1.12	26.03	+0.97	+0.15	25.86	+1.14	−0.02
∑(Cl)	37.82	−2.82	37.67	−2.67	−0.15	37.83	−2.83	+0.01
[RuCl5NO]		−1.70		−1.70			−1.69

---

The total charges on the atoms are calculated with respect to the charge enclosed in the Bader volume defined by the surface of minimal charge density between atoms; the resulting charge q on the atom is given by the difference with respect to the neutral atom. In GS the NO is negative (−0.15e), in MS2 it gets even more negative (−0.25e) while in MS1 it is almost neutral (−0.08e). Hence, the downshift of [small nu, Greek, tilde](NO) cannot be explained by a pure charge redistribution effect. The simple rule that the more negative the NO the lower the ν(NO) stretching vibration, does not apply to the present case, and we have to search for further mechanisms.

In MS1 we observe a charge redistribution between N, O and Ru upon NO inversion. The negative charge on the oxygen atom increases by 0.14e, that on the nitrogen decreases by 0.21e and that of the ruthenium atom increases by 0.05e. Moreover, 0.05e are redistributed from the trans-to-NO ligand Cl4_trans to the equatorial Cl-ligands, which also receive the minimal excess charge from RuNO. The decisive charge redistribution occurs thus, as might be expected, on the N and O atoms. In MS2 the negative charge on the Ru, N, O atoms is equally increased by 0.05e. This charge stems from the Cl ligands, in particular from Cl4_trans and Cl3, so that in MS2 the Cl-ligands contribute much more charge for the stabilization of this structural configuration.

Such a charge redistribution when going from GS to MS1 was also calculated for the complex trans-[Ru(py)₄(NO)F](ClO₄)₂,⁴⁸ for which the NO has a Bader charge of −0.13e in the GS, which reduces to -0.03e in the MS1. The frequency of the [small nu, Greek, tilde](NO) stretching vibration changes from [small nu, Greek, tilde]_GS(NO) = 1909 cm⁻¹ to [small nu, Greek, tilde]_MS1(NO) = 1761 cm⁻¹, i.e. by 148 cm⁻¹, which compares well with the observations of the shift of 146/153 cm⁻¹ in K₂[RuCl₅NO]. Hence, also for this second ruthenium-nitrosyl complex (cation instead of anion) the downshift of [small nu, Greek, tilde](NO) cannot be explained by a simple increase of the total charge on the NO.

Overall one could thus potentially explain the downshift of the ν(NO) stretching vibration, and hence the reduced force constant, for MS2 by the increase in charge of 0.10e and in bond length of 0.058 Å (in case of O–Cl1 geometry). But for MS1 this argument no longer holds, since the charge on the NO ligand is reduced by 0.07e with respect to GS and the change in bond length amounts to only 0.002 Å. Already Sizova and co-workers³⁰ discussed this discrepancy between the calculated and experimental results for the vibrational frequencies, which occur especially for MS1. They investigated the influence of the environment by applying a polarizable continuum model (PCM), which nevertheless did not resolve the issue for MS1. In such a simple picture, the contribution of the coupling between [small nu, Greek, tilde](RuN) and [small nu, Greek, tilde](NO) to the experimentally observed values is neglected. As a matter of fact, Sizova et al.³⁰ indicated the contributions of the internal coordinates to the NO and RuNO vibrations for the [RuCl₅NO]²⁻ complex, which amounts up to 11% of [small nu, Greek, tilde](RuN) to 89% [small nu, Greek, tilde](NO) in GS using a valence force model, but without proceeding to a detailed analysis including further calculations of local force constants. Such a complete decoupling for the solid state by the transformation of all vibrations into a pure two-atomic behavior can be obtained by using the local vibrational mode theory formalism.³² Using the PyMol plugin, named LModeA-nano, implementing the local vibrational mode theory for periodic systems,⁴⁶ we obtain the decoupled wavenumbers and force constants k^dc. The coupled force constants k^c, which are given in Table 9, can then be obtained from the equation k^c/k^dc = ([small nu, Greek, tilde]^c/[small nu, Greek, tilde]^dc)² with the calculated wavenumbers.

Table 9 Coupled and decoupled vibrational frequencies ([small nu, Greek, tilde]) and force constants (k) as well as corresponding differences Δ

[small nu, Greek, tilde], k	Decoupled ([small nu, Greek, tilde]^dc, k^dc)			Coupled ([small nu, Greek, tilde]^c, k^c)			Δ(coupled–decoupled)
cm^−1, N cm^−1	GS	MS2	MS1	GS	MS2	MS1	GS	MS2	MS1
[small nu, Greek, tilde](NO) calc.	1799	1408	1741	1869	1484	1772	+70	+76	+31
[small nu, Greek, tilde](NO) exp.				1912	1550	1766	+113	+142	+25
[small nu, Greek, tilde](RuN,O) calc.	884	636	643	641	422	482	−243	−214	−161
[small nu, Greek, tilde](RuN,O) exp.				609	—	467	−275	—	−176
k(NO)	14.239	8.72	13.334	15.369	9.687	13.813	1.130	0.967	0.479
k(RuN,O)	5.658	2.930	3.368	2.975	1.290	1.893	−2.683	−1.640	−1.475

---

The most important result of the decoupling is the blueshift of the [small nu, Greek, tilde]^dc(RuN), [small nu, Greek, tilde]^dc(RuO) vibrations and the redshift of [small nu, Greek, tilde]^dc(NO) with respect to the coupled [small nu, Greek, tilde]^c values, which demonstrates together with the resulting force constants the strong coupling of the corresponding atomic movements. Since the transformation into local modes is a linear operation, the resulting decoupled parameters still reflect the same physical properties. So, if there would be an unusual behavior of the vibrations in the metastable states it should remain visible in the uncoupled parameters. 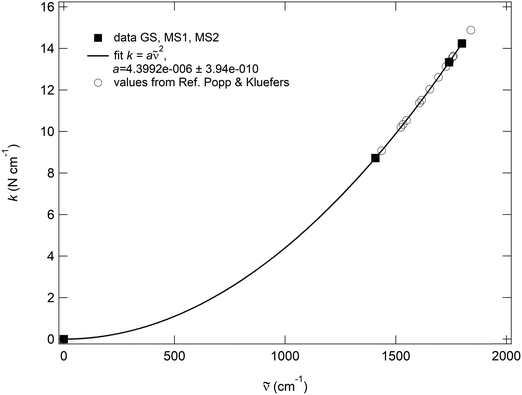Due to the fact that these local modes are harmonic oscillators, the force constants depend on the wavenumbers as k = 4π²c²μ[small nu, Greek, tilde]² in which c is the light velocity, μ is the reduced mass of the corresponding atoms and [small nu, Greek, tilde] is the wavenumber. The pre-factor 4π²c²μ is then exactly the same for GS, MS2 and MS1, so that the decoupled wavenumbers of these three states need all follow the same quadratic dependence k ∼ [small nu, Greek, tilde]². Additionally, the fitted pre-factor must be identical with the calculated one, which is indeed the case for the NO, since the calculated pre-factor is 4.399096 × 10⁻⁴ cm² kg s⁻² and the fitted one is 4.3992(4) × 10⁻⁴ cm² kg s⁻² (Fig. 7). This quadratic dependence of the local force constants on the calculated decoupled vibrations shows the pure functional dependence of the harmonic oscillator, e.g., the two-atomic system NO, which then should be true, independent of the system in which the NO is integrated. This can be clearly seen when inserting the calculated decoupled values from the study of Popp & Kluefers²⁸ for different metal-nitrosyl complexes, as shown in Fig. 7.

Fig. 7 Quadratic dependence k^dc = a([small nu, Greek, tilde]^dc)², (a = 4π²c²μ) for the NO stretching vibration of GS, MS1, and MS2 in K₂[RuCl₅NO], resulting from the decoupling into two-atomic harmonic oscillators. For the fit, the point k = [small nu, Greek, tilde] = 0 has been added.

An immediate consequence of these findings is that the experimentally measured red- or blueshifts for the vibrations of an atomic group (pair) cannot be used as a direct measure of possible underlying distance changes or charge redistributions, since the experimentally observed vibrations are always the result of coupled motions. However, the calculated decoupled force constants, being local force constants, confirm the softening of the N–O and Ru–N, Ru–O bonds, which is more pronounced for the side-on geometry. In order to properly interpret the observations, we might estimate the coupling of the modes, in particular between the [small nu, Greek, tilde](NO) and [small nu, Greek, tilde](RuN) and [small nu, Greek, tilde](RuO). Comparing the coupled and uncoupled values, we can see from Table 9 that for NO all coupled force constants, k^c, are higher than their uncoupled counterparts, k^dc. For Ru–N/O the coupled force constants are lower than the uncoupled ones. Thus, there is transfer of bond strength from the Ru–N/O to the N–O. This transfer varies significantly between the three states as we can estimate using the ratios Δ(coupled–decoupled)/k^c for the gain in NO bond strength and Δ(coupled–decoupled)/k^dc for the loss in Ru–N and Ru–O bond strength. While for GS the N–O receives 7.35% bond strength at a cost of 47.42% loss of bond strength in Ru–N, for MS1 the N–O receives only 3.47% with a loss of 43.79% for the Ru–O. Thus, the seemingly unusually large redshift of [small nu, Greek, tilde](NO) observed in MS1 is actually largely due to the fact that there is less transfer from the Ru–O bond to the N–O bond than in the GS (Ru–N to N–O). For MS2, the N–O receives 9.98% at a loss of 55.97% for Ru-N. Note that these are all calculated values as we have no means to access experimentally the uncoupled parameters. Furthermore, we have to keep in mind that the calculated coupled vibrational frequencies are underestimated compared to the experimental values (Table 9) except for MS1.

Still, one problem remains unresolved by the local vibrational mode transformation: the anharmonicity of the measured values. The strong change of the dipole moment allows to measure the first and second overtones, which show the anharmonicity of the NO potential. This is not considered in the local mode calculation. Nevertheless, the quadratic dependence k ∼ [small nu, Greek, tilde]² of all vibrations after the local mode transformation clearly shows that all photoinduced linkage isomers behave as expected and that the observed, seemingly atypical, large shift of the [small nu, Greek, tilde](NO) stretching vibration is due to a significant change in the coupling of the N–O and Ru–N/O modes, and thus does not properly reflect the intrinsic changes in bond strength. One should therefore refrain from interpreting this observed shift directly into changes of bond length or even redistribution of charge on the NO group. In view of the fact that we can now treat the decoupled vibrations of NO in the framework of a two-atomic harmonic oscillator, the observed redshift of the [small nu, Greek, tilde](NO) vibration when going from GS to MS1 and MS2 might be explained by the influence of an external lateral charge-ligand interaction, as proposed by Popp & Klufers²⁸ for diatomic ligands like NO or CO. Additionally, an internal contribution due to modified occupations of the N(2s), N(2p), O(2s), O(2p) and Ru(4d) orbitals, as can be seen from a Mulliken population analysis (see discussion in Supplementary material and Table S6), might also contribute to this shift. Further calculations are necessary to shine light on these potential external and internal contributions.

5. Conclusion

The solid-state DFT calculations reproduce with good accuracy the structures and vibrational frequencies in the three linkage isomers GS, MS1 and MS2 of K₂[RuCl₅NO], such that the calculated Bader charges represent an excellent model for the real charges on the atoms. Based on this Bader charge analysis we show that the downshift of the [small nu, Greek, tilde](NO) stretching vibration in MS1 and MS2 cannot be explained by an increase of the charge on the NO. The local mode transformations of [small nu, Greek, tilde](NO), [small nu, Greek, tilde](RuN) and [small nu, Greek, tilde](RuO) decouples these vibrations into two-atomic harmonic oscillators, revealing a significant change in coupling between ν(NO) and ν(RuN) in GS compared to ν(NO) and ν(RuO) in MS1. Hence, the experimentally observed redshift of the ν(NO) stretching vibration should not be directly used for a physical interpretation of possible photoinduced changes of the NO bond strength.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank B. A. Kolesov for measurement of Raman spectra. The work has been financially supported by RSF (22-43-09001) in the part of synthesis and spectroscopy and ANR (grant no. ANR-21-CE30-0045-01). We thank the PMD2X platform of Université de Lorraine for granting access to XRD diffractometers. High Performance Computing resources were partially provided by the EXPLOR centre hosted by the Université de Lorraine.

References

1. D. Awasabisah and G. B. Richter-Addo, Advances in Inorganic Chemistry, Elsevier, 2015, vol. 67, pp. 1–86.
2. T. E. Bitterwolf, Photochemical nitrosyl linkage isomerism/metastable states, Coord. Chem. Rev., 2006, 250, 1196–1207.
3. P. Coppens, I. Novozhilova and A. Kovalevsky, Photoinduced Linkage Isomers of Transition-Metal Nitrosyl Compounds and Related Complexes, Chem. Rev., 2002, 102, 861–884.
4. C. Daniel and C. Gourlaouen, Chemical bonding alteration upon electronic excitation in transition metal complexes, Coord. Chem. Rev., 2017, 344, 131–149.
5. P. Gütlich, Y. Garcia and T. Woike, Photoswitchable coordination compounds, Coord. Chem. Rev., 2001, 219–221, 839–879.
6. I. Stepanenko, M. Zalibera, D. Schaniel, J. Telser and V. B. Arion, Ruthenium-nitrosyl complexes as NO-releasing molecules, potential anticancer drugs, and photoswitches based on linkage isomerism, Dalton Trans., 2022, 51, 5367–5393.
7. J. V. Esplugues, NO as a signalling molecule in the nervous system: NO in the nervous system, Br. J. Pharmacol., 2002, 135, 1079–1095.
8. P. Picón-Pagès, J. Garcia-Buendia and F. J. Muñoz, Functions and dysfunctions of nitric oxide in brain, Biochim. Biophys. Acta, Mol. Basis Dis., 2019, 1865, 1949–1967.
9. D. Schaniel, M. Imlau, T. Weisemoeller, T. Woike, K. W. Krämer and H.-U. Güdel, Photoinduced Nitrosyl Linkage Isomers Uncover a Variety of Unconventional Photorefractive Media, Adv. Mater., 2007, 19, 723–726.
10. M. Goulkov, D. Schaniel and T. Woike, Pulse recording of thermal and linkage isomer gratings in nitrosyl compounds, J. Opt. Soc. Am. B, 2010, 27, 927.
11. A. Hasil, D. Beck, D. Schröder, S. Pillet, E. Wenger, T. Woike, P. Klüfers and D. Schaniel, Pas de Deux of an NO Couple: Synchronous Photoswitching from a Double-Linear to a Double-Bent Ru(NO)₂ Core under Nitrosyl Charge Conservation, Angew. Chem., Int. Ed., 2022, 61(42), e202210671.
12. R. D. Yamaletdinov and I. L. Zilberberg, The Effect of trans Ligands in the NO-Linkage Reverse Isomerization for Ruthenium–Nitrosyl–Tetraammine Complexes: A DFT Study, Eur. J. Inorg. Chem., 2017, 2951–2954.
13. A. A. Mikhailov, G. A. Kostin and D. Schaniel, The influence of the trans-ligand to NO on the thermal stability of the photoinduced side-bond coordinated linkage isomer, New J. Chem., 2022, 46, 12641–12650.
14. A. A. Mikhailov, E. Wenger, G. A. Kostin and D. Schaniel, Room-Temperature Photogeneration of Nitrosyl Linkage Isomers in Ruthenium Nitrosyl Complexes, Chem. – Eur. J., 2019, 25, 7569–7574.
15. A. A. Mikhailov, T. S. Sukhikh, N. V. Kuratieva, D. P. Pishchur and G. A. Kostin, Remarkable thermal stability of light-induced Ru–ON linkage isomers in mixed salts of a ruthenium amine complex with a trans -ON–Ru–F coordinate, Dalton Trans., 2021, 50, 2864–2871.
16. A. In-Iam, M. Wolf, C. Wilfer, D. Schaniel, T. Woike and P. Klüfers, {FeNO}⁷-Type Halogenido Nitrosyl Ferrates: Syntheses, Bonding, and Photoinduced Linkage Isomerism, Chem. – Eur. J., 2019, 25, 1304–1325.
17. D. Schaniel, J. Schefer, B. Delley, M. Imlau and T. Woike, Light-induced absorption changes by excitation of metastable states in Na₂[Fe(CN)₅NO]2H₂O single crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 085103.
18. D. Schaniel and T. Woike, Necessary conditions for the photogeneration of nitrosyl linkage isomers, Phys. Chem. Chem. Phys., 2009, 11, 4391.
19. D. Schaniel, M. Nicoul and T. Woike, Ultrafast reversible ligand isomerisation in Na₂[Fe(CN)₅NO]·2H₂O single crystals, Phys. Chem. Chem. Phys., 2010, 12, 9029.
20. G. Gallé, M. Nicoul, T. Woike, D. Schaniel and E. Freysz, Unraveling the mechanism of NO ligand photoisomerism by time-resolved infrared spectroscopy, Chem. Phys. Lett., 2012, 552, 64–68.
21. F. Talotta, M. Boggio-Pasqua and L. González, Early Relaxation Dynamics in the Photoswitchable Complex trans-[RuCl(NO)(py)₄]²⁺, Chem. – Eur. J., 2020, 26, 11522–11528.
22. D. Schaniel, T. Woike, B. Delley, D. Biner, K. W. Krämer and H.-U. Güdel, Generation of one light-induced metastable nitrosyl linkage isomer in [Pt(NH₃)₄Cl(NO)]Cl₂ in the red spectral range, Phys. Chem. Chem. Phys., 2007, 9, 5149.
23. D. Schaniel, T. Woike, N.-R. Behrnd, J. Hauser, K. W. Krämer, T. Todorova and B. Delley, Photogeneration of Nitrosyl Linkage Isomers in Octahedrally Coordinated Platinum Complexes in the Red Spectral Range, Inorg. Chem., 2009, 48, 11399–11406.
24. Y. Divó-Matos, Y. Avila, R. Mojica and E. Reguera, Nature of the observed ν(NO) band shift and splitting during the 3D to 2D structural change in transition metal nitroprussides, Spectrochim. Acta, Part A, 2022, 276, 121210.
25. M. E. Jacox and W. E. Thompson, The vibrational spectra of molecular ions isolated in solid neon. IV. NO⁺, NO⁻, ONNO⁺, and ONNO⁻, J. Chem. Phys., 1990, 93, 7609–7621.
26. J. H. Enemark and R. D. Feltham, Principles of structure, bonding, and reactivity for metal nitrosyl complexes, Coord. Chem. Rev., 1974, 13, 339–406.
27. J. Popp, T. Riggenmann, D. Schröder, T. Ampßler, P. Salvador and P. Klüfers, Bent and Linear {CoNO}⁸ Entities: Structure and Bonding in a Prototypic Class of Nitrosyls, Inorg. Chem., 2021, 60, 15980–15996.
28. J. Popp and P. Klüfers, Bond Strength of a Diatomic Acceptor Ligand: A Reliable Measure of Its Antibond Occupation and Its Charge?, Eur. J. Inorg. Chem., 2022,(32), e202200374.
29. B. Delley, DFT study of crystalline nitrosyl compounds, Z. Kristallogr. – Cryst. Mater., 2008, 223, 329–333.
30. O. V. Sizova, O. O. Lubimova, V. V. Sizov and N. V. Ivanova, DFT study of metastable linkage isomers of six-coordinate ruthenium nitrosyl complexes, Z. Kristallogr. – Cryst. Mater., 2008, 223, 343–355.
31. R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928.
32. Y. Tao, W. Zou, D. Sethio, N. Verma, Y. Qiu, C. Tian, D. Cremer and E. Kraka, In Situ Measure of Intrinsic Bond Strength in Crystalline Structures: Local Vibrational Mode Theory for Periodic Systems, J. Chem. Theory Comput., 2019, 15, 1761–1776.
33. V. A. Emel’yanov, M. A. Fedotov, A. V. Belyaev and S. V. Tkachev, A multinuclear magnetic resonance study of transformations of ruthenium(II) nitrosyl chloride complexes in aqueous solutions, Russ. J. Inorg. Chem., 2013, 58, 956–963.
34. G. M. Sheldrick, SHELXT – Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
35. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341.
36. E. E. Mercer, W. M. Campbell and R. M. Wallace, Chloro Complexes of Nitrosylruthenium, Inorg. Chem., 1964, 3, 1018–1024.
37. D. Guenzburger, A. Garnier and J. Danon, Electronic structure, electronic spectra and Mössbauer hyperfine interactions in ruthenium complexes, Inorg. Chim. Acta, 1977, 21, 119–131.
38. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567–570.
39. C. J. Pickard and F. Mauri, All-electron magnetic response with pseudopotentials: NMR chemical shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
41. E. V. Lenthe, E. J. Baerends and J. G. Snijders, Relativistic regular two-component Hamiltonians, J. Chem. Phys., 1993, 99, 4597–4610.
42. A. A. Mikhailov, T. Woike, A. Gansmüller, D. Schaniel and G. A. Kostin, Photoinduced linkage isomers in a model ruthenium nitrosyl complex: Identification and assignment of vibrational modes, Spectrochim. Acta, Part A, 2021, 263, 120217.
43. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
44. A. Tkatchenko and M. Scheffler, Accurate Molecular van der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data, Phys. Rev. Lett., 2009, 102, 073005.
45. J. Kendrick and A. D. Burnett, PDielec: The calculation of infrared and terahertz absorption for powdered crystals, J. Comput. Chem., 2016, 37, 1491–1504.
46. Y. Tao, W. Zou, S. Nanayakkara and E. Kraka, LModeA-nano: A PyMOL Plugin for Calculating Bond Strength in Solids, Surfaces, and Molecules via Local Vibrational Mode Analysis, J. Chem. Theory Comput., 2022, 18, 1821–1837.
47. M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134, 064111.
48. A. Gansmüller, A. A. Mikhailov, G. A. Kostin, J. Raya, C. Palin, T. Woike and D. Schaniel, Solid-State Photo-NMR Study on Light-Induced Nitrosyl Linkage Isomers Uncovers Their Structural, Electronic, and Diamagnetic Nature, Anal. Chem., 2022, 94, 4474–4483.
49. T. S. Khodashova and B. Bokii, Structure of potassium nitroso-pentachlororuthenate, J. Struct. Chem., 1960, 1, 138–145.
50. T. S. Khodashova and G. B. Bokii, Refinement of the structure of potassium nitrosopentachlororu thenate, J. Struct. Chem., 1964, 5, 130–131.
51. J. T. Veal and D. J. Hodgson, The crystal and molecular structure of potassium pentachloronitrosylruthenate(II), K₂[Ru(NO)Cl₅], Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3525–3529.
52. R. Zarhloul, R. Faure and J.-P. Deloume, Structural study of bonding in halogeno ruthenium complexes: Application to ruthenium nitrosyls, J. Crystallogr. Spectrosc. Res., 1992, 22, 601–606.
53. M. Rüdlinger, J. Schefer, P. Fischer, N. Furer and H. U. Güdel, Temperature-Dependence of the Crystal Structure of K₂[RuCl₅NO]: A Powder Neutron Diffraction Study, J. Solid State Chem., 1993, 103, 170–175.
54. L. K. Bell, J. Mason, D. M. P. Mingos and D. G. Tew, Nitrogen-15 NMR studies of nitrosyl (bent and linear), nitro, and nitrito ligands in 4-, 5-, and 6-coordinate complexes of the platinum metals, Inorg. Chem., 1983, 22, 3497–3502.
55. J. Mason, D. M. P. Mingos, J. Schaefer, D. Sherman and E. O. Stejskal, Nitrogen-15 n.m.r. characterization of bent and linear nitrosyl ligands in the solid state by cross-polarisation magic-angle-spinning spectroscopy of complexes of ruthenium, J. Chem. Soc., Chem. Commun., 1985, 444.
56. J. Mason, L. F. Larkworthy and E. A. Moore, Nitrogen NMR Spectroscopy of Metal Nitrosyls and Related Compounds, Chem. Rev., 2002, 102, 913–934.
57. T. Woike, H. Zöllner, W. Krasser and S. Haussühl, Raman-spectroscopic and differential scanning calorimetric studies of the light induced metastable states in K₂[RuCl₅NO], Solid State Commun., 1990, 73, 149–152.
58. J. R. Durig, W. A. McAllister, J. N. Willis and E. E. Mercer, Far infrared spectra of potassium and ammonium pentahalonitrosylruthenates, Spectrochim. Acta, 1966, 22, 1091–1100.
59. E. Miki, Infrared Studies of Transition-Metal Nitrosyl (¹⁴NO and ¹⁵NO) Complexes—Nitrosylruthenium(III), Nitrosylchromium(II) and Nitrosylcobalt(II) Complexes, Bull. Chem. Soc. Jpn., 1968, 41, 1835–1844.
60. E. Miki, T. Ishimori, H. Yamatera and H. Okuno, The Effects of Outer Sphere Cations and Halide Ions on Infrared Spectra of Pentahalogenonitrosylruthenium(III) Complexes, Bull. Chem. Soc. Jpn., 1969, 42, 3007–3008.
61. E. Miki, K. Mizumachi, T. Ishimori and H. Okuno, Infrared Spectra of Some Transition-metal (Fe, Co, Ru, and Ir) Nitrosyl (¹⁴NO and ¹⁵NO) Complexes, Bull. Chem. Soc. Jpn., 1973, 46, 3779–3784.
62. M. J. Cleare, H. P. Fritz and W. P. Griffith, Vibrational spectra of nitrosyl and carbonyl complexes—I, Spectrochim. Acta, Part A, 1972, 28, 2013–2018.
63. L. Tosi, The polarized Raman and infrared spectra of K₂[RuCl₅NO], J. Raman Spectrosc., 1977, 6, 20–25.
64. J. A. Güida, M. A. Ramos, O. E. Piro and P. J. Aymonino, Infrared spectra of K₂[RuCl₅NO] in two excited metastable states and the evidence for the NO linkage photoisomerization of metastable state I (MSI) in [RuX₅NO]²⁻(X = Cl, CN), J. Mol. Struct., 2002, 609, 39–46.
65. O. E. Piro, E. E. Castellano, J. A. Güida and P. J. Aymonino, Kramers-Kronig dispersive analysis and optical properties in the infrared, and revised vibrational behavior of orthorhombic Na₂[Fe(CN)₅NO]·2H₂O, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 1919–1926.
66. S. I. Gorelsky and A. B. P. Lever, Metastable states of ruthenium (II) nitrosyl complexes and comparison with [Fe(CN)₅NO]²⁻, Int. J. Quantum Chem., 2000, 80, 636–645.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2336093. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cp01374c

---