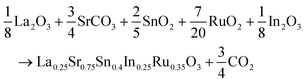First-principles prediction of half metallic-ferromagnetism in La0.25Sr0.75Sn0.4In0.25Ru0.35O3 and enhanced experimental electrical and magnetic behaviours†
Samira
Barouni
 a,
Ameni
Brahmia
b,
Hanen
Chaker
a,
Mikhail M.
Maslov
a,
Ameni
Brahmia
b,
Hanen
Chaker
a,
Mikhail M.
Maslov
 c,
Akram
Alhussein
d and
Rached
Ben Hassen
c,
Akram
Alhussein
d and
Rached
Ben Hassen
 *a
*a
aLaboratory of Materials and Environment for Sustainable Development (LR18ES10), University of Tunis El Manar, Tunisia. E-mail: rached.benhassen@issbat.utm.tn
bDepartment of Chemistry, College of Science, King Khalid University, P.O. Box 9004, 61413 Abha, Saudi Arabia
cNanoengineering in Electronics, Spintronics and Photonics Institute, National Research Nuclear University “MEPhI”, Kashirskoe Shosse 31, Moscow 115409, Russia
dLASMIS, Université de Technologie de Troyes, Pôle Technologique Sud Champagne, 26 rue Lavoisier, Nogent 52800, France
First published on 11th June 2024
Abstract
A successful mechanochemical synthesis of a new nanoscale semi-conductive perovskite, La0.25Sr0.75Sn0.4In0.25Ru0.35O3 (LSSIRuO) was achieved through co-doping of SrSnO3. XRD and IR analyses confirmed that the sample crystallized in a pure perovskite GdFeO3 type structure (Pnma space group). Diffuse reflectance measurements revealed a direct band gap of 1.3 eV, which was significantly narrowed compared to that of SrSnO3 (4.1 eV). The investigation of DFT calculations into the sextenary systems La0.25Sr0.75[Sn0.4Ru0.35]In0.25O3 and La0.25Sr0.75[Sn0.5Ru0.25]In0.25O3 has revealed semiconductor behavior, very close to a semiconductor–semi metal transition. Importantly, Arrhenius-type charge transport was confirmed through a temperature-dependent conductivity study of the sample, showing good electrical conductivity of 3.6 S m−1 at 513 K with an activation energy of Ea = 0.19 eV. Furthermore, the compound exhibited ferromagnetic ordering at temperatures lower than 155 K, contrasting the diamagnetic behavior of SrSnO3. The narrower band gap value (1.3 eV) and improved electrical properties of LSSIRuO, in addition to its ferromagnetic characteristics, distinguish it as a promising candidate for applications in optoelectronics, as well as in memory and spintronic devices.
1. Introduction
Tin-based perovskites with general formula ABO3 have attracted the attention of researchers in the fields of photocatalysis,1 energy,2 and gas sensing.3 One of the key compounds in this stannate family is SrSnO3 (SSO), which stands out due to its structural flexibility, reduced lattice parameters, and high transparency with a wide band gap ranging from 3.9 to 4.5 eV.4 Compared to conventional binary oxides such as ZnO, In2O3, and SnO2, the perovskite structure of SrSnO3 offers a better control over its optical properties.5 Visible light absorption is observed in SSO by increasing the doping level, thanks to the orthorhombic distortion of its perovskite structure.6 The tilting of octahedra in tin-based perovskites is also a crucial factor in determining their physical properties, as slight changes can lead to drastic variations in these properties.7 SrSnO3 is classified as an n-type material6 and is used, both doped and undoped, as a humidity sensor. Sensitivity increases with donor substitution, while electrical conductivity is enhanced in acceptor-doped SrSnO3.8 To meet the growing demand for high-performance oxides in multiple applications with commercial viability, SrSnO3 is often doped with alkali metals, transition metals, post-transition elements, and rare earth elements, either on the A-site, B-site, or simultaneously on both sites. Thus tuned new obtained materials could present innovative properties by enhancing or refining characteristics such as thermal stability, chemical stability, electrical conductivity, magnetic effects, catalytic activity, and electrolytic compatibility.9,10According to the literature, A-site doping of SrSnO3 with lanthanum (La) has been observed.7 Lanthanum is a rare earth element known for its ability to retain parent crystal structures and promote electrical conductivity.11 Furthermore, ruthenium (Ru), a transition metal with good catalytic and magnetic properties, as well as excellent chemical stability, is often used as a substitute to enhance the activity and selectivity of catalytic materials.12 Indium (In) is well known as a dopant in semiconductors often used in electronics, optics and solar cells due to its ability to improve electrical conductivity and form thin films.13 Thus, the selection of these substitutes La, Ru and In in the new material has the essential objective of contributing to improving the performance and characteristics of the material for some intended applications.
Significant efforts have been dedicated to the development of highly efficient and air-stable tin-based perovskite solar cells.14,15 In this context, an intriguing alternative as a light absorber for lead-free solar cells is CsSnI3, with a band gap of 1.3 eV,15 a low excitonic binding energy of 18 × 10−3 eV,16 and a high optical absorption coefficient of 104 cm−1 (comparable to that of MAPbI3).16 Nevertheless, it is imperative to overcome the major challenge related to the instability of CsSnI3, as its black phase tends to easily transform into a yellow phase after oxidation in the atmosphere.16 The preferred solution in this case is the development of new tin-based perovskite oxides due to their advantages, such as greater stability than halide-based perovskites or halide-based hybrid perovskites. In addition, they exhibit better optical absorption in the visible range than halides.16
The exploration of ferromagnetic half-metallic materials is crucial due to their potential applications in memory and spintronic devices. In order to develop new promising candidates for achieving half-metallic ferromagnets (HMFs),17 several attempts were carried out by substituting B-site ions in SrRuO3 with Ti4+ and Sn4+ to explore transforming of a simple ferromagnetic metal, into a half-metal.18–21 Despite theoretical advances in the search for new HMFs, the experimental realization of these materials remains challenging. The few well-established examples of half-metallic ferromagnetism were materials adopting a double perovskite type structure,22 where a double-exchange mechanism leading to a half-metallic state with associated magnetic properties should be expected as suggested by J. H. Park et al.23 The transition from double perovskite systems to simple perovskites to achieve ferromagnetic half-metallicity is motivated by the stringent constraints of B-site ordering in the former.20
In this study, we report the structure as well as the electrical, magnetic and optical properties of SrSnO3 (perovskite oxide) doped with La, Ru and In. To date, no experimental studies or DFT analyzes exist on how the co-doping of In and Ru systematically influences the electronic and magnetic properties of SrSnO3, whether in bulk or in thin film form.
2. Experimental and theoretical section
2.1 Synthesis of La0.25Sr0.75Sn0.4In0.25Ru0.35O3
The synthesis of LSSIRuO powder employed the eco-friendly mechanosynthesis method, known for its simplicity and cost-effectiveness. This is achieved through the use of affordable starting materials and the omission of solvents, effectively addressing waste disposal concerns. Moreover, mechanosynthesis provides a versatile and efficient approach, affording control over composition and properties. In this particular process, precise amounts of La2O3 (99.9+%; Sigma-Aldrich), SrCO3 (99.9+%; Sigma-Aldrich), SnO2 (99.9%; Alfa), RuO2 (99.9%; Sigma-Aldrich) and In2O3 (99.9%; Sigma-Aldrich) precursors, with purity exceeding 99.9%, were dried and weighed using a high-precision balance. The weighed precursors were then introduced into the mill (FRITSCH GmbH), and ground for 3 hours at a speed of 500 rpm, with a ball-to-precursor ratio of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. After the initial grinding, a second grinding step was carried out, followed by calcination at 950 °C and subsequent XRD diffraction analysis. Based on the presence of diffraction lines corresponding to the SnO2 precursor, the calcination temperature was increased to 1000 °C for 12 hours. Subsequently, through XRD analysis, it was observed that the intensity of the SnO2 lines decreased, prompting a further sintering cycle at 1050 °C. This led to the disappearance of the lines associated with the aforementioned precursor. All heating processes were conducted in the presence of air. The stoichiometric proportions of the reagents used in the synthesis are represented by the following equation:
2. After the initial grinding, a second grinding step was carried out, followed by calcination at 950 °C and subsequent XRD diffraction analysis. Based on the presence of diffraction lines corresponding to the SnO2 precursor, the calcination temperature was increased to 1000 °C for 12 hours. Subsequently, through XRD analysis, it was observed that the intensity of the SnO2 lines decreased, prompting a further sintering cycle at 1050 °C. This led to the disappearance of the lines associated with the aforementioned precursor. All heating processes were conducted in the presence of air. The stoichiometric proportions of the reagents used in the synthesis are represented by the following equation:2.2 Characterization
Powder X-ray diffraction (XRD) measurements were conducted using an X’Pert3 powder PANalytical diffractometer equipped with Cu Kα radiation (λ = 0.15406 nm). The experimental parameters were carefully set to ensure accurate data acquisition, including a step size of 0.013° and an accumulation time of 30 seconds. The 2θ range covered was from 10° to 110°, and the measurements were performed in a continuous scan mode.For the analysis of the obtained XRD data, Rietveld refinement was conducted following the established methodology described by Rodriguez-Carvajal in the FullProf program.24
To accurately determine the instrumental line broadening, a standard microcrystalline powder was utilized, and its XRD pattern was recorded under identical experimental conditions. This reference measurement served as a benchmark for evaluating and accounting for any broadening effects inherent to the XRD instrument itself.
High-resolution scanning electron microscopy (SEM) measurements were conducted using a cutting-edge FE-SEM instrument (Hitachi SU8030) operating at 10 kV. This advanced SEM instrument allowed us to capture detailed images of the sample surface, providing valuable insights into its microstructure and morphology. Additionally, energy-dispersive X-ray analysis (EDX) was performed using an Oxford INCA x-act system at an acceleration voltage of 15 kV. The EDX analysis enabled the determination of the elemental composition of the sample. Importantly, the analytical errors associated with the elemental content were found to be less than 5 atomic percent (at%), ensuring high accuracy. Quantification of the elements was achieved using the Proza algorithm (Phi-Rho-Z), a reliable method for elemental analysis.
Infrared (IR) measurements were realized using a highly precise spectrometer, BRUKER “TENSOR 27,” covering a spectral range from 4000 to 400 cm−1. For the measurements, approximately 1 mg of the sample was mixed with 300 mg of potassium bromide (KBr) and ground in an agate mortar. The resulting mixture was then pressed into pellets under a pressure of 10 bar.
Diffuse reflectance (DR) spectra were obtained using a UVD-3500 UV-Vis spectrophotometer equipped with a BaSO4-coated integrating sphere. The spectral range covered wavelengths from 190 to 900 nm, with measurements taken at 1 nm intervals. The use of an integrating sphere ensured accurate and reliable measurement of the diffuse reflectance properties of the sample. By analysing the DR spectra, valuable information about the optical properties, such as band gap energy and light absorption behaviour, could be obtained, contributing to a comprehensive characterization of the material.
For the theoretical geometry optimization and study of the electronic structure and optical properties of LaSrSnInRuO compound, we employed the implementation of density functional theory (DFT) calculations in the QUANTUM Espresso 6.5 program package.25,26 The plane-wave basis set for valence electron states with the cutoff energy of 120 Ry (1632 eV), corresponding to 800 Ry (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 eV) for the charge density cutoff, was taken. We considered the Perdew–Burke–Ernzerhof (GGA-PBE) functional for the description of exchange–correlation energy.27 Pseudopotentials for the electronic structure calculations were taken from the standard solid-state pseudopotentials (SSSP) library.28,29 The projector-augmented-wave (PAW) method for the electron–ion interaction30,31 was also applied to perform the numerical simulation. To take into account the magnetic order in the LaSrSnInRuO compound we used the generalized gradient spin approximation (GGSA). The calculations were performed within the Hubbard-corrected DFT energy functionals (GGSA+U) for the ruthenium atoms. The GGSA+U approach32–34 can overcome the lack of a DFT-based correlation–exchange functional by combining DFT with the Hubbard model. To consider the strong correlation induced by Ru 4d electrons, an on-site Coulomb interaction U = 5.0 eV is chosen in GGSA+U calculations. The Brillouin zone integrations were performed using the Monkhorst–Pack k-point sampling scheme35 with the 4 × 4 × 4 mesh grid (for the non-self-consistent field calculations, the k-point grid size of 8 × 8 × 8 was used) together with the Methfessel–Paxton smearing36 with the smearing width of 0.02 Ry. For the calculations of the electronic density of states, the Böchl tetrahedron method37 was employed. Periodical boundary conditions were used. The atomic equilibrium positions were obtained by the complete minimization of the unit cell using the calculated forces and stress on the atoms. The convergence criterion of self-consistent calculations for ionic relaxations is 10−8 eV between two consecutive steps. Furthermore, all atomic positions and the supercell itself were optimized until all components of all forces acting on the atoms became smaller than 10−4 hartree per Bohr. Such criteria ensure that the absolute value of stress is less than 0.01 kbar. The electronic structure properties were elucidated by analyzing the sample band structure and its electronic density of states. In order to get the accurate band gaps, the beyond GGA methods such as Gaussian attenuating Perdew–Burke–Ernzerhof (Gau-PBE) that uses a Gaussian function as a modified Coulomb potential for the exact exchange,38 and Heyd–Scuseria–Ernzerhof (HSE) hybrid functional approaches39 were included. The use of these approaches allowed us to refine the values of band gaps.
880 eV) for the charge density cutoff, was taken. We considered the Perdew–Burke–Ernzerhof (GGA-PBE) functional for the description of exchange–correlation energy.27 Pseudopotentials for the electronic structure calculations were taken from the standard solid-state pseudopotentials (SSSP) library.28,29 The projector-augmented-wave (PAW) method for the electron–ion interaction30,31 was also applied to perform the numerical simulation. To take into account the magnetic order in the LaSrSnInRuO compound we used the generalized gradient spin approximation (GGSA). The calculations were performed within the Hubbard-corrected DFT energy functionals (GGSA+U) for the ruthenium atoms. The GGSA+U approach32–34 can overcome the lack of a DFT-based correlation–exchange functional by combining DFT with the Hubbard model. To consider the strong correlation induced by Ru 4d electrons, an on-site Coulomb interaction U = 5.0 eV is chosen in GGSA+U calculations. The Brillouin zone integrations were performed using the Monkhorst–Pack k-point sampling scheme35 with the 4 × 4 × 4 mesh grid (for the non-self-consistent field calculations, the k-point grid size of 8 × 8 × 8 was used) together with the Methfessel–Paxton smearing36 with the smearing width of 0.02 Ry. For the calculations of the electronic density of states, the Böchl tetrahedron method37 was employed. Periodical boundary conditions were used. The atomic equilibrium positions were obtained by the complete minimization of the unit cell using the calculated forces and stress on the atoms. The convergence criterion of self-consistent calculations for ionic relaxations is 10−8 eV between two consecutive steps. Furthermore, all atomic positions and the supercell itself were optimized until all components of all forces acting on the atoms became smaller than 10−4 hartree per Bohr. Such criteria ensure that the absolute value of stress is less than 0.01 kbar. The electronic structure properties were elucidated by analyzing the sample band structure and its electronic density of states. In order to get the accurate band gaps, the beyond GGA methods such as Gaussian attenuating Perdew–Burke–Ernzerhof (Gau-PBE) that uses a Gaussian function as a modified Coulomb potential for the exact exchange,38 and Heyd–Scuseria–Ernzerhof (HSE) hybrid functional approaches39 were included. The use of these approaches allowed us to refine the values of band gaps.
Direct current electrical measurements were conducted using a Lucas Labs S-302 four-point probe and a Keithley 2400 digital source counter (Keithley Instruments, Inc., Cleveland, Ohio). The measurements were performed over a temperature range of 330–520 K. The sample used for the measurements had a diameter of 8 mm and a thickness of 2 mm.
To investigate the magnetic properties of the samples, a MANICS DSM-8 differential magneto-susceptometer was employed. The measurements were carried out under an applied magnetic field of up to 1.5 T. The magnetization of the samples was measured using two modes: FC (field-cooled) and ZFC (zero-field-cooled). Additionally, hysteresis measurements were performed for a deeper understanding of the magnetic properties exhibited by the samples.
3. Results and discussion
3.1 Structural analysis
The crystallographic parameters derived from this analysis are presented in Table 1, providing valuable insights into the structural characteristics of the material. Fig. 1 illustrates the profiles obtained from the Rietveld refinement process, including the observed, calculated, and difference profiles. Additionally, Fig. 1 presents the structure of the LSSIRuO compound. It is noteworthy that nearly all reflections are successfully indexed. The refinement results and atomic positions are presented in Table 1. The stability of this structure is supported by three well-established factors: the Goldschmidt tolerance factor40t, the octahedral factor41μ and the newly introduced tolerance factor42τ.
| Temperature | 300 K |
| Chemical formula | (La0.25Sr0.75)(Sn0.4In0.25Ru0.35)O3 |
| Formula weight (M) | 844.023 g mol−1 |
| Space group | Pnma (no. 62) |
| Lattice parameters | |
| a (Å) | 5.6848(8) |
| b (Å) | 8.0676(8) |
| c (Å) | 5.6961(10) |
| V (Å3) | 261.24(6) |
| Z | 4 |
| χ 2 | 1.84 |
| R p | 2.72 |
| R Expected | 2.57 |
| R wp | 3.49 |
| R I | 2.02 |
| D W–H (nm) | 98 |
| D MEB (nm) | 135 |
| Strain | 0.0095 |
| Atomic positions | ||||||
|---|---|---|---|---|---|---|
| Atoms | Sites | Occupancy | X | Y | Z | U iso |
| La | 4c | 0.25 | 0.0024 | 0.2500 | 0.4962 | 0.0320(9) |
| Sr | 4c | 0.75 | 0.0024 | 0.2500 | 0.4962 | 0.0320(9) |
| Ru | 4a | 0.35 | 0.0000 | 0.0000 | 0.0000 | 0.0087(6) |
| In | 4a | 0.25 | 0.0000 | 0.0000 | 0.0000 | 0.0087(6) |
| Sn | 4a | 0.40 | 0.0000 | 0.0000 | 0.0000 | 0.0087(6) |
| O1 | 8d | 1.00 | 0.2825 | 0.0342 | 0.2154 | 0.01312 |
| O2 | 4c | 1.00 | 0.4891 | 0.2500 | 0.5666 | 1.03989 |
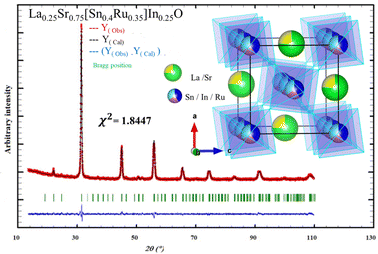 | ||
| Fig. 1 Observed, calculated and difference of X-ray diffraction patterns of La0.25Sr0.75Sn0.4In0.25Ru0.35O3 powder calcined at 1050 °C with structure inset. | ||
The formulas for these factors are presented in equations (eqn (1)–(3)), and their corresponding values are illustrated in Table 2. In these expressions, r(A) and r(B) represent the Shanon ionic radii43 of A (Sr2+ or La3+) and B (Sn4+, In3+, or Ru4+), respectively, while nA denotes the oxidation state of A. The ionic radii, considering a coordination of twelve for (Sr, La), six for (Sn, In, and Ru), and two for oxygen, are as follows: r(O2−) = 1.4 Å, r(Sr2+) = 1.44 Å, r(La3+) = 1.36 Å, r(Sn4+) = 0.69 Å, r(In3+) = 0.8 Å, and r(Ru4+) = 0.62 Å.43
 | (1) |
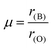 | (2) |
 | (3) |
| t | μ | τ | |
|---|---|---|---|
| LSSIRuO | 0.9478 | 0.4928; 0.5714; 0.4428 | 3.3947 |
| Tolerated values in the perovskite structure | 0.825 < t < 1 | 0.414 < μ < 0.732 | τ < 4.18 |
This structure consists of interconnected (Sn/In/Ru)O6 octahedra at the corners, with each Sn, In, or Ru surrounded by six oxygen ions. These octahedra are adjacent to large (La/Sr)O9 cavities. In this orthorhombic structure, all B cations occupy the same crystallographic site 4a (0, 0, 0), while the A cations reside in 4c. The two oxygen atoms, O1 and O2, occupy non-equivalent crystallographic sites, 8d and 4c, respectively. Surrounding each oxygen, there are 2 Sn4+ ions and 4 Sr2+ ions, forming octahedral coordination environments. The Sn–O1 distances range from 2.0394(2) Å to 2.0576(2) Å, with an average of 2.0485 Å. The Sn–O2 distance is 2.0532(2) Å, resulting in an average Sn–O bond length of 2.0501 Å, which is slightly smaller than the average value in SrSnO3 (2.0504 Å).7 The Sr–O bond lengths vary between 2.4590(2) Å and 2.9455(5) Å, with an average value of 2.7352 Å, compared to 2.8685 Å in SrSnO3 and related compounds.7,44 These bond lengths fall within the typical range observed in octahedral environments.45,46 With doping, the covalency of the bonds increases, resulting in a slight decrease in the average Sn–O and Sr–O bond lengths. The values of the Sn–O1–Sn and Sn–O2–Sn angles (θ1 and θ2, respectively) are 158.276(4)° and 158.420(2)°, respectively, which are consistent with the findings of Mizoguchi et al.47 In SrSnO3, these values are Sn–O1–Sn = 160.73° and Sn–O2–Sn = 158.60°.7 Using the mathematical relations (eqn (4)) proposed by O’keeffe et al.,7,48 which established the connection between these angles and the tilting angles, we calculated the tilt in our material, resulting in an average value of 13.242°, compared to 12.44° in SrSnO3.7
 | (4) |
The relationship between octahedral rotations and the covalent nature of metal–oxygen bonds in orthorhombic perovskites was explored by Cammarata et al.49 Their research indicated that the covalency of the metal–oxygen bond influenced the degree of octahedral rotation, with a less covalent B–O bond resulting in a more distorted structure. Consequently, co-doping with less electronegative atoms (Ru, In) is expected to enhance the conduction bandwidth and reduce the band gap, which will be verified through UV-Vis spectroscopy in next paragraphs and DFT calculations.
 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ” on the y-axis and “4
θ” on the y-axis and “4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ” on the x-axis, the average crystallite size and microstrain can be estimated by extrapolating the y-intercept and slope of the line (Fig. 2).
θ” on the x-axis, the average crystallite size and microstrain can be estimated by extrapolating the y-intercept and slope of the line (Fig. 2).
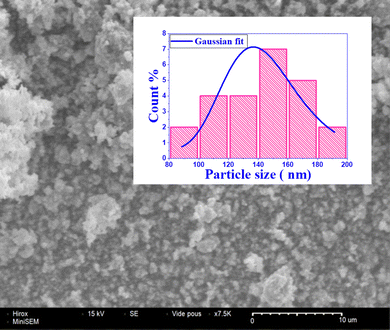
The line in the Fig. 2 passes through nearly all points, suggesting a microstructural homogeneity. Additionally, according to the Hume-Rothery crystallographic defect model,50 the ionic radius difference between the dopant and host cation should be less than 15% to form a stable crystalline system. In the present case, the ionic radius of the dopant In3+ (0.8 Å) is 15% higher than that of the host cation Sn4+ (0.69 Å), the ionic radius of the dopant Ru4+ (0.62 Å) is 10% smaller than that of the host cation Sn4+, while the ionic radius of the dopant La3+ (1.36 Å) is 6% higher than that of the host cation Sr2+ (1.44 Å). This likely rules out the possibility of oxygen vacancy formation5 and the incorporation of In, Ru, and La in both cationic sites. The calculated average size is found to be D = 98 nm, while the microstrain is on the order of ε = 0.0095, confirming the nanoscale nature of the particles as shown in Table 1.
To evaluate the chemical purity and elemental composition of LSSIRuO, we employed energy-dispersive spectroscopy (EDS). The EDS analysis confirmed the presence only of the anticipated elements, including La, Sr, Sn, In, Ru, and O, demonstrating the elemental homogeneity of the material and the absence of any foreign elements (Fig. 4). Furthermore, the mass, atomic, theoretical (based on the empirical formula), and experimental (from EDS) percentages within the unit cell of the perovskite LSSIRuO are determined and presented in Table 3. The rather remarkable coincidence between these values and estimates and their agreement and provide information on the chemical coherence of the material.
| The theoretical mass and atomic percentages | The experimental mass and atomic percentages | ||||
|---|---|---|---|---|---|
| Element | Mass (%) | Atom (%) | Mass (%) | Atom (%) | Absolute error (%) |
| Strontium | 25.27 | 15 | 25.48 | 14.61 | 0.99 |
| Oxygen | 18.46 | 60 | 19.80 | 62.17 | 3.77 |
| Tin | 18.26 | 8 | 17.72 | 7.50 | 0.65 |
| Lanthanum | 13.35 | 5 | 13.15 | 5.51 | 0.70 |
| Ruthenium | 13.6 | 7 | 11.55 | 5.74 | 0.45 |
| Indium | 11.04 | 5 | 10.21 | 4.47 | 0.42 |
3.2 Optical properties
 | ||
| Fig. 5 FTIR spectrum of La0.25Sr0.75Sn0.4In0.25Ru0.35O3 and deconvolution of the spectral band at 663 cm−1. | ||
The strong band at 663 cm−1 may be associated with various O–M–O bends and M–O stretch in the octahedra of InO6, SnO6, and RuO6. As per the literature, the stretching and bending vibrations of SnO6 are typically identified between 624 and 687 cm−1.52 Those corresponding to the In–O bonds within InO6 octahedra are commonly observed within the range of 405 to 560 cm−1.4,52 In the case of ruthenates, the absorptions linked to the stretching and bending of the Ru–O bond are reported to be located between 414 cm−1 and 524 cm−1 with weak intensity.53 The deconvolution of this broad band that spreads from 500 to 800 cm−1, using Gaussian function, gives three absorption peaks, shown in Fig. 5 to characterize the various O–M–O bends and M–O stretch (with M being Sn, In or Ru). In addition to the metal–oxygen bands, vibrations attributed to carbonates, water, and the Sn–OH bond are also observed. The carbonate can be formed by the absorption of atmospheric CO2 or, alternatively, it can be derived from the strontium carbonate used as a starting precursor in the solid-state synthesis.54 If carbonate is trapped in the perovskite structure, it would replace the O2− anions and is bound to Sr2+. The presence of these carbonates in the perovskite lattice leads to greater disorder in the (Sn/In/Ru)O6 octahedra. Nyquist and Kagel showed that carbonate bands are located at 1320–1530, 1040–1100, and 800–890 cm−1.55 Our compound exhibits bands around 1456, 1083, and 860 cm−1. The presence of water is probably observed due to its adsorption by LSSIRuO as SrO is a hygroscopic oxide.56 The broad band located between 3450 and 3900 cm−1 is probably due to the stretching vibration of the hydroxyl group O–H (free and bound). This presence is confirmed by a weak band around 1627 cm−1, which is caused by the bending vibration of H2O and Sn–OH.57 This OH group may also be bound, in addition to water and Sn, to oxygen atoms on the surface.
| F(R) = (1 − R)2/2R = K/S | (6) |
 | ||
| Fig. 6 (a) Kubelka–Munk function F(R) for La0.25Sr0.75Sn0.4In0.25Ru0.35O3 as a function of wavelength λ. (b) Tauc plot for La0.25Sr0.75Sn0.4In0.25Ru0.35O3. (c) Plot of ln(F(R) × hv) vs. ln(hν − Eg). | ||
This was facilitated by the common hypothesis that the Kubelka–Munk function was analogous to the absorbance function in transmission spectroscopy.
To determine the optical band gap of LSSIRuO, the Tauc method was employed, using the relation (F(R)·hν)p = A(hν − Eg). Here, Eg represents the band gap energy, A is a constant, and p is the index that can take on various values (1/2, and 2) corresponding to indirect allowed and direct allowed transitions, respectively. We graphed the Tauc relation with various exponents against hν to precisely determine the optical band gap. The analysis disclosed an Eg value of 1.3 eV in Fig. 6(b), indicating a direct allowed transition as illustrated in Fig. 6(c). Remarkably, the band gap showed a significant decrease with La, In, and Ru doping compared to pure SrSnO3, which had a band gap of 4.1 eV,10 Sr(Ru, Sn)O3 with 0.4 eV,20 Sr(In, Sn)O3 with 3.8 eV58 and (La, Sr)SnO3 with 3.97 eV.7
It is noteworthy that this band gap is smaller than those of CH3NH3PbBr3 (2.26 eV) and CH3NH3PbCl3 (3 eV), but of the same order as that of CH3NH3BiSeI2, MASnI3, and CsSnI3.16 These findings highlight the potential of this simple oxide perovskite semiconductor as an environmentally friendly alternative to lead halide-based perovskite semiconductors.
3.3 Density functional theory calculations
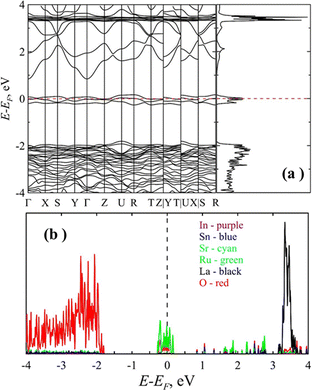
To study the electronic properties of the LSSIRuO compound, we analyze the electronic characteristics, namely band structure and density of electronic states of the sample's equilibrium structure. The total density of states (DOS) and the band structure along high symmetry directions of the optimized sample are shown in Fig. 7(a). The Fermi level is set to zero energy.The nature of the electronic band structure and the density of states indicate that the LSSIRuO sample exhibits metallic nature. The finite value of the density of electronic states at the Fermi level and the absence of the explicit dielectric gap indicate that the LSSIRuO belongs to the class of semi-metals or even metals. Additional analysis of the partial density of electronic states (PDOS, Fig. 7(b)) demonstrates that the number of states at the Fermi level in the conduction band is primarily composed of ruthenium and oxygen atoms. Thus, the GGA approximation predicts the absence of energy gap at the Fermi level. It should be noted that taking into account the magnetic order in the LaSrSnInRuO compound using the generalized gradient spin approximation (GGSA) and within the framework of the Hubbard model (U = 5.0 eV) indicates the presence of a semiconductor gap in the sample. The nature of the density of electronic states in this case indicates that the LaSrSnInRuO sample exhibits the semiconducting properties (see Fig. 8). The density of electronic states is equal to zero at the Fermi level and possesses a gap. An estimation of the band gap at the GGSA+U level of theory gives the value of 1.55 eV, which agrees well with the experimentally obtained value of 1.3 eV.
 | ||
| Fig. 8 The density of electronic states of the LaSrSnInRuO sample obtained at the GGSA+U approach. The Fermi level is assigned at zero. | ||
Adjusting the substitution ratio of Sn by Ru and increasing the Sn content to 0.5 in our formulation, corresponding to a Sn to Ru ratio of x = 0.66, results in the compound La0.25Sr0.75Sn0.5In0.25Ru0.25O3, which, according to our DFT results, exhibits semiconductor behavior with a gap of 0.75 eV (Fig. 9). It should be noted that GGA level of theory tends to underestimate the dielectric gap. So, we made a refinement using the Gau-PBE and HSE hybrid functional. The HSE approach gives an estimate of 11.69 eV for the bottom of the conduction band and 9.69 eV for the top of the valence band. Thus, the determined band gap using the HSE approach is equal to 2 eV, which corresponds to a value more characteristic of a semiconductor. Data obtained within the framework of the Gau-PBE approach confirm this result. The estimated semiconductor gap in this case is 1.93 eV. Increasing tin content leads to a shift in the Fermi level, and a gap appears.
 | ||
| Fig. 9 Band structures and density of electronic states of La0.25Sr0.75Sn0.4In0.25Ru0.35O3 and La0.25Sr0.75Sn0.5In0.25Ru0.25O3. | ||
This finding agreed well with the detailed experimental study on the effects of Sn substitution in SrRuO3 done by Amand et al.21 in which they classified all the compositions with x > 0.44 as semiconductors or even insulators.
On the other hand, calculations with LSDA (local spin-density approximation) and LSDA+U method led by Kim et al.20 showed that Ru's electron hopping ‘d’ is blocked by Sn-substituted sites, resulting in a reduction of the Rut2g bandwidth as doping x increases. Transitions from ferromagnetic metal (FM) to ferromagnetic half-metal (HMF) up to the insulator are described by the Rut2g bandwidth (W), the position of the maximum valence band (Δ) in the majority spin channel, and the band gap. The HMF region is observed for 0.5 ≤ x ≤ 0.7, with a potential half-metal-to-insulator transition at x ≈ 0.7. It is noteworthy that our compound's doping ratio (Sn/Ru) x = 0.53 falls within the semiconductor region close to the HMF region. Probably, by decreasing the Sn content in our formulation, we could reach the half-metal to insulator transition.
3.4 Electrical properties
The electrical properties of the sample were analyzed by studying the electrical conductivity as a function of temperature. It is well established that the dc conductivity of the sample is related to temperature according to Arrhenius equation (eqn (7)) | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ(dc)vs. 1000/T is presented in Fig. 10. The linear correlation observed between values of log
σ(dc)vs. 1000/T is presented in Fig. 10. The linear correlation observed between values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ(dc)vs. 1000/T strongly indicates Arrhenius-type conduction in the sample. Within 333–513 K temperature range, a singular conduction process prevails in the LSSIRuO sample, characterized by an activation energy of 0.19 eV. Such a low activation energy value of LSSIRuO sample could suggest a more favored ionic conduction process within degenerate sites of (Sn4+/Sn2+) and (Ru4+/Ru3+).59
σ(dc)vs. 1000/T strongly indicates Arrhenius-type conduction in the sample. Within 333–513 K temperature range, a singular conduction process prevails in the LSSIRuO sample, characterized by an activation energy of 0.19 eV. Such a low activation energy value of LSSIRuO sample could suggest a more favored ionic conduction process within degenerate sites of (Sn4+/Sn2+) and (Ru4+/Ru3+).59
For instance, the dc conductivity shows a 100-fold increase from 3.2 10−2 S m−1 at 333 K to 3.6 S m−1 at 513 K. This improvement in conductivity is expected for several reasons:
(i) Doping perovskite oxides with trivalent (3+), such as La3+, is known to enhance their electrical properties.7
(ii) Substituting La3+ for Sr2+ creates a mixed valence state of Sn2+–Sn4+, Ru4+–Ru3+ generating mobile charge carriers. This process strongly influences electrical conductivity, with sensitivity to chemical composition and oxygen content.44
3.5 Magnetic properties
The temperature dependence of the magnetization M(T) of LSSIRuO was characterized using a differential sample susceptometer under an applied magnetic field of 1 T, in both field-cooled (FC) mode (cooling under field) and zero-field-cooled (ZFC) mode (cooling without field), with a heating rate of 5 K per minute (Fig. 11). | ||
| Fig. 11 Temperature dependence of the M(FC) and (ZFC) magnetization of LSSIRuO compound under μ0H = 1 T. (The inset shows the local enlargement where ZFC and FC curves begin to diverge.) | ||
The ferromagnetic isotropy is confirmed by the overlap of the magnetization curves M(FC) and M(ZFC), even at low temperatures. Paramagnetic behaviour is observed at high temperatures, and a second-order ferromagnetic–paramagnetic phase transition occurs around the Curie temperature of Tc = 155 K, as evidenced by the FC curve that does not exhibit a sharp change in slope when the temperature decreases to low temperatures. As shown in the inset of Fig. 11, the Curie temperature has been determined to be 155 K, corresponding to that at which the ZFC and FC curves begin to diverge when cooling the sample. The region where this occurs has been magnified (inset of Fig. 11).
The magnetic hysteresis loops M(H) of LSSIRuO powder at 8 K and 100 K are shown in Fig. 12 with an applied field reaching 10 T.
 | ||
| Fig. 12 Magnetization dependence of LSSIRuO as a function of the magnetic field. (Inset: (a) an enlarged view of the central region of the curves; (b) magnetisation of SrSnO3.60) | ||
As the magnetic field increases, this compound undergoes a transition from a weak magnetic state to a strong one, it all depends on the applied field and temperature. The hysteresis loops exhibit a small area, highlighting the low energy loss during the magnetization–demagnetization process.61 The parameters obtained from the curves are summarized in Table 4. As the temperature decreases, μ0HC increases, and the ferromagnetic ordering becomes significantly enhanced. The value of MR/MS indicates a weak multi-domain structure in our case.
| T (K) | M S (emu g−1) | M R (emu g−1) | M R/MS | μ 0 H C (T) |
|---|---|---|---|---|
| With MS (saturation magnetization), MR (remanence), and μ0HC (coercive field). | ||||
| 8 | 2.048 | 0.0623 | 0.0304 | 0.0724 |
| 100 | 0.63 | 0.0689 | 0.1093 | 0.0230 |
The occurrence of ferromagnetism in LSSIRuO, despite the diamagnetic nature of the mother compound SSO is intriguing. Various already known factors may contribute to the emergence of ferromagnetism in oxide-based semiconductors such as the incorporation of magnetic or mixed-valence ions,62 as well as the existence of magnetic impurities and defects.63 However, at high doping concentrations, defects are likely to hinder the establishment of magnetic order.5 This could explain the relatively low magnitude of ferromagnetism in our compound. Furthermore, the surface-level imperfections such as grain boundaries, deep point defects, and interstitials5 are supposed to be absent and could not contribute to the observed ferromagnetism in our compound.
In our case, the observed ferromagnetism can only be explained by models involving free charge carriers, such as the Ruderman–Kittel–Kasuya–Yosida (RKKY) theory, superexchange, and double exchange interactions. According to the RKKY interaction theory, ferromagnetism arises from spin injection by the dopant, which interacts with the free electrons in the conduction band, inducing a ferromagnetic order.60 In the superexchange interaction, each oxygen anion positioned between two Ru4+ ions in the Ru4+–O–Ru4+ configuration leads to an antiferromagnetic order. Conversely, the order becomes ferromagnetic in the double exchange if this oxygen is situated in the Ru3+–O–Ru4+ configuration, since Ru4+ is a magnetic ion with mixed valence.62
4. Conclusions
The La0.25Sr0.75Sn0.4In0.25Ru0.35O3 (LSSIRuO) compound has been successfully synthesized using a rapid, mild, effective, and reproducible mechanosynthesis method. This process resulted in an orthorhombic perovskite structure akin to GdFeO3. XRD analysis confirmed the excellent crystallinity of the material, and the systematic doping of La, In, and Ru influenced the lattice constants. EDS analysis provided the chemical composition of each element, while IR spectroscopy validated the perovskite structure by identifying vibrational bands associated with LSSIRuO groups, such as SnO6, RuO6, and InO6. The sample exhibited a significantly narrow band gap of 1.3 eV, as determined through diffuse reflection measurements. Intermediate energy states were identified as crucial for this band gap reduction. Additionally, LSSIRuO displayed substantially improved electrical conductivity compared to SrSnO3, as evidenced by conductivity-as-a-function-of-temperature analysis, which indicated Arrhenius-type charge transport. Investigation into the magnetic properties, when doping SrSnO3 with La, In and Ru, revealed a transition from dia- to ferromagnetic nature induced by superexchange and double exchange interactions. DFT predictions with an estimation of the band gap at the GGSA+U level of theory give a value of 1.55 eV, which agrees well with the experimentally obtained value of 1.3 eV. It could be concluded that the increase in Ru doping favors the transition from the insulating state to the semiconductor state, then to the semi-metal/metal state. This chemical doping on both A and B sites demonstrates control over the functional properties, facilitating a transition from insulating to semi-metallic states and enabling exploration of optical, electrical, and magnetic properties. The highly reduced band gap, coupled with excellent electrical and magnetic characteristics, positions LSSIRuO as a promising candidate for optoelectronic, memory, and spintronic applications. Future applications in thin films aim to reveal the intricate interplay of these properties, further unveiling the semi-metallic ferromagnetic state.Author contributions
Samira Barouni with Rached Ben Hassen carried out the synthesis, the powder XRD structure determination, the UV-vis, FTIR characterization and the electrical measurements of the material and participated in drafting the manuscript. Mikhail Maslov conducted the DFT calculations and drafted the corresponding section. Scanning electron microscopy and energy-dispersive X-ray analysis were carried out by Akram Alhussein. Magnetic measurements were conducted by Hanen Chaker. Amani Brahmia participated in the powder XRD structure determination and FTIR characterization. Revision and editing were performed by Rached Ben Hassen, Mikhail Maslov and Samira Barouni. All authors read and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the ICDD for the financial support (grant number: 09-04) and extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through a Large Research Project under grant number RGP2/53/45.Notes and references
- O. V. Nkwachukwu and O. A. Arotiba, Front. Chem., 2021, 9, 634630 CrossRef CAS.
- A. Kostopoulou, K. Brintakis, N. K. Nasikas and E. Stratakis, Nanophotonics, 2019, 8(10), 1607–1640 CrossRef CAS.
- M. S. Hossain and A. Takshi, MRS Adv., 2021, 6, 645–649 CrossRef CAS.
- B. Belgacem, M. M. Maslov, S. Kaya, I. H. Ali and R. Ben Hassen, J. Mol. Struct., 2022, 1259, 132716 CrossRef CAS.
- M. Avinash, M. Muralidharan, S. Selvakuma, S. Selvakumar and K. Sivaji, J. Mater. Sci.: Mater. Electron., 2020, 31(4), 3375–3386 CrossRef CAS.
- K. P. Ong, X. Fan, A. Subedi, M. B. Sullivan and D. J. Singh, APL Mater., 2015, 3(6), 062505 CrossRef.
- Y. Kumar, R. Kumar, R. J. Choudhary, A. Thakur and A. P. Singh, Ceram. Int., 2020, 46(11), 17569–17576 CrossRef CAS.
- M. M. Kumar, P. Singh, D. Kumar and O. Parkash, Adv. Appl. Ceram., 2006, 105(6), 280–284 CrossRef.
- S. Ouni, S. Nouri, J. Rohlicek and R. Ben Hassen, J. Solid State Chem., 2012, 192, 132–138 CrossRef CAS.
- A. Kumar, V. Sahrawat, A. A. Kumar and S. Priya, Trans. Indian Inst. Met., 2017, 70(3), 573–579 CrossRef CAS.
- Q. Gao, K. Li, L. Zhao, K. Zhang, H. Li, J. Zhang and Q. Liu, ACS Appl. Mater. Interfaces, 2019, 11, 25605–25612 CrossRef CAS.
- S. Halder, R. A. Kumar, R. Maity and T. P. Sinha, Ceram. Int., 2023, 49(5), 8634–8645 CrossRef CAS.
- A. Malešević, A. Radojković, M. Žunić, S. M. Savić, S. Perać, Z. Branković and G. Branković, Ceram. Int., 2023, 49(10), 15673–15679 CrossRef.
- W. Ming, H. Shi and M.-H. Du, J. Mater. Chem., 2016, 4(36), 13852–13858 RSC.
- Y. Zhou, H. F. Garces, B. S. Senturk, A. L. Ortiz and N. P. Padture, Mater. Lett., 2013, 110, 127–129 CrossRef CAS.
- M. Wang, W. Wang, B. Ma, W. Shen, L. Liu, K. Cao, S. Chen and W. Huang, Nano-Micro Lett., 2021, 13(1), 62 CrossRef.
- M. I. Katsnelson, V. Y. Irkhin, L. Chioncel, A. I. Lichtenstein and R. A. de Groot, Rev. Mod. Phys., 2008, 80(2), 315–378 CrossRef CAS.
- P. A. Lin, H. T. Jeng and C. S. Hsue, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(8), 085118 CrossRef.
- J. Kim, J. Y. Kim, B. G. Park and S. J. Oh, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(23), 235109 CrossRef.
- N. Kim, R. Kim and J. Yu, J. Magn. Magn. Mater., 2018, 460, 54–60 CrossRef CAS.
- A. Huon, S. Yoon, M. R. Fitzsimmons, T. R. Charlton, J. M. Ok, C. D. Cruz and H. N. Lee, Appl. Phys. Lett., 2021, 119, 112404 CrossRef CAS.
- K. W. Lee and K. H. Ahn, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(22), 224404 CrossRef.
- K. I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395(65), 677–680 CrossRef CAS.
- J. R. Carvajal, FULLPROF Program for Rietveld Refinement, Laboratorie Leon Brillouin, CEA Saclay, France, 2000 Search PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. O. de la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys. Condens. Matter, 2017, 29(46), 465901 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS.
- G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet and N. Marzari, npj Comput. Mater., 2018, 4(1), 72 CrossRef.
- E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G. M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G. X. Zhang and S. Cottenier, Science, 2016, 351(6280), 1415-U81 Search PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(24), 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(3), 943–954 CrossRef CAS.
- V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyżyk and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(23), 16929–16934 CrossRef CAS.
- M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(3), 035105 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192 CrossRef.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(6), 3616–3621 CrossRef CAS.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(23), 16223–16233 CrossRef.
- J. W. Song, K. Yamashita and K. Hirao, J. Chem. Phys., 2011, 135, 071103 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118(18), 8207–8215 CrossRef CAS.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14(21), 477–485 CrossRef CAS.
- W. Li, E. Ionescu, R. Riedel and A. Gurlo, J. Mater. Chem. A, 2013, 1(39), 12239 RSC.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5(2), eaav0693 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32(5), 751–767 CrossRef.
- S. Ouni, S. Nouri, J. Rohlicek and R. Ben Hassen, J. Solid State Chem., 2012, 192, 132–138 CrossRef CAS.
- O. C. Gagné and F. C. Hawthorne, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74(1), 63–78 CrossRef.
- O. C. Gagné and F. C. Hawthorne, IUCrJ, 2020, 7, 581–629 CrossRef.
- H. Mizoguchi, H. W. Eng and P. M. Woodward, Inorg. Chem., 2004, 43(5), 1667–1680 CrossRef CAS.
- M. O’keeffe and B. G. Hyde, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33(12), 3802–3813 CrossRef.
- A. Cammarata and J. M. Rondinelli, J. Chem. Phys., 2014, 141(11), 114704 CrossRef.
- W. Hume-Rothery and G. V. Raynor, The Structure of Metals and Alloys, Institute of Metals Monograph and Report Series, 1962, No. 1, pp. 210–217.
- W. D. Kingery, H. K. Bowen and D. R. Uhlmann, Introduction to ceramics, Wiley, 1976 Search PubMed.
- A. Zouaghi, B. Belgacem, A. Alhussein, A. Brahmia and R. Ben Hassen, J. Solid State Chem., 2023, 328, 124303 CrossRef CAS.
- M. B. Khanvilkar, A. K. Nikumbh, R. A. Pawar, N. J. Karale, D. V. Nighot, R. C. Ambare, P. A. Nagwade, M. D. Sangale, G. S. Gugale and S. B. Misal, Phys. Chem. Solid State, 2021, 22(4), 664–686 CrossRef CAS.
- M. C. F. Alves, M. R. Nascimento, S. J. G. Lima, P. S. Pizani, J. W. M. Espinosa, E. Longo, L. E. B. Soledade, A. G. Souza and L. M. G. Santos, Mater. Lett., 2008, 63(1), 118–120 CrossRef.
- R. A. Nyquist and R. O. Kagel, Infrared Spectra Atlas of Inorganic Compounds, Academic Press, 1971 Search PubMed.
- J. Hong, S. J. Heo and P. Singh, Sci. Rep., 2021, 11, 3368 CrossRef CAS.
- R. Malik, V. K. Tomer, S. Duhan, S. P. Nehra and P. S. Rana, Energy Environ. Focus, 2015, 4(4), 340–345 CrossRef.
- T. Mohan, S. Kuppusamy and R. J. V. Michael, ACS Omega, 2022, 7(22), 18531–18541 CrossRef CAS.
- A. Kumar, B. Khan, V. Yadav, A. Dixit, U. Kumar and M. K. Singh, J. Mater. Sci.: Mater. Electron., 2020, 31, 16838–16848 CrossRef CAS.
- M. Muralidharan, V. Anbarasu, A. Elaya Perumal and K. Sivakumar, J. Mater. Sci.: Mater. Electron., 2016, 28(5), 4125–4137 CrossRef.
- N. Amri, J. Massoudi, K. Nouri, M. Triki, E. Dhahri and L. Bessais, RSC Adv., 2021, 11(22), 13256–13268 RSC.
- J. M. D. Coey, M. Venkatesan and C. B. Fitzgerald, Nat. Mater., 2005, 4(2), 173–179 CrossRef CAS.
- J. M. D. Coey, K. Wongsaprom, J. Alaria and M. Venkatesan, J. Phys. D: Appl. Phys., 2008, 41(13), 134012 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01233j |
| This journal is © the Owner Societies 2024 |